A Differential Privacy Federated Learning Scheme Based on Adaptive Gaussian Noise

1  Introduction

In recent years, with the continuous innovation of algorithms and the continuous collection of training data, deep learning technology (Deep Learning, DL) has been applied in the field of image processing [1–3], natural language processing [4–6] and speech recognition [7–9] Rapid development. The success of current deep learning is based on a large amount of data. However, with the increase in training data, the risk of privacy leakage also increases accordingly. In addition, people’s attention to user privacy and data security is also increasing. Existing studies have shown that launching privacy attacks on deep learning models will lead to the leakage of training data, and data privacy issues hinder the improvement of deep learning algorithm models.

FL is a key technology to solve the data privacy problem in deep learning. The core concept of federated learning is that the data does not move and the model moves, while the data is usable but not visible. This can ensure that all participants collaborate to train the model on the premise that the data does not leave the local area. On the one hand, the privacy of users’ data can be well protected by keeping the data out of the local area; on the other hand, it can make full use of the data of all participants to collaboratively train the model. Compared with traditional centralized machine learning methods, federated learning effectively reduces the risk of user privacy data leakage. However, attackers may launch attribute inference attacks or membership inference attacks on the model by analyzing the parameters of the model [10–17], etc. For example, Phong et al. [18] pointed out that the attacker recovers private data based on the gradient of the weights being proportional to the gradient of the bias. Reference [19] proposed a reconstruction attack based on generative adversarial networks (GANs), which also used a shared model as a discriminator to train a GAN model and generates raw samples of the model’s training data. Therefore, additional measures are required to protect data privacy in federated learning.

In recent years, DP [20] has become an important means of privacy protection and is widely used for privacy protection in machine learning. In order to prevent the model from leaking the private information in the dataset, there have been a series of works applying DP to deep learning [21–28]. For example, Abadi et al. [21] first used DP for deep learning and proposed a differential privacy stochastic gradient descent algorithm (DPSGD). Truex et al. [29] proposed a hybrid approach based on DP and Secure Multi-Party Computation (SMC) to prevent inferred threats and generate high-precision models, but this also consumed more communication resources. Recently, DP has also been applied to privacy protection in federated learning [29–38]. For example, Wei et al. [30] proposed a new framework (NbAFL) based on the concept of differential privacy, that is, artificial noise is added before client parameter aggregation, and the loss function of the trained federated learning model is given. Xu et al. [37] proposed an Adaptive Rapidly Convergent Learning Algorithm (ADADP) with provable privacy guarantees, which outperformed differential privacy methods in terms of both privacy cost and model accuracy. When clients participate in model training, the model could achieve good training performance at a given level of privacy. However, this does not guarantee that the client’s private data will not be leaked by an honest but curious server. Therefore, it is necessary to design an algorithm that can not only ensure the security of local private data but also improve the performance of the model.

To address these challenges, this paper proposes a novel differential privacy federated learning scheme based on adaptive Gaussian noise. In summary, our contributions are as follows:

•   This paper proposes a DPFL-AGN scheme, which solves the privacy problem existing in the training process of federated learning.

•   This paper adds adaptive Gaussian noise to the DPFL-AGN algorithm to hide the real parameters uploaded by the client during federated learning training. Furthermore, this paper proposes an adaptive noise reduction method, as the model converges, the noise is reduced adaptively in the later stages of the federated learning training process. The algorithm balances data security and availability under a shared model.

•   This paper conducts comparative experiments on two real datasets, MNIST and CIFATR-10, and the experimental results show that the DPFL-AGN method proposed in this article is superior to other methods.

The rest of this paper is organized as follows. Section 2 presents the related work. Section 3 details our approach. Section 4 presents the privacy analysis. Section 5 presents the experimental results and related analysis. The conclusion of this paper is in Section 6. The basic concepts and meanings of the symbols are summarized in Table 1.

2  Related Work

2.1 Federated Learning

As shown in Fig. 1, a federated learning system with one aggregation server 𝒩 clients is considered. 𝒩 clients are recorded as {ℱj}j=1𝒩, and their respective training data sets are recorded as {Dj}j=1𝒩. Let Dj represent the local dataset held by the j−th client, where j∈{1,2,⋯,𝒩}. The goal of the server is to learn a model with data from 𝒩 related clients and minimize the model's loss function. Formally, the server adds weights received from 𝒩 clients as:

Figure 1: A federated learning training model with a hidden adversary

ω=∑j=1𝒩pjωj(1)

where ω is the parameter vector aggregated by the server, ωj is the parameter vector trained on the j−th client, and 𝒩 is the number of clients. pj=|Dj||D|≥0, ∑j=1𝒩pj=1, |D|=∑j=1𝒩|Dj| is the total number of all data samples. The optimization task of federated learning can be expressed as:

ω∗=argminω∑j=1𝒩pjℱj(Dj,ω)(2)

where ℱj(.) is the local loss function of the j−th client. Usually, the local loss function is given by the local empirical risk. Each round of training in the federated learning system can usually be divided into the following steps:

•   Step 1: local training:All clients perform isolated calculations based on original data locally, each use local samples to update the model, and send the locally trained parameters to the aggregation server.

•   Step 2: model aggregation:The aggregation server securely aggregates the parameters uploaded by each client, and updates the global model parameters according to the local statistical results of each client.

•   Step 3: parameter broadcasting:The aggregation server broadcasts the aggregated updated parameters to each client.

•   Step 4: model updating:Each client updates the local model parameters with the new parameters received and tests the performance of the updated model.

In the FL process, the server and 𝒩 clients collaborate to learn a machine learning (ML) model, and finally the optimization Eq. (2) converges to the solution of the globally optimal model.

2.2 Threat Model

In this paper, we assume that the aggregator server is honest but curious, suggesting that while it honestly follows the FL protocol, it may also try to learn information other than output from locally received information.

Semi-honest adversary models are vulnerable to reconstruction attacks and membership inference attacks. Specifically, the adversary can extract training data during model training, or extract feature vectors of training data to carry out reconstruction attacks [39–43]. As Lacharité et al. [39] proposed an approximate refactoring attack, current approaches to enabling range queries provide little security to the model. Furthermore, Salem et al. [40] proposed a hybrid generative model (CBM-GAN) based on generative adversarial networks (GANs) with strong attack performance. Assuming that the adversary has black-box access to the model and has a specific sample as its prior knowledge, the adversary can judge whether the training set of the model contains a specific sample to launch membership inference attacks. For example, Hu et al. [41] proposed a new over representation-based membership inference attack. Carlini et al. [13] improved a new likelihood-ratio-based membership inference attack (LiRA). To sum up, the adversary may integrate the parameter information stolen during model training to launch an attack. Therefore, our threat model is reasonable and realistic.

2.3 Differential Privacy

Differential privacy strictly defines the privacy loss of data analysis algorithms mathematically, and its implementation process is relatively simple and the system overhead is smaller, so it is widely used. It uses a random mechanism when a single sample in the input is changed, but the distribution of the output does not change significantly.

Definition 1: ((ε,δ)−DP[18]). A randomized mechanism ℳ:D→ℛ with domain D and range ℛ satisfies (ε,δ)−DP if for any two adjacent datasets d,d′∈D and for any subset of outputs 𝒪∈ℛ it holds that

Pr[ℳ(d)∈𝒪]≤Pr[ℳ(d′)∈𝒪]×eε+δ(3)

If δ=0, ℳ is the original definition of ε—differential privacy. Generally. 1/|d| is selected for δ, and the default δ=10−5 in this paper.

Definition 2: (RényiDivergence [42]). For two probability distributions P and Q defined over R, the Renyi divergence of order α>1 is

Dα(P∥Q)≜1α−1log⁡Ex∼Q(P(x)Q(x))α(4)

Definition 3: ((α,ε) – RDP [42]). randomized mechanism ℳ:D→ℛ is said to have ε−Rényi differential privacy of order α, or (α,ε)−RDP for short, if for any adjacent datasets d,d′∈D it holds that

Dα(ℳ(d)∥ℳ(d′))≤ε(5)

3  Our Approach

Using an adaptive learning rate can make the model converge faster. Therefore, DPFL-AGN adds Gaussian noise to the gradient and uses an adaptive learning rate for gradient descent training, thereby improving the performance of model training. To further reduce the impact of noise on model performance, we adaptively reduce noise in the later stages of federated learning training. In this section, we introduce methods for adaptive Gaussian noise (AGN), adaptive noise reducton (ANR), and differential privacy federated learning scheme with adaptive Gaussian noise (DPFL-AGN).

3.1 Adaptive Gaussian Noise (AGN)

Gradient descent is the most commonly used method for training deep learning models. The goal of training the model is to obtain the minimum loss function ℱ(w) value. In order to minimize ℱ(w), stochastic gradient descent (SGD) is usually used, that is, in each iteration training Randomly select a subset of the data and update the parameter ωt+1←ωt−α∇ωtℱi(xi,ωt). The step size of the gradient descent update is determined by the learning rate. If the learning rate is too large, it is easy to skip the optimal solution and fall into the embarrassment of the local optimal solution. However, if the learning rate is too small, it takes a lot of time to obtain the optimal solution. Therefore, how to set the appropriate learning rate and how to avoid falling into the local optimal solution are the challenges we face. To solve the above problems, more advanced optimizers, such as Adam, Adagrad, Adadelta, RMSprop, Nadam, etc. are proposed. They are self-Adaptively adjust the learning rate to update the parameters.

DPFL-AGN uses a similar approach to Adam’s adaptive learning rate. It is worth noting that the framework proposed in this paper is not only applicable to other types of adaptive gradient descent algorithms, but also adaptive gradient descent algorithms with noise added.

In DPFL-AGN, let Δωt be expressed as the update item of step t, which is

•   Calculate moving average of noise gradients

mt←β1mt−1+(1−β1).g~t(6)

vt←β2νt−1+(1−β2).g~t2(7)

•   Bias Correction for Noise Gradients

m^t←mt/(1−β1t)(8)

v^t←vt/(1−β2t)(9)

•   Update the parameters after adding noise

ωt←ωt−1−ηv^t+ϵ.m^t(10)

We have Δωt=ηv^t+ϵ.m^t, where g~t is the noise gradient of the noise with Gaussian added, g~t2 is the square of the noise gradient with Gaussian noise added. In other words, DPFL-AGN uses ηv^t+ϵ.m^t to perform adaptive gradient descent on gradients with Gaussian noise added train.

3.2 Adaptive Noise Reduction (ANR)

Usually in the early training stages of federated learning, adding noise to the gradient has less impact on the model. During training, the gradient gets smaller and smaller, and adding noise to the gradient gradually increases the impact on the model. Excessive noise in the later stages of training can prevent the model from converging to the optimum. Therefore, as the model converges, we expect to adaptively reduce the noise later in the training, resulting in better model performance. Improvement stops when the convergence performance is determined by the following formula.

ν(ωt)−ν(ωt+1)<μ(11)

The ANR method is triggered when the server satisfies Eq. (11). Among them, μ is the threshold, which is used to predict whether the training process stops and determine when to trigger the ANR method. Therefore, in our experiments, we use a positive value of 0.001 as the value of μ. ν(ωt) is the test loss of the model ωt, and ν(ωt+1) is the test loss of the next round of training model ωt+1.

When the server detects that the test loss reaches the condition to trigger ANR, the noise scale of all clients decays according to Eq. (12).

σt+1={ ρ*σt,ν(ωt)−ν(ωt+1)  < μσt,else(12)

where ρ(0<ρ<1) is the decay rate. σt is the Gaussian noise added to the gradient by the t−th round of federated learning, and σt+1 is the Gaussian noise added to the gradient by the t+1 round of federated learning.

3.3 Differential Privacy Federated Learning Scheme with Adaptive Gaussian Noise (DPFL-AGN)

Combining the above two methods, we propose the DPFL-AGN method. Its training process is shown in Algorithm 1, including the following steps:

Initial:The server initializes and broadcasts the global model ω0, initial noise scale σ0 to all clients.

Step 1: Gradient calculation:At each client, gradients are computed using a per-sample gradient algorithm.

Step 2: Gradient clipping: The contribution of each sample to the local gradient is bounded by a clipping threshold Θ. Each gradient vector will be clipped in the L2 norm, the j−th local gradient vector gt(xj) of the t−th communication cycle is replaced by gt(xj)/max(1,‖gt(xj)‖2Θ).

Step 3: Adaptive Gaussian noise:Each client adds artificial noise according to the differential privacy rule of the Gaussian mechanism, and performs gradient descent with an adaptive learning rate on the gradient with Gaussian noise added to obtain the model ωt+1j.

Step 4: Model uploading:Each client updates the local model and uploads the updated model to the server.

Step 5: Model aggregating:The server weights and averages the models uploaded by each client.

Step 6: Adaptive noise reduction:The server executes Eq. (12) for adaptive noise reduction to obtain σt+1 for the next round of all clients.

Step 7: Model broadcasting:The server broadcasts the current global model and noise level to each client.

4  Privacy Analysis

All clients participating in local training add Gaussian noise satisfying differential privacy to the model, which can resist the inference attack in the above threat model. The privacy loss of each client will be analyzed next.

Theorem1:(Privacy Loss of Algorithm 1). Given the sampling probability q=ℋ/𝒩. The number of steps T, the Gaussian mechanism satisfies (ε,δ)−DP if σ satisfies:

ε≤Tα−1∑j=0α(αj)qj(1−q)α−jexp(j(j−1)2σ2)+log1/δα−1(13)

where (..) denotes the binomial coefficient and α can be any integer satisfies α≥2.

To prove Theorem 1, we adopt the sampling Gauss theorem of RDP to analyze the privacy cost, and then convert the obtained RDP to DP.

Lemma 1: (RDP Privacy Budget of Subsampled Gaussian Mechanism): A Gaussian mechanism function f sensitivity is 1 and satisfies (α,ε)−RDP whenever

ε≤1α−1log⁡max(E1,E2)(14)

Let μ0 denotes the probability density function (pdf) of N(0,σ2), μ1 denote the pdf of N(1,σ2), and μ=(1−q)μ0+qμ1.

E1=Ez∼μ0[(μ0(z)/μ1(z)α](15)

E2=Ez∼μ0[(μ(z)/μ0(z)α](16)

Further, reference [42] described the compute method of E1 on integer α.

E1=∑j=0α(αj)qj(1−q)α−jexp(j(j−1)2σ2)(17)

The two Gaussian distribution μ0 and μ1 used in the RDP, and they satisfy E1≥E2. Thus, f satisfies (α,1α−1log⁡(E1))−RDP.

Lemma 2. (Composition of RDP [42]). For two randomized mechanisms, f and g, such that f is (α,ε1)−RDP and g is (α,ε2)−RDP, the composition of f and g which is defined as (X,Y), where X∼f and Y∼g, satisfies (α,ε1+ε2)−RDP.

Lemma 3. Given the sampling probability q=ℋ/𝒩, after T training steps of DPFL-AGN, we could obtain the total privacy loss Tε′(α) via composing such T subsampled Gaussian mechanism depending on Lemma 2 for any integer α≥2. Tε′(α) can be expressed as:

Tε′(α)≤Tα−1∑j=0α(αj)qj(1−q)α−jexp(j(j−1)2σ2)(18)

Definition 4. (From RDP to (ε,δ)−DP [42]). If f is an (α,ε)−RDP mechanism, it also satisfies (ε+log1/δα−1,δ)−DP for any 0<δ<1.

With Lemma 3 and Definition 4, Theorem 1 is proved. We use the result of Theorem 1 to calculate the privacy cost. Specifically, given ε, σ, and q, at each communication round, we select α from {2,3,…,64} and determine the smallest ε∗ in Theorem 1.

5  Experiment

In this section, we conduct three comparative experiments on the MNIST dataset and the CIFAR-10 dataset. We choose the state-of-the-art research methods [21,31] as the baseline for comparison. First, we analyze the impact of the model on the performance of the model in the adaptive Gaussian noise method. Second, we compare the impact of adaptive noise reduction methods on model performance. Finally, the effect of differential privacy federated learning methods with adaptive Gaussian noise on model performance is compared.

Experiment setup:MNIST is a standard dataset for handwritten digit recognition, consisting of 60,000 training samples and 10,000 testing samples. Each sample is a 28 × 28 grayscale image. CIFAR-10 consists of 6000 labeled samples of 32 × 32 RGB images. There are 50,000 training images and 10,000 testing images. This article performs non IID partitioning of data from 10 clients. The training data is sorted based on digital tags and divided into an average of 400 segments. Each customer is assigned 40 random data segments, so each customer’s sample has two or five tags. Each round of experiments is set at 1000 epochs. This paper uses a shallow convolutional neural network, which consists of two convolutional layers and two fully connected layers. Convolutional Layer Use 5 × 5 convolutions with stride 1. The first convolution outputs 12 for each image 6 × 6 × 64 tensors, second convolution for each image output 6 × 6 × 64 Tensor. The experiment was completed under NVIDIA GeForce RTX 2080TI GPU (64 GB RAM) and Windows10 system, and the model training was implemented under the PyTorch framework.

Parameter settings:In order to facilitate the experiment, we use a fixed value δ=10−5, the initial learning rate of the experiment using the MNIST dataset is 0.001, and the initial learning rate of the experiment using the CIFAR-10 dataset is 0.002. β1 in adaptive Gaussian noise is set to 0.9 and β2 is set to 0.999. The threshold ρ in the adaptive noise reduction method was set to 0.001. The parameter clipping threshold C is a popular component of SGD and ML, and for DP-based FL frameworks, an appropriate value of clipping threshold Θ should be considered. In the following experiments, we use the method in [31] and choose Θ by taking the median of the norm of the unclipped parameters during training.

5.1 Adaptive Gaussian Noise

Figs. 2 and 3 investigate the effect of the adaptive Gaussian noise approach on model performance. The accuracy and loss of the adaptive Gaussian noise method (AGN) and the method without adaptive noise (DP-SGD) are compared. We set cropping threshold Θ=1 and privacy budget ε=2 in MNIST dataset and CIFAR-10 dataset. Both methods in MNIST dataset and CIFAR-10 dataset use constant noise scale σ=1.0 and constant δ=10−5. Set the initial learning rate of the experiment to 0.001 in the MNIST dataset, set the initial learning rate of the experiment to 0.002 in the CIFAR-10 dataset, set β1 to 0.9, and β2 to 0.999. We can see that in the MNIST dataset, the final convergence accuracy of the adaptive Gaussian noise model is 94.31%, and the final convergence accuracy of the DP-SGD method without adaptive noise is 92.43%. In the CIFAR-10 dataset, the final convergence accuracy of the model using adaptive Gaussian noise is 92.21%, and the final convergence accuracy of the DP-SGD method without adaptive noise is 87.92%. For both datasets, the adaptive Gaussian noise method converges faster and the final accuracy is higher than the method without adaptive noise.

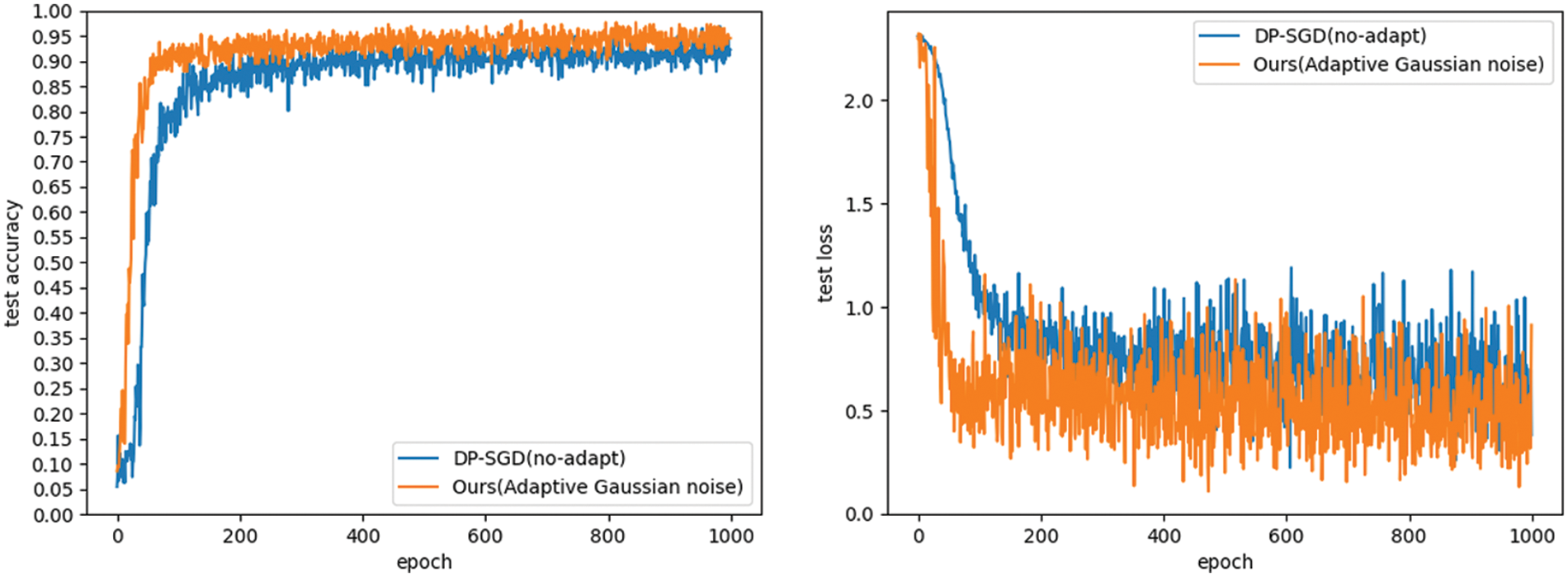
Figure 2: The effect of adaptive Gaussian noise method on model performance on MNIST dataset

Figure 3: The effect of adaptive Gaussian noise method on model performance on CIFAR-10 datasets

5.2 Adaptive Noise Reduction

Figs. 4 and 5 investigate the impact of adaptive noise reduction methods on model performance. The accuracy and loss of adaptive noise reduction (ANR) and constant noise are compared. We set the clipping threshold Θ=1 in MNIST dataset and CIFAR-10 dataset. The two methods in the MNIST dataset and the CIFAR-10 dataset have constant noise scale σ=4.0 and constant δ=10−5, privacy budget ε=2, and noise decay rate ρ is set to 0.001. We can see that in the MNIST dataset, the final convergence accuracy of the model using adaptive noise reduction is 93.74%, and the final convergence accuracy of the model using constant noise is 92.56%. In the CIFAR-10 dataset, the final convergence accuracy of the model using adaptive noise reduction is 91.43%, and the final convergence accuracy of the model using constant noise is 88.38%. For these two datasets, the final accuracy with adaptive noise reduction is 1.18% and 3.05% higher than the method with constant noise, respectively, and the model with adaptive noise reduction converges faster.

Figure 4: The effect of adaptive noise reduction method on model performance on MNIST dataset

Figure 5: The effect of adaptive noise reduction method on model performance on CIFAR-10 dataset

5.3 DPFL-AGN

Figs. 6 and 7 investigate the effect of a differential privacy federated learning method with adaptive Gaussian noise on model performance. The accuracy and loss of differential privacy federated learning methods with adaptive Gaussian noise and constant noise without adaptation are compared. We set the clipping threshold Θ=1 in MNIST dataset and CIFAR-10 dataset. The two methods in the MNIST dataset and the CIFAR-10 dataset have constant noise scale σ=4.0 and constant δ=10−5, privacy budget ε=2, and noise decay rate ρ is set to 0.001. Set the initial learning rate of the experiment to 0.001 in the MNIST dataset, set the initial learning rate of the experiment to 0.002 in the CIFAR-10 dataset, set β1 to 0.9, and β2 to 0.999. We can see that in the MNIST dataset, the final convergence accuracy of the model using adaptive Gaussian noise for differential privacy federated learning is 95.23%, and the final convergence accuracy of the model using non-adaptive constant noise is 94.68%. In the CIFAR-10 data set, the final convergence accuracy of the model using adaptive Gaussian noise for differential privacy federated learning is 92.78%, and the final convergence accuracy of the model using non-adaptive constant noise is 89.68%. For these two datasets, the final accuracy of differential privacy federated learning with adaptive Gaussian noise is 0.55%, 3.1% higher than the method with constant noise without adaptation, and the differential privacy with adaptive Gaussian noise Federated learning models converge faster. Additionally, we also observe that the DPFL-AGN method (combining AGN and ANR) outperforms previous AGN and ANR methods on both datasets. On the MNIST dataset, the final accuracy of DPFL-AGN is 2.8% and 1.49% higher than that of AGN and ANR methods alone. On the CIFAR-10 dataset, the final accuracy of DPFL-AGN is 4.86% and 4.4% higher than that of AGN and ANR methods alone.

Figure 6: The effect of differential privacy federated learning method with adaptive Gaussian noise on model performance on MNIST dataset

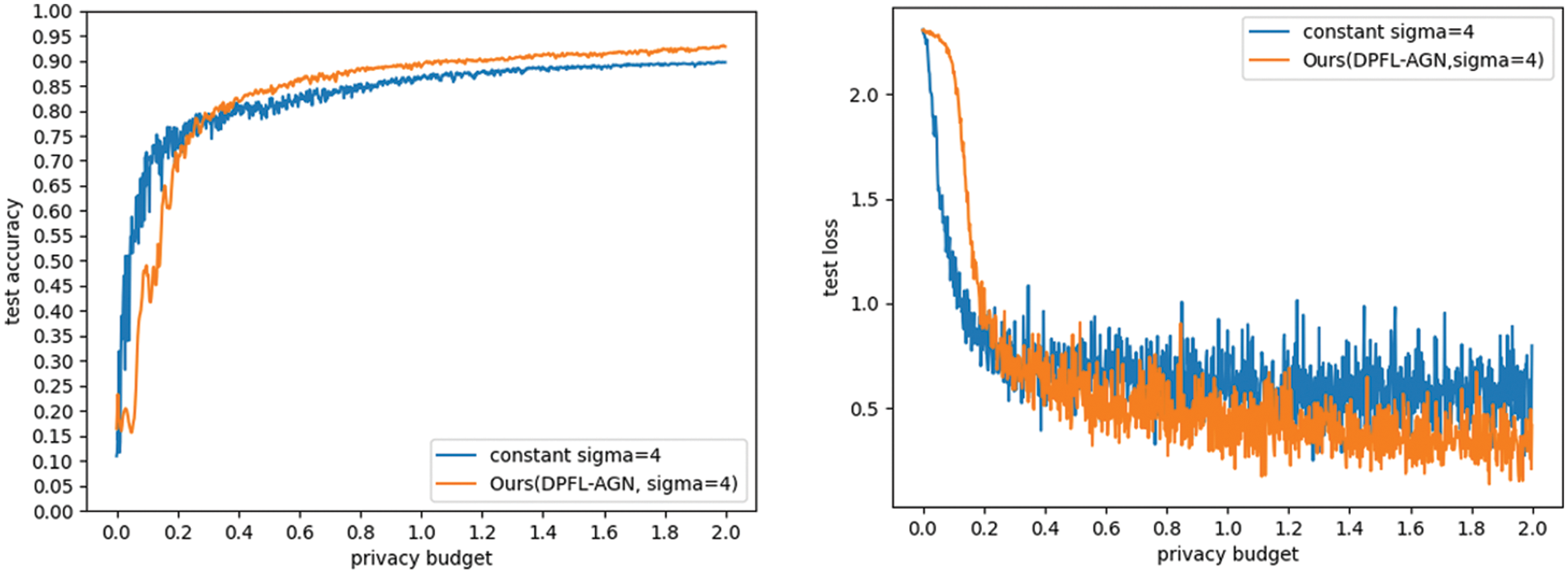
Figure 7: The effect of differential privacy federated learning method with adaptive Gaussian noise on model performance on CIFAR-10 dataset

Fig. 8 studies the effect of different algorithms on model performance. The accuracy and loss of DPSGD, NbAFL, and the proposed algorithm are compared. The final accuracy of DPSGD without adaptive algorithm is 88.42%, and the convergence speed is the slowest. The final accuracy of NbAFL that adds precisely calculated Gaussian noise to the gradient before federated learning training is 92.75%, which is slightly higher than DPSGD and has a slower convergence speed. The final accuracy of the proposed algorithm is 94.86%, which has the fastest convergence speed, and is 6.66% and 2.11% higher than that of DPSGD and NbAFL.

Figure 8: The effect of different algorithms on model performance

6  Conclusion

The main contributions of this paper are in three aspects. Firstly, a differential privacy joint learning scheme based on adaptive Gaussian noise (DPFL-AGN) is proposed, which converges faster and has higher accuracy compared to existing methods. Secondly, this article mathematically rigorously proves that DPFL-AGN satisfies differential privacy through RDP. Thirdly, DPFL-AGN is applied to train models on deep learning networks on real datasets. Experimental results show that DPFL-AGN has a better performance compared to previous methods.

Acknowledgement: Thanks to the help of four anonymous reviewers and journal editors, the logical organization and content quality of this paper have been improved.

Funding Statement: This work was supported in part by the Sichuan Provincial Science and Technology Department Project under Grant 2019YFN0104, in part by the Yibin Science and Technology Plan Project under Grant 2021GY008, and in part by the Sichuan University of Science and Engineering Postgraduate Innovation Fund Project under Grant Y2022154.

Author Contributions: Study conception and design: Sanxiu Jiao; analysis and interpretation of results: Lecai Cai; draft manuscript preparation: Xinjie Wang, Kui Cheng, Xiang Gao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The study used a public dataset and did not generate any new data.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Monga, V., Li, Y., Eldar, Y. C. (2021). Algorithm unrolling: Interpretable, efficient deep learning for signal and image processing. IEEE Signal Processing Magazine, 38(2), 18–44. [Google Scholar]

2. Hatt, M., Parmar, C., Qi, J., Naqa, I. E. (2019). Machine (deep) learning methods for image processing and radiomics. IEEE Transactions on Radiation and Plasma Medical Sciences, 3(2), 104–108. [Google Scholar]

3. Bhattacharya, S., Maddikunta, P. K. R., Pham, Q. V., Gadekallu, T. R., Chowdhary, C. L. et al. (2021). Deep learning and medical image processing for coronavirus (COVID-19) pandemic: A survey. Sustainable Cities and Society, 65(13), 102589. [Google Scholar] [PubMed]

4. Lauriola, I., Lavelli, A., Aiolli, F. (2022). An introduction to deep learning in natural language processing: Models, techniques, and tools. Neurocomputing, 470(1), 443–456. [Google Scholar]

5. Caucheteux, C., King, J. R. (2022). Brains and algorithms partially converge in natural language processing. Communications Biology, 5(1), 134. [Google Scholar] [PubMed]

6. Raina, V., Krishnamurthy, S., Raina, V. (2022). Building an effective data science practice. CA, USA: Apress BerNeley Press. [Google Scholar]

7. Mukhamadiyev, A., Khujayarov, I., Djuraev, O., Cho, J. (2022). Automatic speech recognition method based on deep learning approaches for Uzbek language. Sensors, 22(10), 3683. [Google Scholar] [PubMed]

8. Kumar, L. A., Renuka, D. K., Rose, S. L., Wartana, I. M. (2022). Deep learning based assistive technology on audio visual speech recognition for hearing impaired. International Journal of Cognitive Computing in Engineering, 3(2022), 24–30. [Google Scholar]

9. Li, J. (2022). Recent advances in end-to-end automatic speech recognition. APSIPA Transactions on Signal and Information Processing, 11(1), 1–64. [Google Scholar]

10. Cretu, A. M., Houssiau, F., Cully, A., de Montjoye, Y. A. (2022). QuerySnout: Automating the discovery of attribute inference attacks against query-based systems. Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, pp. 623–637. Los Angeles, CA, USA. [Google Scholar]

11. Feng, T., Peri, R., Narayanan, S. (2022). User-level differential privacy against attribute inference attack of speech emotion recognition in federated learning. arXiv:2204.02500. https://doi.org/10.21437/Interspeech.2022-10060 [Google Scholar] [CrossRef]

12. Hu, H., Salcic, Z., Sun, L., Dobbie, G., Yu, P. S. et al. (2022). Membership inference attacks on machine learning: A survey. ACM Computing Surveys, 54(11s), 1–37. [Google Scholar]

13. Carlini, N., Chien, S., Nasr, M., Song, S., Terzis, A. et al. (2022). Membership inference attacks from first principles. 2022 IEEE Symposium on Security and Privacy (SP), pp. 1897–1914. San Francisco, CA, USA. [Google Scholar]

14. Mei, Q., Yang, M., Chen, J., Wang, L., Xiong, H. (2022). Expressive data sharing and self-controlled fine-grained data deletion in cloud-assisted IoT. IEEE Transactions on Dependable and Secure Computing, 20(3), 2625–2640. [Google Scholar]

15. Li, W., Wang, P., Liang, K. (2022). HPAKE: Honey password-authenticated key exchange for fast and safer online authentication. IEEE Transactions on Information Forensics and Security, 18, 1596–1609. [Google Scholar]

16. Wang, L., Lin, Y., Yao, T., Xiong, H., Liang, K. (2023). FABRIC: Fast and secure unbounded cross-system encrypted data sharing in cloud computing. IEEE Transactions on Dependable and Secure Computing, 1–13. https://doi.org/10.1109/TDSC.2023.3240820 [Google Scholar] [CrossRef]

17. Feng, J., Xiong, H., Chen, J., Xiang, Y., Yeh, K. H. (2022). Scalable and revocable attribute-based data sharing with short revocation list for IIoT. IEEE Internet of Things Journal, 10(6), 4815–4829. [Google Scholar]

18. Phong, L. T., Aono, Y., Hayashi, T., Wang, L., Moriai, S. (2017). Privacy-preserving deep learning: Revisited and enhanced. International Conference on Applications and Techniques in Information Security, pp. 100–110. Auckland, New Zealand. [Google Scholar]

19. Wang, Z., Song, M., Zhang, Z., Song, Y., Wang, Q. et al. (2019). Beyond inferring class representatives: User-level privacy leakage from federated learning. IEEE INFOCOM 2019-IEEE Conference on Computer Communications, pp. 2512–2520. Paris, France. [Google Scholar]

20. Dwork, C. (2006). Differential privacy. Automata, Languages and Programming: 33rd International Colloquium, ICALP 2006, pp. 1–12. Venice, Italy. [Google Scholar]

21. Abadi, M., Chu, A., Goodfellow, I., McMahan, H. B., Mironov, I. et al. (2016). Deep learning with differential privacy. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, pp. 308–318. Vienna, Austria. [Google Scholar]

22. Dwork, C., Roth, A. (2014). The algorithmic foundations of differential privacy. Foundations and Trends® in Theoretical Computer Science, 9(3–4), 211–407. [Google Scholar]

23. Lee, J., Kifer, D. (2018). Concentrated differentially private gradient descent with adaptive per-iteration privacy budget. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 1656–1665. London, UK. [Google Scholar]

24. Lu, Y., Huang, X., Dai, Y., Maharjan, S., Zhang, Y. (2019). Differentially private asynchronous federated learning for mobile edge computing in urban informatics. IEEE Transactions on Industrial Informatics, 16(3), 2134–2143. [Google Scholar]

25. Wang, L., Qin, G., Yang, D., Han, X., Ma, X. (2018). Geographic differential privacy for mobile crowd coverage maximization. Proceedings of the AAAI Conference on Artificial Intelligence, vol. 32, no. 1. New Orleans, Lousiana, USA. [Google Scholar]

26. Bu, Z., Dong, J., Long, Q., Su, W. J. (2020). Deep learning with gaussian differential privacy. Harvard Data Science Review, 2020(23), 10–1162. [Google Scholar]

27. Arachchige, P. C. M., Bertok, P., Khalil, I., Liu, D., Camtepe, S. et al. (2020). Local differential privacy for deep learning. IEEE Internet of Things Journal, 7(7), 5827–5842. [Google Scholar]

28. Arachchige, P. C. M., Bertok, P., Khalil, I., Liu, D., Camtepe, S. et al. (2019). Local differential privacy for deep learning. IEEE Internet of Things Journal, 7(7), 5827–5842. [Google Scholar]

29. Truex, S., Baracaldo, N., Anwar, A., Steinke, T., Ludwig, H. et al. (2019). A hybrid approach to privacy-preserving federated learning. Proceedings of the 12th ACM Workshop on Artificial Intelligence and Security, pp. 1–11. London, UK. [Google Scholar]

30. Wei, K., Li, J., Ding, M., Ma, C., Yang, H. H. et al. (2020). Federated learning with differential privacy: Algorithms and performance analysis. IEEE Transactions on Information Forensics and Security, 15(2020), 3454–3469. [Google Scholar]

31. Wei, K., Li, J., Ding, M., Ma, C., Su, H. et al. (2021). User-level privacy-preserving federated learning: Analysis and performance optimization. IEEE Transactions on Mobile Computing, 21(9), 3388–3401. [Google Scholar]

32. Girgis, A., Data, D., Diggavi, S., Kairouz, P., Suresh, A. T. (2021). Shuffled model of differential privacy in federated learning. Proceedings of the 24th International Conference on Artificial Intelligence and Statistics, pp. 2521–2529, Breckenridge, Colorado, USA. [Google Scholar]

33. Jia, B., Zhang, X., Liu, J., Zhang, Y., Huang, K. et al. (2021). Blockchain-enabled federated learning data protection aggregation scheme with differential privacy and homomorphic encryption in IIoT. IEEE Transactions on Industrial Informatics, 18(6), 4049–4058. [Google Scholar]

34. Kim, M., Günlü, O., Schaefer, R. F. (2021). Federated learning with local differential privacy: Trade-offs between privacy, utility, and communication. ICASSP 2021–2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 2650–2654. Toronto, ON, Canada. [Google Scholar]

35. Lian, Z., Wang, W., Su, C. (2021). COFEL: Communication-efficient and optimized federated learning with local differential privacy. ICC 2021-IEEE International Conference on Communications, pp. 1–6. Montreal, QC, Canada. [Google Scholar]

36. Wu, X., Zhang, Y., Shi, M., Li, P., Li, R. et al. (2022). An adaptive federated learning scheme with differential privacy preserving. Future Generation Computer Systems, 127(2022), 362–372. [Google Scholar]

37. Xu, Z., Shi, S., Liu, A. X., Zhao, J., Chen, L. (2020). An adaptive and fast convergent approach to differentially private deep learning. IEEE INFOCOM 2020-IEEE Conference on Computer Communications, pp. 1867–1876. Toronto, ON, Canada. [Google Scholar]

38. Hu, R., Guo, Y., Li, H., Pei, Q., Gong, Y. (2020). Personalized federated learning with differential privacy. IEEE Internet of Things Journal, 7(10), 9530–9539. [Google Scholar]

39. Lacharité, M. S., Minaud, B., Paterson, K. G. (2018). Improved reconstruction attacks on encrypted data using range query leakage. 2018 IEEE Symposium on Security and Privacy (SP), pp. 297–314. San Francisco, CA, USA. [Google Scholar]

40. Salem, A., Bhattacharya, A., Backes, M., Fritz, M., Zhang, Y. (2020). Updates-leak: Data set inference and reconstruction attacks in online learning. 29th USENIX Security Symposium (USENIX Security 20), pp. 1291–1308. Boston, MA, USA. [Google Scholar]

41. Hu, H., Pang, J. (2021). Membership inference attacks against GANs by leveraging over-representationregions. Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, pp. 2387–2389. Virtual Event, Republic of Korea. [Google Scholar]

42. Mironov, I. (2017). Rényi differential privacy. 2017 IEEE 30th Computer Security Foundations Symposium (CSF), pp. 263–275. Santa Barbara, CA, USA. [Google Scholar]

43. Huang, X., Xion, H., Chen, J., Yang, M. (2021). Efficient revocable storage attribute-based encryption with arithmetic span programs in cloud-assisted Internet of Things. IEEE Transactions on Cloud Computing, 11(2), 1273–1285. [Google Scholar]