Case Retrieval Strategy of Turning Process Based on Grey Relational Analysis

1  Introduction

How to achieve metal cutting in a low-cost and high-efficiency way has always been the purpose of machinists, many attempts have been done to improve the cutting efficiency or reduce cost. These include 1) Modifying the cutting item material, such as improvement of tool substrate material [1], coating [2] or both [3]; 2) Optimizing machining processes, such as proper selection of tools [4], development of novel special inserts [5–7], and optimization of cutting parameters [8,9]. Among them, improving tool materials and developing novel inserts are not time-saving and cost-friendly, due to the requirement of the complex preparation process and expensive equipment. These works are often done by tool developers. Hence, cutting parameters optimization provides a better solution for machining enterprises.

Cutting parameters optimization is a complex non-linear, multi-constrained, and multi-objective problem [10]. Fortunately, with the applications of intelligent technology (such as Genetic algorithm [11], Machine learning [8], artificial neuron networks [12], and Particle swarm algorithm [13], etc.), many methods have been studied to provide solutions to this problem. These means have also been used in CAPP (Computer Aided Process Planning), which have been proven quite effective, although these platforms are isolated and time-consuming.

However, with the development of the network-based public service manufacturing model [14–16], the above methods are not applicable anymore because too much time is consumed. It is unacceptable for users if the response time is too long when they access the Internet to obtain service. This work aims to provide a solution for the problem in the application of the CBR (Case-based reasoning) [17,18] that has been applied to many fields to provide a solution for an unknown problem. For example, a CBR model was proposed for the decision support of building envelop design [19]. Focusing on the multivariable adaption problem in CBR adaptation, a modularized adaptation method was developed [20]. Based on the vector space model (VSM), case-based reasoning and methods of Grey Correlation Analysis, the intelligent method was designed for DfRem (Design for Remanufacturing) [21]. This method can transform different kinds of feature information into the same representation method and combine the similarity of feature information and user preference to obtain processing information which is more suitable for the scene. It can greatly improve the response speed while ensuring accuracy and suitability for users. It solves the problem that the processing parameters cannot match the actual situation of users and the waiting time is too long in the current industrial production.

A cutting process involves many features with both numeric and category properties. To digitally express a cutting case and search for the most similar one quickly, a framework based on the Intent is proposed, where the case reasoning process is completed online with a fast response and the case supplement is completed offline. Accordingly, the remainder of this paper is organized as follows. Section 2 presents the proposed framework. Section 3 introduces the Case retrieval approach. Platform development and case study are demonstrated in Section 4. Finally, Section 5 concludes the paper.

2  The Proposed Framework

The framework shown in Fig. 1 is proposed to provide the cutting process optimization service, where users only get services quickly through the Internet and no longer manage optimization programs.

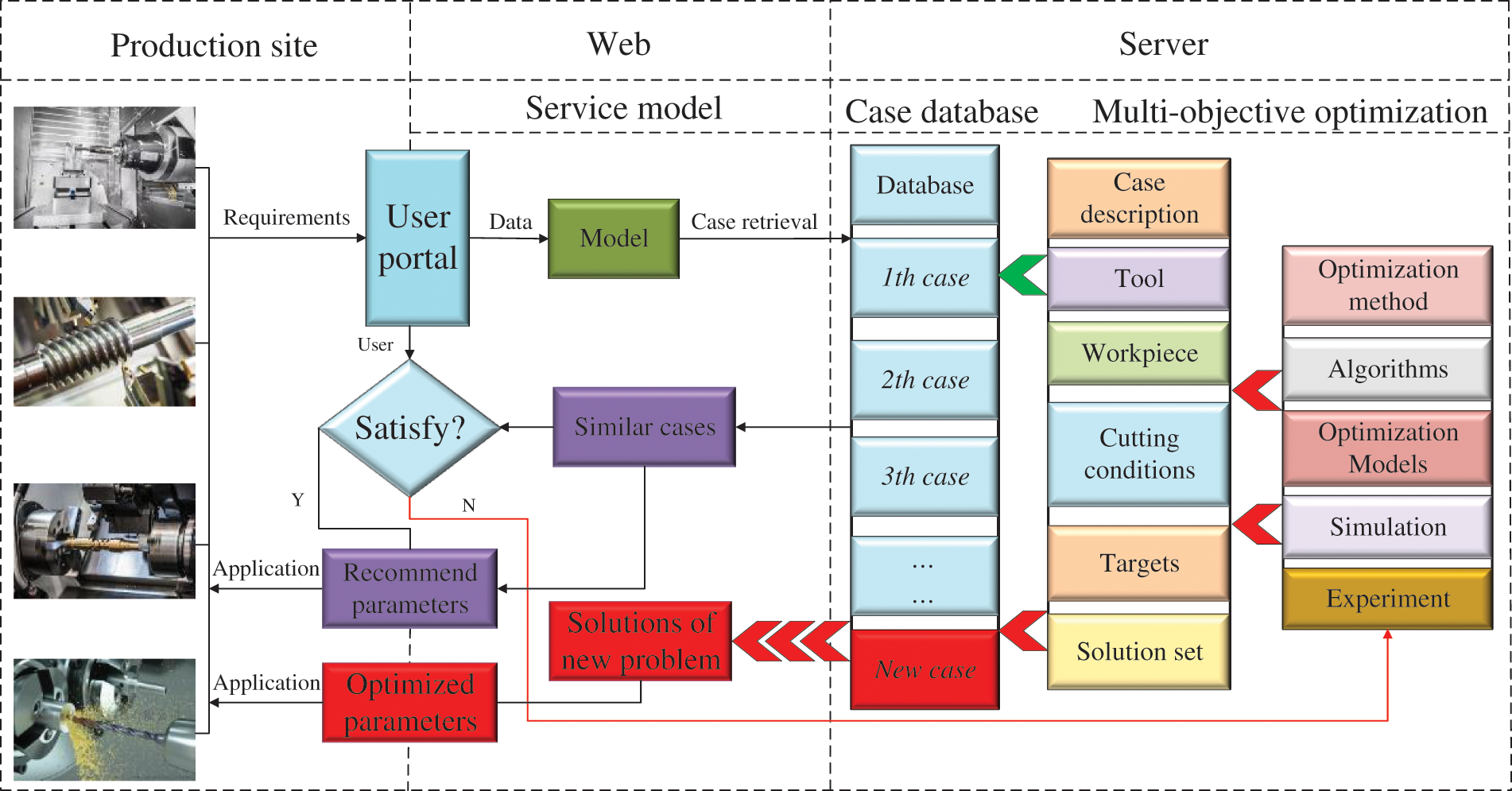
Figure 1: The proposed framework

As shown in Fig. 1, the user submits requirements of the production site to the Web through the user portal, and a service model based on the requirements data is established. Then, the model is submitted to the server to retrieve similar cases in the cases database. The server will use the algorithm proposed in this paper to retrieve cases according to the properties of new problems and user preferences and similar cases are recommended to the user portal. If the user is satisfied with a similar case, the processing parameters of the similar case are recommended to solve the new problem; otherwise, the user requirements data is submitted to the multi-objective optimization program interface of the server to obtain the optimized cutting parameters.

2.1 Problem Statement

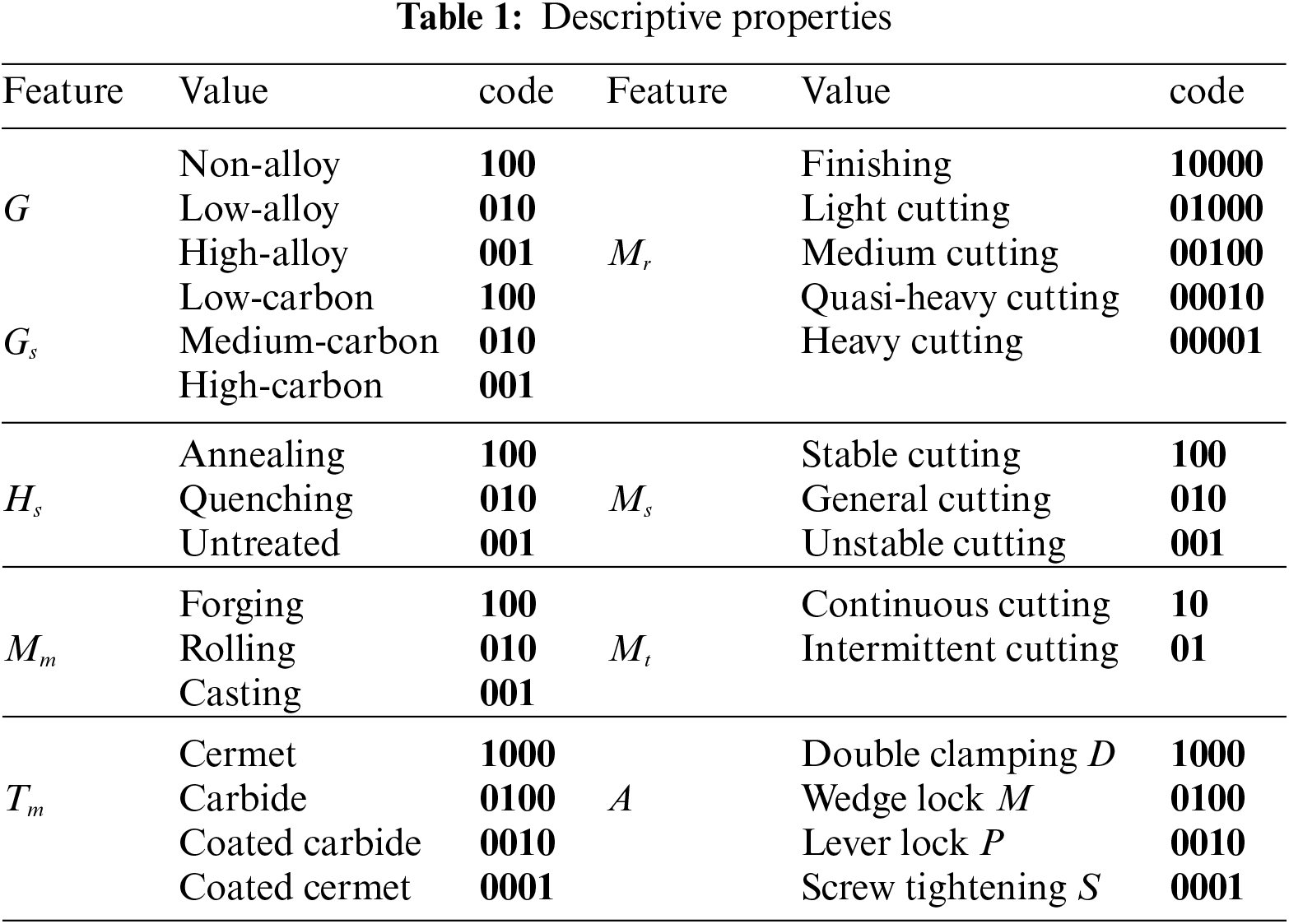
The requirements of a case consist of two parts: 1) The cutting process consists of the workpiece, machine tool, cutting tool, and cutting conditions. Specifically, workpiece Wm includes group G, sub-group Gs, heat treatment state Hs, molding method Mm, hardness H, unit cutting force Kc, retract distance Lb, cutting length L, radial allowance Lm, and workpiece diameter D. Cutting conditions Cc involves machining range Mr; machining purpose Mp; machining state Ms, machining type Mt, and maximum required surface quality Ra−req. The machine tool includes maximum cutting power Pmax and maximum feed power Pf−max. Cutting tool T includes rake angle γ; clearance angle α; tool material Tm, assembly method A, and nose radius r. 2) User objectives include cost, processing time, carbon emission, these properties have both numeric and descriptive properties.

To digitally express cutting cases, the descriptive properties are classified and coded as shown in Table 1.

2.2 Case Description

The case describes as two parts: requirements description X and solution set Y; case reasoning obtains the most similar one to the new problem by calculating the similarity between requirements. X consists of several features, and each feature consists of several properties. For the ith case X(i) with n features, where the jth feature expressed in Eq. (1) has kj properties.

X(i)=[x1(i),x2(i)…xn(i)]xj(i)=(p1,p2,…pkj)(j=1,2…n)Y(i)=[y1(i),y2(i),…ym(i)]ym(i)=(sm1,sm2…smq)(1)

x(i)j is the jth feature vector of X(i); pk is the kth property value; Y(i) is the solution set of the X(i); y(i)m is the mth solution in Y(i); smq is the qth parameter of the solution y(i)m. Correspondingly, a new problem is expressed as Eq. (2):

X(0)=[x1(0),x2(0)…xn(0)]xj(0)=(p1,p2,…pkj)(j=1,2…n)Y(0)=[y1(0),y2(0),…ym(0)]ym(0)=(sm1,sm2…smq)(2)

As mentioned in Section 2.1, the required features of a cutting process include the workpiece x(i)1, machine tool x(i)2, cutting tool x(i)j, and cutting conditions x(i)j.

3  Case Retrieval Approach

This work combines the AHP and entropy methods to propose a multi-level comprehensive case retrieval algorithm. Specifically, AHP is used to obtain the subjective weights, while entropy is adopted to obtain the objective weights of each feature. Then, combining subjective and objective weights, a multi-level comprehensive evaluation algorithm for case retrieval is designed. The algorithm flow is shown in Fig. 2.

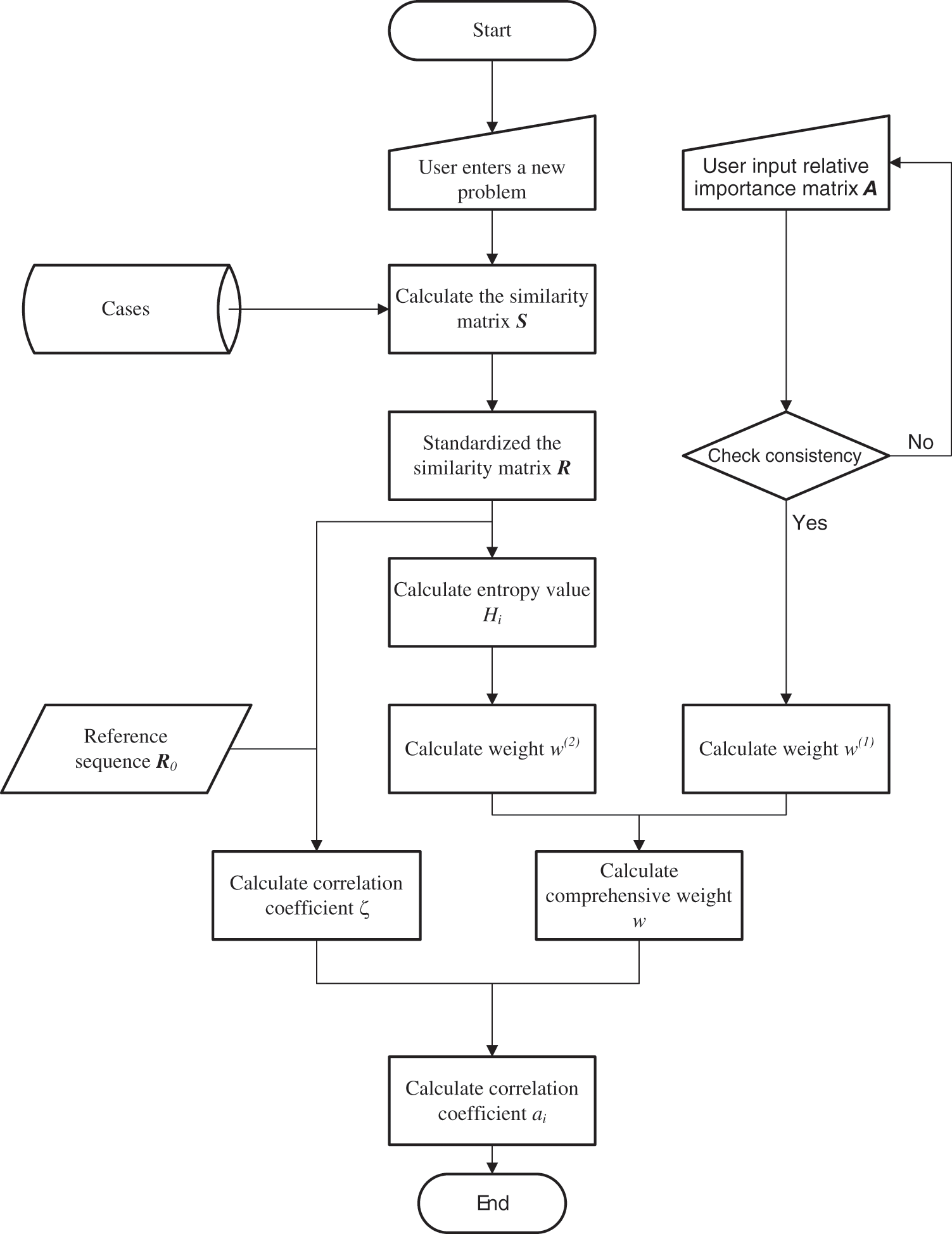
Figure 2: Flow chart of cutting parameter recommendation algorithm

3.1 Feature Similarity

For a new problem X(0) = (x1(0), x2(0),…, xn(0)), and a case X(i) = (x1(i), x2(i),…, xn(i)). The problem translates into how to measure the similarity between X(0) and X(i). Hence, a similarity matrix shown in Eq. (3) is established.

x1(0)x2(0)⋯xn(0)x1(i)s10⋯0x2(i)0s2⋯0⋯⋮⋮⋱⋮xn(i)00⋯sn(3)

si is the similarity of the ith feature between X(0) and X(i). Since properties of features have both numbers and coding, this work combined Hamming distance with Euclidean distance to generate the similarity measurement method which is shown in Eq. (4):

sin=∑i=1k1(yj1−yji)2sic=∑i=1k2Pjr∗⊕Pjrisi=Sn+w∗Sc(4)

For a feature of a case, yj1 is the normalized value of the jth property of xn(0); yji is the normalized value of the jth property of xn(i), which is obtained through Eqs. (5) and (6); k1 is the number of numerical properties; k2 is the number of coding properties; Pr*j is the jth coding properties; Prij is the jth coding properties.

M=x∗11x12⋯x1mx∗21x22⋯x2m⋮⋮⋱⋮x∗k11xk12⋯xk1m(5)

x*j1 is the original value of the jth numerical property of xn(0); xij is the original value of the jth numerical property of xn(i).

yij=xij−VjMINVjMAX−VjMIN(6)

V jMIN and V jMAX are the maximum and minimum of the jth numerical property of all cases (including X(0) and X(i)), respectively. Then, si indicates the similarity of the feature between X(0) and X(i).

3.2 Combination Weight

Weights that reflect the decision of user preference are defined as w(1), and that reflects the contribution of the information contained in the data are defined as w(2).

3.2.1 Determining w(1) Based on AHP

AHP was widely used in recommendation and decision-making problems and performed well [22–24]. When faced with a variety of programs to compare, judge, evaluate and make decisions, often use the analytic hierarchy process. AHP decomposes the problem according to the nature of the problem and the overall goal, and then combines the decomposed factors according to their mutual correlation, so as to form a multi-level analysis structure model. Such a model would translate a complex problem into a ranking of the relative importance or relative merits of different factors relative to the overall goal. This work adopts AHP to obtain weights that reflect the decision maker’s preference. Given by the user, the relative importance matrix A of features is shown in Eq. (7):

A=C1C2⋯CnC11a2…anC21/a21⋯bn⋮⋮⋮⋱⋮Cn1/an1/bn⋯1(7)

The consistency of A must be checked to determine the logical correctness of the description of the user. The specific checking method is shown in Eq. (8), and RI values of factors 3 to 13 are shown in Table 2.

CI=λmax−nn−1CR=CIRI(8)

If CR < 0.1, consistency check passed, else adjust A. If the consistency checks of A passed, the weight of each factor can be calculated via Eq. (9):

w(1)i=wi∗∑j=1nw∗j(9)

3.2.2 Determining w(2) Based on Entropy Method

Entropy is a measure of the uncertainty of information, which can be used to judge the degree of dispersion of a certain index. Generally, the greater the degree of dispersion of the index, the greater the comprehensive impact of the index on the decision. The similarity of n features of X(0) to m cases X(i)(i = 1, 2,…, m) form the decision matrix S=(sij)m × n (i = 1, 2,…, m; j = 1, 2, …, n). S is standardized as R = (rij)m × n, the specific formula is shown in Eq. (10):

rij=sij−siminsimax−simin(10)

smini and smaxi are the maximum and minimum of the ith feature, respectively.

The entropy of the ith feature is defined as Hi, which is shown in Eq. (11):

Hi=−K∑j=1mfijlnfijK=(lnm)−1fij=rij∑j=1mrij(11)

The entropy weight of the ith feature for decision-making is shown in Eq. (12):

wi(2)=1−Hin−∑i=1nHi(12)

where 0 < Hi ≤ 1, the smaller the Hi, the larger the comprehensive influence of the ith feature on the decision-making.

3.2.3 Comprehensive Weight

The weight that considers the preference of the decision-maker comprehensively and the objectivity of the information can be obtained by Eq. (13):

wi=wi(1)wi(2)∑i=1mwi(1)wi(2)(13)

3.3 Gray Correlation-Based Case Similarity

Grey relation analysis is a useful method to solve MCDM problems in an uncertain environment and in situations with multiple attributes [25], which includes the following three steps:

1) Generate the compared sequence Ri = (ri1, ri2, …, rin) and the reference sequence R0 = (r01, r02, …, r0n).

2) According to Eq. (14), calculate the correlation coefficient ζij between Ri(j) and R0(j), in the standardized decision matrix R, i = 1, 2,…, m, and j = 1, 2, …, n.

ζij=miniminj(σij)+ρmaximaxj(σij)|σij|+ρmaximaxj(σij)σij=|r0j−rij|(14)

ρ (0 ≤  ρ ≤ 1) is the distinguishing coefficient that represents the significance of maximaxj(σij). The smaller ρ is, the higher the distinguishing is. In most situations, ρ = 0.5, because this value usually offers moderate distinguishing effects and good stability [26].

3) Calculate the grey relational degree. A grey relational degree is a weighted sum of the grey relational coefficients obtained via Eq. (15).

ai=∑i=1nwiξij(15)

ai is the grey relational degree, which represents the magnitude of correlation measured between the reference sequence and Riand R0. The case with the highest ai is identified as the most similar case to the new problem.

4  Platform Development and Case Study

The platform is developed based on the proposed method, which integrated Visual Studio 2015, and SQL Server 2012. The ASP.NET in Visual Studio 2015 was adopted to build the portal of users, where users can input their requirements and obtain services via the Internet. The application process of the platform is shown in Fig. 3.

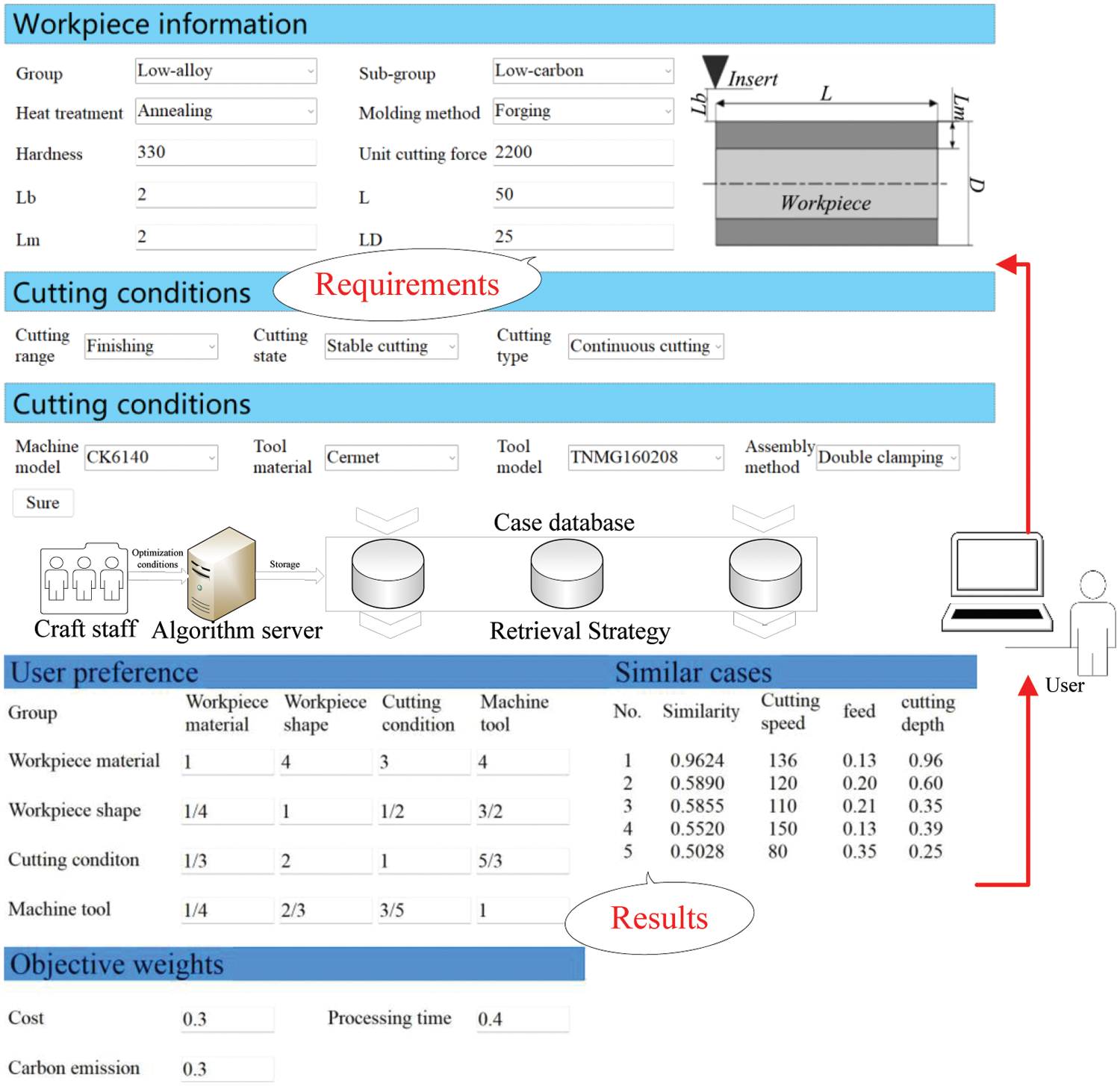
Figure 3: Platform workflow

4.1 A Case Study

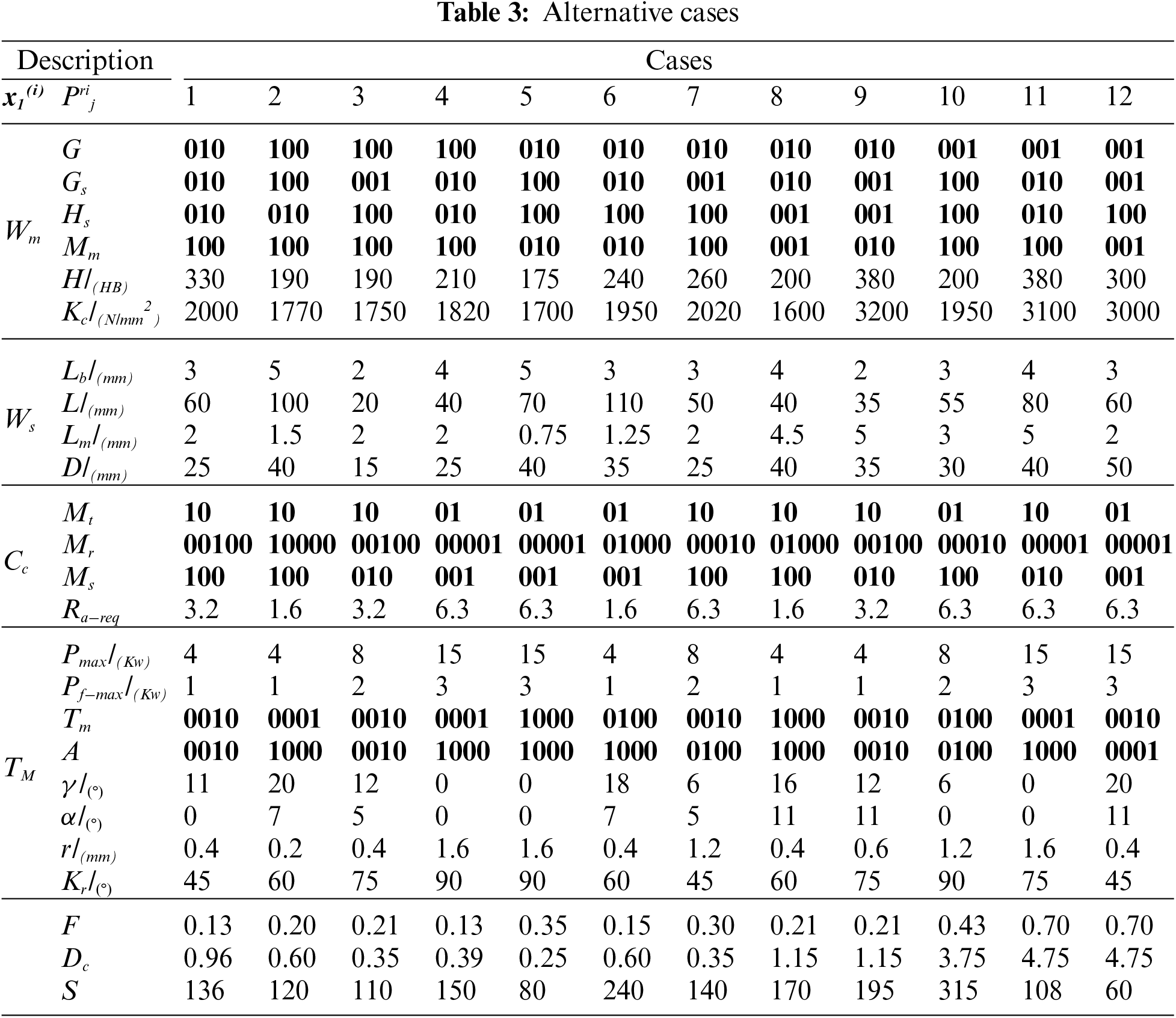
Twelve cases of the new problem stored in the database on the server are shown in Table 3, and user requirements are shown in Table 4.

4.2 Solving Process

(1) The relative importance matrix A and its standardized form A* given by the user are shown as follows:

A=WmWsCcTMWm1434Ws1/411/23/2Cc1/3215/3TM1/42/33/51  A∗=WmWsCcTMWm0.54550.52170.58820.4898Ws0.13640.13040.0980.1837Cc0.18180.26090.19610.2041TM0.13640.0870.11760.1224

The maximum eigenvalue of A is 4.0455, according to Eq. (8), CI = 0.0152 and CR = 0.017 < 0.1. Hence, the consistency check is passed. By row summation and normalization, w(1) = (0.5363, 0.1371, 0.2107, 0.1159).

(2) Entropy Standard Decision Matrix M is obtained through Eq. (10).

M=00.6920.9870.38240.99860.65950.63950.689610.97730.40210.97840.20210.11820.32320.91210.541700.73820.49920.11470.87160.517600.24920.3003110.84980.39940.24920.30030.69970.699710.108400.13480.473210.50830.74660.60650.12340.80590.45130.8701

The similarity between each candidate case and the new problem is a = (0.9624, 0.5520, 0.5855, 0.5028, 0.3382, 0.4392, 0.589, 0.4801, 0.5162, 0.4729, 0.4736, 0.3764), the case 1 is the most similar one whose solution set will be recommended.

4.3 Discussion

4.3.1 Cases Similarity Analysis

The purpose of the method is to measure the similarity between the new problem of alternative cases with both user preference and the degree of dispersion of information. The similarity with only user preference a1 or the degree of dispersion of information a2 concerned is compared with a, respectively. The results are shown in Fig. 4.

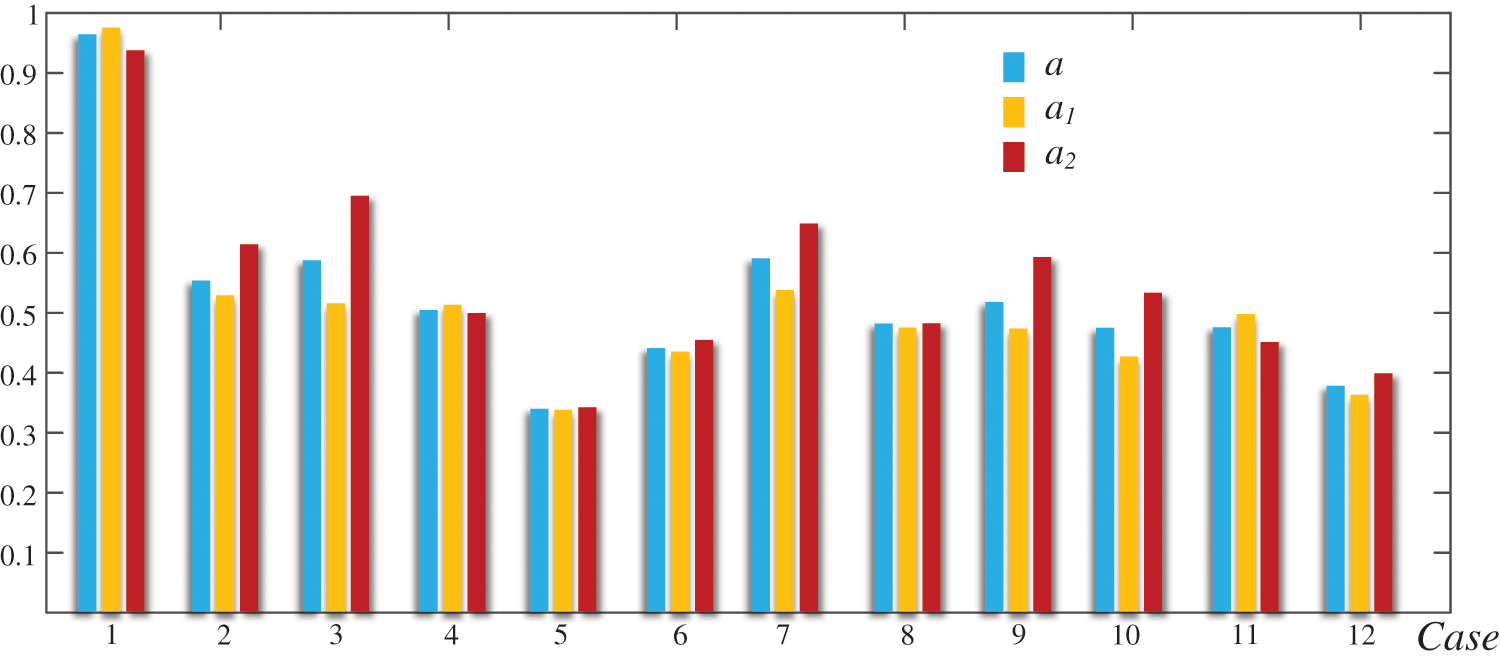
Figure 4: Similarity comparation

It can be observed that although a1, a2 and a show the same order of similarity, a1 and a2 only focus on a single aspect, a can descript the case similarity in a comprehension way.

4.3.2 Cutting Simulation Analysis

As shown in Table 4, the new issues have determined the properties of the processed parts including G, Gs, Hs, Mm, H, Kc; the shape characteristics including Lb, L, Lm, D; the heat treatment process including Mt, Mr, Ms; the parameters of the processing machine tools including Pmax, Pf−max and the cutting tools including Tm, A, γ, α, r, Kr. The forming process and surface quality of the processed parts vary depending on the use of different cutting parameters including F, Hc, S. Through cutting simulation, 12 groups of different cutting parameters shown in Table 3 were verified on The Third AdvantEdge, and the results of the cutting force are shown in Figs. 5 and 6.

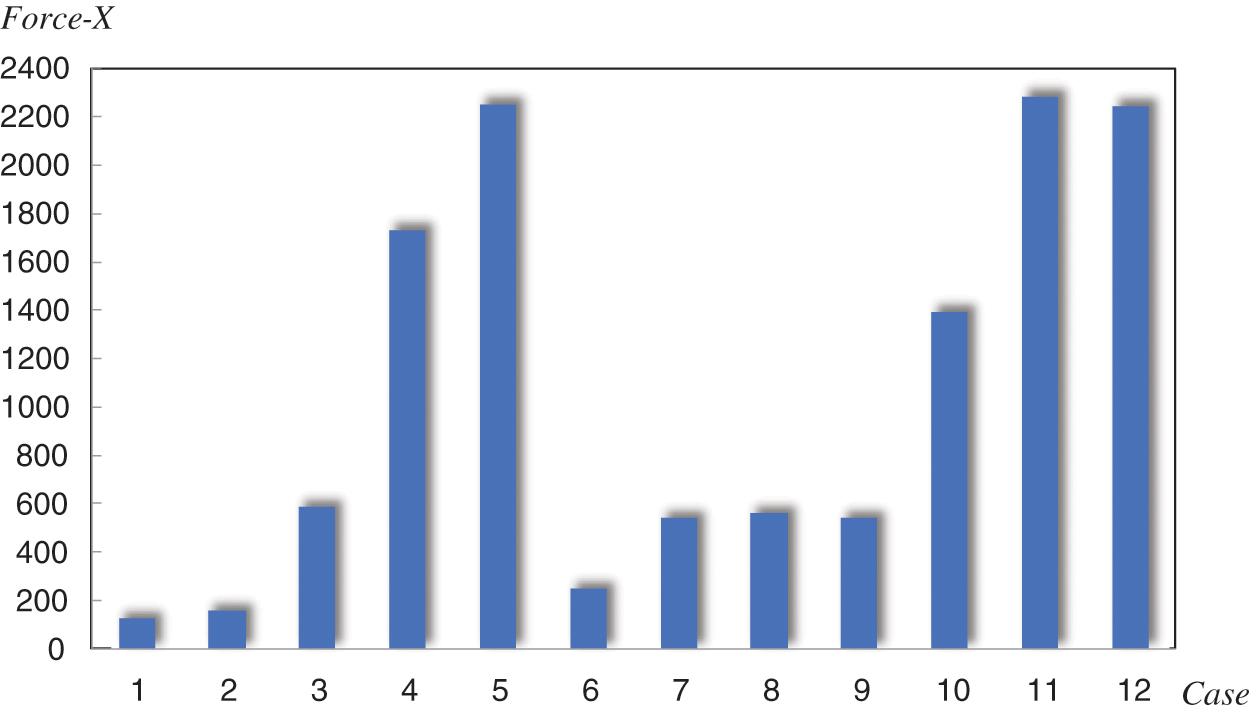
Figure 5: Cutting simulation results

Figure 6: Cutting simulation results

From the perspective of cutting force, case 1 has the best performance. In 12 groups of simulation experiments, no matter axial force or radial force, case 1 shows a smaller value and more stable fluctuation, followed by case 2, case 6 and case 7. In several cases, the cutting force exceeds the normal value range, so it is not suitable for this new problem. As for the cutting temperature, due to the cutting speed, feed, and depth of cutting, will cause different sizes of the cutting temperature, the above situations of the cutting temperature are within the normal range. In summary, the cutting parameters provided by case 1 are more suitable for the newly proposed problem.

As shown in Figs. 6c and 6d, using the parameters of case 1 and case 2 for simulation, their cutting forces are lower and similar. By comparing the stress distribution in the vertical direction, as shown in Fig. 6a, it can be seen that when the parameters of case 1 are used for cutting, the stress distribution is more uniform, and there is no stress concentration, while when the parameters of case 2 are used for cutting, the stress is more concentrated and the edge collapse is more likely to occur. The results are shown in Fig. 6b.

4.3.3 Efficiency Analysis

The purpose of the work is to improve the response speed when users obtain the cutting parameters. Thus, the consumed time Tc is a significant index to show the responsiveness. Tc obtained through this method is compared with the current cutting parameters recommendation methods (Particle swarm optimization PSO [27] and Genetic algorithm GA [28]), and the results are shown in Fig. 7.

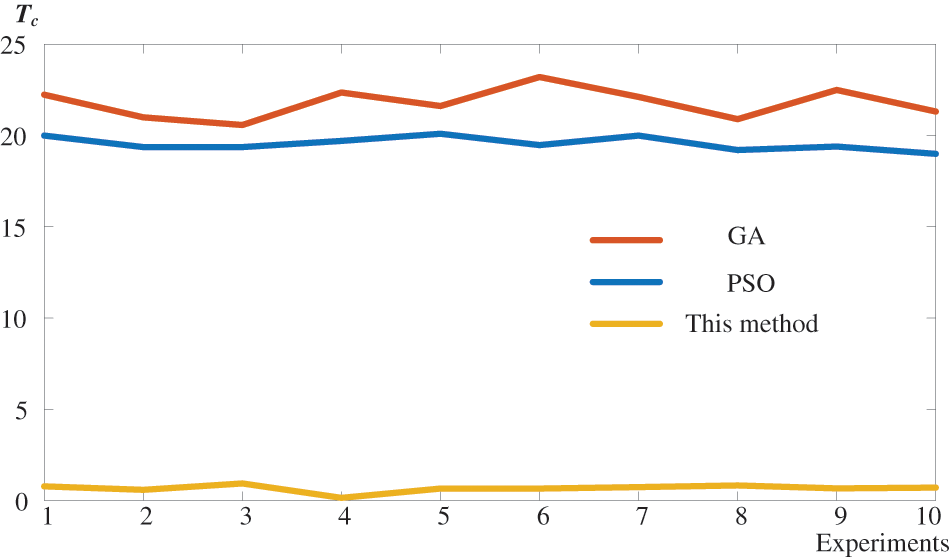
Figure 7: Time consumed comparation

As shown in Fig. 7, the proposed method performs well than the PSO and GA which are widely used in cutting parameter optimization. Namely, the proposed method is more quickly responding to user requirements and is more suitable for providing online services that require high response speed.

4.3.4 Solution Set Comparison

To show the deviation between the solution obtained through the proposed method and current optimization method, the function S shown in Eq. (16) is designed to show the relationship between the similarity of the case and the deviation of retrieving solution.

S=11+|f∗if|f=∑j=1mwj∗Fj(16)

f is the fitness value of the objective problem obtained through PSO; fi∗ is the fitness value of the ith similarity case; Fj is the jth objective value; wj∗ is the weight of the jth objective given by the user. In this work, the weight for carbon emissions, processing time, and cost are set as w* = (0.3, 0.4, 0.3). The relation of S and case similarity ai are shown in Fig. 8.

Figure 8: Relation of S and ai

It can be observed that the gap between the solution of the similar case and the solution obtained by the multi-objective algorithm is the same as the similarity of the alternative case. Hence, the retrieval method can give a suitable solution if there is a case with high similarity.

5  Conclusions

With the growing development of the Internet, network-based public service manufacturing platforms have been developed to provide service for users without constraints of scene and location. However, current cutting parameters optimization methods mainly focus on the offline dedicated model, which is not suitable for the online platform because they are time-consuming and need a long response time.

This work has made the following contributions to solve the problem; 1) A cutting parameters optimization framework under the Internet was proposed; 2) Turning case description and retrieval method were studied, and a platform of the turning process was developed, where the case study showed that the proposed method can provide the reliable and optimized cutting parameters if there are high similarity cases in alternative cases; 3) A cutting case retrieval platform was developed on Visual Studio 2015. Compared with Particle swarm optimization and Genetic algorithm, the response time of the algorithm based on grey correlation in the platform can be greatly reduced.

The limitation of this study is that the sample size of the case base is small at this stage, and the response time may be prolonged when a large number of sample retrieval is carried out. Future research work will focus on collecting more research data and expanding the database so that the proposed method can provide more accurate and reliable turning parameters. At the same time, the algorithm will be optimized so that the running time of the proposed method can be shortened to improve efficiency.

Acknowledgement: The research described in this paper was financially supported by the Sichuan Science and Technology Program, SCU-SUINING Project; We also appreciate Zhuojun Ma form Sichuan University and Tao Xiong from MingWu Technology Co., Ltd. for their support and assistance.

Funding Statement: The research described in this paper was financially supported by the Sichuan Science and Technology Program (Nos. 23ZHCG0049, 2023YFG0078, 23ZHCG0030, 2021ZDZX0007), SCU-SUINING Project (2022CDSN-14).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jianfeng Zhao, Yunliang Huo and Qingxian Li; data collection: Jianfeng Zhao and Zhixing Guo; analysis and interpretation of results: Jianfeng Zhao and Junbo Liu; draft manuscript preparation: Jianfeng Zhao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used or analysed during the current study are available from the corresponding author on reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Liu, Y., Deng, J., Liu, L., Wang, W., Meng, R. et al. (2018). Effect of nano-scale texture pretreatment on wear resistance of WC/Co tools with/without TiAlN coated flank-face in dry turning of green Al2O3 ceramics. Ceramics International, 44(17), 21176–21187. [Google Scholar]

2. You, Q., Xiong, J., Guo, Z., Liu, J., Yang, T. E. et al. (2019). Microstructure and properties of CVD coated Ti(C, N)-based cermets with varying WC additions. International Journal of Refractory Metals and Hard Materials, 81, 299–306. [Google Scholar]

3. Fox-Rabinovich, G. S., Yamamoto, K., Veldhuis, S. C., Kovalev, A. I., Shuster, L. S. et al. (2006). Self-adaptive wear behavior of nano-multilayered TiAlCrN/WN coatings under severe machining conditions. Surface and Coatings Technology, 201(3), 1852–1860. [Google Scholar]

4. Huo, Y., Xiong, J., Ze, Y., Chen, S., Guo, Z. (2022). Turning inserts the selection approach based on fuzzy comprehensive evaluation. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 236(11), 6103–6116. [Google Scholar]

5. Liao, Z., Xu, D., Axinte, D., M’Saoubi, R., Thelin, J. et al. (2020). Novel cutting inserts with multi-channel irrigation at the chip-tool interface: Modelling, design and experiments. CIRP Annals, 69(1), 65–68. [Google Scholar]

6. Shanmugapriya, P., Baskaran, J., Nayanatara, C., Kothari, D. P. (2019). IoT based approach in a power system network for optimizing distributed generation parameters. Computer Modeling in Engineering & Sciences, 119(3), 541–558. https://doi.org/10.32604/cmes.2019.04074 [Google Scholar] [PubMed] [CrossRef]

7. Patil, S. S., Pardeshi, S. S., Patange, A. D. (2023). Health monitoring of milling tool inserts using CNN architectures trained by vibration spectrograms. Computer Modeling in Engineering & Sciences, 136(1), 177–199. https://doi.org/10.32604/cmes.2023.025516 [Google Scholar] [PubMed] [CrossRef]

8. Lin, W., Yu, D., Zhang, C., Zhang, S., Tian, Y. et al. (2015). Multi-objective optimization of machining parameters in multi-pass turning operations for low-carbon manufacturing. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 231(13), 2372–2383. [Google Scholar]

9. Zhou, G., Zhang, C., Lu, F., Zhang, J. (2020). Integrated optimization of cutting parameters and tool path for cavity milling considering carbon emissions. Journal of Cleaner Production, 250, 119454. [Google Scholar]

10. Jiang, Z., Gao, D., Lu, Y., Liu, X. (2019). Optimization of cutting parameters for trade-off among carbon emissions, surface roughness, and processing time. Chinese Journal of Mechanical Engineering, 32(1), 94. [Google Scholar]

11. Mokhtari, A., Jalili, M. M., Mazidi, A. (2020). Optimization of different parameters related to milling tools to maximize the allowable cutting depth for chatter-free machining. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 235(1–2), 230–241. [Google Scholar]

12. Ming, W., Hou, J., Zhang, Z., Huang, H., Xu, Z. et al. (2016). Integrated ANN-LWPA for cutting parameter optimization in WEDM. International Journal of Advanced Manufacturing Technology, 84(5–8), 1277–1294. [Google Scholar]

13. Xu, L., Huang, C., Li, C., Wang, J., Liu, H. et al. (2020). Prediction of tool wear width size and optimization of cutting parameters in milling process using novel ANFIS-PSO method. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 236(1–2), 111–122. [Google Scholar]

14. Huo, Y., Xiong, J., You, Q., Guo, Z., Xiang, H. (2021). A personalized method of cloud manufacturing service customization. International Journal of Computer Integrated Manufacturing, 34(4), 440–454. [Google Scholar]

15. Huo, Y., Xiong, J., Guo, Z., You, Q., Peng, Y. (2021). A homogeneous cloud task distribution method based on an improved leapfrog algorithm. Computer Modeling in Engineering & Sciences, 128(1), 359–379. https://doi.org/10.32604/cmes.2021.015314 [Google Scholar] [PubMed] [CrossRef]

16. Xu, S., Chen, J., Wu, M., Zhao, C. (2021). E-commerce supply chain process optimization based on whole-process sharing of internet of things identification technology. Computer Modeling in Engineering & Sciences, 126(2), 843–854. https://doi.org/10.32604/cmes.2021.014265 [Google Scholar] [PubMed] [CrossRef]

17. Li, S., Li, Y., Li, W., Chen, C. (2019). An extended case-based reasoning method and corresponding product design process. Proceedings of the Institution of Mechanical Engineers. Part C: Journal of Mechanical Engineering Science, 233(19–20), 6673–6688. [Google Scholar]

18. Qi, J., Hu, J., Peng, Y. (2016). Hybrid weighted mean for CBR adaptation in mechanical design by exploring effective, correlative and adaptative values. Computers in Industry, 75, 58–66. [Google Scholar]

19. Zhang, B., Li, X., Lin, B., Zhu, Y. (2021). A CBR-based decision-making model for supporting the intelligent energy-efficient design of the exterior envelope of public and commercial buildings. Energy and Buildings, 231, 110625. [Google Scholar]

20. Qi, J., Hu, J., Peng, Y. (2017). A modularized case adaptation method of case-based reasoning in parametric machinery design. Engineering Applications of Artificial Intelligence, 64, 352–366. [Google Scholar]

21. Ke, C., Jiang, Z., Zhang, H., Wang, Y., Zhu, S. (2020). An intelligent design for remanufacturing method based on vector space model and case-based reasoning. Journal of Cleaner Production, 277, 123269. [Google Scholar]

22. Mathew, M., Chakrabortty, R. K., Ryan, M. J. (2020). A novel approach integrating AHP and TOPSIS under spherical fuzzy sets for advanced manufacturing system selection. Engineering Applications of Artificial Intelligence, 96, 103988. [Google Scholar]

23. Ogundoyin, S. O., Kamil, I. A. (2020). A fuzzy-AHP based prioritization of trust criteria in fog computing services. Applied Soft Computing, 97, 106789. [Google Scholar]

24. Zyoud, S. H., Fuchs-Hanusch, D. (2017). A bibliometric-based survey on AHP and TOPSIS techniques. Expert Systems with Applications, 78, 158–181. [Google Scholar]

25. Wang, Q., Wu, C., Sun, Y. (2015). Evaluating corporate social responsibility of airlines using entropy weight and grey relation analysis. Journal of Air Transport Management, 42, 55–62. [Google Scholar]

26. Chang, T. C., Lin, S. J. (1999). Grey relation analysis of carbon dioxide emissions from industrial production and energy uses in Taiwan. Journal of Environmental Management, 56(4), 247–257. [Google Scholar]

27. Osorio-Pinzon, J. C., Abolghasem, S., Maraon, A., Casas-Rodriguez, J. P. (2020). Cutting parameter optimization of Al-6063-O using numerical simulations and particle swarm optimization. The International Journal of Advanced Manufacturing Technology, 111(9–10), 1–26. [Google Scholar]

28. Ramón, Q. S., Reis, P., Davim, J. P. (2006). Multi-objective optimization of cutting parameters for drilling laminate composite materials by using genetic algorithms. Composites Science & Technology, 66(15), 3083–3088. [Google Scholar]