 Open Access
Open Access
ARTICLE
Decision Making Based on Valued Fuzzy Superhypergraphs
1 Department of Mathematics, University of Payame Noor, Tehran, 19395-4697, Iran
2 Department of Mathematics, University of New Mexico, Gallup, 87301 NM, USA
* Corresponding Author: Mohammad Hamidi. Email:
(This article belongs to the Special Issue: Advances in Ambient Intelligence and Social Computing under uncertainty and indeterminacy: From Theory to Applications)
Computer Modeling in Engineering & Sciences 2024, 138(2), 1907-1923. https://doi.org/10.32604/cmes.2023.030284
Received 29 March 2023; Accepted 14 June 2023; Issue published 17 November 2023
Abstract
This paper explores the defects in fuzzy (hyper) graphs (as complex (hyper) networks) and extends the fuzzy (hyper) graphs to fuzzy (quasi) superhypergraphs as a new concept. We have modeled the fuzzy superhypergraphs as complex superhypernetworks in order to make a relation between labeled objects in the form of details and generalities. Indeed, the structure of fuzzy (quasi) superhypergraphs collects groups of labeled objects and analyzes them in the form of the part to part of objects, the part of objects to the whole group of objects, and the whole to the whole group of objects at the same time. We have investigated the properties of fuzzy (quasi) superhypergraphs based on any positive real number as valued fuzzy (quasi) superhypergraphs, considering the complement of valued fuzzy (quasi) superhypergraphs, the notation of isomorphism of valued fuzzy (quasi) superhypergraphs based on the permutations, and we have presented the isomorphic conditions of (self complemented) valued fuzzy (quasi) superhypergraphs. The concept of impact membership value of fuzzy (quasi) superhypergraphs is introduced in this study and it is applied in designing the real problem in the real world. Finally, the problem of business superhypernetworks is presented as an application of fuzzy valued quasi superhypergraphs in the real world.Keywords
The theory of hypergraph as a model of hypernetwork has been introduced by Berge as a generalization of graph theory in 1960 [1]. A graph cannot connect more than two elements, which is a defect when discussing the connection between a group of elements is considered. A hypergraph is a generalization of a graph such that its edge can relate any number of vertices, in which a graph, and its edge connects exactly two vertices. Indeed, a hypergraph is a useful tool to analyze the structure of a system that connects a group of elements (more than two elements) together, and in this sense, it can play an important role in embedding, classifying, partitioning, covering, and clustering elements in different classes. Therefore, a hypergraph as an extension and covering of the graph has attracted the attention of many researchers, and this theory has spread rapidly, especially since it has many applications in real world (its uses in model gene interactions (ER-type hypergraph [2]), machine learning (spectral hypergraph [3]), computer networks (WIS hypergraph [4]), chemistry (molecular hypergraph [5]), visual classification (hypergraph-induced convolutional network [6]), and social media (soft hypergraph [7])). Because of the more important and updated hypergraphs, a hypergraph structure as a hypernetwork has various applications, among which it can refer to updated works such as soft hypergraph for modeling global interactions via social media networks [7], session-based recommendation with hypergraph convolutional networks and sequential information embeddings [8], hypergraph-based analysis and design of intelligent collaborative manufacturing space [9] and hypergraph-based centrality metrics for maritime container service networks: a worldwide application [10]. In classical set theory, the mathematical concepts introduce purely, and without any quality or criteria, it is not attractive to be used in the world. Zadeh introduced the concept of fuzzy set theory as a generalization of set theory to deal with uncertainties [11]. Furthermore, the Plithogenic set (as a generalization of crisp, fuzzy, Intuitionistic fuzzy, and neutrosophic sets) was introduced by Smarandache in 2017. The Plithogenic set is a set whose elements are characterized by attribute values. Recently, Edalatpanah et al. considered new and recent developments in methodologies, techniques, and applications of Neutrosophic and Plithogenic sets for various practical problems and demonstrated the challenging issues as a generalization of fuzzy sets [12]. Sometimes graphs are not able to correctly analyze many phenomena because the uncertainty of various characteristics of systems naturally exists, so fuzzy graphs can cover this defect and this is an important motivation to introduce fuzzy graph theory. After that, the fuzzy graph theory was proposed as a generalization of the graph by Rosenfeld [13], which has many applications in real world (see more details in [14]). Since a fuzzy graph as a complex graph theory gives very limited information about complex networks, so we propose that the main motivation of complex hypergraph structures is for covering fuzzy graph defects in applications. Lee-Kwang et al. [15], generalized and redefined the concept of fuzzy hypergraphs (as a useful tool for the analysis and fuzzy partition of a system) whose basic idea was given by Kaufmann [16]. Akram et al. have written a book on fuzzy hypergraph which presents the fundamental and technical concepts of fuzzy hypergraphs and explains their extensions and applications. It discusses applied generalized mathematical models of hypergraphs, including complex, intuitionistic, bipolar, m-polar fuzzy, Pythagorean, complex Pythagorean, and q-rung ortho-pair hypergraphs, as well as single-valued neutrosophic, complex neutrosophic, and bipolar neutrosophic hypergraphs. In addition, the book also sheds light on real-world applications of these hypergraphs, making it a valuable resource for students and researchers in the field of mathematics, as well as computer and social scientists [17]. There is also some research about fuzzy (hyper) graphs and their applications in complex hypernetworks, such as the implementation of single-valued neutrosophic soft hypergraphs on the human nervous system [18], decision-making methods based on fuzzy soft competition hypergraphs [19], hypergraph and network flow-based quality function deployment [20], global domination in fuzzy graphs using strong arcs [21], fuzzy hypergraph modeling, analysis and prediction of crimes [22], single-valued neutrosophic directed (hyper) graphs and applications in networks [23], achievable single-valued neutrosophic graphs in wireless sensor networks [24], fuzzy hypergraph network for recommending top-k profitable stocks [25], an algorithm to compute the strength of competing interactions in the bearing sea based on Pythagorean fuzzy hypergraphs [26] and centrality measures in fuzzy social networks [27]. Recently, Smarandache extended hypergraphs to a new concept as n-superhypergraph and Plithogenic n-superhypergraph which have several properties and are connected with the real-world [28]. Indeed, n-superhypergraphs are a generalization of hypergraphs, with the advantage that they can communicate between the hyperedges. Recently, Hamidi et al. introduced the concept of quasi superhypergraphs as a special concept of n-superhypergraphs and showed that in hypergraph theory, any hypergraph can relate a set of elements, while without any details, it makes some conflicts, defects, and shortcomings in hypergraph theory [29]. Thus, by introducing superhypergraph, they try to eliminate defects of graphs (sometimes graph structures give very limited information about complex networks) structures and hypergraph structures (although the hypergraph structures are for covering graph defects in the applications in hypergraphs, the relation between vertices can’t be described in full details). They introduced the incidence matrix of superhypergraph and computed the characteristic polynomial for the incidence matrix of superhypergraph, so they obtained the spectrum of superhypergraphs. Also, by computingthe number of superedges of any given superhypergraphs and based on superedges and partitions of an underlying set of superhypergraph, the number of all superhypergraphs on any nonempty set is obtained.
Regarding these points, we introduce the concept of valued fuzzy superhypergraphs as a generalization of fuzzy hypergraphs. Valued fuzzy superhypergraphs are dependent on the concept of fuzzy supervertices and fuzzy superedges or fuzzy links, which are defined in this study. The motivation of valued fuzzy superhypergraphs is based on a design of real problems as complex superhypernetworks. Indeed, we modify a real problem as a fuzzy superhypergraph, and with respect to the notation of the impact membership value of modeled fuzzy superhypergraph, we have made the best decision. This paper presents the fuzzy algebraic structures on valued fuzzy superhypergraphs such as strong valued fuzzy superhypergraphs, isomorphic valued fuzzy superhypergraphs, the complement of fuzzy link, and self-complemented valued fuzzy superhypergraphs. Also, the relation between fuzzy hypergraphs and strongly valued fuzzy superhypergraphs has been investigated.
Motivation and advantage: Modeling based on fuzzy (hyper) graphs is a clustering or grouping of elements based on certain properties, in which the properties of its elements are checked in each cluster, and this check has nothing to do with the properties of other clusters. We need more complete modeling in order to be able to analyze the effect of the elements in the entire modeling and with other cluster elements at the same time. Our motivation in introducing valued fuzzy superhypergraphs is the coverage of this problem in fuzzy (hyper) graphs and therefore we define it such a way that in each cluster and group the elements are related to the elements of other clusters and groups in order to analyze the effect of each element in the (super) hypernetwork on the whole (super) hypernetwork. One of the motivations for valued fuzzy superhypergraphs is that we can have the best modeling of complex (super) hypernetworks where the role of all the details that make up this complex (super) hypernetwork is important in detail and in general. In fact, in this modeling, for each complex (super) hypernetwork, we examine the relationship between all the components of the systems that make up the complex (super) hypernetwork in detail and analyze the impact of these components in the entire complex (super) hypernetwork. The highest advantage of modeling the world’s issues based on valued fuzzy superhypergraph regarding the modeling of the fuzzy (hyper) graph is in the complex (super) hypernetworks based on the fuzzy superhypergraph, and the relationship between the components is checked only in the components of all clusters based on the map of clusters. This advantage leads to obtaining, the optimal results in the complex (super) hypernetwork, based on our mathematical methods and computations. In this method, we consider the values of components in clusters, the values between clusters, and the weight of clusters and closely and carefully find the suitable positive real values for optimal computations in complex (super) hypernetworks. The positive real values play the main role in the extremum in calculus and so the optimization problem plays a significant role in these calculations.
In this section, we recall some definitions and results, which we need as follows:
Definition 2.1. [1] Let X be a finite set. A hypergraph on X is a pair
Definition 2.2. [30] Let
Definition 2.3. [29] Let X be a non-empty set. Then
(i)
(ii) the quasi superhypergraph
(iii) The superhypergraph
Let X be a nonempty set,
Theorem 2.1. [29] Let X be a nonempty set and |X| = n. If
In this section, we introduce the novel concept of fuzzy supervertices, fuzzy superedges or fuzzy links, and fuzzy superhypergraph.
Example 3.1. Let X = {a, b, c, d, e, f} and consider the fuzzy hypergraph
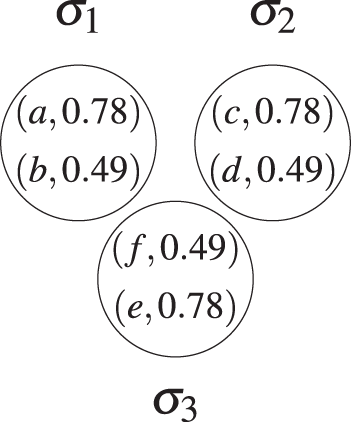
Figure 1: Hypergraph
Definition 3.1. Let
From now on, if there is not any fuzzy links from
Example 3.2. Let
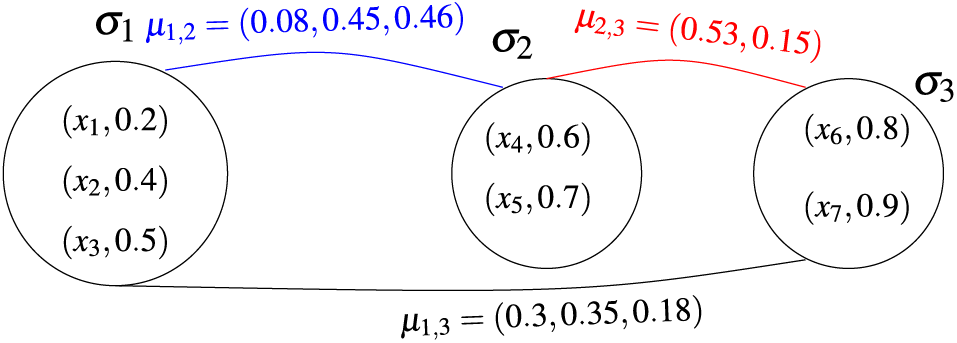
Figure 2:
Theorem 3.1. Let
Proof. Let
Proposition 3.1. The following hold:
(i) Every fuzzy hypergraph is a fuzzy quasi superhypergraph.
(ii) Every fuzzy graph is a fuzzy quasi superhypergraph.
Proof. The proof is clear by definition.
Theorem 3.2. Let
(i) For all x ∈ X,
(ii) If q ∈ [t, s], then
(iii) If q ≤ 1, then for all
Proof. Let x ∈ X. Then
(i)
It follows that q ≤ s.
(ii) By (i), q ≤ s. Let x ∈ X. If
(iii) It is obtained from (ii), (iii) and Theorem 3.1.
Corollary 3.1. Let
Definition 3.2. Let
(i) A bijective mapping
(ii) H is called a self complemented fuzzy quasi superhypergraph, if
Example 3.3. Let X = {x, y, z, w} and X′ = {x′, y′, z′, w′}. Then
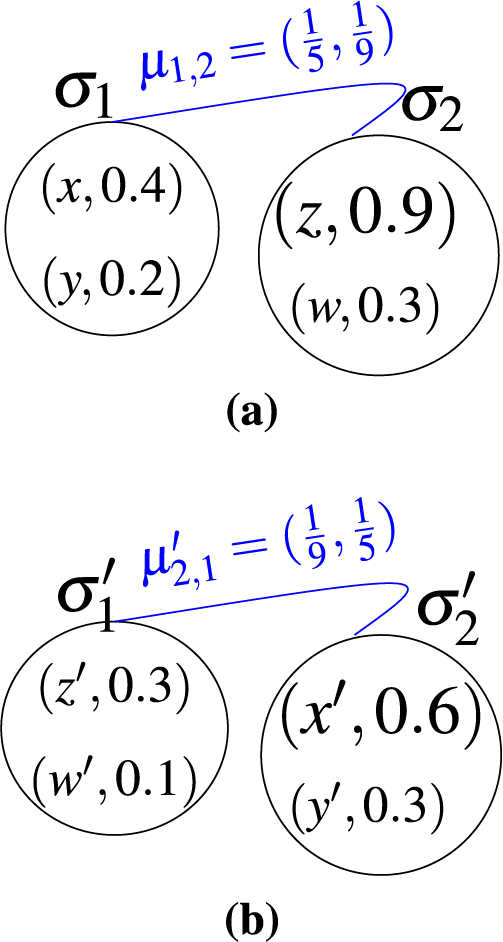
Figure 3: Isomorphic fuzzy 2-quasi superhypergraphs H, H′
Theorem 3.3. Let
Proof. Since H ≅ H′, there exists a bijective mapping
Let
Theorem 3.4. Let
(i) For any given fuzzy supervertex
(ii) For any x ∈ X, there exist
Proof. (i) Let
(ii) Let x ∈ X. Since
Example 3.4. Consider 2-fuzzy quasi superhypergraphs
Definition 3.3. Let
Lemma 3.1. Let
Theorem 3.5. Let
Proof. Let x ∈ X. Then for any
It follows that for any
Theorem 3.6. Let
Proof. Since H ≅ H′, there exists a bijective mapping
Hence
Theorem 3.7. Let
Proof. Since
so
It follows that
Example 3.5. Let
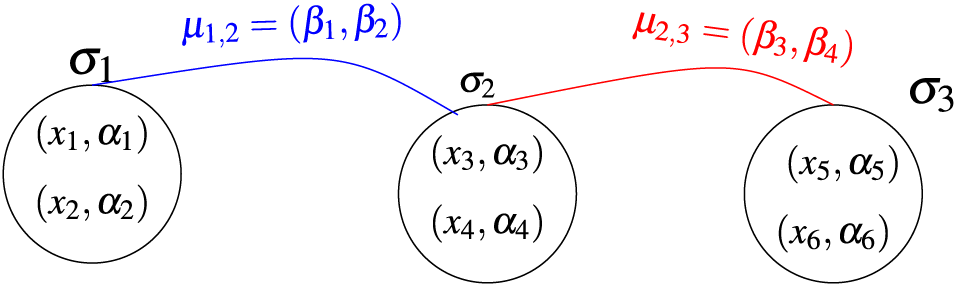
Figure 4: Fuzzy quasi superhypergraph
where
It follows that
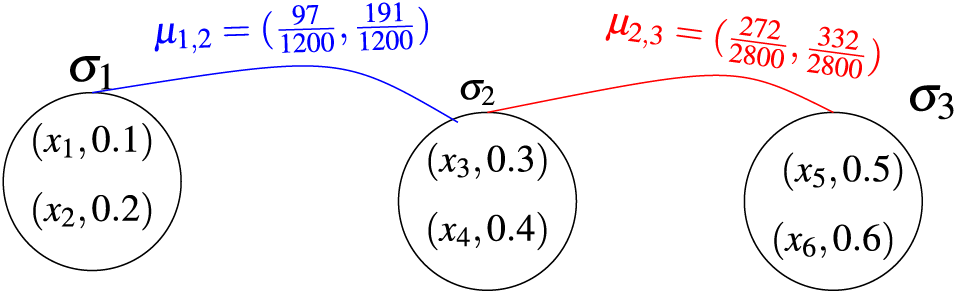
Figure 5: Fuzzy quasi superhypergraph
Theorem 3.8. Let
Proof. Define
It follows that
Definition 3.4. Let
Theorem 3.9. Let
Proof. Let x ∈ X. Since
Thus for any x ∈ X, we have
Definition 3.5. Let
Theorem 3.10. Let
(i) if
(ii)
(iii) if
Proof. I is clear by Definition 3.3 and Theorem 3.9.
Corollary 3.2. Let
4 Application of Fuzzy q-quasi Superhypergraph in Real World
In this section, we apply the concept of fuzzy valued quasi superhypergraph in the real world. To simplify and better display the method of application of fuzzy q-quasi superhypergraph in a practical problem, the following algorithm can be used:
Step 1: Consider a real problem as a complex (super)hypernetwork,
Step 2: Separate the factors and components of this complex (super)hypernetwork according to the type of application,
Step 3: Put the factors and constituent factors classified according to their values in different tables,
Step 4: According to the tables of step 3, model the relationship between components in an optimal state through a fuzzy q-quasi superhypergraph (in this step, one must find the q, and compute the maximum of fuzzy superedges based on fuzzy supervertices)
Step 5: Compute the impact membership value of components of the q-fuzzy quasi superhypergraph,
Step 6: Find the extremum case based on step 5 and the conditions we need to solve the real problem.
In the following section, we consider a real problem as a business (super)hypernetwork, and in this regard, first, we analyze and describe a business network. A business network is a complex network of companies, working together to accomplish certain objectives. These objectives, which are strategic and operational, are adopted by business networks based on their role in the market. In follows, we define a fuzzy (super)hypernetwork as a q-fuzzy quasi superhypergraph, such that its objects are called fuzzy supervertices and their connections are called fuzzy superedges or fuzzy links. For example, when we represent the business superhyper network, it concludes a collection of people and their fund, products and their quality, and the buying and selling market and their liquidity as a fuzzy quasi superhypergraph. The fuzzy supervertices are the people under consideration, products, and their quality and the buying and selling market and their liquidity, while the fuzzy superedges list all ability level, communication level, and the service time between them.
Business superhypernetwork: Business fuzzy superhypernetworking is the process of establishing a mutually beneficial relationship with other business people and potential clients or customers. The main purpose of business fuzzy superhypernetworking is to tell others about your business and hopefully convert them into customers. The most valuable advantage of the fuzzy superhypernetwork is meeting potential customers or creating referrals that you can then follow up to hopefully add to your customer base. In Table 1, we introduce a group of people with capital percentage for the participation of a business superhypernetwork that is supposed to work. In Table 2, we introduce a carpet production factory with high production quality for the participation of business superhypernetwork and in Table 3, we introduce shopping markets with liquidity for the participation of a business superhypernetwork.

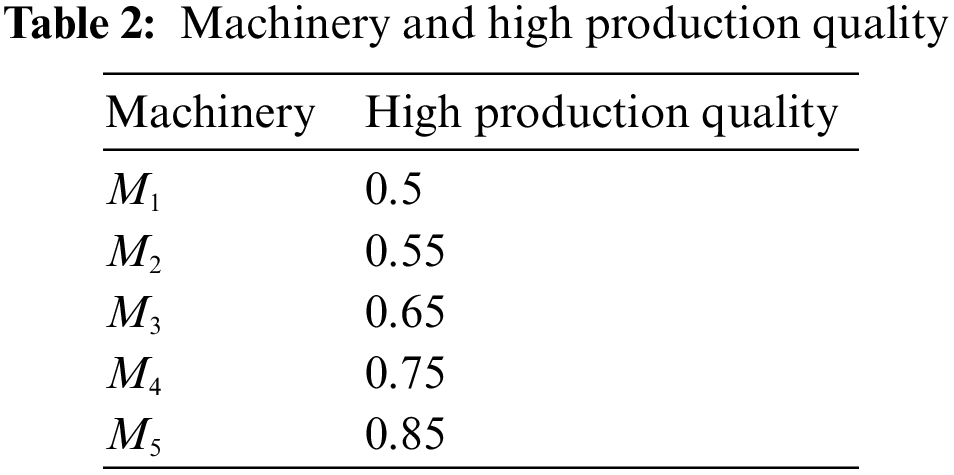
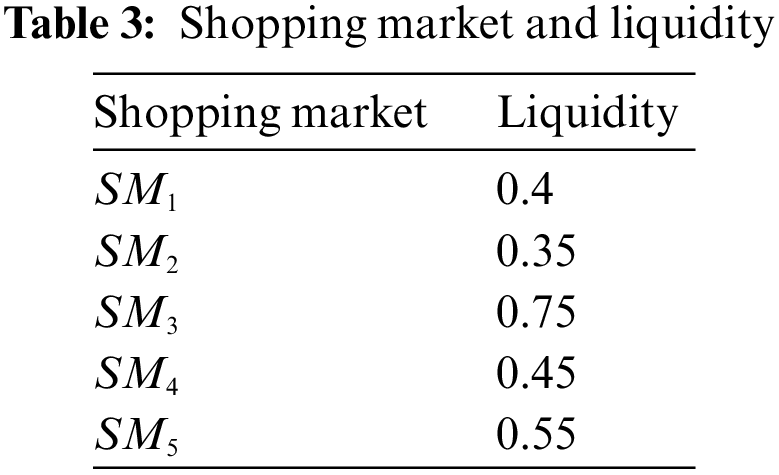
Case 1: We want to analyze the minimum ability of people on machines, the minimum consultation of people with the capital market, and the minimum distance between factories and the capital market. For instance, we compute the minimum ability of Benjamin and Machinery
It follows that:
All these qualities will be represented in the fuzzy quasi superhypergraph, where the fuzzy supervertices are the people, Machinery and the fuzzy superedges list all the ability levels, communication levels, and service time (Fig. 6). Now we see the minimum ability of people on machines, the minimum consultation of people with the capital market, and the minimum distance between factories and the capital market as shown in Tables 4–6.
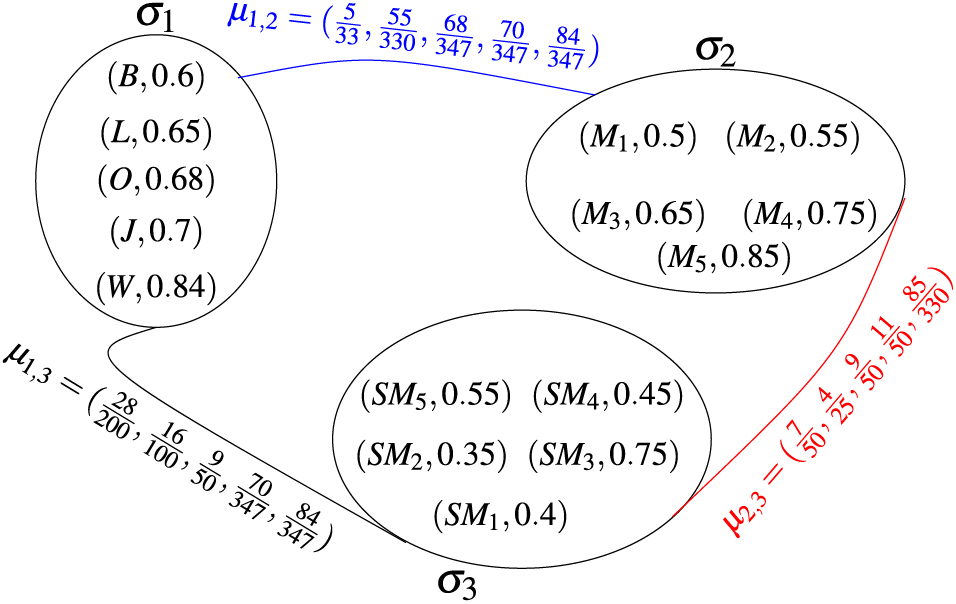
Figure 6: Fuzzy quasi superhypergraph
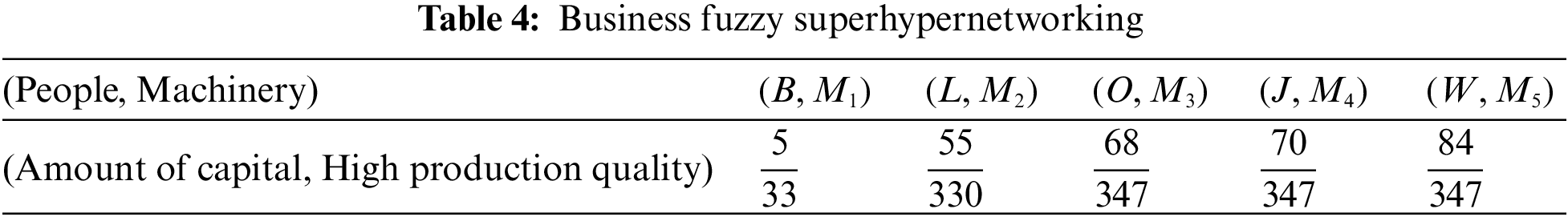
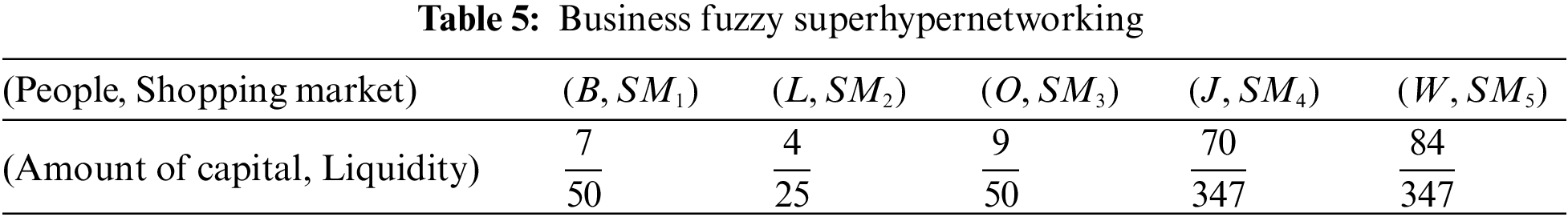

Case 2: We want to identify the best one in terms of the impact membership value in this superhypernetwork. For instance, we compute the impact membership value of William as follows:
In Table 7, we compute that

The current paper has defined and explored the notion of fuzzy quasi superhypergraphs. This study has tried to prove that the fuzzy links in the concept of fuzzy quasi superhypergraphs are fundamental and play a main role in the impact value of quasi superhypergraphs. The main motivation of this work is to apply fuzzy quasi superhypergraphs in the real world and to generalize the application of fuzzy hypergraphs in the real world. Indeed, all results of fuzzy hypergraphs can be extended to fuzzy quasi superhypergraphs both theoretically and practically. The merit of the proposed method is to fix the defects of fuzzy hypergraph theory. Indeed, fuzzy hypergraph theory investigates the optimal case for limited elements, while fuzzy quasi superhypergraphs consider the optimal case for the set of elements or object (object can be set). Also, we have shown that:
(i) The extension of a valued fuzzy quasi superhypergraph depends on its value.
(ii) Every fuzzy hypergraph is a fuzzy quasi superhypergraph.
(iii) The supremum of fuzzy superedges is less than or equal to the inverse of the real value.
(iv) Every fuzzy graph is a fuzzy quasi superhypergraph.
(v) The concept of isomorphic valued fuzzy quasi superhypergraphs is introduced and proved that the necessary condition for isomorphism of two valued fuzzy quasi superhypergraphs is equality of their values.
(vi) The concept of the complement of valued fuzzy quasi superhypergraphs is introduced and proved that the complement of isomorphic valued fuzzy quasi superhypergraphs is isomorphic. Also, it is proved that the complement of valued fuzzy quasi superhypergraphs satisfies involution properties.
(vii) The concept of self complemented valued fuzzy quasi superhypergraphs is introduced and the conditions for a valued fuzzy quasi-superhypergraph to be self-complemented have been investigated.
(viii) The impacts membership value of any valued fuzzy quasi superhypergraph is introduced and the properties of impact membership value of strong valued fuzzy quasi superhypergraph have been explored. We have particularly proven that the impact membership value of strong valued fuzzy quasi superhypergraph is zero.
(ix) We proved that the sum of all impact membership values of isomorphic valued fuzzy quasi superhypergraphs is equal.
(x) Based on the impact membership value of valued fuzzy quasi superhypergraph, we presented business superhypernetwork as a real-world problem and reached an optimal decision in this type of problem.
We hope that these results are helpful for further studies in complex (super)hypernetwork via algebraic structures and hyperstructures and fuzzy quasi superhypergraphs. In our future studies, we hope to obtain more results through the comparison of the suggested method with some existing methods and prove the effectiveness of the method, the fundamental relation on fuzzy quasi superhypergraphs, and their applications in other research. Also, we intend to work on the Plithogenics and new types of (hyper)soft sets and on superhypergraph and its relation to real-world problems.
Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: Idea of superhypergraph: Florentin Smarandache; data collection: Mohammad Hamidi; analysis and interpretation of results: Mohammad Hamidi, Mohadesheh Taghinezhad; draft manuscript preparation: Mohammad Hamidi. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: This statement should make clear how readers can access the data used in the study and explain why any unavailable data cannot be released.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Berge, C. (1973). Graphs and hypergraphs. North Holland: Amsterdam. [Google Scholar]
2. Klimm, F., Deane, M. C., Reinert, G. (2021). Hypergraphs for predicting essential genes using multiprotein complex data. Journal of Complex Networks, 9(2), 1–16. [Google Scholar]
3. Gunopulos, D., Khardont, R., Mannila, H., Toivonen, H. (1997). Data mining, hypergraph transversals, and machine learning. Proceedings of the Sixteenth ACM SIGACT-SIGMOD-SIGART Symposium on Principles of Database and Knowledgebase Systems (PODS’97), pp. 209–216. Tucson, Arizona, ACM. [Google Scholar]
4. Molnar, B. (2014). Applications of hypergraphs in informatics: A survey and oppporrtunities for research. Annales Universitatis Scientiarum Budapestinensis de Rolando Eotvos Nominatae, Sectio Geologica, 42, 261–282. [Google Scholar]
5. Konstantinova, E. V., Skorobogatov, V. A. (2001). Application of hypergraph theory in chemistry. Discrete Mathematics, 235, 365–383. [Google Scholar]
6. Shi, H., Zhang, Y., Zhang, Z., Ma, N., Zhao, X. et al. (2019). Hypergraph-induced convolutional networks for visual classification. IEEE Transactions on Neural Networks and Learning Systems, 30(10), 2963–2972 [Google Scholar] [PubMed]
7. Amini, A., Firouzkouhi, N., Gholami, A., Gupta, A. R., Cheng, C. et al. (2022). Soft hypergraph for modeling global interactions via social media networks. Expert Systems with Applications, 203(1), 117466. [Google Scholar]
8. Ding, C., Zhao, Z., Li, C., Yu, Y., Zeng, Q. (2023). Session-based recommendation with hypergraph convolutional networks and sequential information embeddings. Expert Systems with Applications, 223(1), 119875. [Google Scholar]
9. Nagy, L., Ruppert, T. (2022). Hypergraph-based analysis and design of intelligent collaborative manufacturing space. Journal of Manufacturing Systems, 65, 88–103. [Google Scholar]
10. Tocchi, D., Sys, C., Papola, A., Tinessa, F., Simonelli, F. et al. (2022). Hypergraph-based centrality metrics for maritime container service networks: A worldwide application. Journal of Transport Geography, 98, 103225. [Google Scholar]
11. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. [Google Scholar]
12. Edalatpanah, S. A., Smarandache, F. (2023). Introduction to the special issue on advances in neutrosophic and plithogenic sets for engineering and sciences: Theory, models,and applications. Computer Modeling in Engineering & Sciences, 134(2), 817–819. https://doi.org/10.32604/cmes.2022.024060 [Google Scholar] [CrossRef]
13. Rosenfeld, A. (1971). Fuzzy groups. Journal of Mathematical Analysis and Applications, 35, 512–517. [Google Scholar]
14. Sitara, M., Akram, M., Bhatti, Y. M. (2010). Fuzzy graph structures with application. Mathematics, 7(1), 63. [Google Scholar]
15. Lee-Kwang, H., Lee, K. M. (1995). Fuzzy hypergraph and fuzzy partition. IEEE Transactions on Systems, Man, and Cybernetics, 25(1), 196–201. [Google Scholar]
16. Kaufmann, A. (1977). Introduction a la thiorie des sous-ensemble flous, pp. 1. Paris: Masson. [Google Scholar]
17. Akram, M., Luqman, A. (2020). Fuzzy hypergraphs and related extensions. Singapore: Springer. [Google Scholar]
18. Akram, M., Nawaz, H. S. (2023). Implementation of single-valued neutrosophic soft hypergraphs on human nervous system. Journal of Artificial Intelligence Research, 56, 1387–1425. [Google Scholar]
19. Akram, M., Shahzadi, S., Rasool, A., Sarwar, M. (2022). Decision-making methods based on fuzzy soft competition hypergraphs. Complex & Intelligent Systems, 8(3), 2325–2348. [Google Scholar]
20. Abonyi, J., Czvetko, T. (2022). Hypergraph and network flow-based quality function deployment. Heliyon, 8(12), e12263 [Google Scholar] [PubMed]
21. Manjusha, O. T. (2023). Global domination in fuzzy graphs using strong arcs. Journal of Fuzzy Extension and Applications, 4(1), 8–17. [Google Scholar]
22. Dhanya, P. M., Ramkumar, P. B., Nirmaljith, C., Paul, J. (2022). Fuzzy hypergraph modeling, analysis and prediction of crimes. International Journal of Computing and Digital Systems, 11(1), 649–661. [Google Scholar]
23. Hamidi, M., Smarandache, F. (2019). Single-valued neutrosophic directed (Hyper) graphs and applications in networks. Journal of Intelligent & Fuzzy Systems, 37(2), 2869–2885. [Google Scholar]
24. Hamidi, M., Borumand Saeid, A. (2018). Achievable single-valued neutrosophic graphs in wireless sensor networks. New Mathematics and Natural Computation, 14(2), 157–185. [Google Scholar]
25. Ma, X., Zhao, T., Guo, Q., Li, X., Zhang, C. (2022). Fuzzy hypergraph network for recommending top-K profitable stocks. Journal of Information Science, 613, 239–255. [Google Scholar]
26. Nawaz, H. S., Akram, M., Alcantud, J. C. R. (2022). An algorithm to compute the strength of competing interactions in the Bering Sea based on pythagorean fuzzy hypergraphs. Neural Computing and Applications, 34, 1099–1121. [Google Scholar]
27. Zareie, A., Sakellariou, R. (2023). Centrality measures in fuzzy social networks. Journal Information Systems, 114, 102179. [Google Scholar]
28. Smarandache, F. (2020). Extension of hypergraph to n-super hypergraph and to plithogenic n-super hypergraph, and extension of hyperalgebra to n-ary (Classical-/Neutro-/Anti-) hyperalgebra. Neutrosophic Sets and Systems, 33, 290–296. [Google Scholar]
29. Hamidi, M., Smarandache, F., Davneshvar, E. (2022). Spectrum of superhypergraphs via flows. Journal of Mathematics, 2022, 12. [Google Scholar]
30. Smarandache, F. (2022). Introduction to the n-SuperHyperGraph-the most general form of graph today. Neutrosophic Sets and Systems, 48, 483–485. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools