 Open Access
Open Access
ARTICLE
Deep Structure Optimization for Incremental Hierarchical Fuzzy Systems Using Improved Differential Evolution Algorithm
College of Electrical Engineering, Sichuan University, Chengdu, 610065, China
* Corresponding Author: Tao Zhao. Email:
Computer Modeling in Engineering & Sciences 2024, 138(2), 1139-1158. https://doi.org/10.32604/cmes.2023.030178
Received 24 March 2023; Accepted 21 June 2023; Issue published 17 November 2023
Abstract
The optimization of the rule base of a fuzzy logic system (FLS) based on evolutionary algorithm has achieved notable results. However, due to the diversity of the deep structure in the hierarchical fuzzy system (HFS) and the correlation of each sub fuzzy system, the uncertainty of the HFS's deep structure increases. For the HFS, a large number of studies mainly use fixed structures, which cannot be selected automatically. To solve this problem, this paper proposes a novel approach for constructing the incremental HFS. During system design, the deep structure and the rule base of the HFS are encoded separately. Subsequently, the deep structure is adaptively mutated based on the fitness value, so as to realize the diversity of deep structures while ensuring reasonable competition among the structures. Finally, the differential evolution (DE) is used to optimize the deep structure of HFS and the parameters of antecedent and consequent simultaneously. The simulation results confirm the effectiveness of the model. Specifically, the root mean square errors in the Laser dataset and Friedman dataset are 0.0395 and 0.0725, respectively with rule counts of rules is 8 and 12, respectively. When compared to alternative methods, the results indicate that the proposed method offers improvements in accuracy and rule counts.Keywords
The fuzzy system was first proposed by Zadeh [1] in 1965, and it has been well applied in many fields [2–5]. The traditional fuzzy system performs well with low-dimensional input, but with the increase of input variables, the fuzzy system often encounters the problem of “dimension disaster”, which makes the number of rules and the calculation cost increase sharply. Raju et al. [6] proposed the HFS for addressing this problem. HFS comprises multiple sub-fuzzy systems with low dimensional input, connected in the form of layering and blocking, mainly including incremental, aggregated and cascaded structures [7], as shown in Fig. 1. Compared with the traditional fuzzy system, the construction process of the rule base of the HFS is more complex due to the correlation between the sub fuzzy systems. With the increase of the layers of the HFS, the expert experience is not enough to realize the establishment of the fuzzy rule base.
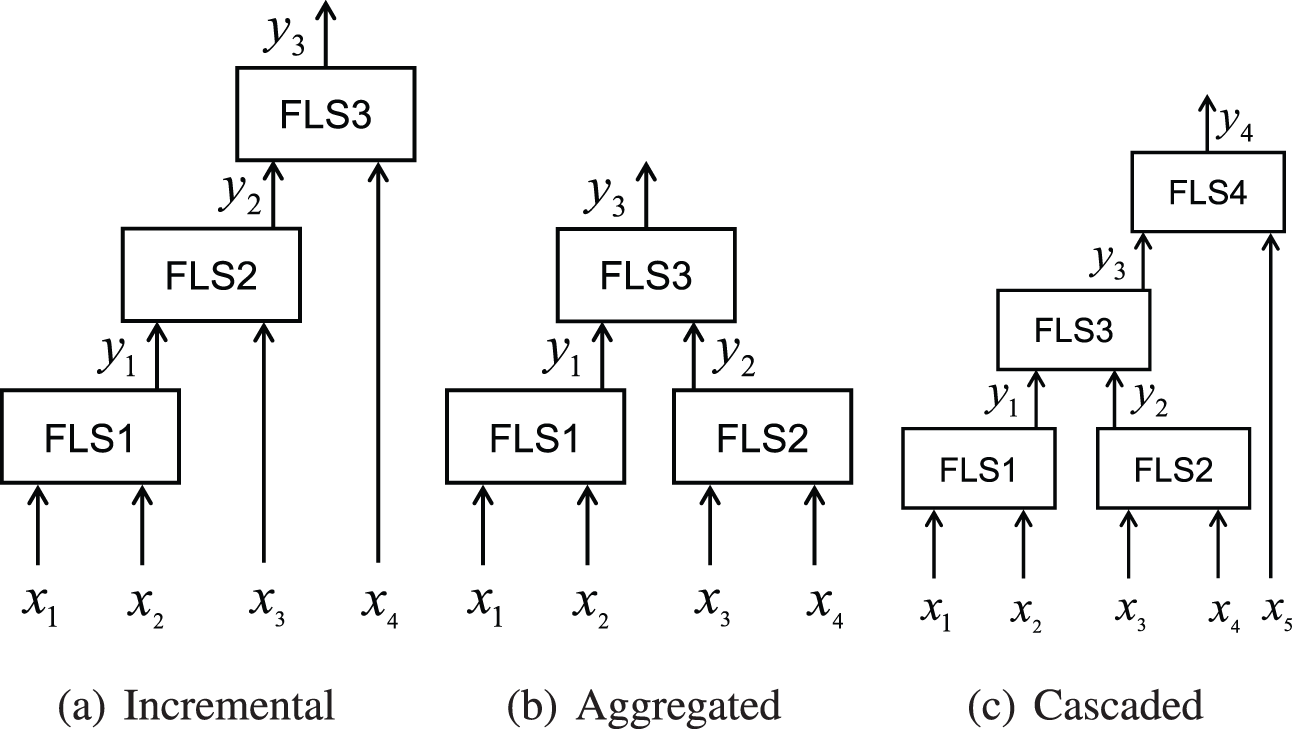
Figure 1: Common deep structures of HFS
Due to the difficulty in obtaining the fuzzy rule base, Jang [8] proposed the adaptive-network-based fuzzy inference system (ANFIS) for known input and output data pairs. ANFIS used the hybrid learning method of gradient descent and least square to make the system have strong self-learning ability to rules. Zhao et al. [9] proposed the deep neural fuzzy system (DNFS) based on ANFIS, which realized the fast learning of the HFS rule base. Talpur et al. [10] proposed a novel Bitwise Arithmetic Optimization Algorithm, which is implemented as a feature selection approach to solve the problem of large rule base in DNFS. Wang [11] designed a deep convolutional fuzzy system (DCFS) based on the Wang-Mendel (WM) method, which realized the application of HFS in prediction problems. The DNFS and DCFS methods used a bottom-up approach to design a low-dimensional fuzzy system layer by layer and finally constructed a HFS. This construction method reduced the complexity of the HFS, and can achieve better prediction and classification effects. However, DNFS and DCFS were only researched based on a specific hierarchical deep structure, and cannot be combined with different hierarchical and block methods adaptively. The prediction effect of different data sets was contingent, and it may be difficult to achieve the target effect.
Considering the diversity and complexity of HFS, it is difficult to manually select a suitable deep structure. In [12], Razak et al. proposed a method for constructing the HFS using a participatory design approach to reduce the complexity of the model. Moreover, some studies [13,14] optimized the structures of the HFS by optimizing the selection and ordering of input features according to the characteristics of hierarchical fuzzy systems. In [15], a fuzzy autoencoder and a self-organizing fuzzy partition method were designed to construct the HFS. Table 1 summarized the different techniques used in modeling the HFS.
At present, many studies have proved that it is effective to use the global search ability of heuristic algorithms such as genetic algorithm, particle swarm optimization algorithm and differential evolution to learn the antecedent and consequent parameters of rules when building a rule base of complex fuzzy system [24–28]. Velliangiri et al. [4] used the Taylor series and elephant herding optimization algorithm to optimize the fuzzy classifier. Zhao et al. [29] designed the training algorithm of a fuzzy second curvelet neural network based on an improved firefly algorithm. Traditional fuzzy systems have ante-hoc interpretability, and the performance of the model is bounded by its own interpretability and is related to the parameter settings of the system [30]. All the fuzzy system can obtain is the optimal result under the current constraints, which is consistent with the strategy principle of heuristic algorithms. In HFS, there are many parameters that need to be determined, such as the number of layers, the number of FLSs in each layer, the number of fuzzy sets divided by input variables, the number of input variables in each FLS, the rule base and so on. However, these parameters cannot be verified whether it is the optimal solution. Therefore, the heuristic algorithm is selected to optimize these parameters automatically. Considering the convenience of real-number encodings, the DE algorithm is utilized to realize the automatic optimization of HFS deep structure.
The main contributions of this paper can be summarized in the following aspects:
• This paper proposes a new encoding method for the automatic deep structure optimization of HFS. The deep structure optimization strategy of HFS adopts the joint encoding of the number of hierarchical layers and the number of input variables of each fuzzy system, which is intuitive and easy to understand. And it is also convenient for the encoding and decoding of deep structures. The parameters of the antecedent and consequent of the rules adopt the traditional parameter optimization method based on the evolutionary algorithm. The two are encoded separately, and then jointly enter the iterative process of the heuristic algorithm, which is the encoding basis for the simultaneous optimization of the deep structures and rules.
• A new mutation method for deep structures is proposed and we optimize the architecture of DE algorithm. The improved DE algorithm is adaptive to the dynamic environment. With the iterative evolution of structures and rules, the algorithm can not only ensure reasonable optimization of antecedent and consequent parameters of rules under the same deep structure, but also ensure the reasonable competition between different deep structures.
• The usefulness of the algorithm proposed for deep structures optimization of HFS is demonstrated. The algorithm achieves acceptable accuracy on prediction problems and greatly reduces the number of rules of HFS, solving the problem of “rule explosion”. Moreover, the algorithm also reduces the difficulty of HFS construction.
The rest of this paper is structured as follows. Section 2 describes the basic framework and characteristics of the HFS. Section 3 introduces the new encoding method based on HFS deep structure and rule base, and the improved DE algorithm architecture under the new encoding method. In Section 4, we perform simulation verification of the algorithm designed in this paper, and finally, Section 5 summarizes the current research.
The sub fuzzy systems of the HFS adopt the Takagi-Sugeno (T-S) fuzzy system proposed by Takagi et al. in 1985 [31]. Compared with the Mamdani fuzzy system [32], the T-S fuzzy system outputs crisp values without defuzzifying the fuzzy set, which greatly simplifies the construction process of the HFS. Each sub fuzzy system adopts a 0-order T-S fuzzy system. For a fuzzy system with r fuzzy rules, n inputs and single output, the ith fuzzy rule is:
Ri: IF x1 is Ai1 and x2 is Ai2 and ... xk is Aik and xk ... and xn is Ain THEN yi is ai(1)
where Aik is the ith fuzzy set of the kth variable, ai is the crisp value of the rule consequent parameter of the ith fuzzy rule, and each fuzzy set is described by the Gaussian membership function shown in Eq. (2):
μik(xk)=exp[−(xk−mikσik)2](2)
where k=1,2,...,n, μik is the membership value of each input xk on the corresponding fuzzy set Aik, mik is the center of the Gaussian membership function of the ith fuzzy set of the kth variable, σik is the corresponding variance, and the output of the fuzzy system is obtained as shown in Eq. (3). When the output y1 of the first layer fuzzy system is obtained, then the first input of the sub fuzzy system of the lth layer is given by the output yl−1 of the previous layer.
y=∑ri=1∏kj=1μij(xj)ai∑ri=1∏kj=1μij(xj)(3)
When dealing with high-dimensional problems, the number of rules in traditional fuzzy systems increases exponentially with the number of input variables [15]. Consider a fuzzy system as shown in Fig. 2a, in which the number of input variables is n and each variable is divided into m fuzzy sets, the number of fuzzy rules in this fuzzy system is mn. For the HFS shown in Fig. 2b, when the number of input variables is n, the number of sub fuzzy systems is n−1, the total number of rules in this HFS is (n−1)m2. The relationship between fuzzy rules and the number of input variables changes from an exponential relationship to a linear relationship. For example, when the number of input variables of the fuzzy system is 6, if each input number is divided into 4 fuzzy sets, the number of rules of the traditional fuzzy system is 46=4096, and the total number of rules of the HFS is (6−1)×42. Obviously, the number of rules is greatly reduced, which reduces the complexity of the fuzzy reasoning process. In addition, Wang [33] has proved that HFS still has the universal approximation property, so HFS has the potential to solve the problem of rule explosion with high-dimensional input.
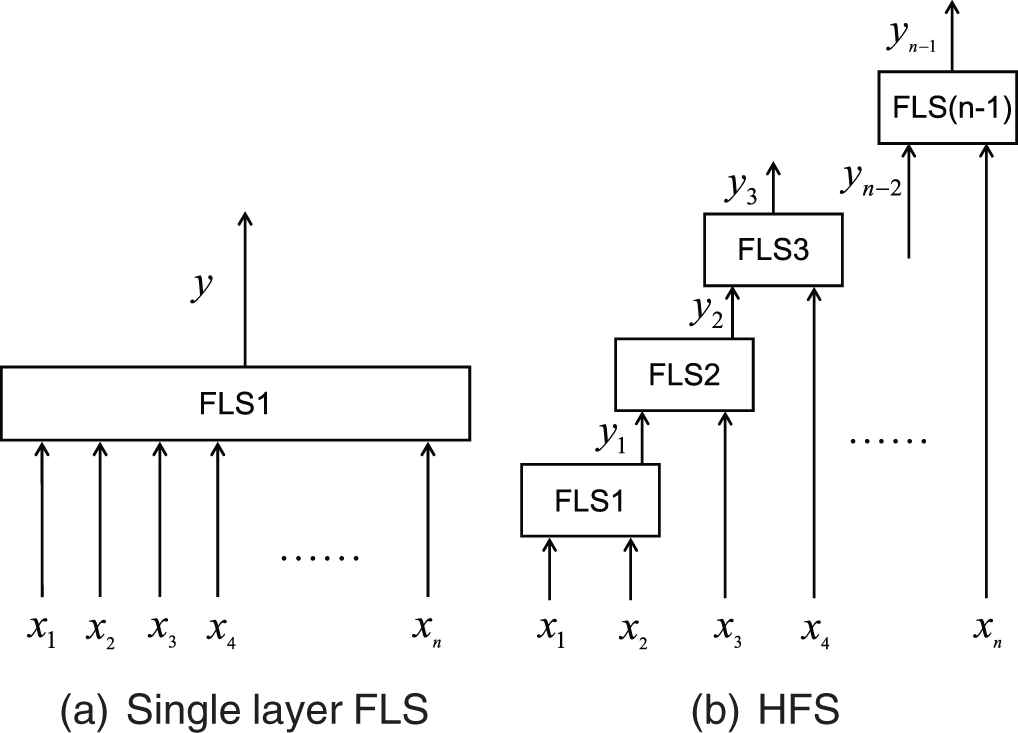
Figure 2: Single layer FLS and HFS
The HFS shown in Fig. 2b is an incremental structure with the simplest form and the largest number of layers. Since each layer has only one sub fuzzy system and each sub fuzzy system has the same number of input variables, this deep structure is more convenient in model construction for high-dimensional input. In this structure, each sub fuzzy system has two input ports. Except that the first layer uses two input variables, each other layer uses only one input variable, and the other port is the output of the previous sub fuzzy system. Wang [11], Zhao et al. [9] have done great research on the design of HFS with specific incremental structure and aggregated structure, and have applied it in the prediction model. However, when designing the deep structure of HFS, how many input variables should be designed for each layer of sub fuzzy system and how to construct the rule base are still challenging problems.
For the number of input variables n, an incremental structure with only one sub fuzzy system per layer similar to the structure of Fig. 2b. HFS is constructed layer by layer from bottom to top, and each layer except the first layer uses at least one input variable. Each sub fuzzy system has at least two input ports, the input ports of the sub fuzzy system of the first layer are all used for the input of variables, and each other layer has one port for the input of the output of the sub fuzzy system of the previous layer. Therefore, the number of input variables used in the first layer may be 2∼(n−1), and each subsequent layer may be 1∼(n−2). The maximum number of layers in the deep structure is n−1, and the sum of the number of input variables used in all layers should be n. Table 2 shows all structures existing in the HFS based on incremental deep structure described in Fig. 2b when the number of input variables is 6.
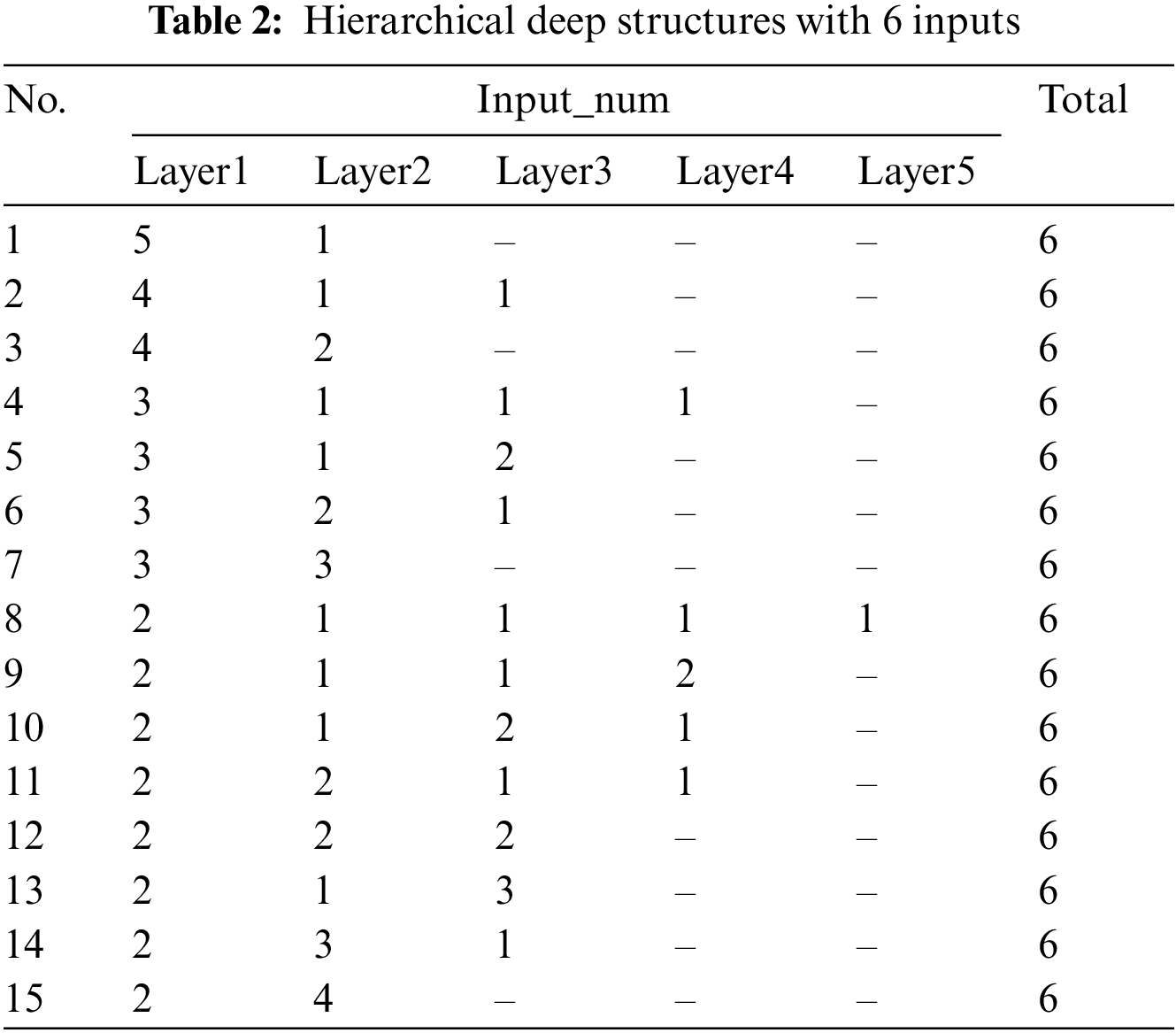
Obviously, there are 15 hierarchical deep structures with 6 inputs in Table 2. The first column is the label of each structure, and the Input_num column is the number of input variables used by each layer of sub fuzzy system. The final number of inputs used by each structure is 6. Fig. 3 showsthe hierarchical structure of the 5th and the 6th groups in Table 2. For the 5th structure in Fig. 3a, the order of the number of input variables used by each sub fuzzy system is 3-1-2, while the order of the number of input ports is 3-2-3. Actually, the first sub fuzzy system of the two structures in Fig. 3 both have three input ports, but due to the difference in the configuration of the subsequent input ports, the performance of the fuzzy system will also be different. With the increase of dimension, it is difficult to determine a reasonable hierarchical deep structure by manual experience, so exploring the automatic optimization of hierarchical deep structures has important theoretical and practical application value.
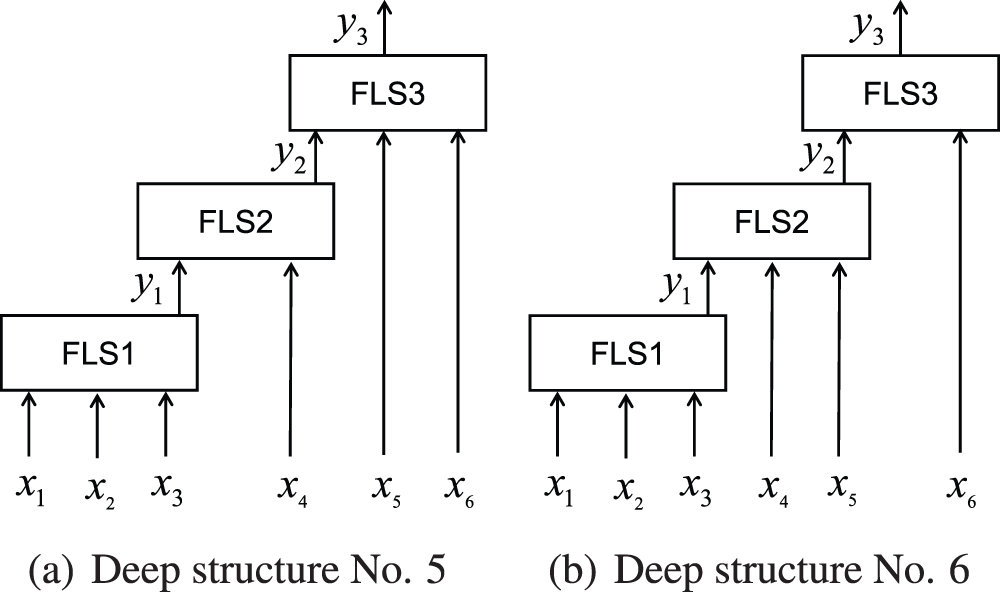
Figure 3: Hierarchical deep structures
In practical application, HFS is not only difficult to choose in the face of many hierarchical deep structures, but also difficult to establish the rule base of fuzzy system and determine the parameters of antecedent and consequent when the deep structure of HFS has already determined. The traditional method of establishing the rule base manually is ineffective in complex fuzzy systems. The rule base of DCFS is constructed by using WM method to train each sub fuzzy system from top to bottom and then combine them. DNFS adopts ANFIS method in the training mode of each sub fuzzy system. Constructing HFS in a hierarchical and block way reduces the training difficulty of the rule base, but both DCFS and DNFS methods take the final target output as the target output of each sub fuzzy system. Although each sub fuzzy system has good performance under the current constraints, it is difficult to guarantee the performance of HFS formed by combination, and the subsequent optimization of parameters is also difficult. Juang et al. [34–36] used evolutionary algorithms to learn the rule base for traditional fuzzy systems, and have achieved good results in robot control. HFS is a connection combination of multiple fuzzy systems, and considering the characteristics of fuzzy system and the adaptability of evolutionary algorithm, it is feasible to apply evolutionary algorithms to the learning of the rule base of HFS. The algorithm proposed in this paper can simultaneously optimize the deep structure of HFS and the antecedent and consequent parameters, so as to achieve an acceptable realization result.
3 An Optimal Algorithm for Deep Structures of HFS
In the classical DE algorithm, first of all, select three different individuals from the population randomly, two of which are selected to subtract, and then add the difference to the third individual according to the rule. Then, cross the result with the original individual. After natural selection, retain the better one to achieve the evolution of the population [37,38]. In order to improve the ability of global search, Juang et al. [34] proposed an adaptive group-based differential evolution (AGDE) algorithm. AGDE dynamically divides the entire population into different groups, and the mutation is based on individuals in different groups, which increases the global search ability of the algorithm and accelerates the convergence speed. Based on the idea of population grouping in [34], this paper encodes the HFS deep structure and antecedent and consequent parameters respectively, and improves the architecture of the classical DE algorithm based on this new encoding method, which makes HFS have both hierarchical deep structure and rule base self-learning ability.
3.1 Description of the New Encoding Method
Degenerate the possible deep structure shown in Table 2 into a structure in which the number of input variables used in the first layer may only be 2 or 3, and the number of input variables used in each subsequent layer may be 1 or 2, so as to faciltate subsequent encoding descriptions. That is, the maximum number of input ports of each sub fuzzy system is set to 3.
When the number of input ports in the first layer is 2, the maximum layer number Lmax of HFS is n−1, and the minimum layer number Lmin is n/2. If n is odd, Lmin is rounded down, and the list of possible deep structures is shown in Table 3. When the number of input ports in the first layer is 3, the maximum layer number Lmax of HFS is n−2, and the minimum layer number Lmin is (n−1)/2. If n is odd, Lmin is rounded up, and the list of possible deep structures is shown in Table 4. Where Layer_num is the number of HFS layers under Description, Stru_num is the number of deep structures existing under the current number of layers. The total number of deep structures N of HFS is shown in Eq. (4).


{N=3+k−3∑i=1[Cin−3−i+Cin−2−i],k=(n+2)/2, if n is even N=2+k−3∑i=1[Cin−3−i+Cin−2−i],k=(n+3)/2, if n is odd (4)
where n is the dimension of the input, and N is the number of deep structures in the corresponding dimension in HFS. There are different calculation formulas when n is odd or even. For HFS with 6 inputs, the total number of deep structures calculated by Eq. (4) is 8, which has a maximum of 5 layers of hierarchical deep structures.
For HFS with n inputs, since it has at most n−1 layers of hierarchical deep structure, the solution vector of deep structure s1 can be randomly initialized to NP vectors with dimension n−1. Each bit of the encoding is the number of input ports of the sub fuzzy system. For input ports that do not exist, set the corresponding encoding position to 0. The deep structures of HFS and the corresponding encoding results are shown in Table 5.
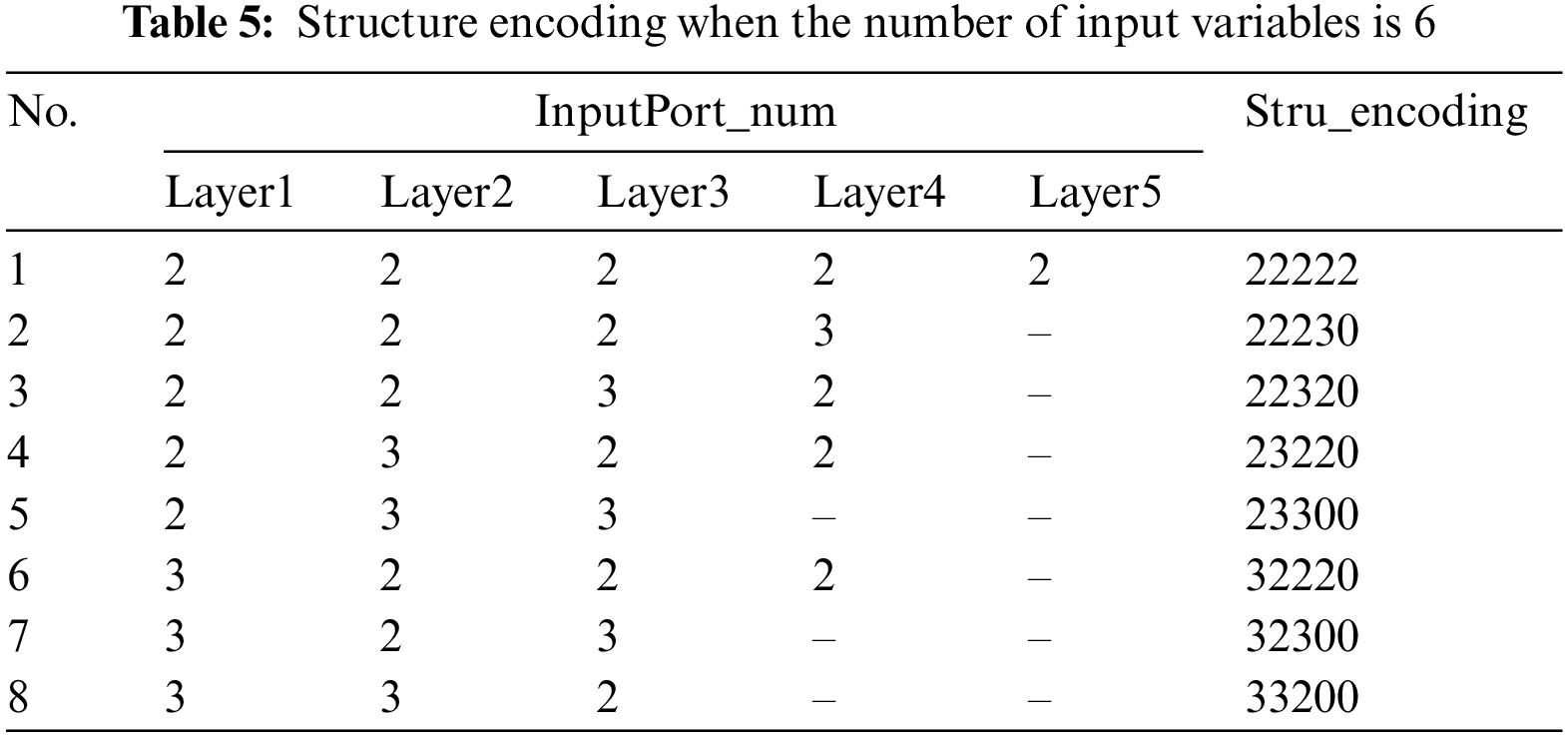
In Table 5, since the input dimension is 6, the encoding length of each hierarchical deep structure is 5. This encoding method makes s1 only need to randomly generate a sequence containing 2 and 3 during initialization, and then according to the constraint of the number of inputs, the subsequent elements of s1 are subtracted or set to 0. Algorithm 3.1 describes the algorithm flow of constraint on the solution vector of initializing deep structures, where size_x is the size of input dimension. For example, when s1 is initialized to 23233, after the constraint of Algorithm 3.1, s1_new is obtained as 23220.

Considering learning the antecedent and consequent parameters of the rules of HFS by evolutionary algorithm, when the input dimension is n, and each input is divided into r fuzzy sets, HFS has N−1 layers of the HFS deep structure if uses the deep structure shown in Fig. 2b. The number of rules in each sub fuzzy system is equal to the number of fuzzy sets. Assuming that each sub fuzzy system has only 2 inputs, so the number of parameters of each rule is 5, and the single individual description of the parameter solution vector of the antecedent and consequent of the rule is shown in Eq. (5).
s2=[m111,σ111,m112,σ112,a11⏟FLS 1, Rule 1,⋯,m1r1,σ1r1,m1r2,σ1r2,a1r⏟FLS 1, Rule r ,⋯,mLr1,σLr1,mLr2,σLr2,aLr⏟FLS L, Rule r ](5)
where m, σ and a are parameters given in Eqs. (1) and (2), L is the number of the sub fuzzy systems, and r is the number of rules. When the deep structure of HFS has already selected, the rule base of HFS can be obtained by evolutionary algorithm to learn s2. In this case, the number of fuzzy rules is only related to the number of fuzzy sets and the number of sub fuzzy systems, which further reduces the number of the rules of HFS.
Considering that each sub fuzzy system has at most p inputs, and each input is divided into r fuzzy sets, s2 can be randomly initialized as NP vectors with dimension r(2p+1)(n−1) to form a regular evolutionary population of the evolutionary algorithm. For the HFS with 6 input variables shown in Table 5, assuming that the number of rules is 4, the deep structure solution vector s1 after random initialization contains only 2 and 3. Then, according to the relationship between the total number of inputs and the number of inputs in each layer, s1 can be adjusted adaptively. Finally s1 is composed of NP vectors with dimension 7, and s2 is composed of NP vectors with dimension 140.
3.2 Improved DE Algorithm Based on New Encoding Method
On the basis of the classical DE algorithm, the improved DE algorithm adds the mutation of HFS deep structure. Algorithm 3.2 describes the mutation process of the deep structure solution vector s1. When initializing s1, there may be same encodings of deep structure. After grouping the same deep structures in the population, the mean fitness of each group was calculated. Then, according to the rank order of each group, the proportion of mutation is allocated to each group. The worse the rank of the group, the more mutation individuals within the group. And the mutation individuals were selected from the individuals with lower fitness rank in the group. Adding the mutation of the solution vector of deep structure s1 into DE algorithm can increase the number of population and ensure the diversity of deep structures.

In the mutation process of deep structures, each individual has three directions of mutation. The purpose of mutating to the forward adjacent deep structure and the backward adjacent deep structure is to increase the diversity of the population and avoid falling into a local optimum in deep structure selection. Mutation to the best deep structure is to increase the weight of the current optimal deep structure, so that the antecedent and consequent parameters of the rule can be better learned.
For HFS with 6 input variables, all deep structures are shown in Table 5. If the optimal deep structure s3 is encoded as 23300, and the individual s4 of the deep structure to be mutated is encoded as 22230, the forward adjacent deep structure s5 is encoded as 22222, and the backward adjacent deep structure s6 is encoded as 22320. According to the initial set probability, s4 will mutate to s3 with probability p1, mutate to s5 with probability p2, and mutate to s6 with probability p3, where p1+p2+p3=1. The method of multi-direction mutation can ensure that the existing optimal deep structure is stabilized, while maintaining the diversity of the population and reasonable competition between individuals, and avoid the deep structure from falling into a local optimum to a certain extent. For groups lacking forward or backward neighbors, the corresponding mutation probability can be set to 0.
The improved DE algorithm flow is shown in Fig. 4. Firstly, import the dataset and initialize the parameters of the algorithm. To eliminate the influence of dimensionality, the dataset needs to be normalized in advance. Min-max normalization can ensure that mutation, crossover and selection in DE algorithm are performed reasonably. Then, calculate the fitness and start the iteration. The iteration terminates when the maximum number of iterations N_iter is reached or the fitness reaches the requirement of accuracy. The mutation and crossover strategy of the solution vectors of rule parameters s2 are shown in Eqs. (6) and (7).

Figure 4: Flowchart of the improved DE algorithm
vi,j=xa,j+F(xb,j−xc,j)(6)
ui,j={vi,j, if rand(0,1)<Cr or j=rand(1,n)xi,j, otherwise (7)
where F is the scaling factor of mutation, Cr is the crossover probability, and xi,j represents the jth dimension of the ith solution vector of the initial population. a, b, c, and i are random integers that are different from each other. v is the population obtained after mutation, and u is the population obtained after crossover.
The solution vectors of deep structures s1 mutates when the set iteration step g is reached. Mutation of s1 is performed every g iterations of s2. For example, if N_iter is 20000 and g is 20, s1 mutates when s2 iterates a multiple of 20. So that s1 can mutate a total of 100 times. The mutation strategy of s1 is described in Algorithm 3.2.
In this section, two simulations are used to verify the proposed method. We select the Laser data set and Friedman data set from the KEEL database [39] for prediction simulation implementation. The Laser prediction dataset is a far-infrared laser recording of continuous time series in a chaotic state. The friedman prediction dataset is a comprehensive benchmark dataset, which is generated by Eq. (8) and is Gaussian random noise.
y=10sin(πx1x2)+20(x3−0.5)2+10x4+5x5+σ(0,1)(8)
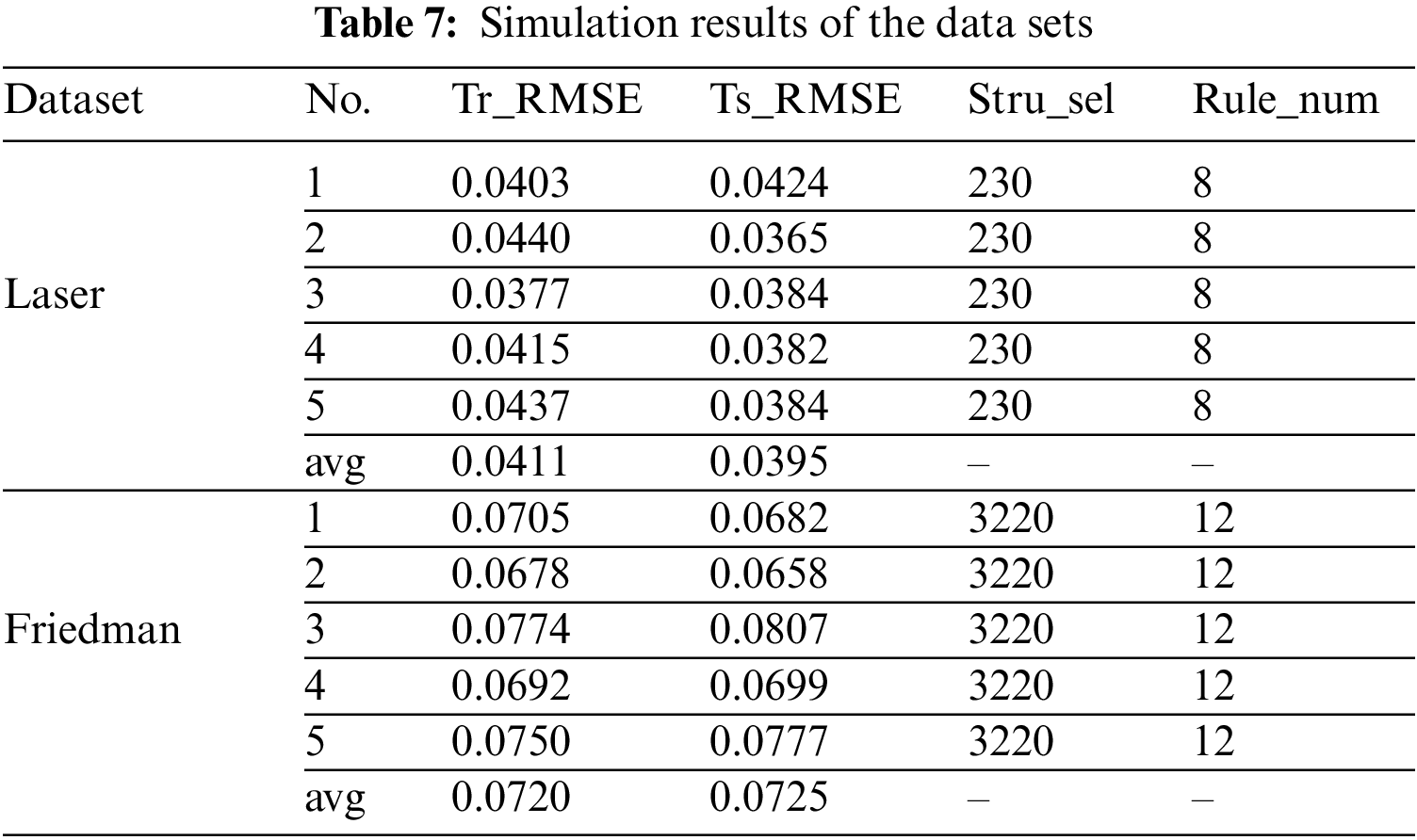
The evaluation index of the fitness function used in the simulation is root mean square error (RMSE). In Eq. (9), n is the number of samples, y is the real output, and ˆy is the predicted output. According to the basic information of the data set, the population number NP of DE algorithm was set as 50, the maximum input number p of each sub fuzzy system is 3, the number of fuzzy sets r divided by each input is 4, the iteration step g of deep structure mutation is 20, and the total number of iterations N_iter is 20000. Moreover, the scaling factor of mutation F is 0.4 and the crossover probability V is 0.7. Table 6 briefly describes the basic information of the data set used for simulation, where Stru_num is the number of deep structures calculated by Eq. (5). And 70% of the samples are used for training the HFS and 30% for testing [40,41]. Considering the randomness of the results obtained by a single simulation, each data set is repeated 5 times. Table 7 shows the implementation results of predictions on the laser dataset and the friedman dataset.

RMSE=√1nn∑i=1(^yi−yi)(9)
Figs. 5 and 6 show the prediction results and error curves of the laser dataset and the friedman dataset respectively, where the data in Figs. 5 and 6 are the first group of each data set in the simulation results in Table 7. The results show that the algorithm proposed in this paper can obtain better prediction accuracy and fewer fuzzy rules. Compared with the Laser data set, the Friedman data set has higher input dimensions, resulting in a larger number of possible deep structure for HFS. And the resulting precision reduction can be improved by increasing the number of population or iteration. Moreover, the use of 1-order or higher-order T-S fuzzy systems can also improve the prediction ability of HFS for complex models, but it will increase the complexity of the system and the amount of calculation. And this paper mainly analyzes and verifies the feasibility of the proposed algorithm. Although there are differences in the prediction accuracy obtained by the five repeated experiments, they all obtain the same hierarchical deep structure in the end. However, because the number of fuzzy rules is only linear with the number of fuzzy sets and the number of sub fuzzy systems, the number of fuzzy rules is less than that of the traditional HFS construction method. Figs. 7 and 8 show the deep structure change curves of the two data sets, respectively. Where Label represents the label of possible deep structures, Struc_iter_num represents the number of deep structure iterations, and Class_num represents the number of current deep structure in the population.
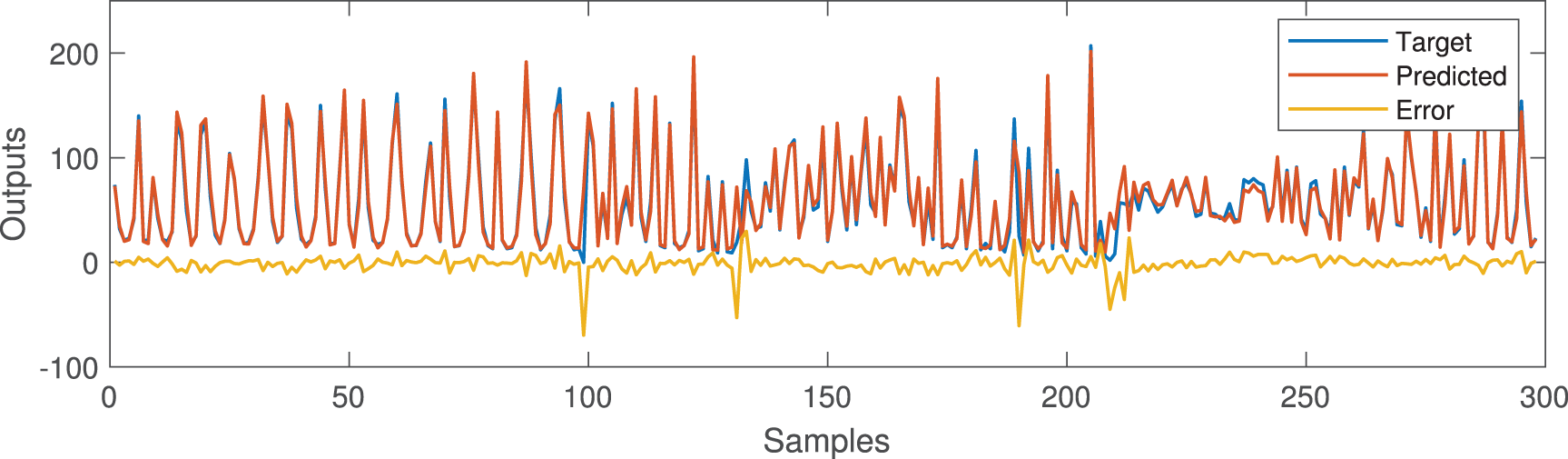
Figure 5: Laser dataset prediction results

Figure 6: Friedman dataset prediction results
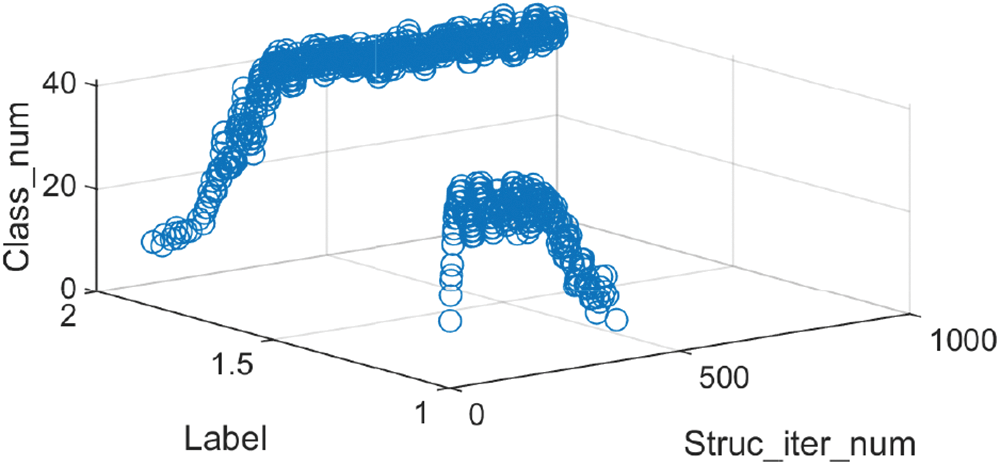
Figure 7: Iterative process of deep structure of Laser dataset (No. 1) (label_1: 222, label_2: 230, label_3: 320)

Figure 8: Iterative process of deep structure of Friedman dataset (No. 1) (label_1: 2222, label_2: 2230, label_3: 3220, label_4: 3300)
For the Laser dataset, the optimal deep structure finally obtained is shown in Fig. 9a. In the iterative process, three optimal structures with encoding 222, 230, and 320 appeared. The initial optimal deep structure of HFS is 222. In the subsequent evolution, the number of this deep structure first increases and then decreases in the population. Then at about the 3000th iteration, it oscillates with the final optimal deep structure 230. Finally, the optimal deep structure converges and stabilizes in the deep structure with encoding 230, and 36 of the 50 solution vectors are the current optimal deep structure.

Figure 9: Structures of the HFS
For the Friedman dataset, the optimal deep structure finally obtained is shown in Fig. 9b. Compared with the laser dataset, the deep structure transformation process of the Friedman dataset is more complex due to the larger number of possible topological structures. In the iterative process, four optimal deep structures with encoding 2222, 2230, 3220, and 3300 appeared, and it achieves stable convergence in the 3220 encoding deep structure in the end. Moreover, 30 of the 50 solution vectors are the current optimal deep structure.
The optimal deep structures finally obtained in Figs. 7 and 8 are neither the optimal deep structures at the beginning of iteration nor the deep structures with the largest number, but is obtained through continuous evolutionary learning of the improved DE algorithm. Figs. 7 and 10 compare the deep structure iteration process of No. 1 and No. 2 of the Friedman dataset simulation results in Table 7. The results show that the initial optimal deep structure of the two groups is 2230. Although there are differences in the iterative process of the deep structures, due to the characteristics of the data set, they eventually converge and stabilize in the same deep structure. The simulation results verify that the algorithm proposed in this paper has good reasonable competition among deep structure populations and can maintain species diversity during the evolution of deep structures.
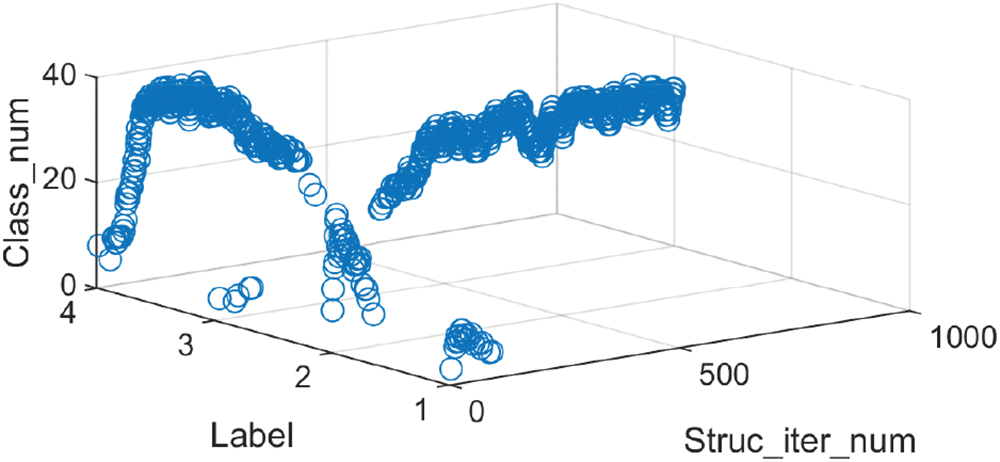
Figure 10: Iterative process of deep structure of Friedman dataset (No. 2) (label_1: 2222, label_2: 2230, label_3: 3220, label_4: 3300)
For further evaluation of the proposed algorithm, Table 8 shows the simulation results of Laser dataset and Friedman dataset in DCFS [11] and DNFS [9]. Each sub fuzzy system in DCFS is constructed by WM method. In DCFS, the fuzzy set is generated by meshing each variable, so the number of rules for each sub fuzzy system is large, which makes the total number of the rules of HFS not significantly reduced. And each sub fuzzy system in DNFS is constructed by ANFIS method. In DNFS, the rule base of each sub fuzzy system is trial-calculated through grid division, subtraction clustering and fuzzy c-means clustering, and then the rule base with better performance is selected as the final rule base, which may have fewer rules than DCFS. Compared with DCFS and DNFS, the algorithm proposed in this paper has fewer rules and greatly simplifies the complexity of HFS.
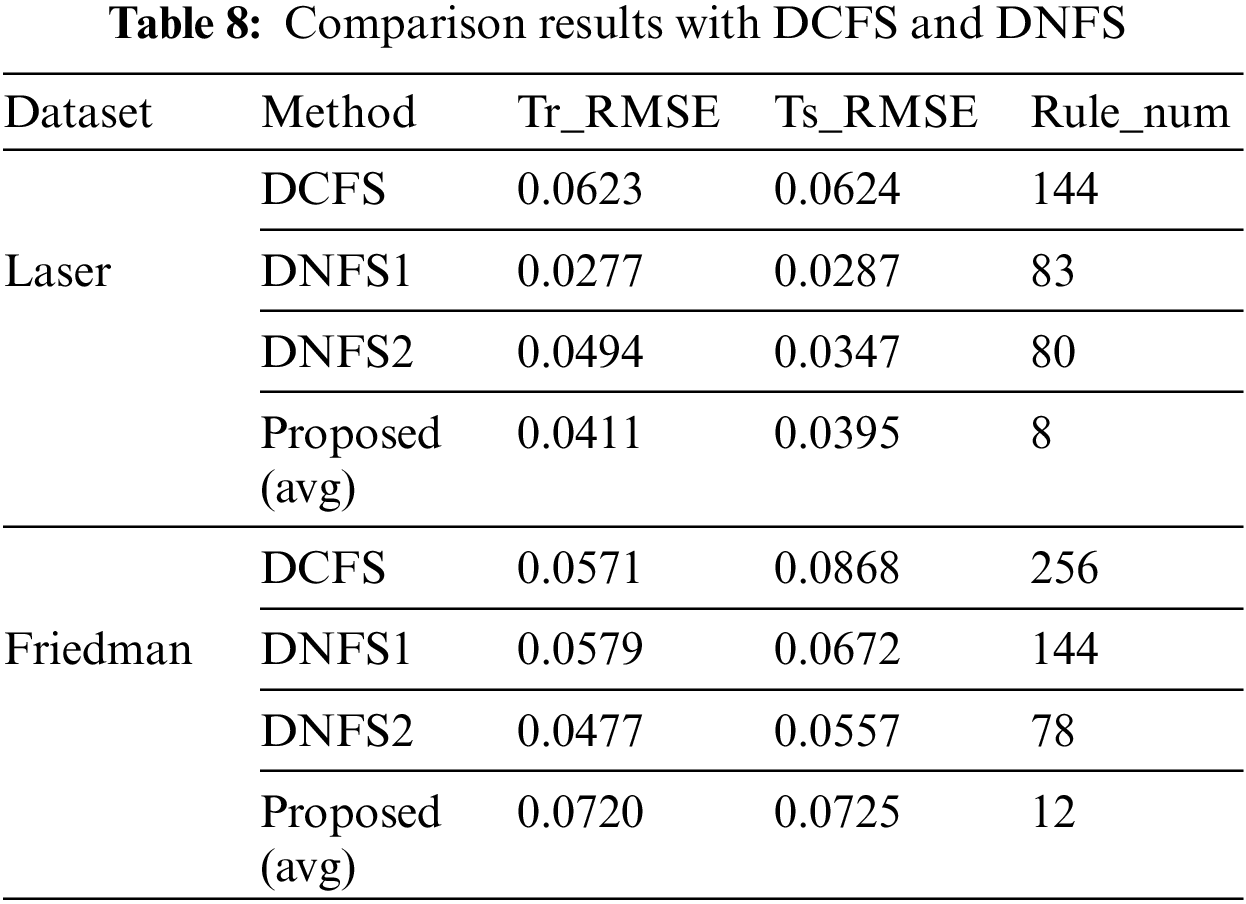
Because the hierarchical deep structures of DCFS and DNFS are both fixed, there are great differences in accuracy results for different data sets. The results with DCFS is not very good in the two datasets. Although increasing the number of rules can improve the accuracy to a certain extent, it is also related to the construction method of the rule base and the characteristics of the dataset itself. In addition, overfitting appeared in Friedman data set, resulting in a large difference between the test set and the training set. As for DNFS, the accuracy is slightly better than the algorithm proposed in this paper, but there are a large number of rules in HFS and the implementation effect is not stable for different data sets. In the Laser dataset, DNFS1 performed better than DNFS2, while in the Friedman dataset, DNFS2 performed better than DNFS21. It also shows that different topologies have a great impact on the accuracy of HFS, and manual selection is difficult.
The algorithm proposed in this paper can make the system automatically optimization and select the hierarchical deep structure, and get the optimal deep structure and its matching rule base based on the characteristics of the data set. This greatly reduces the number of rules while achieving precision similar to that of fixed deep structure. As increase the number of rules or enrich the architecture of the improved DE algorithm, the accuracy can be further improved. In terms of the number of rules, the algorithm proposed in this paper strikes a balance between interpretability and accuracy to a certain extent. In the iterative process, the algorithm maintains reasonable competition among different deep structures and ensures the diversity of deep structure types. Finally, realize the automatic deep structure optimization of HFS.
In this paper, an improved DE algorithm based on the new encoding method is proposed to optimize the deep structure of HFS. The new encoding method combines architecture encoding and rule encoding, so that the application of HFS is no longer limited to a fixed hierarchical deep structure, but automatically finds and selects the appropriate hierarchical deep structure according to the characteristics of the data set itself. At the same time, the use of evolutionary algorithm to learn the deep structures and rule base can further reduce the number of rules in HFS compared with traditional manual design. Finally, the proposed method is verified on the prediction data set, and the simulation results illustrate the effectiveness of the proposed method. The establishment of the deep structure of HFS can also show the relationship between the variables of the dataset from the side to a certain extent. In the future, we will optimize the coding mode of the hierarchical fuzzy system to make the combination of input features and sub-fuzzy systems more diversified, and reduce the complexity of the fuzzy system while ensuring the accuracy of the model.
Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.
Funding Statement: This study was funded by the Sichuan Science and Technology Program (2021ZYD0016).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Tao Zhao; data collection: Yue Zhu; analysis and interpretation of results: Yue Zhu; draft manuscript preparation: Yue Zhu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data used in this article are freely available in the mentioned references.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zadeh, L. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. https://doi.org/10.1016/S0019-9958(65)90241-X [Google Scholar] [CrossRef]
2. Zhao, T., Tong, W., Mao, Y. (2023). Hybrid non-singleton fuzzy strong tracking kalman filtering for high precision photoelectric tracking system. IEEE Transactions on Industrial Informatics, 19(3), 2395–2408. [Google Scholar]
3. Min, X., Li, Y., Tong, S. (2020). Adaptive fuzzy output feedback inverse optimal control for vehicle active suspension systems. Neurocomputing, 403, 257–267. https://doi.org/10.1016/j.neucom.2020.04.096 [Google Scholar] [CrossRef]
4. Velliangiri, S., Pandey, H. M. (2020). Fuzzy-taylor-elephant herd optimization inspired deep belief network for ddos attack detection and comparison with state-of-the-arts algorithms. Future Generation Computer Systems, 110, 80–90. https://doi.org/10.1016/j.future.2020.03.049 [Google Scholar] [CrossRef]
5. Zhao, T., Liu, J., Dian, S., Guo, R., Li, S. (2020). Sliding-mode-control-theory-based adaptive general type-2 fuzzy neural network control for power-line inspection robots. Neurocomputing, 401, 281–294. https://doi.org/10.1016/j.neucom.2020.03.050 [Google Scholar] [CrossRef]
6. Raju, G., Zhou, J., Kisner, R. A. (1991). Hierarchical fuzzy control. International Journal of Control, 54(5), 1201–1216. https://doi.org/10.1080/00207179108934205 [Google Scholar] [CrossRef]
7. Magdalena, L. (2019). Semantic interpretability in hierarchical fuzzy systems: Creating semantically decouplable hierarchies. Information Sciences, 496, 109–123. https://doi.org/10.1016/j.ins.2019.05.016 [Google Scholar] [CrossRef]
8. Jang, J. S. (1993). ANFIS: Adaptive-network-based fuzzy inference system. IEEE Transactions on Systems, Man, and Cybernetics, 23(3), 665–685. https://doi.org/10.1109/21.256541 [Google Scholar] [CrossRef]
9. Zhao, W., Chen, D., Zhuo, Y., Huang, Y. (2020). Deep neural fuzzy system algorithm and its regression application. Acta Automatica Sinica, 46(11), 2350–2358. [Google Scholar]
10. Talpur, N., Abdulkadir, S. J., Akhir, E. A. P., Hasan, M. H., Alhussian, H. et al. (2023). A novel bitwise arithmetic optimization algorithm for the rule base optimization of deep neuro-fuzzy system. Journal of King Saud University-Computer and Information Sciences, 35(2), 821–842. https://doi.org/10.1016/j.jksuci.2023.01.020 [Google Scholar] [CrossRef]
11. Wang, L. X. (2019). Fast training algorithms for deep convolutional fuzzy systems with application to stock index prediction. IEEE Transactions on Fuzzy Systems, 28(7), 1301–1314. https://doi.org/10.1109/TFUZZ.2019.2930488 [Google Scholar] [CrossRef]
12. Razak, T. R., Garibaldi, J. M., Wagner, C., Pourabdollah, A., Soria, D. (2020). Toward a framework for capturing interpretability of hierarchical fuzzy systems–A participatory design approach. IEEE Transactions on Fuzzy Systems, 29(5), 1160–1172. https://doi.org/10.1109/TFUZZ.2020.2969901 [Google Scholar] [CrossRef]
13. Zhang, X., Onieva, E., Perallos, A., Osaba, E. (2020). Genetic optimised serial hierarchical fuzzy classifier for breast cancer diagnosis. International Journal of Bio-Inspired Computation, 15(3), 194–205. https://doi.org/10.1504/IJBIC.2020.107490 [Google Scholar] [PubMed] [CrossRef]
14. Kerr-Wilson, J., Pedrycz, W. (2020). Generating a hierarchical fuzzy rule-based model. Fuzzy Sets and Systems, 381, 124–139. https://doi.org/10.1016/j.fss.2019.07.013 [Google Scholar] [CrossRef]
15. Zhao, T., Cao, H., Dian, S. (2022). A self-organized method for a hierarchical fuzzy logic system based on a fuzzy autoencoder. IEEE Transactions on Fuzzy Systems, 30(12), 5104–5115. https://doi.org/10.1109/TFUZZ.2022.3165690 [Google Scholar] [CrossRef]
16. Chang, C. W., Tao, C. W. (2019). A simplified implementation of hierarchical fuzzy systems. Soft Computing, 23, 4471–4481. https://doi.org/10.1007/s00500-018-3111-3 [Google Scholar] [CrossRef]
17. Fan, Z., Chiong, R., Hu, Z., Lin, Y. (2020). A multi-layer fuzzy model based on fuzzy-rule clustering for prediction tasks. Neurocomputing, 410, 114–124. https://doi.org/10.1016/j.neucom.2020.04.031 [Google Scholar] [CrossRef]
18. Zhao, T., Xiang, Y., Dian, S., Guo, R., Li, S. (2020). Hierarchical interval type-2 fuzzy path planning based on genetic optimization. Journal of Intelligent & Fuzzy Systems, 39(1), 937–948. https://doi.org/10.3233/JIFS-191864 [Google Scholar] [CrossRef]
19. Wang, F. S., Wang, T. Y., Wu, W. H. (2022). Fuzzy multiobjective hierarchical optimization with application to identify antienzymes of colon cancer cells. Journal of the Taiwan Institute of Chemical Engineers, 132, 104121. https://doi.org/10.1016/j.jtice.2021.10.021 [Google Scholar] [CrossRef]
20. Zhang, L., Shi, Y., Chang, Y. C., Lin, C. T. (2020). Hierarchical fuzzy neural networks with privacy preservation for heterogeneous big data. IEEE Transactions on Fuzzy Systems, 29(1), 46–58. https://doi.org/10.1109/TFUZZ.2020.3021713 [Google Scholar] [CrossRef]
21. Zhou, T., Zhou, Y., Gao, S. (2021). Quantitative-integration-based TSK fuzzy classification through improving the consistency of multi-hierarchical structure. Applied Soft Computing, 106, 107350. https://doi.org/10.1016/j.asoc.2021.107350 [Google Scholar] [CrossRef]
22. Zouari, M., Baklouti, N., Kammoun, M. H., Ayed, M. B., Alimi, A. M. et al. (2021). A multi-agent system for road traffic decision making based on hierarchical interval type-2 fuzzy knowledge representation system. 2021 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), pp. 1–6. Luxembourg, IEEE. [Google Scholar]
23. Kamthan, S., Singh, H. (2023). Hierarchical fuzzy deep learning system for various classes of images. Memories-Materials, Devices, Circuits and Systems, 4, 100023. https://doi.org/10.1016/j.memori.2022.100023 [Google Scholar] [CrossRef]
24. Bernal, E., Lagunes, M. L., Castillo, O., Soria, J., Valdez, F. (2021). Optimization of type-2 fuzzy logic controller design using the GSO and FA algorithms. International Journal of Fuzzy Systems, 23(1), 42–57. https://doi.org/10.1007/s40815-020-00976-w [Google Scholar] [CrossRef]
25. Kacimi, M. A., Guenounou, O., Brikh, L., Yahiaoui, F., Hadid, N. (2020). New mixed-coding PSO algorithm for a self-adaptive and automatic learning of mamdani fuzzy rules. Engineering Applications of Artificial Intelligence, 89, 103417. https://doi.org/10.1016/j.engappai.2019.103417 [Google Scholar] [CrossRef]
26. Mohsenpourian, M., Asharioun, H., Mosharafian, N. (2021). Training fuzzy inference system-based classifiers with krill herd optimization. Knowledge-Based Systems, 214, 106625. https://doi.org/10.1016/j.knosys.2020.106625 [Google Scholar] [CrossRef]
27. Zhao, T., Chen, C., Cao, H., Dian, S., Xie, X. (2023). Multiobjective optimization design of interpretable evolutionary fuzzy systems with type self-organizing learning of fuzzy sets. IEEE Transactions on Fuzzy Systems, 31(5), 1638–1652. [Google Scholar]
28. Chauhan, N. K., Tyagi, I., Kumar, H., Sharma, D. (2022). Tasks scheduling through hybrid genetic algorithm in real-time system on heterogeneous environment. SN Computer Science, 3(1), 75. https://doi.org/10.1007/s42979-021-00959-0 [Google Scholar] [CrossRef]
29. Zhao, B., Chen, H., Gao, D., Xu, L. (2020). Risk assessment of refinery unit maintenance based on fuzzy second generation curvelet neural network. Alexandria Engineering Journal, 59(3), 1823–1831. https://doi.org/10.1016/j.aej.2020.04.052 [Google Scholar] [CrossRef]
30. Alonso, J. M., Castiello, C., Mencar, C. (2015). Interpretability of fuzzy systems: Current research trends and prospects. In: Springer handbook of computational intelligence, pp. 219–237. Berlin, Heidelberg: Springer. [Google Scholar]
31. Takagi, T., Sugeno, M. (1985). Fuzzy identification of systems and its applications to modeling and control. IEEE Transactions on Systems, Man, and Cybernetics, SMC-15(1), 116–132. https://doi.org/10.1109/TSMC.1985.6313399 [Google Scholar] [CrossRef]
32. Mamdani, E. H., Assilian, S. (1975). An experiment in linguistic synthesis with a fuzzy logic controller. International Journal of Man-Machine Studies, 7(1), 1–13. https://doi.org/10.1016/S0020-7373(75)80002-2 [Google Scholar] [CrossRef]
33. Wang, L. X. (1998). Universal approximation by hierarchical fuzzy systems. Fuzzy Sets and Systems, 93(2), 223–230. https://doi.org/10.1016/S0165-0114(96)00197-2 [Google Scholar] [CrossRef]
34. Juang, C. F., Chen, Y. H., Jhan, Y. H. (2014). Wall-following control of a hexapod robot using a data-driven fuzzy controller learned through differential evolution. IEEE Transactions on Industrial electronics, 62(1), 611–619. https://doi.org/10.1109/TIE.2014.2319213 [Google Scholar] [CrossRef]
35. Juang, C. F., Lin, C. H., Bui, T. B. (2018). Multiobjective rule-based cooperative continuous ant colony optimized fuzzy systems with a robot control application. IEEE Transactions on Cybernetics, 50(2), 650–663. https://doi.org/10.1109/TCYB.2018.2870981 [Google Scholar] [PubMed] [CrossRef]
36. Hsu, C. H., Juang, C. F. (2012). Evolutionary robot wall-following control using type-2 fuzzy controller with species-de-activated continuous ACO. IEEE Transactions on Fuzzy Systems, 21(1), 100–112. https://doi.org/10.1109/TFUZZ.2012.2202665 [Google Scholar] [CrossRef]
37. Das, S., Suganthan, P. N. (2010). Differential evolution: A survey of the state-of-the-art. IEEE Transactions on Evolutionary Computation, 15(1), 4–31. https://doi.org/10.1109/TEVC.2010.2059031 [Google Scholar] [CrossRef]
38. Pant, M., Zaheer, H., Garcia-Hernandez, L., Abraham, A. (2020). Differential evolution: A review of more than two decades of research. Engineering Applications of Artificial Intelligence, 90(1), 103479. https://doi.org/10.1016/j.engappai.2020.103479 [Google Scholar] [CrossRef]
39. Alcalá-Fdez, J., Fernández, A., Luengo, J., Derrac, J., García, S. et al. (2011). Keel data-mining software tool: Data set repository, integration of algorithms and experimental analysis framework. Journal of Multiple-Valued Logic & Soft Computing, 17(2–3), 255–287. [Google Scholar]
40. Zhou, Z. H. (2021). Machine learning, pp. 25–26. Berlin, Heidelberg: Springer Nature. [Google Scholar]
41. Liu, H., Cocea, M. (2017). Semi-random partitioning of data into training and test sets in granular computing context. Granular Computing, 2, 357–386. https://doi.org/10.1007/s41066-017-0049-2 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF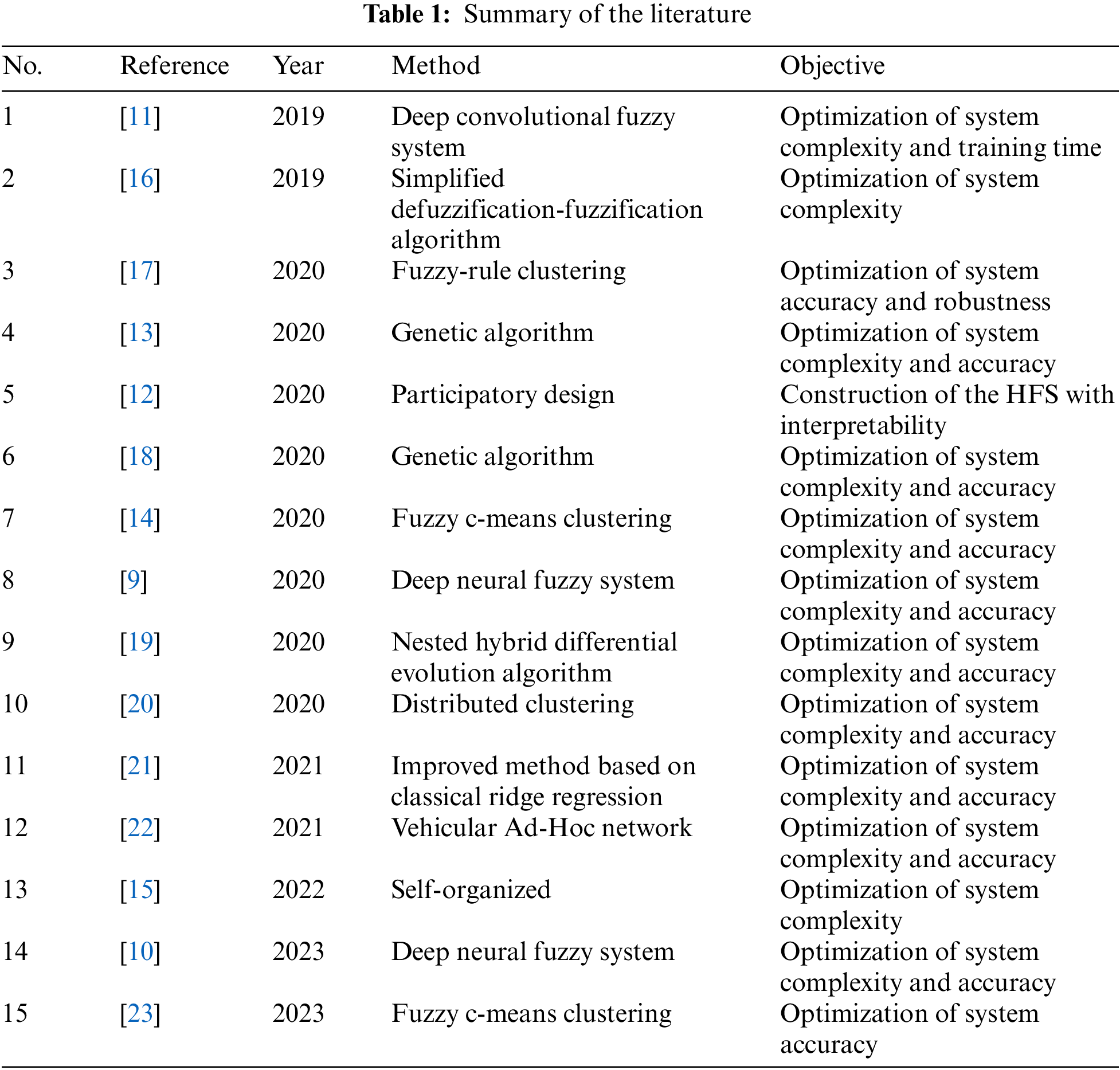
 Downloads
Downloads
 Citation Tools
Citation Tools
