Energy Efficiency Maximization in Mobile Edge Computing Networks via IRS assisted UAV Communications

1  Introduction

Recently, unmanned aerial vehicle (UAV) technology has aroused widespread concern in industry and academia [1–3]. The unique advantages of the UAV are its flexibility and mobility [4,5]. The glider UAV can move to different positions at different time slots, while the rotor UAV can hover at the same position, which could significantly improve channel gain and thus improve the transmission rate [6–8].

In [9], the authors have done some basic research on the flexibility of UAVs, which can effectively improve the communication rate when a UAV is used as a base station. The author focuses on the flexible deployment of UAVs, and can adjust the position of UAVs under different channel conditions to improve channel gain; In [10], the author considered the mobility of UAVs. When the UAV hovers, its energy consumption is a huge expense, and the glider UAV cannot hover. The author designs the trajectory of the UAV, making full use of the mobility of the UAV.

Intelligent reflector technology is also an emerging technology, which is used to improve the channel environment and is applied to scenes with poor channel conditions [11,12]. In [13], the authors combined the IRS technology with the UAV technology and uses the UAV to carry the IRS to further improve the flexibility of the IRS, thus further improving the communication rate.

With the continuous development of communication technology, the demand for communication rate is increasing [14,15]. Due to the limitation of Shannon’s information theory, the upper limit of the communication rate is closely related to the communication bandwidth and the background noise in the communication [16,7]. Under the existing technical framework, the use of mobile edge computing technology is undoubtedly an important means to improve the communication user experience in a new way [17,18].

Mobile edge computing technology transmits the user’s computing tasks to the ECS for computing [19,20], and then transmits the computing results back. Although the transmission of computing tasks will increase the communication frequency, the advantage of this is that the computing efficiency of cloud servers is usually higher than that of local computing [21–23]. The data volume of the calculation result is much smaller than that of the local calculation. The research on mobile edge computing has made some progress [24–26]. For example, in [26], two modes of partial unloading and full unloading were considered, and it is proposed that the total delay of computing can be greatly reduced under the partial unloading mode.

The research on the combination of mobile edge computing and IRS technology has also made great progress [27,28]. As a means of channel reconstruction, IRS can effectively reduce the transmission delay of data, thus reducing the overall delay of mobile edge computing.

In this paper, we consider using UAVs to carry IRS to assist mobile edge computing tasks. The main contributions of this paper are summarized as follows:

(1) We consider a new paradigm that uses IRS to assist users in mobile edge computing tasks. Meanwhile, the UAV is applied as a cloud server to improve the efficiency of computing and transmission.

(2) We propose an original optimization problem. We jointly design the unloading ratio, the phase shift matrix of the IRS, the flight path of the UAV, and the user’s unloading strategy to minimize the computing delay.

(3) After relaxing the original optimization problem, we put forward three subproblems, put forward the results of closed expressions for two subproblems, and transform the other subproblem into a convex problem to solve.

(4) The simulation results show that the proposed scheme is better than the existing scheme in terms of energy efficiency.

The rest of the paper is organized as follows: In Section 2, we introduce the system model and formulate the original problem; In Section 3, we propose the solution to the original problem, which could be divided into several sub-problem solutions and the AO based algorithm is proposed; In Section 4, we take a discussion of this paper; In Section 5, we take the simulation results and Section 6concludes this paper.

2  System Model and Problem Formulation

As shown in Fig. 1, the system consists of a UAV, and IRS and several users. All transmission nodes are equipped with multi-antennas.

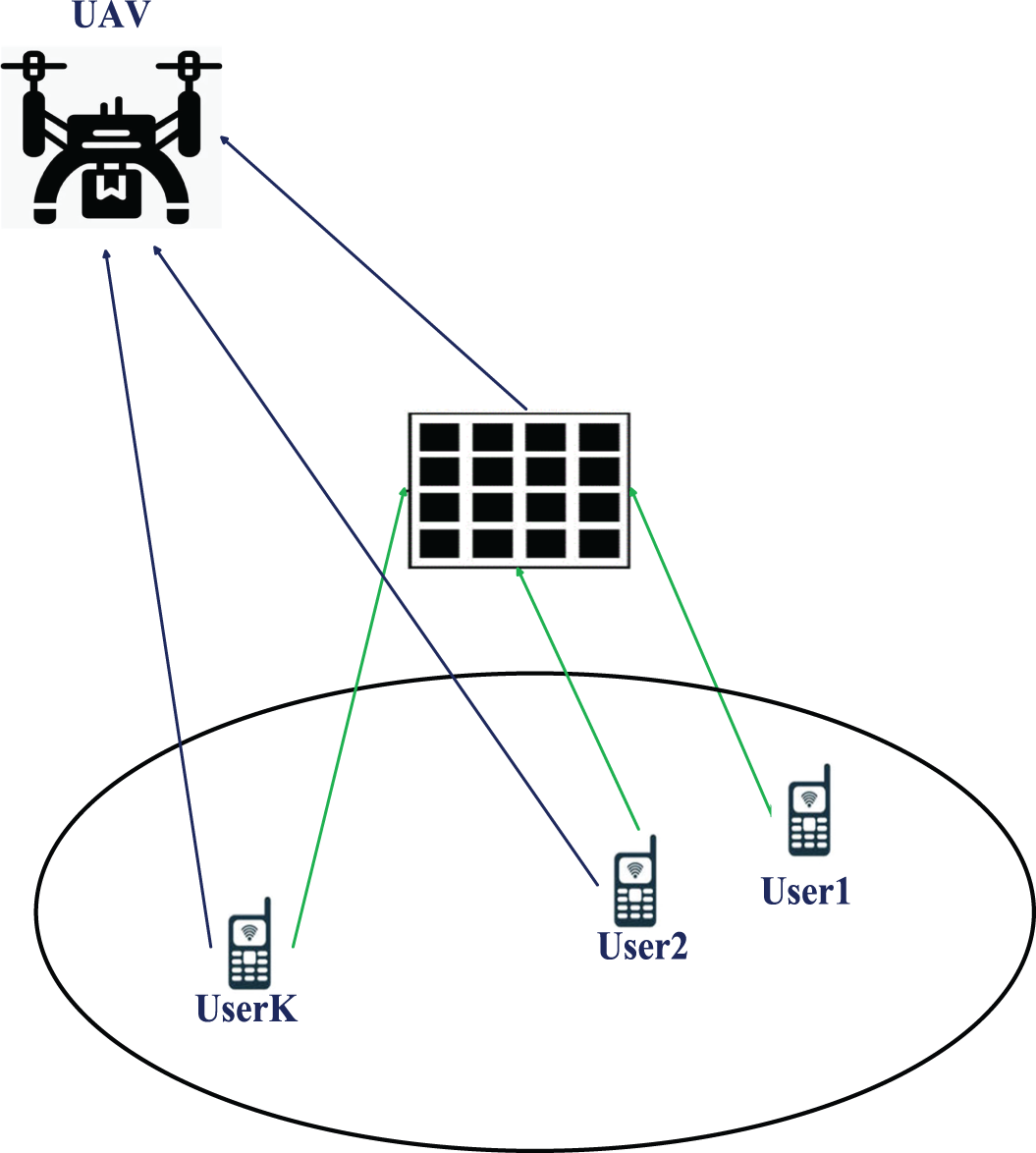
Figure 1: System model

If we consider a UAV as a mobile cloud server, its movement is limited by its hardware performance. We first obtain the flight speed of the UAV as

v[n]=Q[n]−Q[n−1]ΔT,(1)

Following the general assumption, we set the channel between the UAV and the ground user as the LOS link, that is, the channel gain is only related to the distance between the UAV and the ground user. Specifically, the air-ground channel is modeled as

hk[n]=g0‖Q[n]−qk‖22+H2,(2)

where g0 represents the empirical gain of the line-of-sight link at the specified distance (set to 1 m for simplicity). Let qk represent the physical position of user k, and H represents the fixed flight altitude of the UAV [29].

We consider that all users are transmitting in the same frequency band. At this time, the data between different users is not interconnected, and some interference will occur, which is expressed as

Rk[n]=BΔTlog⁡(1+pkhk[n]∑j≠kpjhj[n]+σ2),(3)

where pj represents the transmission power of the user j, and j represents the background Gaussian white noise.

Consider the scenario of partial unloading. We define all tasks of the user k as Dk, and the local computing part is m, so the available offload part is 1−m. As in [30], the user’s uninstall task constraint is

∑nRk[n]≥(1−mk)Dk.(4)

In addition, considering the delay between the transmission task and the calculation task, we define the task amount to be calculated by each timeslot server as W[n], and then we need to define the following constraints:

∑n=1n0Rk[n]≥∑n=1n0Wk[n].(5)

When the UAV flight ends, all tasks are processed, namely

∑n=1NRk[n]=∑n=1NWk[n].(6)

Since all computing tasks are divided into two parts, the above constraints only restrict the transmission and computing tasks. For local computing tasks, the following constraints need to be met:

fmaxT≥Wk.(7)

In addition, both UAVs and users are subject to power limitations. The user’s power consumption is divided into two parts. One part is the energy consumption generated in the communication process when the user sends a task. It can be expressed as

Ek,1[n]=Pk,1[n]T,(8)

where Pk,1 is the communication energy consumption of the user k in unit time. It is worth noting that the communication energy consumption of users is mainly determined by channel gain. When the distance between the UAV and the user is longer, the user needs to consume more energy and vice versa. Therefore, air-ground channel gain can not only improve the communication rate but also reduce the energy consumption of users.

In addition, because some tasks are calculated locally by users, the calculation of tasks will consume additional energy at this time, expressed as

Ek,2=Pk,2mk.(9)

Unlike the communication energy consumption of users, the calculation energy consumption of users is independent of the channel state information but only depends on the local calculation task. In order to simplify the process, we assume that the energy consumption is linear with the local computing task share, which has been described in detail in [4].

Further, we consider the energy consumption of UAVs. Similar to the energy consumption of users, the energy consumption of UAVs consists of the following two parts: (1) the flight energy consumption of UAVs; (2) the calculated energy consumption of UAVs. The flight energy consumption of UAV is expressed by the following formula:

Eu,1[n]=α1‖v[n]‖2+α2‖v[n]‖2(1+‖a[n]‖2g2).(10)

Symbol α1,α2,g are all fixed parameters, determined by the UAV structure, and represent the acceleration of the UAV, expressed by the following expression:

a[n]=v[n]−v[n−1]T.(11)

The calculated energy consumption of the UAV is as follows:

Eu,1=2[n]=Pu,2mk.(12)

Based on the above energy consumption expression, we can get the energy constraints for users and UAVs as follows:

∑nEk,1[n]+Ek,2≤Ek,sum,(13)

∑nEu,1[n]+Eu,2≤Eu,sum.(14)

In this paper, our goal is to maximize the system’s computing power by assigning tasks to mobile edge computing, UAV flight path, and IRS dependency matrix. At this time, the problem is established as follows:

maxm,Q,W,G∑n∑kRk[n]s.t. 0≤m≤1,∑nEk,1[n]+Ek,2≤Ek,sum,∑nEu,1[n]+Eu,2≤Eu,sum∑n=1n0Rk[n]≥∑n=1n0Wk[n],∑n=1NRk[n]=∑n=1NWk[n],∑nRk[n]≥(1−mk)Dk,v[n]≤vmax,a[n]≤amax,(15)

where vmax and amax respectively represent the maximum instantaneous speed and maximum instantaneous acceleration allowed by UAVs. Since the variables of the problem are highly non-convex, we use the method of iteratively finding the local optimal solution to solve the original problem in the subsequent solving process.

3  Proposed Solution

In this section, due to the highly non-convex nature of the original problem, we first introduce auxiliary variables according to the definition of R as follows:

Rk[n]≥BTNlog⁡(1+κk,n),(16)

we convert rate maximization to rate lower bound maximization, and introduce the following equation:

κk,n=Psk,nqk,n,(17)

qk,n=1gk,n.(18)

Note that non-convex variables in the target are converted into a linear format. Then, we deal with the non-convex form in the condition, mainly including the energy consumption form of UAV. We introduce new variables as follows [31]:

α1‖v[n]‖2+α2‖v[n]‖2(1+‖a[n]‖2g2)≤α1‖v[n]‖2+α2A[n].(19)

Further, we relax the upper bound of energy consumption into linear representation, and then the original problem is expressed as

maxm,Q,W,G∑n∑kBTNlog⁡(1+κk,n)s.t. 0≤m≤1,∑nEk,1[n]+Ek,2≤Ek,sum,∑nEu,1[n]+Eu,2≤Eu,sum,A[n]≥(1+‖a[n]‖2g2),∑n=1n0Rk[n]≥∑n=1n0Wk[n],∑n=1NRk[n]=∑n=1NWk[n],∑nRk[n]≥(1−mk)Dk,v[n]≤vmax,a[n]≤amax.(20)

It is worth noting that the problem is still non-convex at this time. For this kind of problem, we use the first-order Taylor expansion method to solve it.

3.1 First-Order Taylor Based Method

In this subsection, we propose the local optimal solution for the beamforming vector and the phase shift matrix of IRS.

We first introduce the following variables:

f=−∑nlog⁡(∑kTr(gkgkHWr)+σn,k2),g=−∑nlog⁡(∑K∖kTr(gkgkHWr)+σn,k2).(21)

Further, we define the first order partial derivative as

R(Wk)≥R(Wk(j))+∑kTr(∂R(Wk(j))∂Wk)H(Wk(j)−Wk),(22)

where

Tr(∂R(Wk(j))∂Wk)=−1ln⁡2∑K∖kgkgkHTr(gkgkHW)+σn,k.(23)

The local optimal solution of the beamforming vector is thus obtained via CVX toolbox [32].

We then focus on the optimization of the phase shift matrix of IRS. We deal with the form of the sum of two non-convex terms in the target. It is worth noting that due to the high coupling of variables, direct derivation is very difficult. We therefore introduce the following inequality:

P(1+‖w‖2Up2)+m0A‖w‖3+αv2[n]≤Ev[n],(24)

which comes from the following triangular inequality:

(a2+b2)12≤(a+b).(25)

According to (24) and (25), we take the alternative definitions as

1Lk[n]+(Lk[n]−Lk[n−1])(−1Lk2[n])≥(fk)2Uk.(26)

Then we transform the numerator and denominator of the problem into convex form. Therefore, the problem can be transformed into a quasi-convex problem in general.

maxQ,y,P,f∑kLkα∑nE[n]+∑kEk+χk,s.t.yk≥‖q[n]−wk‖2+H2,pk≥‖q[n]‖2+‖wk‖2,∑n=1n0Rk[n]≥∑n=1n0Wk[n],∑n=1NRk[n]=∑n=1NWk[n],∑nRk[n]≥(1−mk)Dk.(27)

Here, the user beam transmission can be completed by solving multiple second-order convex cone constraints. However, due to the flexibility of UAV, with the passage of time, UAV needs to maintain communication with users to exchange information. Therefore, we consider using the distributed solution as follows.

We use the ADMM method in the following format to solve the above problems:

G=[A1,1⋯AN,1B1,1⋯BN,1⋮⋱⋮⋮⋱⋮A1,N⋯AN,NB1,N⋯BN,N]T,(28)

where A represents the position of the UAV in each time slot, and B represents the beam vector of the user in different time slots. The user’s beam will change according to the different position of the UAV. Then the UAV calculates the energy consumption required for its flight and whether it meets the constraints of speed and acceleration according to the information in A. If the above constraints are met, the user beam in B will be further updated. Finally, the updates of A and B will be stable and meet the constraints of the UAV’s speed and computing ability.

The optimal G should meet the following conditions:

[IN00Λ]G=[IN,V],(29)

where IN refers to a identity matrix with dimension N, and V is an orthogonal matrix.

However, we gradually optimize the composition of G by iteration, and the two sides of the equation are not fixed matrices, so we can not directly obtain the optimal solution by solving the inverse of the matrix. We try to reduce the interval of the equation as follows:

Δ=−∑n∑kRn,k+α(∑n∑kEk[n]+∑nEup[n])+Tr(UT(PTG−H))+12‖PTG−H‖2+β2(en,k+σn,k2)2(30)

By substituting the expression of Δ into (27), the problem (27) is then transformed as

maxQ,y,P,f−∑n∑kRn,k+α(∑n∑kEk[n]+∑nEup[n])+Tr(UT(PTG−H))+12‖PTG−H‖2+β2(en,k+σn,k2)2,s.t.yk≥‖q[n]−wk‖2+H2,pk≥‖q[n]‖2+‖wk‖2,∑n=1n0Rk[n]≥∑n=1n0Wk[n],∑n=1NRk[n]=∑n=1NWk[n],∑nRk[n]≥(1−mk)Dk.(31)

According to the constraints in (31), we can obtain the local optimal solution of the n+1 th iteration according to the results of the n th iteration, so as to realize the distributed solution of the problem. Specifically,

P1(n)=P1(n−1)+α1(PTG−H)(n)P2(n)=P2(n−1)+α2θ,(32)

where θ is the difference between the preset variable and the actual variable used in the calculation process, which is calculated by the following:

θ=ϕ(n)−ϕ¯(n).(33)

According to the iterative solution process, we propose an iterative algorithm. By confirming the maximum iteration number and the minimum iteration interval, the algorithm can achieve the balance of time complexity and algorithm performance.

3.2 Offloading Allocation

For the fixed UAV flight path and user-sending strategy, we optimize the resource unloading scheme. At this time, the problem is simplified as follows:

maxm,Q,W,G∑n∑kRk[n]s.t. 0≤m≤1,∑nEk,1[n]+Ek,2≤Ek,sum,∑nEu,1[n]+Eu,2≤Eu,sum.(34)

For the resource allocation problem, we first determine it as a convex problem according to its second derivative. Specifically, the first derivative of the target is

∂Rk[n]∂mk=−mk−2Blog⁡(1+PGσ2).(35)

Further, its second partial derivative is

∂2Rk[n]∂2mk=−2mk−3Blog⁡(1+PGσ2).(36)

The second order partial derivative of the objective is constantly positive, so the objective of the problem is convex. Further, the problem constraint is linear with respect to m, that is, the problem is convex.

In order to solve the problem, we simplified the energy constraint into a linear form as follows:

L(β1,β2,mk)=∑n∑k(1Blog⁡(1+PGσ2))+β1∑k(Ek,sum−Eu,sum)+β2(1−m),(37)

At this time, (37) establishes a convex problem. According to Slater condition, we can obtain a unique optimal solution as follows.

We first calculate the partial derivative of (37) as follows:

∂L(β1,β2,mk)∂mk=∑n(1Blog⁡(1+PGσ2))+β1∑k(Ek,sum−Eu,sum)−β2.(38)

Finally, the point where the partial derivative is 0 can be considered as the optimal solution of the KKT condition as follows:

mk∗=1+PBlog⁡(1+PGσ2).(39)

3.3 Trajectory Optimization

In this subsection, we focus on the trajectory optimization for the fixed beamforming vector in UEs, the phase shift matrix of IRS and the offloading allocation. The original problem is simplified as follows:

maxm,Q,W,G∑n∑kBTNlog⁡(1+κk,n)s.t. ∑nEk,1[n]+Ek,2≤Ek,sum,∑n=1n0Rk[n]≥∑n=1n0Wk[n],∑n=1NRk[n]=∑n=1NWk[n],∑nRk[n]≥(1−mk)Dk,v[n]≤vmax,a[n]≤amax.(40)

Note that (40) is non-convex due to the non-convex of the constraints. We introduce the following variables:

x={xk[n],∀k,n},p={p[n],∀n},(41)

where xk[n] and yk could be obtained via the following consumption:

xk[n]≥‖q[n]−wk‖2+H2,yk=1N∑n=1NmkBR~k[n],∀k.(42)

We thus obtain the transmission rate as

R~k[n]=log21p[n]xk[n]+σk.(43)

By introducing auxiliary variables, we transform the problem into a convex problem. Using SCA technology, we first established the following:

Q[n]=Blog⁡(∑j=1ipj[n]‖hj[n]‖2).(44)

Further, we consider the reachability rate with noise and interference, expressed as

Q[n]=Blog⁡(∑j=1i−1pj[n]‖hj[n]‖2+σ2).(45)

This means that in order to maximize the use efficiency of computing power at the achievable rate at the current time, it is necessary to transmit data not less than the sum of current computing power. This also indicates the physical distance required by the UAV at the current moment.

maxm,Q,W,G∑n∑kBTNlog⁡(1+κk,n)s.t. ∑nEk,1[n]+Ek,2≤Ek,sum,∑n=1n0Rk[n]≥∑n=1n0Wk[n],∑n=1NRk[n]=∑n=1NWk[n],∑nRk[n]≥(1−mk)Dk,v[n]≤vmax,a[n]≤amax.(46)

We can obtain the optimal solution of the problem (46) by means of first-order Taylor expansion.

3.4 Alternate Optimization Algorithm Design

According to the local optimal solution, closed expression and iterative solution obtained in the above section, we can carry out the local optimal design for the user’s transmitted beam, the user’s unloading ratio and the flight path of the UAV. We finally get the overall algorithm summarized as Algorithm 1. The convergence and superiority of the algorithm are verified in the simulation experiment.

Due to the high coupling between variables, the convergence of the algorithm is given by simulation experiments.

4  Complexity Analysis

We focus on the complexity of proposed schemes and two traditional schemes: MRT scheme and OA algorithm. The specific expression is shown in Table 1.

Note that MRT scheme gets the minimum complexity since it has a closed-form solution. The proposed sub-optimal get less complexity than the optimal scheme.

5  Numerical Results

In this section, we first list the parameters required for the simulation environment, then simulate the results under different settings, and analyze the advantages of the proposed algorithm.

5.1 Simulation Results

In this section, we conducted simulation experiments on the proposed scheme, mainly including (1) the proposed scheme; (2) the full offloading scheme; (3) the maximum rate scheme; (4) the scheme against potential eavesdroppers; (5) no IRS scheme; (6) fixed IRS scheme. The setting of transmission if shown in Table 2 and the specific results are as follows.

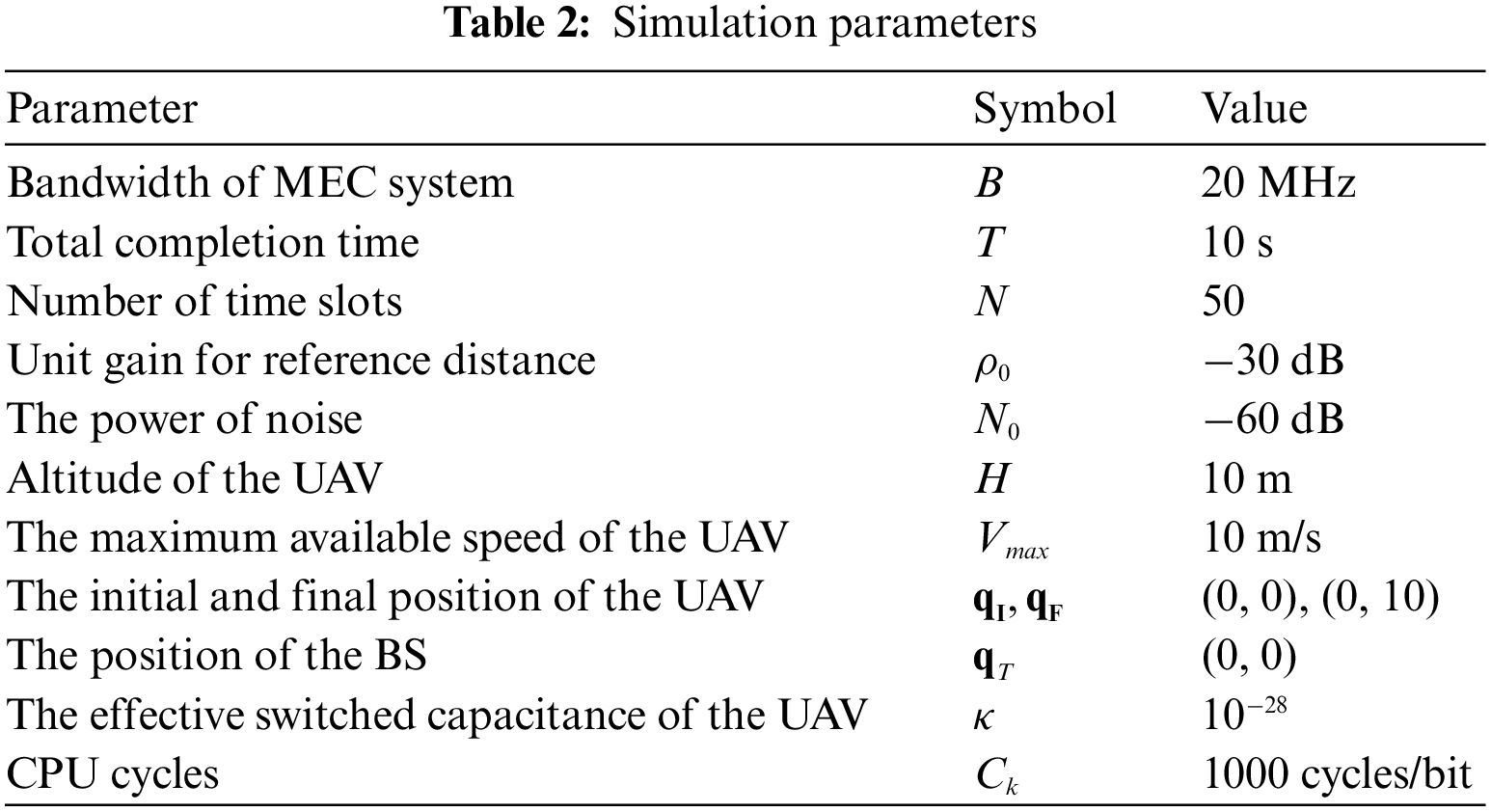
We first focus on the convergence of the algorithm. We have drawn three curves in Fig. 2, two of which represent the convergence curves of iteration from different initial points. In the two initial points, we assume that all the IRS phase-shift matrices are unit matrices, the flight path of the UAV is a straight flight from the initial point to the endpoint, and the unloading mode is full unloading. The difference is that the user-transmitted beam at the initial point 1 is the MRT scheme, and the user-transmitted beam at the initial point 2 is the unit vector. It can be seen that the MRT scheme will obtain higher initial energy efficiency than the unit vector, but with the increase in the number of iterations, both of them converge around 10 iterations. In addition, we also simulate the individual iteration scheme, and the results show that our proposed scheme has higher performance.

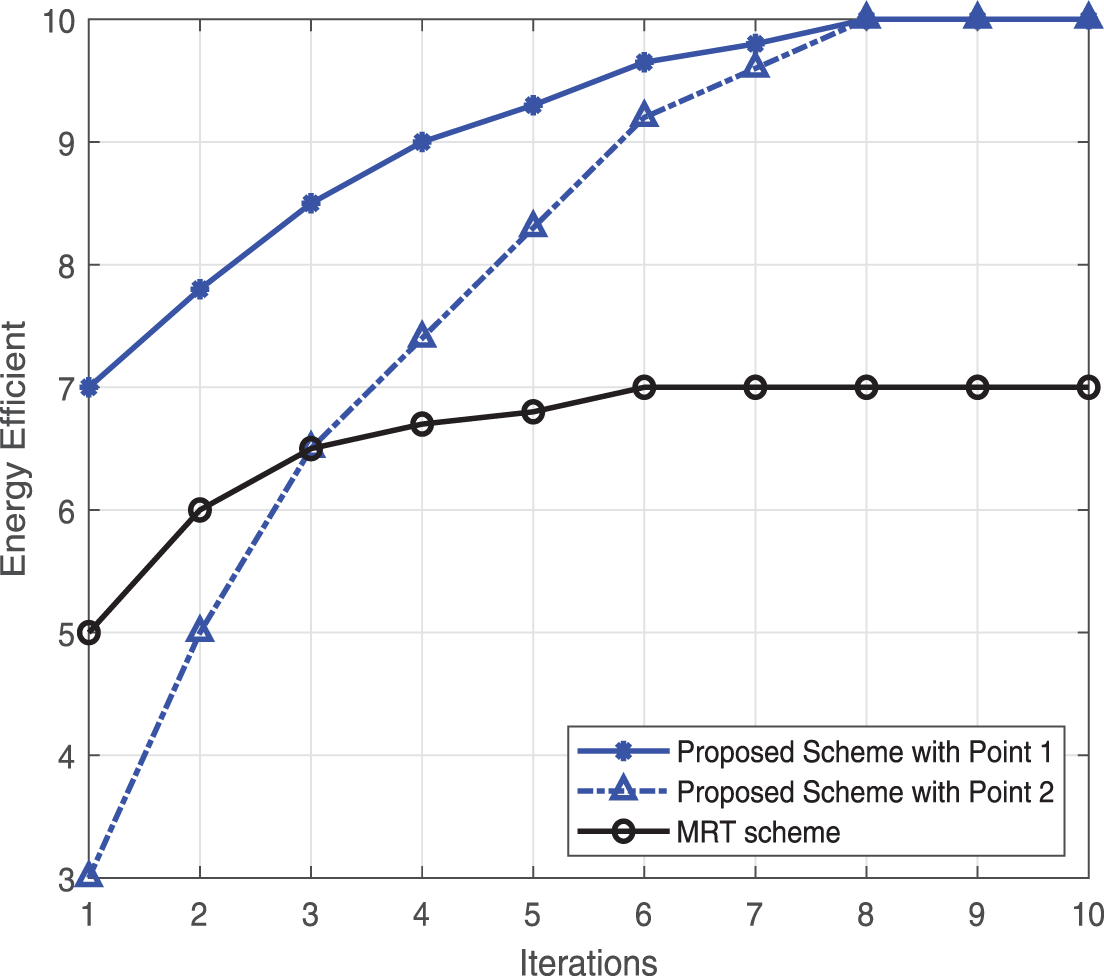
Figure 2: Convergence of the proposed algorithm

The trajectory in a UAV simulation case is shown in Fig. 3. We randomly set 4 users. It can be found that the trajectory of the UAV will be as close as possible to each user. However, in order to maximize fairness and overall energy efficiency, no one has the opportunity to focus on different users in different time slots.

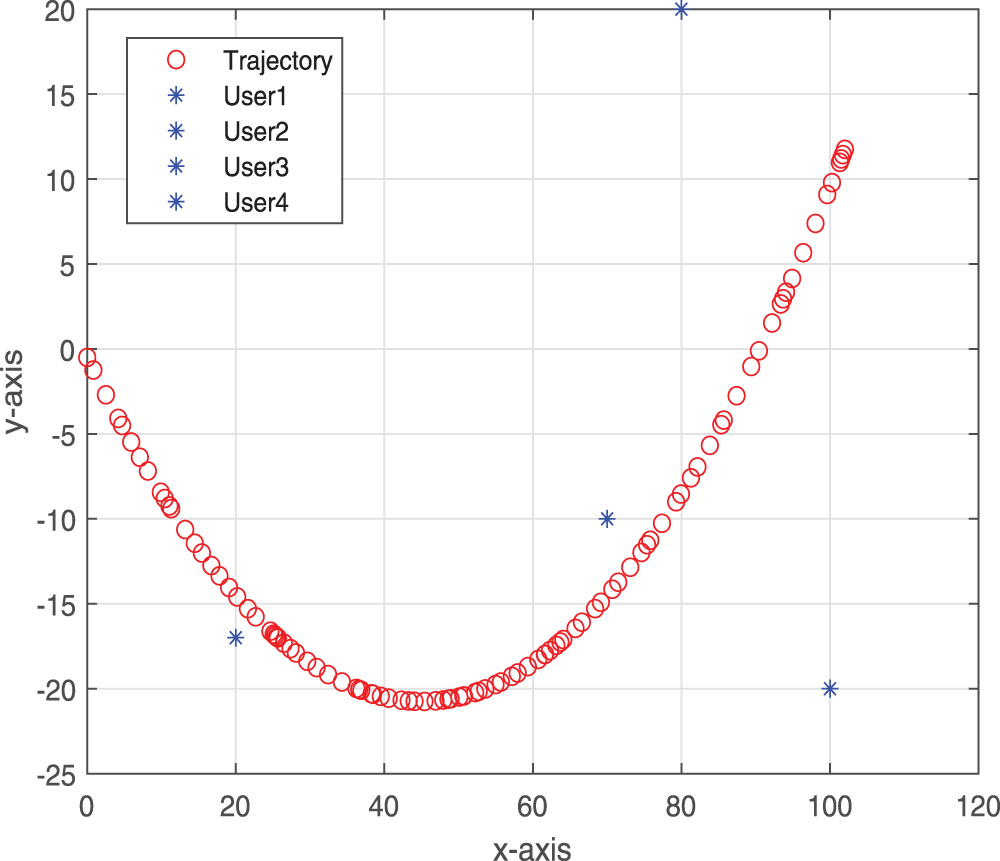
Figure 3: Trajectory of the UAV

We also conducted simulation experiments on the impact of IRS elements. In Fig. 4, we mainly considered the change of IRS in the [10:10:40] range. When the number of IRS is small, that is, when the number of IRS is 10, our proposed scheme still has considerable advantages over other schemes. As the number of IRS elements increases, the proposed scheme will also increase. It is worth noting that the role of the IRS is to reconstruct the channel. It cannot improve energy efficiency without limitation. When the number of IRS is large, the gain it can bring is limited. On the other hand, when IRS is not applicable in the scheme, the increase in the number of elements cannot bring benefits.

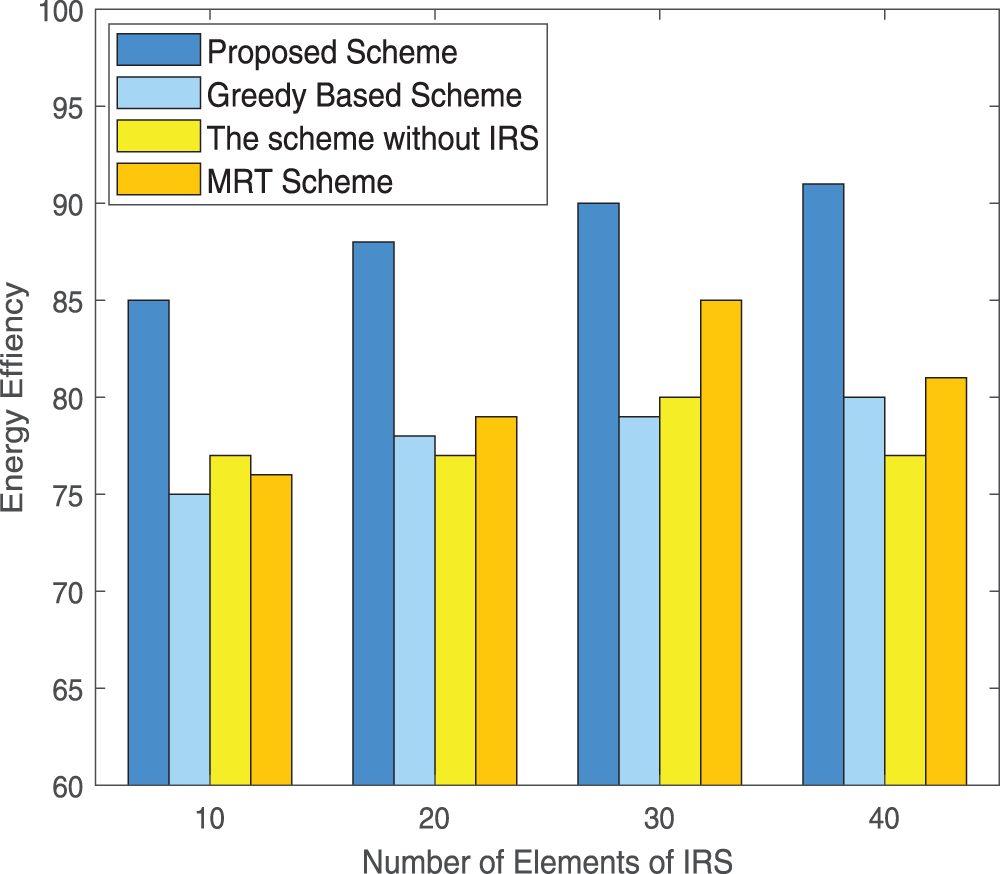
Figure 4: Energy efficiency vs. the number of IRS elements

In Fig. 5, we simulate the relationship between noise power and energy efficiency. The improvement of noise power will inevitably reduce energy efficiency. When the noise power increases, the communication rate from the user to UAV decreases. This means that users need to consume more energy to achieve the set transmission target task.

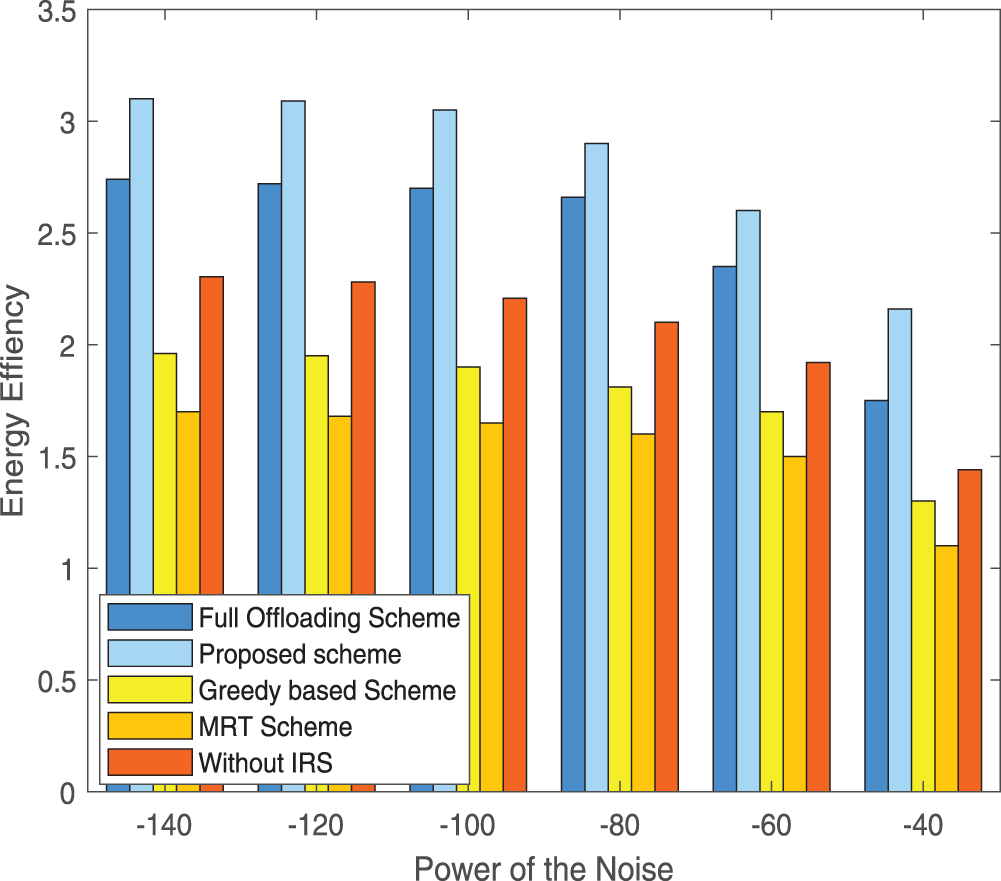
Figure 5: Energy efficiency vs. the maximum power of noise

In Fig. 6, we show the curve of energy efficiency changing with the maximum power of users. It is worth noting that with the increase in the maximum power of users, the growth rate of energy efficiency gradually slows down. Our proposed scheme is always superior to the existing scheme. In addition, when the maximum power of the user is increased, the energy efficiency of all unloading schemes will not be improved, because the extra energy cannot bring additional gain.

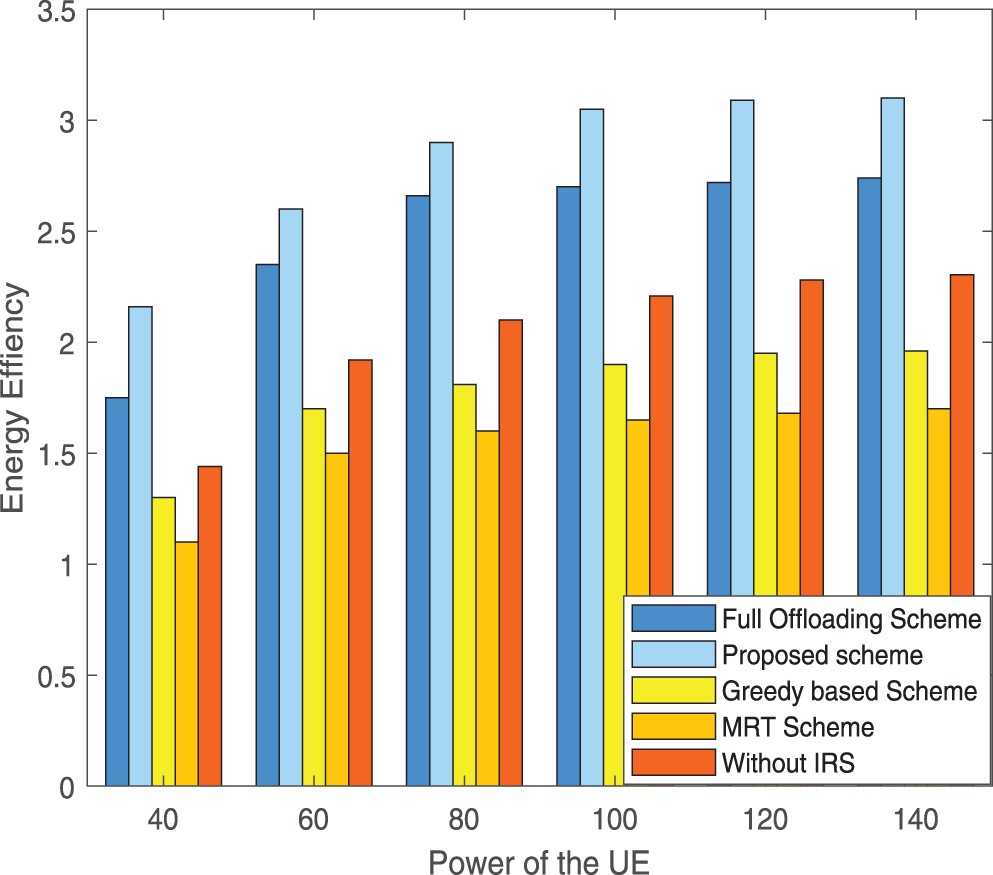
Figure 6: Energy efficiency vs. the maximum power of users

In Fig. 7, we focus on the impact of total tasks on energy efficiency. It is worth noting that the scope of the total task is limited. When the total task is too large, the unloading and calculation of all tasks cannot be completed within the agreed time. When the total number of tasks is small, most of the energy consumed is used to support the UAV flight and the user’s transmission consumption. At this time, the energy efficiency is low. When the total number of tasks increases, the proportion of calculated energy consumption gradually increases, and the energy efficiency also increases. At this point, our proposed scheme can effectively allocate the energy required for calculation and flight transmission energy to improve energy efficiency.

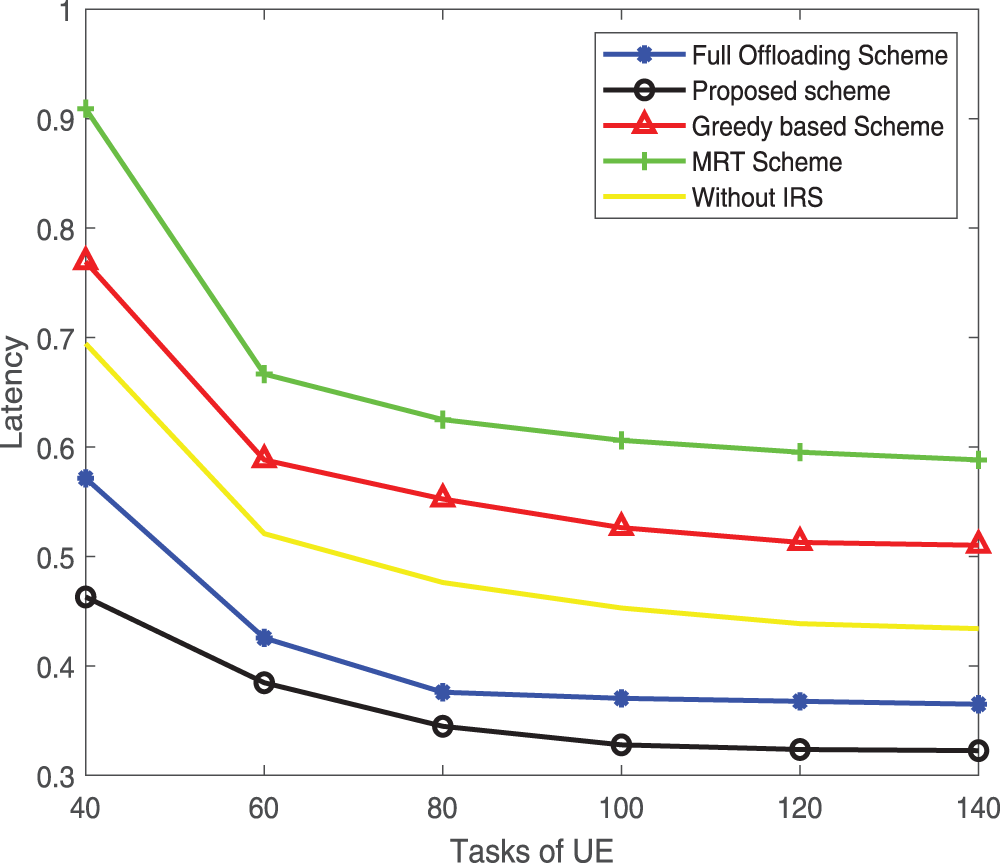
Figure 7: Energy efficiency vs. the tasks

6  Conclusion

In this paper, we design the transmitting beam of the user, the trajectory of the UAV, and the phase shift matrix of the IRS to maximize the user’s secrecy rate. We analyze the two working modes of the eavesdropper and potentially control its transmitting beam. We add the influence factor of the eavesdropper as an optimization variable into the design scheme and propose a local optimization scheme based on the interior point method and alternative optimization. In addition, we designed a suboptimal scheme based on the zero forcing method to reduce the computational complexity. The simulation results show that the proposed iterative scheme is superior to the suboptimal scheme and has a higher secrecy rate than the existing schemes.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This work was supported by the Key Scientific and Technological Project of Henan Province (Grant Number 222102210212), Doctoral Research Start Project of Henan Institute of Technology (Grant Number KQ2005), Doctoral Research Start Project of Henan Institute of Technology (Grant Number KQ2110) and Key Research Projects of Colleges and Universities in Henan Province (Grant Number 23B510006).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Ying Zhang; data collection: WeiMing Niu; analysis and interpretation of results: Supu Xiu, Guangchen Mu; draft manuscript preparation: Ying Zhang, Weiming Niu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data is synthesized using MATLAB and the generation method is described in detail in the simulation section.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Mao, Y., You, C., Zhang, J., Huang, K., Letaief, K. B. (2017). A survey on mobile edge computing: The communication perspective. IEEE Communications Surveys and Tutorials, 19(4), 2322–2358. [Google Scholar]

2. Abbas, N., Zhang, Y., Taherkordi, A., Skeie, T. (2018). Mobile edge computing: A survey. IEEE Internet of Things Journal, 5(1), 450–465. [Google Scholar]

3. Wu, Q., Zhang, R. (2019). Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming. IEEE Transactions on Wireless Communications, 18(11), 5394–5409. [Google Scholar]

4. Wu, Q., Zhang, R. (2020). Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network. IEEE Communications Magazine, 58(1), 106–112. [Google Scholar]

5. Zhou, F., Hu, R. Q. (2020). Computation efficiency maximization in wireless-powered mobile edge computing networks. IEEE Transactions on Wireless Communications, 19(5), 3170–3184. [Google Scholar]

6. Wu, W., Wang, X., Zhou, F., Wong, K. K., Li, C. et al. (2021). Resource allocation for enhancing offloading security in NOMA-enabled MEC networks. IEEE Systems Journal, 15(3), 3789–3792. [Google Scholar]

7. Zeng, Y., Zhang, R., Lim, T. J. (2016). Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Communications Magazine, 54(5), 36–42. [Google Scholar]

8. Mao, S., Wu, J., Liu, L., Lan, D., Taherkordi, A. (2022). Energy-efficient cooperative communication and computation for wireless powered mobile-edge computing. IEEE Systems Journal, 16(1), 287–298. [Google Scholar]

9. Al-Hourani, A., Kandeepan, S., Lardner, S. (2014). Optimal LAP altitude for maximum coverage. IEEE Wireless Communications Letters, 3(6), 569–572. [Google Scholar]

10. Liu, Y., Wang, W., Chen, H. H., Lyu, F., Wang, L. et al. (2021). Physical layer security assisted computation offloading in intelligently connected vehicle networks. IEEE Transactions on Wireless Communications, 20(6), 3555–3570. [Google Scholar]

11. Hu, X., Wong, K. K., Zhang, Y. (2020). Wireless-powered edge computing with cooperative UAV: Task, time scheduling and trajectory design. IEEE Transactions on Wireless Communications, 19(12), 8083–8098. [Google Scholar]

12. Dinh, T. Q., Tang, J., La, Q. D., Quek, T. Q. S. (2017). Offloading in mobile edge computing: Task allocation and computational frequency scaling. IEEE Transactions on Communications, 65(8), 3571–3584. [Google Scholar]

13. Zhang, J., Hu, X., Ning, Z., Ngai, E. C. H., Zhou, L. et al. (2018). Energy-latency tradeoff for energy-aware offloading in mobile edge computing networks. IEEE Internet of Things Journal, 5(4), 2633–2645. [Google Scholar]

14. Tran, T. X., Pompili, D. (2019). Joint task offloading and resource allocation for multi-server mobile-edge computing networks. IEEE Transactions on Vehicular Technology, 68(1), 856–868. [Google Scholar]

15. Liu, M., Yu, F. R., Teng, Y., Leung, V. C. M., Song, M. (2019). Distributed resource allocation in blockchain-based video streaming systems with mobile edge computing. IEEE Transactions on Wireless Communications, 18(1), 695–708. [Google Scholar]

16. Wang, F., Xu, J., Wang, X., Cui, S. (2018). Joint offloading and computing optimization in wireless powered mobile-edge computing systems. IEEE Transactions on Wireless Communications, 17(3), 1784–1797. [Google Scholar]

17. Jeong, S., Simeone, O., Kang, J. (2018). Mobile edge computing via a UAV-mounted cloudlet: Optimization of bit allocation and path planning. IEEE Transactions on Vehicular Technology, 67(3), 2049–2063. [Google Scholar]

18. Hu, X., Wong, K. K., Yang, K., Zheng, Z. (2019). UAV-assisted relaying and edge computing: Scheduling and trajectory optimization. IEEE Transactions on Wireless Communications, 18(10), 4738–4752. [Google Scholar]

19. Zeng, Y., Zhang, R. (2017). Energy-efficient UAV communication with trajectory optimization. IEEE Transactions on Wireless Communications, 16(6), 3747–3760. [Google Scholar]

20. Wu, W., Wang, Z., Yuan, L., Zhou, F., Lang, F. et al. (2021). IRS-enhanced energy detection for spectrum sensing in cognitive radio networks. IEEE Wireless Communications Letters, 10(10), 2254–2258. [Google Scholar]

21. Mao, S., Liu, L., Zhang, N., Dong, M., Zhao, J. et al. (2022). Reconfigurable intelligent surface-assisted secure mobile edge computing networks. IEEE Transactions on Vehicular Technology, 71(6), 6647–6660. [Google Scholar]

22. You, C., Huang, K., Chae, H., Kim, B. H. (2017). Energy-efficient resource allocation for mobile-edge computation offloading. IEEE Transactions on Wireless Communications, 16(3), 1397–1411. [Google Scholar]

23. Wu, W., Zhou, F., Hu, R. Q., Wang, B. (2020). Energy-efficient resource allocation for secure NOMA-enabled mobile edge computing networks. IEEE Transactions on Communications, 68(1), 493–505. [Google Scholar]

24. Zheng, L., Lops, M., Eldar, Y. C., Wang, X. (2019). Radar and communication coexistence: An overview: A review of recent methods. IEEE Signal Processing Magazine, 36(5), 85–99. [Google Scholar]

25. Nartasilpa, N., Salim, A., Tuninetti, D., Devroye, N. (2018). Communications system performance and design in the presence of radar interference. IEEE Transactions on Communications, 66(9), 4170–4185. [Google Scholar]

26. Grossi, E., Lops, M., Venturino, L., Zappone, A. (2018). Opportunistic radar in IEEE 802.11ad networks. IEEE Transactions on Signal Processing, 66(9), 2441–2454. [Google Scholar]

27. Shirin Abkenar, F., Ramezani, P., Iranmanesh, S., Murali, S., Chulerttiyawong, D. et al. (2022). A survey on mobility of edge computing networks in IoT: State-of-the-art, architectures, and challenges. IEEE Communications Surveys and Tutorials, 24(4), 2329–2365. [Google Scholar]

28. Cui, J., Wang, L., Hu, B., Chen, S. (2022). Incidence control units selection scheme to enhance the stability of multiple UAVs network. IEEE Internet of Things Journal, 9(15), 13067–13076. [Google Scholar]

29. Ning, Z., Dong, P., Kong, X., Xia, F. (2019). A cooperative partial computation offloading scheme for mobile edge computing enabled internet of things. IEEE Internet of Things Journal, 6(3), 4804–4814. [Google Scholar]

30. Ju, H., Lim, S., Kim, D., Poor, H. V., Hong, D. (2012). Full duplexity in beamforming-based multi-hop relay networks. IEEE Journal on Selected Areas in Communications, 30(8), 1554–1565. [Google Scholar]

31. Shi, Q., Razaviyayn, M., Luo, Z. Q., He, C. (2011). An iteratively weighted MMSE approach to distributed sum-utility maximization for a MIMO interfering broadcast channel. IEEE Transactions on Signal Processing, 59(9), 4331–4340. [Google Scholar]

32. Grant, M., Boyd, S. P. (2014). CVX: Matlab software for disciplined convex programming. http://cvxr.com/cvx [Google Scholar]