 Open Access
Open Access
ARTICLE
The Spherical q-Linear Diophantine Fuzzy Multiple-Criteria Group Decision-Making Based on Differential Measure
1 Institute of Mathematics, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan
2 Department of Mathematics, Deanship of Applied Sciences, Umm Al-Qura University, Mecca, Saudi Arabia
3 Department of Mathematics, Huzhou University, Huzhou, 313000, China
* Corresponding Authors: Shahzaib Ashraf. Email: ; Yu-Ming Chu. Email:
(This article belongs to the Special Issue: Advances in Ambient Intelligence and Social Computing under uncertainty and indeterminacy: From Theory to Applications)
Computer Modeling in Engineering & Sciences 2024, 138(2), 1925-1950. https://doi.org/10.32604/cmes.2023.030030
Received 19 March 2023; Accepted 19 June 2023; Issue published 17 November 2023
Abstract
Spherical q-linear Diophantine fuzzy sets (Sq-LDFSs) proved more effective for handling uncertainty and vagueness in multi-criteria decision-making (MADM). It does not only cover the data in two variable parameters but is also beneficial for three parametric data. By Pythagorean fuzzy sets, the difference is calculated only between two parameters (membership and non-membership). According to human thoughts, fuzzy data can be found in three parameters (membership uncertainty, and non-membership). So, to make a compromise decision, comparing Sq-LDFSs is essential. Existing measures of different fuzzy sets do, however, can have several flaws that can lead to counterintuitive results. For instance, they treat any increase or decrease in the membership degree as the same as the non-membership degree because the uncertainty does not change, even though each parameter has a different implication. In the Sq-LDFSs comparison, this research develops the differential measure (DFM). The main goal of the DFM is to cover the unfair arguments that come from treating different types of FSs opposing criteria equally. Due to their relative positions in the attribute space and the similarity of their membership and non-membership degrees, two Sq-LDFSs form this preference connection when the uncertainty remains same in both sets. According to the degree of superiority or inferiority, two Sq-LDFSs are shown as identical, equivalent, superior, or inferior over one another. The suggested DFM’s fundamental characteristics are provided. Based on the newly developed DFM, a unique approach to multiple criterion group decision-making is offered. Our suggested method verifies the novel way of calculating the expert weights for Sq-LDFSS as in PFSs. Our proposed technique in three parameters is applied to evaluate solid-state drives and choose the optimum photovoltaic cell in two applications by taking uncertainty parameter zero. The method’s applicability and validity shown by the findings are contrasted with those obtained using various other existing approaches. To assess its stability and usefulness, a sensitivity analysis is done.Keywords
Multiple criteria decision-making
In order to evaluate logistics AVs, Bonab et al. [30] created an enhanced MCDM framework based on the Choquet integral (CI) and a spherical fuzzy set (SFS). By employing spherical fuzzy sets and the spherical fuzzy weight correlation coefficient, Ma et al. [31] initiated a novel failure mode and effect analysis (FMEA) that enhanced the performance of FMEA. Ali et al. [32] introduced a novel approach for making decisions called MCDM-total area based on orthogonal vectors with a few innovative distance measurements made possible by matrix norms. The limitations of the current distance measurements are removed by this measure, which also meets all axiomatic requirements.
Das et al. [33] provided a way for resolving group decision-making issues using intuitionistic fuzzy parameterized intuitionistic multi fuzzy N-soft sets of dimension q by providing its induced IFP-hesitant N-soft set as an addition to the multi-fuzzy N-soft set-based method. Khan et al. [34] provided multi-attribute decision-making in a T-spherical fuzzy environment using the Archimedean aggregation operator for three-dimensional data with n powers.
Measures of similarity and distance are two sides of the same coin. The majority of similarity tests rely on distance measurements. A lot depends on both metrics when comparing two PFSs. Even though several studies suggested various distance measurements, the ones that are currently in use still have certain shortcomings [35]. They can first result in counterintuitive consequences [36]. Second, it is possible that they will not be able to calculate the maximum distance measurement value [35]. This will skew the ranking values of the alternatives and result in inaccurate findings. As a result, Shraf has solved the open problem of determining the distance between two PFSs in the Pythagorean fuzzy environment [36]. But there is still a problem with the idea, which is that it might not function if the raw data is in triplet form. To remove this flaw, we created a new fuzzy set to address this problem.
An integer-coefficiented linear Diophantine equation is included in the fuzzy membership function of Q-linear Diophantine fuzzy sets, a particular kind of fuzzy set. A solution to a q-linear Diophantine equation is the value that is specifically described as the membership function of a q-linear Diophantine fuzzy set. Applications that utilise such fuzzy sets in fuzzy set theory include decision-making, control, pattern recognition, and image processing. Overall, q-linear Diophantine fuzzy sets are a practical tool in fuzzy set theory for representing ambiguous and imprecise information and have many applications in a variety of domains. The human mind extends much beyond TM and FM. As a result, a new fuzzy set was required to take human thinking into account, and Ashraf et al. [37] proposed the concept of a spherical fuzzy set that provides a more adaptable and expressive framework for the ideas of classical (crisp) sets. In spherical fuzzy sets, an element of a set is given a range of membership values rather than a single membership value to represent the degree of uncertainty or ambiguity in that element’s categorization. This study’s objective is to identify the differential measure among three parameters using the Sq-LDFS specified fuzzy set to cover the three degrees of membership (membership, non-membership and indeterminacy). Razzaque et al. [38] proposed a collection of innovative Einstein aggregation operations by using sq-LDF data. Additionally, a better VIKOR method is presented to address the uncertainty in categorising viral hepatitis.
This article introduces the idea of differential measure (DFM), derived from [39] as a novel method for contrasting spherical q-linear Diophantine fuzzy sets (Sq-LDFSs) [40]. When the uncertainty grade has equally in both sets, there is a preference connection between two Sq-LDFS because of their relative positions in the attribute space and the proximity of their membership and non-membership degrees. Due to the equal consideration of the membership and non-membership degrees, and uncertainty grade, although each direction has a distinct connotation, the existing Distance measures and similarity measures across various fuzzy sets, namely PFSs with a zero uncertainty grade have several shortcomings. To take into To account the effects of each element of an Sq-LDFSs evaluation, the DFM uses signed distance. According to the degree of superiority or inferiority, two Sq-LDFSs are shown as the same, equal, superior, or inferior to one another. Based on the newly established DFM, a novel MCGDM approach is certified by our proposed idea. Since Sq-LDFS are more adaptable than IFSs, PFSs, q-LDFSs and SFSs to deal with absurdity and ambiguity, as well as to deal with human evaluation information, it is vital to pay greater attention to collective decision-making in this context. Therefore,
1. The proposal of DFM is proposed as a revolutionary technique for contrasting Sq-LDFSs. It is an association between two Sq-LDFSs based on the position in the attribute space. To cover the limitations of the current distance in discriminating, a DFM maintains the identity of the Sq-LDFSs’ parameters.
2. A novel
3. The experts’ weights in
The rest of the part is structured as follows: The most recent information regarding Sq-LDFSs is provided in the following sections: Literature review in Section 1, preliminary definitions in Section 2, and an explanation of the differential measure in Section 3. We provided the differential rules suggested for Sq-LDFSs with short numerical examples in Section 4. In Section 5, an enhanced framework for MCGDM is proposed to explain all phases of the technique and offer some counter-examples for previously proposed differential measures by our technique. In Subsection 5.1, a numerical example of diagnosing cancer patients using a variety of tests is provided to bolster the differential measure. In Sections 6 and 7, a discussion and a conclusion are offered.
Definition 2.1. [40] A spherical q-linear Diophantine fuzzy set
where each membership grade
1.
2.
Definition 2.2. A compliment of
Definition 2.3. For a Sq-LDFS a score function
where
Definition 2.4. The hamming distance using Sq-LDFSs [38] can be defined as:
Definition 2.5. The euclidean function using Sq-LDFSs can be defined as:
Song et al. [41] presented the analysis of the distinction between psychological distance measure and classical distance measurement. The classical distance measurements’ surprising potential to ignore alternative background information and their competing interactions resolved by psychological distance. To illustrate, we use the SF to evaluate the three alternatives
The differential measure between two Sq-linear Diophantine fuzzy sets
For triplet grades, membership determinacy and non-membership degrees, the datum is one. In case where A’s membership degree exceeds B’s, the difference between the grades is added to one, showing a positive step; in case where A’s membership degree is less than B’s, the difference between the grades is deducted from one, showing a negative step.
Definition 4.1. A differential measurement between two spherical q-linear Diophantine fuzzy sets (Sq-LDFSs)
Definition 4.2. Two Sq-LDFSs
1. If
Proposition 4.1. For Sq-LDFSs
1. If
2. If
Proposition 4.2. For the Sq-LDFSs
We noticed that
Numerical Examples In this subsection a few examples are provided to demonstrate the use of differential measures.
Example 1. Let
Example 2. Let
Following that, either
5 An Improved Proposed Framework for MCGDM
(1) Problem identification. Evaluation of the criteria
(2) The creation of decision matrix and weight vector assigned by experts as Sq-LDFSs.
and
(3) Normalize the information in DM to get the best results.
(4) Create the aggregated decision matrix using the formula (7), and then determine the best rating for each criterion.
(5) Determine the DFM between the ideal rating and the rating of each alternative for a criterion to create the differential matrix.
(6) Calculate the collective differential measure (CDFM) for each option.
(7) Calculate the CDFM’s score function and rank. The crisp value of the CDFM of each A is estimated using the score formula. The total degree to which the ideal ratings for the evaluation criteria outperform the ratings of an alternative is the CDFM. The superiority of the alternative rating decreases with decreasing ideal rating superiority. The option with the lowest value is the best, and the alternatives are arranged in ascending order.
The expert weights evaluation technique: With the socioeconomic environment becoming more complicated, switching from a single expert to a group of experts became necessary since it is challenging for a single expert to manage all the relevant components of a complex problem [42]. A homogenous group of specialists with comparable attitudes, knowledge, and experience is virtually impossible when group decision-making. Consideration should be given to the credibility of expert opinions and how they could influence the choice made. Results may be inaccurate if the relative importance of the experts is ignored. Studies on calculating the weights of the criteria are abundant, but studies on calculating the weights of the experts are few [43]. Usually, the weights of the experts are chosen based on personal preference. They are decided upon by a manager or through peer reviews. Credibility is low for this method of allocating the experts’ weights. To give the experts’ opinions greater weight from a more objective standpoint, objective procedures that make use of quantitative methodologies are used [44]. Based on the similarity between the opinions of the individual experts and the group, Zhang [45] suggested a method to calculate the experts’ unknown weights. Experts are more significant and should be given more weight when their opinions are more in line with the group’s viewpoint. This study suggests a precise approach for calculating the weights of the unknown experts based on their agreement with the ranking of the alternatives. The weighted sum approach is employed to rank each expert (WSM). Spearman’s correlation coefficient is then used to determine the correlation between each pair of experts’ ranks. The correlation between an expert and other experts is added to determine the expert’s overall correlation. The final step is to divide the sum of the total correlations of each expert by that of the experts as a whole. First, each expert’s assessments of a potential replacement for the evaluation criteria are combined using the Pythagorean fuzzy weighted averaging operator (7).
Step1: Create each expert’s judgment vector. The pth expert’s evaluations for the ith alternative are combined utilizing (7).
Step2: Calculate the total rating score for each option and place it in order.
Step3: Use Spearman’s correlation coefficient to calculate the correlation between one expert’s ranking and the other. Using Spearman’s correlation coefficient, the ranking of the pth expert and each of the other experts is correlated.
Step4: Calculate each expert’s overall correlation. The expert’s total correlation is the result of adding up all of the expert’s correlations. Assign a weight to the experts.
Step5: Each expert’s weight is determined by dividing his or her overall correlation by the sum of the total correlations of the other experts. w
Fig. 1 depicts the prescribed MCGDM framework.
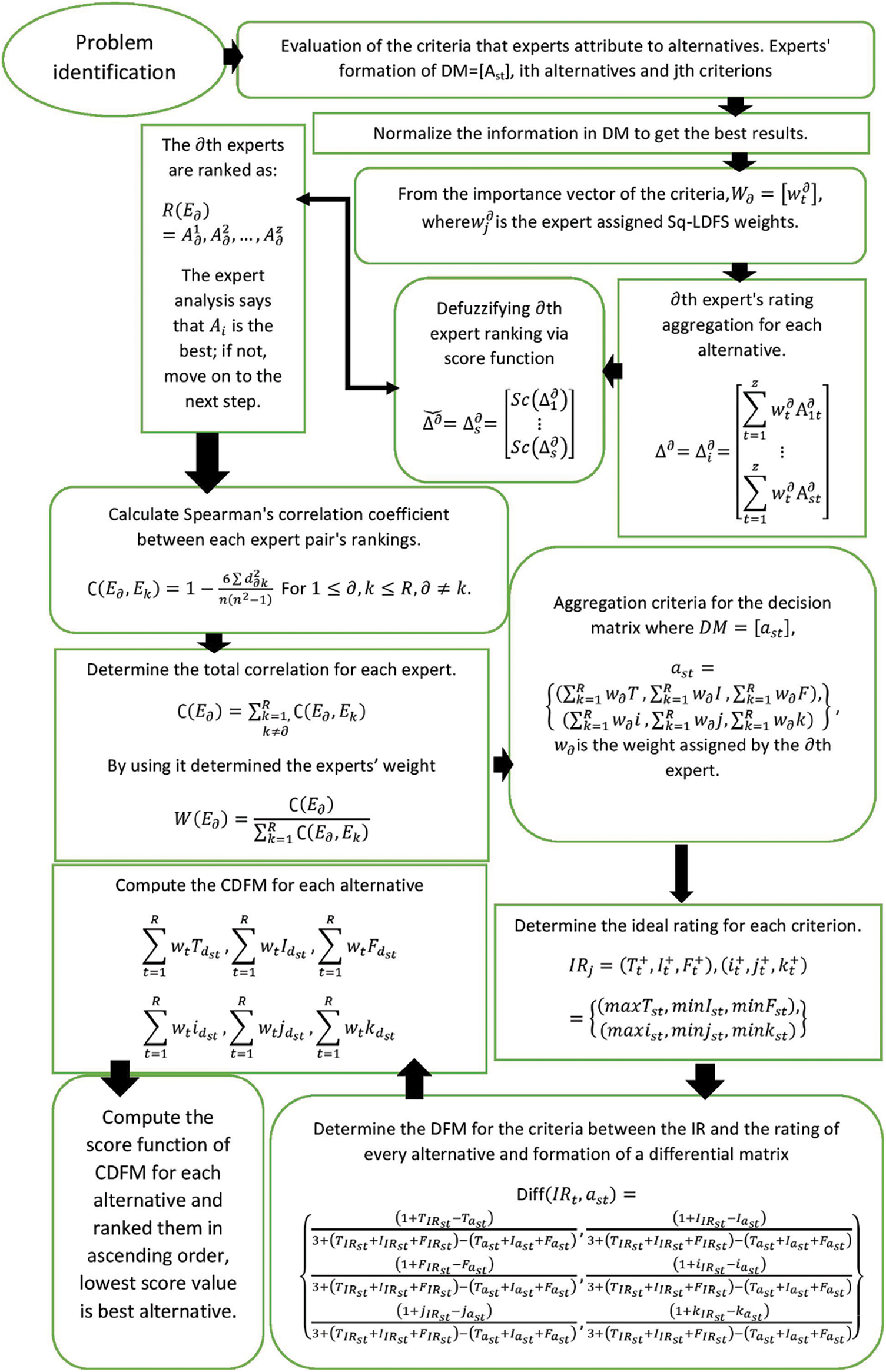
Figure 1: Improved technique for MCGDM
Practical examples: In decision making problem, one of the efficient way to identifying an eligible preferred alternative from a group of alternatives is its similarity degree to the ideal rating. The best alternative is chosen by the degree of similarity. The least differential measurement indicates the ideal option when evaluating the differential measure. In this part, two real-world applications utilizing Pythagorean fuzzy information are discussed in two practically applications. The first application is the evaluation of solid-state drives (SSDs) derived from Huang et al. [35]. The second application is the identification of the finest photovoltaic cell taken from Zhang [45].
Evaluation of SSDs: Flash memory is the primary storage technology used in computers and mobile devices today. Modern computing systems frequently substitute solid-state drives

Utilizing DM, the differential measurement between the ideal rating (IR) and the rating for each criterion is computed with the help of the differential measure formula, as shown in Table 2. To obtain its integrated DiFM, the differential measurements of each alternative are aggregated. After that, the CDiFMs are defuzzified using the score function (2.3), allowing for the evaluation of the total degree of the best ratings’ superiority over the ratings of the alternatives available for the evaluating criterion.

The options are ranked as shown in Table 3 in ascending order. According to Table 3, the ranking order is


Photovoltaic cells: Photovoltaic (PV) thermoelectric technology has gained a great deal of attention as a result of the present global crisis caused by the shortage of natural fuels in the earth’s crust [51]. The most effective alternative to conventional sources of energy power is photovoltaic solar energy, which offers both sustainable and environmentally friendly energy sources [52]. Photovoltaic systems produce zero pollution as they directly harness solar energy to produce electricity [53]. They also provide many benefits, including noiseless operation, low maintenance requirements, and excellent dependability [54]. The advancement of new photovoltaic technologies has recently been the topic of extensive research focused on boosting the effectiveness and sustainability of these devices, integrating with using cheap materials and techniques [52]. These significant efforts combined with outstanding efforts to identify the best alternative and choice based on the requirements, using multi-criteria decision approaches, which have been kept parallel to this ongoing search [55]. A photovoltaic cell is an apparatus that uses the photovoltaic effect, a well-known physical and chemical phenomenon, to transform light energy into electricity. A generational division of several PV cell types in use. The first generation, which is the most widely used and conventional kind consisting of monocrystalline or polycrystalline silicon, controls more than 90% of the market for solar energy today. Due to the expensive manufacture of crystalline silicon, the experts made more efforts to create alternative materials with low-cost fabrication methods. The second generation was created of thin-film cells using less expensive techniques. Amorphous silicon (a-Si), nanocrystalline silicon (nc-Si), cadmium telluride (CdTe), and copper indium gallium selenide are employed the most frequently (CIGS). However, they do not perform much better than first-generation cells. The third generation was created to be highly efficient and inexpensive. They include a range of thin film technologies, some of which employ organic materials to produce energy while others rely on inorganic materials, such as dye-sensitized cells (DSSCs), quantum dot-sensitized cells (QDSSCs), organic solar cells, and hybrid perovskite cells [51]. Table 5 represents the aggregated decision matrix consists of photovoltaic cell data.

After selecting the ideal site for a photovoltaic solar plant installation, it is necessary to choose the kind of cell among the many PV cell options that best optimize the construction, for example, enhances production or efficiency, reduces costs, and provides the highest maturation and reliability [55].
The selection of photovoltaic cells: The selection of optimal photovoltaic is required from the listed alternatives: CdTe and CIGS



It is also obvious that the ranking of the suggested technique is virtually identical to Zhang’s [45] results. The two best technologies and the poorest technologies are unchanged, however, the moderately performing technologies have altered somewhat.
Propose weighting method application: The proposed technique may be used to calculate the weights of the professionals for the previous PV cell selection task. The illustrations of the stages are listed below.
Step 1: From the given weight vector by each decision professional, by using (2.3) WV
Step 2: Evaluate each alternative’s score function (2.3) using Table 10 to rank them.
Step 3: Utilize Spearman’s correlation to identify the relationship between the expert ranks. Table 9 summarizes the results.

Step 4: Computation of each professional’s total correlation
Step 5: Quantify the weights of the experts
After the resolution of PV cell selection by qualities, the weights are calculated by the proposed technique, and the obtained data are summarized in Table 10. The obtained ranking is consistent with previous results. It is worth noting that this methodology can detect the optimum alternative for selecting expert weights. After determining how each expert ranked the choices, if one alternative comes in first among all experts, it is the best option, and thereafter step is not necessary unless a complete ranking list is required. The three professionals select the PV cell at number second

Cancer [57] is not only a disease but rather a collection of diseases that collectively cause the body’s cells to alter and proliferate uncontrollably. Cancers are classed either based on the type of fluid or tissue from which they arise or based on where in the body they first manifested themselves. Some cancers are of mixed kinds. The origins of cancer in the tissues and blood may be subdivided into the five major categories below:
Carcinoma: A carcinoma cancer develops in epithelial tissue, which covers or lines the surfaces of organs, glands, and other body organs. A carcinoma, for instance, is a cancer of the stomach lining. Numerous carcinomas attack organs or glands that secrete substances, such as milk-producing breasts. 80%–90% of all cancer cases are carcinomas.
Sarcoma: Sarcomas are cancerous tumors that grow from connective tissues such as cartilage, fat, muscle, tendons, and bones. The most prevalent sarcoma, a bone tumor, usually affects young individuals. Chondrosarcoma (cartilage) and osteosarcoma are two examples of sarcoma.
Lymphoma: Lymphoma-type cancer develops in the lymph systems nodes or glands, whose job is to produce white blood cells and clean body fluids, as in organs like the brain and breast. The two types of lymphomas are Hodgkin’s lymphoma and Hodgkin’s non-lymphoma.
Leukemia: Leukemia, widely known as blood cancer, is a bone marrow cancer that resists the marrow from creating healthy red, white, and platelet blood cells. To fight infection, white blood cells are necessary. To avoid anemic, red blood cells are necessary. The presence of platelets helps to prevent rapid bleeding and bruising.
Myeloma: Bone marrow plasma cells are where myeloma develops. Myeloma cells can sometimes gather in one bone to create a single tumor known as plasmacytoma. However, in some instances, the myeloma cells assemble in several bones, producing numerous bone tumors. Several medical tests [58] are used to diagnose these cancer types namely CT scan, MRI, Nuclear scan, Bone scan, PET scan, Ultrasound, X-rays, and Biopsy. Suppose a medical expert have five cancer patients namely
Step1: Creation of a decision matrix based on Sq-LDFSs w.r.t the reports of five cancer patients in Table 11.

Step2: Normalized fuzzy data given in Table 12.

Step3: The differential measure between the ideal ratings and the ratings of each alternative for the criterion is derived using the decision matrix. Following that, the differential matrix shows the results in Table 13.

The collective differential measure and ranks for cancer patients can be seen in Table 14. The ranking of patients according to their condition is presented in Table 15.


The purpose of this paper is to discriminate the Sq-LDFSs by the proposed notion of DFM. It is a preference connection between two Sq-LDFSs because of where they are in the attribute space and how closely their degrees of membership, indeterminacy and non-membership with the control parameter are correlated. Overcoming potential flaws in the current measures between fuzzy sets is the primary goal of the DFM. The shortcomings of the current distance and similarity metrics come from treating membership, indeterminacy, and non-membership degree identically, although each direction has a different connotation. Differently, a DFM handles variations in a spherical q-linear diophantine fuzzy assessment’s parameters. A step taken in the support direction is viewed as a +ve point, while an opposite step is shown as −ve with the same indeterminacy values. The degree of superiority or inferiority between two Sq-LDFSs is determined by whether they are classed as identical, equivalent, superior, or inferior to one another. Based on the newly introduced DFM, a new method for calculating the expert weights is created, and an MCGDM method is also defined. To demonstrate the approach, two real-world issues were resolved. The suggested method’s results are contrasted with those of several other existing MCDM approaches. The comparison’s primary goal is to confirm and show the method’s applicability. There is no worst or best methodology; all of the MCDM methods can be compared to one another. Even when processing the same data and information, different methodologies can yield different conclusions. We can determine which approach is most appropriate in a specific circumstance [59]. When the MCDM methods based on distance or similarity measurements are impacted by the aforementioned flaws, resulting to inaccurate findings, the proposed method would be preferable. The assessment of solid-state drives is the first illustration. The proposed method’s outcome is contrasted with that of other decision-making techniques, including the TOPSIS method put forth by Zhang et al. [47], the TODIM approach created by Ren et al. [48], the distance and similarity measures introduced by Zeng et al. [49], the fuzzy weighted and ordered weighted aggregation operators put forth by Garg [50], and the PF-MULTIMOORA method put forth by Huang et al. [35]. The best choice was found using the same techniques. With a few minor differences from previous ranking lists, the ranking list produced by the suggested method is consistent with the outcomes of Zeng et al. The choice of the best photovoltaic cell serves as the second illustration. The outcome of the suggested strategy is contrasted with that of Zhang [45] and Biswas et al. [56]. The best alternative was determined using all three procedures. The ranking list of the suggested technique is almost identical to the ranking list of Zhang [45] and correlates with the ranking list of Biswas et al. [56]. Finally, using Spearman’s correlation coefficient as a base, an improved method for calculating the expert weights is created and used for the photovoltaic cell problem. The weights obtained from the experts differ slightly from those reported by Zhang [45] in some respects. Nevertheless, the experts’ relative weights are equal, and the same answer is reached when the problem is solved using the suggested weights. Practical applications for the proposed DFM include image processing, pattern recognition, machine learning, information retrieval, medical diagnosis, and decision-making. The suggested framework might reduce preferences that might develop in the decision-making process as a result of giving decision-makers subjective weights, which frequently results in outcomes that are not accurate [60]. The framework offers decision-makers objective weights to counteract the unfavorable impact of subjective weights. The suggested approach can therefore help managers make better judgments. It is predicted that the created method will work successfully in any GDM setting, including corporate management and industrial engineering. Fig. 2 represents the differential measurement in both PyFS and Sq-LDFS graphically.
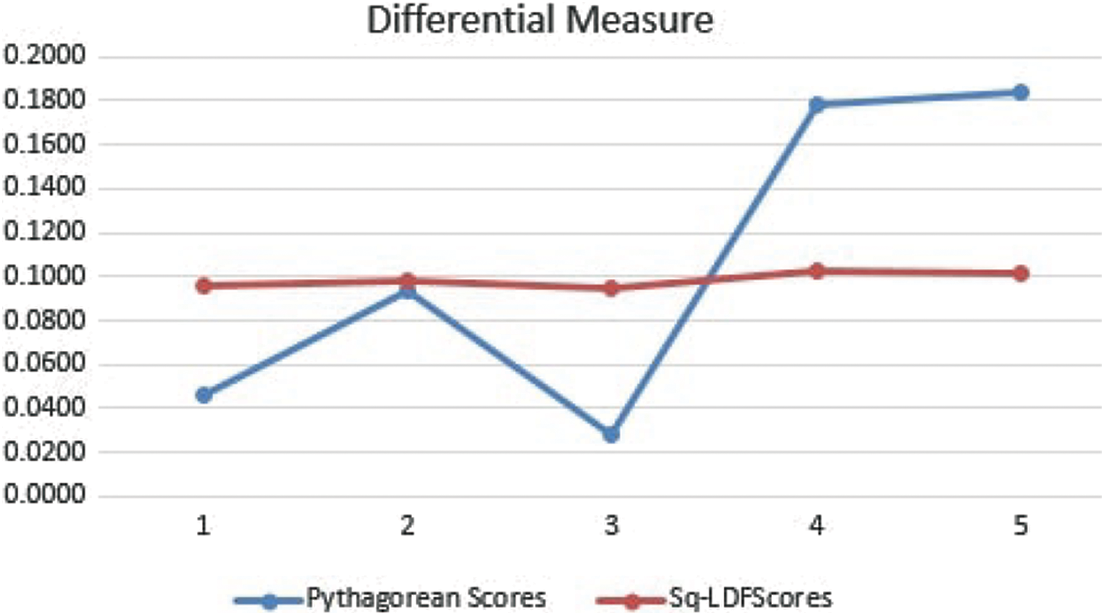
Figure 2: Differential measure comparison
The construction of an appropriate evaluation method for the fuzzy data to find differential measures is essential. There are a lot of techniques to find a difference in fuzzy sets, i.e., similarity measures, distance measures, and methods such as VIKOR, TOPSIS, EDAS, etc. In this article, we proposed differential measures among three grades membership, indeterminacy, and non-membership related to their control variables. The results of our technique show efficient performance. we use the previous examples from Pythagorean fuzzy sets data but got the same results as our proposed technique of differential measure in Sq-LDFSs. The MCGDM method proposed by finding the weights by Spearman’s correlation coefficient got identical results in three grades. “Differential Measure for Pythagorean Fuzzy Sets” only covers two membership grades; however, there is a need for a fuzzy set to fill in this gap and cover the data for the three grades when the Pythagorean fuzzy set constraints fall short in specific situations. Therefore, using data from three grades, we determine the Sq-LDFS and find the differential measure. The outcome validates the effectiveness of the suggested method. We infer that our approach is useful for three parametric data in addition to two degree data based on our ranking results and comparison.
The proposed Sq-LDFS concept can be used in other existing methods, such as MAIRCA, ELECTREE, AHP, or PROMETHEE, to enhance its performance and accuracy. The proposed technique can be applicable to several real-life problems that involve decision-making under uncertainty and imprecision. For instance, in green supplier selection, the proposed method can be used to evaluate and rank potential suppliers based on multiple criteria, such as quality, price, and delivery time etc. In medical field, the proposed method can be used to analyze patient data and provide a diagnosis based on multiple symptoms and test results.
Acknowledgement: Muhammad Naeem would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work.
Funding Statement: This work is supported by the Deanship of Scientific Research at Umm Al-Qura University (Grant Code: 22UQU4310396DSR65).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: H. Razzaque, S. Ashraf; data collection: H. Razzaque; analysis and interpretation of results: H. Razzaque, S. Ashraf, M. Naeem, Y.M. Chu; draft manuscript preparation: H. Razzaque, S. Ashraf, M. Naeem, Y.M. Chu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data used in this paper are hypothetical and can be used by anyone by just citing this article.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Akram, M., Dudek, W. A., Ilyas, F. (2019). Group decision-making based on pythagorean fuzzy TOPSIS method. International Journal of Intelligent Systems, 34(7), 1455–1475. [Google Scholar]
2. Wu, Y., Gao, Y., Zhang, B., Pedrycz, W. (2023). Minimum information-loss transformations to support heterogeneous group decision making in a distributed linguistic context. Information Fusion, 89, 437–451. [Google Scholar]
3. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. [Google Scholar]
4. Atanassova, K., Stoeva, S. (1983). Intuitionistic fuzzy sets. Polish Symposium on Interval and Fuzzy Mathematics, pp. 23–26. Poznan, Poland. [Google Scholar]
5. Yager, R. R. (2013). Pythagorean fuzzy subsets. 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), pp. 57–61. Edmonton, AB, Canada. [Google Scholar]
6. Peng, X., Yuan, H., Yang, Y. (2017). Pythagorean fuzzy information measures and their applications. International Journal of Intelligent Systems, 32(10), 991–1029. [Google Scholar]
7. Peng, X., Selvachandran, G. (2019). Pythagorean fuzzy set: State of the art and future directions. Artificial Intelligence Review, 52, 1873–1927. [Google Scholar]
8. Yager, R. R. (2016). Generalized orthopair fuzzy sets. IEEE Transactions on Fuzzy Systems, 25(5), 1222–1230. [Google Scholar]
9. Wang, P., Wang, J., Wei, G., Wei, C. (2019). Similarity measures of q-rung orthopair fuzzy sets based on cosine function and their applications. Mathematics, 7(4), 340. [Google Scholar]
10. Donyatalab, Y., Farrokhizadeh, E., Seyfi Shishavan, S. A. (2021). Similarity measures of q-rung orthopair fuzzy sets based on square root cosine similarity function. Intelligent and Fuzzy Techniques: Smart and Innovative Solutions: Proceedings of the INFUS 2020 Conference, pp. 475–483. Istanbul, Turkey. [Google Scholar]
11. Jana, C., Senapati, T., Pal, M. (2019). Pythagorean fuzzy Dombi aggregation operators and its applications in multiple attribute decision-making. International Journal of Intelligent Systems, 34(9), 2019–2038. [Google Scholar]
12. Jana, C., Muhiuddin, G., Pal, M. (2019). Some Dombi aggregation of Q-rung orthopair fuzzy numbers in multiple-attribute decision making. International Journal of Intelligent Systems, 34(12), 3220–3240. [Google Scholar]
13. Qiyas, M., Naeem, M., Abdullah, S., Khan, N., Ali, A. (2022). Similarity measures based on q-rung linear diophantine fuzzy sets and their application in logistics and supply chain management. Journal of Mathematics, 2022, 1–19. [Google Scholar]
14. Kutlu Gündoğdu, F., Kahraman, C. (2019). Spherical fuzzy sets and spherical fuzzy TOPSIS method. Journal of Intelligent & Fuzzy Systems, 36(1), 337–352. [Google Scholar]
15. Ahmmad, J., Mahmood, T., Chinram, R., Iampan, A. (2021). Some average aggregation operators based on spherical fuzzy soft sets and their applications in multi-criteria decision making. AIMS Mathematics, 6(7), 7798–7833. [Google Scholar]
16. Kutlu Gündoğdu, F., Kahraman, C. (2021). Properties and arithmetic operations of spherical fuzzy sets. In: Decision making with spherical fuzzy sets: Theory and applications, pp. 3–25. Springer. [Google Scholar]
17. Shishavan, S. A. S., Gündoğdu, F. K., Farrokhizadeh, E., Donyatalab, Y., Kahraman, C. (2020). Novel similarity measures in spherical fuzzy environment and their applications. Engineering Applications of Artificial Intelligence, 94, 103837. [Google Scholar] [PubMed]
18. Rafiq, M., Ashraf, S., Abdullah, S., Mahmood, T., Muhammad, S. (2019). The cosine similarity measures of spherical fuzzy sets and their applications in decision making. Journal of Intelligent & Fuzzy Systems, 36(6), 6059–6073. [Google Scholar]
19. Khan, M. J., Kumam, P., Deebani, W., Kumam, W., Shah, Z. (2020). Distance and similarity measures for spherical fuzzy sets and their applications in selecting mega projects. Mathematics, 8(4), 519. [Google Scholar]
20. Rayappan, P., Mohana, K. (2021). Spherical fuzzy cross entropy for multiple attribute decision making problems. Journal of Fuzzy Extension and Applications, 2(4), 355–363. [Google Scholar]
21. Mao, X., Zhao, G., Fallah, M., Edalatpanah, S. A. (2020). A neutrosophic-based approach in data envelopment analysis with undesirable outputs. Mathematical Problems in Engineering, 2020, 1–8. [Google Scholar]
22. Kouatli, I. (2022). Modeling fuzzimetric cognition of technical analysis decisions: Reducing emotional trading. Journal of Fuzzy Extension and Applications, 3(1), 45–63. [Google Scholar]
23. Iqbal, S., Yaqoob, N. (2023). Ranking of linear Diophantine fuzzy numbers using circumcenter of centroids. AIMS Mathematics, 8(4), 9840–9861. [Google Scholar]
24. Hasan, M. K., Ali, M., Sultana, A., Mitra, N. K. (2022). Some picture fuzzy mean operators and their applications in decision-making. Journal of Fuzzy Extension and Applications, 3(4), 349–361. [Google Scholar]
25. Wang, P., Wang, J., Wei, G. (2021). The generalized dice similarity measures for spherical fuzzy sets and their applications. In: Decision making with spherical fuzzy sets: Theory and applications, pp. 85–110. Springer. [Google Scholar]
26. Wei, G., Wang, J., Lu, M., Wu, J., Wei, C. (2019). Similarity measures of spherical fuzzy sets based on cosine function and their applications. IEEE Access, 7, 159069–159080. [Google Scholar]
27. Mahmood, T., Ilyas, M., Ali, Z., Gumaei, A. (2021). Spherical fuzzy sets-based cosine similarity and information measures for pattern recognition and medical diagnosis. IEEE Access, 9, 25835–25842. [Google Scholar]
28. Mohammad, M. M. S., Abdullah, S., Al-Shomrani, M. M. (2022). Some linear Diophantine fuzzy similarity measures and their application in decision making problem. IEEE Access, 10, 29859–29877. https://doi.org/10.1109/ACCESS.2022.3151684 [Google Scholar] [CrossRef]
29. Donyatalab, Y., Gündoğdu, F. K., Farid, F., Seyfi-Shishavan, S. A., Farrokhizadeh, E. et al. (2022). Novel spherical fuzzy distance and similarity measures and their applications to medical diagnosis. Expert Systems with Applications, 191, 116330. [Google Scholar]
30. Bonab, S. R., Ghoushchi, S. J., Deveci, M., Haseli, G. (2023). Logistic autonomous vehicles assessment using decision support model under spherical fuzzy set integrated Choquet Integral approach. Expert Systems with Applications, 214, 119205. [Google Scholar]
31. Ma, Q. X., Zhu, X. M., Bai, K. Y., Zhang, R. T., Liu, D. W. (2023). A novel failure mode and effect analysis method with spherical fuzzy entropy and spherical fuzzy weight correlation coefficient. Engineering Applications of Artificial Intelligence, 122, 106163. [Google Scholar]
32. Ali, J., Garg, H. (2023). On spherical fuzzy distance measure and TAOV method for decision-making problems with incomplete weight information. Engineering Applications of Artificial Intelligence, 119, 105726. [Google Scholar]
33. Das, A. K., Granados, C. (2023). IFP-intuitionistic multi fuzzy N-soft set and its induced IFP-hesitant N-soft set in decision-making. Journal of Ambient Intelligence and Humanized Computing, 14, 10143–10152. https://doi.org/10.1007/s12652-021-03677-w [Google Scholar] [CrossRef]
34. Khan, M. R., Ullah, K., Khan, Q. (2023). Multi-attribute decision-making using Archimedean aggregation operator in T-spherical fuzzy environment. Reports in Mechanical Engineering, 4(1), 18–38. [Google Scholar]
35. Huang, C., Lin, M., Xu, Z. (2020). Pythagorean fuzzy MULTIMOORA method based on distance measure and score function: Its application in multicriteria decision making process. Knowledge and Information Systems, 62, 4373–4406. [Google Scholar]
36. Xiao, F., Ding, W. (2019). Divergence measure of Pythagorean fuzzy sets and its application in medical diagnosis. Applied Soft Computing, 79, 254–267. [Google Scholar]
37. Ashraf, S., Abdullah, S. (2019). Spherical aggregation operators and their application in multiattribute group decision-making. International Journal of Intelligent Systems, 34(3), 493–523. [Google Scholar]
38. Razzaque, H., Ashraf, S., Kallel, W., Naeem, M., Sohail, M. (2023). A strategy for hepatitis diagnosis by using spherical q-linear Diophantine fuzzy Dombi aggregation information and the VIKOR method. Aims Mathematics, 8(6), 14362–14398. [Google Scholar]
39. Sharaf, I. M. (2023). The differential measure for Pythagorean fuzzy multiple criteria group decision-making. Complex & Intelligent Systems, 9, 3333–3354. https://doi.org/10.1007/s40747-022-00913-4 [Google Scholar] [PubMed] [CrossRef]
40. Ashraf, S., Razzaque, H., Naeem, M., Botmart, T. (2023). Spherical q-linear Diophantine fuzzy aggregation information: Application in decision support systems. AIMS Mathematics, 8(3), 6651–6681. [Google Scholar]
41. Song, C., Xu, Z., Hou, J. (2021). An improved TODIM method based on the hesitant fuzzy psychological distance measure. International Journal of Machine Learning and Cybernetics, 12(4), 973–985. [Google Scholar]
42. Yang, Q., Du, P. A. (2015). A straightforward approach for determining the weights of decision makers based on angle cosine and projection method. International Journal of Industrial and Manufacturing Engineering, 9(10), 3335–3341. [Google Scholar]
43. Koksalmis, E., Kabak, Ö. (2019). Deriving decision makers’ weights in group decision making: An overview of objective methods. Information Fusion, 49, 146–160. [Google Scholar]
44. Qu, S., Xu, Y., Wu, Z., Xu, Z., Ji, Y. et al. (2021). An interval-valued best-worst method with normal distribution for multi-criteria decision-making. Arabian Journal for Science and Engineering, 46, 1771–1785. [Google Scholar]
45. Zhang, X. (2016). A novel approach based on similarity measure for Pythagorean fuzzy multiple criteria group decision making. International Journal of Intelligent Systems, 31(6), 593–611. [Google Scholar]
46. Jin, Y., Lee, B. (2019). A comprehensive survey of issues in solid state drives. Advances in Computers, 114, 1–69. [Google Scholar]
47. Zhang, X., Xu, Z. (2014). Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. International Journal of Intelligent Systems, 29(12), 1061–1078. [Google Scholar]
48. Ren, P., Xu, Z., Gou, X. (2016). Pythagorean fuzzy TODIM approach to multi-criteria decision making. Applied Soft Computing, 42, 246–259. [Google Scholar]
49. Zeng, W., Li, D., Yin, Q. (2018). Distance and similarity measures of Pythagorean fuzzy sets and their applications to multiple criteria group decision making. International Journal of Intelligent Systems, 33(11), 2236–2254. [Google Scholar]
50. Garg, H. (2017). Confidence levels based Pythagorean fuzzy aggregation operators and its application to decision-making process. Computational and Mathematical Organization Theory, 23(4), 546–571. [Google Scholar]
51. Ananthakumar, S., Kumar, J. R., Babu, S. M. (2019). Third-generation solar cells: Concept, materials and performance-an overview. Emerging Nanostructured Materials for Energy and Environmental Science, 23, 305–339. [Google Scholar]
52. Giannouli, M. (2021). Current status of emerging PV technologies: A comparative study of dye-sensitized, organic, and perovskite solar cells. International Journal of Photoenergy, 2021, 1–19. [Google Scholar]
53. Liu, Z., Jin, Z., Li, G., Zhao, X., Badiei, A. (2022). Study on the performance of a novel photovoltaic/thermal system combining photocatalytic and organic photovoltaic cells. Energy Conversion and Management, 251, 114967. [Google Scholar]
54. Zhang, F., Wu, M., Hou, X., Han, C., Wang, X. et al. (2021). The analysis of parameter uncertainty on performance and reliability of photovoltaic cells. Journal of Power Sources, 507, 230265. [Google Scholar]
55. Socorro García-Cascales, M., Teresa Lamata, M., Miguel Sánchez-Lozano, J. (2012). Evaluation of photovoltaic cells in a multi-criteria decision making process. Annals of Operations Research, 199, 373–391. [Google Scholar]
56. Biswas, A., Sarkar, B. (2018). Pythagorean fuzzy multicriteria group decision making through similarity measure based on point operators. International Journal of Intelligent Systems, 33(8), 1731–1744. [Google Scholar]
57. U.S. National Cancer Institute's Surveillance, Epidemiology and End Results (SEER) Program. https://training.seer.cancer.gov/disease/categories/classification.html (Accessed on March 2023). [Google Scholar]
58. National Cancer Institute at the National Institutes of Health, USA. https://www.cancer.gov/about-cancer/diagnosis-staging/diagnosis (Accessed on March 2023). [Google Scholar]
59. Akram, M., Luqman, A., Kahraman, C. (2021). Hesitant pythagorean fuzzy ELECTRE-II method for multi-criteria decision-making problems. Applied Soft Computing, 108, 107479. [Google Scholar]
60. Akram, M., Ilyas, F., Al-Kenani, A. N. (2021). Two-phase group decision-aiding system using ELECTRE III method in Pythagorean fuzzy environment. Arabian Journal for Science and Engineering, 46, 3549–3566. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools