Electricity Carbon Quota Trading Scheme based on Certificateless Signature and Blockchain

1  Introduction

More than forty percent of all carbon emissions in China are produced by the electric power industry, making it a significant sector. In addition, according to a report by Ember, a UK-based independent climate think tank, carbon emissions from the power industry reached a new peak in 2021, rising by 778 million tons annually. According to research, limiting carbon emissions in the electricity industry is essential for achieving an early carbon emissions peak [1].

Carbon emissions are considered a commodity in carbon trading, which uses a market mechanism to raise the price of carbon emissions to regulate and lower them and to foster low-carbon, sustainable development. Government departments assign carbon emission quotas [2–4] to each firm in accordance with predetermined guidelines to attain the objectives of “carbon peaking” and “carbon neutrality”. Suppose the actual carbon emissions of an enterprise are higher than the initial quota allocated by the government. If an enterprise’s actual carbon emissions exceed the initial quota assigned by the government, the enterprise must acquire the additional quota on the carbon trading market. Using energy-saving and emission-reduction technologies, if an enterprise’s actual carbon emissions are lower than the government-allocated quota, it can sell and trade the excess carbon quota to generate revenue. Fig. 1 depicts the carbon quota trading procedure between two businesses.

Figure 1: Overview of carbon quota trading

Blockchain technology has the characteristics of immutability and transaction traceability, providing technical support for the realization of secure and trusted carbon quota trading. Zhang et al. [5] established a carbon quota trading model with blockchain technology to ensure the fairness of carbon quota allocation. Zhu et al. [6] proposed a multi-energy primary energy storage optimization configuration model based on blockchain to improve energy self-sufficiency. Ji et al. [7] designed an electricity carbon rights trading mechanism based on an alliance chain to improve the market returns of all participants. Yuan et al. [8] used blockchain technology to build a carbon emission data-sharing platform to realize the traceability and sharing of carbon trading. However, these schemes still suffered from complex key management and low transaction efficiency.

Certificateless signatures maintain the advantages of identity-based cryptographic systems without vital public certificates and can ensure the integrity, identity authentication, and nonrepudiation of carbon quota trading. Electricity carbon quota trading scheme based on certificateless signature and blockchain offers several advantages:

Efficiency: Traditional carbon quota trading requires the involvement of government regulatory bodies for verification and approval, which is time-consuming and costly. However, Certificateless signature and blockchain-based scheme eliminates the need for certificate verification and enables fast, automated transaction verification and settlement, reducing intermediaries and increasing transaction efficiency.

Security: The scheme based on certificateless signature uses digital signatures to verify information authenticity, while blockchain technology ensures the immutability of transaction records, guaranteeing transaction safety and reliability.

Decentralization: The blockchain-based scheme does not require a centralized platform as an intermediary; all transactions are recorded on the blockchain, enhancing transaction transparency and traceability while removing intermediaries.

Compared to traditional schemes, the proposed Electricity Carbon Quota Trading Scheme based on Certificateless Signature and Blockchain has the following advantages:

1. Traditional schemes rely on third-party certificate authorities for identity verification, adding extra time and expense. But the certificateless public key cryptography-based scheme is decentralized and does not require certificate verification, thus enabling faster transactions.

2. The use of digital signature verification ensures transactional authenticity and integrity, while blockchain technology enforces immutability, guaranteeing transaction safety and reliability.

3. Traditional schemes require businesses to purchase a fixed number of carbon quotas. By contrast, the certificateless signature and blockchain-based scheme allow for instantaneous carbon quota trading, making it more flexible.

4. Traditional schemes require payment of multiple types of fees and costs, while the certificateless signature and blockchain-based solution can reduce transaction costs.

In conclusion, the electricity carbon quota trading scheme based on certificateless signature and blockchain provides greater efficiency, security, and decentralization compared to traditional schemes. Researchers have presented several certificateless signature techniques [9–11] in recent years. The user’s private key is divided into two pieces for the certificateless signature: a secret value chosen randomly by the user and a partial private key derived by the semi-trusted key generation center (KGC). For the security of certificateless signature schemes, attackers are divided into two categories: one is the attacker that imitates malicious users, usually known as the first type of attacker A1. It can launch public key replacement attacks and mastering user secret values but is unaware of KGC’s master key. The KGC attacker is an additional type of attacker that mimics malicious attacks. It is usually called the second type of attacker A2. It has access to the master key of the KGC, but it is prohibited from launching public key replacement attacks and cannot determine the user’s secret value. Mei et al. [12] suggested a certificateless signature scheme that enables conditional privacy protection; however, signature verification efficiency might be improved. Deng et al. [13] proposed a new certificateless signature scheme, but it could not resist replay attacks and did not consider anonymity. To solve these problems, Wang et al. [14] proposed an undocumented signature scheme that supports anonymity and traceability (referred to as Wang et al.’s scheme). Wang et al. [15] have presented a novel blockchain-based smart car carbon emission cap-and-trade system. The proposed system employs a dual-chain architecture, wherein the data chain is utilized to chronicle the data collated from automobiles to guarantee the dependability of the data, thereby ensuring correctness of the carbon emission calculation outcomes. Luo et al. [16] have proposed a carbon quota trading scheme for power generation based on blockchain technology, which integrates lightweight certificateless signature technology and smart contracts to realize an automated carbon quota trading mechanism. However, we find that Wang et al.’s scheme has security defects and cannot resist signature forgery attacks launched by two types of attackers.

Our contributions: To ensure the integrity and identity authentication of electricity carbon quota trading, we propose a scheme of electricity carbon quota trading based on the blockchain and certificateless signatures. The main work is as follows:

(1) We evaluate the security of Wang et al.’s scheme and present two types of forgery attacks.

(2) Aiming at the security defects of Wang et al.’s scheme, we propose an improved certificateless signature scheme.

(3) We suggest an improved signature method and blockchain technology-based trading scheme to make electric carbon quota trading tamper-proof and traceable.

(4) A security study demonstrates that our scheme has low computing and communication costs, provides anonymity and traceability of power enterprise identification, and can withstand forgery and replay attacks.

2  Preparatory Knowledge

Let p and q be two large prime numbers, G1 and G2 be two cyclic groups of order q, G be a cyclic group of order p, and P~ and P be generators of G and G1, respectively.

2.1 Bilinear Mapping

A bilinear map e:G1×G1→G2 has the following properties:

(1) Bilinear: For any a,b∈Zq∗, there is e(aP,bP)=e(P,P)ab.

(2) Nonregressive: e(P,P)≠1.

(3) Validity: There is an effective algorithm to calculate e(aP,bP).

(q,G1,G2,e,P) satisfying the above conditions is usually called a bilinear group [14].

2.2 Difficult Assumptions

Computational Diffie Hellman (CDH) problem: Given a tuple (P,aP,bP)∈G13, where a,b∈Zq∗, calculate abP.

Definition 1 The CDH hypothesis is said to be valid if there is no polynomial-time algorithm that can solve the CDH issue with a nonnegligible probability [8].

Discrete Logarithms (DL) Problem: Given a tuple (P~,P~z)∈G2 and calculate z∈Zp∗.

Definition 2 The DL hypothesis is said to be true if there is no polynomial-time algorithm that can solve the DL problem with a nonnegligible probability [11].

2.3 Security Model

The central objective of our security model is to comprehensively address the security challenges related to carbon emission quotas in the electricity trading market. Specifically, the proposed model strives to prevent various types of malicious attacks, such as data falsification, tampering, forgery, and replay attacks.

To overcome the limitations imposed by traditional cryptography’s reliance on fundamental certification requirements and avoid critical custody issues based on identity-based cryptography, a certificate-free signature scheme has been proposed as a feasible solution. The proposed certificate-free signature scheme is highly secure and efficient, aimed at ensuring the validity and non-repudiation of all transactions involved in carbon emission quota trading. In addition, blockchain technology has been deployed to achieve the immutability and traceability of all power carbon quota transactions. This scheme provides conditional identity privacy protection, enhances defense against replay attacks, and has high computational and communication performance.

In response to the security vulnerabilities of Wang et al.’s scheme, we propose the security model for our scheme and divide the adversaries of the certificate-free signing scheme into two categories: 𝒜1 and A2.

𝒜1: These are adversaries who launch forged attacks against malicious users. They can select a target user with a pseudonym PID1∗, obtain their secret value x1∗ and public key PK1∗=(X1∗,R1∗), and attempt to obtain a legal signature for any message of the target user through a series of forged attacks, as described in detail in the following text.

A2: These are adversaries who launch forged attacks against malicious KGCs. As malicious KGCs, they not only know the main secret key of KGC and partial private key d2∗ of users but also can modify system parameters. They can first select a target user for the attack, obtain their pseudonym PID2∗ and public key PK2∗=(X2∗,R2∗), and then attempt to forge a legal signature for any message of the target user through a series of forged attacks, as described in detail in the following text.

3  Security Analysis of Wang et al.’s Scheme

This section focuses mostly on reviewing the certificateless signature scheme proposed by Wang et al. [14], analyzing its security, and presenting the related enhancement scheme.

3.1 Wang et al.’s Scheme Description

The certificateless signature of Wang et al.’s scheme consists of the six methods listed below:

(1) System establishment: Given a security parameter ζ, the KGC generates system parameters and master keys using the following procedures.

① Select bilinear groups (q,G1,G2,e,P) and Q∈G1.

② Select random number s,k∈Zq∗ as the master key and then calculate Ppub=sP.

③ Select three hash functions H1:G1→Zq∗, H2:{0,1}∗×G1→Zq∗, and H3:{0,1}∗×{0,1}∗×G1× G1×G1→Zq∗.

④ Expose the system parameter params={q,G1,G2,e,P,Ppub,Q,H1,H2,H3}.

(2) Pseudonym generation: The user whose real identity is IDi selects a random number ti∈Zq∗, calculates Ti=tiP, and secretly sends (IDi,Ti) to the KGC.

After receiving (IDi,Ti), the KGC verifies the correctness of IDi, computes PIDi=IDi ⊕H1(kP+Ti) using the master key k, and finally sends the user the pseudonym PIDi.

(3) Generation of partial private keys: The KGC generates partial private keys for users with the alias PIDi using the following methods:

① Select a random number ri∈Zq∗ and then calculate Ri=riP.

② Calculate ki=H2(PIDi,Ri).

③ Calculate partial private key di=ri+kismodq.

④ Send (di,Ri) to the user through the secure channel.

(4) Public/private key generation: After receiving (di,Ri) from KGC, the user using pseudonym PIDi chooses a random number xi∈Zq∗, computes Xi=xiP, and establishes public key PKi=(Xi,Ri) and private key SKi=(xi,di).

(5) Signature generation: For message mi, the user with pseudonym PIDi generates the signature of mi.

① Randomly select ui∈Zq∗, and calculate Ui=uiP and Vi=uiQ.

② Select a timestamp TSi and calculate hi=H3(mi∥TSi,PIDi,Ui,Vi,PKi).

③ Calculate Wi=(di+hixi)Q+Vi.

④ Output a signature σi=(Ui,Vi,Wi) of mi∥TSi.

(6) Signature verification: The verifier goes through the following motions to ensure that mi∥TSi’s signature on σi=(Ui,Vi,Wi) is legitimate.

① Check the freshness of TSi. If TSi is within the effective time, perform the following operation ②; otherwise, terminate the operation.

② Calculate ki=H2(PIDi,Ri) and hi=H3(mi∥TSi,PIDi,Ui,Vi,PKi).

③ Verify equation e(Wi,P)=e(Ri+kiPpub+hiXi+Ui,Q).

The verifier accepts the signature if the aforementioned equation is true; otherwise, σi is rejected.

The relevant process of the Wang et al.’s scheme is shown in Fig. 2.

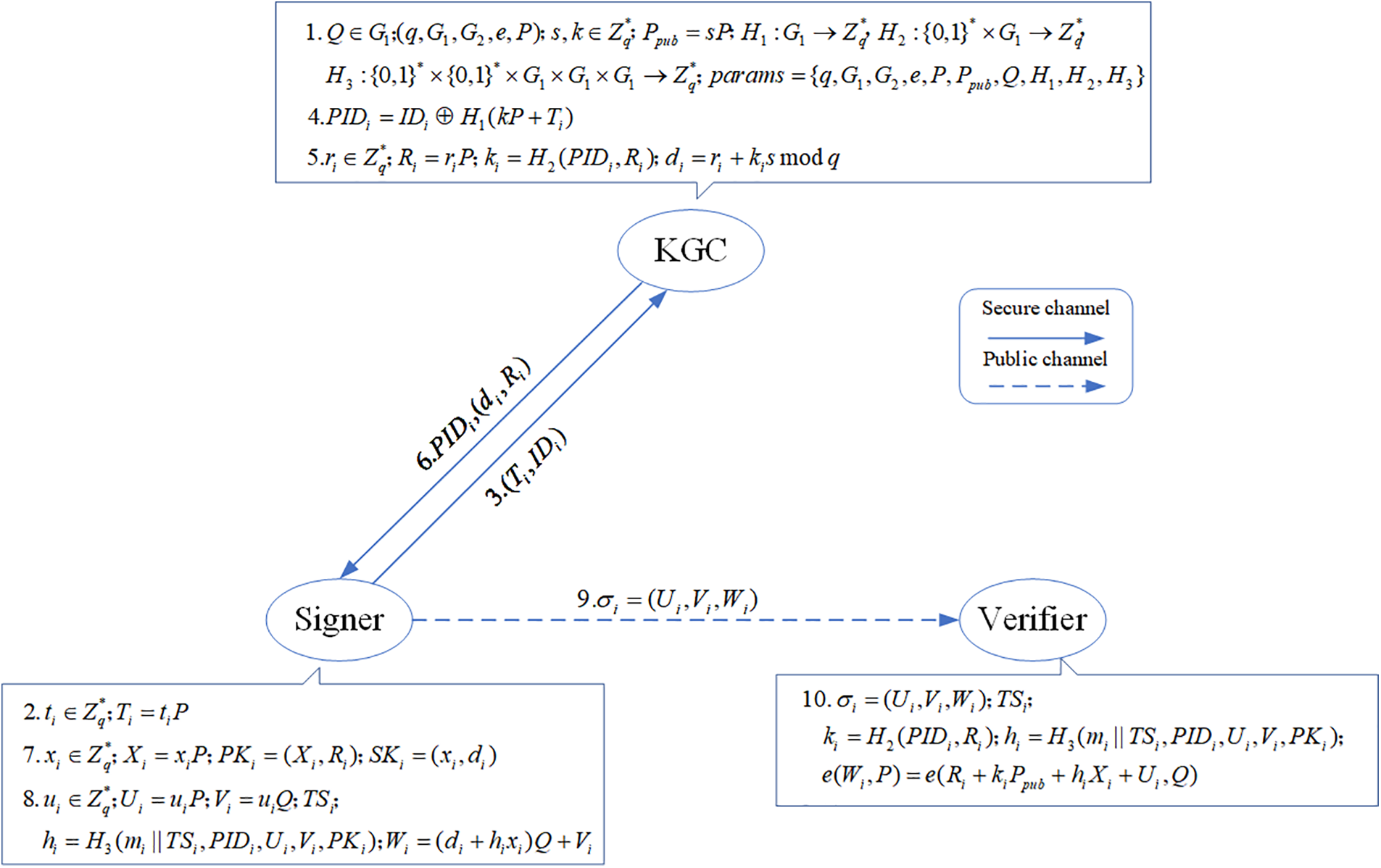
Figure 2: Wang et al.’s scheme

3.2 Forgery Attack of Wang et al.’s Scheme

Here are the specific steps for the two forgery attacks that Wang et al.’s scheme cannot resist.

(1) Forgery attack by malicious users: Let 𝒜1 be the first type of attacker targeting Wang et al.’s scheme. 𝒜1 selects a target user with pseudonym PID1∗ and obtains its secret value x1∗ and public key PK1∗=(X1∗,R1∗). Through the subsequent attack methods, 𝒜1 can falsify the target user’s actual signature on any message.

① Calculate k1∗=H2(PID1∗,R1∗).

② Select z1∗∈Zq∗ at random and compute U1∗=z1∗P−k1∗Ppub−R1∗ and V1∗=z1∗Q.

③ Select message m1∗ and timestamp TS1∗ at random and calculate h1∗=H3(m1∗∥TS1∗,PID1∗,U1∗,V1∗,PK1∗).

④ Calculate W1∗=(z1∗+h1∗x1∗)Q.

⑤ Output m1∗∥TS1∗ to forge signature σ1∗=(U1∗,V1∗,W1∗).

The following verifies the legitimacy of 𝒜1’s forged signature σ1∗:

e(W1∗,P)=e((z1∗+h1∗x1∗)Q,P)=e((z1∗+h1∗x1∗)P,Q)=e(z1∗P+h1∗(x1∗P),Q)=e((U1∗+k1∗Ppub+R1∗)+h1∗X1∗,Q)=e(R1∗+k1∗Ppub+h1∗X1∗+U1∗,Q)

The given reasoning demonstrates that σ1∗ satisfies Wang et al.’s signature verification equation. In the above attack, 𝒜1 does not know the master key of the KGC. Therefore, 𝒜1’s assault based on forgery is successful. Wang et al.’s scheme is not secure against the first type of forgery attacker 𝒜1.

(2) Forgery attack of malicious KGC: Let A2 be the second type of attacker against Wang et al.’s scheme. A2 selects a target user and obtains its pseudonym PID2∗ and public key PK2∗=(X2∗,R2∗). Because A2 is a malicious KGC, it not only knows the KGC’s master key and part of the user’s private key d2∗ but can also modify system parameters. A2 can fake the valid signature of the target user for any information via the following attack techniques:

① Select a random number z2∗∈Zq∗, calculate Q∗=z2∗P, and make parameter params= {q,G1,G2,e,P,Ppub,Q∗,H1,H2,H3} public.

② Select u2∗∈Zq∗ at random and calculate U2∗=u2∗P and V2∗=u2∗Q∗.

③ Select message m2∗ and timestamp TS2∗ at random and calculate h2∗=H3(m2∗∥TS2∗,PID2∗,U2∗,V2∗,PK2∗).

④ Calculate W2∗=d2∗Q∗+h2∗(z2∗X2∗)+V2∗.

⑤ Output m2∗∥TS2∗ to forge signature σ2∗=(U2∗,V2∗,W2∗).

The following verifies the legitimacy of the signature forged by A2:

e(W2∗,P)=e(d2∗Q∗+h2∗(z2∗X2∗)+V2∗,P)=e(d2∗Q∗+h2∗z2∗(x2∗P)+V2∗,P)=e(d2∗Q∗+h2∗x2∗(z2∗P)+V2∗,P)=e(d2∗Q∗+h2∗x2∗Q∗+V2∗,P)=e((d2∗+h2∗x2∗)Q∗+V2∗,P)=e(R2∗+k2∗Ppub+h2∗X2∗+U2∗,Q∗)

The given reasoning demonstrates that σ2∗ satisfies Wang et al.’s signature verification equation. However, A2 does not know the target user’s secret value x2∗ in the above attack. Therefore, A2’s forgery attack is successful. Wang et al.’s scheme is also unsafe for the second type of forgery attacker A2.

3.3 Improved Certificateless Signature Scheme

To address the security flaws of Wang et al.’s scheme, we provide an enhanced certificateless signing scheme below. The cyclic group of the elliptic curve is chosen to improve the communication performance of the updated scheme. The specific description is as follows:

(1) System establishment: The KGC performs the following actions to produce system parameters and master keys based on security parameter ζ:

① Select an elliptic curve cyclic group G of prime p and a generator P of G.

② Select a random number s,k∈Zp∗ as the master key and then calculate Ppub=sP.

③ Select four hash functions: H1:G1→Zq∗, H2:{0,1}∗×G1×G1→Zq∗, H3:{0,1}∗×{0,1}∗×G1×G1 →Zq∗, H4:Zq∗×G1→Zq∗.

④ Expose system parameter params={q,G1,G2,e,P,Ppub,H1,H2,H3,H4}.

(2) Kana generation: This algorithm is the same as Wang et al.’s scheme.

(3) Partial private key generation: This algorithm is the same as Wang et al.’s scheme, but the only difference is that the value of ki is ki=H2(PIDi,Ri,Ppub).

(4) Public/private key generation: This algorithm is the same as Wang et al.’s scheme.

(5) Signature generation: For message mi, the user with pseudonym PIDi generates mi’s signature.

① Randomly select ui∈Zp∗ and then calculate Ui=uiP.

② Select a timestamp TSi and calculate hi=H3(mi∥TSi,PIDi,Ui,PKi), li=H4(hi,Ppub).

③ Calculate wi=ui+hixi+lidimodp.

④ Output signature σi=(Ui,wi) of mi∥TSi.

(6) Signature verification: The verifier performs the following steps to check the validity of mi∥TSi’s signature σi=(Ui,wi).

① Check the freshness of TSi. If TSi is within the valid time, perform the following operation ②; otherwise, terminate the operation.

② Calculate ki=H2(PIDi,Ri,Ppub),

hi=H3(mi∥TSi,PIDi,Ui,PKi),

li=H4(hi,Ppub).

③ Verify equation wiP=Ui+hiXi+li(Ri+kiPpub).

If the above formula is true, the verifier accepts the signature; otherwise, it rejects σi.

The related process of the Improved certificateless signature scheme is shown in Fig. 3.

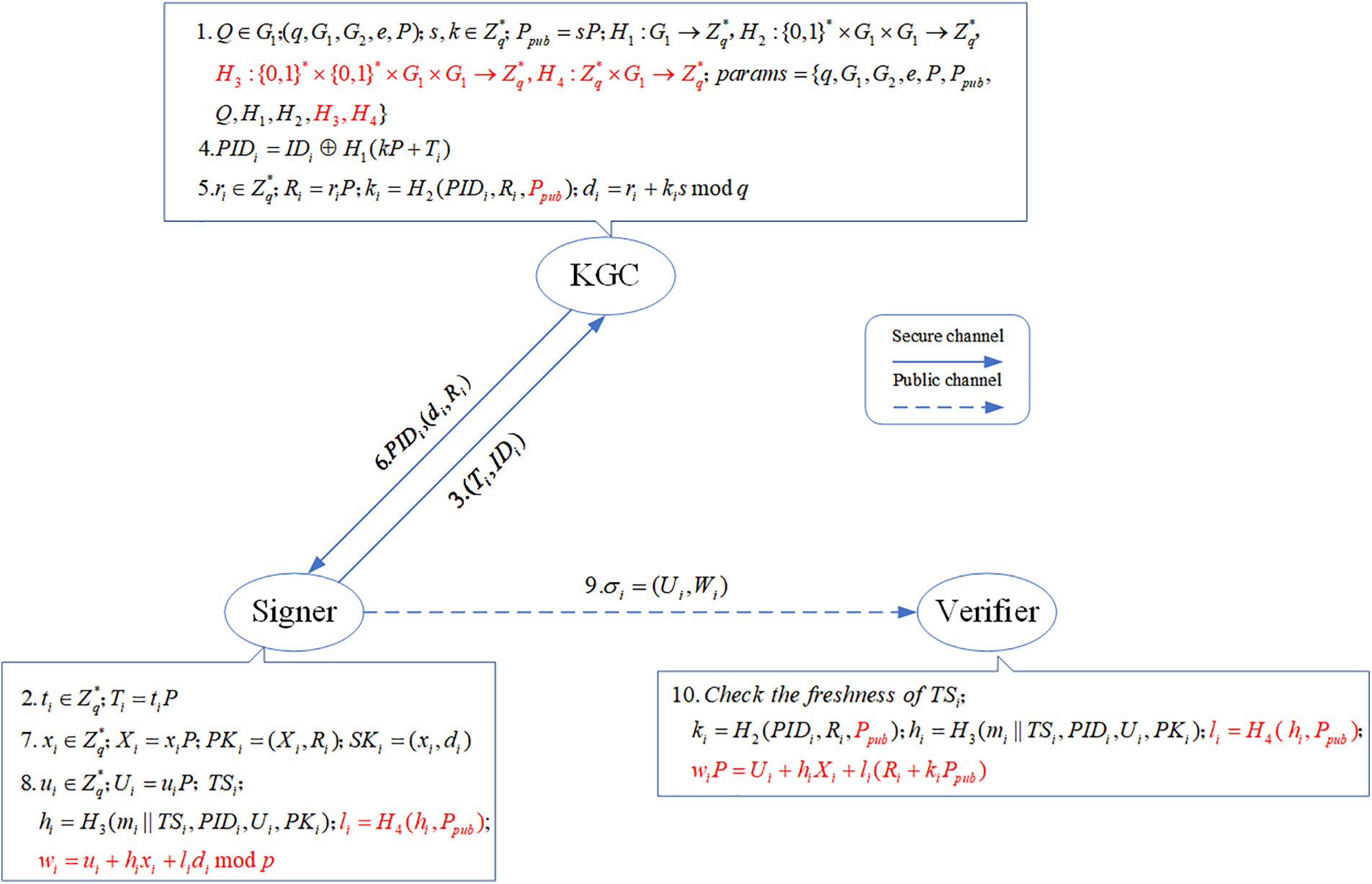
Figure 3: Improved certificateless signature scheme

In the hash value hi=H3(mi∥TSi,PIDi,Ui,PKi), (Ui,PKi) is the input value of hi; in ki=H2 (PIDi,Ri,Ppub), (Ri,Ppub) is the input value of ki; and in li=H4(hi,Ppub), (hi,Ppub) is the input value of li. In addition, wi binds the hash function to the secret value and partial private key. Based on the unidirectional and anti-collision properties of the hash function, the attacker cannot forge valid signatures by modifying system parameters and replacing public keys. Consequently, the modified scheme is resistant to the two types of forgery attacks outlined in Section 3.2.

4  Electricity Carbon Quota Trading Scheme Based on Certificateless Signature and Blockchain

Based on the improved certificateless signing scheme and blockchain technology presented in Section 3.3, we propose and analyze a secure and effective power carbon quota trading scheme.

4.1 System Model

The carbon quota trading model proposed in this paper is shown in Fig. 4, including six participants: the environmental protection management department (EPMD), quota seller enterprise (QSE), blockchain network (BN), quota buyer enterprise (QBE), audit department (AD), and distributed storage hash table (DSHT).

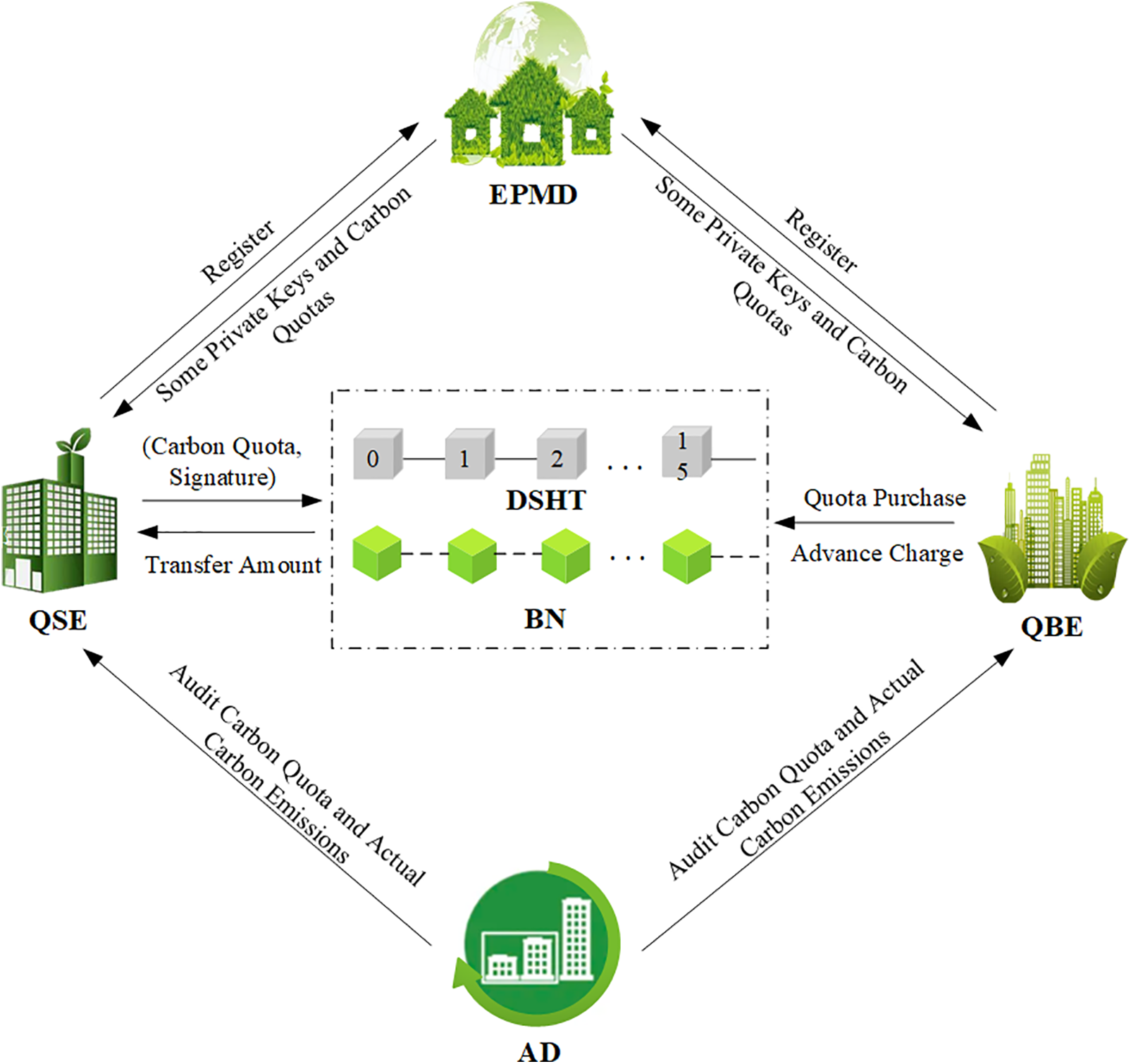
Figure 4: System model

(1) EPMD: Mainly responsible for system initialization, maintenance of the blockchain network, and distribution of some private keys and initial carbon quotas of power enterprises.

(2) QSE: Power enterprises with surplus carbon quotas sign the carbon quota to be sold and then publish it to the blockchain network for trading.

(3) BN: This network is mainly accountable for processing the storage and transaction requests of power carbon quota transactions and validating transaction legitimacy.

(4) QBE: Power enterprises with insufficient carbon quotas purchase carbon quotas through the blockchain network and pay transaction costs to the seller enterprises.

(5) AD: Mainly audits electric power enterprise carbon emission quotas and actual carbon emissions and assists the environmental protection management department in resolving transaction disputes.

(6) DSHT: Mainly stores relevant data on electric power enterprises and carbon quota transactions. Essentially, it is a distributed storage space that divides the data into several small pieces, gives them to different clients for storage, and then uses the storage address to read the data.

4.2 Scheme Description

(1) System initialization: The environmental management department runs the system establishment algorithm of the improved certificateless signature scheme described in Section 3.3 and sets s,k∈Zp∗ as the master secret key and public parameter params={q,G1,G2,e,P,Ppub,H1,H2,H3,H4}.

(2) Enterprise registration: The power enterprise whose real identity is IDi selects a random number ti∈Zp∗, calculates Ti=tiP, and secretly sends (IDi,Ti) to the environmental protection management department.

After receiving (IDi,Ti), the environmental protection management department performs the following operations:

① Verify the identity information of IDi and then calculate the corresponding power enterprise pseudonym PIDi=IDi⊕H1(kP+Ti).

② Save (IDi,PIDi,Ti) in power enterprise information table LID.

③ Select a random number ri∈Zq∗ and then calculate Ri=riP.

④ Calculate ki=H2(PIDi,Ri,Ppub).

⑤ Calculate the partial private key di=ri+kismodq.

⑥ Allocate the initial carbon emission quota mi of power enterprises.

⑦ Send (PIDi,di,Ri,mi) to the enterprise through the secure channel.

⑧ Publish a correctly registered transaction TID={PIDi,mi,AddrIDi} of the power enterprise on the blockchain network, where AddrIDi is the address of the distributed storage hash table used for storage. Create the enterprise credit pool KC in the common storage area and save (PIDi,ci,mi) in KC. ci represents the enterprise credit degree, and the initial value is 0. If ci=0, the enterprise credit rating is good; if ci=1, the enterprise credit rating is poor.

After receiving (PIDi,di,Ri,mi) from the department of environmental protection management, the power enterprise chooses a random number xi∈Zq∗ and generates the private key SKi=(xi,di) and the public key PKi=(Xi=xiP,Ri).

(3) Quota sale: For the surplus electric power carbon emission quota mi,1, the power enterprise with the pseudonym PIDi performs the following sales operations.

① Execute the signature generation process outlined in Section 3.3 of the enhanced certificateless signature scheme and generate the signature σi=(Ui,wi) of mi,1∥TSi.

② Publish on the blockchain a transaction Ti={PIDi,PKi,mi,1,Addri,σi} for the sale of energy carbon quotas, where Addri is the address where (PIDi,PKi,mi,1,TSi,σi) is stored in the distributed storage hash table.

(4) Quota purchase: When the enterprise with the pseudonym PIDj purchases the electricity carbon quota mi,1, the purchase transaction Tj={PIDj,PKj,Addri,θj} is broadcast in the blockchain network, where PIDj and PKj are the pseudonym and public key of the buyer’s enterprise, and θj is the prepayment amount. The blockchain node takes (PIDi,PKi=(Xi,Ri),mi,1,TSi,σi) from address Addri of the distributed storage hash table and then performs the following operations.

① Check the freshness of TSi. If |TSi−TS0|>λ, terminate the operation; otherwise, perform step ②, where TS0 and λ represent the maximum values of the current timestamp and the effective time, respectively.

② Find the cred KC value of the buyer’s enterprise and the seller’s enterprise in the enterprise credit pool KC. If ci=1 or cj=1 indicates that the credit degree of the buying and selling enterprises does not match and the electricity carbon quota transaction is risky, terminate the operation.

③ Perform the signature verification procedure described in Section 3.3 of the improved certificateless signature scheme. If σi is a legal signature, perform step ④; otherwise, terminate the operation.

④ If θj is less than the market selling price of mi,1, terminate the operation; otherwise, transfer to the quota seller according to θj to pay the purchase cost of the electricity carbon quota.

⑤ Send (PIDi,PKi,mi,1,TSi,σi) to the buyer’s enterprise.

⑥ In enterprise credit pool KC, modify the actual carbon quota of the seller’s enterprise to mi−mi,1 and the actual carbon quota of the buyer’s enterprise to mj+mi,1.

⑦ The enterprises of both parties shall go through the relevant carbon quota transfer filing formalities in the environmental protection management department and terminate the carbon quota transaction.

(5) Dispute arbitration: If there is a dispute regarding the electric carbon emission quota mi,1 sold by the seller’s enterprise, the audit department shall investigate the power enterprise’s actual carbon emissions and carbon quota. If there is any violation in the power enterprise, the audit department will set the credit value of the power enterprise to 1 in the enterprise credit pool KC and submit it to the environmental protection management department for corresponding punishment. The specific interaction between QSE, QBE, EPMD and blockchain is shown in Fig. 5.

Figure 5: The interactions between blockchain and entities

5  Security and Performance Analysis

5.1 Security Authentication

Based on the methods in [10,14], Theorem 1 and Theorem 2 prove that our proposed scheme can resist signature forgery attacks from malicious users and malicious KGCs.

Theorem 1 If the DL hypothesis is true, our scheme is unfakable for the first type of attacker.

Proof: If the first type of attacker C forges a valid signature of our scheme, then the DL problem can be solved by constructing an Algorithm C as the challenger. Given an instance of a DL problem (P,aP), C aims to calculate a∈Zp∗.

(1) System initialization: C sets Ppub=aP and then runs the system establishment algorithm to send the generated parameter paramsto𝒜1.

(2) Query: C creates 5 blank initialized tables {L1,L2,L3,L4,Lu} in response to 𝒜1′s request. Let PID∗ indicate the pseudonym of the target user.

① H1 query. When 𝒜1 queries H1(kP+Ti), if (kP+Ti,hti) exists in L1, C sends hit to 𝒜1; Otherwise, select hit∈Zp∗, store (kP+Ti,hti) in L1 and return hit to 𝒜1.

② H2 query. When 𝒜1 queries H2(PIDi,Ri,Ppub), if (PIDi,Ri,Ppub,ki) exists in L2, C sends ki to 𝒜1; Otherwise, select ki∈Zp∗, store (PIDi,Ri,Ppub,ki) in L2 and return ki to 𝒜1.

③ H3 query. When 𝒜1 queries H3(mi∥TSi,PIDi,Ui,PKi), if (mi∥TSi,PIDi,Ui,PKi,hi) exists in L3, C sends hi to 𝒜1; Otherwise, select hi∈Zp∗, return hi to 𝒜1 and store (mi∥TSi,PIDi,Ui,PKi,hi) in L3.

④ H4 query. When 𝒜1 queries H4(hi,Ppub), if (hi,Ppub,li) exists in L4, C sends li to 𝒜1; Otherwise, select li∈Zp∗, store (hi,Ppub,li) in L4 and return li to 𝒜1.

⑤ Public key query: When 𝒜1 queries PIDiʼs public key, if (PIDi,di,Ri,xi,Xi) exists in Lu, C sends (Xi,Ri) to 𝒜1; Otherwise, C performs the following operations:

• If PIDi≠PID∗, C randomly select xi,di,ki∈Zp∗, calculate Xi=xiP and Ri=diP−kiPpub, and there are (PIDi,di,Ri,xi,Xi) and (PIDi,Ri,Ppub,ki) respectively in Lu and L2, send (Xi,Ri) to 𝒜1.

• If PIDi=PID∗, C randomly select x∗,r∗∈Zp∗, calculate X∗=x∗P and R∗=r∗P. If (PID∗,⊥,R∗,x∗,X∗) exists in Lu, send (X∗,R∗) to 𝒜1.

⑥ Secret value query: When 𝒜1 queries the secret value of PIDi, C looks up (PIDi,di,Ri,xi,Xi) in Lu and returns xi to 𝒜1.

⑦ Partial private key query: When 𝒜1 queries PIDi’s partial private key, C looks up (PIDi,di,Ri,xi,Xi) in Lu and returns di to 𝒜1.

⑧ Public key replacement query: When 𝒜1 submits (PIDi,Xi′,Ri′), C replaces PIDi’s public key in Lu and sets Xi=Xi′ and Ri=Ri′.

⑨ Signature query: When 𝒜1 queries (mi∥TSi,PIDi)’s signature, C randomly selects wi,hi,li ∈Zp∗, looks up ki in L2, calculates Ui=wiP−hiXi−li(Ri+kiPpub) and returns (Ui,wi) to 𝒜1.

(3) Forgery: After a finite number of the above queries, 𝒜1 outputs the signature σ∗=(U∗,w∗) of m∗∥TS∗ under PID∗ and public key (X∗,R∗). According to forking lemma [17], C obtains another valid signature σ~=(U∗,w~) by using different output values k~ of the same random values U∗ and H2. Because w∗P=U∗+h∗X∗+l∗(R∗+k∗(aP)), w~P=U∗+h∗X∗+l∗(R∗+k~(aP)).

Therefore, w∗P−w~P=l∗k∗aP−l∗k~aP, so we can calculate a=(w∗−w~)(k∗−k~)−1(l∗)−1modp.

Nevertheless, the DL problem is difficult to solve in polynomial time, indicating that 𝒜1’s proposed attack is not feasible. Therefore, our scheme can resist signature forging attacks from malicious users.

Theorem 2 If the LD hypothesis is valid, our scheme is unforgeable for the second type of attacker.

The proving procedure for Theorem 2 is comparable to that of Theorem 1. Because the second sort of attacker has access to the KGC’s master key, partial private key queries and public key replacement queries are no longer conducted.

5.2 Security Analysis

(1) Anonymity: The real identity IDi of the power enterprise and the master key k of the environmental protection management department generate the pseudonym PIDi=IDi ⊕H1(kP+Ti) of the power enterprise. If the attacker cannot know k and Ti, he cannot calculate IDi from PIDi. The master key k is kept secret by the environmental protection management department, but deriving ti from Ti=tiP is equivalent to solving the DL problem. Therefore, our scheme satisfies the anonymity of power enterprise identity.

(2) Traceability: When there is a dispute in an enterprise-issued energy carbon quota transaction, the environmental protection management department looks up (IDi,PIDi,Ti) in the information table LID of the power enterprise through PIDi in the transaction and calculates IDi′=PIDi⊕H1(kP+Ti). If IDi′=IDi, the environmental protection management department can determine the real identity IDi of the power enterprise participating in the transaction. Therefore, our scheme satisfies the traceability of power enterprise identity.

(3) Integrity, authenticity, and nonrepudiation: The power carbon quota transaction issued by the enterprise of the seller must be appended with signature σi=(Ui,wi), and the transaction information Ti must be maintained in the blockchain. Theorems 1 and 2 demonstrate that adversaries cannot fabricate valid signatures of our scheme, and blockchain ensures the traceability and tamper-proofness of transaction data. Consequently, our scheme satisfies the integrity, authenticity, and nonrepudiation requirements of electrical carbon quota trading and is capable of withstanding attacks such as forgery, impersonation, and tampering.

(4) Resist replay attack: When the buyer’s enterprise purchases the electricity carbon quota, it checks the freshness of the transaction through timestamp TSi. Since TSi is the input value of hash values hi and li, if the attacker attempts to modify TSi, the signature cannot be verified. Therefore, our scheme can resist replay attacks.

5.3 Performance Analysis

Tables 1 and 2 exhibit the performance and function comparisons between our scheme and published schemes [10,11,14]. Reference [18] evaluated the operation time of cryptographic operations, where TM=1.9456 ms, TH=2.3366 ms, and TP=15.0738 ms. To achieve the same level of security in schemes based on the bilinear group and elliptic curve group, 512-bit prime numbers q and 160-bit prime numbers p are selected, respectively. Table 1 only considers the operations with high computational overhead. TM, TH, and TP are used to represent a dot product operation, hash operation mapped to point and bilinear pair operation, respectively; |p|, |G| and |G1| represent the length of an element in Zp, G, and G1, respectively. Our scheme is based on a cyclic group of an elliptic curve. and the signature verification phase does not involve time-consuming bilinear pair operations.

As seen in Tables 1 and 2, Figs. 6, and 7, compared with other schemes [10,11,14], our scheme has the minimum time cost in generating and verifying signatures and the shortest signature length. Our scheme introduces the use of blockchain technology to eliminate intermediaries and improve the efficiency, transparency, and traceability of carbon quota trading in the electricity industry.

Figure 6: Comparison of computational overhead

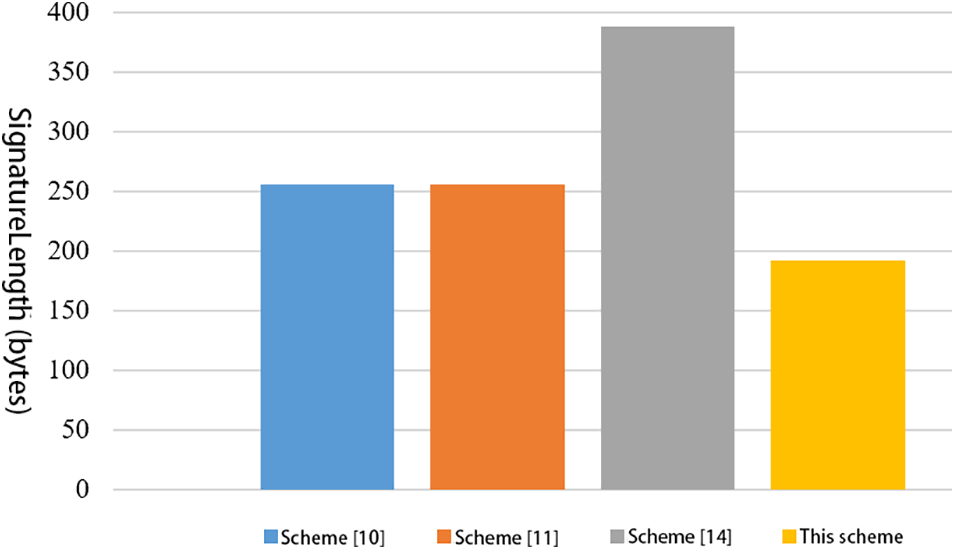
Figure 7: Comparison of signature length

The experimental environment for building the blockchain is Intel(R) Xeon(R) Gold 6133 2.50 GHz with Ubuntu Server 22.04 LTS 64-bit operating system, and the underlying platform for the blockchain is Hyperledger Fabric. The experiment simulated the generation of 1,000 to 5,000 user data entries, and tested the time it takes to upload the user data to the blockchain and the time it takes to retrieve the data from the blockchain. The specific test results are shown in Figs. 8 and 9.

Figure 8: User data upload time

Figure 9: User data return time

The test results show that as the amount of user data increases, the upload time slightly increases and the efficiency decreases slightly, but this decrease is within an acceptable range compared to the significant increase in data volume. When retrieving user data, the blockchain needs to run a consensus algorithm to disclose data to the nodes, and the degree of impact on time varies depending on the consensus algorithm used, so the retrieval time is slightly lower than the upload time.

6  Conclusions

We propose an efficient electricity carbon emission quota trading scheme based on an improved certificateless signature scheme and blockchain technology. Ensure the integrity and security of the transaction by signing without the certificate, and using the blockchain to store the transaction data to improve the anti-tampering and traceability of the power carbon quota transaction.

Our scheme provides conditional privacy protection, not only to protect the identity privacy of power enterprises but also to track the real identity of power enterprises that issue disputed transactions. However, our scheme does not consider the confidentiality of transaction data. Therefore, we plan to design a power carbon quota trading scheme based on blockchain and encryption technology in the future.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This research was supported by the National Fund Project No. 62172337, National Natural Science Foundation of China (No. 61662069) and China Postdoctoral Science Foundation (No. 2017M610817).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Xiaodong Yang, Runze Diao; data collection: Tao Liu, Haoqi Wen; analysis and interpretation of results: Tao Liu, Haoqi Wen. Haoqi Wen; draft manuscript preparation: Xiaodong Yang, Runze Diao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used to support the study's findings are included in the paper.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Lin, B., Zhou, Y. (2021). Does the internet development affect energy and carbon emission performance. Sustainable Production and Consumption, 28(6), 1–10. [Google Scholar]

2. Wang, R., Cheng, S., Zuo, X., Liu, Y. (2022). Optimal management of multi-stakeholder integrated energy system considering dual incentive demand response and carbon trading mechanism. International Journal of Energy Research, 46(5), 6246–6263. [Google Scholar]

3. Zhang, L., Li, S., Nie, Q., Hu, Y. (2022). A two-stage benefit optimization and multi-participant benefit-sharing strategy for hybrid renewable energy systems in rural areas under carbon trading. Renewable Energy, 189, 744–761. [Google Scholar]

4. Wang, X. Q., Su, C. W., Lobont, O. R., Li, H., Nicoleta-Claudia, M. (2022). Is China’s carbon trading market efficient? Evidence from emissions trading scheme pilots. Energy, 245, 123240. [Google Scholar]

5. Zhang, Y., Wu, Q., Hu, W. (2023). Carbon quota trading model based on quantum blockchain. Journal of Systems & Management, 32(2), 300–307. [Google Scholar]

6. Zhu, X., Fu, Q., Wen, H., Zhong, Y., Su, Z. et al. (2020). Optimal allocation model of multi-energy entity energy storage from the perspective of blockchain. Electric Power Automation Equipment, 40(8), 47–56. [Google Scholar]

7. Ji, B., Liu, Y., Zhu, L. (2020). Design of carbon emission permit trading mechanism in power industry based on consortium blockchain. Huadian Technology, 42(8), 32–40. [Google Scholar]

8. Yuan, L., Li, D. (2020). Carbon emission mechanism design based on blockchain technology. Cyberspace Security, 11(2), 111– 117. [Google Scholar]

9. Liu, Y., Wang, D., Wang, Z., Duan, R. (2020). Efficient revocable certificateless signature scheme for cloud computing. Computer Engineering and Design, 41(9), 2442–2446. [Google Scholar]

10. Wang, D., Teng, J. (2018). Probably secure certificate less aggregate signature algorithm for vehicular ad hoc. Network Journal of Electronics & Information Technology, 40(1), 11–17. [Google Scholar]

11. Xu, Z., He, D., Kumar, N., Choo, K. R. (2020). Efficient certificateless aggregate signature scheme for performing secure routing in VANETs. Security and Communication Networks, 2020(2), 1–12. [Google Scholar]

12. Mei, Q., Xiong, H., Chen, J., Yang, M., Kumari, S. et al. (2020). Efficient certificateless aggregate signature with conditional privacy preservation in IoV. IEEE Systems Journal, 15(1), 245–256. [Google Scholar]

13. Deng, L., Ning, B., Jiang, Y. (2020). A lightweight certificateless aggregation signature scheme with provable security in the standard model. IEEE Systems Journal, 14(3), 4242– 4251. [Google Scholar]

14. Wang, H., Wang, L., Zhang, K., Li, J., Luo, Y. (2022). A conditional privacy-preserving certificateless aggregate signature scheme in the standard model for VANETs. IEEE Access, 10, 15605–15618. [Google Scholar]

15. Wang, Y., Li, L., Zhang, Y., Zhao, B. (2022). STRICTs: A blockchain-enabled smart emission cap restrictive and carbon permit trading system. Applied Energy, 306, 117848. https://doi.org/10.1016/j.apenergy.2022.117848 [Google Scholar] [CrossRef]

16. Luo, J., Han, M., Wang, J. (2020). A blockchain-based electricity carbon quota trading scheme with lightweight certificateless signature. IEEE Access, 8, 222830–222840. [Google Scholar]

17. Bagherzandi, A., Cheon, J. H., Jarecki, S. (2008). Multi signatures secure under the discrete logarithm assumption and a generalized forking lemma. Proceedings of the 15th ACM Conference on Computer and Communications Security (CCS’08), pp. 449–458. New York, NY, USA, Association for Computing Machinery. [Google Scholar]

18. Cui, J., Wu, D., Zhang, J., Xu, Y., Zhong, H. (2019). An efficient authentication scheme based on semi-trusted authority in VANETs. IEEE Transactions on Vehicular Technology, 68(3), 2972–2986. [Google Scholar]