Optimization of Cooperative Relaying Molecular Communications for Nanomedical Applications

1  Introduction

Following the COVID-19 crisis with the increase of severe diseases, and the shortage of medical specialists, new healthcare monitoring technologies are required. One of these technologies is the nano-system (NS) for infectious disease diagnosis [1–3]. It can also be used to deliver therapeutic drugs to the targeted tissue. Furthermore, such nano-system networks can be remotely controlled and monitored using the Internet of Bio-Nano Things (IoBNT) technology [4,5]. The IoBNT is a broad paradigm for remotely managing a biological network of nanosystems, and thus interfacing the biological network with external networks such as the Internet [6,7]. The NS is made up of a collection of nanomachines such as nano-transmitter, nano-relay and nano-receiver that artificially mimic the biological cell [8]. Communication between nanomachines is accomplished through molecular communication via diffusion (MCvD). The MCvD has captured a particular interest due to its energy effectiveness and bio-compatibility. The molecular information in MCvD is encoded using a variety of methods, including molecular concentration, time, and molecular type [9]. In this study, we consider a hybrid encoding of molecular information by the emitted concentration and the molecular type. Additionally, in MCvD, the nano-transmitter releases drug molecules in an aqueous medium. They randomly walk in all available directions according to Brownian motion [10]. Subsequently, due to the randomness of the movement of molecules, a lot of therapeutic molecules cannot reach the nano-receiver, especially if the separation distance between the nano-transmitter and the nano-receiver is large. In flow-based diffusion, the drug molecules are restricted in the micro-fluid channels as blood vessels [11]. Therefore, molecular communication suffers from high propagation delay in proportion to the square of the distance between the nano-transmitter and the nano-receiver. Moreover, the concentration of molecules is inversely proportional to the cubic power of the separation between the nano-transmitter and the nano-receiver. These characteristics result in communication unreliability and deterioration between the nano-transmitter and the nano-receiver [12,13]. These problems can be solved using relay capabilities. Relay strategies can be found in biological systems, such as the nervous system and quorum sensing in bacteria [14].

As nano-relaying plays an essential role in nano-networks based on diffusive molecular communication, various research efforts have been presented on flow-based diffusive molecular communication, relay molecular communication and optimization criteria. In [15], a mobile multiple-input multiple-output system for MCvD was introduced by combining decode-and-forward and network coding at relay nano-machines. The authors defined the thresholds at the relay and destination nanomachines by the maximum a posteriori (MAP) probability detection algorithm. A new network coding algorithm was introduced in [16] for mitigating ISI and enabling a larger-range communication. The half-duplex network coding is used for sending the nanomachine symbols to the nano-relay. A flow-induced diffusive channel model was investigated in [17] to study the effect of velocity with different mobility conditions. The performance of the molecular communication system with on-off keying (OOK) modulation was evaluated in terms of bit error rate (BER). A decision rule and an adaptive decision threshold have been derived using the likelihood ratio. A two-hop molecular communication system was introduced in [18]. The authors considered molecular degradation and noise effect over channel. They used a joint optimization method for resource allocation and position determination of relays with given detection thresholds to reduce BER. In [19], a nano-relay has been presented between the sender and destination nodes. It combines the collected portion of molecules released from the sender and stores them for a fraction of time, and then they are released to the receiver. Thereby, the delayed and non-delayed received molecules arrive at the same time, and thus the signal strength is improved. The most accurate vitro biological barrier models created to study the dynamic interaction of nanoconstructs for diagnostic or therapeutic purposes in this constantly changing environment are summarized by the authors of [20]. They assisted nanotechnologists in selecting the best vitro models for their specific experimental needs. The advantages of the most popular drug-carrier system liposomes were discussed by the authors of [21]. They investigated the effects of size, surface charge, and lipid structure on the efficiency of liposomes as well as their composition. The impact of liposome physicochemical characteristics on in vivo cell contact, half-life, tissue infiltration, and final state was also examined. Along with liposome-based drugs that are currently available in clinical trials, the authors also considered a number of strategies that have been created to get around the drawbacks of liposomes’ first generation. On the other hand, partial differential equations were used in [22] to model the fluids’ flow and temperature behavior. In order to study natural heat convection inside square and equilateral triangular cavities, a meshless approach based on a collocation of local radial basis functions was used. To assess the system precision, a number of natural convection test cases in square and triangular cavities were selected. Numerous academic papers examined the chemical and physical characteristics of natural molecular aspects as in [23].

As illustrated by the aforementioned literature, these systems may result in solutions to the problems in MCvD. However, optimization has not been considered widely in engineering aspects of cooperative molecular communication systems. Effective and robust computational algorithms are required to solve optimization problems that arise in such systems. Several global optimization algorithms have recently been presented such as particle swarm optimization (PSO) which is based on swarm movement, and MCFO which is subject to the law of gravity [24,25]. The PSO is simple and effective, with few parameters. The MCFO, on the other hand, is relatively complex, but it is capable of optimizing multiple parameters with high performance [26,27].

Unlike previous literature [15], [18], [28] and [29], this paper presents a new optimization technique that can work on multiple parameters. In the related literature, the drift velocity is the most important parameter. In this work, we investigate the cooperative nano-relay problem in MCvD with drift flow velocity. To improve the reliability of delivering drug molecules from the nano-source to the nano-receiver, a decoding nano-relaying scheme is used. We developed a cooperative decoding nano-relay based on flow velocity to deliver predetermined therapeutic drug molecules with a carefully determined drift velocity (optimized drift velocity) to the targeted cell. Furthermore, we adopt the energy detection method as the diversity combining technique to solve the detection problem at the cooperative nano-relay. The MCFO optimization technique is used to optimize the nano-network parameters for minimizing the probability of error. We believe that the proposed nanonetwork should be implanted in the human body as a form of therapy to effectively deliver therapeutic drug molecules to diseased cells with a carefully-chosen effective velocity. The basic contributions of this work are as follows:

•   Analyzing a nano-system based on a cooperative nano-relaying scheme that depends on drift velocity in molecular communication.

•   Deriving the bit error probability of the proposed detection method, in which the received signals from the cooperative paths are merged linearly at the nano-receiver.

•   Developing an optimization technique, namely MCFO, which is based on the block coordinate descent algorithm (BCDA) in order to obtain the optimal parameters (drift velocity for injection of drug molecules, detection threshold, optimal position of nano-relay and resources allocated for the emitting nano-source) to minimize the bit error probability.

The rest of this work is organized as follows. Section 2 describes the proposed nano-system based on drift velocity in molecular communication, including an analysis of the cooperative nano-relay scheme. It also presents a performance analysis of the detection method. The MCFO optimization technique is also introduced in Section 2. The numerical and simulation results are presented in Section 3. Finally, Section 4 gives the concluding remarks.

2  Proposed Nano-System Model

We consider a scenario of implanting a cooperative nano-system in the intra-body area network (IBAN) based on the advanced achievements of nanotechnology in nanomedical applications. Furthermore, we believe that the nanonetwork should be planted close to the diseased cell to prevent drug molecules from spreading throughout the body, and thus reducing side effects in healthy cells. The aim of the proposed model is to deliver therapeutic drug molecules to the targeted cell. Fig. 1 indicates that the proposed nano-system model consists of a nano-source (S), a nano-receiver (D), and a decoding nano-relay (R). For the sake of simplicity, we assume that R and D are sphere-shaped with radii rr and rd, respectively, and that S is a point source. Furthermore, R is considered as a nano-transceiver that either releases molecules or serves as a destination when it receives molecules. The lengths of S−R, S−D, and R−D are denoted as dsr, dsd, and drd, respectively. R is assumed to release a type of molecules (type B) then S (type A) in order to avoid self-interference, which limits the performance of the nano receiver. The molecular transmission works on a slot-by-slot basis, similar to a conventional wireless system. Ts specifies the length of the time slots. The employed modulation scheme is OOK, which is used by S and R, i.e., a fixed number of drug molecules (doses of drug molecules) is released to transmit the information bit “1” at the beginning of each Ts and nothing is released for information bit “0”. The operation of delivering therapeutic drug molecules at the NS can be summarized as follows:

•   At the beginning of the nth time slot, the nano-source S releases the information bit as molecules of type A to both R and D nano-machines via the diffusive drift channel.

•   The diffusion channel is prone to errors due to noise and ISI at each nano-machine.

•   Nano-relay R receives the information molecules and decodes them. The decoded information bits are then forwarded by R to the nano-receiver D, at the (n+1)th time slot via molecules of type B.

•   The diversity technique is used to improve the performance of the proposed nano-system on the two different combined signals at the nano-receiverD. The two signals come from the S−R−D and the S−D paths.

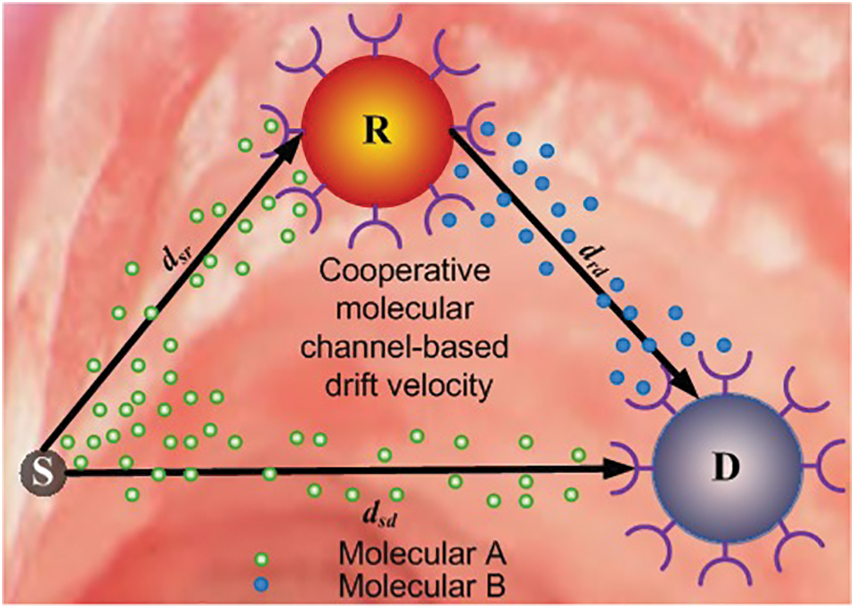
Figure 1: Cooperative molecular communication relaying scheme model based on drift velocity

As previously stated, the proposed nano-system is implanted in the human body, and thus the diffusion of therapeutic drug molecules in blood flow is based on positive drift velocity. According to Fick’s second law, the time it takes for any therapeutic drug molecule of type A released by the S to reach the R or D after the drifting distance, d, follows the probability density function f(t) given as [27]:

f(t)=d(4πDAt3)exp⁡(−(vt−d)24DAt)(1)

where d is the distance between any two nano-machines depending on the analysis of the path, DA is the diffusion coefficient of type A molecules and v is the drift velocity. The probability of a type A molecule striking the receiver within time t can be calculated as [27]:

F(t)=12[1+erf[d4DAt(vtd−1)]]+12exp⁡(vdDA)[1+erf[−d4DAt(vtd+1)]](2)

The cumulative distribution function in Eq. (2) depends on drift velocity, diffusion coefficient, time and distance.

A cooperative molecular communication is presented as a relaying scheme based on drift velocity analysis and its BER analytical expression in the following subsections.

2.1 A Cooperative Molecular Communication Relaying Scheme Based on Drift Velocity Analysis Model

We consider a linear combination of the two received signals from the two paths, namely the first path (S−R−D) which is defined as the path between nano-source (S), nano-relay (R) and nano receiver (D) nano-machines and the (S−D) path between S and D nano-machines, to detect the main signal at the nano-receiver D as represented in Fig. 2. This cooperative manner is implemented similar to diversity combining techniques in which the received signals from previous paths are combined linearly at D. These two signals are detected in different time slots k and k+1 under the effect of positive drift velocity. The nano-receiver D can distinguish between them due to the different types of molecules for each signal.

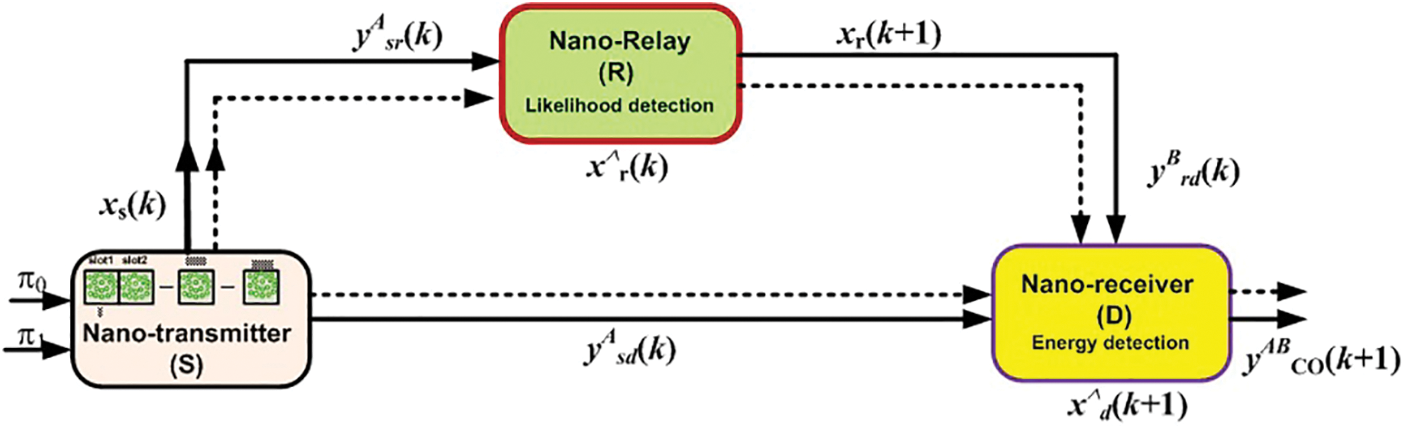
Figure 2: Schematic diagram of the proposed scheme

In the S− R−D path, let ysrA(k) be the total number of A molecules absorbed at nano-relay R, and NCsrA(k) be the number of molecules conveyed and received at the current time slot Ts. The ISI term is represented by NPsrA(k). NNo,srA(k) is the number of molecules acting as noise from other sources and NNc,srA(k) is the counting noise defined as the number of absorbed molecules by the nano relay R. Thereby, ysrA(k) can be represented by the following equation:

ysrA(k)=NCsrA(k)+NPsrA(k)+NNo,srA(k)+NNc,srA(k)(3)

NCsrA(k) obeys binomial distribution and also NPsrA(k).

NCsrA(k)∼B(QAxs(k),P1srA)(4)

NPsrA(k)∼B∑i=1I(QAxs(k−i),P(i+1)srA−P(i)srA)(5)

where I is the length of ISI, xs(k−i) denotes the transmitted bit by nano-source S at the (k−i)th time slot and P(i)srA=F(v,DA,dsr,its). We assume that NNo,srA(k) obeys a normal distribution asfollows [30]:

NNo,srA(k)∼N(µno,sr,σno,sr2)(6)

The counting noise NNc,srA(k) is considered as [30]:

NNc,srA(k)∼N(0,σnc,sr2)(7)

where σnc,sr2 depends on the number of molecules collected by the nano relay R. If QA is very large, and QAF(v,DA,d,t) is not equal to zero, the binomial distribution in Eqs. (6) and (7) can be approximated as a Gaussian distribution as follows:

ysrA(k)∼N(QAxs(k)P1,srA,QAxs(k)P1,srA(1−P1,srA))+∑i=1IN(QAxs(k−i)qi,srA,QAxs(k−i)qi,srA(1−qi,srA))+N(µno,sr,σno,sr2)+N(0,σnc,sr2)(8)

where qi,sr=(Pi+1,sr−Pi,sr). Thereby, ysrA(k) also obeys the Gaussian distribution as [28]:

Pr(ysrA[k]∣xs[k]=0)∼N(µ0,sr,σ0,sr2)(9)

Pr(ysrA[k]∣xs[k]=1)∼N(µ1,sr,σ1,sr2)(10)

where the mean and variance are calculated from Eq. (8) as follows [28]:

µ0,sr=π1QA∑i=1Iqi,srA+µno,sr(11)

µ1,sr=µ0,sr+QAP1,sr(12)

σ0,sr2=π1QA∑i=1Iqi,srA(1−qi,srA)+π1π0QA2∑i=1I(qi,srA)2+σno,sr2+µ0,sr(13)

σ1,sr2=QAP1,srA(1−P1,srA)+σ0,sr2+σno,sr2+µ1,sr(14)

where Pr(xs[k]=1)=π1 and Pr(xs[k]=0)=π0. The received molecules can be detected by the nano-machine R using the likelihood detection method as shown in Fig. 2, and in the equation below [31]:

xr^(k)={1ifysrA[k]≥τR0ifysrA[k]<τR(15)

The detection threshold at the nano-machine R is denoted by τR, and xr^(k) is the bit information detected by the nano-machine R in the kth time slot. τR can be obtained via the likelihood-ratio test Pr(ysrA[k]∣xs(k)=0)Pr(ysrA[k]∣xs(k)=1) as π1π0 as derived in [28]. The steps for computing the detection threshold at node R is provided in the Appendix.

As equations for the absorbed molecules for type A by the nano-machine R are given in Eqs. (3)–(8), we can derive equations for type B molecules absorbed by the nano-receiver D at the (k+1)th time slot, which is represented by yrdB(k+1). In consequence, the distribution of yrdB(k+1) is obtained as follows:

Pr(yrdB[k+1]∣xr[k+1]=0)∼N(µ0,rd,σ0,rd2)(16)

Pr(yrdB[k+1]∣xr[k+1]=1)∼N(µ1,rd,σ1,rd2)(17)

where the mean and variance values are given by Eqs. (11)–(14) with QA, π1, Pi,srA, Pi+1,srA, qi,srA, µnc,sr, σnc,sr2 µno,sr, σno,sr2 replaced by QB, Pr(xr[k+1]=1), Pi,rdB, Pi+1,rdB, qi,rdB, µnc,rd, σnc,rd2 µno,rd, σno,rd2, respectively.

where Pr(xr[k+1]=1) can be represented as [28,29]:

Pr(xr[k+1]=1)=π1Pr(xr^[k+1]=1∣xs[k]=1)+π0Pr(xr^[k+1]=1∣xs[k]=0)=14[(1−erf(τR−µ1,sr2σ1,sr2))+(1−erf(τR−µ0,sr2σ0,sr2))](18)

where erf(.) is the error function.

In the S−D path, the transmission of drug molecules is similar to the transmission of drug molecules in the S−R path, but with different parameters. Thereafter, the number of type A molecules collected by the nano receiver D along the S−D path in the kth time slot is defined by ysdA[k] similar to that of the S − R path. The ysdA[k] also obeys the Gaussian distribution as follows:

Pr(ysdA[k]∣xs[k]=0)∼N(µ0,sd,σ0,sd2)(19)

Pr(ysdA[k]∣xs[k]=1)∼N(µ1,sd,σ1,sd2)(20)

where the mean and variance values given by (11)–(14) can be calculated with the parameters: QA, Pr(xs[k]=1), Pi,sdA, Pi+1,sdA, qi,sdA, µnc,sd, σnc,sd2, µno,sd and σno,sd2.

2.2 Performance Analysis of the Detection Method

Energy detection is used as a diversity combining technique in the detection process. The diversity combining techniques in molecular communication cooperative networks based on drift velocity can be applied to enhance the performance of detection at the nano-receiver D. The linear combination technique gathers the received energy signals that come from the S−D and R−D paths with different types of molecules A and B in different time slots. Therefore, we can detect the signal with the next decision rule:

xd^(k+1)={1ifqDysdA[k]+qRyrdB[k+1]≥τD0ifqDysdA[k]+qRyrdB[k+1]<τD(21)

where xd^(k+1) is the bit detected at the nano-receiver D in the (k+1)th time slot, and qD and qR are the weights of the S−D and R−D paths, respectively. In this paper, the equal gain combining technique is applied at the nano-receiver D, which means that equal weights are considered for the two paths. This technique is preferred because the attenuators and adaptive controller amplifiers are not needed, and also no channel amplitude estimation is needed. So, equal gain combining is simpler to implement than maximum ratio combining (MRC).

The received signals from the two paths are merged as cooperative values with equal gain combining in different time slots as shown in Fig. 2. yrdB[k+1], and ysdA[k] are Gaussian random variables given by Eqs. (16), (17), (19) and (20), respectively. Therefore, the cooperative sum, yCOAB[k+1]=ysdA[k]+yrdB[k+1], is also a Gaussian random variable as follows [28]:

Pr(yCOAB(k+1)∣xs(k)=0,xr(k+1)=0)∼N(µ00,CO,σ00,CO2)(22)

Pr(yCOAB(k+1)∣xs(k)=0,xr(k+1)=1)∼N(µ01,CO,σ01,CO2)(23)

Pr(yCOAB(k+1)∣xs(k)=1,xr(k+1)=0)∼N(µ10,CO,σ10,CO2)(24)

Pr(yCOAB(k+1)∣xs(k)=1,xr(k+1)=1)∼N(µ11,CO,σ11,CO2)(25)

where the mean values can be obtained as:

µlj,CO=µl,sd+µj,rd,∀l,j∈{0,1}(26)

σlj,CO2=σl,sd2+σj,rd2,∀l,j∈{0,1}(27)

where µlj,CO and σlj,CO2 can be calculated from Eqs. (11) to (14).

Finally, the total probability of error for the overall system can be defined as follows [28]:

Pe(k)=π1Pr(xd^(k+1)=0∣xs(k)=1)+π0Pr(xd^(k+1)=1∣xs(k)=0)=12+18[(erf(τD−µ10,CO2σ10,CO2))(1+erf(τR−µ1,sr2σ1,sr2))+(erf(τD−µ11,CO2σ11,CO2))(1−erf(τR−µ1,sr2σ1,sr2))]−18[(erf(τD−µ00,CO2σ00,CO2))(1+erf(τR−µ0,sr2σ0,sr2))−(erf(τD−µ01,CO2σ01,CO2))(1−erf(τR−µ0,sr2σ0,sr2))](28)

2.3 Optimization Problem

The preceding section obtained a closed-form expression of the error probability of the proposed cooperative relaying nano-network with drift velocity. To achieve the best system performance, we must first obtain the optimal solution for the most critical parameters such as drift velocity v and detection threshold (τD) at the destination node by achieving:

minv,τDPe(29)

Then, we optimize the relay position and resources allocated to S and R nodes with fixed optimal v and τD by:

minm,nPe(30)

where m=dsr/dsd and n=QA/(QA+QB).

This study aims to find the optimum drift velocity v and τD required to minimize the system Pe. The MCFO is used as an efficient optimization technique to minimize the objective function Pe. For multi-optimal parameters based on BCDA, the MCFO is superior. The BCDA works by fixing all variables except one in order to minimize the objective function. The operation is then repeated until all parameters get to convergence.

2.4 Original Central Force Optimization (CFO) Algorithm

The CFO algorithm is a particle optimization algorithm that follows the gravity law. Each particle attracts every other particle with the virtual gravity force. The CFO is initialized by user-specified probe positions and acceleration distributions as follows:

Aj−1P=G0∑k=1k≠PNPU(Fj−1k−Fj−1P)(Fj−1k−Fj−1P)αRj−1k−Rj−1P‖Rj−1k−Rj−1P‖β(31)

The position vector of each probe is updated using the equation below:

RjP=Rj−1P+12Aj−1PΔt2(32)

where j⩾1. After updating the position of the probe, the probe may fly outside the DS and the CFO may look in areas other than the DS. A useful one is the reposition factor Frep, which plays an important role in avoiding local trapping which will be explained later.

2.4.1 Modified Central Force Optimization (MCFO)

The MCFO technique is a new smart optimization tool, which fixes the drawbacks of the CFO. That is, CFO occasionally halts progress towards the global optima, even when the population does not converge at the local optima or any other point. In other words, the objective of this development or modification was to enhance the global search during the early parts of the optimization and to lead the probes to converge towards the global optimum at the end of the search.

The pseudo-code of MCFO is given below. It depicts the primary steps of the MCFO algorithm, which are initialized with probe places and acceleration distributions chosen by the user on the points, which represent the Pe solutions on the decision space (DS). It is assumed that the first set of probes is randomly scattered throughout each point. The maxima of an objective function Pe are found using the MCFO optimization, where the objective function Fj−1k=f(x1,j−1k,...,xNd,j−1k) by flying a series of probes through the three dimensions space, where xNd is the decision variables as v, τD, m and n. Each probe P with position vector Rj−1P updates its acceleration Aj−1P:

Aj−1P=Gj∑k=1k≠PNPU(Fj−1k−Fj−1P)(Fj−1k−Fj−1P)αRj−1k−Rj−1P‖Rj−1k−Rj−1P‖β(33)

where Np is the number of probes, the time step j=0,1,…,Nt and Nt is the maximum number of iterations.

Rj−1P is the position vectors, which represent a solution for the optimization problem that determines the optimal values for decision variables (v, τD, m and n) and Fj−1P represents the fitness values (or mass) corresponding to the values of the objective function of the probe p with the (j−1)th step.

U(.) is the unit step function to avoid the probability of negative mass results. If negative masses were permitted, the resulting accelerations would be repulsive rather than attractive. The MCFO exponents are represented by α and β.

where Gj is the computed value of the present gravitational constant represented by:

Gj=G0exp⁡(−jγNt)(34)

where G0 is the gravitational constant and γ represents the descending coefficient factor. The original CFO has no memory, but the MCFO algorithm has a memory that is able to update the probe position. As a result, the probes are attracted towards the best previous positions Rbest. The best position vector discovered by the whole population is introduced as Rbest=(Rbest1,Rbest2,RbestD). As a result, probes near good solutions attempt to attract other probes that investigate the search space. When all probes are close to a satisfactory solution, they move relatively slowly. At this instance, Rbest helps them to exploit the global finest solution. Also, time varying acceleration coefficients C1 and C2 are configured to effectively regulate the global search and convergence toward the optimal global solution. According to these changes, at step j, the position vector of each probe is updated using the equation below:

RjP=Rj−1P+C1jrand1Aj−1PΔt2+C2jrand2(Rbest−Rj−1P)Δt(35)

As mentioned before, some roles may fall outside the DS, and the MCFO may look in areas other than the DS. Hence, we introduce a simple deterministic repositioning strategy for avoiding an unallowable search space and correcting infeasible solutions. If the probe RjP(i) is less than Rimin, it is updated to be

RjP(i)=Rimin+Frep(Rj−1P(i)−Rimin).(36)

However, if the probe RjP(i) is greater than Rimax, therefore:

RjP(i)=Rimax+Frep(Rimax−Rj−1P(i))(37)

where Rimin and Rimax are the minimum and maximum values of the ith spatial dimension of decision variables. The repositioning factor Frep has a significant impact on the algorithm convergence.

C1j=C1max−(C1max−C1minNt)j(38)

C2j=C2min−(C2max−C2minNt)j(39)

The capabilities of global and local search, which affect MCFO can be balanced by by updating C2j and C2j, the current gravitational constant, Gj and the descending coefficient factor, γ. In this development, the acceleration coefficients C1 and C2 change with time. The acceleration constant C1 changes from C1max = 1.5 to C1min = 0.1, whereas C2 is altered from C2min = 0.1 to C2max = 1.5.

The steps of the MCFO pseudo-code are recorded below:

Step 1Initialization NP,Nd,Nt,G0,Frep,α,β,

Step 2 Compute initial probe distribution

Step 3 Compute initial fitness matrix, and select the best probe fitness

Step 4 Assign initial probe Position & acceleration

Step 5 For j=0 to Nt and p=1 to NP

Step 5.1 Compute C1j and C2j using Eqs. (38) and (39)

Step 5.2 Update probe position (35)

Step 5.3 Update probe gravitational Gj (34)

Step 5.4 Retrieve errant probe using (36) and (37)

Step 5.5 Update fitness matrix, and select the best probe fitness

Step 5.6 Compute probe accelerations using (33)

Step 5.7 Shrink decision space matrix by updating Frep

Next J

Find the final solution

3  Numerical Results and Discussions

The performance of the proposed cooperative nano-system in MCvD with positive drift velocity is presented in this section. In fact, we used numerical analysis to demonstrate the proposed nanosystem performance in terms of the probability of error. We also compared the results to those of the direct link case, also known as the direct link relay (DLR) scheme presented in [29]. All of our numerical results are generated with MATLAB code and the parameters are listed in Table 1 [29].

Fig. 3 shows the performance of the probability of error in the proposed nano-system against the drift velocity of molecules with variable symbol duration Ts, when the detection threshold τD is fixed. As expected, the probability of error in the proposed nano-system is significantly reduced when the symbol duration is long, due to the possibility of lowering the ISI. On the other hand, we notice that all probability of error curves in the figure have a quasi-convex behavior, implying that the optimization problem of determining the best velocity is a quasi-convex problem. As a result, the goal of the MCFO algorithm in the cooperative nano-system is to select the optimal velocity of drug molecule injection. It has been observed that the performance of probability of error increases with velocity increase until a certain point is determined by the MCFO. At that point, the performance decreases. As a result, the MCFO can solve the optimization problem of determining the best velocity.

Figure 3: Probability of error of the proposed cooperative scheme as a function of drift velocity (QA = QB = 400 and dsd=2µm)

Fig. 4 shows the performance of the proposed nano-system and the DLR [29] in terms of bit error probability vs. detection threshold, when the drift velocity of molecules is fixed at 0.3 mm/sec. As can be seen, the proposed cooperative nano-system improves performance significantly compared to DLR. Furthermore, the plot shows the impact of the MCFO on performance by selecting an appropriate detection threshold and drug molecule velocity.

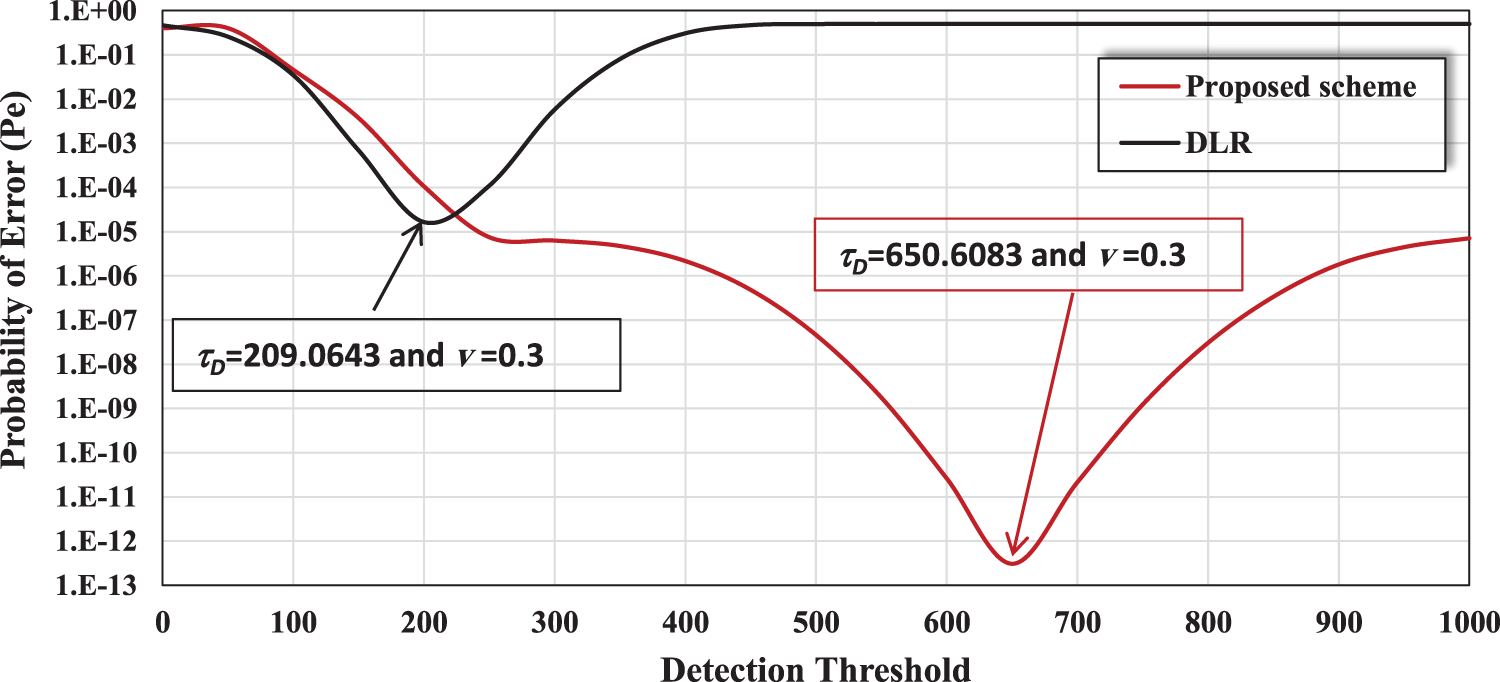
Figure 4: Comparison of the proposed scheme and the DLR scheme in terms of probability of error (QA = QB = 400 and dsd=2µm,Ts=5ms)

Table 2 shows the performance of the probability of error, when employing the proposed nano-system and the DLR system against the molecular budget of types A and B. We consider S and R nano-machines releasing equal molecular budget. The performance of the probability of error is depicted with optimized parameters v and τD obtained by the proposed MCFO as illustrated in Fig. 3.

We observe that the proposed cooperative nano-system with the nano-relay based on a diversity combining technique expends a lower molecular budget, and thus a significant increase in nano-system performance is achieved compared with the DLR system. For example, at Ts = 5 ms and Ts = 7 ms, it is clear that in the proposed cooperative nano-system expends fewer than 300 molecules for transmission to realize a probability of error equal to 10−10 compared with the DLR. In addition, the figure indicates that there is a direct influence of the symbol duration on the ISI issue, which means that with larger symbol duration, ISI is reduced. We can conclude that with increased symbol duration in the proposed cooperative nano-system, the performance is significantly better than that of the DLR.

Figs. 5 and 6 show the joint optimization of nano-relay position and molecular budget for S and R nanomachines with a fixed destination threshold, τD and v parameters. The probability of error is given as a function of nano-relay position m in Fig. 5. Obviously, it is a quasi-convex function. As a result, we can use BCDA method to optimize the nano-relay position with MCFO, which is based on the idea of setting all parameters except one and determining the optimal value that minimizes the objective function Pe, and then fixing m and finding the optimal molecular budget allocated to the S and R nanomachines until convergence is achieved.

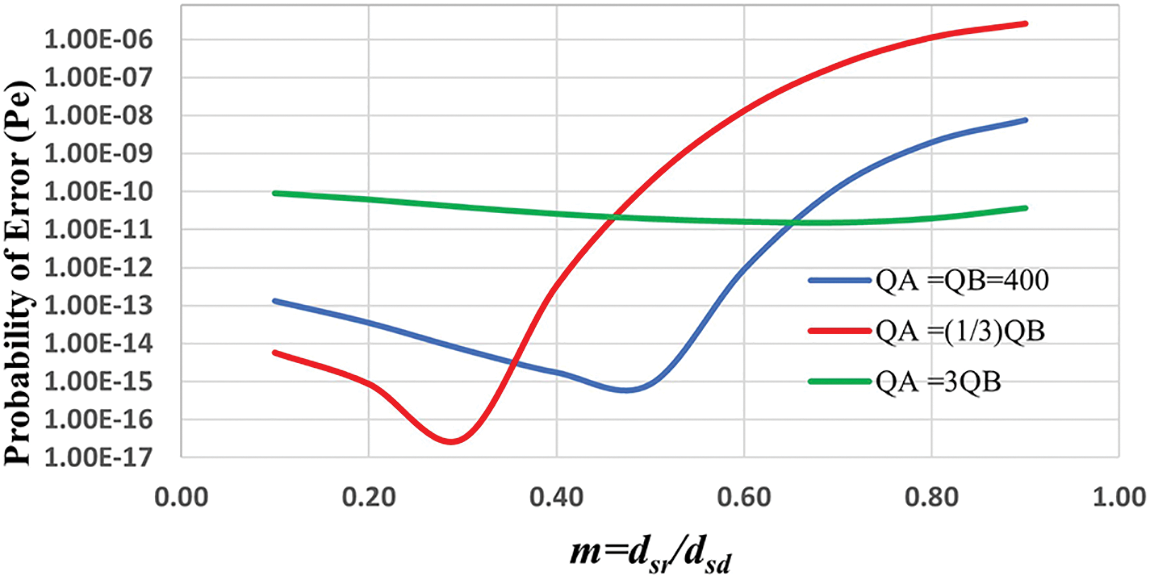
Figure 5: Probability of error vs. relay node position, when the detection threshold and velocity are fixed, (QA + QB = 800)

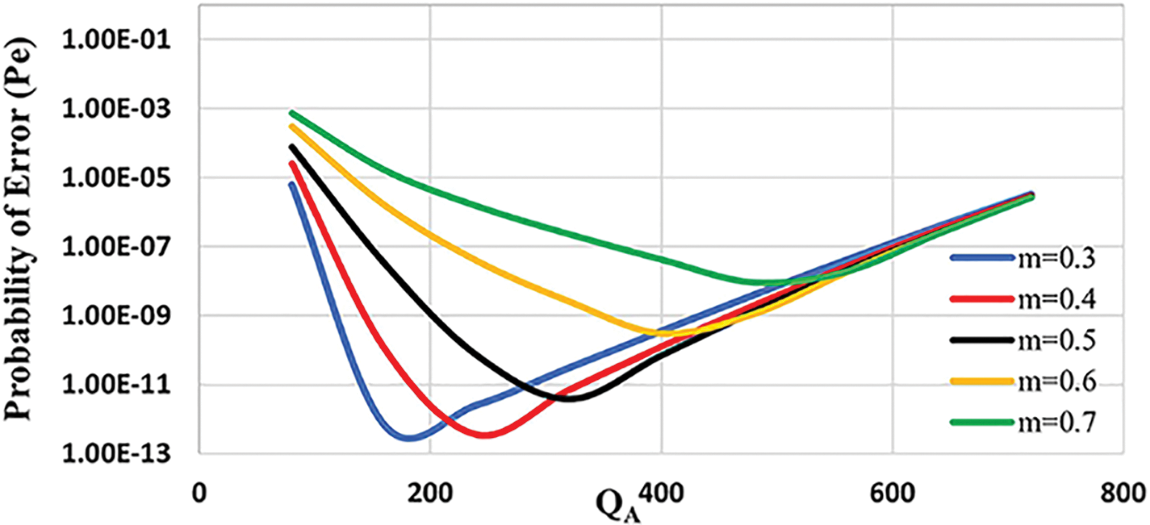
Figure 6: Probability of error vs. number of molecules assigned to node S for various relay node positions when the detection threshold and velocity are fixed (QA+QB=800, dsd=1µm)

Unlike the previous literature, the proposed nano-system is considered non-linear due to the effect of velocity that controls the diffusion of molecules and different types of molecules A and B with different diffusion coefficients, and thus the optimal relay position is obtained when m = 0.3. This indicates that the nano-relay, R is close to the nano-source, S and that an optimal molecular distribution is achieved when the nano-relay QA = 1/3 QB, which means that more molecules are allocated to the nano-relay R than those of the nano-transmitter S, indicating the importance of the (R−D) path and that it has a greater influence on system performance than the (S−R) path.

We can conclude from the preceding analysis that the proposed cooperative nano-system with nano-relay outperforms the DLR system. Furthermore, when compared to the DLR system, the proposed nano-system uses a lower molecular budget with low error probability.

Table 3 illustrates a comparison between PSO and MCFO before and after optimizing the flow velocity v when the distance, dsd is 2 µm, for two different values of Ts=2 and 5 ms. The flow velocity is v=0.6 and 0.4 mm/s before optimization and v=0.5 and 0.3 mm/s after optimization as explained in Fig. 3, when the resource budget QA=QB has 400 and 600 molecules. In fact, we measured the BER of both PSO and MCFO before and after optimization using the nano-system parameters listed in Table 3. As we can see, the performance of the proposed nano-system improves with the optimized flow velocity rather than the original flow velocity. Furthermore, we see that the PSO is slightly better than the MCFO. This is attributed to the PSO algorithm ability to optimize a single value. Furthermore, it is demonstrated that the MCFO algorithm can achieve roughly the same performance as the PSO, and it has the advantage of optimizing more than one parameter, unlike the PSO algorithm.

4  Conclusion

This study proposes a nano-system with cooperative molecular communications based on nano-relaying. It considers the molecular drift velocity in the proposed molecular communication system based on diffusion. The noise and ISI issues have an impact on the molecular diffusion channel. Furthermore, we proposed a collaborative optimization problem for nano relay positioning and determination of the fraction of the drug molecular budget that should be allocated to the nano transmitter and nano receiver. The probability of bit error is expressed in closed form, and this is used as an objective function to determine the optimal velocity of the drug molecules and the detection threshold at the nano receiver. The error probability equation is then used as an objective function to determine the optimal drug molecule velocity and detection threshold to achieve a minimum probability oferror. The numerical results show that the proposed scheme can improve the performance of the nanosystem, when compared to a system with a direct link relay (DLR). Furthermore, this approach can be extended to a multi hop nano relay to make it more realistic for nano receivers with a large number of receptors. Finally, the proposed nano system with the cooperative nano relaying approach combined with the emerging nanotechnology can be implemented in advanced nanomedicine solutions to perform disease detection, health monitoring, and targeted drug delivery more efficiently.

Acknowledgement: None.

Funding Statement: This work was funded by the Researchers Supporting Project Number (RSP2023R102) King Saud University, Riyadh, Saudi Arabia.

Author Contributions: Saied M. Abd El-atty and Eman S. Attia conceived of the main idea, developed the theory, and performed the computations for the presented work. The analytical methods were validated by Ashraf A. M. Khalaf, Fathi E. Abd El-Samie, and Heba M. El-Hosen. The manuscript was written by Saied M. Abd El-atty, Eman S. Attia, Konstantinos A. Lizos, and Osama Alfarraj. The findings were considered by all writers, and they all contributed to the final publication. All authors discussed the results and contributed to the final manuscript.

Availability of Data and Materials: The authors have not used datasets generated during the paper work but the analysis and codes are available from the corresponding author on reasonable request.

Conflicts of Interest: The authors have no relevant financial or non-financial interests to disclose.

References

1. Abd El-atty, S. M. (2020). Health monitoring scheme based forster resonance energy transfer nanocommunications in the Internet of Biological Nanothings. International Journal of Communication Systems, 33(11), e4398. [Google Scholar]

2. Mohamed, S., Dong, J., El-Atty, S. M. A., Eissa, M. A. (2022). Bio-cyber interface parameter estimation with neural network for the Internet of Bio-Nano Things. Wireless Personal Communications, 123(2), 1245–1263. [Google Scholar]

3. El-Fatyany, A., Wang, H., El-atty, A., Saied, M. (2021). Efficient framework analysis for targeted drug delivery based on Internet of Bio-Nanothings. Arabian Journal for Science and Engineering, 46(10), 9965–9980. [Google Scholar] [PubMed]

4. Attia, E. S., Khalaf, A. A. M., Abd El-Samie, F. E., Abd El-Atty, S. M., Lizos, K. A. et al. (2022). Embedded coded relay system for molecular communications. Computers, Materials & Continua, 72, 2729–2748. [Google Scholar]

5. Chude-Okonkwo, U., Malekian, R., Maharaj, B. T. (2020). Advanced targeted nanomedicine a communication engineering solution, Cham: Springer. [Google Scholar]

6. Zafar, S., Nazir, M., Bakhshi, T., Khattak, H. A., Khan, S. et al. (2021). A systematic review of bio-cyber interface technologies and security issues for Internet of Bio-Nano Thing. IEEE Access, 9, 93529–93566. [Google Scholar]

7. Pan, W., Chen, X., Yang, X., Zhao, N., Meng, L. et al. (2022). A molecular communication platform based on Body Area Nanonetwork. Nanomaterials, 12(4), 722. [Google Scholar] [PubMed]

8. Abd El-atty, S. M., Arafa, N. A., Abouelazm, A., Alfarraj, O., Lizos, K. et al. (2022). Performance analysis of an artificial intelligence nanosystem with biological Internet of Nano Things. Computer Modeling in Engineering & Sciences, 133(1), 1–21. https://doi.org/10.32604/cmes.2022.020793 [Google Scholar] [PubMed] [CrossRef]

9. Farsad, N., Yilmaz, H. B., Eckford, A., Chae, C. B., Guo, W. (2016). A comprehensive survey of recent advancements in molecular communication. IEEE Communications Surveys Tutorials, 18(3), 1887–1919. [Google Scholar]

10. Kadloor, S., Adve, R. S., Eckford, A. W. (2012). Molecular communication using Brownian motion with drift. IEEE Transactions on NanoBioscience, 11(2), 89–99. [Google Scholar] [PubMed]

11. Gómez, J. T., Pitke, K., Stratmann, L., Dressler, F. (2022). Age of information in molecular communication channels. Digital Signal Processing, 124, 103108. [Google Scholar]

12. Kuscu, M., Akan, O. B. (2022). Detection in molecular communications with ligand receptors under molecular interference. Digital Signal Processing, 124, 103186. [Google Scholar]

13. He, S., Joseph, N., Feng, S., Jellicoe, M., Raston, C. L. (2020). Application of microfluidic technology in food processing. Food Function, 11(7), 5726–5737. [Google Scholar] [PubMed]

14. Yang, N. J., Chiu, I. M. (2017). Bacterial signaling to the nervous system through toxins and metabolites. Journal of Molecular Biology, 429(5), 587–605. https://doi.org/10.1016/j.jmb.2016.12.023 [Google Scholar] [PubMed] [CrossRef]

15. Cheng, Z., Sun, J., Yan, J., Tu, Y. (2022). Optimizations for mobile MIMO relay molecular communication via diffusion with network coding. KSII Transactions on Internet and Information Systems, 16(4), 1373–1391. [Google Scholar]

16. Akdeniz, B. C., Tepekule, B., Pusane, A. E., TuÄcu, T. (2017). Novel network coding approaches for diffusionabased molecular nanonetworks. Transactions on Emerging Telecommunications Technologies, 28(7), e3105. [Google Scholar]

17. Varshney, N., Haselmayr, W., Guo, W. (2018). On flow-induced diffusive mobile molecular communication: First hitting time and performance analysis. IEEE Transactions on Molecular, Biological and Multi-Scale Communications, 4(4), 195–207. [Google Scholar]

18. Tiwari, S. K., Reddy, T. R. T., Upadhyay, P. K., Da Costa, D. B. (2018). Joint optimization of molecular resource allocation and relay positioning in diffusive nanonetworks. IEEE Access, 6, 67681–67687. [Google Scholar]

19. Angjo, J., Pusane, A. E., Yilmaz, H. B., Basar, E., Tugcu, T. (2022). Optimal relaying in molecular communications. Nano Communication Networks, 32–33, 100404. [Google Scholar]

20. Carton, F., Malatesta, M. (2022). In vitro models of biological barriers for nanomedical research. International Journal of Molecular Sciences, 23(16), 8910. [Google Scholar] [PubMed]

21. Bozzuto, G., Molinari, A. (2015). Liposomes as nanomedical devices. International Journal of Nanomedicine, 10, 975–999. [Google Scholar] [PubMed]

22. Nuwairan, M. A., Chaabelasri, E. (2023). Numerical assessment of nanofluid natural convection using local RBF method coupled with an artificial compressibility model. Computer Modeling in Engineering & Sciences, 135(1), 133–154. https://doi.org/10.32604/cmes.2022.022649 [Google Scholar] [PubMed] [CrossRef]

23. Javaid, M., Alamer, A., Sattar, A. (2023). Topological aspects of dendrimers via connection-based descriptors. Computer Modeling in Engineering & Sciences, 135(2), 1649–1667. https://doi.org/10.32604/cmes.2022.022832 [Google Scholar] [PubMed] [CrossRef]

24. Mahmoud, K. R. (2016). Synthesis of unequally-spaced linear array using modified central force optimisation algorithm. IET Microwaves, Antennas Propagation, 10(10), 1011–1021. [Google Scholar]

25. Siddique, N., Adeli, H. (2015). Central force metaheuristic optimisation. Scientia Iranica, 22(6), 1941–1953. [Google Scholar]

26. Chen, Y., Yu, J., Mei, Y., Wang, Y., Su, X. (2016). Modified central force optimization (MCFO) algorithm for 3D UAV path planning. Neurocomputing, 171(3), 878–888. [Google Scholar]

27. Wang, X., Jia, Z. (2020). Reliability analysis of molecular communication based on drift diffusion in different topologies. Journal of Computer and Communications, 8(1), 71–89. [Google Scholar]

28. Tavakkoli, N., Azmi, P., Mokari, N. (2017). Optimal positioning of relay node in cooperative molecular communication networks. IEEE Transactions on Communications, 65(12), 5293–5304. [Google Scholar]

29. Tavakkoli, N., Azmi, P., Mokari, N. (2016). Performance evaluation and optimal detection of relay-assisted diffusion-based molecular communication with drift. IEEE Transactions on NanoBioscience, 16(1), 34–42. [Google Scholar] [PubMed]

30. Pierobon, M., Akyildiz, I. F. (2011). Diffusion-based noise analysis for molecular communication in nanonetworks. IEEE Transactions on Signal Processing, 59(6), 2532–2547. [Google Scholar]

31. Jamshidi, A., Keshavarz-Haddad, A., Ardeshiri, G. (2019). MAP detector performance analysis in diffusion-based relaying molecular communications. Nano Communication Networks, 19(12), 81–91. [Google Scholar]

32. Wang, J., Peng, M., Liu, Y., Liu, X., Daneshmand, M. (2019). Performance analysis of signal detection for amplify-and-forward relay in diffusion-based molecular communication systems. IEEE Internet of Things Journal, 7(2), 1401–1412. [Google Scholar]

Appendix

The steps for calculating the detection threshold at node R (τR) using the MAP detection approach are provided in this appendix.

The threshold at node R has a closed-form expression and can be determined carefully [28]. The likelihood-ratio test Pr(ysrA[k]∣xs(k)=0)Pr(ysrA[k]∣xs(k)=1) as π1π0 is derived in Eqs. (9) and (10) as in [31,32]:

Π0σ1,sr2Π1σ0,sr2=exp⁡((τR−µ0,sr)22σ0,sr2−(τR−µ1,sr)22σ1,sr2)(40)

τR=−B±B2+2Aln⁡(C)A(41)

A=1σ0,sr2−1σ1,sr2(42)

B=µ1,srσ1,sr2−µ0,srσ0,sr2(43)

C=Π0σ1,srΠ1σ0,srexp⁡[12(µ1,sr2σ1,sr2−µ0,sr2σ0,sr2)](44)

Because the number of molecules in the medium cannot be negative, the negative value should be removed. Furthermore, because the number of molecules is an integer, the final positive answer must be rounded to an integer.