 Open Access
Open Access
ARTICLE
A Large-Scale Group Decision Making Model Based on Trust Relationship and Social Network Updating
1
School of Business Administration, Northeastern University, Shenyang, 110819, China
2
School of Management, Northeastern University at Qinhuangdao, Qinhuangdao, 066004, China
3
School of Modern Logistics, Shanxi Vocational University of Engineering Science and Technology, Taiyuan, 030031, China
4
Business School, Sichuan University, Chengdu, 610064, China
* Corresponding Author: Meng Zhao. Email:
(This article belongs to the Special Issue: Linguistic Approaches for Multiple Criteria Decision Making and Applications)
Computer Modeling in Engineering & Sciences 2024, 138(1), 429-458. https://doi.org/10.32604/cmes.2023.027310
Received 24 October 2022; Accepted 23 March 2023; Issue published 22 September 2023
Abstract
With the development of big data and social computing, large-scale group decision making (LGDM) is now merging with social networks. Using social network analysis (SNA), this study proposes an LGDM consensus model that considers the trust relationship among decision makers (DMs). In the process of consensus measurement: the social network is constructed according to the social relationship among DMs, and the Louvain method is introduced to classify social networks to form subgroups. In this study, the weights of each decision maker and each subgroup are computed by comprehensive network weights and trust weights. In the process of consensus improvement: A feedback mechanism with four identification and two direction rules is designed to guide the consensus of the improvement process. Based on the trust relationship among DMs, the preferences are modified, and the corresponding social network is updated to accelerate the consensus. Compared with the previous research, the proposed model not only allows the subgroups to be reconstructed and updated during the adjustment process, but also improves the accuracy of the adjustment by the feedback mechanism. Finally, an example analysis is conducted to verify the effectiveness and flexibility of the proposed method. Moreover, compared with previous studies, the superiority of the proposed method in solving the LGDM problem is highlighted.Keywords
Due to the increasing complexity of the social and economic environment, it is increasingly difficult to rely on a single decision maker (DM) to make effective decisions. Therefore, many organizations use multiple members in the decision-making process, which is called group decision making (GDM). GDM is a participatory process, which selects the best solution from alternatives by considering the personal opinions of multiple experts [1]. However, with the rapid development of technology and society [2], the group sizes have gradually become larger and more complex [3,4]. Generally, a group with more than 20 members is defined as a large-scale group.
In the background of LGDM, decision makers (DMs) may have diverse opinions because of the different knowledge and experience. Therefore, how to help DMs reach consensus becomes a key issue. In order to deal with the complexity and uncertainty of the LGDM problem, this study starts from the following aspects: the dimensional reduction of large-scale DMs [5], the consensus measure and the improving method.
The dimensional reduction of large-scale DMs. There are two main directions for reducing the size of large-scale DMs. The one is based on the department or field in which the DM belongs. For example, Liu et al. [6] classified the DMs according to the DMs’ school, and determined the percentage distribution on evaluations of each group concerning each alternative. The characteristics of this direction are simple and convenient. But in the real process, judgment information given by the same type of DMs is not necessarily the same. Therefore, the clustering method based on the evaluation value or preference value of DM is used to reduce the dimension of large-scale DMs. For example, Wu et al. [7] used the k-means method to cluster a large amount of hesitant fuzzy preference information and improved consensus level based on three-level consensus measures and a local feedback strategy. Yang et al. [8] investigated the additive consistency of the intuitionistic fuzzy preference relations in group decision making using T-normalized intuitionistic fuzzy priority vectors. In the above studies, DMs are considered as independent individuals. However, there are social relationships among DMs, especially the trust relationship which is clearly existed and important in reality.
Social networking applications generate a huge amount of data daily. Meanwhile, social networks (SNs) have become a growing field of research due to the heterogeneity of data and structures, as well as their size and dynamics [9]. Some studies have proven the advantages of social networking, such as social network-based recommendation systems [10–12], online review websites incorporating the social-networking function [3,13], collaborative networks in the con53text of publications and citations [14,15], preventing the spread of rumors and misinformation by identifying influencers [16–19]. Information on SNs can not only enrich and improve the DMs’ preference information, promote and accelerate consensus reaching process, but more importantly, reduce the dimension of large-scale DMs. Trust is a special case in social relations, and some studies have also analyzed the impact of trust relations on clustering [20,21]. Therefore, in the framework of social network-group decision making (SN-GDM), it is novel and feasible to use trust relationship as a reliable source of member weight information. However, most existing studies only consider the trust relationship between nodes without considering the trust degree of different nodes; they also ignore the generation process of relationship network, and cannot automatically cluster in the process of dimension reduction. In addition, previous studies that applied SNA to large group networks did not consider network construction and update based on DMs feedback, except for the trust relationship among DMs.
The consensus measure and improving method. On the one hand, an interesting issue within the group decision theory is the consensus measure, and the key of the problem is how to determine the DMs’ weight and subgroup weight in the process of decision matrix aggregation. In GDM, the decision matrix is generally aggregated through subjective or objective weighting to perform consensus measures. In particular, expert weights may be adjusted during the consensus reaching process. Pang et al. [22] developed an extended TOPSIS method and aggregation-based method for multi-attribute group decision making (MAGDM) with probabilistic linguistic information in the case where the attribute weights are unknown and partially known. Wu et al. [23] used trust score values to assign importance weights to experts. For LGDM, the weight of individual DMs and the weight of each subgroup need to be determined after clustering. For example, Wu et al. [5] determined the expert weight through the centrality of the network. Wu et al. [7] determined the subgroup weight based on the number of experts in the subgroup. Shi et al. [24] used a uniform aggregation operator to update the weights in the consensus reaching process (CRP). According to the above research, group consensus can be improved quickly by adjusting the weight of DMs and subgroups in the CRP. This is also in line with reality. The influence of some DMs may increase in the process of DM interactions, resulting in the corresponding changes in weights. Although the above studies involve weight changes in the CRP, the trust relationship between DMs is rarely considered. Generally speaking, DM with strong trust relationships has a greater influence. In the process of interaction, DMs with strong trust relationships will affect the preferences of DMs with weaker trust relationships.
On the other hand, scholars have proposed consensus improvement methods for LGDM consensus problems [7,25–28], which are mainly divided into automatic methods [29,30] and interactive methods [31,32]. The automatic feedback mechanism saves time because it does not require additional expert interaction to carry out the consensus-improving process. For example, Zhang et al. [33] proposed an automatic feedback mechanism for group decision making based on the distribution linguistic preference relations. Perez et al. [34] overcame the problem of the moderator, giving a way to use an automatic system to compute and send customized advice to the experts if there is not enough consensus. The interactive feedback mechanism requires expert interaction, which takes more time but the results obtained are more accurate. For example, for the cooperative and noncooperative behaviors of experts, Quesada et al. [35] introduced a method to deal with noncooperative behaviors, which used an informal weighted scheme to assign weights to experts. Gou et al. [36] built a consensus-reaching model of noncooperative behavior and deal with noncooperative behavior and preference information. In addition, Gou et al. [37] used multi-stage interactive consensus reaching algorithms to deal with multi-expert decision making problems with language preference ordering. For the dynamic adjustment process of consensus reaching, in [1], a non-linear programming model was constructed to dynamically adjust the experts’ weights in consensus reaching process. Wu et al. [7] proposed an LGDM consensus model which allowed clusters change. And as the clusters changed in every interactive consensus round, the consensus process evolution could be captured. Besides, some studies have also considered social networks. For example, in [5], after the feedback mechanism is executed, clustering and consensus measures are performed again, the process of consensus improvement is not involved. However, the social network was applied in [5] which applied IT2-TOPSIS to obtain the optimal solution directly. In the above research on consensus improving, social networks, trust networks, interaction rules, and the update and optimization of the entire network structure in the adjustment process are rarely considered. However, in the actual adjustment process, it is necessary to consider the acceptability of information and let DMs with higher trust interact with each other. The interaction process will inevitably lead to changes in the trust relationship among members of the large group. Therefore, it is necessary to consider the update of the trust network in the process of consensus improvement.
Trust relationships have been applied in various fields and have brought great benefits to various industries. In the business field, marketing methods such as fan economy, word-of-mouth bonus, media marketing, onlookers, and participation experience have brought unexpected dividends to enterprises in the era of mobile internet. Among them, the cultivation of trust relationships is the key, and trust is the core of this emotional marketing. Similarly, in academia, the citation relationship between different scholars also reflects the trust between each other, which may further lead to collaboration relationships. In politics, the trust relationship between voters will also greatly affect the election results. Therefore, it is necessary to consider the trust relationship and trust network in LGDM. In addition, considering trust networks based on group classification of decision makers can better reflect the trust relationship, and the trust degree and the degree of information difference can be better reflected in the group consensus. Considering trust relationships can achieve more effective interactions in the feedback adjustment process.
In view of the necessity of trust in decision making, this study will take the trust relationship through the entire decision-making process, from social network construction and clustering to weight determination and consensus measurement, as well as consensus reaching process and network updating. In comparison with the previous consensus model, the consensus model proposed in this study has some distinctive features:
First, in previous studies, the SNA was typically used to simply represent the relationship of DMs. It did not really combine the actual social activities of the DMs. Considering the social trust relationships between DMs for the LGDM, this study builds a social network between DMs and uses the Louvain method to detect community based on the trust relationship.
Second, in the process of determining the weight of individual DMs and the weight of each subgroup, the trust weight and the network weight are fully considered. Compared with weights based on network degree centrality or subgroup size, it is more convincing to assign weights based on trust relationships and to make corresponding weight changes in the feedback adjustment process. In addition, the weight for individual DMs and the weight of each subgroup will update accordingly in the consensus reaching process.
Third, the proposed model allows for changes in the trust network. Individuals are able to modify their preferences in the reaching consensus process, so the trust relationship will change, which will make the number of subgroups and members of each subgroup likely to change. In addition, the consensus rules and adjustment rules proposed in the model are simple and can be used to guide modifications.
The remainder of this study is organized as follows. Section 2 introduces related concepts, such as social relationship and social impact analysis, possibility distribution based on hesitant fuzzy elements, and probability distribution based on fuzzy preference relations. Section 3 presents the proposed SNA-based LGDM method. In Section 4, an illustrative example is provided to show the applicability of the proposed method. Section 5 compares and analyzes the similarities and differences between the proposed method and the other methods in detail, cutting from the three perspectives of trust relationship, social network and subgroup classification method. Finally, Section 6 concludes this paper with future perspectives.
2.1 Measurement of Trust among DMs
In this study, we distinguish senders and receivers of social ties, which means the DM’s online network is directed. The in-degree of a DM refers to the social ties that the DM has received from other DMs. The out-degree indicates the social ties that the DM has sent to other DMs [38]. The definitions of in-degree centrality and out-degree centrality are described as follows.
Definition 1 [39]: Let
(1) The number of edges originating from node
where
(2) The number of edges terminating from the node
where
The relationship strength between members shows the level of trust between those members [38]. Within online social networks, members can declare friendship with one another by establishing social. If two DMs have more common social connections in an online social network, we can conclude that they have deeper social ties. This study uses degree centrality to calculate social connection strength between
where
Social interaction strength is a combination of time length, emotional intensity, intimacy (mutual confiding), and reciprocal services that characterize the ties [40]. This study measures interaction strength between
where
Let
2.2 Possibility Distribution Based Hesitant Fuzzy Element
Let
Each DM gives a judgment on the various alternatives. As we know, preference relations are a classical and powerful preference structure to represent the preferences in GDM problems. Fuzzy preference relations (FPR) have been found to be effective when dealing with uncertain information [41–45]. Therefore, this study uses FPR to represent each DM’s opinion on alternatives
Definition 2 [7]: A FPR on
Definition 3 [7]: The possibility distribution-based hesitant fuzzy element (PDHFE) can be expressed as follows:
where
Definition 4 [7]: A PDFPR on
where
Definition 5 [7]: The expected value or mean for
Definition 6 [7]: The distance between
where
3 Consensus Framework and Model for the LGDM
3.1 Problem Description and Consensus Framework
Suppose that there are
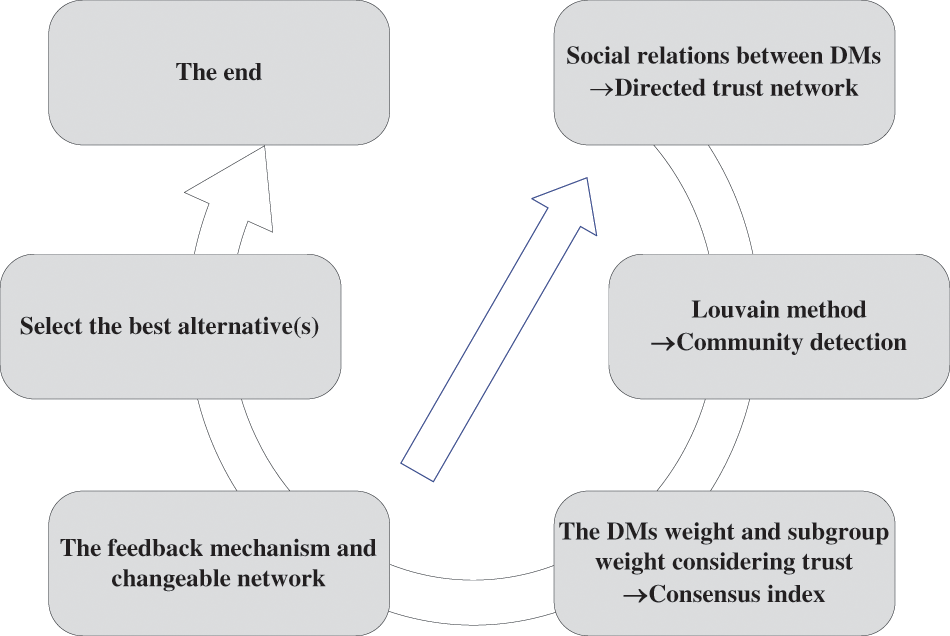
Figure 1: The overall solution for LGDM problems based on trust relation and changeable network
(1) Firstly, according to the social relations between DMs, a directed social relationship network can be constructed. Then the trust relationships among the members are calculated. Using the Louvain method which has been widely used in large-scale network community detection [46], the large-scale social network is divided into several subgroups. This part is detailed in Section 3.2.
(2) Secondly, the weight of the DMs in the subgroup and the weight of each subgroup based on trust relationships are calculated by combining the SNA and the Louvain method, then the consensus index is obtained. Details of trust weight determination and consensus measure are given in Section 3.3.
(3) Thirdly, if the group consensus does not reach the predefined threshold, the feedback mechanism considering the trust relationship between the members is used to adjust the consensus until the threshold is reached, and the network will change during this process. Details of the consensus reaching process are given in Section 3.4.
(4) Finally, the DMs’ preferences are aggregated according to the network relations, and the alternatives are sorted to select the best ones.
3.2 Trust Weight Determination and Consensus Measure
In determining the weight of individual DM and the weight of each subgroup, compared with weighting based on network degree centrality or subgroup size, the trust weight and the network weight are fully considered. Firstly, this study uses the Louvain method to classify DMs, and obtains the comprehensive weight of each DM by the network weights and trust weights. Then, based on the reciprocal of the distance from each subgroup to the network center, the weight of each subgroup is calculated. Finally, based on the work of Herrera-Viedma et al. [47], the main steps of the consensus measure are listed. In addition, the weights for individual DM and the weight of each subgroup will change accordingly in the consensus reaching process.
3.2.1 Trust Network and Louvain Method in Community Detection
Community, also called a cluster or module, is a group of vertices which probably share common properties. Community detection refers to the recognition of modules and their boundaries based on the structural positions of vertices and the classification of vertices [48]. The community detection method is the key based on a trust network for DMs to reduce dimensionality clustering. Some methods have been developed, such as the GN method [49], the spin-glass method [50], the random walk community detection [51], the label propagation method [52] and so on. The Louvain method is a commonly used community detection method, which is based on the modularity theory proposed by Blondel et al. [46]. This method is an agglomerative clustering algorithm, which reveals the complete hierarchical community structure of the network and can cluster subgroups automatically without setting the initial number of subgroups. Therefore, this study uses the Louvain method for DMs in LGDM problems.
Assuming that a network has t nodes, the algorithm of the Louvain method can be expressed as follows [39]:
Step 1: Each node in the network is treated as a separate community. In the beginning, the number of communities is the same as the number of nodes.
Step 2: Assign each node to the community according to the node near each node, calculate the value of
The definition of
where
Step 3: Repeat Step 2 until the network in the community no longer changes.
Step 4: Streamline the entire network and treat the nodes in a community as a new node. The weights between nodes within the community are converted to the weights of the new nodes. The weights between the edges of the community are converted to weights between the edges of the new nodes. The boundary value of the weight is 1.
Step 5: Repeat Steps 1–4 until the modules of the entire network no longer change.
3.2.2 The Comprehensive Weight of Each Decision Maker
(1) Network weights of each DM
Set
Combining the normalized degree centrality
According to [49], the value of
Suppose that
(2) Trust weights of each DM
Assigning weight to each DM is an important part of the decision-making process and plays a key role in obtaining the final solution. For online social networks, historical interaction information can provide a reliable source for accessing DMs.
Social influence is defined as the individual’s thoughts, feelings, attitudes or behaviors can affect others when interacting with other individuals or groups. DMs with higher social impact have the ability to influence the opinions of other members [47]. Using social network analysis techniques, the social impact of each DM in the group can be obtained. The more social relations a person has with others, the more influence the decision maker will be. In the social network analysis method, the centrality of the in-degree is used to quantify the social influence of DM in a network, and the social influence can reflect the importance of DM to a certain extent. Therefore, the social impact of
Then the comprehensive weight of each DM can be calculated as
3.2.3 The Weight of Each Subgroup
The network weight between subgroups can be calculated from the reciprocal of the distance from each subgroup to the network center. The further the distance, the smaller the weight. The main steps for calculating weights are shown below [5]:
Step 1: Calculate the fusion centrality of the network.
where
Step 2: Calculate the fusion centrality of each subgroup.
where
Step 3: Calculate the relative distance
Step 4: Standardize the weight
The trust relation between subgroups can be reconstructed by treating all nodes in a subgroup as a new node, and then calculating the trust weights between subgroups. Finally, the network weights and trust weights of the subgroups are integrated, and the comprehensive weights of the subgroups are obtained.
Next, the consensus measure will be computed based on
Step 1: Calculate the similarity matrix. Let
where
Step 2: Calculate the consensus matrix. By aggregating the similarity matrix of each pair of subgroups
Step 3: Calculate the large-scale group consensus index (LGCI).
(1) Calculate the consensus degree of the pair of alternatives. The consensus degree
(2) Calculate the consensus degree of the alternatives. The consensus degree
(3) Calculate the consensus degree of the preference relationship. This study refers to the consensus degree of the large group preference relationship as the consensus index LGCI, and the formula is as follows:
3.3 Consensus Reaching Process Based on Social Network Updating
Based on the above discussion, this study can get consensus at different levels. Assume
Moreover, the strength of ties between members shows the trust degree between those members. DMs with strong trust relationships have a greater impact. In the process of interaction, DMs with strong trust relationships will affect the preferences of DMs with weaker trust relationships. At the same time, the trust relation between DMs will also change. Therefore, this study will reflect the results of the feedback in the social network and change the connection between DMs to achieve a higher consensus faster according to the trust relationship between DMs.
The identification rules can obtain alternative comparison pairs, subgroups, and DMs continuously and accurately. Therefore, DMs can change their preferences in a precise way.
Identification Rule 1: Identify alternatives whose preferences need to be changed. The identified alternatives can be expressed as follows:
Identification Rule 2: Identify the locations that need to be changed. For any
Identification Rule 3: Determine the ideal and non-ideal sets for each identified part. For
Identification Rule 4: Identify the DMs who need to change their preferences. For the identified non-ideal set
The DMs in the non-ideal set
Set thresholds
3.3.2 Directions Rules and Network Adjustment
For each
Directions Rule 1: If
Directions Rule 2: If
One way to achieve the direction rule is to provide a set of values for
Let
After completing the above adjustment process, the final step is to modify the original social network.
Step 1: Let
Step 2: Calculate the
Step 3: Modify the original social network. According to
3.4 The Procedure of the Proposed Method
The main steps of the LGDM consensus problem are summarized below. Fig. 2 shows the framework of the proposed method.
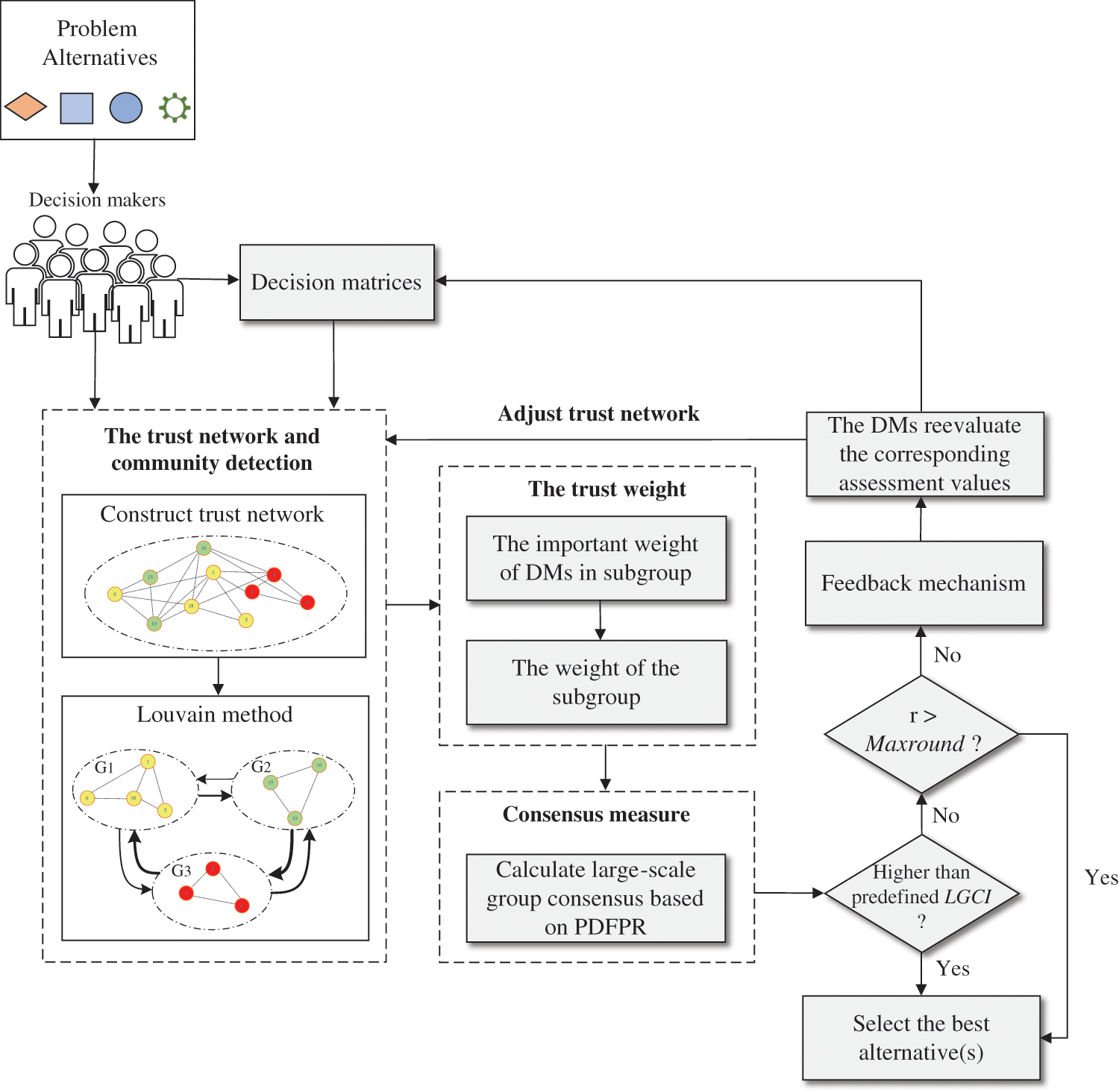
Figure 2: The framework of the proposed method
Part 1: Determine the network structure of the LGDM problem.
(1) The set of DMs and alternatives are represented by
(2) For each DM, a fuzzy preference matrix
(3) The Louvain method is used to determine subgroups of large-scale networks. Suppose this study gets
Part 2: Calculate the trust weight and consensus measure.
(1) Calculate the weights of the
(2) Calculate the PDFRP for each subgroup.
(3) Calculate the consensus of each subgroup.
Subgroup consensus can be obtained according to Section 3.3. Set the consensus is
Part 3: Consensus reaching process.
(1) Determine the identified DM as the corresponding new collection.
According to the four identification rules proposed in Section 3.3.1, the set of non-ideal DM can be expressed as
(2) Direct the DMs in
Modify the FPR of the DM in
(3) Modify the social network.
Part 4: Select the best alternative(s).
(1) Based on the final adjusted network, the weight of each DM within the subgroup and subgroup weights are recalculated, and then the final pairwise comparison matrix is obtained by aggregating the preference matrix of all subgroups for each pair of alternatives according to Eqs. (21)–(24).
(2) After obtaining the final pairwise comparison matrix, the final ranking result is obtained by subtracting the sum of each column value from the sum of each row value of each alternative [53].
(3) Rank all alternatives in descending order by the gap between the column value and row value and choose the alternative with the smallest gap as the best alternative.
Twenty travel enthusiasts with certain social connections are denoted as
The social network relations between the 20 travel enthusiasts as shown in Fig. 3.
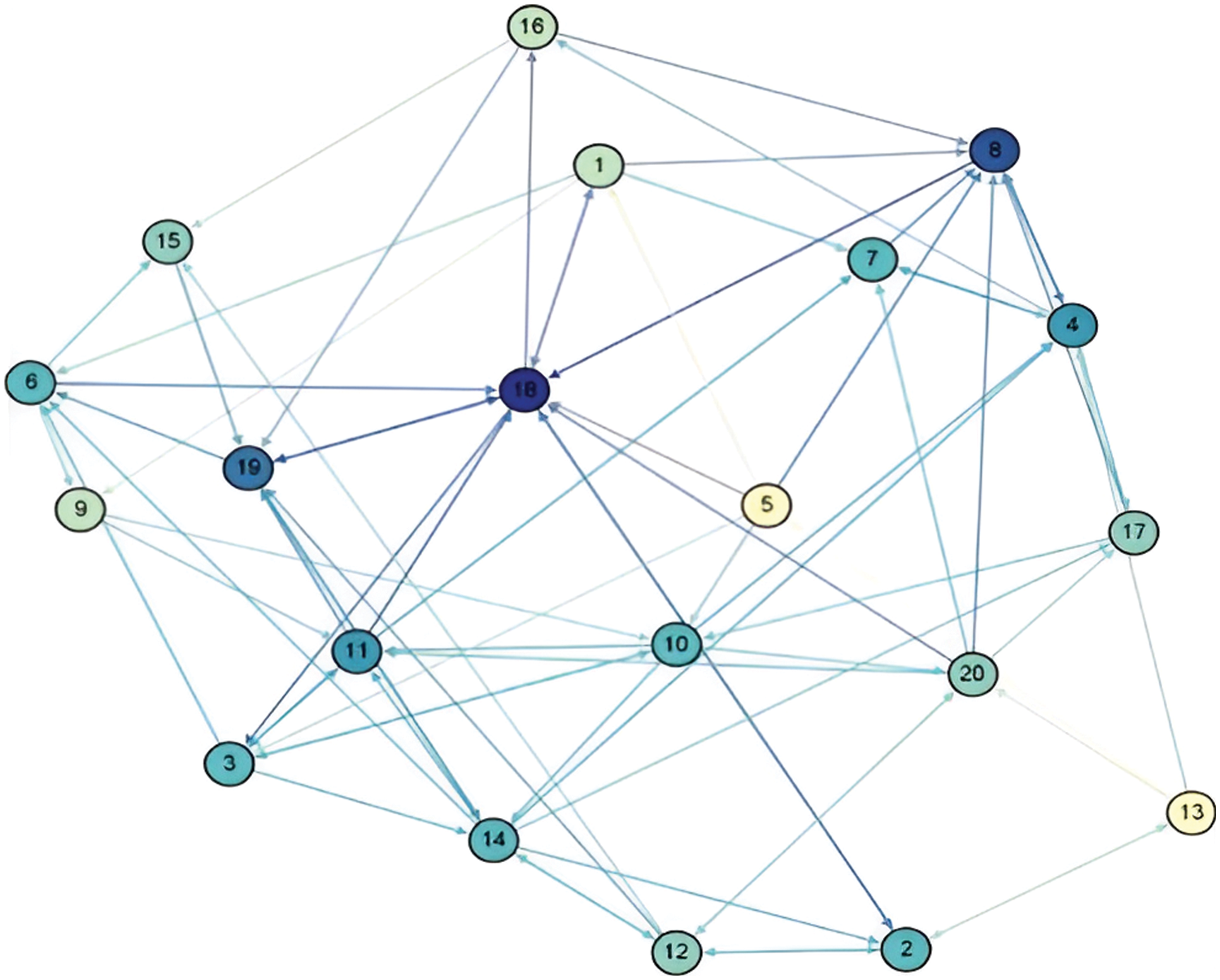
Figure 3: DMs’ social network
In Fig. 3, each travel enthusiast is represented in the network as a node with different colors and used to distinguish the number of ingress connections of the DMs. For example, the DM
4.2.1 Classification of Network Using Lauvain Method
A network corresponding to Fig. 3 is constructed in the complex network analysis tool Pajek, as shown in Fig. 4, where nodes

Figure 4: Network constructed in Pajek software
Using the Lauvain package included in the Pajek software, automatic classification is performed to form the classification results as shown in Fig. 5. The subgroup is represented by the set
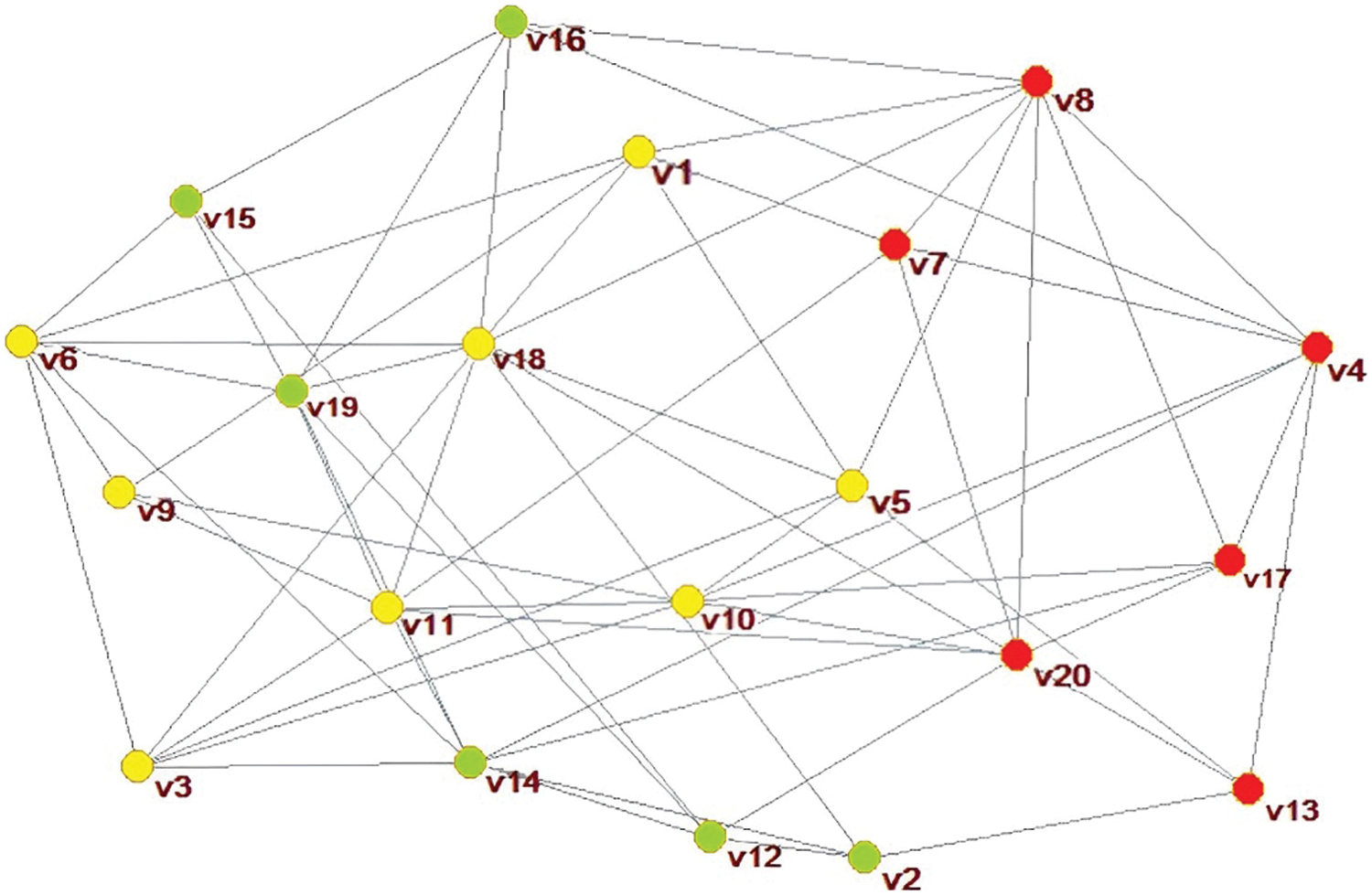
Figure 5: Social network clustering analysis results
4.2.2 Calculate the Trust Weight and Consensus Measure
For the subgroup
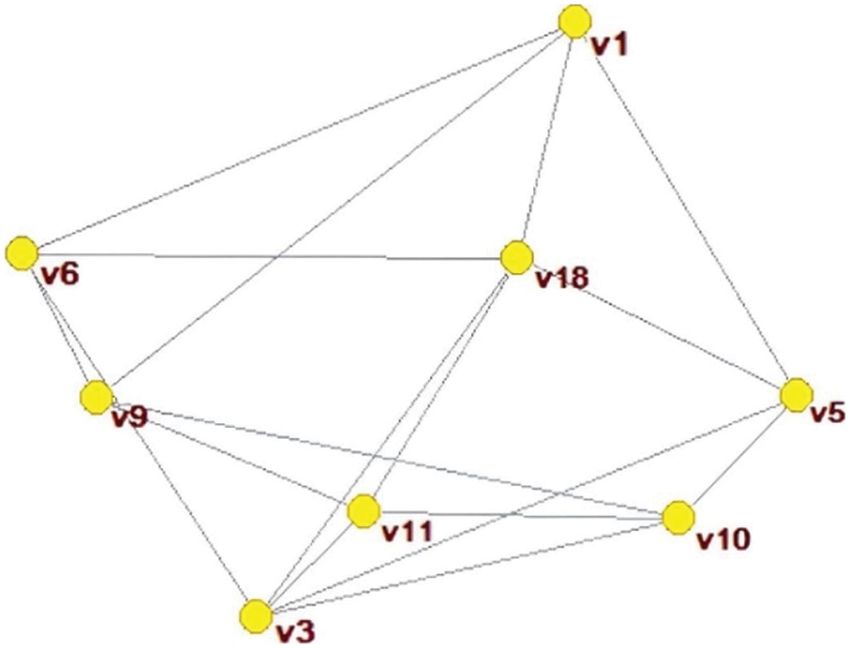
Figure 6: Network of subgroup
According to the original data required by the software and the original data required for the centrality of the feature vector, the network weight of each node in the subgroup

According to the network weights and trust weights, the weight of each DM is aggregated. And this study takes
According to the calculation results by Pajek software and Section 3.2, the network weight of each subgroup is
Considering each subgroup as a node, Fig. 3 can be abstracted into the structure shown in Fig. 7, where the direction of the edge represents the relationship between nodes, and the thickness of the edge represents the connection strength.
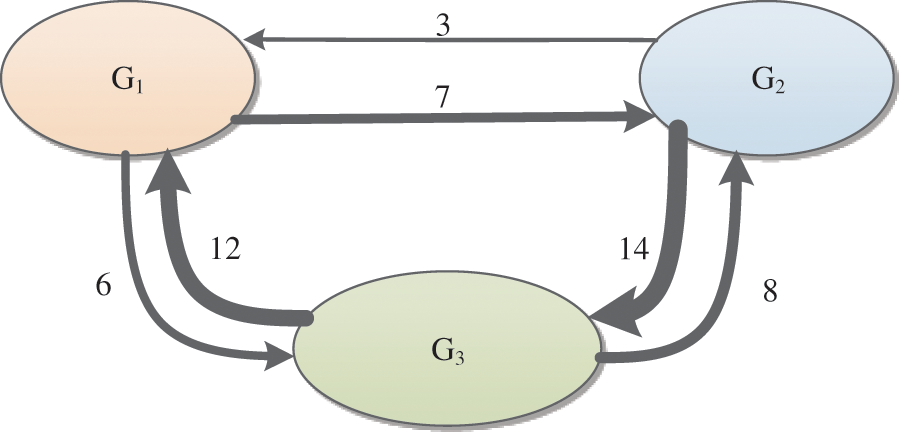
Figure 7: Directed social relationship network between subgroups
The trust weights between subgroups are
Similarly, by aggregating the network weights and trust weights of each subgroup, the comprehensive weight of each subgroup can be obtained
According to their preference for alternatives provided by the 20 DMs through FPR, the preference relationship of each subgroup also forms a probability distribution based on fuzzy preference relations [51]. According to Section 3.4, the corresponding
For the subgroup
For the subgroup
For the subgroup
According to Section 3.4, the consensus degree of the three subgroups can be calculated. First, the similarity matrixes between subgroups are calculated, and the results are as follows:
According to Eq. (13), the normalized weights between subgroups are
Second, the consensus of the group is calculated, and the consensus matrix is as follows:
The consensus degree between alternative pairs is
Third, the consensus degree at the level of the alternative is
Finally, the consensus degree of the group is
4.2.3 Consensus Reaching Process
Set
Let the parameter
DMs in subgroup
DMs in subgroup
Find the most trusted person for DMs
First round of adjustment:
According to Section 3.2.1, this study can get a new social network based on the Louvain method and a new subgroup classified as shown in Figs. 8 and 9.
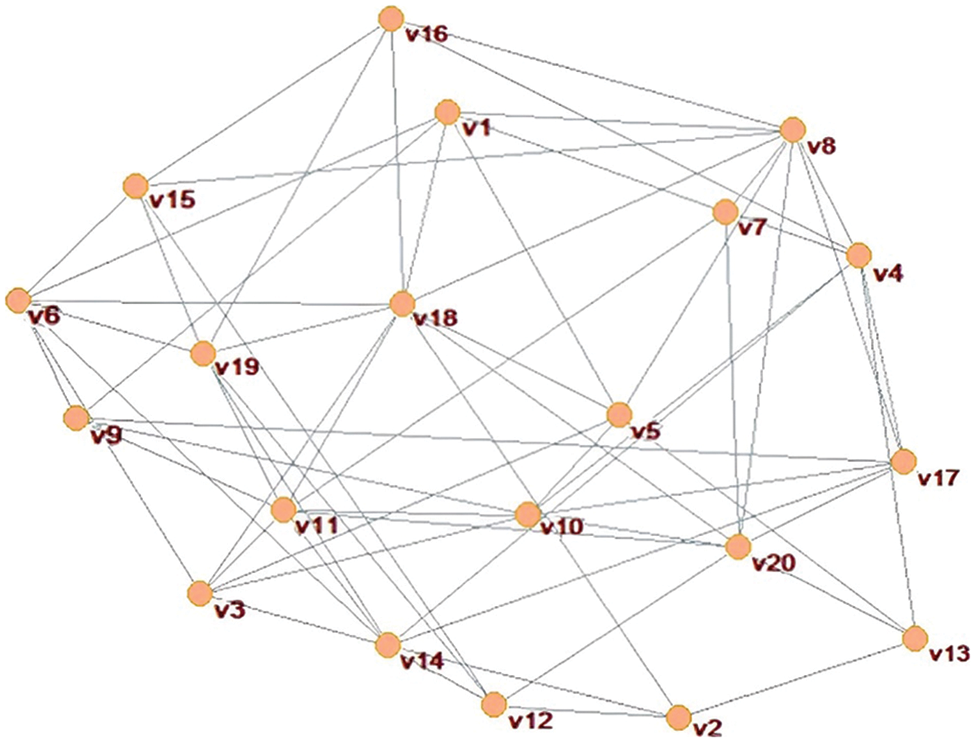
Figure 8: Network in the first round of adjustment
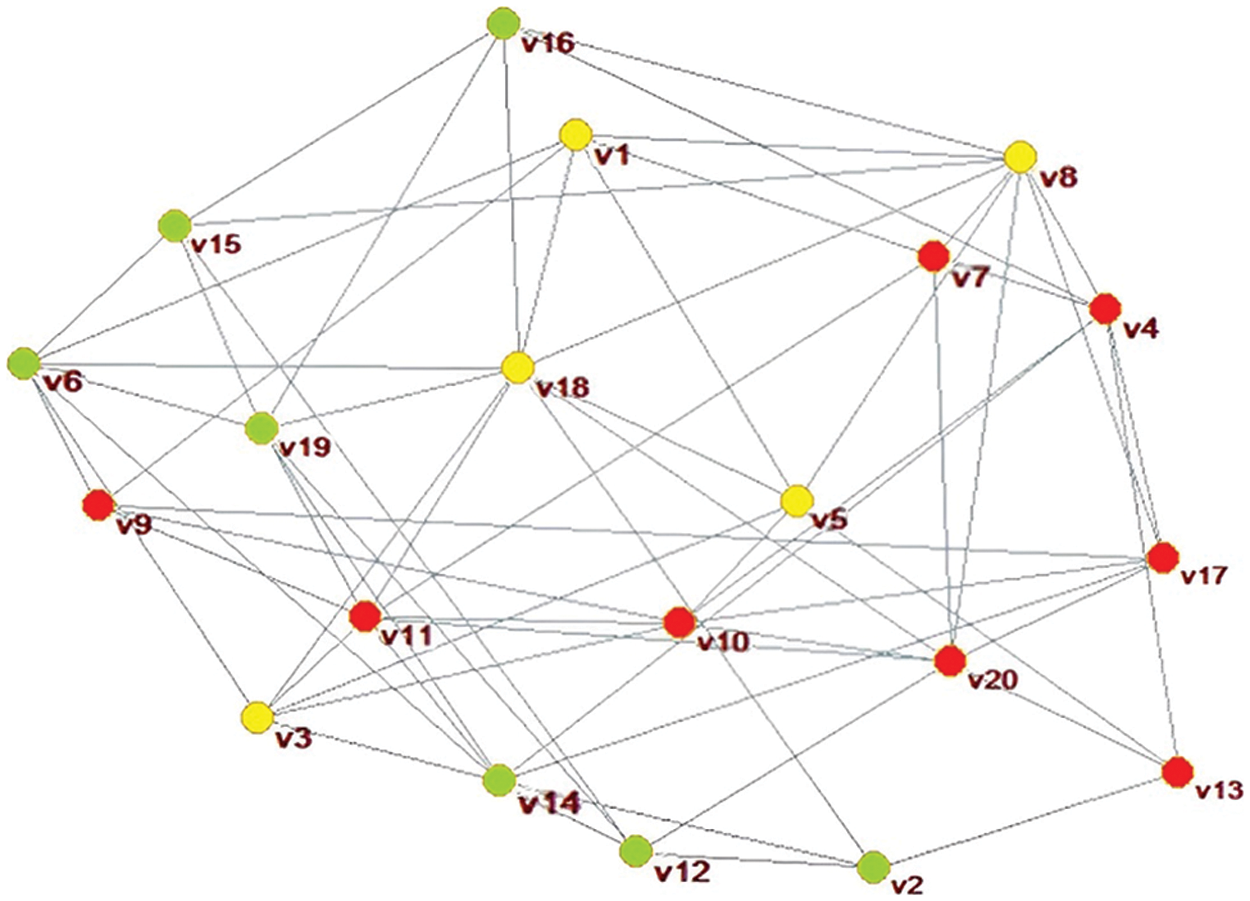
Figure 9: Classification result
As can be seen from the Fig. 9, three new subgroups can be obtained in this adjustment:

For the subgroup
For the subgroup
For the subgroup
The new similarity matrixes between subgroups are:
The normalized weights between pairs of subgroups are
Then the consensus of the group is calculated, and the consensus matrix is as follows:
The consensus degree of the large group
The preference pairs that need to be modified are
4.2.4 Select the Best Alternative(s)
The network obtained at the end of the final adjustment is shown in Fig. 10.

Figure 10: Classification network in the last round of adjustment
According to the network structure, the network weights and trust weights of the nodes are obtained, and the relative weights of the nodes in each subgroup are shown in Table 3. And the relative weights between the subgroups are

According to Eqs. (21)–(24), the preference of each DM is gathered within the subgroup, as shown below:
After obtaining the final pairwise comparison matrix, the final ranking result is obtained by subtracting the sum of each column value from the sum of each row value of each alternative [53]. According to the calculation, this study obtains
5 Comparative and Experiment Analysis
The proposed model considers the trust relationship between DMs, and daily social data are combined when calculating trust weights. The novel Louvain method is adopted in the classification of large groups, which has certain advantages compared with the traditional clustering method. In addition, this study also fully integrates real life when designing the feedback mechanism, and reconstructs the network through trust relations. This section compares the proposed method with other methods, as shown in Table 4.
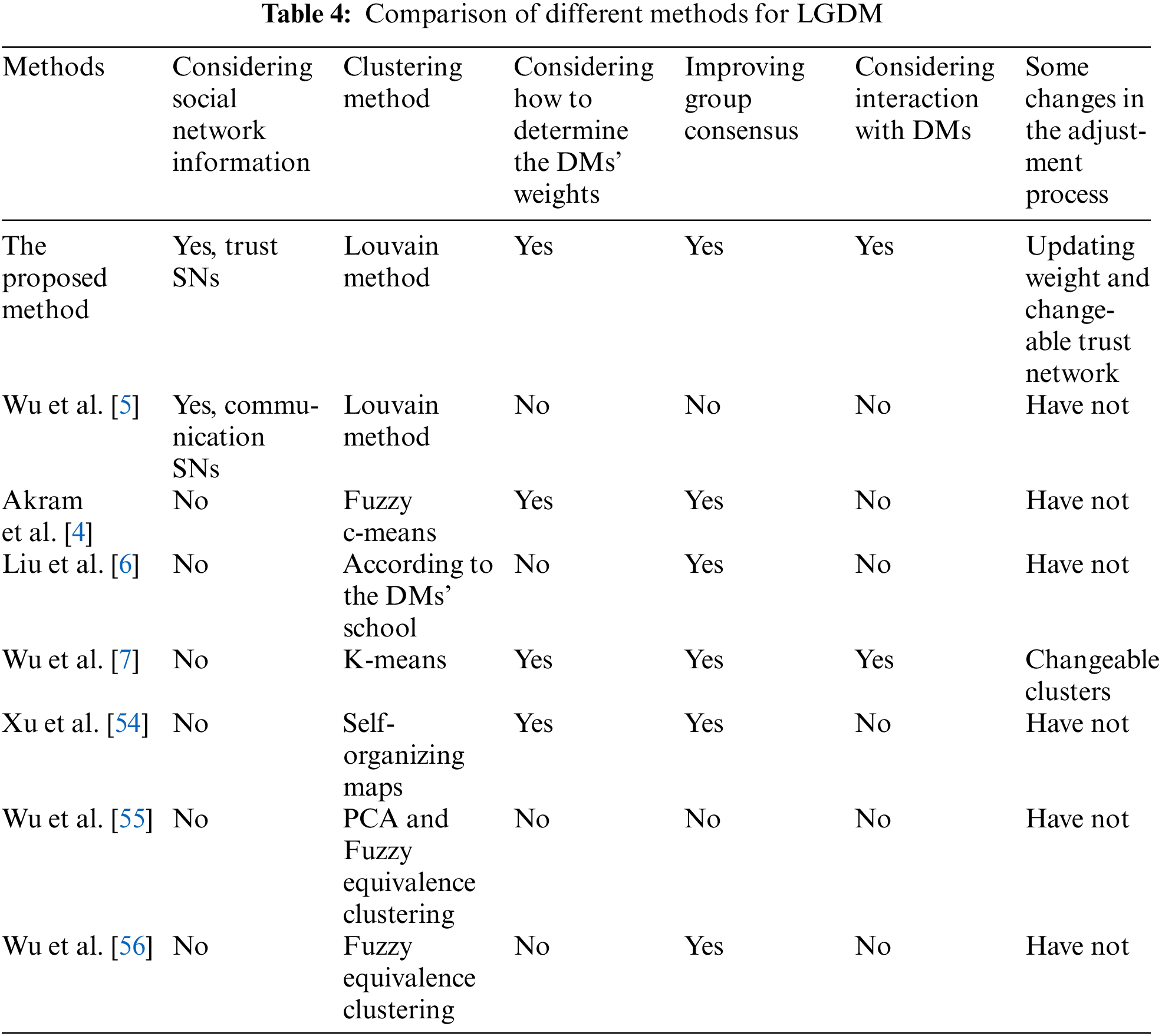
(1) Comparison with the LGDM with the clustering methods.
Akram et al. [4] used fuzzy c-means to cluster the fuzzy preferences, computed the consensus degree and improved consensus. But Akram et al. [4] did not consider the social network information. Liu et al. [6] classified the DMs according to the practical situation (DMs’ school). According to the percentage distribution and the decision weights, the dominance degrees on pairwise comparisons of alternatives are calculated, and a ranking of alternatives can be determined. However, Liu et al. [6] did not involve consensus improvement and interaction with DMs. A two-stage method to support the consensus-reaching process for large-scale multi-attribute group decision making was presented by Xu et al. [54]. The first stage classified the group into sub-subgroups by using the SOM in order to obtain preference of each sub-cluster. Wu et al. [55] developed a solution for LGDM, which used linguistic principal component analysis to reduce the dimensions of the attributes and used fuzzy equivalence clustering with linguistic information aggregate the preferences of the DMs, respectively. Wu et al. [56] incorporated clustering analysis and information aggregation operator into LGDM with interval type-2 fuzzy sets and used fuzzy equivalence clustering analysis to classify DMs to reduce the dimension of the DMs. However, [6] and [55] did not consider the consensus and interaction with DMs. At the same time, they all did not consider the relationship among DMs, such as communication, trust or cooperation.
Wu et al. [5] have built a large-scale undirected and unweighted network of 50 people. The relationship among DMs in the network is communication relationship and the Louvain method is also applied. The objective relationship of trust in the real world is very important in decision-making, but Wu et al. [5] did not take it into consideration. Moreover, it is not involved in the consensus measure and CRP. This study takes the trust relationship through the entire decision-making process, from social network construction and clustering, to weight determination and consensus measure, and finally to CRP and changeable networks.
(2) Comparison with the LGDM with the changeable cluster.
Some existed studies have considered the changeable cluster for LGDM. For example, the k-means clustering method based on Euclidean distance under possibility information was extended to classify the whole group into manageable subgroups [7]. The results showed that the twenty DMs were clustered into three clusters
Due to the low initial consensus of [7], the consensus is improved quickly after three rounds of adjustment; The initial consensus of this study is higher, after three rounds of adjustment, the predefined consensus level is also reached. Compared with the results of [7], The final consensus of this study is higher, which illustrates the effectiveness of the proposed method. In addition, since the decision preference information used by the two methods is the same, the different results of the two methods indicate that the SN information can amplify the difference between the alternatives, which means that social information about the DM does affect the outcome of the LGDM problem. When DM has similar preferences, it is reasonable to consider social information, which will be beneficial to SNA.
The proposed model in this study not only combines social network information, but also the number of subgroups is determined automatically. At the same time, in each round of adjustment process, not only the number of subgroups changes, but also the internal network structure of subgroups changes, which can more realistically aggregate the preference matrix of DMs, the optimal solution can be obtained in a simpler and more efficient way.
In order to determine the appropriate coefficient
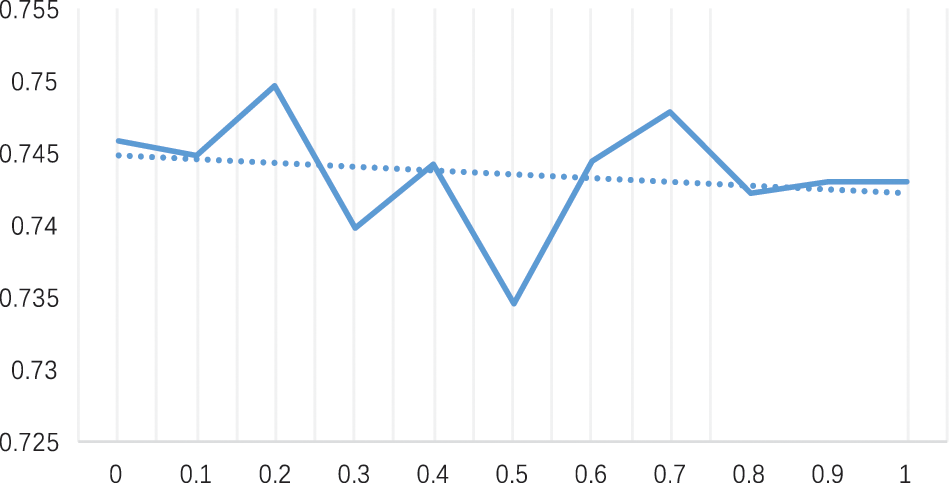
Figure 11: Simulation analysis of θ
In previous studies, DMs were independent of each other in the GDM problems. However, in most practical decision situations, DMs are socially related to each other rather than independent of each other. Moreover, consensus improvement is becoming increasingly important for DMs and stakeholders. This study provides a new perspective on LGDM problems and the main contributions are as follows:
First, this study considers the social trust relationship between DMs for the LGDM problems, builds the social network between DMs, and uses the Louvain method to detect community based on the trust relationship. Social networks built on trust relationships are more convincing than building networks based solely on DMs.
Second, this study fully considers the trust weight and the network weight in the process of determining the weight of individual DMs and the weight of each subgroup. Compared with weighting based on network degree centrality or subgroup size, it is more convincing to assign weights based on trust relationships and to make corresponding changes in weights in the feedback adjustment process. In the process of obtaining the final weight, the parameter
Third, the trust network in the proposed model allows for changes. Individual DMs are able to modify their preferences in the CRP, so the trust relationship will change, which will make the number of subgroups and members of each subgroup likely to change. And the interaction of trust relations is fully considered in the adjustment process. This is more in line with the reality that the influential DMs in the network will influence the opinions of the surrounding DM and enhance their trust.
Some significant opportunities for future work should be pointed out.
Firstly, this study determines the social network, trust weights and network weights by organizing social connections between DMs and the interaction frequency on social platforms. How to more scientifically measure the relationship between DMs is worth studying and improving. Secondly, although the Louvain method has realized automatic classification of the network, the constructed network diagram is still an undirected graph. In fact, a directed network is more reasonable and applicable to represent the social connection between people, and the classification results may differ from undirected networks. If the automatic classification method of directed networks can be added to future research, it will be a good innovation. Finally, the two parameters are fixed in this study: the predefined threshold of
Funding Statement: The work was supported by Humanities and Social Sciences Fund of the Ministry of Education (No. 22YJA630119), the National Natural Science Foundation of China (No. 71971051), and Natural Science Foundation of Hebei Province (No. G2021501004).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zhao, M., Liu, T., Su, J., Liu, M. Y. (2018). A method adjusting consistency and consensus for group decision-making problems with hesitant fuzzy linguistic preference relations based on discrete fuzzy numbers. Complexity, 2018(1), 1–17. https://doi.org/10.1155/2018/9345609 [Google Scholar] [CrossRef]
2. Lin, M., Huang, C., Xu, Z., Chen, R. (2020). Evaluating IoT platforms using integrated probabilistic linguistic MCDM method. IEEE Internet of Things Journal, 7(11), 11195–11208. https://doi.org/10.1109/JIOT.2020.2997133 [Google Scholar] [CrossRef]
3. Morente-Molinera, J. A., Kou, G., Peng, Y., Torres-Albero, C., Herrera-Viedma, E. (2018). Analysing discussions in social networks using group decision making methods and sentiment analysis. Information Sciences, 447(12), 157–168. https://doi.org/10.1016/j.ins.2018.03.020 [Google Scholar] [CrossRef]
4. Akram, M., Ilyas, F., Garg, H. (2021). ELECTRE-II method for group decision-making in Pythagorean fuzzy environment. Applied Intelligence, 51(12), 8701–8719. https://doi.org/10.1007/s10489-021-02200-0 [Google Scholar] [CrossRef]
5. Wu, T., Liu, X., Liu, F. (2018). An interval type-2 fuzzy TOPSIS model for large scale group decision making problems with social network information. Information Sciences, 432(2), 392–410. https://doi.org/10.1016/j.ins.2017.12.006 [Google Scholar] [CrossRef]
6. Liu, Y., Fan, Z. P., Zhang, X. (2016). A method for large group decision-making based on evaluation information provided by participators from multiple groups. Information Fusion, 29(3), 132–141. https://doi.org/10.1016/j.inffus.2015.08.002 [Google Scholar] [CrossRef]
7. Wu, Z., Xu, J. (2018). A consensus model for large-scale group decision making with hesitant fuzzy information and changeable clusters. Information Fusion, 41(3), 217–231. https://doi.org/10.1016/j.inffus.2017.09.011 [Google Scholar] [CrossRef]
8. Yang, W., Jhang, S. T., Shi, S. G., Xu, Z. S., Ma, Z. M. (2020). A novel additive consistency for intuitionistic fuzzy preference relations in group decision making. Applied Intelligence, 50(12), 4342–4356. https://doi.org/10.1007/s10489-020-01796-z [Google Scholar] [CrossRef]
9. Eirinaki, M., Gao, J., Varlamis, I., Tserpes, K. (2018). Recommender systems for large-scale social networks: A review of challenges and solutions. Future Generation Computer Systems, 78(3), 413–418. https://doi.org/10.1016/j.future.2017.09.015 [Google Scholar] [CrossRef]
10. Porcel, C., Ching-López, A., Lefranc, G., Loia, V., Herrera-Viedma, E. (2018). Sharing notes: An academic social network based on a personalized fuzzy linguistic recommender system. Engineering Applications of Artificial Intelligence, 75(1), 1–10. https://doi.org/10.1016/j.engappai.2018.07.007 [Google Scholar] [CrossRef]
11. Ozsoy, M. G., Polat, F., Alhajj, R. (2016). Making recommendations by integrating information from multiple social networks. Applied Intelligence, 45(4), 1047–1065. https://doi.org/10.1007/s10489-016-0803-1 [Google Scholar] [CrossRef]
12. Tu, W., Yang, M., Cheung, D. W., Mamoulis, N. (2018). Investment recommendation by discovering high-quality opinions in investor based social networks. Information Systems, 78(4), 189–198. https://doi.org/10.1016/j.is.2018.02.011 [Google Scholar] [CrossRef]
13. Li, H., Zhang, Z., Meng, F., Janakiraman, R. (2017). Is peer evaluation of consumer online reviews socially embedded?–An examination combining reviewer’s social network and social identity. International Journal of Hospitality Management, 67(51), 143–153. https://doi.org/10.1016/j.ijhm.2017.08.003 [Google Scholar] [CrossRef]
14. Dingyloudi, F., Strijbos, J. W. (2018). Just plain peers across social networks: Peer-feedback networks nested in personal and academic networks in higher education. Learning, Culture and Social Interaction, 18(6), 86–112. https://doi.org/10.1016/j.lcsi.2018.02.002 [Google Scholar] [CrossRef]
15. Leppink, J., Pérez-Fuster, P. (2019). Social networks as an approach to systematic review. Health Professions Education, 5(3), 218–224. https://doi.org/10.1016/j.hpe.2018.09.002 [Google Scholar] [CrossRef]
16. Tsugawa, S., Kimura, K. (2018). Identifying influencers from sampled social networks. Physica A: Statistical Mechanics and its Applications, 507(11), 294–303. https://doi.org/10.1016/j.physa.2018.05.105 [Google Scholar] [CrossRef]
17. Lingam, G., Rout, R. R., Somayajulu, D. V. L. N. (2019). Adaptive deep Q-learning model for detecting social bots and influential users in online social networks. Applied Intelligence, 49(11), 3947–3964. https://doi.org/10.1007/s10489-019-01488-3 [Google Scholar] [CrossRef]
18. Mnasri W., Azaouzi M., Romdhane L. B. (2021). Parallel social behavior-based algorithm for identification of influential users in social network. Applied Intelligence, 51(10), 7365–7383. https://doi.org/10.1007/s10489-021-02203-x [Google Scholar] [PubMed] [CrossRef]
19. Şimşek A., Kara R. (2018). Using swarm intelligence algorithms to detect influential individuals for influence maximization in social networks. Expert Systems with Applications, 114(1), 224–236. https://doi.org/10.1016/j.eswa.2018.07.038 [Google Scholar] [CrossRef]
20. Weng, J., Miao, C., Goh, A. (2006). Improving collaborative filtering with trust-based metrics. Proceedings of the 2006 ACM Symposium on Applied Computing–SAC’06, pp. 1860–1864. New York, USA. [Google Scholar]
21. Ureña, R., Kou, G., Dong, Y., Chiclana, F., Herrera-Viedma, E. (2019). A review on trust propagation and opinion dynamics in social networks and group decision making frameworks. Information Sciences, 478(1), 461–475. https://doi.org/10.1016/j.ins.2018.11.037 [Google Scholar] [CrossRef]
22. Pang, Q., Wang, H., Xu, Z. (2016). Probabilistic linguistic term sets in multi-attribute group decision making. Information Sciences, 369, 128–143. https://doi.org/10.1016/j.ins.2016.06.021 [Google Scholar] [CrossRef]
23. Wu, J., Chiclana, F., Fujita, H., Herrera-Viedma, E. (2017). A visual interaction consensus model for social network group decision making with trust propagation. Knowledge-Based Systems, 122(1), 39–50. https://doi.org/10.1016/j.knosys.2017.01.031 [Google Scholar] [CrossRef]
24. Shi, Z., Wang, X., Palomares, I., Guo, S., Ding, R. X. (2018). A novel consensus model for multi-attribute large-scale group decision making based on comprehensive behavior classification and adaptive weight updating. Knowledge-Based Systems, 158(1), 196–208. https://doi.org/10.1016/j.knosys.2018.06.002 [Google Scholar] [CrossRef]
25. Gou, X., Xu, Z., Herrera, F. (2018). Consensus reaching process for large-scale group decision making with double hierarchy hesitant fuzzy linguistic preference relations. Knowledge-Based Systems, 157(3), 20–33. https://doi.org/10.1016/j.knosys.2018.05.008 [Google Scholar] [CrossRef]
26. Ureña, R., Chiclana, F., Melançon, G., Herrera-Viedma, E. (2019). A social network based approach for consensus achievement in multiperson decision making. Information Fusion, 47(Supplement C), 72–87. https://doi.org/10.1016/j.inffus.2018.07.006 [Google Scholar] [CrossRef]
27. Gou, X., Xu, Z., Liao, H., Herrera, F. (2021). Consensus model handling minority opinions and noncooperative behaviors in large-scale group decision-making under double hierarchy linguistic preference relations. IEEE Transactions on Cybernetics, 51(1), 283–296. https://doi.org/10.1109/TCYB.2020.2985069 [Google Scholar] [PubMed] [CrossRef]
28. Dong, Y., Zha, Q., Zhang, H., Kou, G., Fujita, H. et al. (2018). Consensus reaching in social network group decision making: Research paradigms and challenges. Knowledge-Based Systems, 162(345), 3–13. https://doi.org/10.1016/j.knosys.2018.06.036 [Google Scholar] [CrossRef]
29. Lin, M., Chen, Z., Xu, Z., Gou, X., Herrera, F. (2021). Score function based on concentration degree for probabilistic linguistic term sets: An application to TOPSIS and VIKOR. Information Sciences, 551(3), 270–290. https://doi.org/10.1016/j.ins.2020.10.061 [Google Scholar] [CrossRef]
30. Dong, Q., Cooper, O. (2016). A peer-to-peer dynamic adaptive consensus reaching model for the group AHP decision making. European Journal of Operational Research, 250(2), 521–530. https://doi.org/10.1016/j.ejor.2015.09.016 [Google Scholar] [CrossRef]
31. Li, Y., Zhang, H., Dong, Y. (2017). The interactive consensus reaching process with the minimum and uncertain cost in group decision making. Applied Soft Computing, 60, 202–212. https://doi.org/10.1016/j.asoc.2017.06.056 [Google Scholar] [CrossRef]
32. Wu, Z., Xu, J. (2016). Managing consistency and consensus in group decision making with hesitant fuzzy linguistic preference relations. Omega, 65(2), 28–40. https://doi.org/10.1016/j.omega.2015.12.005 [Google Scholar] [CrossRef]
33. Zhang, G., Dong, Y., Xu, Y. (2014). Consistency and consensus measures for linguistic preference relations based on distribution assessments. Information Fusion, 17(2), 46–55. https://doi.org/10.1016/j.inffus.2012.01.006 [Google Scholar] [CrossRef]
34. Perez, I. J., Cabrerizo, F. J., Alonso, S., Herrera-Viedma, E. (2014). A new consensus model for group decision making problems with non-homogeneous experts. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 44(4), 494–498. https://doi.org/10.1109/TSMC.2013.2259155 [Google Scholar] [CrossRef]
35. Quesada, F. J., Palomares, I., Martínez, L. (2015). Managing experts behavior in large-scale consensus reaching processes with uninorm aggregation operators. Applied Soft Computing, 35, 873–887. https://doi.org/10.1016/j.asoc.2015.02.040 [Google Scholar] [CrossRef]
36. Gou, X., Xu, Z. (2021). Managing noncooperative behaviors in large-scale group decision-making with linguistic preference orderings: The application in internet venture capital. Information Fusion, 69(1), 142–155. https://doi.org/10.1016/j.inffus.2020.12.003 [Google Scholar] [CrossRef]
37. Gou, X., Xu, Z., Zhou, W. (2020). Managing consensus by multi-stage optimization models with linguistic preference orderings and double hierarchy linguistic preferences. Technological and Economic Development of Economy, 26(3), 642–674. https://doi.org/10.3846/tede.2020.12013 [Google Scholar] [CrossRef]
38. Granovetter, M. S. (1973). The strength of weak ties. American Journal of Sociology, 78(6), 1360–1380. https://doi.org/10.1086/225469 [Google Scholar] [CrossRef]
39. Liang, Q., Liao, X., Liu, J. (2017). A social ties-based approach for group decision-making problems with incomplete additive preference relations. Knowledge-Based Systems, 119, 68–86. https://doi.org/10.1016/j.knosys.2016.12.001 [Google Scholar] [CrossRef]
40. Freeman, L. C. (1978). Centrality in social networks conceptual clarification. Social Networks, 1(3), 215–239. https://doi.org/10.1016/0378-8733(78)90021-7 [Google Scholar] [CrossRef]
41. Lin, M., Huang, C., Xu, Z. (2019). TOPSIS method based on correlation coefficient and entropy measure for linguistic pythagorean fuzzy sets and its application to multiple attribute decision making. Complexity. https://doi.org/10.1155/2019/6967390 [Google Scholar] [CrossRef]
42. Huang, C., Lin, M., Xu, Z. (2020). Pythagorean fuzzy MULTIMOORA method based on distance measure and score function: Its application in multicriteria decision making process. Knowledge and Information Systems, 62(11), 4373–4406. https://doi.org/10.1007/s10115-020-01491-y [Google Scholar] [CrossRef]
43. Lin, M., Wang, H., Xu, Z. (2020). TODIM-based multi-criteria decision-making method with hesitant fuzzy linguistic term sets. Artificial Intelligence Review, 53(5), 3647–3671. https://doi.org/10.1007/s10462-019-09774-9 [Google Scholar] [CrossRef]
44. Lin, M., Huang, C., Chen, R., Fujita, H., Wang, X. (2021). Directional correlation coefficient measures for Pythagorean fuzzy sets: Their applications to medical diagnosis and cluster analysis. Complex & Intelligent Systems, 7(2), 1025–1043. https://doi.org/10.1007/s40747-020-00261-1 [Google Scholar] [CrossRef]
45. Lin, M., Li, X., Chen, R., Fujita, H., Lin, J. (2022). Picture fuzzy interactional partitioned Heronian mean aggregation operators: An application to MADM process. Artificial Intelligence Review, 55(2), 1171–1208. https://doi.org/10.1007/s10462-021-09953-7 [Google Scholar] [CrossRef]
46. Blondel, V. D., Guillaume, J. L., Lambiotte, R., Lefebvre, E. (2008). Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment, 2008(10), P10008. https://doi.org/10.1088/1742-5468/2008/10/P10008 [Google Scholar] [CrossRef]
47. Herrera-Viedma, E., Alonso, S., Chiclana, F., Herrera, F. (2007). A consensus model for group decision making with incomplete fuzzy preference relations. IEEE Transactions on Fuzzy Systems, 15(5), 863–877. https://doi.org/10.1109/TFUZZ.2006.889952 [Google Scholar] [CrossRef]
48. Fortunato, S. (2010). Community detection in graphs. Physics Reports, 486(3–5), 75–174. https://doi.org/10.1016/j.physrep.2009.11.002 [Google Scholar] [CrossRef]
49. Newman, M. E. J., Girvan, M. (2004). Finding and evaluating community structure in networks. Physical Review E, 69(2), 026113. https://doi.org/10.1103/PhysRevE.69.026113 [Google Scholar] [PubMed] [CrossRef]
50. Pan, L., Wang, C., Xie, J. (2013). A spin-glass model based local community detection method in social networks. 2013 IEEE 25th International Conference on Tools with Artificial Intelligence, pp. 108–115. Herndon, VA, USA. [Google Scholar]
51. Wang, W., Liu, D., Liu, X., Pan, L. (2013). Fuzzy overlapping community detection based on local random walk and multidimensional scaling. Physica A: Statistical Mechanics and its Applications, 392(24), 6578–6586. https://doi.org/10.1016/j.physa.2013.08.028 [Google Scholar] [CrossRef]
52. Sattari, M., Zamanifar, K. (2018). A cascade information diffusion based label propagation algorithm for community detection in dynamic social networks. Journal of Computational Science, 25(2), 122–133. https://doi.org/10.1016/j.jocs.2018.01.004 [Google Scholar] [CrossRef]
53. Recio-García, J. A., Quijano, L., Díaz-Agudo, B. (2013). Including social factors in an argumentative model for group decision support systems. Decision Support Systems, 56, 48–55. https://doi.org/10.1016/j.dss.2013.05.007 [Google Scholar] [CrossRef]
54. Xu, Y., Wen, X., Zhang, W. (2018). A two-stage consensus method for large-scale multi-attribute group decision making with an application to earthquake shelter selection. Computers & Industrial Engineering, 116, 113–129. https://doi.org/10.1016/j.cie.2017.11.025 [Google Scholar] [CrossRef]
55. Wu, T., Liu, X., Qin, J. (2018). A linguistic solution for double large-scale group decision-making in E-commerce. Computers & Industrial Engineering, 116(1), 97–112. https://doi.org/10.1016/j.cie.2017.11.032 [Google Scholar] [CrossRef]
56. Wu, T., Liu, X. W. (2016). An interval type-2 fuzzy clustering solution for large-scale multiple-criteria group decision-making problems. Knowledge-Based Systems, 114(3), 118–127. https://doi.org/10.1016/j.knosys.2016.10.004 [Google Scholar] [CrossRef]
57. Roselló, L., Sánchez, M., Agell, N., Prats, F., Mazaira, F. A. (2014). Using consensus and distances between generalized multi-attribute linguistic assessments for group decision-making. Information Fusion, 17(23), 83–92. https://doi.org/10.1016/j.inffus.2011.09.001 [Google Scholar] [CrossRef]
58. Dong, Y., Zhao, S., Zhang, H., Chiclana, F., Herrera-Viedma, E. (2018). A self-management mechanism for noncooperative behaviors in large-scale group consensus reaching processes. IEEE Transactions on Fuzzy Systems, 26(6), 3276–3288. https://doi.org/10.1109/TFUZZ.2018.2818078 [Google Scholar] [CrossRef]
59. Zhang, H., Dong, Y., Herrera-Viedma, E. (2018). Consensus building for the heterogeneous large-scale GDM with the individual concerns and satisfactions. IEEE Transactions on Fuzzy Systems, 26(2), 884–898. https://doi.org/10.1109/TFUZZ.2017.2697403 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools