Role Dynamic Allocation of Human-Robot Cooperation Based on Reinforcement Learning in an Installation of Curtain Wall

1  Introduction

With the research on human-robot cooperation and intelligent robot technology, we recognize that tasks can be completed more efficiently and smoothly by endowing the robot with specific initiatives [1,2]. Many studies have examined the claim that the human is the leader and the robot is the follower during cooperation [3]. As auxiliary equipment, the robot can help the human increase or decrease force by collecting interactive signals, reducing the partner’s working intensity [4]. That researches mainly focus on master-slave and follow-up robot control algorithms [5,6]. However, in some practical tasks, human and robots must be leaders and followers [7,8]. An additional complication is that the roles of leader and follower may need to be changed during the task. Several researchers have addressed the issue of the different roles of humans and robots in cooperative tasks. For example, Lawitzky et al. [9] have shown that task performance is improved through a higher degree of assistance by the robot in the human-robot moving an object task. Some researchers [10–12] have tried to create a continuous function by rapidly switching between two distinct extreme behaviors (leader and follower) to change the cooperative role. In order to develop assistance adaptation schemes, Passenberg and others present a force-based criterion for distinguishing between the two scenarios and introduce an approach to optimize the assistance levels for each scenario [13]. According to the observation that human-human interaction is not defined as a proportion of role allocation in advance, some researchers try to study approaches that allow online investigation of the dominance distribution between partners depending on different situations [14]. For comparing the cooperation performance from the fixed role method and the adaptive control role switching method, some researchers [15,16] investigated a method for the simultaneous switching of two roles between a robot and a human participant. They have proven that the adaptive online role-adjusting method has a higher success rate than the fixed role method.

In the recent related research work, literature [17] is a further study of the dynamic role assignment (RDA) algorithm [15,16] based on the homotopy method. Robots know the target location and task content to plan their motion trajectory, while humans act as task correctors. Specifically, when the robot plays the “leader” role, the robot follows a pre-planned trajectory; When the robot’s movement track does not meet the task requirements, the human plays the role of ‘leader’ and intervenes (corrects) the robot’s movement. However, the robot’s trajectory cannot be planned in tasks with unknown and variable targets. Therefore, the above RDA method is no longer applicable, as shown in the scene of the human-robot Cooperative curtain wall assembly in Fig. 1. A three-module framework (HMRDA) of human-robot cooperative motion target prediction module, role dynamic assignment module, and robot motion planning module was designed, and a dynamic role assignment method based on goal prediction and fuzzy reasoning was proposed [18]. According to motion information and prediction information, the robot can adjust its role in human-robot cooperative motion to change the motion trajectory. However, the above HmrDA-based approach can change the binary problem where the role is only leader and follower, rather than the role adjusting more weight to the leader or follower. In addition, the premise of changing the role is that the robot can accurately recognize human intention. Compared with the dynamic adjustment of role, the article’s authors [18] have contributed more to the recognition of robot intention.

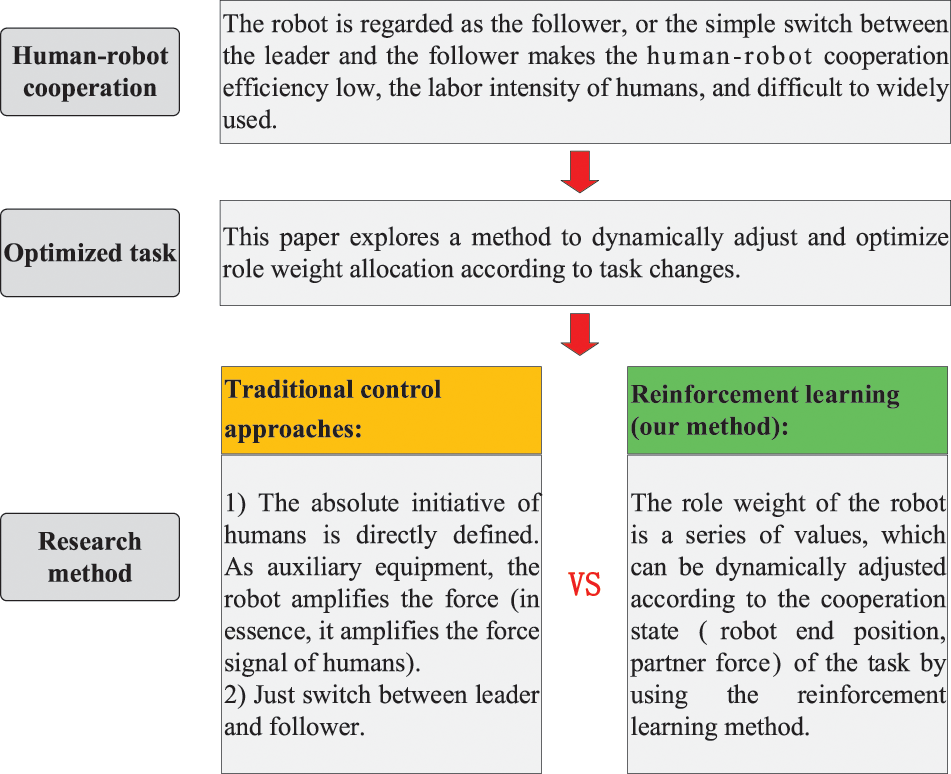
Figure 1: The architecture of the relationship among the optimized task, research methods, and the human-robot cooperation

Reinforcement learning is often an effective method to solve the problem of parameter recognition or robot imitation learning in human-robot cooperation [19]. Like the role allocation problem, reinforcement learning is often used to learn model-free strategies in practical robot control. The online, self, and adaptive learning algorithm is applied not only in human-robot cooperation but also in the problems of dynamic parameter difficulty and nonlinear control. For example, in literature [20], they adopt reinforcement learning methods constructed a control policy inside the multi-dimensional chaotic region to solve the problem of higher-order, coupled, 3D under-actuated manipulator with non-parametric uncertainties, control signal delay (input delay), and actuator saturation. Literature [21] proposed a reinforcement learning method called the ‘CPGactor-critic’ to control a humanoid robot leg, which can successfully control a system with a large DOF but a small number of actor parameters. In addition, the excessive increase in the input dimensionality of the critic could be avoided. The above literature methods provide ideas for using reinforcement learning to solve the role assignment problem in human-robot interaction in this paper.

In this paper, we use reinforcement learning to adjust the roles allocation of the human and robot so that we can install the glass curtain wall unit more efficiently and quickly. First, the physical human-robot cooperation model, including the role factor, is built. Second, a reinforcement learning model which can adjust the role factor in real-time is established, and a reward and action model are designed. The role factor can be adjusted continuously according to the comprehensive performance of the human-robot interaction force and robot’s Jerk during the repeated installation process. Finally, the experiments of the dynamic role allocation and the effect of the performance weighting coefficient on the result have been verified. The results show that the proposed method can realize the role adaptation and achieve the dual optimization goal of reducing the sum of the cooperator’s force and the robot’s Jerk. Compared with the existing role allocation methods, the established role model is not only a leader and a follower but a more precise division of roles, which is more suitable for occasions when the boundary between the leader and the follower is blurred in tasks. In addition, the enhanced learning algorithm is used to learn the changing rules of the role. The intelligence of the robot is enhanced by imitating the idea that human beings use incentives and training methods to improve intelligence to explore and solve the problems caused by the robot mental retardation in man-machine cooperation, such as low cooperation efficiency, the heavy labor intensity of operators and application difficulties. The main contributions of this work are as follows: (1) The role adjustment model and comprehensive performance model of man-machine cooperation are established. (2) A dynamic role assignment method based on reinforcement learning is proposed. Robots can adjust their role in the man-machine cooperative movement in real-time according to the changes in cooperative tasks, giving full play to the advantages of humans and robots.

An architecture is created to visualize the relationship among the optimized task, traditional control approaches, reinforcement learning, and human-robot cooperation, as shown in Fig. 1.

Fig. 1 shows that this paper transforms the role allocation problem in human-robot cooperation into a dynamic adaptive optimization problem. It compares the differences between traditional control methods and the proposed methods in robot role allocation.

2  Problem Statement

2.1 Task Description

In this paper, we assume that one scene in which the human is collaborating with the robot to complete an installation task of a glass curtain wall, as shown in Fig. 2. There is a two-step process. (1) the curtain wall should be moved to near the preinstallation location rapidly in the low-restricted area; (2) the curtain wall should be precisely installed into the frame in the high-restricted area. In step (1), there is a bigger space of movement, the efficiency of the movement should be concerned, and the effort from the human should be minimized. However, step (2), it is an accurate installing mission, and the curtain wall stability of the robot end-effector under multi-force action should be more concerned than the human’s effort.

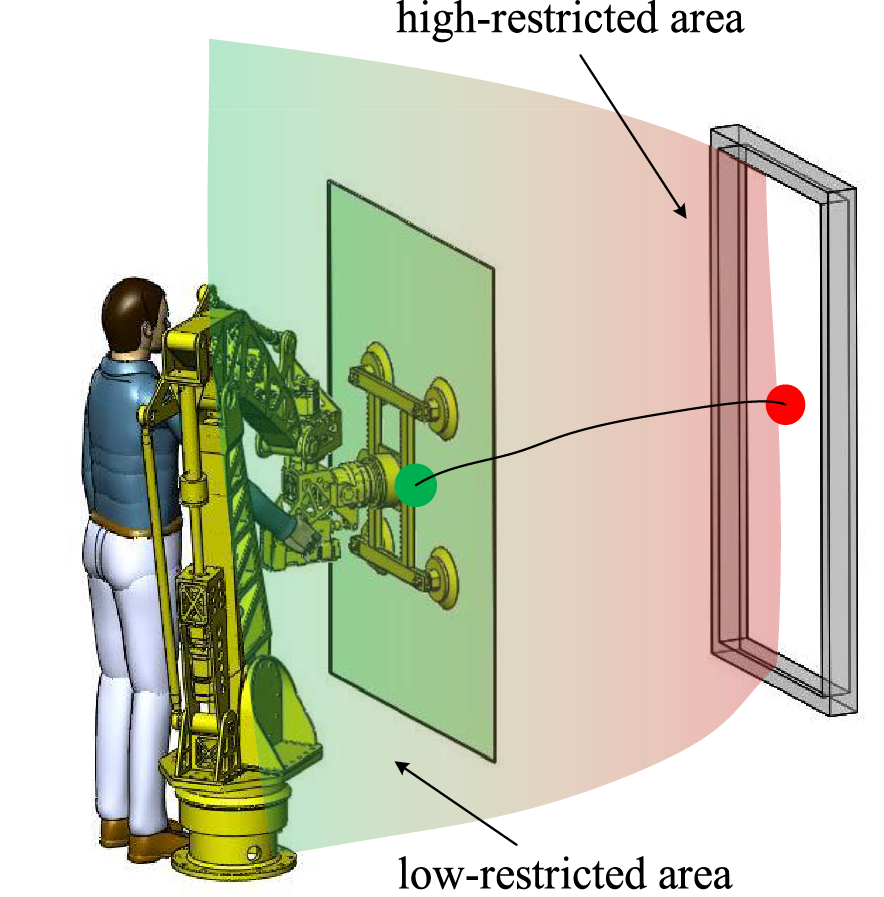
Figure 2: Human-robot cooperation system schematic diagram of curtain wall installation
Note: The knowledge of the high-restricted and low-restricted areas of the robot is not given, and the high-restricted and low-restricted have no apparent boundaries.

2.2 Human-Robot Cooperation Model and Evaluation Model

2.2.1 Cooperation Model

A force-based physical cooperation model is built and discussed. The application scenario involves one human and one robot to do a lifting task, as shown in Fig. 3. In this paper, 1 DOF case is established as a research model. However, the definitions may also be valid for more DOFs and partners.

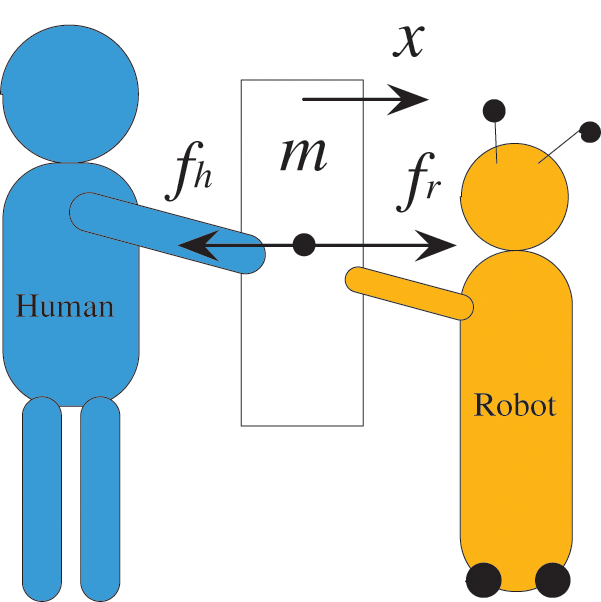
Figure 3: Cooperative model based on force interaction in a lifting task

In Fig. 3, fh and fr respectively represent the interaction force from the human and the robot; x is the object’s displacement; m is the object’s mass. The mathematical model acting on an object by two agents can be described as follow based on Newton’s Second Law:

fh+fr=mx¨(1)

where, x¨ is the acceleration of the object.

2.2.2 Roles Model

From previous studies [14], the expression forms of the contribution level to the contributions for moving the object can be described as follows:

α1=fh/(fh+fr)α2=fr/(fh+fr)α1+α2=1(2)

where, the α1 and the α2 respectively represent the role values of the human and the robot.

2.2.3 Evaluation Model

a) Force Model of Human

The total energy paid by the collaborator or the sum of the interaction force from the human is generally used to be described to evaluate the human’s effort in the cooperation process [14]. The total energy from the partner to complete the task is challenging to measure directly during the cooperation process. However, the total force of the collaborator is more easily measured. Therefore, the partner’s force sum is used to estimate the partner’s effort in this paper. The sum of the force model of the human THF (Total Human Force) is established in Eq. (3):

THF=∑t=0tf‖fh‖(3)

where, tf represents the current time corresponding to the discrete movement steps, fh represents the cooperative force, and ‖⋅‖ represents the norm.

b) Compliant Model of Robot

In the field of robotics, the Jerk is often used to describe the flexibility of a robot. The smaller the Jerk is, the smoother the system is. In this paper, the sum of the Jerk is used to assess the end-point flexibility of the robot, and the compliant model of robot TJerk (Total Jerk) is established in Eq. (4):

TJerk=∑t=0tf‖x⃛‖(4)

where, the x⃛ represents the Jerk at the end of the cooperative robot.

c) Comprehensive Evaluation Model

A comprehensive evaluation model that reflects human effort and robotic compliance is estimated to evaluate the performance of human-robot cooperation in this paper, and it is defined as follows:

OES=ω1⋅THF+ω2⋅TJerk(5)

where, ω1 and ω2 are performance weighting coefficients, and their values meet the following conditions:

{ω1∈[0;1]ω2∈[0;1]ω1+ω2=1(6)

In Eq. (6), if the weighting factor is designed as ω1=1,ω2=0, it indicates that only the human effort is considered in the cooperative performance. On the contrary, if the weighting factor is designed as ω1=0,ω2=1, the single factor of robot compliance is used as the evaluation parameter. However, if the weighting factor is designed as ω1=0.5,ω2=0.5, the human effort and the robot compliance are regarded as equally important. The weighting factor value significantly impacts cooperative performance, which affects the result of role allocation. In this paper, the impact on role allocation is discussed separately under the same and different weighting factor.

3  Dynamic Role Adaptive Allocation Design

3.1 Overall Framework

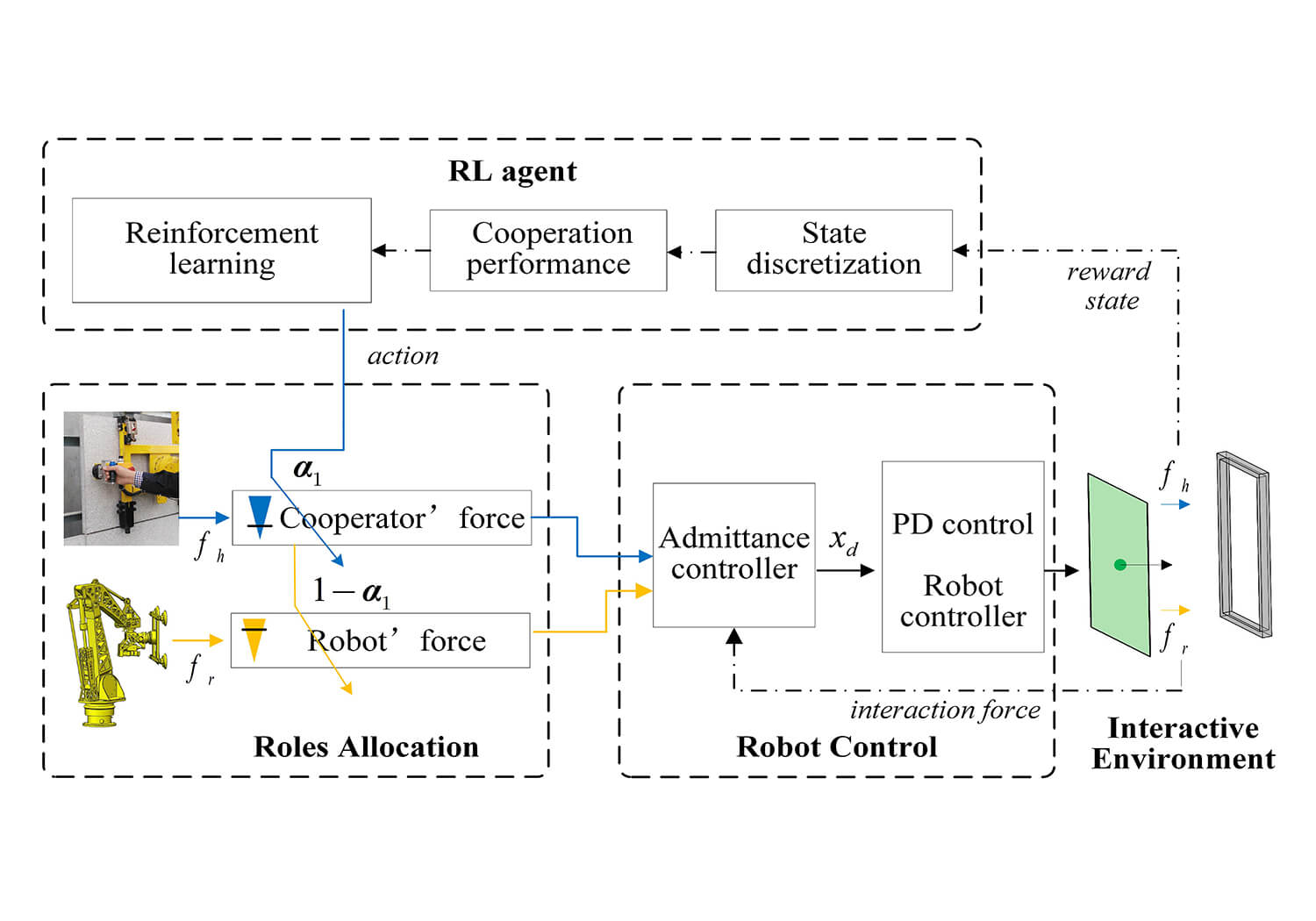
Reinforcement learning is a method that can realize adaptive parameter adjustment online and establish the relationship between action and state uncertainty according to the target. In this paper, this method is used to adjust role parameters during the process of cooperation. The overall architecture of the method is shown in Fig. 4.

Figure 4: Roles allocation method based on reinforcement learning in human-robot cooperation

In Fig. 4, α1 is the role factor, which regulates the active and passive relationship between the collaborator and the robot in a cooperative task. The α1 is dynamically adjusted according to the performance of the comprehensive evaluation model. The robot is controlled by the admittance method [22,23]. The robot admittance control model is shown in Eq. (7):

{x¨d−x¨0)+Dd(x˙d−x˙0)+Kd(xd−x0)=(1−α1)fr+fh(7)

where, Md,Dd,Kd are the expected mass matrix, damping matrix, and stiffness matrix, respectively. The {x¨d,x˙d,xd} are the expected acceleration, velocity, and position of the end of the robot, and the {x¨0,x˙0,x0} are the actual acceleration, velocity, and position of the robot’s end.

3.2 Reinforcement Learning

This paper proposes a reinforcement learning model to change roles allocation weight during the installation of glass curtain walls in human-robot cooperation, as shown in Fig. 5.

Figure 5: Principle diagram of dynamic role allocation based on reinforcement learning method

Here the roles allocation value a1 adjusted online according to the system’s current state and reward value. The current state st is the motion state of the robot and collaborator’s force, and the reward value is calculated as a designed model described below. A Q-learning model [24] generates the roles allocation algorithm since no prior strategy or sample. The algorithm of Q-learning is shown in Algorithm 1.

where, α is the learning rate, s is the current system state, s′ is the next sampling system state, a and a′ is respectively the behavior of the current moment (action) and the next sampling moment, r is the return value of the current moment, and γ is the discount factor. π is the strategy. The machine has to learn, by trial and error in the environment, a “strategy” π, according to which the action to be performed at state x is obtained: a = π (s). In Algorithm 1, the core intermediate variable is Q(s, a), which can be referred to as the Q table for short (mainly used for learning deterministic strategy π, namely updating strategy π), representing the expected cumulative reward obtained by the agent choosing action a under state s. Since the dynamic programming method is used and the model is unknown, it is more convenient to use γ discount cumulative reward in this paper. In formula (8), Q(s, a) is updated incrementally.

3.2.1 Action

In this paper, we aim to adjust the roles allocation weight α1 or α2 using reinforcement learning, so the roles allocation weight α1 or α2 should be established an association with the moment a parameter of reinforcement learning. The roles allocation values α1 are preprocessed by discretization of the parameters and divided into m. The action model can be expressed as α1=a={a1,a2,a3,⋯,am}.

3.2.2 Reward Design

In the physical human-robot cooperation system, the reward in reinforcement learning should be designed to be associated with comprehensive performance. It is based on minimizing the robot’s Jerk and minimizing the partner’s effort. The return value of cooperation performance is described as follows by formula (9):

T∗=min{T}=min{∑τ=0τf(ω1(‖fh‖)+ω2(‖x⃛‖))}(9)

where, T∗,T are non-negative terms, the τf is the duration of discrete motion in the task process, ω1,ω2 are the performance weight coefficients. The reward model is designed as follows:

rt+1=−∑τ=τtτt+1(ω1(‖fh‖)+ω2(‖x⃛‖))(10)

where, τt,τt+1∈N represents the sample time of the reinforcement learning, t,t+1∈N represents the robot-controlled cycle time, and their relationship is shown as follows:

τt=kt(11)

where, k is an integer greater than zero, and it is the asynchronous adjustment coefficient. The function of the asynchronous adjustment coefficient is to enhance the system’s robustness by setting the sampling frequency of the reinforcement learning return value less than the robot control frequency.

At the end of each traversal, the total return value of the traversal can be obtained to evaluate the cooperation performance. The sum of return values is shown as follows:

rtot=−∑t=0τf(ω1(‖fh‖)+ω2(‖x⃛‖))(12)

4  Experiment

4.1 Experimental Setup and Experimental Design

In order to verify the effectiveness of the method proposed in this paper, an experimental platform was designed for human-robot cooperation to complete the curtain wall installation task, as shown in Fig. 6.

Figure 6: Curtain wall installation experimental platform by physical human-robot cooperation

In the experiment, to simulate the installation process and avoid the risk of collision in the actual experimental environment, a laser pointer was fixed to the curtain wall, and a laser point was used to indicate the location of the curtain wall. The curtain wall position indicator experimental device is shown in Fig. 7.

Figure 7: Curtain wall position indicator experimental device

In the installation process of the curtain wall, the movement track can be divided into the low-restricted area and the high-restricted area. In the low-restricted area, the robot has plenty of room to move, and more attention should be paid to the speed of movement and less effort of the partner than to the movement accuracy of the curtain wall. Contrary to the low-restricted area, in the high-restricted area, the movement accuracy of the curtain wall should be paid more attention than the speed of movement and the effort of the collaborator.

Here are the steps:

1)   Firstly, the laser point representing the position of the curtain wall was located in the low-restricted area, which was the starting point. Following the robot’s movement, the location of the laser point was operated according to the interaction force from a six-dimensional force sensor.

2)   Secondly, the laser point was controlled to move quickly to the high-restricted area entrance.

3)   Thirdly, the operator, ensuring that the laser point does not collide with the boundary of the high-restricted area as much as possible, continues to control the robot towards the target point.

4)   The curtain wall was considered to have reached the target point when the distance between the laser point and the end position of the drawing board was less than a specific value. Then the robot will automatically return to the original position.

5)   Repeated steps 1)–4) until the value of the variable that reinforcement learning levels off.

4.2 Experimental Parameters Design

In order to obtain the continuous state input vector X={fh,f˙h,x,x¨}, each variable was divided into five fuzzy sets and evenly distributed to the domain by a triangular membership function, so the total number of states was N=54=625. In this paper, the number of behaviors was set as m = 6, that is, A={a1,a2,a3,a4,a5,a6}={0.1,0.2,0.4,0.6,0.8,1}. In other words, the robot and the partner have been given six different roles allocation weights. Here, the minimum role of the collaborator was chosen as 0.1 instead of 0 for the following reasons. 1) it was needed that the operator makes a particular decision as moving guidance information to control the robot in the physical human-robot cooperation; 2) it was hazardous when the robot was given complete control in actual operation.

In this study, the system frequency was set to 1000 Hz, and the frequency of the reinforcement learning was set to 100 Hz. That was the k = 10 in the formula (10). The learning rate was designed to be α=0.95 and the discount factor was designed to be γ=0.9 in the Q-learning model (7). The role weight initial value of the collaborator was set as a1=α1=0.4.

5  Experimental Results and Performace Assessment

5.1 Dynamic Role Adaptive Allocation Results

The relationship between human-robot cooperation performance and the roles allocation weight was established with changes in the cooperative performance as the number of iterations increased in this experiment, as shown in Fig. 8. The experiment was repeated 30 times by operating the robot from its initial position to its destination. In this process, collisions should be avoided whenever possible by observing the position of the laser point. The comprehensive performance model consisting of robot’s Jerk and human-robot interaction force that were regarded as equally important (ω1=ω2=0.5) was used to estimate the effect of the role change.

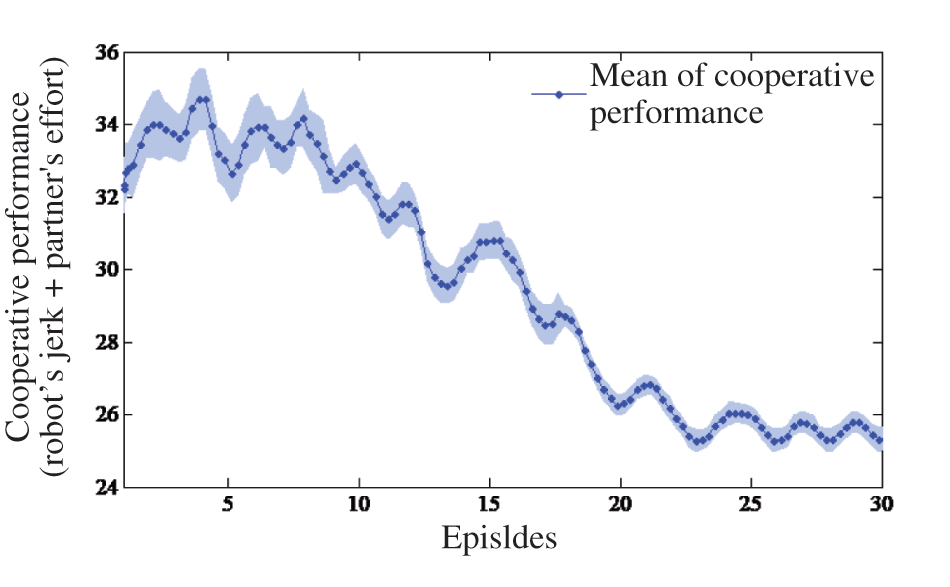
Figure 8: Relationship between number of iterations and cooperative performance

As can be seen from Fig. 8, with the increase in the number of iterations, the comprehensive performance value composed of Jerk and the efforts of the cooperator showed a downward trend. When the number of iterations was more than 25 times, the comprehensive performance value tended to be stable. This experiment showed that it effectively improved robot flexibility and reduced human-robot force by changing the role weight based on reinforcement learning.

In order to evaluate the efficiency of task completion as learning progresses, the relationship between the number of iterations times and task completion time was established, as shown in Fig. 9.

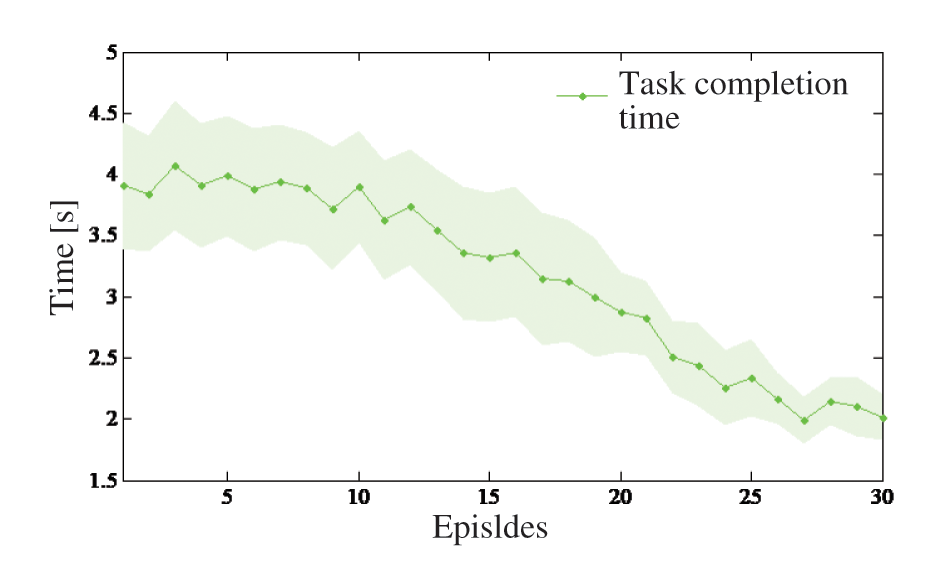
Figure 9: Relationship between number of iterations times and task completion time

From Fig. 9, the time for task completion decreases as the number of iterations increases. When the number of iterations was more than 25 times, the decline of the task completion time was slow and steady. It has shown that the roles allocation method based on reinforcement learning was a great way to improve task completion efficiency.

The Fig. 10 shows the mean value α1 of the last five iterations of the collaborator’s role over time t based on the reinforcement learning method. Initially, the robot was guided by increasing the partner role α1 gradually, and then the partner role α1 dropped rapidly once the robot was identified in free mode. In the low-restricted area, the robot played a significant role in the movement of the curtain wall, which was beneficial in reducing the labor intensity of the collaborator. However, in the stage of approaching and entering the high-restricted area, the collaborator’s role value was rapidly increased to ensure the smooth movement of the robot end curtain wall.

Figure 10: The mean value of the last five iterations of the collaborator’s role over time t

The relationship between the partner’s force and time t for the last five times was established, as shown in Fig. 11. The force change trend of the partner was similar to the collaborator’s role, which was first more prominent, then decreased, and then increased. This pattern of change is consistent with the relationship between the change of force and the role. The greater the weight of the partner’s role, the greater the force applied.

Figure 11: Relationship between the partner’s force and time t for the last 5 times

The cooperation performance of the dynamically changing roles according to the method proposed in this paper and the different fixed role weights was established, as shown in Fig. 12. The result has verified that the continuous adjustment of roles based on the reinforcement learning method was more conducive to the performance of human-robot cooperation than the fixed roles.

Figure 12: Cooperation performance of fixed and adaptive role based reinforcement learning

In Fig. 12, the fixed roles were designed with six levels, which were the α1=0.1,0.2,0.4,0.6,0.8,1. Compared to the fixed roles, the combination of Jerk and the partner’s force was even lower by using the adaptive role based on the reinforcement learning method, which showed that the method proposed in this paper was excellent results.

5.2 Effect of Performance Weighting Coefficient on the Result

In the above experiment, the robot’s Jerk and human-robot interaction force were regarded as equally important (ω1=0.5,ω2=0.5) in the formula (9) of the comprehensive performance model. In order to explore the influence of changing the performance weighting coefficient, the Jerk, the partner’s force, and their overall performance were obtained through experiments based on reinforcement learning, as shown in Fig. 13. The weighting of the partner’s force was set as ω1=0.1,0.2,0.4,0.6,0.8,1.

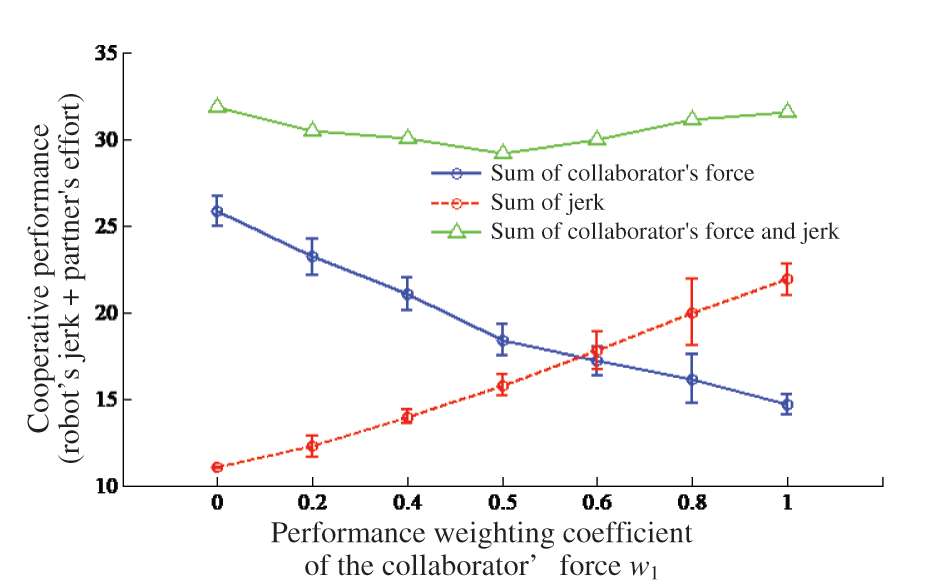
Figure 13: The relationship between overall performance and different performance weighting coefficient of the partner’ force

From Fig. 13, the Jerk was set as the only goal in reinforcement learning when the ω1=0. Even though the sum of the Jerk was minimal, the cooperator’s force was considerable, which led to more effort for humans. If the minimum sum of the partner’s force was designed as the only consideration (ω1=1), the sum of the cooperator’s force was minimum, but the sum of the robot’s accelerations became maximum. Excessive acceleration could lead to vibration at the end of the robot, which would increase control difficulty and danger. The overall performance value was the lowest when the performance weighting coefficient ω1=0.5, that was to say, it was appropriate that the comprehensive performance model consisting of human-robot interaction force and robot’s Jerk were regarded as equally important to estimate the effect of the role change.

6  Conclusion

In this paper, according to the dynamic role allocation problem in contact human-robot cooperation, an online role allocation method based on reinforcement learning is proposed for a curtain wall installation task. First, the physical human-robot cooperation model, including the role factor, is built. Second, a reinforced learning model, including a reward model and action model, which can adjust the role factor in real-time, is established. The role factor can be adjusted continuously according to the comprehensive performance consisting of human-robot interaction force and robot’s Jerk during the repeated installation process. Finally, the comprehensive performance of the human-robot system can be continuously improved by the role adjustment rule established according to reinforcement learning. In order to verify the effectiveness of the proposed method, the dynamic role allocation regarding human force and Jerk and the effect of the performance weighting coefficient have been verified by experiments. The experimental results show that the proposed method can realize the dynamic adjustment of the human-robot role and achieve the dual optimization goal of reducing the sum of the cooperator’s force and the robot’s Jerk. The role assignment method based on reinforcement learning proposed in this paper is of great significance to physical human-robot cooperation. In future work, to further play the advantages of the role dynamic assignment algorithm proposed in this paper, we will improve the degrees of freedom to the role assignment factor to study. In addition, more complex reward models and execution models with more character values will be built. Meanwhile, the generality of this paper’s role dynamic assignment algorithm will be improved to extend it to more practical applications.

Acknowledgement: The authors express their gratitude to the editor and referees for their valuable time and efforts on our manuscript.

Funding Statement: The research has been generously supported by Tianjin Education Commission Scientific Research Program (2020KJ056), China, and Tianjin Science and Technology Planning Project (22YDTPJC00970), China. The authors would like to express their sincere appreciation for all support provided.

Author Contributions: Study conception and design: Zhiguang Liu, Jian Zhao; data collection: ShilinWang; analysis and interpretation of results: Zhiguang Liu, Fei Yu; draft manuscript preparation: Zhiguang Liu, Jianhong Hao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used in this paper is available in the paper.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Moertl, A., Lawitzky, M., Kucukyilmaz, A., Sezgin, M., Basdogan, C. et al. (2012). The role of roles: Physical cooperation between humans and robots. International Journal of Robotics Research, 31(31), 1656–1674. [Google Scholar]

2. Jarrasse, N., Sanguineti, V., Burdet, E. (2013). Slaves no longer: Review on role assignment for human robot joint motor action. Adaptive Behavior, 22(1), 70–82. [Google Scholar]

3. Passenberg, C., Peer, A., Buss, M. (2010). A survey of environment, operator, and task adapted controllers for teleoperation systems. Mechatronics, 20(7), 787–801. [Google Scholar]

4. Tsarouchi, P., Makris, S., Chryssolouris, G. (2016). Human robot interaction review and challenges on task planning and programming. International Journal of Computer Integrated Manufacturing, 29(8), 916–931. [Google Scholar]

5. Dimeas, F., Aspragathos, N. (2016). Online stability in human-robot cooperation with admittance control. IEEE Transactions on Haptics, 9(2), 267–278. [Google Scholar] [PubMed]

6. Lee, H. J., Kim, K. S., Kim, S. (2021). Generalized control framework for exoskeleton robots by interaction force feedback control. International Journal of Control, Automation and systems, 19, 3419–3427. [Google Scholar]

7. Kheddar, A. (2011). Human robot haptic joint actions is an equal control sharing approach possible. International Conference on Human System Interactions, pp. 268–273. Lisbon, Portugal. [Google Scholar]

8. Jarrasse, N., Charalambous, T., Burdet, E. (2012). A framework to describe, analyze and generate interactive motor behaviors. PLoS One, 7(11), e49945. [Google Scholar] [PubMed]

9. Lawitzky, M., Mortl, A., Hirche, S. (2010). Load sharing in human robot cooperative manipulation. 19th International Symposium in Robot and Human Interactive Communication, pp. 185–191. Viareggio, Italy. [Google Scholar]

10. Li, Y. N., Tee, K. P., Chan, W. L., Yan, R., Chua, Y. W. et al. (2017). Continuous role adaptation for human-robot shared control. IEEE Transactions on Robotics, 31(3), 672–681. [Google Scholar]

11. Hang, T., Ueha, R., Hirai, H., Miyazaki, F. (2010). A study on dynamical role division in a crank-rotation task from the viewpoint of kinetics and muscle activity analysis. IEEE/RSJ International Conference on Intelligent Robots & Systems, pp. 2188–2193. Taibei. [Google Scholar]

12. Jaberzadehansari, R., Karayiannidis, Y. (2021). Task-based role adaptation for human-robot cooperative object handling. IEEE Robotics and Automation Letters, 2(6), 3592–3598. [Google Scholar]

13. Passenberg, C., Groten, R., Peer, A., Buss, M. (2011). Towards real time haptic assistance adaptation optimizing task performance and human effort. IEEE World Haptics Conference, pp. 155–160. Istanbul, Turkey. [Google Scholar]

14. Gu, Y., Thobbi, A., Sheng, W. (2011). Human robot collaborative manipulation through imitation and reinforcement learning. IEEE/RSJ International Conference on Intelligent Robots & Systems, pp. 151–156. Shenzhen, China. [Google Scholar]

15. Evrard, P., Kheddar, A. (2009). Homotopy switching model for dyad haptic interaction in physical collaborative tasks. World Haptics Third Joint Eurohaptics Conference & Symposium on Haptic Interfaces for Virtual Environment & Tele-Operator Systems, pp. 45–50. Salt Lake City, USA. [Google Scholar]

16. Evrard, P., Kheddar, A. (2009). Homotopy-based controller for physical human-robot interaction. ROMAN 2009-The 18th IEEE International Symposium on Robot and Human Interactive Communication, pp. 1–6. Toyama, Japan. [Google Scholar]

17. Takagi, A., Li, Y., Burdet, E. (2021). Flexible assimilation of human’s target for versatile human-robot physical interaction. IEEE Transactions on Haptics, 14(2), 421–431. [Google Scholar] [PubMed]

18. Wang, C., Zhao, J. (2023). Role dynamic assignment of human-robot collaboration based on target prediction and fuzzy inference. IEEE Transactions on Industrial Informatics, 1–11. https://doi.org/10.1109/TII.2023.3266378 [Google Scholar] [CrossRef]

19. Modares, H., Ranatunga, I., Lewis, F. L. (2016). Optimized assistive human robot interaction using reinforcement learning. IEEE Transactions on Cybernetics, 46(3), 655–667. [Google Scholar] [PubMed]

20. Tutsoy, O., Barkana, D. E. (2021). Model free adaptive control of the under-actuated robot manipulator with the chaotic dynamics. ISA Transactions, 118, 106–115. [Google Scholar] [PubMed]

21. Nakamura, Y., Mori, T., Sato, M. A., Ishii, S. (2007). Reinforcement learning for a biped robot based on a CPG-actor-critic method. Neural Networks, 20(6), 723–735. [Google Scholar] [PubMed]

22. Dimeas, F., Aspragathos, N. (2015). Reinforcement learning of variable admittance control for human-robot co-manipulation. IEEE/RSJ International Conference on Intelligent Robots & Systems, pp. 1011–1016. Hamburg, Germany. [Google Scholar]

23. Seraji, H. (1994). Adaptive admittance control: An approach to explicit force control in compliant motion. IEEE International Conference on Robotics & Automation, pp. 2705–2712. San Diego, CA, USA. [Google Scholar]

24. Watkins, C. J. C. H., Dayan, P. (1992). Q-learning. Machine Learning, 8(3–4), 279–292. [Google Scholar]