Cooperative Rate Splitting Transmit Design for Full-Duplex-Enabled Multiple Multicast Communication Systems

1  Introduction

As 6G wireless communication technology becomes more popular, mobile data traffic is increasing rapidly. The constant update of wireless devices that are connected to the global mobile network has greatly contributed to the growth of global mobile traffic. Every year, many new devices with different shapes, capabilities and intelligence are launched in the market. As the communication field keeps evolving, in the future, once 6G communication matures, there will be thousands of wireless devices connected to the network. At the same time, people’s demands for data transmission rate, network coverage, connection reliability and other network performance are further improved. When people enjoy the high quality of life brought by it, some problems are becoming more and more obvious, such as: the rise in connected devices, spectrum shortage, large consumption, high carbon emissions which will result in a higher number of high-density connected devices and wireless communication volume. These are a series of issues that need to be solved. Therefore, 6G communication needs to achieve higher spectral efficiency, lower transmission delay and mass connection requirements. Specifically, as 5G opens the door to the Internet of Everything (IoE), the focus of communications has shifted from mobile broadband connections to utilizing ultra-reliable low-latency communications and massive machine-type communications. 6G is expected to become a platform for connected intelligence intelligently connecting a large number of devices to the mobile network. Therefore, in order to meet the key requirements for 6G mobile communication system such as higher spectral efficiency, lower transmission delay massive connections and high data rate under high dynamic scenarios it is necessary to further explore new network architecture and transmission technology.

Orthogonal Multiple Access (OMA) methods are used to avoid orthogonal multiple access interference from 1G to 5G communication systems. However, in massive access scenarios, Non-Orthogonal Multiple Access (NOMA) has advantages of supporting massive connectivity and high spectral efficiency compared with traditional OMA technologies. It was taken seriously. The freedom of wireless communication resources is limited by the low OMA access efficiency, and problems such as blocking and high delay are faced by the system. NOMA is considered as a new technology for cellular communication, which has the potential to provide higher throughput than traditional orthogonal multiple access. The frequency spectrum efficiency of mobile communication network can be improved quickly and significantly by it. A frequency channel can be assigned simultaneously to multiple users within the same cell by NOMA, and a number of benefits are offered by it, including improved Spectral Efficiency (SE), providing higher cell edge throughput and relaxed channel feedback. A downlink version of NOMA, Multi-User Superposition Transmission (MUST) has been proposed for the third Generation Partnership Project LTE-Advanced (3GPP-LTE-A) network. In addition, the use of NOMA is also envisioned as a key component of fifth generation (5G) mobile systems. NOMA has the advantages of fast signal transmission rate, high spectrum utilization rate and low transmission delay, and is considered as a cutting-edge technology in future wireless communication system. Services for multiple users on the same resource block can be provided by it. In other words, NOMA provides the possibility to meet the demanding requirements of 6G ultra-low latency and ultra-high connectivity.

NOMA technology enables users to share the same time/frequency resources with higher spectral efficiency through the use of superposition coding, which multiplexes users in the power domain at the transmitter and Serial Interference Cancellation (SIC) at the receiver. NOMA aims to serve multiple users at the same time frequency resource and assign them different power levels. In the case of two users, users with poor channel conditions usually allocate higher transmission power than those with better channel conditions to improve the edge data rate. SIC, as a multi-user detection technology, was adopted as early as the third generation mobile communication technology CDMA. SIC has a great improvement in performance compared with the traditional detector, and the hardware is not changed much, so it is easy to implement. Users with better channel conditions can eliminate the interference from the former through SIC technology. When multiple users have similar channel conditions, dynamic user pairing and clustering with different channel gains is an effective way to leverage NOMA’s potential to provide large-scale connectivity requirements for 6G networks. Although NOMA based on Superposition Coding (SC) and SIC has significant advantages in degraded single input single output broadcast channels (SISO BC), it still presents many problems in multi-antenna scenarios, such as loss of Degree of Freedom (DoF) and performance degradation in general user deployments.

Due to the exponential growth of wireless communications and the growing demand for higher data rates, there is a great deal of interest in how NOMA can be improved for multi-antenna scenarios.The interference management strategy based on SDMA is limited by the number of antennas at the sending end. In the network overload scenario, interference between users is difficult to be fully suppressed, resulting in the system performance reaching saturation state and difficult to be further improved. Although the interference management strategy based on NOMA can accommodate more users from the power domain dimension, it damages the spatial freedom. Rate splitting multiple access (RSMA) is derived from NOMA technology, which is an emerging technology with strong flexibility. RSMA is a new multiple access scheme proposed in recent work that has proven to be a promising and powerful strategy for improving the lower levels of next generation communication systems. By dividing user messages into public and private parts using linear precoded frequency division at the transmitter and sequentially decoding the encoded public and private streams using SIC at all receivers, compared with space division multiple access (SDMA), which treats residual interference entirely as noise, and power domain NOMA which decodes the interference entirely. RSMA manages interference in a more general and robust way. As a result, RSMA is unified and superior to SDMA and NOMA technologies in more scenarios. At the transmitter end of RSMA communication network, the messages required by users are divided into private information flow and public information flow, and then all the public information is encoded as public flow for transmission. Similar to NOMA technology, RSMA uses SIC technology to demodulate the information on the receiving end. However, unlike NOMA users who demodulate the interference completely, RSMA users partially decode the interference and partially treat it as noise during the demodulation process. Therefore, the cost of spectral efficiency, energy efficiency, robustness and CSI feedback is reduced. In addition, from an encoding structure perspective, combining a universal stream decoded by all users with a private stream dedicated to each user also provides fundamental compatibility with other technologies. This good compatibility further prompts us to study the application of RS in collaborative relay.

In recent years, because of its good performance in many practical application scenarios, Rate Splitting (RS) has attracted extensive attention in the academic circle in the downlink of communication system. From the perspective of information theory, the RS literature of multi-antenna BC studies and compares the RS advantages of perfect CSIT [1–3] and imperfect CSIT [4–6]. The comparison results indeed confirm the gain of RS at high SNR. In addition, RS is also studied in the finite signal-to-noise ratio environments of MIMO [7–10], millimeter-wave systems [11,12], multi-multicast [13,14], synchronous wireless Information and Power Transfer (SWIPT) [15], and multi-pair decoding and forwarding (DF) full-duplex relay channels [16].

In order to break the bottleneck of RS universal flow realization rate limited by the worst user, a promising solution is to use user relay to combine RS and cooperative transport. Cooperative user relaying is therefore considered a promising solution, Cooperative RS (CRS), which relies on user collaboration to improve the rate of common traffic. The transmitter divides the user message into public and private parts, encodes it as a public stream and a private stream, and linearly precodes it before transmission. One user then decodes the common stream and forwards it to another user, helping that user better decode the common stream. After performing SIC and deleting the public stream, both users decode their respective private streams and then reconstruct their originally expected messages from the private and public streams. Decode the public stream before the expected private stream. It can effectively counter shadow effect, expand radio coverage and improve channel capacity at the same time [17]. By designating one or more relay users to assist in receiving data from the BS and forwarding it to other users, spatial diversity can be improved without the deployment of a dedicated relay station. There are some researches on it in unicast system. It mainly adopts the joint optimization strategy of precoding, slot allocation and rate segmentation to solve the problems of maximizing the minimum rate and enhancing the security of physical layer. However, there are still few researches in wireless multicast.

This cooperation strategy is proposed in reference [18], which naturally connects the multi-antenna RS technology (developed for multi-antenna BC) with the three-node relay broadcast channel of one transmitter and two receivers, in which the transmitter is equipped with multiple antennas. Through the proposed flexible framework, CRS not only takes advantage of the RS advantages of multi-antenna BC [2,5,19,20], but also user cooperation [1,5,18]. By separating the user messages and linearly precoding the public and private streams at the transmitter, the relay users are opportunistically required to forward their decoded public messages. Based on the exploration of combined RS in multi-antenna RBC. Mao et al. [1] proposed a linear precoded dual-user cooperative RS (CRS) transmission framework, allowing one of the two users to regularly forward its public messages to the other user. In [2], the authors demonstrated that RSMA has better performance compared to NOMA and SDMA. Mao et al. [21] extend the existing two-user CRS transport policy to the case of k user. Under the constraint of transmitting power of the base station, the problems of preencoder, message segmentation, slot allocation and relay user scheduling are studied with the aim of maximizing the minimum rate between users.

CRS can effectively cope with a wide range of propagation conditions (differences in user channel strength and direction) and compensate for performance degradation due to deep fading. By solving the weighting sum rate (WSR) maximization problem, the design and resource allocation of the preencoder are optimized. The results show that, compared with non-cooperative strategies and other cooperative strategies (such as cooperative NOMA), the proposed CRS scheme can achieve explicit rate domain improvement.

However, in the above related work [1,18], there are still some problems to be solved [21,22]. The CRS scheme in the literature still stays at the stage of two users or even K users, which still has a certain gap with the reality. Secondly, most of the CRS in the literature work in the half-duplex mode and cannot complete the task of transmitting and receiving information at the same time, resulting in a great waste of time. Moreover, user FD C-RSMA in downlink scenario has not been well studied in the literature.

Driven by this, this paper focuses on the SWIPT-assisted Full-Duplex Cooperative Rate Splitting and multicast beam-forming in MISO networks. The main contributions are summarized as follows:

•   This paper investigates the performance of FD C-RSMA with SWIPT assist in MISO networks. The system is composed of the base station and two near and far user groups, and the near user group works in full duplex mode to receive information and assist forwarding. To increase the minimum reachable data rate, we allow all the local user groups to act as relays to assist the transmission of the remote user groups.

•   This paper investigates joint optimization of BS beamvector, common stream segmentation vector, collaborative distributed beamvector, and strong user transmission power, with the goal of solving the constructed convex optimization problem to maximize the minimum achievable data rate within the power budget constraints of BS and the proximal user group.

•   In order to solve non-convex quadratic programming problems with quadratic constraints, this paper explores using a low complexity algorithm based on successive convex approximation (SCA) to find a feasible solution to the problem.

•   Simulation results show that the FD-CRS mechanism has advantages in reducing the average transmission power of the system. Higher performance gains can also be achieved compared to other baseline schemes.

2  System Model

2.1 Network Model

This paper considersr an FD-assisted downlink MISO system as shown in Fig. 1, which consists of a BS and two users represented by K={𝒩,ℱ}. In this model, we assume that BS is equipped with M transmitting antennas and serves K single antenna receivers or users. We represent CCUs as a strong user multicast group with a set of ℱ:={1,...,N} and CEUs as a weak user multicast group with a set of 𝒩:={1,...,F}. The strong user multicast group is located close to the transmitter, and the weak user multicast group is another multicast group away from the transmitter, the cellular edge user group CEUs. And CCUs has better channel conditions than CEUs. To enhance network downlink performance, we allow all CCUs to act as transmitter helpers to assist CEUs in the transmission of public data streams. In Fig. 2, the two channels of information are divided into two parts according to RSMA, and then encoded into one public stream and two private streams. Using PS technology, the power of the near end user group is allocated partly to the monitoring of public and private streams, and the other part is used for information forwarding. The energy harvested by the local user in the direct transmission phase will ensure its own energy.

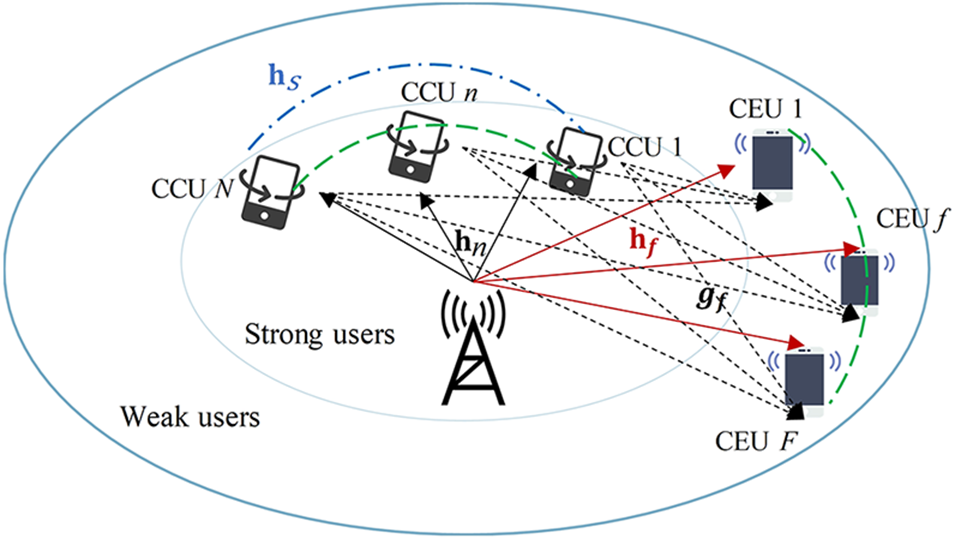
Figure 1: Two groups of users FD C-RSMA system model

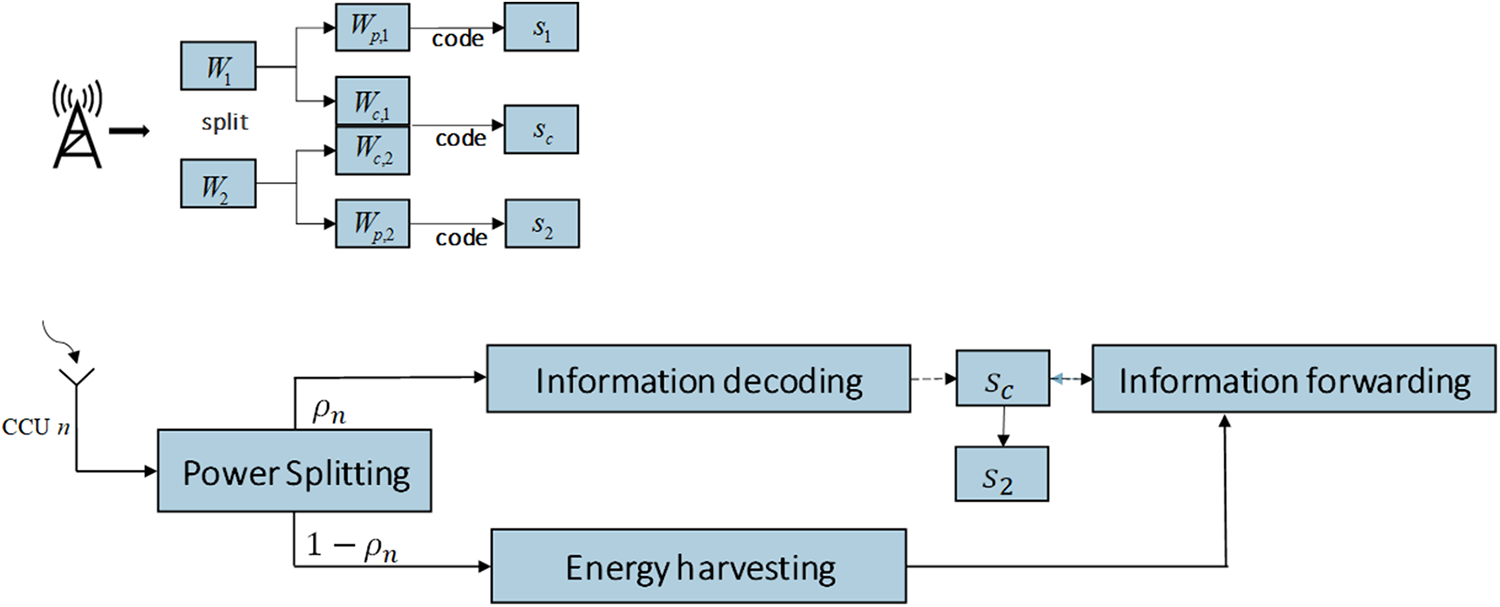
Figure 2: RSMA architecture and power-splitting architecture based on SWIPT

2.2 Transmission Model

The transmission model of two user groups C-RSMA includes direct multicast and cooperative multicast, which are detailed as follows.

Direct transmission: In the solid line, the message sent to CCUs and CEUs is divided into two parts according to RSMA criteria. Then, the common part of the two multicast groups is encoded as a common stream; Encode two private data streams separately at the same time. After that, the transmitter sends the three data streams through linear precoding to all receivers. According to the RSMA principle, a superimposed transmission of a public stream is first decoded by the CCUs, and then removed from the received signal by that user group in order to decode its own private stream.

Cooperative transmission: During collaboration, we use a dotted line. To make full use of time resources, CCUs works in full duplex mode, meaning that information is received and sent simultaneously. In order to maintain the co-operative’s own battery power. All CCUs use the energy harvested during direct transmission to work together to form a distributed common data stream beam to assist the transmission of CEUs information.

Since the near-end user group uses FD relay mode, direct and cooperative transmissions occur in time slots that generate the same self-interference gain (blue dotted lines in the figure). In the next section, we will elaborate the whole communication process and signal decoding process of FD-CRS mechanism. We will give the signal-to-noise ratio (SINR) and the achievable data rate for each user.

2.3 Rate Analysis

Following the RSMA principle, in the scenario of two user groups, BS first divides information W1 of CEUs group, a strong user group, into public part Wc,1 and private part Wp,1. Similarly, for the weak user group CCUs, the requested information W2 is divided into public part Wc,2 and private part Wp,2. The common information is then syndicated into a common stream that is shared by all users. Meanwhile, Wp,1 and Wp,2 are independently encoded as private streams s1 and s2 of the two multicast groups, respectively. On this basis, the total data stream transmitted by BS can be expressed as s=[sc,s1,s2]T. Therefore, these data flows are linearly precoded by the precoded vector W=[wc,w1,w2], where wc,wk∈CM×1. wc∈CM×1 represents the common stream beam-forming vector. w1∈CM×1 and w2∈CM×1 represent private data stream beam-forming vectors. The last transmitted signal can be denoted by s

s=wcsc+w1s1+w2s2(1)

It is noted that the average transmitted power of BS can be given by Pt(wc,w1,w2), which is the trace of the beam vector covariance.

Pt(wc,w1,w2)=||wc||2+||w1||2+||w2||2=wc†wc+w1†w1+w2†w2(2)

It is assumed that BS is fully aware of each user’s channel state information. During direct transmission, the signal received by the local user group CCU in the t time slot can be expressed as

ynD[t]=hn†wcsc[t]+hn†w1s1[t]+hn†w2s2[t]+nn[t],∀n∈𝒩(3)

where, hn†∈C1×M represents the 1×M complex channel coefficient vector from the transmitter to user n, and nn represents the additive white Gaussian noise nn∼𝒞𝒩(0,σn2) at the receiving antenna end of user n.

Similarly, the remote user group is at the CEU end, and the signal received from the transmitter in the t slot can be expressed as

yfD[t]=hf†wcsc[t]+hf†w1s1[t]+hf†w2s2[t]+nf[t],∀f∈ℱ(4)

where, hf†∈C1×M represents the 1×M complex channel coefficient vector from the transmitter to user f, and nf represents the additive white Gaussian noise nf∼𝒞𝒩(0,σf2) at the receiving antenna end of user f.

In collaborative multicast, assuming that CCUs have realized synchronization, distributed virtual beam forming can be realized cooperatively. During the collaboration, the proximal user group CCUs transmits a common stream to the CEUs using the energy it harvested in the direct transmission. All CCUs are distributed beam-forming vectors that generate data streams as virtual antenna arrays. Since the local user group collaboratively forwards the data stream, it actually works in full duplex mode, which also means that CCUs receives both the signal from BS and the interference signal from its own transmitting antenna. In this mode, the signal actually received by the CCU is not only from the transmitter, but also from itself, which is expressed as

yn[t]=ynD[t]+hsvns^c[t−τ]=hn†wcsc[t]+hn†w1s1[t]+hn†w2s2[t]+hsvns^c[t−τ]+nn[t],∀n∈𝒩(5)

s^c represents the delay of the common stream from CCUs to CEUs, in s^c=sc(i−τ), i represents the i th time slot, and T represents the processing time to decode the common stream s^c at a strong user. It is worth noting that τ is insignificant compared to the duration of a time slot. We can think of s^c=sc.

As mentioned above, part of the signal received by CCU n is used for information detection, which can be represented as follows:

ynI[t]=ρnyn[t]=ρn (hn†wcsc[t]+hn†w1s1[t]+hn†w2s2[t]+hsvnsc[t−τ])+nnI[t],∀n∈𝒩(6)

At the CEU f end, the signal from the BS and the signal from the near end collaborative user group CCUs are received, combined and used for signal detection, which can be rewritten as

yfI[t]=yfD[t]+gf†vsc[t−τ]=hf†wcsc[t]+hf†w1s1[t]+hf†w2s2[t]+gf†vsc[t−τ]+nf[t],∀f∈ℱ(7)

where gf† represents the channel coefficient vector from CCUs to CEU f.

After receiving a signal from BS, first the CCUs strong user group decodes the public stream sc by treating all private stream s1,s2 as interference. Based on this, the data rates that can be achieved when a strong user uses serial interference cancellation to decode a common stream can be expressed as follows:

Rc,n=wlog2(1+ξc,n)(8)

The corresponding signal-to-noise ratio is

ξc,n=ρnwc†Hnwcρnw1†Hnw1+ρnw2†Hnw2+ρnvn†Hsvn+σn2,∀n∈𝒩

Hs=hshs† is the residual self-interfering channel covariance. w is the transmission bandwidth.

The decoded common stream sc is then removed from the total received signal by SIC, and the strong user group decodes its own private stream by treating the private stream of the weak user group as interference. Thus, the achievable rate at which a strong user group CCUs decodes its private stream can be expressed as follows:

Rp,n=wlog2(1+ξp,n)(9)

where  ξp,n=ρnw2†Hnw2ρnw1†Hnw1+ρnvn†Hsvn+σn2, n∈𝒩

To facilitate the detection of the common flow at the end of the cooperative transmission, we assume that the weak user group CEUs is fully capable of resolving the signals received after the BS and strong user group cooperative transmission. Thus, these received signals can be appropriately synchronised and combined by the maximum ratio combination (MRC) technique. Therefore, the data rate that a weak client CEU f can achieve when decoding a common stream can be expressed as

Rc,f=wlog2(1+ξc,f)(10)

Rp,f=wlog2(1+ξp,f)(11)

where  ξc,f=wc†Hfwcw1†Hfw1+w2†Hfw2+σf2+v†Gfvσf2, ∀f∈ℱ,ξp,f=w1†Hfw1w2†Hfw2+σf2,∀f∈ℱ  and  Hf=hfhf†≻0.

Since little energy can be harvested from the noise signal, it is negligible. We assume that harvested energy is used solely for information forwarding. The remaining energy consumption for circuit maintenance, signal processing, etc., is ignored. Therefore, the transmitted power of CCU when forwarding signals is limited by its harvesting energy.

|vn|2≤Pn,∀n∈𝒩(12)

We adopt a linear energy harvesting model, and the harvested energy can be modeled as a linear function, that is Pn=ηPin, where η∈[0,1] represents the energy harvesting efficiency of the energy harvesting circuit, and Pin represents the input power of the energy harvesting circuit. We use 0<ρn<1 to represent the power division ratio of CCU n. Then the energy harvested from CCU n in the t slot can be represented. And since part of yn[t] is used for information detection, the other part is used for harvesting energy for CCU n. So Pn can be represented as

Pn=η(1−ρn)Pin=η(1−ρn)(wc†Hnwc+w1†Hnw1+w2†Hnw2+vn†Hsvn),∀n∈𝒩(13)

To ensure that both user groups can successfully decode the common stream, the achievable data rate of the common stream should be the minimum between the achievable common rates of the two user groups, which can be expressed as follows:

Rc≤min{Rc,N,Rc,F}(14)

We know that Rc is shared by two users, and that it is equal to ∑k=12Ck=Rc, where Ck is the part of Rc that sends the common information, and c=[C1,C2]. Therefore, we can obtain the total achievable rate of user-k as

Rk=Ck+Rp,k,∀k∈K(15)

3  Cooperative Full-Duplex-Enabled RSMA Algorithm

3.1 Problem Formulation

It is reasonable to assume that the instantaneous CSI of all links is completely knowable because the transmitter and the user are in the same system and the channel can be estimated in real time in each transmission time block. Our goal is to maximize the minimum transmission rate under power constraints. We study the problem of maximum and minimum fairness under the full duplex cooperative rate segmentation mechanism. By optimizing the beam-forming vector wc,wk, ∀k∈K. Public stream data vector c. Distributed beam vector v, and power division ratio ρ. So the maximum and minimum rate problem can be expressed as 𝒫1

𝒫1:maxw,c,v,ρ⁡min(Ck+Rp,k),∀k∈K,(16a)

s.t.  C1+C2≤Rc,k,∀k∈K,(16b)

0<ρn≤1,∀n∈𝒩,(16c)

Ck≥0,∀k∈K,(16d)

|vn|2≤Pn,∀n∈𝒩,(16e)

wc†wc+w1†w1+w2†w2≤PBS,(16f)

where C1 and C2 represent parts of a common stream, and w† represents Hermite, the complex number of the vector w. Our goal is to ensure fairness between users by maximizing the minimum achievable rate. Constraint (16b) ensures that both users can successfully decode the common stream. (16e) and (16f) are transmitted power constraints and BS power constraints of the strong user group, respectively.

3.2 Proposed Algorithm

It can be observed from the constructed optimization problem 𝒫1 that variables {w,c,v,ρ} are coupled to each other in the constraints, resulting in the non-convexity of the constraint set. Due to the existence of the non-convexity constraint set, it is difficult to find the global optimal solution of the optimization problem 𝒫1.

𝒫1 is a non-convex optimization problem because both the objective (a) and the constraints (b) (e) are non-convex. So 𝒫1 is hard to solve directly. And the complexity of seeking the global minimum is very high. To do this, we want to look for a local minimum as an alternative. Therefore, some auxiliary variables are properly introduced to make the non-convex optimization problem easier to deal with, and the SCA method is used to convexize 𝒫1. First, we rephrase the original problem 𝒫1 as follows:

𝒫2:maxw,c,v,ρ,r⁡r,(17a)

Ck+Rp,k≥r,∀k∈K,(17b)

(16b)−(16f),(17c)

where r is the relaxation variable. Now, problem 𝒫2 is equivalent to problem 𝒫1. But there is still non-convexity in (16b), (16e) and (17b). So let us rewrite (17b) as

C1+Rp,f≥r1C2+Rp,n≥r2

Secondly, we introduce two new relaxation variables δn,∀n∈𝒩 and ϕf,∀f∈𝒩. They respectively represent the disturbance plus noise term in the private flow of the near-end user group and the remote user group. Therefore, (17b) becomes

2r2−C2w−1≤w2†Hnw2δn,∀n∈𝒩,(18a)

w1†Hnw1+vn†Hsvn+σn2tn≤δn,∀n∈𝒩,(18b)

2r1−C1w−1≤w1†Hfw1ϕf,∀f∈ℱ,(18c)

w2†Hfw2+σn2≤ϕf,∀f∈ℱ.(18d)

Following the same process as above, we still introduce the relaxation variable tn and define tn=Δ1ρn≥1, so (16c) can be expressed as (19d), where αn,∀n∈𝒩 represents the common current reachable rate of CCU n. βn,∀n∈𝒩 indicates the SNR of the CCU n for detecting public signals. The non-convex constraint in (16b) can be rewritten as

C1+C2≤αn,∀n∈𝒩,(19a)

2αnw−1≤wc†Hnwcβn,∀n∈𝒩,(19b)

w1†Hnw1+w2†Hnw2+vn†Hsvn+σn2tn≤βn,∀n∈𝒩,(19c)

tn≥1,∀n∈𝒩.(19d)

We continue to introduce λf,∀f∈𝒩, which represents the accessible common flow rate of CEU f. (16b) can be expressed as

C1+C2≤λf,∀f∈ℱ,(19e)

2λfw−1≤wc†Hfwcμf+v†Gfvσf2,∀f∈ℱ,(19f)

w1†Hfw1+w2†Hfw2+σf2≤μf,∀f∈ℱ.(19g)

Since constraint (16e) still has non-convexity, tn=Δ1ρn≥1 has been defined before, so we use Qn(wc,w1,w2,vn,t) and En(wc,w1,w2,vn) to represent non-convexity constraint, where

Qn(wc,w1,w2,vn,t)=|vn|2+η(wc†Hnwctn+w2†Hnw2tn+w1†Hnw1tn+vn†Hsvntn),En(wc,w1,w2,vn)=η(wc†Hnwc+w1†Hnw1+w2†Hnw2+vn†Hsvn).

(16e) can be further expressed as

Qn(wc,w1,w2,vn,t)≤En(wc,w1,w2,vn)(19h)

Using the above approximation, the 𝒫2 problem is converted to

𝒫3:maxw,c,v,t,a,β,λ,μ,δ,ϕ,r⁡r(16d),(16f),(18a)−(18d),(19a)−(19d),(19e)−(19g),(19h)

We will resimplify some of the constraints as follows:

An(w2,δn)=w2†Hnw2δnBf(w1,ϕf)=w1†Hfw1ϕfDn(wc,βn)=wc†HnwcβnJf(wc,μf,v)=wc†Hfwcμf+v†Gfvσf2

Through observation, we find that An(w2,δn), Bf(w1,ϕf), Dn(wc,βn), Jf(wc,μf,v), Qn(wc,w1,w2,vn,t) in (18a), (18c), (19b), (19f) and (19h) all contain a superquadratic linear term

F1(w,y)=w†Hwy,w∈{wc,w1,w2,vn},y∈{βn,μf,δn,ϕf,tn}

Similar to the constraint condition of the hyperquadratic linear term, including that w†Hw in (19f) and (19h) is the joint convex function of the variable {w,y}, from which we can get the form that both ends of the constraint are convex functions. According to the definition of the convex difference problem, if a function can be expressed as the difference of two convex functions, it is called DC. We consider the 𝒫3 problem as a convex difference problem. You just need to convert the convex function on the right-hand side of the inequality into a concave function. Therefore, we use the Taylor approximation to linearize the non-convex parts of these equations iteratively. The Taylor first-order expansions obtained by approximating these functions are affine functions.

Specifically, the right side of constraints (18a), (18c), (19b), (19f) and (19h) can be respectively approximated as first-order Taylor expansions at (w2(i),δn(i)), (w1(i),ϕf(i)), (wc(i),βn(i)), (wc(i),μf(i),v(i)), (wc(i),w1(i),w2(i),vn(i)) point. The approximate linear transformation is expressed as follows:

w2†Hnw2δn≥2Re(w2(i)†Hnw2δn(i))−w2(i)†Hnw2(i)δnδn(i)2,∀n∈𝒩,(20a)

w1†Hfw1ϕf≥2Re(w1(i)†Hfw1ϕf(i))−w1(i)†Hfw1(i)ϕfϕf(i)2,∀f∈ℱ,(20b)

wc†Hnwcβn≥2Re(wc(i)†Hnwcβn(i))−wc(i)†Hnwc(i)βnβn(i)2,∀n∈𝒩,(20c)

Since the last two constraints are more complicated on the right-hand side, we let

J(wc(i),μf(i),v(i))=2Re{wc(i)†Hfwcμf(i)}−wc(i)†Hfwc(i)μfμf(i)2π+1σf2{v(i)†Gfv(i)+2Re(v(i)†Gf(v−v(i))},∀f∈ℱ

E(wc(i),w1(i),w2(i),vn(i))=η{wc(i)†Hnwc(i)+2Re(wc(i)†Hn(wc−wc(i)))+w1(i)†Hnw1(i)+2Re(w1(i)†Hn(w1−w1(i)))+w2(i)†Hnw2(i)+2Re(w2(i)†Hn(w2−w2(i)))+vn(i)†Hsvn(i)+2Re(vn(i)†Hs(vn−vn(i)))},∀n∈𝒩

Therefore, it is expressed as

wc†Hfwcμf+v†Gfvσf2⩾J(wc(i),μf(i),v(i))(20d)

En(wc,w1,w2,vn)⩾E(wc(i),w1(i),w2(i),vn(i))(20e)

Using the above approximation, 𝒫3 is converted to

𝒫4:maxw,c,v,t,α,β,λ,μ,δ,ϕ,r⁡r,(21a)

2r2−C2w−1≤2Re(w2(i)†Hnw2δn(i))−w2(i)†Hnw2(i)δnδn(i)2,∀n∈𝒩,(21b)

2r1−C1w−1≤2Re(w1(i)†Hfw1ϕf(i))−w1(i)†Hfw1(i)ϕfϕf(i)2,∀f∈ℱ,(21c)

2αnw−1≤2Re(wc(i)†Hnwcβn(i))−wc(i)†Hnwc(i)βnβn(i)2,∀n∈𝒩,(21d)

2λfw−1≤J(wc(i),μf(i),v(i)),(21e)

Qn(wc,w1,w2,vn,t)≤E(wc(i),w1(i),w2(i),vn(i)),(21f)

(16d),(16f),(18b),(18d),(19a),(19c),(19d),(19e),(19g).(21g)

After the above approximation, it can be seen that the original non-convex problem 𝒫1 is transformed into convex problem 𝒫4, which can be solved easily using convex solvers such as CVX or YALIMP. Finally, our proposed SCa-based solution is presented in Algorithm 1.

Initialization: The pre-coded vector W=[wc,w1,w2] is initialized by assigning high power to wc and power to w1 and w2. We also initialize the common rate vector cn, assuming that the common rate is uniformly assigned to two users. And the distributed beam vector vn. Finally, rn is the maximum and minimum reachable rate in the n-th iteration. In addition, we have to initialize αn,βn,λn,μn,δn,ϕn. They are obtained by replacing the inequality (19a), (19c), (19e), (19g), (18b), (18d) with an equality. Specifically, in order to initialize the algorithm, an initial feasible point needs to be found. First set the desired variables c,v,t to any initial value. A feasible transmitter beam vector satisfying a given signal-to-noise ratio constraint can be found by using the standard optimization toolbox YALMIP or CVX. By fixing c,v,t, we obtain the transmitting beam shaped vector, and then we can further obtain the remaining initial feasible points.

Convergence and Complexity: The convergence of Algorithm 1 can be guaranteed by ensuring that the series of the target obtained is monotone convergence. It is worth mentioning that the SCA approach guarantees that the result goal of Algorithm 1 is monotone and non-decreasing. This is because the solution obtained by solving problem 𝒫4 when iterating n−1 is the feasible solution of problem 𝒫4 when iterating n. In addition, due to the constrained power budget of the BS sum and the strong user group, the sequence generated by the iterative solution problem 𝒫4 is bounded, thus guaranteeing the convergence of the proposed SCA-based algorithm. On the other hand, problem 𝒫4 is a second-order cone problem whose complexity is, therefore, the total complexity of Algorithm 1 is I⋅O((3M+5N+3F)3.5log⁡(1/ε)).

4  Simulation Results

In this section, we use computer simulations to illustrate the performance of the proposed scheme. We consider that we have two groups of users randomly located near and far. A simulated network of base stations with antennas N=4, serving two user groups. It is also assumed that the channel gain between the base station and the near CCUs and the far CEUs conforms to Rayleigh channel static fading hn∼𝒞𝒩(0,σn2) and hf∼𝒞𝒩(0,βσf2) where β controls the channel strength difference between the two users with respect to BS. Residual self-interfering channels We assume that hs follows a complex symmetric Gaussian random variable hs∼𝒞𝒩(0,ΩSI2). To verify the effectiveness of our proposed full-duplex cooperative RSMA, we compared its performance with that of four other traditional reuse schemes:

(1) RSMA, consider a MU-MISO communication network whose base stations are equipped with N transmitting antennas to serve K single antenna users [15]. Using the RSMA policy of the base station, unicast messages for users are divided into public and private sub-messages. Common submessages are syndicated into a common stream for all users to decode. Depending on the RSMA decoding process, each user decodes the public and private streams in turn to recover their information.

(2) HD C-RSMA [21], BS equipped with N transmitting antennas simultaneously serves K single antenna users. The users are divided into two independent user groups, and the signal transmission is divided into direct transmission stage and collaborative transmission stage. The time slot allocation of the two phases is not equal. During the first time slot (also known as the direct transmission phase), BS sends a signal to all users. In the second time slot (also known as the collaborative transmission phase), the strong user group forwards the signal to the weak user group.

(3) C-NOMA, in NOMA based multi-wave beam shaping strategy, because of the adoption of SIC technology, the proximal user can obtain the prior information of the remote user in addition to their own information. Therefore, in the direct transmission phase, BS uses NOMA technology to send the superimposed signal to two user groups simultaneously. In the cooperative phase, the local user can act as the cooperative relay node and send the prior information to the remote user. Using the full-duplex relay mode, the two phases of direct transmission and cooperative transmission are executed at the same time [23].

(4) Traditional NOMA [22], the NOMA solution allows the base station to use the entire bandwidth to serve all users at the same time through the superimposed coding technology on the transmitter side and the SIC technology on the client side. In addition, user reuse is implemented in the power domain. According to NOMA criteria, the base station allocates total power to the I-th data stream, transmitting a linear superposition of N data streams. Each user uses the SIC technology.

When the fault tolerance between two successive iterations is less than 10−5, the algorithm proposed in this paper will stop. Here, the channel quality of the ID-EH user is conducive to better energy capture. In order to solve convex programming, we use cvx toolbox and mosek solver in MATLAB environment. The simulation results average over 100 random channel implementations.

The Fig. 3 shows the typical convergence behavior of several schemes over a random channel with transmitting antenna N=4 and PBSmax=30dBm. As can be seen from the figure, the algorithm proposed in this paper forms a non-decreasing sequence of target values after dozens of iterations and converges to a fixed point. The convergence curves in the figure tend to be gentle roughly after 10 iterations, and the proposed scheme roughly converges to 1.19 bps, while in the comparison with the baseline scheme, it can be observed that N-CRS roughly converges to 1 bps/Hz, and HD CRS roughly converges to 0.95 bps. The convergence values of NOMA’s two schemes are lower. The results clearly show that our proposed algorithm provides better performance in terms of maximum and minimum rates using collaborative logic schemes for the problems considered. This confirms the effectiveness of using collaboration, so it will be used for performance comparisons in subsequent simulations.

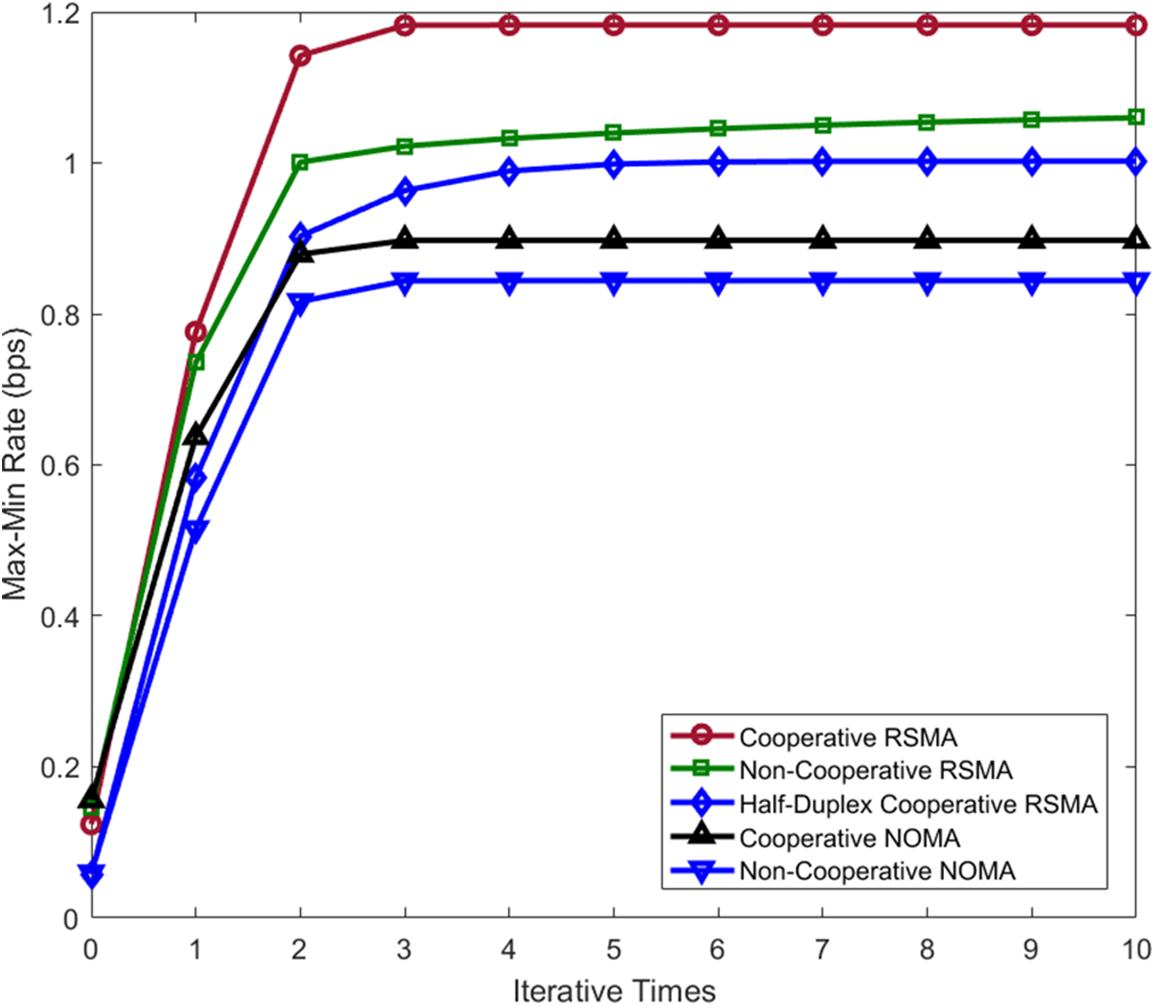
Figure 3: Max-min rate of the considered schemes vs. lterative times

The variation curve of the maximum and minimum speed with the allowable power of the base station is shown in Fig. 4. The results show that the proposed FD CRS scheme is superior to other baseline schemes in terms of maximum and minimum accessibility. It can be observed that when PmaxBS=35dBm, it can be observed that FD CRS proposed by PmaxBS can achieve about 8% rate improvement compared with NRS and HD CRS. Compared with C-NOMA and NC-NOMA, the performance is improved by about 17% and 23%, respectively. We know that RSMA generally has better gain than NOMA [9]. Cooperative full-duplex RSMA improves the performance of RSMA. Due to the cooperative mode, the transmission rate of the remote users with poor conditions is improved, and therefore the overall public reachable rate is improved. In addition, we also found an interesting phenomenon that HD C-RSMA almost overlapped with non-cooperative RSMA when the PmaxBS value was high. This is because when the power budget of the strong user group was similar to that of the base station, the weak user group could gain a large benefit through cooperative transmission, while when the base station power was very large, the benefit would be small. So these two curves tend to overlap.

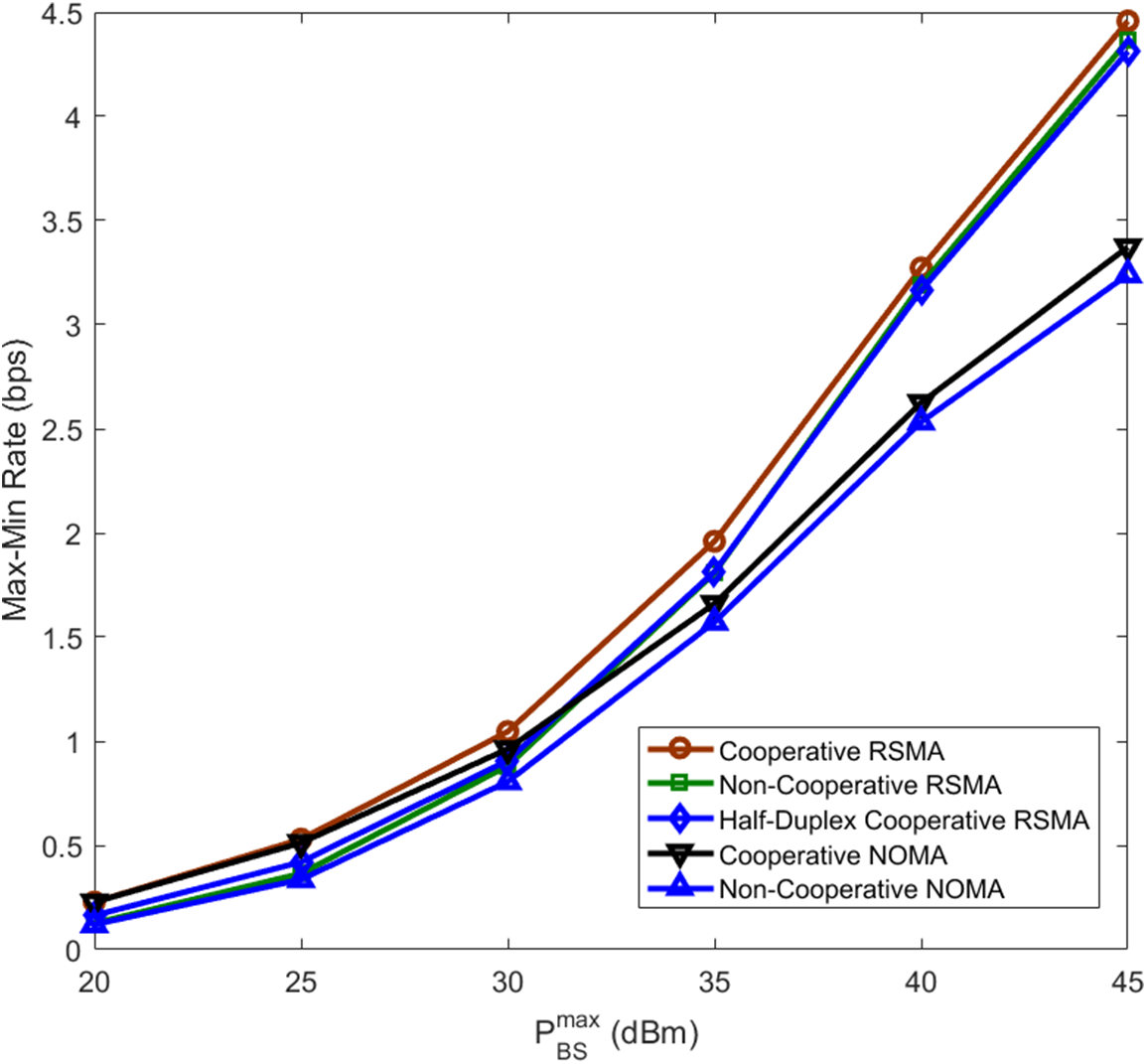
Figure 4: Max-min rate of the considered schemes vs. PmaxBS

In Fig. 5, the effect of the number of antennas equipped on the BS on the maximum and minimum rate performance at PmaxBS=40dBm is shown. It can be clearly observed that our proposed full-duplex assisted CRS scheme has better performance than other baseline methods. And collaborative algorithms, whether RSMA or NOMA, do have better advantages than non-collaborative algorithms. Compared with the non-cooperative RSMA and the half-duplex RSMA, the maximum and minimum rates are roughly stable about 0.1 bps higher. The maximum minimum rate is approximately 0.6 bps higher than that of the cooperative NOMA and non-cooperative NOMA algorithms. As the number of antennas N increases from 4 to 8, it can be found that the maximum and minimum rates of all schemes increase significantly. The result may be that the increase of antenna also increases the degree of freedom of the system, thus improving the utilization rate of resources. When N is small (that is, N<5), the difference between full-duplex mode and half-duplex mode is more obvious due to the lack of degrees of freedom, indicating the superiority of CRS full-duplex mode. Another observation is that after N=5, CRS under half-duplex cooperation is closer to the non-cooperative RS algorithm.

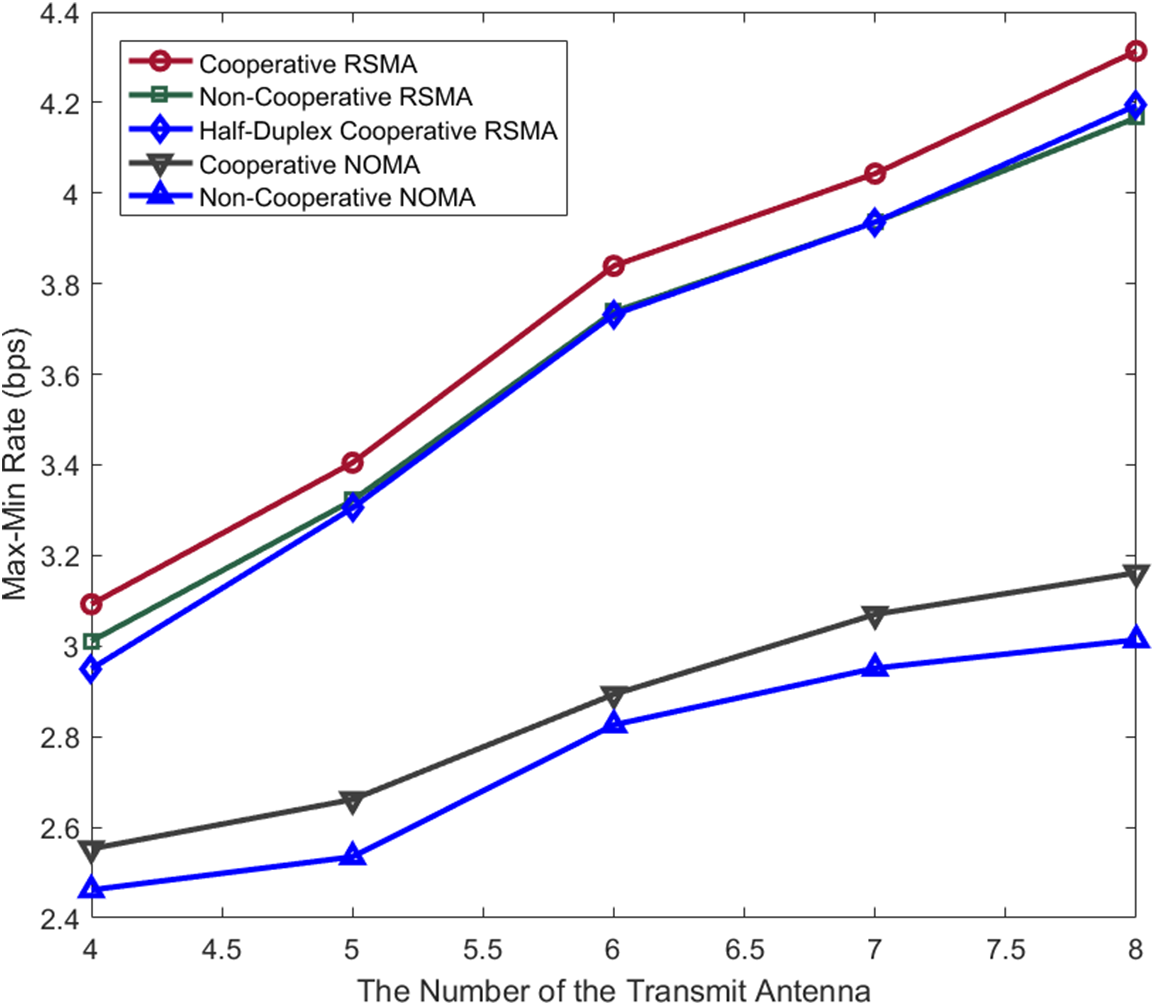
Figure 5: Max-min rate of the considered schemes vs. the number of antennas

The effect of ΩSI2 on the maximum and minimum rate performance that can be achieved is also investigated. As can be seen from Fig. 6, the performance of the full-duplex CRS proposed by us is superior to the other four schemes in terms of the maximum and minimum rate that can be realized. When ΩSI2 is relatively small, FD CRS and FD NOMA schemes perform much better than non-cooperative CRS, half-duplex CRS and non-cooperative NOMA schemes. Since the non-cooperative scheme has almost no self-interference problem, it is a smooth straight line, while the maximum and minimum rate under the cooperative scheme is greatly affected. Half-duplex and non-cooperative RSMA have almost identical performance curves in the figure. It is also observed that by increasing ΩSI2 from −20 dB to 0 dB, the achievable data rates of both FD CRS and FD C-NOMA begin to decrease. This is because increasing ΩSI2 affects the performance of the full-duplex mode. As ΩSI2 increases, more interference is brought to the near end strong user group. It has an impact on both public and private information flows, resulting in a lower signal-to-noise ratio and achievable public rate. In other words, the base station requires the proximal user group to adopt low power transmission to reduce the impact of SI.

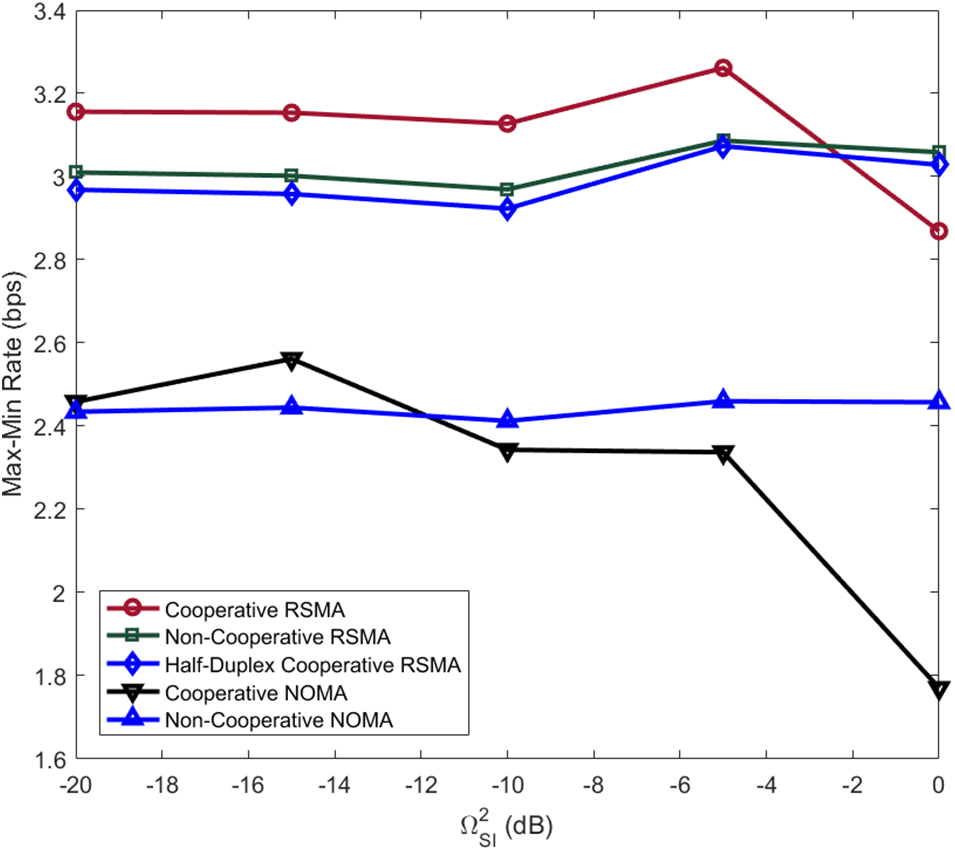
Figure 6: Max-min rate of the considered schemes vs. ΩSI2

Fig. 7 compares the performance difference between the FD CRS proposed by us and the other four baseline schemes when the channel intensity difference between the two groups of users is different, i.e., change β. It can be observed that in the process of β changing from 0.2 to 1, FD CRS proposed by us is generally better than NRS, HD C-RSMA, C-NOMA and traditional NOMA. In the absence of cooperative transmission, the common rate that NRS can achieve is limited by the rate of the user with the worst channel conditions. However, with the increase of channel strength difference, that is, the decrease of β, the performance of FD CRS gradually decreased in line with that of C-NOMA. RSMA and HD RSMA perform well when the channel strength difference is small, and have a large advantage over the NOMA scheme, which is the expected behavior. However, with the increase of β, when the channel conditions of the two groups of users tend to be consistent, which is not consistent with our hypothetical scenario, we can observe that the advantage of collaboration becomes smaller at this time. The three RSMA schemes are almost identical. However, compared with FD C-NOMA, FD CRS scheme using PS strategy can better adapt to different channel intensity differences.

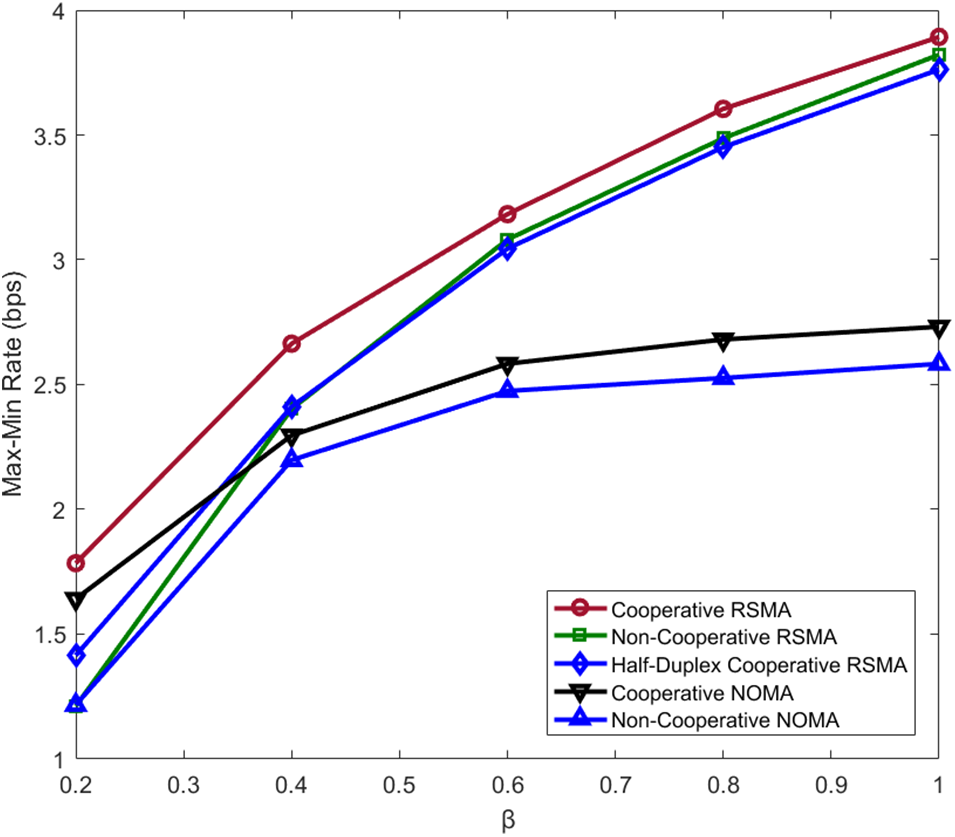
Figure 7: Max-min rate of the considered schemes vs. β

5  Conclusions

This paper studies the performance of FD CRS in MISO system by constructing the joint optimization problem of rate segmentation and multicast beam-forming under full duplex cooperation, aiming at maximizing the minimum transmission rate. We are committed to reducing inter-group interference, and making full use of time resources. The SCA-based method is used to solve the non-convex formula optimization problem iteratively and obtain the local minimum. The simulation results show that the proposed FD-CRS mechanism has a strong advantage in the minimum-rate maximization problem. This model can be used as a general reuse scheme for FD C-NOMA and HD C-RSMA, and is superior to other reference mechanisms. We conclude that the proposed mechanism and iterative algorithm can adapt well to the target rate and network load of various user channel multicast groups. More efficient distributed algorithms with low complexity can be further explored in the future. Compared with the limitations and performance deficiencies of MIMO networks, more complex MIMO networks and large-scale antenna networks can be further studied.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper. This work is supported by Special Fund Project for Technology Innovation of Xuzhou City in 2022 , Jiangsu Province Key Research and Development (Modern Agriculture) Project, Guangzhou Basic Research Program Municipal School (College) Joint Funding Project underGrant and Innovation Project of Jiangsu Province.

Funding Statement: This work is supported by Special Fund Project for Technology Innovation of Xuzhou City in 2022 (KC22083), Jiangsu Province Key Research and Development (Modern Agriculture) Project (BE2019333) and (BE2019334), Guangzhou Basic Research Program Municipal School (College) Joint Funding Project under Grant 2023A03J0111 and Innovation Project of Jiangsu Province (SJCK21_1133).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Siyi Duan, Mingsheng Wei, Shidang Li; data collection: Weiqiang Tan and Bencheng Yu; draft manuscript preparation: Siyi Duan, Mingsheng Wei, Shidang Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data are not publicly available due to [restrictions e.g., their containing information that could compromise the privacy of research participants].

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Mao, Y., Clerckx, B., Li, V. O. (2018). Energy efficiency of rate-splitting multiple access, and performance benefits over SDMA and NOMA. 2018 15th International Symposium on Wireless Communication Systems (ISWCS), pp. 1–5. Lisbon, Portugal. [Google Scholar]

2. Mao, Y., Clerckx, B., Li, V. (2018). Rate-splitting multiple access for downlink communication systems: Bridging, generalizing, and outperforming SDMA and NOMA. EURASIP Journal on Wireless Communications and Networking, 2018(1), 133. [Google Scholar] [PubMed]

3. Yang, S., Lit, Z. (2018). A constant-gap result on the multi-antenna broadcast channels with linearly precoded rate splitting. 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece. [Google Scholar]

4. Clerckx, B., Joudeh, H., Hao, C., Dai, M., Rassouli, B. (2016). Rate splitting for MIMO wireless networks: A promising PHY-layer strategy for LTE evolution. IEEE Communications Magazine, 54(5), 98–105. [Google Scholar]

5. Joudeh, H., Clerckx, B. (2016). Sum-rate maximization for linearly precoded downlink multiuser MISO systems with partial CSIT: A rate-splitting approach. IEEE Transactions on Communications, 64(11), 4847–4861. [Google Scholar]

6. Joudeh, H., Clerckx, B. (2016). Robust transmission in downlink multiuser MISO systems: A rate-splitting approach. IEEE Transactions on Signal Processing, 64(23), 6227–6242. https://doi.org/10.1109/TSP.2016.2591501 [Google Scholar] [CrossRef]

7. Dai, M., Clerckx, B., Gesbert, D., Caire, G. (2016). A rate splitting strategy for massive MIMO with imperfect CSIT. IEEE Transactions on Wireless Communications, 15(7), 4611–4624. https://doi.org/10.1109/TWC.2016.2543212 [Google Scholar] [CrossRef]

8. Papazafeiropoulos, A., Clerckx, B., Ratnarajah, T. (2017). Rate-splitting to mitigate residual transceiver hardware impairments in massive MIMO systems. IEEE Transactions on Vehicular Technology, 66(9), 8196–8211. [Google Scholar]

9. Wang, H., Xiao, P., Li, X. (2022). Channel parameter estimation of mmWave MIMO system in urban traffic scene: A training channel-based method. IEEE Transactions on Intelligent Transportation Systems, 1–9. https://doi.org/10.1109/TITS.2022.3145363 [Google Scholar] [CrossRef]

10. Wang, H., Xu, L., Yan, Z., Gulliver, T. A. (2021). Low-complexity MIMO-FBMC sparse channel parameter estimation for industrial big data communications. IEEE Transactions on Industrial Informatics, 17(5), 3422–3430. [Google Scholar]

11. Dai, M., Clerckx, B. (2017). Multiuser millimeter wave beamforming strategies with quantized and statistical CSIT. IEEE Transactions on Wireless Communications, 16(11), 7025–7038. [Google Scholar]

12. Kolawole, O., Panazafeironoulos, A., Ratnarajah, T. (2018). A rate-splitting strategy for multi-user millimeter-wave systems with imperfect CSI. 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece. [Google Scholar]

13. Joudeh, H., Clerckx, B. (2015). Sum rate maximization for MU-MISO with partial CSIT using joint multicasting and broadcasting. 2015 IEEE International Conference on Communications (ICC), London, UK. [Google Scholar]

14. Tervo, O., Trant, L., Chatzinotas, S., Ottersten, B., Juntti, M. (2018). Multigroup multicast beamforming and antenna selection with rate-splitting in multicell systems. 2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Kalamata, Greece. [Google Scholar]

15. Yin, L., Clerckx, B., Mao, Y. (2021). Rate-splitting multiple access for multi-antenna broadcast channels with statistical CSIT. 2021 IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Nanjing, China. [Google Scholar]

16. Sun, Y., Ng, D. W. K., Zhu, J., Schober, R. (2016). Multi-objective optimization for robust power efficient and secure full-duplex wireless communication systems. IEEE Transactions on Wireless Communications, 15(8), 5511–5526. [Google Scholar]

17. Zhang, Z., Chai, X., Long, K., Vasilakos, A. V., Hanzo, L. (2015). Full duplex techniques for 5G networks: Self-interference cancellation, protocol design, and relay selection. IEEE Communications Magazine, 53(5), 128–137. [Google Scholar]

18. Zhang, J., Clerckx, B., Ge, J., Mao, Y. (2019). Cooperative rate splitting for MISO broadcast channel with user relaying, and performance benefits over cooperative NOMA. IEEE Signal Processing Letters, 26(11), 1678–1682. [Google Scholar]

19. Clerckx, B., Mao, Y., Schober, R., Poor, H. V. (2020). Rate-splitting unifying SDMA, OMA, NOMA, and multicasting in MISO broadcast channel: A simple two-user rate analysis. IEEE Wireless Communications Letters, 9(3), 349–353. [Google Scholar]

20. Hao, C., Wu, Y., Clerckx, B. (2015). Rate analysis of two-receiver MISO broadcast channel with finite rate feedback: A rate-splitting approach. IEEE Transactions on Communications, 63(9), 3232–3246. [Google Scholar]

21. Mao, Y., Clerckx, B., Zhang, J., Li, V. O. K., Arafah, M. A. (2020). Max-min fairness of K-user cooperative rate-splitting in miso broadcast channel with user relaying. IEEE Transactions on Wireless Communications, 19(10), 6362–6376. [Google Scholar]

22. Timotheou, S., Krikidis, I. (2015). Fairness for non-orthogonal multiple access in 5G systems. IEEE Signal Processing Letters, 22(10), 1647–1651. [Google Scholar]

23. Liu, G., Chen, X., Ding, Z., Ma, Z., Yu, F. R. (2018). Hybrid half-duplex/full-duplex cooperative non-orthogonal multiple access with transmit power adaptation. IEEE Transactions on Wireless Communications, 17(1), 506–519. [Google Scholar]