Outage Probability Analysis for D2D-Enabled Heterogeneous Cellular Networks with Exclusion Zone: A Stochastic Geometry Approach

1  Introduction

As the number of wireless connected devices grows explosively in the upcoming sixth generation (6G) era [1,2], it can be foreseen that heterogeneous cellular (i.e., smartphones) and device-to-device (i.e., wearable devices) devices will densely coexist to extensively collect and frequently exchange information [3] and have widespread application prospects in many fields [4,5]. In the device-to-device (D2D)-enabled heterogeneous cellular networks (HetCNets) [6,7], D2D devices reuse the cellular spectrum, which may result in severe interference for the reception of cellular signals at the base stations (BSs). To alleviate the interference, an efficient interference management way is to set exclusion zones around the receivers [8–10]. That is, when a BS is receiving desired signals from cellular devices, the exclusion zone, defined as a cycle region, centered at the BS is set, in which the D2D devices are inhibited to perform any transmissions.

1.1 Motivation

Whether the information can be successfully transmitted is an important performance metric for wireless devices. In this paper, we aim to theoretically analyze the outage probabilities (i.e., unsuccessful transmission probabilities) of cellular and D2D devices in D2D-enabled HetCNets with exclusion zone. However, we are facing the following major difficulties. First, in practical network deployment, cellular and D2D devices are randomly located in the space, while BSs are deployed with strict requirements and restrictions, the two facts affect the outage probabilities greatly. It is difficult to model the location randomness of BSs, cellular and D2D devices in practice. Second, cellular transmissions occur randomly, leading to random exclusion zones around the BS receivers, further leading to random D2D transmissions. It is difficult to capture the randomness and interrelation of cellular and D2D transmissions. Third, different types of cellular and D2D devices perform transmissions concurrently; they mutually interfere with each other. It is difficult to characterize the different types of interference and their impacts on the outage probabilities of cellular and D2D devices. The above three difficulties motivate this study.

1.2 Contributions

Consider a D2D-enabled HetCNet with exclusion-zone, we theoretically analyze the outage probabilities of cellular and D2D devices and make the following novel contributions:

•   We adopt a stochastic geometry (SG) approach to solve the abovementioned three difficulties. To address difficulty 1, we use Matérn hard-core process (MHCP) to model the real location distribution of BSs and use homogeneous Poisson point processes (HPPPs) to capture the location randomness of cellular and D2D devices in practical networks. To address difficulty 2, we first model the transmitting cellular devices by a thinned HPPP, and then model the activated D2D devices outside the exclusion zones by Poisson hole process (PHP). To address difficulty 3, we characterize mutual interference among the concurrent cellular and D2D transmissions by approximating MHCP of receiving BSs and PHP of activated D2D devices with PPPs and further estimating the intensities of different types of transmitting cellular and D2D devices.

•   With our model, we theoretically analyze the outage probabilities of cellular and D2D devices, which are formulated as functions of system parameters, including the intensities of transmitting cellular and D2D devices, the minimum distance among BSs, and the radius of exclusion zones around BSs.

•   We verify the accuracy of our theoretical model via extensive Monte-Carlo simulations.

The rest paper is organized as follows. Section 2 presents the related work. Section 3 introduces some stochastic geometry preliminaries. Section 4 specifies the system model of a D2D-enabled HetCNet with exclusion zone. Section 5 theoretically analyzes the outage probabilities of cellular and D2D devices with SG approach. Section 6 verifies the accuracy of our theoretical model via extensive Monte-Carlo simulations. Finally, Section 7 concludes the paper. For the ease of reference, Table 1 lists the main notations and their meanings.

2  Related Work

This section presents existing works in terms of performance analysis of D2D-enabled HetCNets by setting exclusion zones or enabling D2D devices to operate in half-/full-duplex mode.

2.1 Set Exclusion Zones

Setting exclusion zones can effectively alleviate the interference among cellular and D2D transmissions. Many existing works have studied the exclusion zones set around transmitters or receivers.

Set exclusion zones around transmitters. Chu et al. in [11] adopted SG to study energy-harvesting-based D2D communication, where they set guard zones (also called exclusion zones) around D2D transmitters to protect D2D transmissions from interference emitted from the cellular devices. Flint et al. in [12] set guard zones around first-tier transmitters in two-tier heterogeneous networks, where they consider the exclusive relationship among the first-tier transmitters and model the spatial distribution of first-tier transmitters by Poisson hard-core process (PHCP). However, we study the D2D-enabled HetCNets with SG and set exclusion zones around the receivers to protect cellular transmissions from interference by D2D transmissions.

Set exclusion zones around receivers. Hasan et al. in [8] introduced guard zone around each receiver to balance the interference and spatial reuse, but this study is for wireless ad hoc networks. Tefek et al. in [9] set two types of exclusion zones around primary receivers and secondary transmitters in two-tier cognitive networks, and analyze the transmission capacities and outage probabilities of primary and secondary users with SG approach. Chen et al. in [10] studied decentralized opportunistic access for D2D underlaid cellular networks with SG and impose cellular guard zones around the BSs where no D2D transmitters can lie in, but they do not consider the minimum distance among BSs. Different from the above works, we adopt SG to study the D2D-enabled HetCNets and consider the exclusive relationship among BSs in practical networks. Besides, D2D devices can operate in half-/full-duplex mode optionally. The performance frameworks in the above works are not suitable in our research scenario.

2.2 Operate in Half-/Full-Duplex Mode

Despite the HD mode, each DU can operate in FD mode optionally to further promote to double the spectral efficiency. Some previous works analyze the performance of HD/FD D2D transmissions.

Operate in HD mode. Huang et al. in [13] studied the energy-efficient mode selection for D2D communications in cellular networks, which enable HD D2D users to select approximated modes, and then analyze the success probability and ergodic capacity for both cellular and D2D links using SG. Sun et al. in [14] controled the transmit power for D2D transmitters based on the statistical channel-state information to mitigate interference among D2D and cellular communications in D2D-underlaid cellular networks, and adopt SG to analyze the success probability and the energy efficiency of D2D communications. In contrast, we analyze the D2D transmissions where D2D devices can operate in HD/FD mode optionally, and we employ exclusion zones around the BS receivers to alleviate the interference.

Operate in FD mode. Badri et al. in [15] and [16] studied FD D2D communication in cellular networks, which enable D2D users to optionally work in HD/FD mode to alleviate the interference and guarantee the quality of service (QoS) of the cellular users. However, they do not consider the real deployment of BSs. Different from the above works, our study captures the location randomness of BS, cellular and D2D devices in real networks, the randomness and interrelation of cellular and D2D transmissions as well as the mutual interference and characterize their impacts on the outage probabilities of cellular and D2D transmissions.

3  Stochastic Geometry Preliminaries

Stochastic geometry (SG) approach, which provides various powerful tools to model the spatial location distribution of wireless devices and characterize the interference effect, has been widely used in wireless networks [17]. Many existing works [15,16,18] adopted homogeneous Poisson point process (HPPP) to model the spatial distribution of the wireless devices, which assumes devices are independently distributed and is the most popular spatial point process owing to its mathematical tractability. However, in practical networks, the transmitters are deployed with strict requirements and restrictions in order to alleviate interference, extend coverage region and reduce deployment costs, and thus an exclusion zone among the locations of the transmitters naturally arises. In this context, hard-core point process (HCPP) [12,19,20], which forbids devices to lie closer than a certain minimum distance has drawn much attention, such as PHCP [12] or MHCP [19,20]. According to whether there is a practical exclusive relationship among devices, we assume that the D2D and cellular users follow HPPPs and assume that base stations follow MHCP in our study. Below, we briefly present some terminologies and SG tools involved in this paper. Readers can refer to [21–24] for further details.

Definition 1. (Poisson point process) A spatial point process Φ={xi,i∈N+}⊂Rd with intensity measure ∧ is a Poisson point process (PPP) [18], if the random number of points of Φ for every bounded Borel set ℬ⊂Rd has a Poisson distribution with mean ∧(ℬ), that is,

P[Φ(ℬ)=k]=e−∧(ℬ)(∧(ℬ))kk!

where ∧(ℬ) represents the average number of points falling in the given set ℬ. For an HPPP, ∧(ℬ)=λ|ℬ|, where λ is the intensity of Φ and represents the average number of points falling in per unit area or volume, |ℬ| is the Lebesgue measure (i.e., area) of set ℬ in Euclidean space.

Definition 2. (Matérn hard-core process of type I) An MHCP of type I ΦM1 is formed from a dependent thinning of an HPPP Φ={xi,i∈N+}⊂Rd with intensity λ. First, each point xi∈Φ is marked if it has a neighbor within distance r. Then, remove all marked points. All the remaining points of Φ form an MHCP of type I ΦM1. Mathematically, ΦM1 is described as

ΦM1={xi∈Φ:∀xj∈Φ is not in b(xi,r)}

where b(xi,r) represents a ball centered at xi∈Φ with radius r. The intensity λM1 of ΦM1 is given by λM1=λexp⁡(−λπr2).

Definition 3. (Matérn hard-core process of type II [25]) An MHCP of type II ΦM2 is formed from a dependent thinning of an HPPP Φ={xi,i∈N+}⊂Rd with intensity λ. First, each point xi∈Φ is marked independently with a random mark Mi∈(0,1). Then, a point xi∈Φ is retained in ΦM2 if and only if the ball b(xi,r) does not contain any point of Φ with mark smaller than Mi. Mathematically, ΦM2 is described as

ΦM2={xi∈Φ:Mi<Mj,∀xj∈Φ∩b(xi,r)∖xi}.

The probability that each point xi∈Φ is retained in ΦM2 can be expressed as PM2=1−exp⁡(−λπr2)λπr2 [26]. Then, the intensity λM2 of ΦM2 is given by λM2=λPM2=1−exp⁡(−λπr2)πr2, which can be further written with the intensity λM1 of ΦM1 as λM2=1πr2(1−λM1λ).

Definition 4. (Poisson hole process) Let Φ1={xi,i∈N+}⊂Rd with intensity λ1 and Φ2={yi,i∈N+}⊂Rd with intensity λ2 (λ2≫λ1) be two independent PPPs in a given bounded Borel set ℬ⊂Rd. For each point xi∈Φ1, remove all the points yi∈Φ2 in b(xi,r). All the removed points of Φ2 form the Hole-0 process Φh0 [27] with intensity λh0=λ2(1−exp⁡(−λ1πr2)), and the remaining points of Φ2 form the Poisson hole process (PHP) ΦPHP (also named as Hole-1 process [27]) with intensity λPHP=λ2 exp⁡(−λ1πr2).

Definition 5. (Probability generating functional) Let Φ={xi,i∈N+}⊂Rd be a spatial point process with intensity measure ∧, for any measurable function f(x):Rd→[0,1], the probability generating functional (PGFL) of Φ is defined as

E[∏xi∈Φf(x)]≜exp⁡(−∫Rd(1−f(x))Λ(dx))

where xi∈Φ represents the orthogonal coordinates of points in Φ. For an inhomogeneous PPP with intensity function λ(x), the PGFL of Φ can expressed as

E[∏xi∈Φf(x)]=exp⁡(−∫Rd(1−f(x))λ(x)dx).

For an HPPP with intensity λ, the PGFL of Φ can expressed as

E[∏xi∈Φf(x)]=exp⁡(−λ∫Rd(1−f(x))dx).

We convert the above integral from orthogonal coordinates to polar coordinates, i.e.,

E[∏xi∈Φf(x)]=exp⁡(−λ∫0∞∫02π(1−f(r))dωrdr)=exp⁡(−λ∫02πdω∫0∞(1−f(r))rdr)=exp⁡(−2πλ∫0∞(1−f(r))rdr)

where xi=(rsin⁡ω,rcos⁡ω), ω is the polar angle and follows uniform distribution in [0,2π].

Definition 6. The Laplace transform (LT) ℒ of random variable X is defined as

ℒX(s)=E[exp⁡(−sX)]=∫0∞exp⁡(−sx)fX(x)dx

where fX(x) is the probability density function (PDF) of X.

4  System Model

This section specifies the system model of a D2D-enabled heterogeneous cellular network (HetCNet) with exclusion-zone in terms of network deployment, channel model, intensities of transmitting cellular and D2D users.

4.1 Network Deployment

We study a D2D-enabled HetCNet with exclusion-zone, which consists of multiple base stations (BSs), lots of cellular users (CUs) and D2D users (DUs), as shown in Fig. 1.

Figure 1: Overview of a D2D-enabled heterogeneous cellular network (HetCNet) with exclusion-zones around the BSs

In a typical HetCNet, the CUs and DUs are randomly located in the space, we model the locations of CUs and DUs by two independent HPPPs Φc,Φd⊂R2 with intensities λc and λd, respectively; since any two BSs cannot be arbitrarily close to each other in practical network deployment, we model the location of BSs by an MHCP of type k Φbk with intensity λbMk(k={1,2}), which is formed by dependent thinning of another HPPP Φb0⊂R2 with intensity λb0 (λc≫λb0, λd≫λb0) [19,20]. According to the definition of MHCP (i.e., Definitions 2 and 3), λbMk can be expressed as

λbMk={λb0exp(−λb0πRb2)k=11−exp(−λb0πRb2)πRb2k=2(1)

where Rb is the minimum distance among any two BSs.

We assume that Φb0, Φc and Φd are independent, the locations of BSs, CUs and DUs are independent with each other. We assume that each CU transmits to its geographically nearest BS with a fixed power Pc, where a Voronoi tessellation is formed, as shown in Figs. 2a–2c. The mean area of each Voronoi cell Sv can be expressed as [19,21–23]

E[Sv]=1/λbMk(2)

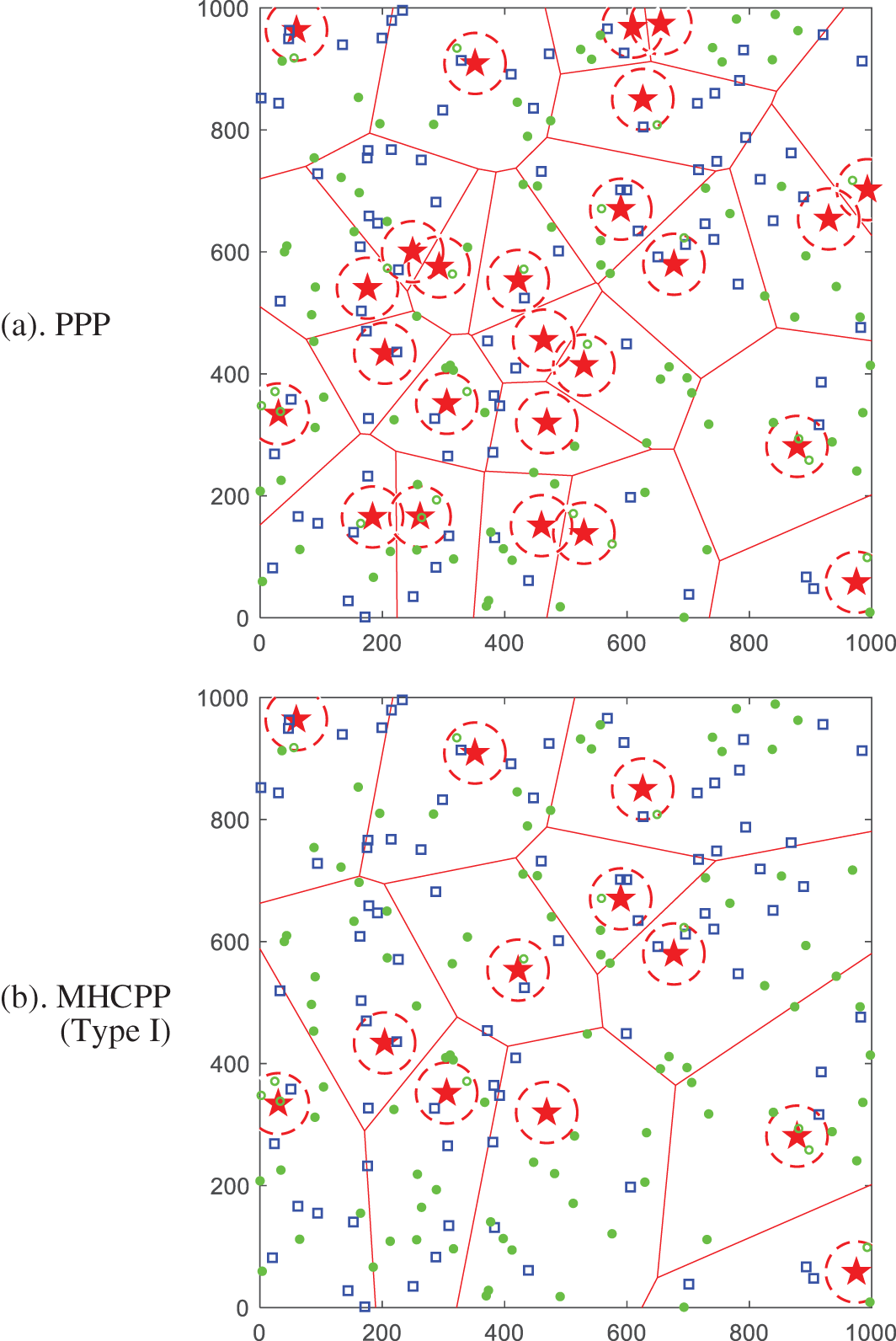
Figure 2: A snapshot of Voronoi tessellation of BSs, CUs and DUs in a 1000 m × 1000 m square region, where λc = 100 CUs km−2, λd = 100 DUs km−2, Rb = 100 m, db = 50 m. (a). BSs follow an HPPP with λb0 = 30 BSs km−2; (b). BSs follow an MHCP of type I with λbM1 = BSs km−2; (c). BSs follow an MHCP of type II with λbM2 = 19.4 BSs km−2

In order to facilitate the analysis, we approximate the Voronoi cell as a circle with radius Rv [28–30], i.e.,

Rv=E[Sv]/π=1/πλbMk(3)

We assume that DUs utilize the uplink cellular channel to perform D2D transmissions and may choose to operate in either HD or FD mode to transmit to its nearest DU with a fixed power Pd. When adopting FD mode, we assume the imperfect self-interference cancellation at the DU receiver side. Due to spectrum sharing, the D2D transmissions may interfere with the reception of cellular signals at the BS. To manage the interference, exclusion zones around BSs are set. In the exclusion zone centered at each receiving BS with radius db, the DUs cannot be activated to perform D2D transmissions. As Figs. 1 and 2 show, DUs in the exclusion zones of BSs are non-activated; in contract, DUs outside the exclusion zones are activated.

4.2 Channel Model

We assume that all the wireless signals in D2D and cellular transmissions undergo large- and small-scale channel fading. We characterize the large-scale channel fading by the distance dependent power-law path loss model l=‖x−y‖−α=R−α [31], where R=‖x−y‖ is Euclidean distance between a transmitter x and a receiver y, and α is the path-loss exponent which usually satisfies 2<α<6 [32]. We characterize the small-scale channel fading with Rayleigh fading that is modeled by an independent and identically distributed (i.i.d.) power fading coefficient H (square of the amplitude fading coefficient) [33], which follows exponential distribution with mean 1/μ, i.e., H∼Exp(μ) [18]. Besides, we assume that the thermal noise at the receiver is additive white Gaussian noise with zero mean and variance σ2 [34,35].

4.3 Intensity of Transmitting CUs

We assume that all CUs perform ALOHA mechanism to access the channel with probability pct to transmit data to its associated BSs [15]. Let Φct denote the set of transmitting CUs with intensity λct. According to independent thinning process of HPPP Φc, Φct is an HPPP and λct can be expressed as

λct=pctλc(4)

4.4 Intensity of Transmitting DUs

Recall that we set exclusion zones at the side of BS which is performing reception from transmitting CUs in its Voronoi cell, that is, when no CUs are transmitting in a cell, the BSs may not perform reception, the exclusion zones are not set. Let pbr denote the receiving probability of BSs, which is equal to the probability that there is at least a transmitting CU in a given Voronoi cell Sv. According to definition of PPP (i.e., Definition 1), pbr can be expressed as

pbr=1−P[Φct(Sv)=0]=1−exp(−∧(E[Sv]))(5)

where ∧(E[Sv]) is the intensity measure of Φct and can be expressed as

∧(E[Sv])=λctE[Sv]=λct/λbMk(6)

Let Φbr denote the set of receiving BSs with intensity λbr. Due to the non-availability of any known PGFL for MHCP, for the ease of analysis, we use a PPP ΦbMk′ with same intensity λbMk to approximate the MHCP ΦbMk of receiving BSs1 [20,36–38], and the accuracy of such approximation is also validated in [39]. According to independent thinning of ΦbMk′, Φbr is a PPP and λbr can be expressed as

λbr=pbrλbMk(7)

Let Ξdb denote the union of exclusion zones formed by all receiving BSs. Since each receiving BS form an exclusion zone, Ξdb can be expressed as

Ξdb≜⋃yi∈Φbrb(yi,db)(8)

where b(yi,db) is an exclusion zone centered at yi∈Φbr with radius db.

In Ξdb, the DUs cannot be activated to perform D2D transmissions. According to the definition of PHP (i.e., Definition 4), for the two PPPs of receiving BSs Φbr and DUs Φd, the activated DUs outside the exclusion zones (i.e., Ξdb) naturally form a PHP Φda with intensity λda, i.e.,

λda=λdexp(−λbrπdb2)(9)

Recall that the DUs can choose to operate in either HD or FD mode [15]. We assume that a DU operates in HD and FD with probability pH and pF, respectively, such that pH+pF=1. Due to the non-availability of any known PGFL for PHP, for the ease of analysis, we use a PPP Φda′ with same intensity λda to approximate the PHP Φda of activated DUs [30,40]. According to independent thinning of PPP Φda′, Φda′ can be regarded as the union of two independent PPPs ΦH of activated HD DUs with intensity λH and ΦF of activated FD DUs with intensity λF, that is, Φda′=ΦH∪ΦF [15]. Hence, λH, λF can be expressed as

λH=pHλda,λF=pFλda(10)

We assume that half of HD DUs are transmitters and half of them are receivers [15]. Hence, the transmitting HD DUs form a thinned PPP ΦHt with intensity λHt=λH/2. Similarly, all FD DUs are transceivers at the same time. The transmitting FD DUs form a thinned PPP ΦFt with intensity λFt=λF.

5  Outage Probability Analysis

This section theoretically analyzes the outage probabilities of CUs and DUs with stochastic geometry approach.

5.1 Outage Probability of CUs Pc

We first analyze the outage probability of CUs. Consider a cellular transmission from a tagged CU c0 to a tagged BS b0 in a distance Rc. Let SINRb(Rc,Ib) denote the signal-to-interference-plus-noise ratio (SINR) between b0 received c0’s signal power Sb and its suffered interference signal power Ib plus noise power σ2. Hence, the SINRb(Rc,Ib) at b0 can be expressed as

SINRb(Rc,Ib)=SbIb+σ2(11)

where σ2 is the noise power. In Eq. (11), Sb can be expressed as

Sb=PcHcRc−α(12)

where Pc is the transmission power of CU, Hc is the power fading coefficient between c0 and b0.

In Eq. (11), Ib can be expressed as

Ib=Ibc+IbH+IbF(13)

where Ibc=∑i∈Φct∖{c0}PcHiRi−α, IbH=∑i∈ΦHtPdHiRi−α, IbF=∑i∈ΦFtPdHiRi−α is b0’s received interference from the other transmitting CUs, HD and FD DUs, respectively. Pd is the transmission power of DU, Hi and Ri are the power fading coefficient and distance between i and b0, respectively.

For the tagged transmitter c0, the transmission is unsuccessful if SINRb(Rc,Ib) at d0 is smaller than a certain SINR threshold θ2. Let Pc denote the outage probability of c0, which is defined as the mean value of P([SINRb(Rc,Ib)]<θ), i.e.,

Pc=EIb,Rc[P(SINRb(Rc,Ib)<θ)]=∫0RvEIb[P(SINRb(rc,Ib)<θ|rc)]⋅fRc(rc)drc(14)

where fRc(rc) is the probability density function (PDF) of Rc [41]. Below, we express fRc(rc) and EIb[P(SINRb(rc,Ib)<θ|rc)] in sequence.

Let FRc(rc) denote the cumulative distribution function (CDF) of Rc. FRc(rc) can be expressed as

FRc(rc)=ℙ(Rc≤rc)=πrc2πRv2=πrc21/λbMk=πλbMkrc2,  0 < rc≤Rv;(15)

Further, fRc(rc) can be obtained by taking derivative of FRc(rc) with respect to rc, i.e.,

fRc(rc)=dFRc(rc)drc=2πλbMkrc,   0 < rc≤Rv;(16)

Then, we express EIb[P(SINRb(rc,Ib)<θ|rc)] as

EIb[P(SINRb(rc,Ib)<θ|rc)]=EIbc,IbH,IbF[P(PcHcrc−αIbc+IbH+IbF+σ2<θ|rc)]=EIbc,IbH,IbF[P(Hc<μθrcαPc(Ibc+IbH+IbF+σ2)|rc)](a)=EIbc,IbH,IbF[1−exp(−μθrcαPc(Ibc+IbH+IbF+σ2))]=1−exp(−sbσ2)EIbc[exp(−sbIbc)]EIbH[exp(−sbIbH)]EIbF[exp(−sbIbF)](b)=1−exp(−sbσ2)ℒIbc(sb)ℒIbH(sb)ℒIbF(sb)(17)

where EX[AX] is the expectation of AX with respect to X. Eq. (a) holds because Hc follows an exponential distribution with mean 1/μ, i.e., Hc∼Exp(μ). According to the CDF of an exponential distribution, if fHc(hc)=μe−μhc, P(Hc<h0)=FHc(h0)=∫0h0μe−μhcdhc=1−exp(−μh0). Eq. (b) follows from the definition of LT (i.e., Definition 6) of interference Ibc, IbH, and IbF evaluated at sb=μθrcαPc, respectively. We express them in sequence below.

In Eq. (17), the LT of Ibc at b0 is given as

ℒIbc(sb)=exp(−λctrc2θ2/α⋅2π2αsin(2π/α))(18)

Proof:

ℒIbc(sb)=EIbc[exp⁡(−sbIbc)]=ERi,Hi[exp⁡(−μθrcαPc∑i∈Φct∖{c0}PcHiRi−α)](a)=ERi[EHi[exp⁡(−∑i∈Φct∖{c0}μθrcαHiRi−α)]](b)=ERi[∏i∈Φct∖{c0}EHi(exp⁡(−μθrcαRi−αHi))](c)=ERi[∏i∈Φct∖{c0}∫0∞exp⁡[−μθrcαRi−αhi]fHi(hi)dhi](d)=ERi[∏i∈Φct∖{c0}∫0∞exp⁡[−μθrcαRi−αhi]μexp⁡(−μhi)dhi]=ERi[∏i∈Φct∖{c0}(μμ+μθrcαRi−α)]=ERi[∏i∈Φct∖{c0}(11+θrcαRi−α)]

In the above proof, Eq. (a) can be obtained from the fact that Ri and Hi are mutually independent. Eq. (b) follows from the property of exponential distribution, i.e., exp⁡(∑ihi)=∏iexp⁡(hi). Eq. (c) is due to the definition of expectation of Hi. Eq. (d) holds because Hi follows an exponential distribution with mean 1/μ3, i.e., fHi(hi)=μe−μhi. According to the PGFL (i.e., Definition 5) of PPP Φct, we can obtain

ℒIbc(sb)(e)=exp⁡(−λct∫R2(1−11+θrcαri−α)dri)(f)=exp⁡(−2πλct∫0∞(θrcαri−α1+θrcαri−α)ridri)=exp⁡(−2πλct∫0∞11+1θrcαri−αridri)(g)=exp⁡(−2πλct∫0∞(11+yα)y(θrcα)2/αdy)=exp⁡(−2πλctrc2θ2/α∫0∞y1+yαdy)(h)=exp⁡(−πλctrc2θ2/α⋅2α⋅Γ(2α)⋅Γ(1−2α))(i)=exp⁡(−λctrc2θ2/α2π2αsin(2π/α))

In Eq. (e), R2 is the area in which the interfering CUs locate. Eq. (f) converts the expression from orthogonal coordinates to polar coordinates. Eq. (g) follows by changing the variable yα=1θrcαri−α, i.e., y=rircθ1α, hence y belongs to (0,∞). Eq. (h) can refer to Eq. 3.241.4 ∫0∞xa−1(p+qxb)n+1dx=1bpn+1(pq)abΓ(ab)Γ(1+n−ab)Γ(1+n),[0<ab<n+1,p≠0,q≠0] of [42]. Eq. (i) follows from the Euler’s reflection formula Γ(x)⋅Γ(1−x)=πsin⁡(πx), where Γ(x)=∫0∞tx−1e−tdt,x>0 is the complete gamma function.

For the special case α=4, we have

ℒIbc(sb)=exp⁡(−λctrc2θπ22sin(π/2))

In Eq. (17), the LT of IbH at b0 is given as

ℒIbH(sb)=exp⁡(−2πλHt(sbPb)2/α∫dbrcθ1/α∞y1+yαdy)(19)

For the special case α=4, we have

ℒIbH(sb)=exp⁡(−2πλHtsbPb∫dbrcθ1/4∞y1+y4dy)(a)=exp⁡(−πλHtsbPb(π2−tan−1⁡(db2rc2θ)))

where (a) follows ∫A∞x1+x4dx=14(π−2tan−1⁡(A2)).

In Eq. (17), the LT of IbF at b0 is given as

ℒIbF(sb)=exp(−2πλFt(sbPb)2/α∫dbrcθ1/α∞y1+yαdy)(20)

5.2 Outage Probability of DUs Pd

We next analyze the outage probability of DUs in HD/FD mode. Consider a D2D transmission from a tagged DU dt0 to the other tagged DU dr0 in a distance Rd. Let SINRd(Rd,Id) denote the SINR between dr0 received dt0’s signal power Sd and its suffered interference signal power Id plus noise power σ2. Hence, the SINRd(Rd,Id) at dr0 can be expressed as

SINRd(Rd,Id)=SdId+σ2(21)

where σ2 is the noise power. In Eq. (21), Sd can be expressed as

Sd=PdHdRd−α(22)

where Pd is the transmission power of DU, Hd is the power fading coefficient between dt0 and dr0.

In Eq. (21), Id can be expressed as

Id=Idc+IdH+IdF+Ids(23)

where Idc=∑i∈ΦctPcHiRi−α, IdH=∑i∈ΦHt∖{dt0}PdHiRi−α, IdF=∑i∈ΦFt∖{dt0}PdHiRi−α is dt0’s received interference from the other transmitting CUs, HD and FD DUs, respectively. Hi and Ri are the power fading coefficient and distance between i and dr0, respectively. Besides, Ids=κPd𝟙FD is the self-interference due to the FD D2D transmission, κ is the self-interference cancellation factor, 𝟙FD is the indicator function which takes value 1 representing DU operating in FD mode and 0 representing DU operating in HD mode.

For the tagged transmitter dt0, the transmission is unsuccessful if SINRd(Rd,Id) at dr0 is smaller than a certain SINR threshold θ. Let Pd denote the outage probability of dt0, which is defined as the mean value of P([SINRd(Rd,Id)]<θ), i.e.,

Pd=EId,Rd[P(SINRd(Rd,Id)<θ)]=∫0∞EId[P(SINRd(rd,Id)<θ|rd)]⋅fRd(rd)drd(24)

where fRd(rd) is the PDF of Rd. Below, we express fRd(rd) and EId[P(SINRd(rd,Id)<θ|rd)].

Recall that the DU transmits to its nearest DU. Given the tagged DU dr0 in the origin and a nearest distance rd, there is no DU closer than rd, which means that there is no DU in the disk b(dr0,rd). According to the definition of PPP Φda (i.e., Definition 1), the PDF that Rd is not smaller than rd [41] can be derived as

P(Rd>rd)=P(No device closer than rd)=P[Φda(|Sb|)=0]=exp(−λda|Sb|)(25)

where |Sb|=πrd2 is the area of b(dr0,rd).

Let FRd(rd) denote the CDF of Rd. FRd(rd) can be expressed as

FRd(rd)=P(Rd≤rd)=1−P(Rd>rd)=1−exp(−λdaπrd2)(26)

Further, fRd(rd) can be obtained by taking derivative of FRd(rd) with respect to rd, i.e.,

fRd(rd)=dFRd(rd)drd=2πλdardexp(−λπrd2)(27)

Then, we express EId[P(SINRd(rd,Id)<θ|rd)] as

EId[P(SINRd(rd,Id)<θ|rd)]=EIdc,IdH,IdF[P(PdHdrd−αIdc+IdH+IdF+Ids+σ2<θ|rd)]=1−exp(−sdσ2)exp(−sdIds)ℒIdc(sd)ℒIdH(sd)ℒIdF(sd)(28)