An Efficient and Provably Secure SM2 Key-Insulated Signature Scheme for Industrial Internet of Things

1  Introduction

In recent years, the Industrial Internet of Things (IIoT), a core subset of the Internet of Things (IoT) [1,2], has seen rapid development and has brought substantial and sustainable advancement to industries [3]. The IIoT is a technology that connects sensors, smart devices and actuators to the existing “Internet” through Wireless Sensor Networks (WSNs) [4]. In IIoT environment, all smart devices can monitor, transmit, collect, and analyze information automatically. Apparently, compared to traditional industries, IIoT achieves more efficient and sustainable production, significantly reducing operating costs and resource consumption [5]. Consequently, the implementation of IIoT-centered smart industry plays a significant role in promoting the development of traditional manufacturing industry to smart manufacturing industry [6]. However, despite IIoT brings plenty of benefits, it also faces thorny data processing issues. Of particular concern is the huge amount of data that is monitored and collected by IIoT smart devices. How to store and process the big data raise serious challenges [7]. Fortunately, cloud computing can provide us with a solution to appropriately deal with the aforementioned problems [8]. Cloud computing has broad network access and resource pooling, as well as formidable processing power and low cost advantages [9]. In IIoT-cloud computing environment, the challenges of big data collection, storage and processing can be properly solved [10].

Although the IIoT-cloud computing environment brings new ideas to solve the aforementioned problems, the authenticity and integrity of the data still need to be addressed urgently [5]. Generally, the channel between the cloud server and the smart device is considered undependable [11]. Therefore, ensuring that the authenticity of data is not maliciously intercepted and modified during transmission is a very difficult challenge. The digital signatures are a promising cryptographic primitive to address these challenges [12] (We give an example of a digital signature in Fig. 1). The data can be signed by the signer’s private key before it is sent from the smart devices to the cloud server. The recipient, in turn, can verify the integrity of the message by verifying the signature [4]. Consequently, a series of public key infrastructure (PKI) signature protocols were progressively presented [13].

Figure 1: Digital signature

In a PKI-based digital signature system, a trusted certification authority (CA) binds a user's identity to a corresponding public key using an issued certificate. In 1976, the first digital signature scheme was proposed by Diffie et al. [14]. It is through the paper [14] that the foundation of Public Key Cryptography (PKC) has been established for the first time. In the next decades, Public Key Infrastructure (PKI) is a popularly applied authentication architecture in traditional PKC-based schemes. Based on the aforementioned knowledge, the U.S. government has released a federal information processing standard: Digital Signature Standard (DSS). And the Chinese government adopts RSA digital signature scheme.

With the development of cryptography and computer technology, the commonly used 1024-bit RSA algorithms are facing serious security threats. In 1987, the Elliptic Curve Cryptography (ECC), which performs better than traditional cryptosystem (such as RSA and DSA) in security and efficiency, was proposed for the first time [15]. On December 17 2010, the public key cryptographic algorithm SM2, published by the Chinese State Cryptography Administration Office in 2010 [16], is also an ECC. Noticeable, it has been standardized by ISO/IEC in ISO/IEC 14888-3:2016/DAMD 1 [17]. Since the algorithm is based on ECC, its signature speed and secret key generation speed are faster than RSA. Compared with RSA algorithm, 256-bit SM2 password strength is already higher than 2048-bit RSA password strength. In order to demonstrate the advantages of SM2 over RSA more intuitively, we have made a comparison between the two dimensions of security and speed. The comparison results are listed in Tables 1 and 2. Thus, SM2 has better performance and security: high password complexity, fast processing speed, and less machine performance consumption. Now, SM2 algorithm is already widely executed in lots of fields, such as electronic authentication systems, E-Commerce systems and E-Government systems.

Another inevitable thorny problem is the key exposure problem since the signature operations are often executed frequently on insecure smart devices. It is obvious that key exposure will lead to disastrous consequences. The primitive of key-insulated was given by Dodis et al. in 2002 [18] for the first time. This cryptographic primitive effectively deals with the problem of catastrophic key exposure. The signer’s temporary signing key completes the key evolution with the assistance of the helper. Without the helper providing an update message, the signer’s key cannot be updated from the last time period to the current time period. With the helper’s key secure, an adversary can only forge the signature scheme for the current time period rather than the next one. After that, A strong key-insulated signature scheme was proposed by Dodis et al. [19]. Then, a number of well-designed key-insulated schemes were gradually constructed based on the work of Hanaoka et al. [20–22]. It is worth noting that the scheme proposed by Zhou et al. [22] does not have the nature of strong key-insulated. This means that an adversary can forge a signature as a legitimate user if the helper’s key is cracked. Therefore, Weng et al. [23] proposed a promising idea, namely secure key-updates. At present, this idea has been widely applied.

Given the above analysis, it faces the key exposure issue when the SM2 digital signature algorithm is integrated into the IIoT-cloud computing environment. This problem has attracted widespread attention from domestic and international authors [24,25]. In order to address the thorny issue of key exposure mentioned above, an efficient and provable secure key-insulated signature scheme based on SM2 (SM2-KI-SIGN) is proposed by us in the IIoT-cloud environment now. Our scheme is inspired by the idea of secure key-updates [23]. Our scheme also has the properties of strong key-insulated and secure key-updates. However, it is more efficient than the Weng et al. [23] due to the use of Elliptic Curve Cryptography (ECC).

Our core contributions in this paper are as follows:

1)   Introduction of an efficient and secure key-insulated signature scheme based on the SM2 cryptosystem, termed SM2-KI-SIGN;

2)   Demonstration that SM2-KI-SIGN achieves EUF-CMA (existential unforgeability under chosen message attacks) and has the key-insulated property, thereby efficiently mitigating the key exposure issue;

3)   Empirical validation of the efficiency and applicability of SM2-KI-SIGN through specific experimental simulations and performance assessments.

The organization is illustrated in this paragraph. In Section 2, we demonstrate some corresponding preliminaries such as elliptic curve, security assumption, and system framework. In Section 3, the concrete construction of SM2-KI-SIGN is provided. In Section 4, the associated security proof, the theoretical as well as experiment evaluation is demonstrated. Finally, Section 5 gives a summary of this paper.

2  Preliminaries

2.1 Elliptic Curve Discrete Logarithm (ECDL) Problem

Set E (Fq) as an elliptic over Fq where G∈E(Fq).There are two points P,Q∈E(Fq) of order q. Besides Q is a multiplicity of points of P. If there exists a positive integer l∈[0,q−1] that makes Q=l⋅P, then obtaining the value of l from P and Q is the ECDL problem.

2.2 ECDLP Assumption

There is a P.P.T algorithm 𝒜 has advantage at least ε to solve ECDL problem in E(Fq).

Pr[A(P,Q)=l|Q=l⋅P,l∈Zq∗]⩾ε

2.3 Bilinear Pairings

Let G be an addictive group and GT be a multiplicative group. G and GT has the equivalent prime order q. P is one of the generators of G. The bilinear map e:G×G→GT satisfies the below properties:

1)   Bilinearity: ∀m,n∈Zq∗, e:(mP,nP)=e:(P,P)mn.

2)   Non-degeneracy: e:(P,P)≠1.

3)   Computability: There exists an algorithm to calculate bilinear map e:G×G→GT.

2.4 Elliptic Curve Cryptography

In recent decades, Elliptic Curve Cryptography (ECC) has been widely studied and applied. In 1985, a mathematician named Victor Miller studied elliptic curves in cryptography and hypothesised that it was highly unlikely that exponential calculus methods would work for elliptic curves. ECC is a public key cryptography method based on the algebraic structure of elliptic curves over a finite field, allowing the use of smaller keys to provide equivalent security. Elliptic curves have now been applied to tasks such as key negotiation, digital signatures, pseudo-random generators. ECC utilises smaller keys, which reduces storage and transmission consumption. Thus, ECC can be better adapted to the IIoT-cloud environment.

2.5 Notations

The notations presented in the SM2-KI-SIGN scheme are defined in Table 3.

2.6 Outline of SM2-KI-SIGN

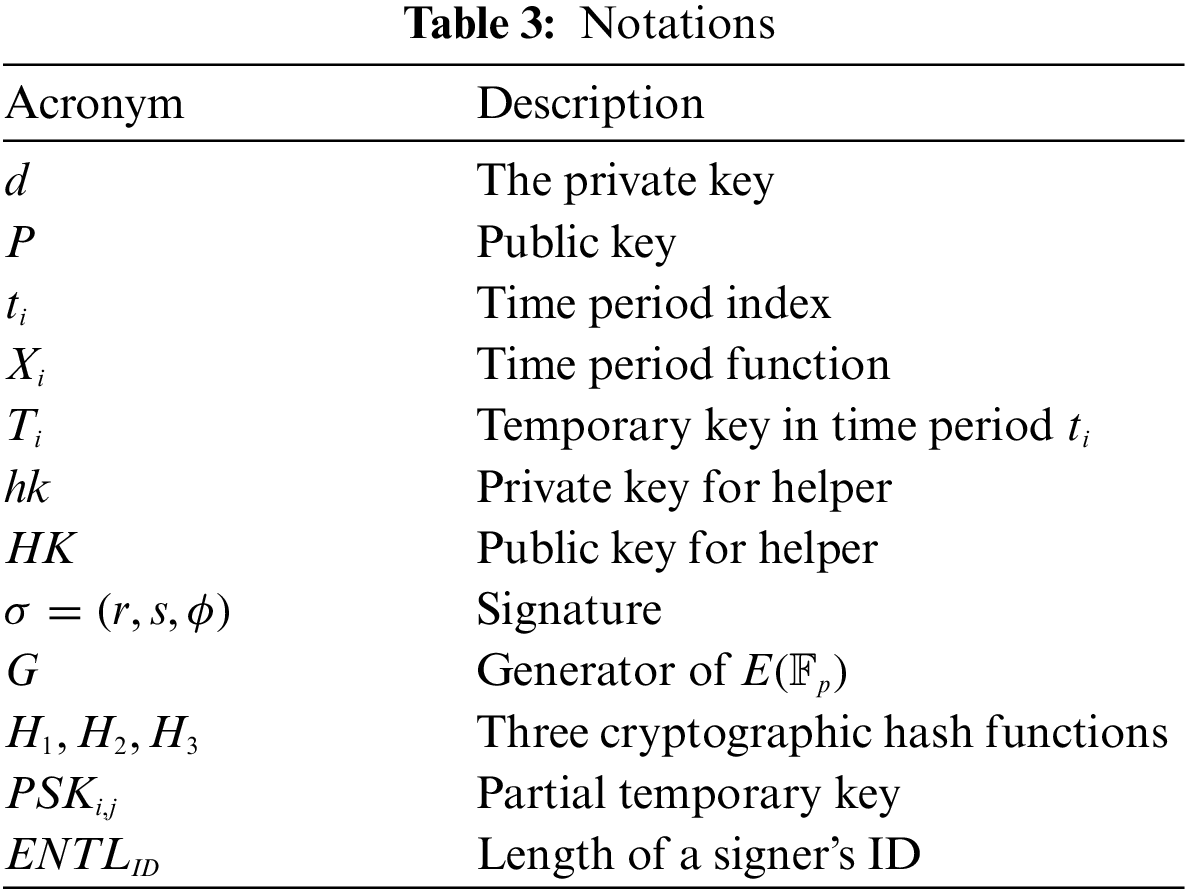
The SM2-KI-SIGN scheme consists of six different algorithms described below:

1)   Setup: Input the security parameter k, the KGC produces params.

2)   KeyGen: Given params, time period t, the user generates the public and private key (d,P) for him/her own as well as generates the public and private key for the helper (hk,HK).

3)   Upd∗: Input params, time period ti and tj, the helper output the partial temporary key PSKi,j.

4)   Upd: Input params, ti, Tj, and PSKi,j, the helper output Ti.

5)   Sign: Input the params, ti, Ti, and the message m, a signer generate a signature ϕ on m.

6)   Verify: Input the params, P, HK, and a message-signature pair (m,ϕ), a verifier output 1 when the signature is valid.

3  Our Proposed SM2-KI-SIGN Scheme

In this section, we further elaborate the detailed construction of SM2-KI-SIGN digital signature scheme we proposed. This scheme consists of six different algorithms as listed below. In these algorithms, Upd∗ and Upd are mainly designed for address the problem of key exposure. The flow of interaction between entities in the SM2-KI-SIGN is illustrated in Fig. 2.

Figure 2: Process of SM2-KI-SIGN scheme

1.    Setup: Input the security parameter k, the administrator operates as follows:

• Generate an elliptic curve y2=x3+ax+b over a finite field Fp as well as the discriminant Δ=4a3+27b2≠0. (p,a,b,q) are the parameters of the curve, where p and q are two large prime numbers. p is the size of Fp.

• Select G∈RE(Fp) as one of the generators. Besides let q be the order of G.

• Set the public parameters params=(p,a,b,q,G) and then output it.

• Select three cryptographic hash functions H1,H2,H3 and describe them with details here: H1:{0,1}∗→E(Fp), H2:{0,1}∗→Zq∗, and H3:{0,1}∗→{0,1}256.

2.    KeyGen: Input params, the user operates as follows:

• Select d∈RZq∗ as the private key.

• Calculate P=d⋅G and set P as the public key.

• Output the pair of the private and public key (d,P).

• Given the time period t0, the helper for the user executes as follows.

• Select hk∈RZq∗ as the private key for the helper.

• Calculate the public key for the helper HK=hk⋅G.

• Output (hk,HK).

• Calculate initial time period key T0=hk⋅X0 and time period function X0=H1(t0).

3.    Upd∗: Input two time period indices ti and tj, the helper for the user executes as below:

• Calculate Xi,j=H1(ti)−H1(tj).

• Calculate the partial temporary key PSKi,j=hk⋅Li,j.

• Return PSKi,j.

4.    Upd: Input a time period index ti, the partial temporary key PSKi,j and the temporary key Tj, the signer obtains the temporary key for the time period ti as below:

• Set Ti=Tj+PSKi,j.

• Return the temporary key Ti.

5.    Sign: Input params, the message m to be signed, time period index ti, as well as the private key d, the signer operates as follows:

• Calculate Z=H3(ENTLID‖ID‖a‖b‖G‖x‖y). ENTLID denotes the length of a signer’s ID.

• Calculate e=H2(m¯), where m¯=Z‖m.

• Select k∈RZq∗, then calculate K=k⋅G.

• Calculate K′=K+k⋅Ti=(x1,y1), r=x1+emodq.

• Calculate s=(1+d)−1⋅(k−r⋅d)modq.

• Calculate ϕ=(1+hk)−1⋅(k−r⋅hk)modq.

• Output the signature σ=(r,s,ϕ).

6.    Verify: Input params, the public key P=d⋅G, the public key of helper HK=hk⋅G, the message m as well as the related signature σ, and then the verifier operates as below:

• Calculate Z=H2(ENTLID‖ID‖a‖b‖G‖x‖y). The definition of ENTLID is the same as the aforementioned one.

• If r∉Zq∗, the verification fails and then terminate the algorithm.

• If s∉Zq∗, the verification fails and then terminate the algorithm.

• Set m¯=Z‖m, and calculate e=H2(m¯).

• Calculate t=(r+s)modq. If t=0, the verification fails and terminate the algorithm.

• Calculate ψ=(r+ϕ)modq. If ψ=0, the verification fails and terminate the algorithm.

• Calculate (x1,y1)=s⋅G+t⋅P+ϕ⋅Xi+ψ⋅Ti.

• Calculate R=(e+x1)modn, if R=r, the signature is valid and the verification passes, otherwise the verification fails.

7.    Correctness

(x1,y1)=s⋅G+t⋅P+ϕ⋅Xi+ψ⋅Ti=s⋅G+(r+s)⋅P+ϕ⋅Xi+(r+ϕ)⋅Ti=s⋅G+(r+s)⋅d⋅G+ϕ⋅Xi+(r+ϕ)⋅hk⋅Li=(1+d)⋅s⋅G+r⋅d⋅G+(1+hk)⋅ϕ⋅Xi+r⋅hk⋅Xi=(1+d)⋅(1+d)−1⋅(k−r⋅d)⋅G+r⋅d⋅G+(1+hk)⋅(1+hk)−1⋅(k−r⋅hk)⋅Xi+r⋅hk⋅Xi=(k−r⋅d)⋅G+r⋅d⋅G+(k−r⋅hk)⋅Xi+r⋅hk⋅Xi=k⋅G+k⋅Ti

4  Analysis

4.1 Security Proof

1)   Theorem 1. The SM2-KI-SIGN scheme we proposed is perfectly key-insulated against a P.P.T adversary 𝒜 in Game.

Proof: Given an ECDL problem instance (P,P0), ℬ computes a∈RZq∗, such that P0=a⋅P, where P is G and ℬ controls the stochastic prediction machine.

Setup: First, ℬ initializes 𝒜 with PKGC=P0, then it sends the public parameters params=(p,a,b,q,G) and (P,PKGC) to 𝒜.

Query: The interaction process between adversary 𝒜 and ℬ is as follows. 𝒜 can execute queries adaptively.

1)   H1 query: ℬ manages the list L1 with the tuple (ti,Xi). After 𝒜 delivered the (ti,Xi) query to the H1() oracle, ℬ retrieves the list L1 at the beginning. If L1 includes (ti,Xi), ℬ answers to 𝒜 with Xi. Otherwise, ℬ selects Xi∈RZq∗, returns Xi to 𝒜 and inserts the tuple (ti, Xi) into L1.

2)   H2 query: ℬ manages the list L2 with the tuple (e,m¯). After 𝒜 delivered the (e,m¯) query to the H2() oracle, ℬ retrieves the list L2 at the beginning. If L2 includes (e,m¯), ℬ answers to 𝒜 with e. Otherwise, ℬ selects e∈RZq∗, returns e to 𝒜 and inserts the tuple (e,m¯) into L2.

3)   H3 query: ℬ manages the list L3 with the tuple (ID, Z). After 𝒜 delivered the (ID, Z) query to the H3() oracle, ℬ retrieves the list L3 at the beginning. If L3 includes (ID, Z), ℬ answers to 𝒜 with Z. Otherwise, ℬ selects Z∈RZq∗, returns Z to 𝒜 and inserts a tuple (ID, Z) into L3.

4)   Extract-Private-Key: ℬ manages the list Lpri with the tuple (ID, d, hk, PSKi,j). After the identity ID is delivered to the oracle, then ℬ retrieves the list Lpri. If IDi=IDI, then ℬ terminate the simulation (Event E1). Otherwise Lpri includes (ID, d, hk, PSKi,j), ℬ gives 𝒜 answers with (d, hk, PSKi,j); If Lpri does not include (ID, d, hk, PSKi,j), ℬ chooses di, hki∈Zq∗ randomly, and computes PSKi,j′=hki⋅Hi,j. Then ℬ inserts the tuple (ID, di, hki, PSKi,j′) into Lpri. Lastly, ℬ answers to 𝒜 with (di, hki, PSKi,j′).

5)   Extract-Public-Key: ℬ manages the list Lpub with the tuple (ID, P, HK). After the identity ID is provided to this oracle, ℬ retrieves the list Lpub. If Lpub includes (ID, P, HK), ℬ answers to 𝒜 with (ID, P, HK). Otherwise Lpub does not include (ID, P, HK), ℬ makes queries to Lpar,Lpri and compute P=d⋅G and HK=hk⋅G as well as inserts the tuple (P, HK) into the Lpub. Lastly, ℬ answers to 𝒜 with (ID, P, HK).

6)   Public-Key-Replace: After 𝒜 makes a query of (ID,P′,HK′), ℬ retrieves the list Lpub. If Lpub does not include (ID, P, HK), ℬ first does a Extract-Public-Key query with identity ID, and then, sets P=P′, HK=HK′. To respond the query, ℬ will update the list Lpub with (P, HK).

7)   Signature query: After 𝒜 makes a query of (ID, M′), ℬ ℬ picks a number a∈Zq∗ at random, and sets hk=a, ϕ=(1+hk)−1⋅(k−r⋅hk)modq. After that, ℬ returns a valid signature θ to 𝒜.

Forgery: After polynomially bounded queries, 𝒜 forges a signature σ=(r1,s1,ϕ1) on message (ID∗,M) with non-negligible probability ε. If ID≠IDi≠IDI, the challenge of ℬ fails and stops (event E2); otherwise, the forgery succeeds. Then, depending on the forking lemma, 𝒜 repeats the aforementioned query using different hash values, two more signature pairs (r2,s2,ϕ2) and (r3,s3,ϕ3) can be generated.

(x1,y1)=sj⋅G+tj⋅P+ϕj⋅XI+ψj⋅TI, j=1,2,3

Set (x1,y1)=c⋅G+c⋅Ti. Because P0=a⋅P⋅G, Ti′=v⋅P⋅Xi, we can obtain c=sj+a⋅P⋅G+ϕj+v⋅P⋅Xi.

There are three unknown numbers c,a,v that are linearly independent of each other. Combining the three equations can find the value of a. ℬ successfully solves an ECDLP instance using the capabilities of 𝒜. To forge a pair of signatures successfully, the following three events need to be satisfied:

1). π1 represents that no partial private key query has been performed on it, i.e., the event E1 does not occur, Pr[π1]⩾(1−1qH1)qppk.

2). π2 The signature forgery under the message M∗ is valid.

3). π3 The forged signature is subject to ID-consistency, i.e., the event E2 does not occur, Pr[π3|π1∧π2]⩾1qH1.

Thus, ℬ uses the ability of 𝒜 in polynomial time with non-negligible probability ε′=Pr[π1∧π2∧π3]=Pr[π1]⋅Pr[π2|π2]⋅Pr[π3∧π2∧π1]⩾(1−1qH1)qppk⋅ε⋅1qH1 successfully solves an ECDLP instance, which contradicts the ECDLP’s difficulty contradiction, so the scheme is able to resist the attacker’s 𝒜 adaptive selection existential forgery under the choice message attack.

2)   Theorem 2. The proposed SM2-KI-SIGN is strong key-insulated secure against adversary ℬ.

Proof: The adversary ℬ has the non-negligible probability ε′⩾(1−1qH1)qppk⋅ε⋅1qH1.

The proof is same as those of Theorem 1, so we omit the proof here.

3)   Theorem 3. The SM2-KI-SIGN scheme we proposes in this paper has secure key updates.

Proof: As to any period indices ti and tj, the update key PSKi,j can be evolved from Ti and Tj.

4)   Theorem 4. The proposed SM2-KI-SIGN is secure against EUF-CMA.

Proof: At first, assume that a P.P.T adversary 𝒜 can exchange information with the signer. Thus, L,r and s,ϕ can be viewed by 𝒜 in the key-insulated signature generating step because of s=(1+d)−1⋅(k−r⋅d)modq and ϕ=(1+hk)−1⋅(k−r⋅hk)modq. 𝒜 obtains the value of r′. If 𝒜 wants to obtain d and hk from s and ϕ, he/she must get the value of k. Although 𝒜 knows L=k⋅G+k⋅Ti, it is a ECDLP to calculate k from K. If ECDLP is difficult to solve, then the private key cannot be received by 𝒜 when he/she exchanges information with the signer. In our proposed SM2-KI-SIGN signature scheme, the signing and verification equations we designed are consistent with the SM2 digital signature scheme. The SM2-KI-SIGN key-insulated signature scheme we proposed is unforgeable under the EUF-CMA attack, since the SM2 signature scheme satisfies EUF-CMA.

4.2 Performance Comparison

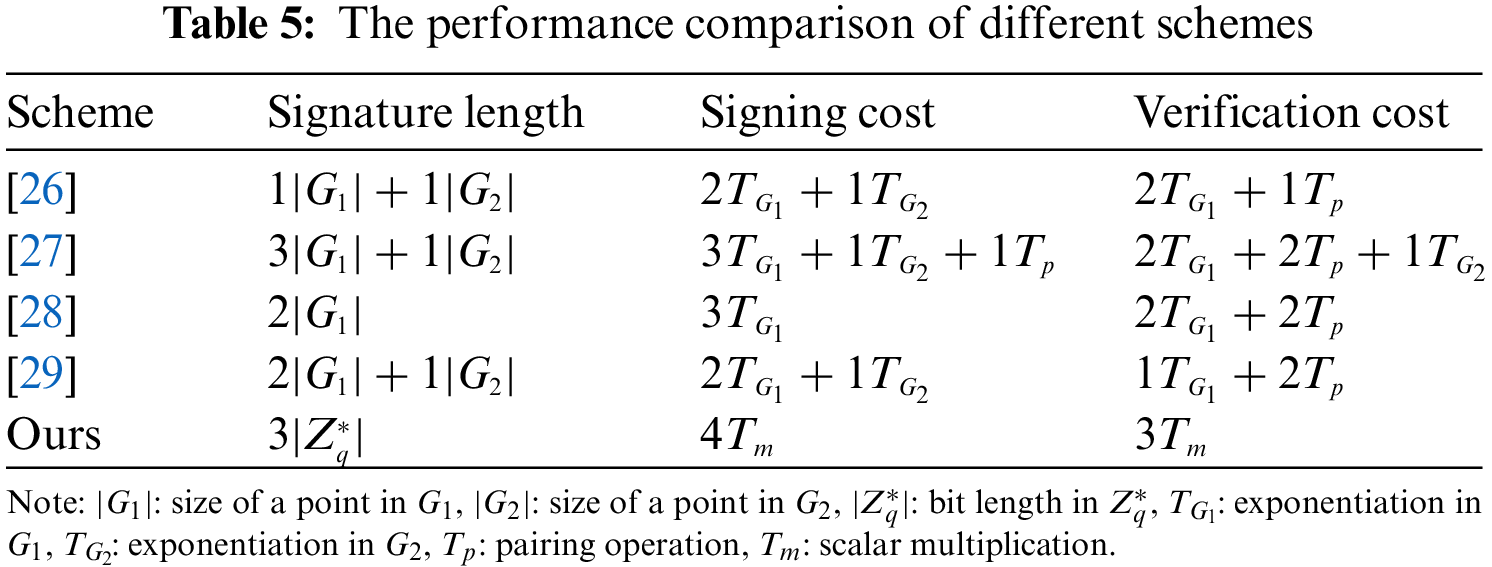
To certify the efficiency and feasibility of the proposed SM2-KI-SIGN scheme, we compare it with the existing works in this subsection. The comparison results are demonstrated in figures and tables.

In Table 4, we summarise and compare the properties between SM2-KI-SIGN scheme and other relevant schemes. We compare the existing schemes from three dimensions: strong key-insulated, secure key-updates and security assumption in Table 4. Here, it should be noted that the symbol “✓” indicates that the scheme satisfies this corresponding property, as well as the symbol “×” means that this capability cannot be achieved by this scheme. Apparently, our proposed SM2-KI-SIGN scheme can satisfy all properties. And this can be proven secure under standard ECDLP assumptions which is weaker than other security assumptions.

Then, a simulation experiment that runs on a Windows 10 computer equipped with an Intel Core i7-6700@2.60-GHz processor, as well as 8 GB, is given in this section. Then, it is implemented in IDEA with Java pairing-based cryptography (JPBC) library. To achieve the same security level as 1024-bit RSA, the super-singular curve y2=x3+x (mod p) with an embedding degree of 2 is utilized, where q=2159+217+1 is a 160-bit Solinas prime and p=12q⋅r−1 is a 512-bit prime. As to the ECC-based scheme, in order to offer the security with the equivalent level, we used the Koblitz elliptic curve y2=x3+a⋅x+b defined on F2163 providing the ECC group. In Table 5, a theoretical evaluation of the signature length, signing cost, as well as verification cost is given. Besides the notations of required signature length and cost of signing and verification are also enumerated in the footnote of Table 5.

Compared with the existing schemes especially the schemes listed here, our scheme has more advantages in cost. This advantage makes SM2-KI-SIGN scheme more suitable for untrusted channels in IIoT-cloud computing environment. At the same time, we show a cost comparison of SM2-KI-SIGN with other schemes [26–29] in Fig. 3.

Figure 3: Comparison of cost

5  Conclusions

This paper presented the first key-insulated digital signature scheme SM2-KI-SIGN based on the SM2 algorithm. The proposed SM2-KI-SIGN scheme can effectively reduce the risk of key exposure due to untrusted channels in IIoT-cloud computing environment. We first gave a formal outline of the scheme. Following this, a concrete scheme and the formal security proof under the ECDLP assumption in the random oracle model were given. Finally, according to the theoretical analysis and simulation experiments, the SM2-KI-SIGN scheme is more efficient and practical than other related key-insulated works. In the current research field, SM2-KI-SIGN introduces a method to make up for the key exposure defects of existing SM2 signature algorithms. On the other hand, our work can provide a new idea for future commercial digital signature schemes.

Acknowledgement: We have already revised the Acknowledgement section in the manuscript.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China (Nos. 62072074, 62076054, 62027827, 62002047), the Sichuan Science and Technology Innovation Platform and Talent Plan (Nos. 2020JDJQ0020, 2022JDJQ0039), the Sichuan Science and Technology Support Plan (Nos. 2020YFSY0010, 2022YFQ0045, 2022YFS0220, 2023YFG0148, 2021YFG0131), the YIBIN Science and Technology Support Plan (No. 2021CG003), the Medico-Engineering Cooperation Funds from University of Electronic Science and Technology of China (Nos. ZYGX2021YGLH212, ZYGX2022YGRH012).

Author Contributions: study conception and design: Senshan Ouyang, Baichuan Shao and Yang Zhao; analysis and interpretation of results: Xiang Liu, Lei Liu, Shangchao Wang; draft manuscript preparation: Senshan Ouyang and Baichuan Shao; figures and tables production: Baichuan Shao.

Availability of Data and Materials: Our current research is limited to algorithm design and analysis, and has not yet applied it to practical scenarios, so we have not yet addressed the source and use of data and materials.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Chen, J., Liu, G., Liu, Y. (2020). Lightweight privacy-preserving raw data publishing scheme. IEEE Transactions on Emerging Topics in Computing, 9(4), 2170–2174. [Google Scholar]

2. Chen, J., Liu, Y., Xiang, Y., Sood, K. (2021). RPPTD: Robust privacy-preserving truth discovery scheme. IEEE Systems Journal, 16(3), 4525–4531. [Google Scholar]

3. Boyes, H., Hallaq, B., Cunningham, J., Watson, T. (2018). The Industrial Internet of Things (IIoTAn Analysis Framework. Computers in Industry, 101(8), 1–12. [Google Scholar]

4. Xiong, H., Mei, Q., Zhao, Y. (2019). Efficient and provably secure certificateless parallel key-insulated signature without pairing for IIoT environments. IEEE Systems Journal, 14(1), 310–320. [Google Scholar]

5. Sisinni, E., Saifullah, A., Han, S., Jennehag, U., Gidlund, M. (2018). Industrial Internet of Things: Challenges, opportunities, and directions. IEEE Transactions on Industrial Informatics, 14(11), 4724–4734. [Google Scholar]

6. Yu, K., Tan, L., Aloqaily, M., Yang, H., Jararweh, Y. (2021). Blockchain-enhanced data sharing with traceable and direct revocation in IIoT. IEEE Transactions on Industrial Informatics, 17(11), 7669–7678. [Google Scholar]

7. Sadeghi, A. R., Wachsmann, C., Waidner, M. (2015). Security and privacy challenges in industrial Internet of Things. 2015 52nd ACM/EDAC/IEEE Design Automation Conference (DAC), IEEE. [Google Scholar]

8. Xiong, H., Zhao, Y., Hou, Y., Huang, X., Jin, C. et al. (2020). Heterogeneous signcryption with equality test for IIoT environment. IEEE Internet of Things Journal, 8(21), 16142–16152. [Google Scholar]

9. Kumar, M., Sharma, S. C., Goel, A., Singh, S. P. (2019). A comprehensive survey for scheduling techniques in cloud computing. Journal of Network and Computer Applications, 143(2), 1–33. [Google Scholar]

10. Li, Q., Yue, Y., Wang, Z. (2020). Deep robust cramer shoup delay optimized fully homomorphic for IIoT secured transmission in cloud computing. Computer Communications, 161(10), 10–18. [Google Scholar]

11. Hou, Y., Xiong, H., Huang, X., Kumari, S. (2021). Certificate-based parallel key-insulated aggregate signature against fully chosen key attacks for Industrial Internet of Things. IEEE Internet of Things Journal, 8(11), 8935–8948. [Google Scholar]

12. Wang, W., Xu, H., Alazab, M., Gadekallu, T. R., Han, Z. et al. (2021). Blockchain-based reliable and efficient certificateless signature for IIoT devices. IEEE Transactions on Industrial Informatics, 18(10), 7059–7067. [Google Scholar]

13. ElGamal, T. (1985). A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Transactions on Information Theory, 31(4), 469–472. [Google Scholar]

14. Diffie, W., Hellman, M. E. (2022). New directions in cryptography. In: Democratizing cryptography: The work of whitfield diffie and martin hellman, pp. 365–390. [Google Scholar]

15. Koblitz, N. (1987). Elliptic curve cryptosystems. Mathematics of Computation, 48(177), 203–209. [Google Scholar]

16. Administration, S. C. (2010). Public key cryptographic algorithm SM2 based on elliptic curves-Part 2: Digital signature algorithm. http://www.sca.gov.cn/sca/xwdt/2010-12/17/1002386/files/b791a9f908bb4803875ab6aeeb7b4e03.pdf [Google Scholar]

17. Administration, S. C. (2016). Our SM2 and SM9 digital signature algorithms officially become ISO/IEC international standard. http://www.sca.gov.cn/sca/qjd/2017-11/17/content_1019960.shtml [Google Scholar]

18. Dodis, Y., Katz, J., Xu, S., Yung, M. (2002). Key-insulated public key cryptosystems. In: International Conference on the Theory and Applications of Cryptographic Techniques, pp. 65–82. Springer. [Google Scholar]

19. Dodis, Y., Katz, J., Xu, S., Yung, M. (2003). Strong key-insulated signature schemes. International Workshop on Public Key Cryptography, Springer. [Google Scholar]

20. Hanaoka, G., Hanaoka, Y., Imai, H. (2006). Parallel key-insulated public key encryption. International workshop on public key cryptography, pp. 105–122. Springer. [Google Scholar]

21. Hanaoka, Y., Hanaoka, G., Shikata, J., Imai, H. (2005). Identity-based hierarchical strongly key-insulated encryption and its application. International Conference on the Theory and Application of Cryptology and Information Security, pp. 495–514. Springer. [Google Scholar]

22. Zhou, Y., Cao, Z., Chai, Z. (2006). Identity based key insulated signature. International Conference on Information Security Practice and Experience, pp. 226–234. Springer. [Google Scholar]

23. Weng, J., Liu, S., Chen, K., Li, X. (2006). Identity-based key-insulated signature with secure key-updates. International Conference on Information Security and Cryptology, pp. 13–26. Springer. [Google Scholar]

24. Hou, H. X., Yang, B., Zhang, L. N., Zhang, M. R. (2020). Secure two-party SM2 signature algorithm. Acta Electonica Sinica, 48(1), 1–8. [Google Scholar]

25. Zhang, Y., He, D., Zhang, F., Huang, X., Li, D. (2020). An efficient blind signature scheme based on SM2 signature algorithm. International Conference on Information Security and Cryptology, pp. 368–384. Springer. [Google Scholar]

26. Karati, A., Islam, S. H., Karuppiah, M. (2018). Provably secure and lightweight certificateless signature scheme for IIoT environments. IEEE Transactions on Industrial Informatics, 14(8), 3701–3711. [Google Scholar]

27. Chen, J., Wang, L., Wen, M., Zhang, K., Chen, K. (2021). Efficient certificateless online/offline signcryption scheme for edge IoT devices. IEEE Internet of Things Journal, 9(11), 8967–8979. [Google Scholar]

28. Cha, S. C., Chen, J. F., Su, C., Yeh, K. H. (2018). A blockchain connected gateway for BLE-based devices in the internet of things. IEEE Access, 6, 24639–24649. [Google Scholar]

29. Reddy, P. V., Gopal, P. (2017). Identity-based key-insulated aggregate signature scheme. Journal of King Saud University-Computer and Information Sciences, 29(3), 303–310. [Google Scholar]