Resource Allocation for IRS Assisted mmWave Wireless Powered Sensor Networks with User Cooperation

1  Introduction

The rapid expansion of the number of mobile devices has brought higher requirements for wireless applications, such as more extensive radio coverage, lower latency, higher data transmission rates and higher security, while the emergence of sixth-generation (6G) wireless technologies can perfectly meet such demands [1,2] describe the vision of future 6G communication and network architecture, which presents emerging technologies such as artificial intelligence, blockchain, quantum communications, integration of wireless information and energy transfer, integrated sensing and communication, intelligent reflecting surface and big data. Millimeter-wave (mmWave) communication has been widely regarded as a key technology of 6G, which owns ultra-wide bandwidth and high transfer speed advantages to meet the enormous capacity demand for 6G wireless communications [3,4]. An exhaustive survey of mmWave wireless communications for future 6G networks is described in [5], where the latest channel measurement, modeling and multiple input multiple output (MIMO) transceiver designs are summarized.

Also, energy harvesting (EH), as one of the main techniques to power future 6G wireless networks, has been introduced as an efficient method that allows wireless devices to capture the energy from external environments [6,7]. Radio frequency (RF) EH technique can enable an aggressive energy supply to the wireless devices (WDs) [8]. As an promising and emerging EH technology, wireless power communication networks (WPCN) are of great interest as they have the potential to provide wireless power to energy-constrained devices such as the internet of things (IoT) and wireless sensor networks (WSN) to ensure their operation [9,10]. Compared to the traditional battery-powered way, WPCN always provides more reliable and sustainable power replenishment. In WPCNs, the placement optimization of power and information access points is researched, where the WDs harvest the RF energy in the downlink and employ the harvested energy to transmit information to a base station in the uplink [11,12].

To improve the radio coverage and signal quality in a green way, an intelligent reflecting surface (IRS) has been proposed to reshape the signal propagation environment via passive reflecting arrays [13,14]. The transmitted signal can be reflected the receiver through the IRS and constitutes the received signal together with the signal transmitted by the direct link [15]. Thus, the reflected signal can be enhanced by properly adjusting the passive components of IRS [16,17].

Recently, some research on IRS-aided wireless powered sensor networks (WPSN) has been studied in [18–38]. For maximizing the sum throughput in an IRS-aided WPCN, the closed-form solution for the phase shifts of the wireless information transfer has been derived, where a low complexity scheme was proposed to reduce the computational complexity of the semidefinite programming (SDP) scheme [18]. Considering user cooperation (UC) in an IRS-assisted WPCN, the maximum throughput performance has been derived by jointly optimizing the power allocations, IRS phase shifts and the transmit time [19]. By obtaining a closed-form solution by the Lagrange dual method and the Karush-Kuhn-Tucker conditions in an IRS-aided WPSN, Chu et al. [20] optimally designed the bandwidth allocation and the transmit time schedule. Li et al. [21] have maximized the minimum throughput performance for IRS-aided UC in a WPCN. To simultaneously improve the performance of uplink information transmission and downlink energy transfer, Lyu et al. [22] investigated a hybrid-relaying self-sustainable IRS WPCN. Zhai et al. [23] has considered multicast transmissions in a game-theoretic way in an IRS-aided WPCN, where the closed-form optimal phase shifts have been derived. For a backscatter-assisted WPCN with an IRS, Ramezani et al. [24] have studied the maximization of total network throughput through a two-stage algorithm. In an IRS-assisted multiuser MISO WPCN, Zheng et al. [25] have maximized the weighted sum rate of all the energy-harvesting users by applying a block-structured optimization method. A novel dynamic IRS beamforming framework has been proposed to boost the sum throughput of an IRS-aided WPCN in [26]. In order to strictly guarantee device quality-of-service (QoS) requirements, Zeng et al. [27] have considered the non-linear energy harvesting in an IRS WPCN. In a multi-user IRS WPCN, Cao et al. [28] have maximized the system throughput by optimizing jointly the energy beamforming, phase shift and time allocation. To maximize the sum throughput by applying the Lagrange dual method, a closed-form solution has been derived for the optimal power allocation, transmission time slots and phase shift for IRS-aided wireless powered IoT system [29].

To tackle the issue of the uplink transmission of WDs in WPCNs depending on the harvested energy from the downlink, Wang et al. [30] proposed an energy efficient optimization method in IRS-assisted WPCN by the variable-substitution approach. In order to ensure fairness, Zeng et al. [31] studied a weighted sum throughput maximization in an active IRS-aided WPCN by applying three beamforming setups. Using the semidefinite relaxation method, Lyu et al. [32] considered a sum rate maximization for the IRS-aided WPCN by jointly iteratively optimizing the time scheduling and the phase shift. In the presence of eavesdropper, Cao et al. [33] proposed three secure modes in physical layer security of an IRS-aided WPC system, where asymptotic ergodic secrecy capacity is analyzed and closed-form expression is obtained. A new transmission policy for an IRS-assisted WPSN with certain phase shifts is proposed by maximizing the system sum throughput in [34], in which IRS can collect energy to achieve its self-sustainability. In a MISO transmission form, a practical IRS can work in EH with a power budget constraint, and then utilize the harvesting energy to sustain its operations in the signal reflecting phase [35]. Considering cognitive loT devices, two transmission policies are studied with a successive interference cancellation technique [36], where the interaction between primary and secondary networks is characterized by a Stackelberg game strategy. An IRS-aided wireless powered over-the-air computation Internet-of-Things network is investigated to propose a joint design of energy beamforming at the access point, downlink and uplink phase-shift matrices, as well as transmit power, in order to minimize the mean-squared error [37]. With the aid of an IRS, in wireless powered non-orthogonal multiple access (NOMA) IoT networks, by jointly optimizing the time allocation and phase shift matrices of wireless energy transfer and wireless information transfer, a novel resource allocation approach is proposed by maximizing the sum throughput in [38].

Integrating the IRS technology with sensor networks can achieve a self-sustaining system, specifically by embedding the IRS to the existing WPSN to reflect energy and information signals to improve the wireless energy transfer (WET) and wireless information transfer (WIT) capabilities of the WPSN. Also, to achieve a better performance with the IRS-assisted scheme, we consider a mmWave WPSN UC system in the uplink, i.e., one user not only completes his own signal transmission task, but also assists other users in completing signal transmission as a relay. Different from the existing works on the IRS-aided WPCN system, the research of transmission strategies in an IRS-assisted WPSN systems with UC in the mmWave band has not been made yet. We summarize our contributions as follows:

1.    First, an IRS has been used to improve the performance of the WPSN system with UC in the mmWave channel, where two single-antenna wireless devices can harvest energy radiated by a hybrid access point (AP) to support the separate information transmission to the AP. Here, the IRS play a role in promoting the system performance of the downlink wireless energy harvesting and the uplink wireless information transmission by energy and information reflection for the IRS, respectively.

2.    Second, it aims to maximize the weighted sum-rate through jointly optimizing the power, the time slots allocation and the IRS phase shift of the WET and WIT is used to evaluate the performance of the proposed system model. Since the original problem is non-convex with respect to the coupled variables of the power and the IRS phase shift, it is hard to solve directly.

3.    Finally, to deal with the non-convexity of the original formulated problem, the semidefinite programming relaxation (SDR) technique is applied to convert the weighted sum-rate maximization (WSRM) problem to a convex optimization framework, which can obtain the global optimal solution. Simulation results proved that the IRS and the UC can improve the system performance compared with the two latest benchmarks.

The rest of the paper is organized as follows. Section 2 introduces the system model of an IRS-aided WPSN system with mmWave channel. In Section 3, a weighted throughput maximization problem with user cooperation is discussed carefully, and we develop a SDR-based algorithm to solve the original problem. In Section 4, our simulation results demonstrate the effectiveness of the proposed SDR algorithm. In Section 5, the paper is summarized.

2  System Model

As shown in Fig. 1, we investigate an IRS-aided mmWave WPSN system, which contains a single-antenna AP and two single-antenna wireless users (WUs). Due to the constrained energy of devices, the wireless communication links (WCLs) of harvesting energy in the UL are established between AP and WUs. In the downlink (DL), information signals also can be transmitted through these links. Without loss of generality, we assume that WU2 is used as a relay between WU1 and AP in the meantime. An IRS with N dynamically adjustable elements is equipped to strengthen WCLs, and only one-time signal reflection by the IRS is considered owing to the path loss. The phase shift matrix of IRS is defined as θ=[θ1,…,θN] and Θ=diag(ejθ1,…,ejθn,…,ejθN). Denote g∈CN×1 and gRk∈CN×1 as the mmWave channel matrix for the channel of AP to IRS, IRS to WUk, where k=1,2. hk, h21 are the channel between AP and WUk, WU1 and WU2, k=1,2, and all channel gains are g=‖g‖2, gRk=‖gRk‖2, ζk=|hk|2, ζ21=|h21|2, respectively. Also, we assume that all channels between different transceiver and receiver are independent and identically distributed complex Gaussian distribution of 𝒞𝒩(0,κ2), where κ2 depending on the path loss. In this paper, our research focuses on finding a suitable optimal algorithm for IRS phase shifting, the power, the time slots allocation and deriving an upper bound on the weighted sum-rate performance of the system model under study. Therefore, we assume that CSI is perfect and we can get the CSI acquisition method under the IRS assisted WPSN system. In the paper, we further elaborate on the reasons for assuming a perfect CSI and how to obtain it.

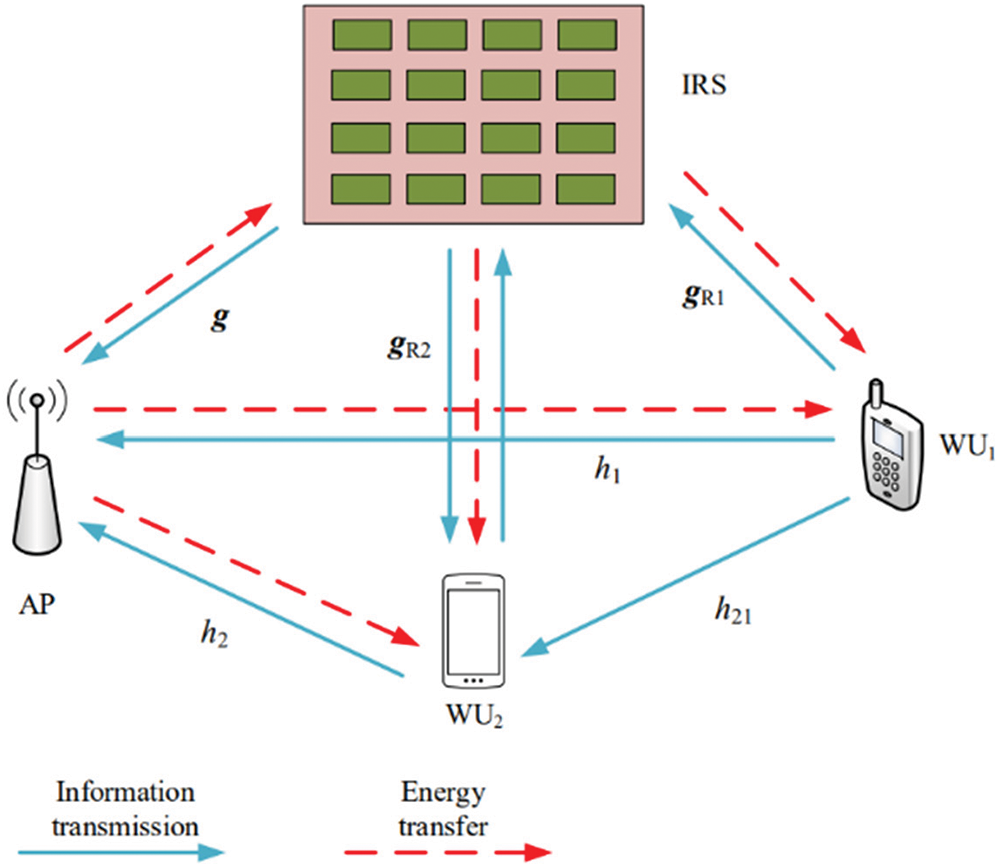
Figure 1: The IRS-aided mmWave WPSN system model

For the mmWave channel of AP to IRS, IRS to WUk, k=1,2, the antenna response can be written as

a(ϕil,θil)=1N[1,…,ej2πλd(psin⁡ϕilsin⁡θil+qcos⁡θil),…,ej2πλd(N−1)sin⁡ϕilsin⁡θil+(N−1)cos⁡θil)]T,(1)

where ϕ and θ represent the incident signal’s angles of azimuth and elevation, λ and d are the wavelength and antenna spacing, respectively. Therefore, the mmWave channel matrix written as

H=ρNtNr∑l=1Lαilar(ϕilr,θilr)at(ϕilt,θilt)H(2)

where Nt and Nr represent the number of transmitting and receiving antennas, and L denotes the total number of paths, including one LOS direct path and (L−1) NLOS paths. ρ is the path loss and ρ=δd−γ, where δ, d, and γ are a constant, the geographical distance and the path-loss exponent, respectively. The WET and WIT processes are considered within the time period T that usually be assumed T=1s. In the WET, the AP charges WUs during time period τ0T(τ0∈(0,1]) in the DL. At the same time, part of the energy transmitted by the AP will be reflected to the WUs through the IRS, and the received energy contains two parts, i.e., AP → WUk, AP → IRS → WUk, k=1,2. Thus, the received information signals at WUs can be expressed as

yk=p0(gRkHΘ1g+hk)x+nk,k=1,2,(3)

where p0 is the transmit power of the AP, and the Θ1=diag(a1,1,…,a1,N) denotes the coefficient matrix of reflected energy by IRS. Define a1,n≜ejθ1,n, θ1,n denotes the phase shift of the IRS and |a1,n|=1,n∈[1,N], x is the energy signals satisfying x∼𝒞𝒩(0,1), and n(t)∼𝒞𝒩(0,σk2) at WUk, k=1,2. Hence, the harvested energy at WUk was donated as

Ek=ητ0Tp0|gRkHΘ1g+hk|2,k=1,2,(4)

where η represents the efficiency of energy harvesting during the WET phase.

The time of the WIT phase is (1−τ0)T, where WUs transmit the information to the AP and the IRS by using the harvested energy. In the WIT scenario, we assume that WU1 and WU2 can transmit information signals directly to the AP simultaneously, and WU2 can act as a passive relay, reflecting some information signals from WU1 to AP. As shown in Fig. 2, to further express this process, the time allocation of the WIT phase is divided into three sub-phases:

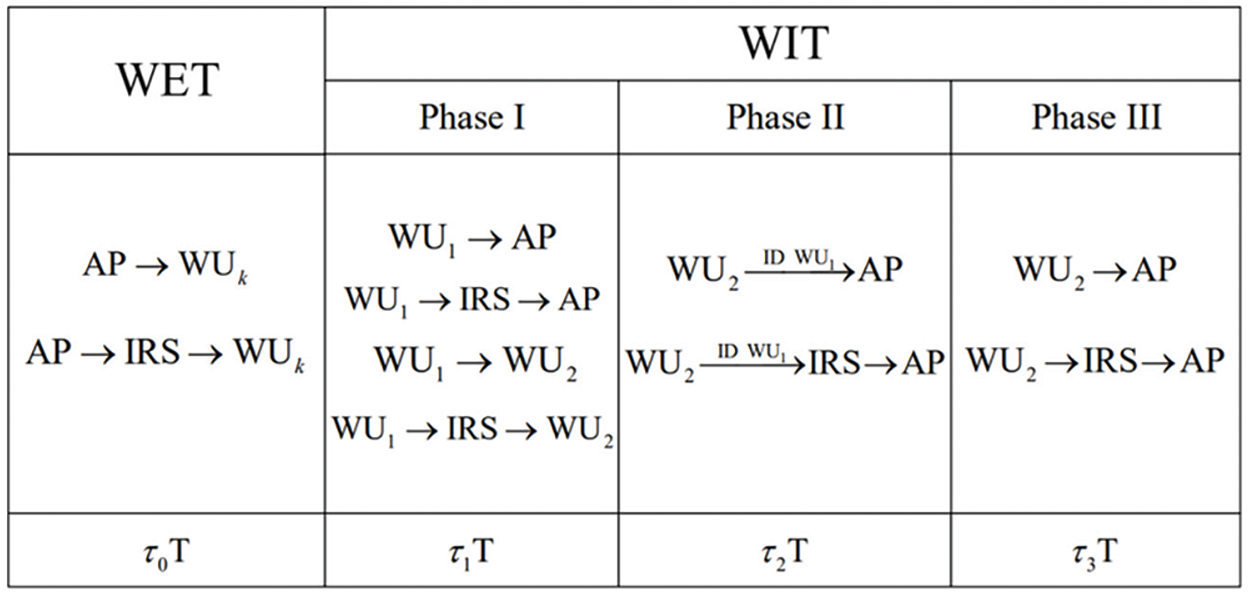
Figure 2: System time allocation of WET and WIT

1.    In the first sub-phase, i.e., τ1T, WU1 transmits the information signal to the AP and WU2 using the harvested energy (i.e., WU1 → AP, WU1 → WU2). Also, the signal of WU1 is reflected to the AP and WU2 via the IRS (i.e., WU1 → IRS → AP, WU1 → IRS → WU2);

2.    In the second sub-phase, i.e., τ2T, WU2 first decodes WU1’s information signal and then forwards it to the AP and the IRS (i.e., WU2 ⟶ID WU1 AP, WU2 ⟶ID WU1 IRS → AP);

3.    In the third sub-phase, i.e., τ3T, WU2 transmits the information signal to the AP and the IRS (i.e., WU2 → AP, WU2 → IRS → AP).

In the first sub-phase, the harvested energy obtained in WET is used in WET and the transmit power of WU1 is

p1=E1τ1T=ητ0p0|gR1HΘ1g+h1|2τ1.(5)

Then, the information signal received at AP and WU2 are expressed respectively as

yAP,1=p1(gR1HΘ2g+h1)s1+nAP,(6)

y2,1=p1(gR1HΘ2gR2+h21)s1+n2,(7)

where s1 is the information signal from WU1 with E[|s1|2]=1, Θ2=diag(a2,1,…,a2,N) denotes the IRS’s reflection coefficient matrix with |a2,n|=1,n∈[1,N], nAP and n2 denote the received noise power of the AP and WU2 with variance σAP2 and σ22, respectively. The achievable rates in this phase are expressed as

RAP,1direct=τ1log⁡(1+p1|gR1HΘ2g+h1|2σAP2),(8)

R21direct=τ1log⁡(1+p1|gR1HΘ2gR2+h21|2σ22).(9)

In the second sub-phase, the signal received at AP given by

yAP,1=p2(2)(gR2HΘ3g+h2)s¯1+nAP,(10)

where p2(2) is the transmit power of WU2 within the subphase, Θ3=diag(a3,1,…,a3,N) denotes the reflection coefficient matrix with |a3,n|=1,n∈[1,N], s¯1 represents the transmit information symbol of WU2 associated with WU1’s information. Then, the achievable direct rates from WU2 to the AP are expressed as

RAP,2relay=τ2log⁡(1+p2(2)|gR2HΘ3g+h2|2σAP2).(11)

The information signals transmitted from WU1 to AP have four different paths, where the signal of AP in the first path is the direct link from WU1 (i.e., WU1 → AP), the signal of AP in the second path is secondarily transmitted by WU2 with proposed UC scheme (i.e., WU2 ⟶ID WU1 AP), the signal of AP in the third path is the direct link from WU1 via IRS (i.e., WU1→ IRS → AP), and the signal in the fourth path is secondarily transmitted by WU2 with UC scheme via IRS to AP (i.e., WU2 ⟶ID WU1 IRS → AP). Therefore, the achievable rate from WU1 to AP is given by

RAp,1=min(Rdirect,1,R21direct),(12)

where

Rdirect,1=RAP,1direct+RAP,2relay.(13)

In the third sub-phase, the information signal received at AP is written as

yAP,3=p2(3)(gR2HΘ3g+h2)s2+nAP,(14)

where p2(3) denotes the transmit power of WU2 in this sub-phase and the achievable rate from WU2 to AP is expressed as

RAP,2=τ3log⁡(1+p2(3)|gR2HΘ3g+h2|2σAP2).(15)

The energy obtained by WU2 in τ0T time period should be greater than that consumed in the latter two sub-phases, so that the later work can be completed normally. So, there is

τ2Tp2(2)+τ3Tp2(3)≤ητ0Tp0|gR2HΘ1g+h2|2.(16)

According to the above transmission process, the time period τ1, τ1, τ2, and τ3 in this WPSN need to satisfy the following time constraints written as

τ0+τ1+τ2+τ3≤1,{τ0,τ1,τ2,τ3}≥0.(17)

3  Weighted Throughput Maximization with User Cooperation

Using the derivation and definition from the previous step, a WSRM problem is formulated based on a UC scheme and then solved by jointly optimizing the phase shift matrices, time allocation, and power allocation. First, the WSRM problem is given by

(P1)maxτ,p,Θ1,Θ2,Θ3αRAP,1+(1−α)RAP,2s.t.τ2p2(2)+τ3p2(3)≤ητ0p0|gR2HΘ1g+h2|2,τ0+τ1+τ2+τ3≤1{τ0,τ1,τ2,τ3}≥0,{p2(2),p2(3)}≥0,|ai,n|=1,i=1,2,3,n∈[1,N],(18)

where α and 1−α are preference constants of RAP,1 and RAP,2, respectively. Problem (P1) is not convex due to the objective function and the constant modulus constraint in the phase shift matrices Θ1,Θ2,Θ3, which leads to the time allocation τ={τ0,τ1,τ2,τ3}, and power allocation p={p2(2),p2(3)} cannot be solved efficiently.

For the non-convexity of problem (P1), we can introduce some transformation forms for the phase shift matrices to tackle it. So, we have

|gRkHΘ1g+hk|2=|a1g^Rk+hk|2,k=1,2,(19)

|gR1HΘ2gR2+h21|2=|a2g^21+h21|2,(20)

|gR2HΘ3g+h2|2=|a3g^R2+h2|2,(21)

where g^Rk=diag(gRkH)g and g^21=diag(gR1H)gR2. The optimal solution Θ2opt can be obtained by maximizing the signal-to-noise ratio (SNR), and it is equivalent to maximizing the expression to the right of equation in (20) with the constraint |a2,n|=1,n∈[1,N].By using the triangle inequality, we can obtain the upper bound of the objective function in (20) as

|a2g^21+h21|≤∑i=1N|a2,i[g^21]i|+|h21|=∑i=1N|[g^21]i|+|h21|,(22)

where [g^21]i denotes the i-th element of g^21.The equal sign in the formula will hold when θ2,i=arg⁡(h21)−arg⁡([g^21]i) and a2,i=ejθ2,i,i∈[1,N], where arg(·) is the phase operator, and the optimal solutions a2opt and Θ2opt can be obtained. It should be noted that according to the asymptotical orthogonality of MIMO channels [39], the reflect path information can be abandoned in (6), i.e., we can reasonably consider the information that AP can only receive directly from WU1 in the first sub-phase. Taking the similar operations for (21), we can also get the optimal solutions a3opt and Θ3opt.

Then, introducing auxiliary variables μ2=τ2p2(2) and μ3=τ3p2(3), another form of RAP,1direct, R21direct, RAP,2relay and RAP,2 can be expressed as

RAP,1direct=τ1log⁡(1+λ1τ0|a1g^R1+h1|2τ1),(23)

R21direct=τ1log⁡(1+λ2τ0|a1g^R1+h1|2τ1),(24)

RAP,2relay=τ2log⁡(1+λ3μ2τ2),(25)

RAP,2=τ3log⁡(1+λ3μ3τ3),(26)

where λ1=ηp0ζ1/σAP2, λ2=ηp0|a2optg^21+h21|2/σ22 and λ3=|a3optg^R2+h2|2/σAP2. Thus, (16) can be reformed as

μ2+μ3≤ητ0p0|a1g^R2+h2|2.(27)

Define a¯1=[a1T1]T, g~Rk=[g^Rkhk]T,k=1,2, A1=a¯1a¯1H and GRk=g~Rkg~RkH. So from the modulus constraint of a1,n, n=1,…,N+1, we have [A1]n,n=1 and

|a1g^Rk+hi|2=tr(GRkA1),(28)

We further define B≜τ0A1⪰0 and the condition Bn,n=τ0,n=1,…,N+1 must hold. In the meantime, B needs to satisfy B⪰0 and rank(B)=1. Therefore, RAP,1direct, R21direct and the constraint in (25) can be reformed as

RAP,1direct=τ1log⁡(1+λ1tr(GR1B)τ1),(29)

R21direct=τ1log⁡(1+λ2tr(GR1B)τ1),(30)

μ2+μ3≤ηp0tr(GR2B).(31)

Accordingly, by introducing another auxiliary variable R^, RAP,1 can be recast as

τ1log⁡(1+λ1tr(GR1B)τ1)+τ2log⁡(1+λ3μ2τ2)≥R^,(32)

τ1log⁡(1+λ2tr(GR1B)τ1)≥R^.(33)

Due to the rank-one constraint causing the problem to be non-convex, so we use the SDR approach to remove this constraint, then (P1) can be reformulated as

(P3)maxR^,μ2,μ3,B,ταR^+(1−α)RAP,2s.t.(29),(30),(31),τ0+τ1+τ2+τ3≤1{τ0,τ1,τ2,τ3}≥0,{μ2,μ3}≥0,B⪰0,Bn,n=τ0,n=1,…,N+1.(34)

Here, the problem (34) is now a convex optimization problem. Thus, the global optimal solution can be obtained by CVX in Matlab [40,41], which is denoted as (R^opt,μ2opt,μ3opt,Bopt,τopt ). The computational complexity of the SDP relaxation scheme is n2N+9(2(N+1)3+(N+1)2+7(n+1)+n2), where n=O(2(N+1)2) [42].

Combined with the above derivation, we can further obtain the optimal values as

A1opt=Boptτ0opt,P2(2)opt=μ2optτ2opt,P2(3)opt=μ3optτ3opt,(35)

The rank-one solution may be obtained from the relaxed WSRM (P3). So we employ the eigenvalue decomposition for A1opt to obtain the a¯1, i.e., A1opt=ΨTΨH, where Ψ∈C(N+1)×(N+1) represents a unitary matrix, T∈C(N+1)×(N+1) represents a diagonal matrix. We can obtain a¯1=ΨT12ν, where ν is complex circularly symmetric Gaussian variables with ν∼𝒞𝒩(0,IN+1). Then, the optimal a1opt is identified by θ1,i=arg⁡([a¯1]i)and a1,i=ejθ1,i,i∈[1,N].

4  Simulation Results

The simulation results are presented to evaluate the performance of the user cooperation scheme in IRS-aided mmWave WPSN. The illustration of the system is shown in Fig. 3. We assume that AP and WUk are on the same level, and the distance between the IRS and this horizontal line is 4 meters and the distance between AP and IRS is d2=5 m. Finally, the settings of other parameters are shown in Table 1. In the specific simulation, some benchmark methods are introduced as the simulation comparison to show the superiority of the proposed method:

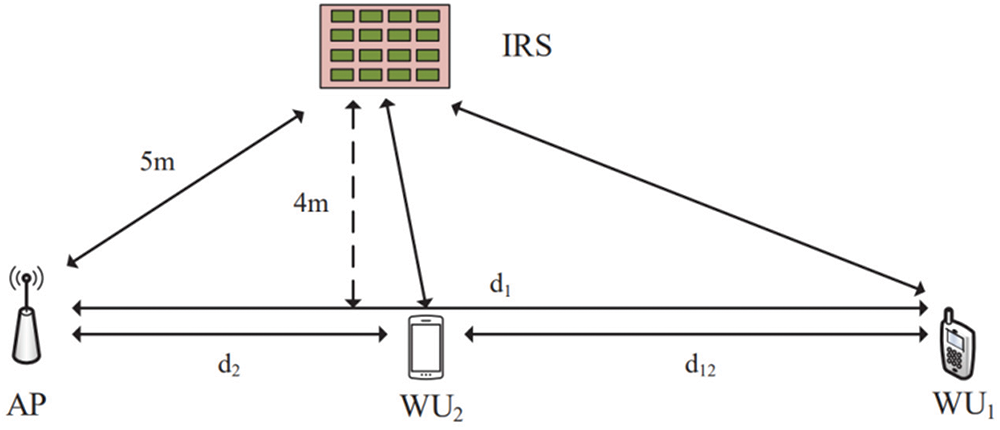
Figure 3: Simulation model

1.    IRS+UC: IRS helps WUs to harvest energy through reflection in the WET phase. In the WIT phase, IRS reflects signals from WUs to AP, and WU2 can receive and secondary transmit signals from WU1 to AP as a relay in the UC scheme.

2.    Non IRS+UC: Following [12], WUs only harvest energy through the direct link from AP in the WET phase and the UC scheme is considered in the WIT.

3.    IRS+Non UC: Following [26], Only IRS works and UC scheme is canceled.

4.    Non IRS+Non UC: There are no IRS and UC schemes in the system.

We first evaluate the sum throughput vs. the distance d1 between the AP and WU1 in Fig. 4. When d1 changes from 5 to 10 m, the channel between AP and WU1 will be influenced, which will affect the sum throughput. In this simulation, p0=30 dBm, N=25. Whether equipped with IRS or not, sum throughput using UC outperform the sum throughput without the UC scheme, which shows that the UC scheme can effectively improve sum throughput in IRS-aided mmWave WPSN. When d1=10 m, the gap of sum throughput between “IRS + UC” and “IRS + Non UC” or “Non IRS + UC” and “Non IRS + Non UC” become smaller compared with d1=5 m. This is because the efficiency of the UC scheme will be affected when the distance between wireless users is large. At the same time, it can be known that the improvement of sum throughput by only using the UC scheme is greater than that only equipping with IRS.

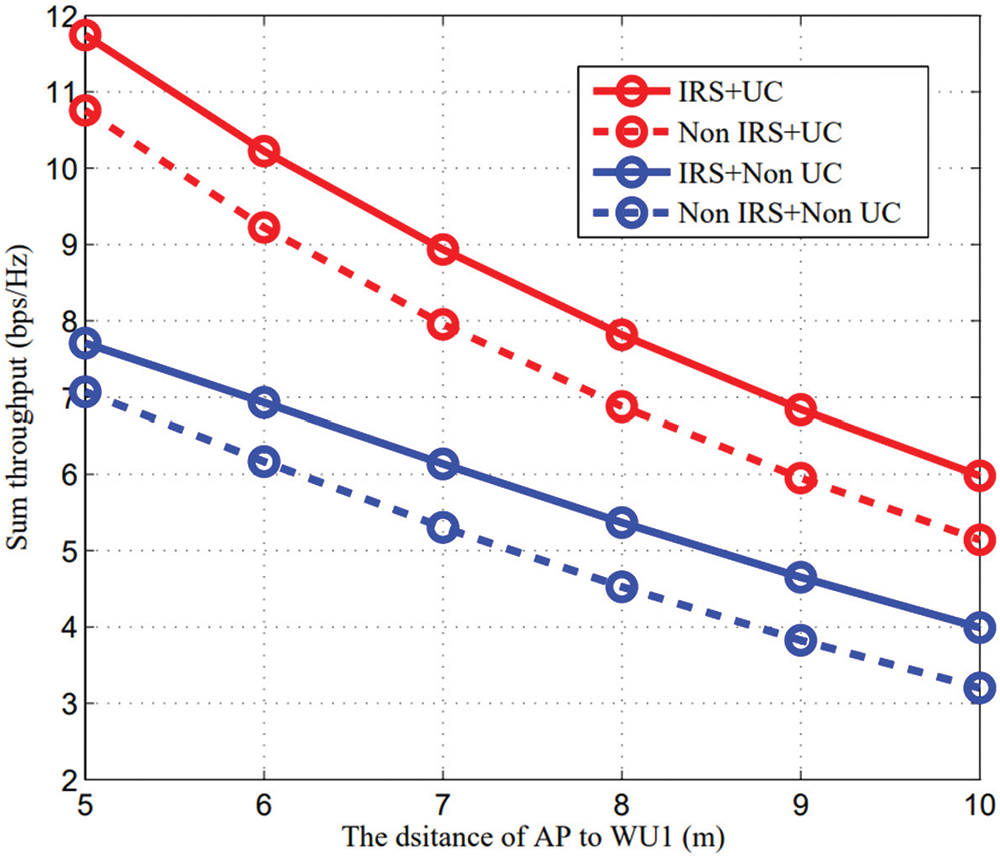
Figure 4: Sum throughput vs. d1

In order to observe the sum throughput improvement with increasing p0, we second compare the performance of some different schemes when p0 increases from 30 to 40 dBm in Fig. 5. We set d1=8 m, N=25 here. It can be seen from the figure that the sum throughput of four schemes increases with the increasing p0, but the “IRS + UC” scheme outperforms that of other schemes. We can realize that the UC scheme can improve sum throughput significantly even if the WUs get less energy in WEL. This also provides a feasible way to make up for the lack of energy by introducing the UC scheme into WPSN.

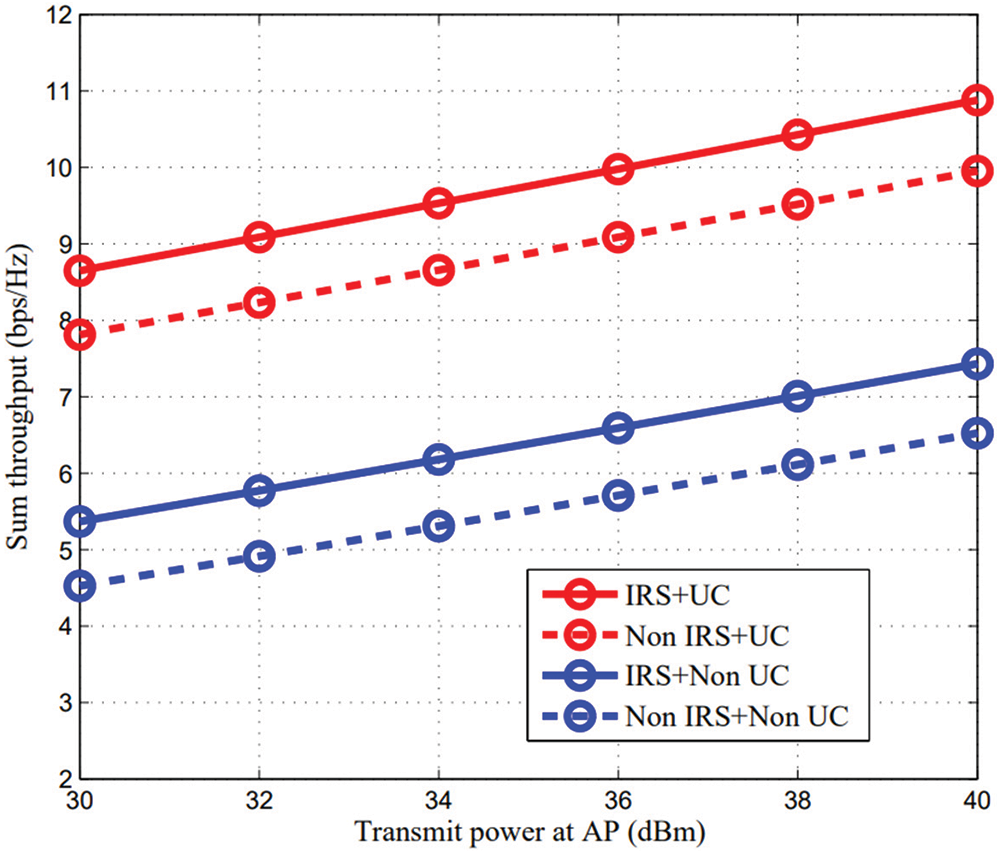
Figure 5: Sum throughput vs. P0

Finally, the impact of the elements number N of IRS on sum throughput is shown in Fig. 6. With the increasing N, the sum throughput obtained by schemes with IRS is gradually increased due to the array gain and the sum throughput of schemes without IRS not changing. When about N<50, “IRS + UC” and “Non IRS + UC” outperforms “IRS + Non UC” and “Non IRS + Non UC”. Then “IRS + Non UC” is greater than “Non IRS + UC” as N continues to grow, and this is because the performance gain of increasing N to that only equipping with IRS is greater than that only using UC scheme in mmWave WPSN.

Figure 6: Sum throughput vs. N

5  Conclusion

In this paper, we proposed a UC scheme for IRS-aided mmWave WPSN. The WSRM problem is formulated to maximize the weighted sum throughout by jointly optimizing the phase shift matrix, time slots, and power allocation. Some efficient variable substitutions and SDP relaxation are introduced to convert the original non-convex problem into a convex problem that is easy to tackle. Finally, numerical results confirm that the weighted sum throughput of our proposed UC scheme is greater than that of non UC whether equipped with IRS or not.

Acknowledgement: This work was supported in part by the open research fund of National Mobile Communications Research Laboratory, Southeast University (No. 2023D11), in part by Sponsored by Program for Science & Technology Innovation Talents in Universities of Henan Province (23HASTIT019), in part by Natural Science Foundation of Henan Province (232300421097), in part by the Project funded by China Postdoctoral Science Foundation (2023T160596, 2020M682345), in part by the Henan Postdoctoral Foundation (202001015).

Funding Statement: This work was supported in part by the open research fund of National Mobile Communications Research Laboratory, Southeast University (No. 2023D11), in part by Sponsored by program for Science & Technology Innovation Talents in Universities of Henan Province (23HASTIT019), in part by Natural Science Foundation of Henan Province (20232300421097), in part by the project funded by China Postdoctoral Science Foundation (2020M682345), in part by the Henan Postdoctoral Foundation (202001015).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Yonghui Lin, Zhengyu Zhu; data collection: Yonghui Lin, Zhengyu Zhu; analysis and interpretation of results: Yonghui Lin, Zhengyu Zhu; draft manuscript preparation: Yonghui Lin. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: This statement should make clear how readers can access the data used in the study and explain why any unavailable data cannot be released.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Alsabah, M., Naser, M. A., Mahmmod, B. M., Abdulhussain, S. H., Eissa, M. R. et al. (2021). 6G wireless communications networks: A comprehensive survey. IEEE Access, 9, 148191–148243. [Google Scholar]

2. Chowdhury, M. Z., Shahjalal, M., Ahmed, S., Jang, Y. M. (2020). 6G wireless communication systems: Applications, requirements, technologies, challenges, and research directions. IEEE Open Journal of the Communications Society, 1, 957–975. [Google Scholar]

3. Roh, W., Seol, J. Y., Park, J., Lee, B., Lee, J. et al. (2014). Millimeter-wave beamforming as an enabling technology for 5G cellular communications: Theoretical feasibility and prototype results. IEEE Communications Magazine, 52(2), 106–113. [Google Scholar]

4. Rappaport, T. S., Xing, Y., MacCartney, G. R., Molisch, A. F., Mellios, E. et al. (2017). Overview of millimeter wave communications for fifth-generation (5G) wireless networks-with a focus on propagation models. IEEE Transactions on Antennas and Propagation, 65(12), 6213–6230. [Google Scholar]

5. Xiao, M., Mumtaz, S., Huang, Y., Dai, L., Li, Y. et al. (2017). Millimeter wave communications for future mobile networks. IEEE Journal on Selected Areas in Communications, 35(9), 1909–1935. [Google Scholar]

6. Zhu, Z., Huang, S., Chu, Z., Zhou, F., Zhang, D. et al. (2019). Robust designs of beamforming and power splitting for distributed antenna systems with wireless energy harvesting. IEEE Systems Journal, 13(1), 30–41. [Google Scholar]

7. Lu, X., Wang, P., Niyato, D., Kim, D. I., Han, Z. (2015). Wireless networks with RF energy harvesting: A contemporary survey. IEEE Communications Surveys & Tutorials, 17(2), 757–789. [Google Scholar]

8. Zhu, Z., Wang, N., Hao, W., Wang, Z., Lee, I. (2021). Robust beamforming designs in secure MIMO SWIPT IoT networks with a non-linear channel model. IEEE Internet Things Journal, 8(3), 1702–1715. [Google Scholar]

9. Bi, S., Ho, C. K., Zhang, R. (2015). Wireless powered communication: Opportunities and challenges. IEEE Communications Magazine, 53(4), 117–125. [Google Scholar]

10. Niu, H., Chu, Z., Zhou, F., Zhu, Z., Zhang, M. et al. (2021). Weighted sum secrecy rate maximization using intelligent reflecting surface. IEEE Transactions on Communications, 69(9), 6170–6184. [Google Scholar]

11. Bi, S., Zhang, R. (2016). Placement optimization of energy and information access points in wireless powered communication networks. IEEE Transactions on Wireless Communications, 15(3), 2351–2364. [Google Scholar]

12. Chu, Z., Zhou, F., Xiao, P., Zhu, Z., Mi, D. (2019). Resource allocation for secure wireless powered integrated multicast and unicast services with full duplex self-energy recycling. IEEE Transactions on Wireless Communications, 18(1), 620–636. [Google Scholar]

13. Niu, H., Chu, Z., Zhou, F., Zhu, Z., Zhen, L. et al. (2022). Robust design for intelligent reflecting surface assisted secrecy SWIPT network. IEEE Transactions on Wireless Communications, 21(6), 4133–4149. [Google Scholar]

14. Zhu, Z., Ma, M., Sun, G., Hao, W., Liu, P. et al. (2022). Secrecy rate optimizations in nonlinear energy harvesting model-based mmWave IoT systems with SWIPT. IEEE Systems Journal, 16(4), 5939–5949. [Google Scholar]

15. Niu, H., Chu, Z., Zhou, F., Zhu, Z. (2021). Simultaneous transmission and reflection reconfigurable intelligent surface assisted secrecy MISO networks. IEEE Communications Letters, 25(11), 3498–3502. [Google Scholar]

16. Zhu, Z., Xu, J., Sun, G., Hao, W., Chu, Z. et al. (2022). Robust beamforming design for IRS-aided secure SWIPT Terahertz systems with non-linear EH model. IEEE Wireless Communications Letters, 11(4), 746–750. [Google Scholar]

17. Liu, H., Li, G., Li, X., Huang, G., Liu, Y. et al. (2022). Effective capacity analysis of STAR-RIS assisted NOMA networks. IEEE Wireless Communications Letters, 11(9), 1930–1934. [Google Scholar]

18. Chu, Z., Zhu, Z., Zhou, F., Zhang, M., Al-Dhahir, N. (2021). Intelligent reflecting surface assisted wireless powered sensor networks for internet of things. IEEE Transactions on Communications, 69(7), 4877–4889. [Google Scholar]

19. Zheng, Y., Bi, S., Zhang, J., Quan, Z., Wang, H. (2020). Intelligent reflecting surface enhanced user cooperation in wireless powered communication networks. IEEE Wireless Communications Letters, 9(6), 901–905. [Google Scholar]

20. Chu, Z., Zhu, Z., Li, X., Zhou, F., Zhen, L. et al. (2022). Resource allocation for IRS assisted wireless powered FDMA IoT networks. IEEE Internet of Things Journal, 9(11), 8774–8785. [Google Scholar]

21. Li, G., Liu, H., Huang, G., Li, X., Raj, B. et al. (2021). Effective capacity analysis of reconfigurable intelligent surfaces aided NOMA network. EURASIP Journal on Wireless Communications and Networking, 198(1), 1–16. [Google Scholar]

22. Lyu, B., Ramezani, P., Hoang, D. T., Gong, S., Yang, Z. et al. (2021). Optimized energy and information relaying in self-sustainable IRS-empowered WPCN. IEEE Transactions on Communications, 69(1), 619–633. [Google Scholar]

23. Zhai, L., Zou, Y., Zhu, J., Guo, H. (2022). A stackelberg game approach for IRS-aided WPCN multicast systems. IEEE Transactions on Wireless Communications, 21(5), 3249–3262. [Google Scholar]

24. Ramezani, P., Jamalipour, A. (2021). Backscatter-assisted wireless powered communication networks empowered by intelligent reflecting surface. IEEE Transactions on Vehicular Technology, 70(11), 11908–11922. [Google Scholar]

25. Zheng, Y., Bi, S., Zhang, Y. J. A., Lin, X., Wang, H. (2021). Joint beamforming and power control for throughput maximization in IRS-assisted MISO WPCNs. IEEE Internet Things Journal, 8(10), 8399–8410. [Google Scholar]

26. Wu, Q., Zhou, X., Chen, W., Li, J., Zhang, X. (2022). IRS-aided WPCNs: A new optimization framework for dynamic IRS beamforming. IEEE Transactions on Wireless Communications, 21(7), 4725–4739. [Google Scholar]

27. Zeng, P., Wu, Q., Qiao, D. (2021). Energy minimization for IRS-aided WPCNs with non-linear energy harvesting model. IEEE Wireless Communications Letters, 10(11), 2592–2596. [Google Scholar]

28. Cao, H., Li, Z., Chen, W. (2021). Resource allocation for IRS-assisted wireless powered communication networks. IEEE Wireless Communications Letters, 10(11), 2450–2454. [Google Scholar]

29. Zhu, Z., Li, Z., Chu, Z., Sun, G., Hao, W. et al. (2022). Resource allocation for intelligent reflecting surface assisted wireless powered IoT systems with power splitting. IEEE Transactions on Wireless Communications, 21(5), 2987–2998. [Google Scholar]

30. Wang, Q., Gao, Z., Xu, Y., Xie, H. (2021). Energy-efficient optimization for IRS-assisted wireless-powered communication networks. IEEE 93rd Vehicular Technology Conference, Helsinki, Finland. [Google Scholar]

31. Zeng, P., Qiao, D., Wu, Q., Wu, Y. (2022). Throughput maximization for active intelligent reflecting surface-aided wireless powered communications. IEEE Wireless Communications Letters, 11(5), 992–996. [Google Scholar]

32. Lyu, B., Hoang, D. T., Gong, S., Yang, Z. (2020). Intelligent reflecting surface assisted wireless powered communication networks. IEEE Wireless Communications and Networking Conference Workshops (WCNCW), Seoul, Korea (South). [Google Scholar]

33. Cao, K., Ding, H., Li, W., Lv, L., Gao, M. et al. (2022). On the ergodic secrecy capacity of intelligent reflecting surface aided wireless powered communication systems. IEEE Wireless Communications Letters, 11(11), 2275–2279. [Google Scholar]

34. Chu, Z., Xiao, P., Mi, D., Hao, W., Khalily, M. et al. (2021). A novel transmission policy for intelligent reflecting surface assisted wireless powered sensor networks. IEEE Journal of Selected Topics in Signal Processing, 15(5), 1143–1158. [Google Scholar]

35. Zou, Y., Gong, S., Xu, J., Cheng, W., Hoang, D. T. et al. (2020). Wireless powered intelligent reflecting surfaces for enhancing wireless communications. IEEE Transactions on Vehicular Technology, 69(10), 12369–12373. [Google Scholar]

36. Chu, Z., Xiao, P., Mi, D., Chen, H., Hao, W. (2020). Intelligent reflecting surfaces enabled cognitive internet of things based on practical pathloss model. China Communications, 17(12), 1–16. [Google Scholar]

37. Wang, Z., Shi, Y., Zhou, Y., Zhou, H., Zhang, N. (2021). Wireless-powered over-the-air computation in intelligent reflecting surface-aided IoT networks. IEEE Internet of Things Journal, 8(3), 1585–1598. [Google Scholar]

38. Li, X., Xie, Z., Chu, Z., Menon, V. G., Mumtaz, S. et al. (2022). Exploiting benefits of IRS in wireless powered NOMA networks. IEEE Transactions on Green Communications and Networking, 6(1), 175–186. [Google Scholar]

39. Rusek, F., Persson, D., Lau, B. K. (2013). Scaling up MIMO: Opportunities and challenges with very large arrays. IEEE Signal Processing Magazine, 30(1), 40–60. [Google Scholar]

40. Boyd, S., Vandenberghe, L. (2004). Convex optimization. Cambridge, UK: Cambridge University Press. [Google Scholar]

41. Grant, M., Boyd, S. (2012). CVX: Matlab software for disciplined convex programming. http://cvxr.com/cvx/ [Google Scholar]

42. Zhang, Y., He, W., Li, X., Peng, H., Rabie, K. M. et al. (2022). Covert communication in downlink NOMA systems with channel uncertainty. IEEE Sensors Journal, 22(19), 19101–19112. [Google Scholar]