 Open Access
Open Access
ARTICLE
Computational Analysis of Heat and Mass Transfer in Magnetized Darcy-Forchheimer Hybrid Nanofluid Flow with Porous Medium and Slip Effects
1
Faculty of Basic and Applied Sciences, Department of Mathematics, Air University, PAF Complex E-9, Islamabad, 44000, Pakistan
2
Department of Mathematics and Sciences, College of Humanities and Sciences, Prince Sultan University, Riyadh, 11586,
Saudi Arabia
3
Department of Mathematics, Air University, PAF Complex E-9, Islamabad, 44000, Pakistan
4
Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, 40402, Taiwan
5
Department of Mathematics, Faculty of Science, The Hashemite University, P.O Box 330127, Zarqa, 13133, Jordan
* Corresponding Author: Khalil Ur Rehman. Email:
(This article belongs to the Special Issue: Advanced Computational Methods in Fluid Mechanics and Heat Transfer)
Computer Modeling in Engineering & Sciences 2023, 137(3), 2311-2330. https://doi.org/10.32604/cmes.2023.026994
Received 08 October 2022; Accepted 03 April 2023; Issue published 03 August 2023
Abstract
A computational analysis of magnetized hybrid Darcy-Forchheimer nanofluid flow across a flat surface is presented in this work. For the study of heat and mass transfer aspects viscous dissipation, activation energy, Joule heating, thermal radiation, and heat generation effects are considered. The suspension of nanoparticles singlewalled carbon nanotubes (SWCNTs) and multi-walled carbon nanotubes (MWCNTs) are created by hybrid nanofluids. However, single-walled carbon nanotubes (SWCNTs) produce nanofluids, with water acting as conventional fluid, respectively. Nonlinear partial differential equations (PDEs) that describe the ultimate flow are converted to nonlinear ordinary differential equations (ODEs) using appropriate similarity transformation. The ODEs are dealt with numerically by means of MATLAB’s inbuilt routine function bvp4c. Velocity, temperature, and concentration profiles are explained pictorially whereas Sherwood number, local skin friction coefficient, and Nusselt number values are represented through bar charts. Thermal radiation and activation parameters shows direct impact on flow field. Furthermore, hybrid nanofluid admits a higher magnitude of velocity and temperature than nanofluid, but the concentration profile exhibits the opposite trend. The notable findings of the present investigation have significant applications in heat combustion and cooling chambers, space technology, the ceramics industry, paint and conductive coatings, bio-sensors, and many more.Keywords
Nanofluids are created when simple nanoparticles are disseminated in basic fluids like oil, ethylene glycol, and water. Compared to regular liquids, these fluids have a higher thermal conductivity. Choi and Eastman [1] were the first to conduct a nanoparticle study at Argonne National Laboratory in 1995. They indicated that the nanofluid is made up of solid nanoparticles that are dispersed in the base fluid. Applications of nanofluids are microelectronics, hybrid-powered engines, pharmaceutical procedures, particle storage facilities, chemical catalytic reactors, electronic equipment cooling, and medicine diffusion in blood veins. Recently, scientists have focused their research on nanofluids to improve heat transfer fluids. Ibrahim and Shankar [2] examined the influence of MHD and heat radiation with slip boundary conditions over permeable stretched sheets using nanofluid. The shooting method combined with the fourth-order Runge–Kutta approach was used in solving higher-order ODEs numerically. Outcomes of concentration, velocity, and temperature distributions against various parameters were displayed numerically. They showed that when thermophoresis and Brownian motion parameters rise, then the Nusselt number falls whereas the Sherwood number becomes grows by raising the Brownian motion parameter. Maraj et al. [3] studied carbon nanotubes gravity-driven flow through vertical stretching surface. MHD effects are incorporated along the active and passive control models to calculate heat and mass transfer. To solve ODEs, the shooting approach was applied with the Runge Kutta Fehlberg method. The consequences of the velocity profile, temperature profile, rate of heat transfer, and coefficient of skin friction for various fluid flow parameters were explained using graphs and tables. They concluded that thermal radiation impacts drop fluid temperature while opposite behavior against Biot number. Hybrid nanofluids (HNFs) are an advanced category of nanofluids. HNFs are suspended into two distinct types of nanoparticles with diameters of less than 100 nanometers with conventional fluids like water. The thermal conductivity and thermo-physical parameters of this new type of nanofluid are greater than those of conventional fluids. Hybrid nanofluids have numerous heat transfer applications, including heat pipes, solar energy, heat exchangers, biomedical, spacecraft, coolant in machining and manufacturing, biomedical, ventilation, and air conditioning systems, to mention a few. Metals (e.g., Ag/silver, Cu/copper), Metal oxides (e.g.,
Carbon nanotubes (CNTs) have a cylindrical shape and are made up of carbon atoms. CNTs are classified into three categories based on graphene layers: single-walled CNTs (SWCNTs) with 0.5 to 1.5 nm diameter, double-walled CNTs (DWCNTs), and multi-walled CNTs (MWCNTs), with 10 to 100 nm diameter. Hardness, adhesion, high mechanical strength, stiffness, chemical steadiness, great thermal and electrical conductivity, biological and chemical sensors, nanotechnology, catalysis, conductive polymers, and structural composite materials are just a few applications of hybrid nanofluids. Carbon nanotube suspensions have better thermal conductivity than the same volume fraction of other nanoparticles, according to references [5,6]. Shanmugapriya et al. [7] examined the moving wedge by taking the effects of MHD, heat radiation, and activation energy for two types of hybrid nanoparticles, SWCNTs and MWCNTs. The equations were numerically solved by utilizing the shooting approach in association with RKF 4-5th order. Graphs and tables were used to represent the findings. They reached the conclusion that heat transfer in a hybrid nanofluid has a greater impact than in a common fluid.Several scientists have recently studied the exact and numerical solutions for heat and mass transfer flow over various geometries, as indicated in [8–12].
Porous media is a porous material that has pores that are usually filled with fluid. There are numerous applications related to porous media, including paper manufacture, nonwoven materials, electrical technology, energy storage, heat pipe technology. Darcy’s law does not apply at greater rate of flow because of inertial and boundary effects. To circumvent this limitation, in 1901 a Dutch scientist, Philippes Forchheimer, modified that by predicting the flow of inertia and the flow of the boundary layer, Darcian velocity expression was changed by introducing the square velocity term to momentum equation [13]. Firstly, Muskat [14] invented the term “Forchheimer factor” to express this unique idea. Sajid et al. [15] analyzed a linearly stretching surface with Darcy-Forchheimer by considering Maxwell nanofluid flow. They added the assumptions like thermal radiation, activation energy, variable thermal conductivity, convective boundary conditions, and zero mass flux. They concluded that thermophoresis and activation energy parameter had an increasing influence on the concentration profile. Khan et al. [16] observed a hybrid nanofluid (
The least amount of energy required to initiate a chemical reaction is known as activation energy. The Arrhenius equation describes the change in rate constants with temperature and is used to determine activation energy. In the mass transfer equation, activation energy is combined with binary chemical reactions that have various uses in food processing, oil reservoirs, water and oil suspensions, chemical and geothermal engineering, and other disciplines. Bestman [23] was the first to introduce this concept. Khan et al. [24] researched Casson nanofluid flow across a stretching sheet by accounting for the effects of activation energy, thermal radiation, heat sink/source, and entropy generation. Under these effects, they formulated the governing equations and solved them numerically using bvp4c technique. Graphical representations were utilized to depict the various flow parameters affected by the profiles of velocity, temperature, concentration, and entropy generation. They noticed that the concentration profile decreases against higher values of the activation energy parameter. Activation energy impact on hybrid nanofluids under various circumstances was identified by a group of scientists, see [25–28].
According to the literature review, the main purpose of this study is to investigate MHD stagnation point flow through a porous medium with mixed convection across a permeable stretched sheet. For a more realistic study, the Darcy-Forchheimer approach has been incorporated. Moreover, the effect of Joule heating due to the external magnetic field is also explored with existence of viscous dissipation, thermal radiation, and heat generation phenomena. Furthermore, solute concentration is also examined under the influence of activation energy and concentration slip at the surface. This study is essentially a comparison of hybrid nanofluids (MWCNTs-SWCNTs/water) and nanofluid (SWCNTs/water) with concentration, thermal, and momentum boundary layer. To the best of the author’s knowledge no such attempt is mentioned in literature. The novel findings for the present investigation may impart noteworthy contributions to the hybrid CNTs as coolants in mechanical procedures and space technology, conductive coating, the polymer industry, and so forth.
We are considering laminar, two-dimensional, steady, and incompressible stagnation point flow for electrically conducting hybrid nanofluid and nanofluid above a porous stretching sheet, with impacts: viscosity dissipation, joule heating, and velocity slip. This study also involves these effects activation energy, heat generation, nonlinearly variable thermal radiation, concentration slip, Soret effect, and uniformly heated boundary condition. Fluid flows in
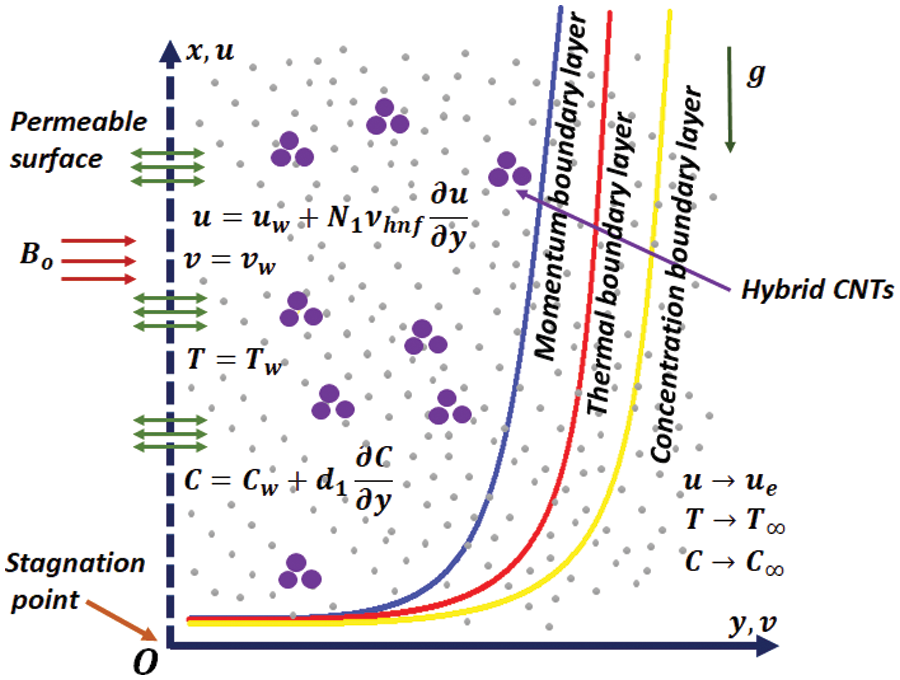
Figure 1: Physical configuration of the current model
Table 1 demonstrates the thermo-physical properties of nanoparticles and base fluid. Table 2 displays thermo-physical properties of single and multi-walled CNTs with base fluid

The governing system of equations based on boundary layer approximation theory is followed by:
where, u and v are horizontal and vertical velocity components, respectively. Subscript
The Rosseland approximation for thermal radiation is implemented to compute radiative heat flux
here
By invoking following similarity variables (according to [34]).
Here prime means differentiation with respect to
The non-dimensional parameters are the velocity ratio parameter
For an engineering perspective, the local skin friction coefficient
where
By invoking Eq. (9), the expressions defined in Eq. (16) take the following form:
where
Nonlinear ODEs are written in Eqs. (10)–(12) and their boundary conditions in Eq. (13) are tackled with the bvp4c function in MATLAB numerically. The finite difference approach is used by the bvp4c solver to implement three steps of the Lobatto IIIa formula. The procedure of the bvp4c technique is listed in Fig. 2. To begin the bvp4c method. We should first convert Eqs. (10)–(12) into first-order ODEs. We suggest different parameters for this purpose:
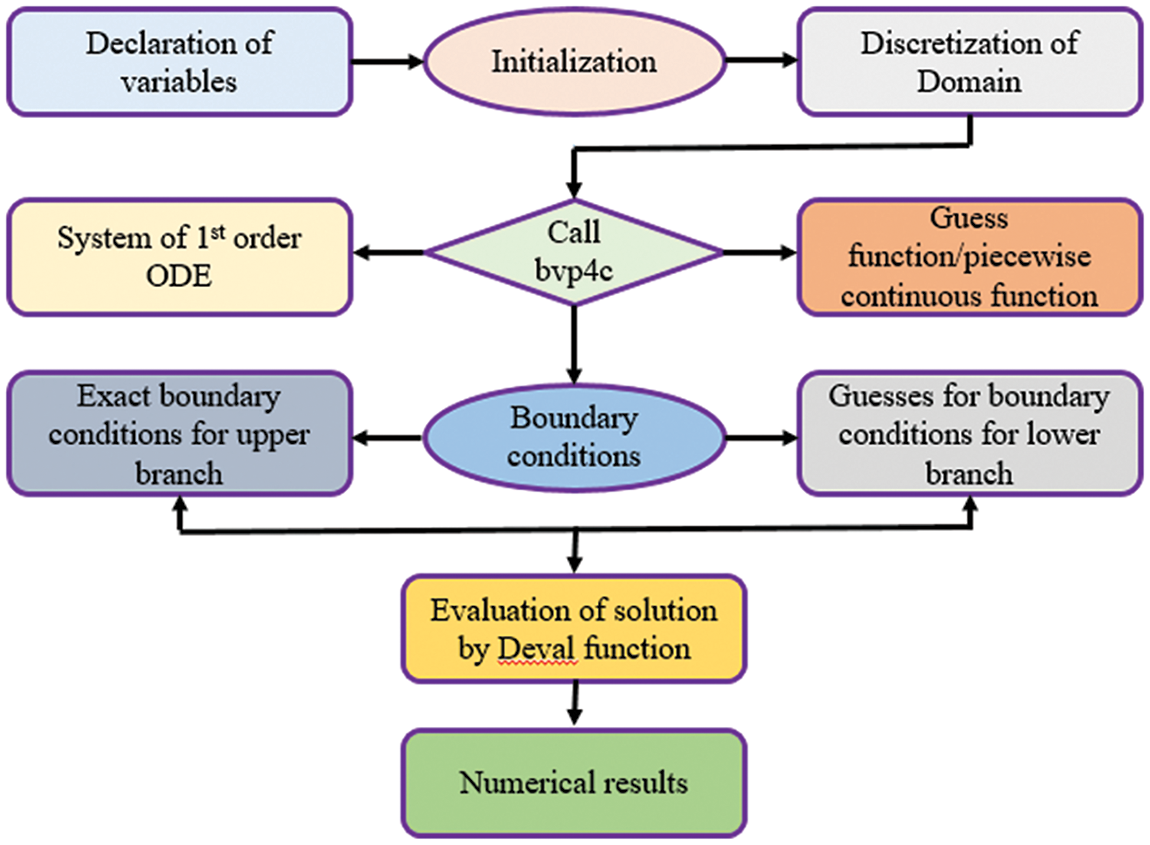
Figure 2: Phases for scheme bvp4c
by inserting Eq. (18) into Eqs. (10)–(12), we get
Using Eq. (18), the boundary conditions given in Eq. (13) are as follows:
We calculated skin friction coefficient values for varying the velocity slip parameter

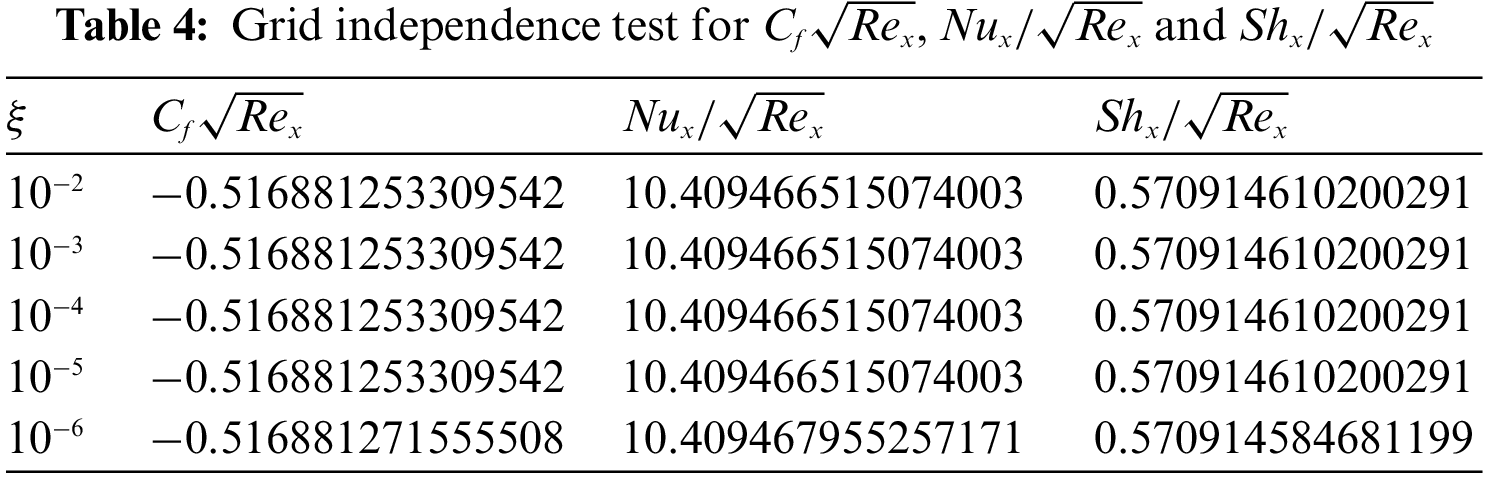
Table 4 represents the grid independence test for various values of tolerance by setting
We examine the heat and mass properties of both nanofluid and hybrid nanofluid in this article. Multi-walled carbon nanotubes (MWCNTs) have volume fraction
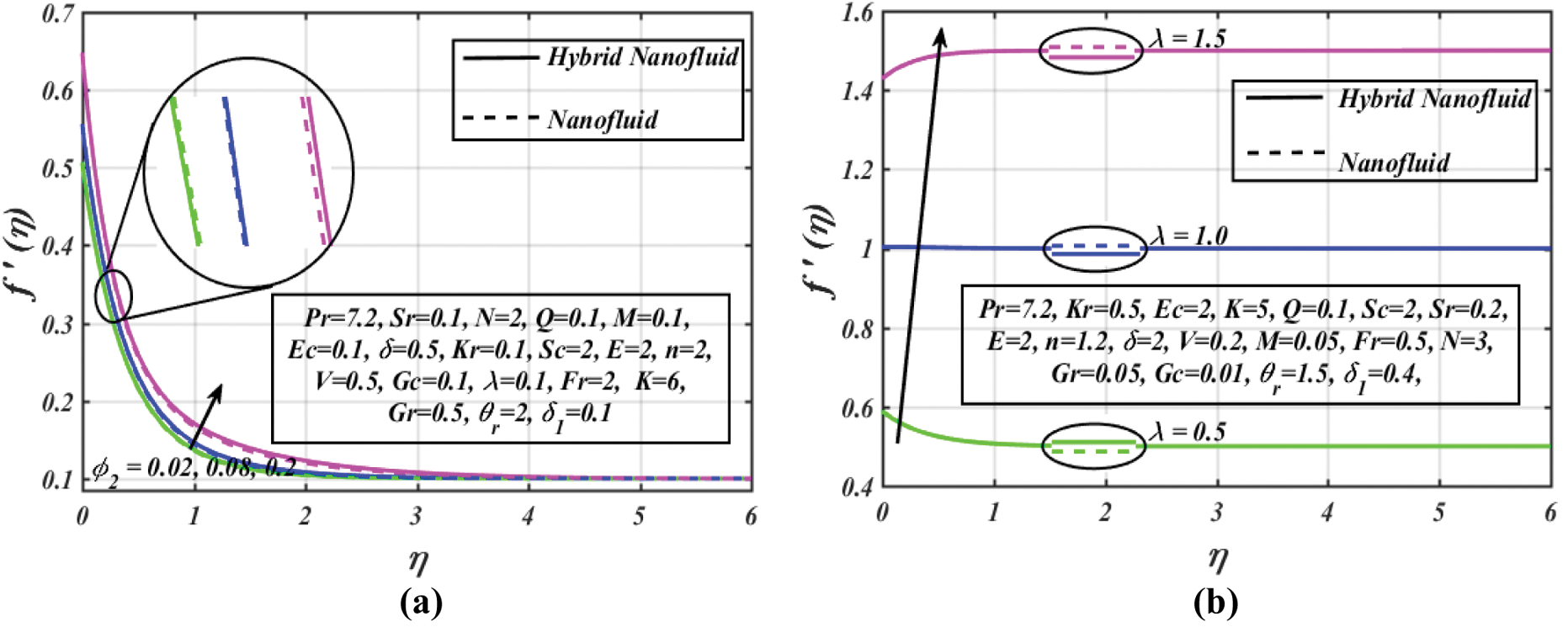
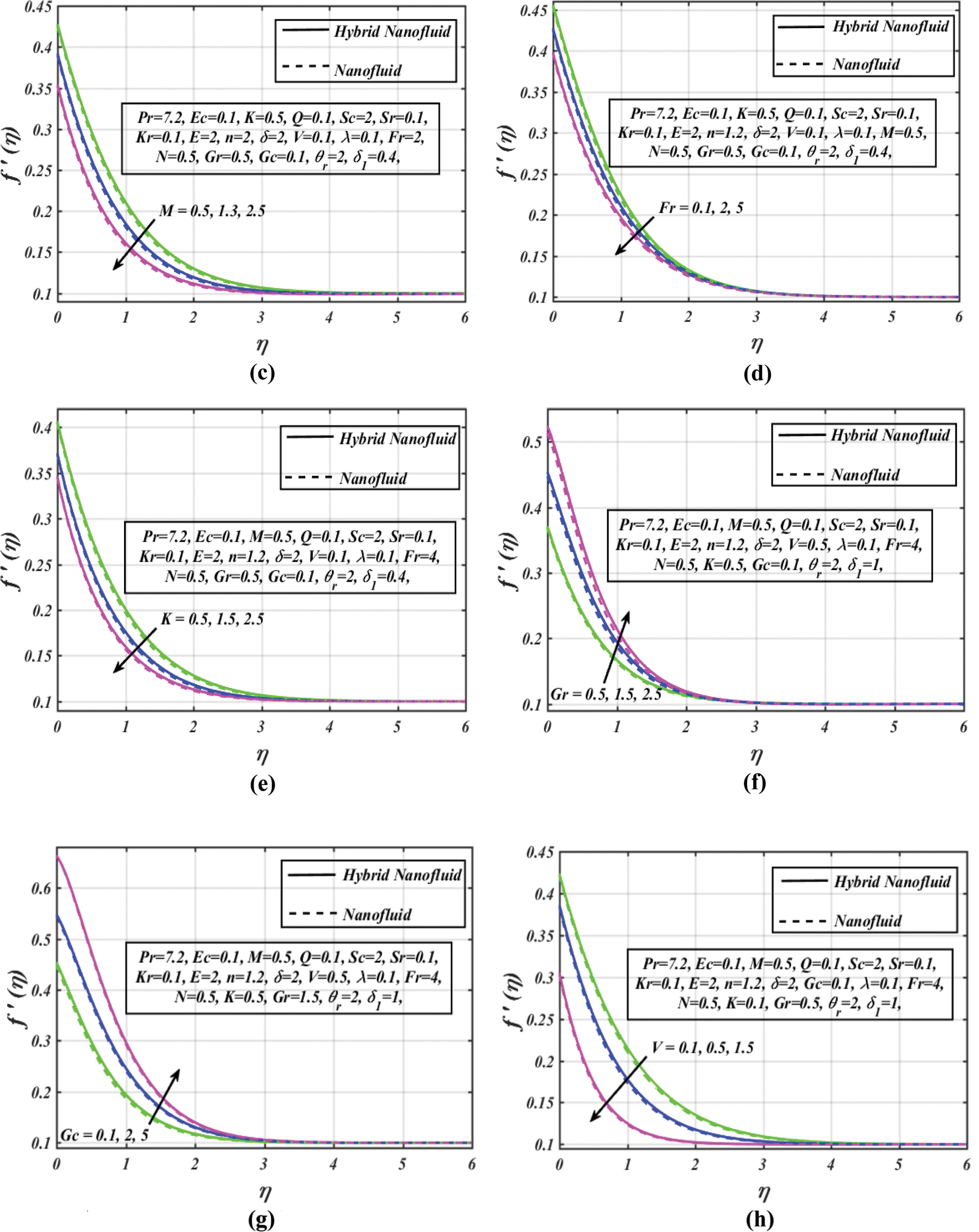
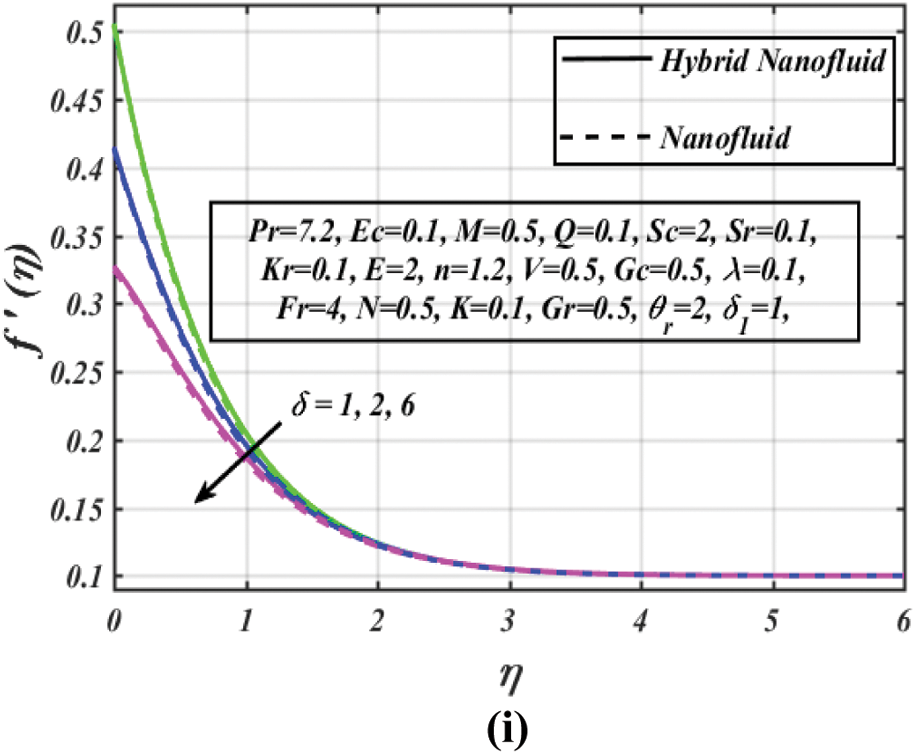
Figure 3: (a) Velocity profile vs. several
Figs. 4a–4f show a series of graphs that assist us to visualize the variations in temperature profiles induced by various prominent parameters. Fig. 4a provides sway of nanoparticles volume fraction
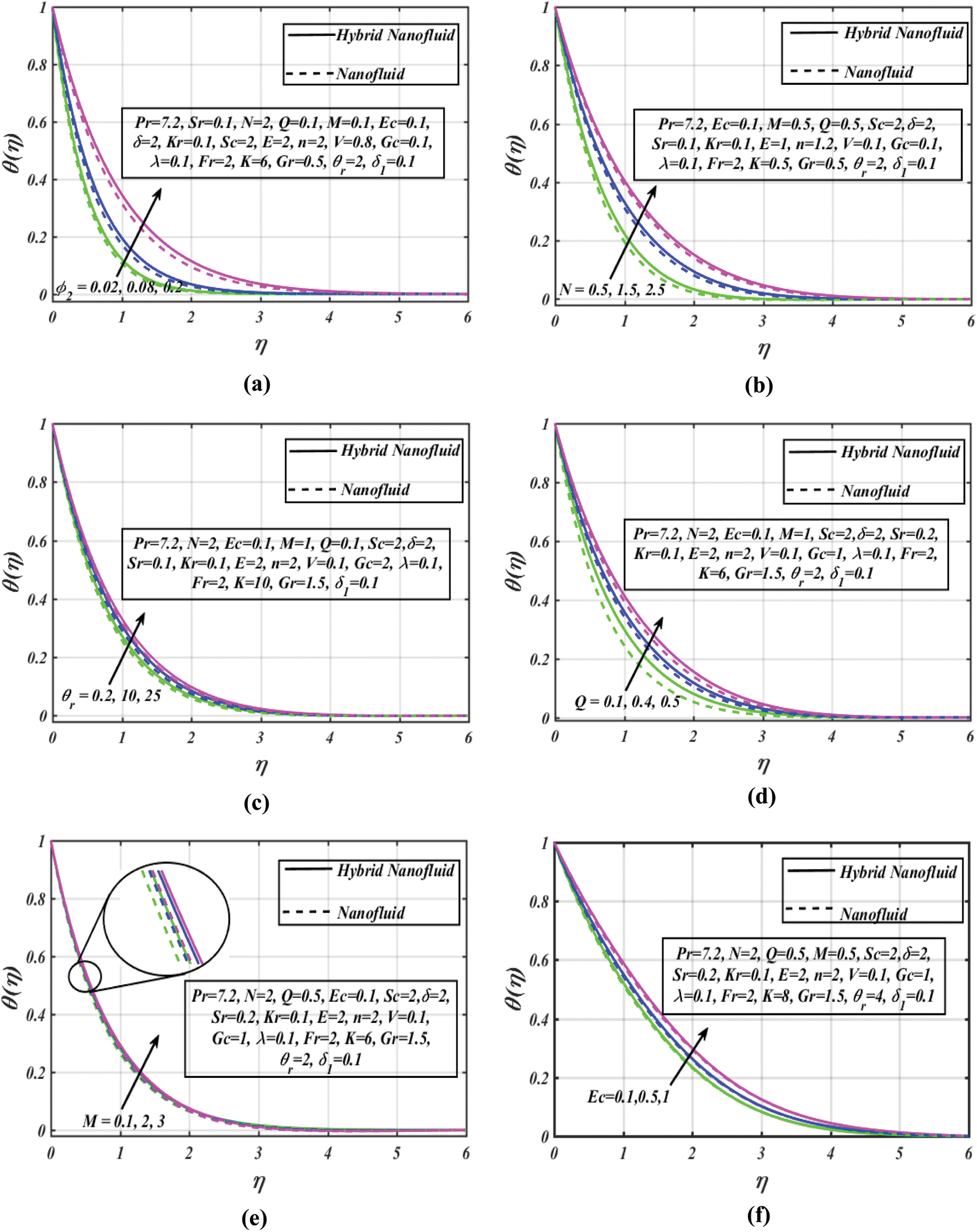
Figure 4: (a) Temperature profile vs. several
The next contention towards the sway of included parameters on the concentration profile, is presented in Figs. 5a–5g. Fig. 5a demonstrates the effect of volume fraction
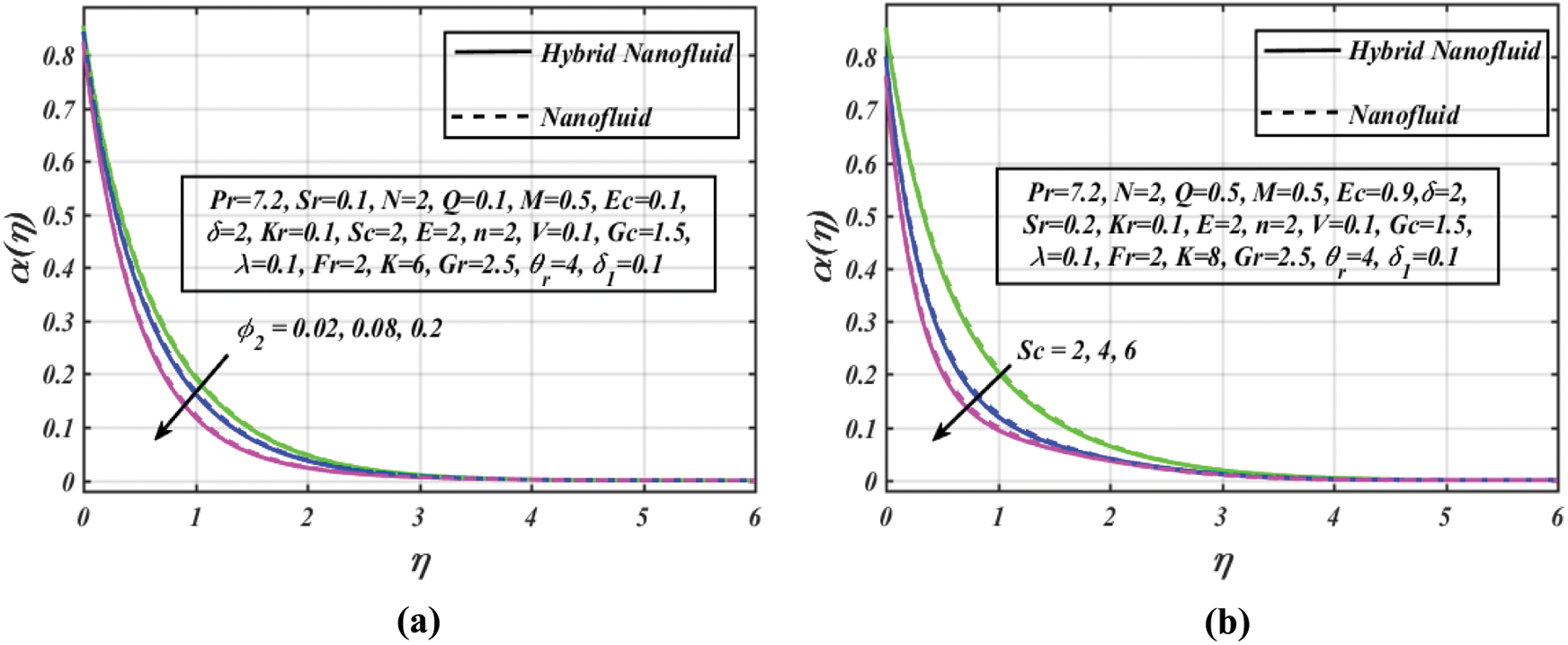
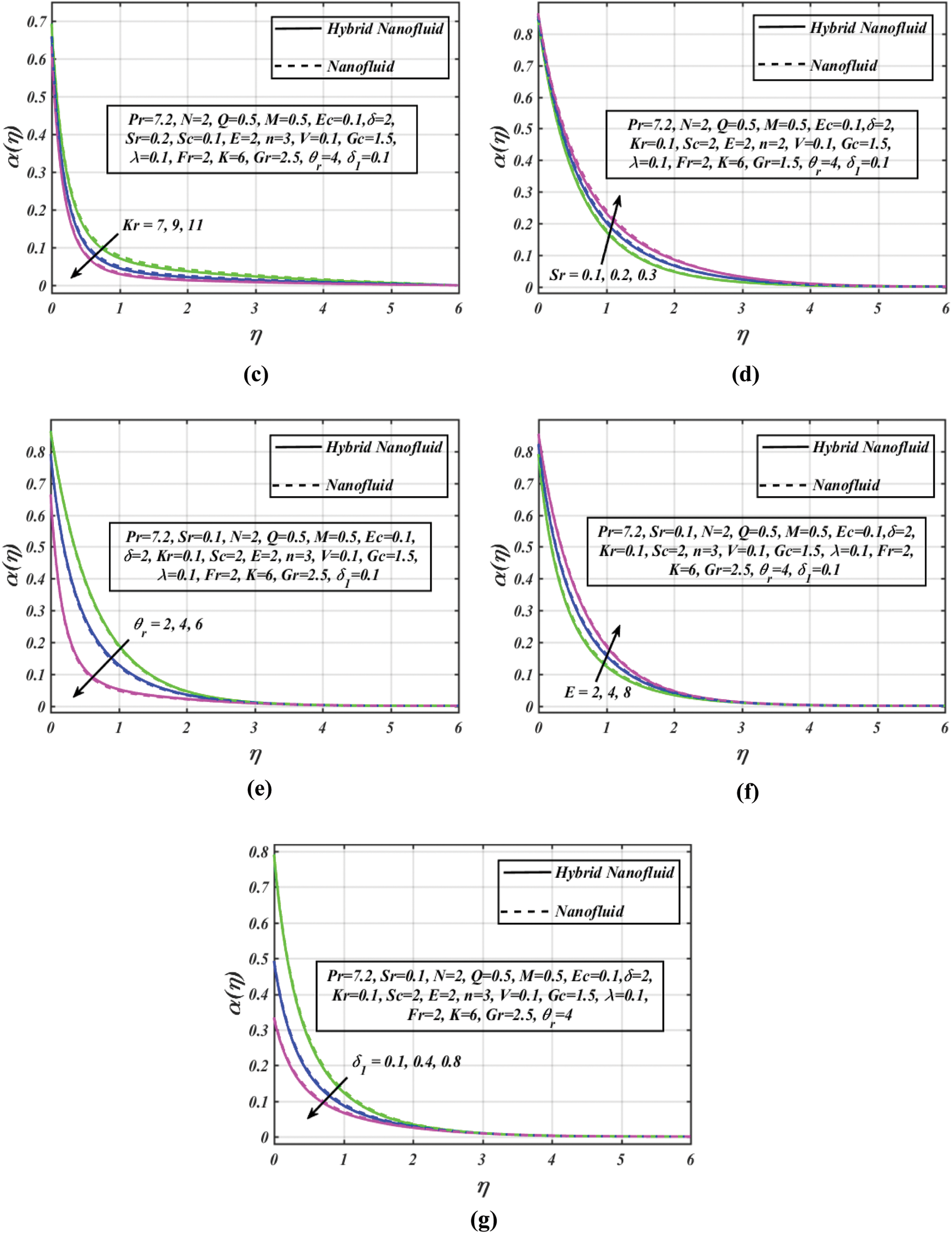
Figure 5: (a) Concentration profile vs. several
Figs. 6–8 provide values for local skin friction coefficient, Nusselt number, and Sherwood number vs. a variety of fluid flow parameters using a bar chart. The impact of
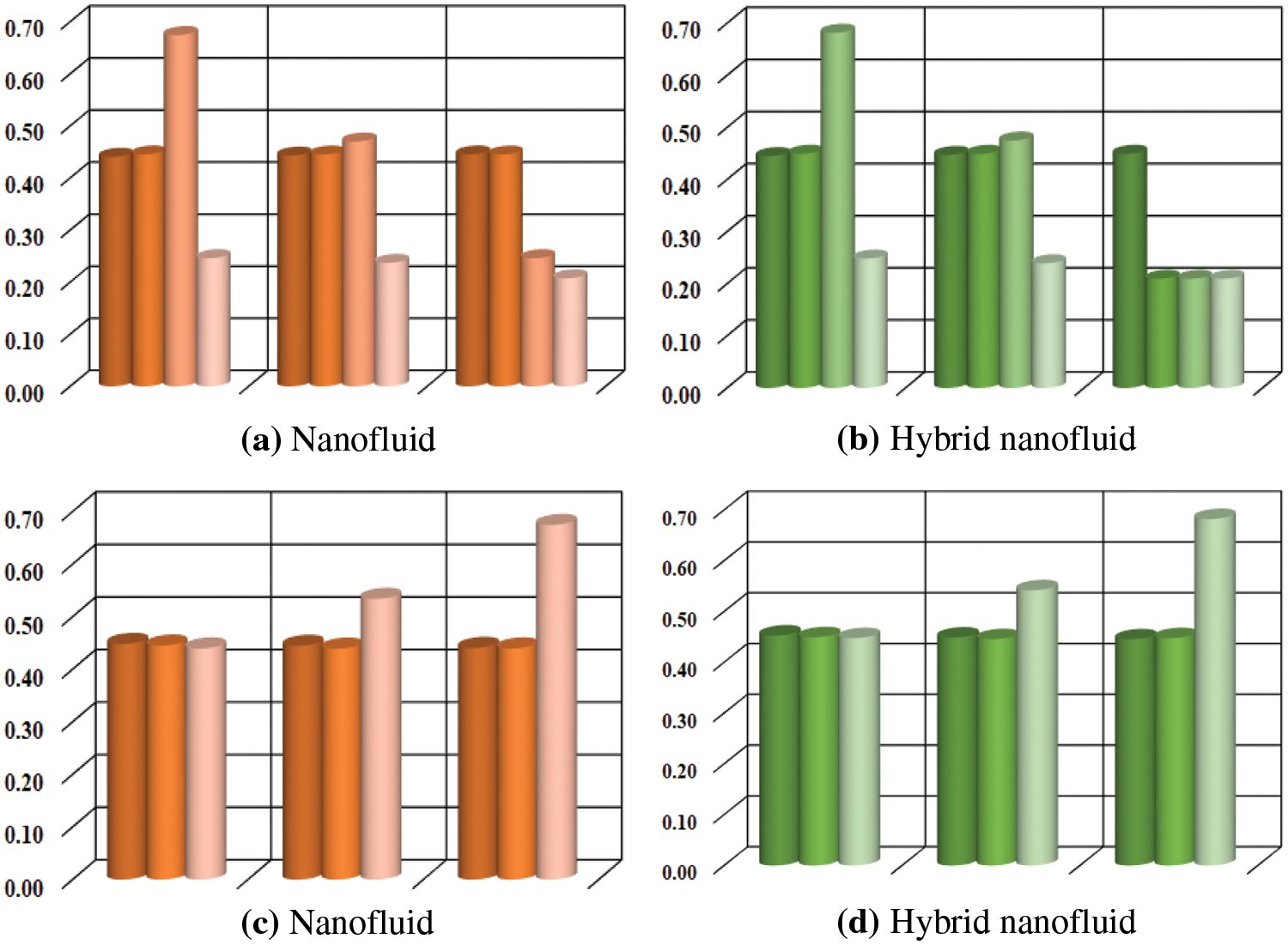
Figure 6: (a–b) Bar chart representation of
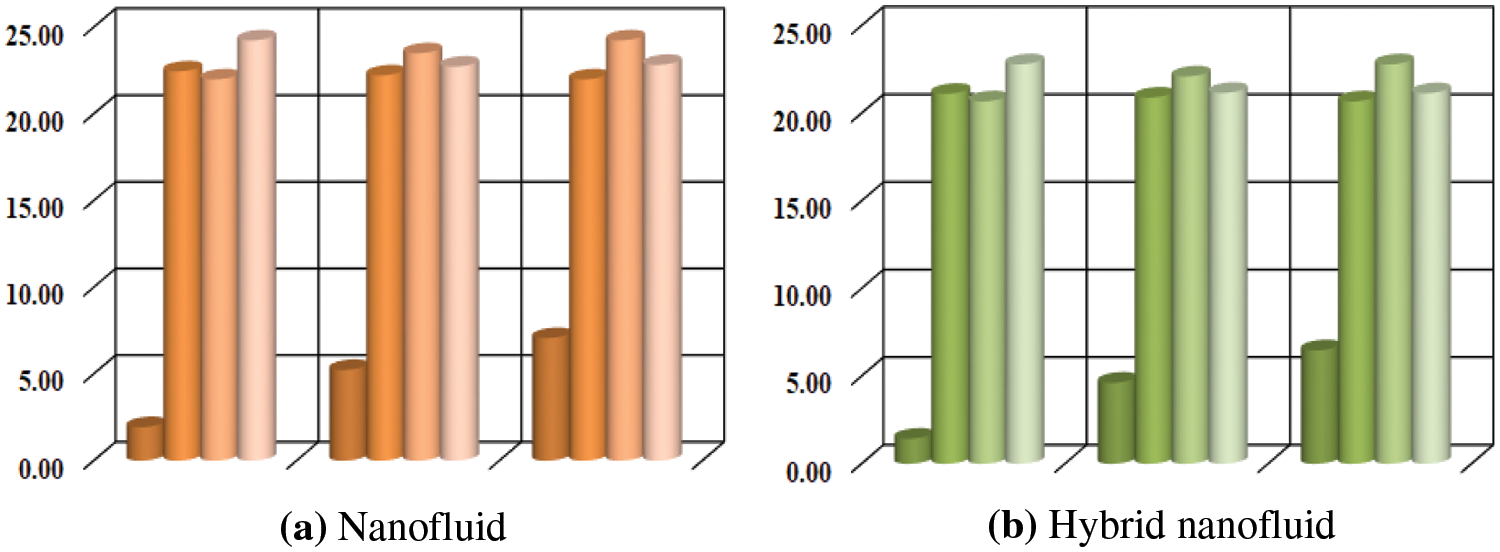
Figure 7: (a–b) Bar chart representation of
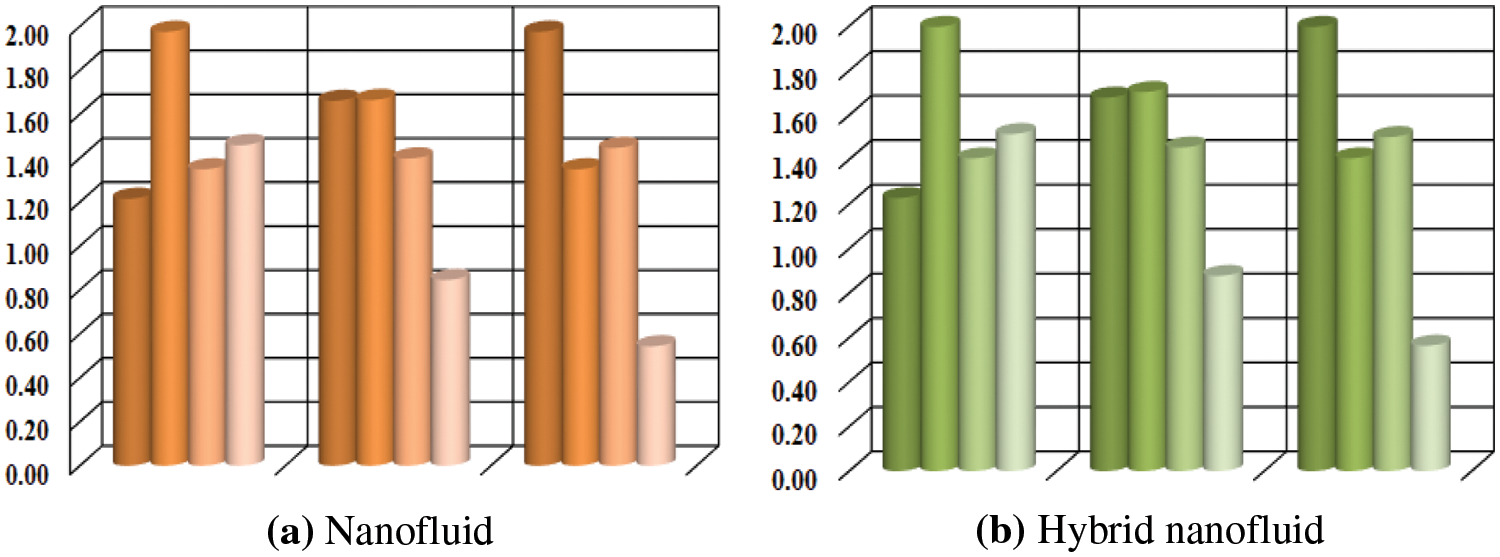
Figure 8: (a–b) Bar chart representation of
Figs. 7a–7b provide the bar chart distribution of
The present comprehensive numerical study on heat and mass transfer CNTs hybrid fluid flow over a porous surface with the presence of an external magnetic field led to the following notable findings:
• Darcy-Forchheimer parameter contributes to fluid flow deceleration. Moreover, this deceleration is significantly less in the case of CNTs hybrid nanofluid.
• Hartmann number, thermal radiation, heat generation, Eckert number, and temperature ratio parameters show an increasing trend for temperature profile. The temperature of fluid for hybrid nanofluid is higher than nanofluid.
• The Joule heating effect and viscous dissipation lead to an upsurge in fluid temperature and the rise in temperature distribution is prominently more in the presence of hybrid nanofluid. Thus, we conclude that the use of CNTs is more efficient than the utilization of hybrid CNTs.
• Activation energy contributes significantly to enhancing solute particles concentration. Furthermore, we identified that nanofluid has a greater concentration profile than hybrid nanofluid, but the temperature ratio parameter has reversed impact.
Acknowledgement: The authors would like to thank Prince Sultan University for their support through the TAS Research Lab.
Funding Statement: The authors received no specific funding for this study.
Availability of Data and Materials: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Choi, S. U., Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles (No. ANL/MSD/CP-84938; CONF-951135-29). Argonne, IL (USAArgonne National Lab (ANL). [Google Scholar]
2. Ibrahim, W., Shankar, B. (2013). MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Computers & Fluids, 75, 1–10. [Google Scholar]
3. Maraj, E. N., Bibi, A., Ijaz, S., Mehmood, R. (2022). MHD carbon nanotubes gravity driven flow along a thermal sensitive porous surface. Arabian Journal for Science and Engineering, 1–11. https://doi.org/10.1007/s13369-022-06775-9 [Google Scholar] [CrossRef]
4. Rekha, M. B., Sarris, I. E., Madhukesh, J. K., Raghunatha, K. R., Prasannakumara, B. C. (2022). Activation energy impact on flow of AA7072-AA7075/water-based hybrid nanofluid through a cone, wedge and plate. Micromachines, 13(2), 302. [Google Scholar] [PubMed]
5. Liu, M. S., Lin, M. C. C., Huang, I. T., Wang, C. C. (2005). Enhancement of thermal conductivity with carbon nanotube for nanofluids. International Communications in Heat and Mass Transfer, 32(9), 1202–1210. [Google Scholar]
6. Maré, T., Halelfadl, S., Sow, O., Estellé, P., Duret, S. et al. (2011). Comparison of the thermal performances of two nanofluids at low temperature in a plate heat exchanger. Experimental Thermal and Fluid Science, 35(8), 1535–1543. [Google Scholar]
7. Shanmugapriya, M., Sundareswaran, R., Senthil Kumar, P. (2021). Heat and mass transfer enhancement of MHD hybrid nanofluid flow in the presence of activation energy. International Journal of Chemical Engineering, 2021, 1–12. [Google Scholar]
8. Kumar, V., Madhukesh, J. K., Jyothi, A. M., Prasannakumara, B. C., Khan, M. I. et al. (2021). Analysis of single and multi-wall carbon nanotubes (SWCNT/MWCNT) in the flow of Maxwell nanofluid with the impact of magnetic dipole. Computational and Theoretical Chemistry, 1200, 113223. [Google Scholar]
9. Ali, M. R., Sadat, R. (2021). Lie symmetry analysis, new group invariant for the (3 + 1)-dimensional and variable coefficients for liquids with gas bubbles models. Chinese Journal of Physics, 71, 539–547. [Google Scholar]
10. Ali, M. R., Sadat, R. (2021). Construction of lump and optical solitons solutions for (3 + 1) model for the propagation of nonlinear dispersive waves in inhomogeneous media. Optical and Quantum Electronics, 53(6), 279. [Google Scholar]
11. Dul, S., Gutierrez, B. J. A., Pegoretti, A., Alvarez-Quintana, J., Fambri, L. (2022). 3D printing of ABS nanocomposites. Comparison of processing and effects of multi-wall and single-wall carbon nanotubes on thermal, mechanical and electrical properties. Journal of Materials Science & Technology, 121, 52–66. [Google Scholar]
12. Wang, Y., Mansir, I. B., Al-Khaled, K., Raza, A., Khan, S. U. et al. (2022). Thermal outcomes for blood-based carbon nanotubes (SWCNT and MWCNTs) with Newtonian heating by using new Prabhakar fractional derivative simulations. Case Studies in Thermal Engineering, 32, 101904. [Google Scholar]
13. Forchheimer, P. (1901). Wasserbewegung durch boden. Zeitschrift des Vereins Deutscher Ingenieure, 45, 1782–1788. [Google Scholar]
14. Muskat, M. (1946). The flow of homogeneous fluids through porous media. Ann Arbor, Michigan: JW Edwards. Inc. [Google Scholar]
15. Sajid, T., Sagheer, M., Hussain, S., Bilal, M. (2018). Darcy-Forchheimer flow of Maxwell nanofluid flow with nonlinear thermal radiation and activation energy. AIP Advances, 8(3), 035102. [Google Scholar]
16. Khan, S. A., Khan, M. I., Hayat, T., Alsaedi, A. (2020). Darcy-Forchheimer hybrid (MoS2, SiO2) nanofluid flow with entropy generation. Computer Methods and Programs in Biomedicine, 185, 105152. [Google Scholar] [PubMed]
17. Yusuf, T. A., Mabood, F., Khan, W. A., Gbadeyan, J. A. (2020). Irreversibility analysis of Cu-TiO2-H2O hybrid-nanofluid impinging on a 3-D stretching sheet in a porous medium with nonlinear radiation: Darcy-Forchhiemer’s model. Alexandria Engineering Journal, 59(6), 5247–5261. [Google Scholar]
18. Gautam, A. K., Verma, A. K., Bhattacharyya, K., Mukhopadhyay, S., Chamkha, A. J. (2021). Impacts of activation energy and binary chemical reaction on MHD flow of Williamson nanofluid in Darcy–Forchheimer porous medium: A case of expanding sheet of variable thickness. Waves in Random and Complex Media, 31, 1–22. [Google Scholar]
19. Raja, M. A. Z., Shoaib, M., Zubair, G., Khan, M. I., Ahmad, S. et al. (2022). Neural artificial networking for a nonlinear Darcy–Forchheimer chemically reactive flow: Levenberg marquardt analysis. Modern Physics Letters B, 36(20), 2250095. [Google Scholar]
20. Joshi, N., Upreti, H., Pandey, A. K. (2022). MHD Darcy-Forchheimer Cu-Ag/H2O-C2H6O2 hybrid nanofluid flow via a porous stretching sheet with suction/blowing and viscous dissipation. International Journal for Computational Methods in Engineering Science and Mechanics, 23(6), 527–535. [Google Scholar]
21. Alshehri, A., Shah, Z. (2022). Computational analysis of viscous dissipation and Darcy-Forchheimer porous medium on radioactive hybrid nanofluid. Case Studies in Thermal Engineering, 30, 101728. [Google Scholar]
22. Mabood, F., Berrehal, H., Yusuf, T. A., Khan, W. A. (2022). Carbon nanotubes-water between stretchable rotating disks with convective boundary conditions: Darcy-Forchheimer scheme. International Journal of Ambient Energy, 43(1), 3981–3994. [Google Scholar]
23. Bestman, A. R. (1990). Natural convection boundary layer with suction and mass transfer in a porous medium. International Journal of Energy Research, 14(4), 389–396. [Google Scholar]
24. Khan, M. I., Qayyum, S., Hayat, T., Waqas, M., Khan, M. I. et al. (2018). Entropy generation minimization and binary chemical reaction with arrhenius activation energy in MHD radiative flow of nanomaterial. Journal of Molecular Liquids, 259, 274–283. [Google Scholar]
25. Ahmad, S., Nadeem, S. (2020). Analysis of activation energy and its impact on hybrid nanofluid in the presence of hall and ion slip currents. Applied Nanoscience, 10, 5315–5330. [Google Scholar]
26. Khan, N. S., Kumam, P., Thounthong, P. (2020). Second law analysis with effects of arrhenius activation energy and binary chemical reaction on nanofluid flow. Scientific Reports, 10(1), 1–16. [Google Scholar]
27. Maraj, E. N., Khatoon, Z., Ijaz, S., Mehmood, R. (2021). Effect of arrhenius activation energy and medium porosity on mixed convective diluted ethylene glycol nanofluid flow towards a curved stretching surface. International Communications in Heat and Mass Transfer, 129, 105691. [Google Scholar]
28. Raza, Q., Qureshi, M. Z. A., Khan, B. A., Kadhim Hussein, A., Ali, B. et al. (2022). Insight into dynamic of mono and hybrid nanofluids subject to binary chemical reaction, activation energy, and magnetic field through the porous surfaces. Mathematics, 10(16), 3013. [Google Scholar]
29. Maxwell, J. C. (1873). A treatise on electricity and magnetism, vol. 1. Oxford: Clarendon Press. [Google Scholar]
30. Brinkman, H. C. (1952). The viscosity of concentrated suspensions and solutions. The Journal of Chemical Physics, 20(4), 571. [Google Scholar]
31. Xuan, Y., Li, Q., Hu, W. (2003). Aggregation structure and thermal conductivity of nanofluids. AIChE Journal, 49(4), 1038–1043. [Google Scholar]
32. Hayat, T., Hussain, Z., Alsaedi, A., Mustafa, M. (2017). Nanofluid flow through a porous space with convective conditions and heterogeneous–homogeneous reactions. Journal of the Taiwan Institute of Chemical Engineers, 70, 119–126. [Google Scholar]
33. Nandi, S., Kumbhakar, B., Seth, G. S., Chamkha, A. J. (2021). Features of 3D magneto-convective nonlinear radiative Williamson nanofluid flow with activation energy, multiple slips and hall effect. Physica Scripta, 96(6), 065206. [Google Scholar]
34. Nandi, S., Kumbhakar, B., Sarkar, S. (2022). MHD stagnation point flow of Fe3O4/Cu/Ag-CH3OH nanofluid along a convectively heated stretching sheet with partial slip and activation energy: Numerical and statistical approach. International Communications in Heat and Mass Transfer, 130, 105791. [Google Scholar]
35. Wang, C. Y. (2002). Flow due to a stretching boundary with partial slip—An exact solution of the Navier–Stokes equations. Chemical Engineering Science, 57(17), 3745–3747. [Google Scholar]
36. Noghrehabadi, A., Saffarian, M. R., Pourrajab, R., Ghalambaz, M. (2013). Entropy analysis for nanofluid flow over a stretching sheet in the presence of heat generation/absorption and partial slip. Journal of Mechanical Science and Technology, 27, 927–937. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF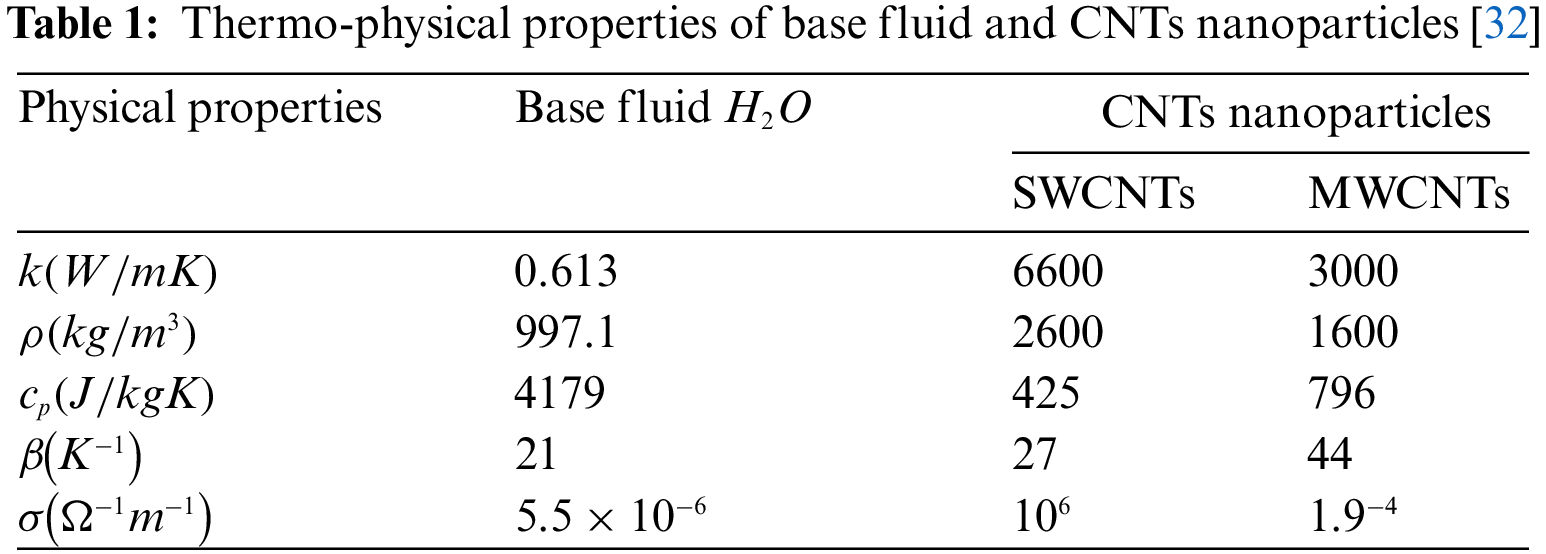
 Downloads
Downloads
 Citation Tools
Citation Tools