 Open Access
Open Access
ARTICLE
Modeling and Validation of Base Pressure for Aerodynamic Vehicles Based on Machine Learning Models
1
Senior Lecturer of Mechanical Engineering, University of Bolton, RAK Academic Center, Ras Al Khaimah, 16038, UAE
2
Department of Mechanical and Aerospace Engineering, Faculty of Engineering, International Islamic University Malaysia,
Selangor, 53100, Malaysia
3
Department of Engineering Management, College of Engineering, Prince Sultan University, Riyadh, 11586, Saudi Arabia
* Corresponding Author: Abdul Aabid. Email:
(This article belongs to the Special Issue: Advanced Computational Methods in Fluid Mechanics and Heat Transfer)
Computer Modeling in Engineering & Sciences 2023, 137(3), 2331-2352. https://doi.org/10.32604/cmes.2023.028925
Received 17 January 2023; Accepted 15 May 2023; Issue published 03 August 2023
Abstract
The application of abruptly enlarged flows to adjust the drag of aerodynamic vehicles using machine learning models has not been investigated previously. The process variables (Mach number (M), nozzle pressure ratio (η), area ratio (α), and length to diameter ratio (γ )) were numerically explored to address several aspects of this process, namely base pressure (β) and base pressure with cavity (βcav). In this work, the optimal base pressure is determined using the PCA-BAS-ENN based algorithm to modify the base pressure presetting accuracy, thereby regulating the base drag required for smooth flow of aerodynamic vehicles. Based on the identical dataset, the GA-BP and PSO-BP algorithms are also compared to the PCA-BAS-ENN algorithm. The data for training and testing the algorithms was derived using the regression equation developed using the Box-Behnken Design (BBD). The results show that the PCA-BAS-ENN model delivered highly accurate predictions when compared to the other two models. As a result, the advantages of these results are two-fold, providing: (i) a detailed examination of the efficiency of different neural network algorithms in dealing with a genuine aerodynamic problem, and (ii) helpful insights for regulating process variables to improve technological, operational, and financial factors, simultaneouslyGraphic Abstract
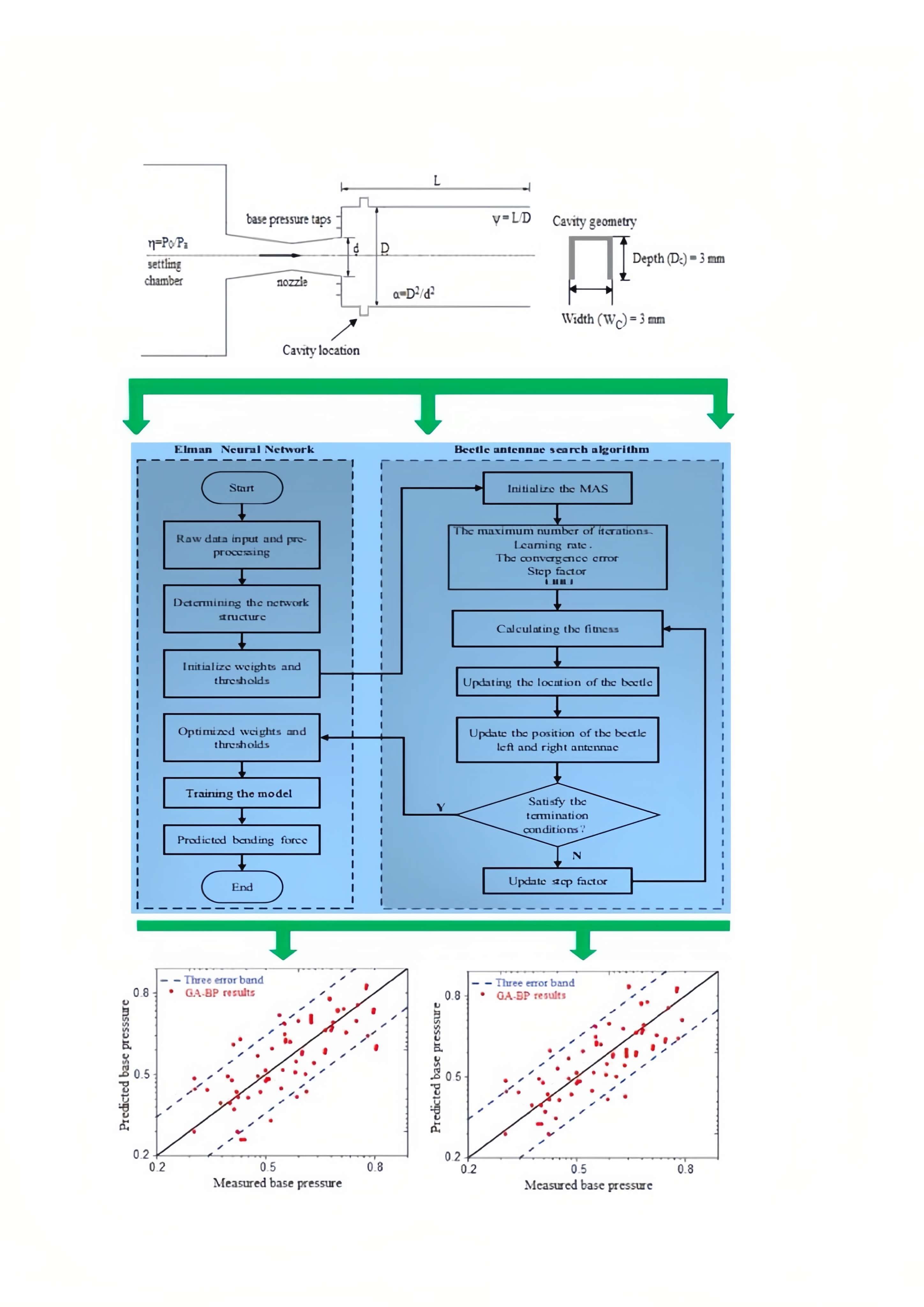
Keywords
Nomenclature
| Convergence precision | |
| Measured value of base pressure (Pa) | |
| BBD | Box-Behnken Design |
| CCD | Central composite design |
| CFD | Computation fluid dynamics |
| IL | Input layer |
| HL | Hidden layer |
| CL | Context layer |
| Spacing between two beetle antennae (mm) | |
| i | Number of iterations |
| OL | Output layer |
| M | Mach number |
| n | Number of samples |
| Specific beetle movement | |
| GA-BP | Genetic algorithm back propagation |
| Learning rate | |
| Mean absolute error | |
| Mean absolute percent error | |
| NN | Nueral network |
| Crossover probability | |
| Nutation probability | |
| PCA-BAS-ENN | Principal component analysis-beetle search algorithm—elman neural network |
| PSO-BP | Particle swarm optimization-back propagation |
| Regression coefficient | |
| Root mean square error | |
| Population size | |
| Highest time for training | |
| TEB | Three error band |
| Location of the simplified center | |
| Output representation of the Elman neural network |
Greek Symbols
| Area ratio (ratio of duct area to nozzle exit area) | |
| Non-dimensionnal base pressure or base pressure | |
| Step decay co-eeficient | |
| η | Nozzle pressure ratio |
| Weights | |
| Length to diameter ratio of the duct |
Subscripts
| Second order | |
| Fifth order | |
| Cavity/cavities in the expanded duct | |
| Predicted | |
| Actual | |
| Desired |
Fluid flows with sudden axisymmetric expansions are a challenging topic in fluid dynamics that may be encountered in a wide range of areas and industrial applications. In most situations, a round tube with a smooth inner surface is adopted. A drop in the pressure in the wake zone is seen while the duct area ascends rapidly. Such type of expanded flows undergoes flow separation and reattachment. Although significant work has been done, these flows are still not completely realized. The area of concern is at the nozzle-duct interface where the nature of the fluid flow phenomena is quite complicated, as it involves shock waves, expansion waves, and high pressure gradients [1]. The shear layer developed at the nozzle exit in the base region results in recirculation flow, which is often said to be highly turbulent and compressible. The intensity of recirculation flow plays a crucial role in controlling the base drag, through which, the performance of high-speed rockets, projectiles, missiles, and other aerodynamic vehicles could be monitored. Recent issues raised concern that the recirculation flow was wave dominated, with not enough mass flow in the base region, causing an increase in the base drag for a certain set of parameters [2]. Hence, it is important to identify such parameters and control their levels, so that their influence on base drag is minimal. As there are quite a few flow and geometric parameters affecting base drag independently [3], varying these parameters experimentally and numerically is quite complex. This explores the possibility of using computational models to know the different input parameters and their combinations that could minimize base drag.
Studies have been carried out by many researchers using a sudden expansion duct with ribs and splitter plates [1,4–6]. These techniques were mostly employed to reduce base drag. Additionally, few investigations demonstrated the application of active control for flow modulation [3,7,8]. These studies employed dynamic control in the form of 1 mm diameter jets to manage
Following the investigative and numerical techniques to passive flow regulation, a numerical approach was also implemented to solve the suddenly expanded flow process. The computational fluid dynamic (CFD) approach is most commonly used for this type of analysis. This approach was undoubtedly used by multiple researchers associated with the current investigation. Over the previous two decades, both passive and active control approaches have been successfully used in CFD investigations. Turbulence modeling is an important aspect of fluid analysis and in most cases; a density-based model was proven to be more suitable for compressible flows. CFD analysis revealed that flow control via tiny jets was favorable for regulating pressure in the separated zone at large η for nozzles flowing under favorable pressure in a convergent-divergent nozzle [9,10]. CFD was also utilized to explore the external flow generation over several types of airfoils, such as the CH10 and wedge, respectively [11]. Utilizing the CFD methodology, the flow control technique in a bluff body was also discovered using a non-circular section in a front face and splitter plate [12].
Several Taguchi designs, response surface methods (RSM), and soft computing approaches have been implemented to determine the level of accuracy and reliability. A study regarding wind tunnel adjustments with variable throat diameters was conducted by Cameron et al. [13] by implementing an operational algorithm. This algorithm was optimized with the genetic algorithm (GA) [14], and the outcomes were matched to those produced with a standard PID controller. CFD simulations were used to construct input-output correlations for recirculation zone length in suddenly expanded flows using a Mamdani-based fuzzy logic technique [15]. The technique included multiple membership functions, and the operating variables were M, η, and expansion corners. The CFD findings indicated that the flow field near the corner vertex was composed of several elemental features. The Triangular function fared the best, having the least uncertainty rate of 9.0705%. Quadros et al. [16] predicted
In a suddenly expanded flow process, a sudden change in the cross-sectional area of the flow from the nozzle to the expanded duct, creates massive changes in velocity and pressure of flow. The dynamics of the flow are dependent on a number of factors that include, M, η, α, γ, etc., and analyzing these factors experimentally is quite complicated [16]. The implementation of cavity/cavities in the expanded duct also creates significant changes in the flow field, and has not been explored much previously. All these factors are critical for creating an optimal design of a suddenly expanded flow process, and can maximize or minimize the base drag. Analyzing such studies experimentally becomes challenging and time consuming, as parameter variation becomes a laborious process. Additionally, although numerical simulations can predict the behavior of suddenly expanded flows, turbulence modelling at the nozzle-duct interface becomes a challenging area due to random fluctuations that result in changes in pressure and velocity. Apart from this, the resolution and stability of the numerical scheme also plays a vital role in determining the accuracy of the numerical model. Considering the issues addressed, and vast amount of data available on experimental and numerical suddenly expanded flows, there is a high potential of implementing the artificial intelligence-based algorithms to model complex fluid systems, due to their ability to capture both linear and non-linear relationships with different parameters of the flow process. These techniques have the ability to handle high dimensional data involving multiple input variables, which otherwise becomes difficult using traditional methods.
Based on the literature cited above, the authors found numerous works that apply different neural network computational techniques on suddenly expanded flows. Also, techniques such as, genetic algorithm and particle swarm optimization in different forms have been applied to similar fluid flow problems. The regression co-efficients
The flow process to be explored experimentally is shown in Fig. 1. Figs. 2 and 3 provide a schematic representation of the experimental setup for determining
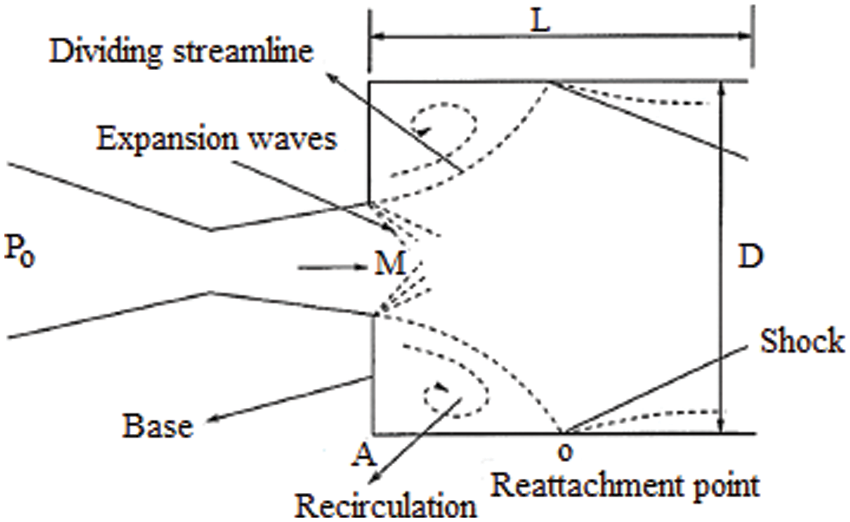
Figure 1: Characteristics of a suddenly expanded flow process
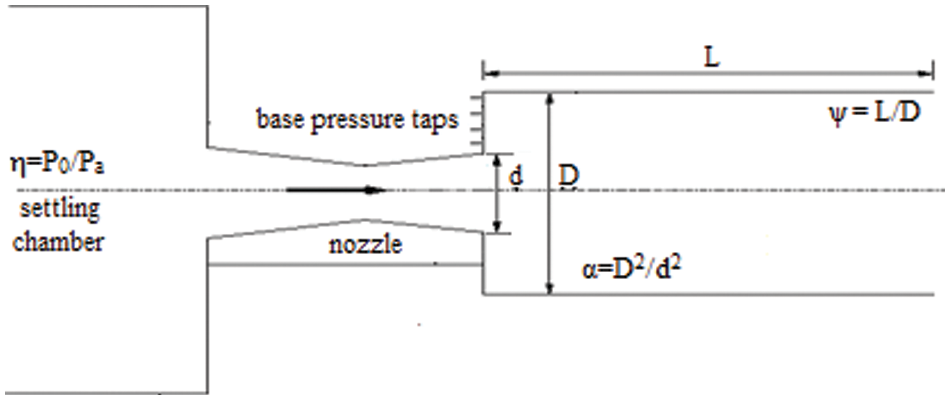
Figure 2: Experimental set up for determing
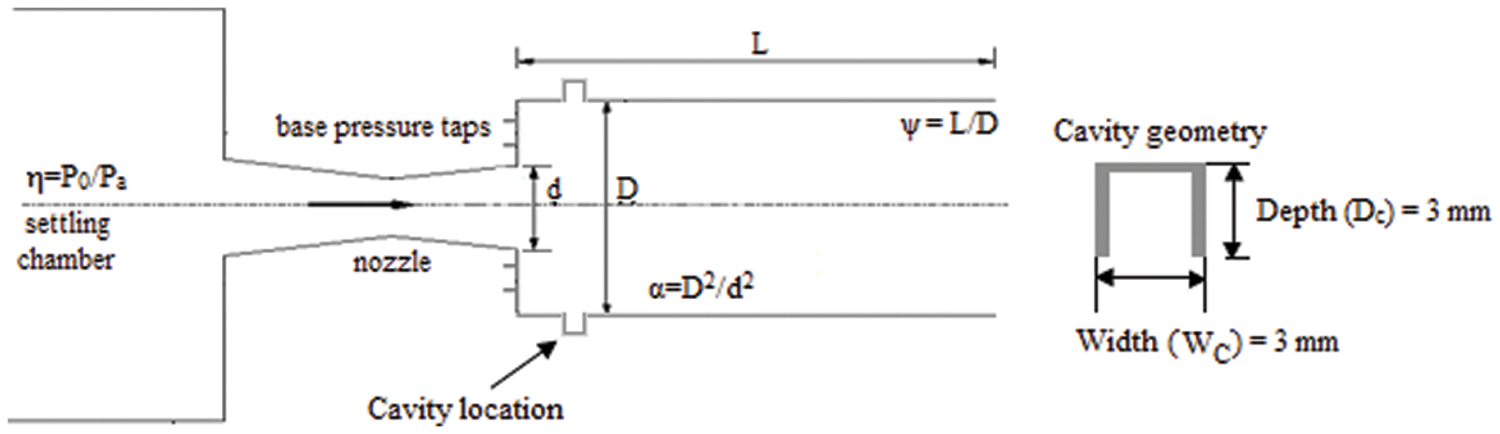
Figure 3: Experimental set up for determining
Nozzles having exit Mach values of 2.0, 2.5, and 3.0 were constructed for the proposed study. The nozzles’ exit Mach numbers were optimized utilizing isentropic relations by Genick [24]. A 1.5 mm thick brass tube was used to fabricate the duct. At the preliminary phase of the experiments, the diameter and length of the duct were maintained at a pre-requisite value. After obtaining the necessary readings for the preceding γ, the duct was partitioned progressively at γ = 9, 6, and 3. In this study, the
3 Design of Suddenly Expanded Flow Preset Model
J. E. Elman suggested introducing a context layer to a feedforward NN to create a one-step postponement manipulator for transitory memory functions, for the NN to respond to time-varying features, thereby improving network stability. The network might then be utilized to tackle quick optimization-seeking challenges that effectively represent the properties of compelling process systems, giving rise to Elman NN [25,26]. The Elman NN is partitioned over four layers: the input layer (IL), the hidden layer (HL), the context layer (CL), and the output layer (OL) (Song et al. [27]). Here,
where,
3.2 BAS Algorithm Optimizing the ENN (BAS‑ENN)
Jiang et al. [29] introduced the BAS algorithm, an intelligent optimization method. The BAS algorithm simulates the natural foraging activity of beetles. When hunting for food, its distinct odor draws the beetle's attention to it. The two antennae of the beetle can smell food through the air, and the strength of the smell they pick up changes depending on how close the food is to them. While the feed is positioned on the left end of the beetle, the left antennae are better able to identify odors than the right antennae. According to the variation in attention observed by the two tentacles, the beetle moves arbitrarily towards the end with stronger intensity. As demonstrated in Wang et al. [30], the position of the food was eventually discovered by repetitive iterations [31].
The beetle is modeled as a parameter that receives input in an n-dimensional space and to compute values, it chooses locations close to oneself based on multiple values obtained throughout either side of the multi spatial domain to obtain the optimal global value. The simplified model was shown in Wang et al. [30].
• Two antennae are located on either ends of the simplified center of the beetle head.
• The ratio of the movement of a specific beetle
• The positioning of the beetle’s head upon approaching the next place from the existing position is random.
The following are the stages of the BAS algorithm:
1. Create and standardize a T-dimensional random vector of the beetle’s original direction (Wei et al. [26]) as seen in Eq. (7):
where
2. At the ith iteration, beetle takes the coordinates as stated by (Lin et al. [32]):
3. The intensity of the food odor is determined by the estimated value of the orientation of the beetle antennas; the next travel direction is then modified (Yue et al. [33]):
Here,
4. As we use the step factor
The BAS-ENN algorithm is eventually established based on the theories presented above, as illustrated in Fig. 4. The following are the steps:
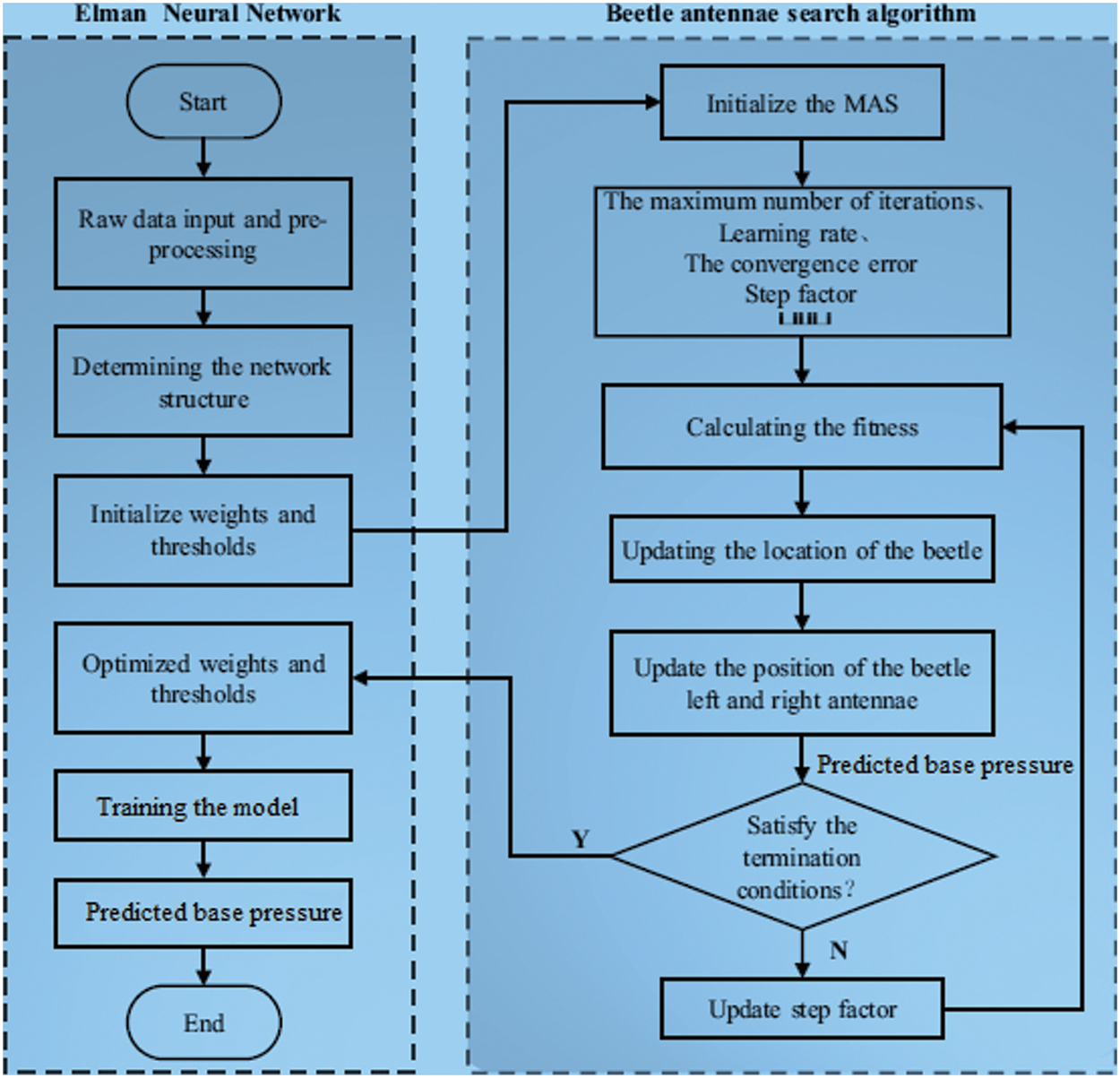
Figure 4: BAS-ENN algorithm flow chart
Step 1: Compute the Elman NN model’s topology and dimensional vector. Assume the suggested model is I-H-O. The neuron numbers in the model’s IL, HL, and OL are denoted by I, H, and O, respectively. Eq. (12) is used to compute H, where is
Step 2: Set up the BAS algorithm’s settings. Calculate the spacing
Step 3: Compute the FF and its value. As demonstrated in Eq. (10), the R
Step 4: Updating the beetle location. Initially, using Eq. (8) the positions of the beetle’s antennae are calculated, and the fitness values of the antennae’s, i.e.,
Step 5: Stop the judgment by iterating. Evaluate if the fitness function value is accurate enough. If a significant level of accuracy is obtained after the completion of iterations, proceed over to Step 6; if not, Step 4 is repeated.
Step 6: Model training and optimal solution creation. The optimum initial weights and thresholds for Elman NN training are found once the BAS algorithm finishes iterating, and this response is used to train the Elman NN until the model’s training accuracy is reached.
Step 7: A unique test set is used to forecast the model to be trained.
The trained model forecasts for the fresh test set. The calculations are performed for this specified test set, and the findings obtained are output.
3.3 Base Pressure Prediction Based on the PCA‑BAS‑ENN Model
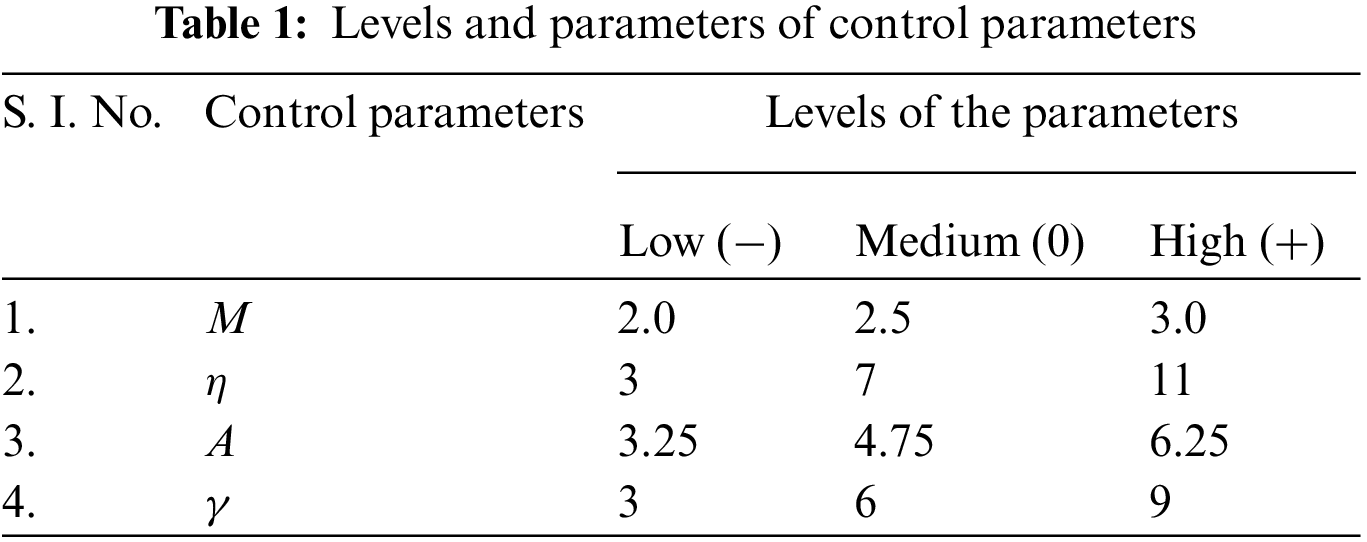
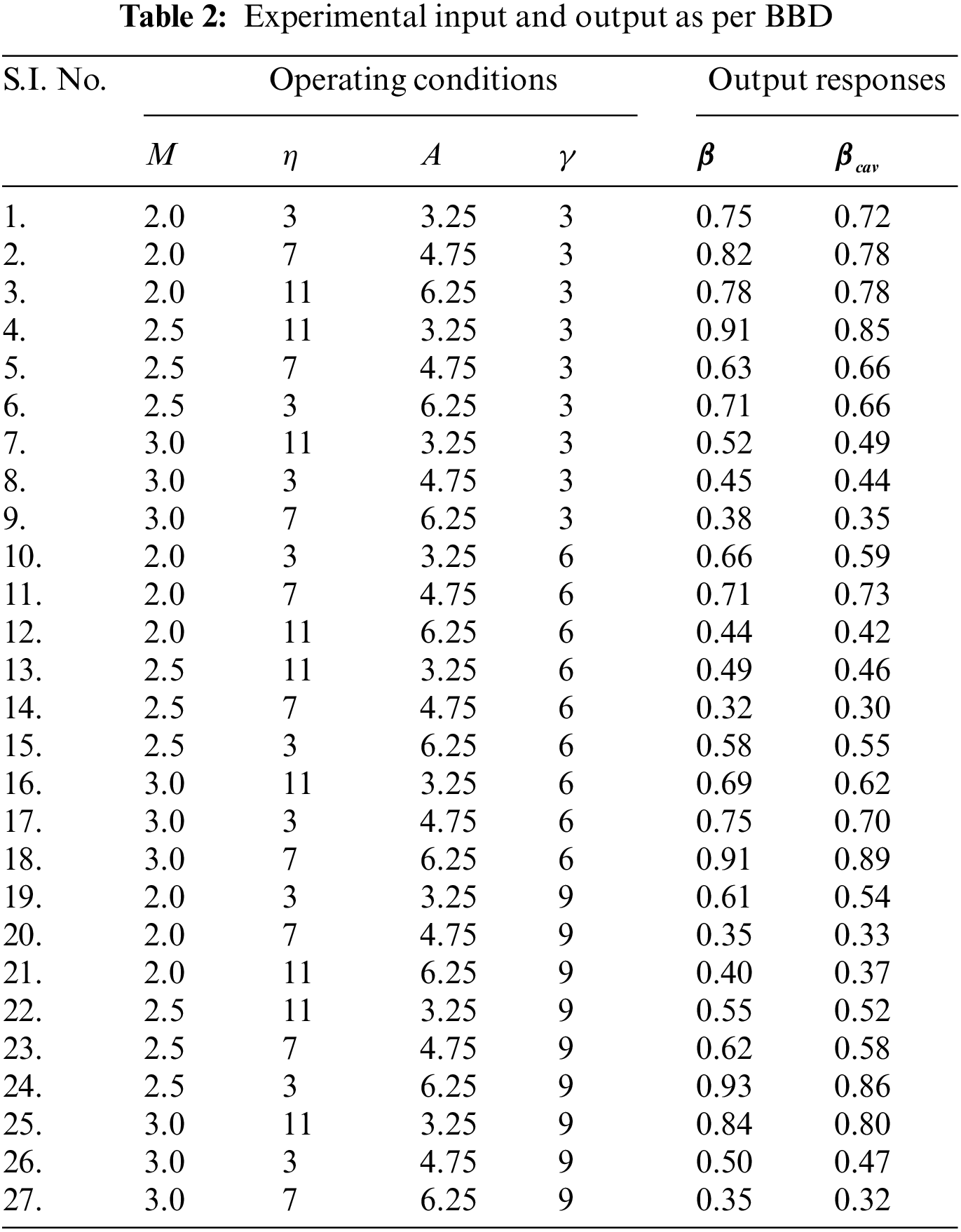
According to the literature, the parameters influencing the suddenly expanded flow process are numerous and complicated. However, in the flow process, M may be selected before experimentation. η, α, γ, and cavity dimensions in the expanded flow process are the other important parameters. Table 1 summarizes the control parameters of the model. For training and testing, data were generated using the Box-Behnken Design (BBD) of response surface methodology (RSM) as shown in Table 2. A MATLAB software was used for this purpose. In response surface methodology (RSM), multiple factors and their interactions are taken into consideration using different experimental designs such as, central composite design (CCD), and Box-Behnken design (BBD), etc. [34]. These designs plan the number of experiments according to the number of parameters and their levels, and as a result develop non-linear regression equations. A statistical Minitab software is used for this purpose. For our study, the BBD was found suitable as per (Quadros et al. [34]). The experimental data have been used to generate nonlinear regression equations that create huge amounts of data required for training and testing. The non-linear regression equations indicate the distribution of the distinctive factors and variables that influence the
The actual
The confidence intervals [
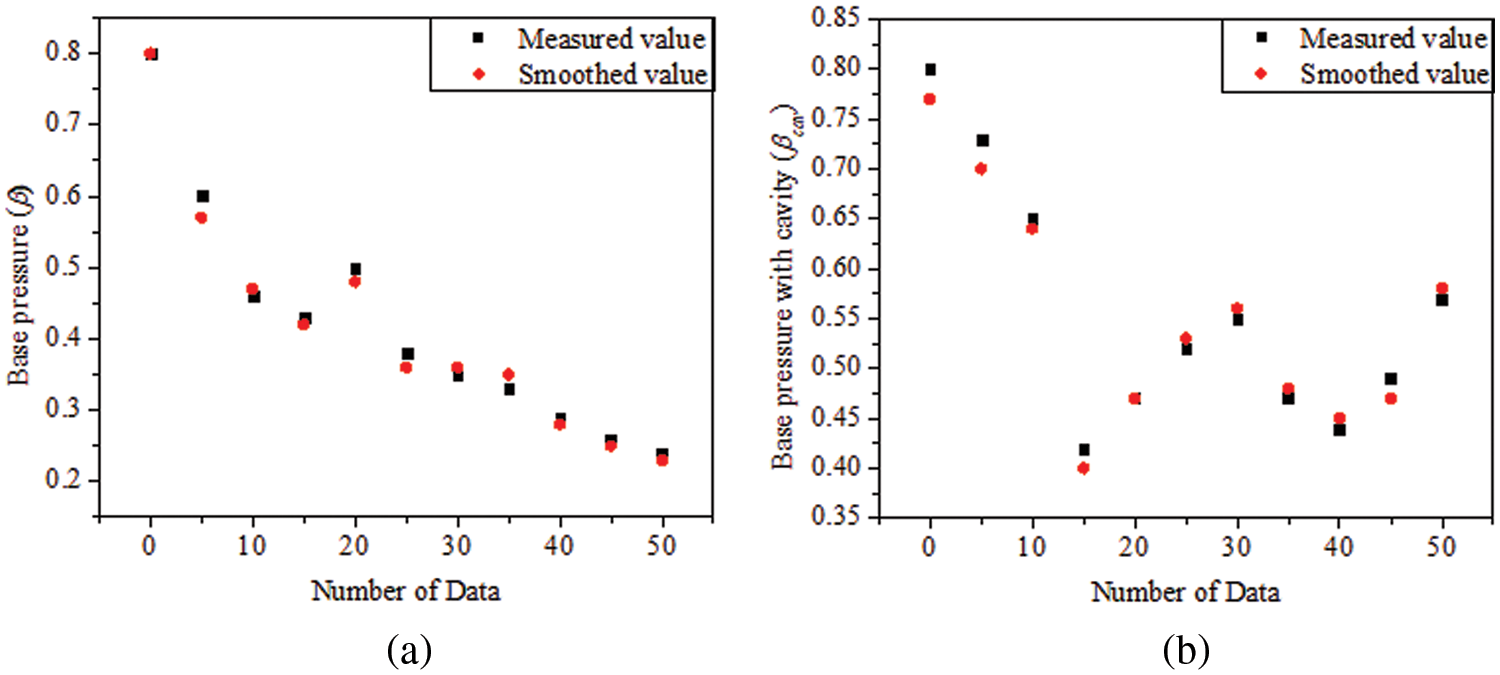
Figure 5: Five-spot triple smoothing
Before the NN analysis, we must understand the behavior of base pressure for the different parameters. For this purpose, variation of
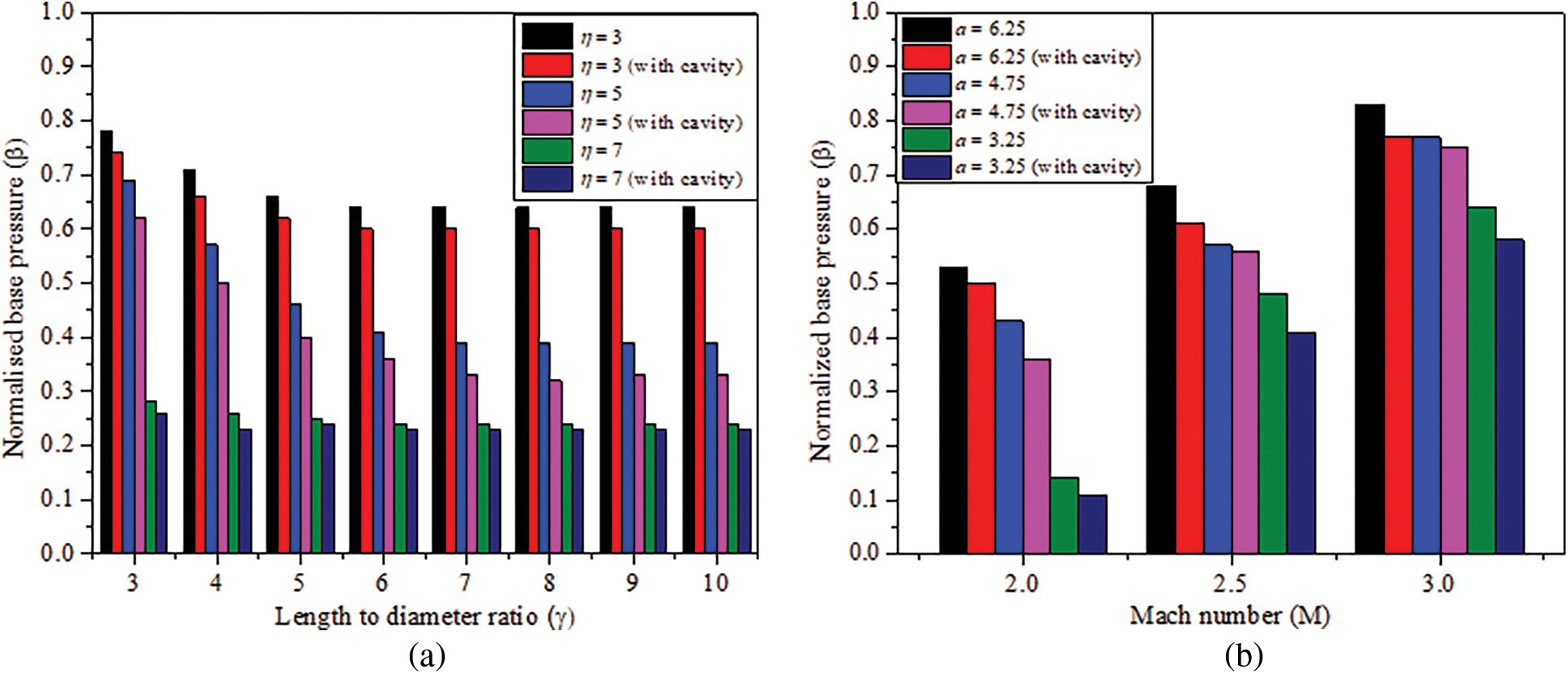
Figure 6: Variation of
It is important to note that, a higher value for
The model contains multiple input parameters, as indicated in Table 1, and these parameters are interconnected. Assume that these are the input variables for explicitely constructing the
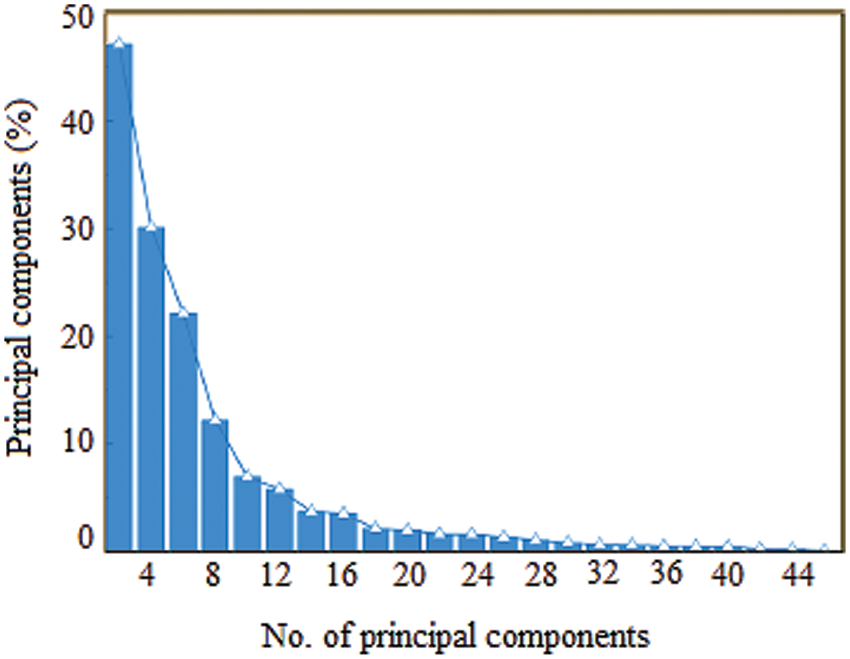
Figure 7: Five-spot triple smoothing
4.2 Performance Analysis of Models
To evaluate the performance of various algorithms on the

Meanwhile, three performances of
where,
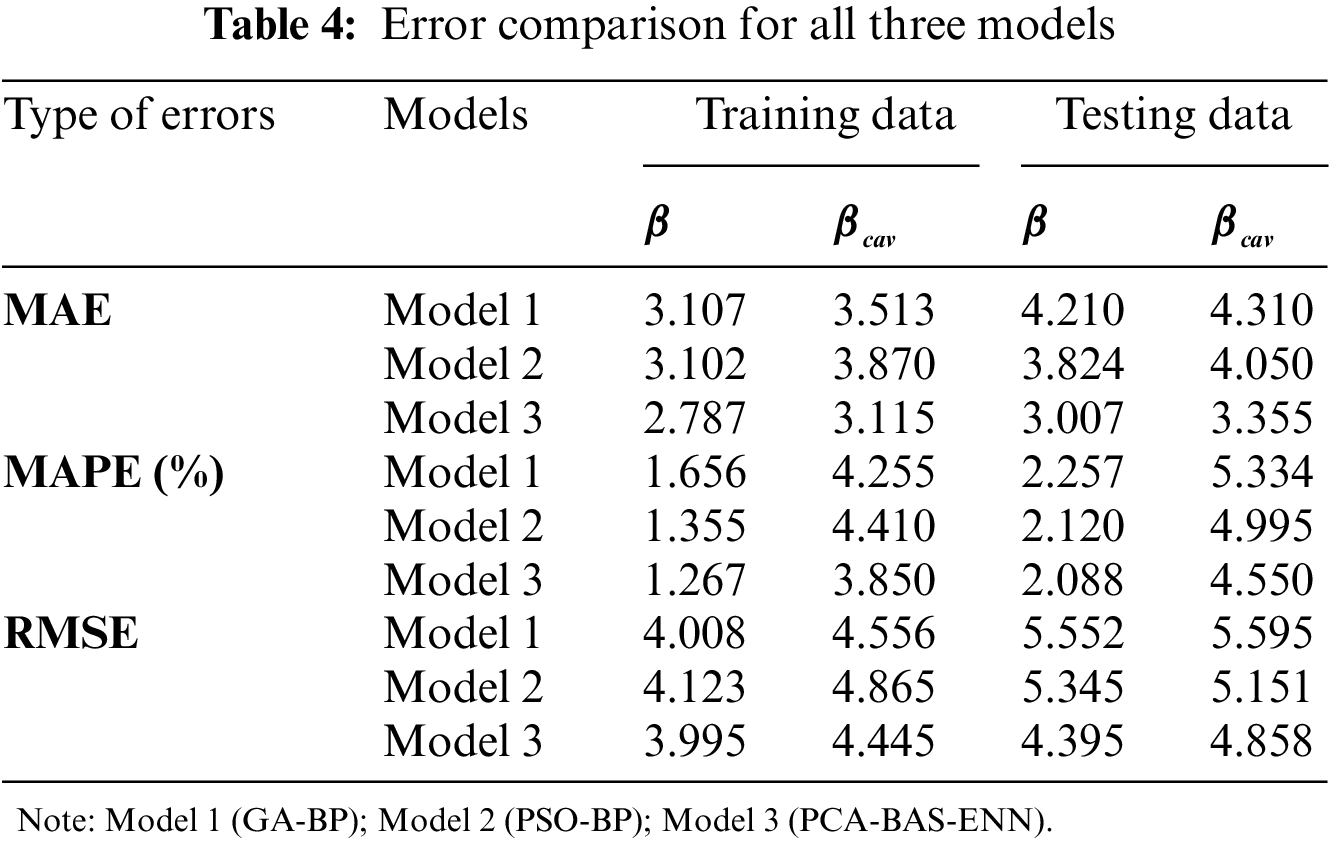
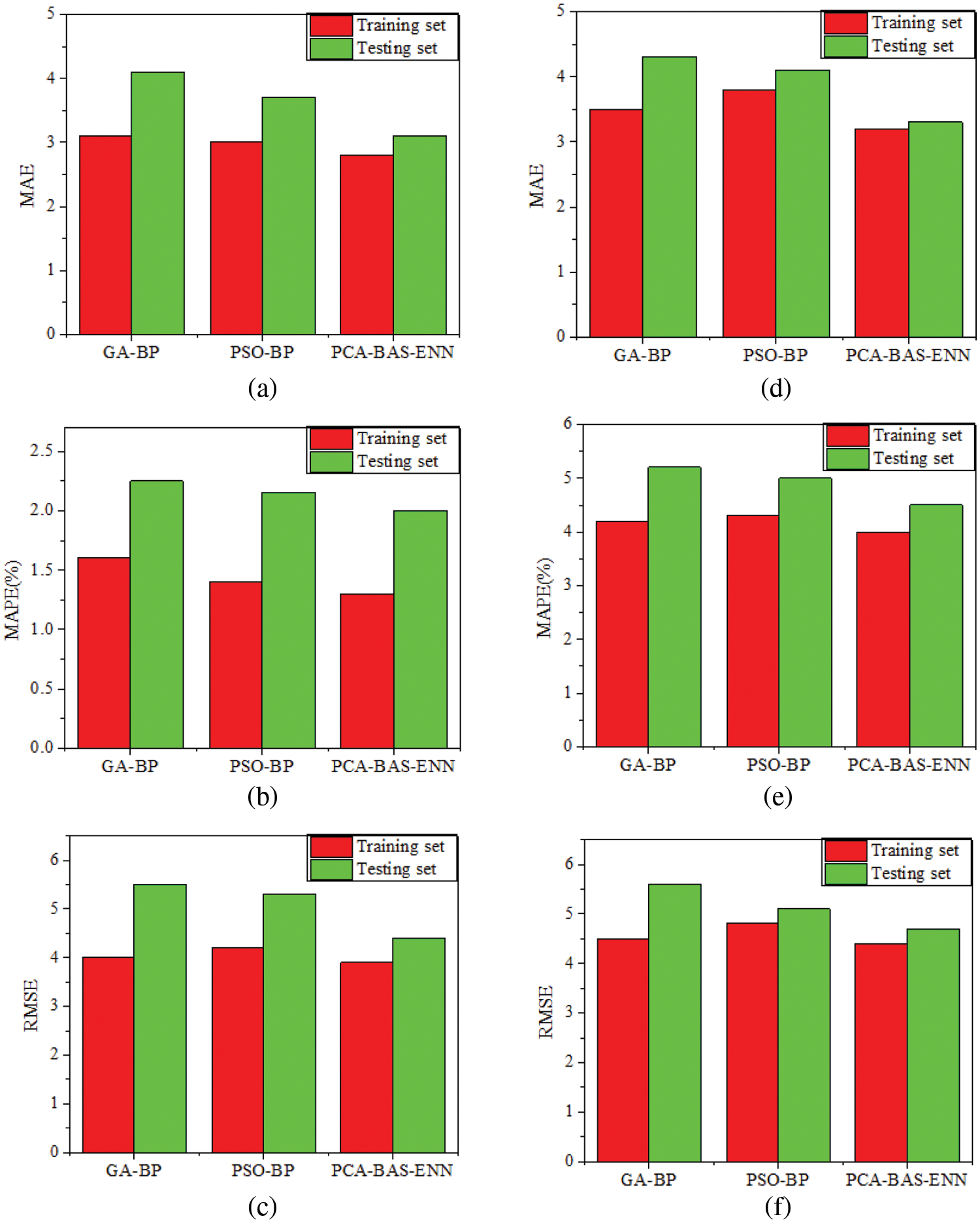
Figure 8: Error comparison of the three models. (a–c) for
From Table 4 and Fig. 8, the following points may be concluded: On the training set, the PCA-BAS-ENN models’ three error indicators for predicting
The primary reason for the poor performance of the GA-BP model (Fig. 8) in prediction of
4.3 Comparison of the Prediction Results of All Three Models
Fig. 9 shows the comparison of performance prediction of all three models for the testing data set. Each models’ performance is determined by the set of data points that fall within the three-error band (TEB), which represents an absolute error of ≤0.05. An increase in the number of data points that fall beyond the TEB indicates the poor performance of the model. From Figs. 9a–9c, the absolute error for prediction of
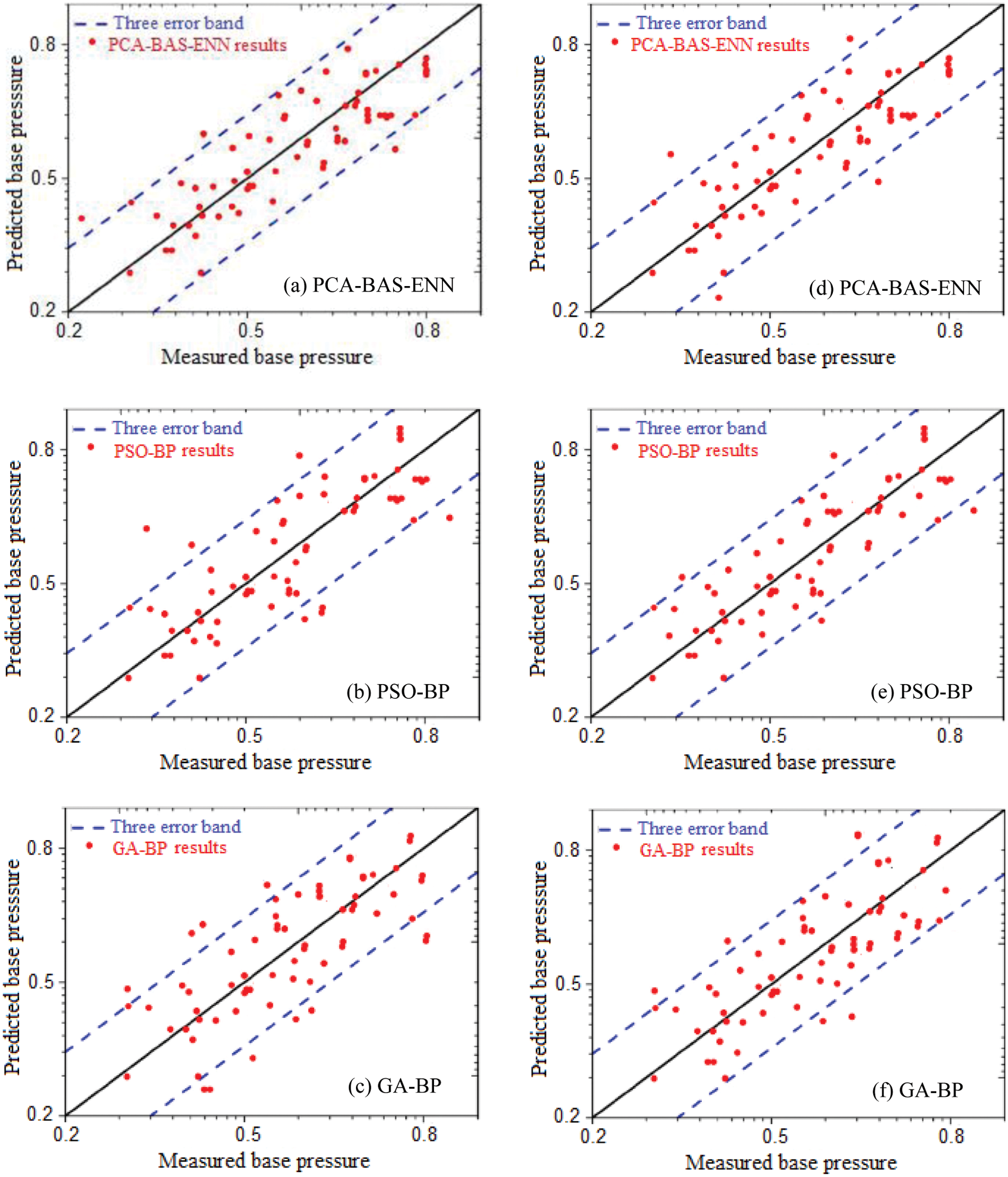
Figure 9: Comparison of performance prediction for all the three models. (a–c) for
The hybrid PCA-BAS-ENN model as seen in Figs. 9a and 9d achieves a low training error due to less deviation, indicating that the model fits the training data very well. The ability of the PCA-BAS-ENN model to perform well in the TEB is due to its robustness and generalization ability. The models ability to reduce input variable dimensionality [27], optimize parameters using the BAS algorithm, and handle various other noise and outliers are the primary reasons that make it a powerfull tool to forecast the
The frequency distribution of the absolute error has been presented in Fig. 10. This type of frequency distribution is plotted as an x-y plot wherein, x-axis represents the absolute error value and y-axis represents the frequency of each error. The model here is said to perform well when its distribution is centered around zero with relatively few errors of high magnitude. Similarly, the model performs poorly when the distribution is spread and sees larger errors of higher magnitude. It can be seen that the errors associated with the PCA-BAS-ENN model prediction are highly pronounced in the 0 range. This is primarily due to reduction of dimensionality of the input data, that moderates the complexity of the data leading to a faster training process [27]. This signifies that there are less significant prediction error samples in this model in comparison to the other two models, thereby confirming that the model is highly secure, balanced and error-tolerant.
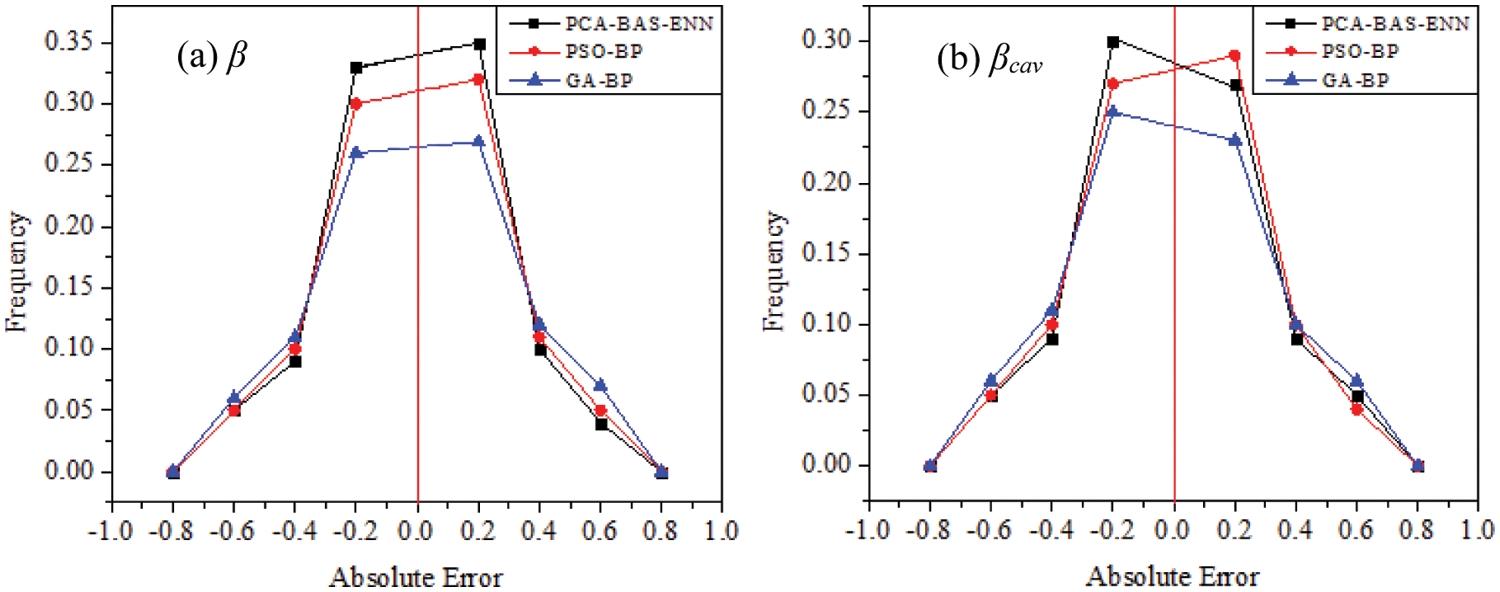
Figure 10: Frequancy distribution of asbsolute errors for (a)
The theoretical
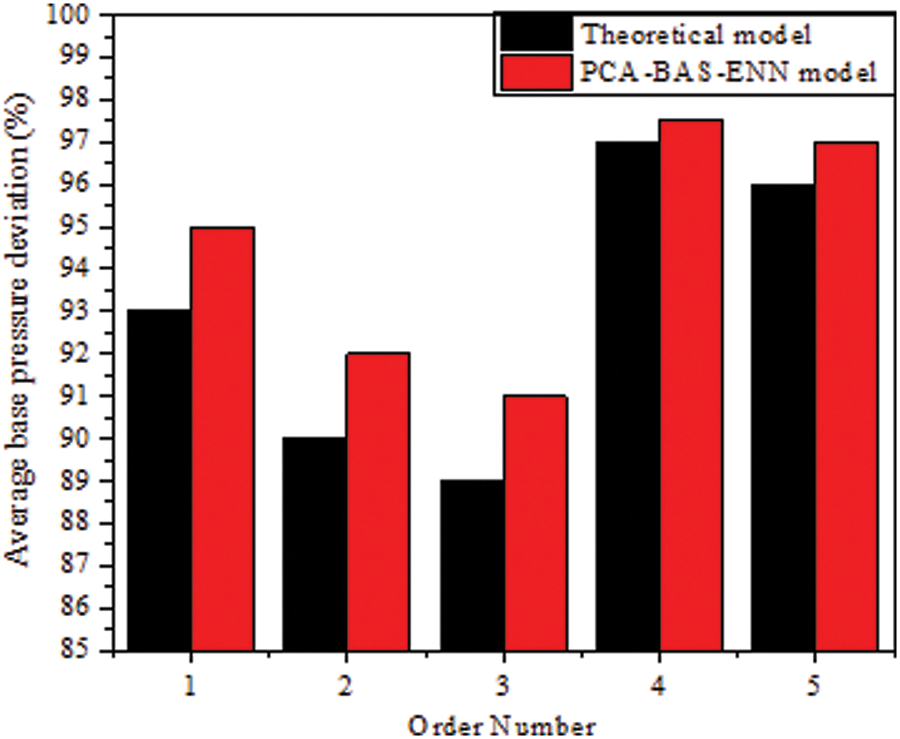
Figure 11: Comparison of base pressure values for varying model settings
Here, n is the sample number,
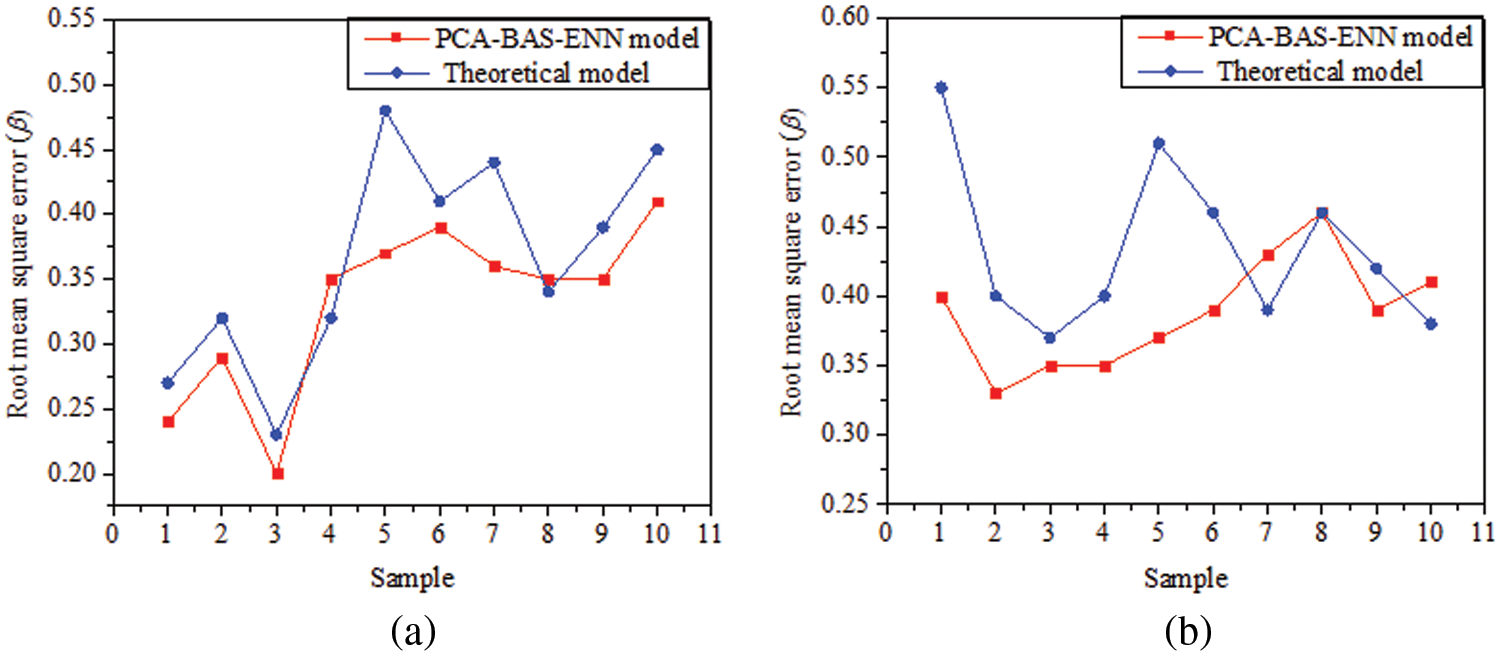
Figure 12: Comparison of base pressure for different models. (a) 2-order, (b) 5-order
Supersonic expanded flow process has been found to be very handy in regulating the base drag of aerodynamic vehicles. Numerous experimental and numerical investigations carried out by researchers previously, supported the implementation of internal modifications in the abruptly expanded duct in order to achieve favourable performance characteristics. However, analyzing such flows for a number of input parameters becomes time-consuming, challenging, and expensive. In this regard, the use of machine learning models in non-linear fluid flow problems still remains unexplored. Therefore, the current study developed a data-driven forecasting model by employing the PCA and BAS-ENN algorithms to determine the optimal setting of
•
• The induction of a cavity into the expanded duct decreased
• Under identical settings, the PCA-BAS-ENN model was compared to the other two algorithms, for determining
• Upon having integrated with the PCA-BAS-ENN model, the practical field implementation displays that the average
• All the machine learning models of the present study for
Acknowledgement: The authors acknowledge the support of Prince Sultan University for paying the article processing charges (APC) of this publication.
Funding Statement: This research is supported by the Structures and Materials (S&M) Research Lab of Prince Sultan University.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Rathakrishnan, E. (2001). Effect of ribs on suddenly expanded flows. American Institute Astronautics and Aeronautics Journal, 9(7), 1402–1404. https://doi.org/10.2514/2.1461 [Google Scholar] [CrossRef]
2. Afzal, A., Aabid, A., Ambareen, K., Khan, S. A., Upendra, R. et al. (2020). Response surface analysis, clustering, and random forest regression of pressure in suddenly expanded high speed aerodynamic flows. Aerospace Science and Technology, 107(1), 106318. https://doi.org/10.1016/j.ast.2020.106318 [Google Scholar] [CrossRef]
3. Khan, S. A., Rathakrishnan, E. (2002). Active control of suddenly expanded flows from over expanded nozzles. International Journal of Turbo and Jet Engines, 19(1–2), 119–126. https://doi.org/10.1515/TJJ.2002.19.1-2.119 [Google Scholar] [CrossRef]
4. Pandey, K. M., Rathakrishnan, E. (2006). Annular cavities for base flow control. International Journal of Turbo and Jet Engines, 23(2), 113–127. https://doi.org/10.1515/TJJ.2006.23.2.113 [Google Scholar] [CrossRef]
5. Sandeep, Y., Ashish, V., Vijayaraja, K., Rathakrishnan, E. (2008). Base pressure control by using ribs in subsonic and sonic suddenly expanded flows. 2nd International Conference on Recent Advances in Experimental Fluid Mechanics, Vijayawada, India. [Google Scholar]
6. Vijayaraja, K., Elongovan, S., Rathakrishnan, E. (2008). Effect of rib on suddenly expanded supersonic flow. International Review of Aerospace Engineering, 39(7), 196–199. https://doi.org/10.2514/2.1461 [Google Scholar] [CrossRef]
7. Baig, M. A. A., Al-Mufadi, F., Khan, S. A., Rathakrishnan, E. (2011). Control of base flows with micro jets. International Journal of Turbo and Jet Engines, 28(1), 259–269. https://doi.org/10.1515/tjj.2011.009 [Google Scholar] [CrossRef]
8. Khan, S. A., Rathakrishnan, E. (2003). Control of suddenly expanded flows with micro jets. International Journal of Turbo and Jet Engines, 20(1), 63–81. https://doi.org/10.1515/TJJ.2003.20.1.63 [Google Scholar] [CrossRef]
9. Fharukh, A. G. M., Alrobaian, A. A., Aabid, A., Khan, S. A. (2018). Numerical analysis of convergent-divergent nozzle using finite element method. International Journal of Mechanical and Production Engineering and Development, 8(6), 373–382. https://doi.org/10.24247/ijmperddec201842 [Google Scholar] [CrossRef]
10. Sajali, M. F. M., Aabid, A., Khan, S. A., Mehaboobali, F. A. G., Sulaeman, E. (2019). Numerical investigation of flow field of a non-circular cylinder. CFD Letters, 11(5), 37–49. [Google Scholar]
11. Aabid, A., Nabilah, L., Khairulaman, B., Khan, S. A. (2021). Analysis of flows and prediction of CH10 airfoil for unmanned arial vehicle wing design. Advances in Aircraft and Spacecraft Science, 8(2), 24–35. https://doi.org/10.12989/aas.2021.8.2.087 [Google Scholar] [CrossRef]
12. Sajali, M. F. M., Ashfaq, S., Aabid, A., Khan, S. A. (2019). Simulation of effect of various distances between front and rear body on drag of a non-circular cylinder. Journal of Advanced Research in Fluid Mechanics and Thermal Sciences, 62(1), 53–65. [Google Scholar]
13. Cameron, R. N., Semih, M. Ö., Daniel, R. L., Keith, W. (2008). Supersonic, variable-throat, blow-down wind tunnel control using genetic algorithms, neural networks, and gain scheduled PID. Applied Intelligence, 29(1), 79–89. https://doi.org/10.1007/s10489-007-0082-y [Google Scholar] [CrossRef]
14. Zhang, D., Liang, Y., Dong, H. (2023). Dendritic cell algorithm with grouping genetic algorithm for input signal generation. Computer Modeling in Engineering & Sciences, 135(3), 2025–2045. https://doi.org/10.32604/cmes.2023.022864 [Google Scholar] [CrossRef]
15. Quadros, J. D., Khan, S. A., Sapkota, S., Vikram, J., Prashanth, T. (2020). On recirculation region length of suddenly expanded supersonic flows, using CFD and fuzzy logic. International Journal of Computational Fluid Dynamics, 34(10), 757–773. https://doi.org/10.1080/10618562.2020.1828580 [Google Scholar] [CrossRef]
16. Quadros, J. D., Khan, S. A. (2020). Prediction of base pressure in a suddenly expanded flow process at supersonic Mach number regimes using ANN and CFD. Journal of Applied Fluid Mechanics, 13(2), 499–511. https://doi.org/10.29252/jafm.13.02.30049 [Google Scholar] [CrossRef]
17. Aabid, A., Khan, S. A. (2020). Investigation of high-speed flow control from C-D nozzle using design of experiments and CFD methods. Arabian Journal of Science and Engineering, 46(3), 2201–2230. https://doi.org/10.1007/s13369-020-05042-z [Google Scholar] [CrossRef]
18. Han, H., Wang, W. (2023). A hybrid BPNN-GARF-SVR prediction model based on EEMD for ship motion. Computer Modeling in Engineering & Sciences, 134(2), 1353–1370. https://doi.org/10.32604/cmes.2022.021494 [Google Scholar] [CrossRef]
19. Afzal, A., Khan, S. A., Islam, T. M., Jilte, R. D., Ambareen, K. et al. (2020). Investigation and back-propagation modeling of base pressure at sonic and supersonic Mach numbers. Physics of Fluids, 32(9), 096109. https://doi.org/10.1063/5.0022015 [Google Scholar] [CrossRef]
20. Aabid, A., Khan, S. A., Afzal, A., Baig, M. (2021). Investigation of tiny jet locations effect in a sudden expansion duct for high-speed flows control using experimental and optimization methods. Meccanica, 6(1), 17–42. https://doi.org/10.1007/s11012-021-01449-6 [Google Scholar] [CrossRef]
21. Al-khalifah, T., Aabid, A., Khan, S. A., Bin Azami, M. H., Baig, M. (2019). Response surface analysis of the nozzle flow parameters at supersonic flow through microjets. Australian Journal of Mechanical Engineering, 13(2), 1–15. https://doi.org/10.1080/14484846.2021.1938954 [Google Scholar] [CrossRef]
22. Quadros, J. D., Nagpal, C., Khan, S. A., Aabid, A., Baig, M. (2022). Investigation of suddenly expanded flows at subsonic Mach numbers using an artificial neural networks approach. PLoS One, 17(10), 1–28. https://doi.org/10.1371/journal.pone.0276074 [Google Scholar] [PubMed] [CrossRef]
23. Quadros, J. D., Suhas Khan, S. A., Aabid, A., Baig, M. (2022). Fuzzy-based prediction for suddenly expanded axisymmetric nozzle flows with microjets. Bulletin of Polish Academy of Technical Sciences, 70(5), 1–11. https://doi.org/10.24425/bpasts.2022.142654 [Google Scholar] [CrossRef]
24. Genick, B. M. (2007). Gas dynamics tables. Version 1.3. https://doi.org/10.5281/zenodo.5523531 [Google Scholar] [CrossRef]
25. Yang, L., Wang, F., Zhang, J. J., Ren, W. H. (2019). Remaining useful life prediction of ultrasonic motor based on Elman neural network with improved particle swarm optimization. Measurement, 143, 27–38. https://doi.org/10.1016/j.measurement.2019.05.013 [Google Scholar] [CrossRef]
26. Wei, L., Wu, Y. Q., Fu, H., Yin, Y. P. (2018). Modeling and simulation of gas emission based on recursive modified Elman neural network. Mathematical Problems in Engineering, 2018(1), 1–10. https://doi.org/10.1155/2018/9013839 [Google Scholar] [CrossRef]
27. Song, L. B., Xu, D., Wang, X. C., Yang, Q., Ji, Y. F. (2022). Application of machine learning to predict and diagnose for hot-rolled strip crown. International Journal of Advanced Manufacturing Technology, 120(1–2), 881–890. https://doi.org/10.1007/s00170-022-08825-w [Google Scholar] [CrossRef]
28. Jiang, X. Y., Lin, Z. Y., He, T. H., Ma, X. J., Ma, S. et al. (2020). Optimal path finding with beetle antennae search algorithm by using ant colony optimization initialization and different searching strategies. IEEE Access, 8, 15459–15471. https://doi.org/10.1109/ACCESS.2020.2965579 [Google Scholar] [CrossRef]
29. Jiang, X. Y., Li, S. (2017). BAS: Beetle antennae search algorithm for optimization problems. International Journal of Robotics and Control, 1(1), 1–5. https://doi.org/10.5430/ijrc.v1n1p1 [Google Scholar] [CrossRef]
30. Wang, Z. H., Gong, D. Y., Li, X., Li, G. T., Zhang, D. H. (2017). Prediction of bending force in the hot strip rolling process using artificial neural network and genetic algorithm (ANN-GA). International Journal of Advanced Manufacturing Technology, 93(9–12), 3325–3338. https://doi.org/10.1007/s00170-017-0711-5 [Google Scholar] [CrossRef]
31. Jiang, X. Y., Li, S. (2017). Beetle antennae search without parameter tuning (BAS-WPT) for multi-objective optimization. Filomat, 34(15), 5113–5119. https://doi.org/10.2298/FIL2015113J [Google Scholar] [CrossRef]
32. Lin, Z. Y., Ma, S., Ma, X. J., Jiang, X. Y., Li, S. (2018). Two new beetle antennae search (BAS) algorithms and their comparative investigation. International Journal of Robotics and Control, 2(1), 9–17. https://doi.org/10.5430/ijrc.v2n1p9 [Google Scholar] [CrossRef]
33. Yue, Z. C., Li, G., Jiang, X. Y., Li, S., Chen, J. et al. (2020). A hardware descriptive approach to beetle antennae search. IEEE Access, 8, 89059–89070. https://doi.org/10.1109/ACCESS.2020.2993600 [Google Scholar] [CrossRef]
34. Quadros, J. D., Khan, S. A., Antony, A. J. (2018). Modelling of suddenly expanded flow process in the Supersonic Mach number regime using DOE and RSM. Journal of Computational Applied Mechanics, 49(1), 149–160. https://doi.org/10.22059/jcamech.2018.248043.221 [Google Scholar] [CrossRef]
35. Deng, J. F., Sun, J., Peng, W., Hu, Y. H., Zhang, D. H. (2019). Application of neural networks for predicting hot-rolled strip crown. Applied Soft Computing, 78, 119–131. https://doi.org/10.1016/j.asoc.2019.02.030 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools