Open Access

ARTICLE

Dynamical Analysis of the Stochastic COVID-19 Model Using Piecewise Differential Equation Technique

Yu-Ming Chu¹, Sobia Sultana², Saima Rashid^3,*, Mohammed Shaaf Alharthi⁴

1 Department of Mathematics, Huzhou University, Huzhou, 313000, China
2 Department of Mathematics, Imam Mohammad Ibn Saud Islamic University, Riyadh, 12211, Saudi Arabia
3 Department of Mathematics, Government College University, Faisalabad, 38000, Pakistan
4 Department of Mathematics and Statistics, College of Science, Taif University, P.O.Box 11099, Taif, 21944, Saudi Arabia

* Corresponding Author: Saima Rashid. Email:

(This article belongs to the Special Issue: Recent Developments on Computational Biology-I)

Computer Modeling in Engineering & Sciences 2023, 137(3), 2427-2464. https://doi.org/10.32604/cmes.2023.028771

Received 06 January 2023; Accepted 20 March 2023; Issue published 03 August 2023

Abstract

Various data sets showing the prevalence of numerous viral diseases have demonstrated that the transmission is not truly homogeneous. Two examples are the spread of Spanish flu and COVID-19. The aim of this research is to develop a comprehensive nonlinear stochastic model having six cohorts relying on ordinary differential equations via piecewise fractional differential operators. Firstly, the strength number of the deterministic case is carried out. Then, for the stochastic model, we show that there is a critical number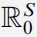 that can predict virus persistence and infection eradication. Because of the peculiarity of this notion, an interesting way to ensure the existence and uniqueness of the global positive solution characterized by the stochastic COVID-19 model is established by creating a sequence of appropriate Lyapunov candidates. A detailed ergodic stationary distribution for the stochastic COVID-19 model is provided. Our findings demonstrate a piecewise numerical technique to generate simulation studies for these frameworks. The collected outcomes leave no doubt that this conception is a revolutionary doorway that will assist mankind in good perspective nature.

---

Keywords

---