 Open Access
Open Access
ARTICLE
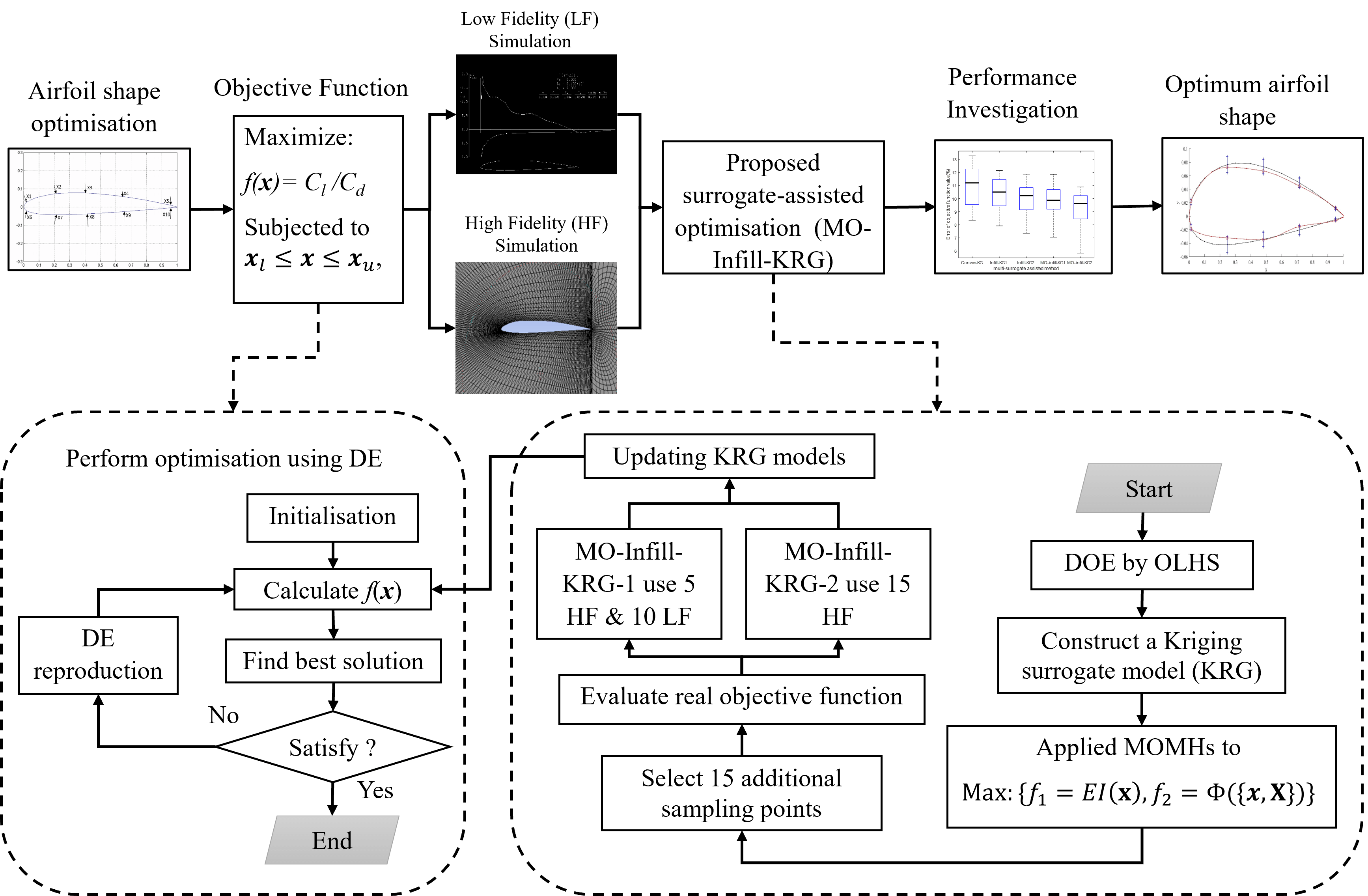
Airfoil Shape Optimisation Using a Multi-Fidelity Surrogate-Assisted Metaheuristic with a New Multi-Objective Infill Sampling Technique
1
Sustainable and Infrastructure Research and Development Center, Department of Mechanical Engineering,
Faculty of Engineering, Khon Kaen University, Khon Kaen, 40002, Thailand
2
Department of Mechanical Engineering, Faculty of Engineering, Mahasarakham University, Mahasarakham, 44150, Thailand
3
Australian Maritime College, College of Science and Engineering, University of Tasmania, Launceston, 7248, Australia
4
Department of Mechanical Engineering, School of Technology, GSFC University, Vadodara, Gujarat, 391750, India
5
Department of Mechanical Engineering, Bursa Uludag University, Bursa, 16059, Türkiye
* Corresponding Author: Nantiwat Pholdee. Email:
Computer Modeling in Engineering & Sciences 2023, 137(3), 2111-2128. https://doi.org/10.32604/cmes.2023.028632
Received 29 December 2022; Accepted 17 March 2023; Issue published 03 August 2023
Abstract
This work presents multi-fidelity multi-objective infill-sampling surrogate-assisted optimization for airfoil shape optimization. The optimization problem is posed to maximize the lift and drag coefficient ratio subject to airfoil geometry constraints. Computational Fluid Dynamic (CFD) and XFoil tools are used for high and low-fidelity simulations of the airfoil to find the real objective function value. A special multi-objective sub-optimization problem is proposed for multiple points infill sampling exploration to improve the surrogate model constructed. To validate and further assess the proposed methods, a conventional surrogate-assisted optimization method and an infill sampling surrogate-assisted optimization criterion are applied with multi-fidelity simulation, while their numerical performance is investigated. The results obtained show that the proposed technique is the best performer for the demonstrated airfoil shape optimization. According to this study, applying multi-fidelity with multi-objective infill sampling criteria for surrogate-assisted optimization is a powerful design tool.Graphic Abstract
Keywords
Nomenclature
| CFD | Computational Fluid Dynamics |
| MHs | Metaheuristics |
| HF | High Fidelity |
| LF | Low Fidelity |
| DOE | Design of Experiment |
| Cl | Coefficient of Lift |
| Cd | Coefficient of Drag |
| RANS | Reynold-Averaged Navier Stoke |
| AOA | Angle of Attack |
| EI | Expect Improvement Function |
| Conventional-KRG | Conventional Kriging Based Surrogate Assisted Optimisation |
| Infill-KRG | Infill Sampling Kriging-Based Surrogate-Assisted Metaheuristics |
| MO-infill KRG | Proposed Multi-objective infill sampling Kriging Based Surrogate-Assisted Metaheuristics |
| f(x) | Objective function value |
| x | Vector of design variables |
| xlb | Lower bound of x |
| xub | Upper bound of x |
| Φ(X) | Space-filling quality of the sampling set X |
| m | Number of sampling points |
| q | Exponent parameter |
| Std | Standard deviation |
| Minimum objective function value in the sampling set | |
| Approximate function value of an additional point x | |
| Mean squared error in a Gaussian process based prediction | |
| Variance of objective function values of the sampling points | |
| Basis function of the sampling point | |
| dj | Euclidean distance of a pair of points in the sampling design X |
| Jj | Number of pairs of points in sampling design X divided by the distance dj |
Burning fossil fuels leads to increased greenhouse gas emissions, which will be one of the major environmental issues for years to come. This results in the development of fuel-efficient vehicles around the world, of which an aircraft is one. It is well known that an aircraft wing with a higher lift-to-drag ratio leads to longer endurance and range. Therefore, airfoil shape design is a critical aspect of aircraft wings and other aerodynamic structure designs, as it affects aerodynamic performance significantly, including lift and drag [1,2]. Another important aspect of airfoil shape optimization is the trade-off between maximum lift and minimum drag. In some cases, a highly cambered airfoil shape may provide increased lift, but at the cost of increased drag. As a result, the design of the airfoil shape needs to be performed by means of optimization, which is usually purposed to explore the trade-off between lift and drag, as well as other objectives, such as stall angle, angle of attack and maximum lift-to-drag ratio [3,4].
An important factor in airfoil shape optimization design is the selection of a tool for aerodynamic analysis. This analysis can either be low-fidelity, e.g., using the vertex lattice method [5], or high-fidelity, using computational fluid dynamics (CFD) [5–7]. Although CFD is more accurate, it also requires complex, computationally expensive models, and design optimization through this approach is nearly impossible. To address this, surrogate models are utilized to approximate the airfoil's aerodynamic performance through the limited number of CFD simulations, enabling a rapid optimization process [8–11]. Despite their advantages, the use of surrogate models presents certain challenges, including the risk of misfit and overfitting. Nevertheless, ongoing development and refinement in this field hold the promise of overcoming these challenges. Enhancement of surrogate-assisted optimization can be attained by implementing multiple surrogate models [12–14], utilizing infill criteria [8,9], or applying multi-fidelity simulation techniques [15,16]. Although infill criteria and multi-fidelity surrogate models have proven effective in improving surrogate models, most research tends to focus on one approach at a time, rather than utilizing both techniques simultaneously. Furthermore, the majority of infill sampling studies focus on single-objective optimization problems, making the exploration of multi-objective optimization with multiple points infill sampling a unique and challenging area of study.
Therefore, this work proposes multi-fidelity multi-objective infill-sampling surrogate-assisted optimization for an airfoil shape design optimization [17,18]. The objective function is set to be maximization of the ratio of lift-to-drag coefficients subjected to airfoil geometry constraints. Computational Fluid Dynamics is used for high-fidelity simulation of airfoils, while the XFoil flow solver is used for low-fidelity simulation of the airfoil. To validate and further assess the proposed method, conventional surrogate assisted optimization and a traditional infill sampling criterion with multi-fidelity simulation are applied. In Section 3, the multi-fidelity analysis tools are described in more details. Section 4 provides details of the multi-surrogate-assisted metaheuristics case. The numerical experiment of each methodology at each test case is illustrated in Section 5. Section 6 demonstrates the results obtained and discusses them, followed by conclusions expressed in Section 7.
Optimization has become a vital part of multi-disciplinary design optimization [19–24], while computational tools based on both high-fidelity simulation [25–27] and low-fidelity simulation [23,28,29] are used practically to simulate the real-world environment and render the outcomes as a function of design variables within the design objectives and constraints framework. Typically, high-fidelity simulation requires extensive computational cost; however, the outcome is more precise than low-fidelity simulation [23,30]. Conversely, the low-fidelity simulations take short times but are less accurate. Therefore, multi-disciplinary design optimization, which requires several function evaluations or simulation runs, is almost impossible based on using high-fidelity simulation alone, while using low-fidelity simulation obtains unacceptable “optimum” solutions. Consequently, the techniques of surrogate-assisted optimization are being used extensively for numerous applications of multi-disciplinary design optimization to reduce [25,31–33] computational competency and analysis times, based on the high-fidelity simulation.
Generally, the surrogate-assisted optimization technique consists of three main steps; generating a set of sampling points, constructing the surrogate model (SuMo), and performing optimization based on the constructed surrogate model [33]. The set of sampling points can be searched for using a design of experiment method, such as the Latin hypercube sampling method (LHS) or the Optimum Latin hypercube sampling method (OLHS) [34,35], while SuMo can be constructed based on several approaches such as Response Surface Methods (RSM) [36], a Gaussian Process or Kriging Model [20,37–41], Radial Basis Functions (RBFs) [42,43], Artificial Neural Networks (ANNs) [44], Support Vector Machines (SVMs) [36], etc. [19,45]. Among these models, Kriging is arguably the most popular one, due to its ability to effectively capture complicated responses and its ability to provide an exact interpolation, objective prediction, and error estimation in the spatial distribution.
Improving the surrogate model method can be achieved by applying infill criteria strategies. The infill sampling technique finds additional points to improve the model by solving an optimization sub-problem, such as maximising an Expected Improvement (EI) indicator [46–49], maximizing the Probability of Improvement function (PI) [50], minimizing the Lower Confidence Bounding (LCB) [51], and Minimizing the Prediction of surrogate models (MP) [52]. Among the various infill criteria, maximizing EI is arguably the most preferred and efficient criterion, while others are also still in use [42,53,54]. Rather than using infill criteria strategies for improving the surrogate model, multi-fidelity surrogate models can also be applied for the reduction of expensive high-fidelity computations with the enhancement of cheaper low-fidelity data [19,53]. Successful use of multi-fidelity surrogate models for several applications of multi-disciplinary design optimization has been reported worldwide [26,27,55,56], e.g., the use in aircraft design [57]. Although the strategy of infill criteria and multi-fidelity surrogate models are used successfully for improving the surrogate model, most of the research usually applies a single strategy; either infill sampling or multi-fidelity modelling in a single work, while the application of using both techniques at the same time is rarely studied. In addition, the infill sampling technique is mostly performed based on a single objective optimization problem, while studying a multi-objective optimization problem for multiple points infill sampling is interesting and challenging.
3 Formulation of Airfoil Shape Optimization Problem
Numerical simulation and optimization techniques [58–60] are widely used in the aerodynamic shape optimization field. Lift and Drag are counted as aerodynamic forces because they exist due to the movement of the aircraft through the air. For aircraft aerodynamic design, a majority of researchers have investigated the lift to drag ratio as a metric of aircraft range and endurance. The literature depicts that the panel method with low-fidelity simulation and CFD simulation with high-fidelity are the two most widely applied and preferred techniques. However, the present work explored both fidelity tools in an effort to accelerate the design process to predict the lift to drag ratio. The airfoil shape design problem is posted to maximize the ratio of lift to drag coefficients which can be expressed as:
Subject to
where f(x) is an objective function; xl and xu are lower bound and upper bound of the design variables of vector x; Cl = coefficient of lift and Cd = coefficient of drag. Here,
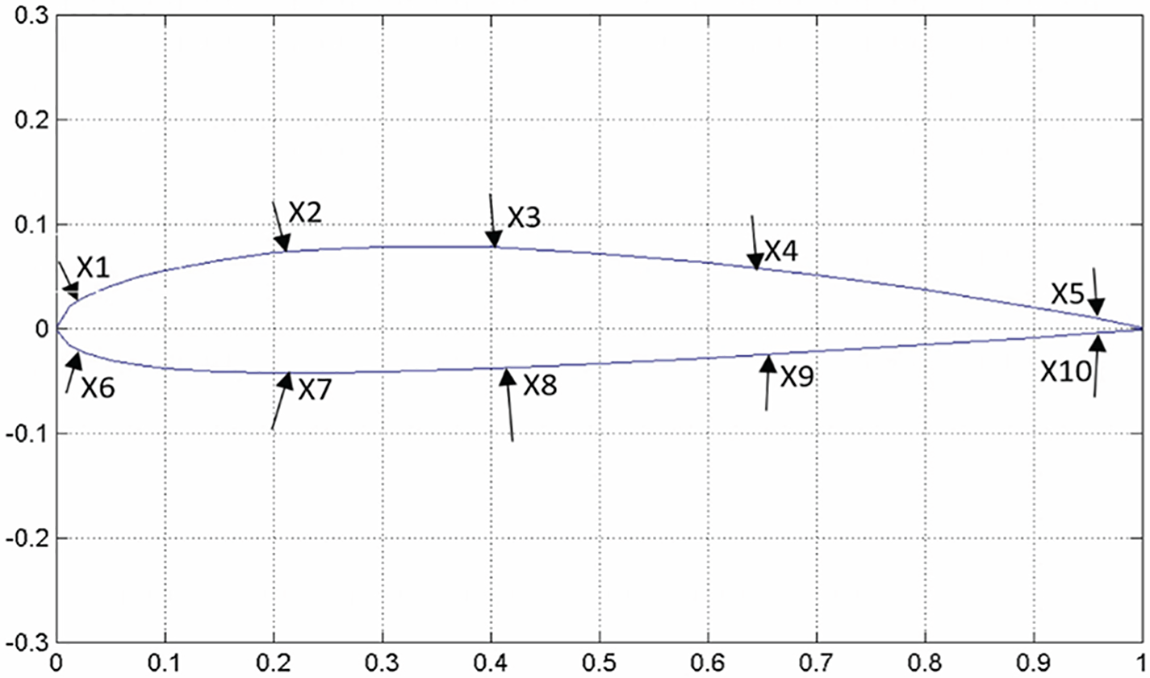
Figure 1: Based line geometry of NACA2412 airfoil and the ten design variables
Multi-fidelity tools are applied for the airfoil aerodynamic analysis to balance between accuracy performance and computational time. The XFoil tool and ANSYS 2020 student version are applied to perform numerical simulation for low-fidelity and high-fidelity, respectively.
3.1 High Fidelity Simulation of Airfoil
The high-fidelity simulation is performed using the ANSYS Fluent student version with the pressure-based finite volume method. The flow conditions are set based on Table 1. A C-type computational Domain is used while the upstream, top and bottom edges of the computational domain are located 12 m radius chord wise away from the trailing edge of the airfoil and the downstream edge is located 12 m chord wise away. An unstructured C-type mesh was used while the meshed model is shown in Fig. 2. Here, a medium mesh is used because the mesh size is limited to 512k cells/nodes for the Ansys student license for a CFD model [56,61,62]. The ANSYS fluent solver is used with steady-state governing equations of continuity and momentum conservation of the Reynold-averaged Navier–Stoke (RANS) simulation. Here, incompressible fluid flow and a pressure-based solver with a 2nd order upwind discretisation scheme are applied. Also, the Spalart–Allmaras turbulence flow model which is found to be effective and robust in the flow analysis of an airfoil as reported in the references [63,64] is used to simulate the 2D flow over the airfoil.
Figure 2: Simulation results of an airfoil with C-type tunnel
Fig. 3 shows the effect of the number of elements on the Cl/Cd values obtained from the CFD analysis; it was found that the Cl/Cd ratio changed when the number of elements ranged from 10,000 to 35,000 elements. However, when the number of elements is higher than approximately 36,000 elements, the lift-to-drag ratio tends to be constant. As a result, in this work, 36,000 elements were used for the CFD analysis.
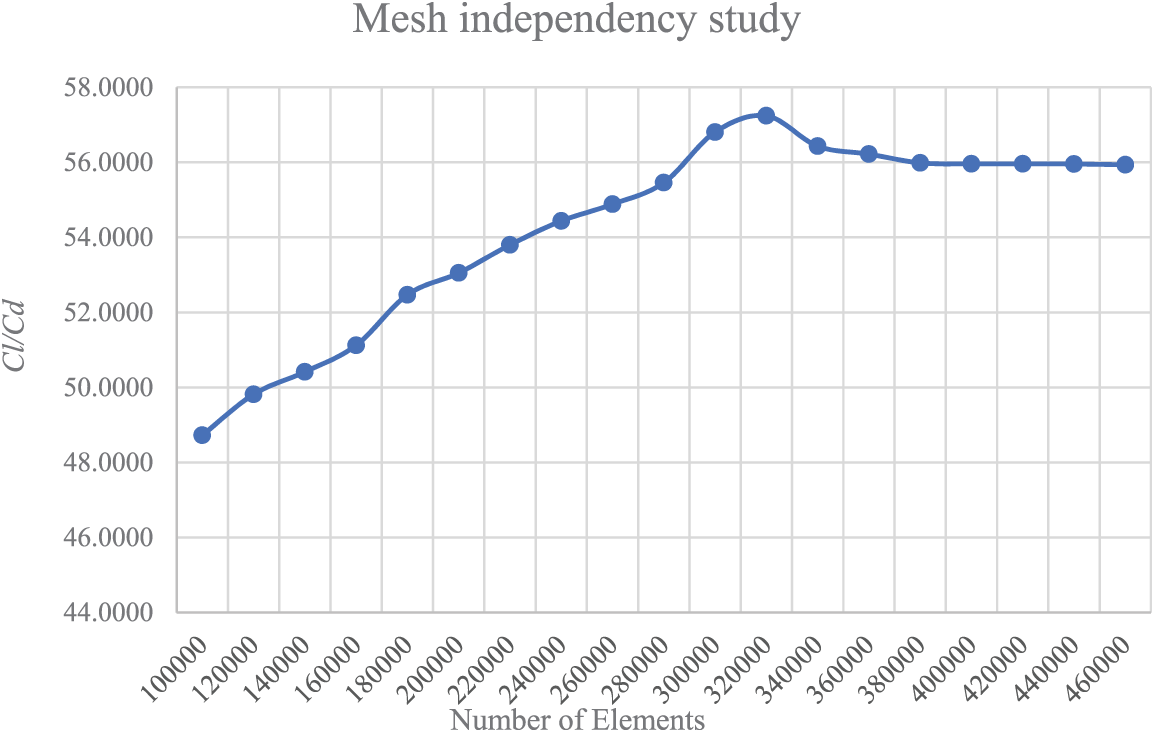
Figure 3: Effect of element size on the Cl/Cd based on the CFD simulation
The XFoil flow solver [65] is applied for low-fidelity simulation by combining the panel method and an integral boundary layer formulation with the subsonic panel code for the analysis of potential flow around the airfoils. The panel method is used to calculate the velocity distribution along the surface of the airfoil by using a given coordinate. The airfoil was imported to XFoil tools to calculate the airfoil performance, and then the number of coordinate points was set as 250 points to resolve the flow properties in the curved region [50,51,66]. To predict the airfoil performance at low Reynolds numbers, a code was developed. The essential design parameters are the airfoil geometry, the Mach number and the Reynolds number, which are set to be the same as for the high-fidelity simulation and also the number of iterations was defined as 400. The results are shown as a graph of the lift and drag coefficient vs. the angle of attack, while pressure distribution around the airfoil can be acquired. Fig. 4 shows the airfoil model simulation in the XFoil with the example results obtained.
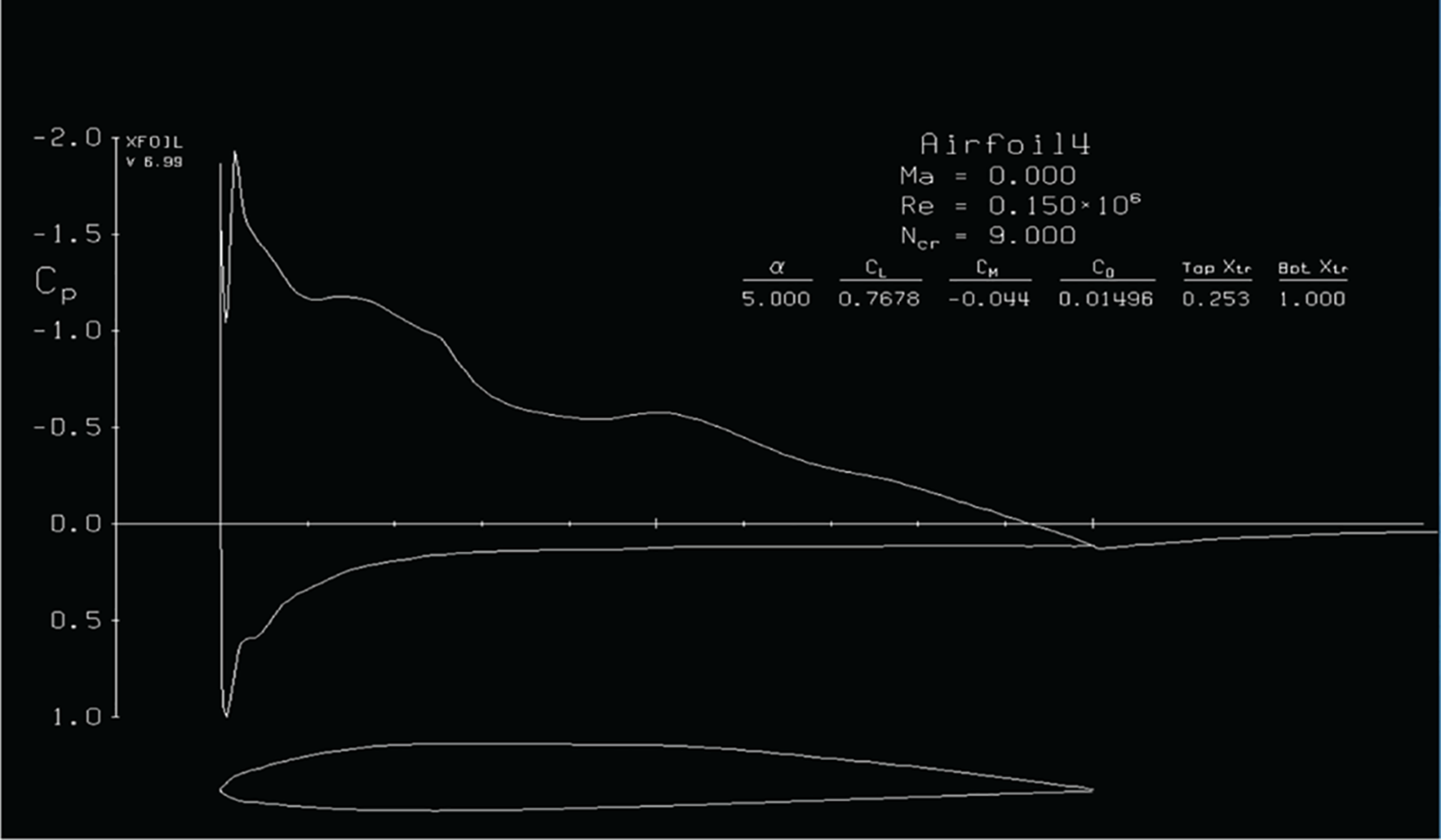
Figure 4: Example results obtained in XFoil
4 Multi-Objective Infill Sampling Kriging Based Surrogate-Assisted Metaheuristics
In real-world problems, optimization is usually time-consuming and computationally expensive in the evaluation of objective functions. Surrogate models can successfully alleviate this problem by reducing the computation time for every numerical simulation code.
4.1 Kriging Based Surrogate-Assisted Metaheuristics
Conventional Kriging based surrogate-assisted optimization (Conventional-KRG) consists of three main steps. Firstly, a set of sampling points is generated throughout the design domain while real expensive objective function values are evaluated. Afterwards, the Kriging surrogate model is constructed [40,67] and optimization is performed based on the constructed inexpensive Kriging model. Finally, the real expensive objective function value at the optimum point is evaluated.
The KG approximation function can be expressed as follows:
where
where f is a vector of function values of the sampling points.
4.2 Infill Sampling Kriging Based Surrogate-Assisted Metaheuristics (Infill-KRG)
Infill sampling is a technique used to improve the model accuracy, which leads to the improvement of the optimum solution. The main idea of an infill sample technique is to add a sampling point to update the already constructed surrogate model, which is expected to obtain the global optimum solution. The additional solution can be found by solving an optimization sub-problem posed to maximize the expected improvement function, expressed as:
subject to
where x is a vector of design variables or a sampling solution and EI is the expected improvement function. The
where
The Kriging based infill sampling surrogate-assisted optimization starts with generating a set of sampling points using a design of experiment method (DOE), and then performing real objective function evaluations. Then, the Kriging surrogate model is constructed. After that, the optimization sub-problem (Eq. (4)) is solved to find the additional point, with its actual expensive objective function value being evaluated. The constructed Kriging model is then updated while optimization is operated based on the updated Kriging model. After the optimum solution is obtained, a real expensive objective function at the optimum point is evaluated. The computational steps for constructing the infill-KRG surrogate model are shown in Algorithm 1.

4.3 Proposed Multi-Objective Infill Sampling Kriging Based Surrogate-Assisted Metaheuristics (MO-Infill Sampling-KRG)
The proposed infill sampling technique is based on the findings of a previous study [68]. It was found that the EI indicator is used for improving an optimum solution to the design problem. However, in such work, it is seen that using a surrogate model that can capture the true objective function landscape, even though the overall root mean square error is high, can lead to better optimum results. This implies that the diversity of the sampling points plays a very vital role in improving the performance of surrogate-assisted optimization. As a result, this work proposes an infill sampling strategy that optimizes EI and sampling point diversity. The optimization sub-problem then becomes multi-objective optimization. For the diversity indicator, a space-filling function proposed by Morris et al. [68,69] is used as another objective function to balance between improving the optimum and capturing a true function landscape. The optimization problem is proposed as a multi-objective optimization problem. A few solutions from the Pareto front obtained from solving the proposed optimization sub-problem are selected to be additional points. The space-filling quality used can be expressed as:
where
The optimization problem can be expressed as:
subject to
Similarly, for the Kriging based infill sampling surrogate assisted optimization strategy, the proposed multi-objective infill sampling surrogate assisted optimization strategy starts with generating a set of sampling points (X) and performing real expensive objective function evaluation (using high-fidelity or low-fidelity). Then, the Kriging surrogate model is constructed and an optimization sub-problem (Eq. (7)) is solved using a multi-objective MH. After the Pareto front is obtained, a Pareto selection process for the multi-objective MH is applied to search for the additional points with their real expensive objective function values being evaluated. The constructed Kriging model is then updated while optimization is performed based on the updated Kriging model. After the optimum solution is obtained, a really expensive objective function at the optimum point is evaluated. The computational steps of the proposed MO-infill-KRG are shown in Algorithm 2.

In order to examine the performance of the proposed method, three surrogate assisted optimization techniques including the conventional Kriging based surrogate assisted optimization, infill sampling Kriging based surrogate assisted optimization and the proposed multi-objective infill sampling Kriging based surrogate assisted optimization are applied for solving the proposed airfoil shape optimization problem as detailed in Section 2. Multi-fidelity modeling is also applied for objective function calculation. The details of the surrogate model techniques used in this study are as follows:
• Conventional-KRG; Conventional Kriging-based surrogate model is used. The Kriging model is constructed based on the high-fidelity simulation for 75 samplings.
• Infill-KRG1 (detailed in Section 3.1). The Kriging model is initially constructed based on the high-fidelity simulation for 60 samplings points. Then, sampling points from high-fidelity simulations are added to update the Kriging model after solving the optimization sub-problem as detailed in Section 3.1. The Kriging model is updated 15 times, which means 15 sampling points are added. Among the 15 sampling points, 5 sampling points are from high-fidelity simulation while the other 10 sampling points are from low-fidelity simulation. The total number of high-fidelity simulations is 60 + 5 = 65 for this case.
• Infill-KRG2 (detailed in Section 3.1). The Kriging model is initially constructed based on the high-fidelity simulation for 60 samplings points. Then, sampling points from high-fidelity simulations are added to update the Kriging model after solving the optimization sub-problem as detailed in Section 3.1. The Kriging model is updated 15 times while 15 sampling points are added. Among the 15 sampling points, 10 sampling points are from high-fidelity simulation while the other 5 sampling points are from low-fidelity simulation. The total number of high-fidelity simulations is 60 + 10 = 70 for this case.
• MO-infill-KRG1 (detailed in Section 3.2). The Kriging model is initially constructed based on the 40 high-fidelity sampling points and 20 low-fidelity samplings points. Then, 15 additional sampling points are generated based on the proposed multi-objective-infill sampling technique. The high-fidelity simulation is applied for the 5 sampling points and low-fidelity simulation is applied for 10 sampling points and all 15 sampling points are used to update the KRG model. The total number of high-fidelity simulations is 40 + 5 = 45 for this case.
• MO-infill-KRG2 (detailed in Section 3.2). The Kriging model is initially constructed based on the 40 high-fidelity samplings points and 20 low-fidelity samplings points. Then, 15 sampling points are generated based on the proposed multi-objective-infill sampling technique. High-fidelity simulation is applied for all 15 sampling points and used to update the KRG model. The total number of high-fidelity simulations is 40 + 15 = 55 for this case.
For each surrogate model strategy, the initial sampling points are generated using an optimum Latin hypercube sampling technique proposed by Pholdee et al. [34]. A differential evolution (DE) algorithm [70] is used for solving the infill sampling sub-problem, while for the main airfoil shape optimization, the hybrid real-code population-based incremental learning and differential evolution (RPBILDE) [71,72] is used to solve the proposed multi-objective infill sampling sub-problem.
In order to investigate the performance of the above surrogate assisted MH methods, each method is used to tackle the proposed airfoil shape optimization design problem for 20 optimization runs. The number of iterations is set to be 200 while the population size is 50 in the present work. The termination criterion for all optimizers is set as 10,000 function evaluations, which is the multiplication of 50 population size and 200 iterations.
In this investigation, the airfoil shape optimization is executed using the multi-fidelity surrogate assisted MH while the surrogate models are constructed based on the Kriging model, infill sampling, and the MO-infill sampling methods. The performance of the various surrogate-assisted MH techniques is investigated based on the percentage error between surrogate model approximation and the real objective function values by high-fidelity obtained at the optimum points of each techniques. After performing the optimization process for 20 independent runs, Fig. 5 shows the box plot of the percent error of the objective function values at the optimum points for all techniques. For each boxplot, the upper and lower horizontal lines correspond to the maximum and minimum percent error at the optimum points, while the internal line shows the median of the percent error at the optimum points. According to Fig. 5, the best performer based on the median values is the proposed MO-infill-KRG2, while the second best and the third best are MO-infill-KRG1 and infill-KRG2, respectively. The minimum percent of error can be archived from the proposed MO-infill-KRG2.
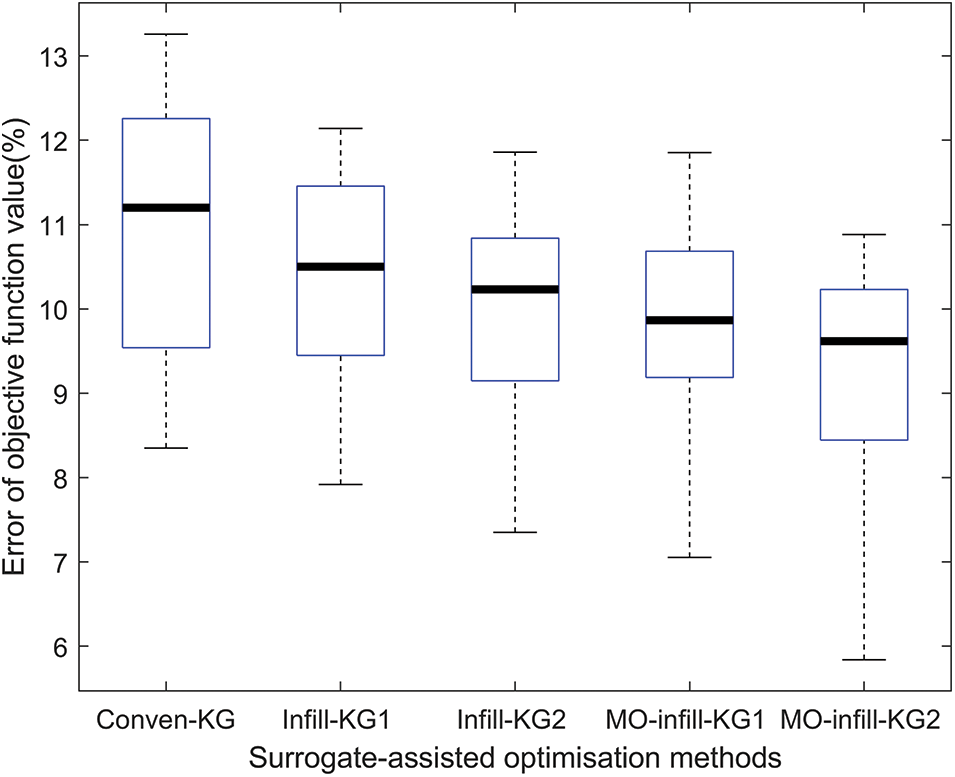
Figure 5: Percentage of error at the optimum point for 20 optimization runs
Table 2 shows the real objective function values at the optimum points for each method after performing high-fidelity simulation. From the results, the best performer according to the mean of the real optimum values is MO-infill-KRG2, while the second and third best are MO-infill-KRG1 and infill-KRG2, respectively. For the consistency performance according to the standard deviation (STD), the best algorithm is Conventional-KRG, while the second and third best methods are Infill-KRG1 and Infill-KRG2, respectively. The best objective function value obtained is from using MO-infill-KRG2. Table 3 shows the real objective function value of the baseline airfoil, and the optimum airfoil obtained from the various surrogate-assisted MH techniques. According to this table, MO-infill-KRG2 obtained the best optimum airfoil while the second and third optimum airfoils are from MO-infill-KRG1 and Infill-KRG2, respectively.
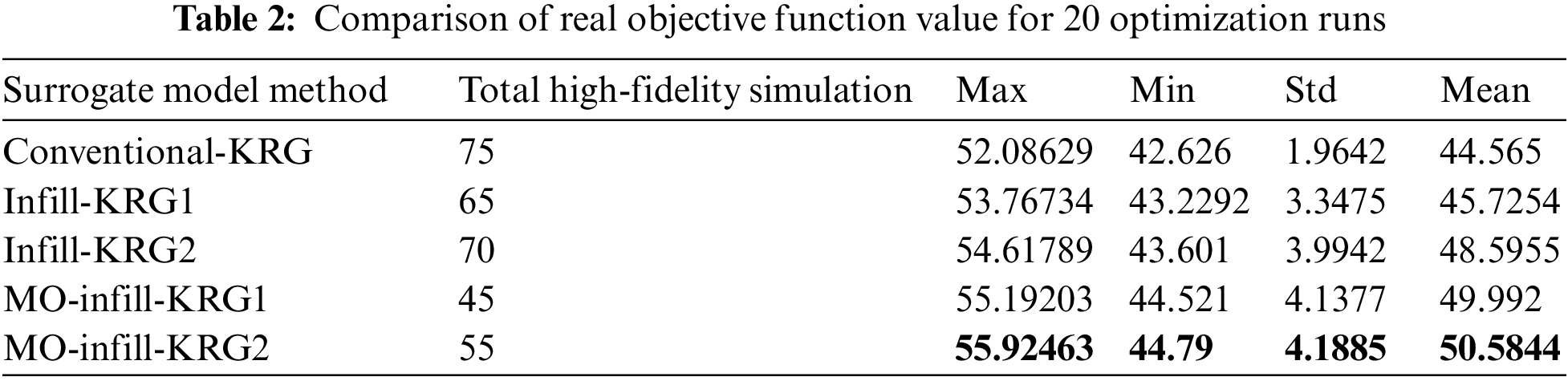
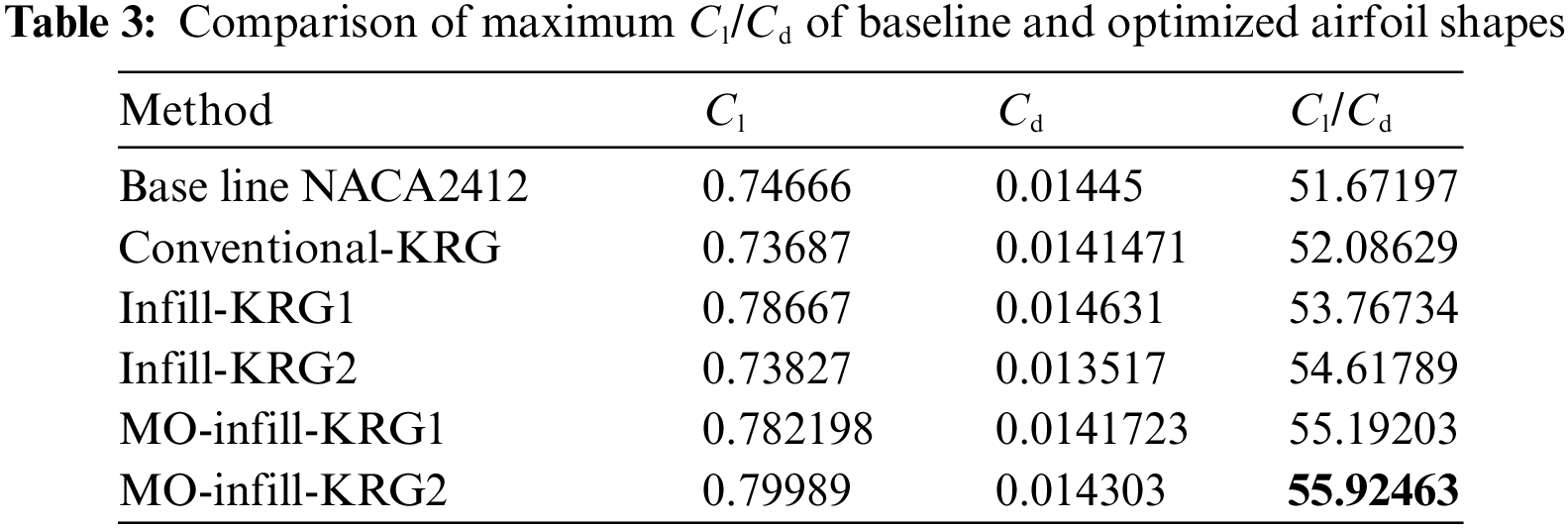
Fig. 6 shows the best airfoil accomplished by MO-infill-KRG2 after the optimization process. The black line represents the baseline geometry, the red line depicts the optimized airfoil shape, and the blue line illustrates the upper and lower bounds of the airfoil nodal points. From Fig. 6, the optimum airfoil geometry shows the lower leading-edge radius, smaller airfoil thickness and different lower and upper surfaces, leading to the aerodynamic efficiency obtained as illustrated in Figs. 7–9. Figs. 7–9 respectively show the comparison of variation of drag coefficient, lift coefficient and ratio of lift and drag coefficient with respect of the angle of attack of the optimized airfoil from MO-infill-KRG2 and the base line airfoil (NACA2412) obtained from CFD analysis. From Figs. 7 and 8, the drag coefficient obtained from the optimum airfoil is better than the base line airfoil for the angle of attack more than 6°, while the lift coefficient obtained from the optimum airfoil is better than the base line airfoil for the angle of attack lower than 8°. For the angle of attack between 8° and 10°, the lift coefficient of both the optimum airfoil and the base line airfoil stall, whereas the optimum airfoil still has higher lift coefficient. Based on Fig. 9, the ratio of lift to drag coefficient obtained from the optimum airfoil is better than the base line airfoil for all angles of attack. Overall, the optimum airfoil obtained from the proposed MO-infill-KRG2 is aerodynamically superior to the baseline airfoil.
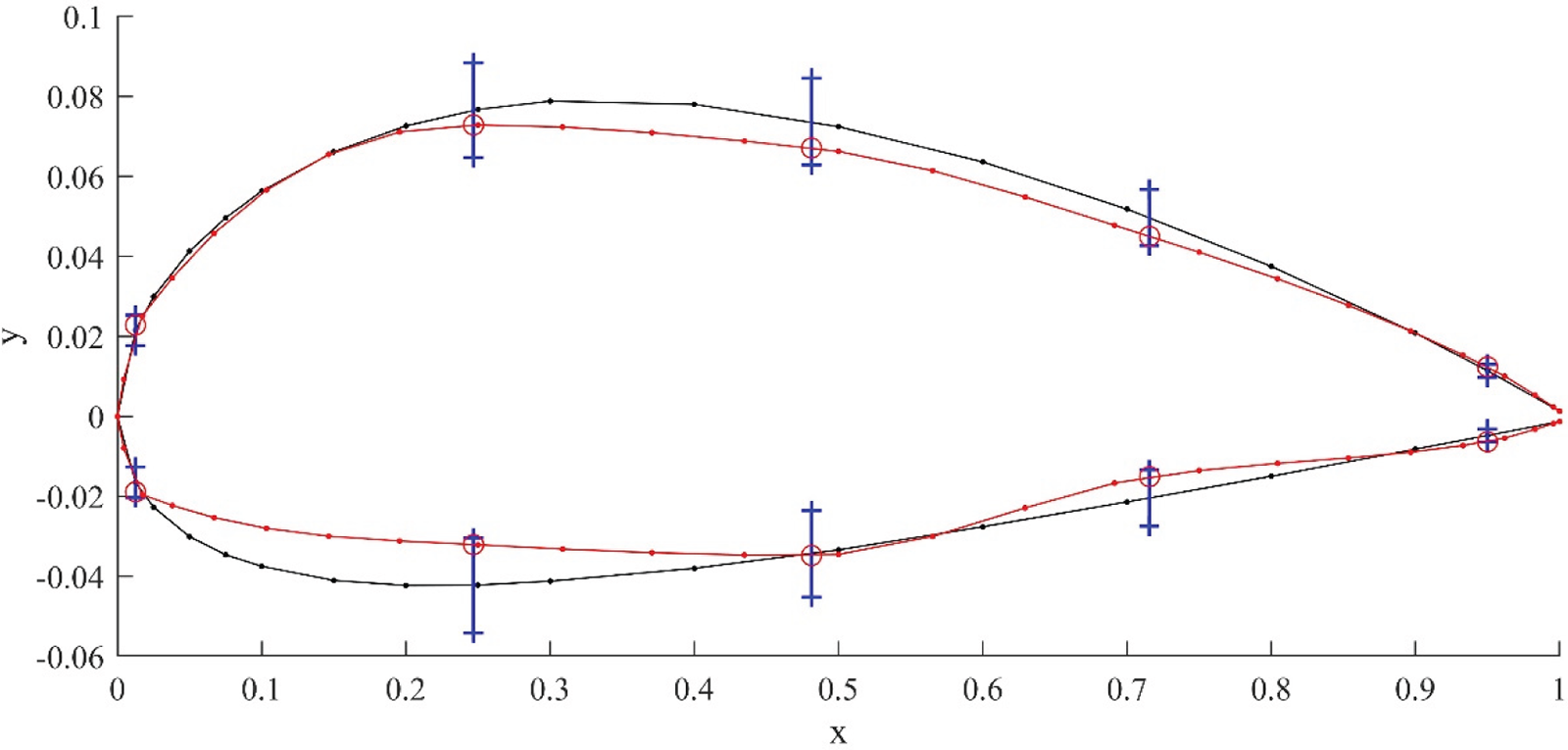
Figure 6: Optimised airfoil obtained by MO-infill sampling-KRG2
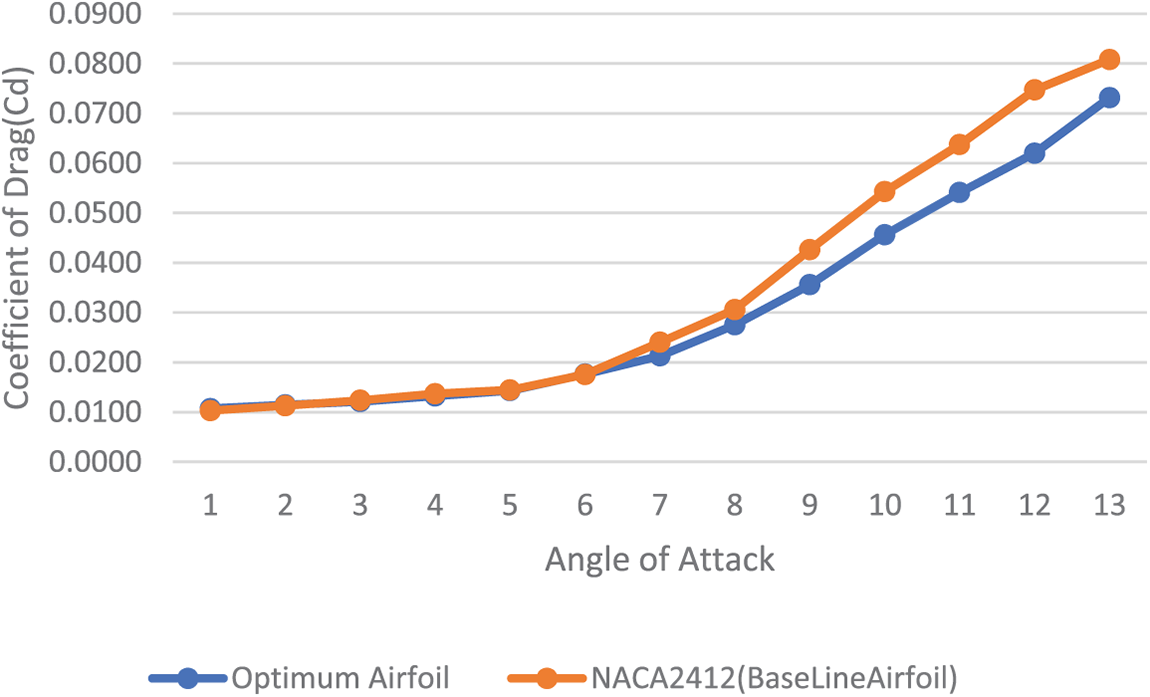
Figure 7: Comparison of the coefficient of drag and angle of attack for optimum airfoil and base line airfoil
Figure 8: Comparison of the coefficient of lift and angle of attack for optimum airfoil and base line airfoil
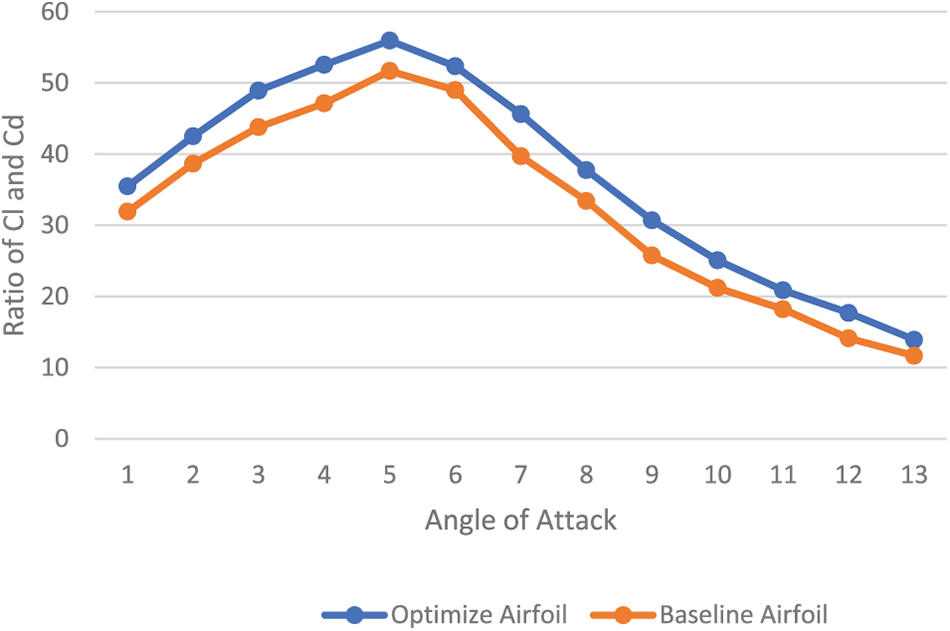
Figure 9: Comparison of the ratio of coefficient of lift and drag with angle of attack for optimum and base line airfoil
As per the aforementioned data, it can be argued that MO-infill-KRG2 is the best while MO-infill-KRG1 is the second-best technique in the vicinity of the Infill-KRG2 approach for airfoil optimization with the investigated surrogate-assisted MHs. Applying EI and space-filling quality functions in the proposed technique can balance model accuracy and function landscape capturing, leading to the best percentage error at the optimum points and the best optimum solution with a smaller number of high-fidelity simulations. In addition, when considering the same surrogate model technique, it was found that using higher fidelity gives better model accuracy at the optimum points and a better optimum solution.
This work successfully proposes multi-objective infill sampling surrogate-assisted metaheuristic based on multi-fidelity simulation for airfoil shape optimization. The optimum LHS technique along with the Kriging surrogate model is applied, while a differential evolution algorithm is used as an optimizer. A special multi-objective optimization sub-problem is proposed for multiple points infill sampling exploration to improve the constructed surrogate model. To validate and further assess the proposed methods, a conventional surrogate-assisted optimization method and infill sampling surrogate-assisted optimization methods are applied with multi-fidelity simulation and their performances are investigated. The quantitative and qualitative comparative analysis demonstrates the dominance of the proposed method (MO-infill-KRG2) over other considered techniques for the presented airfoil shape optimization problem. This work only studied aerodynamics at a single value of AOA with a computational fluid dynamic simulation and various surrogate model method with one optimizer. Future work may try to study various AOAs with various algorithms based on this work. The whole aircraft design based on this simulation process and various algorithms is also a future topic of interest.
Funding Statement: The authors are grateful for the support from Khon Kaen University Scholarship for ASEAN and GMS Countries’ Personnel of Academic Year and the National Research Council of Thailand (N42A650549).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Auteri, F., Savino, A., Zanotti, A., Gibertini, G., Zagaglia, D. et al. (2022). Experimental evaluation of the aerodynamic performance of a large-scale high-lift morphing wing. Aerospace Science and Technology, 124(11), 107515. https://doi.org/10.1016/j.ast.2022.107515 [Google Scholar] [CrossRef]
2. Li H., Zhang Y., Chen H. (2022). Optimization design of airfoils under atmospheric icing conditions for UAV. Chinese Journal of Aeronautics, 35(4), 118–133. https://doi.org/10.1016/j.cja.2021.04.031 [Google Scholar] [CrossRef]
3. Hu, H., Zhang, G., Li, D., Zhang, Z., Sun, T. et al. (2022). Shape optimization of airfoil in ground effect based on free-form deformation utilizing sensitivity analysis and surrogate model of artificial neural network. Ocean Engineering, 257(1), 111514. https://doi.org/10.1016/j.oceaneng.2022.111514 [Google Scholar] [CrossRef]
4. Karbasian, H. K., Vermeire, B. C. (2022). Gradient-free aerodynamic shape optimization using large eddy simulation. Computers and Fluids, 232, 105185. https://doi.org/10.1016/j.compfluid.2021.105185 [Google Scholar] [CrossRef]
5. Bergmann, O., Götten, F., Braun, C., Janser, F. (2022). Comparison and evaluation of blade element methods against RANS simulations and test data. CEAS Aeronautical Journal, 13, 535–557. https://doi.org/10.1007/s13272-022-00579-1 [Google Scholar] [CrossRef]
6. Lewthwaite, M. T., Amaechi, C. V. (2022). Numerical investigation of winglet aerodynamics and dimple effect of NACA, 0017 airfoil for a freight aircraft. Inventions, 7(1). https://doi.org/10.3390/inventions7010031 [Google Scholar] [CrossRef]
7. Zargar, O. A., Lin, T., Zebua, A. G., Lai, T. J., Shih, Y. C. et al. (2022). The effects of surface modification on aerodynamic characteristics of airfoil DU 06 W 200 at low Reynolds numbers. International Journal of Thermofluids, 16(3), 100208. https://doi.org/10.1016/j.ijft.2022.100208 [Google Scholar] [CrossRef]
8. Liu, B., Liang, H., Han, Z. H., Yang, G. (2022). Surrogate-based aerodynamic shape optimization of a morphing wing considering a wide Mach-number range. Aerospace Science and Technology, 124, 107557. https://doi.org/10.1016/j.ast.2022.107557 [Google Scholar] [CrossRef]
9. Liu, X., Wei, F., Zhang, G. (2022). Uncertainty optimization design of airfoil based on adaptive point adding strategy. Aerospace Science and Technology, 130(6), 107875. https://doi.org/10.1016/j.ast.2022.107875 [Google Scholar] [CrossRef]
10. Du, X., He, P., Martins, J. R. R. A. (2021). Rapid airfoil design optimization via neural networks-based parameterization and surrogate modeling. Aerospace Science and Technology, 113(3), 106701. https://doi.org/10.1016/j.ast.2021.106701 [Google Scholar] [CrossRef]
11. Phiboon, T., Khankwa, K., Petcharat, N., Phoksombat, N., Kanazaki, M. et al. (2021). Experiment and computation multi-fidelity multi-objective airfoil design optimization of fixed-wing UAV. Journal of Mechanical Science and Technology, 35(9), 4065–4072. https://doi.org/10.1007/s12206-021-0818-3 [Google Scholar] [CrossRef]
12. Hu, P., Pan, J. S., Chu, S. C., Sun, C. (2022). Multi-surrogate assisted binary particle swarm optimization algorithm and its application for feature selection. Applied Soft Computing, 121(11), 108736. https://doi.org/10.1016/j.asoc.2022.108736 [Google Scholar] [CrossRef]
13. Jim, T. M. S., Faza, G. A., Palar, P. S., Shimoyama, K. (2022). A multi-objective surrogate-assisted optimization and exploration of low-boom supersonic transport planforms. Aerospace Science and Technology, 128(17), 107747. https://doi.org/10.1016/j.ast.2022.107747 [Google Scholar] [CrossRef]
14. Wu, X., Zuo, Z., Ma, L. (2022). Aerodynamic data-driven surrogate-assisted teaching-learning-based optimization (TLBO) framework. Aerospace, 9(10), 610. [Google Scholar]
15. Zhao, H., Gao, Z. H., Xia, L. (2022). Efficient aerodynamic analysis and optimization under uncertainty using multi-fidelity polynomial chaos-Kriging surrogate model. Computers and Fluids, 246(3), 105643. https://doi.org/10.1016/j.compfluid.2022.105643 [Google Scholar] [CrossRef]
16. Shang, X., Su, L., Fang, H., Zeng, B., Zhang, Z. (2023). An efficient multi-fidelity Kriging surrogate model-based method for global sensitivity analysis. Reliability Engineering and System Safety, 229(4), 108858. https://doi.org/10.1016/j.ress.2022.108858 [Google Scholar] [CrossRef]
17. Trapani, G., Kipouros, T., Savill, A. M. (2012). The design of multi-element airfoils through multi-objective optimization techniques. Computer Modeling in Engineering & Sciences, 88(2), 107–140. https://doi.org/10.3970/cmes.2012.088.107 [Google Scholar] [CrossRef]
18. Diwakar, A., Srinath, D. N., Mittal, S. (2010). Aerodynamic shape optimization of airfoils in unsteady flow. Computer Modelling in Engineering & Sciences, 69(1), 61–90. https://doi.org/10.3970/cmes.2010.069.061 [Google Scholar] [CrossRef]
19. Silisteanu, P. D., Botez, R. M. (2012). Two-dimensional airfoil shape optimization for airfoils at low speeds. AIAA Atmospheric Flight Mechanics Conference, Minneapolis, MN, USA. https://doi.org/10.2514/6.2012-4790 [Google Scholar] [CrossRef]
20. Chen, X., Wang, P., Dong, H., Zhao, X., Xue, D. (2021). Coupled-analysis assisted gradient-enhanced kriging method for global multi-disciplinary design optimization. Engineering Optiimization, 53(6), 1081–1100. https://doi.org/10.1080/0305215X.2020.1773812 [Google Scholar] [CrossRef]
21. Wang, H., Jin, Y., Doherty, J. (2018). A generic test suite for evolutionary multifidelity optimization. IEEE Transcation on Evolutionary Computation, 22(6), 836–850. https://doi.org/10.1109/TEVC.2017.2758360 [Google Scholar] [CrossRef]
22. Mukesh, R., Lingadurai, K., Selvakumar, U. (2018). Airfoil shape optimization based on surrogate model. Journal of the Institutional Engineers Series, 99(1), 1–8. https://doi.org/10.1007/s40032-017-0382-x [Google Scholar] [CrossRef]
23. Kontogiannis, S. G., Demange, J., Savill, A. M., Kipouros, T. (2020). A comparison study of two multifidelity methods for aerodynamic optimization. Aerospace Science and Technology, 97(3), 105592. https://doi.org/10.1016/j.ast.2019.105592 [Google Scholar] [CrossRef]
24. Zhao Y., Wang C. (2021). Shape optimization of labyrinth seals to improve sealing performance. Aerospace, 8(4), 92. https://doi.org/10.3390/aerospace8040092 [Google Scholar] [CrossRef]
25. Wilson, B., Wakes, S., Mayo, M. (2017). Surrogate modeling a computational fluid dynamics-based wind turbine wake simulation using machine learning. 2017 IEEE Symposium Series on Computational Intelligence (SSCI), pp. 1–8. Honolulu, HI, USA. https://doi.org/10.1109/SSCI.2017.8280844 [Google Scholar] [CrossRef]
26. Arias-Montaño, A., Coello, C. A. C., Mezura-Montes, E. (2012). Multi-objective airfoil shape optimization using a multiple-surrogate approach. IEEE Congress on Evolutionary Computation, Brisbane, QLD, Australia. https://doi.org/10.1109/CEC.2012.6256491 [Google Scholar] [CrossRef]
27. Aye, C. M., Pholdee, N., Yildiz, A. R., Bureerat, S., Sait, S. M. (2019). Multi-surrogate-assisted metaheuristics for crashworthiness optimization. International Journal of Vehicle Design, 80(2–4), 223–240. https://doi.org/10.1504/IJVD.2019.109866 [Google Scholar] [CrossRef]
28. Priyanka, R., Sivapragasam, M. (2021). Multi-fidelity surrogate model-based airfoil optimization at a transitional low Reynolds number. Sādhanā, 46, 58. https://doi.org/10.1007/s12046-021-01580-w [Google Scholar] [CrossRef]
29. Gillebaart, E., de Breuker, R. (2016). Low-fidelity 2D isogeometric aeroelastic analysis and optimization method with application to a morphing airfoil. Computer Methods and Applied Mechanics and Engineering, 305(39–41), 512–536. https://doi.org/10.1016/j.cma.2016.03.014 [Google Scholar] [CrossRef]
30. Federico, N. (2011). Aerodynamic shape optimization with physics-based surrogate models (Doctorate Thesis). Università degli Studi di Napoli Federico II. [Google Scholar]
31. Baer, K., Ericson, L., Krus, P. (2020). Robustness and performance evaluations for simulation-based control and component parameter optimization for a series hydraulic hybrid vehicle. Engineering Optimization, 52(3), 446–464. https://doi.org/10.1080/0305215X.2019.1590566 [Google Scholar] [CrossRef]
32. Iterative, U., Guidance, T. (2022). Surrogate-based optimization design for air-launched vehicle. Aerospace, 9(6), 300. [Google Scholar]
33. Zhang, M., Xia, S., Li, X., Yao, Q., Xu, Y. et al. (2022). Systematic reliability-based multi-disciplinary optimization by parallel adaptive importance candidate region. Aerospace, 9(5), 240. https://doi.org/10.3390/aerospace9050240 [Google Scholar] [CrossRef]
34. Pholdee, N., Bureerat, S. (2015). An efficient optimum Latin hypercube sampling technique based on sequencing optimization using simulated annealing. International Journal of System Science, 46(10), 1780–1789. https://doi.org/10.1080/00207721.2013.835003 [Google Scholar] [CrossRef]
35. Stocki, R. (2005). A method to improve design reliability using optimal Latin hypercube sampling. Computer Assisted Mechanics and Engineering Sciences, 12(4), 393–411. [Google Scholar]
36. Zhou, Q., Shao, X., Jiang, P., Zhou, H., Shu, L. (2015). An adaptive global variable fidelity metamodeling strategy using a support vector regression based scaling function. Simulation Modelling Practice and Theory, 59(3), 18–35. https://doi.org/10.1016/j.simpat.2015.08.002 [Google Scholar] [CrossRef]
37. Li, Y., Wang, S., Wu, Y. (2020). Kriging-based unconstrained global optimization through multi-point sampling. Engineering Optimization, 52(6), 1082–1095. https://doi.org/10.1080/0305215X.2019.1668934 [Google Scholar] [CrossRef]
38. Liu, J., Han, Z., Song, W. (2012). Comparison of infill sampling criteria in kriging-based aerodynamic optimization. 28th International Congress of the Aeronautical Sciences, pp. 23–28. Brisbane, Australia. [Google Scholar]
39. Jouhaud, J. C., Sagaut, P., Montagnac, M., Laurenceau, J. (2007). A surrogate-model based multi-disciplinary shape optimization method with application to a 2D subsonic airfoil. Computer and Fluids, 36(3), 520–529. https://doi.org/10.1016/j.compfluid.2006.04.001 [Google Scholar] [CrossRef]
40. Zhang, T. T., Huang, W., Wang, Z. G., Yan, L. (2016). A study of airfoil parameterization, modeling, and optimization based on the computational fluid dynamics method. Journal of Zhejiang University Science A, 17(8), 632–645. https://doi.org/10.1631/jzus.A1500308 [Google Scholar] [CrossRef]
41. Pholdee, N., Bureerat, S., Nuantong, W. (2021). Kriging surrogate-based genetic algorithm optimization for blade design of a horizontal axis wind Turbine. Computer Modeling in Engineering & Sciences, 126(1), 261–273. https://doi.org/10.32604/CMES.2021.012349 [Google Scholar] [CrossRef]
42. Song, X., Lv, L., Sun, W., Zhang, J. (2019). A radial basis function-based multi-fidelity surrogate model: Exploring correlation between high-fidelity and low-fidelity models. Structural and Multi-Disciplinary Optimization, 60(3), 965–981. https://doi.org/10.1007/s00158-019-02248-0 [Google Scholar] [CrossRef]
43. Šarler, B. (2005). A radial basis function collocation approach in computational fluid dynamics. Computer Modelling in Engineering & Sciences, 7, 185–194. https://doi.org/10.3970/cmes.2005.007.185 [Google Scholar] [CrossRef]
44. Ruan, X., Jiang, P., Zhou, Q., Hu, J., Shu, L. (2020). Variable-fidelity probability of improvement method for efficient global optimization of expensive black-box problems. Structural and Multi-Disciplinary Optimization, 62(6), 3021–3052. https://doi.org/10.1007/s00158-020-02646-9 [Google Scholar] [CrossRef]
45. Rehman, S. U., Langelaar, M. (2017). Expected improvement based infill sampling for global robust optimization of constrained problems. Optimization and Engineering, 18(3), 723–753. https://doi.org/10.1007/s11081-016-9346-x [Google Scholar] [CrossRef]
46. Parenteau, M. (2017). Aerodynamic optimization of aircraft wings using a coupled VLM-2.5D RANS Approach. Université de Montréal. https://publications.polymtl.ca/2555 [Google Scholar]
47. Liu Z., Liu X., Cai X. (2018). A new hybrid aerodynamic optimization framework based on differential evolution and invasive weed optimization. Chinese Journal of Aeronautics, 31(7), 1437–1448. https://doi.org/10.1016/j.cja.2018.05.002 [Google Scholar] [CrossRef]
48. Pereira, J. M. C., Maia, N. A. R., Pereira, J. C. F. J. (2009). A computational fluid dynamics study of a 2D airfoil in hovering flight under ground effect. Computer Modeling in Engineering & Sciences, 49(2), 113–142. https://doi.org/10.3970/cmes.2009.049.113 [Google Scholar] [CrossRef]
49. Yaohui, L. (2017). A Kriging-based global optimization method using multi-points infill search criterion. Journal of Algorithms and Computational Technology, 11(4), 366–377. https://doi.org/10.1177/1748301817725307 [Google Scholar] [CrossRef]
50. Chen, G., Fidkowski, K. J. (2020). Variable-fidelity multipoint aerodynamic shape optimization with output-based adapted meshes. Aerospace Science and Technology, 105(1), 106004. https://doi.org/10.1016/j.ast.2020.106004 [Google Scholar] [CrossRef]
51. Cheng, J., Jiang, P., Zhou, Q., Hu, J., Yu, T. et al. (2019). A lower confidence bounding approach based on the coefficient of variation for expensive global design optimization. Engineering Computation, 36(3), 830–849. https://doi.org/10.1108/EC-08-2018-0390 [Google Scholar] [CrossRef]
52. Du, X., Amrit, A., Thelen, A., Leifsson, L., Zhang, Y. et al. (2017). Aerodynamic design of a rectangular wing in subsonic inviscid flow by direct and surrogate-based optimization. 35th AIAA Applied aerodynamics Conference, 4366. Denver, Colorado. https://doi.org/10.2514/6.2017-4366 [Google Scholar] [CrossRef]
53. Gunel, O., Koç, E., Yavuz, T. (2016). Comparison of CFD and Xfoil airfoil analyses for low Reynolds number. International Journal of Energy Applications and Technologies, 3(2), 83–86. [Google Scholar]
54. Leifsson, L., Koziel, S. (2010). Multi-fidelity design optimization of transonic airfoils using physics-based surrogate modeling and shape-preserving response predictio. Journal of Computational Science, 1(2), 98–106. https://doi.org/10.1016/j.jocs.2010.03.007 [Google Scholar] [CrossRef]
55. Song C., Yang X., Song W. (2018). Multi-infill strategy for kriging models used in variable fidelity optimization. Chinese Journal of Aeronautics, 31(3), 448–456. https://doi.org/10.1016/j.cja.2018.01.011 [Google Scholar] [CrossRef]
56. Shah, H., Hosder, S., Koziel, S., Tesfahunegn, Y. A., Leifsson, L. (2015). Multi-fidelity robust aerodynamic design optimization under mixed uncertainty. Aerospace Science and Technology, 45(1–3), 17–29. https://doi.org/10.1016/j.ast.2015.04.011 [Google Scholar] [CrossRef]
57. Kafkas, A., Kilimtzidis, S., Kotzakolios, A., Kostopoulos, V., Lampeas, G. (2021). Multi-fidelity optimization of a composite airliner wing subject to structural and aeroelastic constraints. Aerospace, 8(12), 1–34. https://doi.org/10.3390/aerospace8120398 [Google Scholar] [CrossRef]
58. Guo, H., Zhang, C., Lv, B., Yu, L. (2022). Numerical simulation research on static aeroelastic effect of the transonic aileron of a high aspect ratio aircraft. Computer Modeling in Engineering & Sciences, 132(3), 991–1010. https://doi.org/10.32604/cmes.2022.020638 [Google Scholar] [CrossRef]
Kim, C., Lee, Y. G. (2011). Multi-disciplinary design optimization of unmanned aerial vehicle, a review of recent advancements. International Journal of Aerospace Engineering, 4258020. https://doi.org/10.1115/PVP2011-57567 [Google Scholar] [CrossRef]
60. Wang, L., Wang, T., Wu, J., Chen, G. (2017). Multi-objective differential evolution optimization based on uniform decomposition for wind turbine blade design. Energy, 120(4), 346–361. https://doi.org/10.1016/j.energy.2016.11.087 [Google Scholar] [CrossRef]
61. Benaouali, A., Kachel, S. (2019). Multi-disciplinary design optimization of aircraft wing using commercial software integration. Aerospace Science and Technology, 92(1), 766–776. https://doi.org/10.1016/j.ast.2019.06.040 [Google Scholar] [CrossRef]
62. Jin, Y. (2011). Surrogate-assisted evolutionary computation: Recent advances and future challenges. Swarm and Evolutionary Computation, 1(2), 61–70. https://doi.org/10.1016/j.swevo.2011.05.001 [Google Scholar] [CrossRef]
63. D’Alessandro, V., Montelpare, S., Ricci, R. (2021). Assessment of a Spalart–Allmaras model coupled with local correlation based transition approaches for wind turbine airfoils. Applied Science, 11(4), 1872. https://doi.org/10.3390/app11041872 [Google Scholar] [CrossRef]
64. Nordanger K., Holdahl R., Kvamsdal T., Kvarving A. M., Rasheed A. (2015). Simulation of airflow past a 2D NACA0015 airfoil using an isogeometric incompressible Navier–Stokes solver with the Spalart–Allmaras turbulence model. Computational Methods in Applied Mechanics and Engineering, 290(4), 183–208. https://doi.org/10.1016/j.cma.2015.02.030 [Google Scholar] [CrossRef]
65. Zhang, J., Chowdhury, S., Messac, A. (2012). An adaptive hybrid surrogate model. Structural Multi-Disciplinary Optimization, 46(2), 223–238. https://doi.org/10.1007/s00158-012-0764-x [Google Scholar] [CrossRef]
66. Götten, F., Finger, F., Havermann, M., Braun, C., Bil, C. et al. (2019). A highly automated method for simulating airfoil characteristics at low reynolds number using a RANS-transition approach. Deutscher Luft- und Raumfahrtkongress, 490026. https://doi.org/10.25967/490026 [Google Scholar] [CrossRef]
67. Iliev, S. P. (2017). Aerofoil analysis using XFOIL practical implementation for preliminary wing design. London, UK, SW7 2AZ: Department of Aeronautics South Kensington Campus. [Google Scholar]
68. Sleesongsom, K. W. S., Pholdee, N. (2020). Surrogate-assisted reliability optimization of an aircraft wing with static and dynamic aeroelastic constraints. International Journal of Aeronautical and Space Sciences, 21(3), 723–732. https://doi.org/10.1007/s42405-019-00246-6 [Google Scholar] [CrossRef]
69. Morris M. D., Mitchell T. J. (1995). Exploratory designs for computational experiments. Journal of Statistical Planning and Inference, 43(3), 381–402. https://doi.org/10.1016/0378-3758(94)00035-T [Google Scholar] [CrossRef]
70. Mallipeddi, R., Suganthan, P. N., Pan, Q. K., Tasgetiren, M. F. (2011). Differential evolution algorithm with ensemble of parameters and mutation strategies. Applied Soft Computing, 11(2), 1679–1696. https://doi.org/10.1016/j.asoc.2010.04.024 [Google Scholar] [CrossRef]
71. Pholdee, N., Bureerat, S., Yildiz, A. R. (2017). Hybrid real-code population-based incremental learning and differential evolution for many-objective optimization of an automotive floor-frame. International Journal of Vehicle Design, 73(1–3), 20–53. https://doi.org/10.1504/IJVD.2017.082578 [Google Scholar] [CrossRef]
72. Pholdee, N., Bureerat, S. (2013). Hybridisation of real-code population-based incremental learning and differential evolution for multi-objective design of trusses. Informatics and Computer Science Intelligent Systems Applications, 223(6), 136–152. https://doi.org/10.1016/j.ins.2012.10.008 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools