Migration Algorithm: A New Human-Based Metaheuristic Approach for Solving Optimization Problems

1  Introduction

Optimization problems are a type of problems that have more than one feasible solution. Thus, the optimization process consists of finding the best feasible solution among all the available solutions [1]. Numerous optimization problems in science, engineering, and industry, and real-world applications have become more complex as science and technology advance. Therefore, solving these problems requires effective optimization tools [2]. Problem-solving techniques in optimization studies are classified into two groups: deterministic and stochastic approaches [3].

Deterministic approaches in gradient-based and non-gradient-based categories have good efficiency in solving linear, convex, differentiable, continuous, low-dimensional, and simple problems [4]. However, as optimization problems become more complex, deterministic approaches lose their efficiency and, by getting stuck in local optima, cannot provide suitable solutions. Meanwhile, many existing and emerging optimization problems in science and real-world applications are nonlinear, non-convex, non-differentiable, non-continuous, high-dimensional, and complex in nature. The difficulties of deterministic approaches, on the one hand, and the increasing complexity of optimization problems, on the other hand, have led researchers to develop stochastic approaches to deal with these problems [5,6].

Metaheuristic algorithms are one of the most effective stochastic approaches that can solve optimization problems based on random search in the problem-solving space using random operators and trial and error processes [7]. The optimization process in metaheuristic algorithms is such that first, several candidate solutions are initialized under the name of the algorithm population. Then, in a repetition-based process, these initial solutions are improved based on algorithm update steps. Finally, the best solution obtained during the iterations of the algorithm is presented as the solution to the problem [8]. Advantages such as simplicity of concepts, easy implementation, no need for derivative process, efficiency in complex, high dimensions, and NP-hard problems, and efficiency in unknown and discrete search spaces have led to the popularity of metaheuristic algorithms among researchers [9].

Metaheuristic algorithms must be able to accurately search the problem-solving space at global and local levels to achieve optimal solutions [10]. Global search with the concept of discovery leads to the ability of the algorithm to comprehensively scan the problem-solving space and prevent the algorithm from getting stuck in local optima. Local search with the concept of exploitation enables the algorithm to converge to possible better solutions near the discovered solutions. In addition to having high power in exploration and exploitation, the primary key to the success of metaheuristic algorithms in optimization is balancing exploration and exploitation during the search process. Due to the nature of random search in metaheuristic algorithms, there is no guarantee that metaheuristic algorithms will provide global optimal. However, the solutions obtained from these methods are acceptable as quasi-optimal solutions due to their proximity to the global optimal [11].

Since the search process and updating steps in metaheuristic algorithms differ, implementing metaheuristic algorithms on a similar optimization problem provides different solutions. Therefore, in comparing the performance of several metaheuristic algorithms, the more effectively an algorithm provides the search process, it will converge to a better solution and be superior to other algorithms. The desire to achieve more effective solutions for optimization problems has led to the design of numerous metaheuristic algorithms. These algorithms are employed in various optimization applications in science, such as energy [12–15], protection [16], energy carriers [17,18], and electrical engineering [19–24].

The main research question is, considering that countless metaheuristic algorithms have been designed so far, whether there is still a need for newer metaheuristic algorithms. In response to this question, the No Free Lunch (NFL) theorem [25] explains that the effective performance of an algorithm in solving a set of optimization problems is not a guarantee of providing the same performance of that algorithm in other optimization problems. Hence, a successful algorithm in solving some optimization problems may even fail in solving another optimization problem. Based on the NFL theorem concept, no specific metaheuristic algorithm is the best optimizer for all optimization problems. The NFL theorem encourages researchers to be able to provide more effective solutions to optimization problems by designing newer algorithms. The NFL theorem also motivates the authors of this paper to introduce and design a new metaheuristic algorithm to handle optimization tasks in science and engineering.

The aspects of innovation and novelty of this paper are in the design of a new metaheuristic algorithm called the Migration Algorithm (MA), which has applications in solving optimization problems. The contributions of this article are as follows:

•   The fundamental inspiration of MA is the strategies of choosing the migration destination and adapting to the new environment in the migration process, which are mathematically modeled in two phases of exploration and exploitation.

•   The performance of MA in optimization applications is evaluated on fifty-two standard benchmark functions and is compared with twelve well-known metaheuristic algorithms.

•   The effectiveness of the proposed MA approach in real-world applications is evaluated on four engineering design problems.

The rest of the paper is organized, so the literature review is presented in Section 2. Then the proposed MA approach is introduced and modeled in Section 3. Simulation studies and results are presented in Section 4. The efficiency of MA in handling real-world applications is evaluated in Section 5. Finally, conclusions and suggestions for future works are provided in Section 6.

2  Literature Review

Metaheuristic algorithms are inspired by various natural phenomena, living organisms’ behaviors, biological sciences, laws of physics, rules of games, human activities, etc. Based on the design idea, metaheuristic algorithms are classified into five groups: swarm-based, evolutionary-based, physics-based, game-based, and human-based approaches.

Swarm-based metaheuristic algorithms are designed based on the simulation of swarm behaviors of living organisms such as animals, insects, birds, aquatic animals, plants, etc., in nature. Particle Swarm Optimization (PSO) [26], Ant Colony Optimization (ACO) [27], Artificial Bee Colony (ABC) [28], and Firefly Algorithm (FA) [29] are among the most widely used crowd-based approaches. Design of PSO is based on the movement of flocks of birds or fish and their strategy in searching for food. ACO is derived from the ant colony’s ability to identify the shortest path between the food source and the nest. ABC is proposed based on modeling the hierarchical activities of honeybees in the colony to access food resources. FA is inspired by the behavior of fireflies in attracting prey and the opposite sex by using their luminous ability to produce flashing light based on the biological phenomenon of bioluminescence. Grey Wolf Optimization (GWO) is a swarm-based method based on simulating gray wolves’ hierarchical strategy during hunting [30]. Some other swarm-based algorithms are Penicillium Reproduction Algorithm (PRA) [31], Dandelion Algorithm (DA) [32], Pelican Optimization Algorithm (POA) [33], Emperor Penguin Optimizer (EPO) [34], Marine Predators Algorithm (MPA) [35], Rat Swarm Optimization (RSO) [36], Mutated Leader Algorithm (MLA) [37], Reptile Search Algorithm (RSA) [38], Cat and Mouse Based Optimizer (CMBO) [39], Donkey Theorem Optimization (DTO) [40], All Member Based Optimizer (AMBO) [41], Group Mean-Based Optimizer (GMBO) [42], Tunicate Swarm Algorithm (TSA) [43], Two Stage Optimization (TSO) [44], White Shark Optimizer (WSO) [45], and African Vultures Optimization Algorithm (AVOA) [46].

Evolutionary-based metaheuristic algorithms are developed inspired by the concepts of biological, genetics sciences, and natural selection. Genetic Algorithm (GA) [47] and Differential Evolution (DE) [48] are the most famous evolutionary-based algorithms that have been widely used in solving various optimization problems. The design of these algorithms has been inspired by the reproduction process, the concepts of survival of the fittest, Darwin’s evolutionary theory, and the use of random selection, crossover, and mutation operators. Some other evolutionary-based metaheuristic algorithms are Biogeography-based Optimizer (BBO) [49], Artificial Immune System (AIS) [50], Evolution Strategy (ES) [51], Cultural Algorithm (CA) [52], and Genetic Programming (GP) [53].

Physics-based metaheuristic algorithms are introduced based on modeling phenomena, laws, forces, and physics concepts. Simulated Annealing (SA) is one of the most famous physics-based algorithms developed based on the simulation of the physical process of metal annealing. In this physical process, the metal is first melted under heat and then slowly cooled so that the crystals are perfectly formed [54]. Physical forces have been sources of inspiration in designing algorithms such as the Gravitational Search Algorithm (GSA) based on gravitational force [55] and Momentum Search Algorithm (MSA) based on impulse force [56]. Cosmological concepts are employed in the design of algorithms such as the Galaxy-Based Search Algorithm (GbSA) [57], Multi-Verse Optimizer (MVO) [58], and Black Hole (BH) [59]. Some other physics-based algorithms are Small World Optimization Algorithm (SWOA) [60], Magnetic Optimization Algorithm (MOA) [61], Ray Optimization (RO) [62] algorithm, and Artificial Chemical Reaction Optimization Algorithm (ACROA) [63].

Game-based metaheuristic algorithms are proposed based on simulating the rules of different individual and group games, as well as the strategies and behaviors of people influencing games such as players, referees, and coaches. Holding matches in different sports has been the source of inspiration for designing algorithms, such as Volleyball Premier League (VPL) [64] based on the simulation of the volleyball league and Football Game Based Optimizer (FGBO) [65] based on the simulation of the football league. The main idea in the design of the Orientation Search algorithm (OSA) has been the players’ efforts to change the direction of movement on the playing field based on the direction determined by the reference [66].

Human behaviors, activities, interactions, and communication in individual and social life inspire human-based metaheuristic algorithms. Teaching-Learning Based Optimization (TLBO) is one of the most widely used human-based approaches, which is designed based on modeling students’ interactions with each other and students with the teacher in the classroom learning environment [67]. People’s effort to improve society by following the leader of that society has been used in the design of the Following Optimization Algorithm (FOA) [68]. The process of learning a foreign language by people by referring to language schools is employed in the design of Language Education Optimization (LEO) [69], and Election Based Optimization Algorithm (EBOA) [70] mimics the voting process to select the leader. Some other human-based metaheuristic algorithms are Multimodal Nomad Algorithm (MNA) [71], Archery Algorithm (AA) [72], War Strategy Optimization (WSO) [73], and Brain Storm Optimization (BSO) [74].

A short description of the algorithms mentioned in this paper is presented in Table 1.

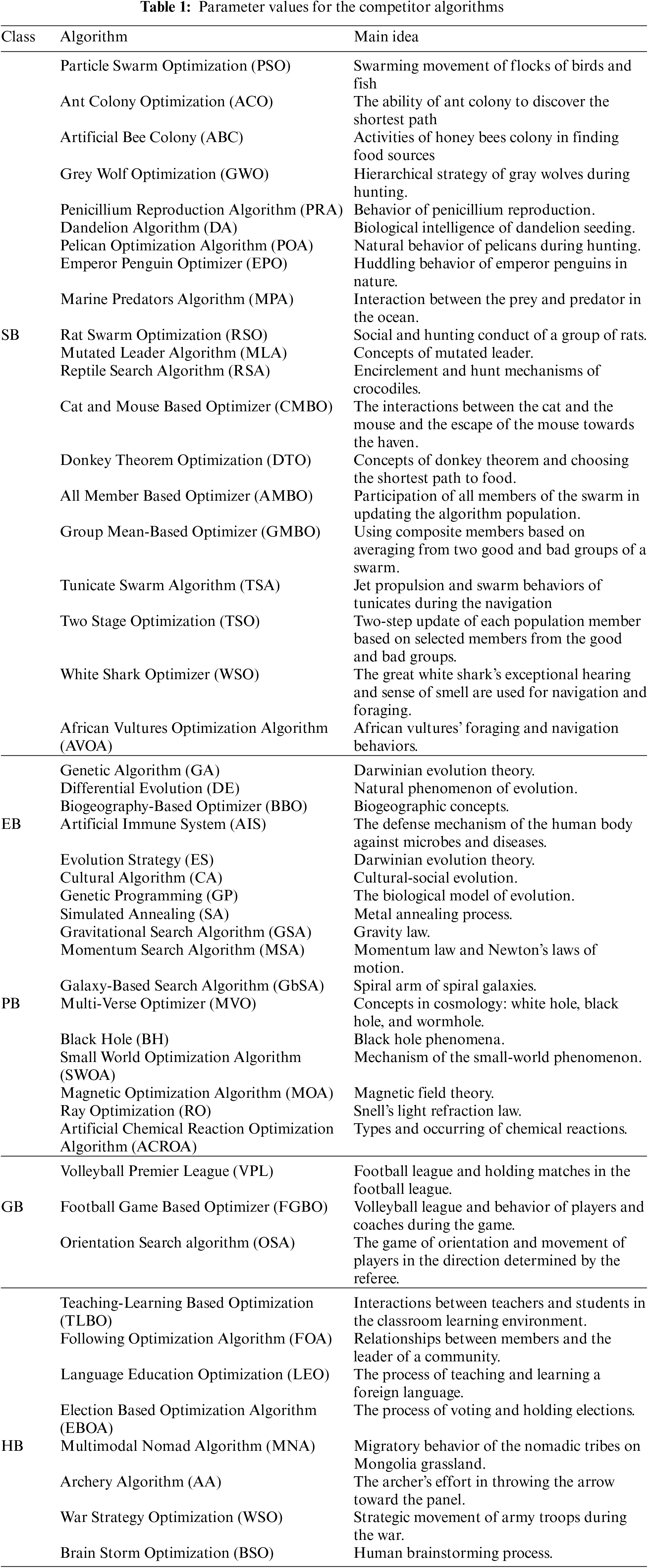
Based on the best knowledge obtained from the literature review, no metaheuristic algorithm has been designed based on the modeling of the human migration process. Meanwhile, the migration process is an intelligent human activity with extraordinary potential as a new metaheuristic algorithm design. In order to address this research gap, in this paper, a new human-based metaheuristic algorithm is designed based on the mathematical modeling of the human migration process, which is discussed in the next section.

3  Migration Algorithm

In this section, the proposed Migration Algorithm (MA) is introduced, and its mathematical model is presented.

3.1 Inspiration

Human migration refers to the movement of people from one place to another for work or life [75]. People usually migrate to escape adverse circumstances, such as poverty, disease, political issues, food shortages, natural disasters, war, unemployment, and lack of security. In addition, the favorable conditions of the migration destination, such as more health facilities, better education, more income, better housing, political freedoms, and a better atmosphere, are the other reasons for people to migrate [76]. Based on their own needs and criteria, people choose the final destination among the immigration options. After moving to the migration destination, people try to adapt to the new environment.

When people decide to migrate, based on their expectations and conditions, they will have different candidates for the migration destination. After analyzing each destination’s conditions, they choose their final migration destination. Then they immigrate. When a person is in a new situation, they try to adapt themself to the new conditions in the immigration destination. The steps of the immigration process are considered as follows:

•   A person checks different destinations for immigration.

•   From among the candidate destinations, a person finally chooses the immigration destination based on examining their benefits and conditions.

•   The person migrates to the chosen destination.

•   In a new situation, a person tries to adapt to the conditions of the new society.

Among humans’ activities in the migration process, the two strategies of (i) choosing and moving to the migration destination and (ii) trying to adapt to the new environment at the migration destination are more significant. Mathematical modeling of these two strategies of the migration process is employed in the design of the proposed MA approach.

3.2 Initialization

The proposed MA approach is a population-based metaheuristic algorithm that can solve optimization problems by using the search power of this population in the problem-solving space in a repetition-based process. The members of the MA population are people in different life situations who are trying to improve their situation by migrating to new places. Each population member, according to its position in the search space, determines the values for the decision variables of the problem. Therefore, each member of the population is a candidate solution to the problem, which is mathematically modeled using a vector. Together, these members form the population of the algorithm, which can be represented from a mathematical point of view using a matrix according to Eq. (1). At the beginning of the MA execution, the initial position of the population members in the search space is initialized using Eq. (2).

X=[X1⋮Xi⋮XN]N×m=[x1,1⋯x1,j⋯x1,m⋮⋱⋮⋰⋮xi,1⋯xi,j⋯xi,m⋮⋰⋮⋱⋮xN,1⋯xN,j⋯xN,m]N×m,(1)

Xi:xi,j=lbj+r⋅(ubj−lbj),i=1,2,…,N,j=1,2,…,m,(2)

where X is the population matrix of the proposed MA, N is the number of population members, m is the number of decision variables, Xi is the ith candidate solution, xi,j is its jth variable, r is a random number in the interval [0,1], lbj is the lower bound, and ubj is the upper bound of the jth decision variable.

Considering that each population member is a candidate solution for the problem, a value for the objective function of the problem is evaluated corresponding to each population member. The set of calculated values for the objective function can be represented using a vector according to Eq. (3).

F=[F1⋮Fi⋮FN]N×1=[F(X1)⋮F(Xi)⋮F(XN)]N×1,(3)

where F is the vector of values of the objective function and Fi is the value of the objective function for the ith candidate solution.

The calculated values for the objective function are suitable for the qualitative assessment of candidate solutions. Therefore, the best value calculated for the objective function corresponds to the best member of the population. Similarly, the worst value calculated for the objective function corresponds to the worst member of the population. Considering that the position of the population members in the search space is updated in each iteration, the best member must also be updated. At the end of the algorithm execution, the best member of the population is available as a solution to the problem.

In the design of the proposed MA approach, the position of the population members is updated based on the simulation of the human migration process in two phases, which are explained below. In the following, mathematical equations of the proposed MA are presented to minimize the objective functions of optimization problems. It should be noted that MA can also be used for maximization problems, but the relevant equations would have to be rewritten for these problems.

3.3 Phase 1: Choosing and Moving to the Migration Destination (Exploration Phase)

One of the most important actions in the migration process is choosing the migration destination among all the available options. When people migrate, they choose a destination based on their criteria and move there. The simulation of this behavior is employed in the design of the first phase of population update in the proposed MA approach. Modeling this strategy leads to significant changes in the population position of the algorithm, which leads to increased algorithm ability in global search and exploration. In the MA design, for each population member, the position of other population members (with the better fitness function value) is considered a set of possible destinations for its migration. This set of candidate destinations for each member is determined using Eq. (4). Then, the migration destination MD is randomly chosen for each member of the population among the options selected in this set. Then, the proposed new position for each member is calculated based on the displacement towards the migration destination using Eq. (5). Finally, if the value of the objective function is improved in the new position, the proposed position is accepted as the position of the corresponding member according to Eq. (6).

CDi={Xk,Fk<Fi and k∈{1,2,..,N}},where i=1,2,…,N,(4)

xi,jP1=xi,j+ri,j⋅(MDi,j−Ii,j⋅xi,j),(5)

Xi={XiP1,FiP1≤Fi,Xi,else,(6)

where CDi is the set of all possible candidate destinations for the ith member, Xk is the kth row of X matrix which has better objective function value than the ith member, MDi is the migration destination for ith member, MDi,j is its jth dimension, XiP1 is the new position calculated for the ith population member based on first phase of the proposed MA, xi,jP1 is its jth dimension, FiP1 is its objective function value, ri,j are random numbers from the interval [0,1], and Ii,j are numbers which are randomly selected as 1 or 2. The random numbers used in MA design create a random nature in changing the position of the population members. Random parameters determined automatically during the execution of the algorithm are used in many metaheuristic algorithms. These random numbers can cause random changes in the population members in the search space and improve the optimization operation.

3.4 Phase 2: Adaptation to the New Environment in the Migration Destination (Exploitation Phase)

After a person migrates and enters a new environment and society, they try to adapt themself to the new conditions. In this activity, a person achieves better performance and social needs. This human activity in the migration process is employed in the second phase of population update in the proposed MA algorithm. Modeling this behavior leads to small changes in the position of the population members, which leads to an increase in the ability of local search and exploitation in the proposed MA approach. To simulate people’s efforts in adapting to the new environment, for each member of the population, a proposed random position near the same member is generated using Eq. (7). This proposed position, if it leads to the improvement of the objective function value, replaces the position of the corresponding member according to Eq. (8).

xi,jP2=xi,j+(1−2ri,j)⋅ubj−lbjt(7)

Xi={XiP2,FiP2≤FiXi,else(8)

where XiP2 is the new position calculated for the ith population member based on second phase of the proposed MA, xi,jP2 is its jth dimension, FiP2 is its objective function value, ri,j are random numbers from the interval [0,1], and t is the iteration counter.

3.5 Repetitions Process, Flowchart, and Pseudocode of MA

After updating all population members based on the first and second phases of the proposed MA approach, the first iteration of the algorithm is completed. After that, with the new values calculated for the position of the population members and the objective function, the algorithm enters the next iteration. The population update process is repeated until the last iteration of the algorithm based on Eqs. (4) to (8). In each iteration, the best member of the population is updated as the best-obtained solution until that iteration. After completing the implementation of the algorithm, the best candidate solution saved during the iterations of the algorithm is presented as a solution to the problem. The implementation steps of the proposed MA approach are shown in the form of a flowchart in Fig. 1 and the form of pseudocode in Algorithm 1.

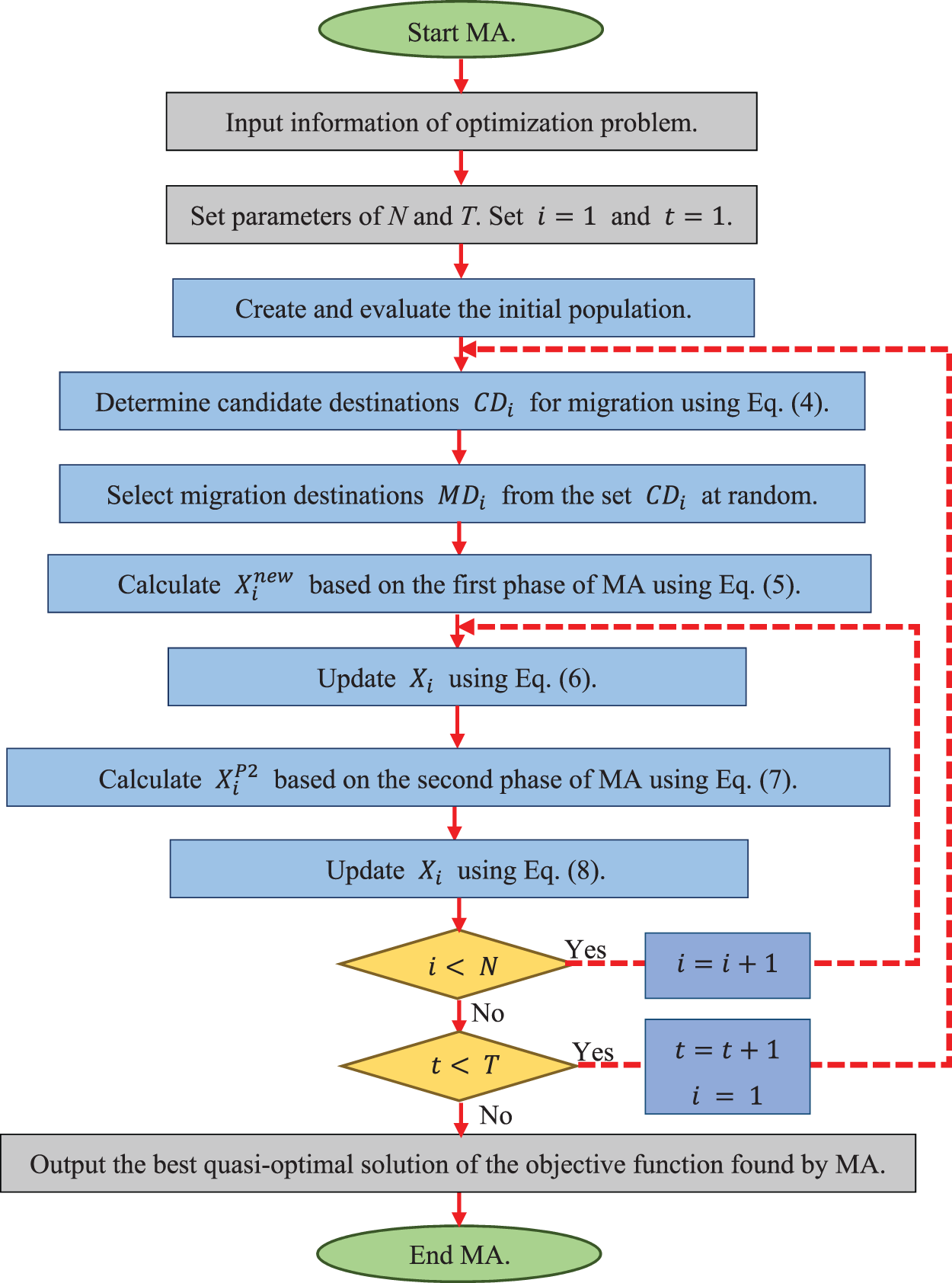
Figure 1: Flowchart of the proposed MA

4  Simulation Studies

In this section, the performance of the proposed MA approach in optimization tasks is evaluated. For this purpose, a set of fifty-two standard benchmark functions consisting of unimodal, high-dimensional multimodal, and fixed-dimensional multimodal types [77] and also the CEC 2017 test suite [78] are employed. The details of these functions are specified in the appendix and in Tables A1 to A4. The results obtained from MA have been compared with the performance of twelve well-known metaheuristic algorithms: GA, PSO, GSA, GWO, MVO, WOA, TSA, MPA, AVOA, WSO, and RSA. The adjusted values for the control parameters are specified in Table 2. Optimization results are reported using six statistical indicators: mean, best, worst, standard deviation, median, and rank. It should be noted that the mean value is chosen as the ranking criterion of metaheuristic algorithms.

4.1 Evaluation of Unimodal Objective Functions

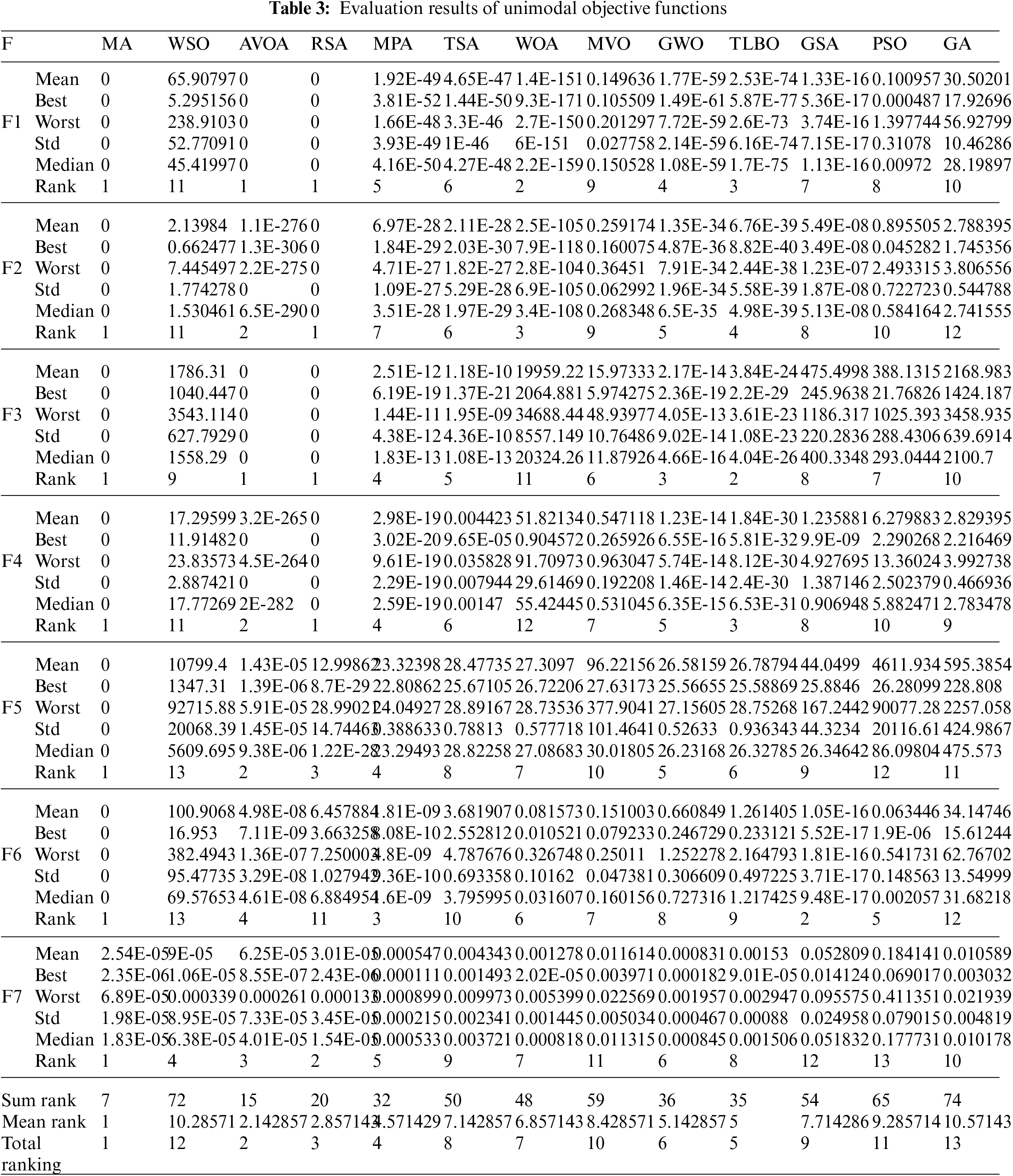
Seven benchmark functions, F1 to F7, have been selected from the unimodal type to evaluate the ability to exploit metaheuristic algorithms. The optimization results of unimodal functions F1 to F7 using MA and competitor algorithms are reported in Table 3. Based on the optimization results, MA, with high exploitation ability in optimizing functions F1, F2, F3, F4, F5, and F6, has converged to the global optimal. In the optimization of the F7 function, MA is the first best optimizer. The analysis of the optimization results shows that MA has provided superior performance in the optimization of unimodal functions F1 to F7 by providing high power in exploitation and local search compared to competitor algorithms.

4.2 Evaluation of High-Dimensional Multimodal Objective Functions

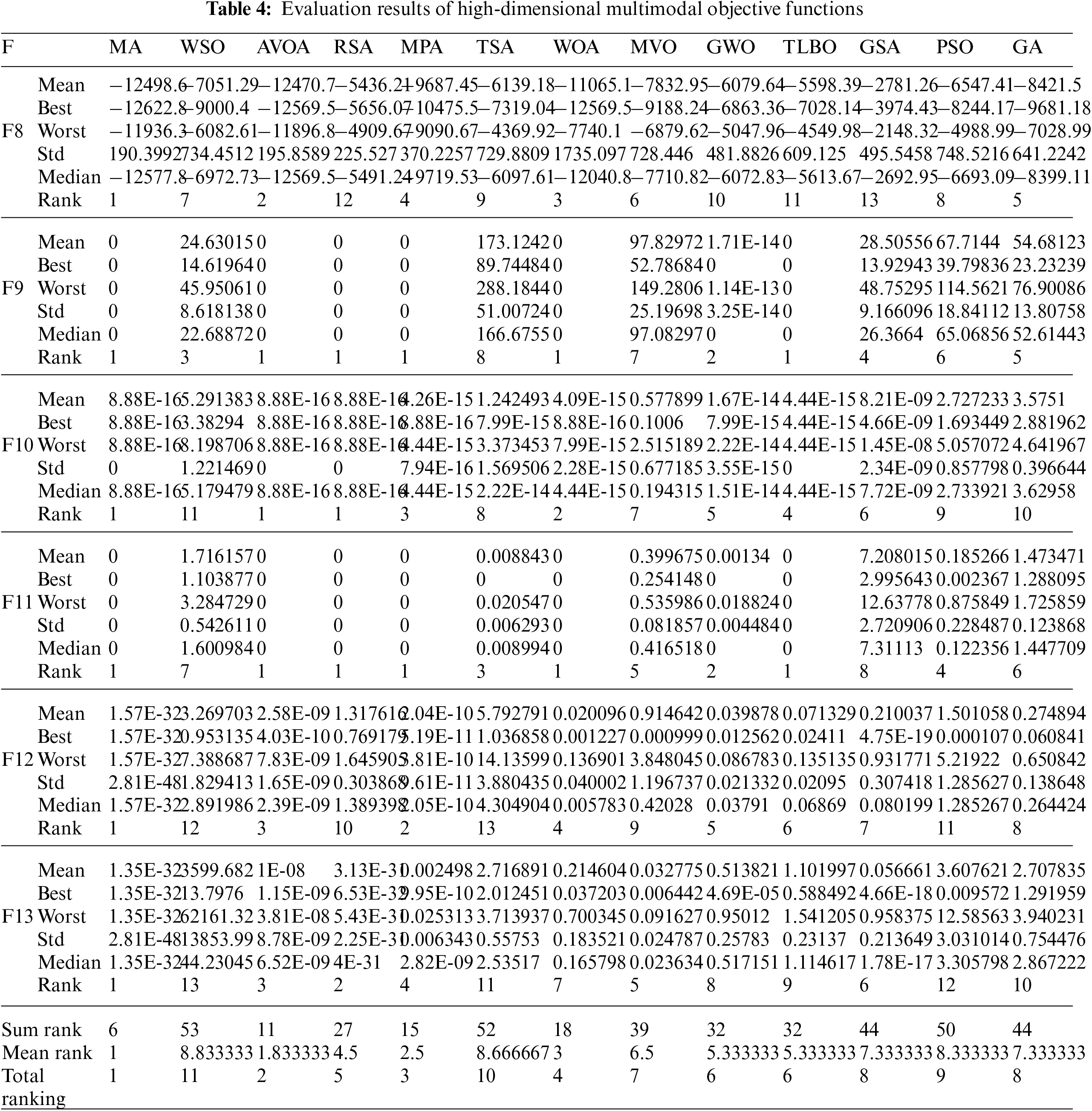
Six benchmark functions F8 to F13, have been selected from the high-dimensional multimodal type to evaluate the exploration ability of metaheuristic algorithms. The implementation results of MA and competitor algorithms on functions F8 to F13 are presented in Table 4. The optimization results show that MA, with high exploration ability, in optimizing F9 and F11 functions, has converged to the global optimal by accurately identifying the main optimal area in the search space. Also, MA is the first best optimizer for solving functions F8, F10, F12, and F13. Based on the analysis of the simulation results, it is concluded that the proposed MA approach with high exploration ability and optimal global search has provided superior performance in the optimization of high-dimensional multimodal functions compared to competitor algorithms.

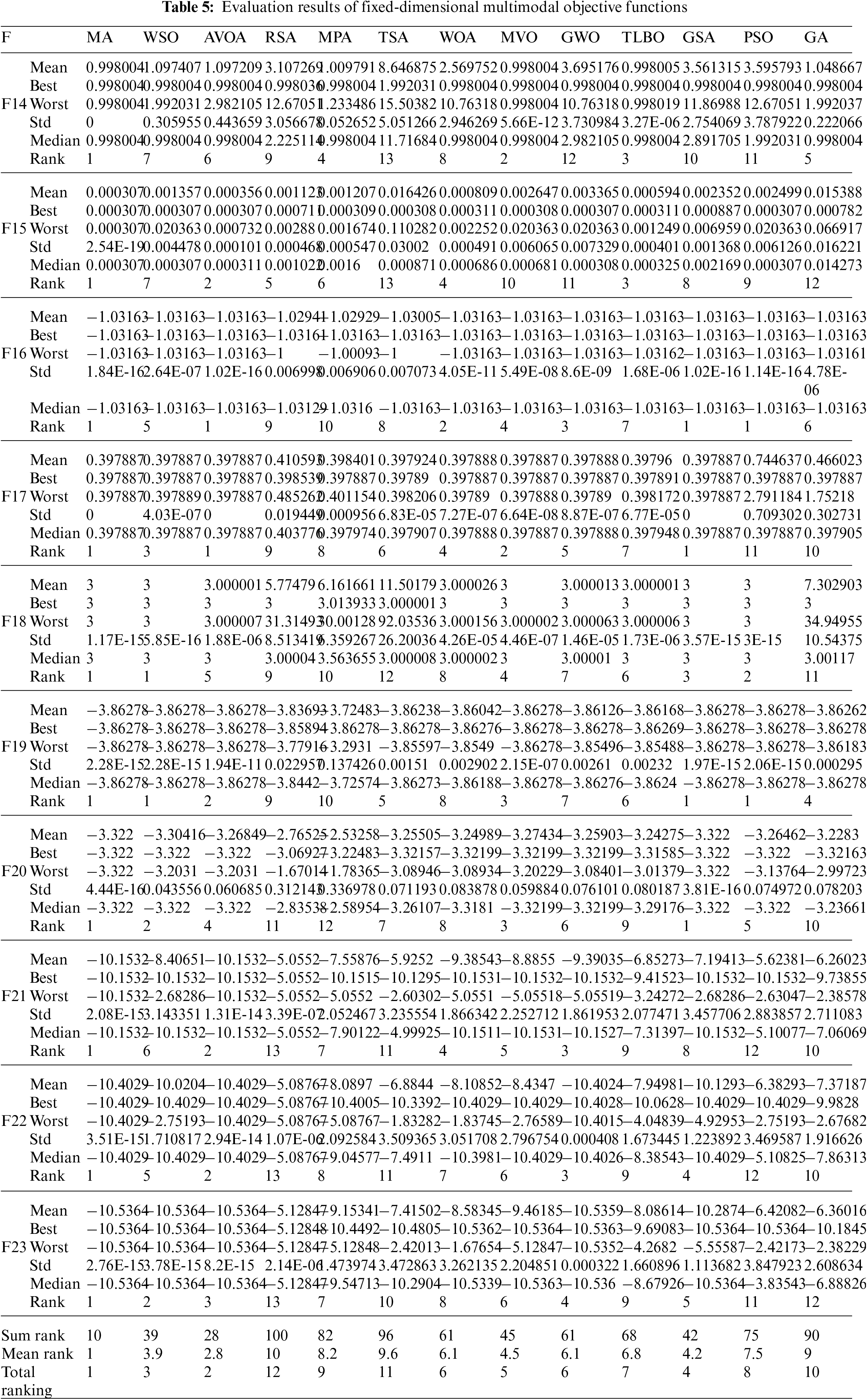
4.3 Evaluation of Fixed-Dimensional Multimodal Objective Functions

Ten benchmark functions, F14 to F23, are selected from the fixed-dimension multimodal to evaluate the ability of metaheuristic algorithms to balance exploration and exploitation during the search process. The results of employing MA and competitor algorithms are reported in Table 5. The results show that MA is the first best optimizer for functions F14, F15, F21, F22, and F23. Furthermore, in solving functions F16 to F20, although MA has similar conditions with some competitor algorithms in the mean criterion, by providing better results for the std index, it has provided a more effective performance in optimizing these functions. What is clear from the analysis of the simulation results is that the proposed MA approach, with a high ability to balance exploration and exploitation, has provided superior performance in the optimization of fixed-dimension multimodal functions compared to competitor algorithms.

The performance of MA and competitor algorithms in optimizing functions F1 to F23 is presented in the form of boxplot diagrams in Fig. 2. Also, the effectiveness of MA and competitor algorithms in obtaining the first rank of the best optimizer and solving the set of unimodal functions, high-dimensional multimodal, and fixed-dimensional multimodal is presented in the form of the bar graphs in Fig. 3. These charts visually show that MA has been ranked as the first best optimizer in 100% of the objective functions in the mentioned sets.

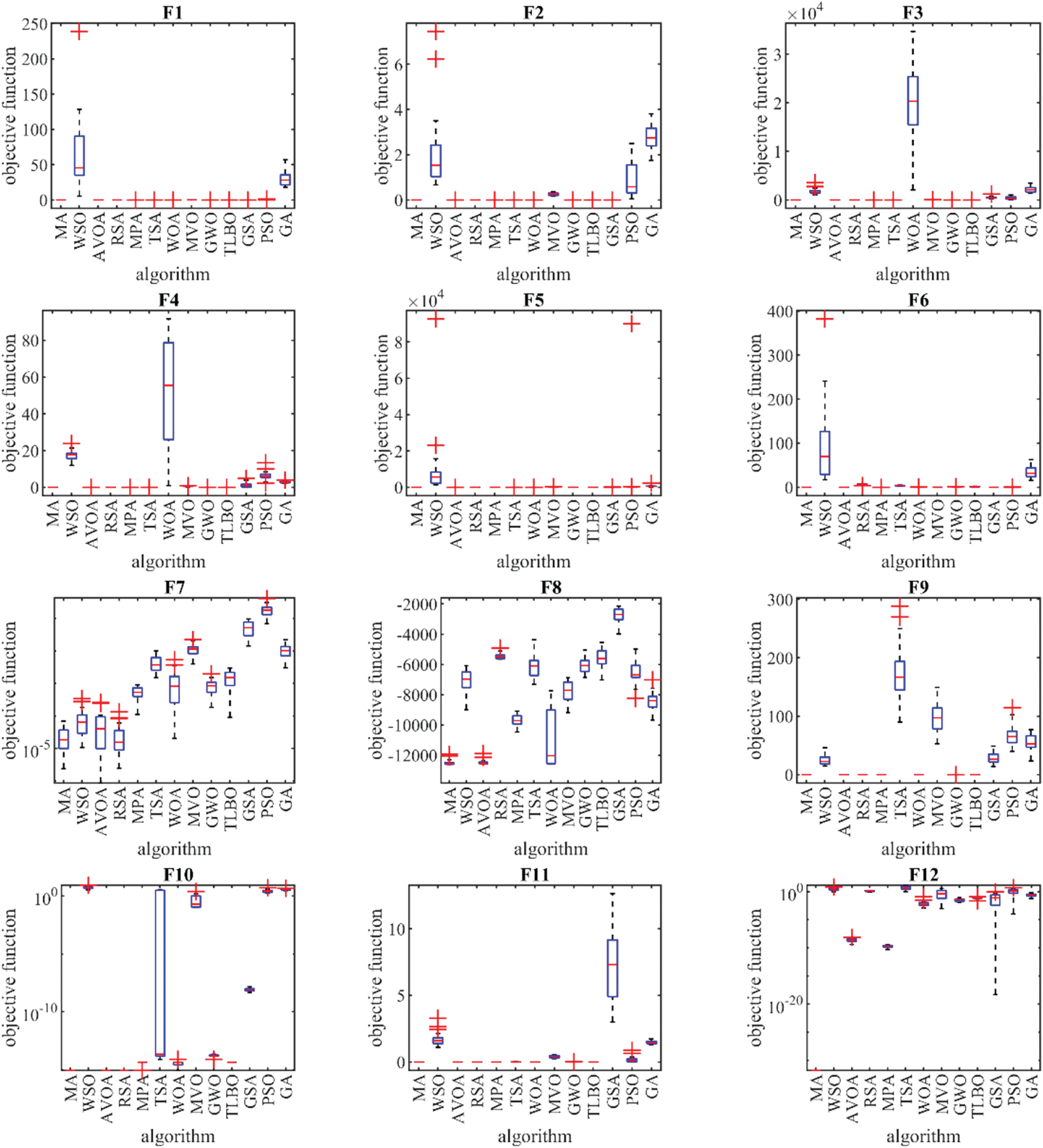
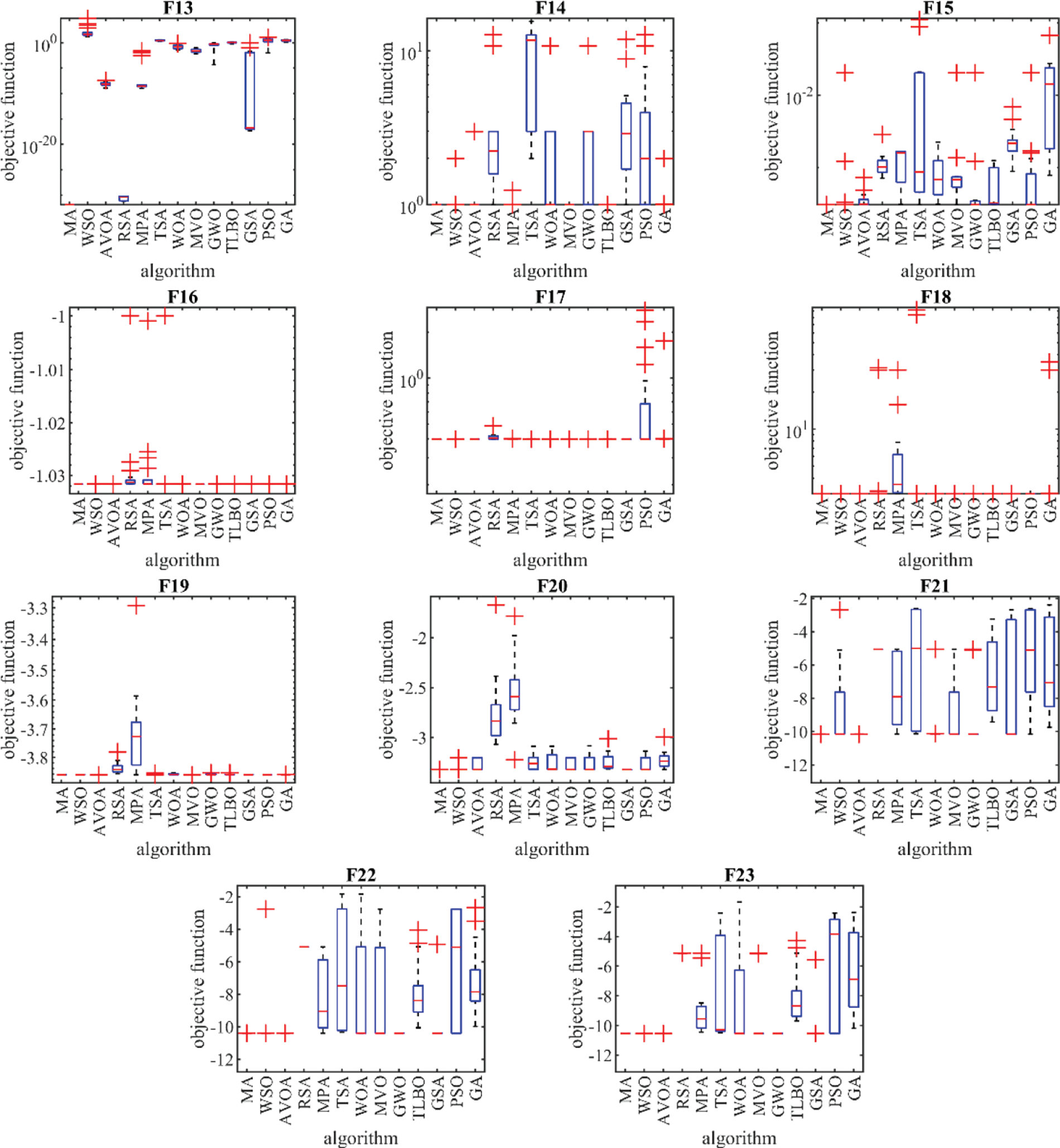
Figure 2: Boxplots of MA and competitor algorithms performances on the F1 to F23

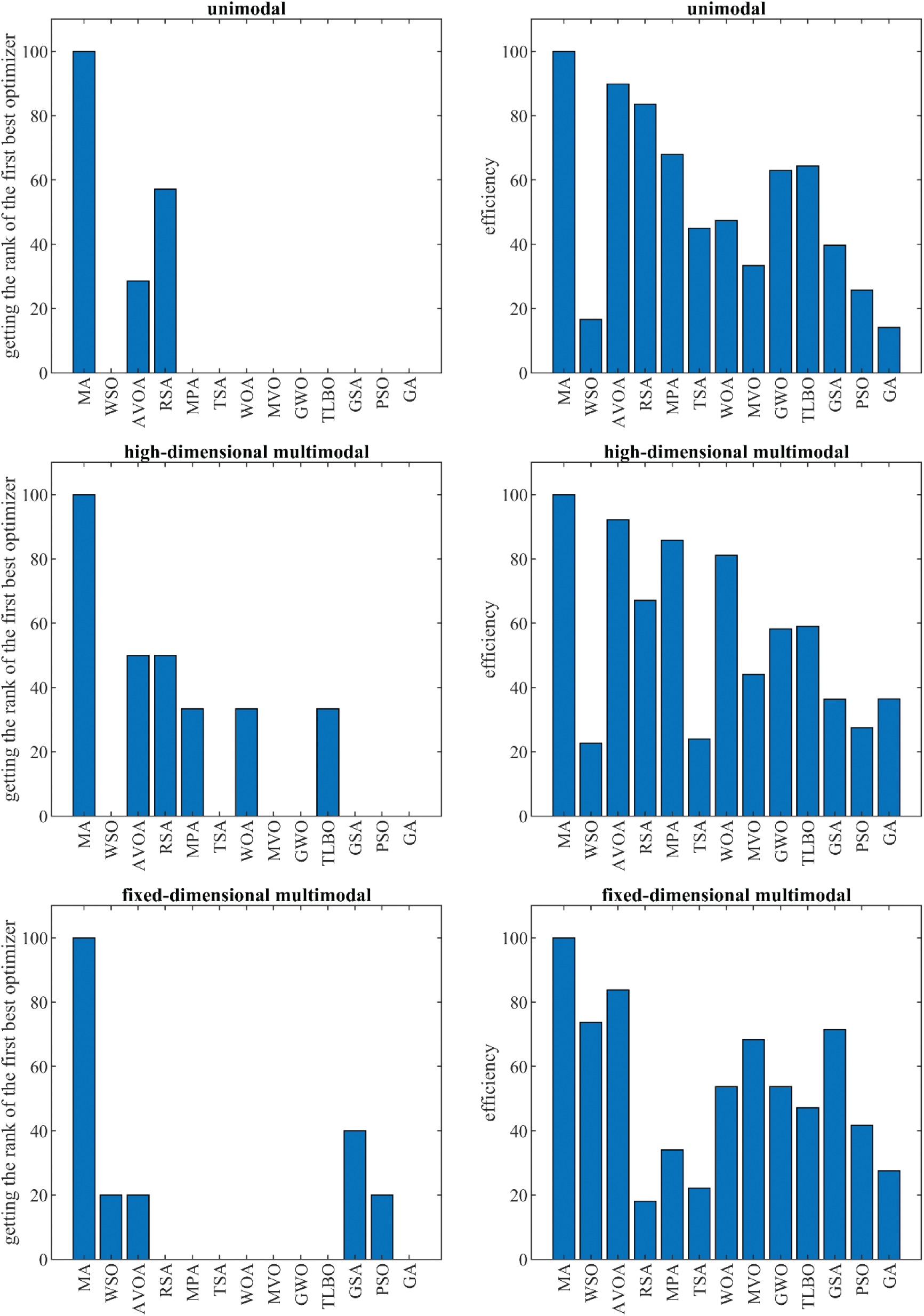
Figure 3: Bar graph of MA and competitor algorithms performances on the F1 to F23

4.4 Evaluation of the CEC 2017 Test Suite

In this subsection, the performance of the proposed MA approach has been tested in optimizing the CEC 2017 test suite benchmark functions. The CEC 2017 test suite has thirty benchmark functions C17-F1 to C17-F30. The C17-F2 function is not considered in the simulation studies due to its unstable behavior. The optimization results of this test suite using MA and competitor algorithms are reported in Table 6. Based on the optimization results, MA is the first best optimizer for functions C17-F1, C17-F3 to C17-F6, C17-F8 to C17-F21, and C17-F23 to C17-F30. Analysis of the simulation results shows that the proposed MA algorithm, by providing better results in most functions, has delivered superior performance in optimization of the CEC 2017 test suite compared to competitor algorithms. The effectiveness of the proposed MA approach and competitor algorithms in solving the CEC 2017 test suite is presented in Fig. 4. The visual analysis of these graphs shows that MA has been ranked as the first-best optimizer in 92% of the functions of this test suite.

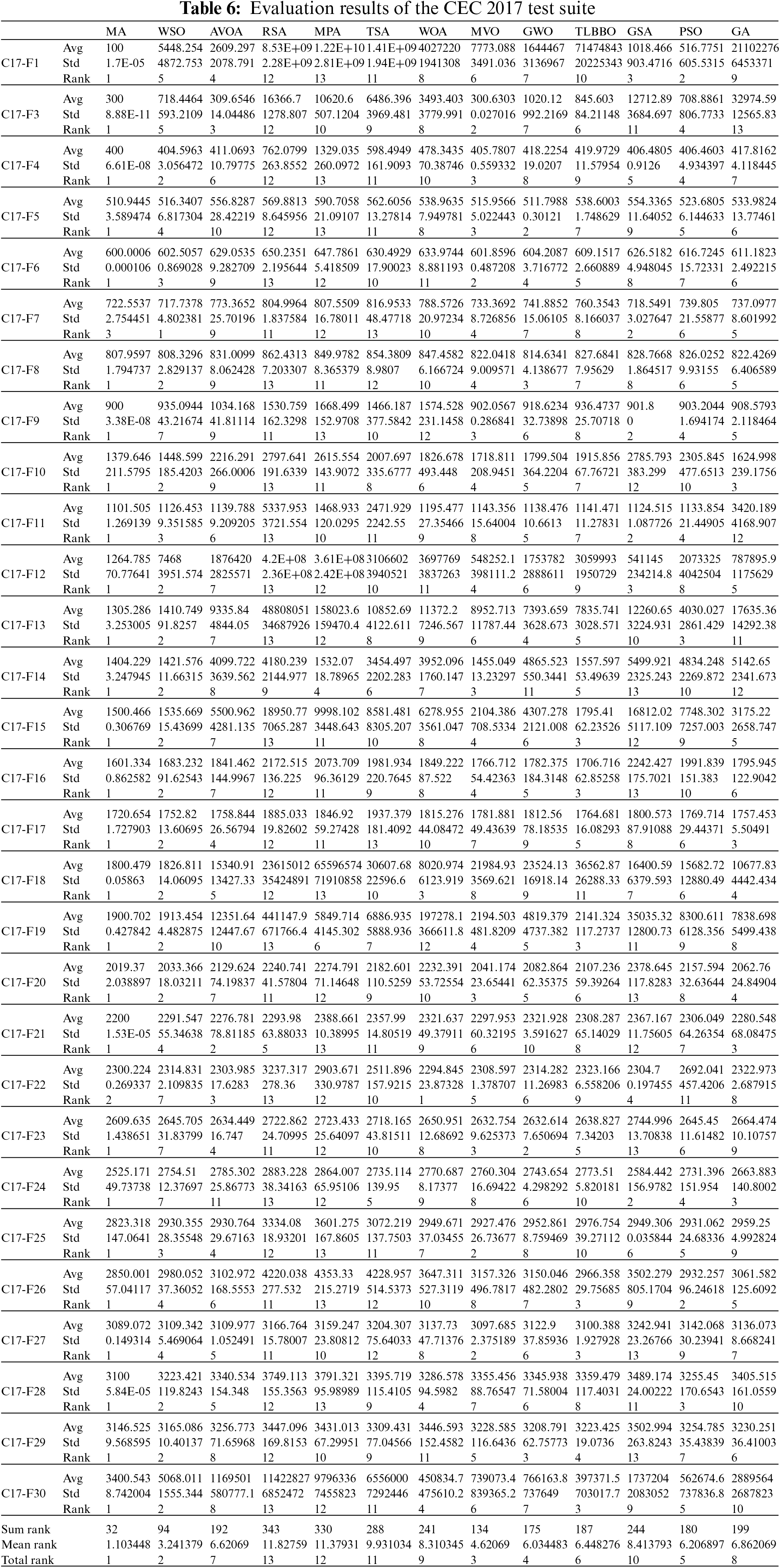
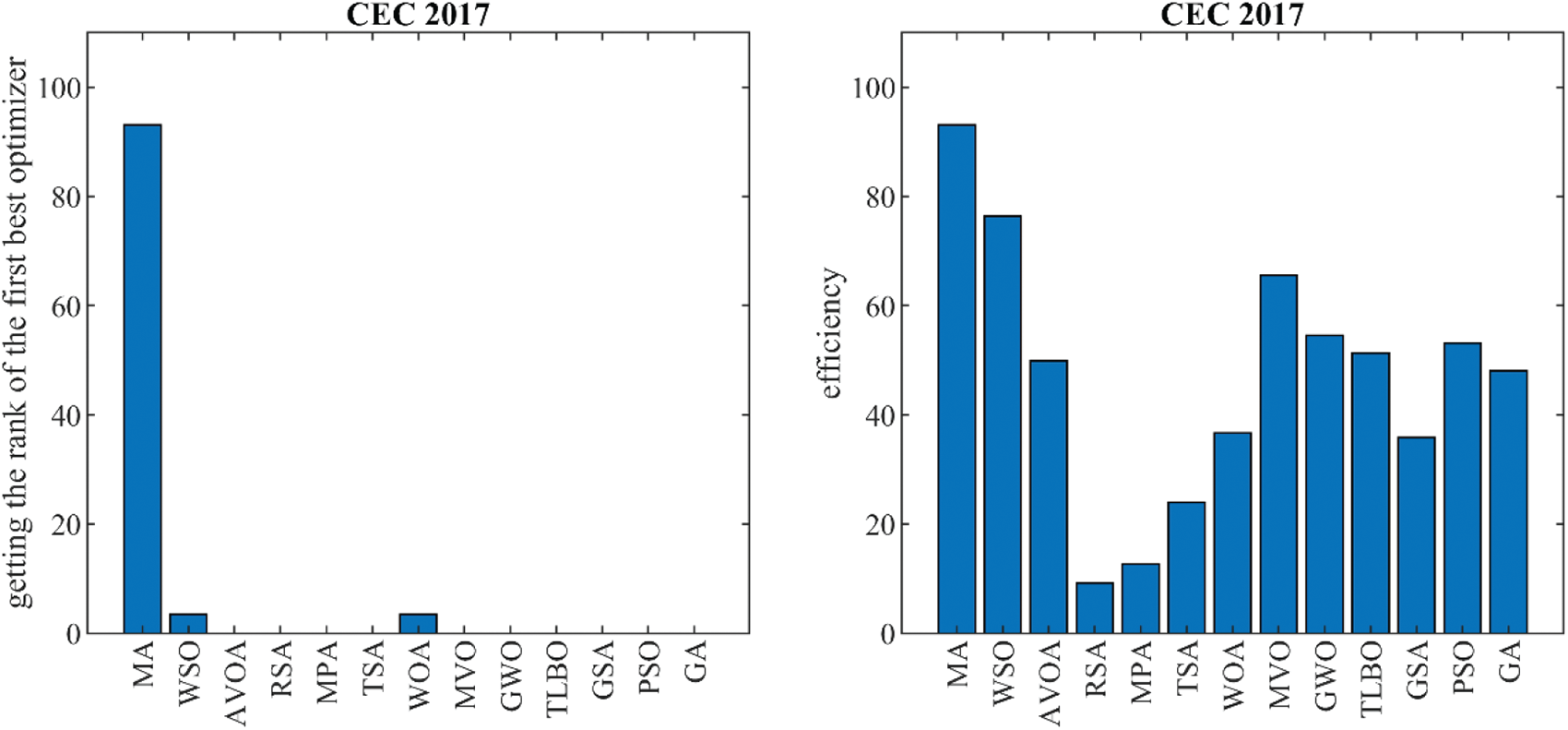
Figure 4: Bar graph of MA and competitor algorithms performances on the CEC 2017 test suite

4.5 Statistical Analysis

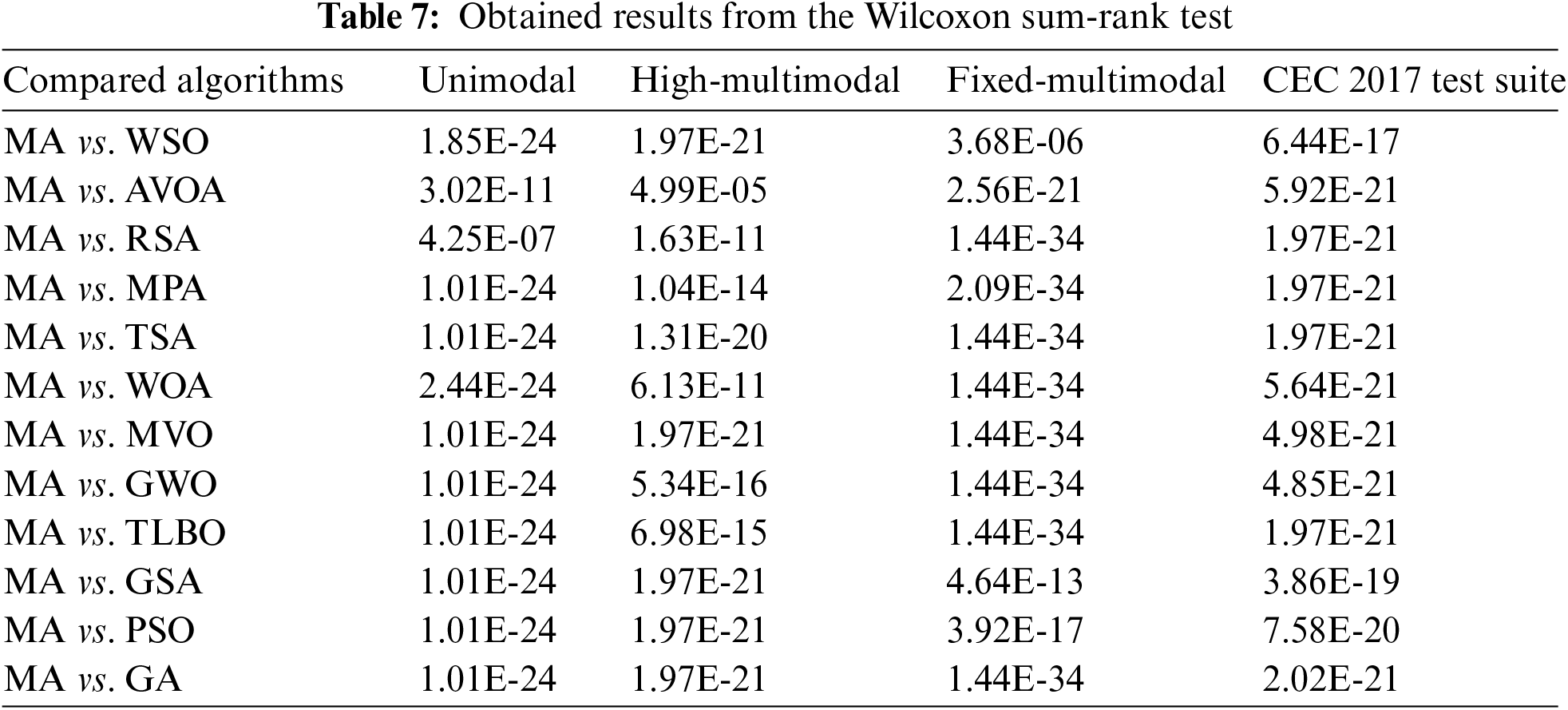
In this subsection, statistical analysis is presented on the performance of MA and competitor algorithms to determine whether the superiority of the proposed approach is significant from a statistical point of view. Wilcoxon sign-rank test [79] statistical analysis is employed for this purpose. Wilcoxon sign-rank test is a non-parametric test used to determine the significant difference between the averages of two data samples. In this test, the presence or absence of a substantial difference is determined using an index called “p-value”.

The results of implementing Weil’s statistical analysis on the performance of MA compared to each of the competing algorithms are presented in Table 7. Based on the obtained results, in cases where the p-value is less than 0.05, the proposed MA approach has a significant statistical advantage compared to the corresponding competing algorithm.

5  Application of MA to Real-World Problems

In this section, the effectiveness of the proposed MA approach in solving real-world applications is evaluated. For this purpose, MA is employed in the optimization of four engineering design problems, including tension/compression spring (TCS) design, welded beam (WB) design, speed reducer (SR) design, and pressure vessel (PV) design. The full description and mathematical model of these problems are provided for TCS in [80], WB in [80], SR in [81,82], and PV in [83].

The results of implementing the proposed MA approach and competing algorithms on these four engineering problems are reported in Table 8. The optimization results show that the proposed MA approach has provided the optimal solution for the TCS problem with the values of the design variables equal to (0.051689, 0.356718, 11.28897) and the value of the corresponding objective function is equal to 2996.348. MA has presented the optimal design of the WB problem with optimal values of the design variables equal to (0.20573, 3.470489, 9.036624, 0.20573) and the value of the corresponding objective function equal to 5882.901. In optimizing the SR problem, the proposed MA approach has provided the optimal design with the optimal values of the design variables equal to (3.5, 0.7, 17, 7.3, 7.8, 3.350215, 5.286683) and the value of the corresponding objective function equal to 1.724852. In dealing with the PV problem, the MA has provided the optimal design with the found values of the design variables equal to (0.778027, 0.384579, 40.31228, 200) and the value of the corresponding objective function equal to 0.012665. The analysis of the simulation results shows that the proposed MA approach by providing better outcomes for statistical indicators and more suitable designs for engineering problems has delivered superior performance compared to competitor algorithms. The simulation results show that the proposed MA approach has effective performance in real-world handling applications. The efficiency of MA and competitor algorithms in dealing with engineering design problems is drawn as bar graphs in Fig. 5. The visual analysis of these graphs indicates that MA was the first best optimizer in 100% of the investigated engineering problems (including four problems).

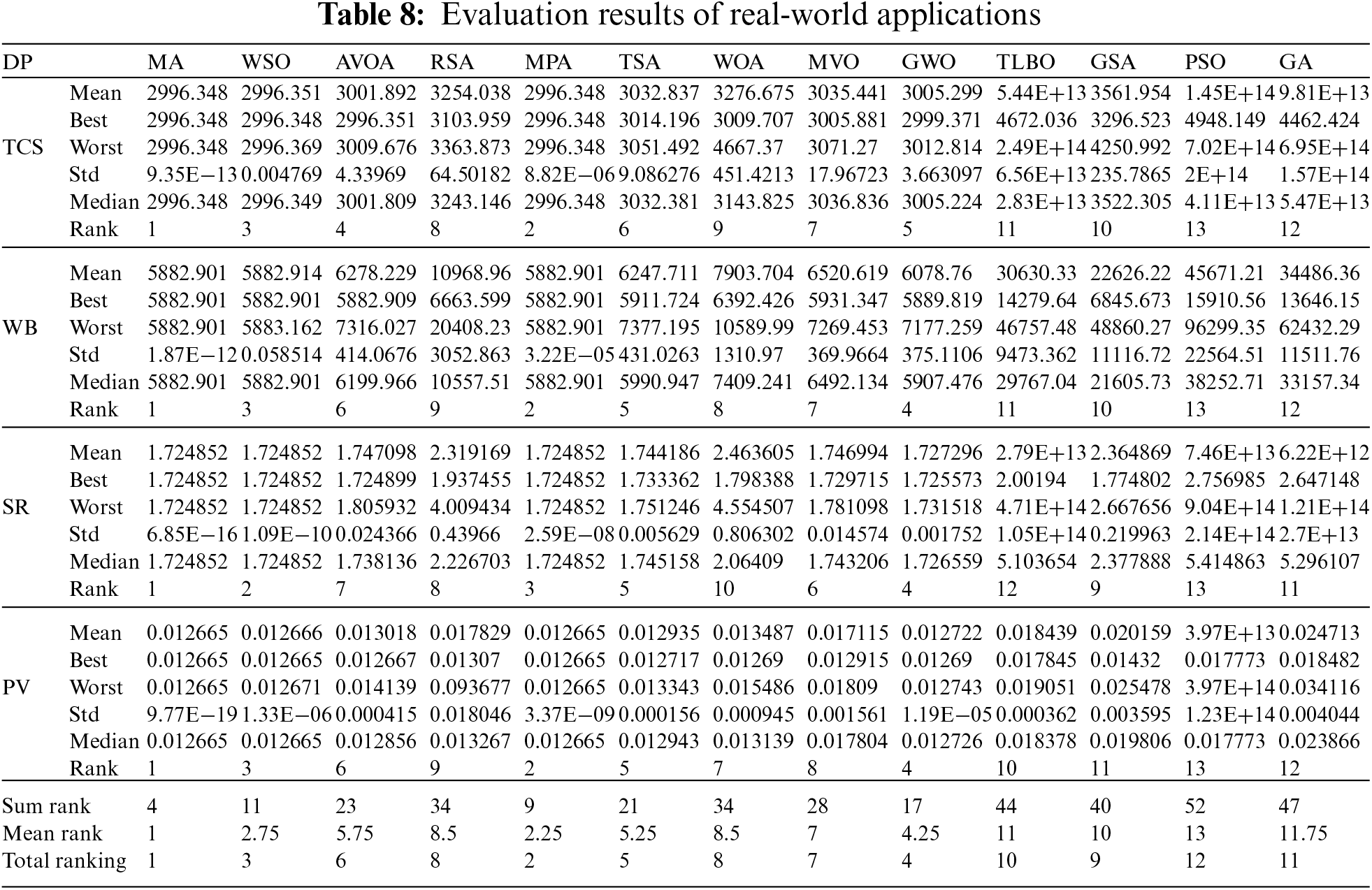
Figure 5: Bar graph of MA and competitor algorithms performances on the engineering problems

6  Conclusion and Future Works

In this paper, a new human-based metaheuristic algorithm called Migration Algorithm (MA) was introduced to solve optimization problems in various sciences. Human activities in the migration process are the fundamental inspiration in MA design. The proposed approach was mathematically modeled based on the simulation of two strategies of choosing the migration destination and adapting to the new environment in two phases of exploration and exploitation. Fifty-two standard benchmark functions including unimodal, multimodal, and the CEC 2017 test suite were employed to evaluate MA performance in solving optimization problems. The optimization results showed that the proposed MA approach with high ability in exploration and exploitation has a favorable performance in optimization. The quality of MA was compared with the performance of twelve well-known metaheuristic algorithms. The results obtained from solving the unimodal functions showed that MA had provided high efficiency in 100% of the functions of this set by winning the first rank. The findings obtained from optimizing unimodal functions showed that MA is highly capable of exploitation and local search. The results of solving high-dimensional multimodal functions indicated the 100% efficiency of the proposed approach and the high capability of MA in exploration and global search. The results of solving fixed-dimensional multimodal functions show 100% efficiency of the proposed approach in getting the rank of the first best optimizer compared to competitor algorithms. The findings obtained from solving the CEC 2017 test suite showed that MA was ranked the first-best optimizer in 92% of the functions of this test suite. Also, the Wilcoxon sign-rank statistical analysis showed that the superiority of the proposed MA approach against competitor algorithms is significant from a statistical point of view. The simulation results showed that the proposed approach with a high ability to balance exploration and exploitation has a superior and far more competitive performance against the compared algorithms. Moreover, the implementation of MA on four engineering design problems indicated the effective performance of the proposed approach in handling real-world applications.

Introducing the proposed MA approach enables several research topics for further studies. One of the most special research potentials for future works is the design of binary and multi-objective versions of the proposed approach. Employing MA in optimization problems in different sciences as well as optimization tasks in real-world applications are other research suggestions for future work.

Acknowledgement: The authors thank Dušan Bednařík from the University of Hradec Kralove for our fruitful and informative discussions.

Funding Statement: The research was supported by the Project of Excellence PřF UHK No. 2210/2023–2024, University of Hradec Kralove, Czech Republic.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Dehghani, M., Montazeri, Z., Dhiman, G., Malik, O., Morales-Menendez, R. et al. (2020). A spring search algorithm applied to engineering optimization problems. Applied Sciences, 10(18), 6173. https://doi.org/10.3390/app10186173 [Google Scholar] [CrossRef]

2. Assiri, A. S., Hussien, A. G., Amin, M. (2020). Ant lion optimization: Variants, hybrids, and applications. IEEE Access, 8, 77746–77764. https://doi.org/10.1109/ACCESS.2020.2990338 [Google Scholar] [CrossRef]

3. Coufal, P., Hubálovský, Š., Hubálovská, M., Balogh, Z. (2021). Snow leopard optimization algorithm: A new nature-based optimization algorithm for solving optimization problems. Mathematics, 9(21), 2832. https://doi.org/10.3390/math9212832 [Google Scholar] [CrossRef]

4. Kvasov, D. E., Mukhametzhanov, M. S. (2018). Metaheuristic vs. deterministic global optimization algorithms: The univariate case. Applied Mathematics and Computation, 318(9), 245–259. https://doi.org/10.1016/j.amc.2017.05.014 [Google Scholar] [CrossRef]

5. Mirjalili, S. (2015). The ant lion optimizer. Advances in Engineering Software, 83, 80–98. https://doi.org/10.1016/j.advengsoft.2015.01.010 [Google Scholar] [CrossRef]

6. Boussaïd, I., Lepagnot, J., Siarry, P. (2013). A survey on optimization metaheuristics. Information Sciences, 237, 82–117. https://doi.org/10.1016/j.ins.2013.02.041 [Google Scholar] [CrossRef]

7. Rakotonirainy, R. G., van Vuuren, J. H. (2020). Improved metaheuristics for the two-dimensional strip packing problem. Applied Soft Computing, 92(1), 106268. https://doi.org/10.1016/j.asoc.2020.106268 [Google Scholar] [CrossRef]

8. Dehghani, M., Montazeri, Z., Dehghani, A., Malik, O. P., Morales-Menendez, R. et al. (2021). Binary spring search algorithm for solving various optimization problems. Applied Sciences, 11(3), 1286. https://doi.org/10.3390/app11031286 [Google Scholar] [CrossRef]

9. Dokeroglu, T., Sevinc, E., Kucukyilmaz, T., Cosar, A. (2019). A survey on new generation metaheuristic algorithms. Computers & Industrial Engineering, 137(5), 106040. https://doi.org/10.1016/j.cie.2019.106040 [Google Scholar] [CrossRef]

10. Hussain, K., Salleh, M. N. M., Cheng, S., Shi, Y. (2019). Metaheuristic research: A comprehensive survey. Artificial Intelligence Review, 52(4), 2191–2233. https://doi.org/10.1007/s10462-017-9605-z [Google Scholar] [CrossRef]

11. Iba, K. (1994). Reactive power optimization by genetic algorithm. IEEE Transactions on Power Systems, 9(2), 685–692. https://doi.org/10.1109/59.317674 [Google Scholar] [CrossRef]

12. Pandya, S., Jariwala, H. R. (2022). Single- and multiobjective optimal power flow with stochastic wind and solar power plants using moth flame optimization algorithm. Smart Science, 10(2), 77–117. https://doi.org/10.1080/23080477.2021.1964692 [Google Scholar] [CrossRef]

13. Dehghani, M., Mardaneh, M., Malik, O. P., Guerrero, J. M., Sotelo, C. et al. (2020). Genetic algorithm for energy commitment in a power system supplied by multiple energy carriers. Sustainability, 12(23), 10053. https://doi.org/10.3390/su122310053 [Google Scholar] [CrossRef]

14. Shaheen, A., El-Sehiemy, R., El-Fergany, A., Ginidi, A. (2022). Representations of solar photovoltaic triple-diode models using artificial hummingbird optimizer. Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, 44(4), 8787–8810. https://doi.org/10.1080/15567036.2022.2125126 [Google Scholar] [CrossRef]

15. Rezk, H., Fathy, A., Aly, M., Ibrahim, M. N. F. (2021). Energy management control strategy for renewable energy system based on spotted hyena optimizer. Computers, Materials & Continua, 67(2), 2271–2281. https://doi.org/10.32604/cmc.2021.014590 [Google Scholar] [CrossRef]

16. Ghasemi, M., Ghavidel, S., Ghanbarian, M. M., Gitizadeh, M. (2015). Multi-objective optimal electric power planning in the power system using Gaussian bare-bones imperialist competitive algorithm. Information Sciences, 294, 286–304. https://doi.org/10.1016/j.ins.2014.09.051 [Google Scholar] [CrossRef]

17. Akbari, E., Ghasemi, M., Gil, M., Rahimnejad, A., Gadsden, S. A. (2021). Optimal power flow via teaching-learning-studying-based optimization algorithm. Electric Power Components and Systems, 49(6–7), 584–601. https://doi.org/10.1080/15325008.2021.1971331 [Google Scholar] [CrossRef]

18. Montazeri, Z., Niknam, T. (2017). Energy carriers management based on energy consumption. Proceedings of the IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI2017), pp. 539–543. Tehran, Iran. https://doi.org/10.1109/KBEI.2017.8325036 [Google Scholar] [CrossRef]

19. Dehghani, M., Montazeri, Z., Malik, O. (2020). Optimal sizing and placement of capacitor banks and distributed generation in distribution systems using spring search algorithm. International Journal of Emerging Electric Power Systems, 21(1), 20190217. https://doi.org/10.1515/ijeeps-2019-0217 [Google Scholar] [CrossRef]

20. Dehghani, M., Montazeri, Z., Malik, O. P., Al-Haddad, K., Guerrero, J. M. et al. (2020). A new methodology called dice game optimizer for capacitor placement in distribution systems. Electrical Engineering & Electromechanics, 1(1), 61–64. https://doi.org/10.20998/2074-272X.2020.1.10 [Google Scholar] [CrossRef]

21. Dehbozorgi, S., Ehsanifar, A., Montazeri, Z., Dehghani, M., Seifi, A. (2017). Line loss reduction and voltage profile improvement in radial distribution networks using battery energy storage system. Proceedings of the 2017 IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI2017), pp. 215–219. Tehran, Iran. https://doi.org/10.1109/KBEI.2017.8324976 [Google Scholar] [CrossRef]

22. Montazeri, Z., Niknam, T. (2018). Optimal utilization of electrical energy from power plants based on final energy consumption using gravitational search algorithm. Electrical Engineering & Electromechanics, 4(4), 70–73. https://doi.org/10.20998/2074-272X.2018.4.12 [Google Scholar] [CrossRef]

23. Dehghani, M., Mardaneh, M., Montazeri, Z., Ehsanifar, A., Ebadi, M. J. et al. (2018). Spring search algorithm for simultaneous placement of distributed generation and capacitors. Electrical Engineering & Electromechanics, 6(6), 68–73. https://doi.org/10.20998/2074-272X.2018.6.10 [Google Scholar] [CrossRef]

24. Premkumar, M., Sowmya, R., Jangir, P., Nisar, K. S., Aldhaifallah, M. (2021). A new metaheuristic optimization algorithms for brushless direct current wheel motor design problem. Computers, Materials & Continua, 67(2), 2227–2242. https://doi.org/10.32604/cmc.2021.015565 [Google Scholar] [CrossRef]

25. Wolpert, D. H., Macready, W. G. (1997). No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1(1), 67–82. https://doi.org/10.1109/4235.585893 [Google Scholar] [CrossRef]

26. Kennedy, J., Eberhart, R. (1995). Particle swarm optimization. Proceedings of the International Conference on Neural Networks (ICNN’95), pp. 1942–1948. Perth, WA, Australia. https://doi.org/10.1109/ICNN.1995.488968 [Google Scholar] [CrossRef]

27. Dorigo, M., Maniezzo, V., Colorni, A. (1996). Ant system: Optimization by a colony of cooperating agents. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 26(1), 29–41. https://doi.org/10.1109/3477.484436 [Google Scholar] [PubMed] [CrossRef]

28. Karaboga, D., Basturk, B. (2007). Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems. In: Foundations of fuzzy logic and soft computing. IFSA 2007. Lecture notes in computer science, pp. 789–798. Berlin, Heidelberg: Springer. https://doi.org/10.1007/978-3-540-72950-1_77 [Google Scholar] [CrossRef]

29. Yang, X. S. (2009). Firefly algorithms for multimodal optimization. In: Watanabe, O., Zeugmann, T. (Eds.Stochastic algorithms: Foundations and applications, SAGA 2009. Lecture notes in computer science, vol. 5792. Berlin, Heidelberg: Springer. https://doi.org/10.1007/978-3-642-04944-6_14 [Google Scholar] [CrossRef]

30. Mirjalili, S., Mirjalili, S. M., Lewis, A. (2014). Grey wolf optimizer. Advances in Engineering Software, 69, 46–61. https://doi.org/10.1016/j.advengsoft.2013.12.007 [Google Scholar] [CrossRef]

31. Zhao, L., Zhao, W., Hawbani, A., Al-Dubai, A. Y., Min, G. et al. (2020). Novel online sequential learning-based adaptive routing for edge software-defined vehicular networks. IEEE Transactions on Wireless Communications, 20(5), 2991–3004. https://doi.org/10.1109/TWC.2020.3046275 [Google Scholar] [CrossRef]

32. Li, X., Han, S., Zhao, L., Gong, C., Liu, X. (2017). New dandelion algorithm optimizes extreme learning machine for biomedical classification problems. Computational Intelligence and Neuroscience, 2017, 4523754. https://doi.org/10.1155/2017/4523754 [Google Scholar] [PubMed] [CrossRef]

33. Trojovský, P., Dehghani, M. (2022). Pelican optimization algorithm: A novel nature-inspired algorithm for engineering applications. Sensors, 22(3), 855. https://doi.org/10.3390/s22030855 [Google Scholar] [PubMed] [CrossRef]

34. Dhiman, G., Kumar, V. (2018). Emperor penguin optimizer: A bio-inspired algorithm for engineering problems. Knowledge-Based Systems, 159(2), 20–50. https://doi.org/10.1016/j.knosys.2018.06.001 [Google Scholar] [CrossRef]

35. Faramarzi, A., Heidarinejad, M., Mirjalili, S., Gandomi, A. H. (2020). Marine predators algorithm: A nature-inspired metaheuristic. Expert Systems with Applications, 152(4), 113377. https://doi.org/10.1016/j.eswa.2020.113377 [Google Scholar] [CrossRef]

36. Dhiman, G., Garg, M., Nagar, A., Kumar, V., Dehghani, M. (2020). A novel algorithm for global optimization: Rat swarm optimizer. Journal of Ambient Intelligence and Humanized Computing, 12, 1–26. https://doi.org/10.1007/s12652-020-02580-0 [Google Scholar] [CrossRef]

37. Zeidabadi, F. A., Doumari, S. A., Dehghani, M., Montazeri, Z., Trojovský, P. et al. (2022a). MLA: A new mutated leader algorithm for solving optimization problems. Computers, Materials & Continua, 70(3), 5631–5649. https://doi.org/10.32604/cmc.2022.021072 [Google Scholar] [CrossRef]

38. Abualigah, L., Abd Elaziz, M., Sumari, P., Geem, Z. W., Gandomi, A. H. (2022). Reptile search algorithm (RSAA nature-inspired meta-heuristic optimizer. Expert Systems with Applications, 191(11), 116158. https://doi.org/10.1016/j.eswa.2021.116158 [Google Scholar] [CrossRef]

39. Dehghani, M., Hubálovský, Š., Trojovský, P. (2021). Cat and mouse based optimizer: A new nature-inspired optimization algorithm. Sensors, 21(15), 5214. https://doi.org/10.3390/s21155214 [Google Scholar] [PubMed] [CrossRef]

40. Dehghani, M., Mardaneh, M., Malik, O. P., NouraeiPour, S. M. (2019). DTO: Donkey theorem optimization. Proceedings of the 27th Iranian Conference on Electrical Engineering (ICEE2019), pp. 1855–1859. Yazd, Iran. https://doi.org/10.3390/math9111190 [Google Scholar] [CrossRef]

41. Zeidabadi, F. A., Doumari, S. A., Dehghani, M., Montazeri, Z., Trojovský, P. et al. (2022b). AMBO: All members-based optimizer for solving optimization problems. Computers, Materials & Continua, 70(2), 2905–2921. https://doi.org/10.32604/cmc.2022.019867 [Google Scholar] [CrossRef]

42. Dehghani, M., Montazeri, Z., Hubálovský, Š. (2021). GMBO: Group mean-based optimizer for solving various optimization problems. Mathematics, 9(11), 1190. https://doi.org/10.3390/math9111190 [Google Scholar] [CrossRef]

43. Kaur, S., Awasthi, L. K., Sangal, A. L., Dhiman, G. (2020). Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Engineering Applications of Artificial Intelligence, 90(2), 103541. https://doi.org/10.1016/j.engappai.2020.103541 [Google Scholar] [CrossRef]

44. Doumari, S. A., Givi, H., Dehghani, M., Montazeri, Z., Leiva, V. et al. (2021). A new two-stage algorithm for solving optimization problems. Entropy, 23(4), 491. https://doi.org/10.3390/e23040491 [Google Scholar] [PubMed] [CrossRef]

45. Braik, M., Hammouri, A., Atwan, J., Al-Betar, M. A., Awadallah, M. A. (2022). White shark optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems. Knowledge-Based Systems, 243(7), 108457. https://doi.org/10.1016/j.knosys.2022.108457 [Google Scholar] [CrossRef]

46. Abdollahzadeh, B., Gharehchopogh, F. S., Mirjalili, S. (2021). African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Computers & Industrial Engineering, 158(4), 107408. https://doi.org/10.1016/j.cie.2021.107408 [Google Scholar] [CrossRef]

47. Goldberg, D. E., Holland, J. H. (1988). Genetic algorithms and machine learning. Machine Learning, 3(2), 95–99. https://doi.org/10.1023/A:1022602019183 [Google Scholar] [CrossRef]

48. Storn, R., Price, K. (1997). Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 11(4), 341–359. https://doi.org/10.1023/A:1008202821328 [Google Scholar] [CrossRef]

49. Simon, D. (2008). Biogeography-based optimization. IEEE Transactions on Evolutionary Computation, 12(6), 702–713. https://doi.org/10.1109/TEVC.2008.919004 [Google Scholar] [CrossRef]

50. de Castro, L. N., Timmis, J. I. (2003). Artificial immune systems as a novel soft computing paradigm. Soft Computing, 7(8), 526–544. https://doi.org/10.1007/s00500-002-0237-z [Google Scholar] [CrossRef]

51. Beyer, H. G., Schwefel, H. P. (2002). Evolution strategies—A comprehensive introduction. Natural Computing, 1(1), 3–52. https://doi.org/10.1023/A:1015059928466 [Google Scholar] [CrossRef]

52. Reynolds, R. G. (1994). An introduction to cultural algorithms. Proceedings of the Third Annual Conference on Evolutionary Programming, pp. 131–139. San Diego: World Scientific. https://doi.org/10.1142/9789814534116 [Google Scholar] [CrossRef]

53. Banzhaf, W., Nordin, P., Keller, R. E., Francone, F. D. (1997). Genetic programming: An introduction, 1st edition. San Francisco: Morgan Kaufmann Publishers. [Google Scholar]

54. Kirkpatrick, S., Gelatt, C. D., Vecchi, M. P. (1983). Optimization by simulated annealing. Science, 220(4598), 671–680. https://doi.org/10.1126/science.220.4598.671 [Google Scholar] [PubMed] [CrossRef]

55. Rashedi, E., Nezamabadi-Pour, H., Saryazdi, S. (2009). GSA: A gravitational search algorithm. Information Sciences, 179(13), 2232–2248. https://doi.org/10.1016/j.ins.2009.03.004 [Google Scholar] [CrossRef]

56. Dehghani, M., Samet, H. (2020). Momentum search algorithm: A new meta-heuristic optimization algorithm inspired by momentum conservation law. SN Applied Sciences, 2(10), 1–15. https://doi.org/10.1007/s42452-020-03511-6 [Google Scholar] [CrossRef]

57. Shah-Hosseini, H. (2011). Principal components analysis by the galaxy-based search algorithm: A novel metaheuristic for continuous optimisation. International Journal of Computational Science and Engineering, 6(1–2), 132–140. https://doi.org/10.1504/IJCSE.2011.041221 [Google Scholar] [CrossRef]

58. Mirjalili, S., Mirjalili, S. M., Hatamlou, A. (2016). Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Computing and Applications, 27(2), 495–513. https://doi.org/10.1007/s00521-015-1870-7 [Google Scholar] [CrossRef]

59. Hatamlou, A. (2013). Black hole: A new heuristic optimization approach for data clustering. Information Sciences, 222, 175–184. https://doi.org/10.1016/j.ins.2012.08.023 [Google Scholar] [CrossRef]

60. Du, H., Wu, X., Zhuang, J. (2006). Small-world optimization algorithm for function optimization. In: Jiao, L., Wang, L., Gao, X., Liu, J., Wu, F. (Eds.Advances in natural computation, ICNC 2006. Lecture notes in computer science, vol. 4222. Berlin, Heidelberg: Springer. [Google Scholar]

61. Tayarani-N, M. H., Akbarzadeh-T, M. R. (2008). Magnetic optimization algorithms a new synthesis. Proceedings of the 2008 IEEE Congress on Evolutionary Computation (IEEE World Congress on Computational Intelligence), pp. 2659–2664. China: Hong Kong. [Google Scholar]

62. Kaveh, A., Khayatazad, M. (2012). A new meta-heuristic method: Ray optimization. Computers & Structures, 112–113, 283–294. https://doi.org/10.1016/j.compstruc.2012.09.003 [Google Scholar] [CrossRef]

63. Alatas, B. (2011). ACROA: Artificial chemical reaction optimization algorithm for global optimization. Expert Systems with Applications, 38(10), 13170–13180. https://doi.org/10.1016/j.eswa.2011.04.126 [Google Scholar] [CrossRef]

64. Moghdani, R., Salimifard, K. (2018). Volleyball premier league algorithm. Applied Soft Computing, 64(5), 161–185. https://doi.org/10.1016/j.asoc.2017.11.043 [Google Scholar] [CrossRef]

65. Dehghani, M., Mardaneh, M., Guerrero, J. M., Malik, O., Kumar, V. (2020). Football game-based optimization: An application to solve energy commitment problem. International Journal of Intelligent Engineering and Systems, 13(5), 514–523. https://doi.org/10.22266/ijies2020.1031.45 [Google Scholar] [CrossRef]

66. Dehghani, M., Montazeri, Z., Malik, O. P., Ehsanifar, A., Dehghani, A. (2019). OSA: Orientation search algorithm. International Journal of Industrial Electronics, Control and Optimization, 2(2), 99–112. https://doi.org/10.22111/ieco.2018.26308.1072 [Google Scholar] [CrossRef]

67. Rao, R. V., Savsani, V. J., Vakharia, D. (2011). Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Computer-Aided Design, 43(3), 303–315. https://doi.org/10.1016/j.cad.2010.12.015 [Google Scholar] [CrossRef]

68. Dehghani, M., Mardaneh, M., Malik, O. P. (2020). FOA: ‘Following’ optimization algorithm for solving power engineering optimization problems. Journal of Operation and Automation in Power Engineering, 8(1), 57–64. https://doi.org/10.22098/JOAPE.2019.5522.1414 [Google Scholar] [CrossRef]

69. Trojovský, P., Dehghani, M., Trojovská, E., Milkova, E. (2022). The language education optimization: A new human-based metaheuristic algorithm for solving optimization problems. Computer Modeling in Engineering & Sciences, 136(2), 1527–1573. https://doi.org/10.32604/cmes.2023.025908 [Google Scholar] [CrossRef]

70. Trojovský, P., Dehghani, M. (2022). A new optimization algorithm based on mimicking the voting process for leader selection. PeerJ Computer Science, 8(4), e976. https://doi.org/10.7717/peerj-cs.976 [Google Scholar] [PubMed] [CrossRef]

71. Lin, N., Fu, L., Zhao, L., Min, G., Al-Dubai, A. et al. (2020). A novel multimodal collaborative drone-assisted VANET networking model. IEEE Transactions on Wireless Communications, 19(7), 4919–4933. https://doi.org/10.1109/TWC.2020.2988363 [Google Scholar] [CrossRef]

72. Zeidabadi, F. A., Dehghani, M., Trojovský, P., Hubálovský, Š., Leiva, V. et al. (2022). Archery algorithm: A novel stochastic optimization algorithm for solving optimization problems. Computers, Materials & Continua, 72(1), 399–416. https://doi.org/10.32604/cmc.2022.024736 [Google Scholar] [CrossRef]

73. Ayyarao, T. L., RamaKrishna, N., Elavarasam, R. M., Polumahanthi, N., Rambabu, M. et al. (2022). War strategy optimization algorithm: A new effective metaheuristic algorithm for global optimization. IEEE Access, 10, 25073–25105. https://doi.org/10.1109/ACCESS.2022.3153493 [Google Scholar] [CrossRef]

74. Shi, Y. (2011). Brain storm optimization algorithm. In: Advances in swarm intelligence, ICSI 2011. Lecture notes in computer science, vol. 6728. Berlin, Heidelberg: Springer. https://doi.org/10.1007/978-3-642-21515-5_36 [Google Scholar] [CrossRef]

75. Veeramoothoo, S. (2022). Social justice and the portrayal of migrants in international organization for migration’s world migration reports. Journal of Technical Writing and Communication, 52(1), 57–93. https://doi.org/10.1177/0047281620953377 [Google Scholar] [CrossRef]

76. Razum, O., Samkange-Zeeb, F. (2008). Populations at special health risk: Migrants. In: Heggenhougen, K. (Ed.International encyclopedia of public health, pp. 233–241. Amsterdam: Elsevier, Academic Press. [Google Scholar]

77. Yao, X., Liu, Y., Lin, G. (1999). Evolutionary programming made faster. IEEE Transactions on Evolutionary Computation, 3(2), 82–102. https://doi.org/10.1109/4235.771163 [Google Scholar] [CrossRef]

78. Awad, N., Ali, M., Liang, J., Qu, B., Suganthan, P. et al. (2016). Evaluation criteria for the CEC, 2017 special session and competition on single objective real-parameter numerical optimization. Technology Report. https://doi.org/10.13140/RG.2.2.12568.70403 [Google Scholar] [CrossRef]

79. Wilcoxon, F. (1992). Individual comparisons by ranking methods. Biometrics Bulletin, 1(6), 80–83. https://doi.org/10.2307/3001968 [Google Scholar] [CrossRef]

80. Mirjalili, S., Lewis, A. (2016). The whale optimization algorithm. Advances in Engineering Software, 95(12), 51–67. https://doi.org/10.1016/j.advengsoft.2016.01.008 [Google Scholar] [CrossRef]

81. Gandomi, A. H., Yang, X. S. (2011). Benchmark problems in structural optimization. In: Koziel, S., Yang, X. S. (Eds.Computational optimization, methods and algorithms. Studies in computational intelligence, vol. 356. Berlin, Heidelberg: Springer. [Google Scholar]

82. Mezura-Montes, E., Coello, C. A. C. (2005). Useful infeasible solutions in engineering optimization with evolutionary algorithms. In: Gelbukh, A., de Albornoz, Á., Terashima-Marín, H. (Eds.Advances in artificial intelligence, MICAI 2005. Lecture notes in computer science, vol. 3789. Berlin, Heidelberg: Springer. [Google Scholar]

83. Kannan, B., Kramer, S. N. (1994). An augmented Lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. Journal of Mechanical Design, 116(2), 405–411. https://doi.org/10.1115/1.2919393 [Google Scholar] [CrossRef]

Appendix A. Objective Functions

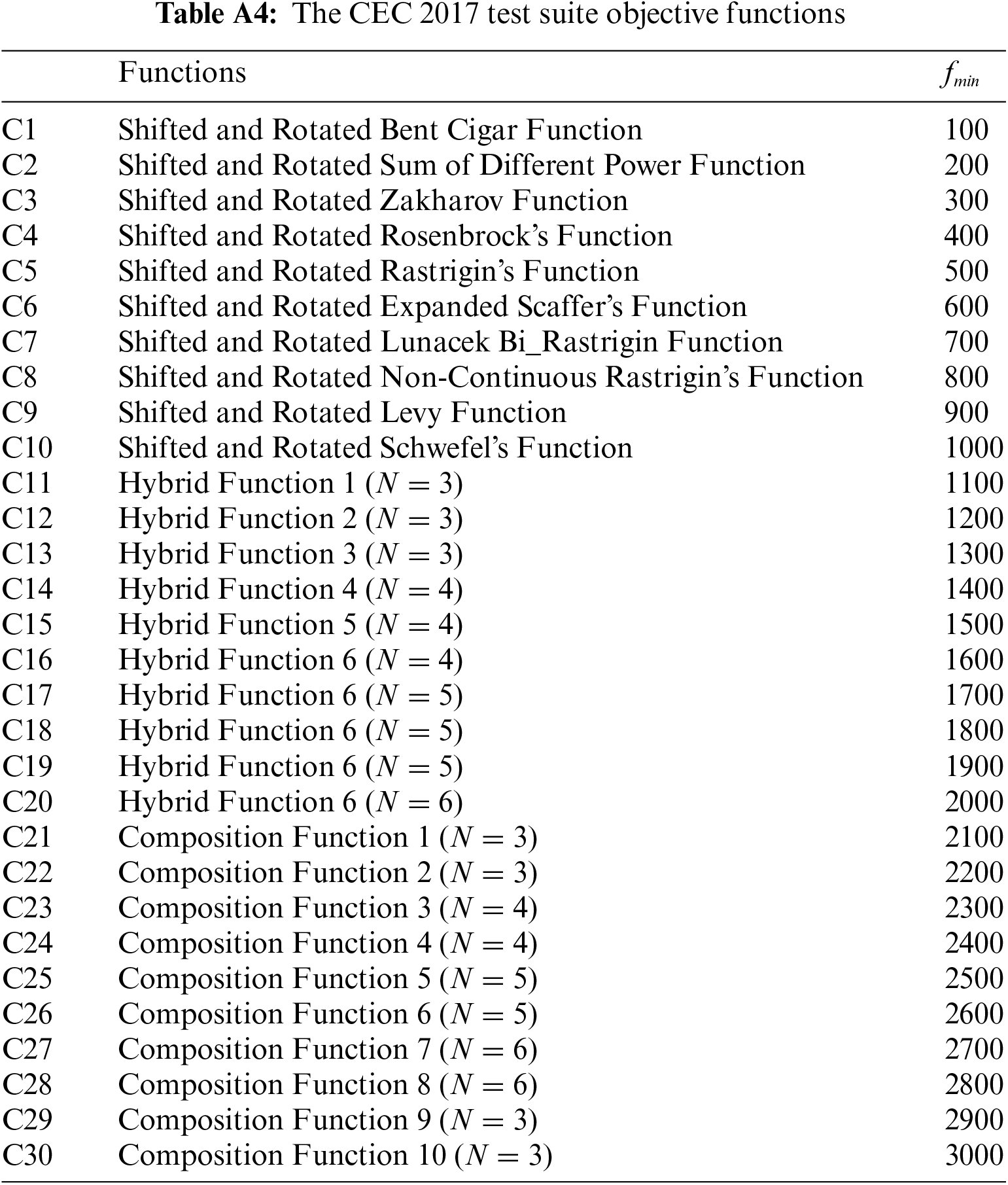
The information of the objective functions used in the simulation section is specified in Tables A1 to A4.