 Open Access
Open Access
ARTICLE
On Fractional Differential Inclusion for an Epidemic Model via L-Fuzzy Fixed Point Results
1
Department of Mathematics, King Abdulaziz University, Jeddah, Saudi Arabia
2
Department of Mathematics, Faculty of Physical Sciences, Ahmadu Bello University, Zaria, Nigeria
* Corresponding Author: Mohammed Shehu Shagari. Email:
(This article belongs to the Special Issue: Computational Aspects of Nonlinear Operator and Fixed Point Theory with Applications)
Computer Modeling in Engineering & Sciences 2023, 137(2), 1937-1956. https://doi.org/10.32604/cmes.2023.028239
Received 06 December 2022; Accepted 30 January 2023; Issue published 26 June 2023
Abstract
The real world is filled with uncertainty, vagueness, and imprecision. The concepts we meet in everyday life are vague rather than precise. In real-world situations, if a model requires that conclusions drawn from it have some bearings on reality, then two major problems immediately arise, viz. real situations are not usually crisp and deterministic; complete descriptions of real systems often require more comprehensive data than human beings could recognize simultaneously, process and understand. Conventional mathematical tools which require all inferences to be exact, are not always efficient to handle imprecisions in a wide variety of practical situations. Following the latter development, a lot of attention has been paid to examining novel L-fuzzy analogues of conventional functional equations and their various applications. In this paper, new coincidence point results for single-valued mappings and an L-fuzzy set-valued map in metric spaces are proposed. Regarding novelty and generality, the obtained invariant point notions are compared with some well-known related concepts via non-trivial examples. It is observed that our principal results subsume and refine some important ones in the corresponding domains. As an application, one of our results is utilized to discuss more general existence conditions for realizing the solutions of a non-integer order inclusion model for COVID-19.Keywords
From the beginning of the universe, man has been exerting great efforts in understanding nature and then coming up with a good connection between life and what it requires. This struggle is broken down into three phases, namely, understanding the surrounding ambient, acknowledgment of creativity, and preparing for the future. In these strives, a lot of challenges like linguistic interpretation, characterization of inter-connected phenomena into suitable categories, application of non-liberal ideas, vagueness in data analysis, and more than a handful of others, affect the precision of results. These problems, common with everyday activities can be avoided by using the concepts of fuzzy sets because they are more flexible than crisp sets. Numerous fields of mathematics, the social sciences, and engineering have undergone enormous upheavals since Zadeh [1] introduced fuzzy sets. The fundamental ideas of fuzzy sets have been refined and used in several contexts. In 1981, Heilpern [2] proved an invariant point theorem for fuzzy contraction mappings, which is a fuzzy analogue of invariant point theorems due to Nadler [3] and Banach [4]. Following [2], a number of authors have studied the existence of invariant points of fuzzy set-valued maps; for example, see [5–9]. Initiated by Goguen [10], L-fuzzy sets are a particularly intriguing development of the fuzzy set notion that substitutes a complete distributive lattice for the range set’s interval [0,1].
A recent study by Rashid et al. [11] introduced the idea of L-fuzzy mappings (Lmap) and examined a pair of Lmaps that are
On the other hand, fractional differential inclusions arise in different problems in mathematical physics, bio-mathematics, control theory, critical point theory for non-smooth energy functionals, differential variational inequalities, fuzzy set arithmetic, traffic theory, and so on. Usually, the first most investigated problem in the study of differential inclusion is the criteria for the existence of its solutions. In this context, several authors have applied different invariant point techniques and topological methods to establish the existence results of differential inclusions in abstract spaces. In the current literature, we can find much work on fractional-order models coming-up with different measures for curbing the novel corona virus (COVID-19). Lately, Rahman et al. [13] investigated a fractional non-integer order fuzzy dynamical system and established an epidemic model for COVID-19. Their proposed model is examined for solvability, using an invariant point method. On close developments, we can cite [14–18].
Following the existing findings, we notice that L-fuzzy invariant point results using the characterizations of
The rest of the paper is structured as follows: Section 2 contains the fundamentals needed to establish our principal proposal. Results and discussion are presented in Section 3. Section 4 is concerned with the application of one of the proposed notions in the fractional differential inclusion model for COVID-19. The summary and conclusion of our obtained key notions are presented in Section 5.
We collate, herein, a few fundamentals which are useful to our principal results. These basic concepts are picked from [1–3,8,9,19,20]. Throughout this paper, the sets
Let
where
Definition 2.1. [21] The mapping
Definition 2.2. [22] The mapping
Recently, Monairah et al. [23] came up with variants of Definitions 2.1 and 2.2 in the fashion given hereunder.
Definition 2.3 [23]. The mapping
Definition 2.4. [23]
The following two lemmas are essential to the discussion of our principal findings:
Lemma 2.1. [23] Let
Lemma 2.2. [23] Let
(i)
(ii) For each
(iii) For each
(iv) For each
(v) For each
(vi) For any sequence
(vii)
Definition 2.5. [24] A relation
(i) reflexive;
(ii) antisymmetric;
(iii) transitive.
A set L together with a partial ordering
Definition 2.6. [24] Let L be a nonempty set and (L,
Definition 2.7. [24] A pset
(i) a lattice, if
(ii) a complete lattice, if
(iii) distributive lattice if
A pset L is called a complete lattice if for every doubleton
Definition 2.8. [10] An L-fuzzy set (L-fset) ∇ on a nonempty set
Denote the class of all L-fuzzy sets on a nonempty set
Definition 2.9. [10] The
Definition 2.10. [11,12] Let
Consistent with Rashid et al. [11,12], let
Definition 2.11. [19,25] Let
We represent the set of all L-fuzzy invariant points of
We begin this section by introducing the idea of coincidence point results for an Lmap and single-valued mappings.
Theorem 3.1. Let
(
(
(
for all
Then,
Proof. By
Further, for every
Let
Given that
From (4), we claim that there exists
Assume that this claim is not true, that is,
that is,
Let
Given that
Hence, it if follows from (8) that
For any
Thus,
Employing the defining property of
We propose that
a contradiction for all
Definition 3.1. [26] A nonempty subset ∇ of
We denote the class of all bounded proximal subsets of
In what follows, we study another coincidence point result in connection with
Theorem 3.2.Let
(
(
for all
Then,
Proof. Let
Since
Hence, Theorem 3.1 can be applied to find
We provide the following example to support the hypotheses of Theorem 3.1.
Example 3.1. Let
Consider an Lmap
Then, for every
Further, define the mappings
Then, we observe that the following hold:
(
(
and
To prove that
(i)
(iii)
(iv)
(vi)
This shows that
Define
Since
Now, we claim that
for all
To verify (11), we check the possibilities:
Case 1. If x = 1, m = 2 and
Case 2. For x = 1, m > 2 and
Case 3. For x = 2, m > 2 and
Case 4. For x > 2, m > x and
Thus, following cases (1)−(4), we have demonstrated that (11) is valid. Hence, all the assumptions of Theorem 3.1 are agreed with. Whence,
Now, notice that if we take L = [0,1] and w = 1,
for all
Similarly, let
for all
Also, we note that
for all m > 2. Thus, all the Mizoguchi-Takahashi type results are not valid here.
Fig. 1 represents the Lattice in Example 3.1.
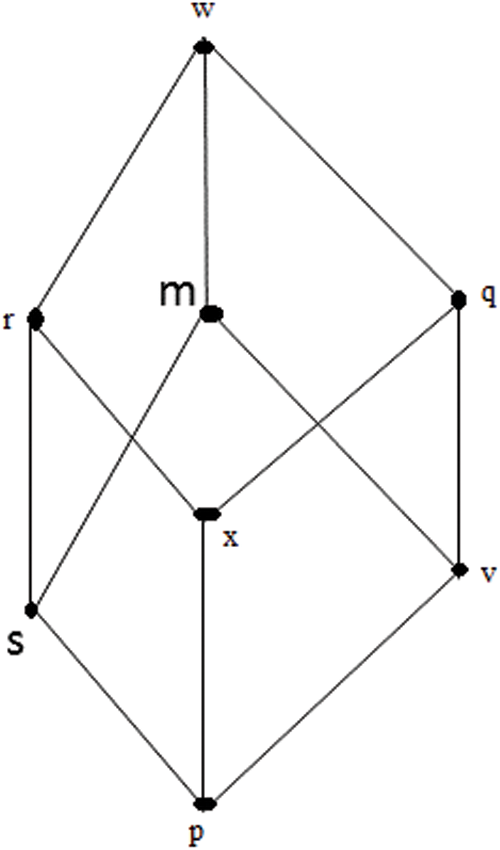
Figure 1: The lattice in example 3.1
Consider a nonempty subset A of
Corollary 3.1. Let
(i) for every
(ii)
(iii) there exists
Then,
Proof. Define the mappings
The next observation follows from Corollary 3.1.
Corollary 3.2. Let
(i) for every
(ii)
(iii) there exist
Then,
Corollary 3.3.Let
(i) for every
(ii)
(iii) there exists
Then,
Proof. Take
Corollary 3.4. Let
for all
Then,
Proof. Take
Corollary 3.5. Let
for all
Proof. First, note that
4 An Application to Fractional Differential Inclusion for an Epidemic Model
Of recent, Ahmed et al. [14] examined the importance of lock-down in managing the escalation of COVID-19, using the following non-integer order epidemic model:
where the total population under study, P(t) is partitioned into four units, viz. a susceptible population that is free from lock-down W(t), a susceptible population that is not free from lock-down
where
Consequently, the model (14) takes the form:
with the conditions:
where
It is a fact that in general, differential equations are not efficient tools to analyze non-statistical uncertainties, since the derivative of a solution to any differential equation automatically enjoys all the regularity properties of the concerned mapping and of the solution itself. This hereditary property is not found under the setting of differential inclusions. With this information, we extend problem (14) to its set-valued version given as
where
Definition 4.1. [33] Let
where
Definition 4.2. [33] Let
Lemma 4.1. [33] Let
In particular, if
Given Lemma 4.1, the integral reformulation of problem (17) which is equivalent to the model (14) is given by
Let
where
and
Definition 4.3. [34] Let
For each
Let
Then, the set of all selections of V can be regarded as the set of all selections of an Lmap
Definition 4.4. A function
and
Definition 4.5. [34] A set-valued mapping
Definition 4.6. An Lmap
Let
Theorem 4.1. Assume that the following conditions are satisfied:
(
(
for almost all
Then, the differential inclusion (19) has at least one solution in
Proof. We start by resolving (19) into an L-fuzzy invariant point problem. Accordingly, let
Then, define an Lmap
By setting
It is clear that the L-fuzzy invariant points of
Case I.
Since V has compact values, it follows that
Hence,
Case 2. Next, we prove that (13) is satisfied. Recall that for every
By
Define
Then, from (22) and (23), we obtain
Whence,
Taking supremum over all of
for all
This article established new coincidence point results for single-valued mappings and an Lmap (Theorems 3.1 and 3.2) by using a modified version of an
The results of this paper, examined in metric space, are indeed fundamental. It follows that an ample amount of future work can be highlighted. Accordingly, the underlying space can be taken to other generalized, pseudo or quasi-metric spaces, such as b-MS, metric-like space, and fuzzy MS. On the flip side, the involved Lmap can be extended to some hybrid set-valued maps, such as fuzzy soft set-valued maps, intuitionistic maps, L-fuzzy soft set-valued maps, and so on. As a result of these suggested modifications, the contractive inequalities obtained herein will be modified. The latter possible variants will pave the way for better applications.
Acknowledgement: The authors gratefully acknowledge the technical and financial support provided by the Deanship of Scientific Research (DSR) at King Abdulaziz University (KAU), Jeddah, Saudi Arabia.
Funding Statement: The Deanship of Scientific Research (DSR) at King Abdulaziz University (KAU), Jeddah, Saudi Arabia has funded this project under Grant Number (G: 220-247-1443).
Conflicts of Interest: The authors declare that they have no conflicts to report regarding the present study.
References
1. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. [Google Scholar]
2. Heilpern, S. (1981). Fuzzy mappings and fixed point theorem. Journal of Mathematical Analysis and Applications, 83(2), 566–569. [Google Scholar]
3. Nadler, S. B. (1969). Multi-valued contraction mappings. Pacific Journal of Mathematics, 30(2), 475–488. [Google Scholar]
4. Banach, S. (1922). Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundamenta Mathematicae, 3(1), 133–181. [Google Scholar]
5. Alansari, M., Shehu, S. M., Akbar, A. (2020). Fuzzy fixed point results in F-metric spaces with applications. Journal of Function Spaces, 2020, 5142815. https://doi.org/10.1155/2020/5142815 [Google Scholar] [CrossRef]
6. Al-Mazrooei, A. E., Ahmad, J. (2019). Fixed point theorems for fuzzy mappings with applications. Journal of Intelligent and Fuzzy Systems, 36(4), 3903–3909. [Google Scholar]
7. Azam, A., Arshad, M., Vetro, P. (2010). On a pair of fuzzy φ-contractive mappings. Mathematical and Computer Modelling, 52(2), 207–214. [Google Scholar]
8. Mohammed, S. S., Azam, A. (2019). Fixed points of soft-set valued and fuzzy set-valued maps with applications. Journal of Intelligent and Fuzzy Systems, 37(3), 3865–3877. [Google Scholar]
9. Mohammed, S. S., Azam, A. (2020). Fixed point theorems of fuzzy set-valued maps with applications. Issues of Analysis, 9(27), 2. [Google Scholar]
10. Goguen, J. A. (1967). L-fuzzy sets. Journal of Mathematical Analysis and Applications, 18(1), 145–174. [Google Scholar]
11. Rashid, M., Azam, A., Mehmood, N. (2014). L-fuzzy fixed points theorems for L-fuzzy mappings via βFL-admissible pair. The Scientific World Journal, 2014, 1–8. [Google Scholar]
12. Rashid, M., Kutbi, M. A., Azam, A. (2014). Coincidence theorems via alpha cuts of L-fuzzy sets with applications. Fixed Point Theory and Applications, 2014(1), 212. [Google Scholar]
13. Rahman, U., Arfan, M., Shah, K., Gomez-Aguilar, J. F. (2020). Investigating a nonlinear dynamical model of COVID-19 disease under fuzzy Caputo, random and ABC fractional order derivative. Chaos, Solitons and Fractals, 140, 110232. [Google Scholar] [PubMed]
14. Ahmed, I., Baba, I. A., Yusuf, A., Kumam, P., Kumam, W. (2020). Analysis of Caputo fractional-order model for COVID-19 with lockdown. Advances in Difference Equations, 2020(1), 1–14. [Google Scholar]
15. Chen, Y., Cheng, J., Jiang, X. Y., Xu, X. (2020). The reconstruction and prediction algorithm of the fractional TDD for the local outbreak of COVID-19. arXiv preprint arXiv: 2002.10302. [Google Scholar]
16. Li, B., Liang, H., He, Q. (2021). Multiple and generic bifurcation analysis of a discrete Hindmarsh-Rose model. Chaos, Solitons and Fractals, 146, 110856. [Google Scholar]
17. Shaikh, A. S., Shaikh, I. N., Nisar, K. S. (2020). A mathematical model of COVID-19 using fractional derivative: Outbreak in India with dynamics of transmission and control. Advances in Difference Equations, 2020, 373. [Google Scholar] [PubMed]
18. Xu, C., Yu, Y., Yang, Q., Lu, Z. (2020). Forecast analysis of the epidemics trend of COVID-19 in the United States by a generalized fractional-order SEIR model. arXiv preprint arXiv: 2004.12541. [Google Scholar]
19. Mohammed, S. S. (2020). On bilateral fuzzy contractions. Functional Analysis, Approximation and Computation, 12(1), 1–13. [Google Scholar]
20. Mohammed, S. S. (2020). On fuzzy soft set-valued maps with application. Journal of the Nigerian Society of Physical Sciences, 2(1), 26–35. [Google Scholar]
21. Du, W. S. (2010). Some new results and generalizations in metric fixed point theory. Nonlinear Analysis: Theory, Methods and Applications, 73(5), 1439–1446. [Google Scholar]
22. Du, W. S. (2012). On coincidence point and fixed point theorems for nonlinear multivalued maps. Topology and its Applications, 159(1), 49–56. [Google Scholar]
23. Monairah, A., Mohammed, S. S. (2022). Analysis of fractional differential inclusion models for COVID-19 via fixed point results in metric space. Journal of Function Spaces, 2022(2), 1–14. https://doi.org/10.1155/2022/8311587 [Google Scholar] [CrossRef]
24. Davey, B. A., Priestly, H. A. (2000). Introduction to lattices and order. Cambridge, New York, Melbourne: Cambridge University Press. [Google Scholar]
25. Azam, A., Beg, I. (2013). Common fuzzy fixed points for fuzzy mappings. Fixed Point Theory and Applications, 2013(1), 14. [Google Scholar]
26. Kaneko, H., Sessa, S. (1989). Fixed point theorems for compatible multi-valued and single-valued mappings. International Journal of Mathematics and Mathematical Sciences, 12(2), 257–262. [Google Scholar]
27. El Naschie, M. S. (2002). Wild topology, hyperbolic geometry and fusion algebra of high energy particle physics. Chaos, Solitons and Fractals, 13(9), 1935–1945. [Google Scholar]
28. El Naschie, M. S. (2000). On the unification of the fundamental forces and complex time in the E∞ space. Chaos, Solitons and Fractals, 11(7), 1149–1162. [Google Scholar]
29. Chen, S. B., Rajaee, F., Yousefpour, A., Alcaraz, R., Chu, Y. M. et al. (2021). Antiretroviral therapy of HIV infection using a novel optimal type-2 fuzzy control strategy. Alexandria Engineering Journal, 60(1), 1545–1555. [Google Scholar]
30. Eskandari, Z., Avazzadeh, Z., Khoshsiar Ghaziani, R., Li, B. (2022). Dynamics and bifurcations of a discrete-time Lotka-Volterra model using nonstandard finite difference discretization method. Mathematical Methods in the Applied Sciences, 13(6), 2050040. https://doi.org/10.1002/mma.8859 [Google Scholar] [CrossRef]
31. Li, B., Liang, H., Shi, L., He, Q. (2022). Complex dynamics of Kopel model with nonsymmetric response between oligopolists. Chaos, Solitons and Fractals, 156, 111860. [Google Scholar]
32. Riaz, M., Hashmi, M. R., Pamucar, D., Chu, Y. M. (2021). Spherical linear Diophantine fuzzy sets with modeling uncertainties in MCDM. Computer Modeling in Engineering & Sciences, 126(3), 1125–1164. https://doi.org/10.32604/cmes.2021.013699 [Google Scholar] [CrossRef]
33. Kilbas, A. A., Srivastava, H. M., Trujillo, J. J. (2006). Theory and applications of fractional differential equations, vol. 204. Oxford, UK: Elsevier Ltd., The Boulevand, Lagford Lane Kidlington. [Google Scholar]
34. Castaing, C., Valadier, M. (1977). Measurable multifunctions. In: Convex analysis and measurable multifunctions, pp. 59–90. Berlin, Heidelberg: Springer. [Google Scholar]
35. Berinde, M., Berinde, V. (2007). On a general class of multi-valued weakly Picard mappings. Journal of Mathematical Analysis and Applications, 326(2), 772–782. [Google Scholar]
36. Mizoguchi, N., Takahashi, W. (1989). Fixed point theorems for multivalued mappings on complete metric spaces. Journal of Mathematical Analysis and Applications, 141(1), 177–188. [Google Scholar]
37. Reich, S. (1972). A fixed point theorem for locally contractive multi-valued functions. Revue Roumaine de Matheematiques Pures et Appliqusees, 17, 569–572. [Google Scholar]
38. Rus, I. A. (1991). Basic problems of the metric fixed point theory revisited (II). University Babes-Bolyai, 36, 81–99. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools