Open Access

ARTICLE

Chaotic Motion Analysis for a Coupled Magnetic-Flow-Mechanical Model of the Rectangular Conductive Thin Plate

Xinzong Wang¹, Xiaofang Kang^1,2,*, Qingguan Lei¹

1 School of Civil Engineering, Anhui Jianzhu University, Hefei, 230601, China
2 Key Laboratory of Intelligent Underground Detection Technology, Anhui Jianzhu University, Hefei, 230601, China

* Corresponding Author: Xiaofang Kang. Email:

(This article belongs to the Special Issue: Vibration Control and Utilization)

Computer Modeling in Engineering & Sciences 2023, 137(2), 1749-1771. https://doi.org/10.32604/cmes.2023.027745

Received 13 November 2022; Accepted 13 February 2023; Issue published 26 June 2023

Abstract

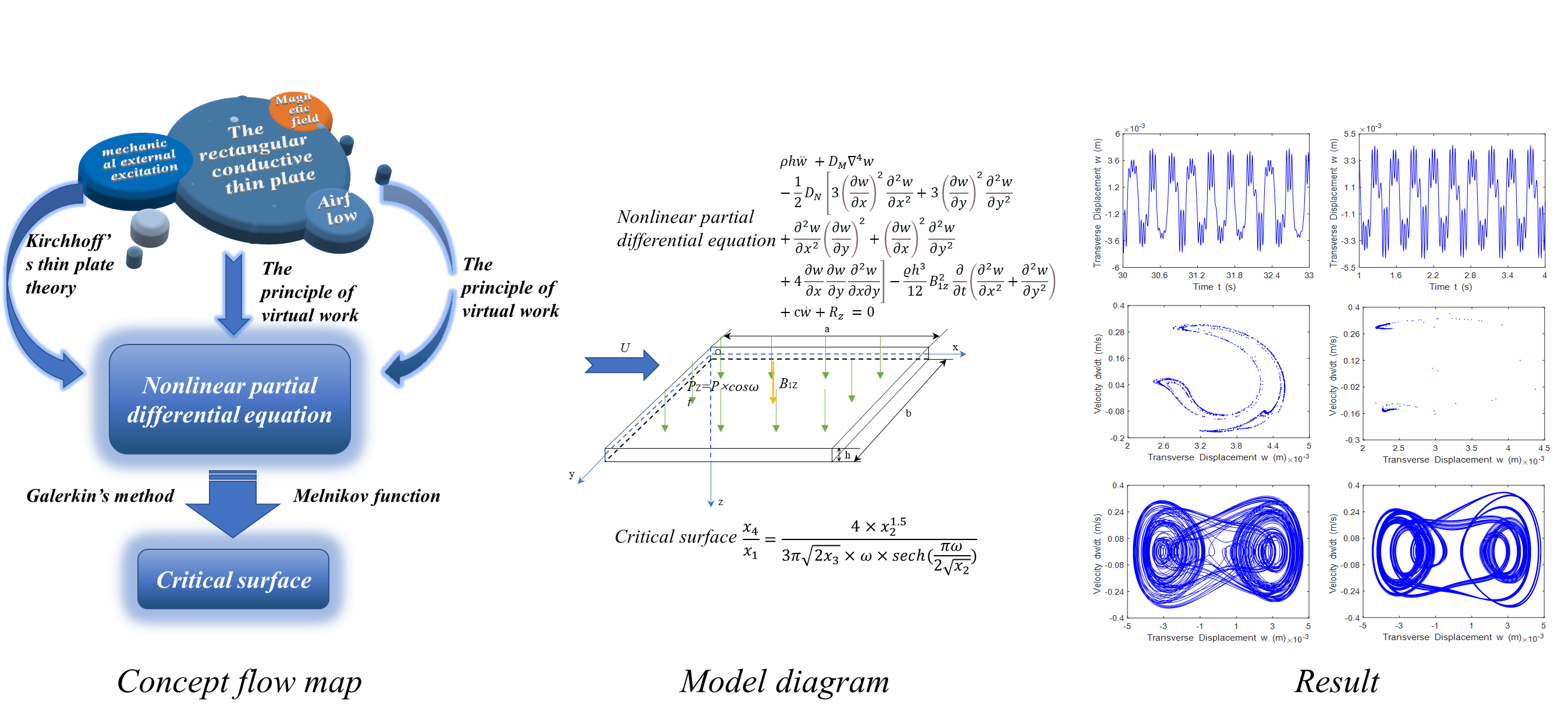
The chaotic motion behavior of the rectangular conductive thin plate that is simply supported on four sides by airflow and mechanical external excitation in a magnetic field is studied. According to Kirchhoff ’s thin plate theory, considering geometric nonlinearity and using the principle of virtual work, the nonlinear motion partial differential equation of the rectangular conductive thin plate is deduced. Using the separate variable method and Galerkin’s method, the system motion partial differential equation is converted into the general equation of the Duffing equation; the Hamilton system is introduced, and the Melnikov function is used to analyze the Hamilton system, and obtain the critical surface for the existence of chaos. The bifurcation diagram, phase portrait, time history response and Poincaré map of the vibration system are obtained by numerical simulation, and the correctness is demonstrated. The results show that when the ratio of external excitation amplitude to damping coefficient is higher than the critical surface, the system will enter chaotic state. The chaotic motion of the rectangular conductive thin plate is affected by different magnetic field distributions and airflow.

---

Graphic Abstract

---

Keywords

---