 Open Access
Open Access
ARTICLE
A Novel Collaborative Evolutionary Algorithm with Two-Population for Multi-Objective Flexible Job Shop Scheduling
State Key Laboratory of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan, 430074, China
* Corresponding Author: Yiping Gao. Email:
(This article belongs to the Special Issue: Computing Methods for Industrial Artificial Intelligence)
Computer Modeling in Engineering & Sciences 2023, 137(2), 1849-1870. https://doi.org/10.32604/cmes.2023.028098
Received 29 November 2022; Accepted 13 February 2023; Issue published 26 June 2023
Abstract
Job shop scheduling (JS) is an important technology for modern manufacturing. Flexible job shop scheduling (FJS) is critical in JS, and it has been widely employed in many industries, including aerospace and energy. FJS enables any machine from a certain set to handle an operation, and this is an NP-hard problem. Furthermore, due to the requirements in real-world cases, multi-objective FJS is increasingly widespread, thus increasing the challenge of solving the FJS problems. As a result, it is necessary to develop a novel method to address this challenge. To achieve this goal, a novel collaborative evolutionary algorithm with two-population based on Pareto optimality is proposed for FJS, which improves the solutions of FJS by interacting in each generation. In addition, several experimental results have demonstrated that the proposed method is promising and effective for multi-objective FJS, which has discovered some new Pareto solutions in the well-known benchmark problems, and some solutions can dominate the solutions of some other methods.Keywords
Planning is a very crucial problem in modern industries [1]. Through the elimination of scheduling conflicts, the decrease of flow time, the improvement of production resource usage, and the adaptation to unpredictable shop floor disruptions, the optimization of production scheduling can lead to considerable improvements. Job shop scheduling (JS) is a challenging problem for production planning [2]. This problem is an NP-hard problem, which is difficult to solve [3]. However, traditional JS, which assumes no flexibility of the resources for each operation of every job, might not be able to fulfill the demand of modern industries, because manufacturing systems have become increasingly flexible, and a considerable amount of automation equipment has been used [4,5]. Therefore, flexible job shop scheduling (FJS) is increasingly interesting for both industry and research.
FJS is a kind of JS that enables any machine from a certain set to process an operation, and it was first introduced in the 1990s by Bruker et al. [6]. Compared with JS, FJS is more complex, which means that JSP is NP-hard as well. Recently, a considerable amount of research has been examined, most of which has focused on a single object. However, different departments of a company expect to maximize their objectives, such as cost and efficiency. Therefore, a single objective is not sufficient to meet the requirements of realistic production, and there is a need for further research on multi-objective FJS (MOFJS). Recently, MOFJS has attracted increasing attention from both the industrial and academic, and several methods, including evolutionary algorithms [7], and ant colony algorithms [8]. Traditionally, MOFJS contains 2 subproblems: operation sorting (OS) and machine selection (MS). Most of the related work employs integrated encoding to solve MOFJS [9]. However, OS and MS are quite different, thereby limiting the global searching ability of the current methods and seriously affecting the solving effect. Therefore, a novel collaborative evolutionary algorithm with two populations based on Pareto optimality is proposed for MOFJS. The proposed method uses Pareto optimality to address the Mutli-objectives problems, and develops a collaborative optimization strategy, which simulates the optimization process of OS and MS wherein the subsystems interact with each other. The interaction with each other in every generation can improve the solution of FJS. Thus, the proposed method takes the merits of collaborative optimization and evolutionary algorithms, and combines them to prompt the solving. The experimental results also show the availability of the proposed method.
The rest of this paper is organized as follows. Section 2 is the literature review. Section 3 is the problem formulation. Section 4 is the proposed method and Section 5 presents the experimental results. Section 6 is the conclusion.
FJS has been a research hotspot for many years, and a considerable amount of research has been conducted in recent years. For the single objective, the FJS can be categorized by exact approaches, such as mathematical programming, and approximation approaches, such as GA [10]. Meng et al. [11] presented a novel integer linear programming for FJS. Alvarez-Valdes et al. [12] developed a heuristic algorithm and applied it to glass production.
Currently, MOFJS has attracted an increasing amount of attention from both academia and industry, and several approaches have been proposed, involving evolutionary algorithms, local search methods, and swarm intelligence. Tay et al. [13] evolved the dispatching rules by genetic programming. Baykasoğlu et al. [14] performed a deep analysis of the effects of dispatching rules. Rajkumar et al. [15] introduced a greedy adaptive search, which considered the maintenance and limited resource constraints. Caldeira et al. [16] developed a multi-objective discrete Jaya by maximizing the makespan, and workload. Li et al. [17] introduced a rescheduling method with a Monte Carlo tree search, and it considered the MOFJS with dynamic events.
In summary, most of the existing approaches use an integrated encoding. However, the two subproblems in FJS (MS and OS) are quite different, and the integrated encoding might cause the solution space to be more complex, and lead to a worse solution. Thus, this paper aims to address this drawback by proposing a novel collaborative evolutionary algorithm with two populations.
The formulation of an
Given a set with
In this research, the following criteria are involved:
Makespan: the maximal finish time;
Maximal machine workload (MMW): the maximal time on a machine.
Total workload of machines (TWM): the total running time of all machines.
Based on these criteria, the MOFJS in this research has three objectives, and the descriptions of these objectives are shown below.
The model of FJS is followed to [18], and the summary of the notations is presented in Table 1.

Generally, the formulation of a multi-objective optimization [19,20] (contains
Non-dominated solution: if the objective function

Figure 1: NDS and Pareto front
Pareto-optimal: when the solution cannot be dominated, it is called Pareto-optimal (PO). Fig. 1b shows the Pareto front of a two objectives problem.
4.2.1 The Optimization Strategy for Collaborative Evolution
The proposed method uses a collaborative strategy to search for a solution in both the OS and MS. The OS and MS are optimized alternatively, and evaluated together. Moreover, it should be noted that this strategy is generic, and it can be suitable to combine with various algorithms, such as GA. In this paper, the proposed method uses an evolutionary algorithm (EA) for both OS and MS, and the optimization strategy is shown in Fig. 2 and below:
1): Parameter Initialization. Assum given
2): Fitness Evaluation. Select the Popsize randomly, and calculate the solutions population. After that, evaluate each solution individually and choose the NDS (NDS);
3): Condition judgement. If it meets the end condition, just terminate and output the solution. Otherwise, going to 4);
4): Collaborative evolution. Generate some new individuals. Go back to 2).
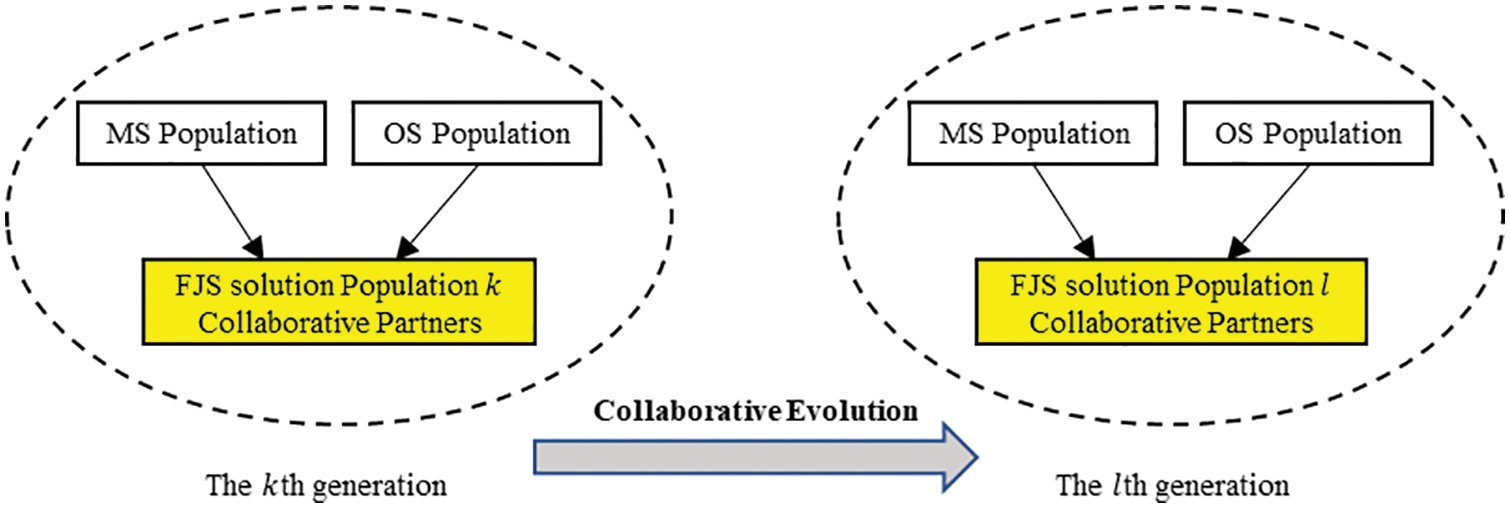
Figure 2: Optimization strategy of the proposed method
For the diversity, a Pareto archive set (PAS) is employed in the proposed method, which can retain the quantity of the NDS with the user requirement [21]. When optimizing, the PAS is moving to the Pareto-optimality front by replenishing some new NDS and eliminating some dominant solutions. Once the number of NDSs is sufficient, a crowding similarity in Eq. (5) is employed (CD) to remove the redundant solutions and guarantee diversity. Individuals with higher CD are preferentially kept in the PAS.
where
In MO problems, one objective is not enough to evaluate the quality of the solution individually, and all of the objectives must be involved. Thus, a sorting algorithm is essential, and the non-dominated sorting method [22] is adopted. The sorting algorithm separates the solutions into different levels. For example, as shown in Fig. 3, the solutions have three levels, and the lower level has the better fitness. For the same levels, the solutions that have higher CDs are also a priority. With this separation, the good solutions can be retained as a priority by the PAS.

Figure 3: NDS levels
4.2.4 Encoding and Decoding Method
The encoding method is essential for an EA, and the proposed method adopts the method in [23] for encoding. Moreover, since the OS and MS are quite different, the details of the encoding method for each subproblem are also different. The encoding for OS is based on the operation representation. In addition, the representation employs an undivided arrangement. With this encoding, each job can be selected by
The MS chromosome refers to the
An encoding solution contains an OS chromosome and an MS chromosome, and the decoding manner involves semi-active, active, non-delay, and hybrid. In the proposed method, to achieve a better solution, an active schedule is used. The decoding process is shown below:
m: number of the machines.
The process of decoding in the proposed method:
1): Generate the machine of each operation by the MS chromosome.
2): Choose a set of the operations for each machine:
3): Choose a set of machines for each job:
4): The allowable begin time for every operation:
5): Checking the unused time of the machine of
6): Calculate the finish time of each operation by
7): Generate the sets of the begin time and finish time for each operation of each job by
In the decoding process, it can obtain the set of start time and finish time for each operation of each job, and it is a schedule solution for the workshop. Fig. 4 gives an example of the encoding and decoding in the proposed method. Fig. 4a is the background of this case, which involves 3 jobs and 3 machines. Fig. 4b presents an OS chromosome with repetitions of job numbers, and Fig. 4c is an MS chromosome. The OS and MS chromosomes in Fig. 4 form a solution of FJS. And this solution can be converted into a schedule by decoding, as shown in Fig. 4d. The decoding steps are as follows:
1): Generate the machine of each operation,
2): Choose the set of operations for each machine:
3): Choose the set of machines for each job:
4): The allowable begin time for each operation is calculated as follows:
5): Check the unused time of the machine of
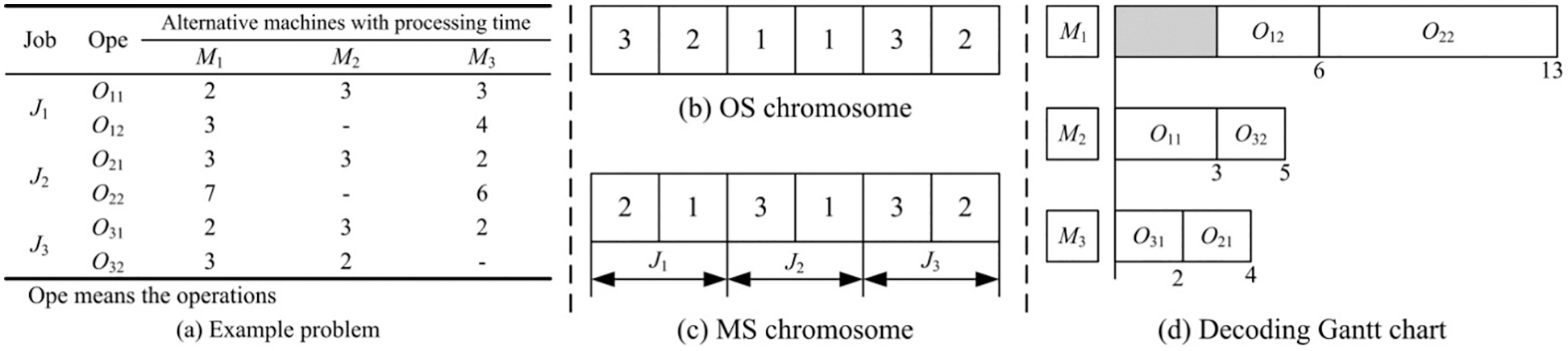
Figure 4: Encoding and decoding example
Step 6: The finish time of each operation is calculated as follows:
Step 7: Generate the sets of begin time and finish time:
The genetic operator (GO) is important for good individuals and solutions. Generally, GO is classified into three categories: selection, crossover and mutation. In the proposed method, for a better solution, OS and MS use different genetic operators. The details of the genetic operations are shown below:
(1) Selection
OS and MS randomly select the individuals.
(2) Crossover
A precedence operation (PO) is used for the crossover in the OS. The PO crossover can retain the good of the parents and propagate it to the offspring. The flowchart of the PO is shown below (P1 and P2 are parents, and O1 and O2 are offspring).
1): Dividing the job set
2): For an element belonging to Jobset1 in P1, it is retained in the same position in O1 and removed in P1. For an element belonging to Jobset2 in P1, it is retained in the same position in O2 and removed in P2.
3): Remains in P2 are moved to the empty positions in O1, while the remainder in P1 are moved to O1.
The MS population uses a two-point crossover, which selects two positions randomly first, and the two strings swap all elements.
Fig. 5a is an example of the PO for OS and Fig. 5b is for MS.
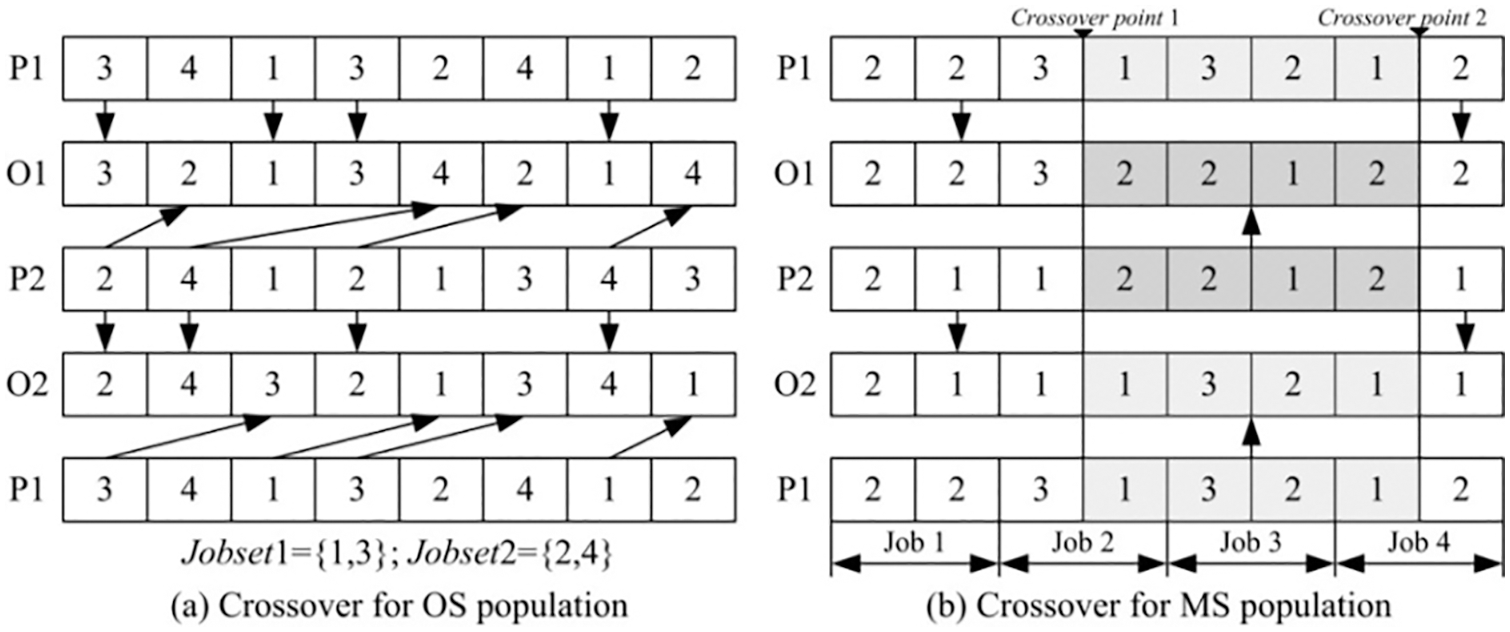
Figure 5: The crossover operations for OS and MS
(3) Mutation
The OS uses a neighborhood mutation operator.
1): Select three elements in a parent (each element has different value), and generate the neighborhood chromosomes.
2): Choose a chromosome randomly for the chromosome.
MS uses the mutation operator below.
1):Select
2): For each position, change the value of the chosen position to the corresponding operations.
If the iteration has reached the maximum epoch, the proposed method stops running.
4.2.7 Framework of the Proposed Method
Fig. 6 presents the flowchart, and the description of the proposed method is shown below:
1): Setting the parameters, including
2): Initialization. For
3): Evaluation. Randomly select
4): If the model meets the stop condition, go to 6), otherwise, go to Step 5).
5): Collaboration evaluating. Upgrade the populations: generate new individuals for each population;
5.1): For the
5.2): If
5.3): Set
6): Output the NDS in PAS.
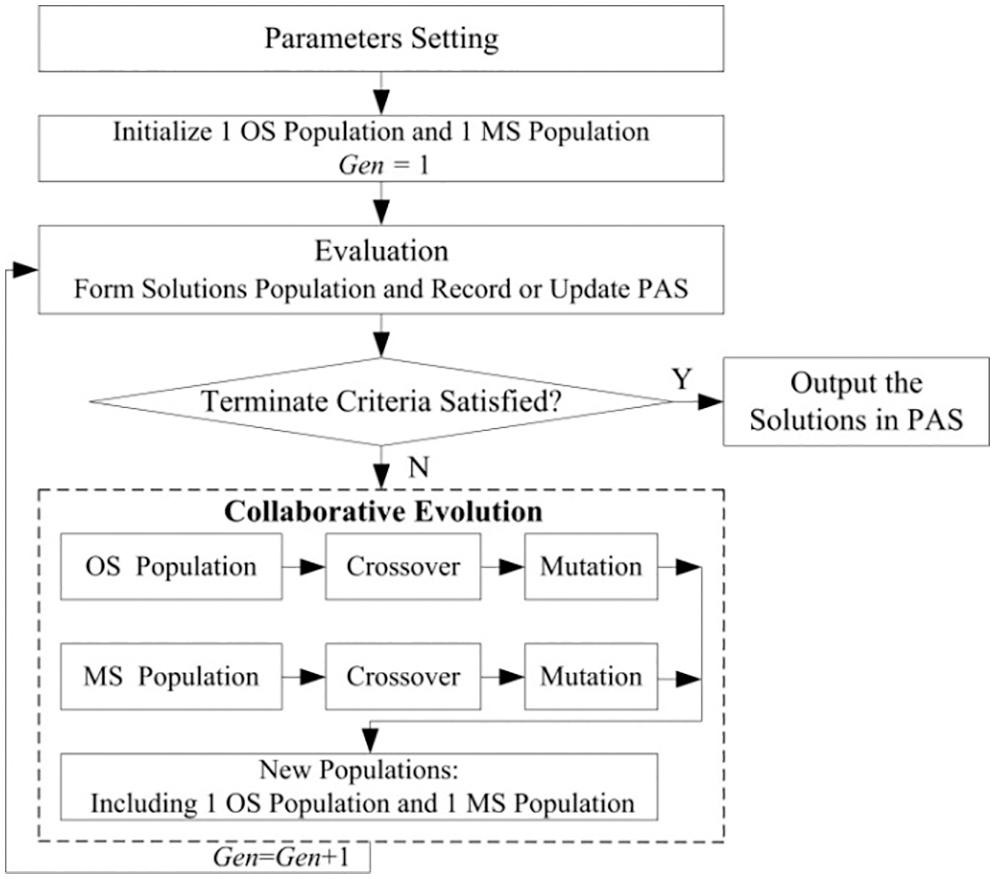
Figure 6: Work flow of the proposed method
5 Experimental Results of the Proposed Method
5.1 Experimental Setting and Results
The proposed method codes in C++ on a laptop. To evaluate the proposed method, six experiments were selected. The five experiments are adopted from the related papers, and the last experiment is employed by the author themselves. For the parameters, the sizes of the OS and MS populations are
This experimental problem is from [24], which includes 5 kinds of problems. Tables 2 and 3 show the comparison results. From Table 2, the proposed method finds another new Pareto solution for problem 4 × 5, which is (13, 7, 33), as shown in Fig. 7a. For problem 10 × 7, compared with other algorithms, the proposed algorithm also finds two Pareto solutions. Based on Table 2, the proposed method finds two solutions that dominate the P-DABC. One solution (11, 11, 61) is shown in Fig. 7b.
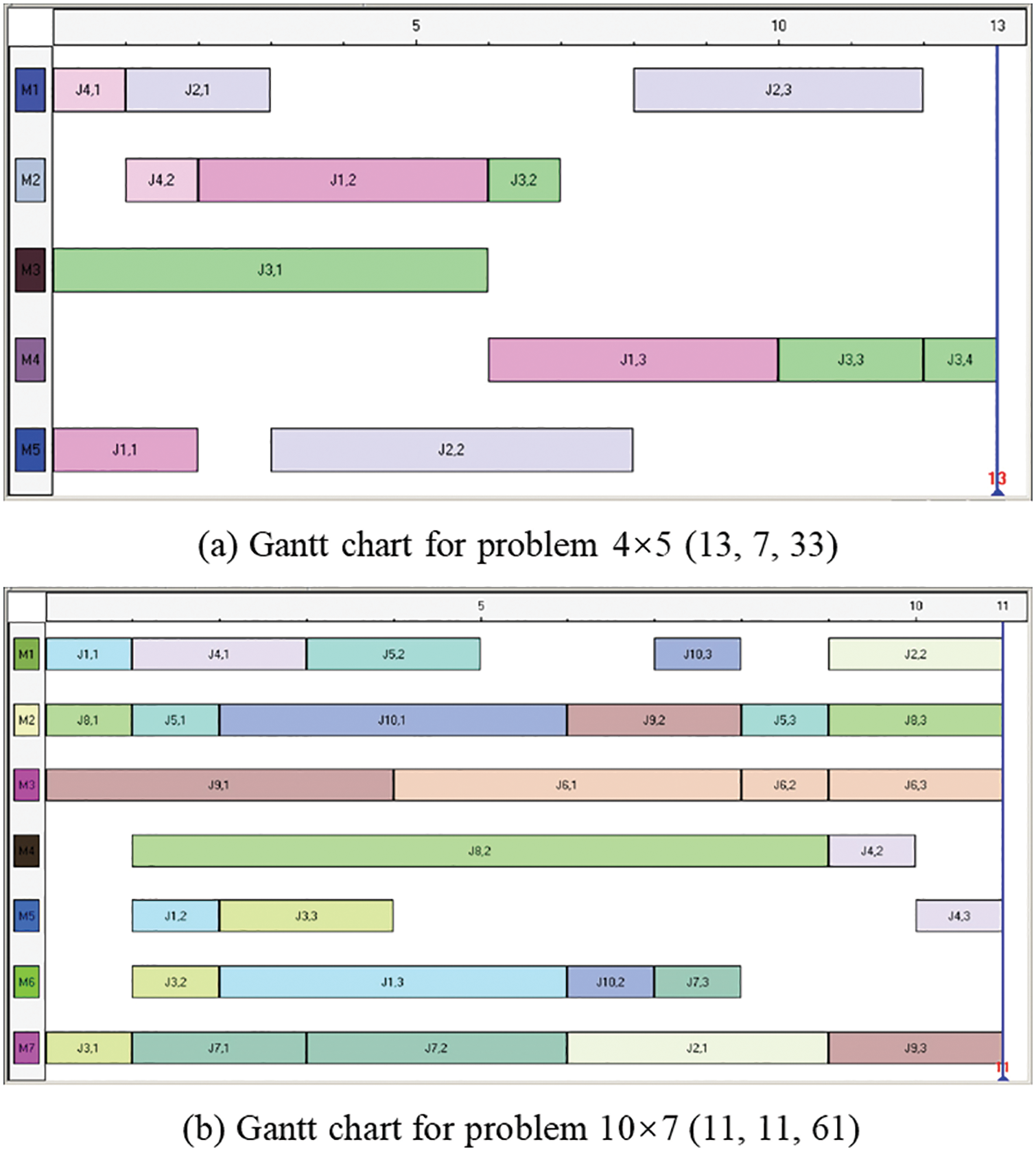
Figure 7: Gantt charts for problem 4 × 5 and problem 10 × 7
Table 3 is the comparisons with the other methods for problems 8 × 8, 10 × 10 and 15 × 10. From Table 3, the proposed method finds several solutions that dominate the other methods. Fig. 8 is the Gantt chart with different solutions that are solved by the proposed method. From the experimental results, it can be seen that the proposed method achieves the best performance. Compared with the other methods, the results of the proposed method are improved for the makespan, MMW and TWM, which means that the proposed method can find new Pareto solutions.
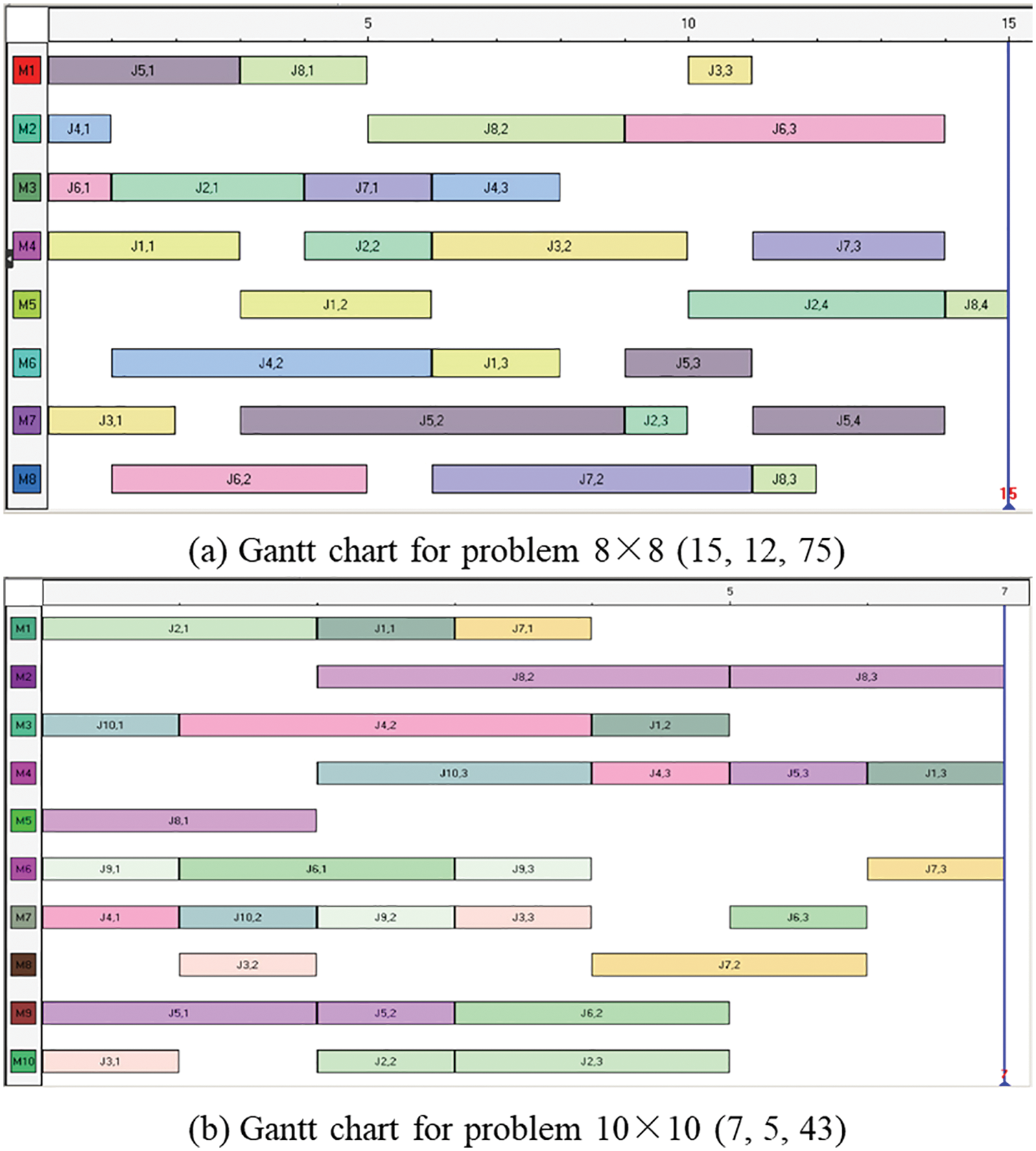
Figure 8: Gantt charts solved by the proposed method
This experimental problem is from [15], which includes 3 kinds of problems. Table 4 is the comparison with the other algorithms. From Table 4, the proposed method finds several solutions that dominate the other methods. Fig. 9 is the Gantt chart of a solution for problem 12 × 5. Similar to the experimental results in Section 5.1.1, the experimental results also suggest that the proposed method has improved performance. Compared with the other methods, the proposed method can find a better solution.

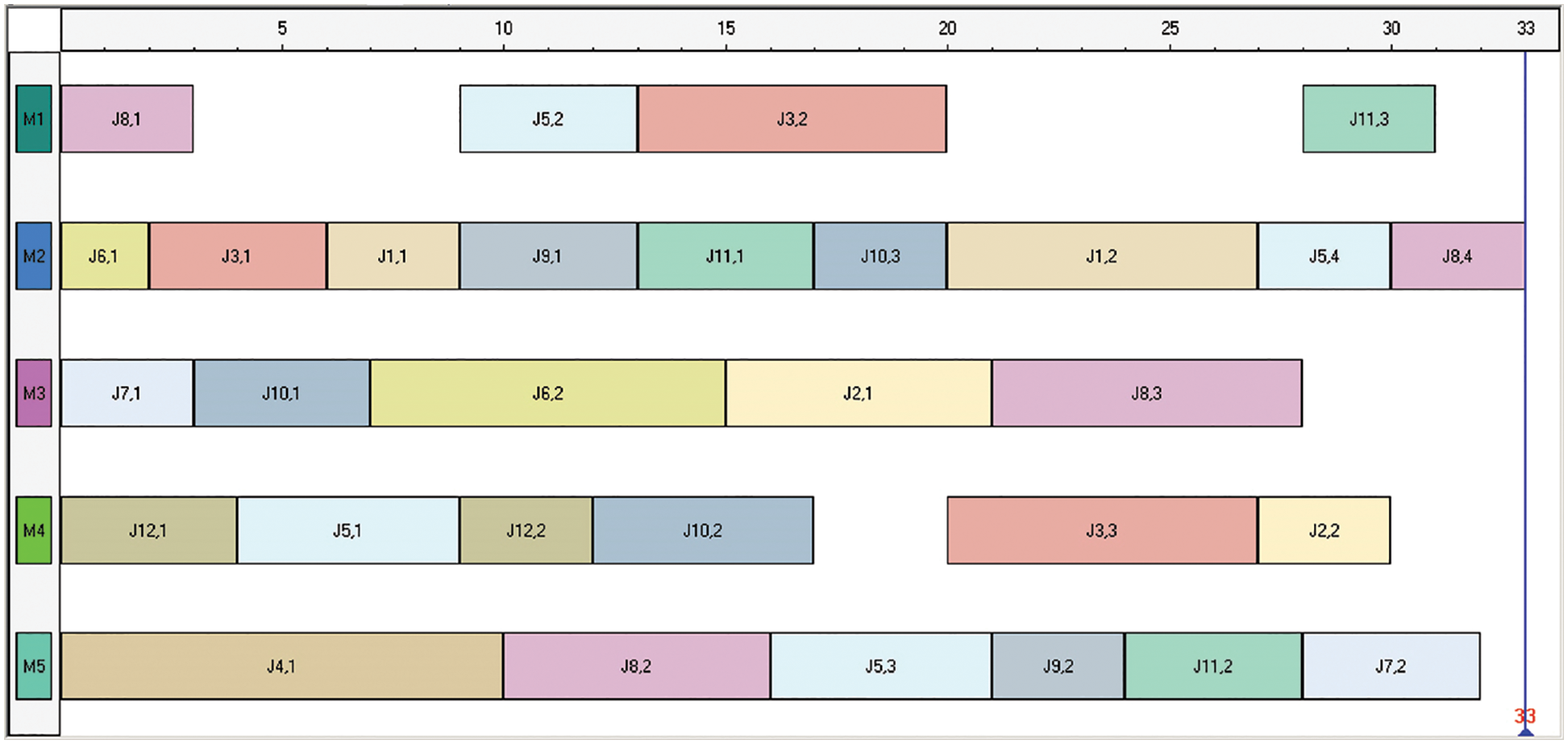
Figure 9: Gantt chart of one solution for problem 12 × 5 (33, 33, 137)
This experimental problem is from [36], which is the famous benchmark instance for the single objective FJS. This data contains 10 problems. Table 5 is the comparison with the other method, which also shows that the proposed method finds several dominant solutions.
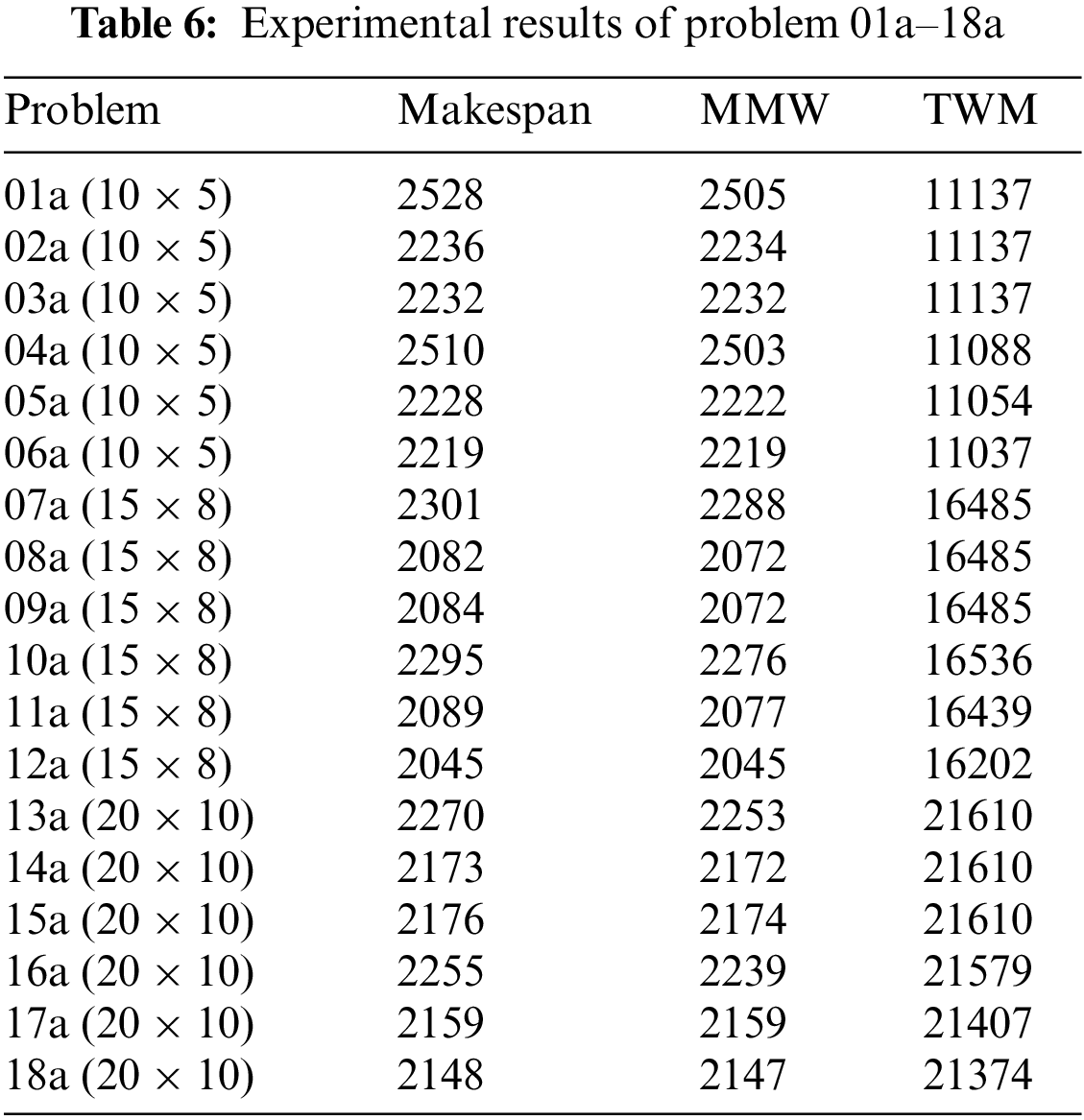
This experimental problem is from [38], which is another famous benchmark instance for the single objective FJS and is very hard to solve. The data contain 18 problems, and the range of the problems is from 8 × 5 to 20 × 10. Table 6 shows the experimental results. The results indicate that the proposed method can address the multi-objective FJS well.
This experimental problem is from [39], which is another famous benchmark instance for the single objective FJSP and is very hard to solve. The experiment contains 21 problems and Table 7 presents the experimental results. The experimental results indicate the proposed method has significant improvement.

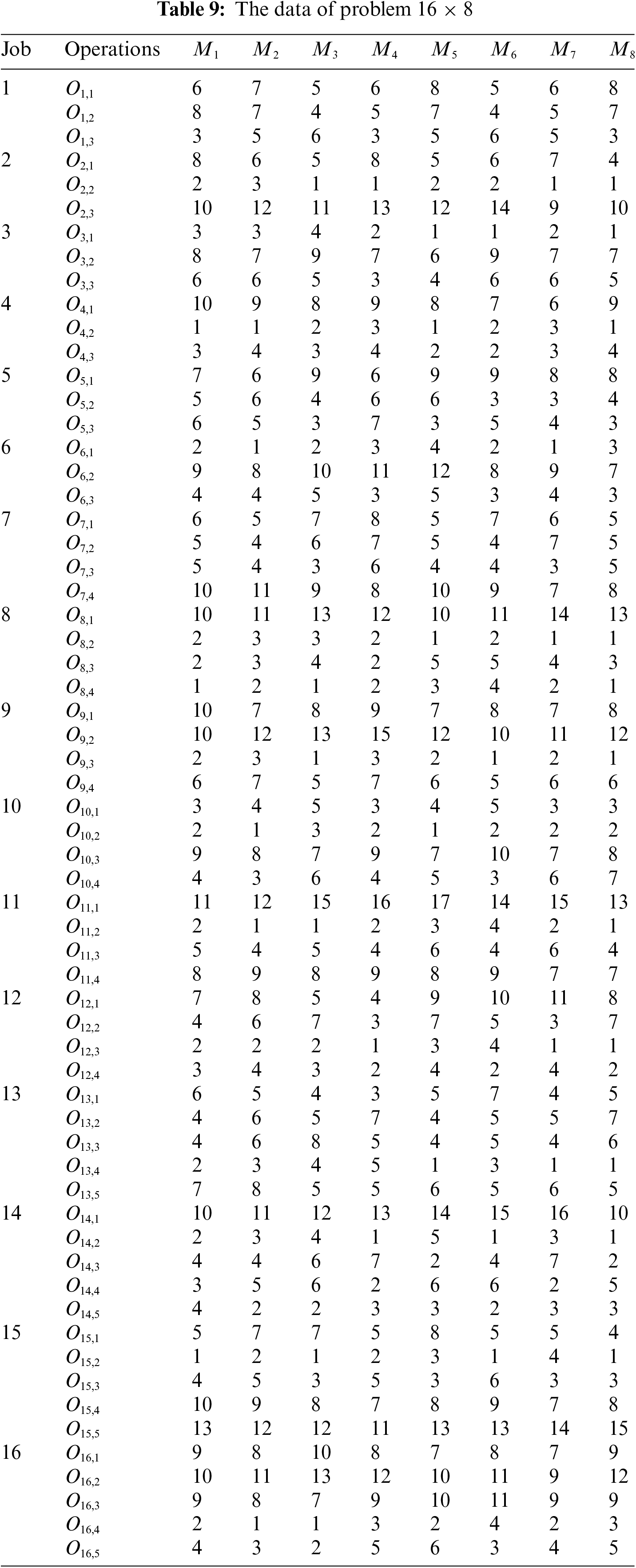
The experimental problems are built by the authors. The range of the problems involves 10 × 8 and 16 × 8, which are shown in Table 8. The data of problem 16 × 8 are shown in Table 9. Table 10 shows the experimental results. From Table 10, the proposed method provides several Pareto solutions for each problem.


In the experimental results, the proposed method finds some dominant solutions of the other methods. These results suggest that the proposed method addresses the MOFJS well. The main reasons for the good performance are because the OS and MS are quite different, and the integrated encoding might cause solution space intricacy and complexity. The complex space might prevent the search ability of the existing methods. Moreover, the proposed method evolves OS and MS separately, which can improve the overall searching ability. With this improvement, the proposed method achieves the more effective results. Furthermore, the proposed method uses PAS to save the solutions, and uses crowd similarity for diversity, which is also effective for the improvement of MOFJS.
FJS is very important for production, and a novel collaborative evolutionary algorithm with two-population based on Pareto optimality is proposed for MOFJS. The experimental results suggest that the proposed method is feasible for improving the solution of MOFJS, and several dominant solutions are found by the proposed method, which achieved significant improvement. The main contributions of this paper are as follows:
• With the problem features of MOFJS, a collaborative evolutionary method is designed. The proposed method reflects the essential feature of MOFJS, and the PAS is used to save the Pareto solutions. The comparison demonstrates that the proposed method can address MOFJS successfully with a promising result.
• The proposed method combines the merits of collaborative optimization and EA. It uses crowd similarity to guarantee diversity. It provides a novel way to solve MO problems by containing several sub-problems. The experimental results of the multi-objective FJSP show that the proposed method may solve these problems effectively.
Funding Statement: This research work is the Key R&D Program of Hubei Province under Grant No. 2021AAB001, and National Natural Science Foundation of China under Grant No. U21B2029.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zhou, J., Li, P., Zhou, Y., Wang, B., Zang, J. et al. (2018). Toward new-generation intelligent manufacturing. Engineering, 4(1), 11–20. https://doi.org/10.1016/j.eng.2018.01.002 [Google Scholar] [CrossRef]
2. Wang, J., Wang, L. (2022). A cooperative memetic algorithm with feedback for the energy-aware distributed flow-shops with flexible assembly scheduling. Computers & Industrial Engineering, 168(4), 108126. https://doi.org/10.1016/j.cie.2022.108126 [Google Scholar] [CrossRef]
3. Liu, Q., Li, X., Gao, L. (2021). A novel MILP model based on the topology of a network graph for process planning in an intelligent manufacturing system. Engineering, 7(6), 807–817. https://doi.org/10.1016/j.eng.2021.04.011 [Google Scholar] [CrossRef]
4. Gao, Y., Gao, L., Li, X. (2023). A hierarchical training-convolutional neural network with feature alignment for steel surface defect recognition. Robotics and Computer-Integrated Manufacturing, 81, 102507. https://doi.org/10.1016/j.rcim.2022.102507 [Google Scholar] [CrossRef]
5. Gao, Y., Gao, L., Li, X., Yan, X. (2020). A semi-supervised convolutional neural network-based method for steel surface defect recognition. Robotics and Computer-Integrated Manufacturing, 61(1), 101825. https://doi.org/10.1016/j.rcim.2019.101825 [Google Scholar] [CrossRef]
6. Brucker, P., Schlie, R. (1990). Job-shop scheduling with multi-purpose machines. Computing, 45(4), 369–375. https://doi.org/10.1007/BF02238804 [Google Scholar] [CrossRef]
7. Sun, J., Zhang, G., Lu, J., Zhang, W. (2021). A hybrid many-objective evolutionary algorithm for flexible job-shop scheduling problem with transportation and setup times. Computers & Operations Research, 132(3), 105263. https://doi.org/10.1016/j.cor.2021.105263 [Google Scholar] [CrossRef]
8. Gu, X. (2021). Application research for multiobjective low-carbon flexible job-shop scheduling problem based on hybrid artificial bee colony algorithm. IEEE Access, 9, 135899–135914. https://doi.org/10.1109/ACCESS.2021.3117270 [Google Scholar] [CrossRef]
9. Zhang, P., Song, S., Niu, S., Zhang, R. (2021). A hybrid artificial immune-simulated annealing algorithm for multiroute job shop scheduling problem with continuous limited output buffers. IEEE Transactions on Cybernetics, 52(11), 12112–12125. https://doi.org/10.1109/TCYB.2021.3081805 [Google Scholar] [PubMed] [CrossRef]
10. Park, J. S., Ng, H. Y., Chua, T. J., Ng, Y. T., Kim, J. W. (2021). Unified genetic algorithm approach for solving flexible job-shop scheduling problem. Applied Sciences, 11(14), 6454. https://doi.org/10.3390/app11146454 [Google Scholar] [CrossRef]
11. Meng, L., Zhang, C., Ren, Y., Zhang, B., Lv, C. (2020). Mixed-integer linear programming and constraint programming formulations for solving distributed flexible job shop scheduling problem. Computers & Industrial Engineering, 142(19), 106347. https://doi.org/10.1016/j.cie.2020.106347 [Google Scholar] [CrossRef]
12. Alvarez-Valdes, R., Fuertes, A., Tamarit, J. M., Giménez, G., Ramos, R. (2005). A heuristic to schedule flexible job-shop in a glass factory. European Journal of Operational Research, 165(2), 525–534. https://doi.org/10.1016/j.ejor.2004.04.020 [Google Scholar] [CrossRef]
13. Tay, J. C., Ho, N. B. (2008). Evolving dispatching rules using genetic programming for solving multi-objective flexible job-shop problems. Computers & Industrial Engineering, 54(3), 453–473. https://doi.org/10.1016/j.cie.2007.08.008 [Google Scholar] [CrossRef]
14. Baykasoğlu, A., Özbakır, L. (2010). Analyzing the effect of dispatching rules on the scheduling performance through grammar based flexible scheduling system. International Journal of Production Economics, 124(2), 369–381. https://doi.org/10.1016/j.ijpe.2009.11.032 [Google Scholar] [CrossRef]
15. Rajkumar, M., Asokan, P., Anilkumar, N., Page, T. (2011). A GRASP algorithm for flexible job-shop scheduling problem with limited resource constraints. International Journal of Production Research, 49(8), 2409–2423. https://doi.org/10.1080/00207541003709544 [Google Scholar] [CrossRef]
16. Caldeira, R. H., Gnanavelbabu, A. (2021). A Pareto based discrete Jaya algorithm for multi-objective flexible job shop scheduling problem. Expert Systems with Applications, 170(1), 114567. https://doi.org/10.1016/j.eswa.2021.114567 [Google Scholar] [CrossRef]
17. Li, K., Deng, Q., Zhang, L., Fan, Q., Gong, G. et al. (2021). An effective MCTS-based algorithm for minimizing makespan in dynamic flexible job shop scheduling problem. Computers & Industrial Engineering, 155(1), 107211. https://doi.org/10.1016/j.cie.2021.107211 [Google Scholar] [CrossRef]
18. Fattahi, P., Saidi Mehrabad, M., Jolai, F. (2007). Mathematical modeling and heuristic approaches to flexible job shop scheduling problems. Journal Intelligent Manufacturing, 18(3), 331–342. https://doi.org/10.1007/s10845-007-0026-8 [Google Scholar] [CrossRef]
19. Lei, D., Yuan, Y., Cai, J. (2021). An improved artificial bee colony for multi-objective distributed unrelated parallel machine scheduling. International Journal of Production Research, 59(17), 5259–5271. https://doi.org/10.1080/00207543.2020.1775911 [Google Scholar] [CrossRef]
20. Xia, W., Wu, Z. (2005). An effective hybrid optimization approach for multi-objective flexible job-shop scheduling problems. Computers & Industrial Engineering, 48(2), 409–425. https://doi.org/10.1016/j.cie.2005.01.018 [Google Scholar] [CrossRef]
21. Lei, D., Yuan, Y., Cai, J. (2021). An improved artificial bee colony for multi-objective distributed unrelated parallel machine scheduling. International Journal of Production Research, 59(17), 5259–5271. https://doi.org/10.1080/00207543.2020.1775911 [Google Scholar] [CrossRef]
22. Deb, K., Pratap, A., Agarwal, S., Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182–197. https://doi.org/10.1109/4235.996017 [Google Scholar] [CrossRef]
23. Gao, L., Peng, C., Zhou, C., Li, P. (2006). Solving flexible job-shop scheduling problem using general particle swarm optimization. Proceedings of the 36th CIE Conference on Computers & Industrial Engineering, pp. 3018–3027. Taipei, China. [Google Scholar]
24. Kacem, I., Hammadi, S., Borne, P. (2002). Approach by localization and multiobjective evolutionary optimization for flexible job-shop scheduling problems. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 32(1), 1–13. https://doi.org/10.1109/TSMCC.2002.1009117 [Google Scholar] [CrossRef]
25. Zhang, G., Shao, X., Li, P., Gao, L. (2009). An effective hybrid particle swarm optimization algorithm for multi-objective flexible job-shop scheduling problem. Computers & Industrial Engineering, 56(4), 1309–1318. https://doi.org/10.1016/j.cie.2008.07.021 [Google Scholar] [CrossRef]
26. Xing, L., Chen, Y., Yang, K. (2009). An efficient search method for multi-objective flexible job shop scheduling problems. Journal Intelligent Manufacturing, 20(3), 283–293. https://doi.org/10.1007/s10845-008-0216-z [Google Scholar] [CrossRef]
27. Xing, L., Chen, Y., Yang, K. (2009). Multi-objective flexible job shop schedule: Design and evaluation by simulation modeling. Applied Soft Computing, 9(1), 362–376. https://doi.org/10.1016/j.asoc.2008.04.013 [Google Scholar] [CrossRef]
28. Wang, X., Gao, L., Zhang, C., Shao, X. (2010). A multi-objective genetic algorithm based on immune and entropy principle for flexible job-shop scheduling problem. International Journal Advanced Manufacturing Technology, 51(5–8), 757–767. https://doi.org/10.1007/s00170-010-2642-2 [Google Scholar] [CrossRef]
29. Li, J., Pan, Q., Gao, K. (2011). Pareto-based discrete artificial bee colony algorithm for multi-objective flexible job shop scheduling problems. International Journal Advanced Manufacturing Technology, 55(9–12), 1159–1169. https://doi.org/10.1007/s00170-010-3140-2 [Google Scholar] [CrossRef]
30. Ho, N., Tay, J. (2008). Solving multiple-objective flexible job shop problems by evolution and local search. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 38(5), 674–685. https://doi.org/10.1109/TSMCC.2008.923888 [Google Scholar] [CrossRef]
31. Xia, W. J., Wu, Z. M. (2005). An effective hybrid optimization approach for multi-objective flexible job shop scheduling problems. Computers & Industrial Engineering, 48(2), 409–425. https://doi.org/10.1016/j.cie.2005.01.018 [Google Scholar] [CrossRef]
32. Zhang, H., Gen, M. (2005). Multistage-based genetic algorithm for flexible job-shop scheduling problem. Journal of Complexity International, 11, 223–232. [Google Scholar]
33. Gao, J., Gen, M., Sun, L., Zhao, X. (2007). A hybrid of genetic algorithm and bottleneck shifting for multiobjective flexible job shop scheduling problems. Computers & Industrial Engineering, 53(1), 149–162. https://doi.org/10.1016/j.cie.2007.04.010 [Google Scholar] [CrossRef]
34. Xing, L. N., Chen, Y. W., Yang, K. W. (2009). An efficient search method for multi-objective flexible job shop scheduling problems. Journal of Intelligent Manufacturing, 20(3), 283–293. https://doi.org/10.1007/s10845-008-0216-z [Google Scholar] [CrossRef]
35. Moslehi, G., Mahnam, M. (2011). A Pareto approach to multi-objective flexible job-shop scheduling problem using particle swarm optimization and local search. International Journal of Production Economics, 129(1), 14–22. https://doi.org/10.1016/j.ijpe.2010.08.004 [Google Scholar] [CrossRef]
36. Brandimarte, P. (1993). Routing and scheduling in a flexible job shop by taboo search. Annals of Operations Research, 41(3), 157–183. https://doi.org/10.1007/BF02023073 [Google Scholar] [CrossRef]
37. Li, J., Pan, Q., Liang, Y. (2010). An effective hybrid tabu search algorithm for multi-objective flexible job-shop scheduling problems. Computers & Industrial Engineering, 59(4), 647–662. https://doi.org/10.1016/j.cie.2010.07.014 [Google Scholar] [CrossRef]
38. Peres, S. D., Paulli, J. (1997). An integrated approach for modeling and solving the general multiprocessor job shop scheduling using tabu search. Annals of Operations Research, 70, 281–306. https://doi.org/10.1023/A:1018930406487 [Google Scholar] [CrossRef]
39. Barnes, J. (1996). Flexible job shop scheduling by tabu search (Ph.D. Thesis). University of Texas at Austin. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF


 Downloads
Downloads
 Citation Tools
Citation Tools