QBFO-BOMP Based Channel Estimation Algorithm for mmWave Massive MIMO Systems

1  Introduction

The main expectation of the next generation wireless communication system is to obtain higher data rates and better user service quality, so as to meet the needs of national economic and social development. The communication system has gradually expanded to more and more application scenarios, such as intelligent transportation, cloud computing, medical treatment, automatic driving and other new fields. Therefore, data transmission with low latency, high throughput and high rate has become the requirement of communication development. In mmWave massive MIMO systems, the acquisition of channel state information is of great significance to the reliability of communication. Among them, the optimization and research of channel estimation for mmWave massive MIMO systems is a popular direction of research in the evolution of communication systems [1–3]. In 1997, Towsend et al. had completed the first multi-user quantum communication network experiment. In this experiment, the quantum communication terminal was used as the network controller, and multi-user key distribution was achieved through an optical splitter [4]. Since then, quantum communication has gradually entered the field of wireless transmission and successfully its unique superiority. Standardization is an important step to transform quantum communication from practicality to industrialization. However, the quantum communication involves various new technologies at present [5–10]. And there are too many unknown factors from theory to practical application, which brings many difficulties to the standardization of quantum communication [11–24].

In mmWave massive MIMO systems, due to the sparsity of mmWave, the combination of channel estimation and compressed sensing (CS) technology is a research hotspot [15–19]. The orthogonal matching pursuit (OMP) algorithms perform successfully in solving the problem of mmWave channel estimation based on CS. In [20], the channel estimation scheme based on simultaneous orthogonal match tracking (SOMP) was proposed. Firstly, the channel estimation problem in broadband beam space was considered as the multiple measurement vector (MMV) problem, and then the SOMP-based algorithm was used to estimate the channel. Lee et al. [21] used the OMP-based algorithm for preliminary estimation. Then, the refinement process based on the Newton method was added to improve the signal recovery accuracy. Wang et al. [22] proposed the OMP-LMM-based channel estimation algorithm. The basic idea of [22] was that the residual likelihood function of each path parameter was used for channel estimation. In [23], the multi-grid OMP based algorithm was proposed. This algorithm determined firstly the approximate regions of angle of departure (AoD) and angle of arrival (AoA) through the coarse grids and then refined the mesh, which greatly improved the estimation accuracy. Jing et al. [24] proposed the OMP-based algorithm for fine quantization of angular meshes. Under the hybrid beamforming structure, Tropp et al. [25] solved the problem of sparse restoration of parametric channel model based on AoD/AoA quantization through the OMP-based algorithm according to the sparsity of mmWave. The key point of [25] was that the redundant dictionary composed of array response vectors with fine quantization angle grid was generated. Weiland et al. [26] used the OMP-based algorithm to solve the design problem of analog digital mixed precoding, achieving better performance of mixed precoding. In [27], the differential channel feedback scheme based on OMP was proposed based on the time correlation of time-varying channels, which effectively reduced the feedback overhead. In [28], the rapid OMP-based algorithm was proposed to estimate samples by running atomic cycles. And the running time was several orders of magnitude faster in the actual scene. But Chatterjee et al. [28] did not give the situation in terms of estimation accuracy.

Traditional channel estimation algorithms are easy to fall into the local optimization and depend on initial conditions. However, the quantum optimization algorithms have the advantages of independent of initial conditions, independent of the solution space, and well-stabilized. In the quantum optimization algorithms, there are interaction between personals and between personal and environment, and thus it has good self-organization ability [29,30].

Dasgupta et al. [31] proposed the BFO-based algorithm. The basic idea of the BFO-based algorithm was that the position of the bacteria was expressed as the potential solution of the problem. The convergence of the entire bacterial population to the optimal solution was realized through the bacterial chemotaxis, reproduction, and dispersion operations. But the mathematical theory of the BFO-based algorithm was weak and it was easy to fall into local optimum. The QBFO-based algorithm was proposed in [32]. The bacterial population was represented by quantum bits with linear superposition, so that the quantum bacterial population can better represent diversity and parallelism. And Li et al. [32] used multiple benchmark functions to test the practicability of the QBFO-based algorithm. Simulation results showed that the QBFO-based algorithm was superior in terms of convergence speed and global search ability. For 3D MIMO downlink wireless communication system, the optimization scheme based on QBFO was proposed in [33]. The cell edge users were transmitted by introducing joint transmission technology. The total spectral efficiency of the cell was taken as the objective function. The beam down tilt angle and power sent to the cell center users and the cell edge users were optimized, and the QBFO-based algorithm was introduced to solve the non-convex optimization problem. Finally, the higher spectral efficiency was achieved for cell-edge users. In [34], the QBFO-based algorithm was applied to the non-orthogonal multi-access systems of cellular massive MIMO to solve the access point (AP) selection problem. Li et al. [34] turned the connection between AP and users into the form of quantum bits. By optimizing and updating the quantum bacterial population, the optimal solution of AP selection for all users was obtained. Meanwhile, the impace of the AP number, the number of user, the incomplete continuous interference cancellation and the number of AP antennas were analyzed for different AP selection schemes. It was proved that the proposed scheme effectively improved the downlink average rate of users and reduced the backhand overhead. In [35], the QBFO-based algorithm was used to study the channel estimation of 3D MIMO systems. Xue et al. [35] proposed the combinatorial estimation optimization criterion, which was used as the fitness function.

Inspired by the above works, the QBFO-BOMP-based algorithm is proposed for mmWave massive MIMO in this paper. When the measured value of signal is corrupted by noisy, the support set of the sparse signal can be recovered via the BOMP-based algorithm. The binary matrix is constructed depending on whether the atom is selected, and then the received signal is projected onto the linear subspace of the selected column to update the residual. In particular, the QBFO-based algorithm is used to obtain the channel matrix to be estimated. The optimization function of the least squares method is used as the fitness function. The bacterial population is measured to collapse into a classical state. The bacterial location is then updated by chemotaxis, reproduction, and dispersal operations. Finally, the optimal solution is obtained.

The remainder of this paper is summarized as follows. Section 2 is the signal model. The proposed QBFO-BOMP-based algorithm is specifically described in Section 3. Section 4 gives simulation figures to illustrate the estimation performance of the proposed algorithm. Section 5 is the conclusion.

2  System Model

MmWave massive MIMO systems is considered. The numbers of transmitter and receiver are Nt and Nr, respectively. The received signal is:

Y=UHHPs+n,(1)

where Y∈CNrRF×1 is the received signal, the hybrid precoding matrix and the hybrid combination matrixis are P∈CNt×NtRF and U∈CNr×NrRF, respectively. s is the pilot signal at transmitter, n is the additive Gaussian white noise (n∼𝒞𝒩(0,σ2I)). σ2 is the noise power.

H∈CNr×Nt is the channel matrix and is written as:

H=NtNrL∑l=1Lβlb(θr,l)bH(θt,l),(2)

where L is the number of scattering paths and satisfies L≪min(Nr,Nt). The gain of the l-th path is βl. b(θr,l) and b(θt,l) are the steering vectors at the transmitter and the receiver, respectively.

For the uniform linear arrays (ULA) adopted in this paper, b(θr,l) and b(θt,l) can be expressed as:

b(θr)=1Nr[1,ej2πdsin⁡θr/λ,…,ej2π(Nt−1)dsin⁡θr/λ]T,(3)

b(θt)=1Nt[1,ej2πdsin⁡θt/λ,…,ej2π(Nr−1)dsin⁡θt/λ]T,(4)

where λ is the wavelength. The distance between the array elements is specified as equal to the half-wavelength of the signal, that is, d=λ2.

Therefore, H can also be denoted as:

H=B(θr)βBH(θt),(5)

where β=NtNrLdiag[β1,…,βL], θr=[θr,1,…,θr,L]T, θt=[θt,1,…,θt,L]T, B(θr)=[b(θr,1),…,b(θr,L)]∈CNr×L, B(θt)=[b(θt,1),…,b(θt,L)]∈CNt×L.

Assuming that the channel remains stationary for the duration of the transmission unit training symbol, where a pilot transmitted signal is written as x=Ps. The transmitter sends N different pilot sequences. By collecting M received pilot signals, the p-th received signal can be expressed as [23]:

yp=UHHxp+np,(6)

where yp=[yp,1T,yp,2T…,yp,MT]T. So the received pilot signal can be simplified as:

Y=UHHX+N,(7)

where Y∈CN×M.

3  Description of the Proposed QMDOMP Based Algorithm

In this paper, a QBFO-BOMP-based algorithm is proposed for the channel eatimation.

3.1 Description of BOMP Based Algorithm

3.1.1 Sensing Matrix

Firstly, Y is vectorized:

Y^=vec(Y),(8)

where Y^∈CMN×1.

The grid, which quantizes the angular parameters, is defined as follows:

Γ={ϕv:ϕv∈[−π2,π2],v=1,…,V},(9)

where ϕ1=−π2, ϕV=π2. {ϕv} is selected from the definition of the steering vectors and related by {sin(ϕv)}, which satisfies:

sin(ϕv)=2V(v−1)−1,v=1,…,V(10)

where V≥max{Nr,Nt}. Eq. (10) is limited to [−π2,π2].

The corresponding rows of the array response matrix are orthogonal and can be represented as follows:

B~r=[br(ϕ1),…,br(ϕV)]B~t=[bt(ϕ1),…,bt(ϕV)].(11)

Thus, Eq. (5) can also be rewritten as:

H=B~rH~B~tH+C,(12)

where B~rH~B~tH is the quantizated-channel. H~∈CV×V is an L-sparse matrix. C is the quantizated error matrix. The sensing matrix can be represented as:

S~=(B~tTX)T⊗(UHB~r),(13)

where S~∈CMN×NrNt.

3.1.2 Selection Atom

The key point of the selection atom step is to find the atom that is highly correlated with the received signal. Although Λ=|S~HY| is a matrix operation, the maximum value needs to be chosen in the different ways to avoid the loop of the signal. For each atom with k cycles, the BOMP determines whether it has all samples with the maximum value.

The signal of the k-th atom with the highest residual does not have positive value in ∑(S~HY−(S~HY)k). Ik,Y reverts the binary Boolean value of the k-th atom and Y. Ik,Y can be denoted as [28]:

Ik,Y={1selected atom0not selected atom.(14)

3.1.3 Update Residual

In this paper, the residual error is updated in the following ways:

κ(t)=Y^−S~(t)h^k(t),s.t. ‖κ(t)‖2<υ,(15)

where υ is the error threshold. The value of υ needs to be set appropriately. If the value of υ is too large, the estimation accuracy is affected. When the value of υ is too small, the convergence speed of the algorithm is reduced. Therefore, it is necessary to choose an appropriate value of υ.

The specific processes of the BOMP-based algorithm are summarized in Algorithm 1. Noting, the QBFO-based algorithm is used to obtain the estimated channel matrix in Algorithm 1. The corresponding specific steps are described in Section 3.2.

3.2 Description of QBFO Based Algorithm

3.2.1 Fitness Function

In this section, QBFO is applied to mmWave massive MIMO, and the fitness corresponding function is:

h^(t)=arg min‖Y^−S~(t)h^‖2f(h^)=exp(−μ|Ω(h^)|).(16)

Firstly, the quantum state bacteria is expressed as the possible value of the channel matrix by using binary coding. Each quantum state is then measured and collapsed to the binary of classical state. Finally, it is decoded into the decimal system, such that each bacterium represents the value of the channel matrix. In addition, the number of bacterial population K represents the corresponding value of the channel matrix in the first generation search for the optimal solution.

Therefore, the corresponding value of the channel matrix in K is substituted into the fitness function to obtain the fitness function value. Then, the chemotaxis, reproduction and dispersion operations are carried out according to the magnitude of K fitness function values and the relative positional relationship between the bacteria. Finally, the optimal fitness function value is obtained through multiple iterations. In other words, the channel matrix obtained by quantum bacteria decoding is the channel matrix obtained by using the QBFO-based algorithm to solve mmWave massive MIMO channel estimation.

3.2.2 Quantum Chemotactic Operation

In quantum theory, the quantum state can collapse by measurement. Specifically, the initial quantum state collapses to the state given by the measurement. The n-bit quantum bit is actually the superposition of 2n basic states, which is given by:

|η⟩=∑z∈{0,1}ncz|z⟩,(17)

where |η⟩ is the quantum state, and |z⟩ is a group of the orthogonal bases of the vector space, called the ground state of quantum state. |cz|2 indicates the corresponding probability amplitude, which satisfies the normalization condition ∑z∈{0,1}n|cz|2=1. Therefore, the quantum states have more randomness and the parallel operation.

In the QBFO-based algorithm, the position information of the bacteria is converted into multiple qubits via quantum states. So every bacteria is in a superposition state. However, the quantum state of each bacteria is determined by the probability amplitude. According to (17), the bacteria of n-bit quantum bit can be written as:

ci=[μ1ν1|μ2ν2|……|μzνz].(18)

The bacterial population composed of K bacteria is prepared as R(t), R(t)={c1t,…,cit,…,cKt}. R(t) collapses to the classical state W(t) after measurement. The measured bacterial population is represented as follows:

W(t)={w1t,…,wit,…,wKt},(19)

where wit is the representation of the classical state, which is obtained by collapsing cit through measurement.

The chemotactic operation refers to the optimization process of the entire bacterial population. The quantum rotating gate is used to update the quantum state of the bacteria in this paper. Fig. 1 is the schematic diagram of the quantum rotating gate. The purpose of the quantum rotating gate is to adjust the state of the qubit, so that it can rotate in the direction of the better value of the fitness function. (μi,νi)T becomes (μ¯i,ν¯i)T through the quantum rotating gate. For any qubit, the update mode of the bacteria state by the quantum rotating gate is [36]:

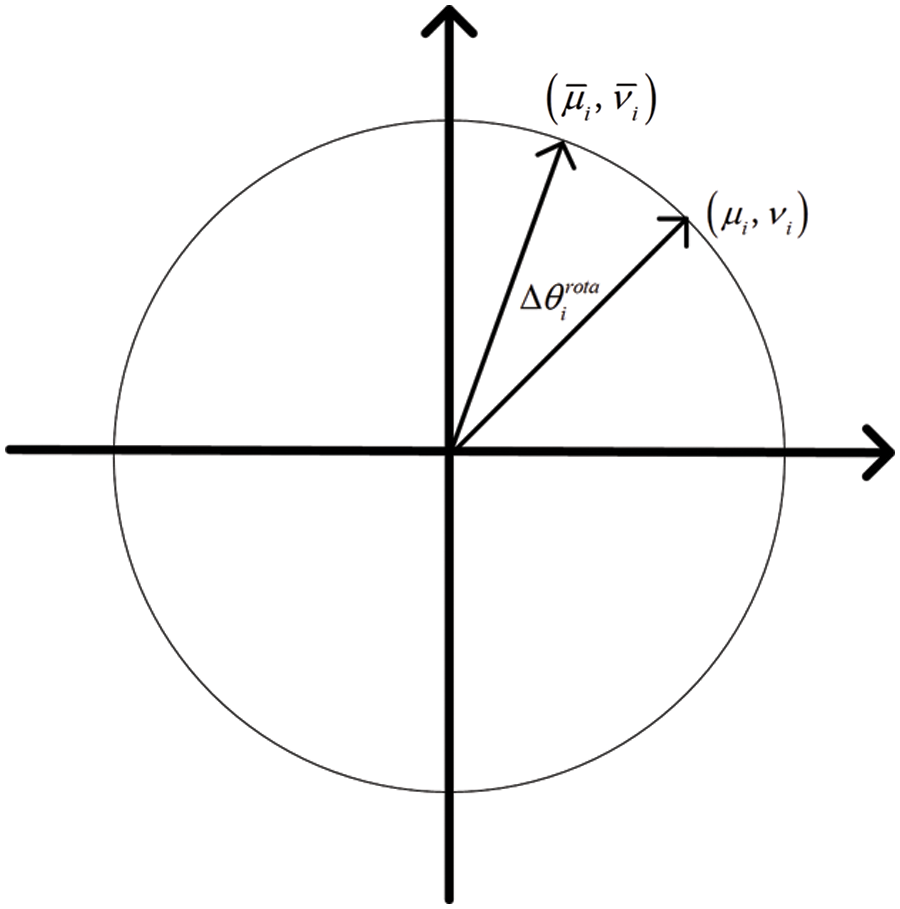
Figure 1: Schematic diagram of quantum rotating gate

(μ¯iν¯i)=(cosθirota−sinθirotasinθirotacosθirota)(μiνi),(20)

θirota=d(μi,νi)Δθirota,(21)

where θirota is the rotation angle of the i-th quantum bit. Δθirota denotes the rotation angle of the i-th qubit of the current bacteria. This paper realizes the adjustment of θirota through adaptive rotation operation.

d(μi,νi) expresses the direction of the rotation angle, and its specific expression is [37–39]:

d(μi,νi)=−sig(Ai).(22)

Ai=|μ0μiν0νi|.(23)

The direction of rotation can be positive or negative when Ai=0. The phase rotation direction is −sig(Ai) when Ai≠0. (μi,νi)T represents the probability amplitude of the i-th quantum bit of the current bacteria. (μ0,ν0)T denotes the probability amplitude corresponding to the historical best personal. Δθirota determines the step size of the quantum state adjustment and the speed of the algorithm convergence. The value of Δθirota is not fixed and the update method is [39,40]:

Δθirota=|θ0rota−θirotaπ/2−(−π/2)|(θmax−θmin)+θmin,(24)

where θmax is the upper bound of the rotation angle, and θmin is the lower bound.

3.2.3 Reproduction Operation

This paper uses the fitness function f of (16) as the standard of reproduction operation. It is randomly selected e bacteria from K bacteria, and the bacteria personal with the highest fitness function value is retained. K personals can be obtained by repeating K times. In order to keep the population size unchanged, e satisfies e=K/2. This reproduction operation has no requirements for the positive and negative values of personal fitness function. In addition, there is a high probability that the best personal can be selected. The specific operations are as follows:

(1)   It is determined that the number of bacteria entering the new population is one.

(2)   K bacteria are randomly selected from the bacterial population, and the personal with the largest fitness value is selected to enter the next generation population.

(3)   A new population is get by repeating K times.

3.2.4 Dispersion Operation

After the reproduction operation is completed, it enters the dispersion stage. At this stage, each bacteria corresponds to a random number. Given a dispersion probability gdis, if the random number of the bacteria is smaller than gdis, it is immediately cleaned. Furthermore, the corresponding alternatives appear randomly in the search space. This operation avoids the situation that the algorithm falls into local optimum.

The value of gdis affects the optimization results. When gdis is too large, most of the bacteria are dispersed, which makes the earlier chemotaxis and reproduction operations ineffective. When gdis is too small, the dispersion operation is meaningless, making the fitness function easily trapped in the local optimal solution.

Fig. 2 shows the final convergence under different dispersal probabilities. The value range of gdis is [0.1 0.6]. It can be seen from Fig. 2 that too large or too small gdis lead to a decrease in the success rate of convergence. Thus, according to the experimental results, gdis is taken as 0.3 in this paper.

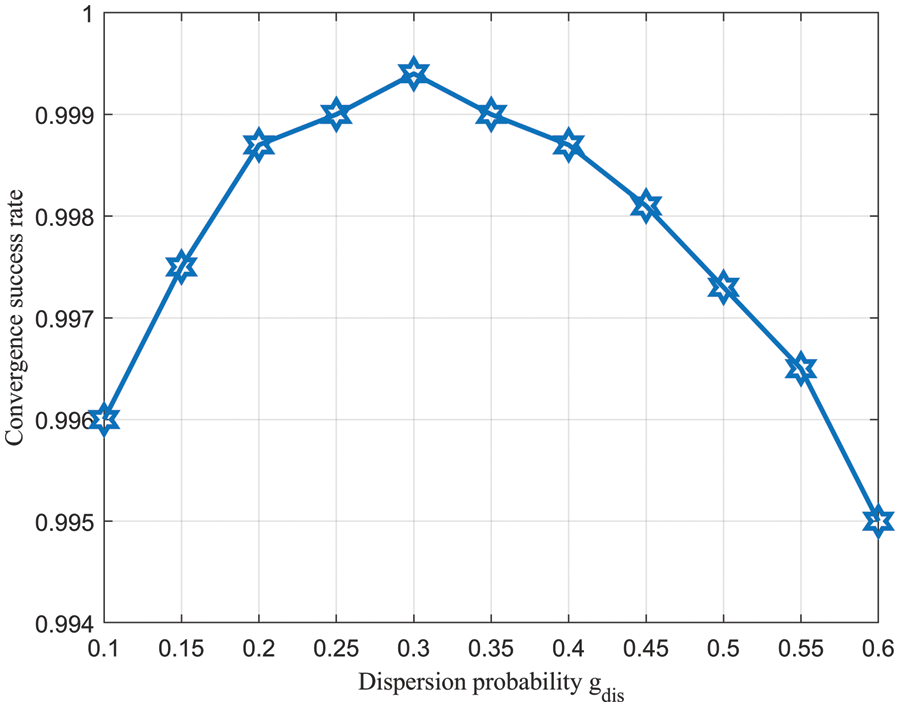
Figure 2: Convergence success rate vs. gdis

The flow chart and steps of the QBFO-based algorithm are shown in Fig. 3 and Algorithm 2, respectively. Fig. 3 shows the important structure of the proposed QBFO-based channel estimation algorithm. Firstly, the population parameters are initialized, namely R(t) and R(t0). Then, R(t) is measured and collapsed to generate W(t). The fitness function value is calculated to record and track the information of the current optimal fitness value and the best personal. Finally, quantum chemotaxis, reproduction and dispersion operations are used to output the optimal personal and the optimal fitness value of the bacterial.

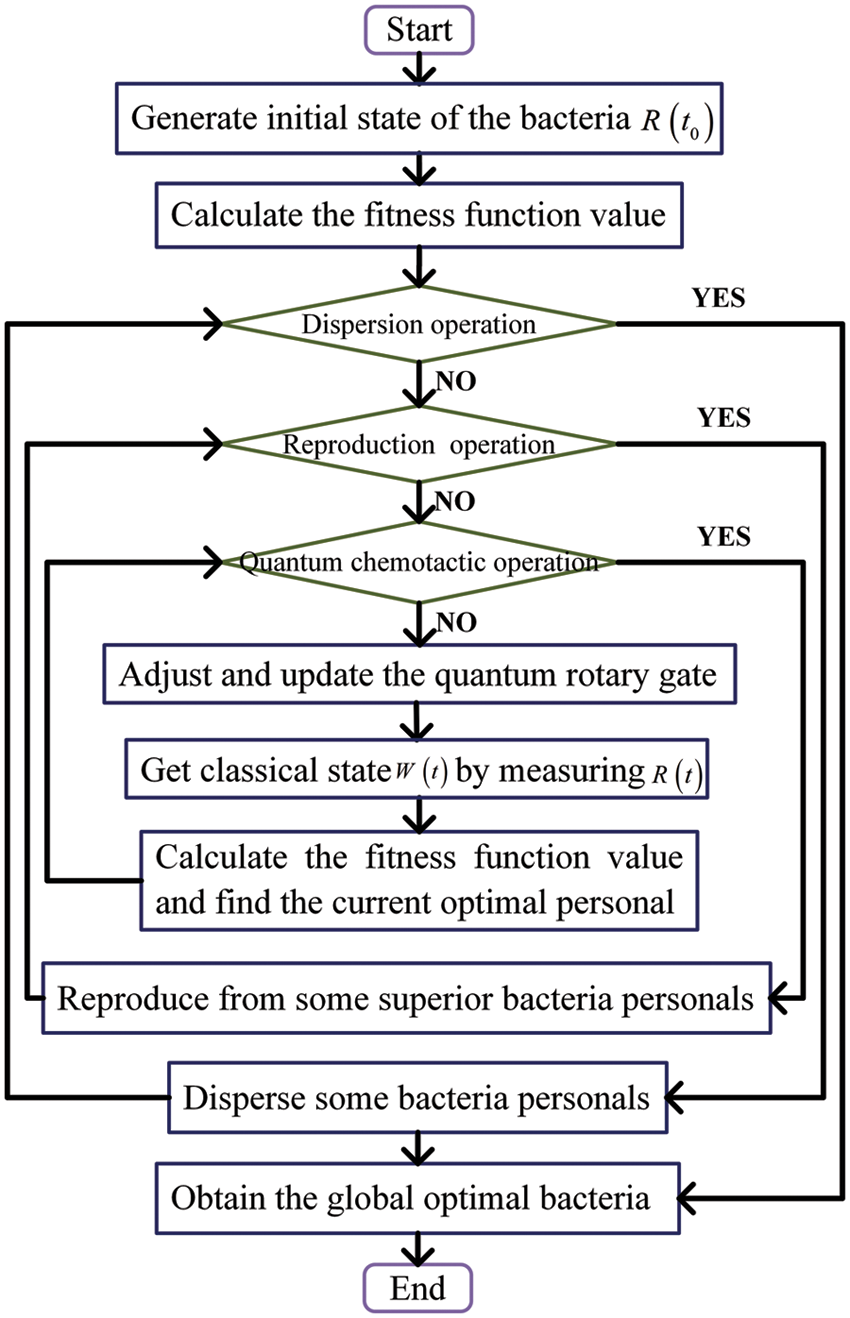
Figure 3: Flow chart of the QBFO-based algorithm

The proposed QBFO-based algorithm does not have the process of derivation and inversion. Instead, the possible values of the channel matrix are directly given in terms of the actual situation. That is to get the minimum value of the fitness function. Therefore, the proposed QBFO-based algorithm is simple to operate and does not depend on the solution range space of the function.

Noting, the expression of the initial state of each quantum bacteria is [41–43]:

R(t0)=[1212|1212|1212……|1212].(25)

It can be shown from (25) that the quantum state of each bacterium in the initial state is the superposition of |1⟩ and |0⟩ with equal probability. As a result, quantum bacteria can represent more possible states during the renewal process.

4  Simulation Results

This paper selects the traditional OMP-based algorithm [21], the orthogonal matching pursuit levenberg marquardt method (OMP-LMM)-based algorithm [26], the binary orthogonal matching pursuit (BOMP)-based algorithm [28], and the bacterial foraging optimization (BFO)-based algorithm [40] as the comparison algorithms. Among them, the BFO-based algorithm is the basic algorithm, which is modified as the basis to obtain the proposed QBFO-BOMP algorithm.

4.1 Simulation Parameters

The parameters are set to: L=3, Nr=Nt=32, V=180, K=40, Kc=60, Kre=8, Ked=3, gdis=0.3, θmax=0.05π, θmin=0.3π, d=0.5, SNR={0,5,10,15,20,25} dB.

4.2 Simulation Results and Analysis

Fig. 4 shows the change curve of the fitness function value of the QBFO-based algorithm and the BFO-based algorithm with the number of iterations. It can be seen from Fig. 4 that the convergence rate of the BFO-based algorithm is faster than that of the QBFO-based algorithm at the beginning of the iteration. But in the later period of iteration, the convergence rate and accuracy of the QBFO-based algorithm is better than the BFO-based algorithm. The main reason is that the BFO-based algorithm is easy to fall into the local extreme value at the later iterations, which affects the convergence accuracy. After 50 iterations, the QBFO-based algorithm gradually reaches the optimal value, which indicates that the QBFO algorithm has strong global search ability.

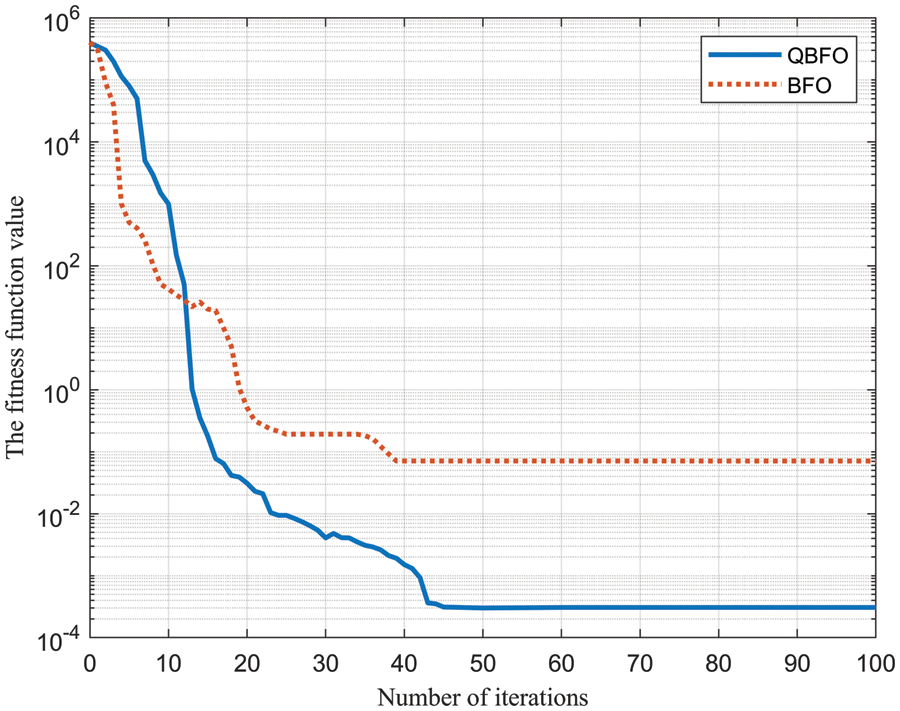
Figure 4: Fitness function value vs. number of iterations

Fig. 5 shows the normalized mean square error (NMSE) performance of different algorithms under different signal-to-noise ratios (SNRs). The estimation accuracy of the proposed QBFO-BOMP-based algorithm is higher than that of other comparison algorithms. The main reason is that the bacteria represented by multiple qubits in the proposed QBFO-BOMP-based algorithm are in the superposition state, which can significantly increase the search space of the algorithm. The worst simulation result is the traditional OMP-based algorithm, which indicates that it does not effectively estimate the channel matrix.

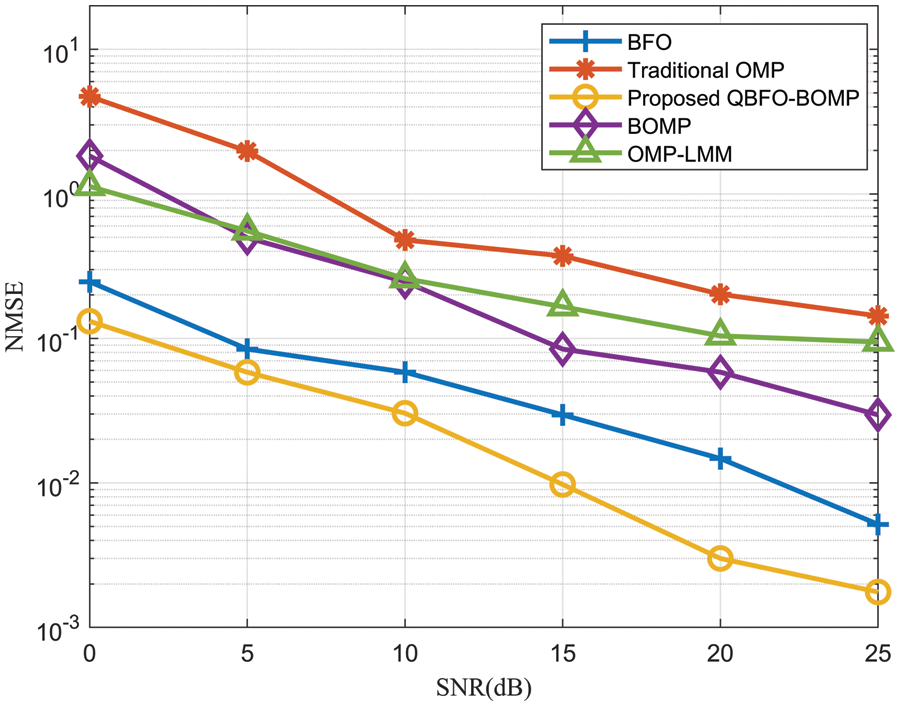
Figure 5: NMSE vs. SNRs

Fig. 6 is the achievable spectral efficiency (ASE) of different algorithms under different SNRs. The proposed algorithm is superior to other comparison algorithms in ASE. The main reason is that the proposed QBFO-BOMP-based algorithm is simple to operate and does not depend on the solution range space of the function, which is different from the traditional channel estimation algorithm. The introduction of quantum basis has certain superiority. In addition, the ASE of the proposed algorithm is closer to the perfect CSI.

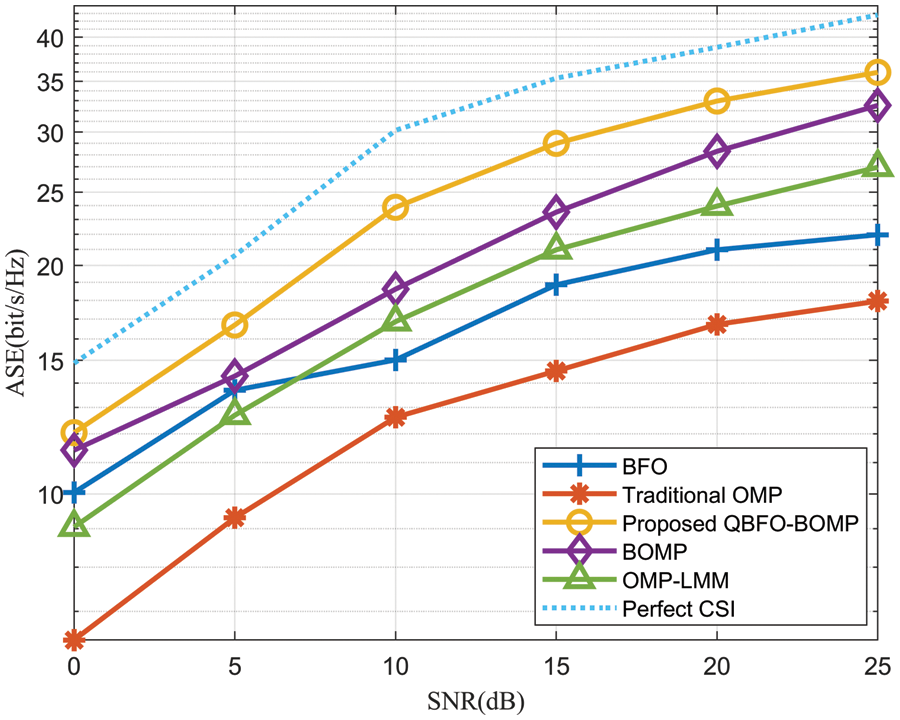
Figure 6: ASE vs. SNRs

Fig. 7 compares the time ratio of the proposed QBFO-BOMP-based algorithm, the BFO-based algorithm, the BOMP-based algorithm and the traditional OMP-based algorithm. It can be observed from Fig. 7 that the time ratio between the proposed QBFO-BOMP-based algorithm and the traditional OMP-based algorithm is about 0.6. The proposed QBFO-BOMP-based algorithm obtains information through the chemotaxis, reproduction and dispersion operations of quantum bacteria, which saves the steps of channel matrix in traditional channel estimation algorithm. The time ratio between the BFO-based algorithm and the traditional OMP-based algorithm is about 0.9. It can be concluded that the complexity of the proposed QBFO-BOMP-based algorithm is similar to that of the BFO-based algorithm. Quantization of the bacteria does not significantly increase the complexity of the algorithm.

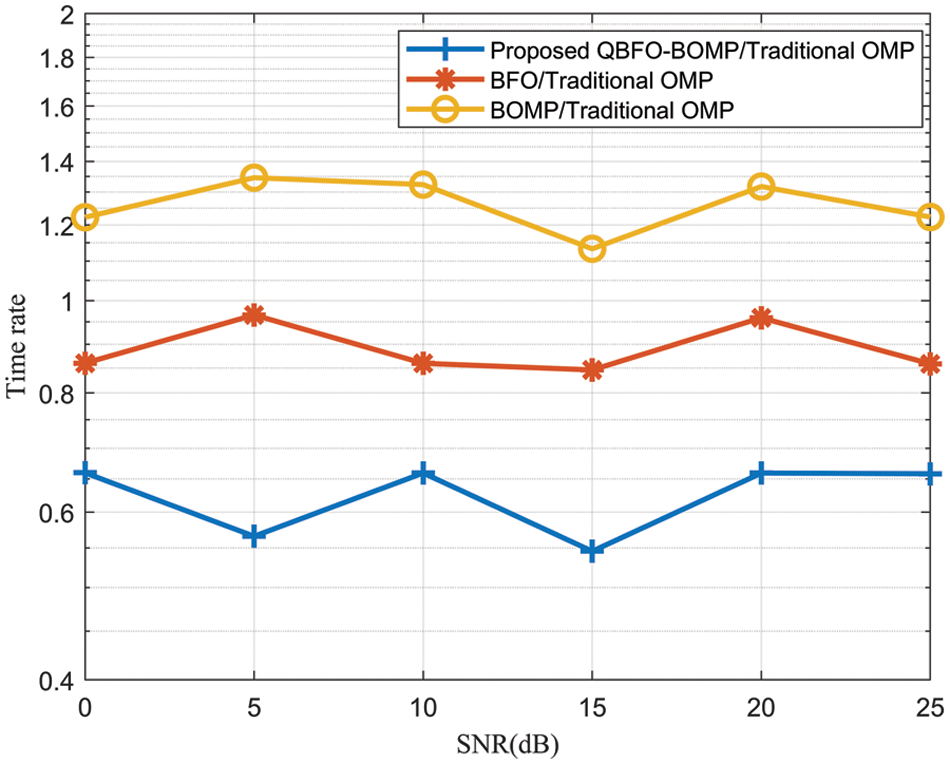
Figure 7: Time rate vs. SNRs

5  Conclusions

This paper focuses on the channel estimation of mmWave massive MIMO systems and proposes the QBFO-BOMP-based algorithm. The quantum transmission technique is introduced to estimate the channel matrix. The proposed QBFO-BOMP-based algorithm mainly consists of two main components. The first part is the BOMP-based algorithm. Firstly, the BOMP-based algorithm is used to recover the support set of the sparse signal. The binary matrix is constructed according to whether the atom is chosen, and then the residual is updated by projecting the received signal onto the linear subspace of the selected column. The second part is to use the QBFO-based algorithm to get the estimated channel matrix. According to the communication between quantum bacteria and the fitness function value, chemotaxis, reproduction and dispersion operations are carried out to update the bacterial position. Simulation analysis shows that the proposed QBFO-BOMP-based algorithm has better estimation performance than other algorithms.

Acknowledgement: The authors express their gratitude to the editor and referees for their valuable time and efforts on our manuscript.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Nos. 61861015, 62061013 and 61961013), Key Research and Development Program of Hainan Province (No. ZDYF2019011), National Key Research and Development Program of China (No. 2019CXTD400), Young Elite Scientists Sponsorship Program by CAST (No. 2018QNRC001), the Scientific Research Setup Fund of Hainan University (No. KYQD(ZR) 1731) and the Natural Science Foundation High-Level Talent Project of Hainan Province (No. 622RC619).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Wen, F., Wymeersch, H., Peng, B., Tay, W. (2019). A survey on 5G massive MIMO localization. Digital Signal Processing, 19, 21–28. https://doi.org/10.1016/j.dsp.2019.05.005 [Google Scholar] [CrossRef]

2. Cong, J., Wang, X., Huang, M., Wan, L. (2021). Robust DOA estimation method for MIMO radar via deep neural networks. IEEE Sensors Journal, 21(6), 7498–7507. https://doi.org/10.1109/JSEN.2020.3046291 [Google Scholar] [CrossRef]

3. Cong, J., Wang, X., Lan, X., Huang, M., Wan, L. (2021). Fast target localization method for FMCW MIMO radar via VDSR neural network. Remote Sensing, 13(10), 1956. https://doi.org/10.3390/rs13101956 [Google Scholar] [CrossRef]

4. Cong, J., Wang, X., Wan, L., Huang, M. (2022). Neural network-aided sparse convex optimization algorithm for fast DOA estimation. IEEE Transactions of the Institute of Measurement and Control, 44(8), 1649–1655. https://doi.org/10.1177/01423312211049067 [Google Scholar] [CrossRef]

5. Wang, X., Huang, M., Wan, L. (2021). Joint 2D-DOD and 2D-DOA estimation for coprime EMVS-MIMO radar. Circuits, Systems, and Signal Processing, 40(1), 1–17. https://doi.org/10.1007/s00034-020-01605-5 [Google Scholar] [CrossRef]

6. Shao, J., Wang, X., Lan, X. (2021). GAMP-SBL-based channel estimation for millimeter-wave MIMO systems. EURASIP Journal on Advances in Signal Processing, 1, 1–22. https://doi.org/10.1186/s13634-021-00792-w [Google Scholar] [CrossRef]

7. Wang, X., Yang, L., Meng, D., Dong, M., Ota, K. et al. (2021). Multi-UAV cooperative localization for marine targets based on weighted subspace fitting in SAGIN environment. IEEE Internet of Things Journal, 9(8), 5708–5718. https://doi.org/10.1109/JIOT.2021.3066504 [Google Scholar] [CrossRef]

8. Wang, X., Wan, L., Huang, M., Shen, C., Han, Z. et al. (2021). Low-complexity channel estimation for circular and noncircular signals in virtual MIMO vehicle communication systems. IEEE Transactions on Vehicular Technology, 69(4), 3916–3928. https://doi.org/10.1109/TVT.2020.2970967 [Google Scholar] [CrossRef]

9. Rezai, M., Salehi, J. A. (2021). Quantum CDMA communication systems. IEEE Transactions on Information Theory, 67(8), 5526–5547. https://doi.org/10.1109/TIT.2021.3087959 [Google Scholar] [CrossRef]

10. Chandra, D., Cacciapuoti, A. S., Caleffi, M., Hanzo, L. (2022). Direct quantum communications in the presence of realistic noisy entanglement. IEEE Transactions on Communications, 70(1), 469–484. https://doi.org/10.1109/TCOMM.2021.3122786 [Google Scholar] [CrossRef]

11. Wengerowsky, S., Joshi, S. K., Steinlechner, F., Hübel, H., Ursin, R. (2019). An entanglement-based wavelength multiplexed quantum communication network. 2019 Conference on Lasers and Electro-Optics Europe European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany. https://doi.org/10.1117/12.2327000 [Google Scholar] [CrossRef]

12. Chandra, D., Caleffi, M., Cacciapuoti, A. S. (2022). The entanglement-assisted communication capacity over quantum trajectories. IEEE Transactions on Wireless Communications, 21(6), 3632–3647. https://doi.org/10.1109/TWC.2021.3122962 [Google Scholar] [CrossRef]

13. Li, J., Guo, Z., Ma, H. (2021). Development of hybrid ARQ protocol for the quantum communication system on stabilizer codes. China Communications, 18(2), 40–48. https://doi.org/10.23919/JCC.2021.02.004 [Google Scholar] [CrossRef]

14. Cacciapuoti, A. S., Caleffi, M. (2020). When entanglement meets classical communications: Quantum teleportation for the quantum internet. IEEE Transactions on Communications, 68(6), 3808–3833. https://doi.org/10.1109/TCOMM.2020.2978071 [Google Scholar] [CrossRef]

15. DiAdamo, S., Nötzel, J., Sekavnik, S., Bassoli, R., Ferrara, R. (2021). Integrating quantum simulation for quantum-enhanced classical network emulation. IEEE Communications Letters, 25(12), 3922–3926. https://doi.org/10.1109/LCOMM.2021.3115982 [Google Scholar] [CrossRef]

16. Zhang, G., Wu, Y., Tan, Y. (2014). Bacterial foraging optimization algorithm with quantum behavior. IEEE Open Journal of the Communications Society, 35(3), 614–621. https://doi.org/10.3724/SP.J.1146.2012.00892 [Google Scholar] [CrossRef]

17. Waqas, A. B., Saifullah, Y., Ashraf, M. M. (2021). A hybrid quantum inspired particle swarm optimization and least square framework for real-time harmonic estimation. Journal of Modern Power Systems and Clean Energy, 9(6), 1548–1556. https://doi.org/10.35833/MPCE.2019.000098 [Google Scholar] [CrossRef]

18. Liu, L., Shan, L., Dai, Y., Liu, C., Qi, Z. (2018). A modified quantum bacterial foraging algorithm for parameters identification of fractional-order system. IEEE Access, 6, 6610–6619. https://doi.org/10.1109/ACCESS.2018.2791976 [Google Scholar] [CrossRef]

19. Jing, X., Wang, X., Lan, X. (2021). l1/2-SVD based channel estimation for mmWave massive MIMO. 2021 5th International Conference on Wireless Communications and Applications (ICWCA), pp. 1–5. Haikou, China. https://doi.org/10.1007/978-981-19-2255-8-2 [Google Scholar] [CrossRef]

20. Ye, T., Lee, S. (2008). Non-iterative exact inverse scattering using simultaneous orthogonal matching pursuit (S-OMP). 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, pp. 2457–2460. Las Vegas, NV, USA. https://doi.org/10.1109/ICASSP.2008.4518145 [Google Scholar] [CrossRef]

21. Lee, J., Gil, G., Lee, Y. (2016). Channel estimation via orthogonal matching pursuit for hybrid MIMO systems in millimeter wave communications. IEEE Transactions on Communications, 64(6), 2370–2386. https://doi.org/10.1109/TCOMM.2016.2557791 [Google Scholar] [CrossRef]

22. Wang, Y., Zhai, J., Mo, Y., Han, Y., Jiang, M. (2017). 3D reconstruction of human body based on orthogonal matching pursuit and accelerated proximal gradient. Chinese Journal of Biomedical Engineering, 36(4), 385–393. https://doi.org/10.3969/j.issn.0258-8021.2017.04.001 [Google Scholar] [CrossRef]

23. Liu, X., Zhao, G., Kang, J., Huang, S. (2022). Parameters optimization and adaptive control for UAV by quantum bacteria foraging algorithms and local refinement strategy. 2022 41st Chinese Control Conference (CCC), pp. 2451–2458. Heifei, China. https://doi.org/10.23919/CCC55666.2022.9901676 [Google Scholar] [CrossRef]

24. Jing, X., Wang, X., Su, T., Lan, X. (2022). An improved QMDOMP channel estimation algorithm in mmWave massive MIMO systems. 2022 IEEE 5th International Conference on Electronic Information and Communication Technology (ICEICT), pp. 735–740. Hefei, China. https://doi.org/10.1109/ICEICT55736.2022.9908736 [Google Scholar] [CrossRef]

25. Tropp, J., Gilbert, A. (2007). Signal recovery from random measurements via orthogonal matching pursuit. IEEE Transactions on Information Theory, 53(12), 4655–4666. https://doi.org/10.1109/TIT.2007.909108 [Google Scholar] [CrossRef]

26. Weiland, L., Stockle, C., Wurth, M. (2018). OMP with grid-less refinement steps for compressive mmWave MIMO channel estimation. 2018 IEEE 10th Sensor Array and Multichannel Signal Processing Workshop (SAM), pp. 543–547. Sheffield, UK. https://doi.org/10.1109/SAM.2018.8448789 [Google Scholar] [CrossRef]

27. You, Y., Zhang, L., Liu, M. (2019). IP aided OMP based channel estimation for millimeter wave massive MIMO communication. 2019 IEEE Wireless Communications and Networking Conference (WCNC), pp. 1–6. Marrakesh, Morocco. https://doi.org/10.1109/WCNC.2019.8885881 [Google Scholar] [CrossRef]

28. Chatterjee, A., Yuen, P. (2020). Rapid estimation of orthogonal matching pursuit representation. 2020 IEEE International Geoscience and Remote Sensing Symposium, pp. 1315–1318. Waikoloa, HI, USA. https://doi.org/10.1109/IGARSS39084.2020.9323532 [Google Scholar] [CrossRef]

29. Mishra, S. (2005). A hybrid least square-fuzzy bacterial foraging strategy for harmonic estimation. IEEE Transactions on Evolutionary Computation, 9(1), 61–73. https://doi.org/10.1109/TEVC.2004.840144 [Google Scholar] [CrossRef]

30. Dasgupta, S., Das, S., Biswas, A. (2010). Automatic circle detection on digital images with an adaptive bacterial foraging algorithm. Soft Computing, 14(11), 1151–1164. https://doi.org/10.1007/s00500-009-0508-z [Google Scholar] [CrossRef]

31. Dasgupta, S., Das, S., Abraham, A., Biswas, A. (2009). Adaptive computational chemotaxis in bacterial foraging optimization: An analysis. IEEE Transactions on Evolutionary Computation, 13(4), 919–941. https://doi.org/10.1109/TEVC.2009.2021982 [Google Scholar] [CrossRef]

32. Li, F., Zhang, Y., Wu, J., Li, H. (2014). Quantum bacterial foraging optimization algorithm. 2014 IEEE Congress on Evolutionary Computation (CEC), pp. 1265–1272. Beijing, China. https://doi.org/10.1109/CEC.2014.6900230 [Google Scholar] [CrossRef]

33. Qiu, L., Ji, W., Li, D., Liang, Y. (2017). Optimized downlink transmission scheme based on quantum bacterial foraging algorithm in 3D MIMO systems. Journal of Computer Applications, 37(S2), 15–19. https://doi.org/CNKI:SUN:JSJY.0.2017-S2-004 [Google Scholar]

34. Li, F., Yan, Z., Li, D., Song, Y. (2022). Accsee point selection in cell-free massive multiple-input multiple-output non-orthogonal multiple accsee system based on quantum bacterial foraging optimization. Journal of Electronics and Information Technology, 44, 1–8. https://doi.org/10.11999/JEIT220573 [Google Scholar] [CrossRef]

35. Xue, J., Jiang, S., Liangm, Y., Li, F. (2016). Quantum bacterial foraging optimization based sparse channel estimation for 3D MIMO systems. 2016 8th International Conference on Wireless Communications Signal Processing (WCSP), pp. 1–5. Yangzhou, China. https://doi.org/10.1109/WCSP.2016.7752677 [Google Scholar] [CrossRef]

36. Huang, H. (2017). High-accuracy positioning for indoor wireless sensor networks. 2017 IEEE 9th International Conference on Communication Software and Networks (ICCSN), pp. 311–316. Guangzhou, China. https://doi.org/10.1109/ICCSN.2017.8230126 [Google Scholar] [CrossRef]

37. Liu, L., Shan, L., Dai, Y. W., Liu, C. L., Qi, Z. D. (2018). Improved quantum bacterial foraging algorithm for tuning parameters of fractional-order PID controller. Journal of Systems Engineering and Electronics, 29(1), 166–175. https://doi.org/10.21629/JSEE.2018.01.17 [Google Scholar] [CrossRef]

38. Zhu, C., Liang, Y., Li, T., Li, F. (2021). Pilot assignment in cell-free massive MIMO based on quantum bacterial foraging optimization. 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), pp. 1–5. Changsha, China. https://doi.org/10.1109/WCSP.2016.7752677 [Google Scholar] [CrossRef]

39. Gao, H., Li, C. (2015). Quantum-inspired bacterial foraging algorithm for parameter adjustment in green cognitive radio. Journal of Systems Engineering and Electronics, 26(6), 897–907. https://doi.org/10.1109/JSEE.2015.00097 [Google Scholar] [CrossRef]

40. Jain, A. K., Srivastava, S. C., Singh, S. N., Srivastava, L. (2015). Bacteria foraging optimization based bidding strategy under transmission congestion. IEEE Systems Journal, 9(1), 141–151. https://doi.org/10.1109/JSYST.2013.2258229 [Google Scholar] [CrossRef]

41. Bejinariu, S. I. (2013). Image registration using Bacterial Foraging Optimization Algorithm on multi-core processors. 2013 4th International Symposium on Electrical and Electronics Engineering (ISEEE), pp. 1–6. Galati, Romania. https://doi.org/10.1109/ISEEE.2013.6674336 [Google Scholar] [CrossRef]

42. Nouria, H., Hong, T. S. (2013). Development of bacteria foraging optimization algorithm for cell formation in cellular manufacturing system considering cell load variations. Journal of Manufacturing Systems, 32, 20–31. https://doi.org/10.1016/j.jmsy.2012.07.014 [Google Scholar] [CrossRef]

43. Zhou, Y., Tan, S., Song, Y., Li, F. (2019). Quantum bacterial foraging optimization based interference coordination in 3D-MIMO systems. 2019 IEEE Congress on Evolutionary Computation (CEC), pp. 627–633. Wellington, New Zealand. https://doi.org/10.1109/CEC.2019.8790134 [Google Scholar] [CrossRef]