Research Progress of Aerodynamic Multi-Objective Optimization on High-Speed Train Nose Shape

1  Introduction

High-speed trains (HSTs) offer a multitude of advantages, including large passenger capacity, safety, comfort, energy saving, environmental protection, and have become a trend in developing world railway transportation. The operating speed of the HST in Germany is 250 km/h, with the highest rate reaching 317 km/h when it was put into service in 1985. ICE set a speed record of 406.9 km/h on the new high-speed railway line Fulda-Wurzburg in 1988, which was the fastest HSTs speed at that time [1,2]. In 1997, the 500 series HST were put into operation on the Sanyo Shinkansen in Japan, with an operating speed of 300 km/h. Moreover, The Japanese Maglev set a speed record of 581 km/h in 2003 [2,3]. The operating speed of the TGV HST is 300 km/h in French, and the test speed reached 515.3 km/h in May 1990, creating a new world record at that time. In 2007, TGV high-speed test train V150 made a new world record of 574.8 km/h in the test [3,4]. The design and operating speed of HSTs in China are also constantly improving. The maximum operating speed of the first HST introduced was 250 km/h. In 2008, when the Beijing-Tianjin intercity high-speed railway opened, the operating speed of CRH3 was 350 km/h. In 2011, the CRH380 series trains with a maximum speed of 380 km/h were put into operation on the Beijing-Shanghai Line. The CRH380A and CRH380B are the main models of the Beijing-Shanghai high-speed railway, which set the highest operating test speed of 486.1 and 487.3 km/h in the alignment joint-test [4,5].

The increase in the running speed of HSTs makes many problems reasonably ignored at low rates more prominent, such as aerodynamic resistance, aerodynamic lift force of the tail car, crosswind operation safety, air pressure pulse from trains passing by each other, micro-pressure wave in the tunnel exit, aerodynamic noise, etc. These problems primarily affect the safety of train operation and ride comfort, which seriously restricts the further improvement of train speed [6–8]. Academician Shen [9] pointed out that the difference between HSTs and ordinary trains is the dynamic environment in which the trains are located has undergone fundamental changes. The forces on ordinary trains are mainly mechanical and electrical, while HSTs have become primarily pneumatic. The aerodynamic resistance energy consumption of an HST at a speed of 350 km/h accounts for about 85% of the traction system [5,6,9,10]. According to the relationship between the aerodynamic resistance and the running speed, the aerodynamic resistance of an HST at a speed of 400 km/h will account for nearly 95% of the running resistance [10,11]. The sharply increased aerodynamic resistance will seriously affect the energy consumption and economy of train operations. Aerodynamic resistance is closely related to the shape of the train, and the effective way to reduce aerodynamic resistance is to design a reasonable shape. Moreover, the aerodynamic lift force and side force will increase rapidly under the action of a strong crosswind with the increase of train running speed, which will affect the lateral stability of the train and may cause the train to derail in severe cases. Studies have shown that the train is likely to derail or overturn when the train speed exceeds 200 km/h, and the crosswind speed exceeds 30 m/s [12–14]. Furthermore, a robust micro-pressure wave will be generated around the tunnel exit when HSTs travel through the tunnel, forming noise at the tunnel exit and affecting the surrounding environment. The most effective measure to reduce the micro-pressure wave at the tunnel exit is to design a more reasonable nose shape [15–18]. In addition, the aerodynamic noise generated by trains running at ever-increasing speeds is becoming more noticeable. When the train speed reaches 350 km/h and above, the aerodynamic noise surpasses the wheel-rail noise and becomes the main contributor to the noise of the HST [19]. The aerodynamic noise of the HST is proportional to the 6~8 power of the running speed, which will seriously affect ride comfort and aggravate the environmental noise pollution along the railway [20,21].

The sharp increase in aerodynamic resistance caused by the rise in running speed will directly affect energy consumption. The aerodynamic performance under the crosswind will jeopardize the safety and stability of the train. The increase in aerodynamic noise will not only affect the comfort of passengers on the train but also cause noise pollution along the railway. Improving the aerodynamic performance is an essential part of HSTs design. Meanwhile, the nose shape of an HST has a significant impact on its aerodynamic performance, which can be improved by optimizing the nose shape reasonably [22,23]. For example, reduce the aerodynamic resistance, aerodynamic noise of HSTs, the aerodynamic lift force of the tail car, and the micro-pressure wave in the tunnel exit, enhance the safety under the operating conditions of crosswind and passing by each other, and so on. Therefore, the research on the aerodynamic multi-objective optimization design of HSTs nose shape is of great significance to energy saving, environmental protection, operation safety, and speed-up. This paper summarizes the research status and progress of the aerodynamic multi-objective optimization of HSTs nose shapes, aiming to provide references for scholars in related fields to study this issue in depth.

2  Effect of Nose Parameters on Aerodynamic Performance

Due to the limitations of numerical methods, computing resources, and costs, early optimization of the nose shape of HSTs was primarily based on single variables, primarily considering the streamlined length, arch forms, and profiles. In terms of the streamlined length of the train nose shape, Shu et al. [24] studied the aerodynamic characteristics of trains with different streamlined lengths using numerical simulation. The results showed that the aerodynamic drag and aerodynamic lift force of the HST decreased as the streamlined head length increased when other conditions were the same. Hemida et al. [25,26] investigated the three-dimensional effect of the nose on the flow structures of the trains, containing aerodynamic force, pressure coefficient, and flow patterns. A highly unsteady characteristic and more vortex structures were generated around the train nose for the shore-nose model, resulting in more vital aerodynamic forces and boundary layer fluctuations. Moreover, the aerodynamic force frequency of the short-nose model is different from that of the long-nose model, and the time-averaged pressure of the long-nose model was in good agreement with the experimental results than the short-nose model. Huang et al. [27] conducted wind tunnel tests on a 3-car marshalled train with the original nose shape and the optimized nose shape. The test results showed that the aerodynamic resistance of the whole vehicle with the optimized head shape with a longer streamlined nose is smaller than that of the original model. Ku et al. [28] optimized the cross-sectional of an HST nose to minimize the micro-pressure wave at the tunnel exit. The relationship between the nose length and the pressure wave was investigated, and the pressure wave intensity was reduced by 27% for the optimal model. Miu et al. [29] carried out wind tunnel tests on CRH380A with various head shapes, among which the lengths of the head cars corresponding to the three nose shapes were 3372, 3335, and 3310 mm, respectively. The test results showed that the train with the longest nose shape has the best aerodynamic resistance characteristics. The drag force coefficient changes very little when the wind speed is changed in the range of 35–70 m/s, and the aerodynamic resistance of the head, middle, and tail cars was all the smallest. Zhang et al. [30] carried out wind tunnel test research on CRH2, including the original model with four different slenderness ratio nose shapes, as shown in Fig. 1. The study found that the longer the streamlined part of the head car, the smoother the streamlined nose shape. Meanwhile, the sharper near the nose tip, the better the drag reduction effect. When the streamline length was close, the greater the slenderness ratio of the head shape, the smaller the aerodynamic resistance of the train. Choi et al. [31] investigated the effects of the nose length on the aerodynamic performance of the Great Train Express (GTX). With the running speed of the GTX increasing from 100 to 200 km/h, the aerodynamic drag forces were obtained when the train travelled in tunnels. It was found that the aerodynamic drag can be reduced by about 50% by streamlining the head nose. Chen et al. [32] investigated the aerodynamic performance of HSTs with varying nose lengths in the presence of two trains passing each other in a tunnel. It was drawn that the positive peak of the pressure wave has a logarithmically decreasing trend with increasing nose length and the peak-to-peak amplitude of the pressure of the train surface. The aerodynamic resistance of the train will decrease with the increased streamlined length, while it should also be considered the passenger compartment of the head car. Meanwhile, the reduced train aerodynamic drag force caused by the streamlined nose length is limited. As a result, the nose length is unrivalled and infinitely stretchable.

Figure 1: High-speed train with different nose lengths

The single-arch model means that the maximum longitudinal profile of the streamlined nose is convex, and the maximum longitudinal profile of the double-arch model is a combination of convex and concave. In the aspect of arch forms, Tian et al. [33] conducted a wind tunnel test on the single-arch and double-arch nose shapes of the “China Star” HST. The aerodynamic resistance of the combination of a single-arch head car and a double-arch tail car is the smallest, and the aerodynamic resistance of the head and tail car with the double-arch nose is the largest. The results indicated that the aerodynamic resistance of the single-arch nose shape is better than that of the double-arch. Chen et al. [34] carried out numerical simulations on four HSTs with different nose shapes. The results showed that the single-arch nose shape of the head car had a significant impact on its running resistance. Meanwhile, the head car with a single-arch had a more excellent performance on the aerodynamic resistance than the double-arch nose, which is consistent with the conclusion of the wind tunnel test [17]. The CRH2 and CRH380A HSTs of China are double-arch nose shapes, and CRH3, CRH380B, and CR400 series all use single-arch models.

The influence of the maximum longitudinal profile and the sharp flattening of the nose on the aerodynamic performance of the HST cannot be ignored. Howe [35] established three train models, and the effect of the train nose shape on the aerodynamic performance when a train travelled through the tunnel was explored. The results showed that the nose shape greatly influenced the generation time and amplitude of the pressure wave at the tunnel exit. Shu et al. [24] studied train noses with different longitudinal profiles. The results showed that the aerodynamic resistance of the head car with a convex profile in the longitudinal direction of the nose is smaller than that with a concave profile in the case of the same streamlined length. There is almost no difference between the middle car and the aerodynamic resistance of the tail car was relatively large. Feng [36] analyzed the aerodynamic characteristics of various train nose shapes, as shown in Fig. 2. From A to C, the nose shapes of the train gradually become blunt from sharp. Meanwhile, from ① to ③, the nose shapes gradually change from straight to convex. The gently changing arc-shaped profile ② has the best aerodynamic resistance characteristics, and the nose shape of the straight longitudinal profile ① corresponds to the aerodynamic drag force in the middle. The nose shape of the drum-shaped longitudinal profile ③ corresponds to the maximum aerodynamic drag force of the HST. The results showed that the aerodynamic resistance of the train is more negligible when the train nose shape is sharper and the nose gradually changes from a cone shape to a square shape, that is, from profile A to C, the aerodynamic resistance of the train increases significantly. Yang et al. [37] studied the aerodynamic characteristic of the train with the different longitudinal profiles operating in the open air. Three kinds of longitudinal profiles were generated, and the results indicated that the profiles had a noticeable influence on the aerodynamic force, surface pressure, and vortex shedding.

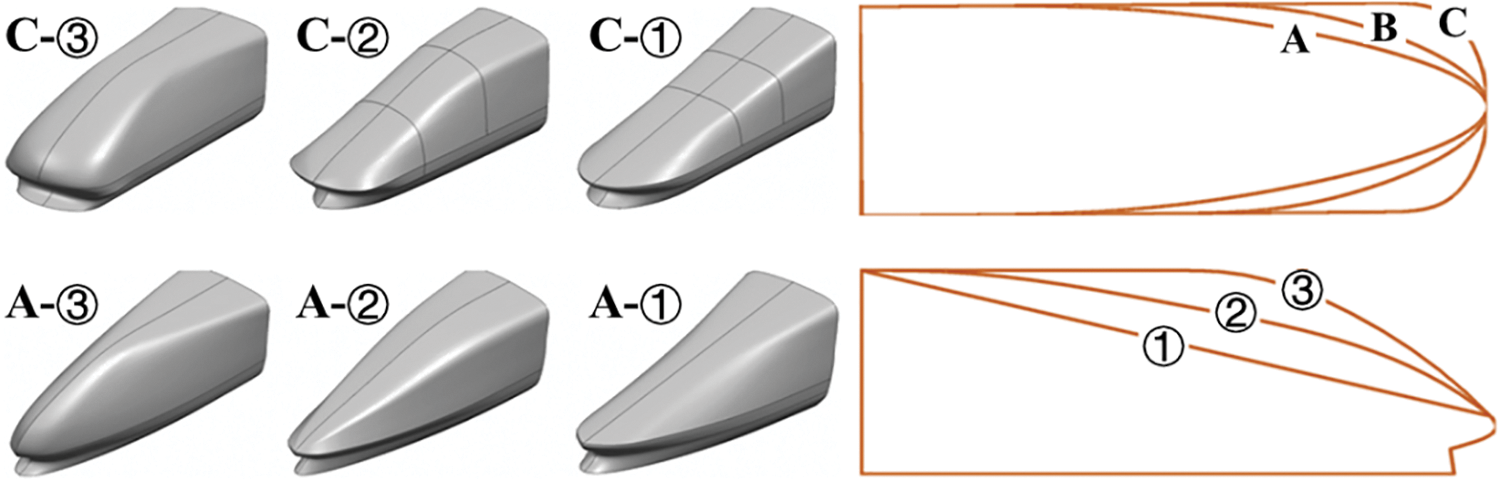
Figure 2: High-speed train noses with different profiles

The early optimization of the train nose shape of the HST is actually “preferable”. Several nose shapes were tested or simulated through wind tunnel tests or numerical simulation methods, and a nose shape with better aerodynamic performance was selected according to the results. This method can only improve the design after selecting a nose shape with relatively good performance from limited samples or improve the design after studying the law between critical parameters and a particular aerodynamic characteristic, which is costly and the design cycle is long. It is necessary to comprehensively consider multiple indicators in HSTs design, such as aerodynamic force, crosswind safety, air pressure pulse from trains passing by each other, tunnel aerodynamic issues, and aerodynamic noise. These objectives may conflict with each other. Therefore, it is difficult to improve the comprehensive performance of trains by using traditional optimization methods. With the development of optimization algorithms, the multi-objective optimization method combined with numerical simulation and surrogate model technology has gradually developed, which can simultaneously take into account multiple aerodynamic characteristics during design, shortening the design cycle and improving optimization efficiency.

3  Parameterization Method of HST Nose Shape

Before the multi-objective optimization process begins, the surface or curve of the HST nose shape needs to be digitally defined, that is, parameterized. The streamlined part of the train nose is composed of free-form surfaces with complex geometric shapes, and the deformation and the transition between adjacent surfaces are relatively large. Therefore, it is crucial to provide a parametric approach that can characterize the curve and surface shape of the nose, as this is what the multi-objective optimization task is based on. There are two types of frequently utilized aerodynamic shape parameterization techniques for the HST nose. The first is the shape-based parameterization method, which enables design without initial shape. The other is the disturbance-based parameterization method, which is appropriate for the design of the existing initial shape.

3.1 Shape-Based Parameterization Method

The shape-based parameterization methods mainly include the analytical method, Non-Uniform Rational B Spline method (NURBS), Class function/Shape function Transformation method (CST), Vehicle Modelling Function method (VMF), etc.

The analytical method expresses the curve by establishing the control equation of the curve. Iida [38] established the two-dimensional cross-sectional profile of the nose shape through the function, took the independent function variable as the parametric variable of the nose, and achieved the purpose of changing the shape by changing the independent variable. Lorriaux et al. [39] established two ellipse portions with five parameters, including two angles and three lengths. The control of the nose shape was realized, such as the nose length, tip taper, and angle, as shown in Fig. 3. The analytical method can accurately describe the geometric shape. Still, it is mainly applied to simple geometric shapes and mainly to two-dimensional models.

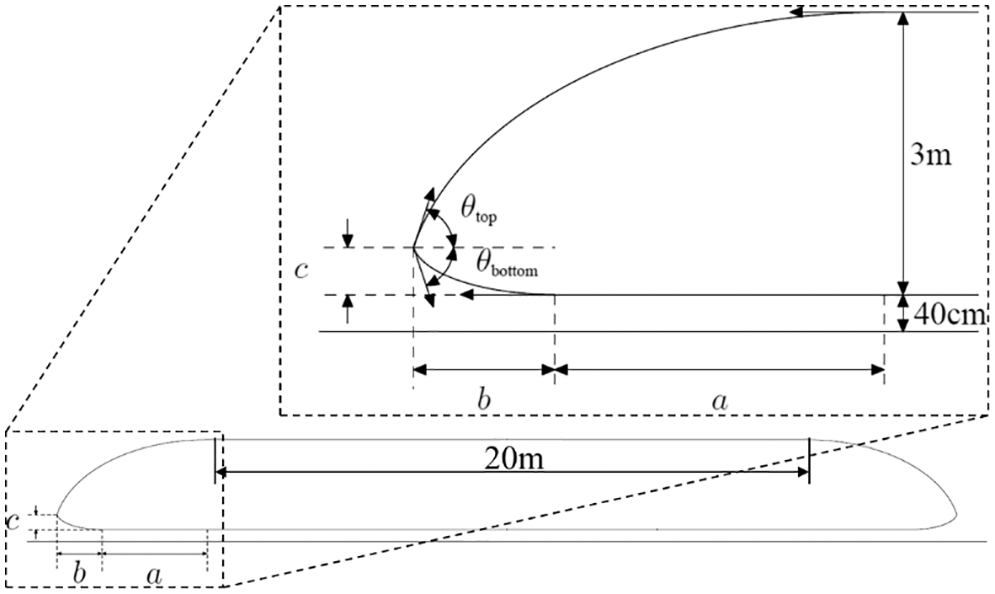
Figure 3: Train nose shape described by elliptic equations

The rational numbers in non-uniform rational B-splines allow NURBS to express precise quadratic and free curves. The curves used to construct surfaces in NURBS have smooth and minimal properties, which can effectively construct various organic 3D shapes [40–42]. Chen et al. [41] applied the NURBS theory in the CATIA software to complete the three-dimensional surface modelling of the CRH1A. The driver’s cab, nose tip, and other parts were improved, and the aerodynamic resistance of the optimized train was reduced by 12.16% compared with the primaeval model. Wang et al. [42] developed a new parametric method that combines the partial differential equation (PDE) and NURBS. The weight deformations and control points of Non-Uniform Rational B Spline surfaces were defined as design variables, and the goal was to minimize the error between the PDE and NURBS surfaces. Furthermore, the study demonstrated the effectiveness of the new modelling approach through examples.

The CST method proposed by Kulfan et al. [43] in 2006 was initially for the shape design of aircraft. A class function (Class) is used to determine the type of airfoil in the CST method, and then the shape function (Shape) is employed as the modification factor. It has the advantages of fewer design parameters and a flexible process to generate simple geometric shapes through analytic function expressions quickly. The original CST method can only describe two-dimensional or quasi-two-dimensional objects, and its ability to express complex surfaces is weak. Su et al. [44] developed a 3D CST geometric modelling method for complex shapes based on Bezier splines. It was applied to the optimal design of unpowered hypersonic gliding reentry vehicles. Liu et al. [45] proposed a mothed based on CST for the hypersonic vehicle, which was adopted to describe the geometric shape. Then, the researchers estimated the aerodynamic force according to the shock wave, and the dynamic features were analyzed compared to the primitive shape using the CST method. Sun et al. [46] implemented the algorithm of the CST method based on the streamlined HST nose shape and established the critical design parameters in the class and shape function, as shown in Fig. 4. Moreover, the CST method was further developed based on the idea of optimal fitting, and the optimized and the practical CST shape are the same in most places.

Figure 4: CST parameterization method

The VMF method expresses the model using Bernstein polynomials and then defines the section function by classifying each subsection. It is a parametric design method proposed by Rho et al. [47] that was first applied to automobile shape design. According to Rho et al. [47], the VMF parametric method improved the efficiency of automobile shape design and optimization. Ku et al. [48] first applied the VMF method to the parametric and optimal design of HST shapes. Four design variables were extracted to control the geometry of the nose shape and carried out multi-objective optimization of the train when the train travelled through the tunnel. The optimal model reduced the maximum micro-pressure wave by 19%, and the aerodynamic drag force was reduced by 5.6%. Yao et al. [49] appropriately modified the VMF parameterization method by using simple functions to describe local shape boundaries. Four main profile lines and two local profile lines were used to control the overall nose shape of the HST. Meanwhile, a separate curved surface controlled the driver's cab, as shown in Fig. 5. Yao et al. [50] combined the VMF parameterization method with the NURBS method. The NURBS method was adopted to make up for the lack of expressive ability of the complex profile of the VMF method. A parametric method that can design any profile line was developed by reasonably setting control points and weights, as shown in Fig. 5. This method was adopted to optimize the aerodynamic resistance of the HST and the aerodynamic lift force of the tail car.

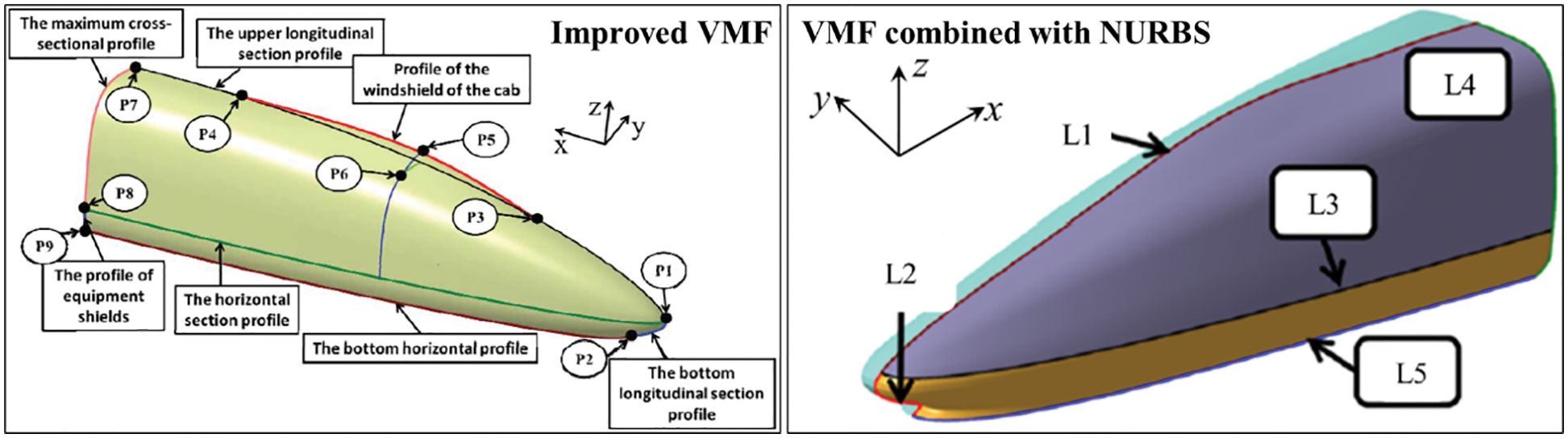
Figure 5: VMF parameterization method

3.2 Disturbance-Based Parameterization Method

The disturbance-based parameterization methods mainly include the Hicks-Henne method, the free-form deformation method (FFD), and the incremental superposition method, etc. Disturbance-based parameterization method generally superimposes the disturbance function on the initial shape to realize the changes, and its function expression is

l=l0+∑i=1nfi(l0)(1)

where l is the changed coordinate, l0 is the initial coordinate, and fi is the basis disturbance function.

The Hicks-Henne method is a disturbance-based parameterization method proposed by Hicks and Henne in 1978 and applied to the optimal aircraft design [51]. The advantage of the Hicks-Henne method is that it is simple in theory and easy to implement, and it can also be parameterized in combination with other disturbance functions. It has an excellent parameterization effect on two-dimensional models, while it has certain limitations on three-dimensional or complex two-dimensional models. Xiong et al. [52] established three-dimensional models of HSTs based on Hicks-Henne functions and studied the impact of shape factors, such as the head vertical contour line, the cowcatcher shape, and the side wing shape, on the aerodynamic performance of HSTs under different operating environments. Kwon et al. [53] and Zhao et al. [54] superimposed the Hicks-Henne method on the basis of Iida [38] and carried out the parameterization of HSTs. The nose shape of the two-dimensional train operating on the open track and travelling through the tunnel was optimized, and obtained the train nose shape with better performance, as shown in Fig. 6 [55]. Lee et al. [56] also employed the Hicks-Henne method to parameterize the two-dimensional train nose shape, as shown in Fig. 6a. The kriging surrogate model was combined with the support vector machine to optimize the micro-pressure wave at the tunnel exit. Optimizing results showed that the optimal nose shape reduced micro-pressure waves over current designs.

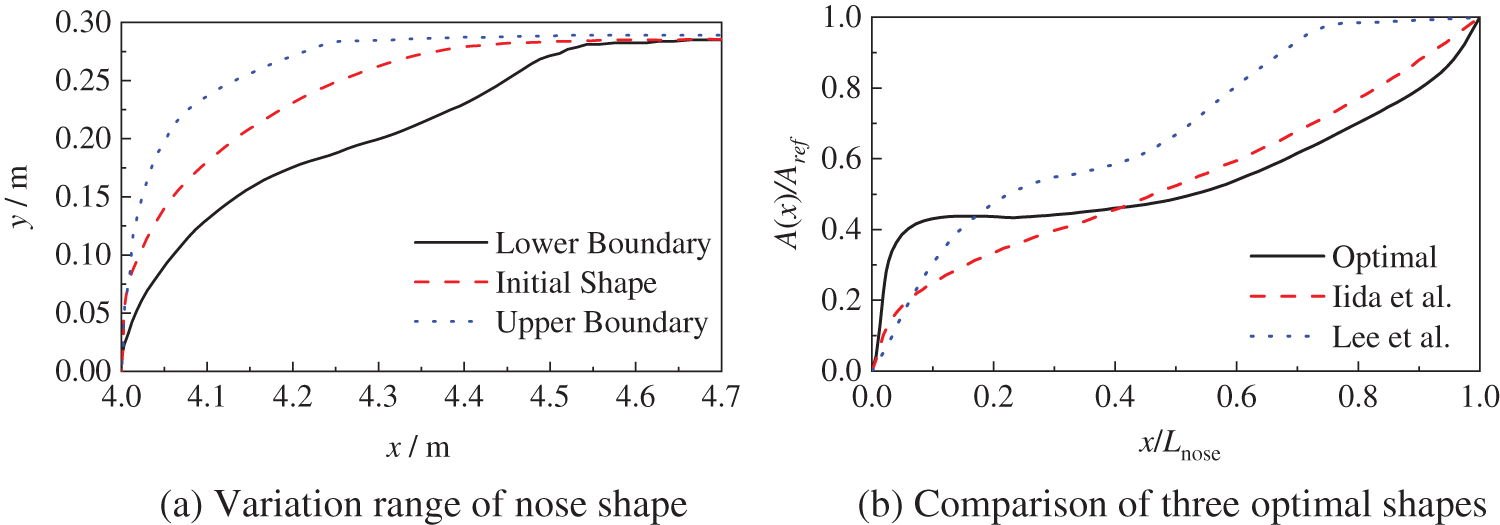
Figure 6: Hicks-Henne parameterization method

The FFD method was proposed by Sederberg in 1986 [57]. A control volume is established around the deformed object, and control points are arranged in the control volume. There is a mapping relationship between the control volume and the control points, and the movement of the control points controls the deformation of the object. This method has a strong deformation ability and can be applied to complex shapes [57]. Li et al. [58] employed the FFD method and five design variables to realize the control of the tip of the nose and the driver’s cab and combined it with the genetic algorithm to optimize the nose shape of the CRH2. The aerodynamic drag force of the whole vehicle and the lift force of the head and tail car in the optimal solution are reduced by 3.6%, 9.6%, and 10.9%, respectively. Zhang et al. [59], Yao et al. [60], Zhang et al. [61], and He et al. [62,63] also adopted the FFD method to parameterize HSTs, including CRH2, CRH380A, and CR400AF, as shown in Fig. 7. And the aerodynamic characteristics such as aerodynamic drag force and lift force of the train are optimized.

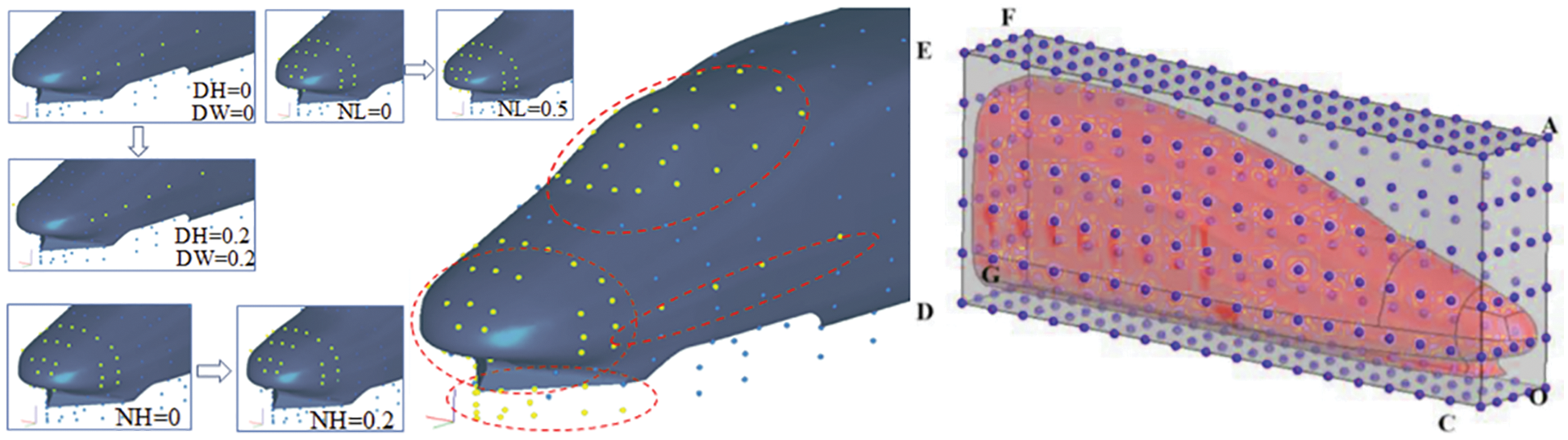
Figure 7: Parameterization of train heads using the FFD method

The primary concept behind the incremental superposition technique is to divide the feature line or feature region on the original shape and define the deformation function and weight factor of each feature separately. The coordinate increment of each feature is then calculated according to the design strategy and the weight factor. Finally, the coordinate value of the deformed shape is obtained by superimposing the original coordinate and the increment. Liu et al. [64] employed the incremental superposition method to parameterize the nose shape of the HST, extracted five design variables and optimized the aerodynamic drag force and dipole noise sources of the train. Yu et al. [65,66] also adopted the incremental superposition method to parameterize the train nose shape, as shown in Fig. 8, and performed optimization on the aerodynamic drag force, lift force, and running safety of the HST. Zhang et al. [67–69] conducted multi-objective optimization on the HSTs and super HSTs using the incremental superposition method, as shown in Fig. 8. The optimization objectives included the aerodynamic resistance of the head car and the whole train, the aerodynamic lift force of the tail car, and the surface acoustic power. The results showed that the parameterization method could improve the optimization efficiency, and the aerodynamic performance of the optimal solution was improved compared with the initial model.

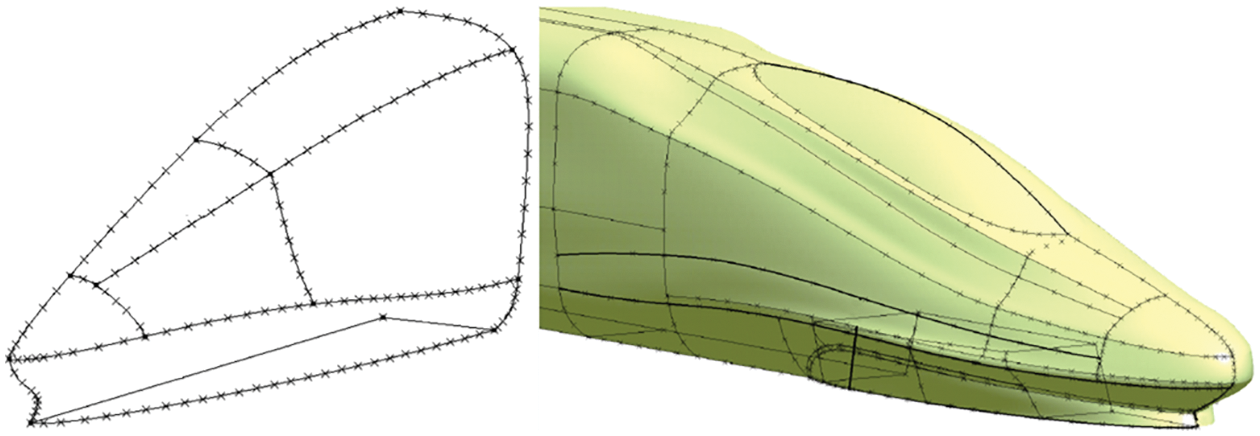
Figure 8: Parameterization of nose shape using the incremental superposition method

4  Multi-Objective Optimization Algorithm and Direct Optimization

One of the key components of train aerodynamic shape optimization is the multi-objective optimization method, the performance of which directly impacts the optimization outcome. Early optimization algorithms, like Newton's method, gradient descent method, quasi-Newton method, etc., were mostly based on gradient algorithms. The aforementioned techniques are effective at locating regionally ideal solutions. The growth of nonlinear and constrained optimization issues gradually draws attention to the drawbacks of local optimization algorithms as optimization problems get more sophisticated. Therefore, the global multi-objective optimization algorithm with intelligent optimization characteristics emerges at the historical moment, such as the genetic algorithm (GA), ant colony algorithm, simulated annealing algorithm, particle swarm algorithm (PSA), etc. [70]. On the basis of multi-objective optimization techniques, a lot of researchers have worked on optimizing the nose shape of HSTs.

4.1 Optimization Algorithm

The multi-objective optimization algorithms applied in the HST aerodynamic optimization mainly include GA, PSA, fish swarm algorithm (FSA), etc. Among them, the Non-dominated Sorting Genetic Algorithms II (NSGA-II) and particle swarm optimization algorithm are widely used. Before introducing commonly used multi-objective optimization algorithms, a brief introduction to the Pareto optimal solution set and the Pareto front is given first.

French Economist V. Pareto proposed the Pareto solution set for multi-objective optimization problems in economics [71]. The sub-objectives often conflict with each other in the multi-objective optimization problem, resulting in the optimal solution being not a single one but a solution set, that is, the Pareto optimal solution set. Correspondingly, the image of the Pareto optimal solution set is called the Pareto front in the objective function space.

4.1.1 NSGA-Ⅱ Algorithm

NSGA-II is an optimization algorithm proposed by Kalyanmoy Deb et al., which uses a non-inferior sorting technique with an elite strategy [72]. It replaces the shared function method by crowding distance comparison. Thus, there is no need to define any parameters for maintaining the diversity of the population. The main difference from the traditional genetic algorithm is that the algorithm is stratified according to the dominant relationship between individuals before the selection operator is executed. The basic idea of NSGA-II is as follows [72]:

1) Randomly generate an initial population of size N and obtain the first-generation offspring population through selection, crossover, and mutation of the genetic algorithm after non-dominated sorting.

2) Merge the parent population with the child population and perform a fast non-dominated sort from the second population. Meanwhile, calculate the crowding degree of individuals in each non-dominated layer, and select appropriate individuals to form a new parent population according to the non-dominated relationship and the degree of crowding of individuals.

3) Generate a new offspring population through the genetic algorithm until the conditions for the end of the program are met.

Among the existing studies, Yao et al. [73] were the first to carry out aerodynamic multi-objective optimization for HSTs using the NSGA-II algorithm. Moreover, Yao et al. [73] improved the traditional algorithm so that crossover and mutation operators could change adaptively. The aerodynamic performances of the CRH380A were optimized, which reduced the drag and lift force by 3.2% and 8.2%. Zhang et al. [67] adopted the basic NSGA-II algorithm to optimize a specific type of HST in China. The initial population was set to 50, the crossover probability was 0.9, and the genetic algebra was 30. The Pareto optimal solution set was obtained. The aerodynamic resistance of the optimal model was reduced by 2.6%, and the lift force of the tail car was reduced by 9.9%. In addition, many scholars have used the basic NSGA-II algorithm to conduct optimization research on HSTs [58,61,65,74–76], which will not be detailed here. It is noteworthy that in the aerodynamic optimization of HSTs, there is also research on improving the NSGA-II algorithm in recent years. Yuan et al. [77] combined the back propagation (BP) neural network with the NSGA-II algorithm to optimize the evolutionary system and adopted the adaptive adjustment mutation operator and the typical distribution crossover operator. The findings revealed that the search space and population adaptability were both optimized, along with a notable acceleration in the search for outstanding members. Therefore, the optimization efficiency was significantly increased.

4.1.2 Particle Swarm Algorithm

Kennedy et al. [78] proposed the particle swarm optimization algorithm in 1995 as an evolutionary technique derived from the study of bird predation behaviour. Particles have only two attributes: velocity v and position x, where velocity represents the movement speed and position represents the movement direction. The basic idea of the particle swarm optimization algorithm is to find the best solution through cooperation and information sharing among individuals in the group [78]:

1) Each particle independently searches for the optimal solution in the search space and records it as the individual extremum Pb at the current moment.

2) Share the individual extremum with other particles in the entire particle swarm and find the optimal individual extremum as the current global optimal solution Gb of the entire particle swarm.

3) All the particles in the particle swarm adjust their speed and position according to the individual extremum Pb and the global optimal solution Gb at the current moment to determine the position at the next moment.

vi,m(t+1)=vi,m(t)+c1r1(Pb(i,m)−xi,m(t))+c2r2(Gb(i,m)−xi,m(t))(2)

xi,m(t+1)=xi,m(t)+vi,m(t+1)(3)

where i = 1, 2, …, I, I is the number of particles; m = 1, 2, …, M, M is the design space dimension; c1 and c2 are learning factors; r1 and r2 are random numbers in the range (0, 1).

Zhang et al. [59] employed the essential PSA to carry out the aerodynamic optimization design of HSTs nose. The optimization algorithm was verified first through the classic multi-objective optimization test function. Then the nose shape of the HST was parameterized using the FFD method, and the design space was 16-dimensional. The results of the test function and aerodynamic optimization of trains showed that the particle swarm optimization algorithm had excellent optimization ability. Many researchers have carried out aerodynamic multi-objective optimization on HSTs using the basic particle swarm optimization algorithm [50,79]. Compared with the single-objective PSA, the particle swarm multi-objective algorithm is different in that it obtains a set of optimal solution sets, and how to select the optimal particles in the solution set is particularly critical. Many scholars have recently improved the existing PSA to improve optimization efficiency. Yao et al. [49] proposed a method to determine the optimal historical particle by using the crowding distance and niche count and making it exist in the area where the particles are relatively sparse in the design space. The results showed that the algorithm constructed based on the crowding distance had a strong optimization ability, especially for high-dimensional problems. He et al. [63] proposed a new particle swarm optimization algorithm combined with an artificial fish swarm algorithm (AFSA), which incorporated the advantages of the fast convergence speed of the FSA. Meanwhile, the backward learning strategy was used for the population initialization of the algorithm, to start the entire population search from a better starting point. The PSA has also received updates and improvements in other fields [80–82], which will not be discussed here. In short, improving the optimization algorithm is an important research direction in the current aerodynamic shape optimization, as well as a way to improve the optimization efficiency further.

4.1.3 Other Optimization Algorithm

In the HST aerodynamic optimization field, there are many other multi-objective optimization algorithms, such as GA, AFSA, ant colony algorithm, and so on. Mohebbi et al. [83] established the two-dimensional HST and windbreaks using the Lattice Boltzmann Method (LBM). The multi-objective genetic algorithm (MOGA) was adopted to optimize the position, height, and angle of the windbreaks. The design space was 4-dimensional, and the optimization objectives included the aerodynamic lateral force, lift force, and roll moment. A windshield model with excellent performance was obtained, and the wind tunnel test was used to verify it. Sun et al. [84] employed the multi-objective genetic algorithm Ⅱ (MOGA-Ⅱ) to optimize. Compared with traditional algorithms, MOGA-Ⅱ introduced a multi-directional search optimization operator, which searches for the optimal global solution more efficiently while guaranteeing the optimal solution of the parent. Muñoz-Paniagua et al. [18,85] conducted optimization for the tunnel pressure wave, lateral stability, and aerodynamic resistance using the GA under the conditions of the train travelling through the tunnel, the train passing each other, as shown in Fig. 9. The multi-objective optimization and the acquisition of the Pareto front solution set are carried out using MATLAB®. Scholars such as Xu et al. [86] also used a genetic algorithm to optimize the aerodynamic characteristics of HSTs.

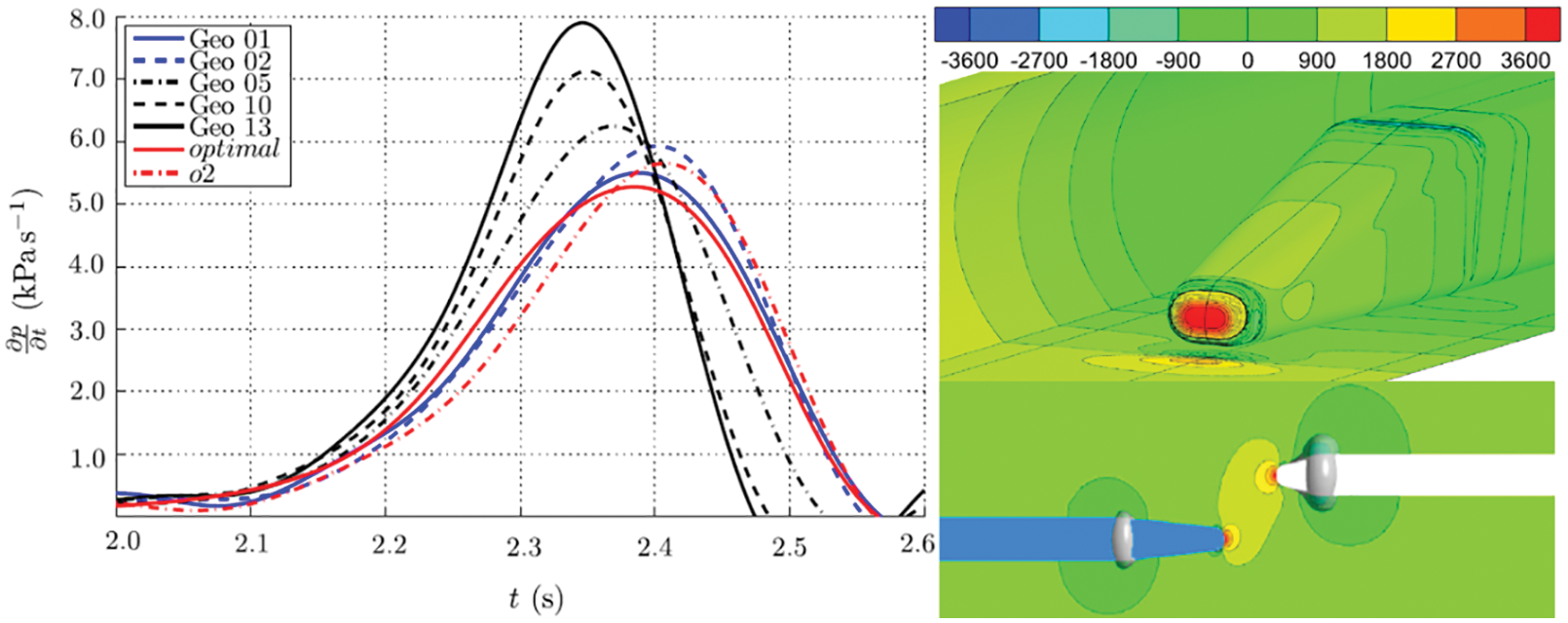
Figure 9: Optimization results of Muñoz-Paniagua

The traditional AFSA algorithm increases the detection range of fish with the visual range, which is conducive to exploring tailing and clustering behaviour. On the contrary, the search will be too detailed if the visual range is small, and it is easy to be limited to the local optimum. Yang et al. [87] combined polynomials to propose an adaptive field of view artificial FSA, which can improve search accuracy and convergence speed. The multi-objective test function and optimization results of the HST proved that improved AFSA using an adaptive method has higher optimization efficiency. Zhang et al. [88] carried out multi-objective optimization on the train aerodynamics after improving the ant colony algorithm. There is no mutation mechanism for the optimal individual obtained in the iteration in the construction process of the traditional ant colony algorithm, resulting in apparent local extremum characteristics, and it is easy to make the multi-objective optimization fall into the local optimum. Zhang et al. [88] developed a multi-objective chaotic ant colony algorithm by introducing the chaotic mutation mechanism and niche-sharing technology. The chaos model was used to initialize in the population initialization stage, and the chaos model was used to generate random disturbance when the pheromone was updated. Research results showed that the time for the individual to converge to the optimal value is reduced, and the efficiency is improved. Meanwhile, the disturbance of the chaotic model can prevent the optimization from falling into a local optimum. In addition to the above-mentioned multi-objective optimization algorithms, Suzuki et al. [89] adopted the basic evolutionary algorithm to optimize the aerodynamic drag force of the HST and the pressure fluctuation around the car body. Zhou et al. [90] employed the multi-island genetic algorithm to optimize the aerodynamic force of the HST, and the design variables include six characteristics of the nose shape.

Many optimization algorithms are used in the aerodynamic multi-objective optimization of HSTs, but most scholars rarely carry out optimization using standard algorithms. The primary development trend at the moment is to improve optimization algorithms with specific working conditions. Second, the calculation amount of HST numerical simulation is gradually increasing with the improvement of engineering and scientific research accuracy requirements, making calculation costs and time-consuming problems more prominent. Therefore, improving the optimization efficiency of the multi-objective optimization algorithm is also a goal that academics strive for and pursue.

4.2 Direct Optimization Based on the Optimization Algorithm

The advancement of the optimization algorithm allows for the simultaneous consideration of multiple aerodynamic performance parameters when optimizing the train nose shape. There are two main types of multi-objective optimization design for HSTs. The first is to parametrically model the HSTs and generate various nose shape models by changing the design variables. Then, results of the aerodynamic drag force, lift force, noise, etc., are obtained through the numerical simulation after the model is divided into grids. The multi-objective optimization algorithm is used for optimization calculations until convergence, and a better performing HST model is obtained. The optimization process is shown in Fig. 10.

Figure 10: Flow chart of multi-objective aerodynamic optimization for the HST

Direct optimization using multi-objective optimization must be performed on an integrated platform. The platform generates a model through parametric modelling when the samples of the next generation or the following position are obtained from optimization. The grid is then generated automatically, and the numerical simulation is run to extract the results. Otherwise, the optimization efficiency will be greatly decreased if the intermediate process is artificially manipulated. Liu et al. [64] integrated CATIA, ICEM, and FLUENT to build a multi-objective optimization platform for HST nose shapes using the Isight® software. Parametric modelling is realized through CATIA macro commands. Then, grid generation and numerical simulation are performed by ICEM and FLUENT, respectively. Moreover, a coupler is built to exchange and transfer data in the middle process. Five control lines of nose shape are selected as the design variables, and the optimization goal is to minimize the aerodynamic resistance and dipole noise source of the train. The multi-objective automatic optimization design of the HST was carried out using the optimized design platform, and the optimization effect is remarkable. Compared with the original train, the aerodynamic resistance of the optimal model is reduced by 4.5%, and the noise is reduced by 5.0 dB. Li et al. [76] built a multi-objective optimization platformto optimize the nose height, slenderness ratio, and longitudinal profile of the train nose shape. The aerodynamic drag forces and the absolute value of lift forces were taken as the optimization objectives, and the NSGA-Ⅱ algorithm was employed for optimization design. Finally, the aerodynamic shape of the HST nose with better all-around performance was obtained. The software integration method is shown in Fig. 11. Zhang et al. [68,69] established an efficient multi-objective aerodynamic optimization design platform to carry out design for the streamlined nose shape. The main control points and lines (C1~C5) of the train nose, include the nose tip, driver's cab, and cowcatcher, to reduce the aerodynamic resistance of the train when it is running at super high speed, as shown in Fig. 8b. Meanwhile, the running safety of the HST in a crosswind is improved through optimization. Yu et al. [91] also adopted a similar approach for multi-objective optimization of the nose shape. Five design variables were extracted to optimize the aerodynamic resistance and wheel load reduction rate. The optimal scheme could reduce the aerodynamic resistance by up to 4.2% and the wheel load reduction rate reduced by up to 1.7%. Sun et al. [84] adopted the modeFRONTIER multi-objective optimization platform to integrate SCULPTOR and FLUENT. SCULPTOR was used for mesh deformation, FLUENT was employed for numerical simulation, and the optimization algorithm adopted MOGA-II of modeFRONTIER. The nose shape of CRH3 was optimized with four variables: nose height, nose forward, nose thickness, and nose top channel. The optimization objective is the aerodynamic resistance of the vertical vehicle.

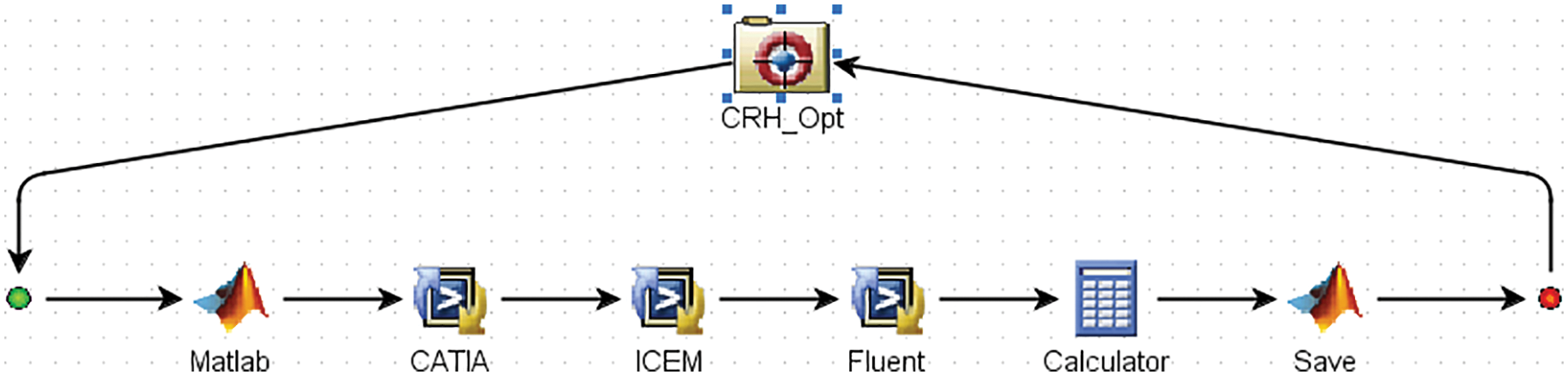
Figure 11: Multi-objective optimization platform for HSTs

Direct optimization utilizing multi-objective optimization algorithms typically needs numerous samples and dozens or even hundreds of iterations to converge. The massive scale and intricate geometry of the HST geometric model result in a high computational cost for numerical simulation, which lengthens the optimization cycle. Meanwhile, the direct optimization strategy strongly depends on the optimization algorithm. The performance of the algorithm directly determines the convergence speed and optimization results of the multi-objective optimization. If the optimization algorithm is poor, it is more likely to fall into the local optimum or even diverge. Therefore, several researchers started investigating aerodynamic multi-objective optimization utilizing surrogate models that were motivated by aerodynamic optimization in other domains.

5  Multi-Objective Optimization Using Surrogate Model

Aerodynamic multi-objective optimization employing a surrogate model emerges as a solution to the optimization cost issue and proves to be extremely effective at reducing the length of the optimization design cycle. The surrogate model was initially applied to the structural optimization, and the response surface model was mainly used. It penetrated the field of aerodynamic optimization design after the advent of multidisciplinary design [92].

5.1 Surrogate Models with More Applications

The radial basis model (RBF), Kriging model, neural network, and support vector regression (SVR) are widely used in aerodynamic multi-objective optimization [93–95]. In the field of HSTs aerodynamic optimization, the Kriging model, neural network and SVR model are mainly used.

5.1.1 Kriging Surrogate Model

The establishment of the standard Kriging surrogate model is as follows:

The design variables of the optimization problem are

x={x(1),x(2),⋅⋅⋅,x(n)}T(4)

The basis function of the Kriging model is [96]

ψ=exp⁡(−∑j=1kθj|xj(i)−xj|2)(5)

where k is the number of variables; θ is the weight, and the bandwidth of the basis function can be changed.

The actual response to the optimization problem is

y={y(1),y(2),⋅⋅⋅,y(n)}T(6)

Assuming the response comes from a random process, its expression is

Y=(Y(x(1)),Y(x(2)),⋅⋅⋅,Y(x(n)))T(7)

The correlation between random variables is correlated with each other using basis functions, and the relationship is as follows [96]:

cor[Y(x(i)),Y(x(l))]=exp⁡(−∑j=1kθj|xj(i)−xj(l)|2)(8)

According to the correlation relationship between variables, the correlation matrix of all observation points is established

Ψ=(cor[Y(x(1)),Y(x(1))]⋅⋅⋅cor[Y(x(1)),Y(x(n))]⋮⋮cor[Y(x(n)),Y(x(n))]⋅⋅⋅cor[Y(x(n)),Y(x(n))])(9)

Then for an unknown vector, its response value can be expressed as [96]

y^(x′)=μ^+ΨTΨ−1(y−1μ^)(10)

where φ is the correlation vector between the point x and the prediction point x', the expression of φ is

φ=(cor[ Y(x(1)),Y(x′) ]⋮cor[ Y(x(n)),Y(x′) ])=(φ(1)⋮φ(n))(11)

μ^ is the mean of the random process

μ^=1TΨ−1y1TΨ−11(12)

In addition to the standard Kriging model, the Gradient-Enhanced Kriging (GEK), Co-Kriging model, Hierarchical Kriging (HK), etc., are widely used in the field of aircraft aerodynamic optimization design [97].

5.1.2 Neural Network Surrogate Model

A neural network is an operational model composed of a large number of nodes, and the specific output function of each node is called an activation function σ. The connection between nodes represents a weighted value for the signal passing through the connection, called weight W. The output of the network is different due to the different connection methods, weights, and activation functions [98–100]. The loss function is a non-negative real-valued function, which can quantify the gap between the network output and the real target, and plays a vital role in the neural network training process. The neural network usually approximates a particular algorithm or function, and the training process roughly includes forward propagation, error backpropagation, and weight update [99–101].

The neural network model contains input, hidden, and output layers. Meanwhile, each layer is composed of multiple neurons. The sample is defined as (x, y), and the input vector is x = (x1, x2, …, xm)T, where m is the dimension of the input layer. The output vector is f = (f1, f2, …, fc)T, where c is the dimension of the output layer. Assuming that the kth (k = 1, 2, ..., L) hidden layer contains nk neurons, the corresponding hidden layer vector is h=(h1, h2,…, hk)T. Wk=(wijk)nk×nk−1 and WL+1=(wijL+1)c×nL are weight matrixes between the (k-1)th hidden and kth hidden layer, the Lth hidden and output layer, respectively. After then, the output of each layer is

{h1=σh1(W1x+a1)hk=σhk(Wkhk−1+ak)f=σc(WL+1hR+aL+1)(13)

where a is the offsets, σ is the activation functions [102].

The mean square error E=12∑‖f−y‖2 is adopted as the loss function. The weight W and the offset a are continuously updated until the E no longer changes [102].

Wk=Wk−η∂E∂Wk(14)

ak=ak−η∂E∂ak(15)

The value of the loss function is only related to the weight W and offset a in the network. The loss of the network depends entirely on the structural parameters of the network. Determining the optimal state of the neural network is equivalent to finding the neural network parameters that minimize the loss function [99–101].

5.1.3 SVR Surrogate Model

Support vector machine is a learning system proposed by Vapnik [103] based on the principle of structural risk minimization using a linear function hypothesis space in a high-dimensional feature space. The SVR model achieves effective conduction reasoning from training samples to prediction samples by avoiding the conventional approach from induction to a deduction. The SVR model needs to define a loss function, which can ignore the error within a specific range of the actual value, that is, the ε insensitive loss function [103,104].

The sample set is (xi, yi), i = 1, 2, …, n. For the nonlinear regression problem, the SVR uses the nonlinear mapping Φ to map the data to the high-dimensional feature space and then performs linear regression in the high-dimensional feature space. According to the theory of functional correlation, as long as a kernel function K(xi, xi) is found to satisfy the Mercer condition and make K(xi, xi) ⩽ {Φ(xi) · Φ(xj)}, the nonlinear transformation can be realized linear regression of [105]. The dual form of the optimization problem is [104]

L(αi,βi)=ε∑i=1n(αi+βi)−yi∑i=1n(αi−βi)+12(αi−βi)(αj−βj)K(xi⋅xj)(16)

subject to constraints

∑i=1nαi=∑i=1nβi,0≤αi≤Cn,0≤βi≤Cn,i=1,…,n(17)

where C is the penalty parameter, α and β are Lagrangian multipliers.

The regression estimation function is [104]

f(x)=∑i=1n(αi−βi)K(xi⋅x)+b(18)

The bias term b is given by

b=yj−∑i=1n(αi−βi)K(xi⋅xj)(19)

The above is the standard SVR model, and there are further developed models on this basis [106,107]. Shao et al. [107] proposed ε-twin support vector regression (ε-TSVR) in 2013. Compared with standard SVR and TSVR [106], it has higher accuracy under the premise of shorter training time, especially for nonlinear problems.

5.2 Construction Methods of Surrogate Models

According to the construction method used in the aerodynamic optimization process, there are two groups of surrogate models. Construction Directly: Surrogate model is constructed using the samples obtained from sampling directly without updating. Construction Iteratively: Samples are obtained by sampling as the initial sample set to establish the initial surrogate model. Then the model is iterated by adding samples until the training results satisfy the predetermined criteria.

5.2.1 Construction Directly

Muñoz-Paniagua et al. [18] optimized the pressure wave and the aerodynamic resistance when the train travelled through the tunnel. Experiments (DOE) were conducted using the Latin Hypercube Design (LHD) method, and 15 samples were drawn to build a neural network surrogate model. The prediction error of the surrogate model was less than 4%. Finally, the genetic algorithm is employed to perform multi-objective optimization using the neural network surrogate model, and an HST model with better all-around aerodynamic performance was obtained. The paper also conducted a sensitivity analysis of design variables based on the surrogate model. The same method was also adopted to optimize running stability in the crosswind and pressure pulse from trains passing by each other [85]. Ku et al. [28] established a response surface model based on different lengths of the streamlined nose to optimize the micro-pressure wave at the tunnel exit. The Broyden Fletcher Goldfarb Shanno (BFGS) algorithm was employed, which reduced the micro pressure wave by 18%~27%. Li et al. [58] established a Kriging model with 26 samples and verified the accuracy of the surrogate model by cross-validation mothed. The results showed that the prediction error of the aerodynamic drag of the whole train was about 6.0%, and the prediction error of the aerodynamic lift force of the tail car was the largest. Then, the NSGA-Ⅱ algorithm was employed to carry out multi-objective optimization using the Kriging model, and the aerodynamic drag force of the HST was reduced by 3.6%. Zhang et al. [88] established an SVR model with 20 samples in combination with the VMF parameterization method, involving five design variables and two optimization objectives. Two samples were selected as the verification set. If the prediction error of the surrogate model was larger than 5%, the hyperparameters C, ε, etc., of the SVR model were optimized until the error standard was satisfied. The aerodynamic drag and aerodynamic lift force of the optimal solution are obtained through optimization reduced by 10.5% and 35.7%, respectively. Yuan et al. [77] carried out multi-objective aerodynamic optimization of HSTs through the neural network surrogate model, but the method is similar to Zhang et al. [88]. The neural network parameters were updated until the model prediction error satisfied the preset requirements.

The advantage of directly constructing the surrogate model is that there is no need to increase the sample size to retrain the model repeatedly, and the steps are relatively simple. It does, however, have some drawbacks. For example, the prediction accuracy of the surrogate model cannot be guaranteed, which may affect the optimization results. Using a fixed validation set to test whether the prediction accuracy of the updated surrogate model satisfies the requirements may lead to the high prediction accuracy of the model only at this position. The accuracy of the optimal solution, on the other hand, cannot be guaranteed. Therefore, many scholars improve the robustness of the surrogate model by adding additional samples, particularly near the optimal solution, which significantly improves the efficiency of multi-objective optimization.

5.2.2 Construction Iteratively

Vytla et al. [108] defined the Expected Improvement Value (EIV) parameter and used 55 sample points to establish the initial surrogate model. If the EIV of the optimal solution obtained by optimization did not meet the requirements, then added two samples and built the next generation model until the EIV requirements were satisfied. Finally, the relationship between the five design variables and the optimization objectives was established through the Kriging surrogate model, and the aerodynamic resistance and aerodynamic noise of the HST were optimized using the hybrid Genetic Algorithm and the Particle Swarm Optimization (GA-PSO) algorithm. Muñoz-Paniagua et al. [109] employed the DOE method to expand the sample design space according to the optimization results and added the samples to update the surrogate model after obtaining the union set, as shown in Fig. 12. Yao et al. [50] established the standard SVR model using 66 initial samples and selected six samples in the Pareto solution set for verification. One of the verification points did not meet the requirements, so researchers added 30 samples to the initial sample set and established a second-generation model, which achieved excellent results. Unfortunately, the paper did not introduce the selection method of 30 samples. The cross-validation technology was adopted to establish the Kriging model [86], and the prediction error was used as the evaluation criterion. If the preset requirements were not met, the samples in the optimized solution set would be added to the sample set to establish the next-generation surrogate model. Still, the paper did not detail select samples from the Pareto solution set. Yao et al. [49,60,73,110] adopted initial samples to establish standard Kriging or cross-validation Kriging (CV-Kriging) models and took the preset samples or samples of the Pareto front set for verification. The limit of the prediction error was defined as the aerodynamic drag and lift force less than 1% and 5%, respectively. The samples of the Pareto front set were added to the sample set to establish the next-generation Kriging model if the accuracy of the model cannot satisfy the requirements simultaneously, as shown in Fig. 13. In addition, literature [61,63,67,87] also adopted a similar method of adding samples, selecting points from the Pareto front set for verification, and adding them to the sample set if the accuracy does not satisfy the preset criteria.

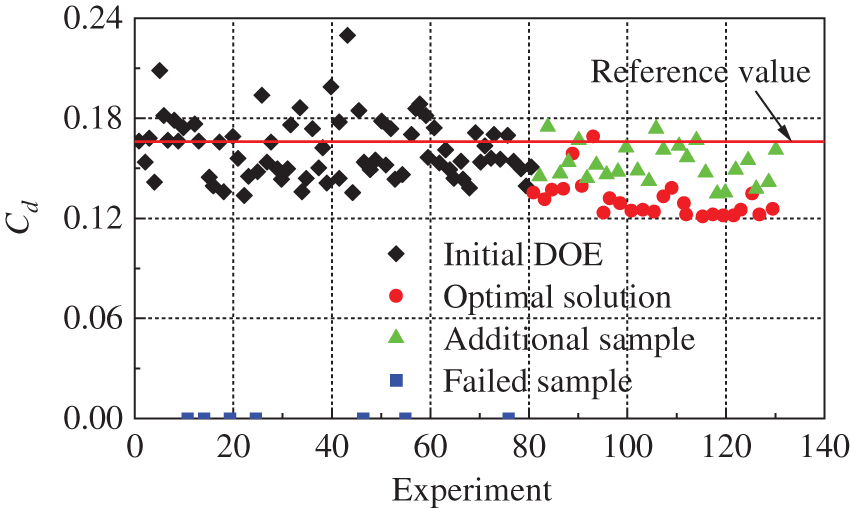
Figure 12: The samples distribution of literature

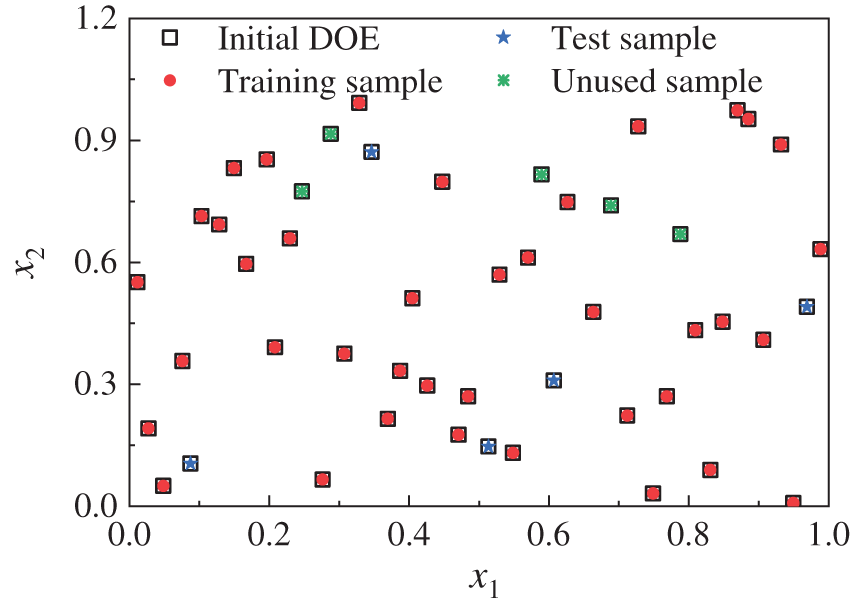
Figure 13: The samples distribution of literature

Selecting the points from the Pareto front set is a method that is widely used and works well at present, which can make the model converge to the optimal solution faster and improve the optimization efficiency. However, how to effectively select one or more samples to add to the sample set, the sample infill criterion, is crucial. Yao et al. [79] introduced a sample infill criterion in the multi-objective aerodynamics of the HST. For the selection of the optimal one, the sample with a balanced aerodynamic drag force of the whole train and the aerodynamic lift of the tail car is preferred. Zhang et al. [111,112] further proposed a sample infill criterion, which selected the best point of each objective in the Pareto solution set for verification and added it to the training set to update the agent if the prediction error was too large. Dai et al. [113] defined the calculation method of comprehensive optimization rate T. The comprehensive optimization rate of all points in the Pareto front solution set was obtained and taken the largest one as the added sample. This sample infill criterion could give the surrogate model higher accuracy in the optimal position of the preferred target and be more conducive to finding the desired optimal solution.

In addition to adding samples in the Pareto front set, there are minimizing the response surface criterion and maximizing the expectation criterion. The latter is widely used in constructing the Kriging model because it can predict the variance of unknown points. Some scholars are also exploring other sample infill criteria for constructing surrogate models in the field of aerodynamic optimization of HSTs. Sun et al. [74] proposed a two-point infill criterion based on the improvement of the research of Gao et al. [114]. The genetic algorithm was employed to search the global forecast standard deviation, and the two points with the largest forecast standard deviation were obtained as adding points. The surrogate model was updated until the preset requirements were satisfied.

The optimization results of the aerodynamic optimization design using the surrogate model are heavily reliant on the prediction accuracy of the model, and a reasonable sample infill criterion can improve the model accuracy and facilitate the convergence of multi-objective optimization. It is also one of the most active research areas, with the goal of developing and proposing a sample infill criterion suitable for aerodynamic multi-objective optimization of HSTs.

5.3 Aerodynamic Multi-Objective Optimization in the Field of Aircraft

Aerodynamic multi-objective optimization in the field of aircraft is the most recent development, and there are more mature research methods and technologies. Laurenceau et al. [115] adopted the Kriging model, the direct GEK model, and the indirect GEK model to predict the aerodynamic force of the RAE2822 airfoil. The research showed that the prediction accuracy of the two GEK models is better than that of the standard Kriging model under the same number of sample points. Han et al. [116] and Chen et al. [117] employed the GEK model to carry out aerodynamic optimization design on ONERA M6 and NACA0012 and obtained airfoils with better aerodynamic performance. Compared with the standard Kriging and quasi-Newton method models, the GEK model had more advantages in terms of convergence speed and optimization results. Shu et al. [118] found that the accurate judgment of the dominance state between the non-dominated solutions in the late stage of optimization greatly influenced the convergence efficiency of the multi-objective optimization algorithm. Then the two-stage update strategy was proposed to reduce the high cost of optimization, which reduced the number of high-precision samples required.

Further, low-fidelity and high-fidelity sample data were introduced to establish a multi-fidelity surrogate model in order to improve the efficiency of optimization and alleviate the curse of dimensionality in the refined aerodynamic design of aircraft. The low-fidelity samples are used to model the changing trend of the characterizing function in the multi-fidelity model, and a small number of high-fidelity samples are adopted for correction, thereby reducing the number of high-fidelity samples required to construct an accurate surrogate model and improving efficiency [119]. The multi-fidelity surrogate construction methods mainly use the scale function, the space map, and the HK model. Han et al. [120] developed a multi-level hierarchical Kriging (MHK) based on the two-level Kriging model. The recursive method was adopted to build Kriging models with different degrees of fidelity from lower to higher until the last level was completed. The MHK optimization efficiency had been further improved compared with the two-level HK model. Some results are shown in Fig. 14. Zhou et al. [121] proposed an individual update strategy considering the estimation uncertainty of multi-fidelity surrogate models and a population update strategy considering the degree of optimization solution dispersion, effectively reducing the cost of optimization. Han et al. [120] and Abdallah et al. [122] carried out aerodynamic multi-objective optimization on NACA0012 and separated turbine blades using the HK model. The results showed that the HK model could overcome the shortcomings of the traditional Kriging model with low global accuracy and the prediction accuracy of the HK model is higher.

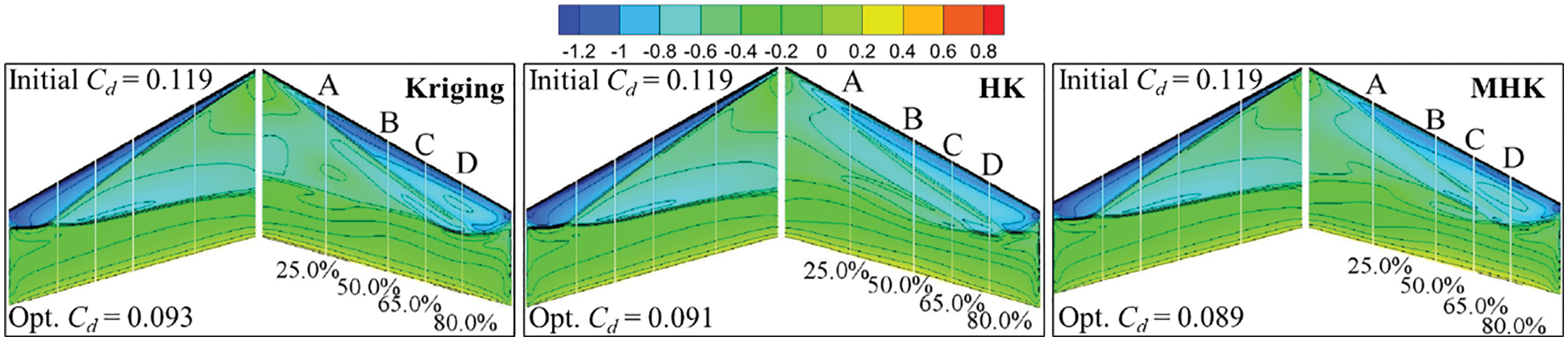
Figure 14: Comparison of pressure distributions obtained from different methods

The geometric shape of HSTs is relatively complex compared with most aircraft. The complex shape dramatically increases the number of grids, and the numerical simulation scales are generally larger than that of aircraft. In the field of aerodynamic optimization for HSTs, most studies optimize the nose shape of HSTs to improve the comprehensive aerodynamic performance using the standard Kriging model. The optimization efficiency is slightly lower than the GEK and HK models widely used in the aircraft field. Therefore, it is urgent to develop a more efficient and convenient parameterization method for dealing with complex shapes and introduce more efficient Kriging methods to optimize the nose shape of HSTs.

6  Conclusion and Outlook

The research status and progress of aerodynamic multi-objective optimization of HSTs, including the parameterization method, multi-objective optimization algorithm, calculation method, and surrogate model technology, are summarized. Overall, there are numerous methods for multi-objective aerodynamic optimization of HSTs, the majority of which achieved significant effects. Based on the research overview provided above, the multi-objective aerodynamic optimization of HSTs warrants further investigation in the following directions:

(1) The current multi-objective aerodynamic optimization design relies on the user’s experience to select the characteristic parameters of the train nose shape to reduce the calculation scale of the optimization problem. As a result, the design space is limited, and the nose shape with relatively large deformation and its aerodynamic performance cannot be achieved. It is possible to study and develop intelligent identification technology for the characteristic parameters of the HST nose shape, to broaden the range and interval of design variables, and to explore the potential of nose shape optimization in the broader spectrum.

(2) The multi-objective aerodynamic optimization of the HST nose shape focuses primarily on the train aerodynamic force and noise in the open air, with less involvement in other operating environments. However, the operating environments of the HSTs are complex and changeable, and it is preferable to avoid situations in which the aerodynamic performance is excellent in one operating condition but poor in another. Therefore, multi-objective aerodynamic optimization of HSTs in multiple operating environments should be regarded as one of the important research directions.

(3) The prediction accuracy of the surrogate model has a large impact on the optimization results of the aerodynamic optimization design using the surrogate model. Meanwhile, the surrogate model is an interpolation technique, and increasing the samples reasonably can effectively improve the accuracy of the model. Therefore, developing the sample infill criteria is a worthwhile research direction to improve the accuracy of the surrogate model and the efficiency of multi-objective optimization, particularly for problems requiring large-scale numerical simulations such as multi-objective aerodynamic optimization of HSTs.

(4) Most studies carry out aerodynamic optimization using the standard surrogate model in the field of HSTs, which is relatively backward compared with the earlier application of aerodynamic multi-objective optimization in the aerospace industry. To improve the efficiency of aerodynamic optimization, it is necessary to learn from efficient optimization strategies in the field of aircraft and develop efficient parameterization and optimization methods in combination with the particularity of HST.

Funding Statement: This project was supported by the Sichuan Science and Technology Program (2023JDRC0062), National Natural Science Foundation of China (12172308) and Project of State Key Laboratory of Traction Power (2023TPL-T05).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Givoni, M. (2006). Development and impact of the modern high-speed train: A review. Transport Reviews, 26(5), 593–611. https://doi.org/10.1080/01441640600589319 [Google Scholar] [CrossRef]

2. Takatsu, T. (2007). The history and future of high-speed railways in Japan. Japan Railway & Transport Review, 48, 6–21. [Google Scholar]

3. Woodward, P. K., El-Kacimi, A., Laghrouche, O., Medero, G. (2012). Breaking the ground speed barriers for ultra speed trains: Rayleigh ground wave modelling and mitigation. International Journal of Railway Technology, 1(1), 105–119. https://doi.org/10.4203/ijrt.1.1.5 [Google Scholar] [CrossRef]

4. Zhou, L., Shen, Z. (2011). Progress in high-speed train technology around the world. Journal of Modern Transportation, 19(1), 1–6. https://doi.org/10.1007/BF03325733 [Google Scholar] [CrossRef]

5. Tian, H. Q. (2019). Review of research on high-speed railway aerodynamics in China. Transportation Safety and Environment, 1(1), 1–21. https://doi.org/10.1093/tse/tdz014 [Google Scholar] [CrossRef]

6. Baker, C. J. (2014). A review of train aerodynamics Part 1-Fundamentals. The Aeronautical Journal, 118(1201), 201–228. https://doi.org/10.1017/S000192400000909X [Google Scholar] [CrossRef]

7. Yu, M., Jiang, R., Zhang, Q., Zhang, J. (2019). Crosswind stability evaluation of high-speed train using different wind models. Chinese Journal of Mechanical Engineering, 32(1), 1–13. https://doi.org/10.1186/s10033-019-0353-7 [Google Scholar] [CrossRef]

8. Rashidi, M. M., Hajipour, A., Li, T., Yang, Z., Li, Q. (2019). A review of recent studies on simulations for flow around high-speed trains. Journal of Applied and Computational Mechanics, 5(2), 311–333. [Google Scholar]

9. Shen, Z. Y. (2006). Dynamic environment of high-speed train and its distinguished technology. Journal of the China Railway Society, 28(4), 1–5. [Google Scholar]

10. Li, T., Dai, Z. Y., Liu, J. L., Wu, N., Zhang, W. H. (2021). Review on aerodynamic drag reduction optimization of high-speed trains in China. Journal of Traffic and Transportation Engineering, 21(1), 59–80. [Google Scholar]

11. Li, T., Liang, H., Zhang, J., Zhang, J. Y. (2023). Numerical study on aerodynamic resistance reduction of high-speed train using vortex generator. Engineering Applications of Computational Fluid Mechanics, 17(1), e2153925. https://doi.org/10.1080/19942060.2022.2153925 [Google Scholar] [CrossRef]

12. Yu, M., Liu, J., Zhang, Q., Dai, Z. (2022). Unsteady aerodynamic characteristics on trains exposed to strong wind and rain environment. Journal of Wind Engineering and Industrial Aerodynamics, 226(7), 105032. https://doi.org/10.1016/j.jweia.2022.105032 [Google Scholar] [CrossRef]

13. Li, T., Dai, Z., Zhang, W. (2020). Effect of RANS model on the aerodynamic characteristics of a train in crosswinds using DDES. Computer Modeling in Engineering & Sciences, 122(2), 555–570. https://doi.org/10.32604/cmes.2020.08101 [Google Scholar] [CrossRef]

14. Liang, H., Sun, Y., Li, T., Zhang, J. (2023). Influence of marshalling length on aerodynamic characteristics of urban emus under crosswind. Journal of Applied Fluid Mechanics, 16(1), 9–20. [Google Scholar]

15. Rabani, M., Faghih, A. K. (2015). Numerical analysis of airflow around a passenger train entering the tunnel. Tunnelling and Underground Space Technology, 45(5), 203–213. https://doi.org/10.1016/j.tust.2014.10.005 [Google Scholar] [CrossRef]

16. Li, T., Dai, Z., Yu, M., Zhang, W. (2021). Numerical investigation on the aerodynamic resistances of double-unit trains with different gap lengths. Engineering Applications of Computational Fluid Mechanics, 15(1), 549–560. https://doi.org/10.1080/19942060.2021.1895321 [Google Scholar] [CrossRef]

17. Li, Z. W., Yang, M. Z., Huang, S., Liang, X. (2017). A new method to measure the aerodynamic drag of high-speed trains passing through tunnels. Journal of Wind Engineering and Industrial Aerodynamics, 171(5), 110–120. https://doi.org/10.1016/j.jweia.2017.09.017 [Google Scholar] [CrossRef]

18. Muñoz-Paniagua, J., García, J., Crespo, A. (2014). Genetically aerodynamic optimization of the nose shape of a high-speed train entering a tunnel. Journal of Wind Engineering and Industrial Aerodynamics, 130(5), 48–61. https://doi.org/10.1016/j.jweia.2014.03.005 [Google Scholar] [CrossRef]

19. Sun, Z. X., Yao, Y. F., Yang, Y., Yang, G. W., Guo, D. L. (2018). Overview of the research progress on aerodynamic noise of high speed trains in China. Acta Aerodynamica Sinica, 36(3), 385–397. [Google Scholar]

20. Dai, Z., Li, T., Deng, J., Zhou, N., Zhang, W. (2022). Effect of the strip spacing on the aerodynamic performance of a high-speed double-strip pantograph. Vehicle System Dynamics, 60(10), 3358–3374. https://doi.org/10.1080/00423114.2021.1945117 [Google Scholar] [CrossRef]

21. Yan, H., Xie, S., Jing, K., Feng, Z. (2022). A review of recent research into the causes and control of noise during high-speed train movement. Applied Sciences, 12(15), 7508. https://doi.org/10.3390/app12157508 [Google Scholar] [CrossRef]

22. Baker, C. (2010). The flow around high speed trains. Journal of Wind Engineering and Industrial Aerodynamics, 98(6–7), 277–298. https://doi.org/10.1016/j.jweia.2009.11.002 [Google Scholar] [CrossRef]

23. Zhang, L., Li, T., Zhang, J. (2021). Research on aerodynamic shape optimization of trains with different dimensional design variables. International Journal of Rail Transportation, 9(5), 479–501. https://doi.org/10.1080/23248378.2020.1817803 [Google Scholar] [CrossRef]

24. Shu, X. W., Gu, C. G., Liang, X. F., Wang, T., Yang, B. (2006). The numerical simulation on the aerodynamic performance of high-speed maglev train with streamlined nose. Journal of Shanghai Jiaotong University, 40(6), 1034–1037. [Google Scholar]

25. Hemida, H., Krajnović, S. (2008). LES study of the influence of a train-nose shape on the flow structures under cross-wind conditions. Journal of Fluids Engineering, 130(9), 091101. https://doi.org/10.1115/1.2953228 [Google Scholar] [CrossRef]

26. Hemida, H., Krajnović, S. (2010). LES study of the influence of the nose shape and yaw angles on flow structures around trains. Journal of Wind Engineering and Industrial Aerodynamics, 98(1), 34–46. https://doi.org/10.1016/j.jweia.2009.08.012 [Google Scholar] [CrossRef]

27. Huang, Z. X., Chen, L., Jiang, K. L. (2011). The wind tunnel test and research on aerodynamics characteristic of high-speed train. Rolling Stock, 49(12), 1–6. [Google Scholar]

28. Ku, Y. C., Rho, J. H., Yun, S. H., Kwak, M. H., Kim, K. H. et al. (2010). Optimal cross-sectional area distribution of a high-speed train nose to minimize the tunnel micro-pressure wave. Structural and Multidisciplinary Optimization, 42(6), 965–976. https://doi.org/10.1007/s00158-010-0550-6 [Google Scholar] [CrossRef]

29. Miu, X. L., Li, M., Yao, Y., Huang, Z. X., Deng, Y. J. (2012). Wind tunnel test investigation on the shape optimization of head car of the high-speed train. Journal of Railway Science and Engineering, 9(2), 94–98. [Google Scholar]

30. Zhang, Z. Z., Zhou, D. (2013). Wind tunnel experiment on aerodynamic characteristic of streamline head of high-speed train with different head shapes. Journal of Central South University (Science and Technology), 44(6), 2603–2608. [Google Scholar]

31. Choi, J. K., Kim, K. H. (2014). Effects of nose shape and tunnel cross-sectional area on aerodynamic drag of train traveling in tunnels. Tunnelling and Underground Space Technology, 41, 62–73. https://doi.org/10.1016/j.tust.2013.11.012 [Google Scholar] [CrossRef]

32. Chen, X. D., Liu, T. H., Zhou, X. S., Li, W. H., Xie, T. Z. et al. (2017). Analysis of the aerodynamic effects of different nose lengths on two trains intersecting in a tunnel at 350 km/h. Tunnelling and Underground Space Technology, 66(9), 77–90. https://doi.org/10.1016/j.tust.2017.04.004 [Google Scholar] [CrossRef]

33. Tian, H. Q., Gao, G. J. (2003). The analysis and evaluation on the aerodynamic behavior of 270 km/h high-speed train. China Railway Science, 24(2), 17–21. [Google Scholar]

34. Chen, B. Z., Zhai, J. J. (2012). Shape optimization of high-speed train head. Journal of Dalian Jiaotong University, 33(4), 16–20. [Google Scholar]

35. Howe, M. S. (1998). The compression wave produced by a high-speed train entering a tunnel. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 454(1974), 1523–1534. https://doi.org/10.1098/rspa.1998.0220 [Google Scholar] [CrossRef]

36. Feng, Z. P. (2008). Aerodynamic performance of high-speed train with the train shape design (Ph.D. Thesis). Southwest Jiaotong Univercity, Chengdu, China. [Google Scholar]

37. Yang, X., Jin, J., Shi, G. (2013). Preliminary study on streamlined design of longitudinal profile of high-speed train head shape. Procedia-Social and Behavioral Sciences, 96(5), 1469–1476. https://doi.org/10.1016/j.sbspro.2013.08.167 [Google Scholar] [CrossRef]

38. Iida, M. (1997). Effective nose shape for reducing tunnel sonic boom. QR of RTRI, 38(4), 206–211. [Google Scholar]

39. Lorriaux, E., Bourabaa, N., Monnoyer, F. (1994). Aerodynamic optimization of railway motor coaches. The 1st World Congress on Railway Research, Paris. [Google Scholar]

40. Xu, P., Tian, H. Q., Yao, S. G. (2007). Shape design method for streamlined train head. China Railway Science, 1(1), 76–80. [Google Scholar]

41. Chen, Z. F., Wu, Z. F. (2014). Optimization method of train surface based on NURBS theory. Railway Locomotive & Car, 34(1), 23–27. [Google Scholar]

42. Wang, S., Xia, Y., Wang, R., You, L., Zhang, J. (2019). Optimal NURBS conversion of PDE surface-represented high-speed train heads. Optimization and Engineering, 20(3), 907–928. https://doi.org/10.1007/s11081-019-09425-6 [Google Scholar] [CrossRef]

43. Kulfan, B., Bussoletti, J. (2006). “Fundamental” parameteric geometry representations for aircraft component shapes. 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Virginia. [Google Scholar]

44. Su, H., Gu, L. Z., Gong, C. L. (2013). Multidisciplinary design optimization of reentry vehicle based on high fidelity model. Journal of Northwestern Polytechnical University, 31(6), 339–344. [Google Scholar]

45. Liu, Y., Hua, B., Xiao, D. (2016). Geometric modeling based on class and shape function transformation technique for hypersonic vehicles. International Journal of Nonlinear Sciences and Numerical Simulation, 17(3–4), 149–158. https://doi.org/10.1515/ijnsns-2014-0106 [Google Scholar] [CrossRef]

46. Sun, Z., Zhang, Y., Yang, G. (2017). Parametrization of high-speed train streamline shape. ASME Fluids Engineering Division Summer Meeting, V01AT04A006. Hawaii. [Google Scholar]

47. Rho, J. H., Ku, Y. C., Yun, S. H., Lee, D. H. (2008). Representation of 3-dimensional automobile configurations with vehicle modeling function for a shape optimization. Proceedings of the KSME Conference, pp. 1057–1062. Korea. [Google Scholar]

48. Ku, Y. C., Park, H. I., Kwak, M. H., Lee, D. H. (2010). Multi-objective optimization of high-speed train nose shape using the vehicle modeling function. 48th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Florida. [Google Scholar]

49. Yao, S., Guo, D., Sun, Z., Yang, G. (2015). A modified multi-objective sorting particle swarm optimization and its application to the design of the nose shape of a high-speed train. Engineering Applications of Computational Fluid Mechanics, 9(1), 513–527. https://doi.org/10.1080/19942060.2015.1061557 [Google Scholar] [CrossRef]

50. Yao, S. B., Guo, D. L., Sun, Z. X., Chen, D. W., Yang, G. W. (2016). Parametric design and optimization of high speed train nose. Optimization and Engineering, 17(3), 605–630. https://doi.org/10.1007/s11081-015-9298-6 [Google Scholar] [CrossRef]

51. Hicks, R. M., Henne, P. A. (1978). Wing design by numerical optimization. Journal of Aircraft, 15(7), 407–412. https://doi.org/10.2514/3.58379 [Google Scholar] [CrossRef]

52. Xiong, J., Li, T., Zhang, J. Y. (2016). Shape optimization of high-speed trains under multi runing conditions. Scientia Sinica Technologica, 46(3), 313–322. https://doi.org/10.1360/N092015-00153 [Google Scholar] [CrossRef]

53. Kwon, H. B., Jang, K. H., Kim, Y. S., Yee, K. J., Lee, D. H. (2001). Nose shape optimization of high-speed train for minimization of tunnel sonic boom. JSME International Journal Series C Mechanical Systems, Machine Elements and Manufacturing, 44(3), 890–899. https://doi.org/10.1299/jsmec.44.890 [Google Scholar] [CrossRef]

54. Zhao, H., Li, Q., Li, X., Rempfer, D. (2012). A design method for high-speed train nose shape under multi-line cases. Structural Longevity, 7(2), 87–103. [Google Scholar]

55. Wang, R., Zhang, J., Bian, S., You, L. (2018). A survey of parametric modelling methods for designing the head of a high-speed train. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 232(7), 1965–1983. https://doi.org/10.1177/0954409718756558 [Google Scholar] [CrossRef]

56. Lee, J., Kim, J. (2008). Approximate optimization of high-speed train nose shape for reducing micropressure wave. Structural and Multidisciplinary Optimization, 35(1), 79–87. https://doi.org/10.1007/s00158-007-0111-9 [Google Scholar] [CrossRef]

57. Sederberg, T. W., Parry, S. R. (1986). Free-form deformation of solid geometric models. ACM Siggraph Computer Graphics, 20(4), 151–160. https://doi.org/10.1145/15886.15903 [Google Scholar] [CrossRef]

58. Li, R., Xu, P., Peng, Y., Ji, P. (2016). Multi-objective optimization of a high-speed train head based on the FFD method. Journal of Wind Engineering and Industrial Aerodynamics, 152(6), 41–49. https://doi.org/10.1016/j.jweia.2016.03.003 [Google Scholar] [CrossRef]

59. Zhang, Y., Yang, G., Sun, Z., Guo, D. (2016). A general shape optimization method based on FFD approach with application to a high-speed train. Journal of Multidisciplinary Engineering Science and Technology, 3(12), 6181–6188. [Google Scholar]

60. Yao, S., Guo, D., Yang, G. (2012). Three-dimensional aerodynamic optimization design of high-speed train nose based on GA-GRNN. Science China Technological Sciences, 55(11), 3118–3130. https://doi.org/10.1007/s11431-012-4934-2 [Google Scholar] [CrossRef]

61. Zhang, L., Zhang, J., Li, T., Zhang, Y. (2018). A multi-objective aerodynamic optimization design of a high-speed train head under crosswinds. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 232(3), 895–912. https://doi.org/10.1177/0954409717701784 [Google Scholar] [CrossRef]

62. He, Z., Xiong, X., Yang, B., Li, H. (2020). Aerodynamic optimization of a high-speed train head shape using an advanced hybrid surrogate-based nonlinear model representation method. Optimization and Engineering, 23(1), 59–84. https://doi.org/10.1007/s11081-020-09554-3 [Google Scholar] [CrossRef]

63. He, Z., Liu, T., Liu, H. (2022). Improved particle swarm optimization algorithms for aerodynamic shape optimization of high-speed train. Advances in Engineering Software, 173(4), 103242. https://doi.org/10.1016/j.advengsoft.2022.103242 [Google Scholar] [CrossRef]

64. Liu, J. L., Li, M. G., Zhang, J. Y., Zhang, W. H., Li, M. (2013). Multi-objective aerodynamic optimization design of streamlined head of high-speed train. Scientia Sinica Technologica, 43(6), 689–698. [Google Scholar]

65. Yu, M. G., Zhang, J. Y., Zhang, W. H. (2014). Multi-objective aerodynamic optimization design of the streamlined head of high-speed trains under crosswinds. Journal of Mechanical Engineering, 50(24), 122–129. https://doi.org/10.3901/JME.2014.24.122 [Google Scholar] [CrossRef]

66. Yu, M. G., Pan, Z. K., Jiang, R. C., Zhang, J. Y. (2019). Multi-objective optimization design of the high-speed train head based on the approximate model. Journal of Mechanical Engineering, 55(24), 178–186. https://doi.org/10.3901/JME.2019.24.178 [Google Scholar] [CrossRef]

67. Zhang, L., Zhang, J. Y., Li, T., Zhang, Y. D. (2017). Multi-objective aerodynamic optimization design of high-speed train head shape. Journal of Zhejiang University-Science A, 18(11), 841–854. https://doi.org/10.1631/jzus.A1600764 [Google Scholar] [CrossRef]

68. Zhang, L., Zhang, J. Y., Li, T., Zhang, Y. D. (2017). Multi-objective optimization design of the streamlined head shape of super high-speed trains. Journal of Mechanical Engineering, 53(2), 106–114. https://doi.org/10.3901/JME.2017.02.106 [Google Scholar] [CrossRef]

69. Zhang, L., Zhang, J. Y., Li, T., Zhang, W. H. (2017). Multi-objective aerodynamic optimization design for head shape of high-speed trains. Journal of Southwest Jiaotong University, 51(6), 1055–1063. [Google Scholar]

70. Gunantara, N. (2018). A review of multi-objective optimization: Methods and its applications. Cogent Engineering, 5(1), 1502242. https://doi.org/10.1080/23311916.2018.1502242 [Google Scholar] [CrossRef]

71. Pareto, V. (1906). Manuale di economia politica con una introduzione alla scienza sociale. Milan: Società Editrice Libreria. [Google Scholar]

72. Deb, K., Pratap, A., Agarwal, S., Meyarivan, T. A. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182–197. https://doi.org/10.1109/4235.996017 [Google Scholar] [CrossRef]

73. Yao, S., Guo, D., Sun, Z., Yang, G., Chen, D. (2012). Multi-objective optimization of the streamlined head of high-speed trains based on the Kriging model. Science China Technological Sciences, 55(12), 3495–3509. https://doi.org/10.1007/s11431-012-5038-8 [Google Scholar] [CrossRef]

74. Sun, Z. X., Wang, M. Y., Wei, L. Y., Kong, F. B., Yang, G. W. (2021). Aerodynamic shape optimization of an urban maglev train. Acta Mechanica Sinica, 37(6), 954–969. https://doi.org/10.1007/s10409-021-01094-y [Google Scholar] [CrossRef]

75. Li, M., Li, M. G., Li, G. Q., Kong, F. B., Liu, B. (2013). Optimized design of parameteric-driven aerodynamic shape of high-speed EMU head-type. Journal of the China Railway Society, 35(11), 14–20. [Google Scholar]

76. Li, M., Li, M. G., Liu, B. (2016). Optimization design on key structural parameter of high speed EMU head-type aerodynamic shape. Journal of Mechanical Engineering, 52(20), 120–125. https://doi.org/10.3901/JME.2016.20.120 [Google Scholar] [CrossRef]

77. Yuan, C. Y., Li, M. Q. (2017). Multi-objective optimization for the aerodynamic noise of the high-speed train in the near and far field based on the improved NSGA-II algorithm. Journal of Vibroengineering, 19(6), 4759–4782. https://doi.org/10.21595/jve [Google Scholar] [CrossRef]

78. Kennedy, J., Eberhart, R. (1995). Particle swarm optimization. Proceeding of the 1995 IEEE International Conference on Neural Network, pp. 1942–1948. WA, Australia. [Google Scholar]

79. Yao, S. B., Chen, D. W., Ding, S. S. (2022). Multi-objective aerodynamic optimization design of high-speed maglev train nose. Railway Sciences, 1(2), 273–288. https://doi.org/10.1108/RS-04-2022-0017 [Google Scholar] [CrossRef]

80. Hoyos, J. D., Jiménez, J. H., Echavarría, C., Alvarado, J. P., Urrea, G. (2022). Aircraft propeller design through constrained aero-structural particle swarm optimization. Aerospace, 9(3), 153. https://doi.org/10.3390/aerospace9030153 [Google Scholar] [CrossRef]

81. Mohamad, A., Karimi, J., Naderi, A. (2020). Dynamic aerodynamic parameter estimation using a dynamic particle swarm optimization algorithm for rolling airframes. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 42(11), 1–16. https://doi.org/10.1007/s40430-020-02658-y [Google Scholar] [CrossRef]

82. Fan, H., Zhan, H., Cheng, S., Mi, B. (2019). Research and application of multi-objective particle swarm optimization algorithm based on α-stable distribution. Journal of Northwestern Polytechnical University, 37(2), 232–241. https://doi.org/10.1051/jnwpu/20193720232 [Google Scholar] [CrossRef]

83. Mohebbi, M., Rezvani, M. A. (2018). Multi objective optimization of aerodynamic design of high speed railway windbreaks using Lattice Boltzmann method and wind tunnel test results. International Journal of Rail Transportation, 6(3), 183–201. https://doi.org/10.1080/23248378.2018.1463873 [Google Scholar] [CrossRef]

84. Sun, Z., Song, J., An, Y. (2010). Optimization of the head shape of the CRH3 high speed train. Science China Technological Sciences, 53(12), 3356–3364. https://doi.org/10.1007/s11431-010-4163-5 [Google Scholar] [CrossRef]

85. Muñoz-Paniagua, J., García, J. (2019). Aerodynamic surrogate-based optimization of the nose shape of a high-speed train for crosswind and passing-by scenarios. Journal of Wind Engineering and Industrial Aerodynamics, 184(1202), 139–152. https://doi.org/10.1016/j.jweia.2018.11.014 [Google Scholar] [CrossRef]

86. Xu, G., Liang, X., Yao, S., Chen, D., Li, Z. (2017). Multi-objective aerodynamic optimization of the streamlined shape of high-speed trains based on the Kriging model. PLoS One, 12(1), e0170803. https://doi.org/10.1371/journal.pone.0170803 [Google Scholar] [PubMed] [CrossRef]

87. Yang, Y., He, Z., Shi, Z., Xiong, X. H. (2022). Multi-objective aerodynamic optimization of a high-speed train head shape based on an optimal kriging model. Journal of Applied Fluid Mechanics, 15(3), 803–813. [Google Scholar]

88. Zhang, Y., Yang, G. W., Guo, D. L., Sun, Z. X., Chen, D. W. (2019). A novel CACOR CACO R-SVR multi-objective optimization approach and its application in aerodynamic shape optimization of high-speed train. Soft Computing, 23(13), 5035–5051. https://doi.org/10.1007/s00500-018-3172-3 [Google Scholar] [CrossRef]

89. Suzuki, M., Nakade, K. (2013). Multi-objective design optimization of high-speed train nose. Journal of Mechanical Systems for Transportation and Logistics, 6(1), 54–64. https://doi.org/10.1299/jmtl.6.54 [Google Scholar] [CrossRef]

90. Zhou, J. L., Bao, F. M., Chen, B. Z. (2017). Shape optimization of high-speed train head based on response surface method. Journal of Dalian Jiaotong University, 38(4), 83–87. [Google Scholar]

91. Yu, M. G., Zhang, J. Y., Zhang, W. H. (2013). Multi-objective optimization design method of the high-speed train head. Journal of Zhejiang University-SCIENCE A, 14(9), 631–641. https://doi.org/10.1631/jzus.A1300109 [Google Scholar] [CrossRef]

92. Jeong, S., Murayama, M., Yamamoto, K. (2005). Efficient optimization design method using kriging model. Journal of Aircraft, 42(2), 413–420. https://doi.org/10.2514/1.6386 [Google Scholar] [CrossRef]

93. Sacks, J., Welch, W. J., Mitchell, T. J., Wynn, H. P. (1989). Design and analysis of computer experiments. Statistical Science, 4(4), 409–423. https://doi.org/10.1214/ss/1177012413 [Google Scholar] [CrossRef]

94. Forrester, A. I., Keane, A. J. (2009). Recent advances in surrogate-based optimization. Progress in Aerospace Sciences, 45(1–3), 50–79. https://doi.org/10.1016/j.paerosci.2008.11.001 [Google Scholar] [CrossRef]

95. Wang, Q., Moin, P., Iaccarino, G. (2010). A rational interpolation scheme with superpolynomial rate of convergence. SIAM Journal on Numerical Analysis, 47(6), 4073–4097. https://doi.org/10.1137/080741574 [Google Scholar] [CrossRef]

96. Sobester, A., Forrester, A., Keane, A. (2008). Engineering design via surrogate modelling: A practical guide. West Sussex: John Wiley & Sons. [Google Scholar]

97. Han, Z. H. (2016). Kriging surrogate model and its application to design optimization: A review of recent progress. Acta Aeronautica et Astronautica Sinica, 37(11), 3197–3225. [Google Scholar]

98. Bishop, C. M. (1994). Neural networks and their applications. Review of Scientific Instruments, 65(6), 1803–1832. https://doi.org/10.1063/1.1144830 [Google Scholar] [CrossRef]

99. Cheng, B., Titterington, D. M. (1994). Neural networks: A review from a statistical perspective. Statistical Science, 9(1), 2–30. [Google Scholar]

100. Gevrey, M., Dimopoulos, I., Lek, S. (2003). Review and comparison of methods to study the contribution of variables in artificial neural network models. Ecological Modelling, 160(3), 249–264. https://doi.org/10.1016/S0304-3800(02)00257-0 [Google Scholar] [CrossRef]

101. Abiodun, O. I., Jantan, A., Omolara, A. E., Dada, K. V., Mohamed, N. A. et al. (2018). State-of-the-art in artificial neural network applications: A survey. Heliyon, 4(11), e00938. https://doi.org/10.1016/j.heliyon.2018.e00938 [Google Scholar] [PubMed] [CrossRef]

102. Rumelhart, D. E., Hinton, G. E., Williams, R. J. (1989). Learning representations by back-propagating errors. Nature, 323(6088), 533–536. https://doi.org/10.1038/323533a0 [Google Scholar] [CrossRef]

103. Vapnik, V. N. (1995). The nature of statistical learning theory. New York: Springer. [Google Scholar]

104. Cherkassky, V. S., Mulier, F. M. (2007). Learning from data: Concepts, theory, and methods. New Jersey: John Wiley & Sons. [Google Scholar]

105. Guo, Z., Bai, G. (2009). Application of least squares support vector machine for regression to reliability analysis. Chinese Journal of Aeronautics, 22(2), 160–166. https://doi.org/10.1016/S1000-9361(08)60082-5 [Google Scholar] [CrossRef]

106. Peng, X. (2010). TSVR: An efficient twin support vector machine for regression. Neural Networks, 23(3), 365–372. https://doi.org/10.1016/j.neunet.2009.07.002 [Google Scholar] [PubMed] [CrossRef]

107. Shao, Y. H., Zhang, C. H., Yang, Z. M., Jing, L., Deng, N. Y. (2013). An ε-twin support vector machine for regression. Neural Computing and Applications, 23(1), 175–185. https://doi.org/10.1007/s00521-012-0924-3 [Google Scholar] [CrossRef]

108. Vytla, V. S., Huang, P., Penmetsa, R. (2010). Multi-objective aerodynamic shape optimization of high speed train nose using adaptive surrogate model. 28th AIAA Applied Aerodynamics Conference, Illinois. https://doi.org/10.2514/6.2010-4383 [Google Scholar] [CrossRef]

109. Muñoz-Paniagua, J., García, J. (2020). Aerodynamic drag optimization of a high-speed train. Journal of Wind Engineering and Industrial Aerodynamics, 204(6), 104215. https://doi.org/10.1016/j.jweia.2020.104215 [Google Scholar] [CrossRef]

110. Yao, S. B., Guo, D. L., Sun, Z. X., Yang, G. W., Chen, D. W. (2014). Optimization design for aerodynamic elements of high speed trains. Computers & Fluids, 95(6–7), 56–73. https://doi.org/10.1016/j.compfluid.2014.02.018 [Google Scholar] [CrossRef]

111. Zhang, L., Li, T., Zhang, J., Piao, R. (2021). Optimization on the crosswind stability of trains using neural network surrogate model. Chinese Journal of Mechanical Engineering, 34(1), 1–17. https://doi.org/10.1186/s10033-021-00604-0 [Google Scholar] [CrossRef]

112. Zhang, L., Dai, Z. Y., Li, T., Zhang, J. Y. (2022). Multi-objective aerodynamic shape optimization of a streamlined high-speed train using Kriging model. Journal of Zhejiang University-SCIENCE A, 23(3), 225–242. https://doi.org/10.1631/jzus.A2100329 [Google Scholar] [CrossRef]

113. Dai, Z. Y., Li, T., Zhang, W. H., Zhang, J. Y. (2022). Multi-objective aerodynamic optimization on the head shape of high-speed train using Kriging surrogate model with hybrid infill criterion. Journal of Southwest Jiaotong University. https://kns.cnki.net/kcms/detail/51.1277.U.20220919.1240.002.html [Google Scholar]

114. Gao, Y. H., Wang, X. C. (2012). Multi-point plus point sequence optimization method based on Kriging proxy model. Engineering Mechanics, 29(4), 90–95. [Google Scholar]

115. Laurenceau, J., Meaux, M., Montagnac, M., Sagaut, P. (2010). Comparison of gradient-based and gradient-enhanced response-surface-based optimizers. AIAA Journal, 48(5), 981–994. https://doi.org/10.2514/1.45331 [Google Scholar] [CrossRef]

116. Han, Z. H., Zhang, Y., Song, C. X., Zhang, K. S. (2017). Weighted gradient-enhanced kriging for high-dimensional surrogate modeling and design optimization. AIAA Journal, 55(12), 4330–4346. https://doi.org/10.2514/1.J055842 [Google Scholar] [CrossRef]

117. Chen, L., Qiu, H., Gao, L., Jiang, C., Yang, Z. (2020). Optimization of expensive black-box problems via Gradient-enhanced Kriging. Computer Methods in Applied Mechanics and Engineering, 362, 112861. https://doi.org/10.1016/j.cma.2020.112861 [Google Scholar] [CrossRef]

118. Shu, L., Jiang, P., Zhou, Q., Xie, T. (2019). An online variable-fidelity optimization approach for multi-objective design optimization. Structural and Multidisciplinary Optimization, 60(3), 1059–1077. https://doi.org/10.1007/s00158-019-02256-0 [Google Scholar] [CrossRef]

119. Zhou, Q., Yang, Y., Song, X. G., Han, Z. H., Cheng, Y. S. et al. (2020). Survey of multi-fidelity surrogate models and their applications in the design and optimization of engineering equipment. Journal of Mechanical Engineering, 56(24), 219–245. https://doi.org/10.3901/JME.2020.24.219 [Google Scholar] [CrossRef]

120. Han, Z. H., Chen, Z. X., Zhang, L., Zhang, Y., Zhang, K. et al. (2020). Efficient aerodynamic shape optimization using variable-fidelity surrogate models and multilevel computational grids. Chinese Journal of Aeronautics, 33(1), 31–47. https://doi.org/10.1016/j.cja.2019.05.001 [Google Scholar] [CrossRef]

121. Zhou, Q., Wu, J., Xue, T., Jin, P. (2021). A two-stage adaptive multi-fidelity surrogate model-assisted multi-objective genetic algorithm for computationally expensive problems. Engineering with Computers, 37(1), 623–639. https://doi.org/10.1007/s00366-019-00844-8 [Google Scholar] [CrossRef]

122. Abdallah, I., Lataniotis, C., Sudret, B. (2019). Parametric hierarchical kriging for multi-fidelity aero-servo-elastic simulators—Application to extreme loads on wind turbines. Probabilistic Engineering Mechanics, 55(1), 67–77. https://doi.org/10.1016/j.probengmech.2018.10.001 [Google Scholar] [CrossRef]