Open Access

ARTICLE

New Configurations of the Fuzzy Fractional Differential Boussinesq Model with Application in Ocean Engineering and Their Analysis in Statistical Theory

Yu-Ming Chu¹, Saima Rashid^2,*, Shazia Karim³, Anam Sultan²

1 Department of Mathematics, Huzhou University, Huzhou, 313000, China
2 Department of Mathematics, Government College University, Faisalabad, 38000, Pakistan
3 Department of Basic Sciences and Humanities, UET Lahore, Faisalabad Campus, Lahore, Pakistan

* Corresponding Author: Saima Rashid. Email:

Computer Modeling in Engineering & Sciences 2023, 137(2), 1573-1611. https://doi.org/10.32604/cmes.2023.027724

Received 11 November 2022; Accepted 21 February 2023; Issue published 26 June 2023

Abstract

The fractional-order Boussinesq equations (FBSQe) are investigated in this work to see if they can effectively improve the situation where the shallow water equation cannot directly handle the dispersion wave. The fuzzy forms of analytical FBSQe solutions are first derived using the Adomian decomposition method. It also occurs on the sea floor as opposed to at the functionality. A set of dynamical partial differential equations (PDEs) in this article exemplify an unconfined aquifer flow implication. This methodology can accurately simulate climatological intrinsic waves, so the ripples are spread across a large demographic zone. The Aboodh transform merged with the mechanism of Adomian decomposition is implemented to obtain the fuzzified FBSQe in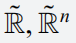 and (2nth)-order involving generalized Hukuhara differentiability. According to the system parameter, we classify the qualitative features of the Aboodh transform in the fuzzified Caputo and Atangana-Baleanu-Caputo fractional derivative formulations, which are addressed in detail. The illustrations depict a comparison analysis between the both fractional operators under gH-differentiability, as well as the appropriate attributes for the fractional-order and unpredictability factors σ ∈ [0, 1]. A statistical experiment is conducted between the findings of both fractional derivatives to prevent changing the hypothesis after the results are known. Based on the suggested analyses, hydrodynamic technicians, as irrigation or aquifer quality experts, may be capable of obtaining an appropriate storage intensity amount, including an unpredictability threshold.

---

Keywords

---