Outage Behaviors of Active Intelligent Reflecting Surface Enabled NOMA Communications

1  Introduction

With the commercialization of the fifth-generation networks, both academia and industry are focusing on the design of the sixth-generation (6G) networks. It will create tremendous research possibilities and enable many new technologies. Compared to the previous wireless communication systems, 6G networks need to take into account the higher performance metrics and are expected to support huge connectivity, high data rates and various heterogeneous communication scenarios [1,2]. Non-orthogonal multiple access (NOMA) has been regarded as one of the promising technologies, which is able to improve spectral efficiency, connectivity and user fairness by encouraging sharing the same time/frequence/code/space resource among plenty of users [3–5]. It has been shown that when the non-orthogonal users have disparate channels to the base station (BS), NOMA is capable of offering better performance gain relative to orthogonal multiple access (OMA) [6–8].

In parallel with the development of NOMA, intelligent reflecting surface (IRS) assisted wireless communications have received a lot of attention due to their superior performance in creating favourable radio propagation environments [9–11]. The basic components of IRS include plenty of low-cost passive reflecting elements, which can independently change the amplitude and phase of incident signals to provide a new degree of freedom. Hence this creates the possibility of realizing a programmable and smart radio communication environments. The continuous deepening researches of passive IRS find that the received signals may suffer from multiplicative fading or double path-loss attenuation [12,13], i.e., the product of path losses from the BS to IRS, and then from IRS to the desired users. To solve the effect of multiplicative fading on system performance, the IRS can be equipped with reflecting amplification elements, such as current-inverting converters and tunnel diode to amplify the reflected signals. The basic approach of designing a reflecting power-amplifying surface was highlighted in [14], where the stability of power amplification was safeguarded by minimizing the nonreciprocal response of the reflecting surface. Moreover, the authors of [15] proposed the concept of active IRS to overcome the multiplicative fading influence, and confirmed that active IRSs are able to achieve the enhanced sum rate gain relative to passive IRS. For the purpose of saving power consumption, the authors in [16] further outlined the sub-connected architecture of active IRS, in which numerous reflecting elements share the integrated power amplifier. The research progresses of NOMA, IRS and IRS assisted NOMA communications are surveyed comprehensively in the following paragraphs.

1.1 Studies on Cooperative NOMA Communications

Many applications of NOMA have been developed to meet the requirements of different communications scenarios. The cooperative NOMA can be categorized into two major types. The first type is that the near-end user with better channel gains is selected as decode-and-forward (DF) or amplify-and-forward (AF) relaying to forward the information. For example, the authors of [17] put forward a cooperative NOMA scheme to achieve the maximum diversity order of users. In [18], the outage probability of energy harvesting based cooperative NOMA was investigated by invoking stochastic geometry. Furthermore, the authors of [19] regarded the near-end user with better channels as decode-and-forward (DF) relaying, which can switch between half-duplex (HD) and full-duplex (FD) modes. Inspired by user collaboration, the integration of NOMA to cognitive radio networks was surveyed in [20], where the secondary users served as HD DF relays to improve the multicast performance. To further enhance the spectrum efficiency, the authors of [21] researched the outage probability of FD device-to-device cooperative NOMA systems. The second type is that the dedicated DF or AF relaying is introduced into NOMA networks to help the BS. In [22], the authors exploited an FD DF relaying based two-way cooperative NOMA system to exchange the information between a pair of users. The ergodic sum rate of AF based cooperative NOMA networks was studied over Nakagami-m fading channels [23]. With an emphasis on hardware impairments, the authors of [24] discussed the outage behaviors and ergodic capacity of AF relaying based cooperative NOMA networks. Except for the above contributions, a novel detection scheme was developed for AF cooperative NOMA networks [25], in which the maximal ratio combining was applied to decode the superposed signals.

1.2 Studies on IRS Assisted Wireless Communications

In contrast with conventional wireless communications, the channel coefficients between the BS and desired users can be adjusted constructively by deploying the IRS for wireless communications [26–28]. From the viewpoint of energy consumption, the authors of [29] revealed the design of energy efficiency for passive IRS aided wireless systems. In [30], the outage probability of passive IRS for wireless communications was studied by employing coherent phase shifting scheme. By emphasizing the performance limits, the authors of [31] researched the achievable rate of passive IRS with sensitive phase shifting. Afterward, the coverage probability of passive IRS aided wireless systems was evaluated in [32] over the real fading channels. To meet diverse requirements, the authors of [33] studied the symbol error probability of single passive IRS in detail. The system performance of passive IRS is usually constrained by the double fading influence, i.e., since the incident signals undergo the cascaded channels of BS-IRS, and then IRS-users. Hence it is necessary to solve this influence introduced by passive IRS. Apart from the aforementioned passive IRS, the growing research interests have been devoted to examine active IRS for overcoming the multiplicative fading [34–36]. The application of active IRS into wireless networks was outlined [34] to balance conflict between the amplification noise and the received signal power at the receiver. The superior of active IRS is able to amplify the incident signals and overcome the double-fading attenuation. The authors of [35] discussed the deployment issues of active IRS and showed that with the IRS’s decreasing amplification power, the active IRS should be deployed closer to the desired users. Conditioned on the small power budget [36], the active IRS assisted wireless communication was capable of supplying the better achievable rate through rational power allocation. It was found in [37] that active IRS not only improves energy efficiency greatly, but also extends transmission coverage with respect to passive IRS.

1.3 Studies on IRS Assisted NOMA Communications

In light of the above discussions, both NOMA and IRS are essential enabling techniques of 6G networks, which are complementary to each other [38,39]. In [40], the closed-form expressions for the outage probability of passive IRS assisted NOMA were derived by designing the passive beamforming weights. To shed light on phase shifting, the authors of [41] analyzed the effect of coherent phase shifting and random phase shifting on active IRS-NOMA networks. Sparked by this work, the outage probability and ergodic rate of passive IRS-NOMA were evaluated by using 1-bit coding scheme [42]. The authors in [43] paid attention to wireless power transfer based NOMA with the aid of the passive IRS. Exploiting the direct links between the BS and users [44], the authors further studied the sum throughput of passive IRS-NOMA networks. The outage probability of NOMA with passive IRS partitioning was evaluated in [45], which denotes the superior of the proposed system over IRS-OMA systems in terms of outage behaviors. Moving forward a single step, the authors of [46] researched the outage performance of multiple passive IRS aided NOMA networks with the use of discrete phase shifts. In [47], the authors outlined the network details of passive IRS aided two-way NOMA, where the outage probability of a pair of users was derived exhaustively. With the emphasis on covert communications, the authors in [48] studied the average error probability of IRS-NOMA networks. In addition, the performance of passive IRS-NOMA was discussed by taking into consideration imperfect successive interference cancellation (SIC) [49].

1.4 Motivation and Contributions

While the before-mentioned enjoyable contributions have laid a substantial foundation for finding out the diverse aspects of passive IRS assisted NOMA networks, the active IRS enabled NOMA communications for 6G networks are far from being well comprehended. It is worth noting that the performance of passive IRS assisted wireless networks may be restricted by its high multiplicative fading. This phenomenon can be alleviated by active IRS equipped with multiple reflecting amplification elements [15], which is able to amplify the incident signals with low cost negative impedance converter or asymmetric current mirrors. At this moment, the fewer reflecting element is required to attain the enhanced performance for users. In contrast to the gain introduced by passive IRS with a large number of elements, the advantages of active IRS with power amplification are more efficient and conspicuous. In [50], two typical active aided multiple access schemes, i.e., time division multiple access and NOMA were surveyed, where the achievable sum throughput was only compared each other from the perspective of system optimization. To the best of our knowledge, the performance analysis of active IRS enabled NOMA networks is not researched yet. Motivated by these, we simultaneously characterize the performance of active/passive IRS-NOMA networks in terms of outage probability and system throughput. The staple issue for active IRS-NOMA are further handled that how amplification noise affects the system performance and how many performance gains can be brought over conventional OMA and cooperative communication schemes. Based on the these explanations, the principal contributions of this manuscript are summarized as follows:

1.   We derive the exact expressions of outage probability for user n and user m in active IRS-NOMA networks. We take advantage of the 1-bit coding scheme to handle the cascade channels. Moreover, we further derive the asymptotic expressions of outage probability for user n and user m and obtain the corresponding diversity orders. The diversity orders of user n and user m are related to the number of reflecting elements and channel order. We also derive both exact and asymptotic expressions of outage probability for orthogonal users in active IRS-OMA networks.

2.   We simultaneously derive the exact and asymptotic expressions of outage probability for user n and user m in passive IRS-NOMA networks. The diversity orders of user n and user m for passive IRS-NOMA networks are attained. We observe that the diversity orders of passive IRS-NOMA networks are associated with the reflecting elements. We compare the outage behaviors of active IRS-NOMA networks with that of passive IRS-NOMA networks and FD/HD DF and AF relaying schemes.

3.   We confirm that the outage probability of user n and user m for active IRS-NOMA is superior to that of passive IRS-NOMA networks. As the reflection amplitude factors increase, the active IRS-NOMA networks are able to provide enhanced performance gains. We further discuss the delay-sensitive system throughput of active/passive IRS-NOMA networks. We observe that the system throughput of active/passive IRS-NOMA is much better than that of conventional FD/HD DF and AF relaying.

1.5 Organization and Notations

The rest of manuscript is organized as below. Section 1 establishes the system model of active RIS enabled NOMA networks; In Section 2, the outage probabilities of a couple of users are analysed and the commensurable high SNR approximated results are provided at length; The computer simulation and analytical discussions are presented in Section 3 to illustrate remarks; Immediately after, the Section 4 gives a summary of this manuscript.

The principal notations in this manuscript are shown as follows. The superscript (⋅)H indicates the conjugate-transpose operation; The cumulative distribution function (CDF) and probability density function (PDF) of a random variable X are denoted by FX(⋅) and fX(⋅), respectively.

2  Network Model

Consider an active IRS enabled NOMA communication scenarios, as illustrated in Fig. 1, where the BS sends the superposed signals to M users with the help of active IRS. The BS and non-orthogonal users are equipped single antenna, while the IRS consists of K active reflecting amplification elements. The IRS is capable of dynamically adjusting the amplitude and phase shifting of each active element through a smart controller. Compared to the passive IRS that just reflects the signals without amplification, active IRS is able to amplify the reflected signals with the additionally active reflection-type amplifier, which can be accomplished by some integrated circuits1. The direct links between the BS and non-orthogonal users are supposed strongly attenuated due to surrounding physical obstacles [41,42]. The assumption can reflect the role of IRS’s deployment between the BS and users. All wireless communication links in the networks are supposed to experience identically and independent Rayleigh fading. Define the phase shift matrix of active IRS as Φ=βΘ, where Θ=Δdiag(ejθ1,...,ejθk,...,ejθK), β and θk denote the reflection amplitude factor and phase shifting of the k-th IRS element, respectively. For passive IRS, the maximum reflection amplitude factor can be set to be one, while the amplitude factor of active IRS is larger than one by invoking the reflection-type amplifier. Without loss of generality, the cascade channel gains from the BS to active IRS, and then to M users are sorted as |hrMHΦhsr|2>⋯>|hrnHΦhsr|2>⋯>|hrmHΦhsr|2⋯>|hr1HΦhsr|2, where hsr=[hsr1,⋯hsrk,⋯,hsrK]H and hrφ=[hrφ1,hrφ2,⋯,hrφK]H denote the channels from the BS to active IRS and active IRS to user φ, i.e., φ∈{n,m} respectively. More specifically, hsrk=dsr−αh~srk with h~srk∼𝒞𝒩(0,1), dsr denotes the distance from the BS to active IRS and α is the path loss exponent. hrφk=drφ−αh~rφk with h~rφk∼𝒞𝒩(0,1) and drφ denotes the distance from the active IRS and user φ. For the sake of brevity, a couple of users, i.e., near-end user n and far-end user m are selected to execute the non-orthogonal communications. Each reflecting element with amplification of active IRS is able to re-scatter the signal independently without cross-interference. Assuming that perfect channel information state at the BS and the feedback information to the active IRS can be attained successfully.

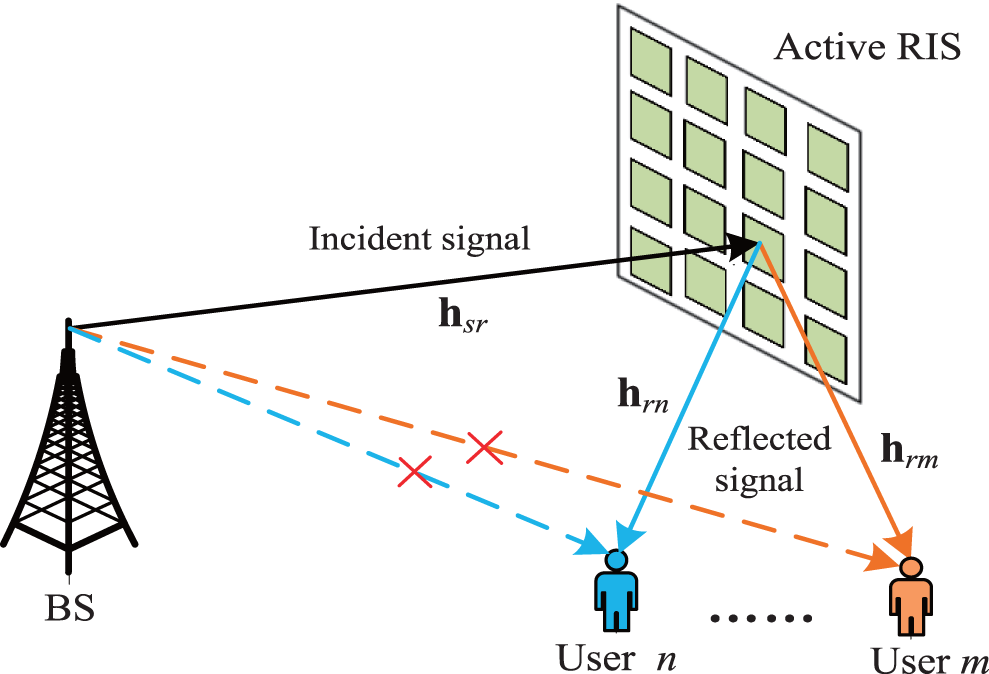
Figure 1: System model of active IRS enabled NOMA networks

2.1 Signal Model

In conformity with the superposition coding principle, the BS broadcasts the superposed signals to non-orthogonal users with the assistance of active IRS. At this moment, the received signals of user φ from the reflecting links can be written as

yφ=hrφHΦhsr(anPsxn+amPsxm)+hrφHΦnr+n~φ,(1)

where xn and xm are the normalized power signals of user n and user m, i.e, E{xn2}=E{xm2}=1 respectively. Ps is the transmit power of the BS. an and am are the power allocation factors of user n and user m, which satisfies the relationship of an+am=1 and am>an for the users’ fairness. nr∼𝒞𝒩(0,NrIK) denotes the amplification noise introduced by the active IRS elements with Nr denoting the amplification noise power. n~φ∼𝒞𝒩(0,N0) represents the received noise at the user φ. To facilitate analyses, we suppose that the amplification noise power of Nr is approximately N0, i.e., Nr≈N0.

For the user n, the SIC scheme is carried out to detect the signal xm of user m firstly, and then decode its own signal xn. The detecting signal-to-interference-plus-noise ratio (SINR) at user n can be respectively given by

γn→m=β|hrnHΘhsr|2ρamβ|hrnHΘhsr|2ρan+ξβ‖hrnHΘ‖2+1,(2)

γn=β|hrnHΘhsr|2ρanξβ‖hrnHΘ‖2+1,(3)

where ρ=PsN0 represents the transmit SNR. ξ=1 and ξ=0 denote the active IRS and passive IRS enabled NOMA networks, respectively.

For the user m, both user n’s signal and amplification noise caused by active IRS are regarded as the interference. Hence the corresponding SINR can be given by

γm=β|hrmHΘhsr|2ρamβ|hrmHΘhsr|2ρan+ξβ‖hrmHΘ‖2+1.(4)

2.2 Active IRS-NOMA with 1-bit Coding

Different to the coherent phase shifting, 1-bit coding scheme is a special case of random phase shifting scheme, which can be easily applicable in practice and avoid the excessive system overhead [41,42]. More specifically, the elements of diagonal matrix Θ are tuned into 1 (on) or 0 (off). We define that the active reflecting amplification elements K are equal to PQ, where P and Q are integers. Assuming V=IP⊗1Q, where ⊗ denotes the Kronecker product and 1Q is a column vector of all ones with Q×1. The p-th column of V is denoted by vp with K×1 and vpHvl=0 for p≠l. This implication is that the inner product of any two columns in V is equal to zero. At this moment, the cascade channel gain |hrφHΘhsr|2 is converted to |vpHDφhsr|2, where Dφ is the diagonal matrix with its diagonal elements obtained from hrφ. It worth pointing out that assuming θ is a vector with K×1, whose elements are from the main diagonal of Θ. As a result, the optimal θ to maximize the SINRs in (2)–(4) can be respectively found based on the following norms:

γ^n→m=maxvp⁡β|vpHDnhsr|2ρamβ|vpHDnhsr|2ρan+ξβ‖vpHDn‖2+1,(5)

γ^n=maxvp⁡β|vpHDnhsr|2ρanξβ‖vpHDn‖2+1,(6)

and

γ^m=maxvp⁡β|vpHDmhsr|2ρamβ|vpHDmhsr|2ρan+ξβ‖vpHDm‖2+1.(7)

2.3 Active IRS-OMA

From the perspective of fair comparison, the active IRS enabled OMA networks are seemed as a benchmark, where the active IRS is deployed between the BS and orthogonal user, i.e., user o to complete the total communication process. By making use of 1-bit coding scheme, the SINR of user o for active IRS-OMA networks can be given by

γo=maxvp⁡β|vpHDohsr|2ρξβ‖vpHDo‖2+1,(8)

where Do is the diagonal matrix with its diagonal elements obtained from hro.

3  Performance Evaluation

In this section, the performance of active IRS-NOMA networks is characterized in terms of outage probability and system throughput. As a further development, the asymptotic outage probabilities for a pair of users are derived in the following part.

3.1 The Outage Probability of User n

The SIC scheme is firstly carried out at user n to detect the signal xm, and then decode its own information xn. As stated in [8,18], if the user n cannot detect xm and the outage will happen. Another event is that on the condition of user n detecting xm successfully, the user n has no ability to decode the information xn. On the basis of its supplementary events, the outage probability of user n for active IRS-NOMA networks can be written as

Pn,act=1−Pr(γ^n→m>γthm,γ^n>γthn),(9)

where γthm=2Rm−1 and Rm denotes the target rate to detect xm at user n and user m. γthn=2Rn−1 and Rn denotes the target rate to detect xn at user n.

Proof. See Appendix A.

As a further advance, the following corollary provides the outage probability of user n for passive IRS-NOMA networks.

3.2 The Outage Probability of User m

Different from the outage events of user n, user m does not implement the SIC scheme and directly detect the signal xm by regarding xn as interference. Hence the outage probability of user m for active IRS-NOMA networks can be expressed as

Pm,act=Pr(γ^m<γthm).(12)

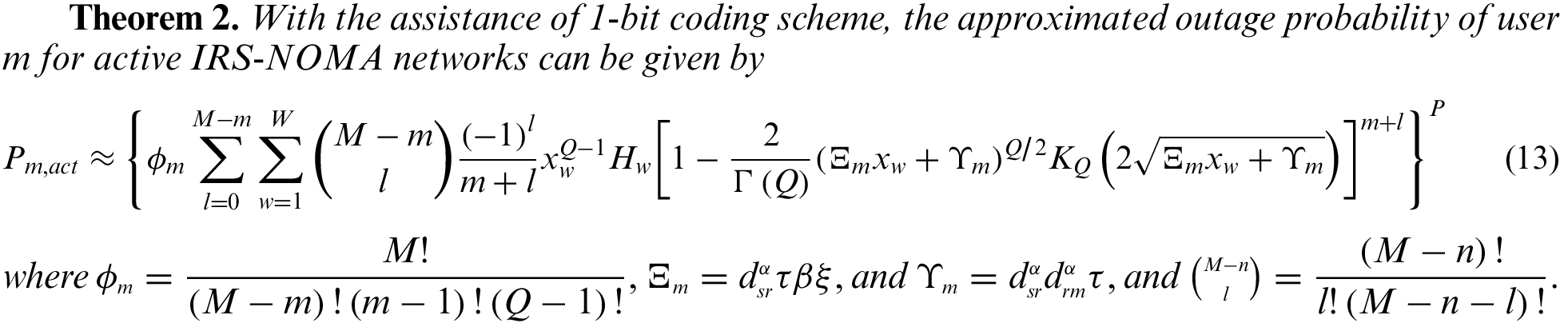
Proof. See Appendix B.

Based on the above analytical result, the following corollary provides the outage probability of user m for passive IRS-NOMA networks.

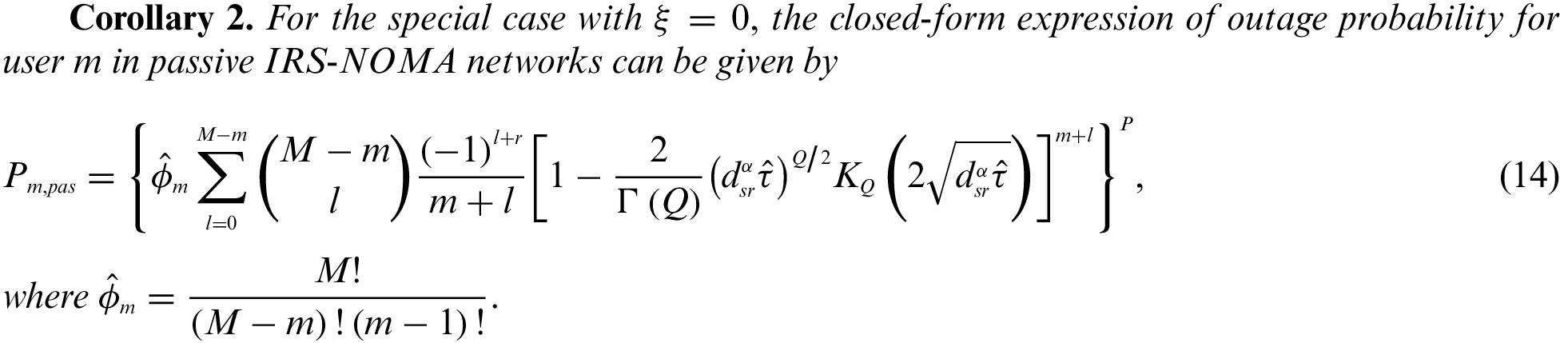
3.3 The Outage Probability of User o

In active IRS-OMA networks, if the detecting SINR of user o is less than the target SNR, i.e., γtho, the communication process will be interrupted. At this moment, the outage probability of orthogonal user o can be expressed as

Po,act=Pr(γo<γtho).(15)

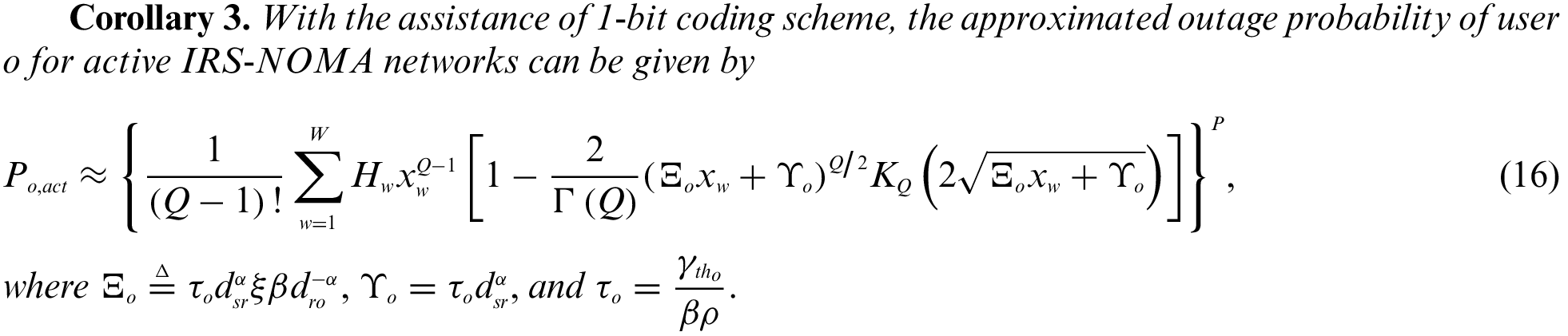
The closed-form and asymptotic expressions for outage probability of orthogonal user in passivea IRS-OMA networks can be found in [42, Eq. (12), Eq. (19), Eq. (20)], which are regarded as a baseline from the comparison point of view.

3.4 Diversity Order

To gain the tractable insights, we provide the diversity orders of user n and user m for active IRS-NOMA networks. It can describe how fast the outage behaviors increase with the transmit SNRs. As a consequence, the diversity order of users for active IRS-NOMA networks can be expressed as

dact=−limρ→∞⁡log⁡[Pasym(ρ)]log⁡ρ,(17)

where Pasym(ρ) is the asymptotic outage probability at the high SNRs.

To calculate the asymptotic outage probability of user n in (10), we should firstly provide the approximated expression of the Bessel function, i.e., KQ(x). When x intends to 0, KQ(x) can be approximated to K1(x)≈1x+x2ln⁡(x2) and KQ(x)≈12[2Q(Q−1)!xQ−2Q−2(Q−2)!xQ−2] with Q=1 and Q≥2, respectively [41,42]. Applying the approximated expressions of Bessel function into (10) and taking the first item (l=0) of summation series, the asymptotic outage probability of user n for active IRS-NOMA networks can be obtained. The following corollary provides the specifical result in detail.

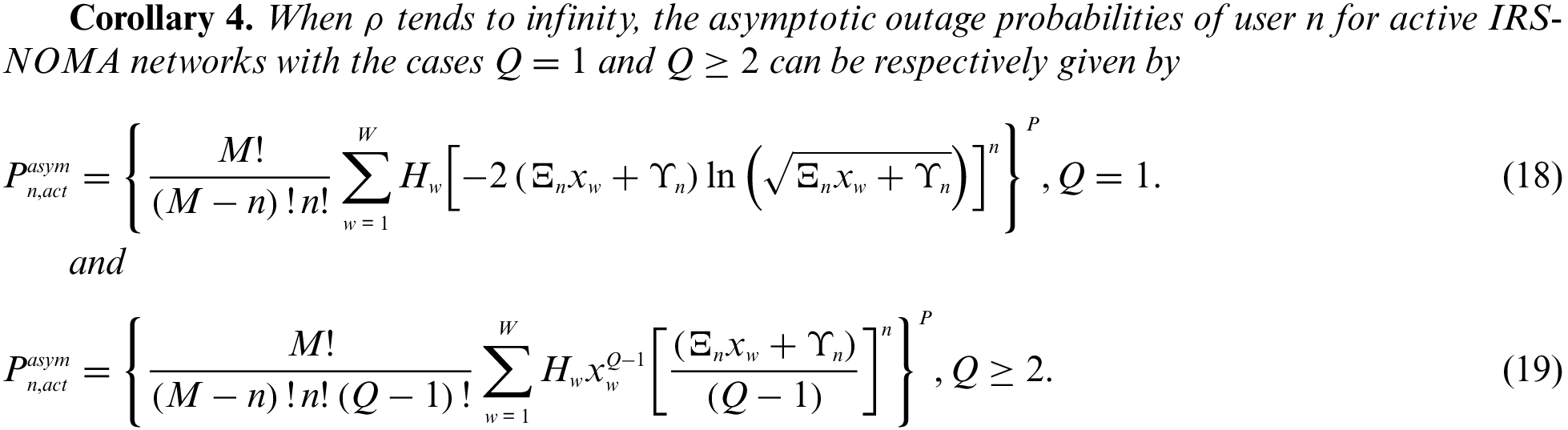
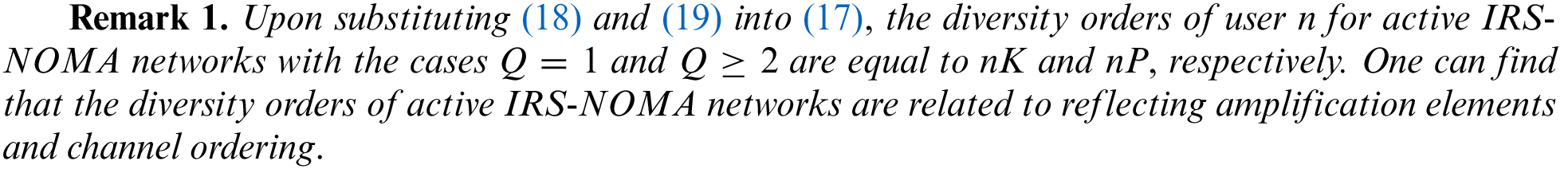
For the special case with ξ=0, the asymptotic outage probabilities of user n for passive IRS-NOMA networks can be given by

Pn,pasasym={M!(M−n)!n![−2dsrαζ^ln⁡(dsrαζ^)]n}K,(20)

and

Pn,pasasym={M!(M−n)!n!(dsrαζ^Q−1)n}P,(21)

on the condition of Q=1 and Q≥2, respectively.

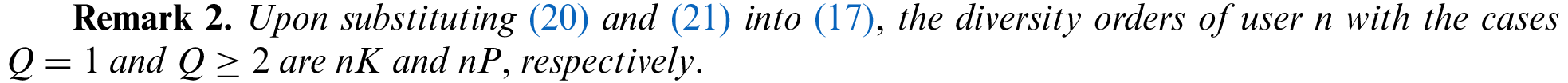
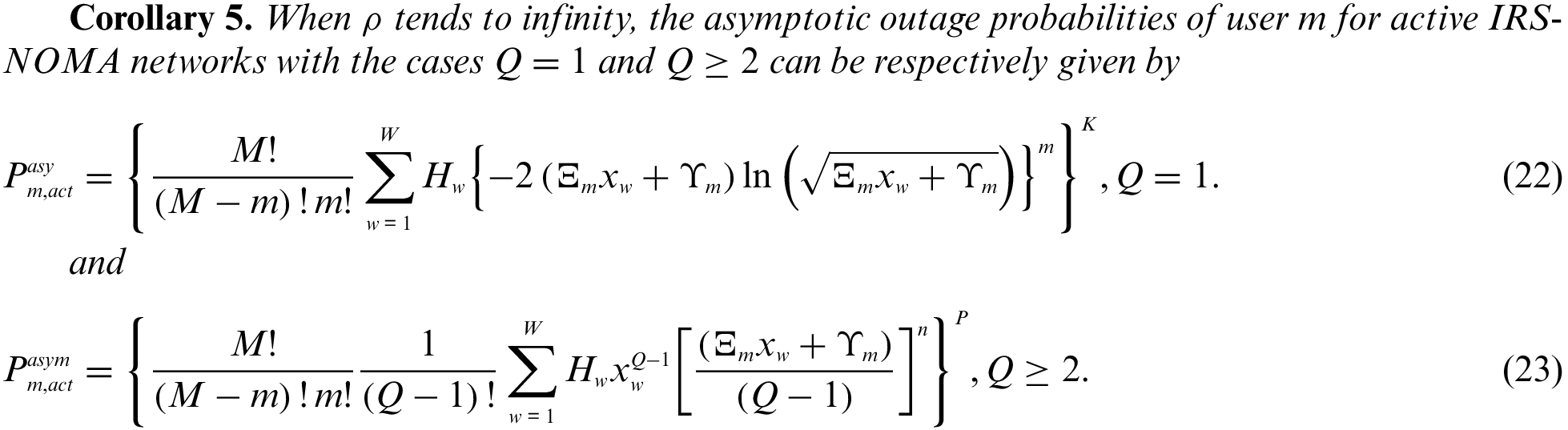
Similar to the calculation processes of user n for passive IRS-NOMA networks, the asymptotic outage probabilities of user m for active IRS-NOMA networks can be given by

Pm,pasasym={M!(M−m)!m![−2dsrατ^ln⁡(dsrατ^)]m}K,(24)

and

Pm,pasasym=[M!(M−m)!m!(dsrατ^Q−1)m]P,(25)

with the cases Q=1 and Q≥2, respectively.

3.5 System Throughput

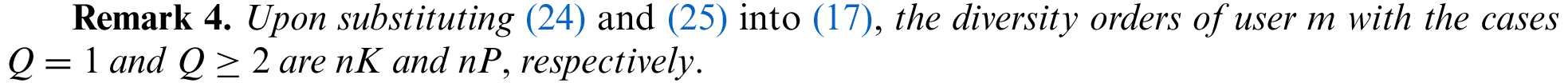
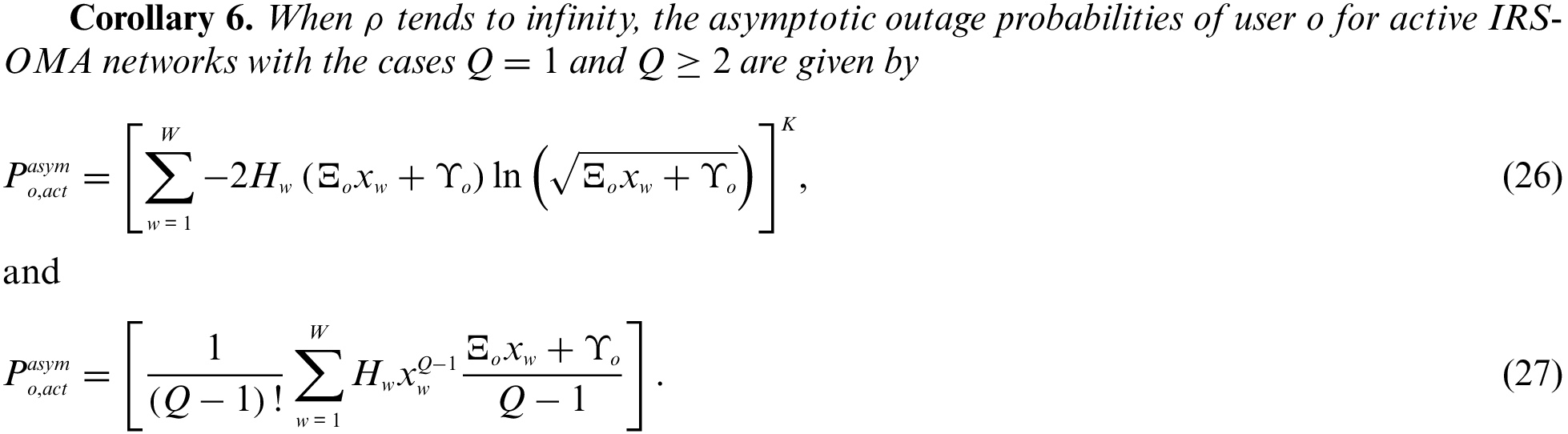
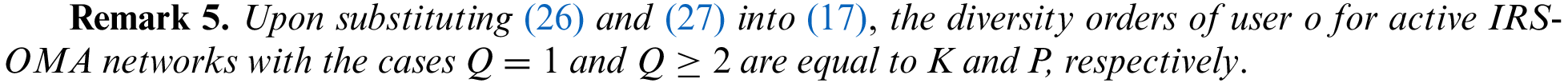
In this subsection, the system throughput of active IRS-NOMA networks is taken into account in delay-sensitive transmission. At this mode, the delay-sensitive throughput system mainly depend on the influence of outage probability. According to the derived outage probability of user n and user m, the system throughput of active IRS-NOMA networks can be given by

Ract=(1−Pn,Φ)Rn+(1−Pm,Φ)Rm,(28)

where Φ∈{act,pas}. Pn,act and Pm,act are obtained from (10) and (13), respectively. Pn,pas and Pm,pas can be obtained from (11) and (14), respectively.

4  Simulation Results

In this section, computer simulations are carried out to verify the analytical results of active IRS-NOMA networks. The impact of reflection amplitude factor on active IRS enabled NOMA is taken into account in detail. For clarity of exposition, the key simulation parameters used are summarized in Table 1, where the BPCU is abbreviation of bit per channel use. The complexity-accuracy tradeoff parameter W is set to be W=300. Noting that the fixed power allocation between users is taken into consideration carefully. We suppose that there are five non-orthogonal users (M=5), where the first user (m=1) and the fourth user (n=4) are paired to carry out the NOMA communications [7,42]. Without loss of generality, the conventional OMA and cooperative communication schemes, i.e., FD/HD AF and DF relaying, are used to compare the performance of active IRS-NOMA networks [54,55]. The target rate of orthogonal users is equal to that of the non-orthogonal users, i.e., Ro=Rn+Rm, from the perspective of fairness.

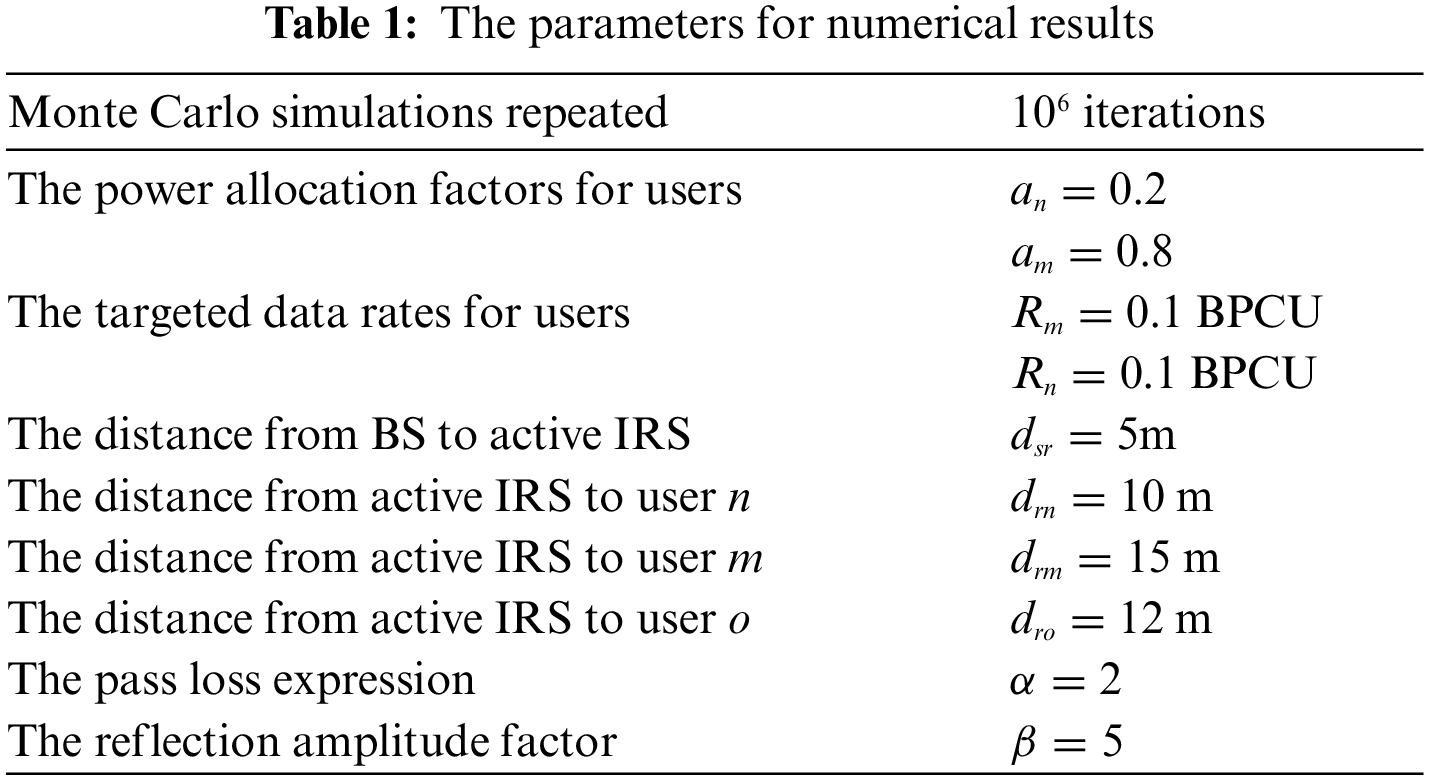
Fig. 2 plots the outage probability of active IRS-NOMA networks vs. SNR for a simulation setting with K=4, P=2, Q=2, β=5, Rn=0.2 BPCU, and Rm=0.1 BPCU. The black diamond and square curves of outage probability for user n and user m are plotted based on the analytical results in (10) and (13), respectively. The red right triangle curve of outage probability for user o is plotted according to (16). The exact outage behaviors of active IRS-NOMA networks are presented by Monte Carlo simulations and perfectly match the derived theoretical results. The asymptotic outage probabilities of user n and user m for active IRS-NOMA networks with the case Q=1 are plotted based on (18) and (22), respectively. The asymptotic outage probability of user o for active IRS-OMA networks with the case Q=1 is plotted according to (26). As can be seen from the figure, the approximated outage probability of user n and user m coincides with theoretical results in the high SNR region. The first important observation is that the outage behaviors of user n and user m for active IRS-NOMA networks are better than that of FD/HD AF and DF relaying, which also verifies the sights in Remark 1 and Remark 3. The reason behind this phenomenon is that the active IRS is capable of producing the line-of-sight between the BS and desired users. It can be seen that although the active IRS brings the amplification noise, it can still provide the enhanced outage behaviors than conventional cooperative communication schemes. Another important observation is that the outage probability of user n is better than that of user m, while the outage probability of user m is inferior to that of user o. This is due to the fact that active IRS-NOMA networks is capable of providing users’ fairness in comparison to active IRS-OMA networks.

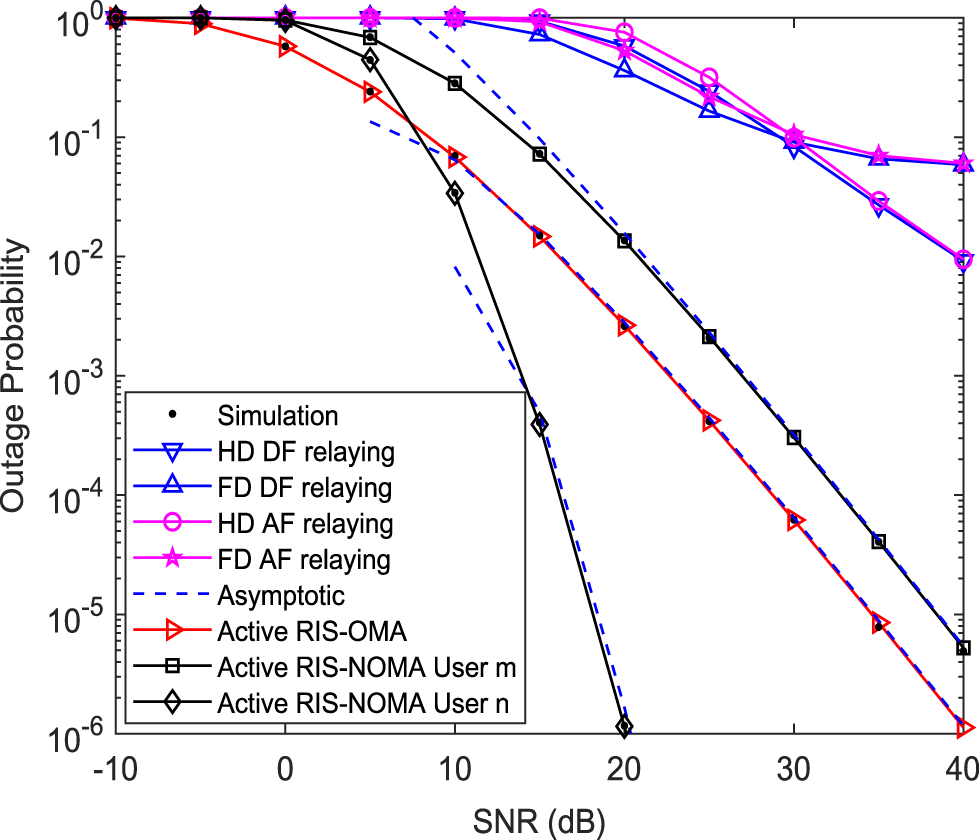
Figure 2: Outage probability vs. the transmit SNR, with K=2, P=2, Q=1, β=5, Rn=0.2 BPCU, and Rm=0.1 BPCU

Fig. 3 plots the outage probability of active IRS-NOMA networks vs. SNR for a simulation setting with K=2, P=2, Q=1, β=5, Rn=0.1 BPCU, and Rm=0.1 BPCU. The outage probability of passive IRS-NOMA networks is selected as the benchmark. More specifically, the blue circle and lower triangle curves of outage probability for user n and user m in passive IRS-NOMA networks are plotted based on (11) and (14), respectively. One can be seen easily that the corresponding simulation and analytical results are overlapped together, which verifies the correctness of the theoretical results derived from the above section. The asymptotic outage probability of user n and user m with the case Q=1 for passive IRS-NOMA networks are plotted according to (20) and (24), respectively. The approximated outage probabilities of passive IRS-NOMA networks finally converge to theoretical results at high SNRs. One of the main insights observed in figure is that the outage probabilities of active IRS-NOMA networks outperform that of passive IRS-NOMA networks. This is due to the fact active IRS can overcome the influence of multiplicative fading compared to passive IRS. We also observe that the active/passive IRS-NOMA networks provide a diversity order that is related with the number of reflection elements and channel order. The amplified noise introduced by active IRS does not lead to the poor outage behaviors.

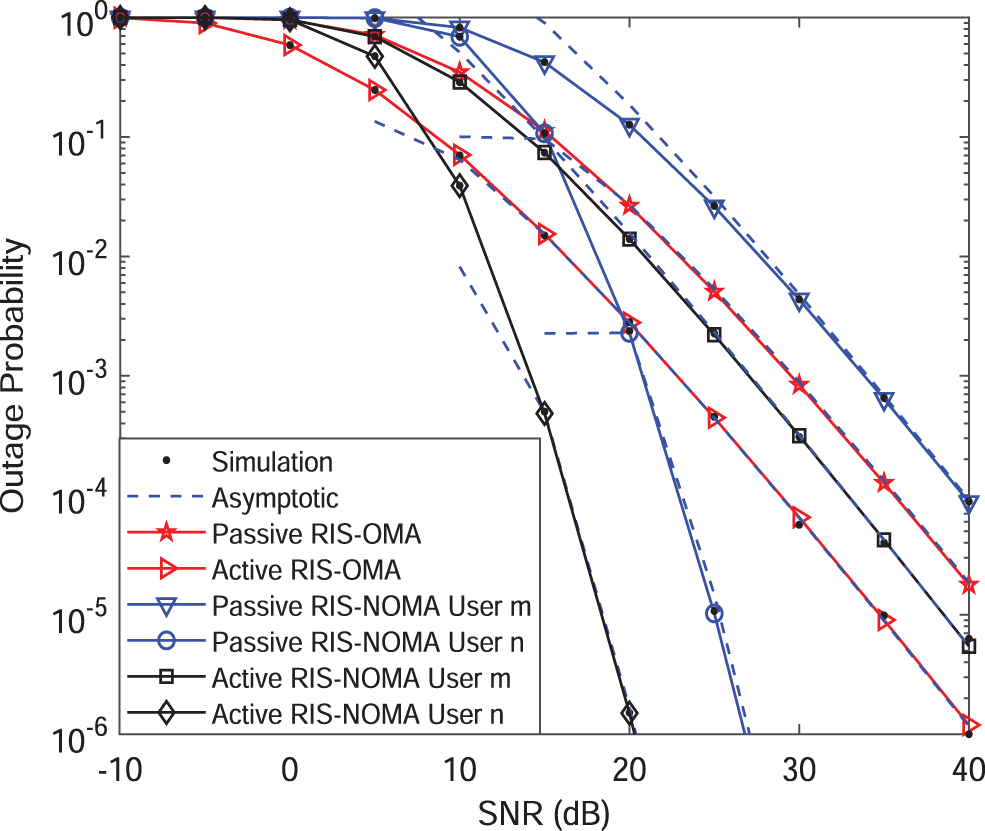
Figure 3: Outage probability vs. the transmit SNR, with K=2, P=2, Q=1, β=5, Rn=0.1 BPCU, and Rm=0.1 BPCU

Fig. 4 plots the outage probability of active IRS-NOMA networks vs. SNR for the different reflection amplitude factors with K=2, P=2, Q=1, β=5, Rn=0.1 BPCU, and Rm=0.1 BPCU. The asymptotic outage probabilities of user n and user m with Q=2 for active IRS-NOMA networks are plotted based on (19) and (23), separately. Additionally, the asymptotic outage probabilities of user n and user m with Q=2 for passive IRS-NOMA networks are plotted according to (21) and (25), separately. It can be observed that the reflection amplitude factors bring enhanced outage performance. As the reflection amplitude factors increase, the active IRS-NOMA networks are capable of attaining much better outage behaviors at low SNRs. This indicates that the active IRS-NOMA tends to achieve superior performance. The main reason is that active IRS-NOMA can utilize a small amount of power to amplify the attenuated signal after transmission in the first hop, and thus significantly increase the signal strength received by the non-orthogonal users. As a result, it is important to design the active IRS-NOMA system, where the IRS can reconfigure its amplification gain according to the requirements of different scenarios.

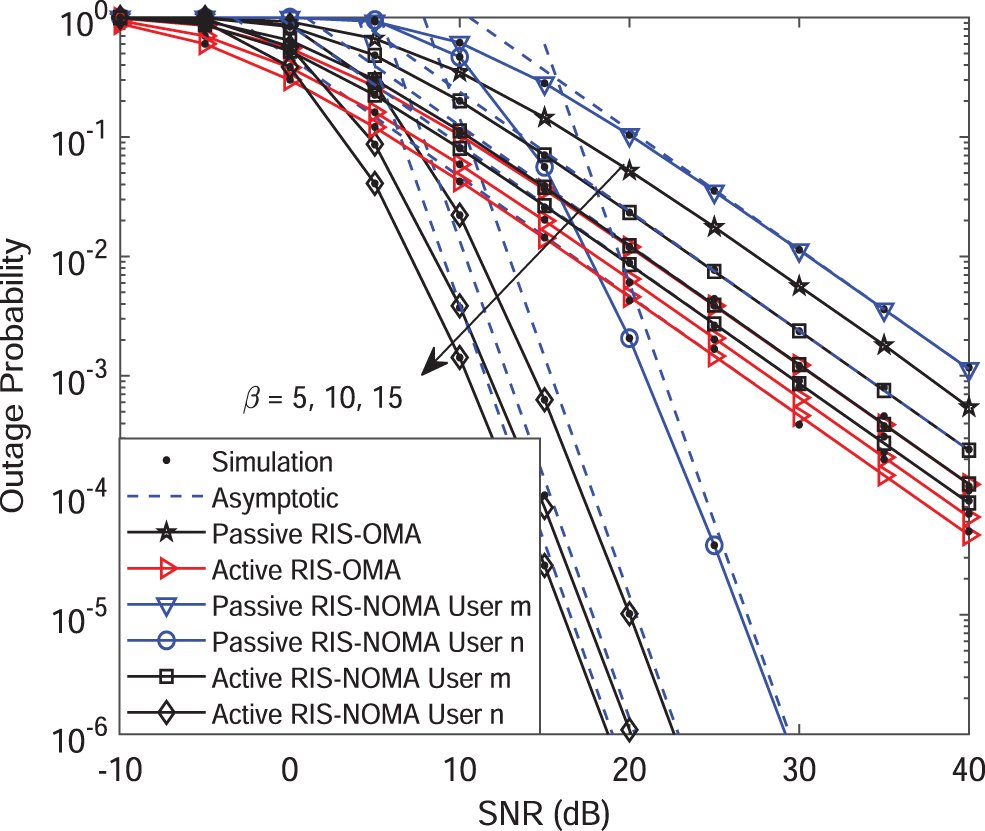
Figure 4: Outage probability vs. the transmit SNR, with K=2, P=1, Q=2, Rn=0.2 BPCU, and Rm=0.1 BPCU

Fig. 5 plots the outage probability of active IRS-NOMA networks vs. SNR for the different reflection elements with P=1, β=5, Rn=0.3 BPCU, and Rm=0.3 BPCU. We can observe that the active RIS-NOMA networks are capable of attaining better outage probability in comparison to passive IRS-NOMA. As the number of reflection elements grows, the outage behaviors of active/passive IRS-NOMA become superior. The main reason behind this is that active IRS depletes the amount of power to supply its amplifier. Apart from this, another reason is that the larger reflection elements lead to stronger amplification noise at the user ends. Moreover, Fig. 6 plots the outage probability of active IRS-NOMA networks vs. SNR for different distances between the BS and active IRS. As can be seen from the figure that as the distance from the BS to passive IRS increases, the outage probability of active IRS-NOMA becomes larger compared to the previous distance. The key reason is that the longer distance between the BS and active IRS, the incident signal attenuation is relatively large. At the same time, we can notice that the outage probability of users increases slowly. This is due to the fact that active IRS amplifies the incident signals and enhances the link performance from active IRS to users.

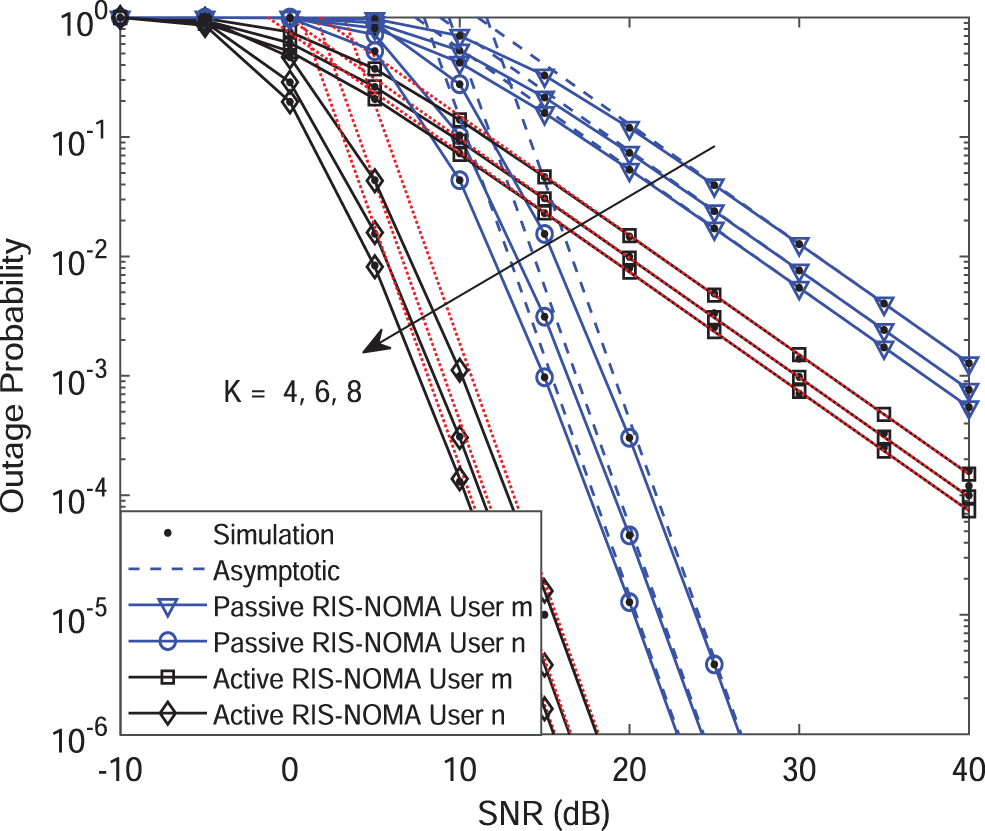
Figure 5: Outage probability vs. the transmit SNR, with P=1, β=10, Rn=0.3 BPCU, and Rm=0.3 BPCU

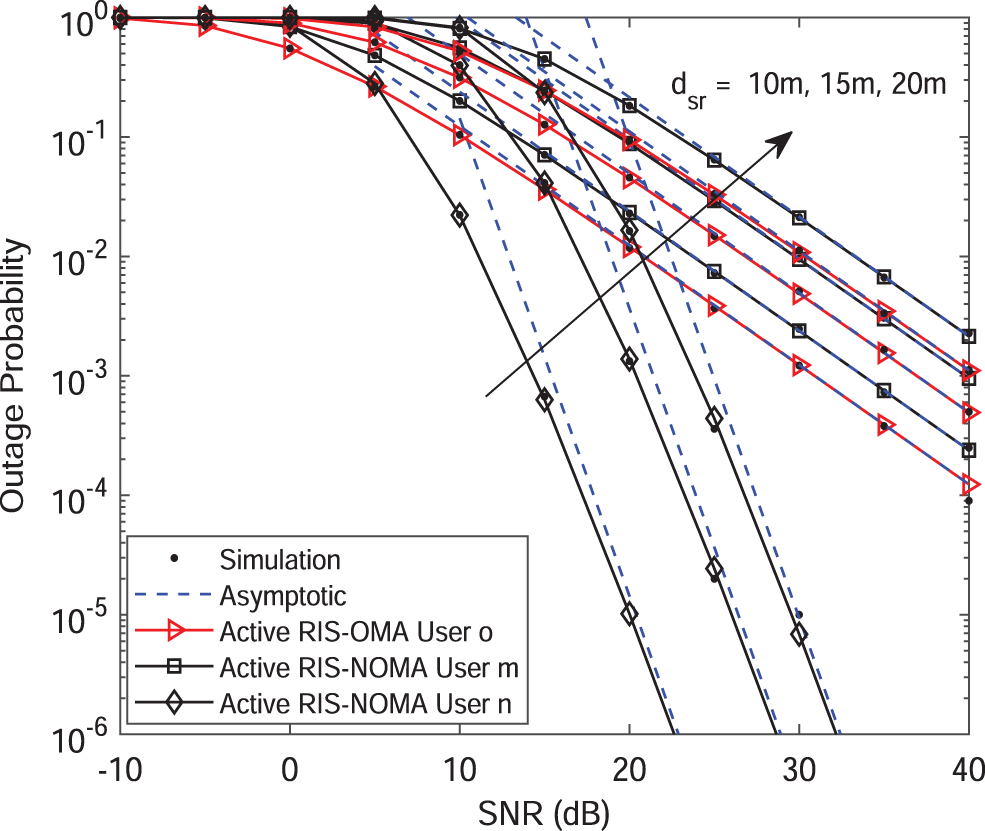
Figure 6: Outage probability vs. the transmit SNR, with K=2, P=2, Q=1, β=5, Rn=0.2 BPCU, and Rm=0.1 BPCU

Fig. 7 plots the outage probability of active IRS-NOMA networks vs. SNR for the different target rates with K=4, P=2, Q=2, and β=5. The size of the user’s target rate has an impact on outage performance of active IRS-NOMA networks. With the increase of target rate value, the outage probability of user n and user m becomes inferior for active IRS-NOMA networks. This phenomenon indicates that active RIS-NOMA can better meet the requirements for Internet of Things scenarios, i.e., low data rate and so on. Immediately after, Fig. 8 plots the outage probability of active IRS-NOMA networks vs. SNR for the different pass loss exponents with K=4, P=2, Q=2, β=5, Rn=0.2 BPCU, and Rm=0.1 BPCU. We can observe that as the value of pass loss exponents increases, the outage probability of active RIS assisted NOMA and OMA becomes smaller in the high SNR region. It is shown that active IRS can improve the enhanced performance when there are many obstacles around the user, i.e., urban cellular shadow scenario. The basic reason for this behavior is that active IRS-NOMA/OMA amplifies the incident superposed signal and overcomes the problem of signal attenuation. On the contrary, active IRS-NOMA/OMA have better outage behaviors with a small pass loss exponent, i.e., free space scenario, in contrast to the larger pass loss exponent in the low SNR region. This is because that the free space is easier for signal transmission under the same power consumed by active IRS.

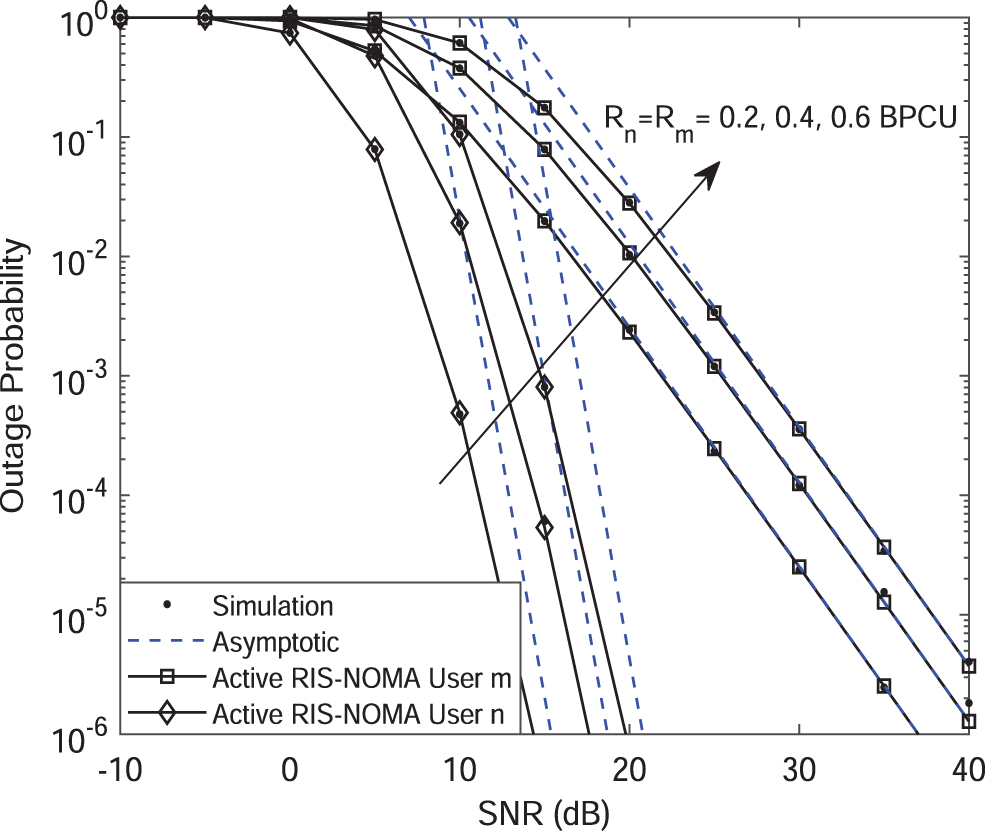
Figure 7: Outage probability vs. the transmit SNR, with K=4, P=2, Q=2, and β=5

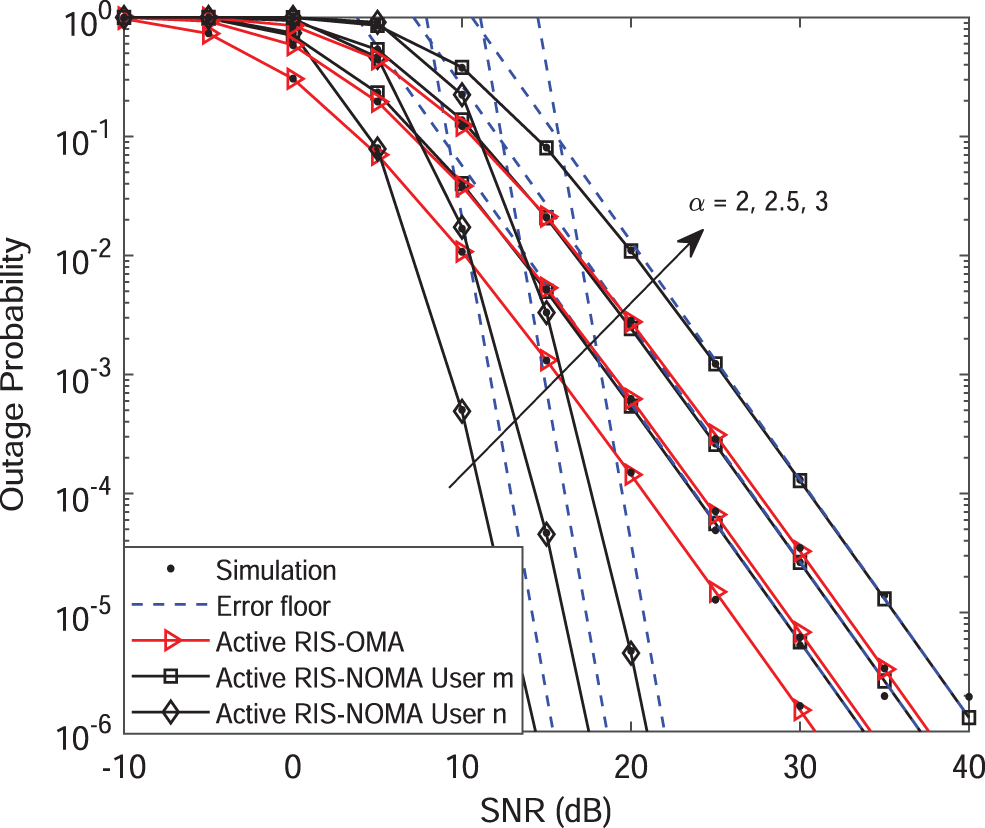
Figure 8: Outage probability vs. the transmit SNR, with K=4, P=2, Q=2, β=5, Rn=0.2 BPCU, and Rm=0.1 BPCU

Fig. 9 plots the delay-sensitive system throughput of active IRS-NOMA networks vs. SNR for a simulation setting with K=4, P=2, Q=2, Rn=0.2 BPCU, and Rm=0.1 BPCU. The system throughput of active/passive IRS-NOMA networks in delay-sensitive transmission mode is plotted based on (28). It is observed that the system throughput of active/passive IRS-NOMA precede that of conventional FD/HD DF and AF relaying. The main reasons are that: i) IRS usually operates in FD mode and does not require the advanced strong self-interference cancellation scheme; and ii) NOMA is able to serve multiple users and has higher spectral efficiency relative to OMA communications. We also can see that the delay-sensitive system throughput of active IRS-NOMA outperforms that of passive IRS-NOMA. With the increasing of reflection amplitude factor, the active IRS-NOMA provides the enhanced delay-sensitive system throughput. This due to the fact that active-IRS NOMA is to amplify the incident signal and improve the signal strength at users.

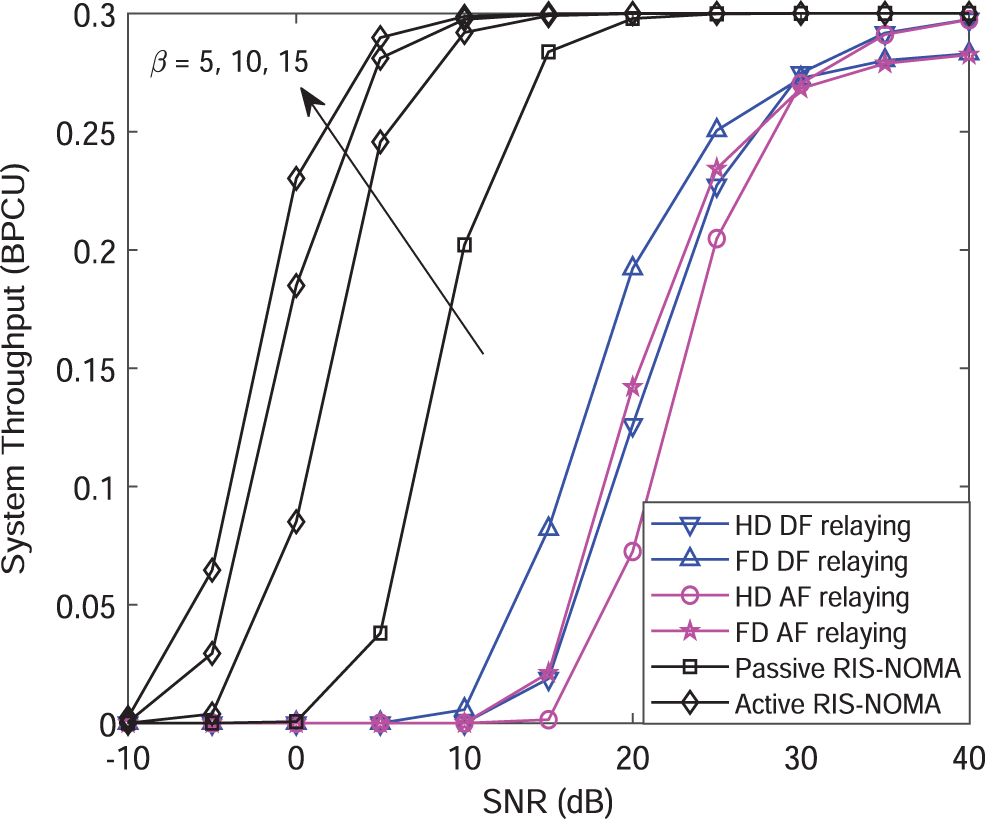
Figure 9: The delay-sensitive system throughput vs. the transmit SNR, with K=4, P=2, Q=2, Rn=0.2 BPCU, and Rm=0.1 BPCU

5  Conclusion

In this paper, the active IRS has been introduced into NOMA networks to help BS forward the incident signals. More specifically, we have investigated the performance of active IRS-NOMA networks by invoking a 1-bit coding scheme. The approximated expressions of outage probability for active/passive IRS-NOMA networks have been derived in detail. Based on these, the diversity orders of user n and user m were achieved for active IRS-NOMA networks. The diversity orders of active IRS-NOMA networks were also in connection with reflection elements and channel order. The amplification noise introduced by active IRS-NOMA did not lead to a worse performance relative to passive IRS-NOMA. In addition, we have studied the impact of reflection amplitude factor on system performance. Numerical results have shown that the outage performance of active IRS-NOMA outperforms that of passive IRS-NOMA and conventional cooperative communications. Finally, the system throughput of active/passive IRS-NOMA has been discussed in a delay-sensitive transmission mode. The promising future research direction is to consider the impact of hardware impairments and limited phase resolution on active IRS-NOMA networks.

Funding Statement: This work was supported by the National Natural Science Foundation of China Grant 61901043.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1Note that the amplification function of active IRS’ reflecting elements can be implemented by the current-inverting converters or tunnel diode and so on [51,52].

References

1. You, X., Wang, C., Huang, J. (2021). Towards 6G wireless communication networks: Vision, enabling technologies, and new paradigm shifts. Science China-Information Sciences, 64(1), 110301:1–110301:74. https://doi.org/10.1007/s11432-020-2955-6 [Google Scholar] [CrossRef]

2. Saad, W., Bennis, M., Chen, M. (2020). A vision of 6G wireless systems: Applications, trends, technologies, and open research problems. IEEE Network, 34(3), 134–142. https://doi.org/10.1109/MNET.001.1900287 [Google Scholar] [CrossRef]

3. Ding, Z., Liu, Y., Choi, J., Sun, Q., Elkashlan, M. et al. (2017). Application of non-orthogonal multiple access in LTE and 5G networks. IEEE Communications Magazine, 55(2), 185–191. https://doi.org/10.1109/MCOM.2017.1500657CM [Google Scholar] [CrossRef]

4. Liu, Y., Yi, W., Ding, Z., Liu, X., Dobre. et al. (2021). Application of NOMA in 6G networks: Future vision and research opportunities for next generation multiple access. https://arxiv.org/abs/2103.02334v1 [Google Scholar]

5. Bouzinis, P. S., Diamantoulakis, P. D., Karagiannidis, G. K. (2022). Wireless federated learning WFL for 6G networks-part II: The compute-then-transmit NOMA paradigm. IEEE Communications Letters, 26(1), 8–12. [Google Scholar]

6. Tse, D., Viswanath, P. (2005). Fundamentals of wireless communication. Cambridge, UK: Cambridge University Press. [Google Scholar]

7. Ding, Z., Yang, Z., Fan, P., Poor, H. V. (2014). On the performance of non-orthogonal multiple access in 5G systems with randomly deployed users. IEEE Signal Processing Letters, 21(12), 1501–1505. https://doi.org/10.1109/LSP.2014.2343971 [Google Scholar] [CrossRef]

8. Yue, X., Qin, Z., Liu, Y., Kang, S., Chen, Y. (2018). A unified framework for non-orthogonal multiple access. IEEE Transactions on Communications, 66(11), 5346–5359. https://doi.org/10.1109/TCOMM.2018.2842217 [Google Scholar] [CrossRef]

9. Wu, Q., Zhang, R. (2020). Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network. IEEE Transactions on Communications, 58(1), 106–112. [Google Scholar]

10. ElMossallamy, M. A., Zhang, H., Song, L., Seddik, K. G., Han, Z. et al. (2020). Reconfigurable intelligent surfaces for wireless communications: Principles, challenges, and opportunities. IEEE Transactions on Cognitive Communications and Networking, 6(3), 990–1002. https://doi.org/10.1109/TCCN.2020.2992604 [Google Scholar] [CrossRef]

11. Liang, Y. C., Chen, J., Long, R., He, Z., Renzo, M. D. (2021). Reconfigurable intelligent surfaces for smart wireless environments: Channel estimation, system design and applications in 6G networks. Science China-Information Sciences, 64(10), 200301:1–200301:21. https://doi.org/10.1007/s11432-020-3261-5 [Google Scholar] [CrossRef]

12. Najafi, M., Jamali, V., Schober, R., Poor, H. V. (2021). Physics-based modeling and scalable optimization of large intelligent reflecting surfaces. IEEE Transactions on Communications, 69(4), 2673–2691. https://doi.org/10.1109/TCOMM.2020.3047098 [Google Scholar] [CrossRef]

13. Basar, E., Poor, H. V. (2021). Present and future of reconfigurable intelligent surface-empowered communications. IEEE Signal Processing Magazine, 38(6), 146–152. [Google Scholar]

14. Lonǎar, J., Šipuš, Z. (2020). Challenges in design of power-amplifying active metasurfaces. 2020 International Symposium ELMAR. [Google Scholar]

15. Zhang, Z., Dai, L., Chen, X., Liu, C., Yang, F. et al. (2022). Active RIS vs. passive RIS: Which will prevail in 6G? https://arxiv.org/abs/2103.15154v4 [Google Scholar]

16. Liu, K., Zhang, Z., Dai, L., Xu, S., Yang, F. (2022). Active reconfigurable intelligent surface: Fully-connected or sub-connected? IEEE Communications Letters, 26(1), 167–171. https://doi.org/10.1109/LCOMM.2021.3119696 [Google Scholar] [CrossRef]

17. Ding, Z., Peng, M., Poor, H. V. (2015). Cooperative non-orthogonal multiple access in 5G systems. IEEE Communications Letters, 19(8), 1462–1465. https://doi.org/10.1109/LCOMM.2015.2441064 [Google Scholar] [CrossRef]

18. Liu, Y., Ding, Z., Elkashlan, M., Poor, H. V. (2016). Cooperative non-orthogonal multiple access with simultaneous wireless information and power transfer. IEEE Journal on Selected Areas in Communications, 34(4), 938–953. https://doi.org/10.1109/JSAC.2016.2549378 [Google Scholar] [CrossRef]

19. Yue, X., Liu, Y., Kang, S., Nallanathan, A., Ding, Z. (2018). Exploiting full/half-duplex user relaying in NOMA systems. IEEE Transactions on Communications, 66(2), 560–575. https://doi.org/10.1109/TCOMM.2017.2749400 [Google Scholar] [CrossRef]

20. Lv, L., Chen, J., Ni, Q., Ding, Z. (2017). Design of cooperative non-orthogonal multicast cognitive multiple access for 5G systems: User scheduling and performance analysis. IEEE Transactions on Communications, 65(6), 2641–2656. https://doi.org/10.1109/TCOMM.2017.2677942 [Google Scholar] [CrossRef]

21. Zhang, Z., Ma, Z., Xiao, M., Ding, Z., Fan, P. (2017). Full-duplex device-to-device-aided cooperative nonorthogonal multiple access. IEEE Transactions on Vehicular Technology, 66(5), 4467–4471. [Google Scholar]

22. Wang, X., Jia, M., Ho, I. W. H., Guo, Q., Lau, F. C. M. (2019). Exploiting full-duplex two-way relay cooperative non-orthogonal multiple access. IEEE Transactions on Communications, 67(4), 2716–2729. [Google Scholar]

23. Men, J., Ge, J., Zhang, C. (2017). Performance analysis for downlink relaying aided non-orthogonal multiple access networks with imperfect CSI over Nakagami-m fading. IEEE Access, 5, 998–1004. [Google Scholar]

24. Li, X., Li, J., Liu, Y., Ding, Z., Nallanathan, A. (2020). Residual transceiver hardware impairments on cooperative NOMA networks. IEEE Transactions on Wireless Communications, 19(1), 680–695. [Google Scholar]

25. Abbasi, O., Ebrahimi, A., Mokari, N. (2019). Noma inspired cooperative relaying system using an AF relay. IEEE Wireless Communications Letters, 8(1), 261–264. [Google Scholar]

26. ElMossallamy, M. A., Zhang, H., Song, L., Seddik, K. G., Han, Z. et al. (2020). Reconfigurable intelligent surfaces for wireless communications: Principles, challenges, and opportunities. IEEE Transactions on Cognitive Communications and Networking, 6(3), 990–1002. [Google Scholar]

27. Liu, Y., Liu, X., Mu, X., Hou, T., Xu, J. et al. (2021). Reconfigurable intelligent surfaces: Principles and opportunities. IEEE Communications Surveys Tutorials, 23(3), 1546–1577. https://doi.org/10.1109/COMST.2021.3077737 [Google Scholar] [CrossRef]

28. Yang, H., Xiong, Z., Zhao, J., Niyato, D., Wu, Q. et al. (2021). Intelligent reflecting surface assisted anti-jamming communications: A fast reinforcement learning approach. IEEE Transactions on Wireless Communications, 20(3), 1963–1974. https://doi.org/10.1109/TWC.2020.3037767 [Google Scholar] [CrossRef]

29. Huang, C., Zappone, A., Alexandropoulos, G. C., Debbah, M., Yuen, C. (2019). Reconfigurable intelligent surfaces for energy efficiency in wireless communication. IEEE Transactions on Wireless Communications, 18(8), 4157–4170. https://doi.org/10.1109/TWC.2019.2922609 [Google Scholar] [CrossRef]

30. Kudathanthirige, D., Gunasinghe, D., Amarasuriya, G. (2020). Performance analysis of intelligent reflective surfaces for wireless communication. IEEE International Communication Conference, pp. 1–6. Dublin, IRL. [Google Scholar]

31. Zhang, H., Di, B., Song, L., Han, Z. (2020). Reconfigurable intelligent surfaces assisted communications with limited phase shifts: How many phase shifts are enough? IEEE Transactions on Vehicular Technology, 69(4), 4498–4502. https://doi.org/10.1109/TVT.2020.2973073 [Google Scholar] [CrossRef]

32. Cui, Z., Guan, K., Zhang, J., Zhong, Z. (2021). SNR coverage probability analysis of RIS-aided communication systems. IEEE Transactions on Vehicular Technology, 70(4), 3914–3919. https://doi.org/10.1109/TVT.2021.3063408 [Google Scholar] [CrossRef]

33. Yildirim, I., Uyrus, A., Basar, E. (2021). Modeling and analysis of reconfigurable intelligent surfaces for indoor and outdoor applications in future wireless networks. IEEE Transactions on Communications, 69(2), 1290–1301. https://doi.org/10.1109/TCOMM.2020.3035391 [Google Scholar] [CrossRef]

34. Long, R., Liang, Y. C., Pei, Y., Larsson, E. G. (2021). Active reconfigurable intelligent surface-aided wireless communications. IEEE Transactions on Communications, 20(8), 4962–4975. [Google Scholar]

35. You, C., Zhang, R. (2021). Wireless communication aided by intelligent reflecting surface: Active or passive? IEEE Wireless Communications Letters, 10(12), 2659–2663. https://doi.org/10.1109/LWC.2021.3111044 [Google Scholar] [CrossRef]

36. Zhi, K., Pan, C., Ren, H., Chai, K. K., Elkashlan, M. (2022). Active RIS vs. passive RIS: Which is superior with the same power budget? IEEE Communications Letters, 26(5), 1150–1154. https://doi.org/10.1109/LCOMM.2022.3159525 [Google Scholar] [CrossRef]

37. Zeng, P., Qiao, D., Wu, Q., Wu, Y. (2021). Active IRS aided WPCNs: A new paradigm towards higher efficiency and wider coverage. https://arxiv.org/abs/2111.11600v1 [Google Scholar]

38. Liu, Y., Mu, X., Liu, X., di Renzo, M., Ding, Z. et al. (2022). Reconfigurable intelligent surface-aided multi-user networks: Interplay between NOMA and RIS. IEEE Wireless Communications, 29(2), 169–176. https://doi.org/10.1109/MWC.102.2100363 [Google Scholar] [CrossRef]

39. Ding, Z., Lv, L., Fang, F., Dobre, O. A., Karagiannidis, G. K. et al. (2022). A state-of-the-art survey on reconfigurable intelligent surface-assisted non-orthogonal multiple access networks. Proceedings of the IEEE, 110(9), 1358–1379. https://doi.org/10.1109/JPROC.2022.3174140 [Google Scholar] [CrossRef]

40. Hou, T., Liu, Y., Song, Z., Sun, X., Chen, Y. et al. (2020). Reconfigurable intelligent surface aided NOMA networks. IEEE Journal on Selected Areas in Communications, 38(11), 2575–2588. https://doi.org/10.1109/JSAC.2020.3007039 [Google Scholar] [CrossRef]

41. Ding, Z., Schober, R., Poor, H. V. (2020). On the impact of phase shifting designs on IRS-NOMA. IEEE Wireless Communications Letters, 9(10), 1596–1600. https://doi.org/10.1109/LWC.2020.2991116 [Google Scholar] [CrossRef]

42. Yue, X., Liu, Y. (2022). Performance analysis of intelligent reflecting surface assisted NOMA networks. IEEE Transactions on Wireless Communications, 21(4), 2623–2636. https://doi.org/10.1109/TWC.2021.3114221 [Google Scholar] [CrossRef]

43. Li, X., Xie, Z., Chu, Z., Menon, V. G., Mumtaz, S. et al. (2022). Exploiting benefits of IRS in wireless powered NOMA networks. IEEE Transactions on Green Communications and Networking, 6(1), 175–186. https://doi.org/10.1109/TGCN.2022.3144744 [Google Scholar] [CrossRef]

44. Li, X., Xie, Z., Huang, G., Zhang, J., Zeng, M. et al. (2022). Sum rate maximization for RIS-aided NOMA with direct links. IEEE Networking Letters, 4(2), 55–58. https://doi.org/10.1109/LNET.2022.3161981 [Google Scholar] [CrossRef]

45. Khaleel, A., Basar, E. (2022). A novel NOMA solution with RIS partitioning. IEEE Journal of Selected Topics in Signal Processing, 16(1), 70–81. https://doi.org/10.1109/JSTSP.2021.3127725 [Google Scholar] [CrossRef]

46. Cheng, Y., Li, K. H., Liu, Y., Teh, K. C., Karagiannidis, G. K. (2021). Non-orthogonal multiple access (NOMA) with multiple intelligent reflecting surfaces. IEEE Transactions on Wireless Communications, 20(11), 7184–7195. https://doi.org/10.1109/TWC.2021.3081423 [Google Scholar] [CrossRef]

47. Liu, Z., Yue, X., Zhang, C., Liu, Y., Wang, Y. et al. (2022). Performance analysis of reconfigurable intelligent surface assisted two-way NOMA networks. IEEE Transactions on Vehicular Technology, 71(12), 13091–13104. [Google Scholar]

48. Lv, L., Wu, Q., Li, Z., Ding, Z., Al-Dhahir, N. et al. (2022). Covert communication in intelligent reflecting surface-assisted NOMA systems: Design, analysis, and optimization. IEEE Transactions on Wireless Communications, 21(3), 1735–1750. https://doi.org/10.1109/TWC.2021.3106346 [Google Scholar] [CrossRef]

49. Wang, H., Shi, Z., Fu, Y., Fu, S. (2022). On intelligent reflecting surface-assisted NOMA uplinks with imperfect SIC. IEEE Wireless Communication Letters, 11(7), 1518–1522. https://doi.org/10.1109/LWC.2022.3177733 [Google Scholar] [CrossRef]

50. Chen, G., Wu, Q., He, C., Chen, W., Tang, J. et al. (2022). Active IRS aided multiple access for energy-constrained IoT systems. https://arxiv.org/abs/2201.12565v1 [Google Scholar]

51. Kishor, K. K., Hum, S. V. (2012). An amplifying reconfigurable reflectarray antenna. IEEE Transactions on Antennas and Propagation, 60(1), 197–205. https://doi.org/10.1109/TAP.2011.2167939 [Google Scholar] [CrossRef]

52. Amato, F., Peterson, C. W., Degnan, B. P., Durgin, G. D. (2018). Tunneling RFID tags for long-range and low-power microwave applications. IEEE Journal of Radio Frequency Identification, 2(2), 93–103. https://doi.org/10.1109/JRFID.2018.2852498 [Google Scholar] [CrossRef]

53. Gradshteyn, I. S., Ryzhik, I. M. (2000). Table of integrals, series and products. sixth edition. New York, NY, USA: Academic Press. [Google Scholar]

54. Laneman, J. N., Tse, D. N. C., Wornell, G. W. (2004). Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Transactions on Information Theory, 50(12), 3062–3080. [Google Scholar]

55. Kwon, T., Lim, S., Choi, S., Hong, D. (2010). Optimal duplex mode for DF relay in terms of the outage probability. IEEE Transactions on Vehicular Technology, 59(7), 3628–3634. [Google Scholar]

56. Liu, H., Ding, H., Xiang, L., Yuana, J., Zhenga, L. (2014). Outage and ber performance analysis of cascade channel in relay networks. Proceedings the 9th International Conference on Future Networks and Communications. [Google Scholar]

57. David, H. A., Nagaraja, H. N. (2003). Order statistics. Third edition. New York: John Wiley. [Google Scholar]

58. Abramowitz, M., Stegun, I. (1972). Handbook of mathematical functions with formulas, graphs, and mathematical tables. New York, NY, USA: Dover. [Google Scholar]

Appendix A: Proof of Theorem 1

The proof process starts by assuming θ = vp and the SINRs in (2) and (3) can be streamlined into γ¯n→m=β|vpHDnhsr|2ρamβ|vpHDnhsr|2ρan+ξβ‖vpHDn‖2+1 and γ¯n=β|vpHDnhsr|2ρanξβ‖vpHDn‖2+1, respectively. Upon substituting γ¯n→m and γ¯n into (9), the outage probability of user n for active IRS-NOMA networks can calculated as follows:

Pn,act=Pr[|vpHDnhsr|2<ζ(βξ‖vpHDn‖2+1)]=Pr[|∑k=1Qhsrkhrnk|2⏟Y<dsrαdrnαζ(βξdrn−α∑k=1Q|hrnk|2⏟X+1)]=∫0∞fX(x)FY[dsrαdrnαζ(βξdrn−αx+1)]dx,(A.1)

where ξ=1, ζ=Δmax(τ,ς), τ=γthmβρ(am−γthman) with the condition of am>γthman, and ς=γthnβρan. As stated in [41,56], the CDF of random variable Y unsorted can be given by

F¯Y(y)=1−2Γ(Q)yQ/Q22KQ(2y),(A.2)

where Γ(⋅) denotes the gamma function and Kv(⋅) is the modified Bessel function of the second kind with order v. Further applying the order statistics [8,57] in the above equation, the CDF of random variable X sorted is given by

FY(y)=M!(M−n)!(n−1)!∑l=0M−n(M−nl)×(−1)ln+l[1−2Γ(Q)yQ/Q22KQ(2y)]n+l,(A.3)

where (M−nl)=(M−n)!l!(M−n−l)!. It may be readily observed that the random variable X obeys a Gamma distribution having the parameters of (Q,1) and its PDF can be given by

fX(x)=xQ−1e−x(Q−1)!.(A.4)

Upon substituting (A.3) and (A.4) into (A.1), the outage probability of user n for active IRS-NOMA networks is expressed as

Pn,act=ϕn∑l=0M−n(M−nl)(−1)ln+l∫0∞xQ−1e−x×{1−2Γ(Q)(Ξnx+Υn)Q/Q22KQ(2Ξnx+Υn)}n+ldx,(A.5)

where ϕn=M!(M−n)!(n−1)!(Q−1)!, Ξn=dsrαζβξ, and Υn=dsrαdrnαζ and β is the reflection amplitude factor.

As a further advance, the Gauss-Laguerre integration [58] can be selected to approximate the above equation. More specifically, this integration is expressed as ∫0∞f(x)e−xdx≈∑w=1WHwf(xw), where Hw=(W!)2xw[LW+1(xw)]2 and xw are the weight and abscissas of Gauss-Laguerre integration, respectively. LW(x)=exW!ddxm(xWe−x) is the m-th Laguerre polynomial. The parameter W is to ensure a complexity-accuracy tradeoff. Applying Gauss-Laguerre integration in (A.5), the outage probability of user n for active IRS-NOMA networks can be approximated as

Pn,act≈ϕn∑l=0M−n∑w=1W(M−nl)(−1)ln+lHwxwQ−1[1−2Γ(Q)∑l=0M−n×[Ξnxw+Υn]Q/Q22KQ(2Ξnxw+Υn)]n+l.(A.6)

With the help of 1-bit coding scheme, vp, i.e., vpHvl=0 for p≠l is selected from V to maximize the SINRs, where the random variables |vpHDnhsr|2 and |vlHDnhsr|2 are independent of each other. Hence choosing an optimal θ to maximize the SINRs of (5) and (6), the outage probability of user n for active IRS-NOMA networks can be finally approximated as

Pn,act≈{ϕn∑l=0M−n∑w=1W(M−nl)(−1)ln+lHwxwQ−1[1−2Γ(Q)∑l=0M−n×[Ξnxw+Υn]Q/Q22KQ(2Ξnxw+Υn)]n+l}P.(A.7)

The proof is completed.

Appendix B: Proof of Theorem 2

When θ is set to be vp, the SINR of (7) is simplified as γ¯m=β|vpHDmhsr|2ρamβ|vpHDmhsr|2ρan+ξβ‖vpHDm‖2+1. Upon substituting γ¯m into (12), the outage probability of user m for active IRS-NOMA networks can be calculated as follows:

Pm=Pr[|vpHDmhsr|2<τ(ξβ‖vpHDm‖2+1)]=Pr[|∑k=1Qhsrkhrmk|2⏟Z1<τdsrαdrmα(βξdrm−α∑k=1Q|hrmk|2⏟Z2+1)]=∫0∞fZ2(z2)FZ1[dsrαdrmατ(βξdrm−αz2+1)]dx.(B.1)

With the assistance of (A.3), the CDF of random variable Z1 can be easily attained as follows:

FZ1(z1)=M!(M−m)!(m−1)!∑l=0M−n(M−ml)×(−1)lm+l[1−2Γ(Q)z1Q/Q22KQ(2z1)]m+l.(B.2)

It is worth noting that the PDF of random variable Z2 is the same as that of random variable X in (A.4). As a result, by substituting (B.2) and (A.4) into (B.1), the outage probability of user m for active IRS-NOMA networks can be given by

Pm,act=ϕm∑l=0M−m(M−nl)(−1)lm+l∫0∞xQ−1e−x×{1−2Γ(Q)(Ξmx+Υm)Q/Q22KQ(2Ξmx+Υm)}m+ldx,(B.3)

where ϕm=M!(M−m)!(m−1)!(Q−1)!, Ξm=dsrατβξ, and Υm=dsrαdrmατ.

Then further applying Gauss-Laguerre integration in the above equation, the outage probability of user m for active IRS-NOMA networks can be approximated as

Pm,act≈ϕm∑l=0M−m∑w=1W(M−ml)(−1)lm+lHwxwQ−1[1−2Γ(Q)∑l=0M−m×[Ξmxw+Υm]Q/Q22KQ(2Ξmxw+Υm)]m+l.(B.4)

It is known from the 1-bit coding scheme that |vpHDmhsr|2 and |vlHDmhsr|2 are independent and identically distributed for p≠l. As a result, choosing an optimal θ to maximize the SINRs of (7), the outage probability of user m for active IRS-NOMA networks can be given by

Pm,act≈{ϕm∑l=0M−m∑w=1W(M−ml)(−1)lm+lxwQ−1Hw[1−2Γ(Q)(Ξmxw+Υm)Q/Q22KQ(2Ξmxw+Υm)]m+l}P.(B.5)

The proof is completed.