High Utility Periodic Frequent Pattern Mining in Multiple Sequences

1  Introduction

With the continuous development of information technology, the modern internet of things (IoT) generates a large amount of complex data that cannot be efficiently acquired, stored, managed, and analyzed using traditional data management techniques. Data mining involves extracting potentially valuable information from large and disorganized data [1,2]; it uses a practical application perspective to extract meaningful information from large amounts of data to make decisions and set solutions [3,4]. Data mining combines different fields by employing other approaches, such as machine learning and statistics, to find and design algorithms for meaningful mining patterns [4–6]. Data mining classifies large amounts of data to identify patterns of interest [3,4]. To date, data mining has been applied to various areas, such as the IoT [7,8], machine learning [9–11], optimization [12,13], smart cities [14–16], and wireless sensors networks [17,18], etc.

Frequent pattern mining (FPM) is an essential branch of data mining research aimed at mining frequently occurring patterns [4,5,19]. For example, FPM has been used to find frequent customer purchases in transaction databases. With the development of FPM in various fields, several algorithms have been proposed for different types of applications, such as malware detection [20], machine learning [21], image classification [22], and activity detection [23]. These algorithms use different measures to identify meaningful patterns to meet the needs of the relevant field [4]. FPM algorithms can be used to determine the correlation between items or transactions in a database. However, they do not consider the order of precedence between transactions [24]. More specifically, FPM algorithms can identify a set of products that customers frequently buy periodically; however, identifying the order of each purchase is impossible. The sequence of events must be considered in practical applications, such as biomedicine [25], electronic information learning [26,27], text analysis [28], website hit comments, and various other fields. For example, in online shopping applications, several customers make the same or different purchases at regular intervals. Analyzing sequential behavior over time can help merchants and e-commerce platforms to develop sales plans and improve sales strategies.

To solve the constraints of FPM, several researchers consider the temporal order between transactions (events) and offer the concept of sequential pattern mining (SPM). SPM mines frequent subsequences in a sequence of transactions. Unlike FPM, SPM considers the sequence of events or transactions [1,26,28–30]. Although SPM algorithms can find frequently occurring patterns in a set of transaction sequences, they cannot be used to find patterns that repeat in a sequence over time, which could be useful. For example, analyzing products that numerous users repeatedly buy every few days or weeks from an online shopping database helps e-commerce platforms develop sales strategies. Research on periodic pattern mining has been conducted to find periodically occurring patterns in sequence databases [31–37]. The task of periodic pattern mining is to find the events or number of events between two occurrences of a pattern in a sequence of transactions that do not exceed a user-defined maximum periodicity threshold. For example, if a customer goes to the gym once a week, and if the maximum period threshold is set to one week, the user goes to the gym at least once a week. Various algorithms have already been proposed for periodic pattern mining [36,38–42],

Existing algorithms for periodic pattern mining focus on patterns occurring periodically in a sequence (one sequence corresponds to one customer). However, this is no longer sufficient to meet real needs. For example, there might be a need to determine the behavior of multiple customers who repeatedly purchase together. Recently, an algorithm called MPFPS was proposed [43] to find periodically frequent patterns in multiple sequences. More significantly, it extends finding periodic patterns in a single sequence to finding periodic patterns that are common to a group of sequences. MPFPS defines a new measure called the periodic standard deviation to guarantee a more stable period for patterns to appear in a sequence. However, MPFPS considers patterns that only appear once in a transaction and does not consider the internal utility (e.g., number of purchases) or external utility (e.g., value, importance) of a pattern. In practical applications, considering the importance and number of patterns based on user preferences is more helpful in discovering which patterns are of higher value in a user’s periodic purchase behavior and mining significant patterns. For example, specific DNA molecules appear regularly in gene sequences [6,33]. However, each DNA molecule carries information of varying importance that directly affects the expression of certain external traits. Hence, the identification of DNA molecules that appear periodically plays an important role. Consequently, designing a new algorithm for mining high-utility periodic frequent patterns (HUPFPS) in multiple sequences is essential.

In this study, we proposed a new algorithm called MHUPFPS to mine HUPFPS in multiple sequences. In contrast to existing algorithms for periodic pattern mining, MHUPFPS considers the value (utility, profit) of patterns in a sequence database to mine patterns that are both periodic and of high value in practical applications. A new measure called the utility ratio is defined to evaluate the percentage of the utility of patterns in a sequence to identify patterns with a high utility percentage. Additionally, traditional algorithms for periodic pattern mining use a fixed number of supports to define the pattern frequency. This is obviously unpractical. In this study, sequence lengths in different databases had different characteristics. Furthermore, MHUPFPS uses a support rate to ensure the fair and effective mining of higher-utility patterns in sequences of different lengths. Moreover, to reduce the search space when MHUPFPS is performed, a new pruning strategy was designed. The key contributions of this study are as follows:

1.   To guarantee the frequency of periodic patterns in each sequence, we defined a new measure: the support ratio. Further, we proposed a high-utility periodic sequence ratio, which defined the high-utility periodic frequent patterns in multiple sequences.

2.   A pruning strategy was proposed to prune the search space. A MHUPFPS was proposed based on this pruning strategy. The proposed algorithm uses the HUPFPS-list structure to avoid scanning the database repeatedly.

3.   Experimental results show that MHUPFPS is correct and efficient in filtering several non-high utility periodic frequent patterns.

The remainder of this paper is organized as follows. Section 2 reviews previous studies related to data mining, and Section 3 presents the necessary definitions. Section 4 describes the proposed algorithm MHUPFPS and Section 5 presents the experimental results. Finally, Section 6 concludes the paper.

2  Related Work

2.1 Sequential Pattern Mining

To date, SPM has been a popular research direction that aims to mine frequent subsequences with at least a threshold minimum number of occurrences in a sequence [4,44]. The first algorithm used for sequential pattern mining was AprioriAll. The AprioriAll algorithm [29] is based on the Apriori algorithm: the mining process was the same. The difference between the two algorithms is that the AprioriAll algorithm considers the order of the last two elements of the pattern when generating the candidate patterns. An algorithm called GSP [44] has also been proposed, which is an extension of the AprioriAll algorithm. The algorithm introduces time constraints, sliding time windows, and classification hierarchy techniques to effectively reduce the number of candidate sequences that need to be scanned. Han et al. [45] proposed the concept of database prefix projection to reduce the cost of scanning the database when mining larger patterns. They then incorporated this concept into the newly proposed freespan algorithm. They further developed the PrefixSpan algorithm [46], which is an improved algorithm based on the freespan algorithm. The PrefixSpan algorithm only introduces the project suffix with the same prefix to obtain the project database. As the PrefixSpan algorithm can significantly reduce the search space and does not generate candidate sequences, the memory consumption of the PrefixSpan algorithm is reduced and relatively stable.

2.2 Utility-Based Pattern Mining

In recent years, high utility pattern mining (HUPM) has become popular in the field of data-mining. HUPM considers that each item in a transaction may have multiple purchase quantities, and each item has equal weight [47–52]. The purpose of HUPM is to find high utility patterns in a transaction database, such as a customer who buys several items in a transaction. HUPM is an important branch of data mining [50,53–55]. If the utility of a pattern is not less than a user-defined minimum utility threshold, it is considered to be a high-utility pattern (HUP). Several HUPM algorithms have been proposed, such as IHUP [50], UP-growth [54], UPgrowth+ [55], HUI-Miner [53], d2HUP [48], FHM [56], HUP-Miner [57], and EFIM [58]. The purpose of HUPM is to discover high utility item sets in transaction databases. HUPM is not only used in market basket analysis but also in website clickstream analysis and biomedical applications. Chan et al. [59] proposed a framework for mining the top-k closed utility patterns by combining positive and negative utilities to find the top-k HUP. Yao et al. [60] considered the problem of internal utility (number of purchases) and external utility (profit per unit) of a transaction to mine HUPs. Liu et al. [61] used the closure property under transaction weighting to discover HUPs and proposed a transaction-weighted utility (TWU) model. Liu et al. [53] also proposed an algorithm called HUI-miner, which uses a new utility list structure to calculate the internal and residual utility of the supported transaction patterns based on the utility list structure. As the challenges of HUPM have been further studied, HUPM algorithms have started to consider the order and utility of transactions, and countless high-utility sequential pattern mining algorithms have been proposed, such as USpan [62], ProUM [63], and HUSP-ULL [64].

2.3 Periodic Pattern Mining

The FPM has been extended from finding periodic patterns in a single sequence to finding those that are common in multiple sequences. In a sequence, a pattern that appears frequently and has two consecutive appearances with a period interval of less than the maximum period threshold is said to be periodic. The PFPM task was defined in a transaction-sequence database by Tanbeer et al. [31]. Several variants of periodic mining patterns in a single sequence have been proposed based on their approach [33–38]. For example, an algorithm called MTKPP was used to mine the top-k frequently occurring patterns in a single sequence [32–34]. Periodic patterns continue to be studied in depth, and some approaches consider the utility (profit) of the periodic patterns. For example, an algorithm called PHM was proposed to find items that are frequently purchased and highly profitable, locating patterns that occur periodically in a single sequence and are of high utility [38]. Additionally, an algorithm called PHUSPM was designed to mine high-utility periodic patterns in multiple-symbol sequences [36]. The PHUSPM algorithm considers a set of sequences as one sequence and mines periodic patterns using the same periodicity measure as for a single sequence. Recently, Philippe et al. proposed two new algorithms for periodic pattern mining in multiple sequences: MPFPS [43] and MRCPPS [65]. These algorithms proposed a new measure called the periodic standard deviation, which was used to evaluate the periodicity of the patterns in the sequence. For MPFPS [43], another new measure was proposed to define a common periodic pattern in multiple sequences: the sequence periodicity ratio (SPR). The MRCPPS algorithm identifies strongly correlated periodic patterns using the bond correlation measure, and defines a new pattern called rare correlated periodic patterns. Recently, the SPP-Growth [66] algorithm was proposed to determine stable periodic patterns in transaction databases with timestamps.

2.4 Problems of Existing Research

Most existing research on periodic patterns does not mine PFPS common to a set of sequences. To the best of our knowledge, MPFPS and MRCPPS are the only recently proposed algorithms that mine PFPS in multiple sequences. However, these algorithms assume that each item has the same weight or value and only appears once in a transaction; this obviously has limitations for practical applications. In contrast, current algorithms for PFPS use a measure called support to define the frequency of patterns; however, this measure does not apply to data with different characteristics.

3  Definition and Problem Statement

In this section, we first present the definitions of periodic and utility patterns in a single sequence [67]. Then, we consider the corresponding definitions for multiple sequences [43]. The terms pattern and itemset are used alternately in the following descriptions.

3.1 Definitions for a Single Sequence

Definition 3.1. Assume that there is a set of items (symbols) I in a sequence database D. An itemset Xi is a subset of I, i.e., Xi ⊆ I. An itemset X with k distinct items {i1, i2,…, ik} is called a k-itemset. A sequence S is an ordered list of itemsets S = {T1, T2,…, Tj}, where Tv ⊆ I (1 ≤ v ≤ j), and Tv represents a transaction in the sequence, where v is a unique transaction identifier in that sequence. A sequence database D is an ordered set containing n sequences, i.e., D = {S1, S2,…, Sn}. Sequence Si (1 ≤ i ≤ n) is defined as the i-th sequence in D, where i is a unique sequence identifier. The itemset X appears in a sequence Sa = {T1, T2,…, Tk}, i.e., X ⊆ Sa, where X is ⊆ Td (1 ≤ d ≤ k). This itemset appears in the transaction Tq.

Example 1. Consider a set of different items I = {a, b, c, d, e}, which represent different types of items sold in a supermarket. As shown in Table 1, sequence S0 contains five transactions. The first transaction (a:6, b:8) indicates that the first transaction in sequence S0 contains two itemsets {a} and {b}. The number of occurrences of {a} in the transaction is six and that of {b} is eight. {a} is called a 1-itemset because it contains only one item, a.

Definition 3.2. Consider an itemset X in Si. The ordered list of transactions in Si containing X is defined as TR(X, S) = ⟨Tg(1), Tg(2),…, Tg(k)⟩⊆ Si. Let Tg(z) and Tg(z+1) (1 ≤ z ≤ k-1) be two consecutive occurrences in Si. The formula for calculating the period of two consecutive occurrences of a transaction containing X is per(Tg(z), Tg(z+1)) = g(z+1) − g(z). The period of X in Si is pr(X, Si)= {per1, per2,…, perk+1}, where per1 = g(1) − g(0), per2 = g(2) − g(1),…, perk = g(k+1) − g(k). g(k) is the unique identifier of the transaction; when X appears, g(0) = 0 and g(k+1) = |Si|. |Si|; the latter denotes the length of Si.

Example 2. In the sequence S0 shown in Table 1, the itemset {a} appears in the transactions T1, T2, T3 and T4; thus, TR({a}, S0) = {T1, T2, T3, T4}. The period {a} in S0 is denoted by pr({a}, S0) = {1, 1, 1, 1, 1}.

Definition 3.3. In a sequence S, an itemset X may appear in multiple transactions, and the number of transactions in a sequence S containing X is defined as sup(X, S) = |TR(X, S)|.

Example 3. In the sequence S0 shown in Table 1, the itemset {a, c} appears in T2, T3, and T4; therefore, the number of occurrences of {a, c} supported for S0 is represented as sup({a, c}, S0) = 3.

Definition 3.4. Each item i has a unit profit, denoted as pl(i), which represents its importance. The unit profit for each item uses a dedicated profit list: profit = {pl(i1), pl(i2), …, pl(im)}. The profit of item ij in Tq in a sequence Sn is defined as u(ij, Tq, Sn) = q(ij, Tq, Sn) × pl(ij), where q(ij, Tq, Sn) is the number of itemsets ij in Tq in Sn.

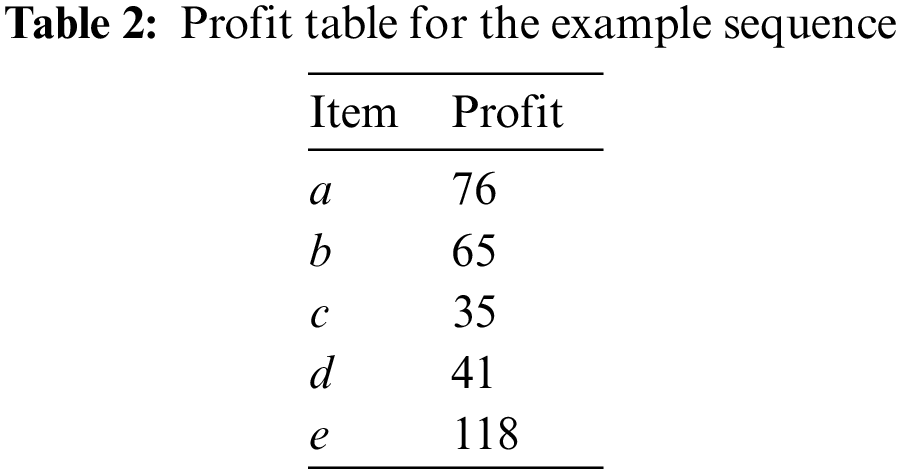
Example 4. In Table 2, the unit profits of the itemsets {a}, {b}, {c}, {d}, {e} are {pl(a): 76, pl(b): 65, pl(c): 35, pl(d): 41, pl(e): 118}, respectively. For S1 and S2 considered in Table 3, {b} in T4 in S1 and {b, d} in T2 in S2 have u({b}, T4, S1) = 65 × 5 = 325 and u({b, d}, T2, S2) = 65 × 8 + 41 × 3 = 643, respectively.

Definition 3.5. The total utility of a transaction Tq in Si is defined as tu(Tq) = ∑j=1|Tq|u(ij,Si), where ij ∈ Tq is the j-th item in Tq.

Example 5. The total utility of T1 in the sequence S1 in Table 3 is tu(T1, S1) = u(a, S1) + u(b, S1) + u(c, S1) = 76 × 6 + 65 × 10 + 35 × 10 = 1456.

Definition 3.6. The total utility of X in S is defined as u(X,S) = ∑q=1|s|u(X,S) where X ∈Tq∧Tq∈S.

Example 6. As shown in Table 3, the total utility of {a, b} in S1 is u({a, b}, S1) = u({a, b}, T1, S1) + u({a, b}, T3, S1) + u({a, b}, T4, S1) + u({a, b}, T5, S1) = 76 × 6 + 65 × 10 + 76 × 5 + 65 × 6 + 76 × 8 + 65 × 5 + 76 × 4 + 65 × 7 = 3568.

Definition 3.7. In a sequence database D, the total utility of Si is defined as su (Si) = ∑q=1|Si|tu(Tq) for Tq∈Si.

Example 7. As shown in Table 3, the total utility of S2 is su(S2) = tu(T1, S2) + tu(T2, S2) + tu(T3, S2) + tu(T4, S2) + tu(T5, S2) = 574 + 1128 + 1309 + 1884 + 3174 = 8069.

Definition 3.8. If a sequence SB = ⟨T1, T2, …, Tl⟩ contains another sequence SA = ⟨Tk1, Tk2, …, Tkm⟩, then it must satisfy the existence of integers 1 ≤ k1 ≤ k2 ≤…≤ km ≤ l such that Tk1 ⊆ T1, Tk2 ⊆ T2, …, Tkm⊆ Tl is defined as SA ⊆ SB.

Example 8. The sequence S0 in Table 1 contains ⟨(a: 6, b: 8), (a: 4, c: 9), (a: 8, d: 4)⟩.

Definition 3.9. In a sequence database D, the standard deviation of the period of the itemset X in the sequence S is denoted by stanDev (X, S).

Example 9. As shown in Table 3, the period of the itemset {a} in sequence S1 is pr({a}, S1) = {1, 2, 1, 1, 0}. The average period is avgPr({a}, S1) = (1 + 2 + 1 + 1 + 0)/5 = 1. The standard deviation of the period is stanDev({a}, S1) = [(1−1)2+(2−1)2+(1−1)2+(1−1)2+(0−1)2]/5 = 0.63.

3.2 Definitions for Multiple Sequences

In the following paragraphs, we described how to combine the utility and periodicity of patterns and apply them to multiple sequences. In addition to the definitions presented in previous works, we defined three measures: utility ratio (Definition 3.10), support ratio (Definition 3.11), and high-utility periodic sequence ratio (Definition 3.14). The utility ratio defines the utility percentage of a pattern in a sequence. The support ratio guarantees the frequency of the periodic patterns in sequences of different lengths. The high-utility periodic sequence ratio is used to discover frequent patterns of high-utility periods in multiple sequences.

Definition 3.10. Let the total utility of an itemset X in a sequence S be u(X,S) and the total utility of S be su(S). Then, the utility ratio is utiRa(X,S) = u(X,S)/su(S). Given a user-defined threshold minHuRa, namely, the minimum high-utility ratio, if utiRa(X,S) ≥ minHuRa for an itemset X, then X is defined as a high-utility itemset in the sequence S.

Example 10. Table 3 outlines an example with S1 and minHuRa = 0.25. The utility of an itemset {a} in S1 is u({a}, S1) = tu(T1, S1) + tu(T3, S1) + tu(T4, S1) + tu(T5, S1) = 456 + 380 + 608 + 304 = 1748. The total utility of S1 is su(S1) = 6815, and that of the itemset {a} in sequence S1 is utiRa({a}, S1) = 1748/6815 = 0.256. Because 0.256 ≥ minHuRa, the itemset {a} is a high-utility itemset in sequence S1.

Definition 3.11. The support ratio of an itemset X in a sequence S is defined as supRa(X, S) = sup({X}, S)/|S|, where |S| is the total number of transactions in S. Given the minimum support ratio threshold, minSuqRa, if supRa(X, S) ≥ minSupRa, then X in S has a high support ratio.

Example 11. The user-defined threshold is set to be minSupRa = 0.6. In Table 3, the itemset {a} appears in T1, T3, T4, and T5 in S1. The support for the itemset X in S1 is sup({a}, S1) = 4. The support ratio of {a} in S1 is supRa({a}, S1) = sup({a}, S1)/|S1| = 0.8. Because 0.8 ≥ minSupRa, X in S1 has a high-support ratio pattern.

Definition 3.12. Let there be four user-defined thresholds, minSupRa, maxPr, maxStd, and minHuRa. If an itemset X in a sequence S satisfies supRa(X, S) ≥ minSupRa, maxPr(X, S) ≤ maxPr, stanDev(X, S) ≤ maxStd, and utiRa(X, S) ≥ minHuRa, then X in S is a high-utility periodic frequent pattern.

Example 12. Let minSupRa = 0.6, maxPr = 3, maxStd = 1, and minHuRa = 0.2. Considering S2 in Table 3, the itemset {a, d} appears in T2, T3, and T4. Thus, supRa({a, d}, S2) = 0.6 ≥ minSupRa, stanDev({a, d}, S2) = 0.433 ≤ maxStd, utiRa({a, d}, S2) = 0.32 ≥ minHuRa, and maxPer{2, 1, 1, 1} = 2 ≤ maxPr; thus, the itemset {a, d} is a high-utility periodic frequent pattern in S2.

Definition 3.13. In a sequence database D, the set of sequences for which an itemset X satisfies supRa(X, S) ≥ minSupRa, stanDev(X, S) ≤ maxStd, maxPr(X, S) ≤ maxPr, and utiRa(X, S) ≥ minHuRa is defined as huPrSeq(X, D) = {S|supRa(X, S) ≥ minSupRa ∧ maxPr(X, S) ≤ maxPr ∧ stanDev(X, S) ≤ maxStd ∧ utiRa(X, S) ≥ minHuRa ∧ S ∈ D}.

Example 13. In Table 3, the itemset {d} satisfies supRa({d}, S) ≥ minSupRa, maxPr({d}, S) ≤ maxPr, stanDev({d}, S) ≤ maxStd, and utiRa({d}, S) ≥ minHuRa in S2, S3, and S4. Thus, the huPrSeq of {d} is huPrSeq({d}) = {S2, S3, S4}.

Definition 3.14. In a sequence database D, the number of sequences in the set huPrSeq(X) is |huPrSeq(X)| and the high utility periodic sequence ratio of X in D is huSeqRa(X) = |huPrSeq(X)|/|D|, where |D| is the number of sequences in D. Given a user-defined threshold minSeqRa, if huSeqRa(X) ≥ minSeqRa, then X is a high utility periodic frequent pattern in D.

Example 14. As shown in Table 3, let minSupRa = 0.6, maxPr = 3, stanDev = 1, and minHuRa = 0.2. The pattern {a, d} in S2, S3, and S4 is a high utility periodic frequent pattern, and the sequence set is huPrSeq(X) = {S2, S3, S4}. Thus, the high-utility periodic sequence ratio of {a, d} is huSeqRa({a, d}) = |huPrSeq(X)|/|D| = 3/4 = 0.75 ≥ minSeqRa; hence, X is a high utility periodic frequent pattern in D.

4  Proposed Algorithm: MHUPFPS

In this section, we first described a new pruning strategy for pruning a search space. Then, we proposed a compact data structure, HUPFPS-list, to store the transactions, sequence information, and utility values of a pattern. Finally, we present the proposed MHUPFPS algorithm.

4.1 Pruning Strategy

To identify high utility periodic frequent patterns in a set of sequences, a method of pruning the search space is required. Thus, in this study, periodicity and utility are combined and an upper bound, upSeqRa, was proposed for the measure huSeqRa and two new pruning properties that were used to prune the vast search space. Note that upSeqRa is defined by Definition 3.14.

Definition 4.1. Given three user-defined thresholds minHuRa, maxPr, and minSupRa, we say that a pattern X is a high-utility periodic frequent candidate pattern in a sequence S if X in S satisfies supRa(X, S) ≥ minSupRa, maxPr(X, S) ≤ maxPr, and utiRa(X, S) ≥ minHuRa.

Example 15. Let minSupRa = 0.6, maxPr = 3, and minHuRa = 0.2. According to the sequence database in Table 3, pattern {a} satisfies the conditions supRa({a}, S1) = 0.8 ≥ minSupRa, maxPr({a}, S1) = 2 ≤ maxPr, and utiRa({a}, S1) = 0.25 ≥ minHuRa. Thus, {a} is a high-utility periodic frequent candidate itemset in S1.

Definition 4.2. In a sequence database D, a set of sequences for which a pattern X satisfies supRa(X, S) ≥ minSupRa, maxPr(X, S) ≤ maxPr, and utiRa(X, S) ≥ minHuRa is defined as huCand(X, D) = {S|supRa(X, S) ≥ minSupRa ∧ maxPr(X, S) ≤ maxPr ∧ utiRa(X, S) ≥ minHuRa ∧ S ∈ D}.

Example 16. As shown in Table 3, the pattern {d} satisfies the conditions supRa({d}, S) ≥ minSupRa, maxPr({d}, S) ≤ maxPr, and utiRa({d}, S) ≥ minHuRa in S2, S3, and S4; thus, {d} is called a high-utility periodic frequent candidate pattern in S2, S3 and S4 and is defined as huCand(X) = {S2, S3, S4}.

Definition 4.3. In a sequence database D, the number of sequences in the set huCand(X) is |huCand(X)|. The upSeqRa of X in D is upSeqRa(X) = |huCand(X)|/|D|, where |D| denotes the number of sequences in D.

Example 17. Let minSupRa = 0.6, maxPr = 3, and minHuRa = 0.2. As shown in Table 3, {a, d} is a high utility period frequent candidate pattern in S2, S3, and S4. Thus, the set of candidate sequences huCand(X) in which the high-utility period frequent candidate pattern is satisfied is huCand(X) = {S2, S3, S4}. Thus, upSeqRa({a, d}) = |huCand({a, d})|/|D| = 3/4 = 0.75.

Theorem 4.1. For a pattern X, upSeqRa(X) is not less than huSeqRa(X), i.e., upSeqRa(X) ≥ huSeqRa(X).

  Proof. For an itemset X:

huSeqRa(X) = |huPrSeq(X)|/|D|

= |{S|supRa(X, S) ≥ minSupRa ∧ maxPr(X, S) ≤ maxPr ∧ stanDev(X, S) ≤ maxStd ∧ utiRa(X, S) ≥ minHuRa ∧ T ∈ S ∧ S ∈ D}|/|D|

≤ |{S|maxPr(X, S) ≤ maxPr ∧ supRa(X, S) ≥ minSupRa ∧ utiRa(X, S) ≥ minHuRa ∧ T ∈ S ∧ S ∈ D}|/|D|

= |huCand(X)|/|D|

= upSeqRa(X)

Theorem 4.2. For two itemsets X ⊂ XY, upSeqRa(XY) ≤ upSeqRa(X).

  Proof. For any sequence S in a sequence database D, if an itemset X is a subset of another itemset XY:

upSeqRa(X) = huCand({X}, S)/|D|

= |{S|maxPr(X, S) ≤ maxPr ∧ supRa(X, S) ≥ minSupRa ∧ utiRa(X, S) ≥ minHuRa ∧ T ∈ S ∧ S ∈ D)|/|D|

≥ |{S|maxPr(XY, S) ≤ maxPr ∧ supRa(XY, S) ≥ minSupRa ∧ utiRa(XY, S) ≥ minHuRa ∧ T ∈ S ∧ S ∈ D)|/|D|

= |huCand(XY)|/|D|

= upSeqRa(XY)

Hence, if X is such that upSeqRa(X) ≤ minSeqRa, then both X and its superset can be pruned without further exploration.

Theorem 4.3. In a sequence database D, if upSeqRa(X) ≤ minSeqRa for any itemset X, then the superset X′ of X is not a HUPFPS.

  Proof. We have upSeqRa(X) < minSeqRa ⇒ upSeqRa(X′) < minSeqRa.

Hence, X is not a HUPFPS, because X ⊂ X′ ⇒ upSeqRa(X′) ≤ upSeqRa(X)

⇒ upSeqRa(X′) < minSeqRa.

Thus, any superset of X is not a HUPFPS.

4.2 The HUPFPS-List Data Structure

To avoid repeated scanning of a database and to improve the performance of MHUPFPS, we proposed a data structure called the HUPFPS-list, which contains four fields. MHUPFPS only scans a database once to generate a HUPFPS-list for each pattern that appears in the sequence database. MHUPFPS combines the HUPFPS-list of different patterns to generate a HUPFPS-list of extended patterns.

Definition 4.4. The HUPFPS-list of a pattern X is denoted Px and contains four fields. The i−set field is defined as Px.i−set = X. The sid−list field is defined as Px.sid−list = {S1, S2, …, Sw}, where Si(1 ≤ i ≤ w) represents the equivalence number at which X appears. The tran−list field represents a list of stored transaction numbers Px.tran−list = {Z1, Z2, …, Zi}(1 ≤ i ≤ |Sw|) where Zi = {Z|X ∈Tz∧Tz∈Si}. The uti−list field is defined as Px.uti−list = {p1, p2, …, pi}, where pi is the utility of X for a particular transaction in the sequence and is defined as pi = {p|(X, pi) ∈ Tz ∧ Tz ∈ Sw}.

Example 18. Tables 4 and 5 represent the HUPFPS-lists of patterns {a} and {d}, respectively. Table 6 shows the HUPFPS-list of pattern {a, d}, which is constructed by combining the HUPFPS-lists of patterns {a} and {d}.

Definition 4.5. The itemsets Px.i-set and Py.i-set with the same prefix are extended to Pxy, which is defined as Pxy = Px ∪ Py (the prefix of a single itemset is an empty itemset).

Example 19. The proposed algorithm uses an intersection procedure to combine the HUPFPS-lists of the itemsets {a} and {d}, in Tables 4 and 5, respectively, to construct the HUPFPS-list of the itemset {a, d}, as shown in Table 6.

4.3 Proposed MHUPFPS Algorithm

Based on the HUPFPS-list and pruning strategy, we designed an algorithm called MHUPFPS. MHUPFPS (Algorithm 1) inputs a multisequence sequence database and five user-defined thresholds: minSupRa, maxPr, maxStd, minHuRa, and minSeqRa. Finally, a set of high utility periodic frequent patterns is output.

In the proposed design, MHUPFPS first scans the database to calculate supRa(X, S), maxPr(X, S), stanDev(X, S), and utiRa(X, S) for each individual itemset. Then, it iterates over every itemset, calculates whether it satisfies the high-utility periodic frequent pattern in each sequence, and stores the sequence that satisfies the condition in the set huPrSeq(X). After it scans all sequences, the set huPrSeq for this pattern is used to calculate the high utility periodic sequence ratio huSeqRa(X). If the value of huSeqRa(X) is not less than the threshold minSeqRa, the output pattern X is a HUPFPS.

Additionally, MHUPFPS prunes the search space using the upper bound upSeqRa(X) of huSeqRa(X). It stores the HUPFPS-list of the pattern whose upSeqRa(X) is not less than minSeqRa in the set boundHUPFPS. The UHPFPS-list of patterns in the set boundHUPFPS is stored in ascending order of upSeqRa(X). Finally, MHUPFPS performs a depth-first search, recursively searching for larger patterns by calling the Search procedure (Algorithm 2) with a set of parameters and the set boundHUPFPS.

The Search procedure (Algorithm 2) takes a HUPFPS-list of patterns and set of user-defined thresholds as input and outputs the high-utility periodic expansion pattern. First, the algorithm iteratively loops over the set boundHUPFPS and sequentially takes the HUPFPS-list of Px.i and Py.i from the set boundHUPFPS. The HUPFPS list of patterns Px.i and Py.i is extended into Pxy using the intersection procedure (Algorithm 3). Then, the set huCand(Pxy.i) of sequences of the itemset Pxy.i is calculated. Finally, the algorithm calculates upSeqRa(Pxy.i) to prune the search space if upSeqRa(Pxy.i) is not less than minSeqRa; Pxy is added to the set ExtenOfPx, which stores the HUPFPS-list of all extended patterns of Px.i for the next iteration. Next, the value of huSeqRa(Pxy.i) is calculated, and if huSeqRa(Pxy.i) is not less than minSeqRa, the output Pxy.i is a HUPFPS. Subsequently, the search procedure recursively calls the HUPFPS-list (ExtenOfPx) of the extended patterns of Px.i to explore larger patterns.

4.4 Concrete Example

In this example, the user-defined thresholds were set to minSupRa = 0.6, maxPr = 3, maxStd = 1.0, minHuRa = 0.2, and minSeqRa = 0.6. According to the example sequence database in Tables 4 and 5, MHUPFPS scans the database once, then uses the HUPFPS-list to calculate pr({a}, S1) = {1, 2, 1, 1, 0}, pr({a}, S2) = {2, 1, 1, 1, 0}, pr({a}, S3) = {2, 1, 2, 0}, pr({a}, S4) = {1, 1, 1, 2}, supRa({a}, S1) = 0.8, supRa({a}, S2) = 0.8, supRa({a}, S3) = 0.6, supRa({a}, S4) = 0.6, maxPr({a}, S1) = 2, maxPr({a}, S2) = 2, maxPr({a}, S3) = 2, maxPr({a}, S4) = 2, stanDev({a}, S1) = 0.63, stanDev({a}, S2) = 0.63, stanDev({a}, S3) = 0.82, and stanDev({a}, S4) = 0.43, based on the HUPFPS-list of {a}. Consider the itemset {a}; because supRa({a}, S1) ≥ minSupRa, maxPr({a}, S1) ≤ maxPr, stanDev({a}, S1) = 0.63 ≤ maxStd, and utiRa({a}, S1) ≥ minHuRa, the pattern {a} is a high-utility periodic frequent pattern in S1. Similarly, the set huPrSeq(a) = {S1, S2, S3, S4} can be calculated, and huSeqRa(a)=|huPrSeq(a)|/|D|=1≥ minSeqRa; thus, pattern {a} is output as a high-utility periodic frequent pattern in a multiple sequence database. MHUPFPS computes patterns {a} and {d} in the same manner as HUPFPS. It adds the HUPFPS-list of the patterns to the set boundHUPFPS to generate a larger HUPFPS. The HUPFPS-list of patterns in boundHUPFPS is sorted in ascending order of upSeqRa values.

According to the HUPFPS-list of pattern {a} in Table 4, the sid-list of {a} is {1, 2, 3, 4}; the tran-list is ({1, 3, 4, 5}, {2, 3, 4, 5}, {2, 3, 5}, {1, 2, 3}); and the uti-list is ([{456}, {380}, {608}, {304}], [{380}, {456}, {684}, {760}], [{608}, {380}, {684}], [{456}, {456}, {684}]). From the HUPFPS-list of pattern {d}, the sid-list is {1, 2, 3, 4}; the tid-list is ({2, 5}, {1, 2, 3, 4}, {1, 2, 3, 4, 5}, {1, 2, 3, 4, 5}); and the uti-list is ([{533}, {410}], [{574}, {123}, {328}, {615}], [{410}, {164}, {492},{492},{492}], [{574}, {328}, {246}, {369}, {328}]). MHUPFPS uses the intersection procedure, which combines the HUPFPS lists of patterns {a} and {d} to generate a HUPFPS list of the pattern {a, d}. MHUPFPS further calculates the parameter values using the field information in the HUPFPS-list of {a, d} and then obtains the set huCand({a, d}) = {S2, S3, S4} and calculates upSeqRa({a, d}) = 0.75 ≥ minSeqRa based on the set huCand({a, d}). Thus, the pattern {a, d} and its superset may be a HUPFPS. The algorithm adds the HUPFPS list of {a, d} to the set boundHUPFPS. Finally, huSeqRa({a, d}) = 0.75 is calculated by obtaining the sequence set huPrSeq({a, d}) = {2, 3, 4}; thus, the algorithm output {a, d} is a HUPFPS. MHUPFPS recursively calls the pattern explorer to explore larger extensions of the patterns.

5  Experiments

5.1 Experimental Setup and Datasets

We conducted experiments on three real datasets (FIFA, Bike, and Leviathan) and a synthetic dataset. The three real datasets were all obtained from the data mining library on the SPMF website, and the synthetic dataset was synthesized by the data generation code provided on the SPMF website [68]. The details of these datasets are provided below:

•   The T23l67kd15k dataset was generated by a Matalab program written by Ashwin Balani that is available on the SPMF website. This dataset contains a total of 15,000 sequences of 68 items; each sequence contains an average of 23 transactions and each transaction contains an average of three items. This dataset is a dense dataset.

•   The FIFA dataset contains a total of 20,450 sequences of 2,990 types of items; each sequence contains an average of 34.74 transactions.

•   The Bike dataset contains a total of 21,078 sequences of 67 types of items; each sequence contains an average of 7.27 transactions.

•   The Leviathan dataset contains 5,834 sequences of 9,025 types of items; each sequence contains an average of 33.8 transactions.

To the best of our knowledge, previous studies have only found periodic patterns that occur together in multiple sequences, whereas the proposed MHUPFPS finds common high-utility periodic frequent patterns in multiple sequences. This means that comparing MHUPFPS with existing approaches is not suitable. Therefore, MHUPFPS was considered to be the baseline. MHUPFPS was implemented in Java on a Windows 11 computer with an Intel(R) Core(TM) i5-1135g7 2.42 ghz CPU and 24 GB of running memory.

In the following, |D|,|Id|,|Tc|, and |Savg| represent the sequence number, distinct item, item count per transaction, and average number of transactions per sequence, respectively. In experiments, the aforementioned datasets with different characteristics were used to comprehensively evaluate the performance of the MHUPFPS algorithm in terms of the running time, number of patterns, and running memory.

5.2 Parameter Analysis

MHUPFPS contains five user-defined parameters: minSeqRa, minSupRa, maxStd, maxPr, and minHuRa. maxStd is used to keep the pattern period stable, maxPr is used to limit the maximum period of the pattern, minSupRa is used to guarantee the HUPFPS support ratio in each sequence, and minHuRa is used to determine whether a pattern is of high utility in a sequence. In experiments, the baseline algorithm was designed with loose settings for each parameter value with the aim of mining more high-frequency periodic patterns. For the baseline algorithm, we set maxPr = 20, minSupRa = 0.1, maxStd = 10, minHuRa = 0.01, and minSeqRa = 0.

In our experiments, we compared the baseline algorithm with MHUPFPS for different parameter sets of minSeqRa, minSupRa, maxStd, maxPr, and minHuRa to evaluate the influence of different parameters and parameter values on the performance of the algorithm. The results showed that when maxStd ≥ 10, the parameter values have almost no influence on the number of patterns, time, or memory required. Thus, we set maxStd to a fixed value of 10. We also evaluated the influence of minSupRa on the performance of MHUPFPS; MHUPFPS(x, y, z) is defined as MHUPFPS when minSeqRa = x, minHuRa = y, and maxPr = z. We evaluated the influence of minHuRa on the performance of MHUPFPS; MHUPFPS(x, y, z) is defined as MHUPFPS when minSeqRa = x, minSupRa = y, and maxPr = z. When evaluating the influence of maxStd on the performance of the algorithm, maxStd was used as the independent variable. To control this variable, the algorithm used minSupRa as a fixed value of minSupRa = 0.1 when the influence of minSupRa on the algorithm was not considered. MHUPFPS(x, y, z) is defined as MHUPFPS when minSeqRa = x, minHuRa = y, and maxPr = z. Finally, when the influence of maxPr on the performance of the algorithm was evaluated, minSupRa was used as the independent variable, and MHUPFPS(x, y, z) is defined as MHUPFPS when minSeqRa = x, minHuRa = y, and maxPr = z.

We investigated the effect of the parameters minSeqRa, minSupRa, maxStd, maxPr, and minHuRa on the algorithm. To investigate the influence of minSupRa and minHuRa on the algorithm, these parameters were sequentially increased from small initial values; this considered the distribution of data in different datasets and length of the sequences. The results of the experiments show that, for both the synthetic and real datasets, the performance of the algorithm was not significantly impacted when the values of minSupRa and minHuRa were set to be greater than 0.5. However, the performance was slightly impacted for some of the real datasets. Thus, the values of minSupRa and minHuRa were set to be in the intervals [0.01,0.5] and [0.1,1], respectively. Because the data in the dataset were unevenly dispersed and relatively sparse, minSeqRa was set to be 0.001 and 0.0001, respectively. The results indicated that these parameters had little influence on the performance of the algorithm when the value of maxStd was above 10. Thus, to better evaluate the parameter maxStd, its value was set to be in the interval [1,10]. Finally, the algorithm was tested with different values of maxPr. The smaller the value of maxPr, the more stringent the filtering of patterns, i.e., a smaller number of patterns were filtered out for larger maxPr values. When the value of maxPr exceeded the sequence length, it had almost no effect on the performance of the algorithm. Thus, the value of maxPr was set to be in the interval [5,20] in experiments.

5.3 Influence Analysis of minSeqRa and minSupRa

In the experiments, we evaluated the performance of the algorithm while varying the value of minSupRa. As the datasets have different characteristics, different values were used for different datasets; for FIFA, T23l67kd15k, and Leviathan, minSupRa was in the interval [0.01,0.5], while for Bike, minSupRa was in the interval [0.1,1].

Fig. 1 shows the effect of different minSupRa values on the runtime of the proposed MHUPFPS. The runtime for the proposed algorithm for FIFA, Leviathan, Bike, and T23l67kd15k were 35%, 50%, 15%, and 18% shorter than that for the baseline algorithm, respectively. The difference between datasets is due to FIFA and Leviathan containing more items; thus, the algorithm generates more itemsets, resulting in a more extensive search space. While the synthetic dataset T23l67kd15k contained fewer items, it contained more items per transaction, generating more candidate patterns and requiring more search space to save them.

Figure 1: MHUPFPS runtime for various minSupRa and maxStd values

As shown in Fig. 2, the number of patterns identified decreases significantly as minSupRa increases. For example, when minSeqRa = 0, minHuRa = 0.01, maxStd = 10, and maxPr = 20, and the value of minSupRa increases from 0.01 to 0.3, the number of patterns found decreases from 2,297 to 45. For the Bike dataset, when minSeqRa = 0.0001, minHuRa = 0.1, maxStd = 10, and maxPr = 20, the number of patterns found decreases from 66 to 15 as minSupRa increases from 0.01 to 0.6. This is because almost all HUPFPS in the Bike dataset are concentrated in a sequence and occur at a high frequency. The value of minSupRa strictly filtered the number of identified patterns when executing MHUPFPS on the synthetic dataset and three real datasets considered in this study. Hence, the results highlight the critical importance of the parameter minSupRa in reducing the search space.

Figure 2: Number of patterns identified for various minSupRa and minSeqRa values

Fig. 3 shows that memory usage decreased as minSupRa increased. For example, for the synthetic dataset T23l67kd15k, the memory occupied by the algorithm reduced from 562 to 325 MB as the value of minSupRa increased from 0.01 to 0.25. In the three real datasets, memory usage decreased as minSupRa increased; this shows that minSupRa has strict support for patterns in the sequence, resulting in a reduced number of candidate patterns stored in the memory. Thus, the memory consumption of the algorithm can be reduced by limiting the value of minSupRa.

Figure 3: Memory usage for different parameter values for different datasets

5.4 Influence Analysis of minSeqRa and minHuRa

Fig. 4 shows the effect of different minHuRa values on the runtime of the proposed MHUPFPS. The runtime remains almost constant as minHuRa increases. For example, the results on the synthetic dataset when minSeqRa = 0.001, minSupRa = 0.1, maxStd = 10, and maxPr = 10, and on the real datasets when minSeqRa = 0.0001, minSupRa = 0.1, and maxStd = 10 are all represented by almost horizontal lines. This means that the parameter minHuRa has little influence on the runtime of MHUPFPS. Fig. 4 shows that for minSeqRa = 0.001 or minSeqRa = 0.0001, the runtime was 20% less than that of the baseline algorithm. This suggests that the search space of MHUPFPS can be reduced by changing the value of minSeqRa.

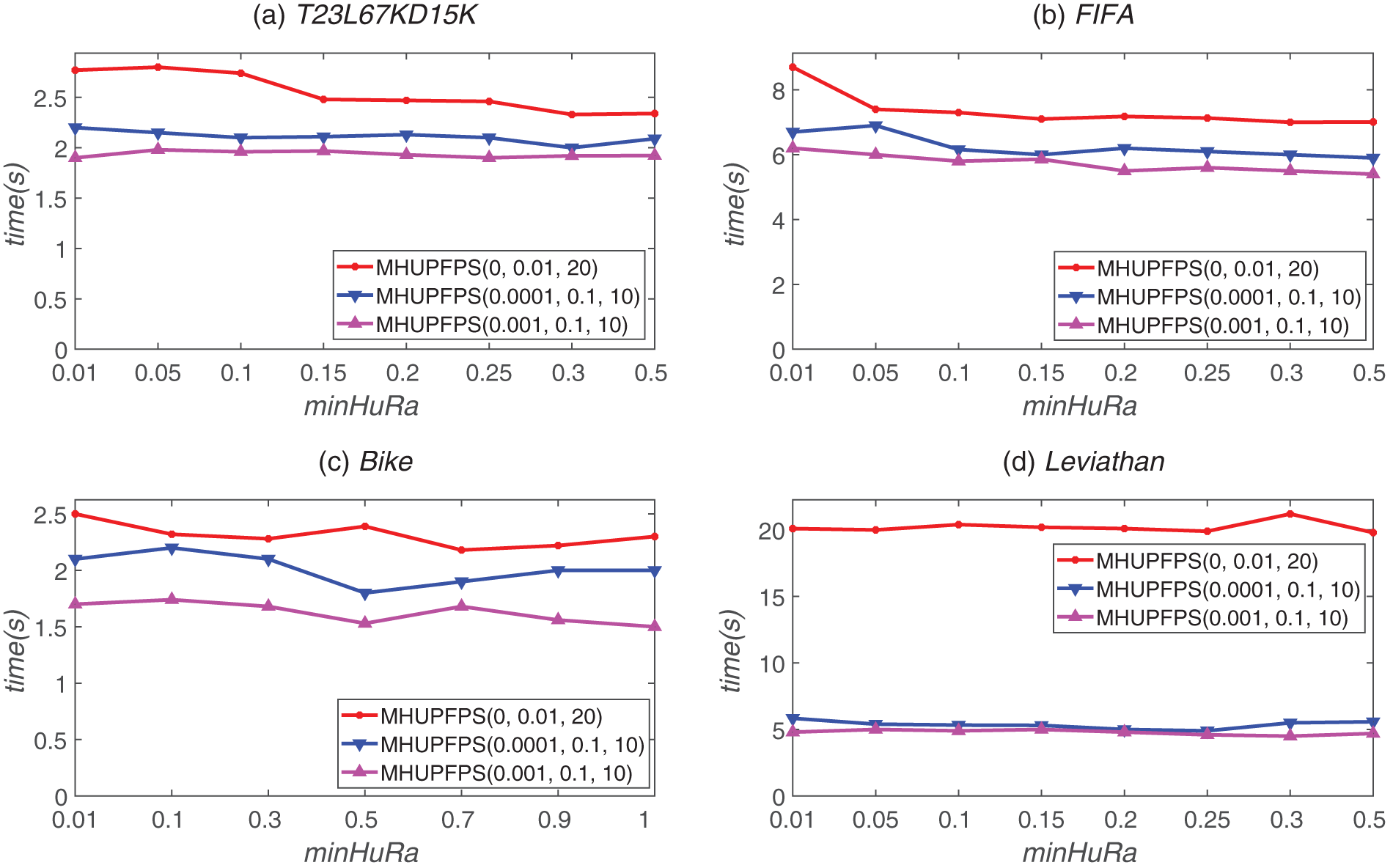
Figure 4: MHUPFPS runtime for various minHuRa and minSeqRa values

As shown in Fig. 5, the number of patterns mined by the algorithm varies for different values of minHuRa. This variation is considerable compared with that of the baseline algorithm. For example, for the FIFA dataset, when minHuRa increased from 0.01 to 0.5, the number of patterns mined by the baseline algorithm decreased from 1,329 to 49. When minSeqRa = 0.001, minSupRa = 0.1, maxStd = 10, and maxPr = 10, and minHuRa increased from 0.01 to 0.5, the number of mined patterns decreased from 122 to 1. Additionally, minSeqRa significantly influenced the number of HUPFPS. For example, for the Leviathan dataset, when minHuRa = 0.01 and minSeqRa increased from 0 to 0.001, the number of mined patterns decreased from 802 to 66. In conclusion, most of the patterns in the sequence are non-high utility frequent periodic patterns, hence the proposed MHUPFPS can prune various non-high utility frequent periodic patterns.

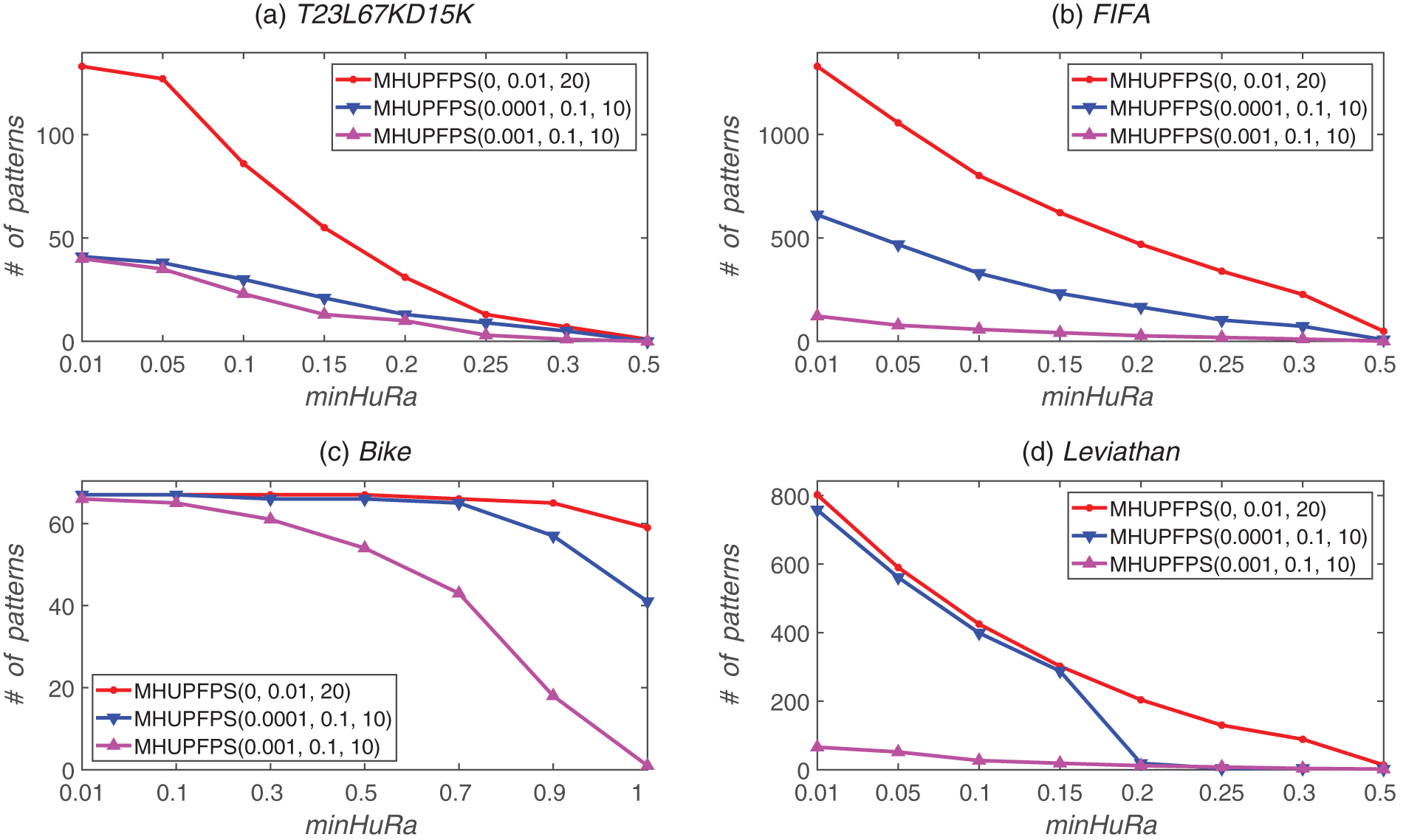
Figure 5: Number of patterns identified for various minHuRa and minSeqRa values

Fig. 6 illustrates the influence of minSeqRa and minHuRa on memory consumption. This figure shows that, for all datasets, the results are all represented by almost horizontal lines as the value of minHuRa increases; this indicates that the value of minHuRa has nearly no influence on the memory usage of MHUPFPS. When minHuRa was fixed, the memory consumption decreased as minSeqRa increased. For example, for the FIFA dataset, when minHuRa = 0.15 and minSeqRa increased from 0 to 0.001, the memory usage decreased from 1,265 to 856 MB; this demonstrates that the value of minSeqRa can reduce the number of patterns that are saved in the memory.

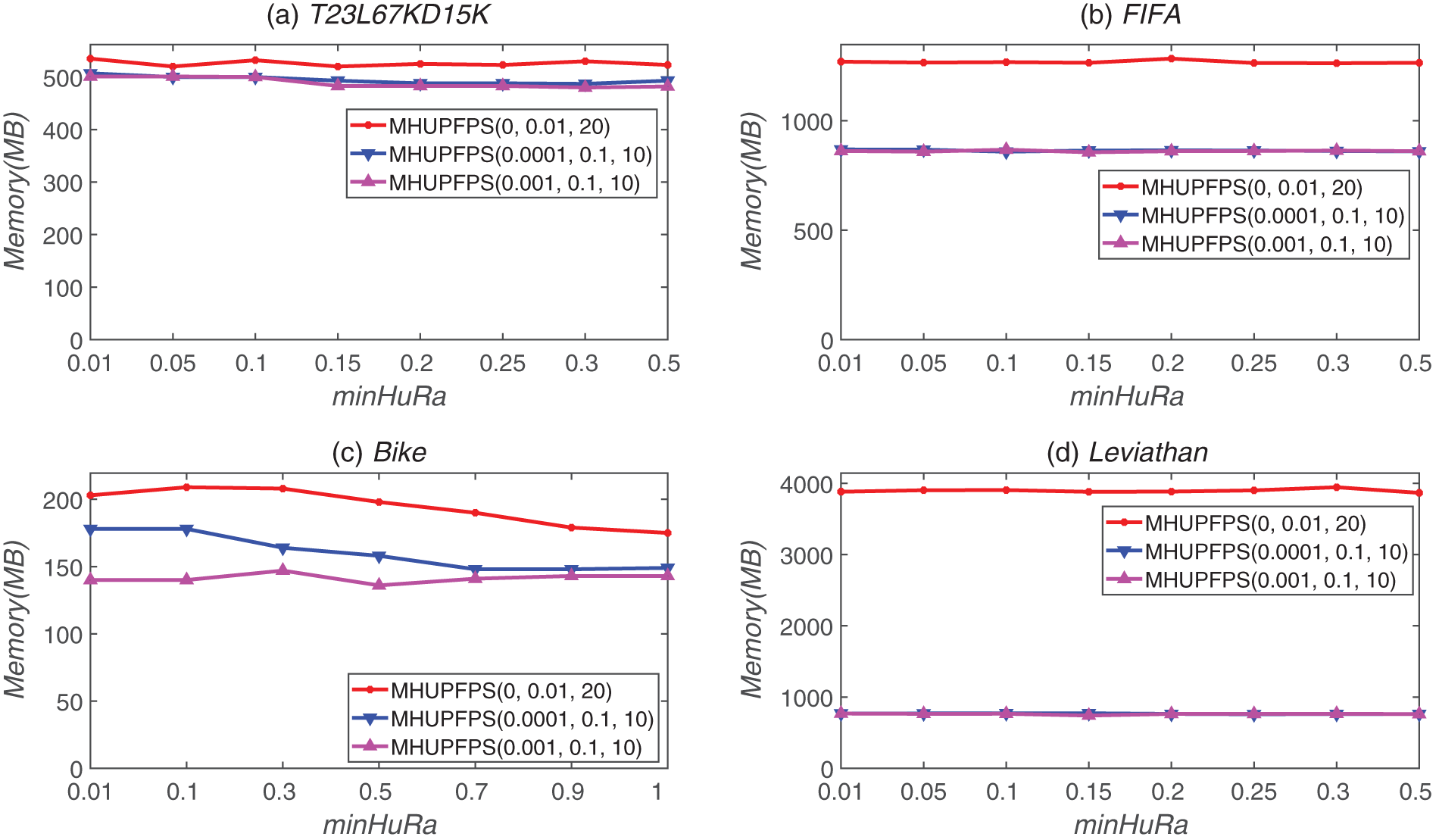
Figure 6: Memory usage for different parameter values for different datasets

5.5 Influence Analysis of minSeqRa and maxStd

We evaluated the combined influence of minSeqRa and maxStd on the algorithm by varying their values. We fixed minHuRa = 0.1, minSupRa = 0.1, and maxPr = 10. Fig. 7 shows the runtime of MHUPFPS for different values of minSeqRa and maxStd; the runtime was 15%, 18%, 12%, and 16% faster than that of the baseline algorithm for mining all HUPFPS in the FIFA, Leviathan, Bike, and synthetic datasets, respectively. The items in the Leviathan dataset are more diverse and the synthetic dataset contains more transactions per transaction; this can lead to a larger search space. Most of the patterns in the Leviathan and T23I67KD15K datasets are non-high-utility periodic frequent patterns, which require considerably more memory space to be saved. MHUPFPS prunes several non-high-utility periodic frequent patterns, resulting in improved performance.

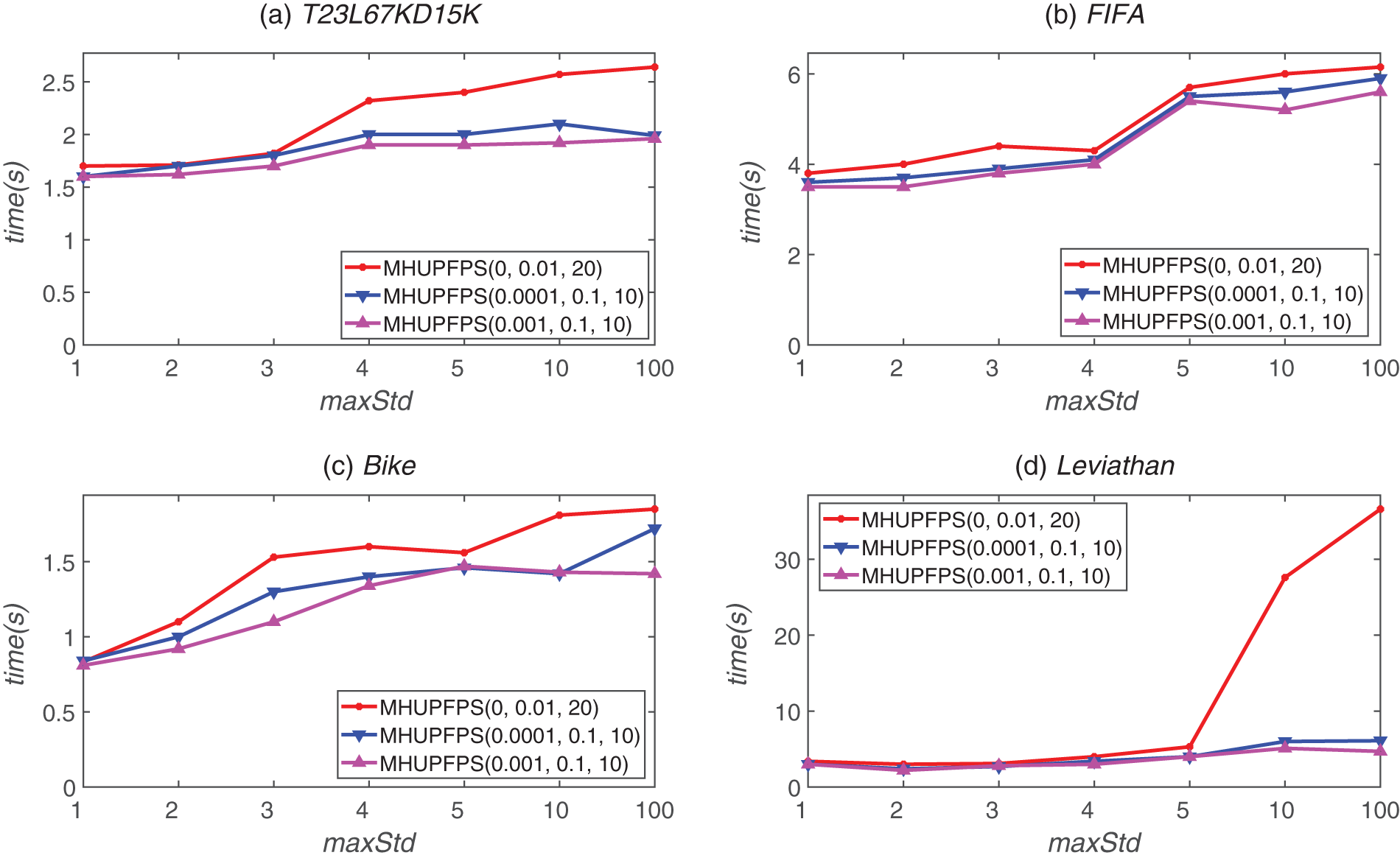
Figure 7: MHUPFPS runtime for various minSeqRa and maxStd values

As shown in Fig. 8, the number of HUPFPS increased as maxStd increased. As maxStd increased, the number of patterns mined by the baseline algorithm was much larger than that in the non-baseline algorithm. For example, for the FIFA dataset, the number of patterns mined by the baseline algorithm decreased from 1,329 to 869 as maxStd decreased from ten to three. When minSeqRa = 0.001 and maxStd decreased from ten to three, the number of patterns mined by the non-baseline algorithm reduced from 58 to 19. Fig. 8 also shows that for a constant minSeqRa, the number of mined patterns decreased as maxStd increased.

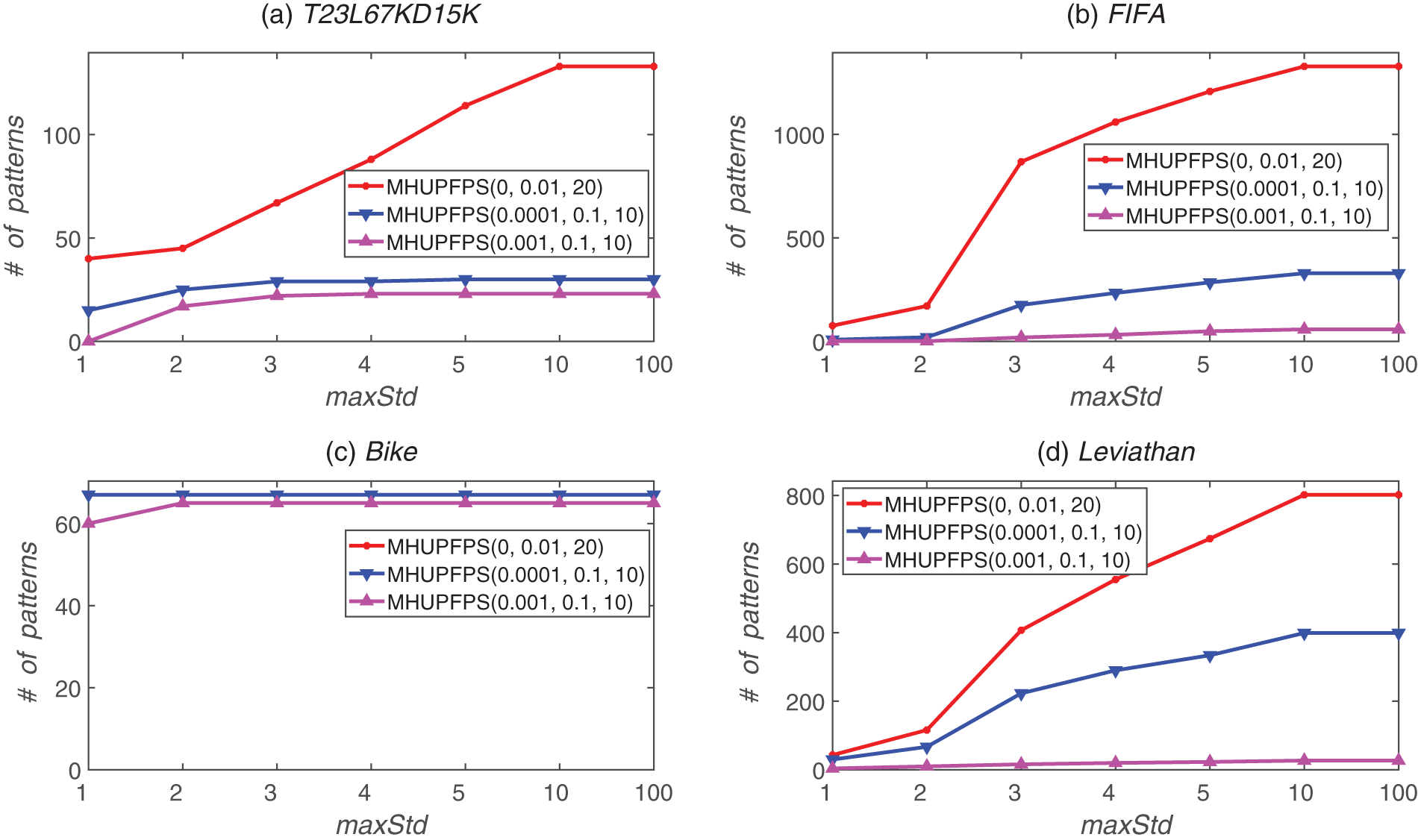
Figure 8: Number of patterns identified for various minSeqRa and maxStd values

The influence of minSeqRa and maxStd on memory consumption is shown in Fig. 9; as maxStd increased, the memory usage increased. This is because when maxStd increases, MHUPFPS requires more space to save the HUPFPS-list of patterns. For example, for the FIFA dataset, the memory consumption of MHUPFPS(0.001, 0.1, 10) increased from 678 to 868 MB as maxStd increased from three to ten (Fig. 9). Our results indicate that changing the value of maxStd can control the number of patterns that are saved in the memory.

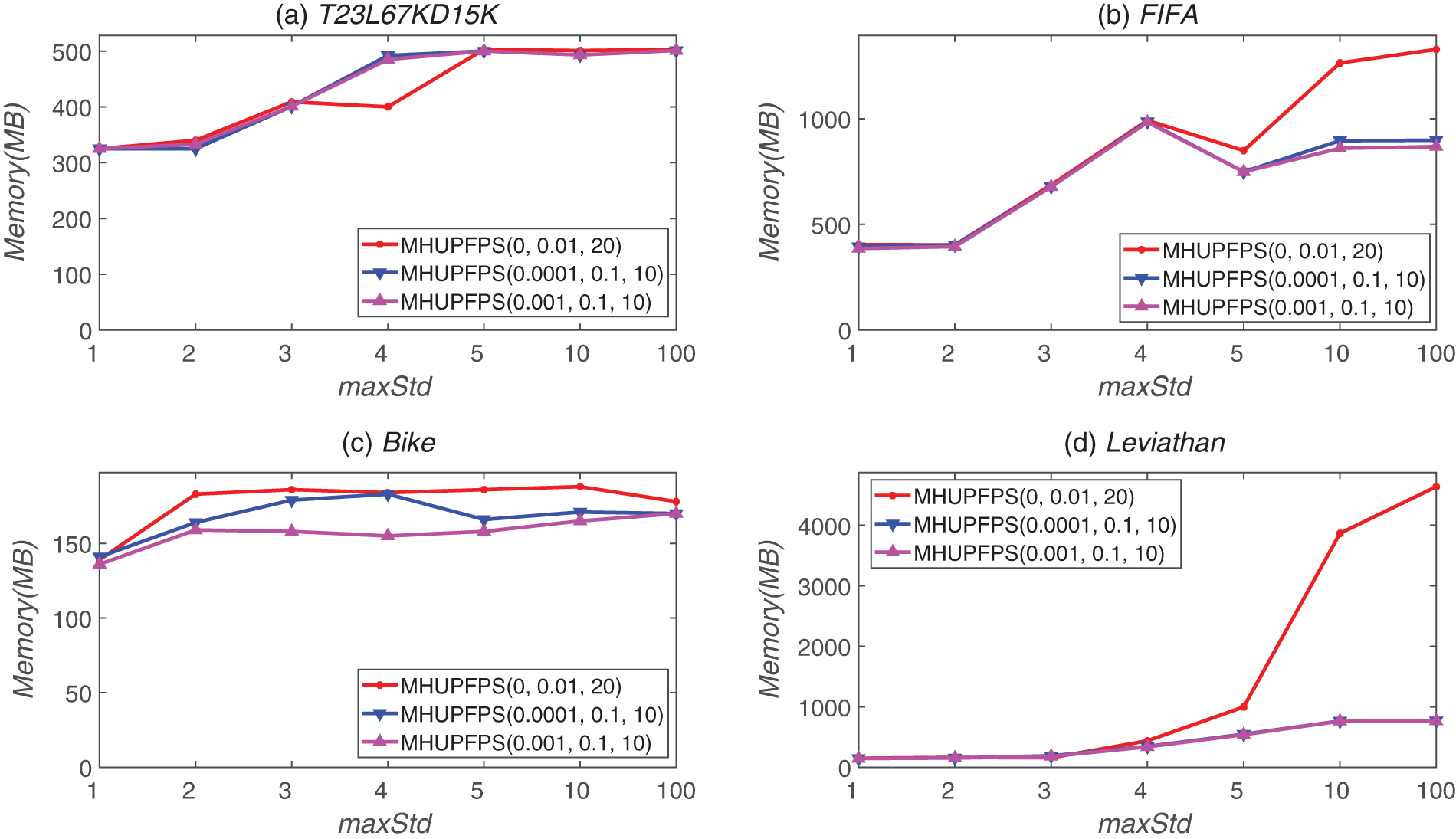
Figure 9: Memory usage for different parameter values for different datasets

5.6 Influence Analysis of maxPr

Fig. 10 shows the time variation of MHUPFPS for different values of maxPr. Figs. 11 and 12 compare the changes in the number of HUPFPS and memory consumption when maxPr is varied. The four datasets had different sequence lengths; the longest was 99 and the shortest was eight. The value of maxPr was fixed at five, ten, and 20. As shown in Fig. 10, decreasing the value of maxPr can significantly reduce the runtime of MHUPFPS. For example, for the FIFA dataset, the runtime was reduced by 12% when minSeqRa increased from 0 to 0.0001, and by 20% when minSeqRa increased from 0. 0001 to 0.001. The runtime also reduced for the other datasets. Because maxPr limits the period of the pattern, the algorithm strictly filters out patterns with a period lower than maxPr.

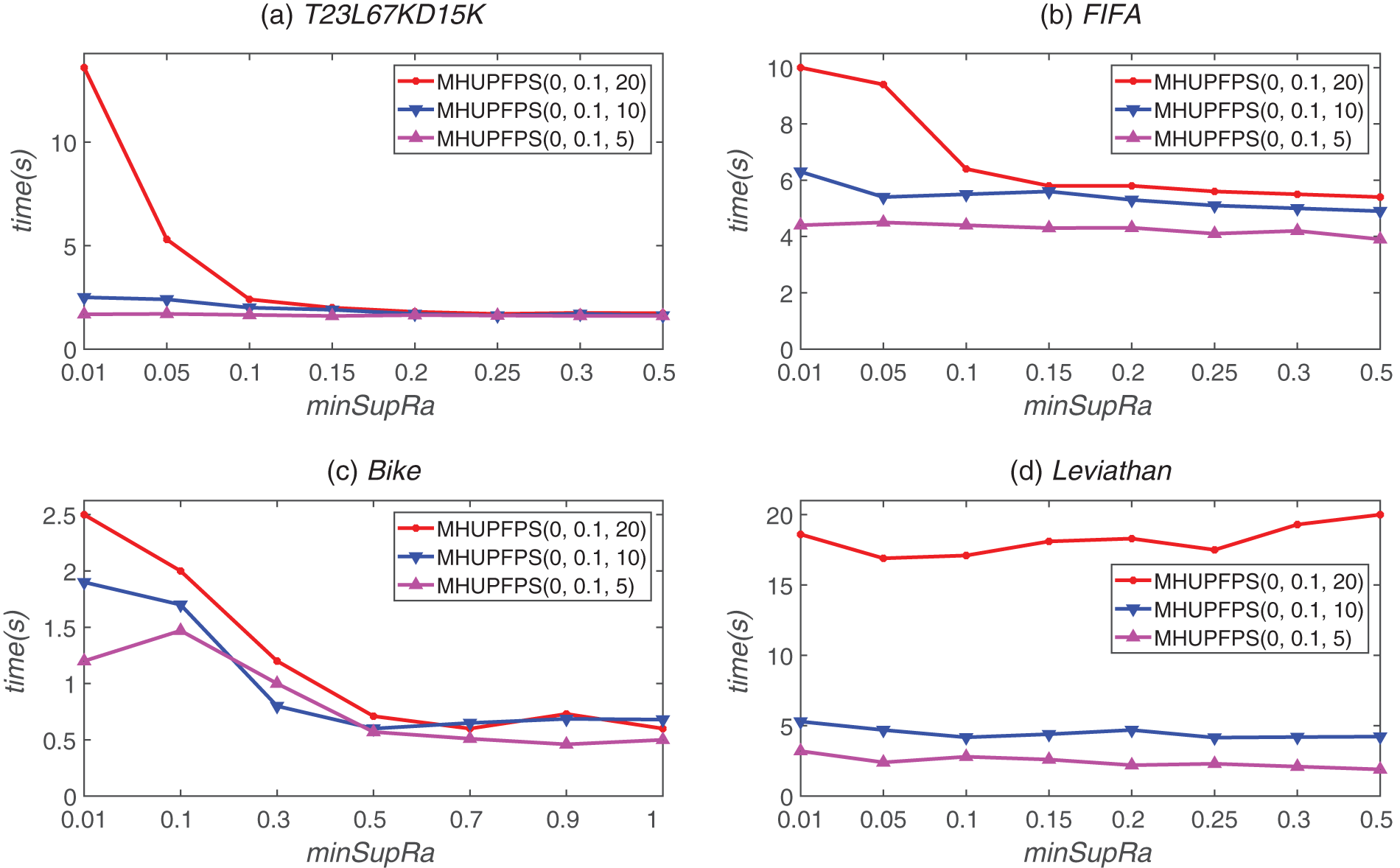
Figure 10: MHUPFPS runtime for various maxPr and minSupRa values

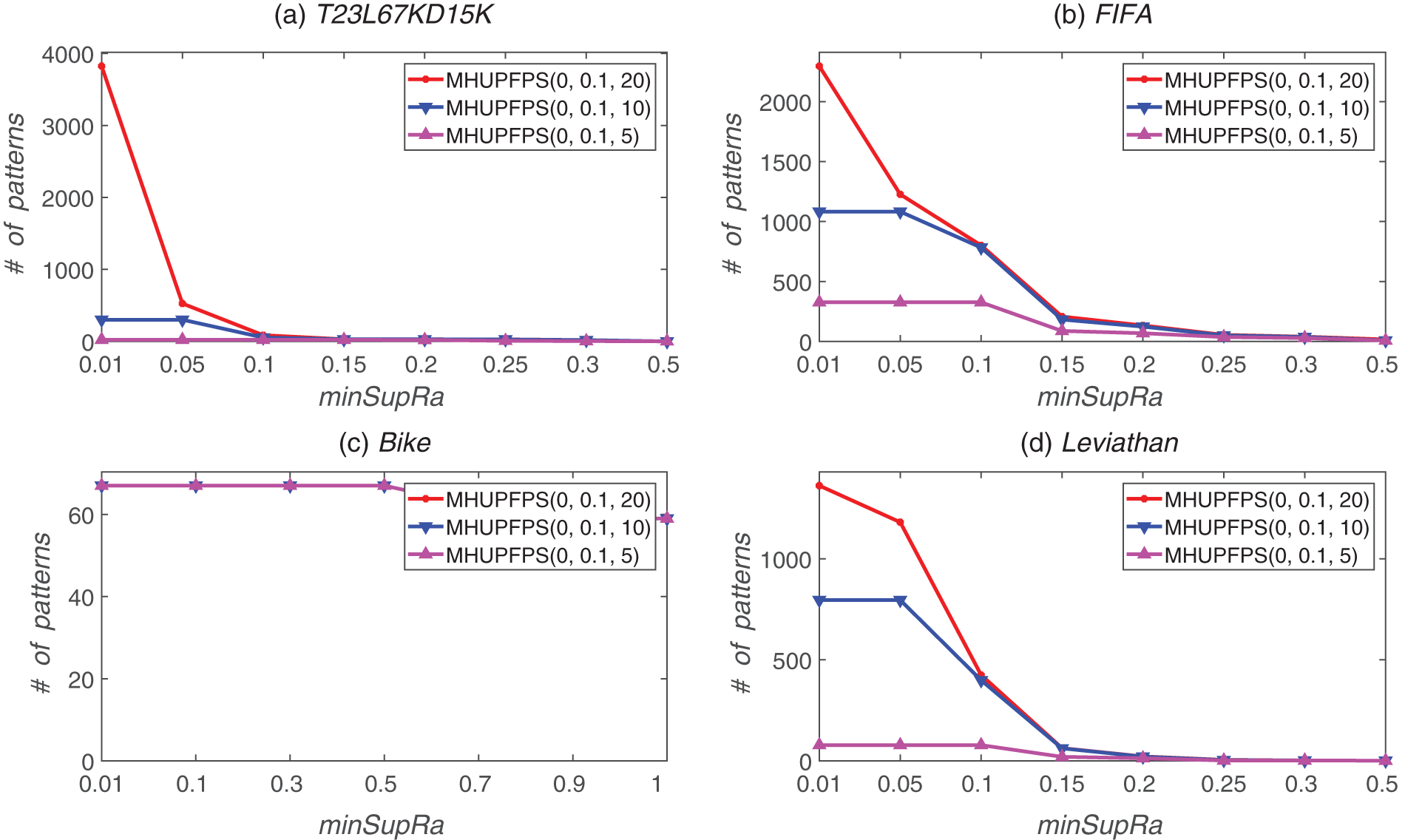
Figure 11: Number of patterns identified for various maxPr and minSupRa values

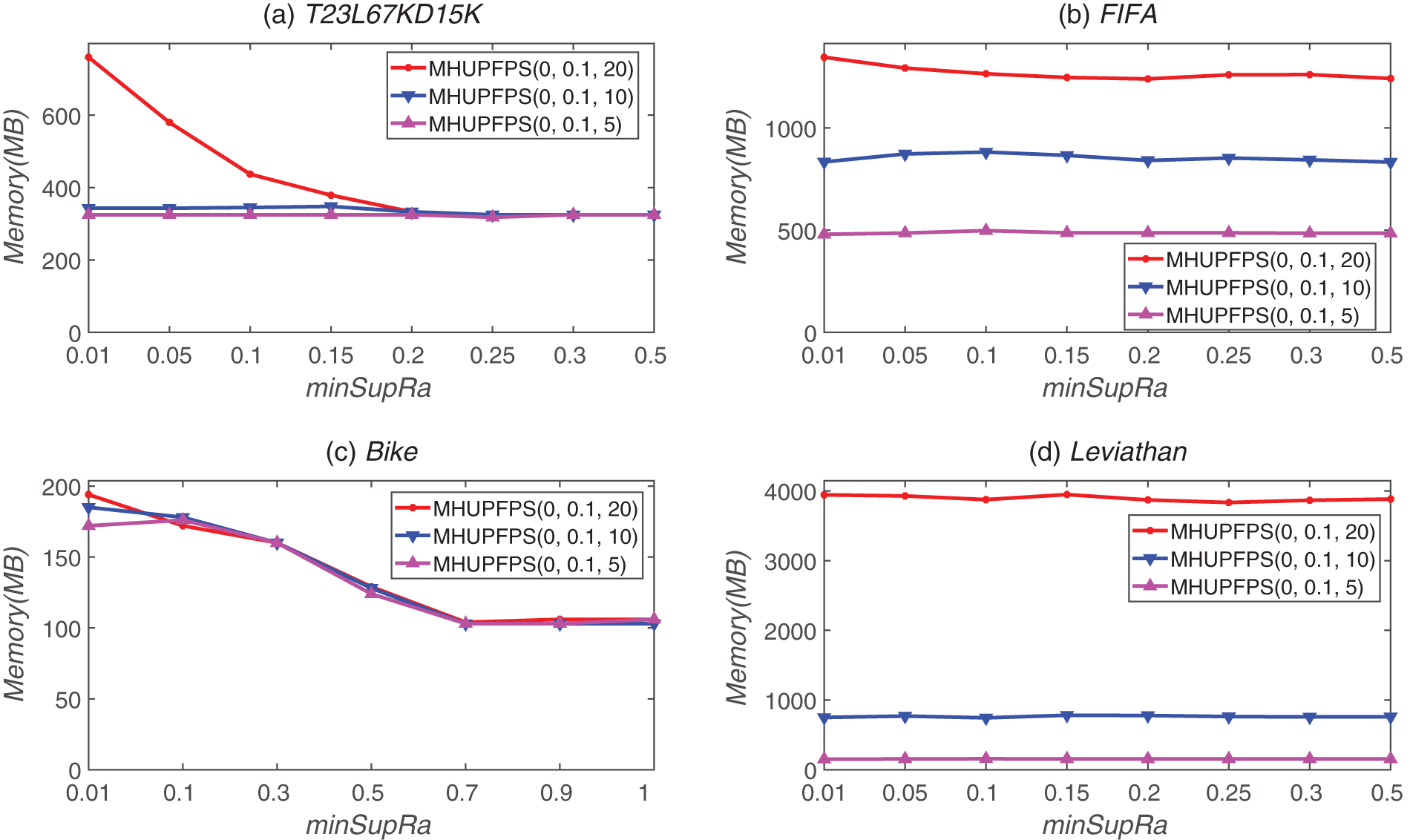
Figure 12: Memory usage for different parameter values for different datasets

Fig. 11 shows that decreasing the value of maxPr can significantly reduce the number of patterns. For example, for the synthetic dataset, the number of mined patterns was 86 for minSupRa = 0.1 and maxPr = 20, which reduced to 54 for minSupRa = 0.1 and maxPr = 10. When minSupRa = 0.1 and maxPr = 5, the number of mined patterns reduced to 22. This is reasonable because maxPr enforces a very strict limit on the period of the patterns; hence, the algorithm requires that every period of every pattern is less than maxPr. Therefore, several patterns were filtered out.

As shown in Fig. 12, as maxPr decreased, the memory usage significantly decreased for all datasets. This is reasonable because the algorithm has a stricter limit on the period of the patterns as maxPr decreases. Thus, MHUPFPS requires less space and reduces the number of patterns in the HUPFPS-list. For example, for the Leviathan dataset, the memory usage decreased from 3,948 to 783 MB as maxStd reduced from 20 to ten for supSupRa = 0.15. The memory usage decreased to 155 MB as maxStd decreased from ten to five for supSupRa = 0.15. This is because when maxPr decreases, the algorithm has a stricter limit on the period of patterns, meaning that MHUPFPS requires less memory to store the HUPFPS-list. Our results show that the number of patterns that are saved in the memory can be reduced by decreasing maxPr.

6  Conclusion

Previous studies have only considered one factor, either periodicity or utility, and have yet to identify valuable patterns in multiple sequences. In this study, we combined the utility and periodicity and mined common high utility period frequent patterns in a set of sequences. The proposed MHUPFPS algorithm is based on a new data structure, HUPFPS-list, and a novel pruning strategy that is used to reduce the search space. The experimental results show that MHUPFPS is efficient and can filter out non-high-utility period frequent patterns. In the future, we plan to further optimize the proposed algorithm in terms of runtime and memory usage. In addition, we aim to locate other meaningful patterns.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest regarding this study.

References

1. Schweizer, D., Zehnder, M., Wache, H., Witschel, H. F., Zanatta, D. et al. (2015). Using consumer behavior data to reduce energy consumption in smart homes: Applying machine learning to save energy without lowering comfort of inhabitants. Proceeding of the IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Florida, USA. [Google Scholar]

2. Zhang, K., Wang, Z., Chen, G., Zhang, L., Yang, Y. et al. (2022). Training effective deep reinforcement learning agents for real-time life-cycle production optimization. Journal of Petroleum Science and Engineering, 208(1), 109766. https://doi.org/10.1016/j.petrol.2021.109766 [Google Scholar] [CrossRef]

3. Aggarwal, C. C., Bhuiyan, M. A., Hasan, M. A. (2014). Frequent pattern mining algorithms: A survey. In: Frequent pattern mining, pp. 19–64. Switzerland: Springer. [Google Scholar]

4. Fournier-Viger, P., Lin, J. C. W., Vo, B., Chi, T. T., Zhang, J. et al. (2017). A survey of itemset mining. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 7(4), e1207. https://doi.org/10.1002/widm.1207 [Google Scholar] [CrossRef]

5. Berlingerio, M., Pinelli, F., Calabrese, F. (2013). Abacus: Frequent pattern mining-based community discovery in multidimensional networks. Data Mining and Knowledge Discovery, 27(3), 294–320. https://doi.org/10.1007/s10618-013-0331-0 [Google Scholar] [CrossRef]

6. Halder, S., Samiullah, M., Lee, Y. K. (2017). Supergraph based periodic pattern mining in dynamic social networks. Expert Systems with Applications, 72(11), 430–442. https://doi.org/10.1016/j.eswa.2016.10.033 [Google Scholar] [CrossRef]

7. Khan, M. A., Ullah, I., Alsharif, M. H., Alghtani, A. H., Aly, A. A. et al. (2022). An efficient certificate-based aggregate signature scheme for internet of drones. Security and Communication Networks, 2022, 1–9. https://doi.org/10.1155/2022/9718580 [Google Scholar] [CrossRef]

8. Mei, Q., Xiong, H., Chen, Y. C., Chen, C. M. (2022). Blockchain-enabled privacy-preserving authentication mechanism for transportation CPS with cloud-edge computing. IEEE Transactions on Engineering Management, 1–12. https://doi.org/10.1109/TEM.2022.3159311 [Google Scholar] [CrossRef]

9. Pan, J. S., Hu, P., Snášel, V., Chu, S. C. (2022). A survey on binary metaheuristic algorithms and their engineering applications. Artificial Intelligence Review, 13(6), 1–67. https://doi.org/10.1007/s10462-022-10328-9 [Google Scholar] [PubMed] [CrossRef]

10. Bhatia, M., Bhatia, S., Hooda, M., Namasudra, S., Taniar, D. (2022). Analyzing and classifying MRI images using robust mathematical modeling. Multimedia Tools and Applications, 81(26), 37519–37540. https://doi.org/10.1007/s11042-022-13505-8 [Google Scholar] [CrossRef]

11. Malviya, S., Kumar, P., Namasudra, S., Tiwary, U. S. (2022). Experience replay-based deep reinforcement learning for dialogue management optimisation. Transactions on Asian and Low-Resource Language Information Processing. https://doi.org/10.1145/3539223 [Google Scholar] [CrossRef]

12. Pan, J. S., Lv, J. X., Yan, L. J., Weng, S. W., Chu, S. C. et al. (2022). Golden eagle optimizer with double learning strategies for 3D path planning of uav in power inspection. Mathematics and Computers in Simulation, 193(10), 509–532. https://doi.org/10.1016/j.matcom.2021.10.032 [Google Scholar] [CrossRef]

13. Song, P. C., Chu, S. C., Pan, J. S., Yang, H. (2022). Simplified phasmatodea population evolution algorithm for optimization. Complex & Intelligent Systems, 8(4), 2749–2767. https://doi.org/10.1007/s40747-021-00402-0 [Google Scholar] [CrossRef]

14. Wu, T. Y., Kong, F., Wang, L., Chen, Y. C., Kumari, S. et al. (2022). Toward smart home authentication using puf and edge-computing paradigm. Sensors, 22(23), 9174. https://doi.org/10.3390/s22239174 [Google Scholar] [PubMed] [CrossRef]

15. Zhao, S., Zhu, S., Wu, Z., Jaing, B. (2022). Cooperative energy dispatch of smart building cluster based on smart contracts. International Journal of Electrical Power & Energy Systems, 138(6), 107896. https://doi.org/10.1016/j.ijepes.2021.107896 [Google Scholar] [CrossRef]

16. Khan, M. A., Kumar, N., Mohsan, S. A. H., Khan, W. U., Nasralla, M. M. et al. (2022). Swarm of UAVs for network management in 6G: A technical review. IEEE Transactions on Network and Service Management, 1. https://doi.org/10.1109/TNSM.2022.3213370 [Google Scholar] [CrossRef]

17. Li, X., Liu, S., Kumari, S., Chen, C. M. (2023). PSAP-WSN: A provably secure authentication protocol for 5G-based wireless sensor networks. Computer Modeling in Engineering & Sciences, 135(1), 711–732. https://doi.org/10.32604/cmes.2022.022667 [Google Scholar] [CrossRef]

18. Wu, T. Y., Meng, Q., Yang, L., Kumari, S., Pirouz, M. (2023). Amassing the security: An enhanced authentication and key agreementprotocol for remote surgery in healthcare environment. Computer Modeling in Engineering & Sciences, 134(1), 317–341. https://doi.org/10.32604/cmes.2022.019595 [Google Scholar] [CrossRef]

19. Han, J., Cheng, H., Xin, D., Yan, X. (2007). Frequent pattern mining: Current status and future directions. Data Mining and Knowledge Discovery, 15(1), 55–86. https://doi.org/10.1007/s10618-006-0059-1 [Google Scholar] [CrossRef]

20. Duan, Y., Fu, X., Luo, B., Wang, Z., Shi, J. et al. (2015). Detective: Automatically identify and analyze malware processes in forensic scenarios via DLLs. Proceedings of the IEEE International Conference on Communications, London, UK. [Google Scholar]

21. Mwamikazi, E., Fournier-Viger, P., Moghrabi, C., Baudouin, R. (2014). A dynamic questionnaire to further reduce questions in learning style assessment. Proceedings of the IFIP International Conference on Artificial Intelligence Applications and Innovations, Rhodes, Greece. [Google Scholar]

22. Fernando, B., Fromont, E., Tuytelaars, T. (2012). Effective use of frequent itemset mining for image classification. Proceedings of the European Conference on Computer Vision, Florence, Italy. [Google Scholar]

23. Liu, Y., Zhao, Y., Chen, L., Pei, J., Han, J. (2011). Mining frequent trajectory patterns for activity monitoring using radio frequency tag arrays. IEEE Transactions on Parallel and Distributed Systems, 23(11), 2138–2149. https://doi.org/10.1109/TPDS.2011.307 [Google Scholar] [CrossRef]

24. Agrawal, R., Srikant, R. (1994). Fast algorithms for mining association rules. Proceedings of the International Conference on Very Large Databases, vol. 1215. Santiago, Chile. [Google Scholar]

25. Wang, J., Han, J., Li, C. (2007). Frequent closed sequence mining without candidate maintenance. IEEE Transactions on Knowledge and Data Engineering, 19(8), 1042–1056. https://doi.org/10.1109/TKDE.2007.1043 [Google Scholar] [CrossRef]

26. Fournier-Viger, P., Nkambou, R., Nguifo, E. M. (2008). A knowledge discovery framework for learning task models from user interactions in intelligent tutoring systems. Proceedings of the Mexican International Conference on Artificial Intelligence, México. [Google Scholar]

27. Ziebarth, S., Chounta, I. A., Hoppe, H. U. (2015). Resource access patterns in exam preparation activities. Proceedings of the European Conference on Technology Enhanced Learning, Toledo, Spain. [Google Scholar]

28. Pokou, Y. J. M., Fournier-Viger, P., Moghrabi, C. (2016). Authorship attribution using small sets of frequent part-of-speech skip-grams. Proceedings of the Twenty-Ninth International Flairs Conference, Florida, USA. [Google Scholar]

29. Agrawal, R., Srikant, R. (1995). Mining sequential patterns. Proceedings of the Eleventh International Conference on Data Engineering, Taipei, Taiwan. [Google Scholar]

30. Fan, Y., Ye, Y., Chen, L. (2016). Malicious sequential pattern mining for automatic malware detection. Expert Systems with Applications, 52, 16–25. https://doi.org/10.1016/j.eswa.2016.01.002 [Google Scholar] [CrossRef]

31. Tanbeer, S. K., Ahmed, C. F., Jeong, B. S., Lee, Y. K. (2009). Discovering periodic-frequent patterns in transactional databases. Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Bangkok, Thailand. [Google Scholar]

32. Amphawan, K., Lenca, P., Surarerks, A. (2009). Mining top-k periodic-frequent pattern from transactional databases without support threshold. Proceedings of the International Conference on Advances in Information Technology, Bangkok, Thailand. [Google Scholar]

33. Surana, A., Kiran, R. U., Reddy, P. K. (2011). An efficient approach to mine periodic-frequent patterns in transactional databases. Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Shenzhen, China. [Google Scholar]

34. Rashid, M., Karim, R., Jeong, B. S., Choi, H. J. et al. (2012). Efficient mining regularly frequent patterns in transactional databases. Proceedings of the International Conference on Database Systems for Advanced Applications, Busan, South Korea. [Google Scholar]

35. Kiran, R. U., Kitsuregawa, M., Reddy, P. K. (2016). Efficient discovery of periodic-frequent patterns in very large databases. Journal of Systems and Software, 112(3), 110–121. https://doi.org/10.1016/j.jss.2015.10.035 [Google Scholar] [CrossRef]

36. Dinh, D. T., Le, B., Fournier-Viger, P., Huynh, V. N. (2018). An efficient algorithm for mining periodic high-utility sequential patterns. Applied Intelligence, 48(12), 4694–4714. https://doi.org/10.1007/s10489-018-1227-x [Google Scholar] [CrossRef]

37. Fournier-Viger, P., Li, Z., Lin, J. C. W., Kiran, R. U., Fujita, H. (2018). Discovering periodic patterns common to multiple sequences. Proceedings of the International Conference on Big Data Analytics and Knowledge Discovery, Regensburg, Germany. [Google Scholar]

38. Fournier-Viger, P., Lin, J. C. W., Duong, Q. H., Dam, T. L. (2016). PHM: Mining periodic high-utility itemsets. Proceedings of the Industrial Conference on Data Mining, New York, USA. [Google Scholar]

39. Dinh, T., Huynh, V. N., Le, B. (2017). Mining periodic high utility sequential patterns. Proceedings of the Asian Conference on Intelligent Information and Database Systems, Kanazawa, Japan. [Google Scholar]

40. Lin, J. C. W., Gan, W., Fournier-Viger, P., Hong, T. P., Chao, H. C. (2017). FDHUP: Fast algorithm for mining discriminative high utility patterns. Knowledge and Information Systems, 51(3), 873–909. https://doi.org/10.1007/s10115-016-0991-3 [Google Scholar] [CrossRef]

41. Zhang, C., Du, Z., Gan, W., Philip, S. Y. (2021). TKUS: Mining top-k high utility sequential patterns. Information Sciences, 570(4), 342–359. https://doi.org/10.1016/j.ins.2021.04.035 [Google Scholar] [CrossRef]

42. Chen, L., Gan, W., Lin, Q., Huang, S., Chen, C. M. (2022). OHUQI: Mining on-shelf high-utility quantitative itemsets. The Journal of Supercomputing, 78(6), 8321–8345. https://doi.org/10.1007/s11227-021-04218-0 [Google Scholar] [CrossRef]

43. Fournier-Viger, P., Li, Z., Lin, J. C. W., Kiran, R. U., Fujita, H. (2019). Efficient algorithms to identify periodic patterns in multiple sequences. Information Sciences, 489(9), 205–226. https://doi.org/10.1016/j.ins.2019.03.050 [Google Scholar] [CrossRef]

44. Srikant, R., Agrawal, R. (1996). Mining sequential patterns: Generalizations and performance improvements. Proceedings of the International Conference on Extending Database Technology, Avignon, France. [Google Scholar]

45. Han, J., Pei, J., Mortazavi-Asl, B., Chen, Q., Dayal, U. et al. (2000). Freespan: Frequent pattern-projected sequential pattern mining. Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Boston, USA. [Google Scholar]

46. Han, J., Pei, J., Mortazavi-Asl, B., Pinto, H., Chen, Q. et al. (2001). Prefixspan: Mining sequential patterns efficiently by prefix-projected pattern growth. Proceedings of the 17th International Conference on Data Engineering, Athens, Greece. [Google Scholar]

47. Tang, L., Zhang, L., Luo, P., Wang, M. (2012). Incorporating occupancy into frequent pattern mining for high quality pattern recommendation. Proceedings of the 21st ACM International Conference on Information and Knowledge Management, Hawaii, USA. [Google Scholar]

48. Liu, J., Wang, K., Fung, B. C. (2012). Direct discovery of high utility itemsets without candidate generation. Proceedings of the IEEE 12th International Conference on Data Mining, Brussels, Belgium. [Google Scholar]

49. Gan, W., Lin, J. C. W., Fournier-Viger, P., Chao, H. C., Tseng, V. S. et al. (2019). A survey of utility-oriented pattern mining. IEEE Transactions on Knowledge and Data Engineering, 33(4), 1306–1327. https://doi.org/10.1109/TKDE.2019.2942594 [Google Scholar] [CrossRef]

50. Ahmed, C. F., Tanbeer, S. K., Jeong, B. S., Lee, Y. K. (2009). Efficient tree structures for high utility pattern mining in incremental databases. IEEE Transactions on Knowledge and Data Engineering, 21(12), 1708–1721. https://doi.org/10.1109/TKDE.2009.46 [Google Scholar] [CrossRef]

51. Han, J., Pei, J., Yin, Y., Mao, R. (2004). Mining frequent patterns without candidate generation: A frequent-pattern tree approach. Data Mining and Knowledge Discovery, 8(1), 53–87. https://doi.org/10.1023/B:DAMI.0000005258.31418.83 [Google Scholar] [CrossRef]

52. Zihayat, M., Davoudi, H., An, A. (2017). Mining significant high utility gene regulation sequential patterns. BMC Systems Biology, 11(6), 1–14. https://doi.org/10.1186/s12918-017-0475-4 [Google Scholar] [PubMed] [CrossRef]

53. Liu, M., Qu, J. (2012). Mining high utility itemsets without candidate generation. Proceedings of the 21st ACM International Conference on Information and Knowledge Management, Hawaii, USA. [Google Scholar]

54. Lin, J. C. W., Gan, W., Fournier-Viger, P., Hong, T. P., Tseng, V. S. (2016). Efficient algorithms for mining high-utility itemsets in uncertain databases. Knowledge-Based Systems, 96(5), 171–187. https://doi.org/10.1016/j.knosys.2015.12.019 [Google Scholar] [CrossRef]

55. Tseng, V. S., Shie, B. E., Wu, C. W., Philip, S. Y. (2012). Efficient algorithms for mining high utility itemsets from transactional databases. IEEE Transactions on Knowledge and Data Engineering, 25(8), 1772–1786. https://doi.org/10.1109/TKDE.2012.59 [Google Scholar] [CrossRef]

56. Fournier-Viger, P., Wu, C. W., Zida, S., Tseng, V. S. (2014). FHM: Faster high-utility itemset mining using estimated utility co-occurrence pruning. Proceedings of the International Symposium on Methodologies for Intelligent Systems, Roskilde, Denmark. [Google Scholar]

57. Krishnamoorthy, S. (2015). Pruning strategies for mining high utility itemsets. Expert Systems with Applications, 42(5), 2371–2381. https://doi.org/10.1016/j.eswa.2014.11.001 [Google Scholar] [CrossRef]

58. Zida, S., Fournier-Viger, P., Lin, J. C. W., Wu, C. W., Tseng, V. S. (2017). EFIM: A fast and memory efficient algorithm for high-utility itemset mining. Knowledge and Information Systems, 51(2), 595–625. https://doi.org/10.1007/s10115-016-0986-0 [Google Scholar] [CrossRef]

59. Chan, R., Yang, Q., Shen, Y. D. (2003). Mining high utility itemsets. Proceeding of the IEEE International Conference on Data Mining, Florida, USA. [Google Scholar]

60. Yao, H., Hamilton, H. J., Butz, C. J. (2004). A foundational approach to mining itemset utilities from databases. Proceedings of the 2004 SIAM International Conference on Data Mining, Florida, USA. [Google Scholar]

61. Liu, Y., Liao, W. K., Choudhary, A. (2005). A two-phase algorithm for fast discovery of high utility itemsets. Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Hanoi, Vietnam. [Google Scholar]

62. Le, B., Dinh, D. T., Huynh, V. N., Nguyen, Q. M., Fournier-Viger, P. (2018). An efficient algorithm for hiding high utility sequential patterns. International Journal of Approximate Reasoning, 95(5), 77–92. https://doi.org/10.1016/j.ijar.2018.01.005 [Google Scholar] [CrossRef]

63. Gan, W., Lin, J. C. W., Zhang, J., Chao, H. C., Fujita, H. et al. (2019). ProUM: High utility sequential pattern mining. Proceedings of the IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy. [Google Scholar]

64. Gan, W., Lin, J. C. W., Zhang, J., Fournier-Viger, P., Chao, H. C. et al. (2020). Fast utility mining on sequence data. IEEE Transactions on Cybernetics, 51(2), 487–500. https://doi.org/10.1109/TCYB.2020.2970176 [Google Scholar] [PubMed] [CrossRef]

65. Fournier-Viger, P., Yang, P., Li, Z., Lin, J. C. W., Kiran, R. U. (2020). Discovering rare correlated periodic patterns in multiple sequences. Data & Knowledge Engineering, 126(1), 101733. https://doi.org/10.1016/j.datak.2019.101733 [Google Scholar] [CrossRef]

66. Fournier-Viger, P., Yang, P., Lin, J. C. W., Kiran, R. U. (2019). Discovering stable periodic-frequent patterns in transactional data. Proceedings of the International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, Kitakyushu, Japan. [Google Scholar]

67. Fournier-Viger, P., Lin, C. W., Duong, Q. H., Dam, T. L., Ševčík, L. et al. (2017). PFPM: Discovering periodic frequent patterns with novel periodicity measures. Proceedings of the 2nd Czech-China Scientific Conference 2016, Ostrava, Czech Republic. [Google Scholar]

68. Fournier-Viger, P., Gomariz, A., Gueniche, T., Soltani, A., Wu, C. W. et al. (2014). SPMF: A Java open-source pattern mining library. The Journal of Machine Learning Research, 15(1), 3389–3393. [Google Scholar]