A Client Selection Method Based on Loss Function Optimization for Federated Learning

1  Introduction

Mobile devices have become the primary electronic devices for billions of users around the world, and we will witness the explosion of IoT devices in the coming years [1,2]. These devices generate vast amounts of valuable data, and machine learning is a popular method for processing those data to make applications more intelligent [3]. Typically, the centralized machine learning method trains all data on the server by gathering data from clients, which can expose data privacy problems [4]. However, with the improvement of users’ awareness of data privacy and the publication of General Data Protection Regulation (GDPR) [5] and Health Insurance Portability and Accountability Act (HIPAA) [6], it is difficult for centralized machine learning to collect and process scattered data. Federated learning is a framework with efficient communication and privacy protection. Since federated learning was proposed by Google in 2016 [7], it has shown potential to promote real-world applications in many domains, e.g., smart healthcare [8], and credit risk assessment [9].

Federated learning consists of three key phrases: (1) Client selection, the server selects random clients and disseminates the global model parameters to the selected clients; (2) Client local training, clients use their local data to update the shared model and upload the new model parameters to the server; (3) Server aggregation, the server aggregates the global model by averaging the updated local parameters. However, due to different client habits, for example, some clients may have more pictures of cats, while others may have more pictures of dogs. In this case, the datasets on each node are not identically and independently distributed, i.e., Non-IID. As a result, the local models trained on these data will also have biases. This means that the local models of clients selected to learn a global model jointly can significantly impact the quality of the global model. Since data distribution divergence between clients may cause parameter divergence between local models, how to select clients becomes essential for training the global model efficiently.

The uniform random selection algorithm is the most frequently used client selection strategy, which makes each client get the same selection probability and keep the same loss expectation. However, in the Non-IID setting, this method cannot accurately select the clients that would be most beneficial for accelerating the training process. As a result, the convergence performance with Non-IID data cannot be improved. The global optimization goal of federated learning is to minimize the loss value of all clients. The loss value generated during the client training can reflect the model’s prediction ability for the data on the client, and the higher the loss value, the poorer the model’s performance. If these losses can be appropriately used, the convergence of the global model can be accelerated.

Driven by the above descriptions, we propose a federated learning client selection method based on the loss function, FedChoice, to improve the convergence of the global model by selecting appropriate local models. The key contributions are as follows:

(1)   It analyzes the principles of selected local models that can affect the convergence of the global model and find that the loss function of the local model is a main influence factor for the convergence of the global model under the Non-IID data.

(2)   It proposes a client selection strategy based on the loss function, which gives a higher selected probability for clients with higher loss values, to speed up the convergence of the global model.

(3)   It introduces a gradient correction method to correct the local gradient vector direction, which can improve the model’s accuracy while keeping the convergence performance of our selection method. It employs a local offset control item to predict the local gradient direction and the global gradient direction and calculates a vector to correct the local gradient vector direction.

(4)   It verifies the effectiveness of our method by comparing the precision and convergence performance against three baseline algorithms FedAvg, FedProx, and FedNova on EMNIST, MNIST, FEMNIST, CINIC-10 and CIFAR-10 datasets. The results show that FedChoice can improve the convergence performance of federated learning in contrast with FedAvg by up to 18.7%.

The rest of this paper is organized as follows. Firstly, we review some related work in Section 2; Then, we describe the proposed problem description and algorithm FedChoice in Sections 3 and 4. Section 5 gives the experimental setup and results of FedChoice in detail. Finally, we summarize the work in Section 6.

2  Related Work

Non-IID data is a challenge for federated learning. There exist extensive works on improving the performance of federated learning via data sharing [10,11], self-supervised [12–14], personalized federated learning [15–17], etc. We review the literature related to our work by dividing them into two categories.

2.1 Statistical Heterogeneity Optimization

Statistical heterogeneity (also known as the Non-IID problem) is a bottleneck of federated learning [18]. McMahan et al. [7] have demonstrated that FedAvg can work with specific Non-IID data. However, Zhao et al. [11] proved that the accuracy of FedAvg became worse under highly skewed Non-IID data. Furthermore, Zhao et al. proposed a strategy to improve training accuracy on Non-IID data by a uniformly distributed dataset.

Many techniques have been proposed to tackle the accuracy degradation of federated learning in the Non-IID setting. FedProx [19] and FedDyn [20] add a proximal term to the local subproblem to limit the impact of local variable updates. SCAFFOLD [21] prevents the model deviation by introducing control variates. However, all these methods focus on balancing the local and global optimization objectives by limiting the updated direction of the local model. Although they can reduce the client drift to some extent, they can only partially eliminate this effect.

In order to improve the convergence performance of the global model, FedNova [22] eliminates this difference by introducing regular terms to keep the local loss function consistent. Lin et al. [23] adopted knowledge distillation technology to accelerate the convergence of the model. Tan et al. [24] proposed a federated prototype learning framework, which communicates the abstract class prototypes instead of the gradients between clients and servers. Zeng et al. [25] proposed a deep learning method to predict models’ training time on heterogeneous clients. However, these methods need to upload more communication data or require a lot of computation.

2.2 Client Selection Optimization

Client selection strategy is a flexible way to improve the performance of federated learning.

There have been some researches on the application of machine learning to client selection strategy. Huang et al. [26] optimized the convergence performance of the model from the perspective of time. They modeled the client selection as a Lyapunov [27] optimization problem, and proposed a client selection method with the model exchange time estimated by an online learning algorithm, between each client and server. Wang et al. [28] proposed an experience-driven federated learning method Favor based on reinforcement learning [29]. These methods can alleviate the deviation introduced by Non-IID data to some extent, but it brings heavy computing tasks to the server.

Some methods use objective indicators as criteria for client selection. Ribero et al. [30] proposed a client selection based on gradient information, which only uploads gradient updates of clients with larger differences from the global model. TiFL [31] accelerates the convergence of the model by selecting clients from the same tier with similar training performance. Similar to TiFL, FedMCCS [32] evaluated the client’s selection value with the client’s resources, including memory, CPU resources, electricity, etc. CSFedAvg [33] introduced the indicator of weight divergence to measure the degree of distribution deviation of Non-IID data. In summary, the indicators proposed by these methods are applied in simple scenarios and lack expansibility.

3  Problem Description

We formally define the problem of federated learning and analyze the effects caused by Non-IID data on federated learning in this section. We take a classification task in sample space X and label space Y={1,…,C} as an example. The data point {x,y} follows distribution q. Let the population cross-entropy ℓ(w) be the loss function, and w is the parameter of the neural network. Then the centralized learning problem is described as Eq. (1):

ℓ(w)=∑i=1Cq(y=i)Ex|y=i[logfi(x,w)].(1)

And the learning task can be expressed as Eq. (2):

minwℓ(w)=minw{∑i=1cq(y=i)Ex|y=i[logfi(x,w)]},(2)

where fi denotes the probability of the i-th class predicted by the neural network.

To determine w, SGD solves the optimization problem iteratively. Let wt(c) denotes the weight of the neural network after t-th update in centralized setting, where η is the learning rate and ∇w represents the gradient update in the t-th round. Then, the centralized SGD performs the following update:

wt(c)=wt−1(c)−η∇wℓ(wt−1(c)).(3)

In federated learning, assuming there are N clients, and the client k has nk training data. Each client executes the local SGD independently, and Eq. (4) describes the t-th round update on client k:

wt(k)=wt−1(k)−η∇wℓ(wt−1(k)).(4)

Assuming that the synchronization is conducted every T step and let wmT(g) be the weight of the global model after m-th synchronization, where wmT(k) denotes the weight of the local model after m-th synchronization, and pk=nk∑iNni denotes the aggregation weight of client k. Then, we have:

wmT(g)=∑k=1KpkwmT(k),∑k=1Npk=1(pk≥0).(5)

In the next synchronization, the server will send wmT(g) to all clients participating in the training.

Limited by the communication conditions, not all clients can be selected to train the global model in each round. A common way is to select a subset of clients, so, the selection strategy π of the subset is very important, which directly affects the data quality of training.

The most common method of client selection in federated learning is uniform selection, that is, all clients have the same probability of being selected qi=1K, where K is the number of clients participating in training. The canonical algorithm FedAvg selects clients with the uniform selection method, and organizes them to do local training and model aggregation. However, different clients have different performances, and the uniform selection algorithm cannot eliminate this difference.

To overcome this problem, Li et al. [19] proposed another unbiased sampling scheme, which modified the sampling probability of clients to qi=nk∑i=1Kni. This sampling scheme may prioritize clients with large data sets, but it does not take into account the distribution and quality of the data, which can significantly impact the convergence speed of the global model.

Specifically, for the global model, the objective of the training is to minimize the loss function of all clients (as defined in Eq. (2)). In the case of uniform random selection, clients with high losses cannot be selected in time to participate in training and optimize their loss values, which will delay the convergence time of the model. For the local model, loss value can reflect the quality of the model. The higher the loss, the worse the prediction ability of the client’s model.

Therefore, this paper will select clients based on the optimization of the loss function to improve the quality of the global model.

4  Methodology

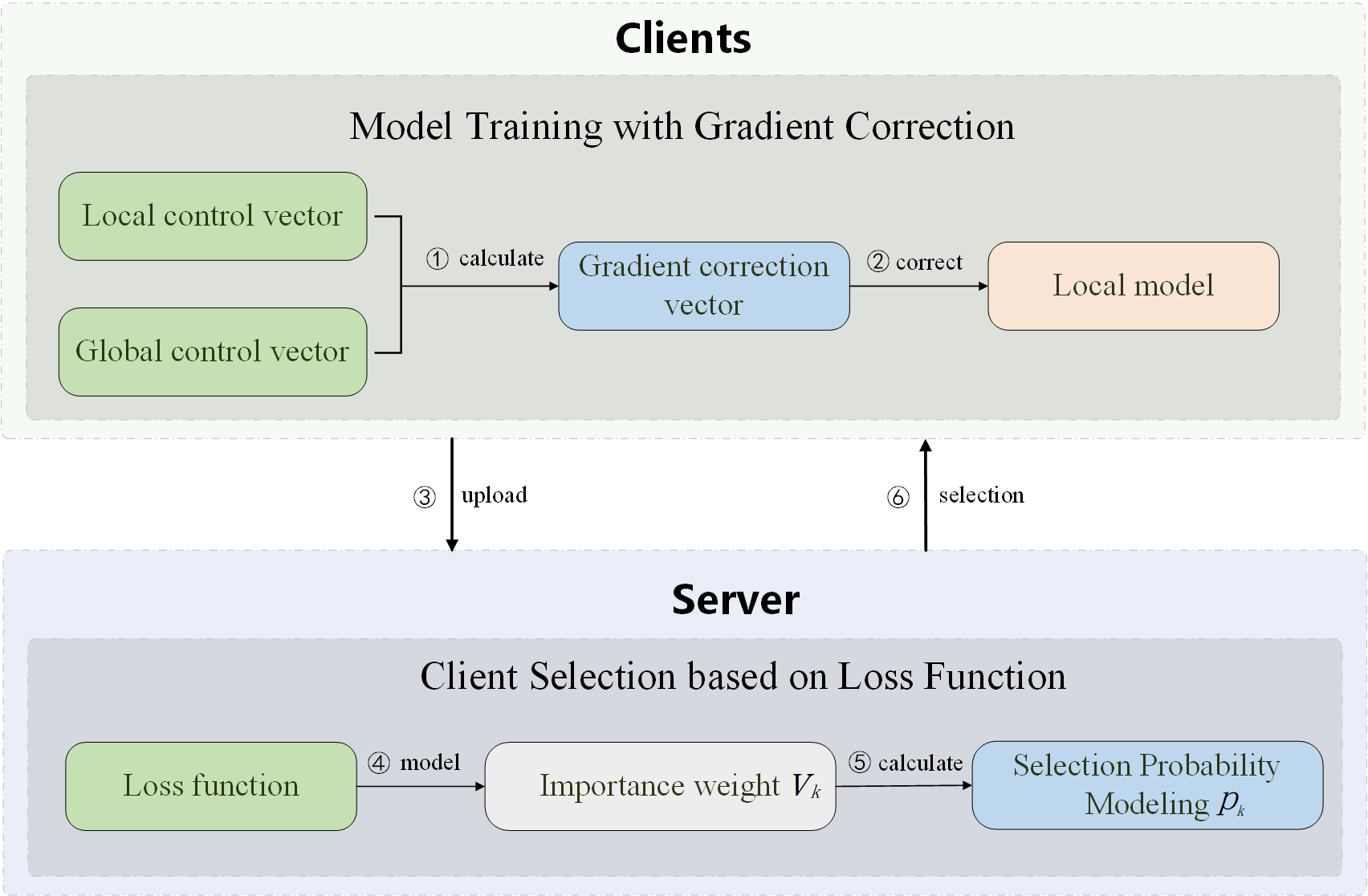
In this section, we introduce FedChoice, which optimizes the client selection method by giving a higher selected probability to the clients with high loss function. The flowchart of FedChoice is shown in Fig. 1. Firstly, we construct the importance weight of clients based on loss function, and calculate the probability of each client being selected in the next round. Then, we employ the model training strategy based on gradient correction vector to reconstruct the local loss function, which can improve the precision of the model under Non-IID environment. Such strategy generates a gradient correction vector through historical training records, which can correct the skewed local gradient update to the global gradient direction.

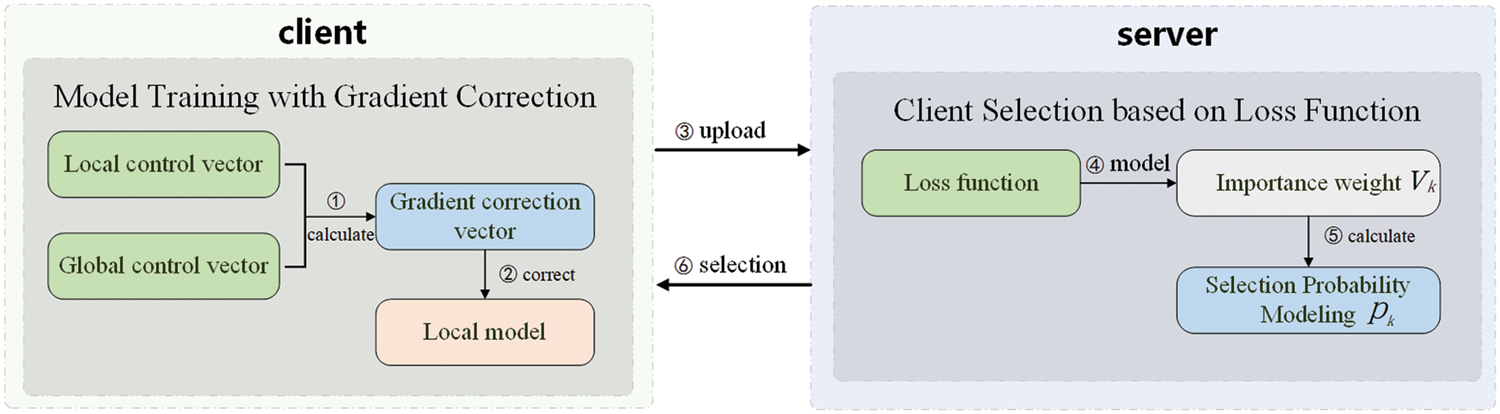
Figure 1: The flow chart of FedChoice

4.1 Client Selection Based on Loss Function

When the training data is highly Non-IID, the client extraction becomes unstable due to its skewed data. The global model cannot quickly get unknown knowledge from the local training, leading to slow convergence. Aiming at accelerating the convergence of the global model, this paper applies the client selection strategy πloss based on the loss function to choose clients with higher loss function values to train.

Assuming there are four clients and one server, and there are circular, square and triangular samples, the data distribution with Non-IID is shown in Fig. 2. If we adopt the random uniform selection strategy πrand, the global model will receive more knowledge about circular and square samples, but less knowledge about triangular samples during training. To avoid the difficulty of the global model convergence, we introduce πloss to give a higher selection probability to the client with a high loss. In this way, the convergence rate will obviously increase since the server can choose more clients with higher loss and poor prediction ability to participate in training. Especially in the case of Non-IID data, a high loss value may mean that the client’s training data is a minority class of the total data. In order to speed up convergence, the server should select more clients with high loss values.

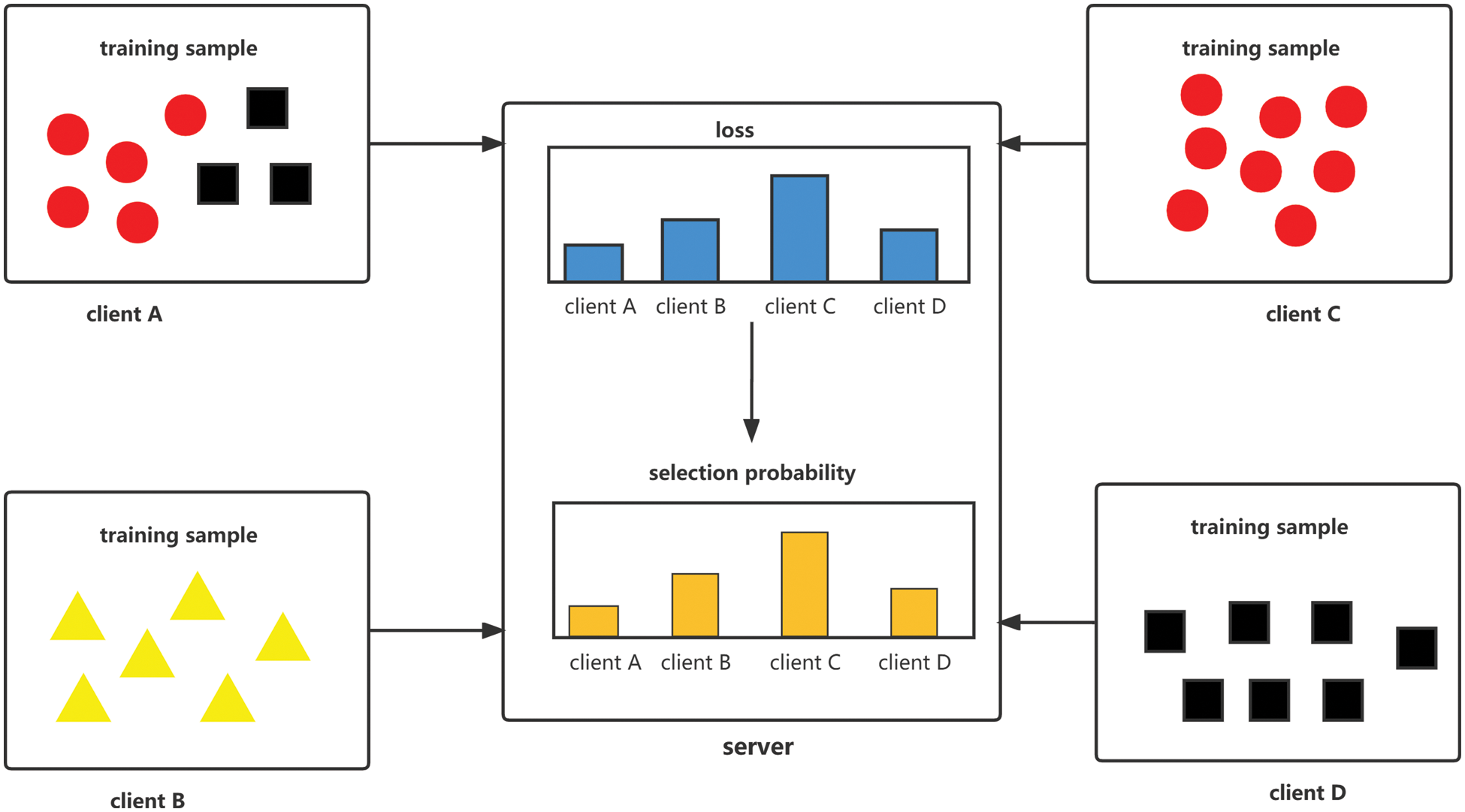
Figure 2: Client selection diagram

The πloss strategy includes the importance weight of client vk and the selection probability function. We firstly define the importance weight vk to indicate the importance of clients to training. Clients with higher value vk will have a greater probability of being selected by the server to participate in training. Then, we construct a selection probability function to compute the selection probability for clients.

4.1.1 Importance Weight of Client Modeling

We define the importance weight of the client in Definition 1 to determine the selection probability for clients.

Definition 1. Importance Weight. The importance weight of client k is defined as vk, with the loss function, which is used to express the potential value of the client k for accelerating the convergence of the model. Taking the cross entropy function in the classification task as an example, importance weight of client k is described in Eq. (6):

vk(t+1)={ℓk(t)(w)=∑i=1cq(y=i)Ex|y=i[logfi(x,w)], if k∈Utvk(t), else, (6)

where k denotes the client k and Ut denotes the selected clients set in the t-th round.

In federated learning, it is difficult for the server to get the loss values of all clients limited by communication and hardware resources. Therefore, for the clients that did not participate in this round of training, we set the client value of the next round to be the same value as the previous round, that is, vk(t+1)=vkt. Although this strategy carries a certain staleness, it does not affect the selection performance, because the loss value of the client will decrease with the increasing number of training rounds. As the newly selected client produces a smaller loss value, its selection probability will be reduced. This gives other clients which are not selected in this round more opportunities to be selected for the next round, so the global model can learn more diverse knowledge.

4.1.2 Selection Probability Modeling

The high selection tendency of clients with high loss value can improve the convergence speed, but it leads to the deviation between the optimal value of the global loss function and the ideal optimal value. That is to say, excessive pursuit of the convergence rate brought by clients with high loss value may result in the decreasing accuracy of the global model. It is not advisable to select all clients by using simple strategy πloss. Thus, FedChoice will control the ratio of using strategies πrand and πloss by hyperparameter α in the client selection stage.

Firstly, we construct a selection probability function with the importance weight of the client. Let pk be the selection probability of client k in the training, αm clients are selected by πloss with the Eq. (7) and added to set Uloss:

pk=eβvk,(7)

where β is an adjustable hyperparameter, vk is the importance weight. The server selects a specified number of clients to participate in the training through weighted randomness by the selection probability p of each client. The selection probability p of a client is calculated based on the loss value, which is a floating-point number. This means that it is highly unlikely for two clients to have the same probability. If two clients have the same probability, the server will randomly select one of them to participate in training.

And then the remaining (1−α)m clients are selected by πrand strategy and added to set Urand. When α=0, the overall client selection strategy is the same as FedAvg, that is, the clients participating in the training are randomly selected.

The details of the FedChoice algorithm are described in Algorithm 1.

4.2 Model Training with Gradient Correction

As stated in 4.1, the client selection strategy based on the loss function may reduce the precision of the global model to a certain extent. In addition, the Non-IID data also affects the model accuracy. To address these limitations, we introduce a model training strategy based on the gradient correction vector. This strategy generates a gradient correction vector with historical training records, to update the skewed local gradient to the global gradient direction and maintain the accuracy of the global model.

Definition 2. Local Control Vector ck. Each client maintains a local control vector ck, which is built from the historical training record of client k and used to predict the client’s future gradient vector.

ckt+1=ckt−cgt+1K(wgt−wkt),(8)

where K denotes the number of participating clients, wg and wk denote the global model parameter and the local model parameter, respectively.

Definition 3. Global Control Vector cg. For the server, we devise a global control vector cg to predict the global gradient vector. It is generated by averaging the local control vectors of all clients participating in the training.

cgt+1=cgt+1N∑k∈K(ckt+1−ckt),(9)

where N is the total number of clients.

Definition 4. Gradient Correction Vector c. The gradient correction vector c is obtained from the local control vector ck and global control vector cg. It is used to correct gradient vector deviation caused by local training and avoid the accumulation of local gradient vector deviation.

c=cg−ck.(10)

In the training process of federated learning, the local model is obtained by optimizing the loss function of local data, while the global model is obtained by aggregating the local models participating in the training. According to the traditional SGD method, the client uploads its update parameters to the server in each step. The local deviation from each step is corrected by the global aggregation process in time. Thus, the global optimization direction is closer to the ideal updated direction and the global optimal can be achieved with fewer steps.

However, communication costs are relatively high in federated learning, so it is hard to aggregate all local models. As shown in Fig. 3, FedAvg performs multiple local SGD before each model aggregation. This approach can greatly reduce the communication cost, but it brings a new problem: there exists skewed data distribution among the clients. Due to the existence of skewed data distribution, the local skewed updates will be accumulated during the local SGD process. Even after global aggregation, the global optimization direction will still deviate from the original optimal direction.

Figure 3: Gradient correction vector effect

In federated learning, the accumulation of local update deviation is inevitable owing to the communication problem. If the local updated direction can be directed to the global updated direction to reduce the local deviation caused by Non-IID data, the performance of the global model will be greatly improved. Therefore, as shown in Fig. 3, we introduce the local control vector ck and the global control vector cg to predict their gradient direction. And a gradient correction term c=cg−ck is generated to make the skewed local update closer to the global update directions. The gradient correction term c will correct the local gradient after each local training, thereby avoiding the accumulation of local model deviation.

4.3 Implement

Based on the above definition and analysis, FedChoice algorithm is proposed to optimize the convergence rate and accuracy of the model in case of Non-IID data in federated learning. Combined with the algorithm architecture shown in Fig. 4 and Algorithm 2, the specific process of FedChoice can be described as follows:

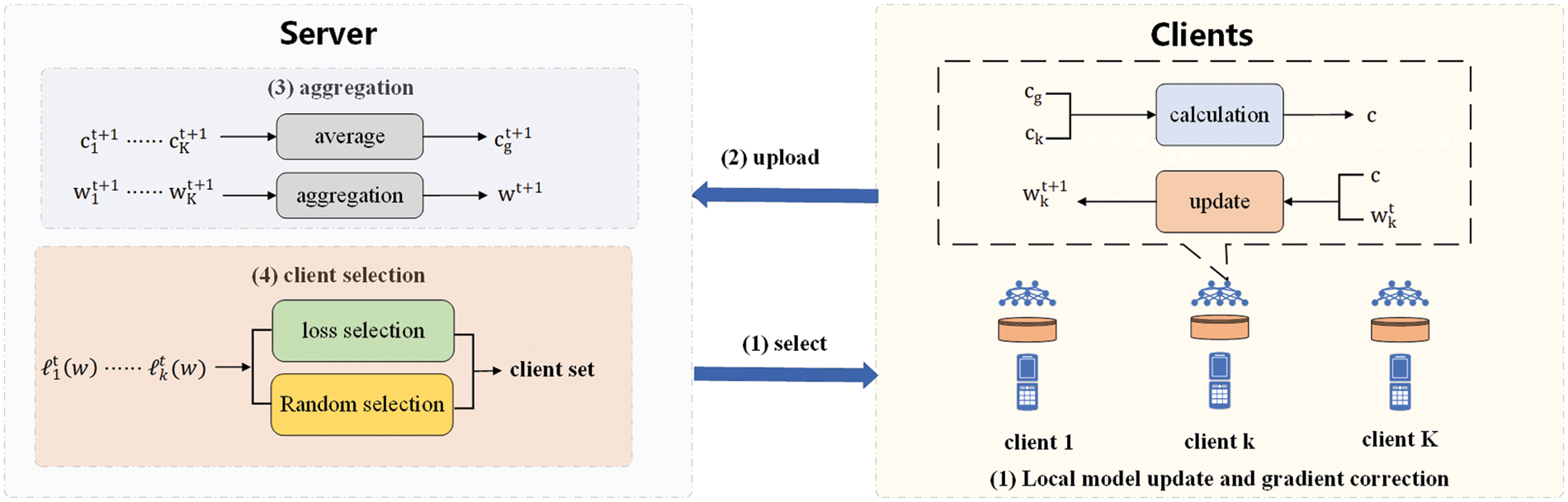
Figure 4: Architecture diagram of FedChoice

Local model update and gradient correction. The selected clients use their local data to train the local models. And each client needs to correct the update gradient (gi(wkt)+c). The purpose of this step is to predict the direction of the current gradient update through the historical gradient updates, so as to reduce the gradient deviation caused by excessive local updates with the correction term.

Upload. The client uploads the local model parameters, loss and local control vector to the server. The loss is used to select the client and the local control vector is used to calculate the new global control vector.

Global model aggregation on server. The server performs an averaging process with the update parameters to formulate an enhanced global model by Eq. (5).

Client selection on server. The server calculates the importance weight based on the loss value, and then calculates the selection probability with the importance weight. Combined with the client selection strategies πrand and πloss, the server selects M clients to participate in the next round of training and broadcasts the global model.

5  Experiments

In order to evaluate the effectiveness of our method, we make experiments on five datasets: MNIST [34], FEMNIST [35], EMNIST [36], CINIC-10 [37] and CIFAR-10 [38], and compare it with three algorithms FedAvg, FedProx and FedNova. For MNIST, FMNIST and EMNIST datasets, we adopt MLP architecture with two hidden layers. For CINIC-10 and CIFAR-10 datasets, we employ CNN architecture with three convolutional layers followed by a fully connected layer. In the experiment, 100 clients were simulated for training, and 10% of the clients were selected to take part in each round.

5.1 Experimental Environment

All the algorithms involved in the experiments are implemented in the Python 3.7.2 with the Pytorch framework. We use Tesla P100 GPU on Ubuntu 18.04.4 LTS system for our experiments. The specific configurations of Linux kernel, graphics card driver and CUDA are shown in Table 1.

5.2 Datasets

We employ MNIST, FMNIST, EMNIST, CINIC-10 and CIFAR-10 to assess the performance of FedChoice. MNIST [34] is an image dataset that contains a large number of images with handwritten digits. It has a training set of 60,000 28 × 28 grayscale examples, and a test set of 10,000 examples. FEMNIST [35] dataset contains 62 different types of handwritten digits and letters (digits 0 to 9, lowercase letters, and uppercase letters), it contains 28 × 28 pixels handwritten digits and letters of 3500 users. Extended MNIST (EMNIST) [36] is a newer dataset to be the successor to MNIST, which is a large database of 62 categories handwritten uppercase and lowercase letters as well as digits. CINIC-10 [37] is a dataset for image classification, and it has a total of 270,000 images constructed from two different sources: ImageNet and CIFAR-10. Similar to CINIC-10, CIFAR-10 [38] is a dataset composed of color images. It consists of 60,000 32 × 32 color images in 10 different classes, with 6000 images per class, and each image is 32×32 in size and has three channels (RGB).

For each dataset, we apply Non-IID settings, that the datasets are sorted by class and divided into 20 partitions and each client is randomly assigned 2 partitions from 2 classes. That is, each client has two classes of data labels. In particular, FEMNIST is a non-independent and identically distributed dataset, which does not need to be re-divided.

5.3 Experimental Results

5.3.1 Hyper-Parameter α Selection

In this section, we will search for the appropriate hyperparameter α on five datasets. As described above, the hyperparameter α is the proportion of πloss strategy, which determines the proportion of πrand and πloss strategy. The larger α is, the more clients will be selected by πloss strategy. The value of α will affect the training accuracy, and we take the values of α as 0.8, 0.4, 0.2, empirically.

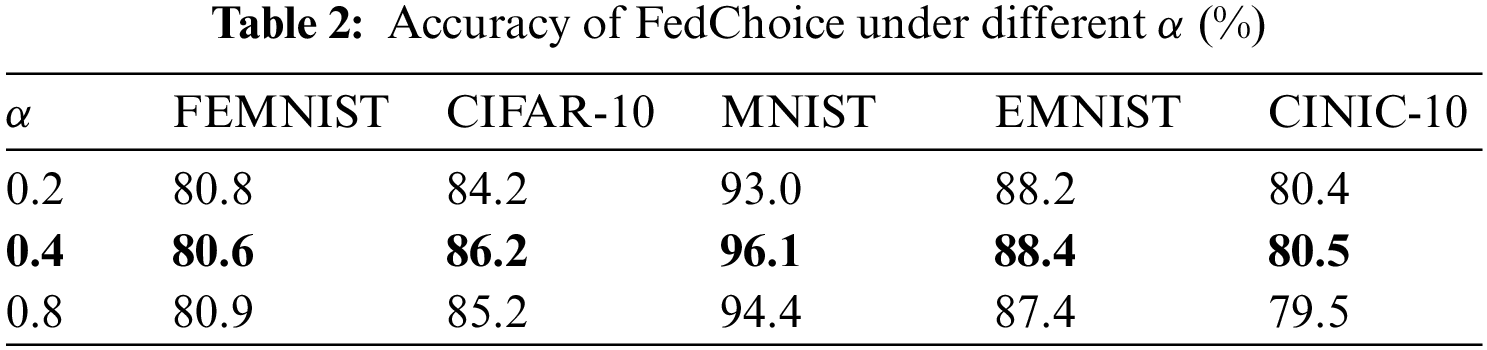
Fig. 5 and Table 2 show the varying performance under different values of α. On FEMNIST and CINIC-10 scenario, the value of α has little effect on accuracy. But in the other three scenarios, when α=0.4, the accuracy of FedChoice is 86.2%, 96.1% and 88.4%, respectively, which is better than the other two options. Based on these results, we set α = 0.4 for the remainder experiments.

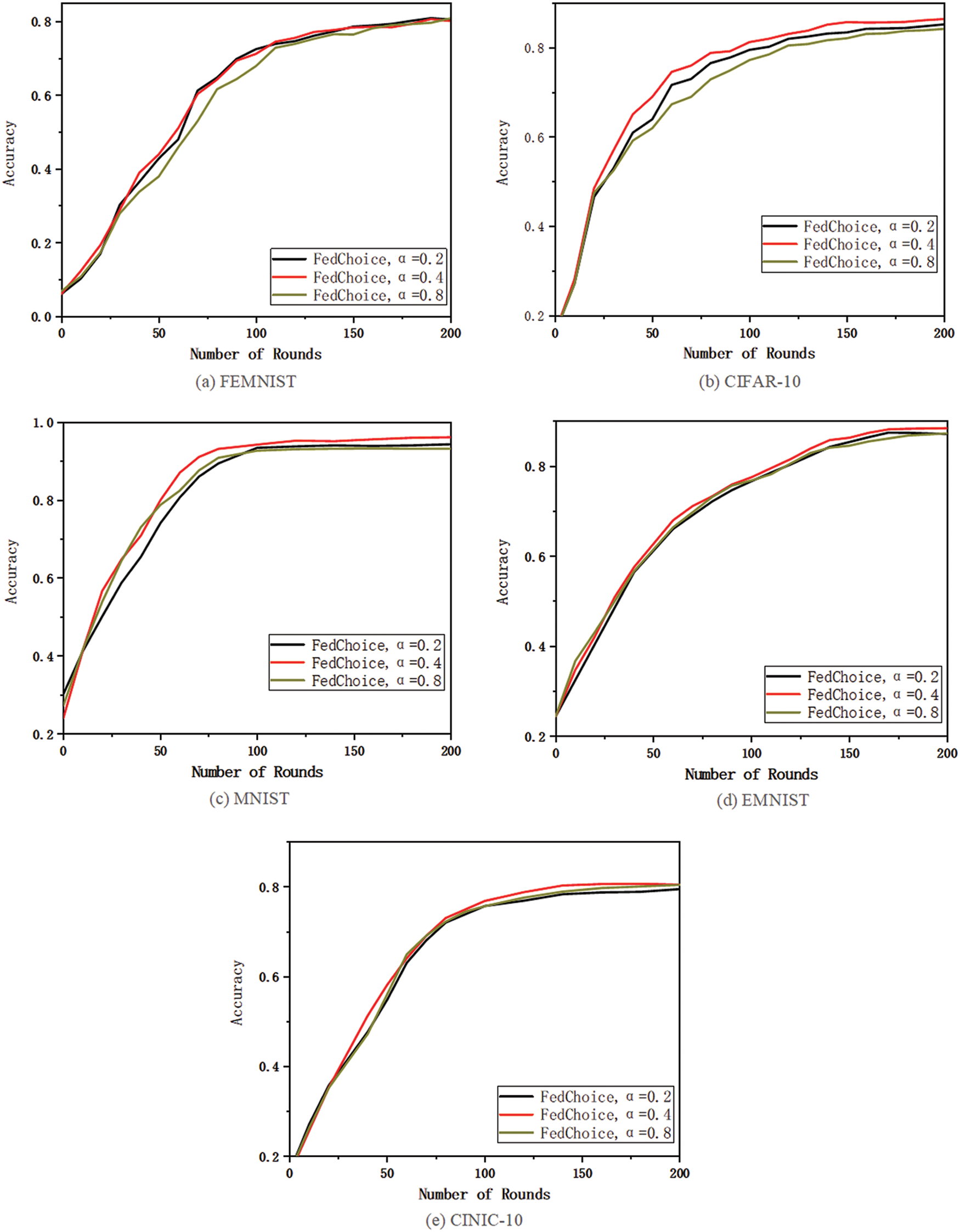
Figure 5: The experiment of hyperparameter α

5.3.2 Accuracy

To investigate the accuracy of FedChoice, we evaluate the accuracy of the global model by comparing with three baseline algorithms on five datasets, and the results are shown in Fig. 6.

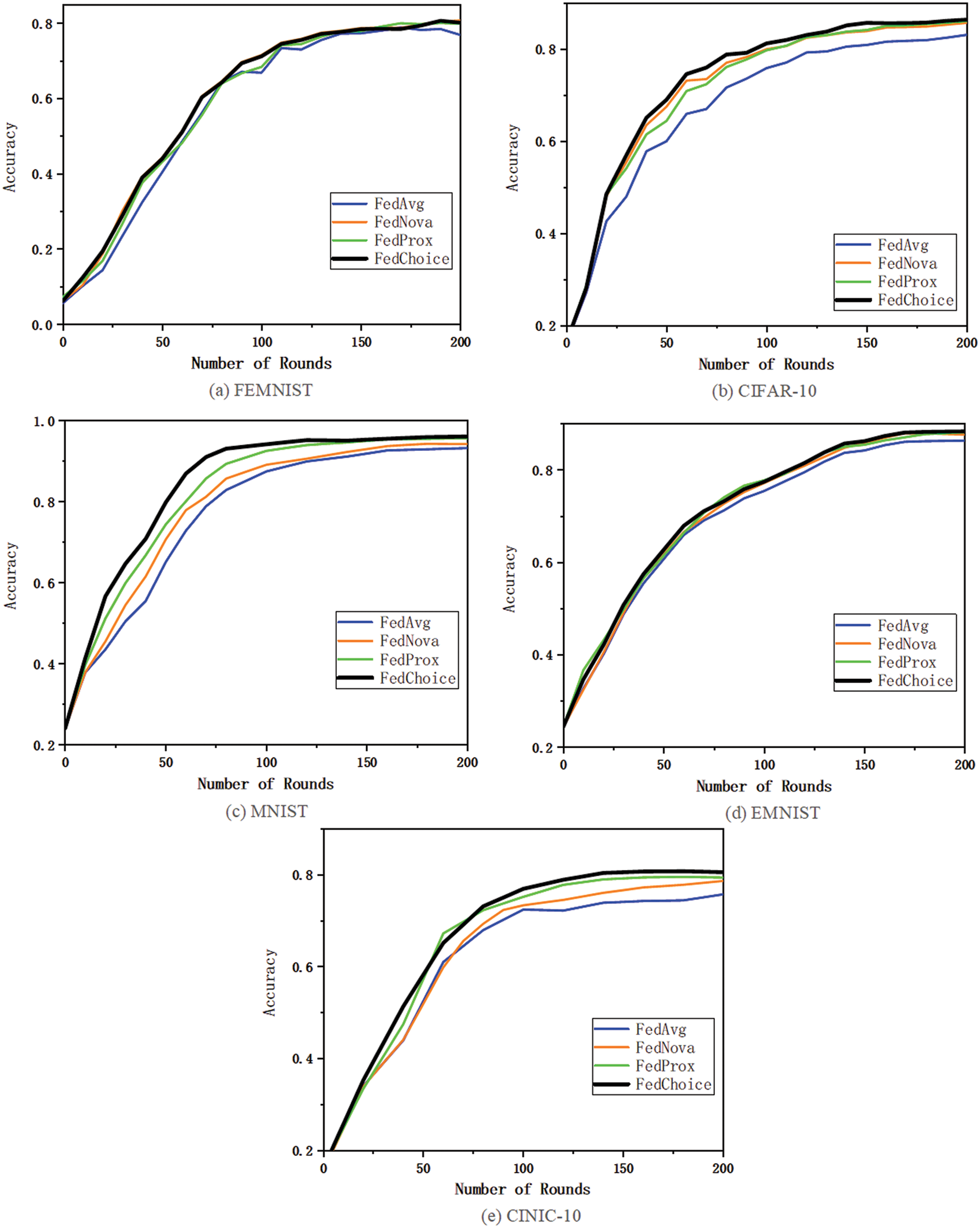
Figure 6: Accuracy of global model trained with different algorithms

Table 3 gives the highest testing accuracy of all methods under Non-IID data setting, from which we can see that FedChoice outperforms all other methods on five datasets. For FEMNIST and EMNIST, the variance of the accuracy across FL methods is much smaller than other datasets, and when compared with FedAvg, the accuracy of FedChoice can be improved by up to 1.7% and 2%, respectively. As for CIFAR-10, MNIST, CINIC-10, FedChoice significantly exceeds other algorithms, especially compared with FedAvg, the accuracy of FedChoice can be improved by up to 3.3%, 2.9%, 4.8%, respectively.

5.4 Convergence Performance

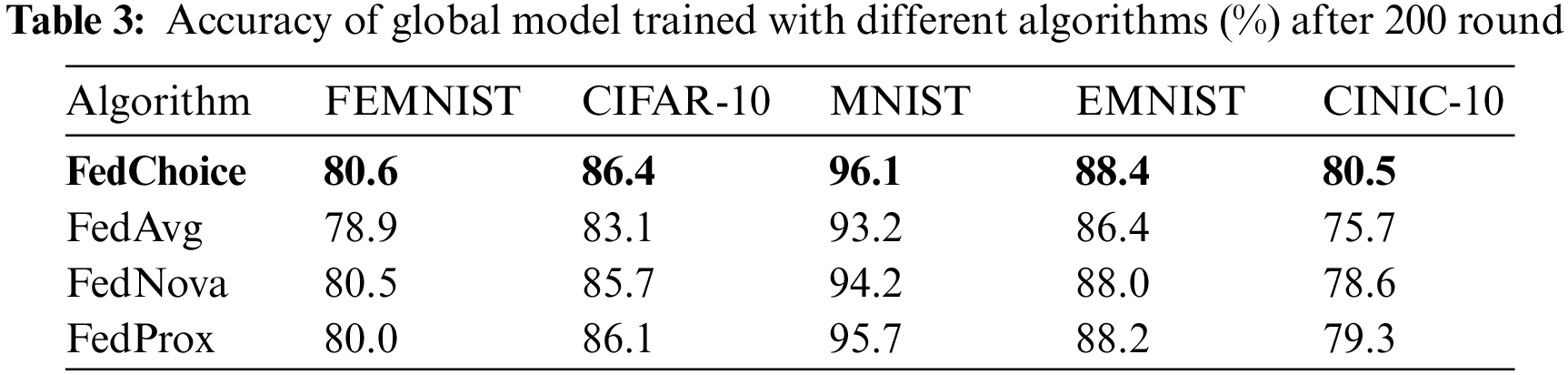
To analyze the convergence of the global model, we set 80% as the convergence accuracy of FEMNIST, EMNIST and CIFAR-10 datasets, 90% as the convergence accuracy of MNIST, and 75% as the convergence accuracy of CINIC-10.

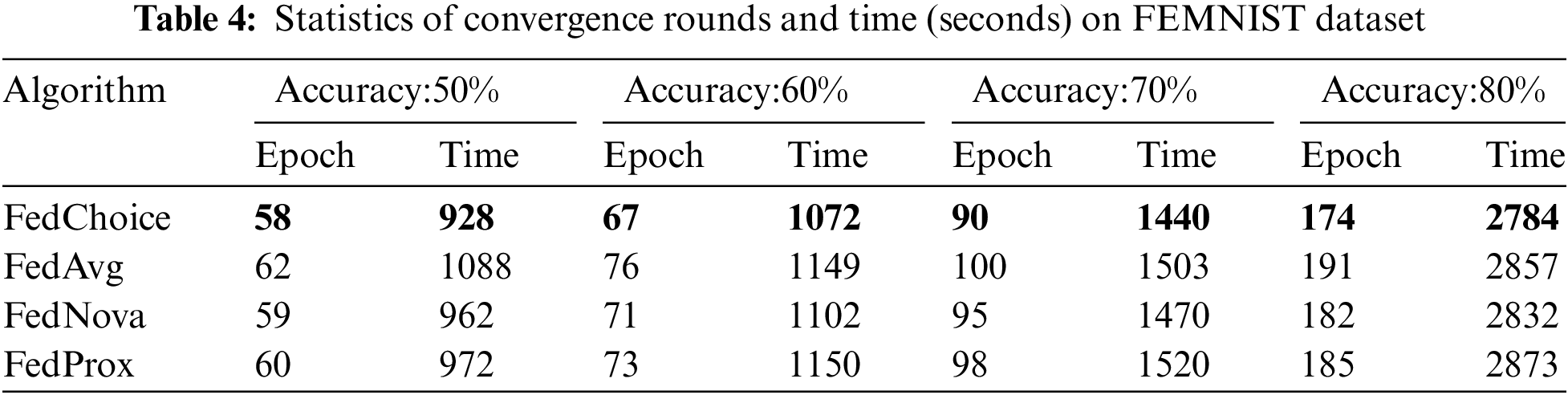
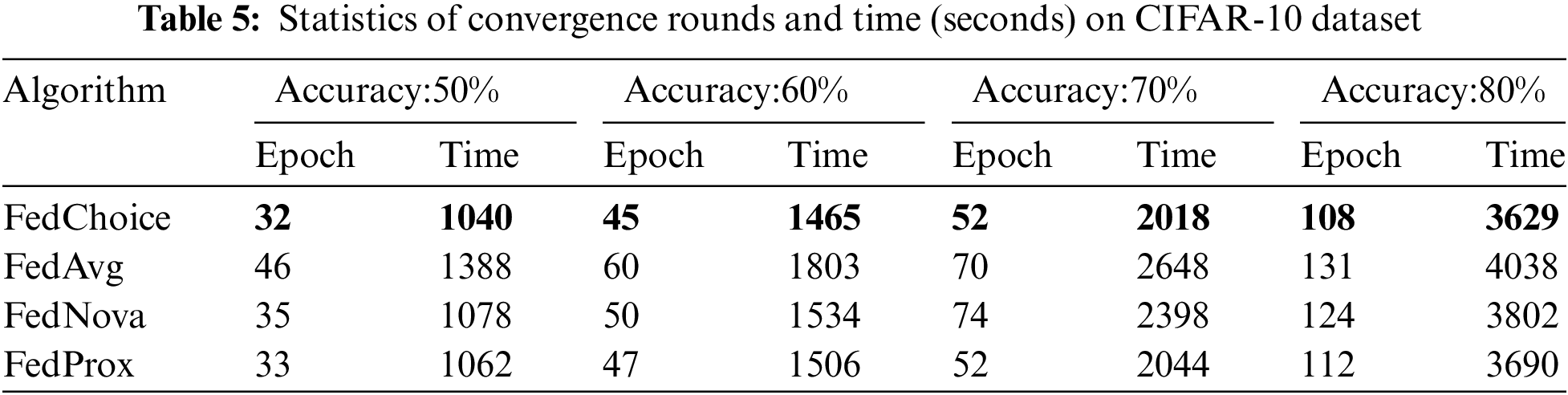
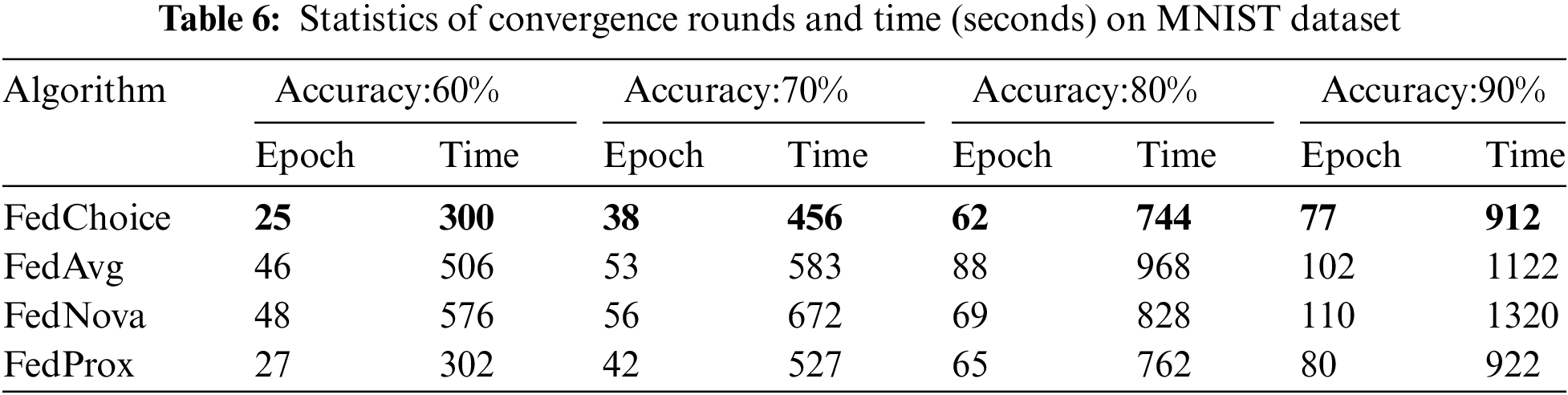
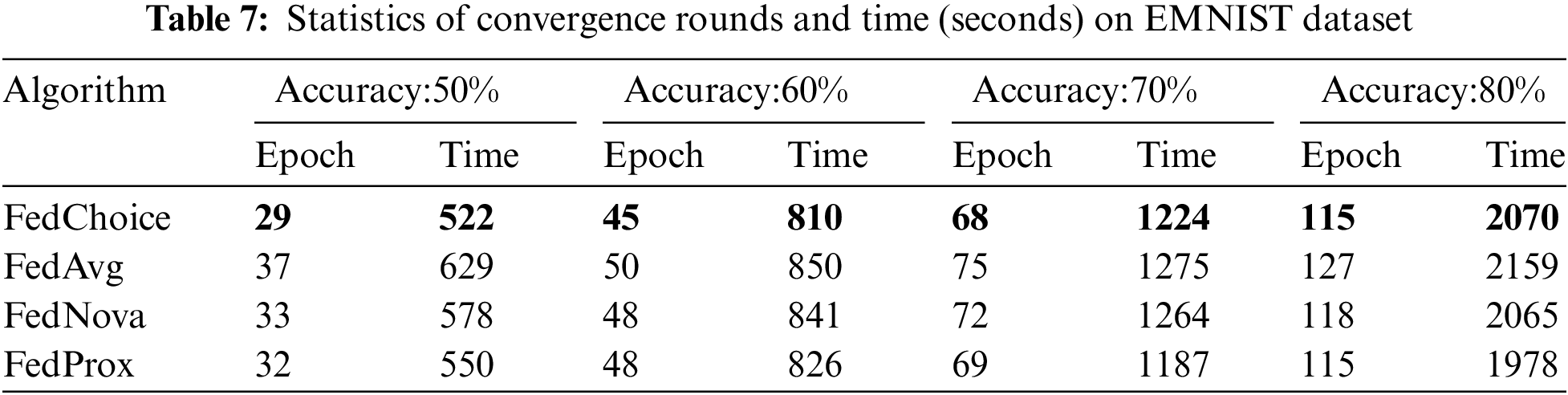
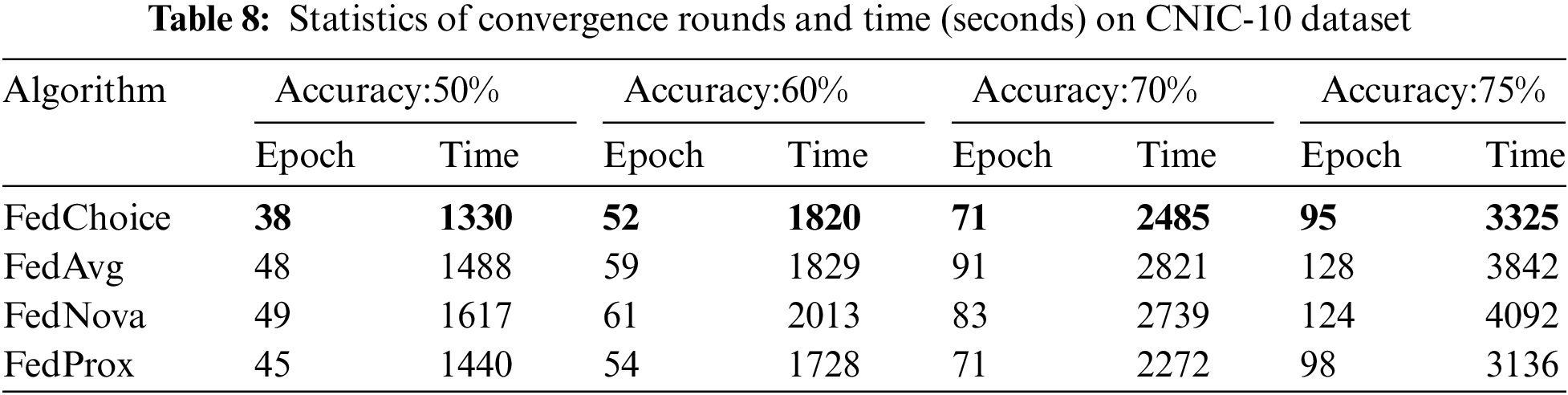
Tables 4~8 give the convergence rounds and time cost of the four algorithms to reach the given accuracy on the five datasets, respectively. Since FedChoice has almost no extra computation for both the client and server, it achieves the best results on all five datasets among the four methods. Specifically, for MNIST dataset, FedChoice requires 24.5% fewer communication rounds and 18.7% less convergence time in comparison with FedAvg. The experiment results show that, the client with a high loss value has a higher training value, because a high loss value means that the weak generalization ability of global models on these clients, and the data stored on these clients is beneficial to enhance the generalization ability of the global model. Compared with the random selection strategy, the strategy based on loss can train a global model with better generalization ability.

6  Conclusion

In this paper, we propose FedChoice, a client selection method based on loss function optimization for federated learning to solve the inefficient convergence problem under Non-IID data. FedChoice gives a higher selection probability to the client with a high loss value, which allows it more likely to participate in training, thus speeding up the convergence of the global model. Besides, we introduce the local offset control item to predict the local gradient direction and the global gradient direction, and calculate a vector to correct the local gradient vector direction, to reduce the accumulated deviation of local gradient caused by Non-IID data. The experiments have validated the effectiveness of FedChoice and demonstrated that FedChoice has significant improvement in convergence and accuracy, compared with FedAvg, FedProx and FedNova. In the future, we will introduce a more effective probability extraction formula from the perspective of gradient update.

Management Implications: Our proposed FedChoice algorithm selects clients based on the importance of the client, which is calculated by loss. It can accelerate the process of minimizing the loss values of all clients and allow the global model to converge in fewer communication rounds while maintaining good accuracy. On the one hand, it is useful for managers and servers of federated learning. Longer training times mean that federated learning is less stable and is more likely to be interrupted. The FedChoice algorithm allows the server to reduce the duration of maintaining federated learning, improving the stability of training and saving the server’s computing power. On the other hand, it is also very beneficial for clients in federated learning, as it reduces the number of communication rounds for clients, reduces the consumption of client resources, and can also mobilize the enthusiasm of clients. Therefore, we recommend that managers decisively adopt the FedChoice algorithm when they want to mobilize clients’ enthusiasm, save communication resources, and save computing power.

Funding Statement: This work is supported by the National Natural Science Foundation of China under Grant No. 62072146, The Key Research and Development Program of Zhejiang Province under Grant No. 2021C03187, National Key Research and Development Program of China 2019YFB2102100. The State Key Laboratory of Computer Architecture (ICT, CAS) under Grant No. CARCHB202120.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Gao, C., Gutierrez, A., Rajan, M., Dreslinski, R. G., Mudge, T. et al. (2015). A study of mobile device utilization. 2015 IEEE International Symposium on Performance Analysis of Systems and Software (ISPASS), pp. 225–234. Philadelphia. [Google Scholar]

2. Zeng, Y., Yan, Z. Y., Zhang, J. L., Zhao, N. L., Ren, Y. J. et al. (2021). Federated learning model training method based on data features perception aggregation. 2021 IEEE 94th Vehicular Technology Conference (VTC2021-Fall), pp. 1–7. Norman. [Google Scholar]

3. Yang, F., Zhang, Q., Ji, X., Zhang, Y., Li, W. et al. (2022). Machine learning applications in drug repurposing. Interdisciplinary Sciences: Computational Life Sciences, 14, 1–7. [Google Scholar]

4. Liu, J. C., Goetz, J., Sen, S., Tewari, A. (2021). Learning from others without sacrificing privacy: Simulation comparing centralized and federated machine learning on mobile health data. JMIR mHealth and uHealth, 9(3), e23728. https://doi.org/10.2196/23728 [Google Scholar] [PubMed] [CrossRef]

5. Tankard, C. (2016). What the gdpr means for businesses. Network Security, 2016(6), 5–8. https://doi.org/10.1016/S1353-4858(16)30056-3 [Google Scholar] [CrossRef]

6. O’herrin, J. K., Fost, N., Kudsk, K. A. (2004). Health insurance portability accountability act (HIPAA) regulations: Effect on medical record research. Annals of Surgery, 239(6), 772–778. https://doi.org/10.1097/01.sla.0000128307.98274.dc [Google Scholar] [PubMed] [CrossRef]

7. McMahan, B., Moore, E., Ramage, D., Hampson, S., Arcas, B. A. (2017). Communication-efficient learning of deep networks from decentralized data. Proceedings of the 20th International Conference on Artificial Intelligence and Statistics, pp. 1273–1282. Ft. Lauderdale. [Google Scholar]

8. Nguyen, D. C., Pham, Q. V., Pathirana, P. N., Ding, M., Seneviratne, A. et al. (2022). Federated learning for smart healthcare: A survey. ACM Computing Surveys, 55(3), 1–37. [Google Scholar]

9. Kawa, D., Punyani, S., Nayak, P., Karkera, A., Jyotinagar, V. (2019). Credit risk assessment from combined bank records using federated learning. International Research Journal of Engineering and Technology (IRJET), 6(4), 1355–1358. [Google Scholar]

10. Duan, M., Liu, D., Chen, X., Tan, Y., Ren, J. et al. (2019). Astraea: Self-balancing federated learning for improving classification accuracy of mobile deep learning applications. 2019 IEEE 37th International Conference on Computer Design (ICCD), pp. 246–254. Abu Dhabi. [Google Scholar]

11. Zhao, Y., Li, M., Lai, L., Suda, N., Civin, D. et al. (2018). Federated learning with non-iid data. arXiv preprint arXiv:1806.00582. [Google Scholar]

12. Li, Q., He, B., Song, D. (2021). Model-contrastive federated learning. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 10713–10722. Nashville. [Google Scholar]

13. Chandrasekaran, R., Ergun, K., Lee, J., Nanjunda, D., Kang, J. et al. (2022). Fhdnn: Communication efficient and robust federated learning for aiot networks. Proceedings of the 59th ACM/IEEE Design Automation Conference, pp. 37–42. San Francisco. [Google Scholar]

14. Ek, S., Rombourg, R., Portet, F., Lalanda, P. (2022). Federated self-supervised learning in heterogeneous settings: Limits of a baseline approach on har. 2022 IEEE International Conference on Pervasive Computing and Communications Workshops and other Affiliated Events (PerCom Workshops), pp. 557–562. Pisa. [Google Scholar]

15. Tan, A. Z., Yu, H., Cui, L., Yang, Q. (2022). Towards personalized federated learning. IEEE Transactions on Neural Networks and Learning Systems, 1–17. https://doi.org/10.1109/TNNLS.2022.3160699 [Google Scholar] [PubMed] [CrossRef]

16. Shang, X., Lu, Y., Huang, G., Wang, H. (2022). Federated learning on heterogeneous and long-tailed data via classifier re-training with federated features. Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence, pp. 2218–2224. Vienna. [Google Scholar]

17. Luo, M., Chen, F., Hu, D., Zhang, Y., Liang, J. et al. (2021). No fear of heterogeneity: Classifier calibration for federated learning with non-iid data. Advances in Neural Information Processing Systems, 34, 5972–5984. [Google Scholar]

18. Li, A., Sun, J., Wang, B., Duan, L., Li, S. et al. (2021). Lotteryfl: Empower edge intelligence with personalized and communication-efficient federated learning. 2021 IEEE/ACM Symposium on Edge Computing (SEC), pp. 68–79. San Jose. [Google Scholar]

19. Li, T., Sahu, A. K., Zaheer, M., Sanjabi, M., Talwalkar, A. et al. (2020). Federated optimization in heterogeneous networks. Proceedings of Machine Learning and Systems, 2, 429–450. [Google Scholar]

20. Acar, D. A. E., Zhao, Y., Navarro, R. M., Mattina, M., Whatmough, P. N. et al. (2021). Federated learning based on dynamic regularization. arXiv preprint arXiv: 2111.04263. [Google Scholar]

21. Karimireddy, S. P., Kale, S., Mohri, M., Reddi, S., Stich, S. et al. (2020). Scaffold: Stochastic controlled averaging for federated learning. International Conference on Machine Learning, pp. 5132–5143. Vienna. [Google Scholar]

22. Wang, J., Liu, Q., Liang, H., Joshi, G., Poor, H. V. (2020). Tackling the objective inconsistency problem in heterogeneous federated optimization. Advances in Neural Information Processing Systems, 33, 7611–7623. [Google Scholar]

23. Lin, T., Kong, L., Stich, S. U., Jaggi, M. (2020). Ensemble distillation for robust model fusion in federated learning. Advances in Neural Information Processing Systems, 33, 2351–2363. [Google Scholar]

24. Tan, Y., Long, G., Liu, L., Zhou, T., Lu, Q. et al. (2022). Fedproto: Federated prototype learning across heterogeneous clients. Proceedings of the AAAI Conference on Artificial Intelligence, pp. 8432–8440. Palo Alto. [Google Scholar]

25. Zeng, Y., Wang, X., Yuan, J., Zhang, J., Wan, J. (2022). Local epochs inefficiency caused by device heterogeneity in federated learning. Wireless Communications and Mobile Computing, 2022, 1530–8669. https://doi.org/10.1155/2022/6887040 [Google Scholar] [CrossRef]

26. Huang, T., Lin, W., Wu, W., He, L., Li, K. et al. (2020). An efficiency-boosting client selection scheme for federated learning with fairness guarantee. IEEE Transactions on Parallel and Distributed Systems, 32(7), 1552–1564. https://doi.org/10.1109/TPDS.2020.3040887 [Google Scholar] [CrossRef]

27. Richards, S. M., Berkenkamp, F., Krause, A. (2018). The lyapunov neural network: Adaptive stability certification for safe learning of dynamical systems. Conference on Robot Learning, pp. 466–476. Zurich. [Google Scholar]

28. Wang, H., Kaplan, Z., Niu, D., Li, B. (2020). Optimizing federated learning on non-iid data with reinforcement learning. IEEE INFOCOM 2020-IEEE Conference on Computer Communications, pp. 1698–1707. Toronto. [Google Scholar]

29. Kaelbling, L. P., Littman, M. L., Moore, A. W. (1996). Reinforcement learning: A survey. Journal of Artificial Intelligence Research, 4, 237–285. https://doi.org/10.1613/jair.301 [Google Scholar] [CrossRef]

30. Ribero, M., Vikalo, H. (2020). Communication-efficient federated learning via optimal client sampling. arXiv preprint arXiv:2007.15197. [Google Scholar]

31. Chai, Z., Ali, A., Zawad, S., Truex, S., Anwar, A. et al. (2020). TiFL: A tier-based federated learning system. Proceedings of the 29th International Symposium on High-Performance Parallel and Distributed Computing, pp. 125–136. New York. [Google Scholar]

32. AbdulRahman, S., Tout, H., Mourad, A., Talhi, C. (2020). FedMCCS: Multicriteria client selection model for optimal iot federated learning. IEEE Internet of Things Journal, 8(6), 4723–4735. https://doi.org/10.1109/JIOT.2020.3028742 [Google Scholar] [CrossRef]

33. Zhang, W., Wang, X., Zhou, P., Wu, W., Zhang, X. (2021). Client selection for federated learning with non-iid data in mobile edge computing. IEEE Access, 9, 24462–24474. https://doi.org/10.1109/ACCESS.2021.3056919 [Google Scholar] [CrossRef]

34. LeCun, Y., Bottou, L., Bengio, Y., Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324. https://doi.org/10.1109/5.726791 [Google Scholar] [CrossRef]

35. Caldas, S., Duddu, S. M. K., Wu, P., Li, T., Konečnỳ, J. et al. (2018). Leaf: A benchmark for federated settings. arXiv preprint arXiv:1812.01097. [Google Scholar]

36. Cohen, G., Afshar, S., Tapson, J., van Schaik, A. (2017). Emnist: Extending mnist to handwritten letters. International Joint Conference on Neural Networks (IJCNN), pp. 2921–2926. Anchorage. [Google Scholar]

37. Darlow, L. N., Crowley, E. J., Antoniou, A., Storkey, A. J. (2018). CINIC-10 is not ImageNet or CIFAR-10. arXiv preprint arXiv:1810.03505. [Google Scholar]

38. Krizhevsky, A., Hinton, G. (2009). Learning multiple layers of features from tiny images. In: Handbook of systemic autoimmune diseases, vol. 1, no. 4, pp. 1–10. http://www.cs.utoronto.ca/~kriz/learning-features-2009-TR.pdf [Google Scholar]