 Open Access
Open Access
ARTICLE
Filter Bank Networks for Few-Shot Class-Incremental Learning
School of Electronic, Electric and Communication Engineering, University of Chinese Academy of Sciences, Beijing, 140018, China
* Corresponding Author: Jianbin Jiao. Email:
Computer Modeling in Engineering & Sciences 2023, 137(1), 647-668. https://doi.org/10.32604/cmes.2023.026745
Received 28 September 2022; Accepted 14 December 2022; Issue published 23 April 2023
Abstract
Deep Convolution Neural Networks (DCNNs) can capture discriminative features from large datasets. However, how to incrementally learn new samples without forgetting old ones and recognize novel classes that arise in the dynamically changing world, e.g., classifying newly discovered fish species, remains an open problem. We address an even more challenging and realistic setting of this problem where new class samples are insufficient, i.e., Few-Shot Class-Incremental Learning (FSCIL). Current FSCIL methods augment the training data to alleviate the overfitting of novel classes. By contrast, we propose Filter Bank Networks (FBNs) that augment the learnable filters to capture fine-detailed features for adapting to future new classes. In the forward pass, FBNs augment each convolutional filter to a virtual filter bank containing the canonical one, i.e., itself, and multiple transformed versions. During back-propagation, FBNs explicitly stimulate fine-detailed features to emerge and collectively align all gradients of each filter bank to learn the canonical one. FBNs capture pattern variants that do not yet exist in the pretraining session, thus making it easy to incorporate new classes in the incremental learning phase. Moreover, FBNs introduce model-level prior knowledge to efficiently utilize the limited few-shot data. Extensive experiments on MNIST, CIFAR100, CUB200, and Mini-ImageNet datasets show that FBNs consistently outperform the baseline by a significant margin, reporting new state-of-the-art FSCIL results. In addition, we contribute a challenging FSCIL benchmark, Fishshot1K, which contains 8261 underwater images covering 1000 ocean fish species. The code is included in the supplementary materials.Keywords
The enormous success of Deep Convolution Neural Networks (DCNNs) [1–3] in computer vision tasks is built upon the collection of large-scale datasets [4,5]. However, with new samples and novel classes emerging, sequential data collection is required for many tasks, e.g., classifying newly discovered fish species in the ocean. Towards lifelong learning ability like humans, deep learning models need to acquire the ability to incorporate new class knowledge incrementally, i.e., Class-Incremental Learning (CIL) [6–12].
Current CIL methods mainly focus on the setting where novel classes arise with sufficient training samples. However, the cost of collecting and labeling new samples is considerably high, and it can be impossible to gather enough new class data in real-world applications. For example, collecting photos of rare fish species in the ocean could take years. Therefore, designing effective deep learning models to incorporate knowledge from limited data and recognize novel classes sequentially, i.e., Few-Shot Class-Incremental Learning (FSCIL), has recently drawn the attention of the deep learning community [13–15]. The FSCIL models are first pretrained with some base classes with sufficient data. Then the model is updated in multiple incremental learning sessions where only a few samples of novel classes, e.g., 1-shot or 5-shots, are provided in each session. The metric of classification accuracy on all seen classes is used to evaluate the model performance of each session.
Why the naive fine-tuning of the model with new samples will not work is twofold. First, the over-parameterized deep learning models tend to overfit the biased distribution of limited few-shot training samples, resulting in poor performance of the new classes. Second, the incremental tuning damages the learned filters of the model, causing the drastic decline of old classes’ classification accuracy, namely the catastrophic forgetting problem. Current few-shot learning methods augment the data of new classes through distribution sampling, e.g., FreeLunch [16], to alleviate the overfitting problem. And to resist the forgetting issue, current approaches mainly concentrate on improving the backward compatibility, which restricts the model parameters from updating in the incremental learning sessions [10–12,17–21]. Despite substantial progress, the problem of addressing the overfitting and forgetting issues in a uniform framework remains open.
In this work, we argue that solving Few-Shot Class-Incremental Learning requires endowing models with the ability to foresee the upcoming new classes and capture the variants of discriminative semantic patterns that do not yet exist in the limited training data. Take an example from software engineering. If the early version is poorly designed, it usually takes significantly more work to improve the later versions without breaking backward compatibility. On the contrary, a proper design of the early version, which foresees the upcoming features and reserves interfaces, can make it considerably easier to maintain and upgrade the software. Consequently, we concentrate on models’ forward compatibility by improving the most fundamental element of Deep Convolution Neural Networks, i.e., convolutional filters.
We propose Filter Bank Networks (FBNs), Fig. 1, a simple yet effective deep learning framework to tackle Few-Shot Class-Incremental Learning (FSCIL). FBNs are built upon the commonly used Deep Convolution Neural Networks (DCNNs) and support modern model architectures, e.g., VGG, Inception, and ResNet. In the forward pass, FBNs augment each convolutional filter to a virtual filter bank containing the canonical one, i.e., itself, and multiple transformed versions, e.g., rotation, flip, or scaling. In the back-propagation, FBNs collectively gather and align gradients of all transformed versions in the filter bank to learn the canonical filter. During incremental learning, FBNs explicitly stimulate fine-detailed features to emerge through mining the instance-aware discriminations.
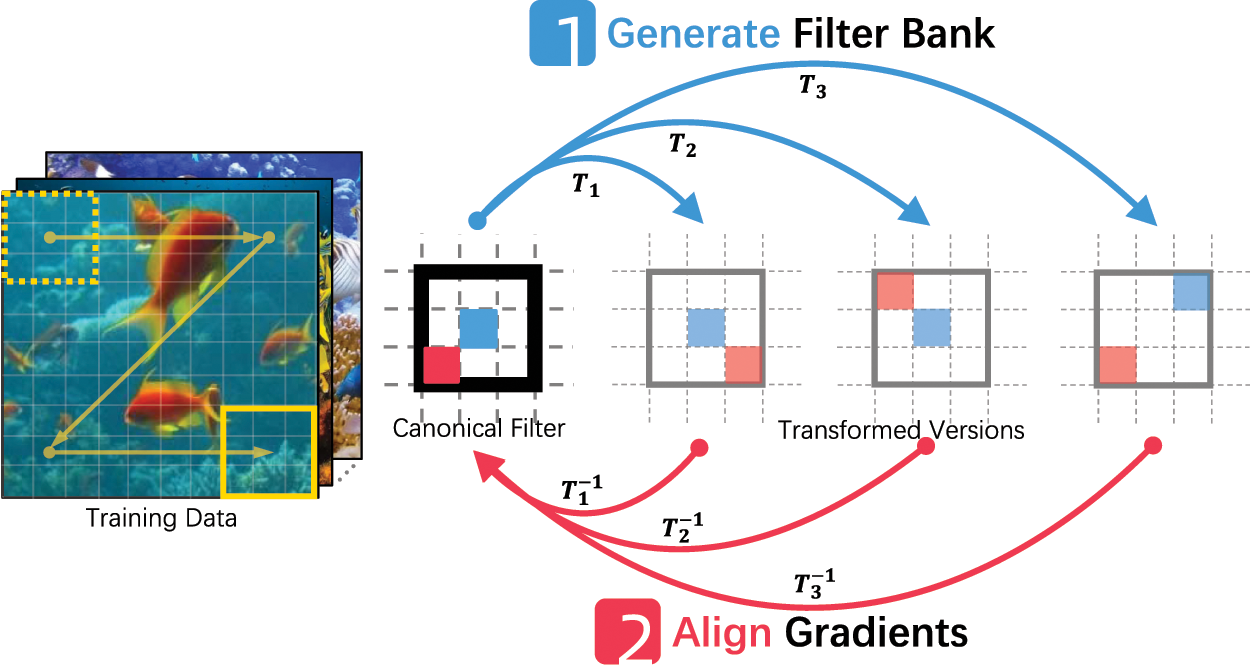
Figure 1: We propose Filter Bank Networks(FBNs) that augment each filter in the Deep Convolution Neural Networks to a virtual filter bank including itself and multiple transformed versions. The filter bank aggregate and align gradients to learn variants of semantic patterns that do not yet exist in the current training session, thus preserving feature space for adapting future novel classes in the Few-Shot Class-Incremental Learning tasks
While conventional models only capture existing patterns in the dataset, FBNs learn semantic patterns that do not yet exist in the pertaining session, thus reserving the feature space for future new classes. During the incremental sessions, FBNs do not need to squeeze former classes’ space, thus alleviating the catastrophic forgetting issue. Note that FBNs augment filters to virtual filter banks in all convolution layers and can model the transformed variants of intermediate representation at different semantic levels, e.g., bird head rotated to its body. Therefore, FBNs are more expressive than the conventional DCNNs trained with image-level data augmentation. Whatsmore, the virtual filter bank in FBNs aggregates gradients from all transformed versions in the dataset to update one canonical filter, thus can utilize the limited few-shot data more efficiently. We conduct extensive experiments and ablation studies on commonly used FSCIL datasets and report new state-of-the-art results, validating the effectiveness of FBNs. The contribution of this paper are summarized as follows:
• We propose Filter Bank Networks (FBNs) to improve the most fundamental element of DCNNs, i.e., convolutional filters. FBNs endow DCNNs with the capability of capturing variants of semantic patterns that do not yet exist in the training session, addressing catastrophic forgetting and overfitting problems of Few-Shot Class-Incremental Learning (FSCIL).
• FBNs achieve new state-of-the-art performance on several commonly used FSCIL datasets, including CIFAR100, CUB200, and Mini-ImageNet.
• We contribute a challenging FSCIL benchmark, i.e., Fishshot1K, which contains 8261 underwater images covering 1000 ocean fish species.
Image Classification. Image Classification [1–3,22], i.e., assigning an input image one label from a fixed set of semantic categories such as fish, cat, or airplane, is one of the fundamental problems in the Computer Vision field. Despite its simplicity, it has a lot of practical applications, and many other computer vision tasks, e.g., object detection [23,24] and scene segmentation [25,26], can be simplified to image classification. Recognizing a visual concept in the image is relatively trivial for a human to perform. However, it is considered challenging for Computer Vision algorithms due to several affecting factors. First, an instance of an object can be oriented in many ways concerning the camera, namely rotation variation. Second, visual concepts often vary in size, namely scale variation. Next, many objects are not rigid bodies and can be deformed in extreme ways, e.g., a bird’s head can significantly rotate relative to its body. Moreover, occlusion, illumination conditions, and background clutter can substantially affect classification accuracy.
Handcrafted Features. Handcrafted image features have been extensively explored in the classical image classification field, e.g., SIFT [27], LBP [28,29], and Gabor features [30,31], to address those challenging variation issues in Image Classification, SIFT-like methods first detect stable feature key points that can be detected across scales. Image gray values of the local regions are then accumulated to summarize local patterns and generate the feature descriptors. The dominant orientations are found according to local gradient directions. With dominant orientation-based feature alignment, SIFT achieves invariance to rotation and robustness to moderate scale transforms. LBP emanates an invariant encoding operator against the monotonic transformation of the grayscale of local regions. LBP minimizes the encoded value via the bit cyclic shift operator based on the gray values of a circularly symmetric neighbor set of pixels in a local region. Other representative handcrafted descriptors include CF-HOG [32], which uses orientation alignment, and RI-HOG [33], which leverages radial gradient transform to be rotation invariant. Despite the progress made in handcrafted features, designing the invariant feature descriptors for different data domains and types of pattern variants is tedious and can not guarantee global optima.
Deep Convolutional Neural Networks (DCNNs). DCNNs can capture discriminative patterns from datasets in a data-driven manner to learn features that can tolerate moderate transformations in the image, such as scale changes and small rotations. DCNNs achieve those abilities through the fundamental design of convolutional operations, redundant convolutional filters, and hierarchical spatial pooling [34]. Modern architectures of DCNNs, e.g., VGG [1], Inception [2], and ResNet [3], achieve great success in image classification. However, it can be seen in the first row of Fig. 2 that the convolution filters in the DCNN can only learn patterns in the training data by rote. And they failed to generally model the variants of semantic patterns. Thus, conventional DCNNs require large-scale training datasets [4,5], which are often expensive to collect and label.
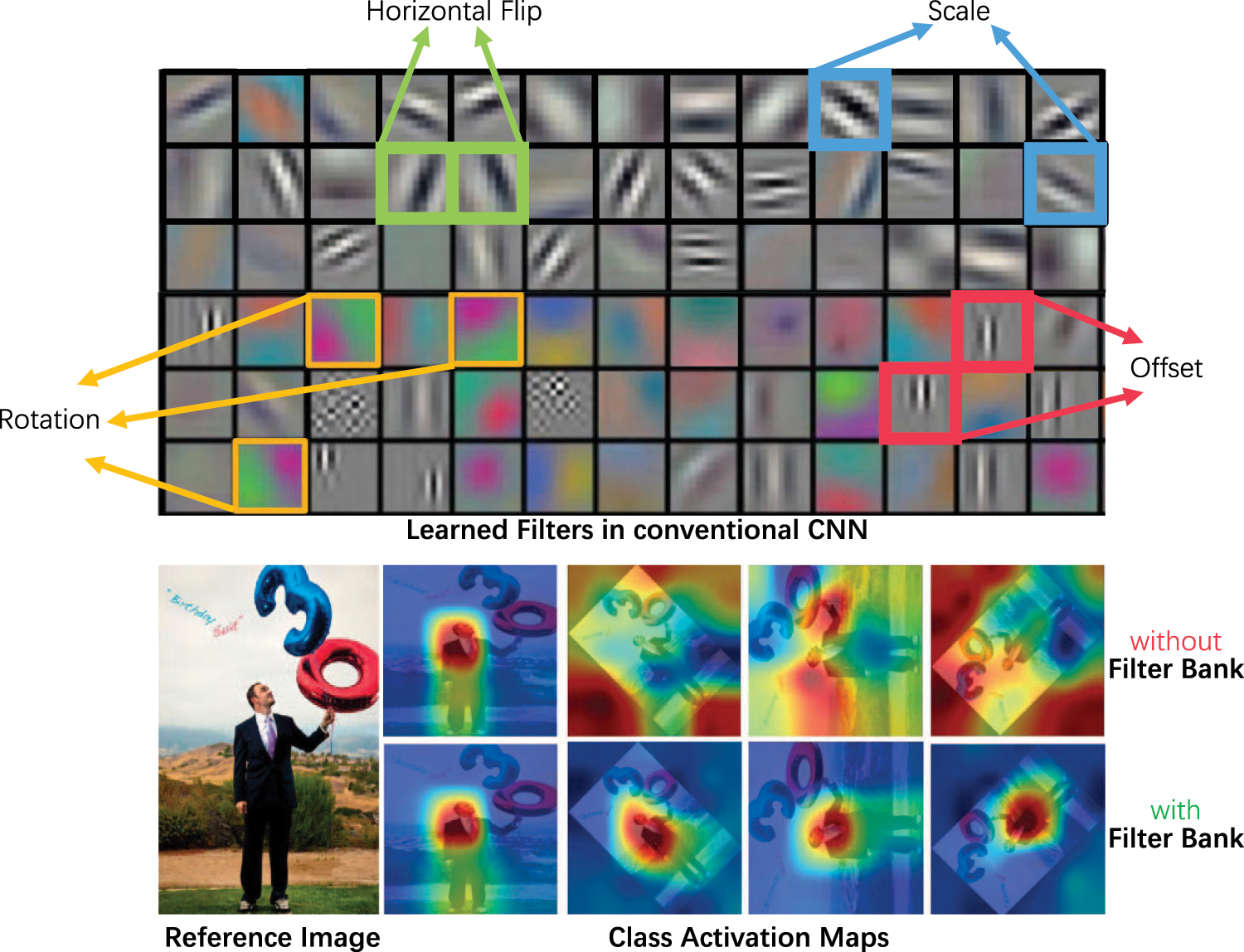
Figure 2: The first row shows the visualization of filters learned in a Deep Convolution Neural Network (DCNN). Transformed variants of patterns are redundantly learned, indicating conventional DCNNs lack the ability to generalize and require abundant data for training. The Class Activation Maps in the second row show that Filter Bank Networks align and learn from all variants of semantic patterns, thus capable of efficiently utilizing the limited few-shot data to update filters. Best viewed in color
Few-Shot Learning (FSL). Few-shot learning focuses on training models to classify novel classes with limited training samples. Conventional methods can be generally grouped into three types, i.e., Metric Learning, Meta-Learning, and Data Augmentation. Metric Learning methods [35–41] find a proper latent embedding space where the feature distances between intra-class samples are significantly smaller than inter-class samples. A typical two-branch network design is used to determine classes of the test images by comparing the feature of few-shot training samples. Meta-Learning methods [42–44] target optimizing the training process to achieve fast adaptation for new classes with limited data. Data augmentation methods [16,45–47] utilize the hidden information of abundant data of base classes to generate pseudo examples for novel classes via sampling techniques, aiming to rectify biased distributions and alleviate the overfitting issue.
Class-Incremental Learning (CIL). With the emergence of new classes, many real-world applications require the capability to incrementally adapt to novel classes, e.g., classifying newly discovered fish categories in the ocean. According to the availability of task IDs, incremental learning methods can be broadly categorized as Task-Incremental or Class-Incremental Learning. CIL methods design models to support learning from data sequence, i.e., incrementally recognizing novel semantics while not forgetting old ones. There are rehearsal, regularization, or architecture configuration methods for the Class-Incremental Learning tasks. Rehearsal methods [7–9,21,48–50] recall samples stored from a previous session to prevent the catastrophic forgetting issue. Regularization methods [10–12,17–21] introduce auxiliary training loss that utilizes prior knowledge or distillation to constrain network parameters from significant changes. Architecture configuration methods restrictedly update parts of network parameters by leveraging attention [51], pruning mechanisms [52], or dynamic expansion [6] to ease model drift.
Few-Shot Class Incremental Learning (FSCIL). The setting of conventional class incremental learning methods assumes sufficient training samples of the novel classes. However, the cost of collecting and labeling new samples is considerably high in many real-world applications. Few-shot Class-Incremental Learning amalgamates the challenges of catastrophic forgetting caused by incremental learning and overfitting caused by biased and insufficient training samples. Tao et al. [13] implemented a Neural Gas structure to address FSCIL by building and preserving feature topology. SKAD [14] designs semantic-aware knowledge distillation [17] to consolidate the features learned from base classes. Continually evolving prototypes [53,54] learn novel classes by optimizing classifier parameters to adjust the decision boundary progressively. The mixture sub-space method [55] synthesizes new samples of incremental classes in the latent embedding space via a variational auto-encoder.
The distribution calibration [16] method initiated the idea of solving the overfitting issue caused by biased distributions. However, it is nontrivial to migrate and apply those to FSCIL due to the enormous memory costs caused by sample storage. Despite substantial progress of FSCIL state-of-the-arts, the problem of solving the forgetting and over-fitting issues in a uniform framework remains open.
Forward Compatible Learning. Compatibility is a core concept in the field of software engineering. Backward Compatibility provides interoperability with an older legacy system, while Forward Compatibility allows a system to accept input intended for an updated later version of itself. The concept of Compatibility has been introduced to FSCIL in recent works [15]. Conventional FSCIL methods concentrate on improving models’ Backward Compatibility by preventing the model from significant changes in the incremental sessions [11,12,17,18]. In contrast, we propose Filter Bank Networks, a simple yet effective model to improve Forward Compatibility by reserving filters for unseen patterns in future novel classes.
Augmented Convolution Filter. Previous works have studied several ways of improving convolution filters. Dilated convolution [56] insert holes between filters to enlarge the effective receptive field. Oriented Response Networks [57] introduce active rotating filters to explicitly model orientation information. Deformable convolution [58] designs learnable offsets to the sampling location of filters, improving data-specific deformation tolerance. Despite the success, those methods aim at single transformation, e.g., rotation, and require abundant data to learn auxiliary parameters, thus are unsuitable for Few-Shot Class-Incremental Learning (FSCIL). We propose Filter Bank Networks (FBNs), a uniform framework that supports arbitrary filter transformations, e.g., rotation, flip, or scaling. FBNs introduce model-level prior knowledge to effectively and sequentially learn from limited few-shot data.
Equivariant Feature Encoding. A number of previous works have addressed the problem of learning or constructing equivariant representations. For instance, transforming autoencoders [59], equivariant Boltzmann machines [60,61], and equivariant filtering [62]. The learned features of conventional Convolutional Neural Networks (CNNs) are naturally equivariant to the translation of image patterns. Nonetheless, CNNs are incapable of handling other transformations like rotations. Group equivariant Convolutional Neural Network (G-CNN) [63] is a representative work that implements equivariant feature encoding in the CNN. However, there are three distinct differences between G-CNNs and our proposed Filter Bank Networks (FBNs). First of all, G-CNNs mainly consider translation, flip, and 90 degrees rotation while FBNs use a set of transformation matrices to support more general feature equivariance such as arbitrary angle rotation. Second, the filter transformation in G-CNNs is implemented as an indices lookup procedure that can not support the change of spatial shape. FBNs introduce a sampling technique to support mixing sizes of filters, e.g., scaling. Last but not least, G-CNNs are evaluated on the regular classification task which assumes abundant training samples. FBNs are designed for the more challenging Few-Shot Class-Incremental Learning benchmark where overfitting and catastrophic forgetting issues can be caused by insufficient training samples.
Filter Bank Networks (FBNs) are built upon Deep Convolution Neural Networks (DCNNs) via augmenting convolution filters to virtual filter banks. Each filter bank contains the canonical filter itself and transformed versions. Thus, a filter bank produces feature maps with additional channels that capture the response of variants of the semantic pattern. Note that all transformed versions are generated on-the-fly, and only one filter in the bank is materialized and learned from the aggregated gradients of the entire filter bank. Model-level prior knowledge is introduced via the design of transformations of the filter bank. Thus, FBNs learn unseen transformed intermediate representations from limited pretraining data, preserving feature space for adopting future novel classes in incremental learning sessions.
In what follows, we address the two problems in implementing FBNs for Few-Shot Class-Incremental Learning (FSCIL). First, we describe the technique of convolution with filter banks. We construct a sampling-based method to efficiently generate virtual filter banks in the forward pass. And we reverse-sampling the gradients to align and aggregate error signals to update one canonical filter in the backward pass. Next, we elaborate on the proposed FBN framework for FSCIL, Fig. 3. We jointly train FBNs with both class- and instance-level losses to stimulate the fine-detailed features to emerge for adapting future novel classes. Last but not least, we discuss the insight into the design of FBNs from the perspective of inductive bias and equivariant representation.
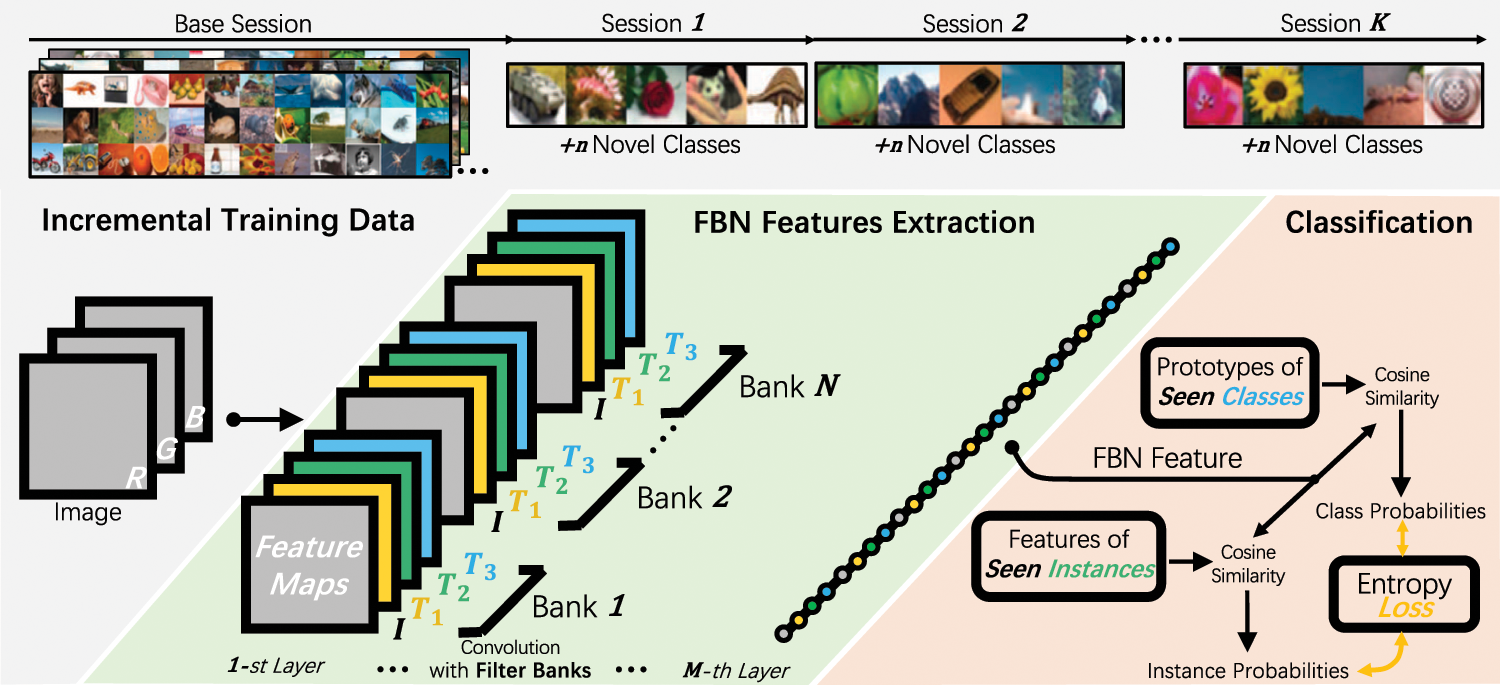
Figure 3: FBN framework
3.1 Convolution with Filter Banks
Filter Bank Generation. Filter Bank Networks are upgraded from conventional Deep Convolution Neural Networks, e.g., ResNet [3]. Without loss of generality, each augmented filter
Each element of
where
Transformations like scaling can alter the size of the filter. And the convolution of the mixing size of filters is not computation-friendly for modern GPUs. Therefore, we implement the generic form of convolution of filter banks based on a fixed-size sampling of input feature maps
Filter Bank Learning. The filter bank represents the semantic patterns of the canonical filter
3.2 Few-Shot Class-Incremental Learning (FSCIL)
FSCIL contains a pretraining session and multiple incremental sessions. During the pretraining session, FSCIL methods learn a representation model to recognize some base classes
It can be seen in Fig. 3 that the proposed Filter Bank Networks (FBN) framework for FSCIL consists of two parts, i.e., a convolutional feature extractor based on FBNs and a classification head that can adapt to the incremental classes. The whole model is jointly trained with multiple losses in an end-to-end manner.
FBN Feature Extraction. To obtain a discriminative feature representation, a feature extractor is developed by upgrading a conventional Deep Convolution Neural Network (DCNN), e.g., VGG [1] or ResNet [3], to the Filter Bank Network via equipping all convolution layers with the Filter Banks. Each filter bank contains the canonical filter itself and multiple transformed versions defined by a predefined transformation matrix set
Through the multiple layers’ convolution, each dimension of
Scalable Classification. The commonly used multi-layer perception (MLP) classifier can not be used in the FSCIL tasks as the number of classes that needs to be recognized is incremental. Therefore, we make classification scalable by allocating class prototypes
where E is a temperature hyperparameter1 and
Model Learning. To train the model parameters, we compute the loss between the predicted classification logits
where
where
Design choices in machine learning signify inductive biases. For example, the composition of layers in Deep Convolution Neural Networks (DCNNs) provides a type of relational inductive bias, i.e., hierarchical processing. And the use of convolution in DCNNs introduces the inductive bias of spatial translation. More generally, anything that imposes constraints on the learning trajectory introduces inductive biases, e.g., dropout, data augmentation, batch normalization, and weight decay. Previous studies have shown that implementing inductive biases to deep learning architectures can facilitate model learning about entities, relations, and rules for composing them and thus improve performance and generalization [66].
The conventional DCNNs leverage inductive biases introduced in convolution, hierarchical structure, and local pooling to handle moderate transforms, i.e., spatial transitions, mild scale changes, and small rotations. However, DCNNs lack the ability to handle significant and generic transforms; thus, the most straightforward way to decrease loss is using the abundant filters to memorize the seen patterns by rote. Transformed variants are often redundantly learned in low-level, middle-level, and relatively high-level filters, Fig. 2. Consequently, the models tend to overfit the existing data and cannot generalize to unseen variants, especially when the data is insufficient.
The proposed Filter Bank Networks approach provides a unified framework for implementing inductive biases within the Deep Convolution Networks (DCNNs) while retaining end-to-end learning capability. Fig. 4 shows the top layer convolutional features of a LeNet-like FBN model trained on the MNIST dataset. It can be seen that the FBN features are intra-class equivariant while maintaining inter-class discrimination. Specifically, the feature difference between the upright 9 and the upside-down 6 is significant despite being visually similar. And the features of the upright 9 and the upside-down 9 are equivariant. FBNs endow DCNNs with equivariant feature representations for generic transformations, improving the essential capability for FSCIL, namely generalization.
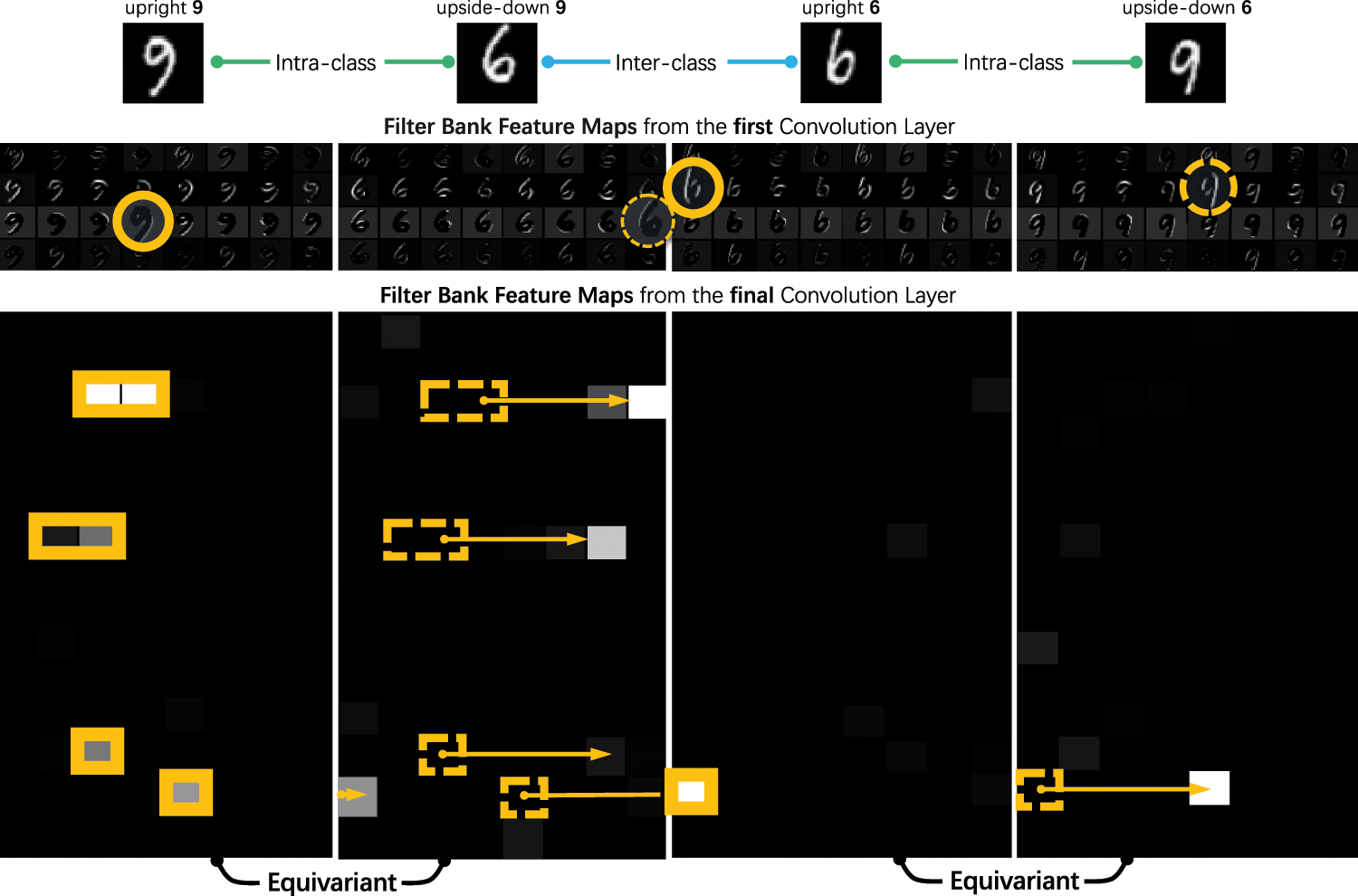
Figure 4: Feature maps produced by filter banks learned from MNIST dataset. FBNs endow DCNNs with equivariant features for transformations. Best viewed by zooming on the screen
The proposed Filter Bank Networks (FBNs) are extensively evaluated. In Section 4.1, experiments on the transformed MNIST dataset [67] are conducted, showing that filter banks can learn transformed variants of intermediate representation and significantly improve the generalization ability of Deep Convolution Neural Networks (DCNNs). In Section 4.2, FBNs are tested on three commonly used benchmarks of Few-Shot Class-Incremental Learning (FSCIL), i.e., CIFAR100, Mini-ImageNet, and CUB200, demonstrating the state-of-the-art performance of FBNs. In Section 4.3, ablation studies are performed to validate the effectiveness of designs in FBNs.
Dataset Description. We transform test samples in the MNIST dataset [67] via bilinear sampling to develop the scaling, flip, and rotation versions. Samples of scaling are resized by a random factor between
Implementation Details. We set up a baseline DCNN with four convolution layers with a kernel size of
Performance. It can be seen in Table 1 that FBN improves the accuracy in scaling and flip setting by
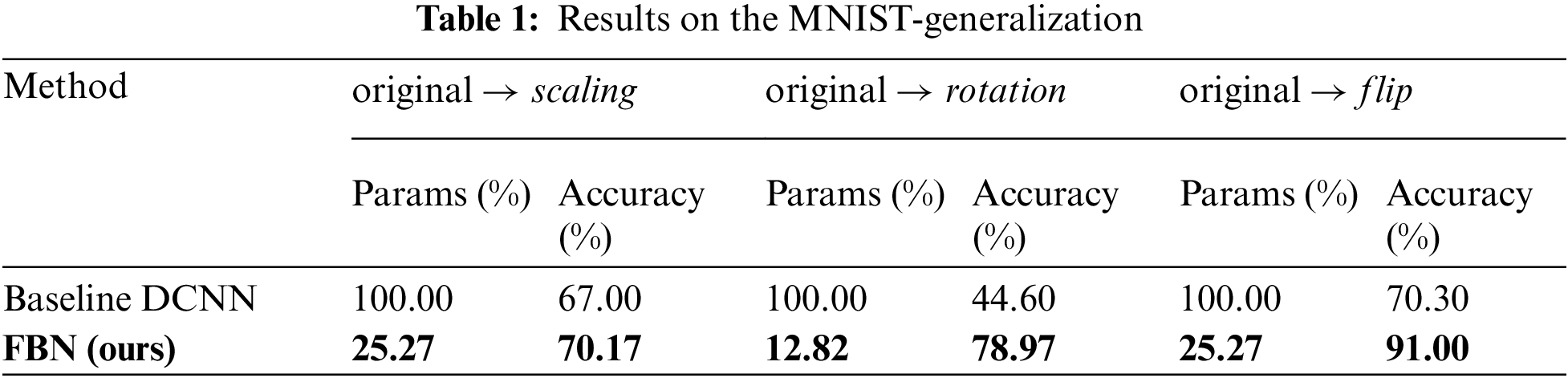
Fig. 5 shows the t-SNE 2D mapping of the features captured by DCNN and FBN where each dot corresponds to a test sample and different colors for different ground truth classes. It can be seen that the FBNs’ features constitute clear clusters and produce a much more explicit feature distribution in manifold than the baseline DCNN.
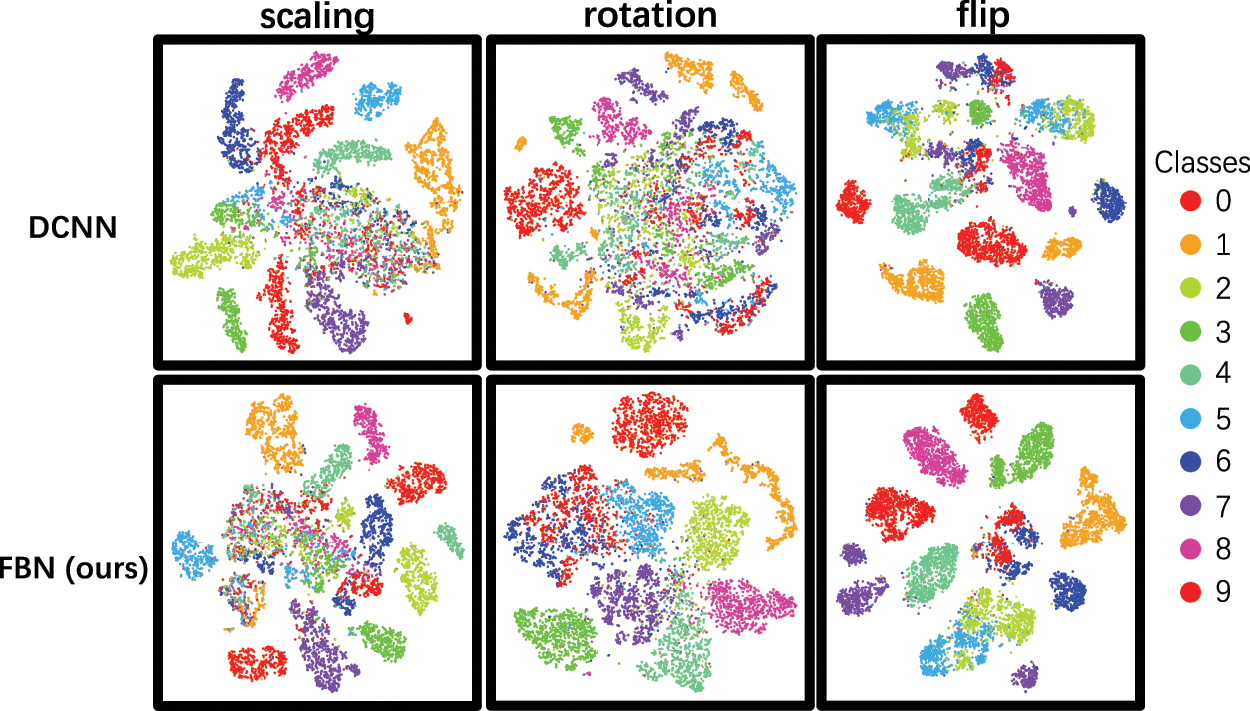
Figure 5: t-SNE visualization of the features produced by DCNN and FBN on the MNIST-generalization dataset. Best viewed in color
The Filter Bank Networks consistently outperform the baselines while using significantly fewer learnable parameters, demonstrating the strong generalization ability of filter banks to the unseen variants of semantic patterns.
4.2 Few-Shot Class-Incremental Learning
We evaluate the proposed FBN on the commonly used FSCIL benchmarks including CIFAR100, CUB200, and Mini-ImageNet. The categories in the datasets are divided into base classes with adequate annotations and new ones with K-shot annotated images. For FSCIL, the network is trained upon base classes for the first pretraining session. New classes are gradually added to train FBN in T incremental sessions. In each incremental session, N-way new classes are added.
Implementation Details. The proposed FBN is built upon the ResNet18/ResNet20 network and optimized with the standard SGD algorithm. We follow the state-of-the-art methods to use four data augmentation strategies, i.e., normalization, horizontal flipping, random cropping, and random resizing. During the first session, FBN is trained using
Dataset Description. CIFAR100 consists of 100 classes, where 60 classes are used as base classes in the pretraining session and 40 as new classes. Each new class has 5-shot annotated images (K = 5). The new classes are divided into 8 sessions (T = 8), each of which has 5 classes (N = 5). In this dataset, the image size is 32
Performance. Table 3 shows the comparison of the proposed FBN and the state-of-the-art methods. We calculate the average classification accuracy of each session’s seen classes. It is shown in Table 3 that FBNs achieve the new state-of-the-art performance. Specifically, FBNs outperform TOPIC by
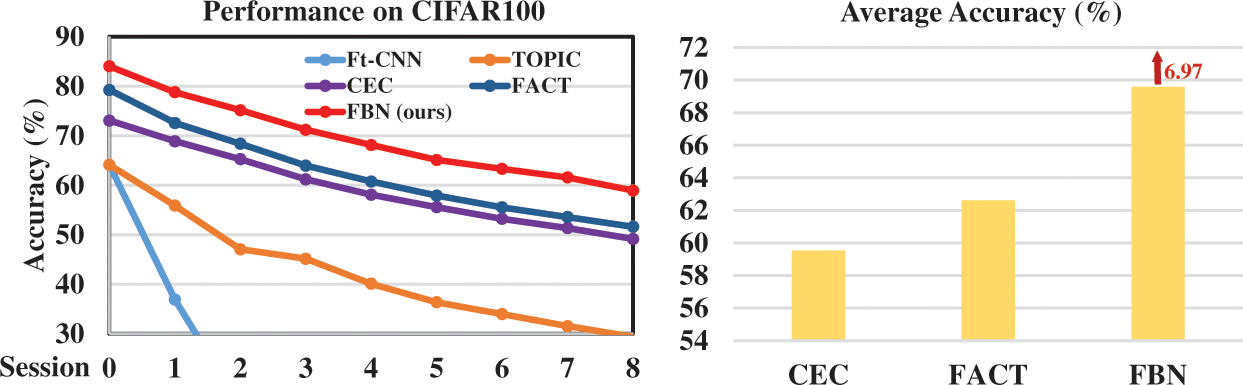
Figure 6: Performance of all the sessions and comparison of average accuracy on CIFAR100
Dataset Description. Mini-ImageNet is a subset of the ImageNet dataset. It is composed of 100 categories sampled from ImageNet, where 60 classes are set as base classes and 40 as new classes. Each new class has 5-shot annotated images (K = 5). The new classes are divided into 8 sessions (T = 8), each of which has 5 classes (N = 5). In this dataset, the image size is 64
Performance. To validate the superiority of our proposed FBN, we compare the performance of all the sessions with state-of-the-art methods. From Table 4 we can see that FBN outperforms CEC [54] and FACT [15] by
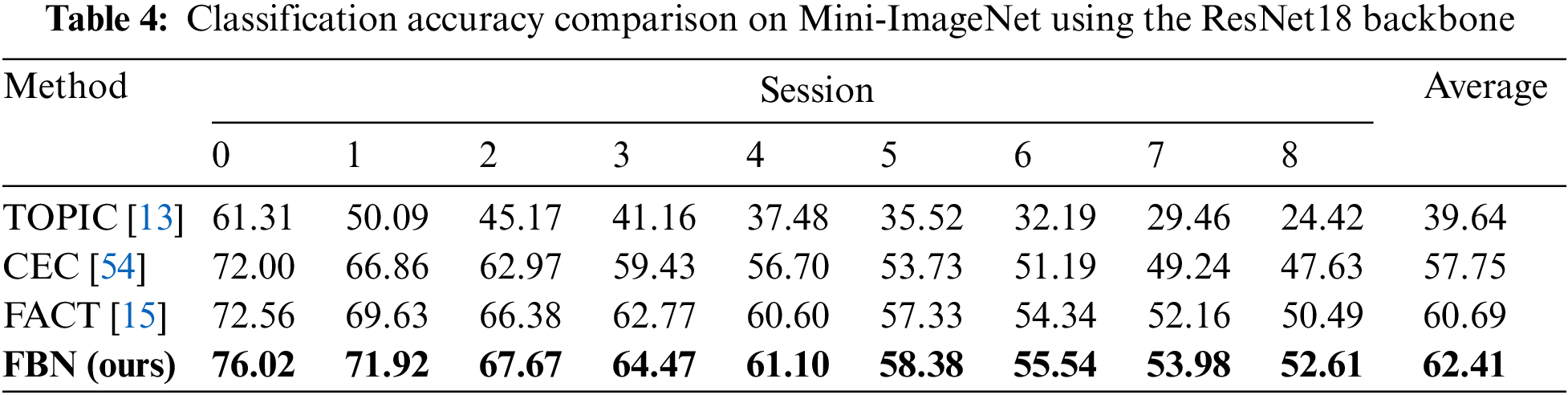
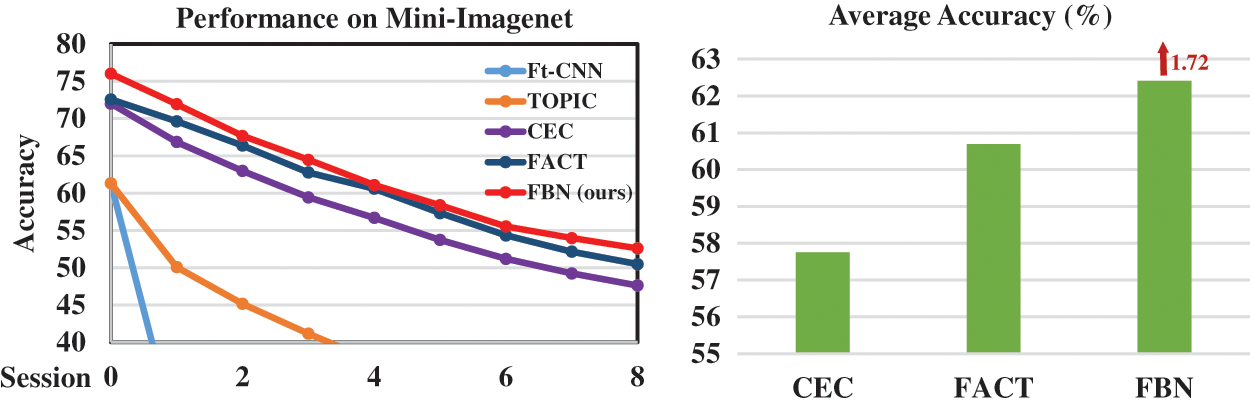
Figure 7: Performance of all the sessions and comparison of average accuracy on Mini-ImageNet
Dataset Description. CUB200 consists of 200 classes where 100 classes are set as base classes and the other 100 classes as new classes under the settings of K = 5, T = 10, N = 10. All the categories in this dataset are birds. Thus it requires the model to learn fine-grained features between classes. The image size of CUB200 is 224
Performance. To validate the models’ ability to mine fine-detailed features, we do not use ImageNet-pretraining in the experiments. For a fair comparison, we re-evaluate CEC [54] and FACT [15] with a consistent setting based on their official implementations, and the result is reported in Table 5. One can see that without pretraining, FBN outperforms CEC [54] and FACT [15] by
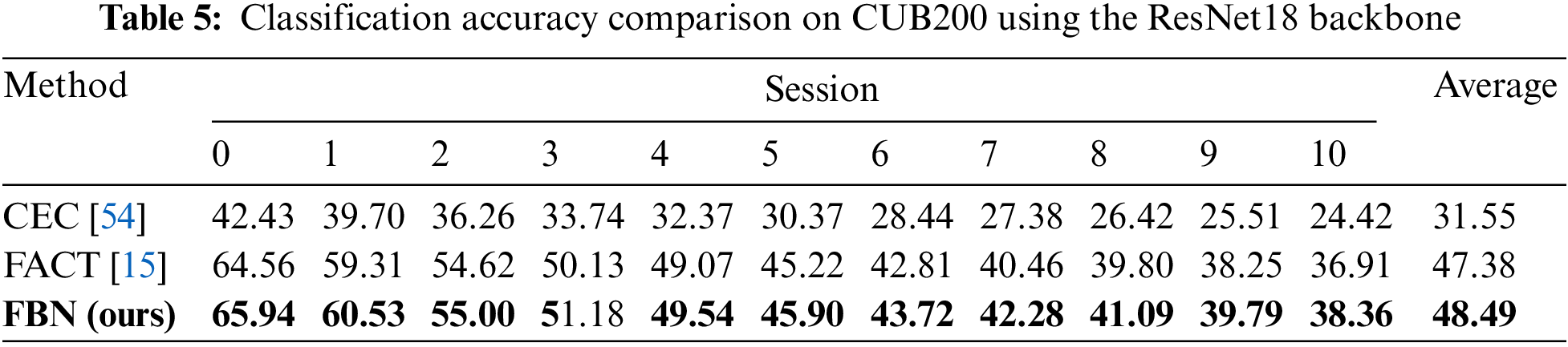

Figure 8: Samples of classes with the highest performance improvements for each session
Dataset Description. To further evaluate Filter Bank Networks, we propose a new challenging Few-Shot Class-Incremental Learning (FSCIL) benchmark, i.e., Fishshot1K, which contains 8261 images covering 1000 ocean fish species. The dataset is built upon an open underwater photography database2. We preprocess and clean the raw data in three steps. First, we sort the fish categories by the number of samples and select the top 1000 classes. Then, we choose 600 classes as the base classes used in the pretraining session and divide the rest 400 classes into 8 incremental sessions, each containing 50 novel classes per session. For each novel class, we use only 1 sample to train the model whereas the rest samples are used for evaluation, i.e., 1-shot learning. Lastly, we resize each raw image to
Performance. We evaluate our proposed Filter Bank Network approach on the challenging Fishshot1K benchmark and compare it with the state-of-the-art method. As shown in Table 6, FBN achieves better classification accuracy for the pretraining and all incremental sessions. The average accuracy significantly outperforms FACT [15] by

Figure 9: Samples of the proposed Fishshot1K dataset which contains 1000 ocean fish species. Images in each row belong to the same category showing significant intra-class differences

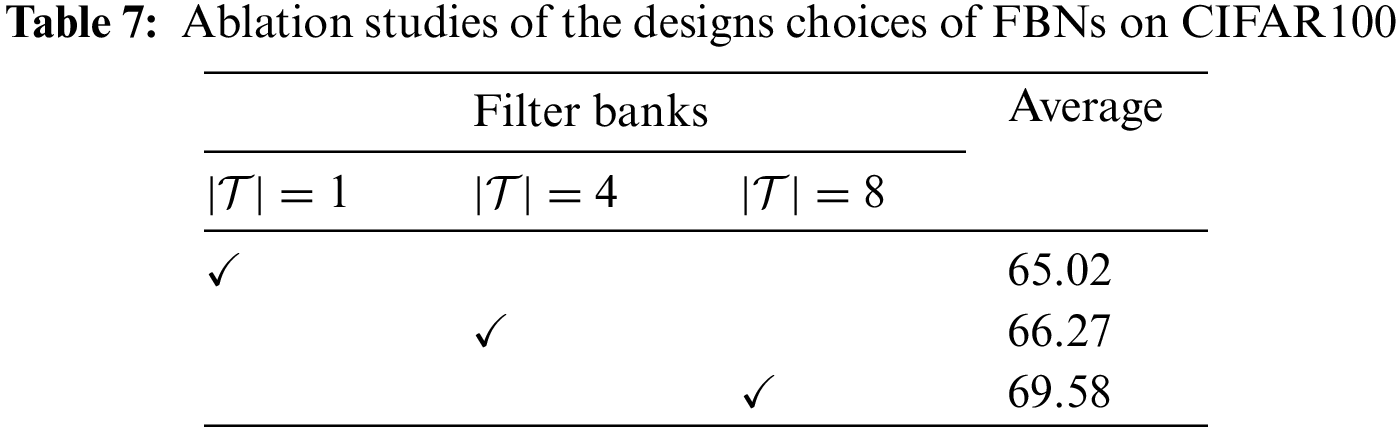
We perform ablation studies on the CIFAR100 FSCIL benchmark to evaluate the effectiveness of the two core designs in FBNs, i.e., the filter banks that learn unseen transformed variants of semantic patterns, and the instance-aware loss which stimulates fine-detailed features to emerge. We sample a subset of
In this paper, we proposed a simple yet effective Few-Shot Class-Incremental Learning (FSCIL) framework, i.e., Filter Bank Networks (FBNs), which introduce learnable inductive biases to address the issue of overfitting and catastrophic forgetting. FBNs improve modern Deep Convolution Neural Networks (DCNNs) to achieve the capability of learning variants of visual patterns that do not exist in the dataset. FBNs augment each learnable filter to a virtual filter bank, containing its canonical form and multiple transformed versions. During back-propagation, gradients of the entire filter bank are collectively aligned and aggregated to update the canonical filter. Moreover, FBNs stimulate instance-aware discriminative patterns to emerge and learn diverse features, reserving latent embedding space for incorporating future novel classes in incremental learning sessions. The primary contributions are three-fold. First, we design the learning paradigm of Filter Bank Networks, including learning augmented filters and mining instance-aware features. Second, we upgrade the modern architecture of DCNNs to FBN and achieve new state-of-the-art results in commonly used Few-Shot Class-Incremental Learning (FSCIL) benchmarks, including CIFAR100, Mini-ImageNet, and CUB200. Last but not least, we contribute a challenging FSCIL benchmark, namely Fishshot1K, which contains 8261 underwater images covering 1000 ocean fish species. With the same training hyperparameters, FBNs consistently outperform their baselines and report the best results, which indicates that the usage of learnable inductive biases is a crucial factor in training growable models which can incrementally learn from limited data.
Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.
Funding Statement: The authors are very grateful for support from the Strategic Priority Research Program of the Chinese Academy of Sciences under Grant No. XDA27000000.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1 We use
References
1. Simonyan, K., Zisserman, A. (2015). Very deep convolutional networks for large-scale image recognition. 3rd International Conference on Learning Representations, San Diego, CA, USA. [Google Scholar]
2. Szegedy, C., Ioffe, S., Vanhoucke, V., Alemi, A. A. (2017). Inception-v4, inception-resnet and the impact of residual connections on learning. Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, California, USA, AAAI Press. [Google Scholar]
3. He, K., Zhang, X., Ren, S., Sun, J. (2016). Deep residual learning for image recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, IEEE Computer Society. [Google Scholar]
4. Deng, J., Dong, W., Socher, R., Li, L., Li, K. et al. (2009). ImageNet: A large-scale hierarchical image database. 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2009), Miami, Florida, USA, IEEE Computer Society. [Google Scholar]
5. Lin, T., Maire, M., Belongie, S. J., Hays, J., Perona, P. et al. (2014). Microsoft COCO: Common objects in context. Computer Vision-ECCV 2014, pp. 740–755. Zurich, Switzerland, Springer. [Google Scholar]
6. Yoon, J., Yang, E., Lee, J., Hwang, S. J. (2018). Lifelong learning with dynamically expandable networks. 6th International Conference on Learning Representations, Vancouver, BC, Canada. [Google Scholar]
7. Xiang, Y., Fu, Y., Ji, P., Huang, H. (2019). Incremental learning using conditional adversarial networks. 2019 IEEE/CVF International Conference on Computer Vision, Seoul, Korea (SouthIEEE. [Google Scholar]
8. Kim, C. D., Jeong, J., Moon, S., Kim, G. (2021). Continual learning on noisy data streams via self-purified replay. 2021 IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, IEEE. [Google Scholar]
9. Smith, J., Hsu, Y., Balloch, J., Shen, Y., Jin, H. et al. (2021). Always be dreaming: A new approach for data-free class-incremental learning. 2021 IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, IEEE. [Google Scholar]
10. Hou, S., Pan, X., Loy, C. C., Wang, Z., Lin, D. (2019). Learning a unified classifier incrementally via rebalancing. IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, Computer Vision Foundation/IEEE. [Google Scholar]
11. Hu, X., Tang, K., Miao, C., Hua, X., Zhang, H. (2021). Distilling causal effect of data in class-incremental learning. IEEE Conference on Computer Vision and Pattern Recognition, Computer Vision Foundation/IEEE. [Google Scholar]
12. Cha, H., Lee, J., Shin, J. (2021). Co2L: Contrastive continual learning. 2021 IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, IEEE. [Google Scholar]
13. Tao, X., Hong, X., Chang, X., Dong, S., Wei, X. et al. (2020). Few-shot class-incremental learning. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, Computer Vision Foundation/IEEE. [Google Scholar]
14. Cheraghian, A., Rahman, S., Fang, P., Roy, S. K., Petersson, L. et al. (2021). Semantic-aware knowledge distillation for few-shot class-incremental learning. IEEE Conference on Computer Vision and Pattern Recognition, Virtual, Computer Vision Foundation/IEEE. [Google Scholar]
15. Zhou, D., Wang, F., Ye, H., Ma, L., Pu, S. et al. (2022). Forward compatible few-shot class-incremental learning. IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, IEEE. [Google Scholar]
16. Yang, S., Liu, L., Xu, M. (2021). Free lunch for few-shot learning: Distribution calibration. 9th International Conference on Learning Representations, Austria. [Google Scholar]
17. Li, Z., Hoiem, D. (2018). Learning without forgetting. IEEE Transactions on Pattern Analysis and Machine Intelligence, 40(12), 2935–2947. https://doi.org/10.1109/TPAMI.2017.2773081 [Google Scholar] [PubMed] [CrossRef]
18. Dhar, P., Singh, R. V., Peng, K., Wu, Z., Chellappa, R. (2019). Learning without memorizing. IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, Computer Vision Foundation/IEEE. [Google Scholar]
19. Zenke, F., Poole, B., Ganguli, S. (2017). Continual learning through synaptic intelligence. Proceedings of the 34th International Conference on Machine Learning, vol. 70. Sydney, NSW, Australia. [Google Scholar]
20. Selvaraju, R. R., Cogswell, M., Das, A., Vedantam, R., Parikh, D. et al. (2017). Grad-CAM: Visual explanations from deep networks via gradient-based localization. IEEE International Conference on Computer Vision, Venice, Italy, IEEE Computer Society. [Google Scholar]
21. Chaudhry, A., Dokania, P. K., Ajanthan, T., Torr, P. H. S. (2018). Riemannian walk for incremental learning: Understanding forgetting and intransigence. Proceedings of the European Conference on Computer Vision (ECCV), pp. 532–547. Munich, Germany, Springer. [Google Scholar]
22. Krizhevsky, A., Sutskever, I., Hinton, G. E., Bartlett, P. L., Pereira, F. C. N. et al. (2012). Imagenet classification with deep convolutional neural networks. 26th Annual Conference on Neural Information Processing Systems, Lake Tahoe, Nevada, USA. [Google Scholar]
23. Girshick, R. B. (2015). Fast R-CNN. 2015 IEEE International Conference on Computer Vision, Santiago, Chile, IEEE Computer Society. [Google Scholar]
24. Ren, S., He, K., Girshick, R., Sun, J., Cortes, C. et al. (2015). Faster R-CNN: Towards real-time object detection with region proposal networks. Advances in Neural Information Processing Systems, vol. 28. Curran Associates, Inc. [Google Scholar]
25. Ronneberger, O., Fischer, P., Brox, T., Navab, N., Hornegger, J. et al. (2015). U-Net: Convolutional networks for biomedical image segmentation. Medical Image Computing and Computer-Assisted Intervention-MICCAI 2015, pp. 234–241. Germany, Springer. [Google Scholar]
26. He, K., Gkioxari, G., Dollár, P., Girshick, R. B. (2017). Mask R-CNN. IEEE International Conference on Computer Vision, Venice, Italy, IEEE Computer Society. [Google Scholar]
27. Lowe, D. G. (1999). Object recognition from local scale-invariant features. Proceedings of the International Conference on Computer Vision, Kerkyra, Corfu, Greece, IEEE Computer Society. [Google Scholar]
28. Ojala, T., Pietikäinen, M., Mäenpää, T. (2000). Gray scale and rotation invariant texture classification with local binary patterns. Computer Vision-ECCV 2000, 6th European Conference on Computer Vision, vol. 1842, Dublin, Ireland, Springer. [Google Scholar]
29. Ahonen, T., Hadid, A., Pietikäinen, M. (2006). Face description with local binary patterns: Application to face recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 28(12), 2037–2041. https://doi.org/10.1109/TPAMI.2006.244 [Google Scholar] [PubMed] [CrossRef]
30. Haley, G. M., Manjunath, B. S. (1995). Rotation-invariant texture classification using modified gabor filters. Proceedings 1995 International Conference on Image Processing, Washington DC, USA, IEEE Computer Society. [Google Scholar]
31. Han, J., Ma, K. (2007). Rotation-invariant and scale-invariant gabor features for texture image retrieval. Image and Vision Computing, 25(9), 1474–1481. https://doi.org/10.1016/j.imavis.2006.12.015 [Google Scholar] [CrossRef]
32. Skibbe, H., Reisert, M. (2012). Circular fourier-hog features for rotation invariant object detection in biomedical images. 9th IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Spain, IEEE. [Google Scholar]
33. Liu, K., Skibbe, H., Schmidt, T., Blein, T., Palme, K. et al. (2014). Rotation-invariant HOG descriptors using fourier analysis in polar and spherical coordinates. International Journal of Computer Vision, 106(3), 342–364. https://doi.org/10.1007/s11263-013-0634-z [Google Scholar] [CrossRef]
34. Scherer, D., Müller, A. C., Behnke, S. (2010). Evaluation of pooling operations in convolutional architectures for object recognition. Artificial Neural Networks-ICANN 2010, pp. 92–101. Thessaloniki, Greece, Springer. [Google Scholar]
35. Vinyals, O., Blundell, C., Lillicrap, T., Kavukcuoglu, K., Wierstra, D. et al. (2016). Matching networks for one shot learning. Advances in Neural Information Processing Systems 29, Barcelona, Spain. [Google Scholar]
36. Snell, J., Swersky, K., Zemel, R. (2017). Prototypical networks for few-shot learning. Advances in Neural Information Processing Systems 30. [Google Scholar]
37. Sung, F., Yang, Y., Zhang, L., Xiang, T., Torr, P. H. S. et al. (2018). Learning to compare: Relation network for few-shot learning. 2018 IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, Computer Vision Foundation/IEEE Computer Society. [Google Scholar]
38. Zhang, C., Cai, Y., Lin, G., Shen, C. (2020). Deepemd: Few-shot image classification with differentiable earth mover’s distance and structured classifiers. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, Computer Vision Foundation/IEEE. [Google Scholar]
39. Liu, B., Ding, Y., Jiao, J., Ji, X., Ye, Q. (2021). Anti-aliasing semantic reconstruction for few-shot semantic segmentation. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 9747–9756. [Google Scholar]
40. Yang, B., Liu, C., Li, B., Jiao, J., Ye, Q. (2020). Prototype mixture models for few-shot semantic segmentation. Computer Vision-ECCV 2020, pp. 763–778. Glasgow, UK, Springer. [Google Scholar]
41. Liu, B., Jiao, J., Ye, Q. (2021). Harmonic feature activation for few-shot semantic segmentation. IEEE Transactions on Image Processing, 30, 3142–3153. https://doi.org/10.1109/TIP.2021.3058512 [Google Scholar] [PubMed] [CrossRef]
42. Finn, C., Abbeel, P., Levine, S. (2017). Model-agnostic meta-learning for fast adaptation of deep networks. Proceedings of the 34th International Conference on Machine Learning, vol. 70. Sydney, NSW, Australia, PMLR. [Google Scholar]
43. Elsken, T., Staffler, B., Metzen, J. H., Hutter, F. (2020). Meta-learning of neural architectures for few-shot learning. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, Computer Vision Foundation/IEEE. [Google Scholar]
44. Sun, Q., Liu, Y., Chua, T., Schiele, B. (2019). Meta-transfer learning for few-shot learning. IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, Computer Vision Foundation/IEEE. [Google Scholar]
45. Zhang, H., Zhang, J., Koniusz, P. (2019). Few-shot learning via saliency-guided hallucination of samples. IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, Computer Vision Foundation/IEEE. [Google Scholar]
46. Li, K., Zhang, Y., Li, K., Fu, Y. (2020). Adversarial feature hallucination networks for few-shot learning. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, Computer Vision Foundation/IEEE. [Google Scholar]
47. Kim, J., Kim, H., Kim, G. (2020). Model-agnostic boundary-adversarial sampling for test-time generalization in few-shot learning. Computer Vision-ECCV 2020-16th European Conference, vol. 12346. Glasgow, UK, Springer. [Google Scholar]
48. Rebuffi, S., Kolesnikov, A., Sperl, G., Lampert, C. H. (2017). ICARL: Incremental classifier and representation learning. 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, IEEE Computer Society. [Google Scholar]
49. Wu, Y., Chen, Y., Wang, L., Ye, Y., Liu, Z. et al. (2019). Large scale incremental learning. IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, Computer Vision Foundation/IEEE. [Google Scholar]
50. Shin, H., Lee, J. K., Kim, J., Kim, J. (2017). Continual learning with deep generative replay. Advances in Neural Information Processing Systems 30. [Google Scholar]
51. Serrà, J., Suris, D., Miron, M., Karatzoglou, A. (2018). Overcoming catastrophic forgetting with hard attention to the task. Proceedings of the 35th International Conference on Machine Learning, vol. 80. Stockholmsmässan, Stockholm, Sweden. [Google Scholar]
52. Mallya, A., Lazebnik, S. (2018). Packnet: Adding multiple tasks to a single network by iterative pruning. 2018 IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, Computer Vision Foundation/IEEE Computer Society. [Google Scholar]
53. Zhu, K., Cao, Y., Zhai, W., Cheng, J., Zha, Z. (2021). Self-promoted prototype refinement for few-shot class-incremental learning. IEEE Conference on Computer Vision and Pattern Recognition, Virtual, Computer Vision Foundation/IEEE. [Google Scholar]
54. Zhang, C., Song, N., Lin, G., Zheng, Y., Pan, P. et al. (2021). Few-shot incremental learning with continually evolved classifiers. IEEE Conference on Computer Vision and Pattern Recognition, Virtual, Computer Vision Foundation/IEEE. [Google Scholar]
55. Cheraghian, A., Rahman, S., Ramasinghe, S., Fang, P., Simon, C. et al. (2021). Synthesized feature based few-shot class-incremental learning on a mixture of subspaces. 2021 IEEE/CVF International Conference on Computer Vision, QC, Canada, IEEE. [Google Scholar]
56. Yu, F., Koltun, V. (2016). Multi-scale context aggregation by dilated convolutions. International Conference on Learning Representations. [Google Scholar]
57. Zhou, Y., Ye, Q., Qiu, Q., Jiao, J. (2017). Oriented response networks. 2017 IEEE Conference on Computer Vision and Pattern Recognition, HI, USA, IEEE Computer Society. [Google Scholar]
58. Dai, J., Qi, H., Xiong, Y., Li, Y., Zhang, G. et al. (2017). Deformable convolutional networks. IEEE International Conference on Computer Vision, Venice, Italy, IEEE Computer Society. [Google Scholar]
59. Hinton, G. E., Krizhevsky, A., Wang, S. D., Honkela, T., Duch, W. et al. (2011). Transforming auto-encoders. Artificial Neural Networks and Machine Learning-ICANN 2011, pp. 44–45. Espoo, Finland, Springer. [Google Scholar]
60. Kivinen, J. J., Williams, C. K. I., Honkela, T., Duch, W., Girolami, M. A. et al. (2011). Transformation equivariant boltzmann machines. Artificial Neural Networks and Machine Learning-ICANN 2011, pp. 1–9. Espoo, Finland, Springer. [Google Scholar]
61. Sohn, K., Lee, H. (2012). Learning invariant representations with local transformations. Proceedings of the 29th International Conference on Machine Learning, Edinburgh, Scotland, UK, icml.cc/Omnipress. [Google Scholar]
62. Skibbe, H. (2013). Spherical tensor algebra for biomedical image analysis = Sphärische Tensor Algebra für die Biomedizinische Bildanalyse (Ph.D. Thesis). University of Freiburg, Germany. [Google Scholar]
63. Cohen, T., Welling, M. (2016). Group equivariant convolutional networks. Proceedings of the 33nd International Conference on Machine Learning, vol. 48. New York, NY, USA. [Google Scholar]
64. Szegedy, C., Liu, W., Jia, Y., Sermanet, P., Reed, S. E. et al. (2015). Going deeper with convolutions. IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, IEEE Computer Society. [Google Scholar]
65. Ding, Y., Zhou, Y., Zhu, Y., Ye, Q., Jiao, J. (2019). Selective sparse sampling for fine-grained image recognition. 2019 IEEE/CVF International Conference on Computer Vision, Seoul, Korea (SouthIEEE. [Google Scholar]
66. Battaglia, P. W., Hamrick, J. B., Bapst, V., Sanchez-Gonzalez, A., Zambaldi, V. F. et al. (2018). Relational inductive biases, deep learning, and graph networks. [Google Scholar]
67. Liu, C., Nakashima, K., Sako, H., Fujisawa, H. (2003). Handwritten digit recognition: Benchmarking of state-of-the-art techniques. Pattern Recognition, 36(10), 2271–2285. https://doi.org/10.1016/S0031-3203(03)00085-2 [Google Scholar] [CrossRef]
68. Castro, F. M., Marín-Jiménez, M. J., Guil, N., Schmid, C., Alahari, K. (2018). End-to-end incremental learning. Proceedings of the European Conference on Computer Vision (ECCV), pp. 233–248. Munich, Germany, Springer. [Google Scholar]
69. Hou, S., Pan, X., Loy, C. C., Wang, Z., Lin, D. (2019). Learning a unified classifier incrementally via rebalancing. IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, Computer Vision Foundation/IEEE. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF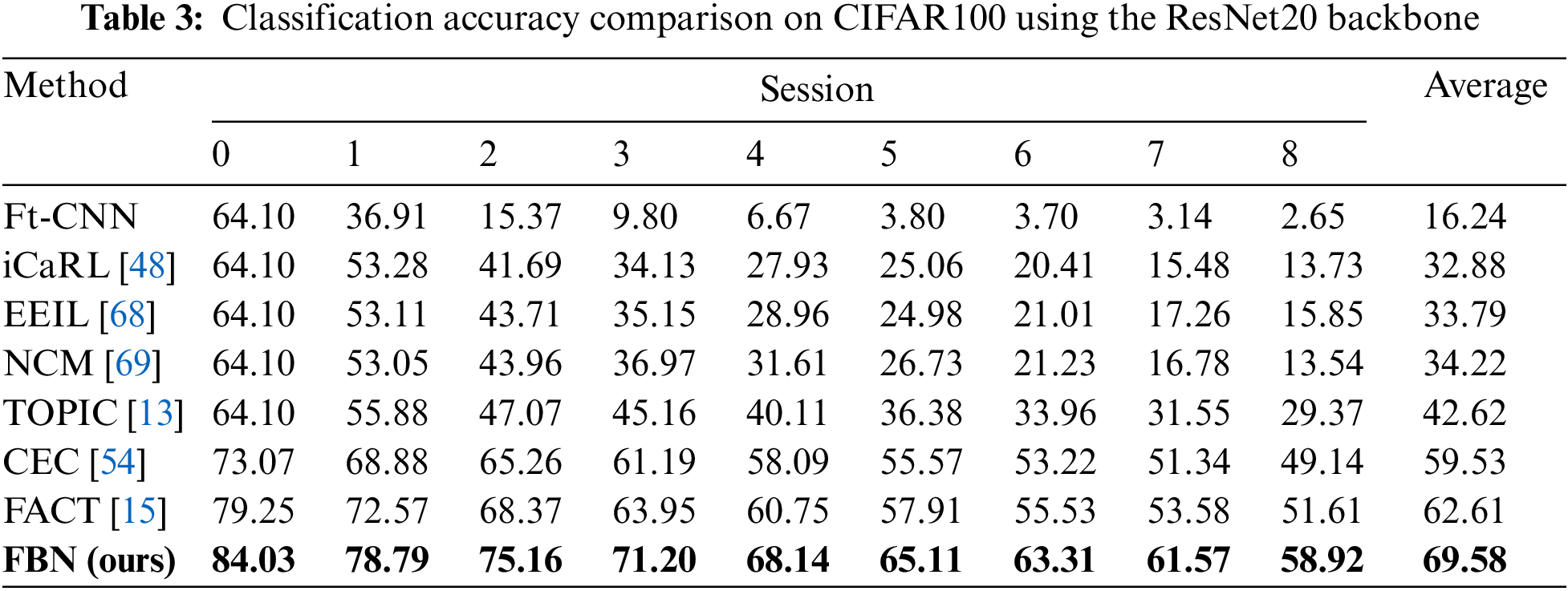
 Downloads
Downloads
 Citation Tools
Citation Tools