 Open Access
Open Access
ARTICLE
3D Human Pose Estimation Using Two-Stream Architecture with Joint Training
1 National and Local Joint Engineering Laboratory of Computer Aided Design, School of Software Engineering, Dalian University, Dalian, 116622, China
2 Dalian Maritime University, Dalian, 116023, China
* Corresponding Author: Dongsheng Zhou. Email:
(This article belongs to the Special Issue: Recent Advances in Virtual Reality)
Computer Modeling in Engineering & Sciences 2023, 137(1), 607-629. https://doi.org/10.32604/cmes.2023.024420
Received 30 May 2022; Accepted 22 December 2022; Issue published 23 April 2023
Abstract
With the advancement of image sensing technology, estimating 3D human pose from monocular video has become a hot research topic in computer vision. 3D human pose estimation is an essential prerequisite for subsequent action analysis and understanding. It empowers a wide spectrum of potential applications in various areas, such as intelligent transportation, human-computer interaction, and medical rehabilitation. Currently, some methods for 3D human pose estimation in monocular video employ temporal convolutional network (TCN) to extract inter-frame feature relationships, but the majority of them suffer from insufficient inter-frame feature relationship extractions. In this paper, we decompose the 3D joint location regression into the bone direction and length, we propose the TCG, a temporal convolutional network incorporating Gaussian error linear units (GELU), to solve bone direction. It enables more inter-frame features to be captured and makes the utmost of the feature relationships between data. Furthermore, we adopt kinematic structural information to solve bone length enhancing the use of intra-frame joint features. Finally, we design a loss function for joint training of the bone direction estimation network with the bone length estimation network. The proposed method has extensively experimented on the public benchmark dataset Human3.6M. Both quantitative and qualitative experimental results showed that the proposed method can achieve more accurate 3D human pose estimations.Keywords
3D human pose estimation has emerged as one of the most important research topic in the field of computer vision [1–5], which has been widely used in animation production [6], medical rehabilitation [7], 3D reconstruction of the human body [8] and simulation of robots. Therefore, 3D human pose estimation based on monocular video has essential research significance and value. In order to acquire 3D human pose, traditional 3D human pose estimation methods usually use specialized equipment for motion capture in an ideal laboratory environment; however, the equipment configuration is time-consuming and expensive, and the equipment is always suitable for certain specific situations. It is difficult to generalize these methods in practice. Therefore, many researchers have shifted their focus to 3D human pose estimation using monocular video. Compared to traditional methods, the equipment required to obtain monocular video is inexpensive and simple to use. In addition, a substantial amount of video data containing human motion is available on the internet. If video data can be fully utilized to accurately estimate human posture or motion, this will provide a substantial amount of real 3D human motion data.
This paper focuses on single 3D human pose estimation based on the monocular video, which is a challenging task due to depth ambiguity and the non-linearity of human dynamics. Recently, works [1,2] used 2D pose estimators to improve 3D human pose estimation methods. Many advanced 3D human pose estimation methods [9–12] also known as two-step methods, first, it uses a 2D human pose estimator to obtain 2D human poses in images or videos, and then use the estimated 2D joints as input and estimate the corresponding 3D joint positions from videos. The two-step method has three main advantages compared to using RGB image as input directly: fewer training resources, lower problem difficulty, and better results. The method proposed in this paper also belongs to the two-step branch.
Despite the two-step approach has made significant advancements, the existing methods also face some limitations at this stage of research. On the one hand, multiple 3D poses with different joint depths may correspond to the same 2D joints, i.e., the depth ambiguity problem. Current works [10,13,14] simply use temporal information, i.e., inter-frame feature relations, to solve this problem. Moreover, what they consider more is the relationship between adjacent frames and the target frame, which makes it difficult to deal with this problem. On the other hand, many of the works do not consider the kinematic structure inherent in the human body. In particular, when the target and neighboring frames correspond to complex actions, the works [10,13,14] caused a decrease in the accuracy of human pose estimation due to lacking of the ability to extract information from frames further away from the target frame. The problem can be effectively addressed by using the human kinematic structure approaches [12,15,16].
Based on the above two problems, this paper adopts the following two solutions. First, we propose TCG, a temporal convolutional network incorporating gaussian error linear units, to extract inter-frame feature relations further. On the one hand, since most of the Natural Language Processing (NLP) tasks need to deal with contextual relations, the language models which are suitable and effective for these tasks are basically equipped with gaussian error linear units. Extraction of inter-frame feature relationship information can be compared to deal with contextual relations in this paper. On the other hand, it is noted that most of the works have focused on macroscopic network structure modification without considering the impact of small parts of the network structure on the network. This paper adopts a kinematic structure approach [12,15,16] to enhance the network’s ability to extract features. The reason for using human kinematic structures lies in that it can further enhance the ability to extract feature relationships between frames. In particular, the model's ability is improved to extract feature relationships between the target frame and more distant frames. In order to link bone length and bone direction tighter, we used a relative joint loss to make a joint training of the two estimation networks, which in turn gave better results.
The main contributions of this paper are summarized as follows:
• This paper proposes the TCG to extract inter-frame feature relations further.
• This paper proposes a relative joint position loss to make a joint training of the two estimation networks.
• This paper demonstrates the effective of the domain of Gaussian error linear units that positively improve the human pose estimation accuracy by experiments.
• To the best of our knowledge, this is the first work to use GELU and Rectified Linear Unit (ReLU) for 3D human pose estimation.
We note that a shorter conference version of this paper appeared in Kang et al. [17]. Our initial conference paper did not discuss the impact of adding relative joint position loss constraints on the network. This manuscript discusses this issue and provides a corresponding analysis of this loss. The manuscript provides a more detailed description of the network structure and algorithm.
This section provides an overview of 3D pose estimation methods based on deep learning. Previous work for 3D human pose estimation can be classified into two main categories based on training methods: direct method and two-step method. With the rise of video pose estimation in recent years, the video-based method has been added to 3D pose estimation.
Direct methods [14,18–27] are to estimate the 3D pose directly from the original input images. In method [19], Li et al. used a shallow network to directly regress 3D joint coordinates, thus enabling a simultaneous task of body joint prediction and detection with sliding windows. Pavlakos et al. [21] integrated a volumetric representation with a supervised scheme for pose estimation from coarse to fine granularity, using voxels instead of joint positions to represent the body and thus estimate a 3D volumetric heatmap. Li et al. [20] designed an embedding subnet that learns information about the underlying pose structure to guide 3D joint coordinate mapping. The subnet employed a maximum cost function to assign corresponding matching scores to the input image-pose pairs. Considering the significance of joint dependencies, Tekin et al. [23] used an autoencoder to learn high-dimensional potential pose representations. Habibie et al. [18] proposed a method for regressing 3D poses using 3D representations and their 2D counterparts. Kocabas et al. [26] used an adversarial learning network with a large-scale motion capture dataset to distinguish between real human actions and human actions generated by the network proposed in this method [26], thereby improving the accuracy of 3D pose and shape estimation.
Two-step methods [9,15,28–38] build a 3D pose estimation model on an off-the-shelf 2D pose estimator. The predicted 2D keypoints are lifted to 3D joint locations by 3D pose model. An earlier approach [28] simply paired the estimated 2D pose with an already integrated 3D pose through a matching strategy and then output the matching 3D pose. The work by Martinez et al. [15] demonstrated that it is possible to map a 2D human pose to a 3D human pose with a simple, lightweight network given 2D ground-truth joints. The difficulty of this method is estimating the exact 2D pose. Ci et al. [34] proposed a general formulation to improve pose representation and pose estimation accuracy by merging Graph Convolutional Network (GCN) with Fully Convolutional Network (FCN). Qammaz et al. [30] proposed an ensemble of self-normalizing neural networks that directly encoded 2D poses and converted them to 3D BVH [39] format, which makes the architecture estimate and render 3D human poses in real-time using only the CPU, and by integrating OpenPose [1]. Zeng et al. [33] proposed to partition the human body into local joint groups and recombine into a low-latitude global contextual information for more efficient learning. Gong et al. [29] designed an automatic enhancement framework for generating more pose data by learning pose data from existing pose datasets, expanding the diversity of pose data available for training and thus improving the generalization capability of 2D-to-3D pose estimators. Xu et al. [32] proposed a graph stacking hourglass network for 2D-to-3D that learns multi-scale graph structure features by stacking graph convolution blocks.
In the case of video-based approaches, recent methods exploited temporal information to alleviate incoherent predictions. As an earlier work, Mehta et al. [40] used simple temporal filtering across 2D and 3D poses from previous frames to predict a temporally consistent 3D pose. Lin et al. [41] applied long short term memory networks (LSTM) to capture temporal information from video. Because of the high computational complexity of LSTM, Pavllo et al. [10] introduced a temporal fully-convolutional model which enables parallel processing of multiple frames and very long 2D keypoint sequence as input.
This paper uses the approach of the second category based on monocular 3D pose estimation. Firstly, a 2D pose detector is used to detect 2D joints of the human body in video frames. Secondly, a sequence of these joints is fed into a 3D pose estimation network for pose estimation. Since 3D pose estimation is more challenging than 2D pose estimation, this paper focuses on the second stage of the second category, i.e., the 3D pose estimation network.
In the video-based 3D human pose estimation task, this paper follows the pipeline of the two-step approach and goes a step further on this pipeline by adopting the method Chen et al. [42] proposed. This article decomposes the task of 3D keypoint estimation into bone length and bone direction estimation, and employs two distinct networks to perform these two tasks concurrently. For the input data, the 2D pose coordinates of each video frame are first obtained using a 2D pose detector. Then the 3D human pose estimation network takes the 2D pose sequences of these consecutive video frames as input to estimate the 3D pose of the target frame. This is the first paper to incorporate gaussian error linear units from natural language processing into the 3D human pose estimation task.
3.1 Overview of the 3D Human Pose Estimation Process
In this paper, the video data is firstly subjected to a frame-splitting operation to obtain the video frames
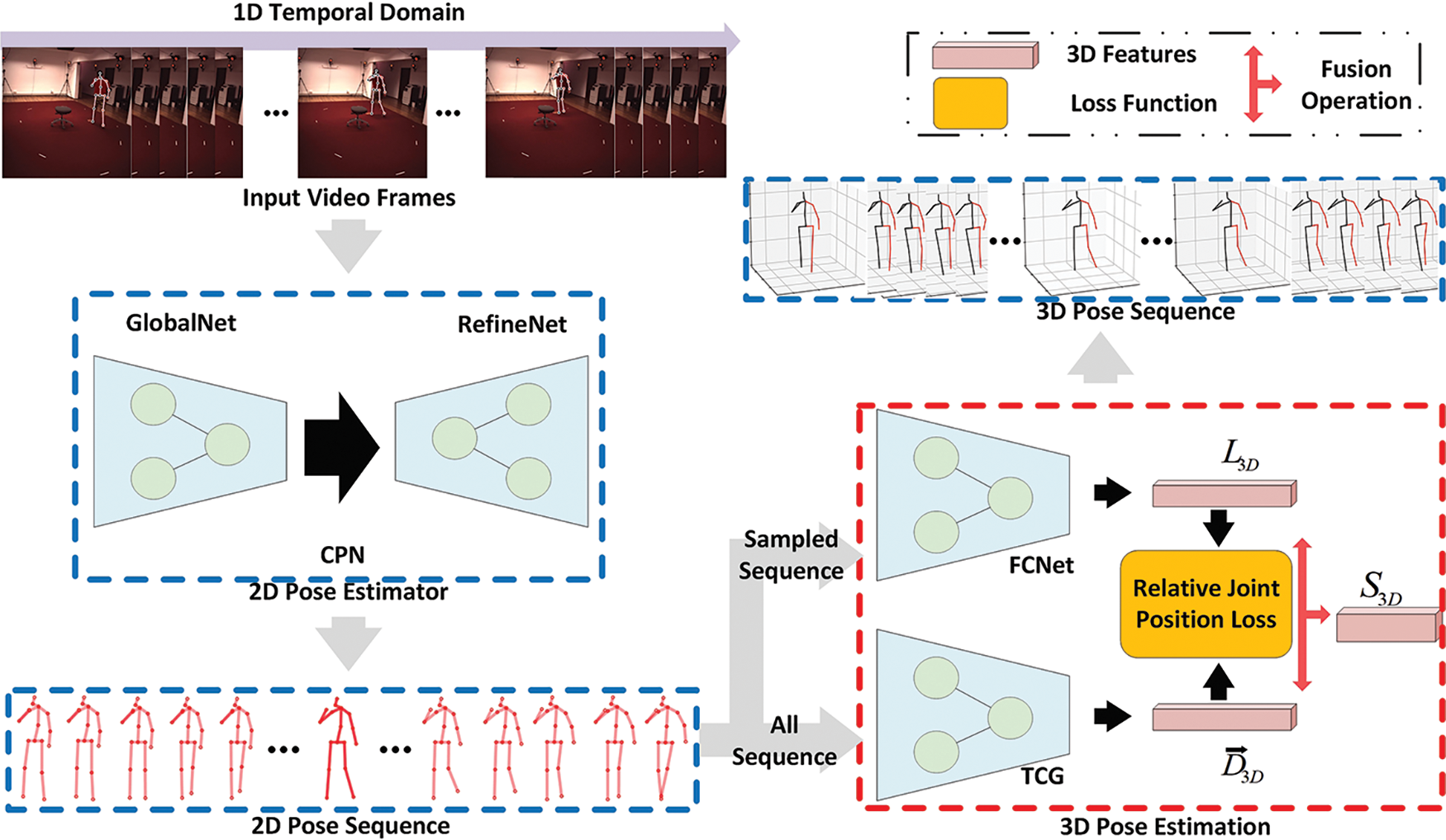
Figure 1: Overview of the 3D human pose estimation process. The red box is the core of this paper, TCG is used to estimate the bone direction, and the loss function is used for the joint training of the two networks
The 2D joint coordinate sequence
After obtaining
Eq. (2) illustrates the detailed process of 3D pose estimation, and the main steps for the whole process is presented in Algorithm 1. The final 3D joint coordinate sequence is
where
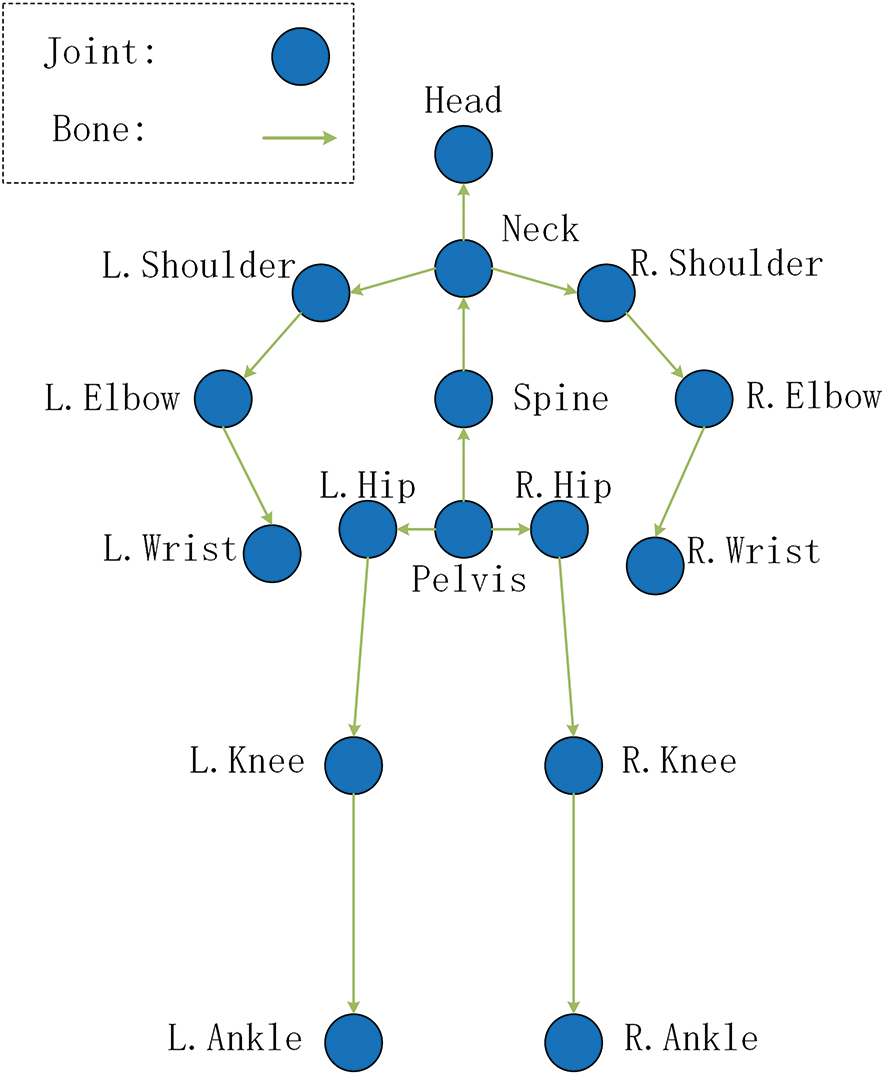
Figure 2: Representation of human joints and bones
The TCG structure is formed by stacking two subnets, as shown in Fig. 3. In subnet_1 and subenet_2, convolution layers are blue where 1024 or 2048, 3d
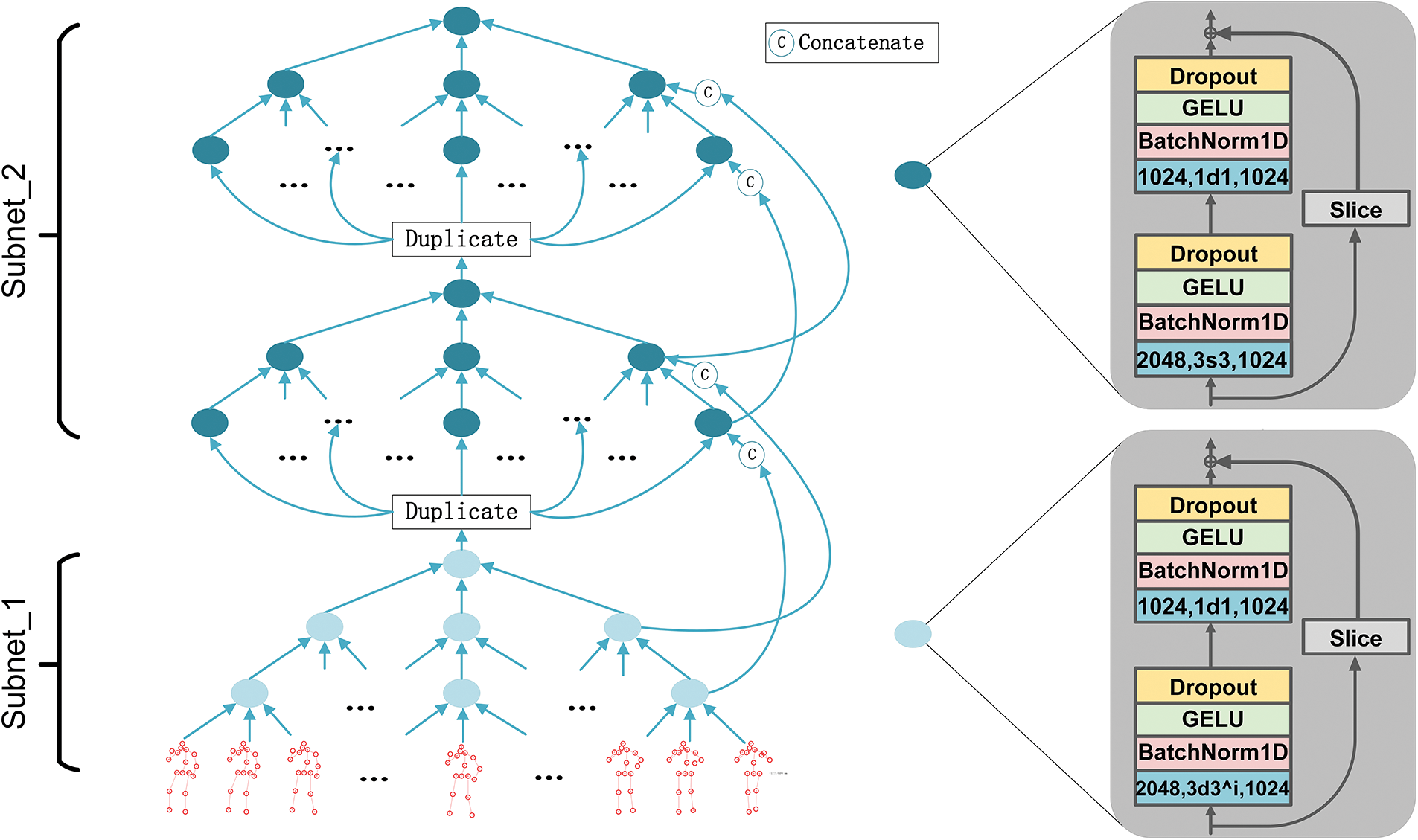
Figure 3: Structure of the TCG
As shown in Fig. 3, centered on the 2D keypoint sequence of the target frame, the 2D keypoint sequence of successive frames is organized together to form the input of TCG. These sequences will be converted into bone direction vectors by TCG, which can be expressed as:
where
where
In TCG, the first subnet obtains the bone direction vector of the target frame by extracting the features of all input frames. The second subnet obtains the bone direction vector by using the output vector of the first subnet and the bone direction feature obtained by long-skip connection. Because ReLU will zero the features less than zero in the convolution output, this operation impairs the ability of works [10,13,14] to extract features. In order to make better use of the feature relationship between the target frame and adjacent and distant frames. This paper replaces the original linear rectification unit with a gaussian error linear unit. GELU and ReLU have a completely different way of dealing with less-than-zero feature values. The ReLU sets less-than-zero and near-zero values to zero, while the GELU performs a scaling transformation. This operation preserves more of the features extracted from the TCG layers, which allows the features extracted from the current TCG layer to participate in the feature computation of subsequent TCG layers, thus contributing more to the estimation of the target frame. Subsequent experiments verify that Gaussian error linear units can achieve improved network estimation accuracy.
3.3 Relative Joint Position Loss Function
A schematic diagram of relative joint position loss is shown in Fig. 4, where
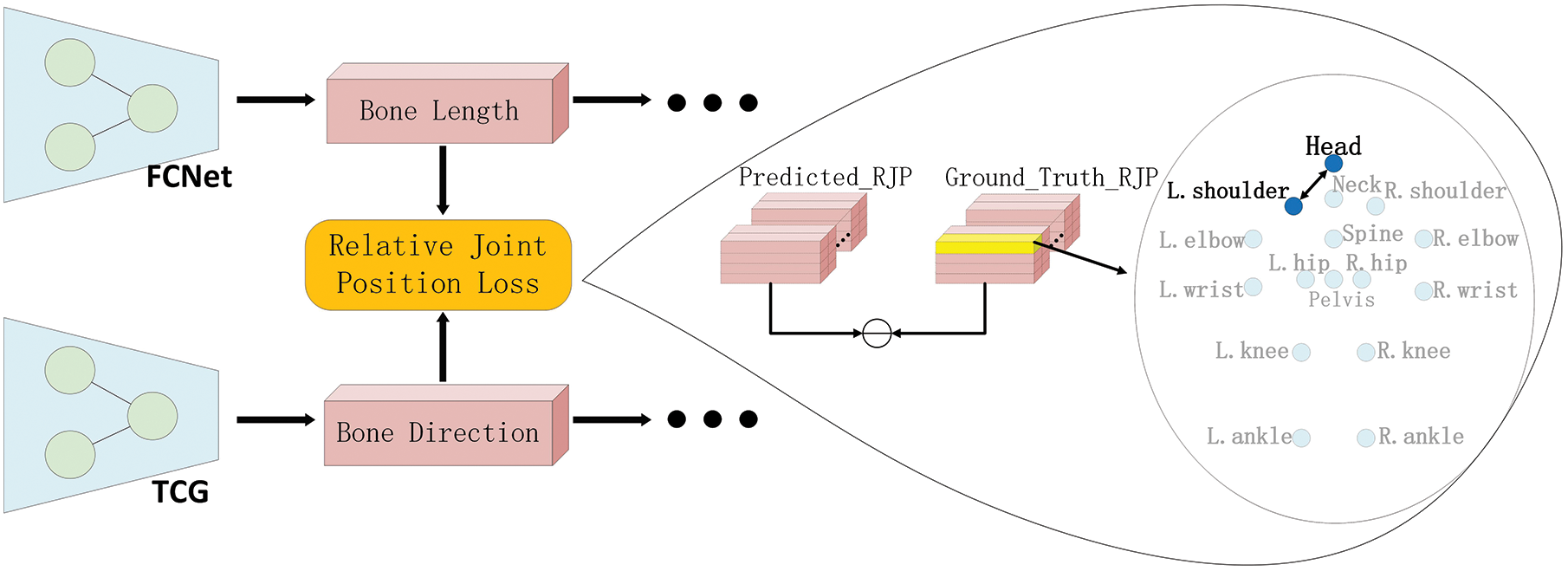
Figure 4: Location of relative joint position loss effects
Since in the 3D human pose estimation, there are 4 joints that are the most easily estimated to be the head, neck, spine and pelvis, and in the 16 joints (see in Fig. 2), the estimation error of these four joints is the smallest compared to the other 12 joints. Therefore, this paper is designed to group the 4 joints into a group and denote them as CenterJoints (CJs):
While this paper not only calculates the relative position distance between limbs and CJs, but also calculates the relative position distance between CJs. Therefore, in this paper, the other 12 joints and two joints in CJs are grouped together as RoundJoints (RJs):
where the
Therefore, the 16 joints in Fig. 2 can be denoted as AllJoints (AJs):

The joint loss function for joint training of the bone direction estimation network (TCG) and the bone length estimation network (FCNet) is defined as follows:
where
Algorithm 2 describes the flow of the relative joint position loss algorithm. The first line initializes the variables used in the algorithm, etc., and lines 2–3 define the order in which the jointpoints are taken. Line 4 makes a judgment on whether the relative joint position calculation condition is satisfied, where the first condition of the judgment statement is to prevent double counting between the four joints in CJs. Line 5 performs a relative position calculation on the joints that satisfy the conditions. Line 9 completes the matching of the ground-truth value to the shape of the predicted value. Lines 10–11 calculate intermediate variable transfer and relative joint position loss.
3.4 Introduced Activation Functions
Rectified linear unit ReLU is an efficient activation function proposed by Nair et al. [43] in 2010, and the image of the function is shown in Fig. 5 with the following equation:
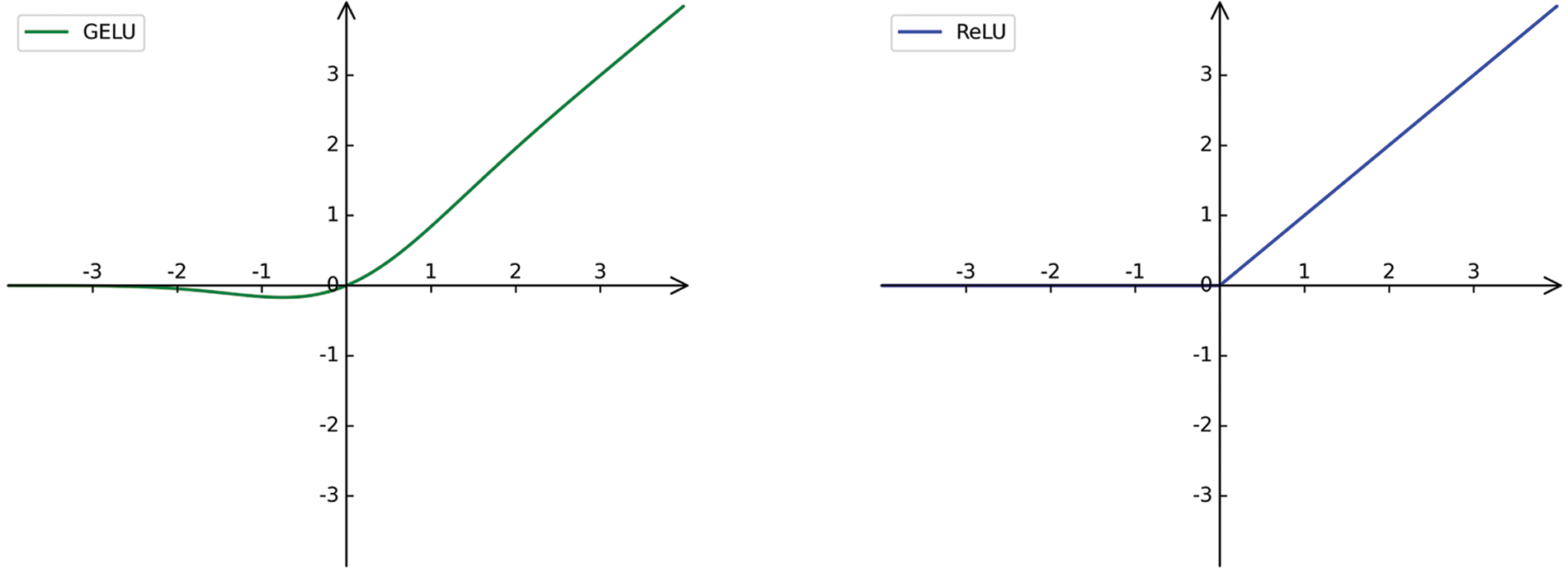
Figure 5: Diagrams of GELU and ReLU functions
For ReLU, it will directly discard the negative value of the input feature, that is, set it to zero. 3D human pose estimation based on the video needs to estimate the human pose of the target frame through adjacent frames, and there are negative values in each frame feature. Therefore, this paper assumes that ReLU sets the negative value of features to zero, it will limit the network's ability to extract feature relationships between frames, thus resulting in reduced estimation accuracy. For this purpose, we draw on the GELU used by BERT [44], RoBERTa [45] and GPT-2 in the field of NLP, all of which use textual, contextual relationships to implement NLP tasks such as text classification and natural language inference tasks (NLI), etc. Since GELU scales all negative values instead of setting them to zero, but scales them, it can be better adapted to tasks that use inter-frame feature relations for video pose estimation than ReLU.
Gaussian error linear unit Hendrycks et al. [46] proposed the GELU function in 2016, which is the preferred choice for many models of NLP. Unlike ReLU's deterministic 0, 1 selection pass, GELU is randomly multiplied by 0 or 1 depending on the input's distribution, which is equivalent to multiplying the neuron’s input
where
The reason for replacing ReLU with GELU in TCG in this paper is that this network processing task performs target frame pose estimation by extracting and fusing joints feature information from individual frames. When GELU encounters negative values in the input data, GELU assigns a weight to the value based on its distribution throughout the data. From Eq. (13), when
Dataset and Evaluation In this paper, the proposed model is trained and evaluated on the largest available human pose dataset, Human3.6M. The dataset is set up in accordance with the standards, and videos of seven professional actors are used for training and evaluation. Videos of five actors (S1, S5, S6, S7, S8) is used for training and two (S9, S11) for evaluation. We follow the standard protocol for evaluating this paper's model on Human3.6M. The first evaluation protocol (Protocol 1): Mean Per Joint Position Error (MPJPE) measures the Euclidean mean distance between the estimated joint position and the ground-truth joint position at the millimeter level. The second evaluation protocol (Protocol 2): Pluck-Mean Per Joint Position Error (P-MPJPE), which requires the estimated 3D pose to be consistent with the ground-truth pose in terms of translation, rotation, and scale. This paper also uses the Mean Per Joint Velocity Error (MPJVE) proposed by Pavllo et al. [10], which corresponds to the first order derivative of the MPJPE 3D pose sequence.
Implementation details In experiments of this paper, for the bone direction estimation task,
All experiments use the PyTorch framework with two Nvidia Tesla V100 graphics cards. The network is trained using the Adam optimizer, with the number of training generations set to 80 and an exponentially decreasing learning rate method, with the initial learning rate set to
Table 1 shows, under protocol 1, the results of quantitative comparison between the proposed method and other methods on the Human3.6M dataset, bold numbers represent the best performance. It can be seen from Table 1, the method in this paper has a lower mean error. Compared with the methods [9,10,42] using the same 2D pose detector, the proposed method achieves better results on various movements. This includes both simple and complex action poses. For example, under protocol 1, the pose estimation errors of the proposed method for the simple actions “Greeting” and “Eating” were 0.4 and 0.1 mm lower than those of Chen et al. [42]. For the complex pose, the pose errors estimated by our method for “SittingDown” and “Smoking” were 0.3 and 0.5 mm lower than those of Chen et al. [42].
Table 2 shows, under protocol 2, the results of the quantitative comparison between the proposed method and other methods on Human3.6M dataset, bold numbers represent the best. As can be seen in Table 2, most of the actions in the proposed method yield the best results. Such as actions “Walking”, “Phoning” and “WalkingDog”.
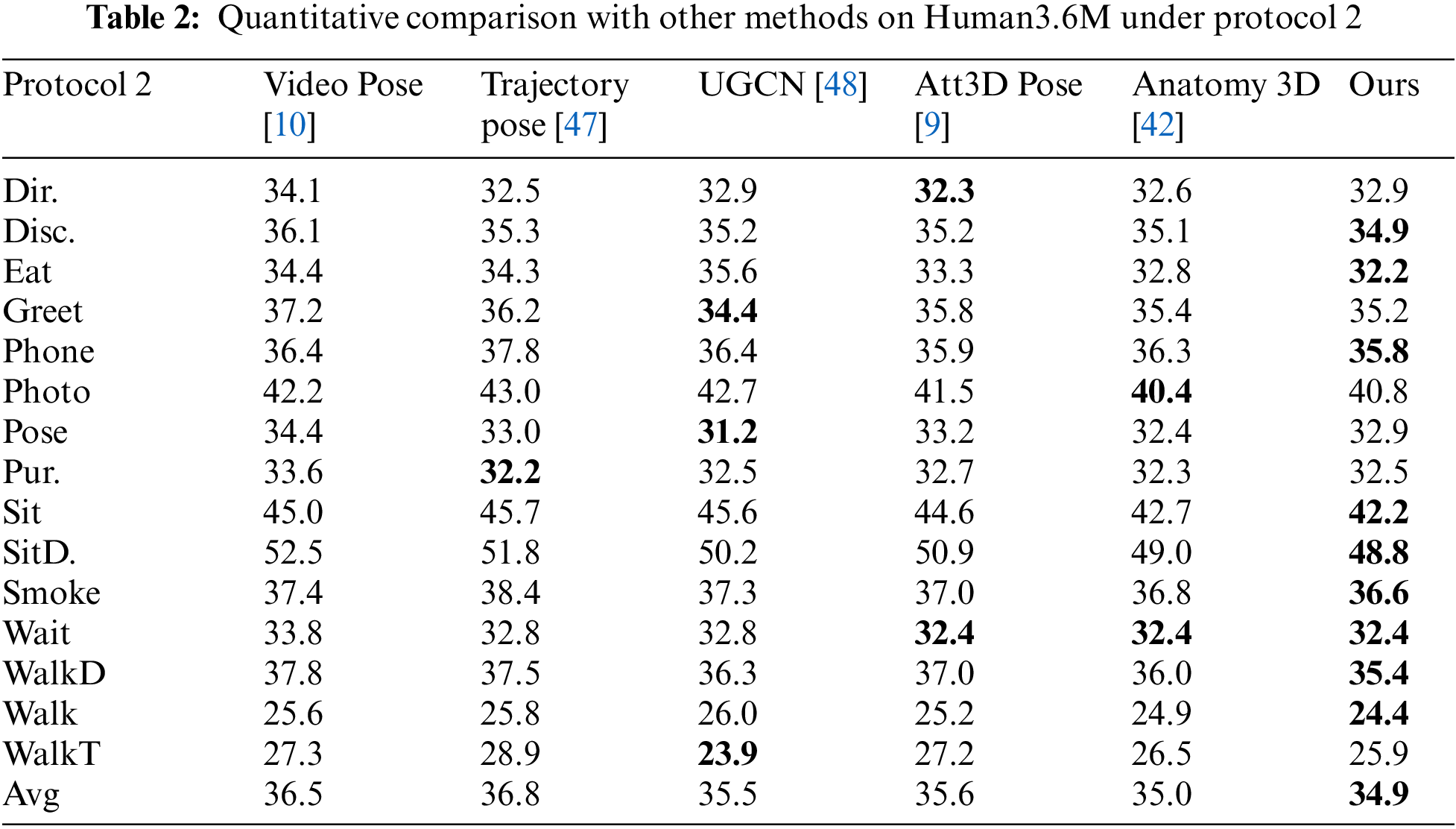
Fig. 6 shows the variation in accuracy of Pavllo et al. [10], Liu et al. [9], Chen et al. [42], and this paper’s model on the validation set. Figs. 7 and 8 show the qualitative comparison between the above three methods and our model on the “Directions,” “Discussion” and “Eating.” Compared to the above three methods, Fig. 7 shows that this method yields better visualization results than three methods; Fig. 8 shows that this method yields visualization results which is less effective than or on par with the other three methods.
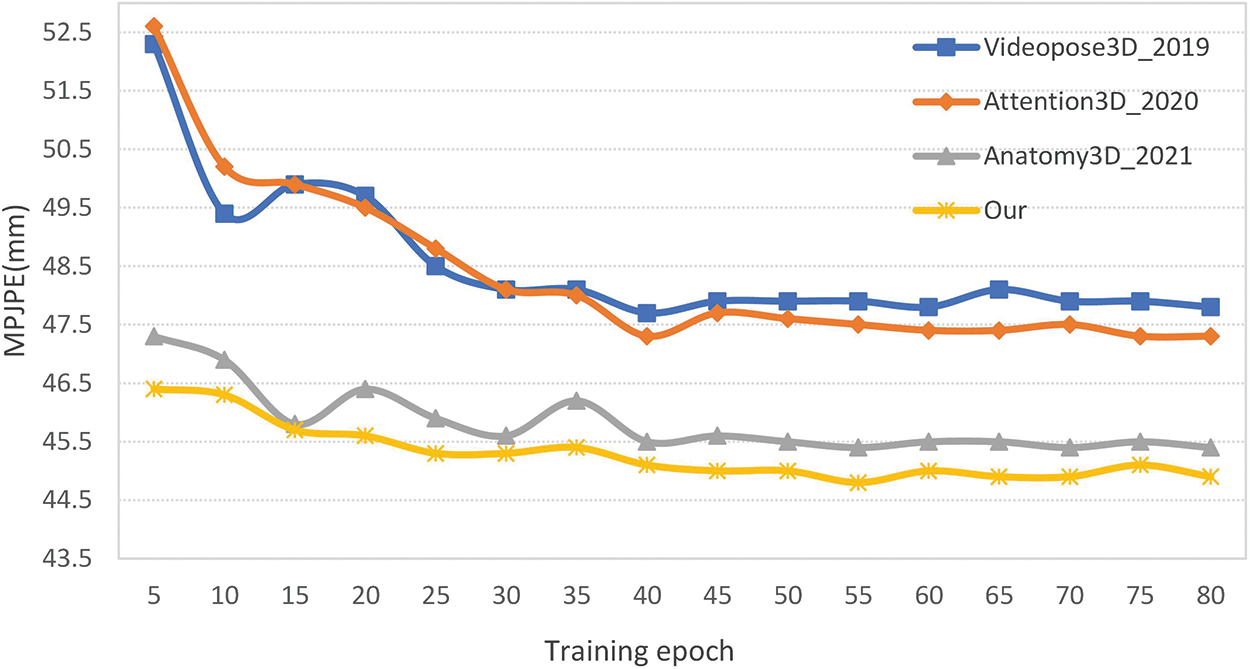
Figure 6: Accuracy variation for four models during validating
Figure 7: Qualitative comparison with other models for visualising actions on the Human3.6M dataset. The locations of the green dashed circles where the present model clearly generates better results

Figure 8: Qualitative comparison with previous state-of-the-art models for visualising actions on the Human3.6M dataset. The blue dashed circle locations where the present visualization is similar to or inferior to the state-of-art approach
As shown in Fig. 7 in Directions action the left arm generated by this model (red arm, position boxed by green circle) is closer to the ground-truth pose than the other three methods. In SittingDown action, the junction of thigh and hip (position boxed in green) generated by the method in this paper is significantly closer to the ground-truth pose than the other three methods.
As shown in Fig. 8 in Phoning action, the direction of the human right arm in the visualization results of this paper is consistent with the other methods. Nonetheless, the arm's length protruding from the point where it intersects the spine is too short, which may be due to excessive bone length restriction. In WalkTogether action, the circled position is where the visualization results in this paper are similar to the other three methods. In Walking action, the right arm (red upper limb) in ground-truth almost overlaps with the spine, in general agreement with the results of the Pavllo et al. [10] and Chen et al. [42] visualizations. The visualization in this paper shows a greater distance between the right arm and the spine.
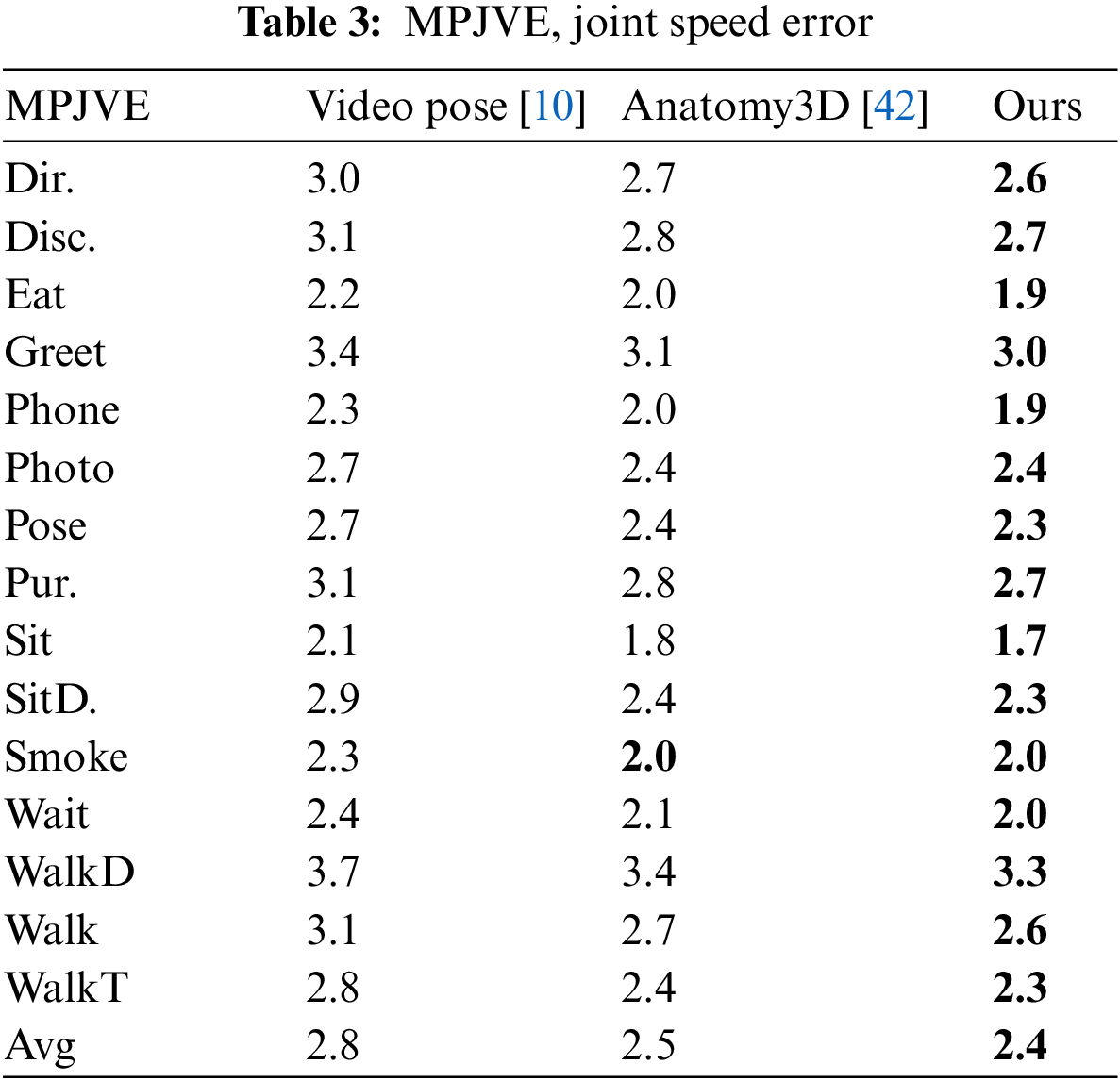
Table 3 shows the comparison results under the MPJVE evaluation protocol, whose high or low corresponds to whether the 3D pose can be estimated more smoothly. As can be seen from the table, compared with Pavllo et al. [10] and Chen et al. [42], the proposed method has lower errors, which indicates that the proposed method has better pose consistency and smoothness in estimating 3D pose. We attribute the accurate estimates achieved in Tables 1 and 2 to the use of TCG in estimating the bone direction, which improves the accuracy of the direction estimation and thus the overall estimation accuracy of the method.
To illustrate the effectiveness of the different modules in this paper, this paper first performs a relative joint position loss experiment to verify its effectiveness. And then, in order to verify the effectiveness of the network incorporating gaussian error linear units for improving the estimation accuracy, four sets of ablation experiments are carried out. These four groups of ablation experiments are divided into All ReLU, All GELU, TC-ReLU FC-GELU and TC-GELU FC-ReLU. Finally, three groups of experiments are designed to explore which regions are effective for improving the accuracy of network estimation in gaussian error linear units.
Through the experimental results in Table 4, compared with Chen et al. [42], the accuracy of network estimation in this paper is slightly improved and almost equal to it. This paper assumes the reason for this situation is that the calculation of some joints is similar, such as the calculation of the relative position of head and shoulder joints. However, this paper uses the four joints of the human central axis to calculate the relative position of the limb joints. The loss proposed by Chen et al. [42], it computes the feature of keypoints 105 times for each frame. In contrast, our method requires less than half the number of computations of Chen’s method, only 47. For the whole training process of the model, Chen’s method needs 6.9M computations and our method needs 3.1M computations. This calculation method makes the calculation times of this paper only half of that. Under the condition of basically consistent accuracy, this paper has advantages in calculation cost.
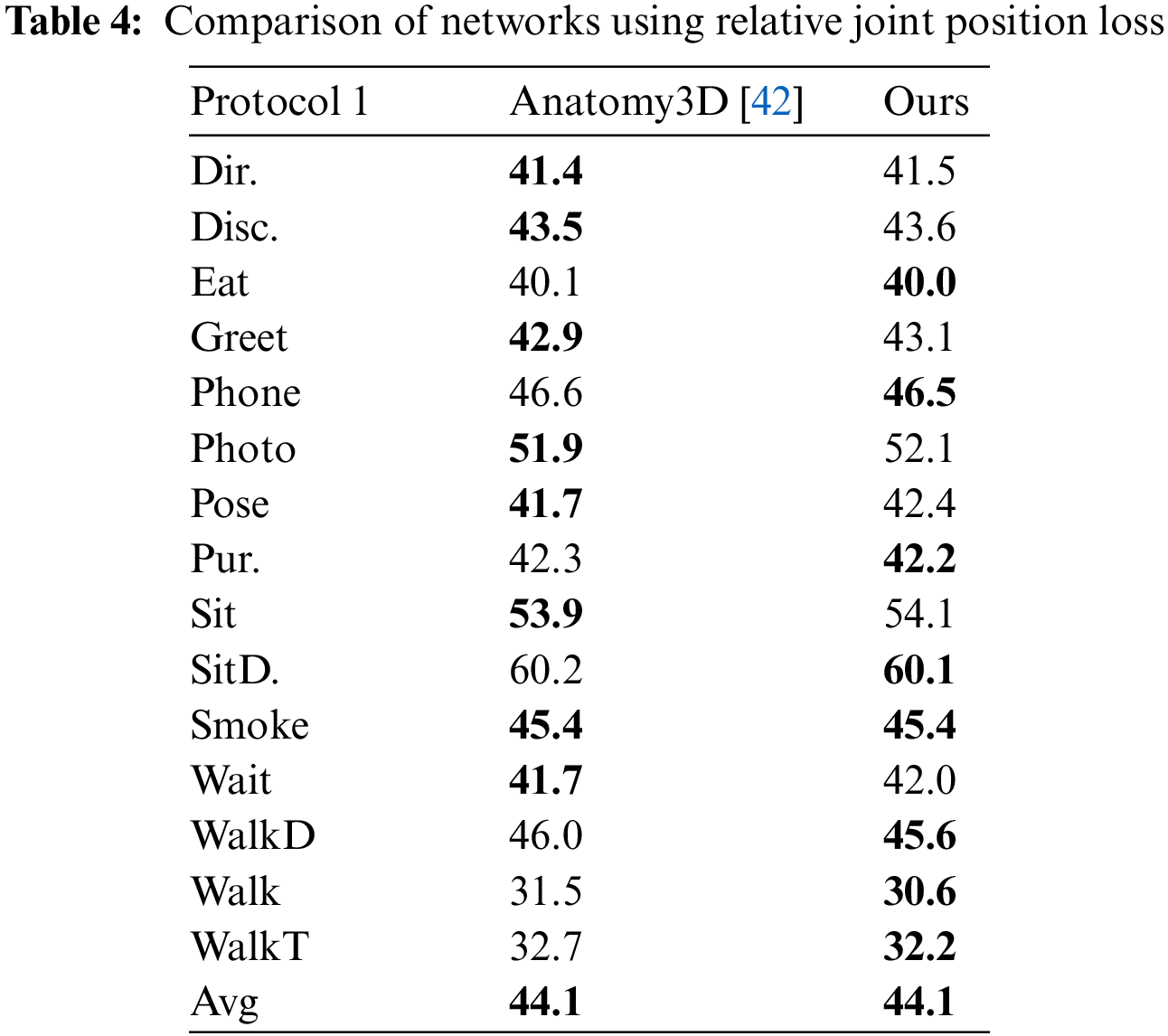
Table 5 shows the effect of using GELU and ReLU in two branching networks.
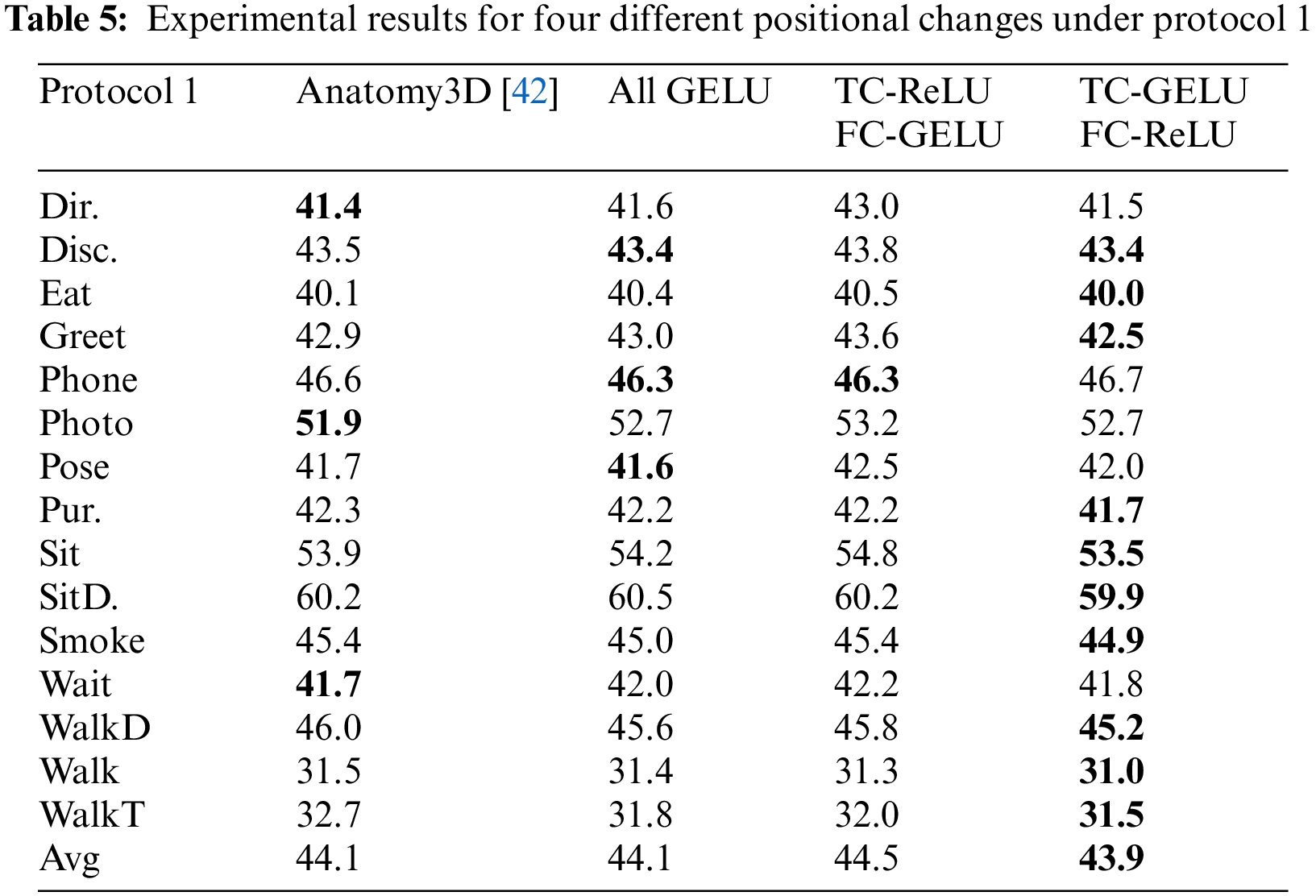
All ReLU The method All ReLU is used by Chen et al. [42], they use the ReLU functions of the residual blocks in the two branching networks in the model. As can be seen from Table 5, their method achieves good results on movements, especially “Direction”, “Photo” and “Wait”.
All GELU In this paper, the ReLU functions of the residual blocks of the two branching networks in the model are all replaced with GELU functions, and experiments are conducted. As can be seen from Table 5, compared to “All ReLU,” the all GELU model achieves accuracy improvements in most of the actions, including the action “WalkToghter” with a large improvement of 0.9 mm, and the actions with a smaller improvement like “Phoning” and “Posing.”
After obtaining the results of All GELU, we consider that the model has two branch networks, which realize different functions and require different input data. Maybe, each branch network has its own adaptive function. For this purpose, two other sets of experiments are performed, “TC-RELU FC-GELU” and “TC-GELU FC-RELU,” where TC and FC represent the networks for estimating the bone direction and the network for estimating the bone length, respectively, and the content behind the horizontal line after the horizontal line represents the function used.
TC-ReLU FC-GELU In this experimental setup, we replaced the functions of the branching network accordingly. Compared with “All ReLU,” the accuracy of most of the actions decreased to varying degrees, except for a few actions, such as “Phoning” and “Walking,” for which the accuracy improved slightly. For example, the accuracy of “Direction,” the easier of the 15 actions to estimate, is 1.6 mm lower, while the accuracy of “Photo” is 1.3 mm lower. As most of the actions have varying degrees of accuracy degradation, our mean value is also 0.4 mm lower than “All ReLU”.
TC-GELU FC-ReLU In this experimental setup, we replaced the functions of the branching network accordingly. By comparing the results with “All ReLU,” the accuracy of 10 of the 15 actions on the Human3.6M dataset is improved. The majority of the improvements are in the region of 0.5 mm, such as “Greeting,” “Sitting” and “Smoking.” There are also a few movements that have improved by less than 0.2 mm, such as “Discussion” and “Eating,” but there are also movements that have improved by 0.6 mm, which are listed in Table 5.
In our analysis, the information in TCG of one frame is estimated by multi-frame information, which indicates that the information of all frames input in the network plays a critical role in the pose estimation of the target frame. GELU allows negative values to be given a smaller weight so that they contribute to the final result without being decisive, which preserves more features of each frame. Therefore, the reason for the improved accuracy of all the above-mentioned action estimates stems from the fact that GELU does not simply set the negative values to zero, as ReLU does.
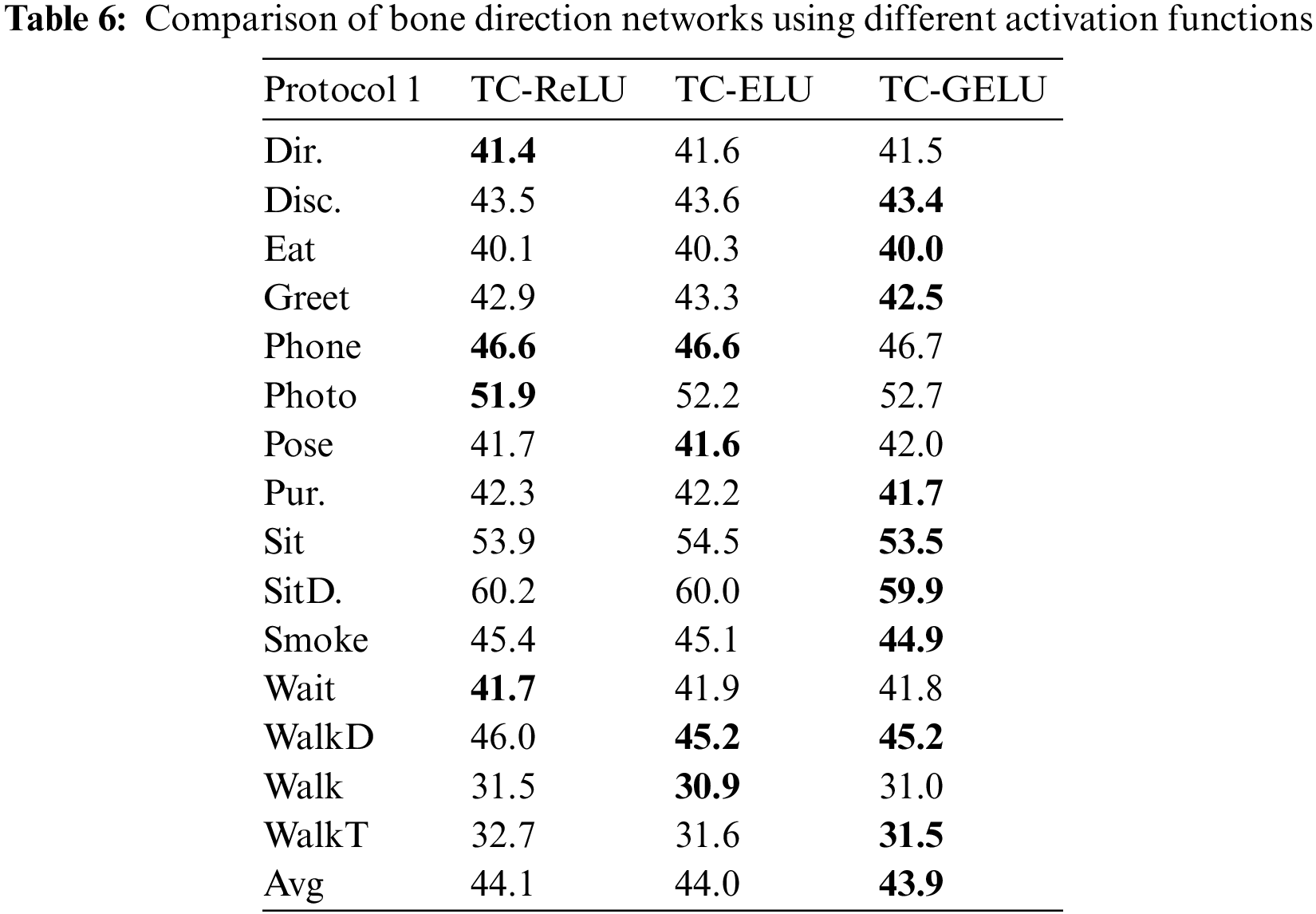
To further explore the effective domain of GELU that plays a positive role in improving the accuracy of human pose estimation. In this paper, the ELU function with similar properties to the ReLU function in the positive half axis is selected for subsequent experiments. Compared to ReLU, ELU retains negative values, which allow them to push the mean cell activation close to zero like batch normalization, but with lower computational complexity. As the bias offset effect is reduced, the mean shifts towards zero, accelerating learning by bringing the normal gradient closer to the natural gradient of the unit. The ELU saturates to negative values for smaller inputs, thus reducing the forward propagation of variation and information. These features are again similar to the negative semi-axis action of the GELU to some extent. Therefore, in this paper, the ELU function is replaced with GELU in TCG, and experiments are conducted. The function images of the three are shown in Fig. 9. A comparison of the experimental results of ReLU, GELU and ELU is shown in Table 6.
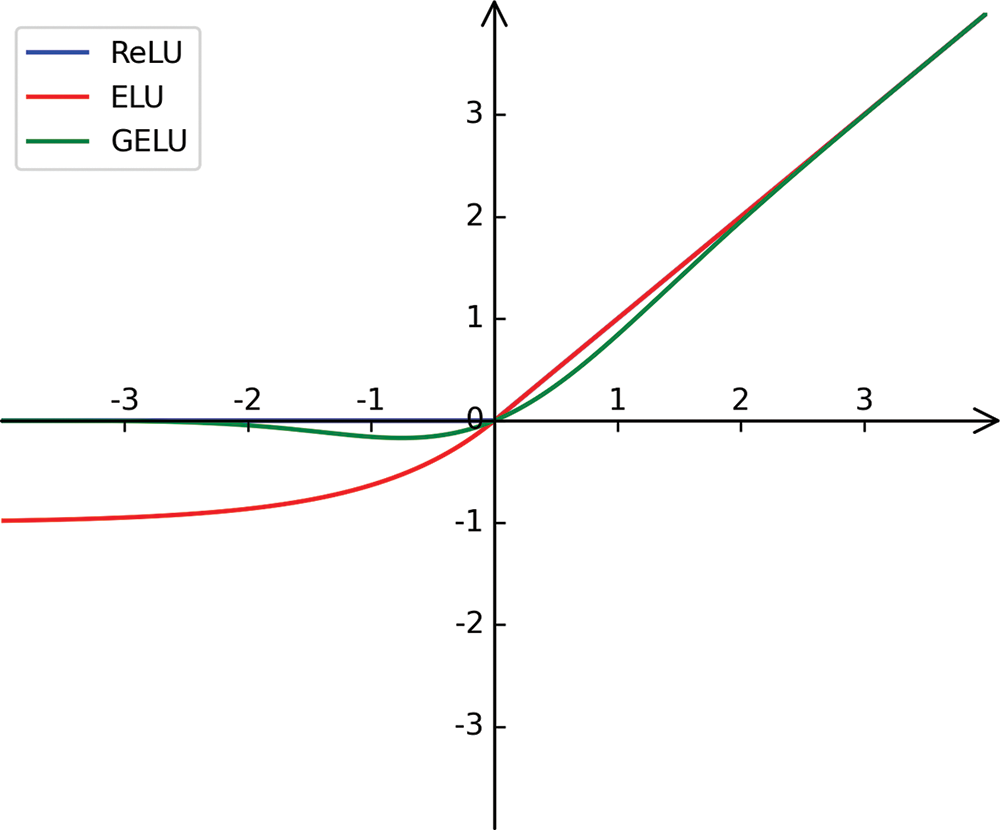
Figure 9: Images of ReLU, ELU, GELU functions
The formula for the ELU (
where the hyperparameter
First of all, this paper hypothesizes that what plays a role in the accuracy improvement is the treatment of the data by GELU when the data is less than 0. Reflected in Fig. 5 is the green curve on the [−2,0] interval. To test this hypothesis, we choose an ELU function with the same function image as ReLU on the positive half-axis. The ELU function is somewhat similar to GELU on the negative half-axis, being also a smooth curve. According to the results in the table, excluding individual actions with a lower accuracy than ReLU and a higher accuracy than GELU, the results obtained by a network using ELU for estimating bone direction fall between the counterparts obtained by networks using the ReLU and GELU functions for the majority of movements. The experimental results based on the comparison between ELU and ReLU illustrate that the retention of negative values in the network for estimating bone direction contributes positively to the final results and can improve the estimation accuracy to some extent; In contrast, the experimental results based on GELU and ELU indicated that for negative values that tend to be close to 0, retention is performed while giving them a relatively small weight, while values far from 0, i.e., outliers, are discarded. It is this mechanism that makes it possible to improve the accuracy of the final pose estimation effectively.
In this paper, the ability of the network to extract inter-frame feature relationships is enhanced by fusing temporal convolutional networks with GELUs. It is experimentally verified that the temporal convolution network proposed in this paper with the fusion of GELUs outperforms the conventional temporal convolution network for the 3D pose estimation task based on videos. The experimental results on Human3.6M showed that, with a comparable number of parameters and computational effort, the average MPJPE obtained by the method used in this paper is reduced by 0.2 mm compared to the method with the lowest error (44.1 mm), specifically for 15 actions we have a reduction of 0.1−1 mm; compared to the method using Transformer, the average MPJPE reduction obtained in this paper is 0.8 mm, with a reduction of 0.2–2.9 mm for the 15 movements. In the future, it is an important subsequent research goal to further exploit the inter-frame feature relationships for achieving more accurate 3D human pose estimation. And we will focus on improving the ability in real-time situations and further exploit the kinematic properties of the human skeleton. In addition, in order to enable the model to cope with more complex scenarios, in future research, we will also invest more energy to conduct experiments on multiple data sets related to personal movement to achieve comprehensive improvement of model performance.
Funding Statement: This work was supported by the Key Project of NSFC (Grant No. U1908214), Special Project of Central Government Guiding Local Science and Technology Development (Grant No. 2021JH6/10500140), the Program for Innovative Research Team in University of Liaoning Province (LT2020015), the Support Plan for Key Field Innovation Team of Dalian (2021RT06), the Support Plan for Leading Innovation Team of Dalian University (XLJ202010); the Science and Technology Innovation Fund of Dalian (Grant No. 2020JJ25CY001), in part by the National Natural Science Foundation of China under Grant 61906032, the Fundamental Research Funds for the Central Universities under Grant DUT21TD107.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Cao, Z., Hidalgo G., Simon T., Wei S., Sheikh Y. (2021). OpenPose: Realtime multi-person 2D pose estimation using part affinity fields. IEEE Transactions on Pattern Analysis and Machine Intelligence, 43(1), 172–186. https://doi.org/10.1109/TPAMI.2019.2929257 [Google Scholar] [CrossRef]
2. Chen, Y., Wang, Z., Peng, Y., Zhang, Z., Yu, G. et al. (2018). Cascaded pyramid network for multi-person pose estimation. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 7103–7112. Salt Lake City, UT, USA. https://doi.org/10.1109/CVPR.2018.00742 [Google Scholar] [CrossRef]
3. Muller, L., Osman, A. A., Tang, S., Huang, C. H. P., Black, M. J. (2021). On self-contact and human pose. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 9985–9994. Nashville, TN, USA. https://doi.org/10.1109/CVPR46437.2021.00986 [Google Scholar] [CrossRef]
4. Tran, T. Q., Nguyen, G. V., Kim, D. (2021). Simple multi-resolution representation learning for human pose estimation. 25th International Conference on Pattern Recognition (ICPR), pp. 511–518. Milan, Italy. https://doi.org/10.1109/ICPR48806.2021.9412729 [Google Scholar] [CrossRef]
5. Wei, S., Ramakrishna, V., Kanade, T., Sheikh, Y. (2016). Convolutional pose machines. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 4724–4732. Las Vegas, NV, USA. https://doi.org/10.1109/CVPR.2016.511 [Google Scholar] [CrossRef]
6. Nakazawa, A., Shiratori, T. (2018). Input device—motion capture. In: The wiley handbook of human computer interaction, vol. 1, pp. 405–419. https://doi.org/10.1002/9781118976005 [Google Scholar] [CrossRef]
7. Knippenberg, E., Verbrugghe, J., Lamers, I., Palmaers, S., Timmermans, A. et al. (2017). Markerless motion capture systems as training device in neurological rehabilitation: A systematic review of their use, application, target population and efficacy. Neuroengineering and Rehabilitation, 14(1), 1–11. https://doi.org/10.1186/s12984-017-0270-x [Google Scholar] [PubMed] [CrossRef]
8. Kanazawa, A., Black, M. J., Jacobs, D. W., Malik, J. (2018). End-to-end recovery of human shape and pose. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 7122–7131. Salt Lake City, UT, USA. https://doi.org/10.1109/CVPR.2018.00744 [Google Scholar] [CrossRef]
9. Liu, R., Shen, J., Wang, H., Chen, C., Cheung, S. C. et al. (2020). Attention mechanism exploits temporal contexts: Real-time 3D human pose reconstruction. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 5064–5073. Seattle, WA, USA. https://doi.org/10.1109/CVPR42600.2020.00511 [Google Scholar] [CrossRef]
10. Pavllo, D., Feichtenhofer, C., Grangier, D., Auli, M. (2019). 3D human pose estimation in video with temporal convolutions and semi-supervised training. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 7753–7762. Long Beach, CA, USA. https://doi.org/10.1109/CVPR.2019.00794 [Google Scholar] [CrossRef]
11. Tripathi, S., Ranade, S., Tyagi, A., Agrawal, A. (2020). PoseNet3D: Learning temporally consistent 3D human pose via knowledge distillation. International Conference on 3D Vision (3DV), pp. 311–321. Fukuoka, Japan. https://doi.org/10.1109/3DV50981.2020.00041 [Google Scholar] [CrossRef]
12. Xu, J., Yu, Z., Ni, B., Yang, J., Yang, X. et al. (2020). Deep kinematics analysis for monocular 3D human pose estimation. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 899–908. Seattle, WA, USA. https://doi.org/10.1109/CVPR42600.2020.00098 [Google Scholar] [CrossRef]
13. Lee, K., Lee, I., Lee, S. (2018). Propagating LSTM: 3D pose estimation based on joint interdependency. Proceedings of the European Conference on Computer Vision (ECCV), pp. 119–135. Munich, Germany. https://doi.org/10.1007/978-3-030-01234-2_8 [Google Scholar] [CrossRef]
14. Wandt, B., Rudolph, M., Zell, P., Rhodin, H., Rosenhahn, B. (2021). Canonpose: Self-supervised monocular 3D human pose estimation in the wild. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 13294–13304. Nashville, TN, USA. https://doi.org/10.1109/CVPR46437.2021.01309 [Google Scholar] [CrossRef]
15. Martinez, J., Hossain, R., Romero, J., Little, J. J. (2017). A simple yet effective baseline for 3D human pose estimation. IEEE International Conference on Computer Vision (ICCV), pp. 2640–2649. Venice, Italy. https://doi.org/10.1109/ICCV.2017.288 [Google Scholar] [CrossRef]
16. Sun, X., Shang, J., Liang, S., Wei, Y. (2017). Compositional human pose regression. International Conference on Computer Vision (ICCV), pp. 2602–2611. Venice, Italy. https://doi.org/10.1109/ICCV.2017.284 [Google Scholar] [CrossRef]
17. Kang, J., Liu, R., Li, Y. J., Liu, Q., Wang, P. F. et al. (2022). An improved 3D human pose estimation model based on temporal convolution with gaussian error linear units. 8th International Conference on Virtual Reality (ICVR), pp. 21–32. Nanjing, China. https://doi.org/10.1109/ICVR55215.2022.9848068 [Google Scholar] [CrossRef]
18. Habibie, I., Xu, W., Mehta, D., Pons-Moll, G., Theobalt, C. (2019). In the wild human pose estimation using explicit 2D features and intermediate 3D representations. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 10905–10914. Long Beach, CA, USA. https://doi.org/10.1109/CVPR.2019.01116 [Google Scholar] [CrossRef]
19. Li, S., Chan, A. B. (2014). 3D human pose estimation from monocular images with deep convolutional neural network. Asian Conference on Computer Vision (ACCV), pp. 332–347. Singapore. https://doi.org/10.1007/978-3-319-16808-1_23 [Google Scholar] [CrossRef]
20. Li, S., Zhang, W., Chan, A. B. (2015). Maximum-margin structured learning with deep networks for 3D human pose estimation. International Conference on Computer Vision (ICCV), pp. 2848–2856. Santiago, Chile. https://doi.org/10.1109/ICCV.2015.326 [Google Scholar] [CrossRef]
21. Pavlakos, G., Zhou, X., Derpanis, K. G., Daniilidis, K. (2017). Coarse-to-fine volumetric prediction for single-image 3D human pose. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 7025–7034. Honolulu, HI, USA. https://doi.org/10.1109/CVPR.2017.139 [Google Scholar] [CrossRef]
22. Pavlakos, G., Zhu, L., Zhou, X., Daniilidis, K. (2018). Learning to estimate 3D human pose and shape from a single color image. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 459–468. Salt Lake City, UT, USA. https://doi.org/10.1109/CVPR.2018.00055 [Google Scholar] [CrossRef]
23. Tekin, B., Katircioglu, I., Salzmann, M., Lepetit, V., Fua, P. (2016). Structured prediction of 3D human pose with deep neural networks. British Machine Vision Conference, pp. 130.131–130.111. York, UK. https://doi.org/10.5244/C.30.130 [Google Scholar] [CrossRef]
24. Tu, H., Wang, C., Zeng, W. (2020). Voxelpose: Towards multi-camera 3D human pose estimation in wild environment. European Conference on Computer Vision (ECCV), pp. 197–212. https://doi.org/10.1007/978-3-030-58452-8_12 [Google Scholar] [CrossRef]
25. Katircioglu, I., Tekin, B., Salzmann, M., Lepetit, V., Fua, P. (2018). Learning latent representations of 3D human pose with deep neural networks. International Journal of Computer Vision, 126(12), 1326–1341. https://doi.org/10.1007/s11263-018-1066-6 [Google Scholar] [CrossRef]
26. Kocabas, M., Athanasiou, N., Black, M. J. (2020). VIBE: Video inference for human body pose and shape estimation. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 5253–5263. Seattle, WA, USA. https://doi.org/10.1109/CVPR42600.2020.00530 [Google Scholar] [CrossRef]
27. Li, Z., Wang, X., Wang, F., Jiang, P. (2019). On boosting single-frame 3D human pose estimation via monocular videos. IEEE/CVF International Conference on Computer Vision (ICCV), pp. 2192–2201. Seoul, Korea (South). https://doi.org/10.1109/ICCV.2019.00228 [Google Scholar] [CrossRef]
28. Chen, C., Ramanan, D. (2017). 3D human pose estimation = 2D pose estimation+ matching. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 7035–7043. Honolulu, HI, USA. https://doi.org/10.1109/CVPR.2017.610 [Google Scholar] [CrossRef]
29. Gong, K., Zhang, J., Feng, J. (2021). PoseAug: A differentiable pose augmentation framework for 3D human pose estimation. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 8575–8584. Nashville, TN, USA. https://doi.org/10.1109/CVPR46437.2021.00847 [Google Scholar] [CrossRef]
30. Qammaz, A., Argyros, A. A. (2019). MocapNET: Ensemble of SNN encoders for 3D human pose estimation in RGB images. British Machine Vision Conference (BMVC), pp. 143.1–143.17. Cardiff, UK. https://doi.org/10.5244/C.33.143 [Google Scholar] [CrossRef]
31. Wang, K., Lin, L., Jiang, C., Qian, C., Wei, P. (2019). 3D human pose machines with self-supervised learning. Transactions on Pattern Analysis & Machine Intelligence, 42(5), 1069–1082. https://doi.org/10.1109/TPAMI.2019.2892452 [Google Scholar] [PubMed] [CrossRef]
32. Xu, T., Takano, W. (2021). Graph stacked hourglass networks for 3D human pose estimation. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 16105–16114. Nashville, TN, USA. https://doi.org/10.1109/CVPR46437.2021.01584 [Google Scholar] [CrossRef]
33. Zeng, A., Sun, X., Huang, F., Liu, M., Xu, Q. et al. (2020). SRNet: Improving generalization in 3D human pose estimation with a split-and-recombine approach. European Conference on Computer Vision, pp. 507–523. https://doi.org/10.1007/978-3-030-58568-6_30 [Google Scholar] [CrossRef]
34. Ci, H., Wang, C., Ma, X., Wang, Y. (2019). Optimizing network structure for 3D human pose estimation. IEEE/CVF International Conference on Computer Vision (ICCV), pp. 2262–2271. Seoul, Korea (South). https://doi.org/10.1109/ICCV.2019.00235 [Google Scholar] [CrossRef]
35. Liu, K., Zou, Z., Tang, W. (2020). Learning global pose features in graph convolutional networks for 3D human pose estimation. Asian Conference on Computer Vision (ACCV), pp. 89–105, Kyoto Japan. https://doi.org/10.1007/978-3-030-69525-5_6 [Google Scholar] [CrossRef]
36. Zhao, L., Peng, X., Tian, Y., Kapadia, M., Metaxas, D. N. (2019). Semantic graph convolutional networks for 3D human pose regression. IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), pp. 3425–3435. Long Beach, CA, USA. https://doi.org/10.1109/CVPR.2019.00354 [Google Scholar] [CrossRef]
37. Cai, Y., Ge, L., Liu, J., Cai, J., Cham, T. J. et al. (2019). Exploiting spatial-temporal relationships for 3D pose estimation via graph convolutional networks. IEEE/CVF International Conference on Computer Vision (ICCV), pp. 2272–2281. Seoul, Korea (South). https://doi.org/10.1109/ICCV.2019.00236 [Google Scholar] [CrossRef]
38. Hossain, M. R. I., Little, J. J. (2018). Exploiting temporal information for 3D human pose estimation. European Conference on Computer Vision (ECCV), pp. 69–86. Munich, Germany. https://doi.org/10.1007/978-3-030-01249-6_5 [Google Scholar] [CrossRef]
39. Meredith, M., Maddock, S. (2001). Motion capture file formats explained. UK: University of Sheffield. [Google Scholar]
40. Mehta, D., Sridhar, S., Sotnychenko, O., Rhodin, H., Theobalt, C. (2017). VNect: Real-time 3D human pose estimation with a single RGB camera. ACM Transactions on Graphics, 36(4), 1–14. https://doi.org/10.1145/3072959.3073596 [Google Scholar] [CrossRef]
41. Lin, M., Lin, L., Liang, X., Wang, K., Cheng, H. (2017). Recurrent 3D pose sequence machines. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 5543–5552. Honolulu, HI, USA. https://doi.org/10.1109/CVPR.2017.588 [Google Scholar] [CrossRef]
42. Chen, T., Fang, C., Shen, X., Zhu, Y., Chen, Z. et al. (2021). Anatomy-aware 3D human pose estimation with bone-based pose decomposition. Transactions on Circuits & Systems for Video Technology, 32(1), 198–209. https://doi.org/10.1109/TCSVT.2021.3057267 [Google Scholar] [CrossRef]
43. Nair, V., Hinton, G. E. (2010). Rectified linear units improve restricted boltzmann machines. International Conference on Machine Learning, 8, 807–814. [Google Scholar]
44. Devlin, J., Chang, M. W., Lee, K., Toutanova, K. (2019). BERT: Pre-training of deep bidirectional transformers for language understanding. North American Chapter of the Association for Computational Linguistics: Human Language Technologies, 1, 4171–4186. [Google Scholar]
45. Liu, Y., Ott, M., Goyal, N., Du, J., Joshi, M. et al. (2019). RoBERTa: A robustly optimized bert pretraining approach. arXiv preprint arXiv:1907.11692. [Google Scholar]
46. Hendrycks, D., Gimpel, K. (2016). Gaussian error linear units (GELUS). arXiv preprint arXiv: 1606.08415. [Google Scholar]
47. Lin, J., Lee, G. H. (2019). Trajectory space factorization for deep video-based 3D human pose estimation. British Machine Vision Conference (BMVC), pp. 42.1–42.13. Cardiff, UK. https://doi.org/10.5244/C.33.42 [Google Scholar] [CrossRef]
48. Wang, J., Yan, S., Xiong, Y., Lin, D. (2020). Motion guided 3D pose estimation from videos. European Conference on Computer Vision (ECCV), pp. 764–780. Glasgow, UK. https://doi.org/10.1007/978-3-030-58601-0_45 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF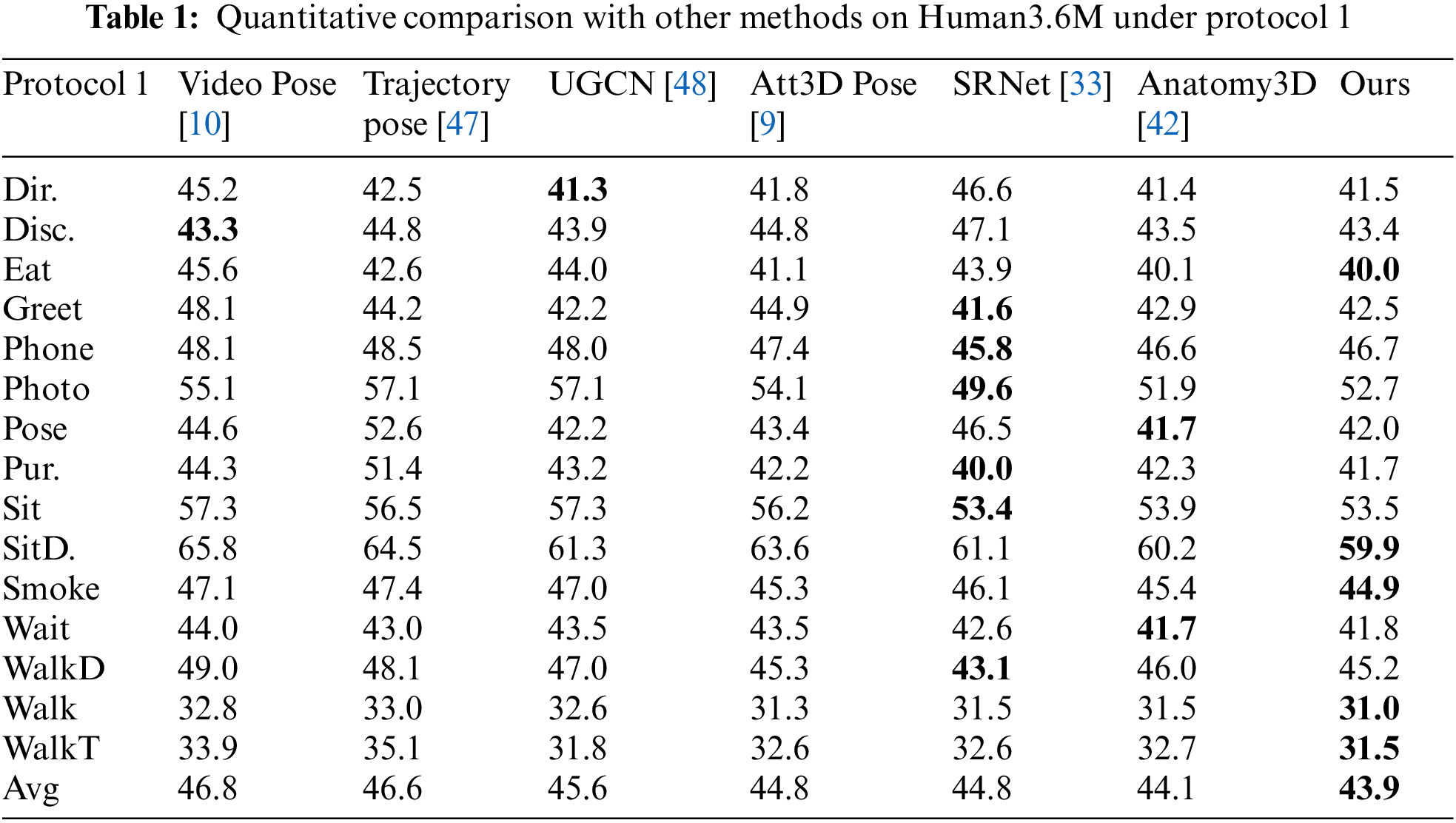
 Downloads
Downloads
 Citation Tools
Citation Tools