A Color Image Encryption Scheme Based on Singular Values and Chaos

1  Introduction

Encryption is the process of transforming information to a random or unintelligible form using a predetermined method or technique, such that only an authorised recipient with a valid secret key can retrieve it. As a result, sensitive data can be retained and transmitted across insecure channels or mediums. Cryptography is another term for the process of encrypting data. While it does provide security for sensitive data, cryptanalysis can be utilized to perform in-depth analysis for data infringement. Data security is essential for a range of applications that operate across unsecured wireless and public networks that are vulnerable to eavesdropping [1,2], hence, it is a critical topic for researchers to address. Cryptography is employed in a variety of fields where data protection is required. Camera security, database security, and internet teleconferencing are a few of these uses [3–5].

The study of cryptography has led to the development of numerous efficient data-protection techniques and algorithms. Because there are many forms of data, each with its unique set of traits and properties, separate cryptographic approaches must be utilised for each type. Modern standard methods such as DES, IDEA, RSA, and AES were intended primarily for text data encryption and decryption and are thus incompatible with multimedia data encryption and decryption [1,6,7].

We avoid utilising typical encryption techniques for image data for two main reasons. For starters, image data is larger than text data and has greater redundancy, necessitating more computational effort. Second, in the case of textual data, the decrypted information must be a precise reconstruction of the original plaintext information, whereas this is not a condition in image data. Because of the nature of human perception, image encryption techniques require a close or near approximation to the plaintext image. The value of close or adjacent pixels in natural photographs can be accurately predicted due to significant correlation and data redundancy.

1.1 Image Cryptography

It is just as important for security reasons to protect visual and image data as it is to protect text data. This is evident in present technology, when multimedia content is often exchanged through the internet, and the bulk of the channels utilised for this purpose are unsecure. Image data, unlike text data, has distinct properties that demand particular treatment. The basics of picture cryptography are the same as those of text data, with the exception that visual data is being processed. The plaintext image is the image that will be encrypted, and the image after encryption is known as ciphertext. An image cryptosystem, like text data, requires the usage of a secret key. Before digging into any modern-day procedures, some historical backdrop is addressed so that classical image cryptosystem methods can be investigated.

1.1.1 Visual Cryptography

Before the time of digitized information, visual cryptography was widely studied. In visual cryptography, the plaintext image is obtained physically and then split into shares. Each of the produced shares is random. Every share acts as a piece of puzzle, when all joined together correctly, forms the actual image. The shares here are considered as ciphertext images. These shares are then distributed among the intended receptors of information and are combined together whenever plaintext is required. This classical method was widely adopted before the image was treated as digital. One such famous technique was proposed in [8], where n shares of plaintext image are produced. All n shares are physically on transparencies. Out of these n shares, specified k shares are stacked together properly to form an actual image. With k − 1 shares or less, the actual image cannot be obtained.

1.1.2 Image Cryptosystems

Image cryptosystems can be created using the concept of image pixels. One could consider using the textual data cryptosystem for the images, but for various reasons, these methods are inefficient and, in some cases, invalid. One of the primary reasons is the larger size of the image with significant redundancy in comparison to text data. Furthermore, requirements for recovering a plaintext image are sometimes different from textual data. Similarly, compression is often a desirable requirement for image cryptosystem but is rarely required for text data.

The positions of pixels in plaintext images can be changed to form ciphertext images in the same way that letters in text data are reallocated to scramble the information. This process of pixel scrambling is often called permutation and is commonly used in chaos based and some other methods. Another approach is to change the grayscale pixel values using a predefined mechanism to obtain encrypted images. This process is often termed as confusion as it further complicate the relationship of pixels with the original image and is often used in conjunction to permutation process. Fig. 1 provides an example of permutation which is performed by performing the operation on fixed sized image block. This block level permutation instead of pixel level permutation is sometimes a requirement of a particular cryptosystem but here they are opted to demonstrate the process through better visualization. Fig. 2 depicts the confusion process which perform the change in graysclae values of pixels which is often used in conjunction to permutation and is part of all modern image cryptosystems.

Figure 1: A coloured plaintext image encrypted by changing pixel locations

Figure 2: Another chaos based method of changing pixels locations

1.1.3 Performance Analysis of Image Cryptosystem

Confidentiality, integrity, and availability are all desirable characteristics for text data, and they are also essential for any effective image cryptosystem. The statistical analysis is mostly used when analysing the performance of image encryption methods. Correlation coefficient, histogram analysis, key space, key sensitivity analysis, and compression friendliness are some statistical performance parameters and test which are often required to evaluate such a system [7,9]. These tests can be run on only the ciphertext image or both the ciphertext and plaintext images.

1.1.4 Image Cryptanalysis

Cryptanalysis can be performed on image encryption methods in the same way that it can be performed on textual data cryptosystems. Normally, intruders find it difficult to perform cryptanalysis due to the large size of the image. Sniffing ciphertext images can sometimes yield blocks of plaintext image, which can be enough to generate an idea for the entire image. As a result, maximum confusion must be introduced into ciphertext images to avoid such attacks.

1.2 Research Motivation

Using highly insecure public networks to transmit confidential data is risky in today’s information and technology world. When some multimedia data is transmitted over insecure internet or wireless LAN networks and then broadcasted without encryption, an intruder can easily breach security and read confidential video or image data. As a result, stringent security measures must be implemented to eliminate such security threats. Several encryption schemes for image data are proposed in the literature, but none is available as a complete and secure cryptographic solution when compared to other highly secured cryptographic standards for textual data.

The available cryptographic techniques for digital image encryption are all intended for a specific application. Creating an algorithm for standard images is a difficult task. A strong encryption algorithm must meet certain security requirements as well as outperform other popular and well-known encryption schemes in terms of performance.

1.3 Research Contribution

An efficient hybrid encryption approach is proposed in this work which incorporates the use of Singular Value Decomposition (SVD) based process and chaos-based process of image encryption. The proposed scheme is compression friendly and can withstand commonly known attacks to image security. The proposed approach can be distinguished by merging the properties of both type of encryption processes. The most desirable feature of image security, which is high randomness in encrypted image data, is provided by chaos-based method. SVD based process, on the other hand, add an extra layer of security as well as make the storage process more efficient by providing a high compression ratio.

Moreover, an in-depth analysis is performed to test the proposed scheme’s effectiveness. It is demonstrated that the presented approach can deal with noisy channel scenarios while also taking into account other factors, most notably compression. Other tests, such as common attacks, key space analysis, key sensitivity analysis, and other performance metrics, are also performed. For the sake of future research, the results show that different types of compression methods can be used with the same devised method.

1.4 Organization of Paper

The sections of this paper are organized according to the following trend:

Section 1 provides the brief overview, background and need for the data encryption methods. Basic essential elements of encryption algorithms are briefly studied. Image cryptography is analyzed separately with some historical significance. Storing of digital images is also briefly studied along with some overview of modern encryption methods and parameters required to analyze its performance.

Section 2 provides a comprehensive analysis of modern encryption methods proposed in recent time.

In Sections 3 and 4, an in-depth discussion is made on proposed method. First, a brief overview of SVD and chaotic maps is presented. Illustrations in the form of flow chart and images are provided for clarity and understanding. Results are also represented in form of graphs and histograms. Robustness of scheme against some well-known attacks are also studied. The discussion is closed by drawing some brief conclusions.

Section 5 is the last section which proposes the future work that can be done to improve the existing encryption algorithm. Different compression methods, that can be deployed within the proposed encryption method, are devised.

2  Literature Review

Data security is a legitimate right of the sender/owner, as discussed in Section 1. A substantial amount of research has been conducted in the most recent available literature to serve this purpose. The objective of this section is to look into the modern cryptosystem proposed for digital images. As previously stated, AES and other advanced proposed methods for text encryption do not appear to be suitable for image encryption. There are several reasons for this, including the size of image data, computational complexities, and difficulties in using compression methods [10]. Image cryptosystems can be classified into three main categories, based on the approaches used [10,11]: (i) transposition based encryption methods, (ii) value transformation based algorithms and (iii) hybrid cryptosystems. Different types of approaches are followed to create a strong image cryptosystem. The content of this section is separated into the following subsections: Sections 2.1 and 2.2 provide the basics for the transposition and value transformation based methods along with the survey of some most recent available literature. In Section 2.3, chaos based image cryptosystems are studied with a brief overview of the latest articles.

2.1 Permutation-Only Algorithms

Image encryption relied on transposition schemes before fast computers. These algorithms altered the positions of image pixels but not their values. A key-generated [10] reference matrix is used to permute pixel locations. These straightforward methods provide quick processing, low computational complexity, and simple decryption [11].

2.1.1 Disadvantages of Permutation-Only Methods

Transposition methods are no longer secure because exhaustive iterative searches can be performed, especially when the image size is small, and the plaintext image or key can be recovered. According to a recent study [10], permutation-only methods are vulnerable. In [10], it cracks a recently proposed permutation-only algorithm in [12], demonstrating that transposition-only methods are vulnerable to modern cryptanalysis. Transposition-only techniques are less resistant to known plaintext attacks, and the plaintext image is generated entirely from the ciphertext image [10].

In conclusion, permutation-only methods are insufficient for image data confidentiality, necessitating the use of other methods. Using multiple level permutations can accomplish this, but it is insufficient for a robust encryption method. To address these issues, value transformation is employed, as discussed in Section 2.2.

2.2 Diffusion Based Image Cryptosystems

To address the shortcomings of permutation-only methods, modern image cryptosystems employ value transformation techniques. Changing the value of a pixel alters its visual and statistical properties which is also known as diffusion. Strong cryptosystems are the result of such techniques. Recent literature proposes such techniques in [13–19] that use substitution and diffusion methods. Permutation and diffusion steps have been combined in [18]. First, a 16-bit secret key is generated and decimalized. This secret key is used to generate a random matrix and 4×4 subkey blocks. DCT transforms is applied and combines subkey blocks to form a final scrambled block. A 256×256 image is divided into four 4×4 blocks. These blocks are permuted by random matrix substitution. To generate diffusion, this permuted sequence is XORed with scrambled subkey blocks. The ciphertext image is created by combining encrypted blocks. To encrypt the image, this process is repeated 16 times. Using confusion and diffusion in the same encryption method is advantageous, as demonstrated in [18]. As a result of such methods, cryptanalysis is difficult, resulting in a strong encryption method.

Reference [20] proposed a cryptosystem that makes use of true random numbers and chaos theory. A cryptosystem (1-dimensional logistic map) is chosen, and a hash function is used to determine the chaotic system’s initial value using a plaintext image. The original image is then scrambled by utilising k-medoids clustering and a chaotic sequence to solve this chaotic system. Finally, a sequence of new random numbers is generated and used for diffusion via the XOR operation. The resulting system is shown to be simpler than AES and other approaches, as well as robust to a variety of classical attacks. Using chaotic maps to generate permuted images only adds to the confusion. Section 2.3 goes into great detail about chaos-based algorithms.

2.3 Chaos Based Image Cryptosystems

The most widely used image encryption method is chaos-based image cryptosystems. There are numerous algorithms based on chaos theory which are proposed in the literature and are widely used. In [21–25], chaos-based image encryption algorithms can be found that are proposed in the literature: In [21], to obtain random values, samples of a W × H array of environmental random noise N are taken. This is a true random number generator, and its values are passed through SHA-256 to generate 256-bit random hashes. These values generate the initial parameters for the Murugan et al. [15] chaotic system, which is proposed as a chaotic attractor in [26]. An input plaintext image of size W × H, the same as the random noise array. The red, green, and blue layers of the plain image are encrypted using Liu’s [21] equations, resulting in the completion of the permutation step. The diffusion process is completed by XORing the three encrypted layers with the three coloured layers of the plaintext image, and the three layers are combined to form the RGB image.

In [25], a new beta-function-based chaotic map system is presented. Beta function is used in many engineering and non-engineering applications. Reference [27] provided a more in-depth discussion of the beta function. Two beta chaotic maps are generated from a 512-bit input. Two random sorting matrices, Q1 and Q2 are used. Q1 shuffles plaintext image columns, while Q2 shuffles rows. The jumbled image is split into four equal blocks before being transformed. When a permuted image is applied to a finite Galois field GF(256), diffusion changes the value of each pixel to complete the encryption process. In [28], a stream cypher based on a hybrid chaotic analog-digital system is proposed. The proposed chaotic map eliminates the possibility of degeneration and ensures synchronisation of the analogue chaotic system for decryption. Furthermore, a modified 3-dimensional logistic map is proposed to improve the uneven distribution, limited parameter space, and low complexity. By combining these modifications, the proposed stream cypher has nearly infinite cycle length, a large key space, and security. As a result, the resulting system is not affected by dynamic degeneration, and its security is demonstrated through a suite of security analyses. Alawida et al. [29] proposed augmenting logistic tent map chaotic features by integrating it with a deterministic finite state machine. The resulting system is known as TM-DFSM, and it has been demonstrated to outperform competing 1-dimensional cryptosystems in terms of non-linearity, key space, and sensitivity to initial conditions. To generate a secure and stable encrypted image, this chaos-based cryptosystem performs both image pixel confusion and diffusion.

2.3.1 Other Advance Cryptosystem Based on Chaos Theory

The list of cryptosystems based on chaos theory includes [1,30–37]. Vast usage of this method in recently proposed literature, as discussed in Section 2.3, indicates that this method is still effective in modern encryption techniques. Other recent research articles, such as in [22,38,39], also utilizes this approach.

Using Colpitts and Duffing oscillators, [22] proposed a new chaotic approach. The paper claims that chaos mixing, in which two generated chaotic maps are mixed for faster results, has a large key size and reduces encryption time. The image is scrambled and secured using the two chaotic maps. For testing the robustness of the scheme, test attacks such as the chosen plaintext attack (CPA) and the chosen ciphertext attack (CCA) are used. Reference [38] is another efficient method for encrypting multiple plaintext images at the same time. The steps of confusion and diffusion are both involved. Plaintext images are first segmented, and all input images are then combined in the encryption process. Reference [39] introduced a new chaotic map system. This new chaotic map produces the S-BOX, which is then used to generate random sequences for image scrambling. Because the XOR operation is used, both the permutation and diffusion stages are implemented.

2.3.2 Image Cryptosystems with Compression

Some image encryption methods are proposed in [12,40,41], where encryption is performed in conjunction with compression to provide data security along with bandwidth efficiency.

In [41], the owner of the plaintext information encrypts the image by permuting the pixels using random number generator. The encrypted image is then transmitted with provided auxiliary information (AI) so that the channel provider can compress data and it can also be retrieved using this information. In [12], authors have suggested an intelligent compression method on encrypted image by using prediction error domain through which both lossy and lossless compression can be achieved.

Similarly, the compressive sensing sampling method is a novel method of sampling signals in such a way that the least number of original signal samples are required for reconstruction. This sampling method also makes use of the Nyquist theorem, which states that a large number of samples are required to reconstruct the original signal. The original signal is regarded as sparse in this approach, and it is mathematically regarded as a sparse matrix with a small number of non-zero entries. These entries represent the bare minimum of samples needed to reconstruct the original signal. This entire theory is also known as sparse signal reconstruction. Reference [42,43] provided a detailed discussion on basics of compresive sensing to perform image encryption.

In [44], combining two chaotic maps, namely the logistic chaotic map and the skew tent map, compresive sensing is used to generate the sensing matrix. These maps guarantee the generation of a random sensing matrix. Moreover, the initial conditions of the selected chaotic map span a vast key space. In this method, the same chaotic maps with a different initial condition or key are used to generate random sequence, followed by an XOR operation with the scrambled ciphertext image to achieve diffusion. A statistical analysis is conducted, and it is determined that the scheme is resistant to attacks and space-efficient.Additional recent articles on compressive sensing-based image cryptosystems research include [45–47].

Similarly, Maqbool et al. [6] have presented an approach which perform simultaneous encryption and compression. The process of simultaneous encryption and compression is achieved by modyfing the JPEG compression algorithm in quantitization step and introducing the SVD method for difusion. Moreover, the permutation is achieved by block level shuffling to ensure the 8×8 block size for JPEG compression. The scheme is termed as SecureJPEG and an extension to their work is proposed to improve the cryptographic security by [1]. They have introduced chaos-based encryption using Bernaulli shift map to improve the security characteristics.

3  Proposed Algorithm

Various image encryption terminologies and existing work are discussed in the prior sections in [1,4,6,48]. In addition, the majority of image encryption types and attacks are also briefly described. A thorough review of the literature is provided, covering the majority of the notable papers published in the last few years. Special emphasis is placed on image encryption schemes that use hybrid approaches, which provide additional benefits to image cryptosystem security such as compression friendliness, channel noise tolerance, and, to some extent, lossy compression tolerance. These characteristics are highlighted because we have presented a novel hybrid approach capable of achieving these benefits. Because of bandwidth constraints or high traffic loads, digital images must be compressed before communication in some cases. Furthermore, in some scenarios, channel noise cannot be avoided, so the cryptosystem should be tolerant towards channel noise so that the data can be viewed with satisfactory performance.

The design of our cryptosystem is inspired from an image cryptosystem presented in [4]. They have used singular value decomposition to decompose a randomly generated matrix into its constituent matrices. Two of these matrices are orthonormal (U and VT) and one is a diagonal matrix of singular values, as described in Eq. (1).

SVD(A)=U∑VT(1)

The diffusion process is achieved by matrix multiplication of permuted image and orthonormal matrix U. This multiplication provides good diffusion but generates an image which has a correlation in its pixels in the horizontal direction. If some rounds of matrix multiplication and image permutation are performed the image gets good mixing of pixels and grayscale values. Another advantage of the use of orthonormal matrices is that taking the inverse of this matrix doesna^t require extensive computation and the transpose of the orthonormal matrix serves as its inverse as described in Eq. (2).

Inv(U)=U−1=UT(2)

The cryptosystem proposed in [4] has a design flaw that makes it unsuitable for use as a general-purpose cryptosystem. The algorithm was designed to generate a random matrix with a long period using Mersenne Twister, but it is not cryptographically secure. As a result of using such an insecure random number generator, the algorithm’s operation is insecure. We replaced the random number generator with a chaotic map generated from four different chaotic systems to obtain a secure chaotic map. Their individual orbits are examined, and a careful combination based on the most recent chaotic system literature is created. As a result, the new system had the same noise and compression tolerance properties as the original systems and used a secure approach to orthonormal matrix formation.

Moreover, the system proposed by [4] used varying block sizes for different image sizes. The reason for this was weak algorithmic approach used to calculate the inverse permutation vector from the original permutation vector. In their approach the operation used two nested loops to check the correct inverse of each pixel position leading to O(N2) speed which resulted in a slowdown for an image of larger size and they used blocks of 32 × 32 pixels for an image of 1024 × 1024 dimension to make the algorithm work in a reasonable time. On the other hand, we have used vectorization to perform the same step which reduced the computation time to O(log N) and reduced the computational time drastically. In our approach we could use the pixel level permutation as well as block permutation to achieve the scrambling. However, as we intended to make the algorithm compression friendly so we decided to use a block size of 8×8 similar to JPEG and experimentation demonstrated that this approach result in better compression characteristics as opposed to pixel level permutation.

Another flaw discovered during testing was the system’s inability to encrypt a pure black image because matrix multiplication produces a zero product, resulting in a black image. We introduced diffusion into the system with an XOR operation in the first iteration, and subsequent operations will result in an avalanche change in the final cypher image. The sections that follow describe the steps involved in chaos-based random number generation, encryption, and decryption algorithms.

3.1 Encryption Process

There are two major stages in the encryption algorithm proposed in this paper. The chaotic map parameters are initialised in the first phase using a secret key and the size of the input image (the initial conditions). The generated chaotic maps are combined using a bitwise XOR operation to produce a hybrid chaotic orbit. The XOR configuration of chaotic maps is depicted in Fig. 3 whereas stepwise flow of hybrid chaotic map generation is depicted in Fig. 4. The first step is to generate four chaotic maps by using a secret key to set their initial conditions. In the second step, the logistic and quadratic maps are bitwise XORed to generate a new chaotic map, and the Tent map is bitwise XORed with the quadratic map to generate a new chaotic map. Finally, these two newly constructed chaotic maps are XORed to create a hybrid chaotic map made up of four different chaotic maps. During testing, it was discovered that a slight correlation exists when the initial conditions in the first few hundred chaotic orbits are changed very slightly. As a result, first 3000 chaotic orbits are discarded to generate the final chaotic map, ensuring that no chaotic maps with slightly different secret keys are similar. The correlation plot for the final hybrid chaotic map is shown in Fig. 5.

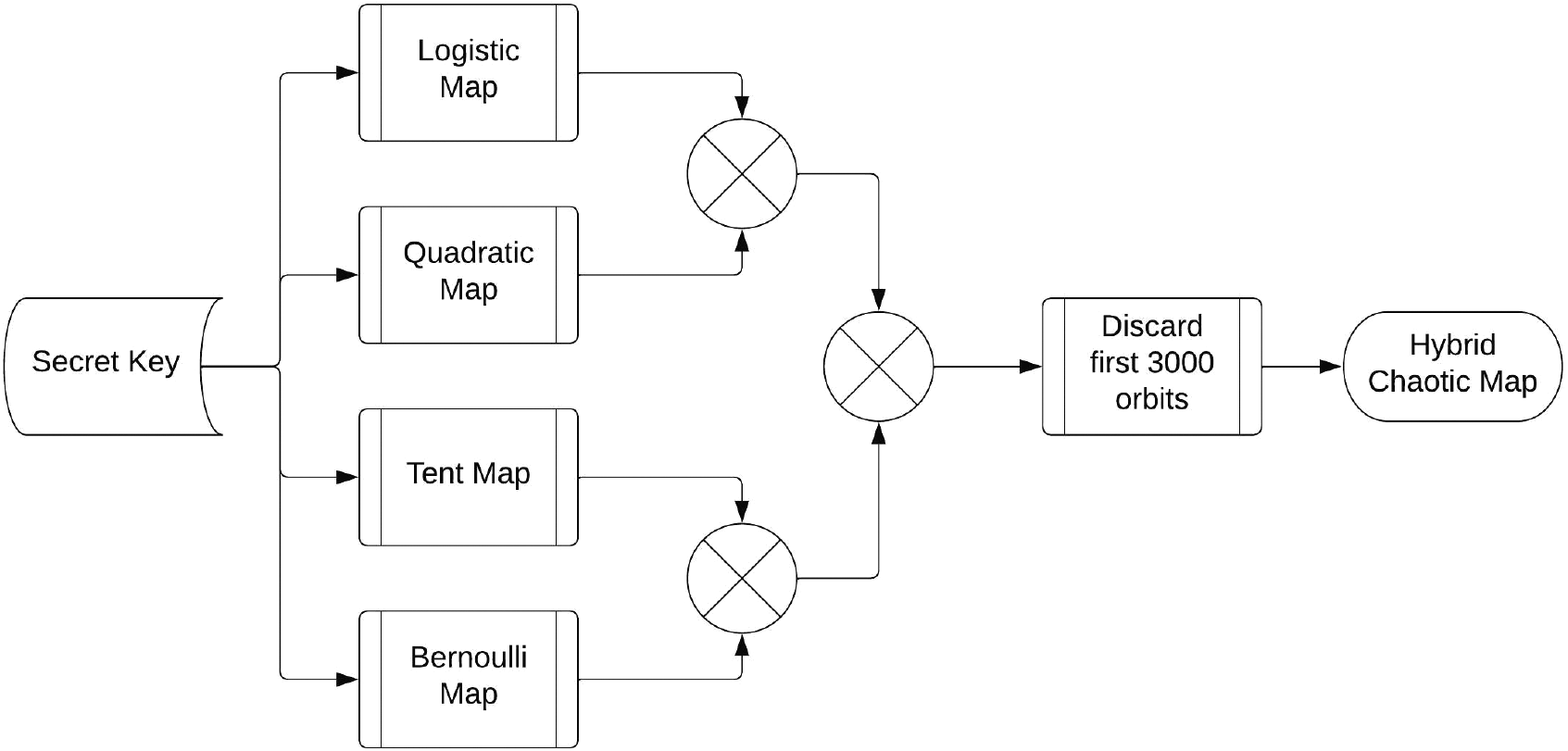
Figure 3: Hybrid chaotic map generation

Figure 4: Steps followed to perform generation of hybrid chaotic map

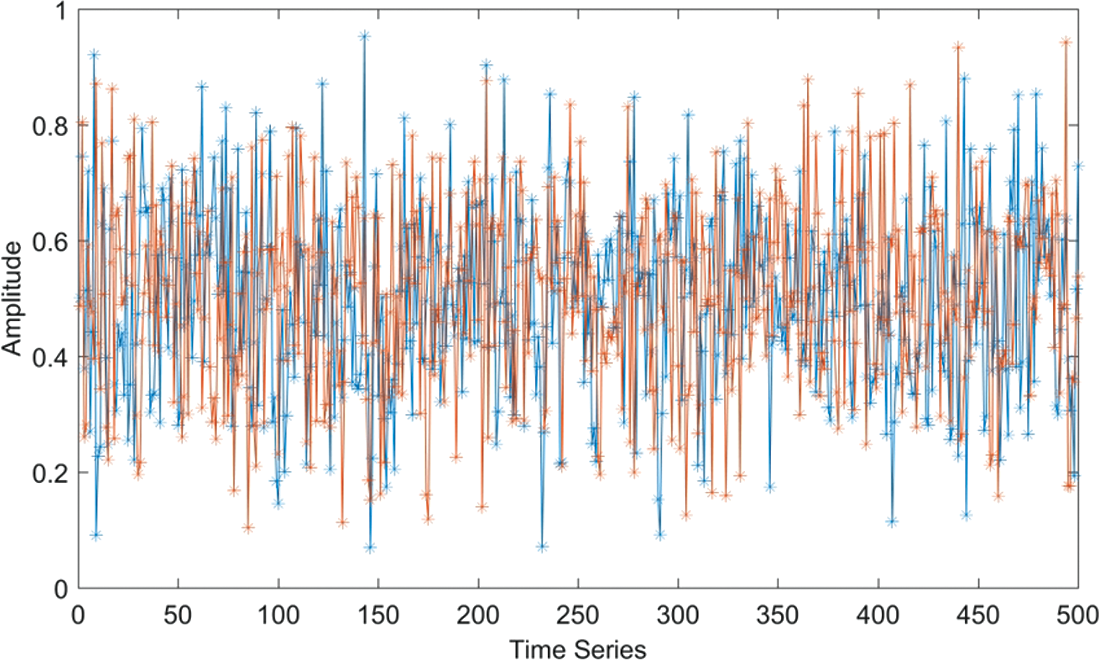
Figure 5: Plot of two different chaotic maps with an initial key difference of 10–12

This randomly generated chaotic map is used as a new random sequence in subsequent encryption stages. Fig. 6 depicts the flow chart of encryption stages used in the proposed approach whereas Fig. 7 provides steps followed in performing encryption. The randomly generated chaotic maps are used in two places in our proposed approach. Initially, this chaotic map is used to generate permutation sequences by sorting the randomly generated numbers and saving their indexes, which are then treated as permutation sequences. This permutation sequence is used to permute the image pixels. In the second step, the randomly generated chaotic map is reshaped to image dimensions, and the Singular Value Decomposition (SVD) of this map is calculated. SVD returns three matrices, as described in Eq. (1). One of these matrices (Left Singular Matrix) is multiplied by the Discrete Cosine Transform (DCT) of the permuted image (right singular matrix will result in horizontally correlated cypher image). This encryption process is repeated several times, and the user can adjust the number of repetitions to obtain a higher level of encryption granularity. Four encryption iterations seemed sufficient in our experimental testing, and additional iterations did not result in a reasonable gain in image security. After four rounds of encryption, the final encrypted matrix is backward DCT transformed. This backward transformed matrix’s pixel values exceed the range of 8-bit image pixels. The cypher matrix is scaled in the range of 0−255 unsigned 8-bit integers to form the cypher image. Because they are required during the decryption process, the maximum and minimum pixel values before scaling are also stored and transmitted with the cypher image.

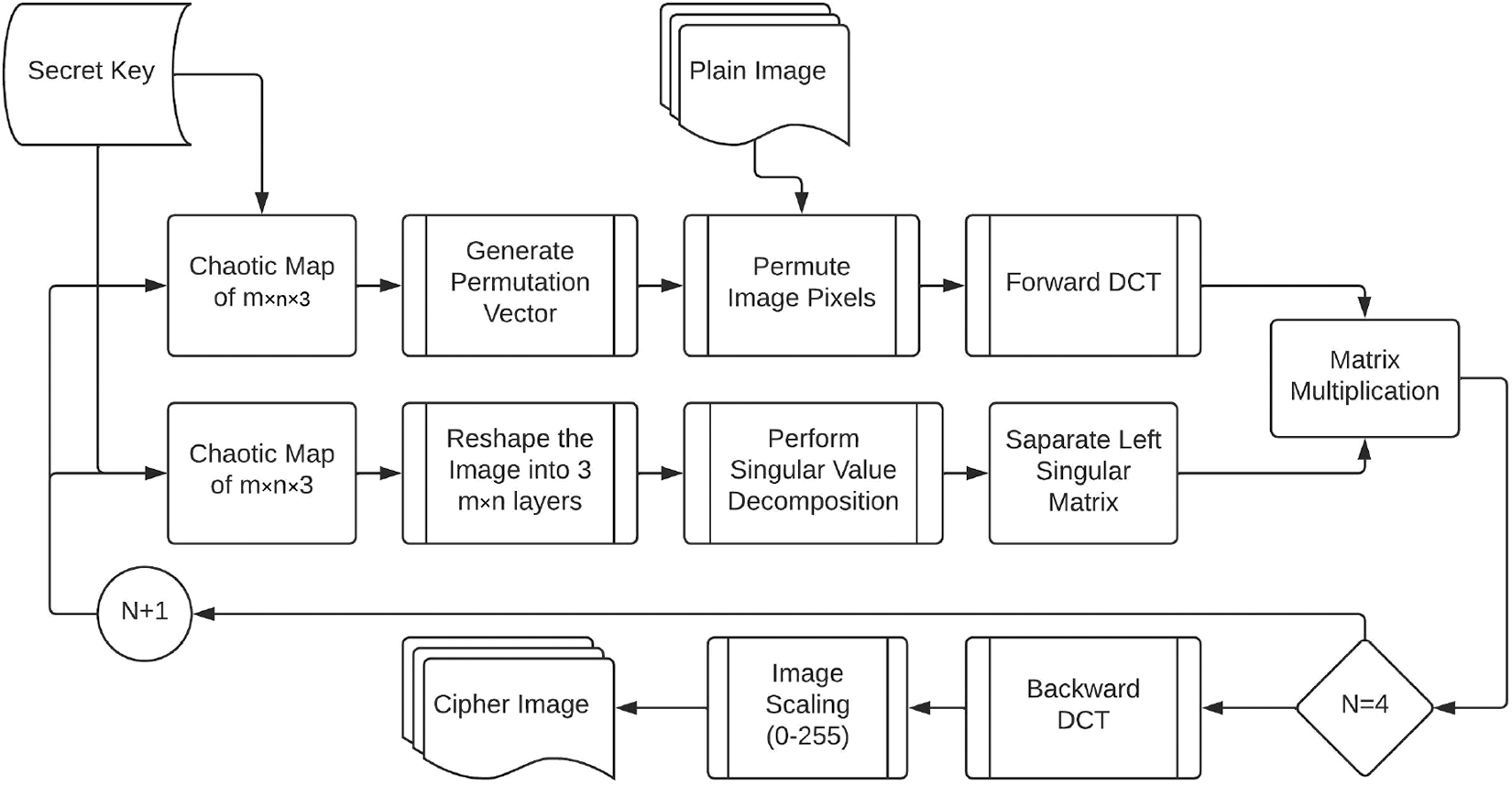
Figure 6: Flow chart of encryption algorithm

Figure 7: Stepwise flow of encryption process

3.2 Decryption Process

The decryption algorithm works similarly to the encryption algorithm, but the steps are reversed. The flowchart of encryption is provided in Fig. 8 and the steps followed in decryption process are provided in Fig. 9. The image is descaled and DCT transformed forward using the original scaling parameters saved during encryption. The secret key is used to generate chaotic maps of image dimension. The first chaotic map is reshaped to image dimension before being decomposed using SVD. The left singular matrix is taken and transposed to create the inverse of this matrix. This inverse matrix is multiplied by the DCT transformed image. The second chaotic map, like the encryption algorithm, is used to compute the permutation sequence. This permutation sequence is used to calculate the inverse permutation sequence via vectorization. It is worth mentioning that the inverse permutation sequence in the original approach [4] was calculated using nested for loop which iterate over all the entries during each pass to calculate the inverse sequence. It lead to higher computational complexity O(N2) which is reduced to O(loga^! N) in our case. It was the reason why the original approach takes more and more time during decryption as image size increases, whereas in our scenario it remains unnoticeably the same. With the inverse permutation sequence, the multiplied image is depermuted. To obtain the cypher image, the entire decryption process is repeated four times (or the number of times specified by the user). The final image is then DCT transformed backwards and scaled to image dimensions ranging from 0–255.

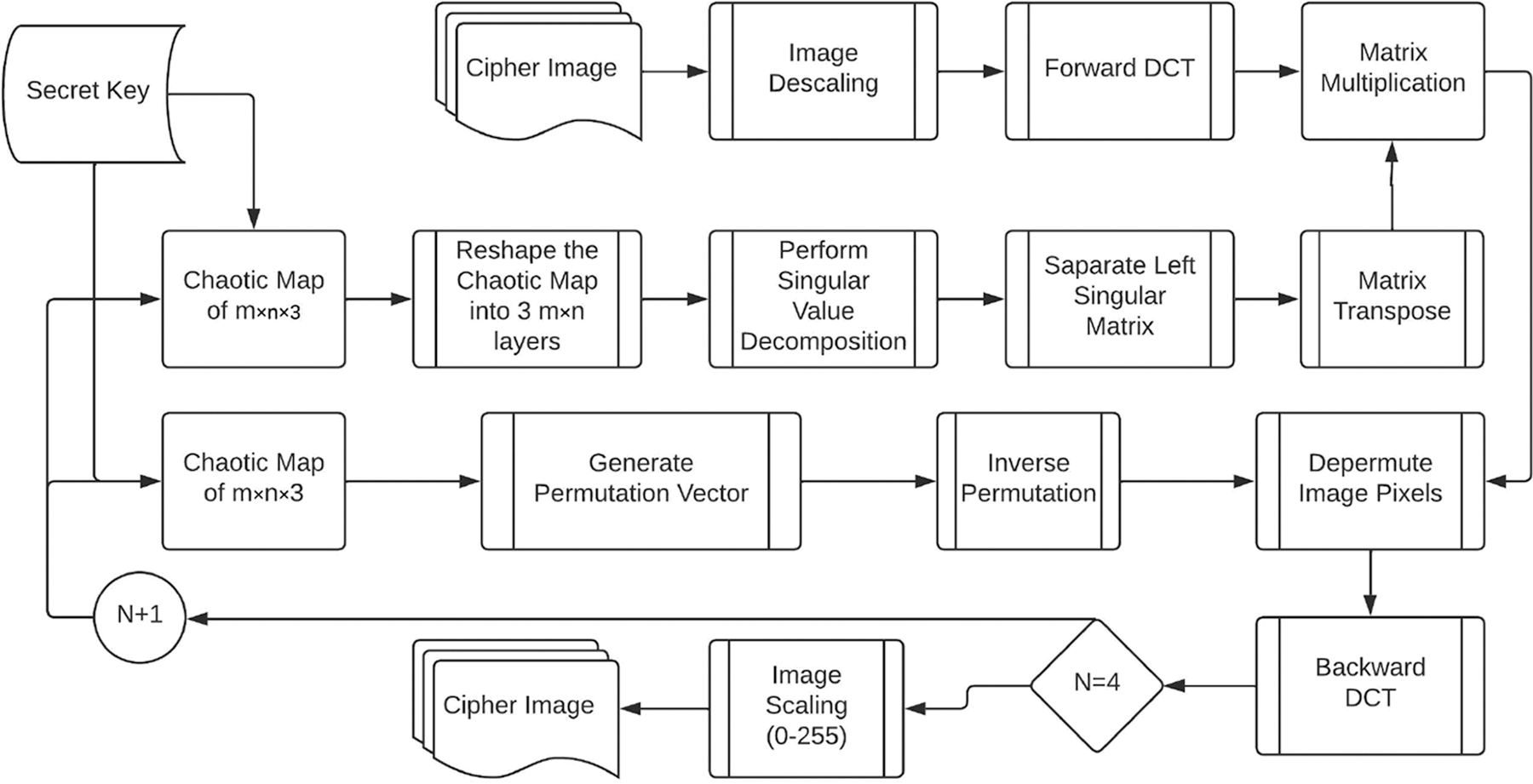
Figure 8: Flow chart of decryption algorithm

Figure 9: Steps for decryption process

3.3 Experimental Results

This section provides the chaotic map and the encryption and decryption results of a number of images to demonstrate the visual security and randomness of decrypted image as well as the decrypted image. Fig. 10 provides the representation of a chaotic map in image form with a pixel dimension of 512 × 512.

Figure 10: Chaotic map of 512×512 pixel

The chaotic map is completely random with very little correlation and high entropy. Similar maps are used for permutation and diffusion. Further tests to verify cryptographic security are provided in the next section. Figs. 11–13 provide the (a) original plaintext image, (b) permuted image produced using chaotic map, (c) encrypted image produced using the proposed encryption scheme and (d) decrypted image.

Figure 11: Encryption results for Lena image

Figure 12: Encryption results for Kodim8 image

Figure 13: Encryption results for Archer image

It should be noted that the decrypted image is not an exact replica of the input plaintext image, but rather a reconstruction that is very close to the original image. Because of contrast stretching and transformation, the corresponding pixel values in both of these images differ slightly. Although both images can be visually inspected to show no difference, image similarity tests such as PSNR and SSIM are used to demonstrate the closeness of two images that can be accepted for visual inspection.

3.4 Secret Key Generation

The initial conditions for the chaotic maps that are provided serve as the basis for the generation of the secret key for the proposed encryption method. Because four different chaotic maps are used, and each individual map necessitates a different set of initial values, the key space is extremely large. In view of the fact that the same key is used at both the encryption and decryption ends, the scheme can be classified as a symmetric key encryption algorithm. Keyspace analysis is discussed in greater depth in Section 4. Specifically, it discusses security and statistical analysis in order to assess the proposed method.

4  Security and Analysis

4.1 Overview

The goal of image encryption is to make the image visually random so that an intruder or any unauthorised person cannot extract any type of information from it. If the cypher images are completely random and unperceivable, visual inspection of digital images can serve the purpose. Furthermore, the encryption process must be repeated on several images to determine whether the scheme is equally effective across all image modalities. Visual inspection is insufficient to check or guarantee the security of an image encryption scheme due to various types of cryptographic attacks that can exploit the encrypted data to deduce the cypher key or extract the original image from the cypher image. As a result, a strong encryption scheme must pass a series of tests that validate its resistance to specific types of attacks. Passing any or all of the cryptographic attacks, however, cannot guarantee the absolute security of an encryption scheme, as new attacks against cryptographic algorithms are being investigated. Passing these cryptographic attacks, on the other hand, will ensure the best possible security measures. Correlation coefficient analysis is the first of these cryptographic security evaluation techniques, as it checks the value of correlation between any pair of adjacent pixels. Information entropy analysis, which is closely related to the visual correlation of image pixels, measures similar characteristics in a different way.

4.2 Correlation Coefficient Analysis

Correlation is a measure of similarity between two different variables. Therefore, it can be used to measure the similarity between two adjacent pixels of an encrypted image to ensure spatial variability. All natural images contain huge correlation in their adjacent pixels as there are very few sharp edges. The value of a pixel is very close to its adjacent pixel value for most of the pixels. Therefore, it can act as an important metric to evaluate the spatial randomness of pixel values. An image cryptosystem is considered effective if it eliminates the spatial correlation or minimize it.

A natural image usually has a correlation nearly one whereas a highly uncorrelated image may have a spatial correlation near zero. Pixel correlation of a digital image can be measured in a pair of horizontally, vertically and diagonally adjacent pixels. The equations for the correlation coefficient analysis and their description can be found in [49]. Tables 1 and 2 below provide the values of correlation coefficient for 20 plain and cipher images respectively. It is evident from Tables 1 and 2 that correlation coefficient have low score (i.e., close to zero) for cipher images in horizontal and diagonal directions. Whereas the pixels in vertical direction are correlated. Whereas for plain images, the pixels are correlated in diagonal, horizontal and vertical directions. The reason for higher correlation in all the directions for natural images is clear from the phenomenon that most of the natural images have high correlations and the pixel values are nearby their neighbors. The proposed system satisfies this security parameter that the cipher image should have low correlation in all direction approaching to zero except for vertical direction. Initially this thing seems to pose a threat to the robustness of system but this correlation is intentionally added to the system so that significant amount of compression can be achieved at later stages in case the image is required to be compressed due to bandwidth limitation. However, this correlation is not due to properties of the image and no information of the image is leaked but it is due to the multiplication of orthonormal vectors. Histogram test will also indicate that the cipher image histogram is independent from the plaintext image which is indicative that information of plaintext image is not disclosed in cipher image.

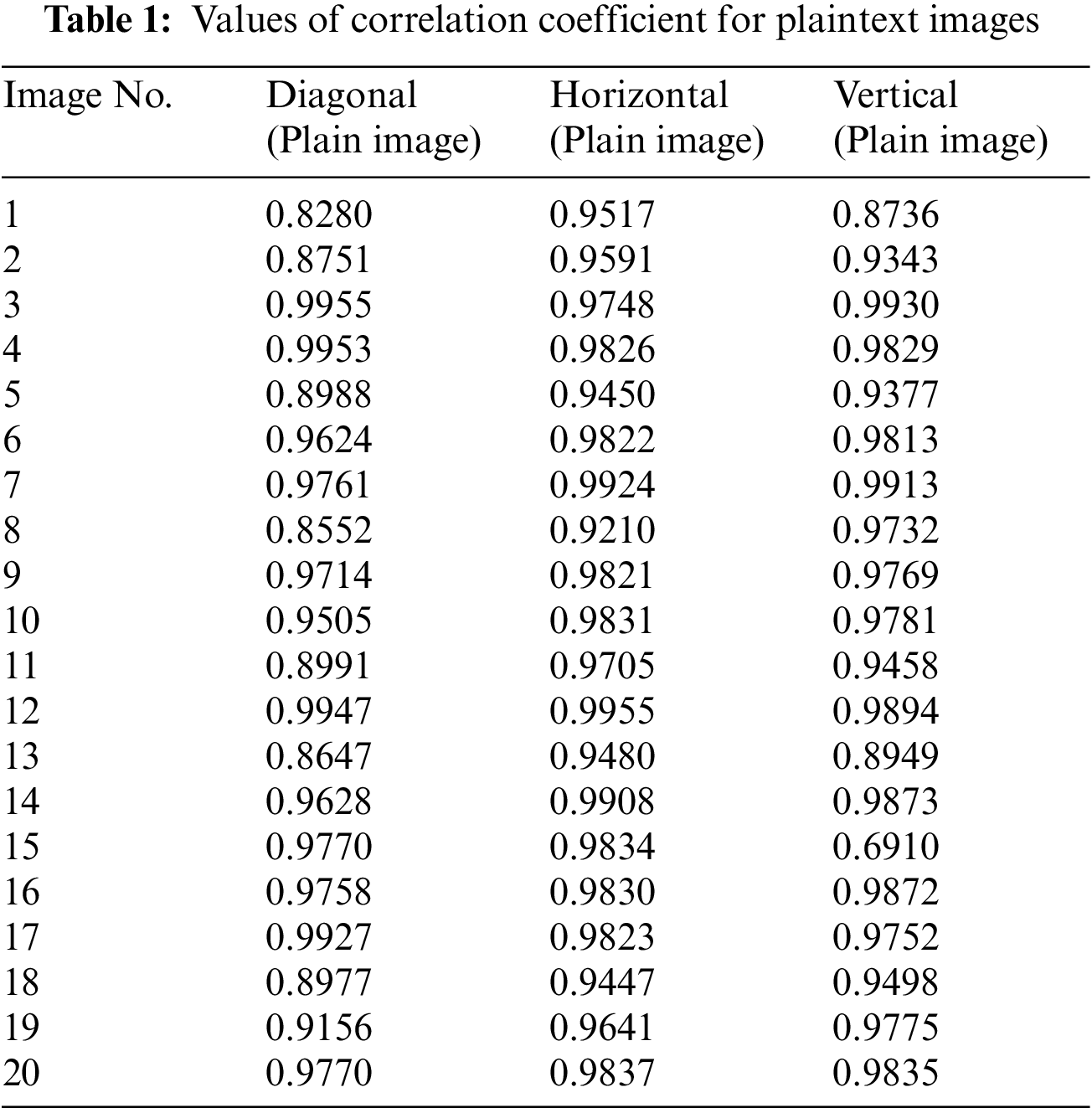
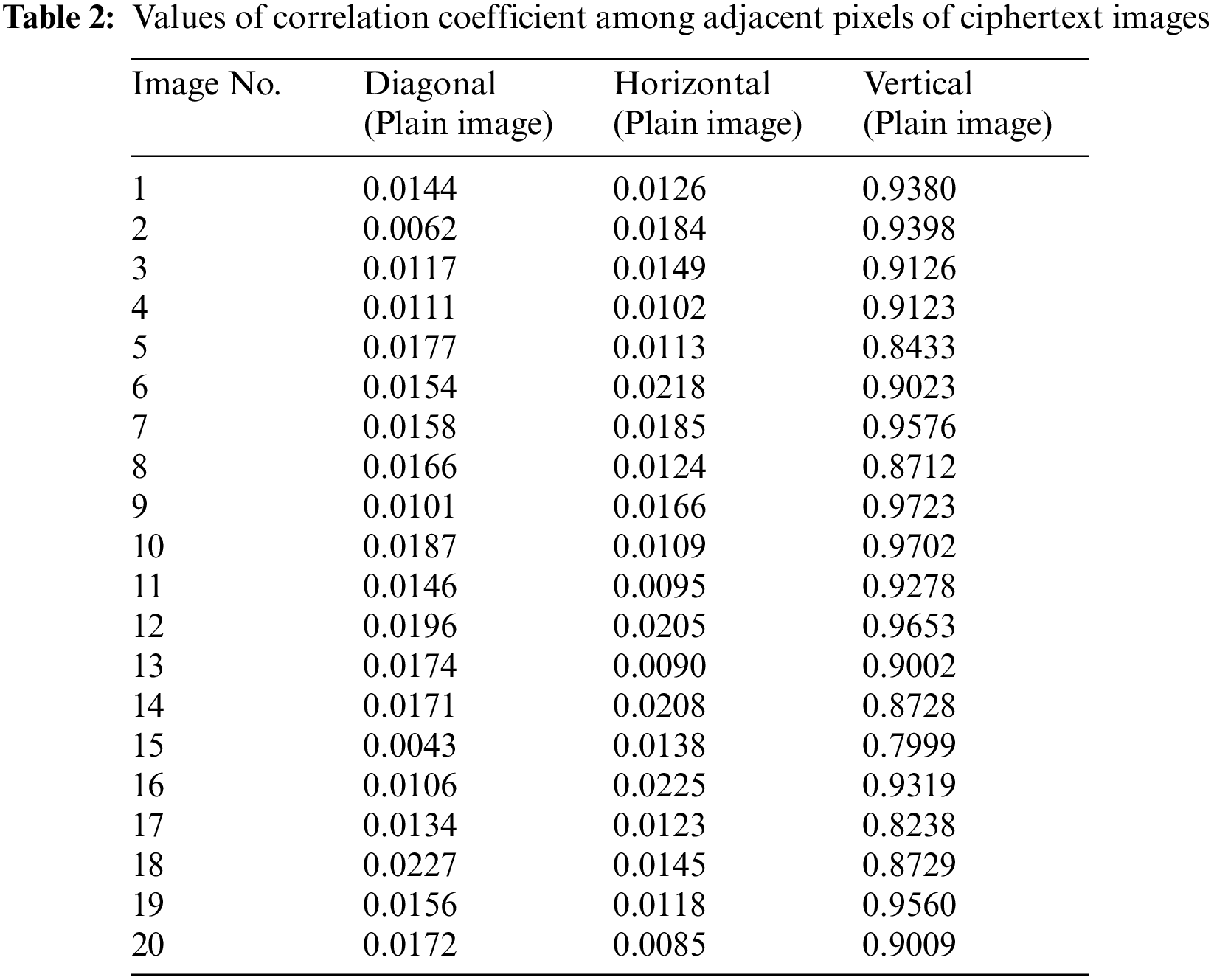
Figs. 14 and 15 show scatter plot of 10,000 randomly selected pixels of cipher image in diagonal and horizontal direction which shows haphazard distribution without any specific correlation. Fig. 16 shows a plot of image pixels of cipher image in vertical direction which shows correlation as the pixels are scattered around linear axes.

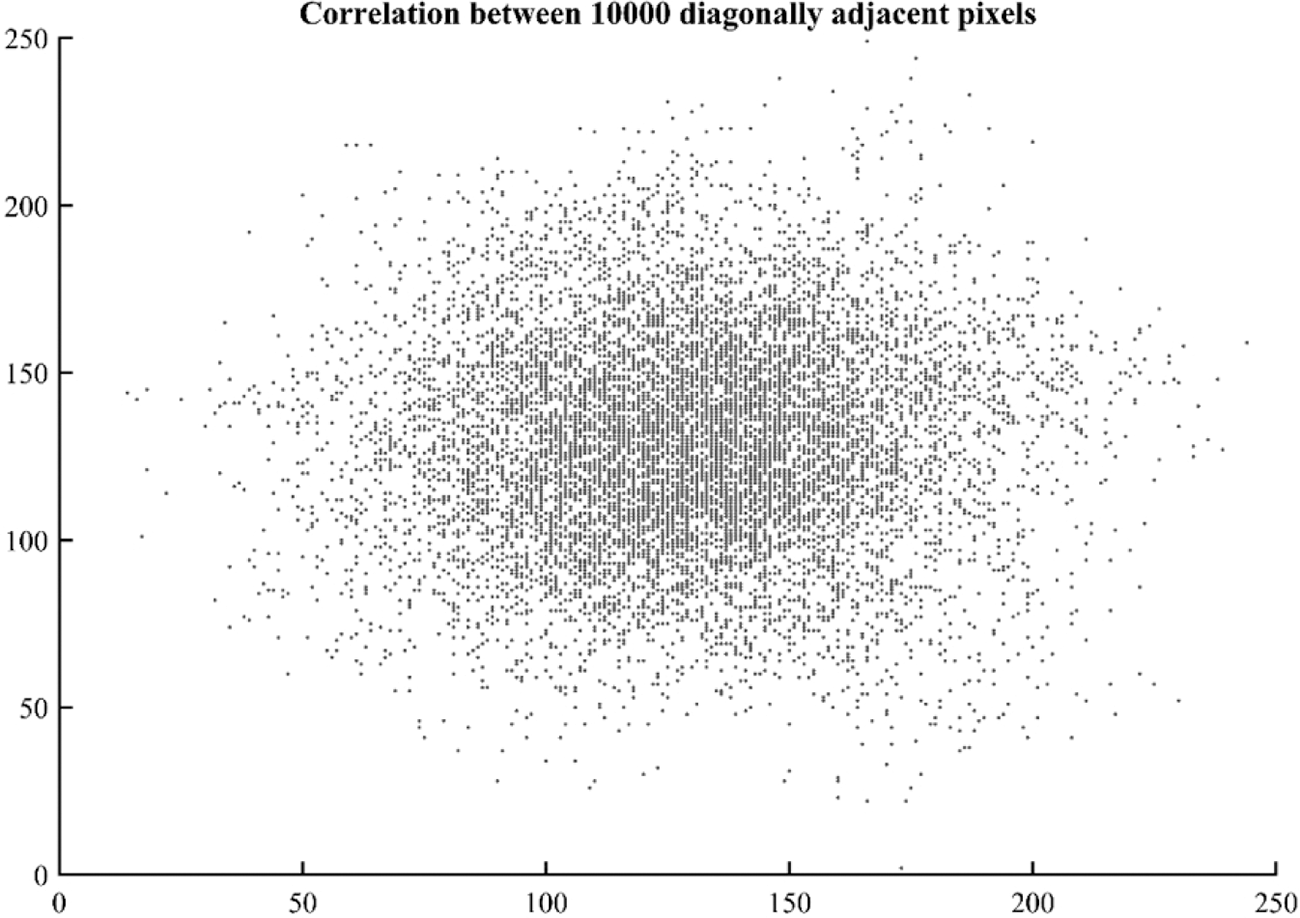
Figure 14: Scatter plot of correlation among 10,000 random diagonally adjacent pixels

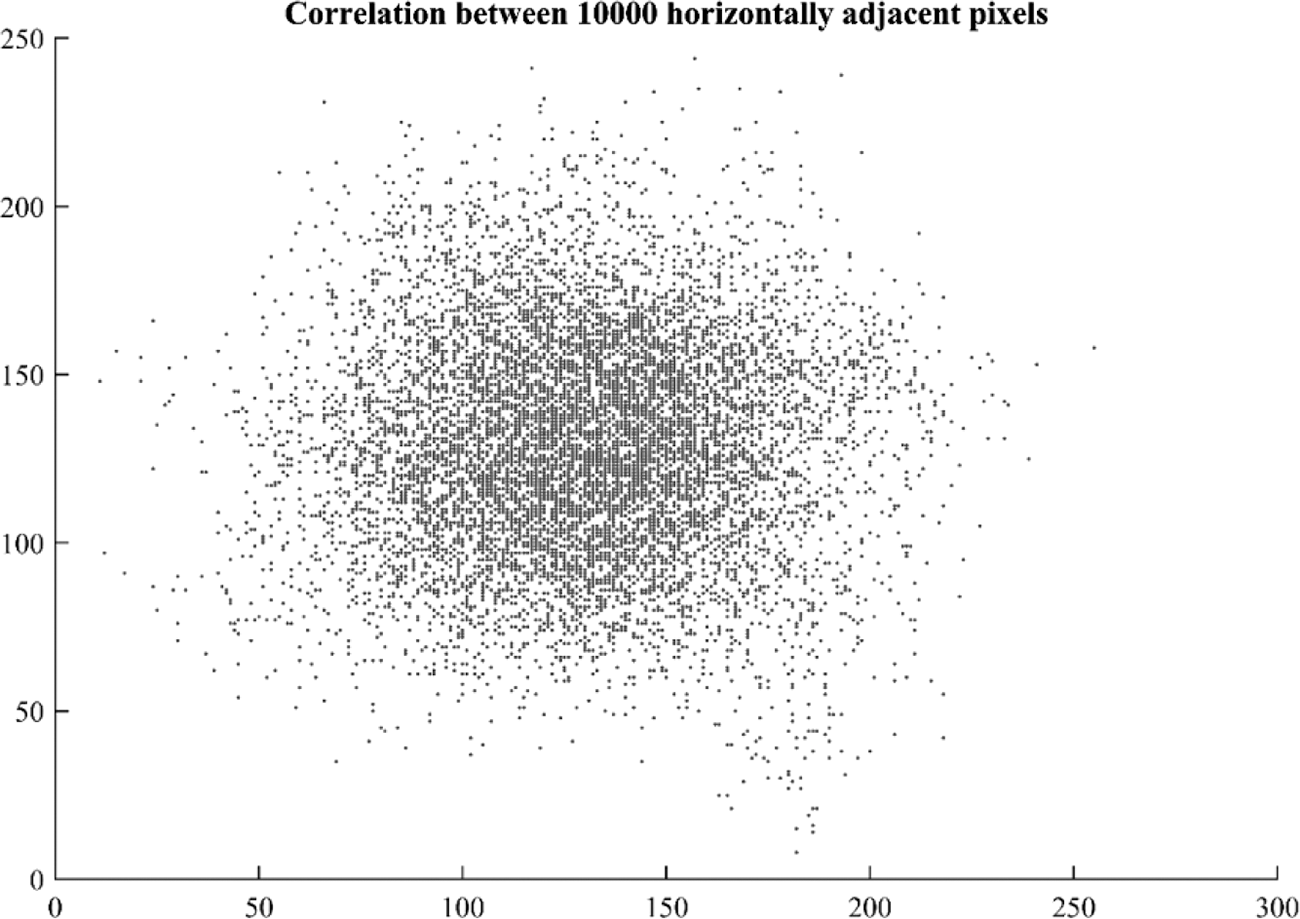
Figure 15: Scatter plot of correlation among 10,000 random horizontally adjacent pixels

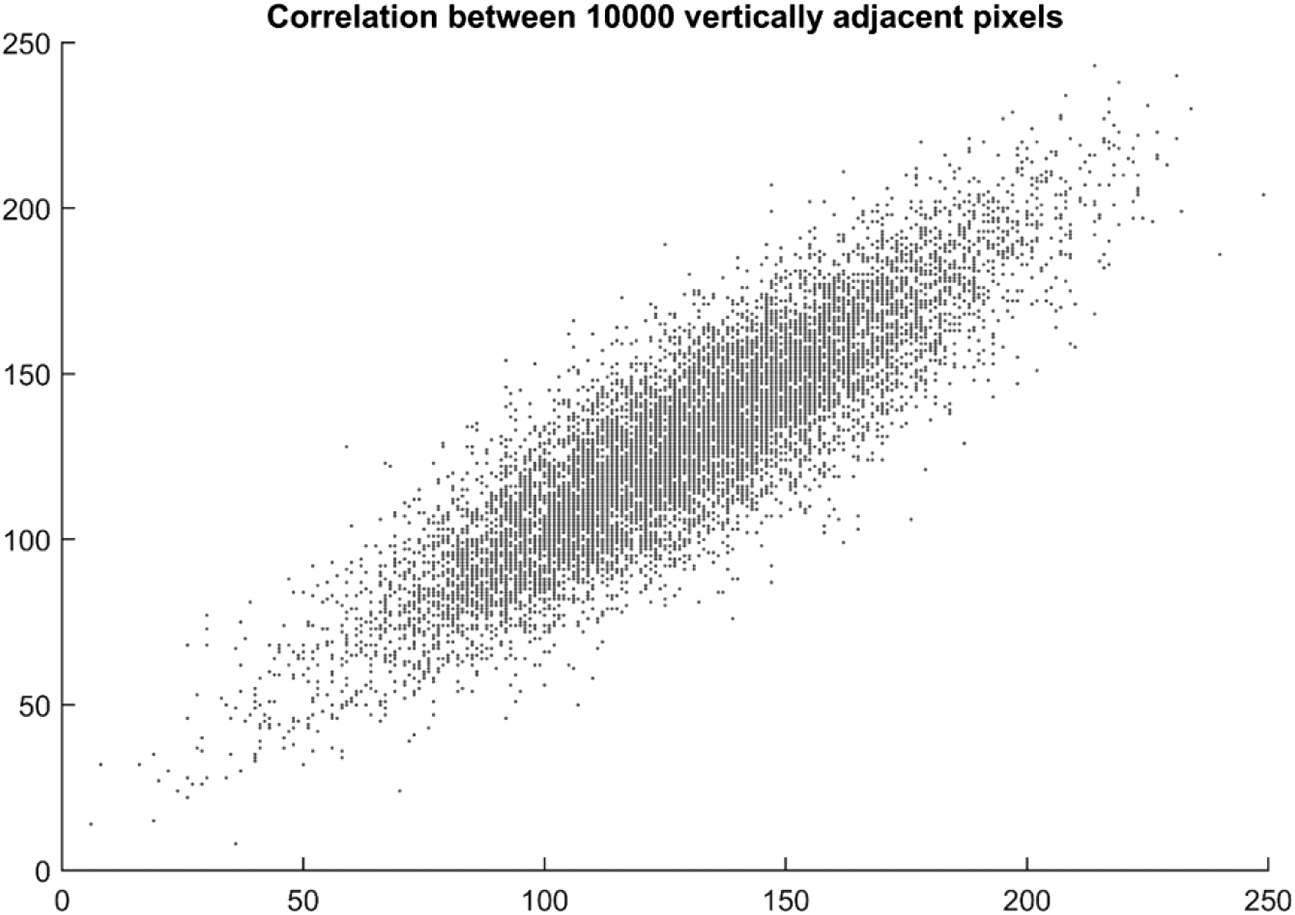
Figure 16: Scatter plot of correlation among 10,000 random vertically adjacent pixels

Pixel correlation plotted in the graphs of Figs. 14–16 are for grayscale image as the cipher image is transformed to grayscale before calculating correlation coefficient and pixel scattering.

The algorithm is designed for color images as well so color cloud is plotted in Fig. 17 which displays random scattering of colors in the space. Moreover, Fig. 18 demonstrates the image gradient indicating random pixel values of cipher image which is also a good measure of random pixel values. It is therefore concluded that the proposed scheme satisfies the requirements of low correlation except in vertically adjacent pixels which can also be witnessed from the cipher image but this correlation provides us the ability to achieve higher compression which is demonstrated in Section 4.8.

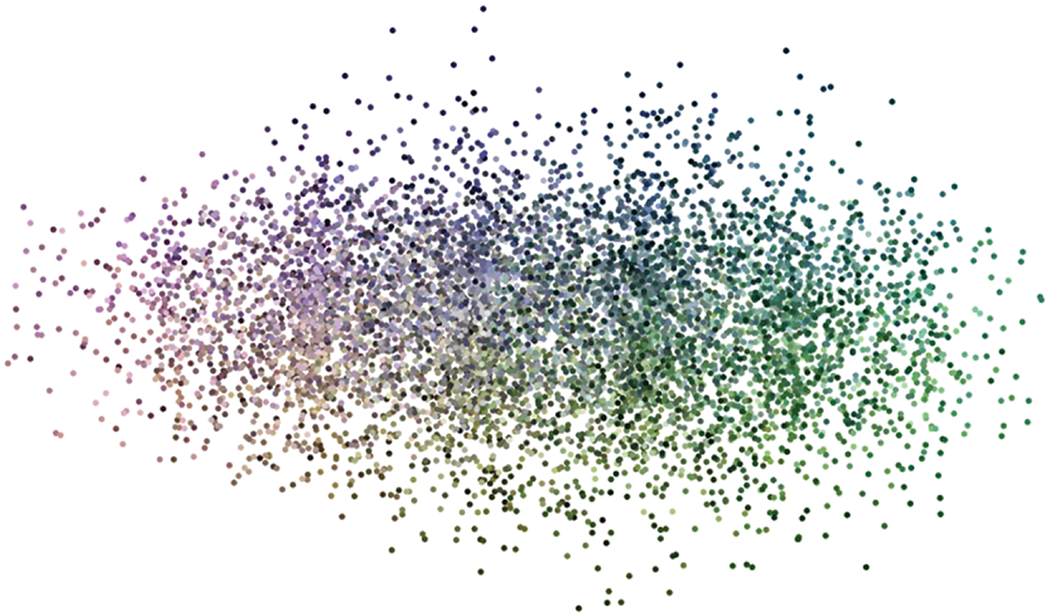
Figure 17: Color cloud of the cipher image showing random distribution of color pixels in the image

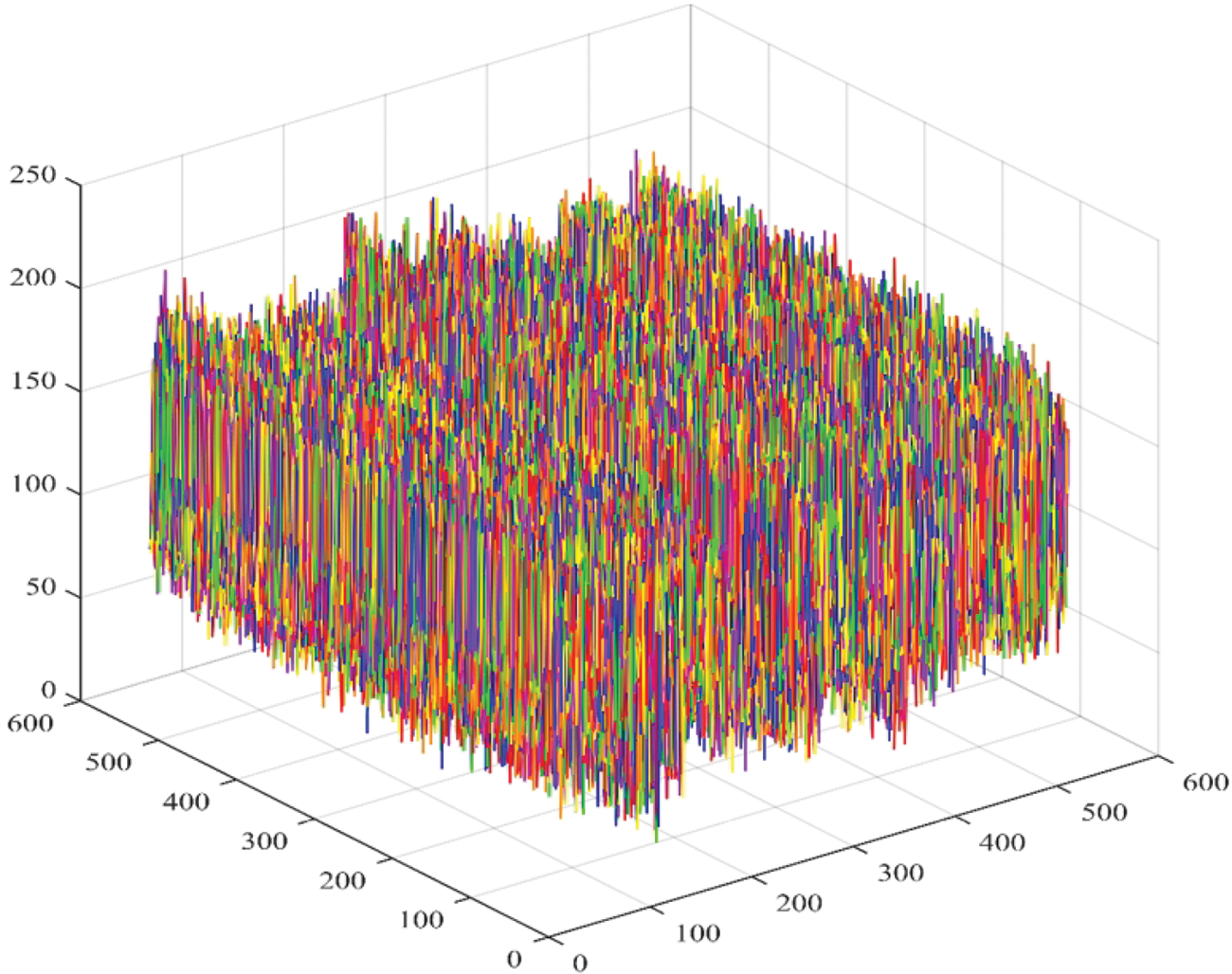
Figure 18: Gradient for image 32 showing randomly distributed pixel values

4.3 Information Entropy Analysis

Information entropy is a mathematical parameter of information and coding theory which measures the statistical randomness of a source. This analysis is carried out to assess the statistical security of an image encryption system. In a natural image, value of a pixel can be reasonably guessed from its neighboring pixels. If it is also true for a cipher image, it cannot be regarded as a secure cipher. Information entropy analysis provides information about the source itself and it is a necessary test to measure the uncertainty and randomness in an image cryptosystem.

The mathematical formulation for this test can be found in [49]. Table 3 and Fig. 19 provide the values of information entropy for cipher images generated from 20 and 36 test images, respectively. It is evident that most of cipher images have high information entropy nearly 7 bits per pixel. It is sometimes desired to plot a histogram of local entropies which is indicative of distribution of information entropy in different spatial regions of the image. The test is demonstrated in [49] and can be used to evaluate the systems which provide good average entropy whereas the local entropies for some regions of the image are very low. For this purpose, the same test is performed on number of test images and the results are shown in Fig. 20. The results of histogram of entropies shows good distribution of entropy values. None of the values are occurring in too low entropy region and most of them are above value of six.

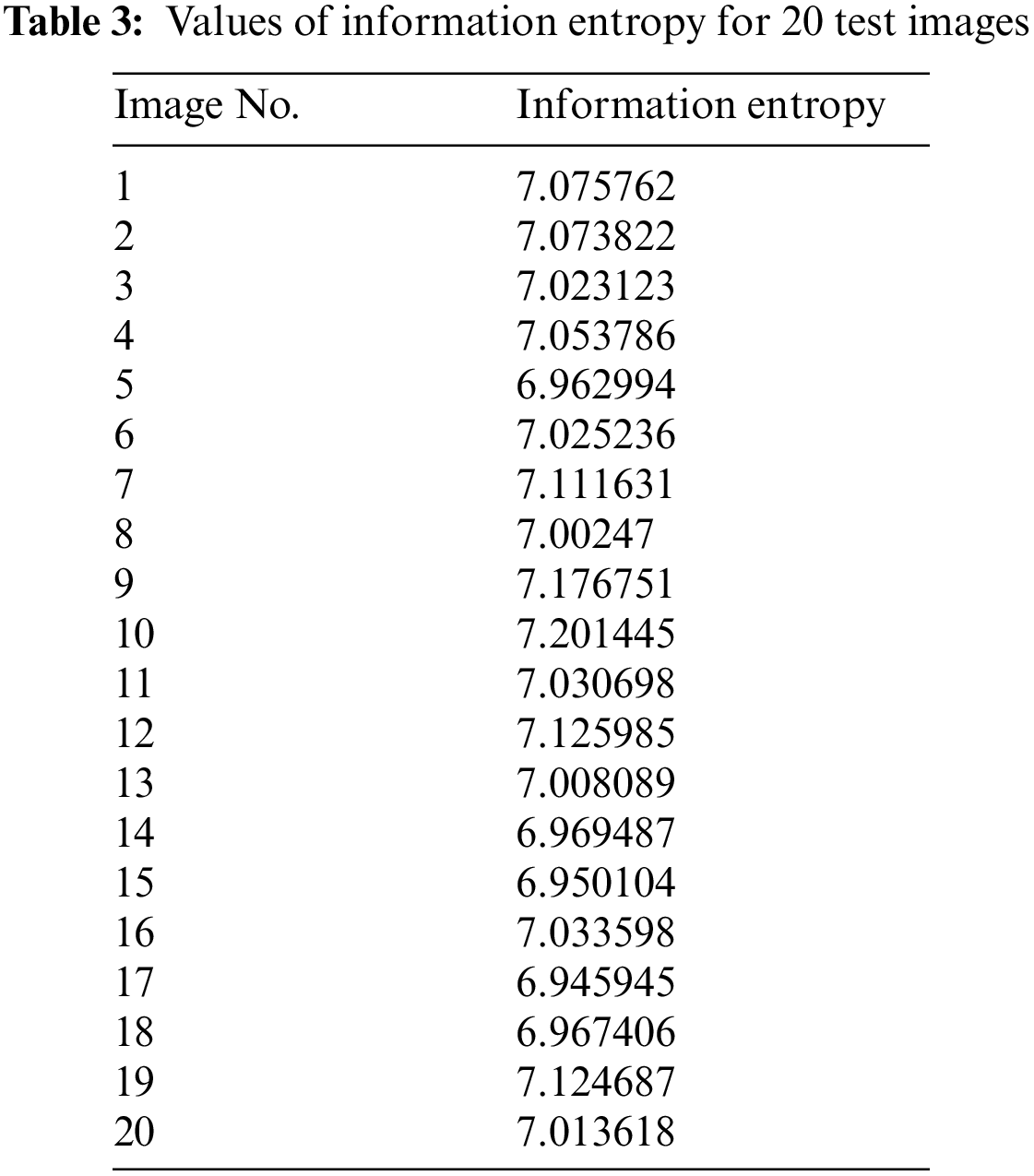
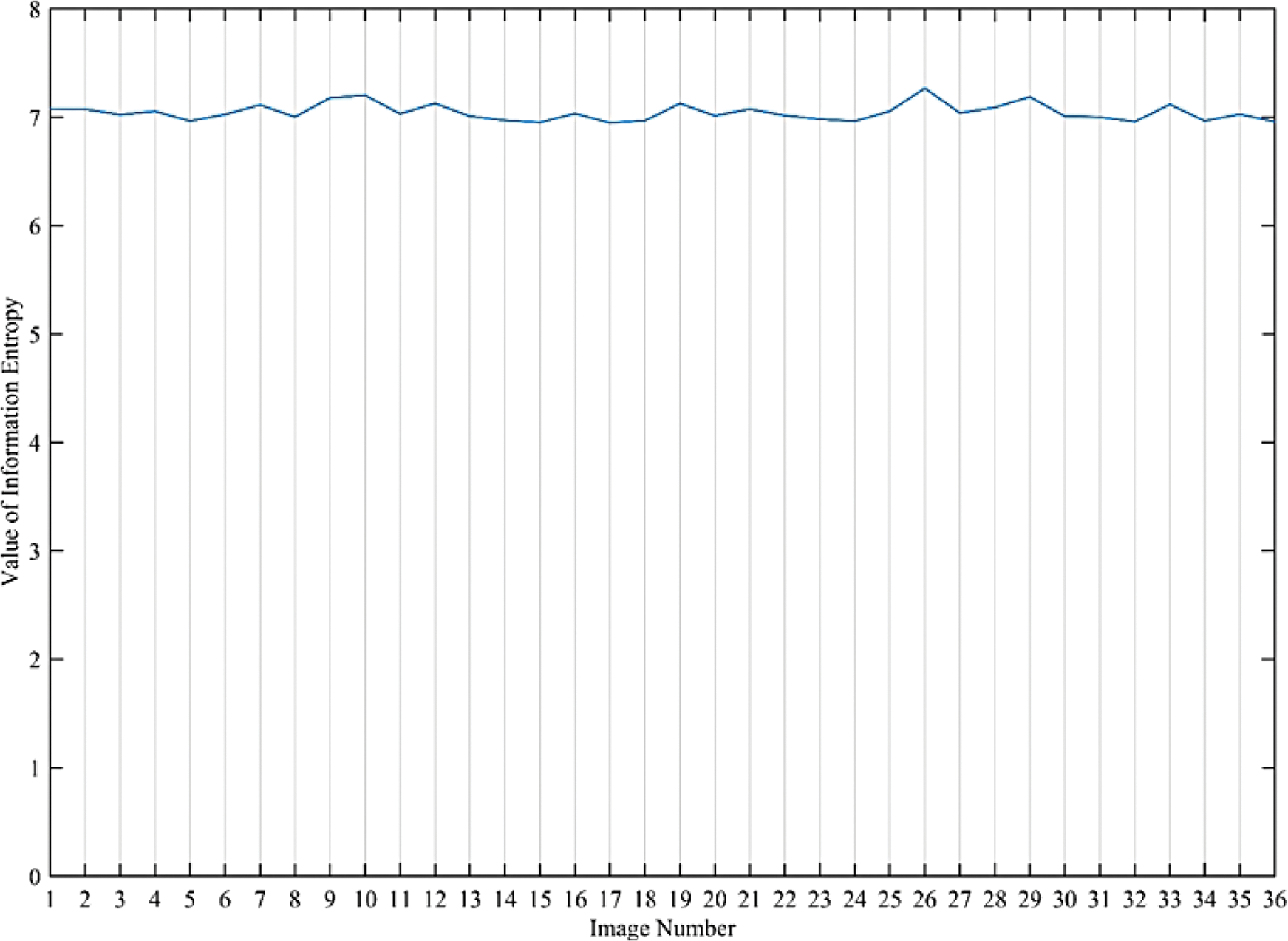
Figure 19: Plot of information entropy values against 36 test images

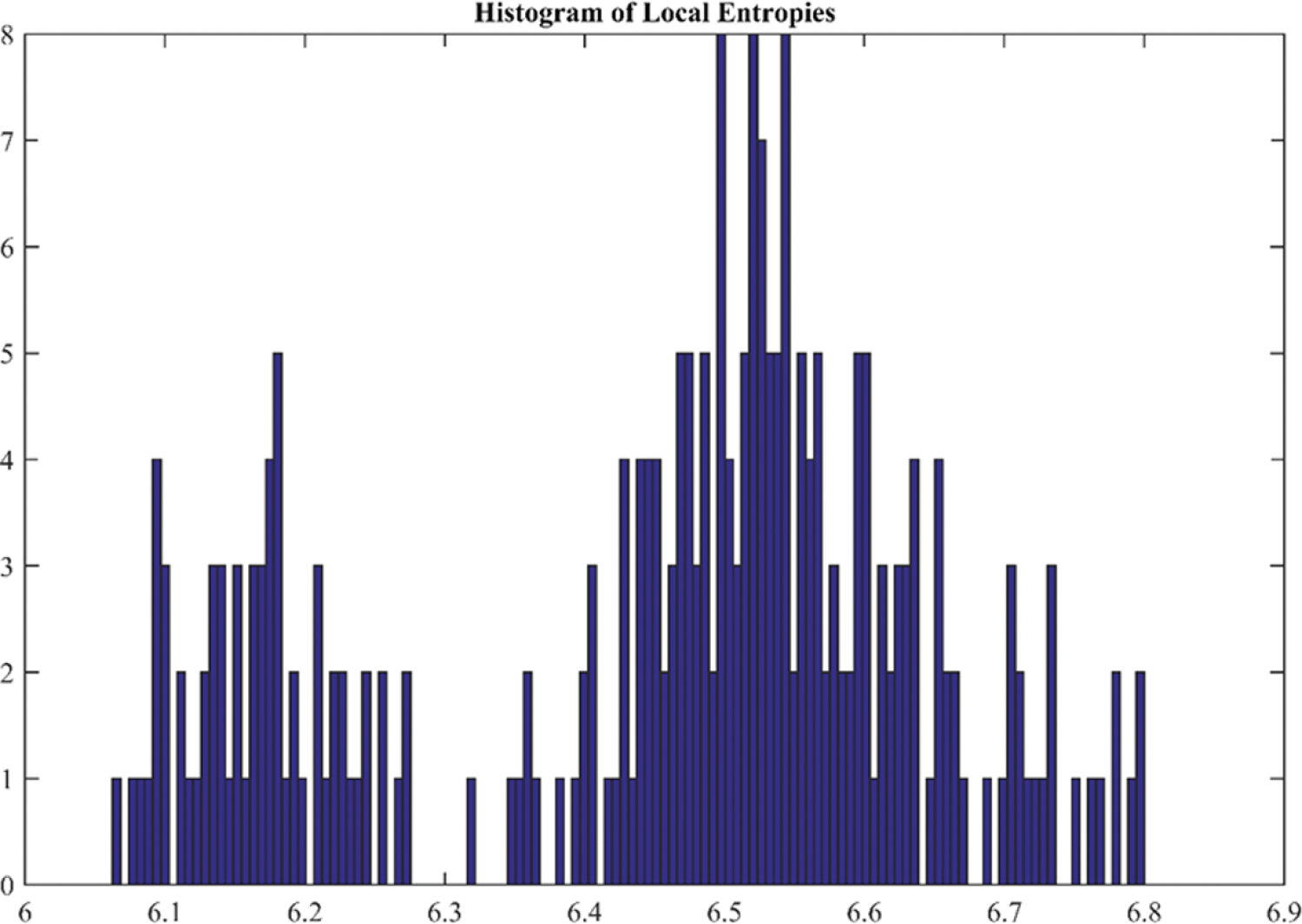
Figure 20: Histogram of local entropies for test image number 36

4.4 Differential Analysis

Differential analysis is used to measure the change in cipher image with a change in plain image. If some part of input image is changed then it should be encrypted in such a way that change should be distributed in the entire image in an unpredictable manner to ensure good diffusion characteristics. Following test are usually carried out to analyze the differential behavior of a system and establish its diffusion characteristics [49].

4.4.1 Avalanche Effect

Avalanche effect is an important test to measure the diffusion characteristics of an image cryptosystem. To perform this test, the cryptosystem is taken as a black box and a small change is performed in the plain image and the cipher image generated is compared to measure the amount of change resulting due to this change. For a successful cryptosystem to have efficient diffusion characteristics this small change should result in a change of more than 50 percent of image pixels.

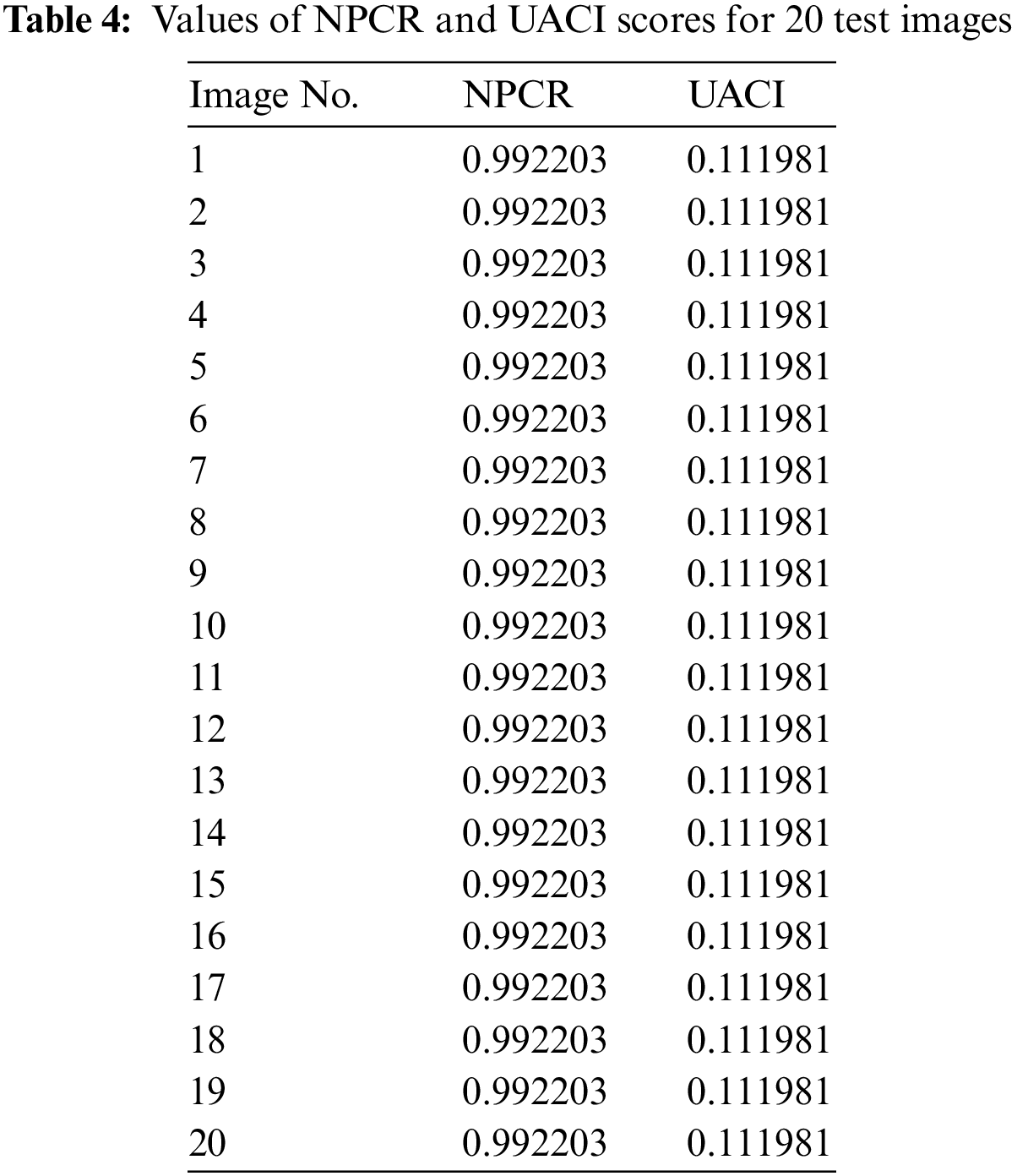
4.4.2 Number of Pixels Change Rate (NPCR)

The number of pixels change rate measures the number of cipher image pixels which are changed in response to a change in plain image. Difference in different cipher images is calculated to measure then number of pixels which are having different values then the other.

4.4.3 Unified Average Change Intensity (UACI)

The number of pixels change rate does not capture all the irregularities of diffusion characteristics so UACI is also used adjacent to NPCR for quantification of diffusion characteristics of an image cryptosystem. This test measures the average intensity change between the two images. However, this test fails to achieve this value and still the cryptosystem is regarded as secure. The results of NPCR and UACI test are provided in the Table 4. It is indicative from the table that NPCR value are quite high as the image have more than 99 percent pixels values different than the other. UACI is 11 percent indicating that there is almost 11 percent change in average image intensity. This change is comparatively low as compared to other image cryptosystems as the cipher image has pixel values distributed as normal distribution so there is not much change in average image intensity.

4.5 Histogram Analysis

Histogram of an image shows the distribution of pixel values in a digital image. This analysis is regarded as an important parameter as it discloses the statistical characteristics of an image cryptosystem. Traditionally, lot of cryptosystem failed only due to statistical analysis and this test became a fundamental test towards measurement of quality of an image cryptosystem. Permutation only ciphers fails only because they donât fulfill this test, no matter what is the randomness of pixel values if the change in plain and cipher image pixel intensities is not reasonable it canât be regarded as a robust image cryptosystem. In no case, the histogram of cipher image should depend on input plain image histogram and ideally it is considered that the histogram should be uniform and pixels intensities should be distributed uniformly in the range.

The experiment has been iterated on all thirty-six test images however due to space limitation results of two of these images are displayed in Figs. 21 and 22. It is evident from the displayed images and the other test images that there is no correlation between the histogram of original image and the cipher image. Although the histogram of cipher image is not uniform as advised by some researchers but still it is not in any way related to plain image histogram and does not result in leakage of information.

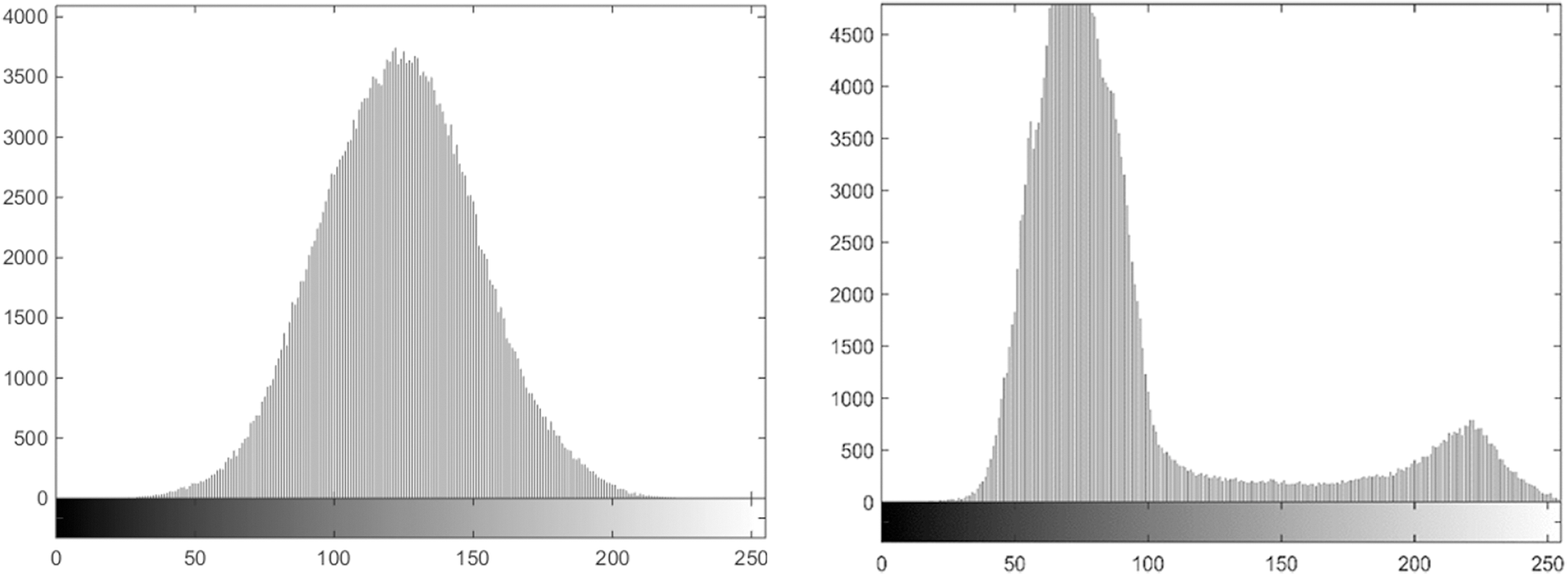
Figure 21: Histogram of cipher image and plain image for test image 32

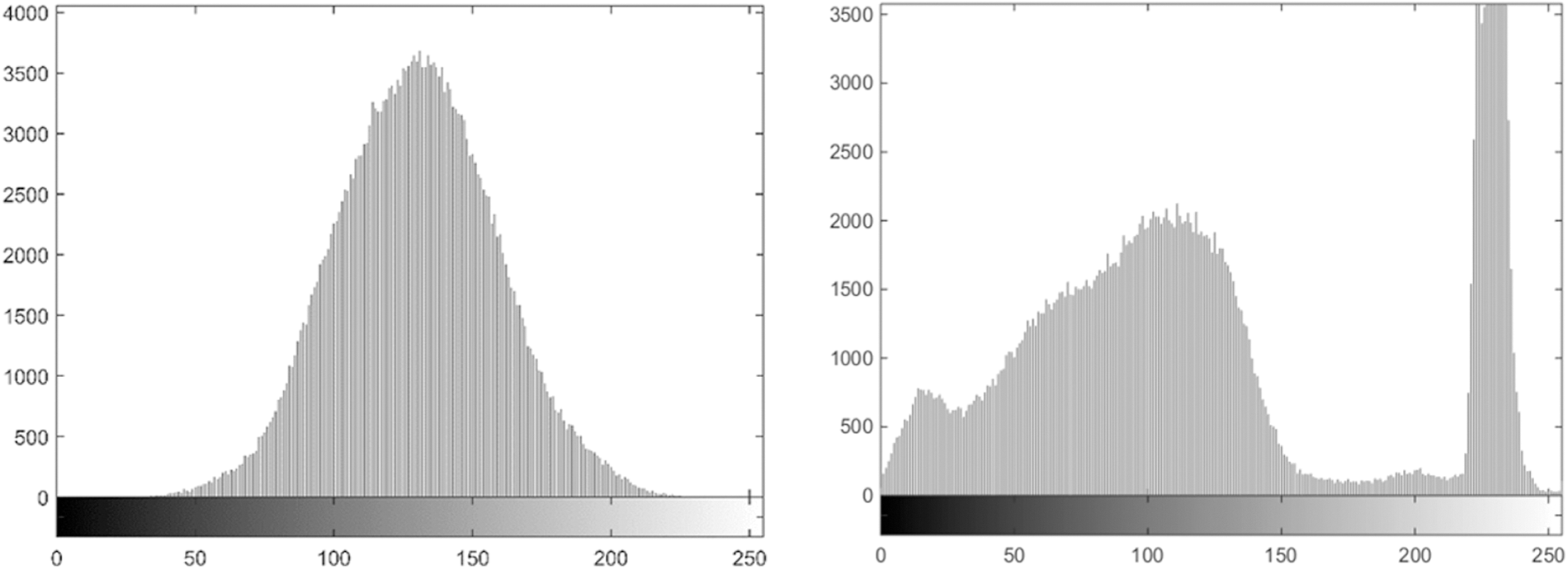
Figure 22: Histogram of cipher image and plain image for test image 36

Moreover, it is worth mentioning that these are grayscale histograms which are taken by converting the input image to grayscale as there is no specified way to plot the histogram of color image. There are few methods which can be used to plot color histogram which are described in [4,49]. Same test is iterated for our test image set and two of them are provided in Figs. 23 and 24 for reference as the results are consistent with the previous observation.

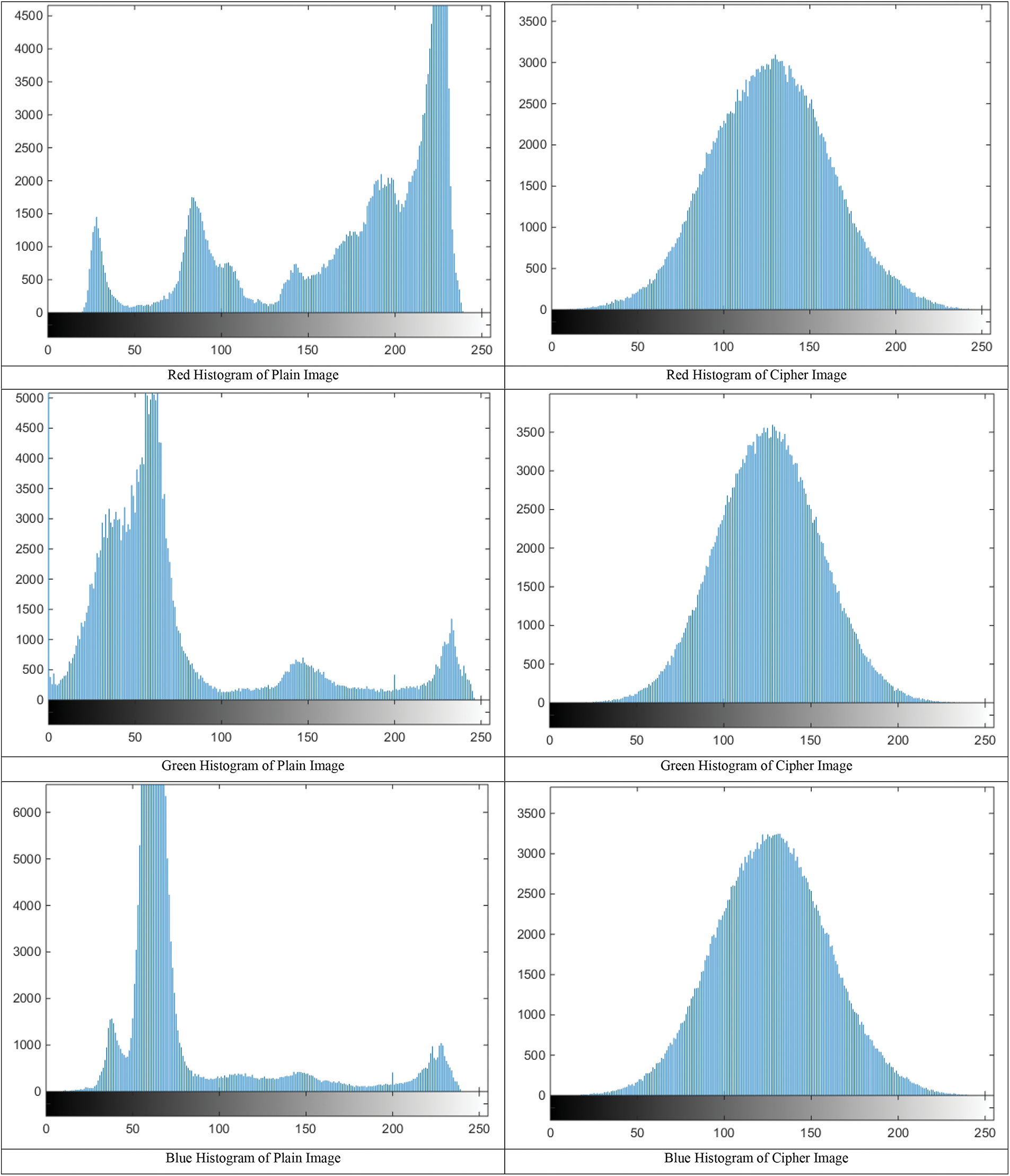
Figure 23: Histogram of three separate RGB channels for a test color image

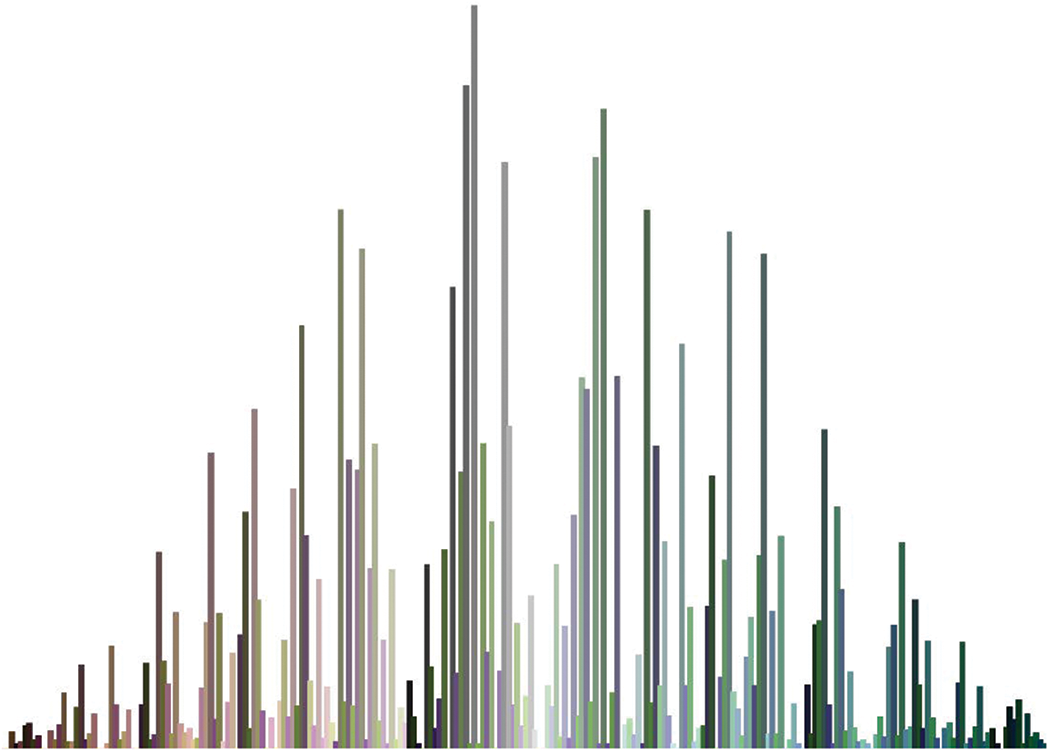
Figure 24: Color histogram of cipher image 32

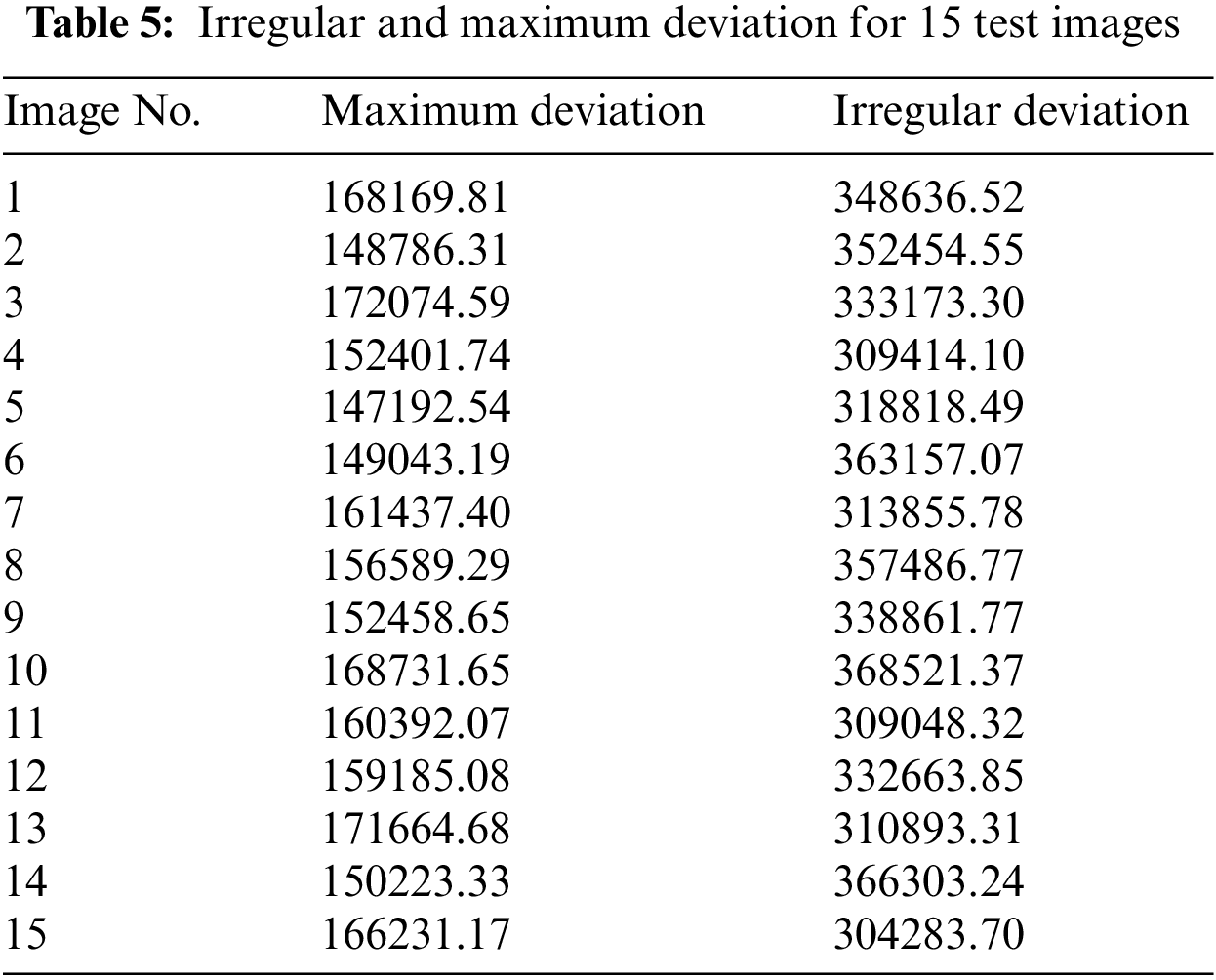
4.6 Maximum Deviation and Irregular Deviation

Visual inspection of histograms does not give accurate results of statistical independence so some histogram-based methods are devised to provide a quantifiable score of histogram analysis. These tests are often regarded as statistical analysis and their formulation can be found in [49]. Maximum deviation measures the deviation in pixel values of the cipher image from the original plain image.

This test provides quantification that how much cipher image pixels values are deviated from the original plain image values. Maximum deviation does not prove to be enough for statistical validation and irregular deviation is also measure to support the claim. It measures the irregular change in pixel values whereas if the cryptosystem yields high deviation in pixel values at some pixel groups and insignificant change in other pixels it would not be a good system. Results of the experiment are provided in Table 5.

4.7 Keyspace Analysis

Keyspace analysis involves the checking of total number of specific combination of secret keys which can be used for the encryption of image and the sensitivity of secret key towards variation in cipher image. This is a fundamental analysis which is required to assess the robustness of cryptosystem towards brute force attacks. A large key space is required for this purpose which can make computation infeasible for deciphering an image with iteration of almost half of possible secret keys. The total number of iterations should be so large that a high speed computer cannot compute in a feasible time to make the attack useful. Moreover, sensitivity of secret key is also a necessary parameter that two cipher images generated with very minor change (usually one bit) in the secret key should produce an entirely random cipher image which must be at least 50 percent different than the other image.

4.7.1 Exhaustive Key Search

This involves the testing of different possible key combinations towards computation of deciphered image. In our cryptosystem the cipher image is produced from the chaos based system which is a combination of four different chaotic systems mixed in single chaotic orbit. The total number of dynamic parameters and initial conditions are therefore enough to form a large key space. The chaotic system is formed from four chaotic orbits and each orbit contains two dynamic parameters in double precision. Total number of variable bits of secret key can be calculated as follows [3–5]:

TotalBits=Bernoulli+Logistic+Qudartaic+Tent(3)

TotalBits=(2×64Bits)+(2×64Bits)+(2×64Bits)+(2×64Bits)=512Bits(4)

Keyspace=2512=1.34×10154(5)

So a total of (1.34 × 10154) possible unique combination of initial conditions (secret keys) are required for full iteration of the key space which is not feasible in a reasonable time.

4.7.2 Key Sensitivity Test

It is an important test which measures the sensitivity of the cryptosystem towards initial conditions. If two slightly different secret key have cipher image which doesnât change very much the usability of large key space is decreased. As the user has no need to check all the keys and few combinations can give a guess which can be further used to fine tune the final secret key. Therefore, to make a brute force attack infeasible, the system should demonstrate high sensitivity towards initial conditions. We have checked the key sensitivity in two ways, one approach involves the iteration of chaotic orbits with slightly different secret key the other involves the encryption of a plain image and decryption of a corresponding cipher image with slightly varying secret keys. A graphical form for analyzing key sensitivity can be found in Fig. 5. Fig. 25 shows the effect of using slightly wrong secret key for decryption. It can be clearly seen the image recovery is not perfect for wrong key and hence making the encryption algorithm highly key sensitive.

Figure 25: Results of key sensitivity test with incorrect secret key with a difference of (10−15)

4.8 Compression Friendliness

An often neglected but important feature of an image cryptosystem is its compression friendliness. Encryption schemes such as AES and some chaos based systems canât be compressed with a lossy compression scheme as it introduces slight variation in the cipher image which result in havoc during decryption and a completely random or highly unintelligible image is obtained as a result [49]. Compression is a very desirable property for digital images and videos otherwise the size of images may result in bandwidth limitations. Compression of digital images therefore become a fundamental necessity in most of the cases.

The other problem with most image cryptosystem is that their image does not result in reduction of size when compressed. A cipher image which is highly random and have very low pixel correlation and high entropy result in such a condition that the compression system rather than reducing the size of image result in increased size. The system proposed in this research has principal property of friendliness to lossy compression and some testing has been performed using JPEG for lossy compression and Portable Network Graphics (PNG) for lossless compression.

Table 6 and Fig. 26 provide the size of compressed image using a lossless compression scheme PNG. It is evident from the results of table that image sizes for chaos based image ciphers are maximum (770 Kbits) which is higher than the plain image size. It is due to the randomness introduced from the chaos based cipher. Whereas in the case of proposed cryptosystem the sizes are higher than the plain image but still lesser then the chaos based cipher. It is therefore evident that the chaos based cipher or other ciphers which have very low correlation doesnât result in reduced size after lossless compression and are not suitable for compression. The proposed scheme on the other hand can be used for the said purpose if the lossless compression is required. However, it is more suited for lossy compression which is used to achieve higher compression ratios.

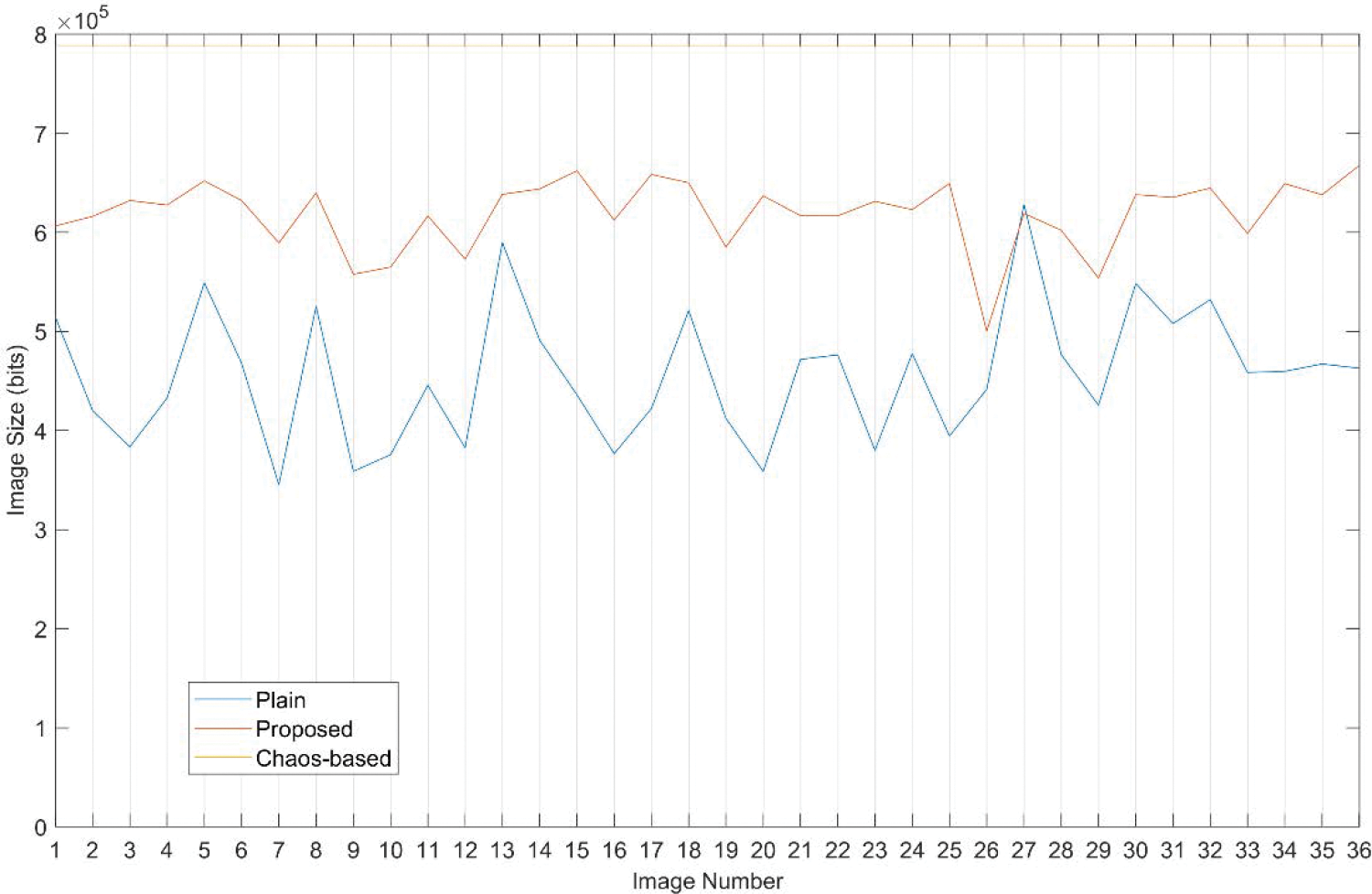
Figure 26: Image sizes of plain, cipher image with proposed scheme and cipher image with chaos based cipher for 36 test images

Fig. 27 provides an excellent demonstration of compression ratio. Chunk of higher plotted lines (36 plots) indicate chaos based cipher images and the lower chunk indicate the cipher images generated from the proposed system. The tabulated results are not provided due to space limitation and less necessity for demonstration. Thirty-six test images are encrypted by proposed cryptosystem and a chaos based cryptosystem. As the chaos based images have very low correlation the compression ratio achieved is significantly lower than the proposed scheme. Moreover, it is worth noting that compression of chaos based cipher image result in highly degraded deciphered image whereas when the same compression is applied on the proposed cipher images the quality is not so much degraded.

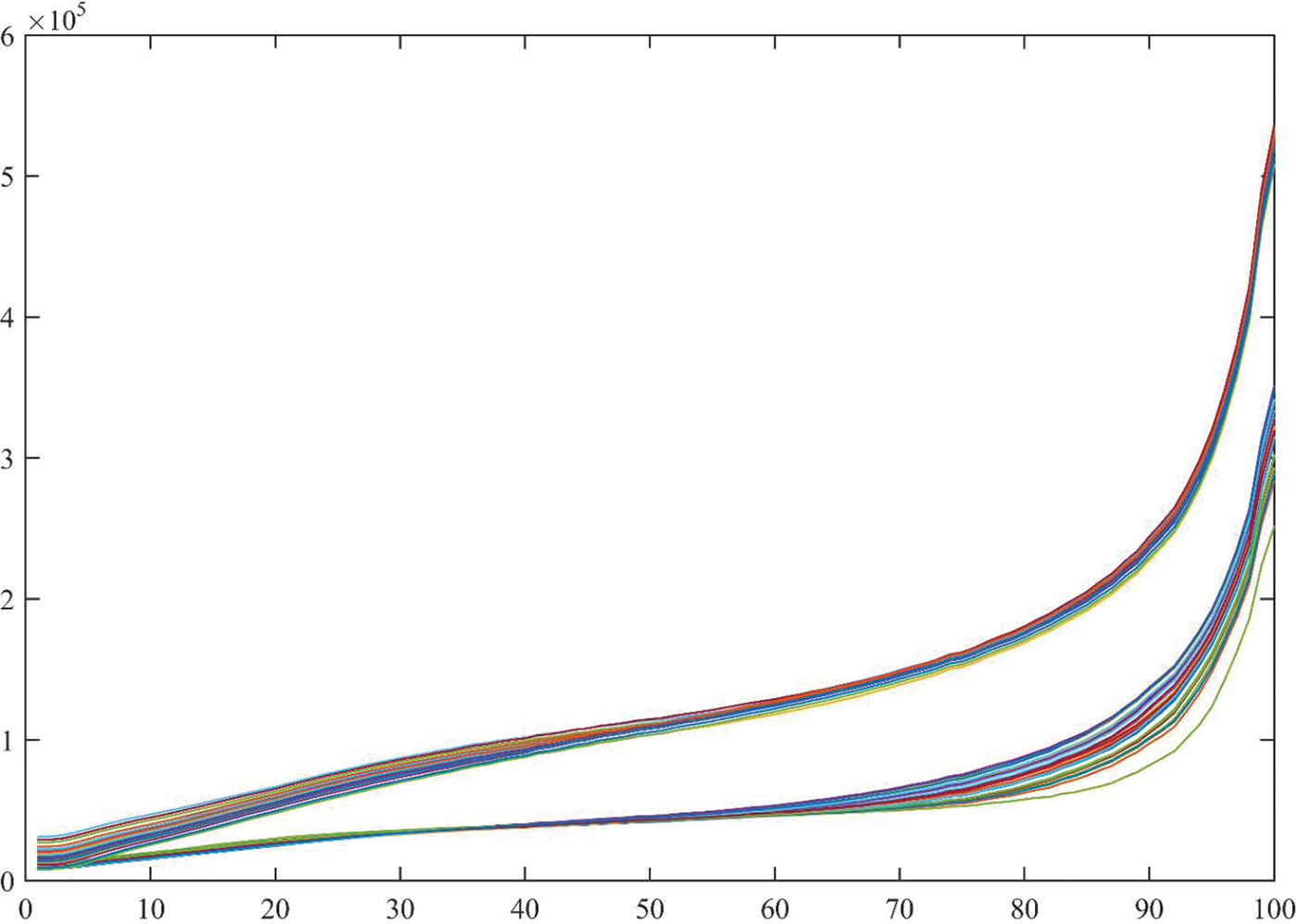
Figure 27: Demonstration of lossy compression (JPEG) at quality factor ranging from zero to 100 for cipher image generated from proposed scheme and chaos based cipher

Fig. 28 provides the decrypted images after compression with JPEG compression with quality factor of 100 percent. It is to note that it is the maximum quality which can be achieved from JPEG and the decrypted image with proposed cipher show no visual degradation whereas the chaos based system has significant distortion. At lower quality factor say 70 percent or lower, the quality of the chaos based system become impermeable. The recovered images can be compared using one of perceptual image quality assessment methods [50–58]. Peak Signal-Noise Ratio (PSNR) and Structural Similarity Index Matrix (SSIM) are one of the widely used image quality assessment metrics. SSIM and PSNR are calculated and provided in Table 7 for both the images in Fig. 28. High PSNR and SSIM values and lower image size indicate that the system demonstrates good tolerance towards lossy compression JPEG and lossless compression PNG.

Figure 28: Demonstration of lossy compression (JPEG) at quality factor ranging from zero to 100 for cipher image generated from proposed scheme and chaos based cipher

5  Conclusions and Future Work

5.1 Conclusions

Data security is a crucial requirement of the modern information era, and numerous approaches have been developed to handle this issue. Digital images and videos require unique security handling due to their inherent redundancy and large size. The goal of this study is to look at a compression-friendly image encryption system and fix some of its flaws to make it more robust and secure. Most image encryption schemes are incompatible with compression or have modest channel noise. Despite best efforts, the security of the compression-friendly technique has several gaps that must be addressed. These methods are susceptible to attack since they rely on pseudorandom number generator that is not cryptographically secure. In the proposed approach, the chaotic system is used to create the permutation sequence and random numbers for image diffusion. Four separate chaotic maps are constructed and then combined to form a more secure chaotic map that serves as the foundation for the proposed approach.

The developed chaotic map is subjected to a series of security checks to ensure it is secure. In addition, several algorithmic improvements are made to the proposed approach’s implementation to improve its efficiency. The finalized technique provides a hybrid encryption scheme for color images that is robust to channel noise and JPEG compression and has good security, as demonstrated by security analysis. It has the potential to be employed for video and image encryption in a number of scenarios, particularly where post-encryption compression is required.

5.2 Future Recommendations

1.   The proposed method could be extended to encrypt audiovisual data or broadcast video.

2.   Real-time encryption can be achieved through the use of an FPGA or DSP kit and optimization of algorithmic operations.

3.   Modification of the proposed algorithm to generate visually meaningful images in order to mitigate the possibility of attack.

4.   Additionally, a recent CS (Compressive Sensing) approach can be used to further compress the image data, in which the chaotic map generated in the previous work can be used to generate a random sensing matrix.

Acknowledgement: The authors extend their gratitude to the Deanship of Scientific Research at King Khalid University for funding this work through research groups program under Grant Number R. G. P. 2/86/43.

Funding Statement: The work is funded by Deanship of Scientific Research at King Khalid University under Grant Number R. G. P. 2/86/43.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Ahmad, N., Younus, M. U., Anjum, M. R., Saleem, G., Gondal, Z. A. et al. (2022). Efficient jpeg encoding using bernoulli shift map for secure communication. Wireless Personal Communications, 125, 3405–3424. https://doi.org/10.1007/s11277-022-09717-8 [Google Scholar] [CrossRef]

2. Ye, G. (2010). Image scrambling encryption algorithm of pixel bit based on chaos map. Pattern Recognition Letters, 31(5), 347–354. https://doi.org/10.1016/j.patrec.2009.11.008 [Google Scholar] [CrossRef]

3. Kessler, G. C. (2014). An overview of cryptography: Cryptographic. In: Handbook on local area networks. https://www.garykessler.net/library/crypto.html [Google Scholar]

4. Ahmed, N., Saleem, Y., Habib, H., Afzal, S., Khurshid, S. (2015). A novel image encryption scheme based on orthogonal vectors. Nucleus, 52(2), 71–78. [Google Scholar]

5. Saleem, G., Ahmed, N., Khalid, H., Ma, S., Wang, H. et al. (2017). Design and analysis of a robust compression friendly image encryption scheme. Algorithms, 8(2), 1–18. [Google Scholar]

6. Maqbool, S., Ahmad, N., Muhammad, A., Martinez Enriquez, A. (2016). Simultaneous encryption and compression of digital images based on secure-jpeg encoding. Pattern Recognition: 8th Mexican Conference. Guanajuato, Mexico, Springer. [Google Scholar]

7. Ahmed, N., Asif, H. M. S., Saleem, G. (2016). A benchmark for performance evaluation and security assessment of image encryption schemes. International Journal of Computer Network & Information Security, 8(12), 28–29. https://doi.org/10.5815/ijcnis.2016.12.03 [Google Scholar] [CrossRef]

8. Naor, M., Shamir, A. (1995). Visual cryptography. In: Advances in cryptology−EUROCRYPT’94: Workshop on the theory and application of cryptographic techniques. Perugia, Italy, Springer. [Google Scholar]

9. Naveed, A., Saleem, Y., Ahmed, N., Rafiq, A. (2015). Performance evaluation and watermark security assessment of digital watermarking techniques. Science International, 27(2), 1271–1276. [Google Scholar]

10. Jolfaei, A., Wu, X. W., Muthukkumarasamy, V. (2016). On the security of permutation-only image encryption schemes. IEEE Transactions on Information Forensics and Security, 11(2), 235–246. https://doi.org/10.1109/TIFS.2015.2489178 [Google Scholar] [CrossRef]

11. Fu, C., Lin, B. B., Miao, Y. S., Liu, X., Chen, J. J. (2011). A novel chaos-based bit-level permutation scheme for digital image encryption. Optics Communications, 284(23), 5415–5423. https://doi.org/10.1016/j.optcom.2011.08.013 [Google Scholar] [CrossRef]

12. Zhou, J., Liu, X., Au, O. C., Tang, Y. Y. (2014). Designing an efficient image encryption-then-compression system via prediction error clustering and random permutation. IEEE Transactions on Information Forensics and Security, 9(1), 39–50. https://doi.org/10.1109/TIFS.2013.2291625 [Google Scholar] [CrossRef]

13. Abd-El-Hafiz, S. K., Radwan, A. G., Haleem, S. H. A., Barakat, M. L. (2014). A fractal-based image encryption system. IET Image Processing, 8(12), 742–752. https://doi.org/10.1049/iet-ipr.2013.0570 [Google Scholar] [CrossRef]

14. Xu, L., Gou, X., Li, Z., Li, J. (2017). A novel chaotic image encryption algorithm using block scrambling and dynamic index based diffusion. Optics and Lasers in Engineering, 91(2), 41–52. https://doi.org/10.1016/j.optlaseng.2016.10.012 [Google Scholar] [CrossRef]

15. Murugan, B., Gounder, A. G. N. (2016). Image encryption scheme based on block-based confusion and multiple levels of diffusion. IET Computer Vision, 10(6), 593–602. https://doi.org/10.1049/iet-cvi.2015.0344 [Google Scholar] [CrossRef]

16. Norouzi, B., Seyedzadeh, S. M., Mirzakuchaki, S., Mosavi, M. R. (2015). A novel image encryption based on row-column, masking and main diffusion processes with hyper chaos. Multimedia Tools and Applications, 74(3), 781–811. https://doi.org/10.1007/s11042-013-1699-y [Google Scholar] [CrossRef]

17. Enayatifar, R., Abdullah, A. H., Isnin, I. F., Altameem, A., Lee, M. (2017). Image encryption using a synchronous permutation-diffusion technique. Optics and Lasers in Engineering, 90, 146–154. https://doi.org/10.1016/j.optlaseng.2016.10.006 [Google Scholar] [CrossRef]

18. Praveenkumar, P., Amirtharajan, R., Thenmozhi, K., Rayappan, J. B. B. (2015). Pixel scattering matrix formalism for image encryptionâa key scheduled substitution and diffusion approach. AEU-International Journal of Electronics and Communications, 69(2), 562–572. https://doi.org/10.1016/j.aeue.2014.11.010 [Google Scholar] [CrossRef]

19. Zhang, Y., Xiao, D. (2014). An image encryption scheme based on rotation matrix bit-level permutation and block diffusion. Communications in Nonlinear Science and Numerical Simulation, 19(1), 74–82. https://doi.org/10.1016/j.cnsns.2013.06.031 [Google Scholar] [CrossRef]

20. Zhou, S., Wang, X., Zhang, Y., Ge, B., Wang, M. et al. (2022). A novel image encryption cryptosystem based on true random numbers and chaotic systems. Multimedia Systems, 28(1), 95–112. https://doi.org/10.1007/s00530-021-00803-8 [Google Scholar] [CrossRef]

21. Liu, H., Kadir, A., Sun, X. (2017). Chaos-based fast colour image encryption scheme with true random number keys from environmental noise. IET Image Processing, 11(5), 324–332. https://doi.org/10.1049/iet-ipr.2016.0040 [Google Scholar] [CrossRef]

22. Abanda, Y., Tiedeu, A. (2016). Image encryption by chaos mixing. IET Image Processing, 10(10), 742–750. https://doi.org/10.1049/iet-ipr.2015.0244 [Google Scholar] [CrossRef]

23. Jakimoski, G., Kocarev, L. (2001). Chaos and cryptography: Block encryption ciphers based on chaotic maps. IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 48(2), 163–169. https://doi.org/10.1109/81.904880 [Google Scholar] [CrossRef]

24. Enayatifar, R., Abdullah, A. H., Isnin, I. F. (2014). Chaos-based image encryption using a hybrid genetic algorithm and a DNA sequence. Optics and Lasers in Engineering, 56, 83–93. https://doi.org/10.1016/j.optlaseng.2013.12.003 [Google Scholar] [CrossRef]

25. Zahmoul, R., Ejbali, R., Zaied, M. (2017). Image encryption based on new beta chaotic maps. Optics and Lasers in Engineering, 96(3), 39–49. https://doi.org/10.1016/j.optlaseng.2017.04.009 [Google Scholar] [CrossRef]

26. Liu, C., Liu, T., Liu, L., Liu, K. (2004). A new chaotic attractor. Chaos, Solitons & Fractals, 22(5), 1031–1038. https://doi.org/10.1016/j.chaos.2004.02.060 [Google Scholar] [CrossRef]

27. Amar, C. B., Zaied, M., Alimi, A. (2005). Beta wavelets. Synthesis and application to lossy image compression. Advances in Engineering Software, 36(7), 459–474. https://doi.org/10.1016/j.advengsoft.2005.01.013 [Google Scholar] [CrossRef]

28. Zheng, J., Hu, H. (2022). A highly secure stream cipher based on analog-digital hybrid chaotic system. Information Sciences, 587(6), 226–246. https://doi.org/10.1016/j.ins.2021.12.030 [Google Scholar] [CrossRef]

29. Moatsum, A., Teh, J. S., Samsudin, A. (2019). An image encryption scheme based on hybridizing digital chaos and finite state machine. Signal Processing, 164(1), 249–266. https://doi.org/10.1016/j.sigpro.2019.06.013 [Google Scholar] [CrossRef]

30. Wang, X. Y., Gu, S. X., Zhang, Y. Q. (2015). Novel image encryption algorithm based on cycle shift and chaotic system. Optics and Lasers in Engineering, 68(6), 126–134. https://doi.org/10.1016/j.optlaseng.2014.12.025 [Google Scholar] [CrossRef]

31. Cheng, P., Yang, H., Wei, P., Zhang, W. (2015). A fast image encryption algorithm based on chaotic map and lookup table. Nonlinear Dynamics, 79(3), 2121–2131. https://doi.org/10.1007/s11071-014-1798-y [Google Scholar] [CrossRef]

32. Wu, X., Kan, H., Kurths, J. (2015). A new color image encryption scheme based on DNA sequences and multiple improved 1D chaotic maps. Applied Soft Computing, 37(5), 24–39. https://doi.org/10.1016/j.asoc.2015.08.008 [Google Scholar] [CrossRef]

33. Norouzi, B., Mirzakuchaki, S. (2014). A fast color image encryption algorithm based on hyper-chaotic systems. Nonlinear Dynamics, 78(2), 995–1015. https://doi.org/10.1007/s11071-014-1492-0 [Google Scholar] [CrossRef]

34. Murillo-Escobar, M., Cruz-Hernández, C., Abundiz-Pérez, F., López-Gutiérrez, R., Del Campo, O. A. (2015). A RGB image encryption algorithm based on total plain image characteristics and chaos. Signal Processing, 109(6), 119–131. https://doi.org/10.1016/j.sigpro.2014.10.033 [Google Scholar] [CrossRef]

35. Chen, J. X., Zhu, Z. L., Fu, C., Yu, H., Zhang, L. B. (2015). A fast chaos-based image encryption scheme with a dynamic state variables selection mechanism. Communications in Nonlinear Science and Numerical Simulation, 20(3), 846–860. https://doi.org/10.1016/j.cnsns.2014.06.032 [Google Scholar] [CrossRef]

36. Wang, L., Song, H., Liu, P. (2016). A novel hybrid color image encryption algorithm using two complex chaotic systems. Optics and Lasers in Engineering, 77(8), 118–125. https://doi.org/10.1016/j.optlaseng.2015.07.015 [Google Scholar] [CrossRef]

37. Praveenkumar, P., Amirtharajan, R., Thenmozhi, K., Rayappan, J. B. B. (2015). Triple chaotic image scrambling on RGB–A random image encryption approach. Security and Communication Networks, 8(18), 3335–3345. https://doi.org/10.1002/sec.1257 [Google Scholar] [CrossRef]

38. Zhang, X., Wang, X. (2017). Multiple-image encryption algorithm based on mixed image element and permutation. Optics and Lasers in Engineering, 92(10), 6–16. https://doi.org/10.1016/j.optlaseng.2016.12.005 [Google Scholar] [CrossRef]

39. Çavuşoğlu, Ü., Kaçar, S., Pehlivan, I., Zengin, A. (2017). Secure image encryption algorithm design using a novel chaos based S-Box. Chaos, Solitons & Fractals, 95(11), 92–101. https://doi.org/10.1016/j.chaos.2016.12.018 [Google Scholar] [CrossRef]

40. Zhou, J., Liu, X., Au, O. C. (2013). On the design of an efficient encryption-then-compression system. 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Vancouver, BC, Canada, IEEE. [Google Scholar]

41. Zhang, X., Ren, Y., Shen, L., Qian, Z., Feng, G. (2014). Compressing encrypted images with auxiliary information. IEEE Transactions on Multimedia, 16(5), 1327–1336. https://doi.org/10.1109/TMM.2014.2315974 [Google Scholar] [CrossRef]

42. Donoho, D. L. (2006). Compressed sensing. IEEE Transactions on Information Theory, 52(4), 1289–1306. https://doi.org/10.1109/TIT.2006.871582 [Google Scholar] [CrossRef]

43. Fay, R. (2016). Introducing the counter mode of operation to compressed sensing based encryption. Information Processing Letters, 116(4), 279–283. https://doi.org/10.1016/j.ipl.2015.11.010 [Google Scholar] [CrossRef]

44. Hu, G., Xiao, D., Wang, Y., Xiang, T. (2017). An image coding scheme using parallel compressive sensing for simultaneous compression-encryption applications. Journal of Visual Communication and Image Representation, 44(4), 116–127. https://doi.org/10.1016/j.jvcir.2017.01.022 [Google Scholar] [CrossRef]

45. Zhou, N., Pan, S., Cheng, S., Zhou, Z. (2016). Image compression–encryption scheme based on hyper-chaotic system and 2D compressive sensing. Optics & Laser Technology, 82, 121–133. https://doi.org/10.1016/j.optlastec.2016.02.018 [Google Scholar] [CrossRef]

46. Liu, X., Zhai, D., Zhou, J., Zhang, X., Zhao, D. et al. (2016). Compressive sampling-based image coding for resource-deficient visual communication. IEEE Transactions on Image Processing, 25(6), 2844–2855. https://doi.org/10.1109/TIP.2016.2554320 [Google Scholar] [PubMed] [CrossRef]

47. Huang, X., Ye, G., Chai, H., Xie, O. (2015). Compression and encryption for remote sensing image using chaotic system. Security and Communication Networks, 8(18), 3659–3666. https://doi.org/10.1002/sec.1289 [Google Scholar] [CrossRef]

48. Zhang, X., Tian, J. (2022). Multiple-image encryption algorithm based on genetic central dogma. Physica Scripta, 97(5), 055213. https://doi.org/10.1088/1402-4896/ac66a1 [Google Scholar] [CrossRef]

49. Nisar, A., Asif, H. M. S., Saleem, G. (2016). A benchmark for performance evaluation and security assessment of image encryption schemes. International Journal of Computer Network and Information Security, 8(12), 18. [Google Scholar]

50. Ahmed, N., Shahzad Asif, H., Bhatti, A. R., Khan, A. (2022). Deep ensembling for perceptual image quality assessment. Soft Computing, 20(16), 7601–7622. [Google Scholar]

51. Ahmed, N., Asif, H. M. S., Khalid, H. (2021). PIQI: Perceptual image quality index based on ensemble of gaussian process regression. Multimedia Tools and Applications, 80(10), 15677–15700. https://doi.org/10.1007/s11042-020-10286-w [Google Scholar] [CrossRef]

52. Ahmed, N., Asif, H. M. S., Khalid, H. (2021). Non-reference quality monitoring of digital images using gradient statistics and feedforward neural networks. arXiv preprint arXiv: 2112.13893. [Google Scholar]

53. Ahmed, N., Asif, H. M. S. (2019). Ensembling convolutional neural networks for perceptual image quality assessment. 2019 13th International Conference on Mathematics, Actuarial Science, Computer Science and Statistics (MACS), Karachi, Pakistan, IEEE. [Google Scholar]

54. Ahmed, N., Asif, H. M. S. (2020). Perceptual quality assessment of digital images using deep features. Computing and Informatics, 39(3), 385–409. https://doi.org/10.31577/cai_2020_3_385 [Google Scholar] [CrossRef]

55. Ahmed, N., Asif, H. M. S., Khalid, H. (2019). Image quality assessment using a combination of hand-crafted and deep features. International Conference on Intelligent Technologies and Applications: Second International Conference, Bahawalpur, Pakistan, Springer. [Google Scholar]

56. Khalid, H., Ali, M., Ahmed, N. (2021). Gaussian process-based feature-enriched blind image quality assessment. Journal of Visual Communication and Image Representation, 77(1), 103092. https://doi.org/10.1016/j.jvcir.2021.103092 [Google Scholar] [CrossRef]

57. Wang, Z., Bovik, A. C., Sheikh, H. R., Simoncelli, E. P. (2004). Image quality assessment: From error visibility to structural similarity. IEEE Transactions on Image Processing, 13(4), 600–612. https://doi.org/10.1109/TIP.2003.819861 [Google Scholar] [PubMed] [CrossRef]

58. Korhonen, J., You, J. (2012). Peak signal-to-noise ratio revisited: Is simple beautiful? 2012 Fourth International Workshop on Quality of Multimedia Experience, Melbourne, VIC, Australia, IEEE. [Google Scholar]