 Open Access
Open Access
REVIEW
Heterogeneous Network Embedding: A Survey
1
School of Computer Science, Wuhan University, Wuhan, 430072, China
2
School of Computer Science, Central China Normal University, Wuhan, 430079, China
* Corresponding Author: Rong Peng. Email:
Computer Modeling in Engineering & Sciences 2023, 137(1), 83-130. https://doi.org/10.32604/cmes.2023.024781
Received 08 June 2022; Accepted 06 December 2022; Issue published 23 April 2023
Abstract
Real-world complex networks are inherently heterogeneous; they have different types of nodes, attributes, and relationships. In recent years, various methods have been proposed to automatically learn how to encode the structural and semantic information contained in heterogeneous information networks (HINs) into low-dimensional embeddings; this task is called heterogeneous network embedding (HNE). Efficient HNE techniques can benefit various HIN-based machine learning tasks such as node classification, recommender systems, and information retrieval. Here, we provide a comprehensive survey of key advancements in the area of HNE. First, we define an encoder-decoder-based HNE model taxonomy. Then, we systematically overview, compare, and summarize various state-of-the-art HNE models and analyze the advantages and disadvantages of various model categories to identify more potentially competitive HNE frameworks. We also summarize the application fields, benchmark datasets, open source tools, and performance evaluation in the HNE area. Finally, we discuss open issues and suggest promising future directions. We anticipate that this survey will provide deep insights into research in the field of HNE.Graphic Abstract
Keywords
Real-world complex networks, such as social, biological protein, and computer networks, are inherently heterogeneous. These networks, called heterogeneous information networks (HINs), contain various types of nodes, attributes, and relationships [1]. In recent years, with the rapid development of artificial intelligence, HIN analysis has attracted significant research attention. Efficient analysis techniques can benefit machine learning (ML) tasks based on HINs, such as node classification, community detection, and recommender systems.
In many HIN-based ML models, the core task is to find a way to convert the structural and semantic information of an HIN into low-dimensional vectors and then input these vectors into various downstream machine learning tasks. Feature engineering, which is the traditional approach used for feature extraction, is inefficient and highly dependent on the experience of engineers. With the successful application of the Word2vec model [2,3] in the field of natural language processing, many recent studies have used ML methods to automatically learn the low-dimensional features of nodes, edges, and subgraphs from networks such that the obtained feature vectors can capture as much structural, semantic, and attribute information in the HINs as possible. This process is called heterogeneous network embedding (HNE). In contrast to the traditional approach, HNE has the advantages of high efficiency and compression. More importantly, most HNE models can learn features from data in a completely unsupervised manner. They do not require labeled data; instead, they generate high-quality feature representations by creating labels from the data themselves using context-based, time series-based, and contrast-based methods, among others. To make the learned feature representation more effective for specific applications, the features generated by unsupervised learning can be input as pretraining parameters to subsequent specific ML tasks, and then fine-tuned using labeled data. Alternatively, the unsupervised and supervised parts can be fused into a model for end-to-end training. When a large amount of manually labeled information is difficult to obtain, HNE can reduce the model’s dependence on labeled information. Therefore, research on HNE is of great significance for artificial intelligence-related applications.
The primary goal of an HNE model is to enable the generated network embeddings to reconstruct various types of information contained in the HINs such that they can be easily used in downstream ML tasks. However, because of the complexity of HINs, existing HNE research often faces the following challenges: 1) Heterogeneity. In an HIN, different types of nodes usually have different types of attributes (multi-modality), and different types of nodes usually establish different types of semantic relationships (multiplex). Numerous existing network embedding models operate on homogeneous networks and are difficult to be extended to HINs. 2) Large-scale. In the real world, HINs are usually large and hyperscale, containing thousands of nodes and complex relationships. Many existing network embedding models are only able to run on small networks and cannot scale to large-scale networks. 3) Dynamism. In the real world, complex heterogeneous networks tend to constantly change. New nodes join and old nodes exit, and new links may be generated anytime and anywhere. Most traditional network embedding models are designed for static snapshot networks and cannot capture the dynamic characteristics of real-time networks. 4) Incomplete data and noise. Real-world network data are often incomplete and noisy. Many existing models do not consider robustness issues, resulting in brittle models and compromised performance. 5) Multi-objectiveness. A good HNE model usually needs to consider multiple modeling goals; such as capturing the local and global structural features of the network, capturing diverse semantic information, attribute information and label information. All the factors outlined above pose serious challenges to research in the field of HNE.
To tackle the issues cited above, numerous HNE models have been proposed over the past several years, such as the meta-path based random walk model metapath2vec [4], the multi-stage non-negative matrix factorization model MNMF [5], and the heterogeneous graph attention network model HGAT [6]. However, there have been few surveys on HNE. Some studies have reviewed the fields of network and graph embedding, but these studies are not specific to HINs [7–14]. To the best of our knowledge, there are several HNE surveys so far [15–19]. Yang et al. [15] reviewed HNE and categorized HNE models into three categories, including proximity-preserving, message-passing, and relation-learning methods. Xie et al. [16] divided current HNE models into path-based, semantic unit-based, and other methods, and each type was further divided into traditional and deep learning-based methods. In addition, from the perspective of modeling goals, Wang et al. [18] categorized existing HNE models into four categories: structure-preserved, attribute-assisted, application-oriented, and dynamic heterogeneous graph embedding models. Dong et al. [17] and Ji et al. [19] also briefly reviewed HNE.
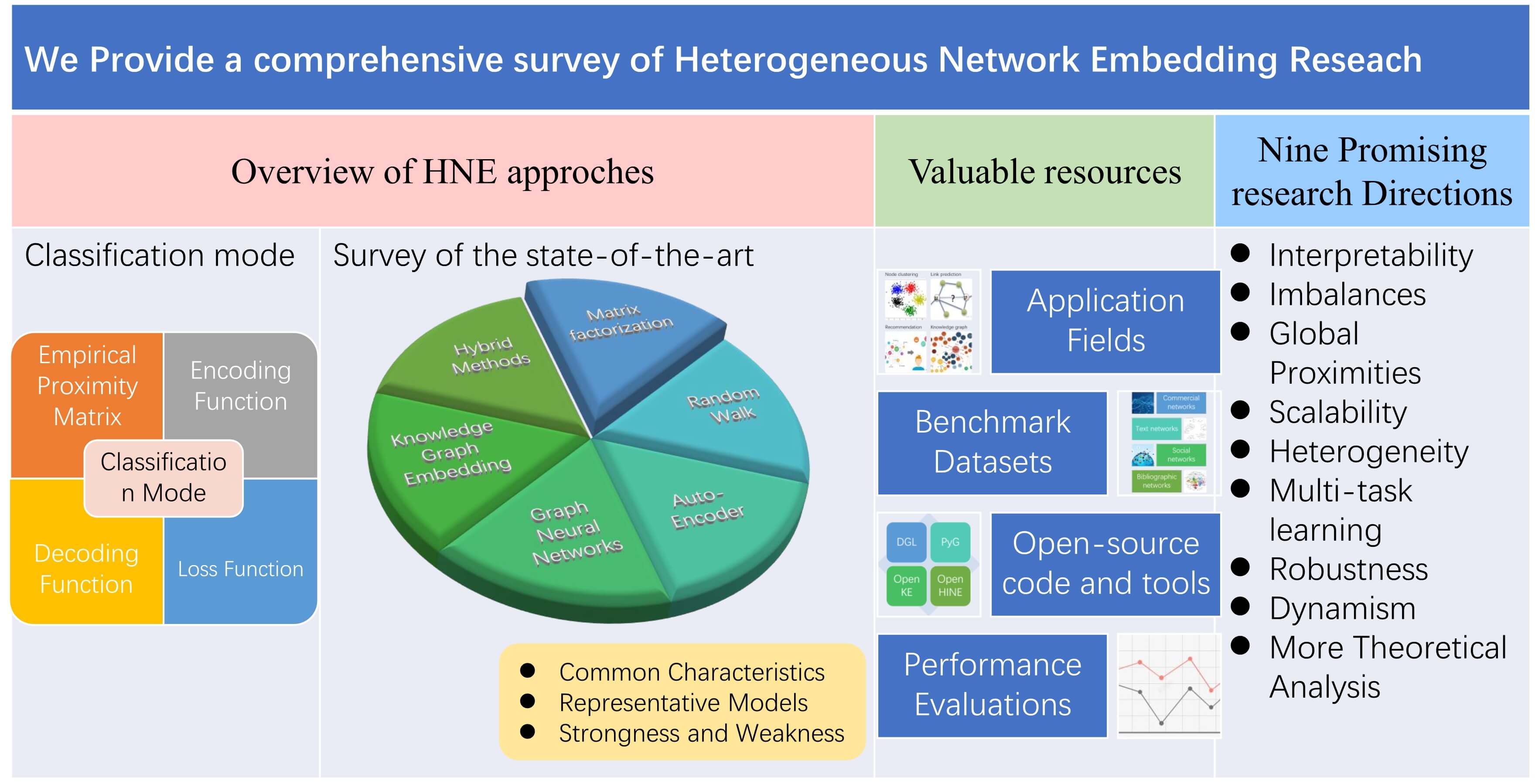
However, these existing surveys on HNE either lack clear classification patterns, or summarize model types in a manner that is not comprehensive and lack in-depth comparison and analysis. To bridge the gap, we provide a comprehensive survey of the state-of-the-art HNE research in this paper. Specifically, we first define a classification mode for HNE study based on an encoder-decoder framework, and explore the major components of an HNE model under the framework. Then, we present a systematic and comprehensive survey of the six categories in the taxonomy. We analyze the basic characteristics, modeling capabilities, advantages and disadvantages of each type of HNE model. Further, we summarize the application areas, publicly available benchmark datasets, open source codes/tools, and give performance comparisons of some typical HNE models on the DBLP dataset for link prediction tasks. Finally, we discuss the open issues and suggest future research directions. The unique contributions of this paper can be summarized as follows:
• From a technical perspective, we use a more primitive, fundamental, and systematic classification mode for HNE approaches. Unlike most surveys that classify models from the perspective of modeling goals, we use the encoder-decoder framework to classify the existing HNE models from a technical perspective. This classification mode is more primitive, fundamental, and systematic. It can explicitly capture the methodological diversity and place the various approaches on an equal symbolic and conceptual basis. We elaborate on major components that an HNE model usually contains under the encoder-decoder framework, including encoder, decoder, empirical proximity matrix, and loss function.
• We provide a comprehensive survey of HNE research. Based on the proposed classification mode, existing HNE methods can be mainly divided into six categories: matrix factorization (MF), random walk (RW), AutoEncoder (AE), graph neural network (GNN), knowledge graph embedding (KGE), and hybrid (HB) methods. We provide a systematic and comprehensive survey of each type of HNE model. For each model type, we first overview its overall common characteristics and modeling ideas. Then, taking the modeling goals and capabilities of the representative HNE models as the main clues, we conduct a systematic and comprehensive overview of each model type. We use extensive tables to analyze and demonstrate the uniqueness of each representative HNE model in the definition of encoder, decoder, loss function, and empirical proximity matrix. We also analyze the modeling capabilities of them and highlight their novel contributions. Finally, we summarize the overall strengths and weaknesses (or challenges) of each type of HNE model to uncover more potentially competitive HNE model frameworks. We believe that these in-depth and extensive analyses and summaries can be helpful in guiding the development of future novel HNE models and aid researchers and practitioners in choosing appropriate HNE frameworks for specific ML tasks.
• We provide a wealth of valuable relevant resources. We summarize the HNE-related application fields, publicly available benchmark datasets, open source codes, and tools, which are rich resources for researchers and practitioners in this field. More over, we provide performance comparisons of some typical HNE models on the DBLP dataset for the link prediction task.
• We suggest nine promising research directions in the field of HNE. We discuss open and challenging issues and propose nine promising research directions in the field of HNE in terms of aspects such as interpretability, scalability, heterogeneity, multi-objectiveness, and robustness. For each direction, we provide an in-depth analysis of the inadequacies in the current research and explore future research directions.
The remainder of this survey paper is organized as follows. Section 2 defines the research problem and elaborates our classification mode. Section 3 provides a comprehensive survey of the state-of-the-art HNE research. Section 4 summarizes the application fields, benchmark datasets, open source codes/tools, and performance evaluations. Section 5 discusses open issues and outlines potential future research directions. Section 6 presents concluding remarks.
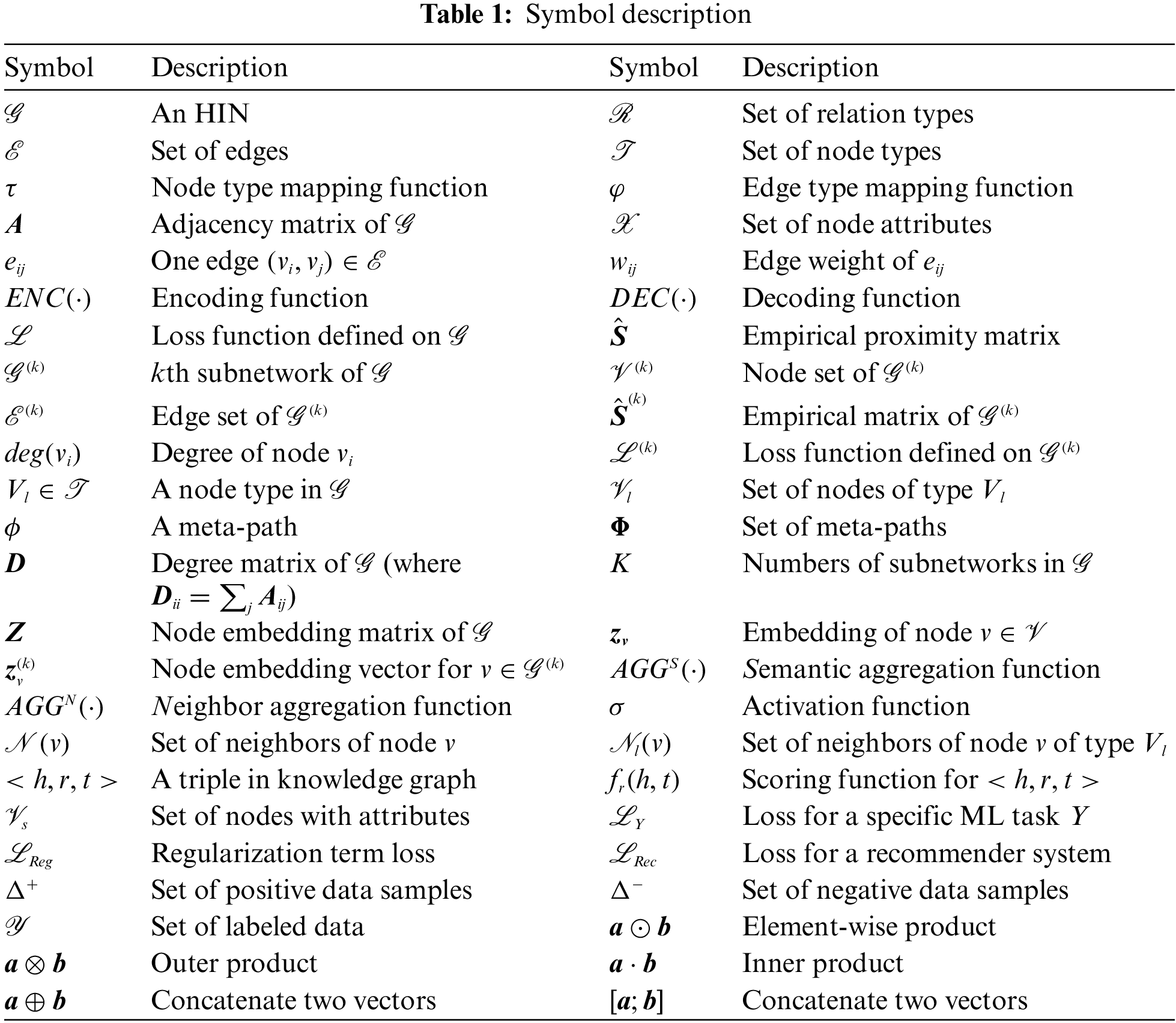
We use uppercase boldface letters for matrices and lowercase boldface letters for vectors. Table 1 lists the key symbols used in this paper.
2.1 Heterogeneous Information Network
Definition 1. Heterogeneous Information Network (HIN) [4]: An HIN can be defined as
Fig. 1 presents two example HINs. The bibliographic network in Fig. 1a is a typical HIN that contains five types of nodes: author (A), paper (P), journal (V), organization (O), and topic (T). A P-type node has different types of links: P-A (a paper is written by an author), P-P (a paper cites another paper), P-V (a paper is published at a venue), among others. The Douban Movie network in Fig. 1b is also an HIN, and it contains four types of entities: user (U), movie (M), director (D), and actor (A).
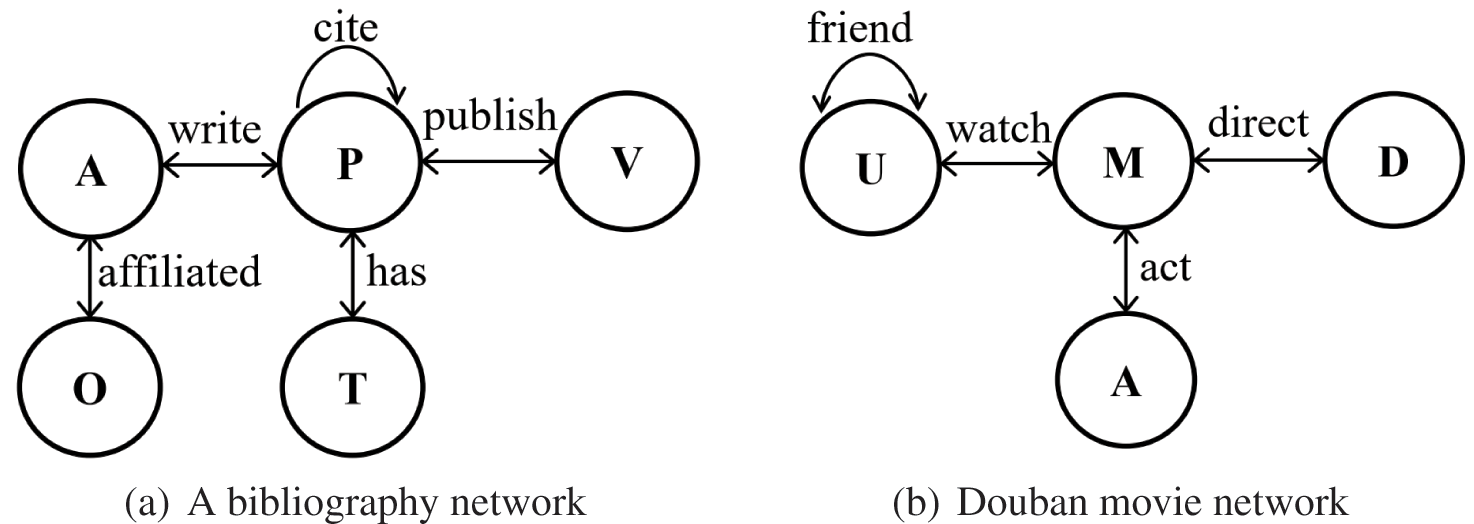
Figure 1: Example Heterogeneous Information Networks (HINs)
According to the different types of semantic relations, a heterogeneous network
2.2 Heterogenous Network Embedding
Definition 2. Heterogeneous Network Embedding (HNE): Given an HIN
Next, we explain the three main modeling goals of general HNE models:
• To preserve structural information (Preserve ST): the generated embeddings are able to preserve the topological proximity (low-order proximity such as
• To preserve attribute information (Preserve AT): the generated embeddings incorporate the affiliated attribute information of nodes or edges in the HINs.
• To preserve semantic information (Preserve SM): the model differentiates between different types of semantic relations when generating network embeddings.
Notably, in addition to generating embeddings for nodes in HINs, some studies generate embeddings for edges, subnetworks, or entire networks. These studies are also studies of HNE. However, because edge and subnet embeddings are also based on node embeddings and generating node embeddings is the main task of most ML models, this survey focuses on the node embedding models and introduces some extended models.
2.3 Overview of Approaches: An Encoder-Decoder Framework
From a technical perspective, we use an encoder-decoder framework depicted in Fig. 2 to classify and review existing state-of-the-art HNE approaches. In this section, we first discuss the methodological components of an HNE model under this framework.
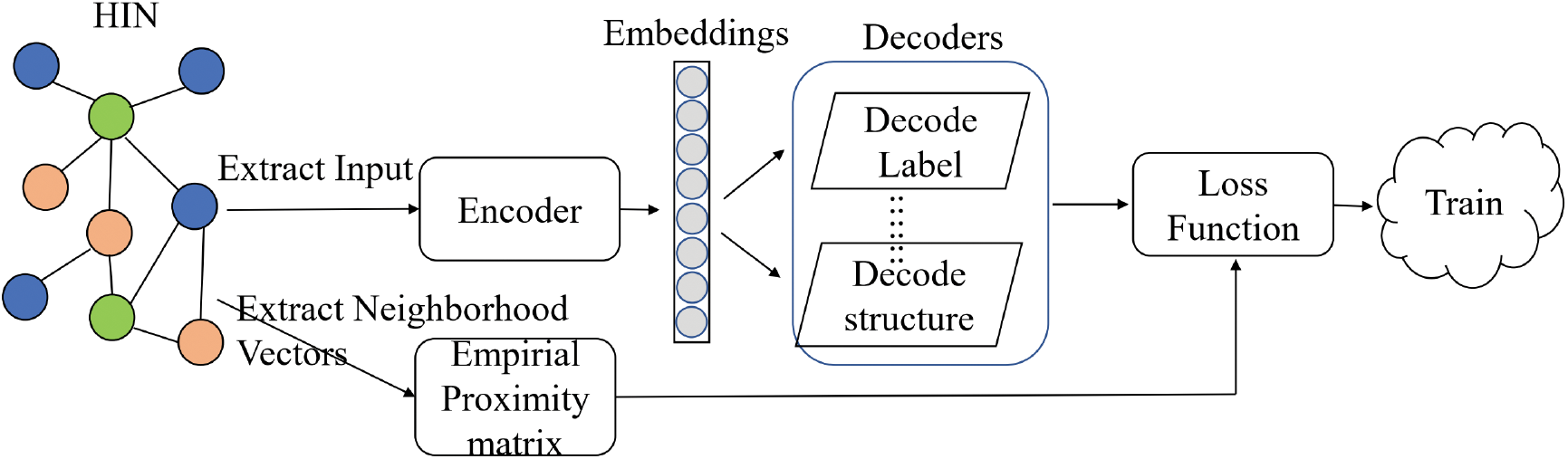
Figure 2: Overview of the encoder-decoder framework
The encoder aims to map each node
maps nodes to low dimensional vecotor embeddings
A decoder is also a function that tries to reconstruct the information of the original HIN from the learned node embeddings. To preserve the structural information of the HIN, many HNE models define a pairwise decoder as
to map the pair of node embeddings
where
In summary, in the encoder-decoder framework, an HNE model typically comprises four components:
• An empirical proximity matrix
• An encoding function
• A decoding function
• A loss function
3 Heterogenous Network Embedding: State-of-the-Art Approaches
Based on the encoder-decoder framework, existing HNE models can be divided into six categories: MF, RW, AE, GNN, KGE, and Hybrid. As explained later, there are distinct differences in the major components of each model type. In Fig. 3, we present the proposed taxonomy for summarizing HNE techniques.
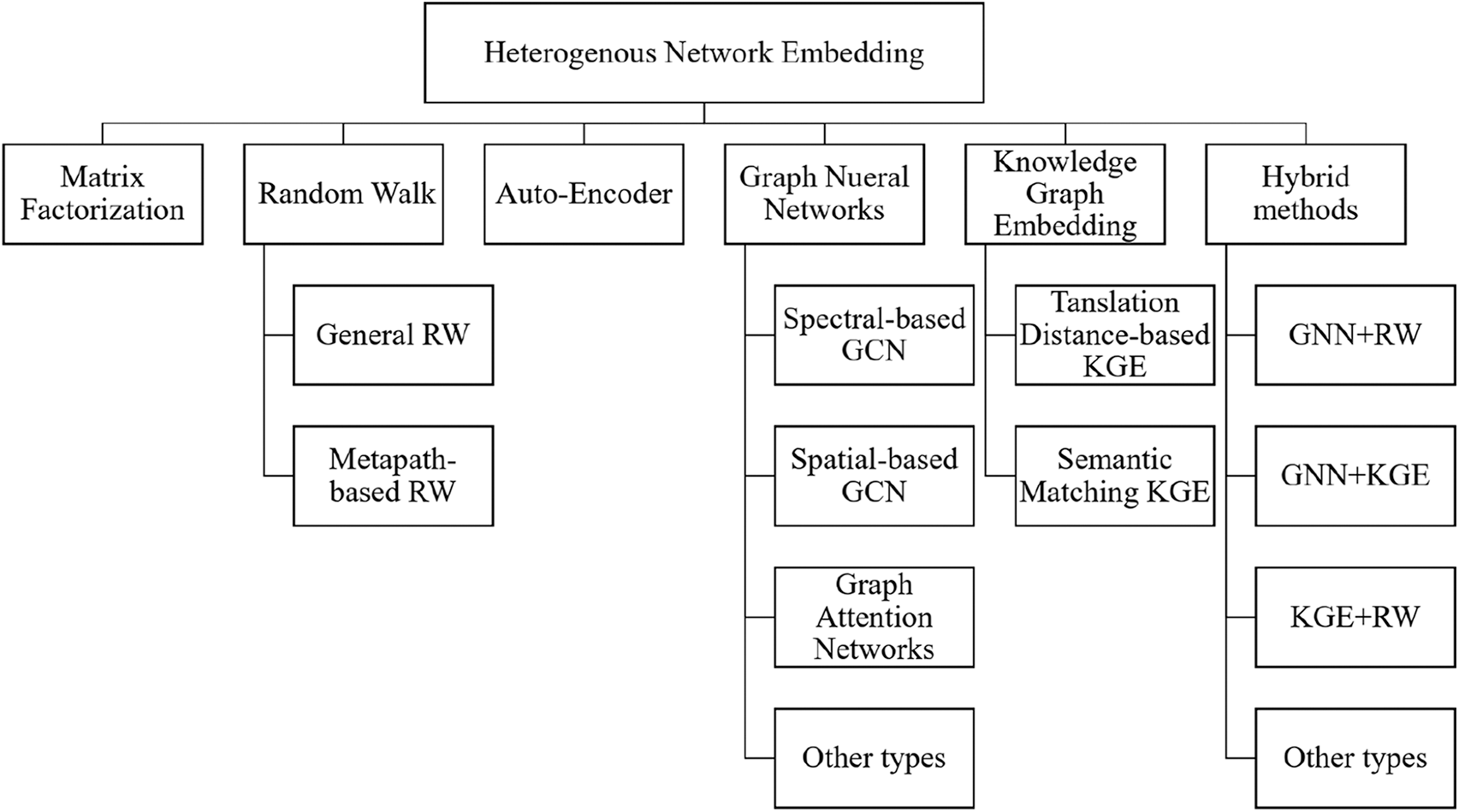
Figure 3: The proposed taxonomy for summarizing Heterogenous Network Embedding (HNE) techniques
3.1 Matrix Factorization-Based Models
Matrix factorization (MF) is an early feature representation learning method. Many MF-based homogeneous network embedding models have been proposed, such as Graph Factorization [23], Laplacian Eigenmaps [24], and HOPE [25]. The encoder of an MF-based model is usually a direct encoding, i.e., the product of a node embedding matrix
In this case, the encoding function is a simple “embedding lookup”, and the embedding matrix
Thus, if the loss function is defined as
Different from homogeneous network embedding, HNE models need to deal with network heterogeneity. In general, the most common idea of extending a homogeneous MF model to an HIN is to 1) use a specific MF model to model the relationships in different subnetworks separately, and 2) sum the losses defined on multiple subnetworks and train them together in an HNE model to get the feature representation of each node in the HIN.
PTE [26] is a semi-supervised model for representation learning of heterogeneous text data. Specifically, to improve the efficiency of text embedding and use the label information in the dataset, PTE represents the text co-occurrence and partial label information in the corpus as an HIN that contains the following subnetworks: the word–word network
To preserve the second-order proximity, the loss function for
where
2) first using the unlabeled networks (
In addition to PTE, HRec [27], ISE [28], and LHNE [29] all use an inner-product decoder as PTE. These models are all able to capture the low-order structural features of the HINs, but they share common defects: 1) These models map the node embeddings in different subnetworks to the same vector space, without considering the diverse semantic information contained in different subnetworks; 2) When the losses of multiple subnetworks are fused together in a single model, these HNE models assign equal weights to different subnetworks. However, the densities of different subnetworks in an HIN are usually quite different. Giving equal weights can easily lead to skew problems, i.e., the HNE model converges in some denser subnetworks but does not in less dense subnetworks.
Inspired by the attention mechanism in neural machine translation in recent years, Qu et al. proposed an MVE model [30] for multi-view heterogeneous networks, which solves the problem of automatically learning the different weights of different views (subnetworks). MVE first maps each node in each subnetwork to a different vector space, and then it also uses the LINE model to obtain the node embedding
where
The final loss of the MVE model is the sum of the model loss for multiple subnets, the regularization term, and the loss for a downstream ML task.
However, the MF-based HNE models mentioned above can only capture low-order structural information of the HINs; they cannot do much for the higher-order structural information. Since the higher-order structural information of the network is equally important in many ML applications, some matrix factorization-based models capture the higher-order structural features by changing the definition of the empirical proximity matrix.
where the residual matrix
where
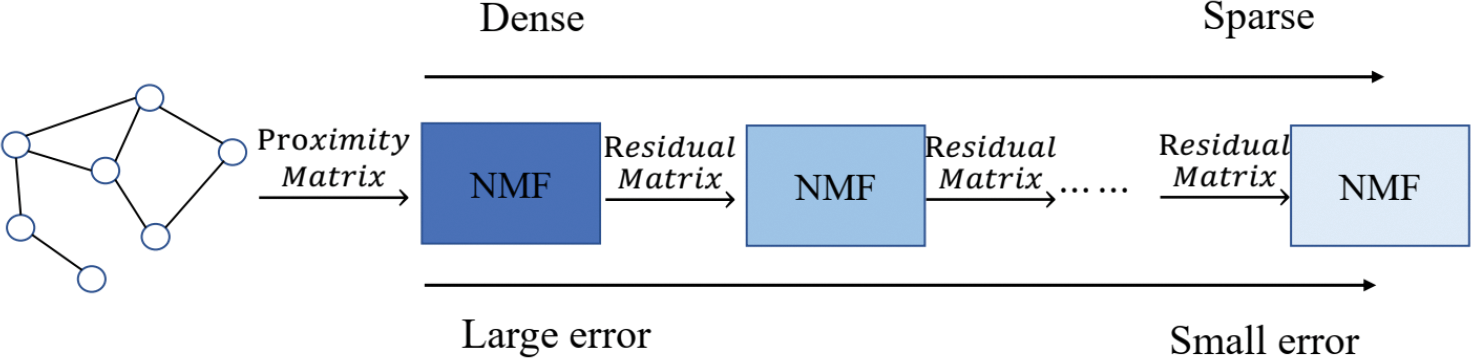
Figure 4: Multi-stage matrix factorization
Table 2 provides an overview of some typical existing MF-based HNE models. In summary, MF-based HNE models are mainly convenient for modeling the structural information of the HINs. They usually have relatively simple encoding and decoding functions and run efficiently. However, this type of model usually has the following disadvantages:
• Such models have poor ability to capture the attribute information and diverse semantic information of heterogeneous networks. Although some MF models take attribute information into account when generating node embeddings (such as MIFHNE and
• In some MF models that consider higher-order proximity (such as MEGA [35], CMF [22], and MNMF [5]), the proximity matrices to be decomposed are usually dense matrices. For a large-scale network, storing and decomposing a large dense proximity matrix consumes significant memory resources, which makes it difficult to implement on ordinary computing platforms.
• Most encoders of such models are direct encoding, and the model input depends on the number of nodes; therefore, they are generally transductive models, which are difficult to extend to dynamic networks.

Random walk (RW) based models are also very common network embedding models. Typical homogeneous random walk models are DeepWalk [33] and node2vec [37]. In contrast to MF-based models, the neighbor nodes in RW-based models are defined as nodes that co-occur in a short sequence of random walks. The optimization goal of most RW models is to make nodes that frequently co-occur in short sequences of random walks on heterogeneous networks have similar embeddings.
That is, this kind of approach is to learn embeddings so that
where
Compared with MF models, random walk-based models have better flexibility and can easily model higher-order neighbor relationships. Furthermore, if the random walk path-sampling process is given some strategic control, such as restricting it to follow a specific relation path (meta-path), it is convenient for a random walk model to capture the specific semantic information contained in the HINs.
Random walk-based HNE models are generally implemented in two stages: 1) sampling a large number of random walk sequences in the HIN from each node according to a specific strategy, 2) learning the optimized node embeddings using the skip-gram (or CBOW) model.
3.2.1 General Heterogeneous Random Walk Embedding Model
In the context of heterogeneous graphs containing nodes from different domains, classical random walks are biased to highly visible domains where nodes are associated with a dominant number of paths [4]. To overcome the skewness problem that random walk may cause, Hussein et al. proposed a JUST model [38] that uses a special
Heterogeneous networks contain rich semantic relationships. If the HNE models do not distinguish between different relationships when modeling, the generated node representations are bound to lose rich semantic information, such as HINE [40] and JUST. To deal with the various semantic relations contained in HINs, the MNE model [41] divides the embedding of each node in the subnetwork
where
Other general RW-based HNE models are summarized in Table 3. In particular, the hyper-gram [42] model uses a novel indicator to describe the indecomposability of the hyperedge in a heterogeneous hypergraph, followed by a random walk sampling algorithm based on a hyper-path and the corresponding hyper-gram optimization algorithm. The GERM [43] model uses a genetic algorithm to select the most informative relation type (subgraph pattern) in a heterogeneous network pattern for a specific ML task, and then uses the generated edge type activation vector (ETAV) to guide the random walk process to reduce noise and model complexity. These two models provide new perspectives for designing random walk sampling procedures. Moreover, because GERM mines the most informative relational patterns for specific ML tasks in the HIN schema, it is also intrinsically related to the automatic mining of meta-paths to be discussed later.
3.2.2 Metapath-Based Random Walk Embedding Models
Since the concept of meta-path was proposed by Sun et al. [44] in 2011, numerous studies have used metapath-based random walk techniques to generate node embeddings. Compared with general RW-based models, metapath-based RW models better capture various types of semantic information contained in the HINs. The characteristic of this type of model is that when a walker performs a random walk in an HIN, it should follow a predefined specific meta-path.
Definition 3. meta-path [4]: A meta-path
Taking Fig. 1a as an example, the three meta-paths shown in Fig. 5a can be defined as
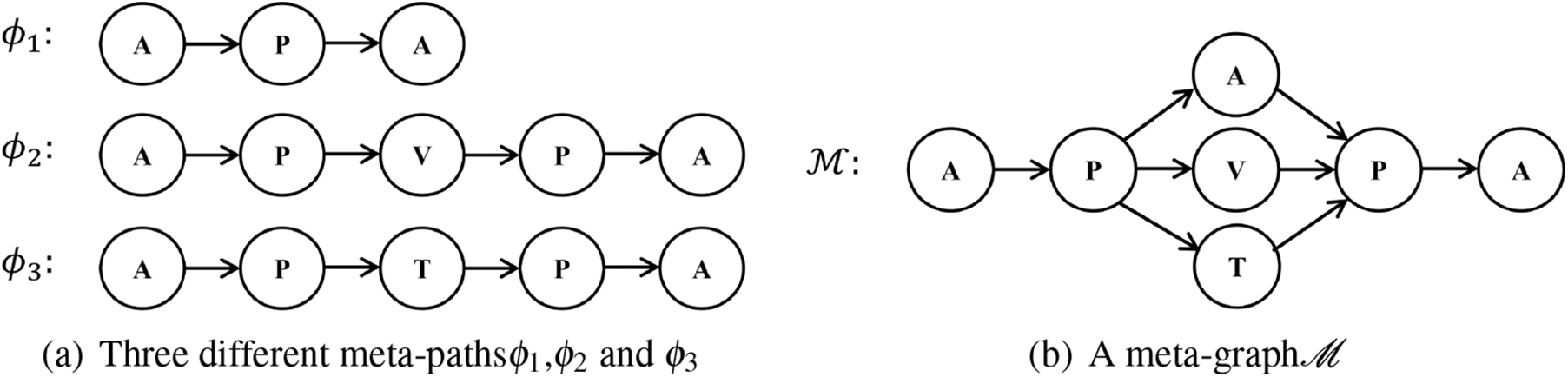
Figure 5: Examples of meta-paths and a meta-graph based on Fig. 1
To address the network heterogeneity challenge, Dong et al. proposed a classic metapath-based random walk model called metapath2vec [4]. The model defines a random walk sampling method based on a meta-path
Then, based on the sampled random walk sequences, the heterogeneous skip-gram algorithm is used to learn the model parameters. The loss function is defined as
Metapath2vec can effectively deal with the heterogeneity issue, and capture the structural and specific semantic information of the HINs. However, it only uses a single meta-path in random walk sequence sampling, which makes the generated node representations capture only limited semantic information; meanwhile, sequence sampling based on a single meta-path can easily lead to the sampling of numerous short random walk sequences, causing the sparsity problem [45].
To capture more diverse semantic relations in HINs, Zhang et al. proposed a MetaGraph2vec model [45] that defines a meta-graph-based random walk strategy. A meta-graph is essentially a combination of multiple meta-paths, e.g., the meta-graph
In addition to the above models, there are many models that also belong to the metapath-based random walk models [31,48–53]. Noted that the HIN2VEC [49] model decomposes all the sampled random walk sequences based on the HIN schema into short meta-path sequences of length no more than
Table 3 presents an overview of the characteristics of some typical RW-based HNE models. In essence, the RW-based models also perform matrix factorization [54]. However, unlike MF models, because the neighbor nodes in RW models are neighbors that co-occur in a sequence of random walks, RW-based HNE models always factorize higher-order proximity matrices. Moreover, most RW models use edge sampling to generate data samples. Therefore, the RW-based model avoids the drawback of directly decomposing large and dense matrices, providing better flexibility than MF models. However, this type of model still has some shortcomings:
• The random walk-based edge sampling can easily lead to skewness issues, which can make the HNE model unbalanced during training; the model is likely to be well-trained in dense subnetworks but far from convergent in sparse subnetworks. Hence, the random walk strategy must be carefully designed to mitigate the skewness problem.
• In random walk models using meta-paths, the definition of the meta-paths generally depends on the engineer’s prior knowledge and experience. If the meta-path is not well defined, it may add noise to the HNE model and useful network information may be lost. It would be appreciable to study the automatic extraction of efficient meta-paths from HINs.
• Similar to MF models, most RW models use direct encoding. Because there are no shared parameters between node embeddings, this may affect the training efficiency of the model.
• The random walk models can capture the low- and high-order structural information of the network, but similar to the MF model, they cannot handle the attribute information well: the attribute information usually needs to be encoded separately. For example, in the SHNE model [50], the text attribute information in the HIN is encoded using a specialized gated recurrent unit-based recurrent neural network.
The AE-based HNE models are different from other types. The model input of this model type is no longer a one-hot identification vector but an adjacency vector

Figure 6: The framework of autoencoder-based models. The encoder of this model type is usually a multi-layer neural network framework (called hidden layers), which maps the input vector
Most AEs are implemented through various types of neural networks, such as feed-forward neural networks (FNNs), sparse AEs, denoising AEs, contractive AEs, and variational AEs. Common AE-based homogeneous network embedding models include SDNE [55], DNGR [56], and VGAE [57]. For HINs, an AE-based HNE model should also fully consider the networks’ heterogeneity.
The SHINE model proposed by Wang et al. [58] is a basic heterogeneous extension of homogeneous network embedding. It first uses three AE neural networks to compress user node adjacency vectors in three different subnetworks; then, it aggregates the node representations in different subnetworks to obtain the unified node embeddings. However, because the input to this model is the node’s first-order adjacency vector, it can only capture the second-order structural features. DHNE [21] and Event2Vec [59] can capture both first- and second-order structural features. Specifically, to capture the first-order structural information, DHNE uses a deep neural network framework to define a nonlinear multivariate function
To capture the second-order structural information, DHNE defines an adjacency matrix
Finally, DHNE merges the two loss functions into one model for unified training.
Besides low-order structural information, the ability of the HNE model to capture high-order structural information is also important. DIME [60] and AMPE [61] extend the definition of neighbor nodes with metapath-based neighbor nodes, thus capturing higher-order structural information of the network. Specifically, DIME first defines multiple meta-paths
and the final loss is defined as
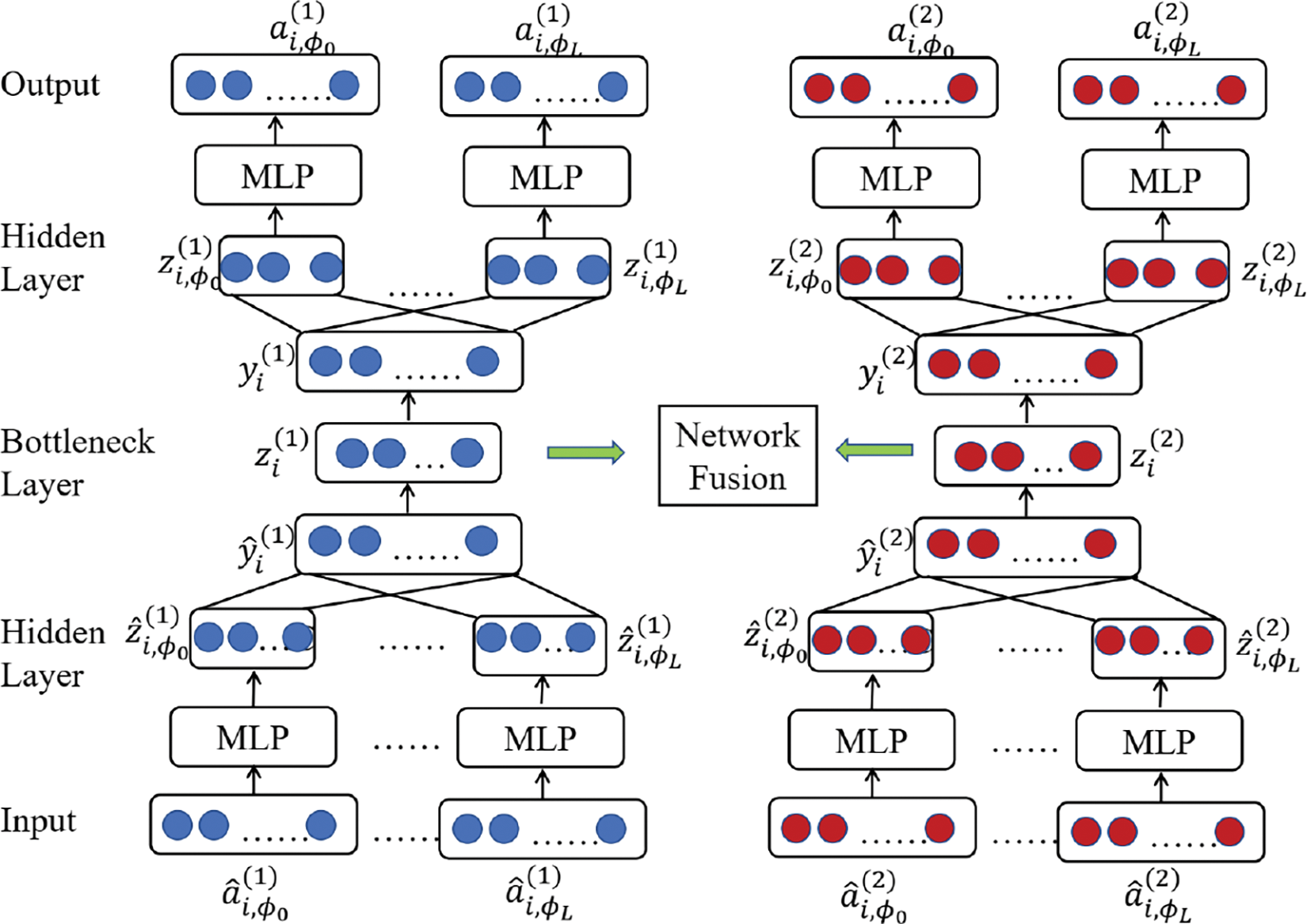
Figure 7: DIME model framework
As mentioned above, in addition to capturing network structure information, HNE models often need to deal with diverse network attribute information. AMVAE [62] and AEHE [63] are two AE-based HNE models that incorporate content attribute embeddings. For the text information
Table 4 gives an overview of the features of some representative AE-based HNE models. In summary, the overall advantage of an AE-based HNE model is that it can easily compress the neighbor vectors through various types of AE frameworks to capture network structural features directly. However, such models often have the following disadvantages:
• For large- and ultra-large-scale heterogeneous information networks, the input adjacency vectors to AE-based models are usually high-dimensional (tens of thousands to hundreds of millions). Building a general multi-layer AE neural network structure usually involves numerous training parameters in the model. Therefore, the training complexity of such HNE models is very high and difficult to implement on general computing platforms.
• As the input of such models depends on the number of nodes in the network, the models are usually transductive and cannot handle dynamic networks.

3.4 Graph Neural Network-Based Models
Inspired by the convolutional neural network (CNN), GNNs, which operate on the graph domain, have been developed in recent years [64,65]. GNNs are able to capture dependencies contained in graphs from graph structural information through information propagation (see Fig. 8). Different from previous types of models, the input of a GNN-based HNE model is usually the nodes’ affiliate attribute vectors, and its encoding function is a multilayer GNN, which continuously aggregates the features of the neighbor nodes around each central node as an update of the feature representation of the current central node. When L rounds of iterations are complete, the final node representation is the output of the encoder. Such models can easily and effectively capture the local structure and affiliated attribute information of HINs. Currently, GNN-based models achieve state-of-the-art performance on many graph-based tasks, including natural language processing, knowledge graphs, and protein networks. According to the way information is propagated in a graph, GNNs are mainly divided into spectral-based graph convolution, spatial-based graph convolution, graph attention networks, and graph spatiotemporal networks, etc. The corresponding representative models for homogeneous networks are GCN [66], GraphSage [67], GAT [68], and GGNN [69], respectively.
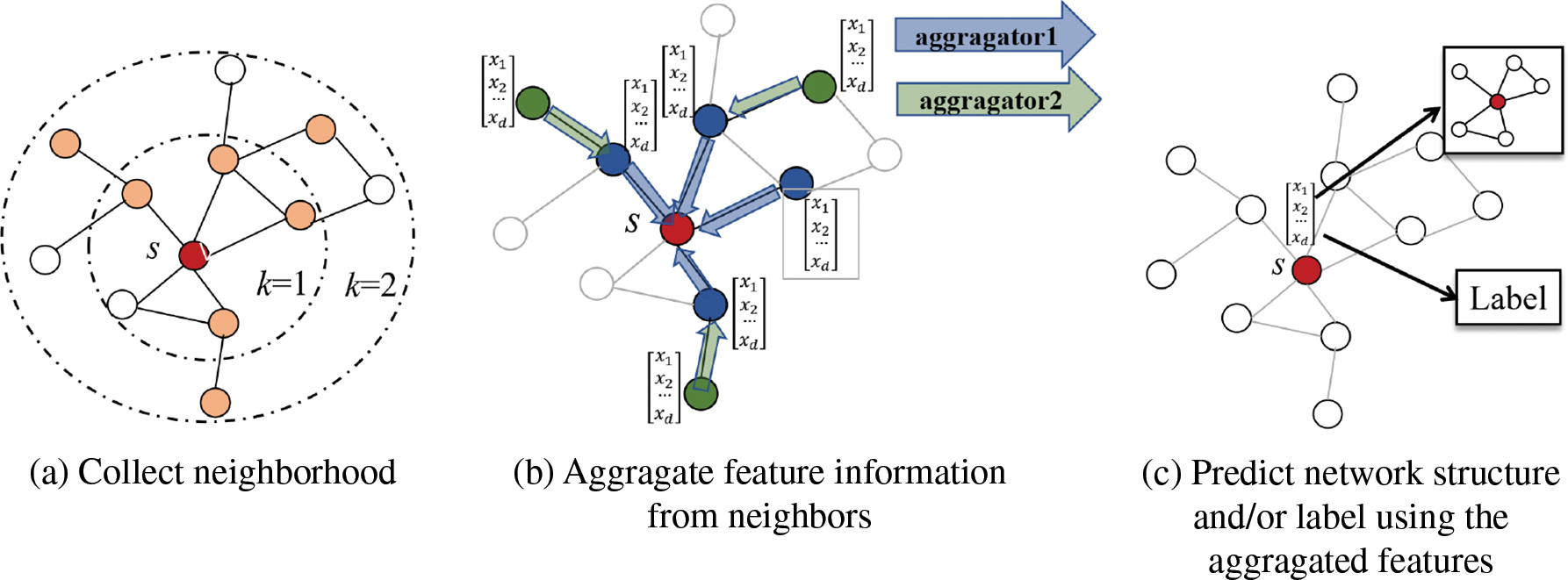
Figure 8: Overview of the GNN models. The figures are adapted from [67]
For HINs, because it is usually necessary to process different types of semantic information, feature aggregation usually follows a hierarchical aggregation strategy. In general, HNE models first use the first-level aggregation function
DMGI [70] is a spectral-based convolutional GNN model designed for multi-relational networks with heterogeneous attributes. The model first uses the GCN model [66] to aggregate the neighbor features of each node inside each subnetwork
where
The model then uses a consensus regularization framework to aggregate the relation-type specific node embeddings to generate the final consensus node embeddings. Owing to the introduction of the DGI method, the DMGI model can not only capture the attribute information and low-level structural information, but also effectively capture the global structural information of the HINs.
However, in many GNN-based models (such as DMGI), the neighbor nodes in the HINs are defined as immediate neighbors. Several studies have extended the definition of neighbor nodes in heterogeneous networks using meta-path-based neighbors [6,72–79]. Such models are able to capture more specific semantic information and overcome possible sparsity issues. The HAN model [6] shown in Fig. 9 is a typical one. The core idea of HAN is to use a metapath-augmented adjacency matrix to replace the original adjacency matrix. It first projects the initial node attribute matrix using the following type-specific transformation:
where
where

Figure 9: HAN model framework
The HAN model can well capture low-order and high-order structural information, as well as specific semantic information, and can distinguish different weights for different neighbor nodes and different semantic relations (different meta-paths). The GraphInception [72], MAGNN [76], RoHe [79], HAHE [73], Player2Vec [74], HDGI [77], and MEIRec [75] models share a similar idea with the HAN model. They all use adjacency matrices based on a specific meta-path to replace the adjacency matrix
Owing to rapid development, the current research on GNNs has shown explosive growth, and there have been many other GNN-related studies [78,80–90]. We list some typical GNN-based HNE models in Table 5. To be specific, the FAME model [87] improves the efficiency of heterogeneous spectral convolution models using sparse random projections; the HWNN model [78] uses wavelet basis instead of Fourier basis for graph convolution operation, avoiding the time-consuming Laplace matrix decomposition operation; when the HetGNN model [80] aggregates the information of neighbor nodes, it selects the top-
In summary, GNN-based HNE models have a good ability to capture attribute information as well as low and high-order structural features. In addition, the input of spatial-based GCN models can be independent of the number of nodes in the current network, so such models are inductive models that can generate embeddings for nodes that are not currently observed. However, this type of model still face the following challenges:
• In a large-scale heterogeneous network, it is very resource intensive to aggregate the features of all the neighbor nodes of one node. Many GNN models use neighbor sampling to reduce model complexity. However, the distribution within different subnets in an HIN may vary substantially. Neighbor sampling must be carefully designed so that the sampling nodes include relatively important neighbor nodes, otherwise important network information may be lost.
• In the GNN model, the number of network layers is key to the performance of the model. A model that is too shallow cannot capture the high-order features of the network; however, blindly increasing the number of layers of a GNN network may degrade the performance of the model while increasing the training complexity of the model [92]. Because the graph convolution operation will make the feature representations of adjacent nodes increasingly more similar, in theory, when there are enough layers, the feature representations of all the nodes in a connected graph will converge to a single point [64], which is called the over-smoothing problem. In addition, when there are too many layers, the model will also amplify some noise due to the continuous iterative convolution operation, making the model more vulnerable to attack. Therefore, how to deal with the problem that the model cannot be deeper remains a challenge in GNN-based models.
3.5 Knowledge Graph Embedding-Based Models
In recent years, knowledge graph techniques have been rapidly developed. Numerous knowledge graphs, such as WordNet [93], Freebase [94], and Yago [95], have been successfully applied to many practical applications. A knowledge graph can be represented by the triple
Most KGE models also use the direct encoding, and the decoder is always a ternary scoring function
3.5.1 Translation Distance-Based KGE Models
TransE [97] is a typical translation distance-based KGE model. Its basic idea is to regard the relationships in the knowledge graph as a transformation from the head to tail entity. Specifically, it assumes that if the triple
The loss function of the TransE model is a margin-based ranking loss defined on the training set:
TransE is very simple and efficient but does not handle one-to-many and many-to-many relationships well. To overcome the shortcomings of TransE, models such as TransH [98], TansR [99], TransD [100] extend the TransE model by allowing entities to have different embeddings for different relations. The simple illustrations of TransE, TransH and transR models are shown in Fig. 10. Furthermore, KG2E [101], TransG [102], and SE [103] are also translation distance-based KGE models. Unlike other models, KG2E and TransG assume that relations and semantics are inherently uncertain, and they use Gaussian distributions to model the entities and relations in knowledge graphs.
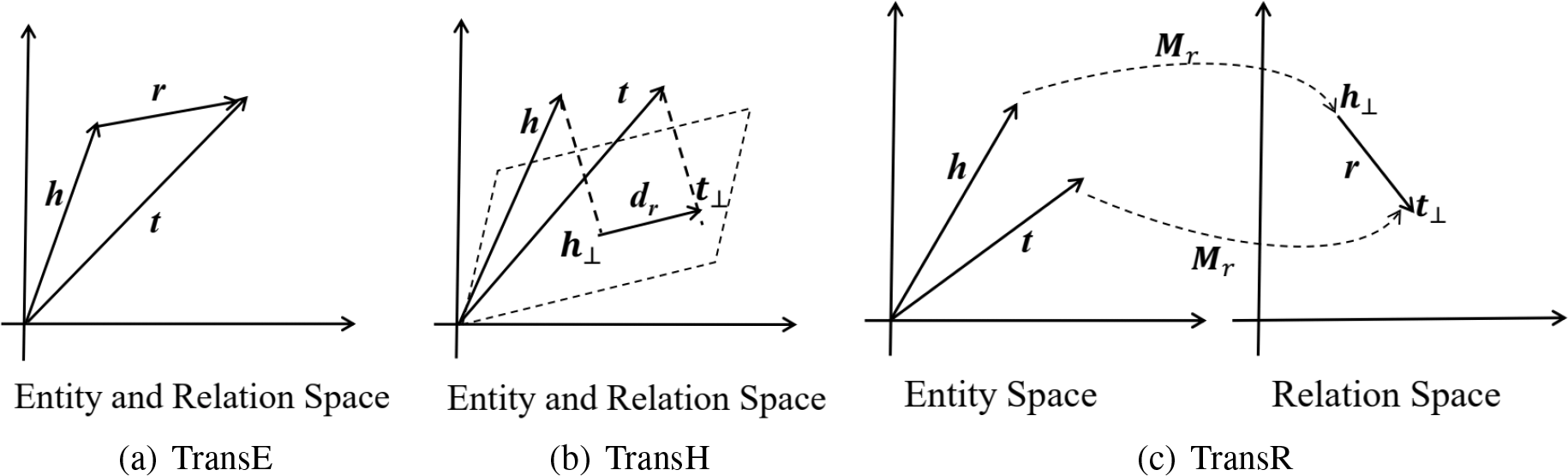
Figure 10: Simple illustrations of TransE, TransH, and TransR models. The figures are adapted from [96]
3.5.2 Semantic Matching KGE Models
The RESCAL model [104] is a typical semantic matching model. In this model, each entity is represented as a vector and each relation
The DistMult model [105] simplifies the matrix
In addition to RESCAL and its extended models, some semantic matching models employ neural network-based frameworks to semantically match entities and relationships [106,107]. ConvE [106] is a semantic matching KGE model that uses a multilayer CNN architecture. The model mainly consists of an encoder and a scorer. For the input triplet
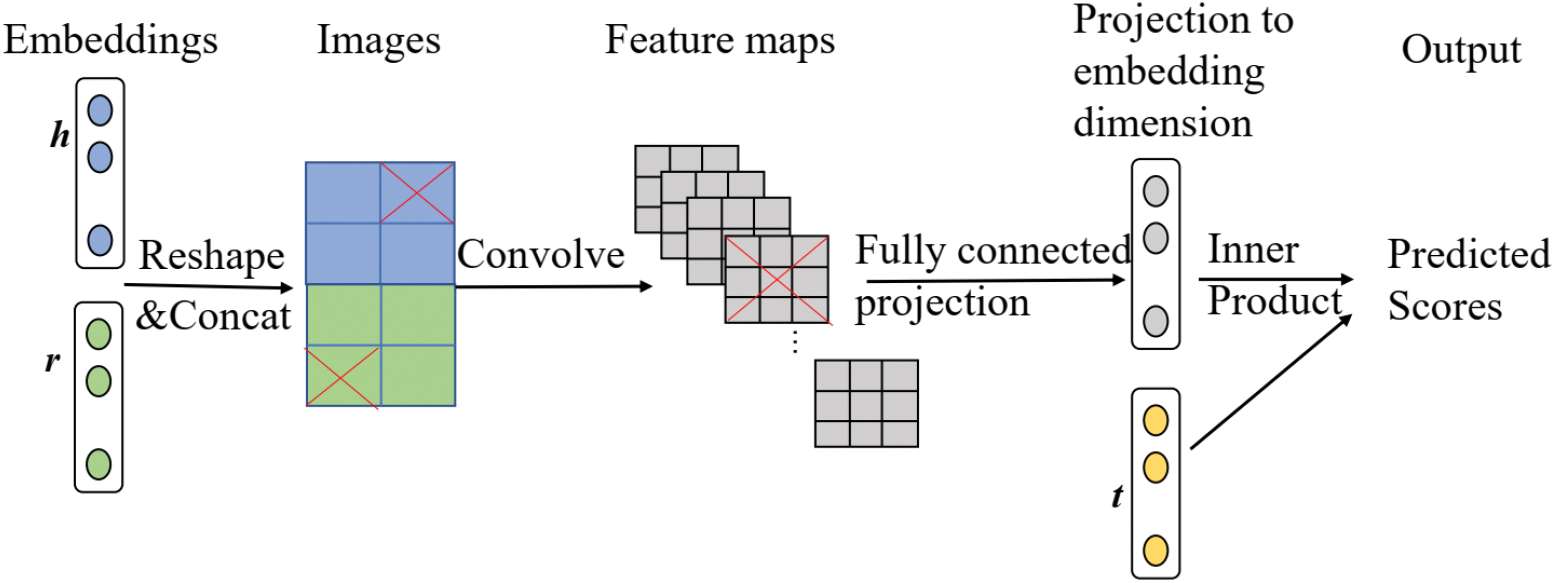
Figure 11: The ConvE model framework. In this model, the entity and relation embeddings are first reshaped and concatenated (Step 1); and then the resulting matrix is then used as input to a convolutional layer (Step 2); the resulting feature map tensor is vectorised and projected into a
Due to the introduction of CNN in the KGE model, the expressive power of the ConvE model is enhanced, and the number of model parameters is controlled.
NTN [107] is another semantic matching model. It uses a neural network structure to describe each triple and gives a score, which is an extension of the SLM model [107]. For a given triple
where
We summarize the basic characteristics of some of the most common KGE models in Table 6. For more other KGE models, we refer the reader to the KGE review [96]. In general, the main difference between KGE and other types of models is that KGE models are able to generate representations for relations in an explicit manner, thus more fully expressing the heterogeneity of relational semantics in the HINs. However, the basic KGE model has the following defects:
• The encoder usually has the disadvantage of direct encoding.
• Such models usually only consider the low-order neighbor relationships when modeling the structural information of the HINs.
• Further, such models usually do not model attribute information.
In order to improve the quality of generated embeddings, some KGE models extend the basic KGE model [110–112], and some models combine more other network information when generating embeddings, including entity attribute information [113], relations path [114], logic rules, and supervision information for some downstream ML tasks. Common downstream ML tasks related to knowledge graphs mainly include knowledge graph completion, link prediction, and recommender systems [115], etc.
To leverage the advantages of multiple techniques, some hybrid models have been proposed.
Some models fuse graph nueral networks and random walk techniques to generate network embeddings. The typical idea of this type of model is to use GNN as the encoder instead of the direct encoding function in the common random walk-based models [116,117].
GATNE [116] is one such type of hybrid model. The idea of GATNE is similar to the MNE model [41], but it is more general. Specifically, GATNE first uses the GNN framework to aggregate the neighbor node features of each node within each sub-network
where
Due to the introduction of the GNN encoder in the random walk-based model, the GATNE model can not only flexibly encode low-order and higher-order structural information, but also capture the attribute information of the network well.
As mentioned in Section 3.5, traditional KGE models are usually not good at handling higher-order structural information and attribute information. Some studies used the GNN encoder to replace the direct encoding function in the basic KGE model to improve the modeling ability of the HNE models [118–121].
LinkNBed is a KGE model that incorporates the idea of GNN. The model contains three layers: atomic, context, and final representation. At the atomic level, the model directly encodes all entities, relationships, entity types, and attribute information contained in the knowledge graph as follows:
where
where
Because of the introduction of GNN encoders based on KGE models, this model can effectively capture more information in HINs, including low-order, high-order structural information, relational semantic information, and attribute information.
Similar to the LinkNBed model, the NKGE [120], CACL [121], SACN [119], LightCAKE [122] and HRAN [123] models are also KG+GNN-type hybrid models. The main difference among these models is the type of encoder or decoder: LinkNBed and LightCAKE use a GAT network when aggregating neighbor node information, SACN uses a GCN model, NKGE uses a deep memory network, and HARN uses a two-level GNN. When defining the ternary scoring function, LinkNBed uses a simplified version of the bilinear function, LightCAKE uses TransE/DistMult, SACN and NKGE use ConvE models, whereas CACL and HRAN use CNN-based deformation models.
To reduce the influence of noise and enhance the robustness of the model, some studies fuse the VAE framework with GNNs [124,125].
The RELEARN model [124] shown in Fig. 12 is a VAE framework designed for relational learning in a multi-relational heterogeneous social network. This model firstly represents the edge embedding
where

Figure 12: RELEARN model framework
Due to the use of the VAE framework, the RELEARN model can not only capture various types of information in the network, but also has good robustness.
Besides the above categories of hybrid models, some other types of hybrid models have been proposed, such as the KGE + RW models [126]. Moreover, some emerging hybrid models use reinforcement learning [127] or adversarial learning [128,129] frameworks. We provide a summary of some common hybrid HNE models in Table 7.

Sections 3.1 to 3.6 present an overview of the six existing HNE model types. For each type, we list the main characteristics of some representative models and use detailed tables to analyze and compare the basic elements of each model. It can be seen that the existing six models have obvious differences in encoder, decoder and empirical proximity matrix. At the same time, we also analyze their modeling ability in terms of capturing structural, relational semantic and attribute network information.
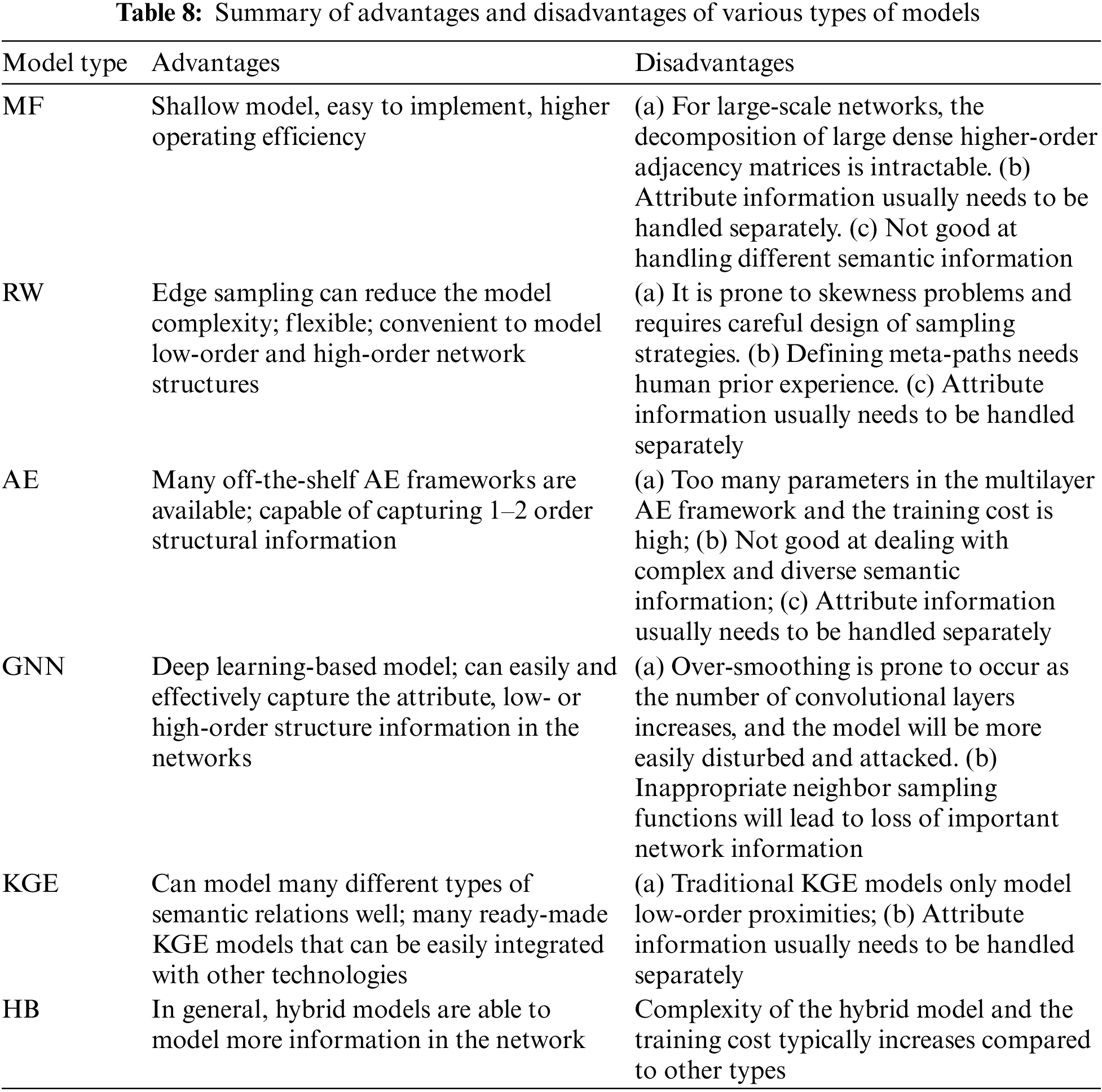
We summarize the advantages and disadvantages of these models in Table 8. From the perspective of modeling capability, MF models and KGE models are good at modeling low-order structural features, whereas other types are good at modeling both low- and high-order structural features. Furthermore, the KGE model has stronger semantic modeling capabilities, whereas GNN models have good ability to capture the attributes and higher-order structural information of the network. Hybrid models are usually able to model more network information by leveraging the advantages of multiple models.
4 Application Fields, Benchmark Datasets, Open Source Code, and Performance Comparison
This section focuses on application fields, benchmark datasets, open source tools, and performance evaluations for HNE.
4.1 Application Fields and Evaluation Metrics
Once new vertex representations are learned via HNE techniques, they can be used to solve various subsequent machine learning tasks. HNE benefits various graph analytics applications such as node classification, node clustering, link prediction, recommender systems, visualization (Fig. 13). Meanwhile, the effectiveness of representation learning can also be validated by evaluating their performance on these various subsequent tasks [12].
Figure 13: Application fields of HNE
Node classification is perhaps the most common benchmark task for evaluating node embeddings. Typically, network vertices are partially or sparsely labeled owing to high labeling costs, and most vertices in a network have unknown labels. The vertex classification problem aims to predict the labels of unlabeled vertices given a partially labeled network, e.g., determining the research field or affiliation information of an author. A good vertex representation improves the accuracy of node classification.
According to the classification task, node classification can be further divided into binary-class classification, multi-class classification, and multi-label classification (each node is associated with one or more labels from a finite label set). In the application of HNE, most cases are multi-class classification [4,21,45,52,72,112] or multi-label classification [5,21,39,48,49,52,61,62,72,80], and these models tipically use the Micro_F1 or Macro_F1 as the performance evaluation metric [5,6,21,26,30,32,38,48,49,52,59,61,70,73,76,77,80,86,87,112,127,129]. A few models use the average accuracy (ACC) [41,45] or the mean average precision (MAP) [62] as the evaluation metric.
Node clustering is also a very common application of HNE models. Its goal is to cluster similar nodes into the same cluster and dissimilar nodes into different clusters as much as possible. Node clustering has a wide range of uses in bioinformatics, computer science, and sociology; for example, clustering a group of proteins with the same function in a biological network or clustering groups of people with similar interests in a social network into a cluster.
For simplicity, most HNE studies choose
Link prediction is a very important ML task in graph mining systems. Its goal is to predict possible connections or existing but not observed relationships in current heterogeneous networks. Link prediction techniques can discover implicit or missing interactions in networks, identify false links, and understand network evolution mechanisms. For example, predicting unknown connections between people in social networks can be used to recommend friendships or identify suspicious relationships. Alternatively, link prediction methods are used in biological networks to predict previously unknown interactions between proteins, thereby significantly reducing the cost of empirical methods. A good network representation should be able to capture both explicit and implicit connections between network vertices, enabling applications to predict links.
Link prediction is often viewed as a simple binary classification problem: for any two potentially linked objects, the task is to predict whether a link exists (1) or does not exist (0). The vast majority of existing link prediction tasks use the area under the receiver operating characteristic curve (AUC) as the performance evaluation metric [30,31,36,39,41,42,48,52,59,60,62,76,80,110,112,116,130–132]. In addition, some studies use the F1-score [58,60,80,112,116], average precision [36,49,53,58,60,76,132], or recall [50,60] as the performance evaluation metric for link prediction tasks.
HNE is also frequently used in Recommender Systems (RSs). RSs can significantly enhance the commercial value of enterprises and effectively reduce the information overload of users. For over a decade, many businesses and companies have used RSs to recommend friends, products, and services to their customers [27,43,47,88,91,115]. Recommendation tasks are closely related to link prediction, but the main difference is that link prediction outputs a binary prediction, whereas RSs output a ranking list of length K.
For RSs, the most commonly used performance evaluation metrics are precision@
4.1.5 Knowledge Graph Related Applications
Compared to general HINs, a knowledge graph has more abundant heterogeneous entity types and semantic relation types. The main application tasks related to KGE are link prediction, triple classification, and relational fact extraction.
Link prediction in a knowledge graph is a typical task of predicting an entity that has a specific relation with another given entity, i.e., predicting
The problem of graph visualization on 2D interfaces has been studied for a long time, with applications in areas such as biology, sociology, and data mining. Researchers can easily leverage existing general-purpose techniques to visualize high-dimensional datasets, which are useful for mining communities and other hidden structures. Common graph visualization approaches include applying a dimensionality reduction technique such as principal component analysis (PCA) [124] or t-distributed stochastic neighbor embedding (t-SNE) [4–6,26,31,51,61,72,73,76,86,88,125,129] to plot the node embedding vectors generated by the HNE models in a 2D space with different colors indicating the nodes’ categories.
Besides the most common HNE applications discussed above, the applications of HNE models also include similarity search [45,51,70,86], information retrieval [50,130], network alignment [29,81], user profiling [83], and anomaly detection [63].
Benchmark datasets play a critical role in the evaluation of HNE models. According to the types of heterogeneous networks contained in the datasets, the commonly used benchmark datasets in existing HNE models can be divided into categories such as social networks, bibliographic networks, text networks, biological networks, knowledge graphs.
DBLP2 and Aminer3 [135] are the most frequently used bibliographic network datasets [4,6,26,28,30,32,36,38,48,49,51,52,59,61,70,72,73,76,78,79,82,86,112], whereas some other models use ACM4 [6,32,48,70,72,77,79,86], Cora [78,82,104,126], DBIS [4,39], or other datasets. Moreover, the most frequently used social network datasets are Twitter5 [26,28,30,41,60,128], Flickr6 [5,30,62,130,136], and Gowalla7 [27]. Among the commercial networks, the Yelp8 and Amazon9 datasets have been widely used [36,39,46–49,51,61,73,88,110]. 20NG10 and WikiPedia11 are commonly used text network datasets [22,26,28,58,113]. MovieLens12, IMDB13, MR14, and YahooMusic15 are widely used video and music datasets [21,26,28,36,39,42,47,52,82,88,91,115]. In the field of KGE, Wordnet16, Freebase17, and Yago18 are widely used knowledge bases [21,42,97–103,105–109,111,113,119–123,126].
4.3 Open Source Code and Tools
Open source codes and platforms are also critical for HNE research. In this section, we list some open source codes and platforms.
Open source code plays a very important role, enabling researchers to reproduce or improve existing HNE models. We extracted the open source code of some common HNE models from related papers, as listed in Table 9.

4.3.2 Open Source Platforms and Toolkits
Open source platforms and toolkits can help researchers quickly and easily build workflows for HNE. We summarize several popular toolkits and platforms for heterogeneous graphs as follows:
• Deep Graph Library (DGL). The DGL is an easy-to-use, high-performance, and scalable open source platform for deep learning on graph data. DGL collects rich example implementations of popular GNN models on a wide range of topics, such as GCMC, MAGNN, and HGT. It provides independent application programming interfaces (APIs) for homogeneous graphs, heterogeneous graphs, and knowledge graphs. The official website of DGL is https://www.dgl.ai/.
• PyTorch Geometric (PyG). PyG is a library for deep learning on irregularly structured input data such as graphs, point clouds and manifolds, built upon PyTorch. In addition to general graph data structures and processing methods, it contains a variety of recently published methods from the domains of relational learning and 3D data processing [137]. Related code and documentation can be found at https://pytorch-geometric.readthedocs.io/en/latest/.
• OpenKE. OpenKE is an open source framework for knowledge embedding organized by THUNLP based on the TensorFlow toolkit [138]. OpenKE provides a fast and stable toolkit including the most popular knowledge representation learning methods such as TansE, TransR, and TransD. OpenKE can support fast model verification and large-scale knowledge representation learning. Moreover, new models can be easily integrated into the OpenKE framework. Related toolkits and documentation are published at http://openke.thunlp.org/.
• OpenHINE. OpenHINE is an open source toolkit for HNE developed by researchers at the DMGroup of Beijing University of Posts and Telecommunications. It unifies the input/output/evaluation interface of the HNE model, and in addition, it revises and reproduces classic HNE models, including DHNE, HAN, HeGAN, HERec, HIN2vec, Metapath2vec, MetaGraph2vec, and RHINE. Related code and datasets can be found at https://github.com/BUPT-GAMMA/OpenHINE.
4.4 Performance Evaluation of Heterogeneous Network Embedding Models
In this subsection, we compare the performance of some typical HNE models on a subset of the publicly available DBLP dataset [139] for the link prediction task [112,125].
The dataset consists of 14,475 authors, 14,376 papers, 20 conferences, 8,920 words, and a total of 170,794 links. There are three types of relationships in the heterogeneous network: “paper-conference,” “paper-author,” and “paper-word.” The HNE models in the comparison include examples from most of the six model types: PTE, metapath2vec, ESim, HIN2Vec, HGT, TransE, ConvE, HEER, RHINE, HGCN, and HeteHG-VAE. For the link prediction task for all models, the heterogeneous edges in the original HIN are divided into two parts: 80% of the edges were used for training, and the remaining 20% were used for testing. The performance evaluation metric was AUC. Table 10 presents the performance comparison of all models on the link prediction task.

As Table 10 reveals, the performances of the various HNE models on the link prediction task differ. The KGE model TransE performs relatively poorly because its model assumptions are too simple and it is only suitable for one-to-one semantic relations. Slightly better than the TransE model are the random walk-based models metapath2vec, Esim, and HIN2Vec. The performances of these three models are mediocre, indicating that the earlier random walk models have some disadvantages: ESim and HIN2Vec use random walk sequences that are too short; metapath2vec uses a single meta-path, which limits the amount of semantic information that can be captured. With performances above the performance of the RW-based models are two other KGE models (ConvE and HEER) and the matrix factorization-based model PTE. The GNN-based model HGT, hybrid model HGCN, and HeteHG-VAE perform relatively well, which demonstrates that GNN-based models capture the network information of HINs well. The hybrid model HeteHG-VAE uses the framework of variational AEs on top of the two-level GNN aggregation, which increases the robustness of the model. Hence, its performance is the best.
5 Future Directions and Open Issues
HNE has made great progress in recent years, which clearly shows that it is a powerful and promising graph analysis paradigm. In this section, we discuss and explore a range of open issues and possible future research directions (Fig. 14).

Figure 14: Future directions and open issues
5.1 Improving the Interpretability
Feature representation learning greatly reduces the workload of manual feature extraction, but such methods usually face the significant problem of poor interpretability, especially in some deep learning-based embedding models. The neural network structure is like a “black box.” A common argument against deep neural networks is that their hidden weights and activations are often unexplainable. Even if it has been experimentally verified that the embeddings generated by their own methods achieve good performance, one cannot gain a deep understanding of the application limitations of the model itself without interpreting the meaning of the learned feature representations. Generally, interpretability has two meanings: 1) interpretability for end users, i.e., explaining to users why the recommendation or prediction models based on HNEs give such results, and 2) interpretability for the implementer, i.e., enabling the researcher to understand the meanings of the weights, biases, and activation functions included in the model.
Some studies have considered the design of interpretable HNE models. Common approaches to improve model interpretability include exploiting the rich information in knowledge graphs to generate interpretable paths [133,140], attention mechanisms, and visual aids. We believe that it would be a good research direction to integrate inference models with ML techniques to design interpretable embedding models for specific ML tasks.
Real-world HINs are often highly skewed. For such heterogeneous networks, if the skewness problem is not considered when designing the HNE model, it is likely that the model will be unbalanced during training, i.e., the model may be well-trained for some densely populated subnetworks but far from convergence in some relatively sparse subnetworks. A good feature representation learning model should overcome this problem.
A typical idea of existing studies that deal with skewness is to control the edge sampling to ensure the number of samples of different relation categories in the dataset is as balanced as possible [4,38,110]. However, this artificial control often changes the original distribution of the data, impacting the effectiveness of the embeddings generated by the model. We believe that future research requires a deeper understanding of the nature of skew phenomena and better solutions.
5.3 Beyond Local Structural Proximity
Many traditional graph representation learning models only consider the local structural proximity between nodes. Node embeddings generated in this type of model are usually based on “homogeneity”. That is, the goal of solving the model is to make the feature representations of nodes with smaller network distances more similar, and vice versa more dissimilar. Most network structure information other than local network structure features is ignored, including structural role proximity, community structures, and motif structural features. This results in the generated node embeddings losing much topological information and they may not meet the needs of various specific ML tasks.
Currently, some studies based on homogeneous network embeddings consider the structural equivalence of nodes [37,141,142]. Moreover, some studies have considered the global structural features [70,77,143] or higher-order triangle motif [144] when generating network embeddings. However, the vast majority of existing HNE models ignore these issues. How future HNE models can improve the ability to capture structural features other than local structural proximity remains a challenging problem.
Real-world networks are constantly changing. However, the vast majority of existing models are designed for static snapshot networks and do not consider the temporal characteristics of the network, resulting in the generated feature embeddings performing poorly on some time series-related ML tasks, such as abnormal event sequence detection and temporal link prediction. In addition, most existing HNE models are transductive and can only generate embeddings for nodes that are currently observed in the network. This leads to the need to constantly retrain the HNE model when the network structure changes, which significantly increases resource consumption.
To handle the dynamics of the HINs, we consider there are two possible solutions: 1) when designing HNE models, consider the timing characteristics of the networks; 2) design inductive models such that they can generate embeddings for currently unobserved nodes in the HINs. There have been some studies devoted to generating embeddings for dynamic networks [145–149]. Such studies often use some deep memory networks, such as LSTM, to capture the temporal characteristics of network events. Moreover, some studies have designed inductive models to overcome the shortcomings of the transductive models [67,116]. The main feature of inductive models is that the input to the model does not depend on the number of nodes in the current networks, e.g., using auxiliary attributes other than the node one-hot encoding vectors as the input of the HNE models. Because of the dynamic and real-time nature of real-world networks, we believe that learning time-dependent embeddings for continuous-time dynamic networks and developing inductive network embedding models are very promising research directions.
5.5 Dealing with Heterogeneity
HINs usually contain rich heterogeneous attribute and relationship information: different types of nodes, different types of attributes, different types of semantic relations, and even the same type of node pairs may contain multiple different semantic relations. Highly heterogeneous networks bring challenges to the design of HNE models.
Of the existing models, GNN-based models usually have better ability to integrate the affiliated attributes. Meanwhile, KGE models perform better in handling various types of semantic relations. In addition, for multimodal heterogeneous networks containing multiple different attribute information (such as text, image, video), many studies have used various types of deep neural networks such as FNN, CNN or RNN to extract attribute features, and fuse the generated content embeddings into the final node embeddings [50,62,130]. This is more common in MF, RW, and AE types of HNE models. Some other studies have treated network node attributes as nodes in the network and generated embeddings for attribute nodes while generating entity node embeddings [84,112]. All of the above approaches have improved the ability of the HNE models to deal with the multimodal and multiplex issues. Owing to the inherent heterogeneity of complex networks, we believe that in the future research field of HNE, fully considering the heterogeneity is still worthwhile.
Most existing HNE models focus on generating feature representations for the nodes in the HINs, whereas some HNE models extend this task to generate edge embeddings, subgraph embeddings [136,150], etc. Meanwhile, some other models combine the network embedding task with specific downstream ML tasks to perform multiple tasks in one model simultaneously [30,31,58,61,63,76,118].
Compared with single-task learning, multi-task learning has the following advantages:
• it usually uses more data labels, which can better overcome the problem of data sparsity.
• it can effectively reduce overfitting of the model to specific task data and generate feature representations with better generalization performance due to the need to meet the training objectives of multiple tasks. For example, if edge and subgraph embeddings are generated simultaneously as a node embedding, the generated network embedding will be able to better capture the semantic information and global structural information contained in the network.
Many existing HNE models are designed for small-scale heterogeneous networks and cannot be scaled to large- and ultra-large-scale networks. However, real-world HINs often contain hundreds of millions of nodes and complex relationships. For such huge networks, in addition to improving the computing power of hardware computing platforms, some researchers have considered using a distributed parallelization strategy to divide large datasets into multiple small data samples in a “divide-and-conquer” manner [85]; there are also some studies that reduce the model complexity by data sampling to reduce the amount of data to be processed [151]. These methods effectively improve the scalability of the HNE model for large-scale networks. However, we believe that besides the above strategies, more and better methods to improve model efficiency and scalability are to be studied.
Available real-world heterogeneous network data is often incomplete, including incomplete nodes, link relationships, or affiliated information. Also, the available data often contains erroneous and noisy information.
A powerful HNE model needs to tolerate such data incompleteness and noise to learn more robust network embeddings. Generally speaking, generative models are more robust than traditional models due to adding noise to the model input [62,124] or using an adversarial learning framework [79,129]. More strategies to improve the robustness of HNE models are to be investigated.
Most existing studies evaluate the performance of HNE models experimentally, and in-depth theoretical analysis is lacking, which may lead to model evaluation limitations and application bias problems. As mere experimental results may be limited to a specific dataset or task, failure to theoretically analyze and demonstrate the properties of the HNE model may result in the essence of the model not being deeply understood. In addition to the complexity analysis, if the theoretical characteristics of the model can be explored in more depth, it will substantially help us understand, apply, and expand the function of the model. For example, we could explore how deep learning models are intrinsically related to traditional models or explore higher-order Markov properties of random walks based on meta-paths. These theoretical analyses will bring more in-depth insights and rich perspectives to researchers.
In this paper, we provide a systematic and comprehensive review of research problems in HNE. From the encoder-decoder perspective, we divide existing HNE research into six categories: MF, RW, AE, GNN, KGE, and hybrid models. For each type of model, we first overview the basic common characteristics. Then, taking typical HNE models as examples, we systematically review each model type. We highlight the novel contribution of each representative HNE model, and summarize the advantages and disadvantages of each model type. We also provide a wealth of valuable relevant resources, including the application areas, benchmark datasets, open-source code and tools of this research field. Finally, we present an in-depth discussion about open issues and future directions. As a result, we believe that future HNE research must better deal with the heterogeneity, dynamics, skewness, and sparsity of the HINs; improve model interpretability, scalability, and robustness; and strengthen theoretical analysis to facilitate model application and expansion.
Acknowledgement: We would like to thank Dr. Rui Zhong for her kind suggestions on revisions to this paper.
Funding Statement: Our research work is supported by the National Key Research and Development Plan of China (2017YFB0503700, 2016YFB0501801); the National Natural Science Foundation of China (61170026, 62173157); the Thirteen Five-Year Research Planning Project of National Language Committee (No. YB135-149); the Fundamental Research Funds for the Central Universities (Nos. CCNU20QN022, CCNU20QN021, CCNU20ZT012).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
1In GNN models, a neighbor aggregation function
2http://dblp.uni-trier.de/xml/.
3https://www.aminer.org/data/.
5https://snap.stanford.edu/data/higgs-twitter.html.
7http://snap.stanford.edu/data/loc-gowalla.html.
8https://www.yelp.com/dataset/.
9http://jmcauley.ucsd.edu/data/amazon/index.html.
10http://qwone.com/jason/20Newsgroups/.
11http://www.mattmahoney.net/dc/textdata.
12https://grouplens.org/datasets/movielens/.
13https://ai.stanford.edu/amaas/data/sentiment/.
14http://www.cs.cornell.edu/people/pabo/movie-review-data/.
15https://github.com/fmonti/mgcnn/tree/master/Data/yahoo_music.
16https://wordnet.princeton.edu/.
17https://developers.google.com/freebase.
18https://yago-knowledge.org/.
References
1. Shi, C., Li, Y., Zhang, J., Sun, Y., Yu, P. S. (2016). A survey of heterogeneous information network analysis. IEEE Transactions on Knowledge and Data Engineering, 29(1), 17–37. https://doi.org/10.1109/TKDE.2016.2598561 [Google Scholar] [CrossRef]
2. Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., Dean, J. (2013). Distributed representations of words and phrases and their compositionality. Proceedings of 27th Annual Conference on Neural Information Processing Systems 2013, pp. 3111–3119. Nevada. [Google Scholar]
3. Levy, O., Goldberg, Y. (2014). Neural word embedding as implicit matrix factorization. Proceedings of Annual Conference on Neural Information Processing Systems 2014, pp. 2177–2185. Quebec. [Google Scholar]
4. Dong, Y., Chawla, N. V., Swami, A. (2017). metapath2vec: Scalable representation learning for heterogeneous networks. Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 135–144. Halifax. [Google Scholar]
5. Huang, H., Song, Y., Ye, F., Xie, X., Shi, X. et al. (2021). Multi-stage network embedding for exploring heterogeneous edges. ACM Transactions on Knowledge Discovery from Data, 15(1), 1–27. https://doi.org/10.1145/3415157 [Google Scholar] [CrossRef]
6. Wang, X., Ji, H., Shi, C., Wang, B., Ye, Y. et al. (2019). Heterogeneous graph attention network. Proceedings of the World Wide Web Conference, pp. 2022–2032. San Francisco. [Google Scholar]
7. Peng, C., Wang, X., Pei, J., Zhu, W. (2019). A survey on network embedding. IEEE Transactions on Knowledge and Data Engineering, 31(5), 833–852. https://doi.org/10.1109/TKDE.2018.2849727 [Google Scholar] [CrossRef]
8. Hamilton, W. L., Ying, R., Leskovec, J. (2017). Representation learning on graphs: Methods and applications. IEEE Data Engineering Bulletin, 40(3), 52–74. [Google Scholar]
9. Cai, H., Zheng, V. W., Chang, C. C. (2018). A comprehensive survey of graph embedding: Problems, techniques, and applications. IEEE Transactions on Knowledge and Data Engineering, 30(9), 1616–1637. https://doi.org/10.1109/TKDE.2018.2807452 [Google Scholar] [CrossRef]
10. Goyal, P., Ferrara, E. (2018). Graph embedding techniques, applications, and performance: A survey. Knowledge-Based Systems, 151(1), 78–94. https://doi.org/10.1016/j.knosys.2018.03.022 [Google Scholar] [CrossRef]
11. Wang, Y., Yao, Y., Tong, H., Xu, F., Lu, J. (2019). A brief review of network embedding. Big Data Mining and Analytics, 2(1), 35–47. https://doi.org/10.26599/BDMA.2018.9020029 [Google Scholar] [CrossRef]
12. Zhang, D., Jie, Y., Zhu, X., Zhang, C. (2020). Network representation learning: A survey. IEEE Transactions on Big Data, 6(1), 3–28. https://doi.org/10.1109/TBDATA.2018.2850013 [Google Scholar] [CrossRef]
13. Li, B., Pi, D. (2020). Network representation learning: A systematic literature review. Neural Computing and Applications, 32(21), 16647–16679. https://doi.org/10.1007/s00521-020-04908-5 [Google Scholar] [CrossRef]
14. Hou, M., Ren, J., Zhang, D., Kong, X., Xia, F. (2020). Network embedding: Taxonomies, frameworks and applications. Computer Science Review, 38(99), 100296. https://doi.org/10.1016/j.cosrev.2020.100296 [Google Scholar] [CrossRef]
15. Yang, C., Xiao, Y., Zhang, Y., Sun, Y., Han, J. (2022). Heterogeneous network representation learning: A unified framework with survey and benchmark. IEEE Transactions on Knowledge and Data Engineering, 34(10), 4854–4873. https://doi.org/10.1109/TKDE.2020.3045924 [Google Scholar] [CrossRef]
16. Xie, Y., Yu, B., Lv, S., Zhang, C., Gong, M. (2021). A survey on heterogeneous network representation learning. Pattern Recognition, 116(7), 107936. https://doi.org/10.1016/j.patcog.2021.107936 [Google Scholar]
17. Dong, Y., Hu, Z., Wang, K., Sun, Y., Tang, J. (2020). Heterogeneous network representation learning. Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, pp. 4861–4867. Yokohama. [Google Scholar]
18. Wang, X., Bo, D., Shi, C., Fan, S., Ye, Y. et al. (2020). A survey on heterogeneous graph embedding: methods, techniques, applications and sources. arXiv:2011.14867v1. [Google Scholar]
19. Ji, F., Zhao, Z., Zhou, H., Chi, H., Li, C. (2020). A comparative study on heterogeneous information network embeddings. Journal of Intelligent & Fuzzy Systems: Applications in Engineering and Technology, 39(3), 3463–3473. https://doi.org/10.3233/JIFS-191796 [Google Scholar] [CrossRef]
20. Tang, J., Qu, M., Wang, M., Zhang, M., Yan, J. et al. (2015). LINE: Large-scale information network embedding. Proceedings of the 24th International Conference on World Wide Web, pp. 1067–1077. Florence. [Google Scholar]
21. Tu, K., Cui, P., Wang, X., Wang, F., Zhu, W. (2018). Structural deep embedding for hyper-networks. Proceedings of the AAAI Conference on Artificial Intelligence, pp. 426–433. New Orleans. [Google Scholar]
22. Zhao, Y., Liu, Z., Sun, M. (2015). Representation learning for measuring entity relatedness with rich information. Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, pp. 1412–1418. Buenos Aires. [Google Scholar]
23. Ahmed, A., Shervashidze, N., Narayanamurthy, S. M., Josifovski, V., Smola, A. J. (2013). Distributed large-scale natural graph factorization. Proceedings of 22nd International World Wide Web Conference, pp. 37–48. Rio de Janeiro. [Google Scholar]
24. Belkin, M., Niyogi, P. (2001). Laplacian eigenmaps and spectral techniques for embedding and clustering. Proceedings of Annual Conference on Neural Information Processing Systems, pp. 585–591. Vancouver. [Google Scholar]
25. Ou, M., Cui, P., Pei, J., Zhang, Z., Zhu, W. (2016). Asymmetric transitivity preserving graph embedding. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 1105–1114. San Francisco. [Google Scholar]
26. Tang, J., Qu, M., Mei, Q. (2015). PTE: predictive text embedding through large-scale heterogeneous text networks. Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 1165–1174. Sydney. [Google Scholar]
27. Su, Y., Li, X., Zha, D., Tang, W., Jiang, Y. et al. (2019). Hrec: Heterogeneous graph embedding-based personalized point-of-interest recommendation. Proceedings of the 26th International Conference on ICONIP 2019, pp. 37–49. Sydney. [Google Scholar]
28. Tang, J., Qu, M., Mei, Q. (2016). Identity-sensitive word embedding through heterogeneous networks. arXiv:1611.09878v1. [Google Scholar]
29. Wang, Y., Feng, C., Chen, L., Yin, H., Guo, C. et al. (2019). User identitylinkage across social networks via linked heterogeneous network embedding. World Wide Web, 22(6), 2611–2632. [Google Scholar]
30. Qu, M., Tang, J., Shang, J., Ren, X., Zhang, M. et al. (2017). An attention-based collaboration framework for multi-view network representation learning. Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, pp. 1767–1776. Singapore. [Google Scholar]
31. Hu, J., Qian, S., Fang, Q., Liu, X., Xu, C. (2019). A2CMHNE: Attention-aware collaborative multimodal heterogeneous network embedding. ACM Transactions on Multimedia Computing Communications and Applications, 15(2), 1–17. [Google Scholar]
32. Bl, A., Dpa, B., Yl, A., Iak, A., Lin, C. C. (2020). Multi-source information fusion based heterogeneous network embedding. Information Sciences, 534(1), 53–71. https://doi.org/10.1016/j.ins.2020.05.012 [Google Scholar] [CrossRef]
33. Perozzi, B., Al-Rfou, R., Skiena, S. (2014). Deepwalk: Online learning of social representations. Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 701–710. New York. [Google Scholar]
34. Zhu, Y., Guan, Z., Tan, S., Liu, H., Cai, D. et al. (2016). Heterogeneous hypergraph embedding for document recommendation. Neurocomputing, 216, 150–162. [Google Scholar]
35. Sun, L., He, L., Huang, Z., Cao, B., Xia, C. et al. (2018). Joint embedding of meta-path and meta-graph for heterogeneous information networks. Proceedings of the 2018 IEEE International Conference on Big Knowledge, pp. 131–138. Singapore. [Google Scholar]
36. Zheng, S., Guan, D., Yuan, W. (2022). Semantic-aware heterogeneous information network embedding with incompatible meta-paths. World Wide Web-internet and Web Information Systems, 25(1), 1–21. [Google Scholar]
37. Grover, A., Leskovec, J. (2016). node2vec: Scalable feature learning for networks. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 855–864. San Francisco. [Google Scholar]
38. Hussein, R., Yang, D., Cudré-Mauroux, P. (2018). Are meta-paths necessary? Revisiting heterogeneous graph embeddings. Proceedings of the 27th ACM International Conference on Information and Knowledge Management, pp. 437–446. Torino. [Google Scholar]
39. Jiang, J., Li, Z., Ju, C. J., Wang, W. (2020). MARU: meta-context aware random walks for heterogeneous network representation learning. Proceedings of The 29th ACM International Conference on Information and Knowledge Management, pp. 575–584. Virtual Event, Ireland. [Google Scholar]
40. Cai, X., Han, J., Pan, S., Yang, L. (2018). Heterogeneous information network embedding based personalized query-focused astronomy reference paper recommendation. International Journal of Computational Intelligence Systems, 11(1), 591–599. https://doi.org/10.2991/ijcis.11.1.44 [Google Scholar] [CrossRef]
41. Zhang, H., Qiu, L., Yi, L., Song, Y. (2018). Scalable multiplex network embedding. Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence, pp. 3082–3088. Stockholm. [Google Scholar]
42. Huang, J., Liu, X., Song, Y. (2019). Hyper-path-based representation learning for hyper-networks. Proceedings of the 28th ACM International Conference on Information and Knowledge Management, pp. 449–458. Beijing. [Google Scholar]
43. Jiang, Z., Gao, Z., Lan, J., Yang, H., Lu, Y. et al. (2020). Task-oriented genetic activation for large-scale complex heterogeneous graph embedding. Proceedings of the Web Conference 2020, pp. 1581–1591. Taipei. [Google Scholar]
44. Sun, Y., Han, J., Yan, X., Yu, P. S., Wu, T. (2011). PathSim: Meta path-based top-k similarity search in heterogeneous information networks. Proceedings of the VLDB Endowment, 4(11), 992–1003. https://doi.org/10.14778/3402707.3402736 [Google Scholar] [CrossRef]
45. Zhang, D., Yin, J., Zhu, X., Zhang, C. (2018). Metagraph2vec: Complex semantic path augmented heterogeneous network embedding. Proceedings of 22nd Pacific-Asia Conference on Knowledge Discovery and Data Mining, pp. 196–208. Melbourne. [Google Scholar]
46. Shi, C., Hu, B., Zhao, X., Yu, P. (2019). Heterogeneous information network embedding for recommendation. IEEE Transactions on Knowledge and Data Engineering, 31(2), 357–370. https://doi.org/10.1109/TKDE.2018.2833443 [Google Scholar] [CrossRef]
47. Wang, Z., Liu, H., Du, Y., Wu, Z., Zhang, X. (2019). Unified embedding model over heterogeneous information network for personalized recommendation. Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, pp. 3813–3819. Macao. [Google Scholar]
48. He, Y., Song, Y., Li, J., Ji, C., Peng, J. et al. (2019). Hetespaceywalk: A heterogeneous spacey random walk for heterogeneous information network embedding. Proceedings of the 28th ACM International Conference on Information and Knowledge Management, pp. 639–648. Beijing. [Google Scholar]
49. Fu, T., Lee, W., Lei, Z. (2017). Hin2vec: Explore meta-paths in heterogeneous information networks for representation learning. Proceedings of the 2017 ACM on Conference on Information and Knowledge Management, pp. 1797–1806. Singapore. [Google Scholar]
50. Zhang, C., Swami, A., Chawla, N. V. (2019). SHNE: Representation learning for semantic-associated heterogeneous networks. Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, pp. 690–698. Melbourne. [Google Scholar]
51. Shang, J., Meng, Q., Liu, J., Kaplan, L. M., Jian, P. (2016). Meta-path guided embedding for similarity search in large-scale heterogeneous information networks. arXiv:1610.09769v1. [Google Scholar]
52. Zhang, Y., Wang, X., Liu, N., Shi, C. (2022). Embedding heterogeneous information network in hyperbolic spaces. ACM Transactions on Knowledge Discovery from Data, 16(2), 1–23. https://doi.org/10.1145/3468674 [Google Scholar] [CrossRef]
53. Chen, T., Sun, Y. (2017). Task-guided and path-augmented heterogeneous network embedding for author identification. Proceedings of the Tenth ACM International Conference on Web Search and Data Mining, pp. 295–304. Cambridge. [Google Scholar]
54. Yang, C., Liu, Z., Zhao, D., Sun, M., Chang, E. Y. (2015). Network representation learning with rich text information. Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence, pp. 2111–2117. Buenos Aires. [Google Scholar]
55. Wang, D., Cui, P., Zhu, W. (2016). Structural deep network embedding. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 1225–1234. San Francisco. [Google Scholar]
56. Cao, S., Lu, W., Xu, Q. (2016). Deep neural networks for learning graph representations. Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, pp. 1145–1152. Phoenix. [Google Scholar]
57. Kipf, T. N., Welling, M. (2016). Variational graph auto-encoders. arXiv:1611.07308v1. [Google Scholar]
58. Wang, H., Zhang, F., Hou, M., Xie, X., Guo, M. et al. (2018). SHINE: Signed heterogeneous information network embedding for sentiment link prediction. Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining, pp. 592–600. Marina Del Rey. [Google Scholar]
59. Fu, G., Yuan, B., Duan, Q., Yao, X. (2019). Representation learning for heterogeneous information networks via embedding events. Proceedings of the 26th International Conference on Neural Information Processing, pp. 327–339. Sydney. [Google Scholar]
60. Zhang, J., Xia, C., Zhang, C., Cui, L., Fu, Y. et al. (2017). BL-MNE: Emerging heterogeneous social network embedding through broad learning with aligned autoencoder. Proceedings of the 2017 IEEE International Conference on Data Mining, pp. 605–614. New Orleans. [Google Scholar]
61. Ji, H., Shi, C., Wang, B. (2018). Attention based meta path fusion for heterogeneous information network embedding. Proceedings of the 15th Pacific Rim International Conference on Artificial Intelligence, pp. 348–360. Nanjing. [Google Scholar]
62. Huang, F., Zhang, X., Li, C., Li, Z., He, Y. et al. (2018). Multimodal network embedding via attention based multi-view variational autoencoder. Proceedings of the 2018 ACM on International Conference on Multimedia Retrieval, pp. 108–116. Yokohama. [Google Scholar]
63. Fan, S., Shi, C., Wang, X. (2018). Abnormal event detection via heterogeneous information network embedding. Proceedings of the 27th ACM International Conference on Information and Knowledge Management, pp. 1483–1486. Torino. [Google Scholar]
64. Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C. et al. (2021). A comprehensive survey on graph neural networks. IEEE Transactions on Neural Networks and Learning Systems, 32(1), 4–24. https://doi.org/10.1109/TNNLS.2020.2978386 [Google Scholar] [PubMed] [CrossRef]
65. Zhou, J., Cui, G., Hu, S., Zhang, Z., Yang, C. et al. (2020). Graph neural networks: A review of methods and applications. AI Open, 1(1), 57–81. https://doi.org/10.1016/j.aiopen.2021.01.001 [Google Scholar] [CrossRef]
66. Kipf, T. N., Welling, M. (2017). Semi-supervised classification with graph convolutional networks. Proceedings of the 5th International Conference on Learning Representations, Toulon. [Google Scholar]
67. Hamilton, W. L., Ying, Z., Leskovec, J. (2017). Inductive representation learning on large graphs. Proceedings of the Annual Conference on Neural Information Processing Systems 2017, pp. 1024–1034. Long Beach, CA. [Google Scholar]
68. Velickovic, P., Cucurull, G., Casanova, A., Romero, A., Liò, P. et al. (2018). Graph attention networks. Proceedings of the 6th International Conference on Learning Representations, Vancouver. [Google Scholar]
69. Li, Y., Tarlow, D., Brockschmidt, M., Zemel, R. S. (2016). Gated graph sequence neural networks. Proceedings of the 4th International Conference on Learning Representations, San Juan. [Google Scholar]
70. Park, C., Kim, D., Han, J., Yu, H. (2020). Unsupervised attributed multiplex network embedding. Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, pp. 5371–5378. New York. [Google Scholar]
71. Velickovic, P., Fedus, W., Hamilton, W. L., Liò, P., Bengio, Y. et al. (2019). Deep graph infomax. Proceedings of the 7th International Conference on Learning Representations, New Orleans. [Google Scholar]
72. Zhang, Y., Xiong, Y., Kong, X., Li, S., Mi, J. et al. (2018). Deep collective classification in heterogeneous information networks. Proceedings of the 2018 World Wide Web Conference on World Wide Web, pp. 399–408. Lyon. [Google Scholar]
73. Zhou, S., Bu, J., Wang, X., Chen, J., Hu, B. et al. (2019). HAHE: Hierarchical attentive heterogeneous information network embedding. arXiv:1902.01475v2. [Google Scholar]
74. Zhang, Y., Fan, Y., Ye, Y., Zhao, L., Shi, C. (2019). Key player identification in underground forums over attributed heterogeneous information network embedding framework. Proceedings of the 28th ACM International Conference on Information and Knowledge Management, pp. 549–558. Beijing. [Google Scholar]
75. Fan, S., Zhu, J., Han, X., Shi, C., Hu, L. et al. (2019). Metapath-guided heterogeneous graph neural network for intent recommendation. Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 2478–2486. Anchorage. [Google Scholar]
76. Fu, X., Zhang, J., Meng, Z., King, I. (2020). MAGNN: Metapath aggregated graph neural network for heterogeneous graph embedding. Proceedings of the Web Conference 2020, pp. 2331–2341. Taipei. [Google Scholar]
77. Ren, Y., Liu, B., Huang, C., Dai, P., Bo, L. et al. (2019). Heterogeneous deep graph infomax. arXiv:1911.08538v5. [Google Scholar]
78. Sun, X., Yin, H., Liu, B., Chen, H., Cao, J. et al. (2021). Heterogeneous hypergraph embedding for graph classification. Proceedings of the Fourteenth ACM International Conference on Web Search and Data Mining, pp. 725–733. Virtual Event, Israel. [Google Scholar]
79. Zhang, M., Wang, X., Zhu, M., Shi, C., Zhang, Z. et al. (2022). Robust heterogeneous graph neural networks against adversarial attacks. Proceedings of the Thirty-Sixth AAAI Conference on Artificial Intelligence, pp. 4363–4370. Virtual Event. [Google Scholar]
80. Zhang, C., Song, D., Huang, C., Swami, A., Chawla, N. V. (2019). Heterogeneous graph neural network. Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 793–803. Anchorage. [Google Scholar]
81. Zheng, V. W., Sha, M., Li, Y., Yang, H., Fang, Y. et al. (2018). Heterogeneous embedding propagation for large-scale e-commerce user alignment. Proceedings of the IEEE International Conference on Data Mining, pp. 1434–1439. Singapore. [Google Scholar]
82. Chen, X., Yu, G., Wang, J., Domeniconi, C., Li, Z. et al. (2019). ActiveHNE: Active heterogeneous network embedding. Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, pp. 2123–2129. Macao. [Google Scholar]
83. Chen, W., Gu, Y., Ren, Z., He, X., Xie, H. et al. (2019). Semi-supervised user profiling with heterogeneous graph attention networks. Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, pp. 2116–2122. Macao. [Google Scholar]
84. Hu, Z., Dong, Y., Wang, K., Sun, Y. (2020). Heterogeneous graph transformer. Proceedings of the Web Conference 2020, pp. 2704–2710. Taipei. [Google Scholar]
85. Imran, M., Yin, H., Chen, T., Huang, Z., Zheng, K. (2022). DeHIN: A decentralized framework for embedding large-scale heterogeneous information networks. arXiv:2201.02757v1. [Google Scholar]
86. Jing, B., Park, C., Tong, H. (2021). HDMI: High-order deep multiplex infomax. Proceedings of the Web Conference 2021, pp. 2414–2424. Virtual Event, Ljubljana. [Google Scholar]
87. Liu, Z., Huang, C., Yu, Y., Fan, B., Dong, J. (2020). Fast attributed multiplex heterogeneous network embedding. Proceedings of the 29th ACM International Conference on Information and Knowledge Management, pp. 995–1004. Virtual Event, Ireland. [Google Scholar]
88. Wang, Y., Tang, S., Lei, Y., Song, W., Wang, S. et al. (2020). Disenhan: Disentangled heterogeneous graph attention network for recommendation. Proceedings of the 29th ACM International Conference on Information and Knowledge Management, pp. 1605–1614. Virtual Event, Ireland. [Google Scholar]
89. Wang, P., Agarwal, K., Ham, C., Choudhury, S., Reddy, C. K. (2021). Self-supervised learning of contextual embeddings for link prediction in heterogeneous networks. Proceedings of the Web Conference 2021, pp. 2946–2957. Virtual Event, Ljubljana. [Google Scholar]
90. Chang, Y., Chen, C., Hu, W., Zheng, Z., Zhou, X. et al. (2022). Megnn: Meta-path extracted graph neural network for heterogeneous graph representation learning. Knowledge-Based Systems, 235(1), 107611. https://doi.org/10.1016/j.knosys.2021.107611 [Google Scholar] [CrossRef]
91. Berg, R., Kipf, T. N., Welling, M. (2017). Graph convolutional matrix completion. arXiv:1706.02263v2. [Google Scholar]
92. Li, Q., Han, Z., Wu, X. (2018). Deeper insights into graph convolutional networks for semi-supervised learning. Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, pp. 3538–3545. New Orleans. [Google Scholar]
93. Miller, George, A. (1995). Wordnet: A lexical database for english. Communications of the ACM, 38(11), 39–41.https://doi.org/10.1145/219717.219748 [Google Scholar] [CrossRef]
94. Bollacker, K. D., Evans, C., Paritosh, P., Sturge, T., Taylor, J. (2008). Freebase: A collaboratively created graph database for structuring human knowledge. Proceedings of the ACM SIGMOD International Conference on Management of Data, pp. 1247–1250. Vancouver. [Google Scholar]
95. Suchanek, F. M., Kasneci, G., Weikum, G. (2007). Yago: A core of semantic knowledge. Proceedings of the 16th International Conference on World Wide Web, pp. 697–706. Banff, Alberta. [Google Scholar]
96. Wang, Q., Mao, Z., Wang, B., Guo, L. (2017). Knowledge graph embedding: A survey of approaches and applications. IEEE Transactions on Knowledge and Data Engineering, 29(12), 2724–2743. https://doi.org/10.1109/TKDE.2017.2754499 [Google Scholar] [CrossRef]
97. Bordes, A., Usunier, N., García-Durán, A., Weston, J., Yakhnenko, O. (2013). Translating embeddings for modeling multi-relational data. Proceedings of the 27th Annual Conference on Neural Information Processing Systems, pp. 2787–2795. Nevada. [Google Scholar]
98. Wang, Z., Zhang, J., Feng, J., Chen, Z. (2014). Knowledge graph embedding by translating on hyperplanes. Proceedings of the Twenty-Eighth AAAI Conference on Artificial Intelligence, pp. 1112–1119. Quebec City. [Google Scholar]
99. Lin, Y., Liu, Z., Sun, M., Liu, Y., Zhu, X. (2015). Learning entity and relation embeddings for knowledge graph completion. Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, pp. 2181–2187. Texas. [Google Scholar]
100. Ji, G., He, S., Xu, L., Liu, K., Zhao, J. (2015). Knowledge graph embedding via dynamic mapping matrix. Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics, pp. 687–696. Beijing. [Google Scholar]
101. He, S., Liu, K., Ji, G., Zhao, J. (2015). Learning to represent knowledge graphs with gaussian embedding. Proceedings of the 24th ACM International Conference on Information and Knowledge Management, pp. 623–632. Melbourne. [Google Scholar]
102. Xiao, H., Huang, M., Zhu, X. (2016). Transg: A generative model for knowledge graph embedding. Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics, pp. 2316–2325. Berlin. [Google Scholar]
103. Bordes, A., Weston, J., Collobert, R., Bengio, Y. (2011). Learning structured embeddings of knowledge bases. Proceedings of the Twenty-Fifth AAAI Conference on Artificial Intelligence, San Francisco. [Google Scholar]
104. Nickel, M., Tresp, V., Kriegel, H. (2011). A three-way model for collective learning on multi-relational data. Proceedings of the 28th International Conference on Machine Learning, pp. 809–816. Bellevue. [Google Scholar]
105. Yang, B., Yih, W., He, X., Gao, J., Deng, L. (2015). Embedding entities and relations for learning and inference in knowledge bases. Proceedings of the 3rd International Conference on Learning Representations, San Diego. [Google Scholar]
106. Dettmers, T., Minervini, P., Stenetorp, P., Riedel, S. (2018). Convolutional 2D knowledge graph embeddings. Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, pp. 1811–1818. New Orleans. [Google Scholar]
107. Socher, R., Chen, D., Manning, C. D., Ng, A. Y. (2013). Reasoning with neural tensor networks for knowledge base completion. Proceedings of the 27th Annual Conference on Neural Information Processing Systems, pp. 926–934. Nevada. [Google Scholar]
108. Sun, Z., Deng, Z., Nie, J., Tang, J. (2019). Rotate: Knowledge graph embedding by relational rotation in complex space. Proceedings of the 7th International Conference on Learning Representations, New Orleans. [Google Scholar]
109. Nickel, M., Rosasco, L., Poggio, T. A. (2016). Holographic embeddings of knowledge graphs. Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, pp. 1955–1961. Phoenix. [Google Scholar]
110. Chen, H., Yin, H., Wang, W., Wang, H., Nguyen, Q. V. H. et al. (2018). PME: Projected metric embedding on heterogeneous networks for link prediction. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 1177–1186. London. [Google Scholar]
111. Shi, Y., Zhu, Q., Guo, F., Zhang, C., Han, J. (2018). Easing embedding learning by comprehensive transcription of heterogeneous information networks. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 2190–2199. London. [Google Scholar]
112. Lu, Y., Shi, C., Hu, L., Liu, Z. (2019). Relation structure-aware heterogeneous information network embedding. Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence, pp. 4456–4463. Honolulu. [Google Scholar]
113. Feng, M., Hsu, C., Li, C., Yeh, M., Lin, S. (2019). MARINE: Multi-relational network embeddings with relational proximity and node attributes. Proceedings of the World Wide Web Conference, pp. 470–479. San Francisco. [Google Scholar]
114. Lin, Y., Liu, Z., Luan, H., Sun, M., Rao, S. et al. (2015). Modeling relation paths for representation learning of knowledge bases. Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, pp. 705–714. Lisbon. [Google Scholar]
115. Cao, Y., Wang, X., He, X., Hu, Z., Chua, T. (2019). Unifying knowledge graph learning and recommendation: Towards a better understanding of user preferences. Proceedings of the World Wide Web Conference, pp. 151–161. San Francisco. [Google Scholar]
116. Cen, Y., Zou, X., Zhang, J., Yang, H., Zhou, J. et al. (2019). Representation learning for attributed multiplex heterogeneous network. Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 1358–1368. Anchorage. [Google Scholar]
117. Qiao, Z., Du, Y., Fu, Y., Wang, P., Zhou, Y. (2019). Unsupervised author disambiguation using heterogeneous graph convolutional network embedding. Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), pp. 910–919. Los Angeles. [Google Scholar]
118. Trivedi, R., Sisman, B., Dong, X. L., Faloutsos, C., Ma, J. et al. (2018). LinkNBed: Multi-graph representation learning with entity linkage. Proceedings of the 56th Annual Meeting of the Association for Computational Linguistics, pp. 252–262. Melbourne. [Google Scholar]
119. Shang, C., Tang, Y., Huang, J., Bi, J., He, X. et al. (2019). End-to-end structure-aware convolutional networks for knowledge base completion. Proceedings of the Thirty-Third AAAI Conference on Artificial Intelligence, pp. 3060–3067. Honolulu. [Google Scholar]
120. Wang, K., Liu, Y., Xu, X., Lin, D. (2018). Knowledge graph embedding with entity neighbors and deep memory network. arXiv:1808.03752v1. [Google Scholar]
121. Oh, B., Seo, S., Lee, K. (2018). Knowledge graph completion by context-aware convolutional learning with multi-hop neighborhoods. Proceedings of the 27th ACM International Conference on Information and Knowledge Management, pp. 257–266. Torino. [Google Scholar]
122. Ning, Z., Qiao, Z., Dong, H., Du, Y., Zhou, Y. (2021). Lightcake: A lightweight framework for context-aware knowledge graph embedding. Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, pp. 181–193. Virtual Event. [Google Scholar]
123. Li, Z., Liu, H., Zhang, Z., Liu, T., Xiong, N. N. (2022). Learning knowledge graph embedding with heterogeneous relation attention networks. IEEE Transactions on Neural Networks and Learning Systems, 33(8), 3961–3973. https://doi.org/10.1109/TNNLS.2021.3055147 [Google Scholar] [PubMed] [CrossRef]
124. Yang, C., Zhang, J., Wang, H., Li, S., Kim, M. et al. (2020). Relation learning on social networks with multi-modal graph edge variational autoencoders. Proceedings of the Thirteenth ACM International Conference on Web Search and Data Mining, pp. 699–707. Houston. [Google Scholar]
125. Fan, H., Zhang, F., Wei, Y., Li, Z., Dai, Q. (2022). Heterogeneous hypergraph variational autoencoder for link prediction. IEEE Transactions on Pattern Analysis and Machine Intelligence, 44(8), 4125–4138. [Google Scholar] [PubMed]
126. Chen, D., Li, Y., Ding, B., Shen, Y. (2020). An adaptive embedding framework for heterogeneous information networks. Proceedings of the 29th ACM International Conference on Information & Knowledge Management, pp. 165–174. Virtual Event, Ireland. [Google Scholar]
127. Zhong, Z., Li, C. T., Pang, J. (2020). Reinforcement learning enhanced heterogeneous graph neural network. arXiv:2010.13735. [Google Scholar]
128. Zhao, K., Bai, T., Wu, B., Wang, B., Zhang, Y. et al. (2020). Deep adversarial completion for sparse heterogeneous information network embedding. Proceedings of The Web Conference 2020, pp. 508–518. Taipei. [Google Scholar]
129. Hu, B., Fang, Y., Shi, C. (2019). Adversarial learning on heterogeneous information networks. Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 120–129. Anchorage. [Google Scholar]
130. Chu, Y., Feng, C., Guo, C. (2018). Social-guided representation learning for images via deep heterogeneous hypergraph embedding. Proceedings of the 2018 IEEE International Conference on Multimedia and Expo, pp. 1–6. San Diego. [Google Scholar]
131. Xu, L., Wei, X., Cao, J., Yu, P. S. (2017). Embedding of embedding (EOEjoint embedding for coupled heterogeneous networks. Proceedings of the Tenth ACM International Conference on Web Search and Data Mining, pp. 741–749. Cambridge. [Google Scholar]
132. Fu, Y., Xiong, Y., Yu, P. S., Tao, T., Zhu, Y. (2019). Metapath enhanced graph attention encoder for hins representation learning. Proceedings of the 2019 IEEE International Conference on Big Data (Big Data), pp. 1103–1110. Los Angeles. [Google Scholar]
133. Ai, Q., Azizi, V., Chen, X., Zhang, Y. (2018). Learning heterogeneous knowledge base embeddings for explainable recommendation. Algorithms, 11(9), 137. https://doi.org/10.3390/a11090137 [Google Scholar] [CrossRef]
134. Schlichtkrull, M. S., Kipf, T. N., Bloem, P., van den Berg, R., Titov, I. et al. (2018). Modeling relational data with graph convolutional networks. Proceedings of the 15th International Conference on the Semantic Web, pp. 593–607. Heraklion. [Google Scholar]
135. Tang, J., Zhang, J., Yao, L., Li, J., Zhang, L. et al. (2008). Arnetminer: Extraction and mining of academic social networks. Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 990–998. Las Vegas. [Google Scholar]
136. Du, B., Tong, H. (2019). MrMine: Multi-resolution multi-network embedding. Proceedings of the 28th ACM International Conference on Information and Knowledge Management, pp. 479–488. Beijing. [Google Scholar]
137. Fey, M., Lenssen, J. E. (2019). Fast graph representation learning with pytorch geometric. arXiv:1903.02428v3. [Google Scholar]
138. Han, X., Cao, S., Lv, X., Lin, Y., Liu, Z. et al. (2018). OpenKE: An open toolkit for knowledge embedding. Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, pp. 139–144. Brussels. [Google Scholar]
139. Ji, M., Sun, Y., Danilevsky, M., Han, J., Gao, J. (2010). Graph regularized transductive classification on heterogeneous information networks. Proceedings of the European Conference on Machine Learning and Knowledge Discovery in Databases, pp. 570–586. Barcelona. [Google Scholar]
140. Chen, H., Li, Y., Sun, X., Xu, G., Yin, H. (2021). Temporal meta-path guided explainable recommendation. Proceedings of the Fourteenth ACM International Conference on Web Search and Data Mining, pp. 1056–1064. Virtual Event, Israel. [Google Scholar]
141. Ribeiro, L. F. R., Saverese, P. H. P., Figueiredo, D. R. (2017). struc2vec: Learning node representations from structural identity. Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 385–394. Halifax. [Google Scholar]
142. Donnat, C., Zitnik, M., Hallac, D., Leskovec, J. (2018). Learning structural node embeddings via diffusion wavelets. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pp. 1320–1329. London. [Google Scholar]
143. Han, X., Jiang, Z., Liu, N., Song, Q., Li, J. et al. (2022). Geometric graph representation learning via maximizing rate reduction. Proceedings of the ACM Web Conference 2022, pp. 1226–1237. Virtual Event, Lyon. [Google Scholar]
144. Hu, Q., Lin, F., Wang, B., Li, C. (2022). MBRep: Motif-based representation learning in heterogeneous networks. Expert Systems with Application, 190(6295), 116031. https://doi.org/10.1016/j.eswa.2021.116031 [Google Scholar] [CrossRef]
145. Yin, Y., Ji, L. X., Zhang, J. P., Pei, Y. L. (2019). DHNE: Network representation learning method for dynamic heterogeneous networks. IEEE Access, 7, 134782–134792. https://doi.org/10.1109/ACCESS.2019.2942221 [Google Scholar] [CrossRef]
146. Xue, H., Yang, L., Jiang, W., Wei, Y., Hu, Y. et al. (2020). Modeling dynamic heterogeneous network for link prediction using hierarchical attention with temporal RNN. Proceedings of the European Conference on Machine Learning and Knowledge Discovery in Databases, pp. 282–298. Ghent. [Google Scholar]
147. Luo, W., Zhang, H., Yang, X., Bo, L., Yang, X. et al. (2020). Dynamic heterogeneous graph neural network for real-time event prediction. Proceedings of the 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, pp. 3213–3223. Virtual Event. [Google Scholar]
148. Wang, X., Lu, Y., Shi, C., Wang, R., Mou, S. (2022). Dynamic heterogeneous information network embedding with meta-path based proximity. IEEE Transactions on Knowledge and Data Engineering, 34(3), 1117–1132. https://doi.org/10.1109/TKDE.2020.2993870 [Google Scholar] [CrossRef]
149. Xie, Y., Ou, Z., Chen, L., Liu, Y., Xu, K. et al. (2021). Learning and updating node embedding on dynamic heterogeneous information network. Proceedings of The Fourteenth ACM International Conference on Web Search and Data Mining, pp. 184–192. Virtual Event, Israel. [Google Scholar]
150. Narayanan, A., Chandramohan, M., Venkatesan, R., Chen, L., Jaiswal, S. (2017). graph2vec: Learning distributed representations of graphs. arXiv:1707.05005v1. [Google Scholar]
151. Yang, Z., Ding, M., Zhou, C., Yang, H., Zhou, J. et al. (2020). Understanding negative sampling in graph representation learning. Proceedings of the 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, pp. 1666–1676. Virtual Event, CA. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
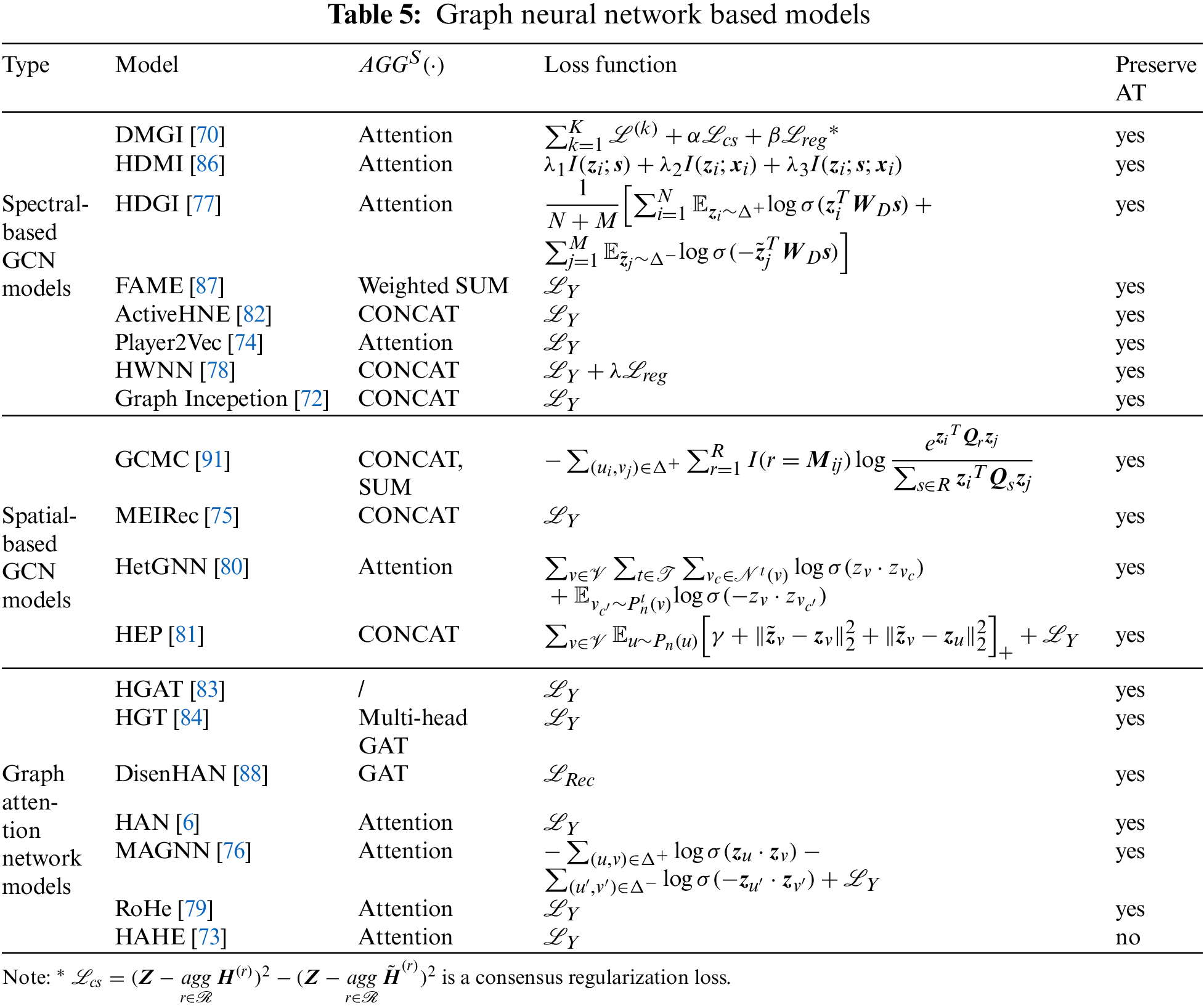

 Downloads
Downloads
 Citation Tools
Citation Tools