Toward Optimal Periodic Crowd Tracking via Unmanned Aerial Vehicle

1  Introduction

The unmanned aerial vehicles (UAVs), also known as drones, refer to pilotless aircraft, flying vehicles without an onboard human pilot or passengers. The term “unmanned” indicates the non-existence of a human who directly and actively pilots the aircraft. The command functions for UAVs may be either on-board or off-board (remote control) [1]. Although the UAVs deployment was initially restricted to the military domain [2,3], it has become widely used within a wide range of domains over the last two decades [4], namely security [5–8], transportation and road management [9–11], networking and communications [12,13], logistics [14], agriculture [15,16], healthcare [17–19], and mining [20], among others.

In real life, each UAV application has been tackled depending on its context, needs, and consequently, took into account the minimum requirements of the used UAVs architecture. Indeed, the drone architecture is determined by its types of build, visual and onboard sensors, communication and power management after specifying its needs for such a real-world application [1,21,22]. A huge number of real-world applications have therefore been implemented and published in the literature. In [22], the authors tried to categorize the unnumbered UAVs applications according to the most important characteristics such as the drone flight zone (outdoor, indoor), mission (military, civil), and environment (underwater, water, ground, air, space). In this research, we focused on the daily life outdoor/civil/ground drone applications related to surveillance, search, and rescue missions. Among this set of applications, we found many recent surveys that specifically concentrated on the development of crowd monitoring and analysis (CMA) systems [21,23–26]. Indeed, UAVs have been used to automatically monitor and analyze several groups of people (crowds) to ensure specified purposes such as security [27–29], rescue [30,31], healthcare [32–35], and jostling avoidance [31,36–38], among others.

In [21], the authors classified UAVs applications and algorithms, for CMA, into five domains, namely, crowd detection [39–49], crowd counting [45,50–59], crowd density estimation [43,53,57,60–62], crowd tracking [49,63–66], and crowd behavior analysis [35,67,68]. In the present study, we were interested in optimally tracking crowds via UAVs. We supposed that the number, density, and behavior of crowds are already known with the help of some detection and prediction techniques (e.g., machine learning, image processing, etc.). The crowd tracking consists of closely following up crowds by UAVs to ensure continuous, real-time supervision in order to achieve the main target of a given CMA system. Using multiple UAVs for crowd tracking gives rise to the huge cost increases on CMA systems due to the swift increase in the acquisition, maintenance, and energy costs of these UAVs [64].

The underlying motivation of this research study was the improvement of crowd-tracking function of the CMA system using UAVs in the context of the annual Islamic pilgrimage (also called Hajj) that hosted about 2.5 million of pilgrims in 20191. In fact, during the Hajj period, which lasts about five days, many rites give rise to very big pilgrims gatherings at the same time in five main places namely: Mina, Arafat, Muzdalifah, Jamarat, Masjid-Al-Haram (see Fig. 1). Additionally, there is a significant number of crowds traveling through these five specific places during the Hajj period which may lead to safety issues. In fact, there have been many serious incidents caused by stampede, trampling to death, crush due to pedestrian collision, and fire outbreaks over the two last decades [69]. In the literature, several works have already tried to develop technologies for CMA systems in the context of Hajj so as to face such issues as control, rescue, and jostling avoidance. The state of the art of some domains indicates that many contributions have focused on the the above mentioned application and algorithm domains using several technologies like traditional/UAVs surveillance systems, communication networks, global positioning systems (GPS), internet of things (IoT), artificial intelligence, computer vision and image processing, big data analytics, etc. For more details and challenges, readers can refer to the literature reviews carried out in [31,70–74]. However, while focusing on the works that consider CMA systems based on UAVs surveillance [31,36–38,75], it can be easily noticed that these studies ignore the UAVs cost optimization when used for tracking crowds.

Figure 1: Mass gatherings places during Hajj period

In order to ensure cost-saving, this study proposed a binary linear program (BLP) to optimize the used UAVs when periodically tracking a set of moving crowds in a determined/bordered open crowded area (OCA) (i.e., a geographical zone with known borders/dimensions and without obstacles where a number of close crowds navigate). Two main objectives were considered, namely the minimization of the UAVs traveled time and the reduction of their energy consumption taking into account their architecture, the crowds characteristics, and power management. Several scenarios were also simulated to prove that the proposed BLP is efficient and can be integrated into many CMA systems using UAVs during crowded events like religious gatherings [31,36,76,77], mass sports events [78,79], social festivals [80], among others. Based on the obtained results, we suggested a set of open research challenges to better improve the optimality of the crowd tracking domain in CMA systems.

The remainder of the paper is structured as follows: Section 2 discussed the literature review of relevant works dealing with crowd tracking systems using UAVs in order to point out their limitations and highlight the importance of our contribution. Section 3 introduced the considered system model of the periodic crowd tracking using UAVs, the different used parameters and variables, and the proposed BLP together with its linear constraints and objective functions. In order to evaluate its performance, Section 4 reported on the computational results obtained by the application of the suggested BLP in the different scenarios of the periodic crowd-tracking problem. Section 5 provided a set of open challenges and perspectives for future works. Section 6 drew the main conclusions of the study.

2  Related Works

A good number of the existing works and approaches in the literature tackle one of the five domains, classified in [21], of CMA systems using UAVs. However, only a few works dealt with the crowd-tracking domain, the focus of our present study, since each of these works refers to the crowd tracking problem from a specific point of view.

In [66], the authors provided an efficient procedure to detect and track a 2D/3D-object using computer vision and image processing technologies, where each tracked object can be considered as a crowd or any other moving object. The proposed procedure is characterized by its computational robustness, and optimized time calculation, but was specifically applied to the military field.

Wang et al. [49] proposed a dynamic-data-driven planning and control framework using collaborative UAVs and unmanned ground vehicles (UGVs). Their suggestion provides three dependent tasks namely crowd motion modeling, crowd motion detection, and crowd motion tracking and controlling. To track crowds, they use the well-known Kalman digital filter [81], also known as linear quadratic estimation (LQE). This allows the prediction of future system states based on past estimations. In [65], the authors extend the proposed framework in [49] by incorporating a multi-resolution data approach, where a grid-based method [82,83] is developed to model crowd motion with UAVs low-resolution global perception. Additionally, an auto-regressive model is employed to model individuals motion based on UGVs detailed perception.

All the above-cited works miss the optimization aspect when tracking target objects or crowds. To the best of our knowledge, de Moraes et al. [64] were pioneers integrating optimization techniques in their tracking mechanism. They proposed a UAVs-based system, that periodically monitors gathered walking individuals, where they integrated auction paradigms and genetic algorithms to distribute UAVs among crowds/targets and calculate the best order to visit them. According to an effective simulation analysis, the authors proved the capabilities, efficiency, and robustness of their system to perform surveillance, visit all targets during a supervising period, minimize the time between visits to each target, and preserve performance and stability under a variety of scenarios.

A second and recent work that considers optimization features was undertaken by Trotta et al. [63]. In this study, the authors proposed an aerial tracking system that deploys a swarm of UAVs for continuous video capture of mobile ground targets. The challenging issues raised in this work deal with energy management, scenario coverage, and multi-device task coordination. To face these issues, they proposed a framework, called PERCEIVE, that considers a modular chain of functionalities to perform crowd mobility prediction, UAVs charging schedules, and mobile charging stations (MCSs) mobility updates. The results showed the capability, efficiency, and robustness of their framework via experimental measurements of an MCS prototype and an extensive and effective simulation analysis on a city-scale monitoring scenario. Regarding the integrated UAV replenishment service, they used a probabilistic charging scheduling algorithm taking into account both UAVs residual energy and the quality of service (QoS) of the system. Concerning the UAVs and MCSs mobility management, they used swarm mobility algorithms based on the potential field force model. The underlying reasons were to maximize the number of targets covered by UAVs and minimize charging operations overhead.

All state-of-the-art contributions, that consider the crowd tracking domain using UAVs, were proposed for a specific application of aerial video surveillance. Even if some works considered the optimization aspect to efficiently track crowds, none of them took into consideration the minimization of the total distance/time traveled by UAVs and the total energy consumed by UAVs via assigning the best set of UAVs for each crowd. Additionally, there is no formal optimization model that can be easily adapted by any CMA system using crowd tracking via UAVs in the literature. The last two issues lead us to the main challenge to face within the current contribution. In this study, we proposed a generic BLP model that optimally assigns UAVs to Crowds in order to enhance the crowd-tracking function offered by a CMA system. Many input parameters are related to OCA characteristics, UAVs features and Crowds behavior. These parameters are outlined and sensitively analyzed to emphasize their impact on the crowd-tracking function of a given CMA system.

3  Model for the Periodic Crowd Tracking Using UAVs

In this section, we first introduced the considered assumptions to define the periodic crowd tracking (PCT) problem using UAVs. Then, we defined the parameters and decision variables used to formulate the linear constraints and objective functions to build the proposed BLP in order to solve the PCT problem.

3.1 Assumptions and Definitions

As mentioned in the previous sections, this study mainly focused on the crowd-tracking domain of CMA systems using UAVs. We assumed that we already had the mechanisms and prediction modules that provided, the following information at each instant:

  (i)   The characteristics of the OCA to be supervised by the CMA such as shape, area, and border dimensions.

 (ii)   The list of charging stations (CSs) that are considered to supply energy to the UAVs. Each CS is characterized by its mobility (fixed or mobile), position (latitude and longitude), and capacity in terms of supported number of UAVs.

(iii)   The list of identified crowds, their positions (latitude and longitude), shapes, areas, cardinalities, densities (number of persons at each squared meter) that depends on the crowds areas and cardinalities, constant speeds that depend on the crowd density, and demands defined by the minimum number of needed UAVs for each crowd.

(iv)   The number of available UAVs in the fleet and their characteristics such as current positions (latitude and longitude), statuses (flying to supervise a crowd, charging in a CS or idle in a CS), energy (batteries) level, constant speeds, and energy (power) charging/discharging functions.

Based on the previous assumptions, the PCT problem is solved periodically (i.e., when UAVs reallocation is needed) in order to satisfy the different crowds demands. This was achieved through assigning the required UAVs for each crowd at the beginning of each period depending on the energy/position variations of each UAV and the crowds movements. The UAVs/crowds assignment process has also to respect some rules such as:

•   A UAV can be assigned to only one crowd during a given period.

•   A UAV cannot be assigned to a crowd if its energy is not enough to supervise the corresponding crowd during the whole current period, and then returns to the nearest available CS.

•   A flying UAV should go back to an available CS if it is not assigned to a crowd in a given period.

The PCT problem using UAVs consists of periodically reallocating the needed number of heterogeneous UAVs to the mobile identified crowds. This is to ensure a continuous efficient coverage while minimizing the UAVs moves in order to reduce energy consumption. Fig. 2a shows the initial system state where ten UAVs remain on the two CSs and the five crowds are not covered. Fig. 2b displays the system state where the PCT problem solver is applied on the initial state to obtain the optimal coverage during the first period (Period 1). During this period, six UAVs are used to ensure the crowds coverage. After solving the PCT at the end of Period 1, we obtained a new reallocation UAVs/crowds to get a new system state during the second period (Period 2) as shown in Fig. 2c. We can see that the number of crowds is reduced to four due to the merge of two crowds. Also, the number of needed UAVs is reduced when allowing one UAV to rejoin a CS.

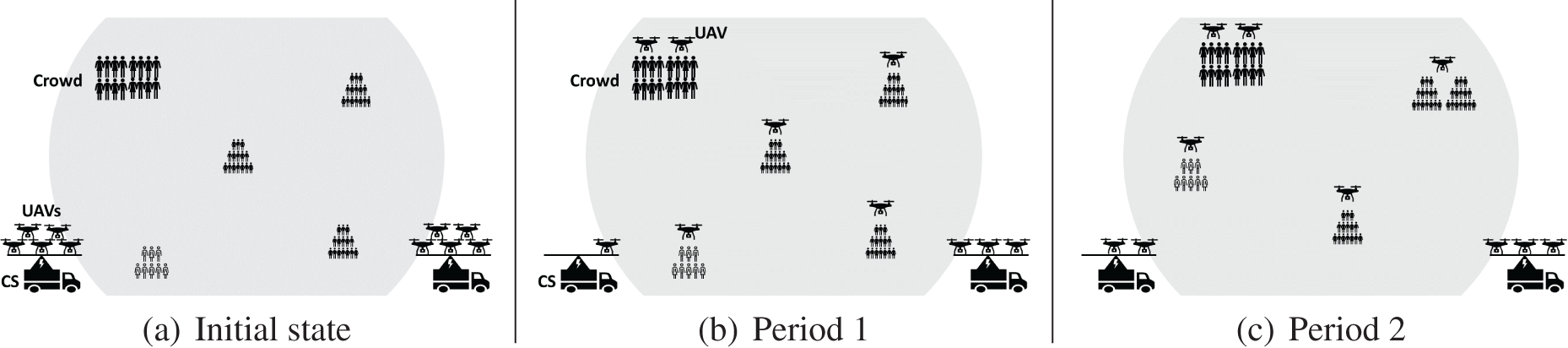
Figure 2: Scenario of three periods

3.2 Parameters (Input Data)

Let C be the total time of a given OCA life cycle and Λ={0,1,…,(λ−1),λ,(λ+1),…,|Λ|} the set of contiguous and non overlapped periods in C. The initial state of the whole system is designated by λ=0 and is not considered a standard period. The first period is designated by λ=1. ∀λ∈Λ,Tλ represents the time in seconds of the period λ where T0=0 and ∑λ∈ΛTλ=C. We considered the following data regarding the end of each period (λ−1)∈Λ to produce the new UAVs assignment of the next (beginning of) period λ∈Λ by solving the PCT problem (noted PCTλ):

•   ∀λ∈Λ,Qλ: the OCA containing the whole sets Uλ of UAVs, Wλ of crowds, and Sλ of charging stations during each period λ. For simplification purpose, we considered that Qλ is a rectangular shaped OCA with length ℓQλ (meters) and width hQλ (meters).

•   ∀λ∈Λ, let the graph Gλ=(Uλ∪Wλ∪Sλ,cwλ∪csλ) where:

–   Uλ: set of UAVs during the period λ.

∗   |Uλ|=n: number of UAVs during the period λ. n is determined according to the OCA initial state it remains fixed during all periods.

∗   ∀u∈Uλ, xcorduλ and ycorduλ: latitude and longitude of the UAV u during the period λ.

∗   ∀u∈Uλ, statuλ∈{0,1}: status of the UAV u during the period λ, 0 when idle/charging on CS, 1 when flying.

∗   ∀u∈Uλ,εuλ∈[0,100]: energy percentage (battery level) of UAV u at the beginning of the period λ.

∗   ∀u∈Uλ,ϑu: constant speed (meter/second) of flying UAV u during all periods in Λ.

∗   ∀u∈Uλ,τˇu: flying time of the UAV u to consume (lose) 1% of its energy.

∗   ∀u∈Uλ,τ^u: charging time of the UAV u to gain 1% of its energy.

∗   ∀u∈Uλ,fuλ: loss energy function of the UAV u caused by its transition movement from its position at the previous period (λ−1) to its position at the current period λ and by its supervising flight during the period λ. Actually, this function depends on the UAV specifications (e.g., speed, engine power, movement angle, battery type, etc.) and on other external factors like climate effects. For a simplification purpose and without loss of generality, we considered that fuλ depends only on the UAVs flying time either in supervising crowd or in shifting from crowd/CS to crowd/CS. For example, if at the end of a period (λ−1)∈Λ, a UAV u∈Uλ should travel from its current position i∈Qλ−1 to a crowd j∈Qλ then flying for Tλ seconds to cover location j during the period λ, then its loss energy fuλ is calculated as follows:

fuλ=⌈cwijλϑu+Tλτˇu⌉(1)

∗   ∀u∈Uλ,δˇuλ: energy percentage threshold forcing UAV u to return to a charging station at the end of a period λ. In general, δˇuλ represents the energy required to travel from any position i to any position j in Qλ. Respecting this threshold, it guarantees the UAV returns to a CS without a total loss of energy. We considered the longest travel distance, the diagonal of the rectangle Qλ, to compute the threshold as follows:

δˇuλ=⌈ℓQλ2+hQλ2ϑu×τˇu⌉(2)

∗   ∀u∈Uλ,δ^uλ: energy percentage threshold allowing UAV u to leave a CS. In general, δ^uλ is fixed according to the required energy of a UAV to travel from its leaved charging station i to a crowd j then to cover it during at least the period Tλ and returning to i. This energy percentage threshold is calculated as follows:

δ^uλ=⌈2×ℓQλ2+hQλ2ϑu+Tλτˇu⌉(3)

–   Wλ: set of crowds during the period λ.

∗   |Wλ|=m: number of crowds during the period λ. m can change from λ to λ+1.

∗   ∀w∈Wλ, xcordwλ and ycordwλ: latitude and longitude of the gravity center of the crowd w during the period λ.

∗   ∀u∈Uλ,w∈Wλ,cwuwλ: distance (meter) between a UAV u during the period (λ−1) and the gravity center of a crowd w during the period λ.

∗   ∀w∈Wλ, raywλ: ray of the crowd w during the period λ.

∗   ∀w∈Wλ,ρwλ: density (person/meter2) of crowd w during the period λ.

∗   ∀w∈Wλ,ϑwλ: speed (meter/second) of crowd w during the period λ according to its density ρwλ. Indeed, the effect of the crowd density on the walking velocity of walkers has been widely studied for the objective of comfort and safety insurance in pedestrian facilities. Regarding crowds with low densities, walkers can retain a free flow velocity without neighbors interruption. However, for crowds with high densities, the velocity decreases by the impact of the neighboring walkers force speed adjustments which is analog to the vehicular traffic situations. This density/velocity relationship is called Fundamental Diagram where Weidmann [84] was one of the first to study this relationship by proposing a systematic description from experimental data in the context of pedestrian facilities. Based on averages of different parameter values taken from the literature, he proposed the following formula to formally define the relationship between crowd density and velocity:

v(ρ)=v0×(1−exp⁡[−γ(1ρ−1ρmax)])(4)

where v0=1.34 meter/second is the free speed at low densities (free flow), ρmax=5.4 person/m2 is the maximal walkers density from which onward movement is not possible anymore and γ=1.913 p/m2 is a fit parameter. These parameter values are widely used in the literature (e.g., [85,86]). Fig. 3 shows a plot of the fundamental diagram given by the last equation and the listed parameters [86].For our case, ϑwλ is calculated as follows:

ϑwλ=1.34×(1−exp⁡[−1.913(1ρwλ−15.4)]),∀w∈Wλ(5)

∗   ∀w∈Wλ, dwλ∈N∗: number of UAVs requested by the crowd w during the period λ.

–   ∀λ∈Λ,Sλ: set of charging stations during the period λ.

∗   |Sλ|=p: number of charging stations. p is fixed during all periods.

∗   ∀u∈Uλ,s∈Sλ,csusλ: distance (meter) between a UAV u during the period (λ−1) and a charging station s during the period λ.

∗   ∀s∈Sλ, xcordsλ and ycordsλ: latitude and longitude of the charging station s during the period λ.

∗   ∀s∈Sλ, mobilsλ∈{0,1}: mobility of the charging station s during the period λ, 0: fixed, 1: mobile. For simplification purposes, we consider that all charging stations are fixed.

∗   ∀s∈Sλ, rs∈N∗: capacity, in terms of UAVs number, of the charging station s during all periods.

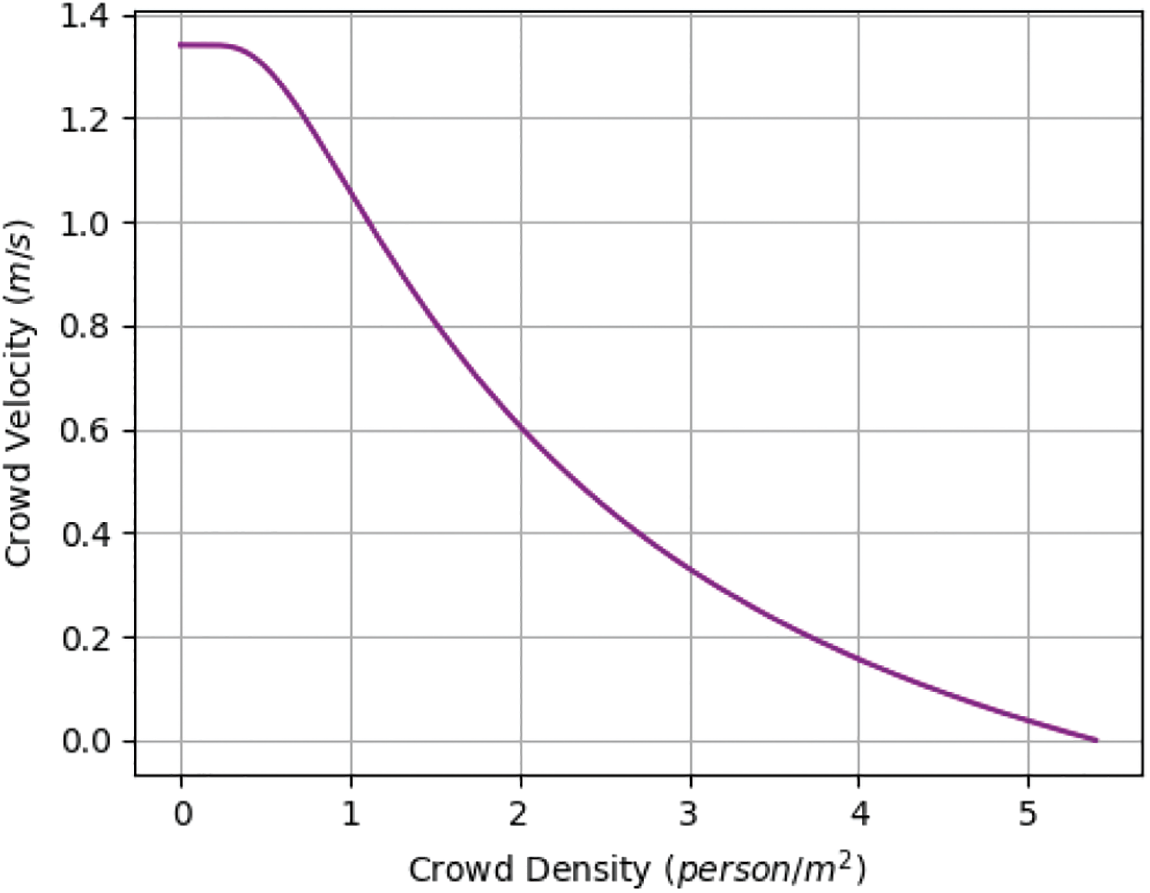
Figure 3: Weidmann’s fundamental diagram. The plot of the density-speed relation according to Weidmann’s fundamental diagram function of Eqs. (4) and (5) [84]

3.3 Decision Variables

Based on the considered parameters and decision variables described in Sections 3.2 and 3.3, we considered the following decision variables of the BLP for the PCTλ relative to solving the PCT at the beginning of each period λ∈Λ according to the whole system state at the ending of period (λ−1):

•   ∀u∈Uλ,∀w∈Wλ,xuwλ=1 if the UAV u is assigned to the crowd w during the period λ, 0 otherwise.

•   ∀u∈Uλ,s∈Sλ, yusλ=1 if the UAV u is assigned to the charging station s during the period λ, 0 otherwise.

3.4 Objective Functions

We defined two objective functions for the PCTλ which take into account the minimization of time and energy consumed by UAVs such as:

•   The first objective (ref. Eq. (6)) considers the minimization of the total time consumed by all UAVs movements during their transition from a period (λ−1) to a period λ. The first and second terms of this objective represent the total movements time of UAVs traveling from their positions during period (λ−1) to their assigned crowds or stations during period λ, respectively. To avoid some restrictions and difficulties caused by floating values during the solving process, we approximated all the coefficients to their upper integer values.

minZ1λ=∑u∈Uλ(∑w∈Wλcwuwλϑuxuwλ+∑s∈Sλcsusλϑuyusλ)≈∑u∈Uλ(∑w∈Wλ⌈cwuwλϑu⌉xuwλ+∑s∈Sλ⌈csusλϑu⌉yusλ)(6)

•   The second objective (ref. Eq. (7)) considers the minimization of the total energy loss of all UAVs during their transition between the two successive periods (λ−1) and λ and during the crowd supervision of the period λ. The first and the second terms of this objective function represent the total energy consumed by UAVs during their movements when traveling from their positions during period (λ−1) to their assigned crowds or stations during period λ, respectively. The third term represents the consumed energy by UAVs following their crowds supervision during the period λ. For the same reason as in the first objective function, we set all the coefficients to their upper integer values.

minZ2λ=∑u∈Uλ∑w∈Wλcwuwλϑuτˇuxuwλ+∑u∈Uλ∑s∈Sλcsusλϑuτˇuyusλ+Tλ∑u∈Uλ∑w∈Wλxuwλτˇu=∑u∈Uλ(∑w∈Wλ(cwuwλϑu+Tλτˇu)xuwλ+∑s∈Sλcsusλϑuτˇuyusλ)≈∑u∈Uλ(∑w∈Wλ⌈cwuwλϑu+Tλτˇu⌉xuwλ+∑s∈Sλ⌈csusλϑuτˇu⌉yusλ)(7)

3.5 Constraints

Based on the considered assumptions, parameters, and decision variables described in Sections 3.1–3.3, we considered the following constraints applied by the BLP solver of PCTλ at the beginning of each period λ∈Λ.

3.5.1 UAVs Constraints

Constraints (8) ensure that each UAV should be assigned to only one crowd or only one charging station.

∑w∈Wλxuwλ+∑s∈Sλyusλ=1,∀u∈Uλ(8)

Constraints (9) ensure that the remaining energy εuλ of each UAV u∈Uλ assigned to a crowd w∈Wλ, after covering the period (λ−1), should be enough to perform its new movement with the distance cwuw and its coverage task during the period λ.

εuλ−∑w∈Wλ⌈cwuwλϑu×τˇu−Tλτˇu⌉xuwλ≥δˇuλ(1−∑s∈Sλyusλ),∀u∈Uλ(9)

Constraints (10) ensure that the energy of each UAV u∈Uλ, that was in a charging station s∈Sλ−1 during the previous period (λ−1) and assigned to a crowd w∈Wλ during a period λ, should not be less than the energy threshold δ^uλ allowing it to leave from a charging station.

(1−statuλ−1)×δ^uλ×∑w∈Wλxuwλ≤εuλ,∀u∈Uλ(10)

3.5.2 Crowds Constraints

Constraints (11) ensure that each crowd demand in a period λ should be satisfied.

∑u∈Uλxuwλ=dwλ,∀w∈Wλ(11)

3.5.3 Charging Station Constraints

Constraints (12) ensure that the number of UAVs in a charging station during a period λ, should not exceed the station capacity.

∑u∈Uλyusλ≤rs,∀s∈Sλ(12)

3.6 PCTs Solver Using the BLP Model

Solving the PCTλ at the beginning of each period λ∈Λ consists in optimally solving the BLP, noted BLP-PCTλ, considering one of the objective functions defined by Eqs. (6) and (7), under all constraints from (8) to (12). Many existing algorithms can solve efficiently each BLP-PCTλ that are embedded in several free or commercial solvers (e.g., GLPK2, IBM-ILOG-CPLEX3, GUROBI4, GAMS5, etc.). Algorithm 1 represents the PCTs solver by calling BLP-PCTλ for each λ∈Λ. This solver can be easily integrated into CMA systems using UAVs by enhancing the reassignment of UAVs to crowds at the beginning of each period λ (see line 5 of Algorithm 1). Fig. 4 shows the processing diagram followed by the PCTs solver to deal with each PCT instance.

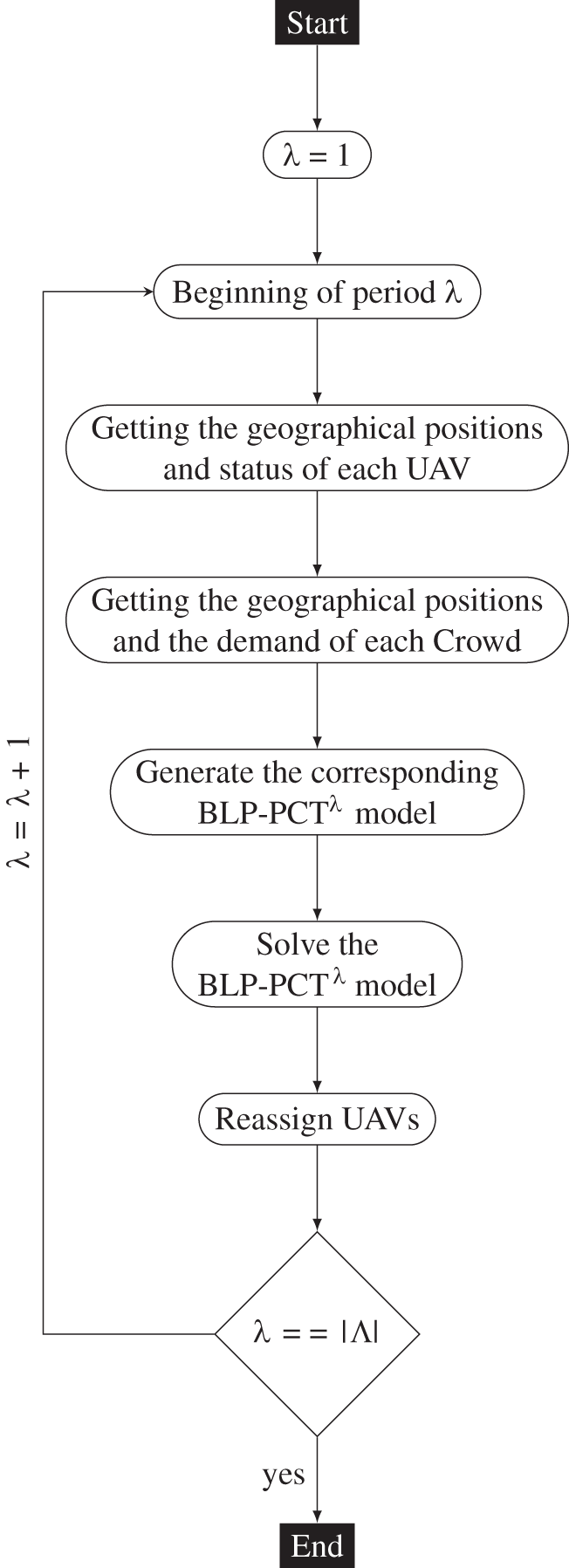
Figure 4: Processing diagram of PCT instances

4  Simulation and Computational Results

Experimental tests were carried out to evaluate the performance of the PCTs solver presented by Algorithm 1. To assess its efficiency, we reported experimental results obtained by the simulation of the PCTs solver on different sets of the PCT problem instances. This section was divided into three subsections. In Section 4.1, we introduced the PCTs instances generated to evaluate the solver performance, then we described our experimental environment settings. In Section 4.2, we revealed the experimental results obtained by the simulation of the PCTs solver, as described in the Section 3, then we discussed its ability to solve PCTs instances under different scenarios and its performance in terms of computational time. To highlight the importance of the initial infrastructure investment in terms of UAVs and CSs availability, in Section 4.3, we detailed the sensitivity analysis of the two considered objective functions according to different scenarios. We start this analysis by showing the behavior of these objective functions according to the variation of UAVs and CSs availability. This analysis showed that the initial infrastructure of a CMA system should be carefully chosen in order to reduce energy and time costs. Then, we introduced the impact of the instances granularity level determined by the BLP-PCTλ application frequency according to the CMA application context. Indeed, the update frequency of UAVs positions and activities during the OCA life cycle has a great significance on the considered objectives. Thus, all the performed analyses in this section, allow us to propose many research challenges to improve CMA systems performances in terms of crowd-tracking process.

4.1 PCTs Instances and Experimental Settings

4.1.1 Instances Generation

To the best of our knowledge, in the literature, there is a lack of accessible generic and diversified use cases and instances of the PCT problem. For this main reason and to effectively evaluate the performance of the PCTs solver, we generated a set of 840 PCTs instances under different scenarios. All these instances are generated under a fixed 1-h OCA life cycle (C=3600) seconds and a rectangular-shaped OCA Qλ with fixed dimensions (ℓQλ×hQλ=2000 m ×1000 m =2.106 m2,∀λ∈Λ). Each instance is generated according to five fixed parameters:

•   The number of periods |Λ| during the life cycle C. This parameter determines the application frequency of the BLP-PCTλ by the PCTs solver. It has a very important impact on the energy and time costs discussed in Section 4.3.3.

•   The number of charging stations |Sλ|=p which is fixed for all periods λ of a given set of periods Λ in C. This parameter has also a very important effect on the PCT objective discussed in Section 4.3. Each charging station s∈Sλ is considered immobile mobilsλ=0, and has a fixed capacity rs,∀λ∈Λ.

•   The maximum number of crowds ϕ1 in each period. Each period λ∈Λ has a specified number of crowds |Wλ|=m≤ϕ1. The characteristics of each crowd w∈Wλ change from one period to another, during the OCA life cycle C, such as: its gravity center coordinates (xcordwλ, ycordwλ), ray raywλ, density ρwλ, speed ϑwλ, and demand dwλ. Two or more crowds can merge during a given period to become only one crowd during the next period. To get closer to the real-world cases, some periods may not have crowds to supervise.

•   The number of required UAVs per 5000 m2 noted ϕ2. The number of UAVs |Uλ|=n,∀λ∈Λ is driven by the crowds demands dw0,∀w∈W0 in the initial CMA system state.

•   The total number of UAVs is determined by increasing the total demand of all crowds by a coefficient ϕ3. Indeed, depending on the CMA application context, the UAVs availability has a very important impact on both costs and QoS.

In order to generate the whole set of 840 PCT instances, the values of the quintuple (|Λ|,|Sλ|,ϕ1,ϕ2,ϕ3) are set to the values from the sets {6,12,30,40,60,120,240}, {2,4,6,8}, {2,4,8,10,12}, {1,2,3}, {2,4}, respectively. There are some other parameters that are fixed randomly or according to some formulas discussed in Section 3.2. Table 1 summarizes all the parameters used to generate the PCT instances that are available for download through the link below6.

4.1.2 Experimental Settings and Metrics

The PCTs solver is implemented in Python programming language. The outlined BLP-PCTλ (see Section 3) is also implemented using DOcplex Python Modeling API of IBM-ILOG-CPLEX (version 12.10) using its default tuning parameters7. All simulations have been conducted on a personal computer (Intel(R) Core(TM) i7-10700 CPU, 2.90 GHz with 8 GB RAM) running with Windows 11 and Python 3.7 compiler.

We empirically evaluated our PCTs solver on the instances set described in Section 4.1.1. In order to discuss the added value of its use, we considered the following metrics to evaluate the PCTs solver performance:

•   Z1=∑λ∈ΛZ1λ: the total of objective function values Z1λ, expressed by Eq. (6), that considers the cumulative time consumed by all UAVs during their transitions through the different periods of the OCA life cycle.

•   Z2=∑λ∈ΛZ2λ: the total of objective function values Z2λ, expressed by Eq. (7), that considers the cumulative energy consumed by all UAVs during their transitions through the different periods of the OCA life cycle.

•   Ψ≤|Λ|: the number of periods during the OCA life cycle that our PCTs solver was able to solve. Indeed, at some periods λ∈Λ, when the BLP-PCTλ is applied on PCTλ with a given objective function, there are some selected UAVs which will be unavailable during the next periods which perturbs PCTλ+1 solvability. This point was discussed in depth in Section 4.2.

•   Δλ: the consumed CPU-time (in seconds) to solve a PCTλ for a given period λ∈Λ of a given PCT instance.

•   Δ=∑λ∈ΛΔλ: the total consumed CPU-time to solve the PCTλ for all periods λ∈Λ of a given PCT instance with a given objective function.

4.2 Simulation Results and PCTs Solver Performance

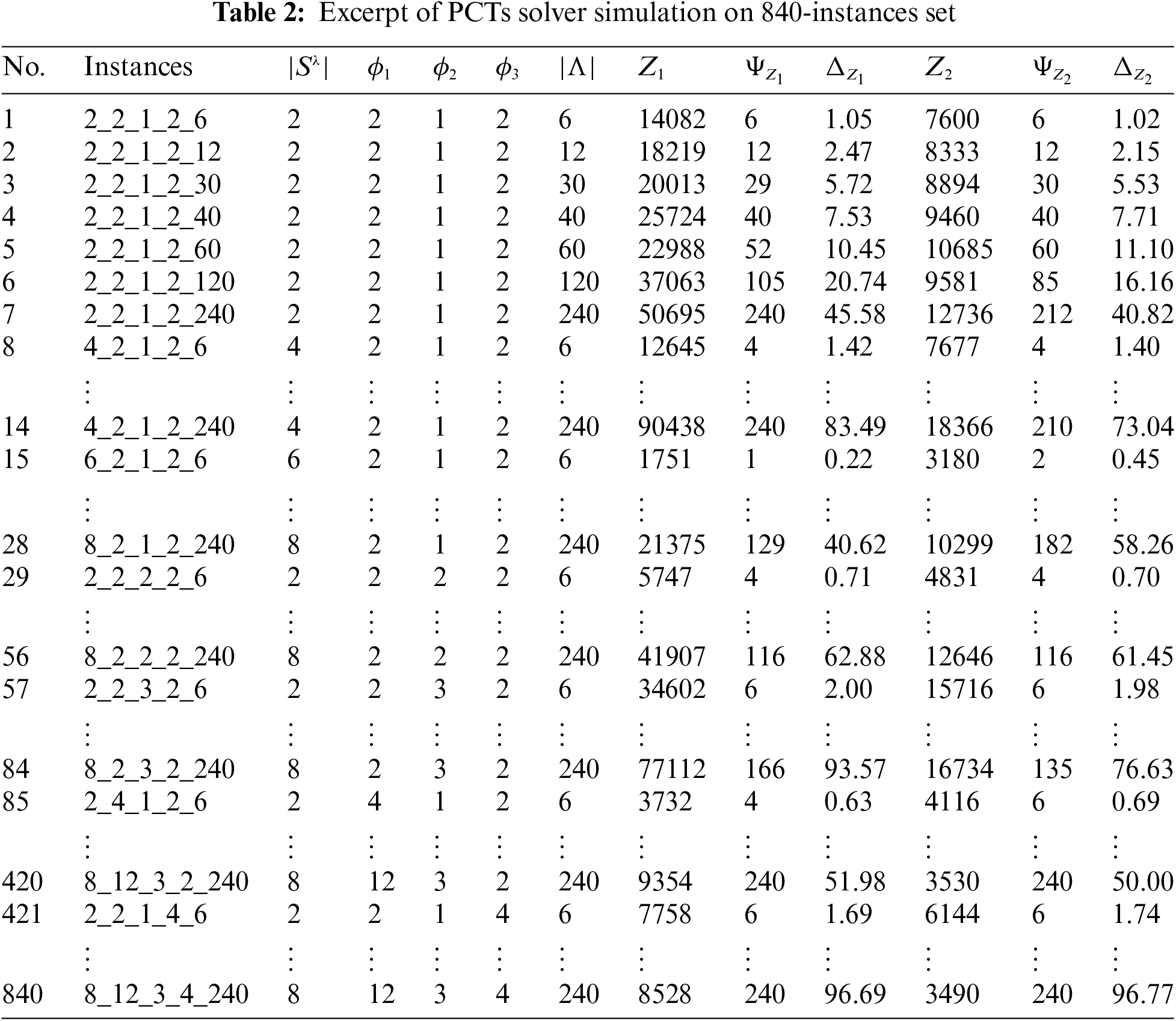
Table 2 displays an excerpt of the results obtained by applying the PCTs solver on the 840-instances set described in Section 4.1.1 according to the metrics described in Section 4.1.2. All the global simulation results file as well as the detailed results of each instance under the two considered objective functions are available to download through the below link8. Instances names follow the pattern (|Sλ|_ϕ1_ϕ2_ϕ3_|Λ|). Each instance was solved for each objective function considered in the BLP-PCTλ such as Z1 and Z2. According to the considered objective functions, we reported the two couples (ΨZ1, ΔZ1) and (ΨZ2, ΔZ2) that represent the number of solved periods and the total consumed CPU-time, respectively, for each instance and for a considered objective function.

4.2.1 PCTs Solver Coverage Ability

When applying the PCTs solver on a given instance with |Λ| periods, it may not cover all the periods in Λ. Indeed, at each period λ∈Λ, the PCTs solver deals with the corresponding BLP-PCTλ according to (i) the considered objective function Z1λ or Z2λ, (ii) the set of stations Sλ and their characteristics, (iii) the set of UAVs Uλ and their characteristics, and (iv) the set of existing crowds Wλ their characteristics.

Fig. 5 shows the PCTs solver coverage ability covab according to the considered objective function and the number of periods |Λ|. The coverage ability is measured by the percentage of solved periods Ψ compared to the total number of periods of each instance |Λ| calculated as follows:

covab=Ψ|Λ|×100(13)

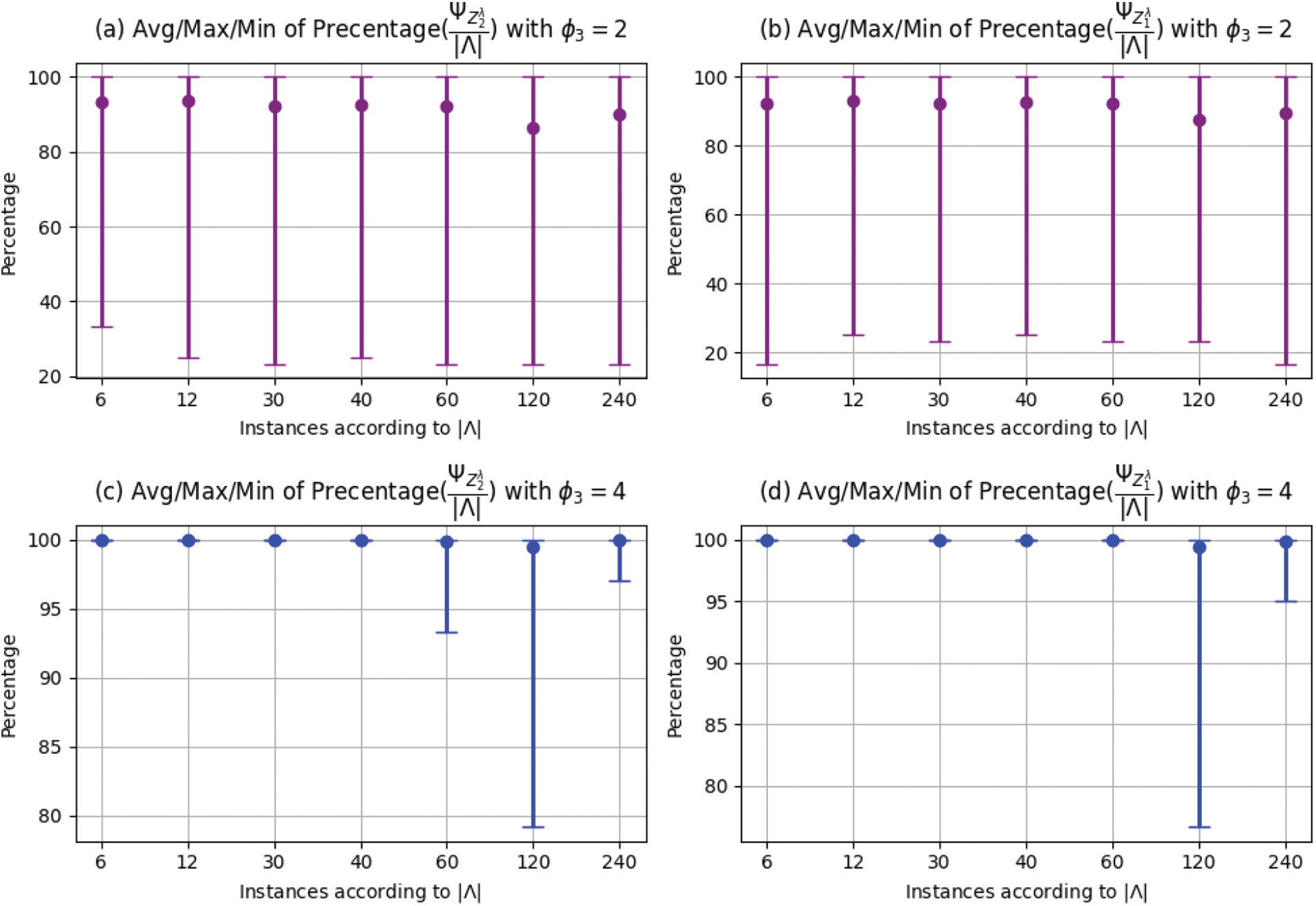
Figure 5: Ability of PCTs solver in terms of periods coverage Ψ according to the number of periods |Λ| and the UAVs availability ϕ3

Figs. 5a–5d show the average, maximum, and minimum covabs obtained by instances combination of the UAVs availability determined by (ϕ3=2,ϕ3=4) and the considered objective functions (Z1λ, Z2λ) in BLP-PCTλ, respectively. It can be noticed that the average of coverage ability is around 90% for ϕ3=2 and 100% for ϕ3=4 for both objective functions Z1λ and Z2λ. This is expected since the number of UAVs plays a key role in the resolution process. It is worth reminding that the availability of each UAV u∈Uλ changes from one period to another because of the decrease in its autonomy in terms of power that is determined by the triple (ϑuλ,τˇu,τ^u). After a certain number of periods in the OCA life cycle, some UAVs lose their energy and the PCTs solver becomes unable to solve the remaining periods. This is explained by the fact that, for each period λ∈Λ, the PCTs solver considers only the current PCTλ parameters and does not take into account the CMA states and the OCA needs in the next periods. This drawback will be discussed in Section 5 as a new challenge to improve the PCTs solver.

Fig. 6 displays the PCTs solver coverage ability according to the considered objective function and the number of stations |Sλ|. Figs. 6a and 6b show instances of low UAVs availability, the PCTs solver average, maximum, and minimum covab relative to the considered objective functions (Z1λ, Z2λ) in BLP-PCTλ, respectively. It can be noted that the covab average is greater than 90% for |Sλ|={2,4,8} and less than 90% for |Sλ|=8 for both objective functions Z1λ and Z2λ. This observation proves that increasing the number of stations does not necessarily improve the coverage ability of the PCTs solver. Indeed, increasing the number of CSs may decrease the travel distance between flying UAVs and CSs, however, it has no effect on flying UAVs movements between different crowds. Also, there are some other important factors that affect the coverage ability namely the location distribution of the CSs over the OCA, the capacity of each CS, and the UAVs distribution over the different CSs. This assumption was also highlighted in Section 4.3 and further discussed in Section 5 as an additional challenge to improve the PCTs solver.

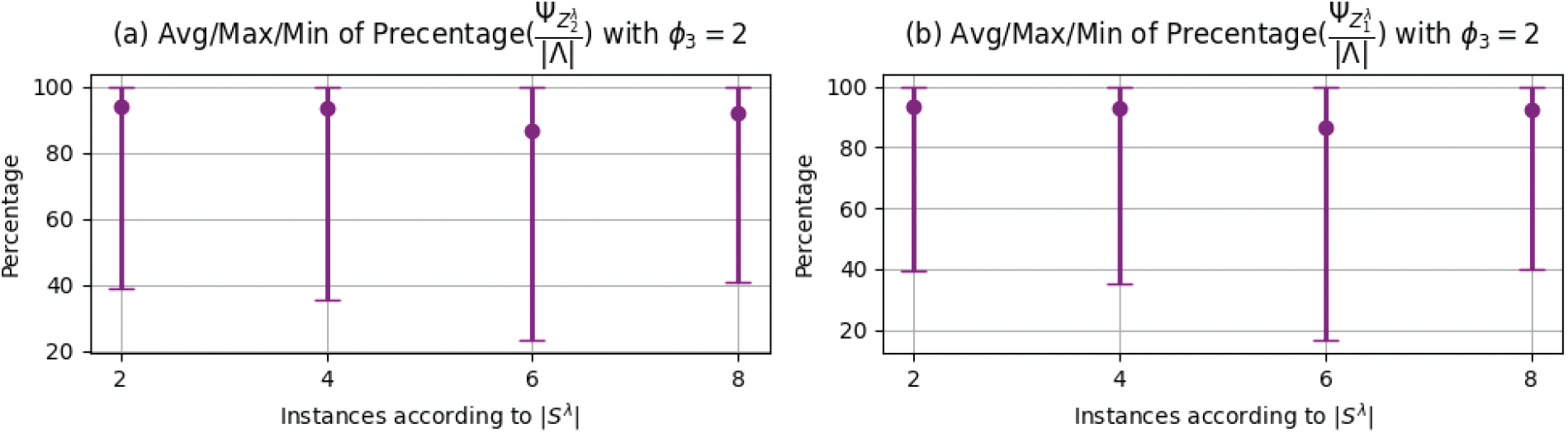
Figure 6: Ability of PCTs solver in terms of periods coverage Ψ according to the number of stations |Sλ|

Fig. 7 shows the PCTs solver coverage ability according to the considered objective function and the maximum number of crowds at each period determined by |ϕ1|. Figs. 7a and 7b show instances of low UAVs availability, the PCTs solver average, maximum, and minimum covab relative to the considered objective functions (Z1λ, Z2λ) in BLP-PCTλ, respectively. A strange behavior can be easily observed which consists in the fact that the covab average increases and reaches 100% when the number of crowds is increased for both objective functions Z1λ and Z2λ. This observation can be explained by the fact that our PCTs solver is always applied on an OCA. Indeed, a crowded area with a low number of crowds does not mean that the area where the crowds are located are small compared to their whole OCA dimensions/area. To preserve the characteristics of the crowds in the OCA, it should be reminded that at each period of all of our generated PCT instances, the total area of the crowds was considered to be very close to that of the OCA (see the crowds rays raywλ calculation way shown in Table 1). For example, if the maximum number of crowds ϕ1 is set to 2, we can find two big crowds that navigate over the whole OCA and require a higher number of UAVs.

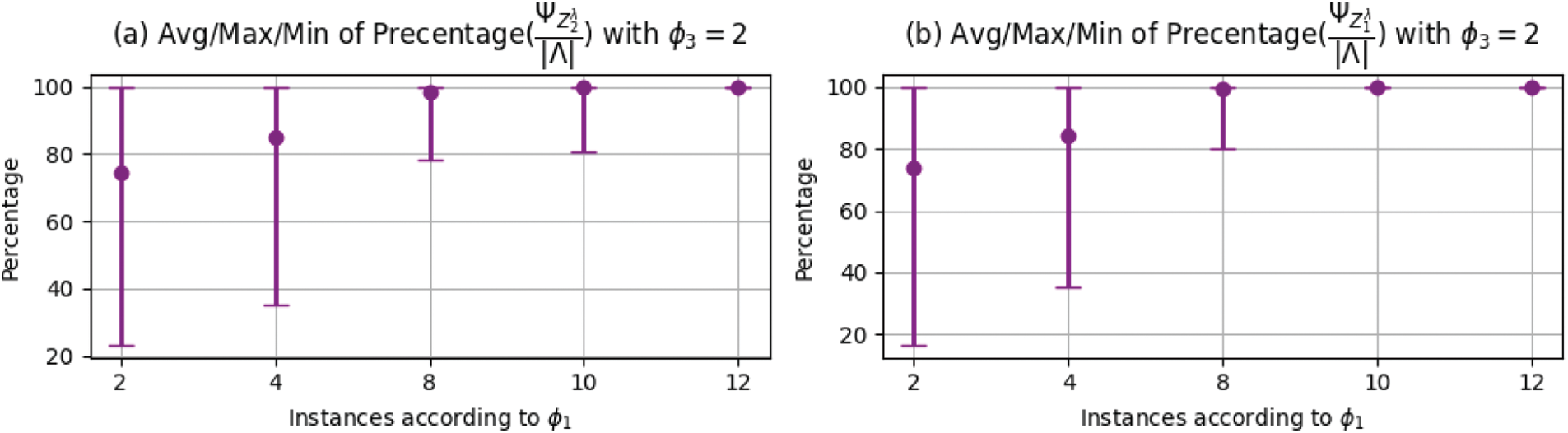
Figure 7: Ability of PCTs solver in terms of periods coverage Ψ according to the number of crowds ϕ1

4.2.2 PCTs Solver Computation Performance

It is worth reminding that solving BLP-PCTλ is performed by the PCTs solver at the beginning of each period λ∈Λ during a given OCA life cycle. To ensure a high QoS of a given CMA, a quick BLP-PCTλ application is needed to provide new UAVs-Crowds/UAVs-CSs assignment. Fig. 8 shows the recorded average, maximum, and minimum CPU-time Δλ consumed by solving BLP-PCTλ for all 840-instances by the PCTs solver. The instances are categorized according to the considered objective function and the UAVs availability. We can confirm that our model BLP-PCTλ is efficient in preserving the QoS of any given CMA. Indeed, for instances with low UAVs availability (ϕ3=2), the average CPU-time is about 0.25 s and does not exceed about 0.75 s for both objective functions Z1λ and Z2λ. For instances with high UAVs availability, the CPU-times are 0.4 and 1.5 s, respectively. It is also worth noting that the average CPU-time is very close to the minimum one.

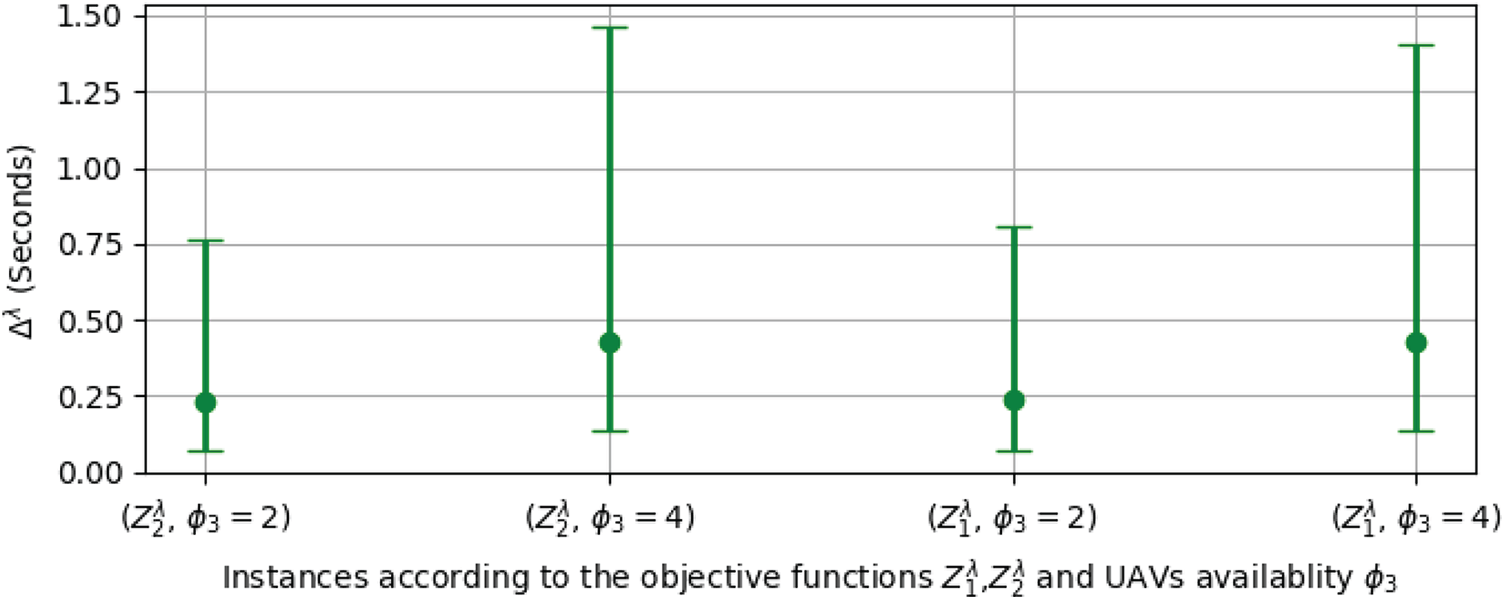
Figure 8: CPU-time consumption Δλ of BLP-PCTλ solving

Figs. 9a–9d represent the average, maximum, and minimum CPU-time Δ taken by PCTs solver to solve BLP-PCTλ for all periods of a given instance. They show these CPU-times according to the combination of the UAVs availability determined by (ϕ3=2,ϕ3=4) and the considered objective functions (Z1λ, Z2λ) in BLP-PCTλ, respectively. Only the CPU-times of instances where the PCTs solver covers all periods are displayed (i.e., covab=100%, Ψ=|Λ|). In the worst case, for each instance, the PCTs solver solves the BLP-PCTλ for |Λ| times. For this reason, Fig. 9 also shows that the average of the global consumed CPU-time increases while increasing the number of periods |Λ|. Likewise, the increase in UAVs availability for instances with ϕ3=4, resulted in the CPU-time to double compared to instances with low UAVs availability. This can be explained by the increase in the decision variables xuwλ and yusλ for each BLP-PCTλ.

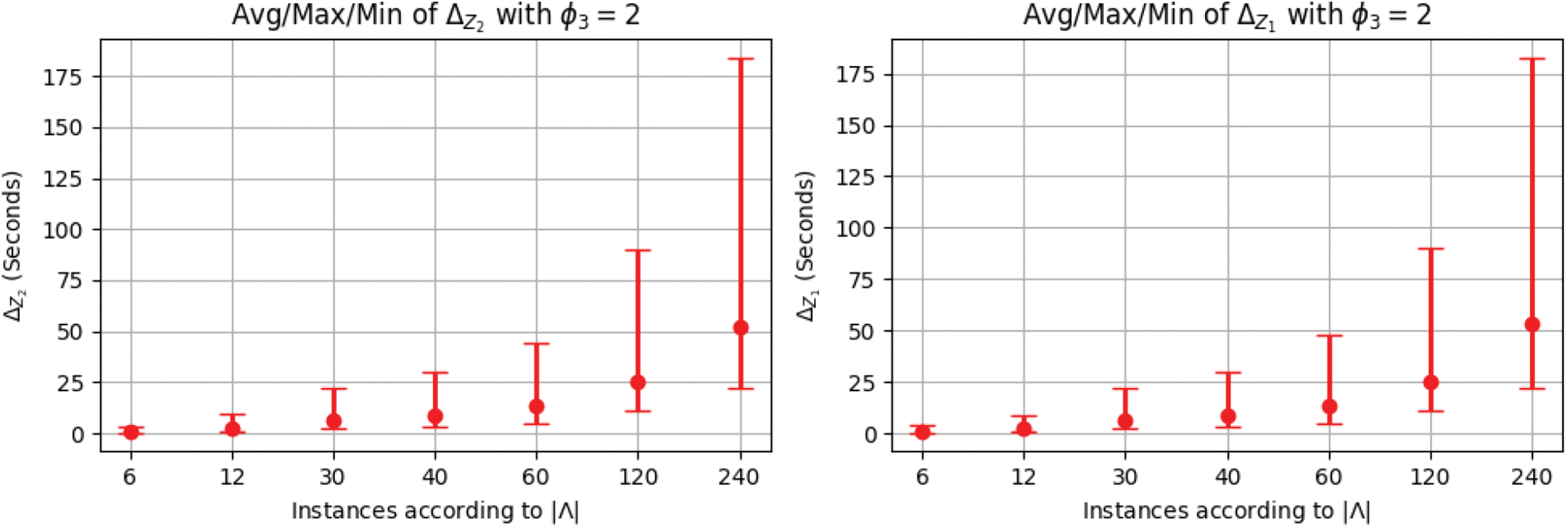
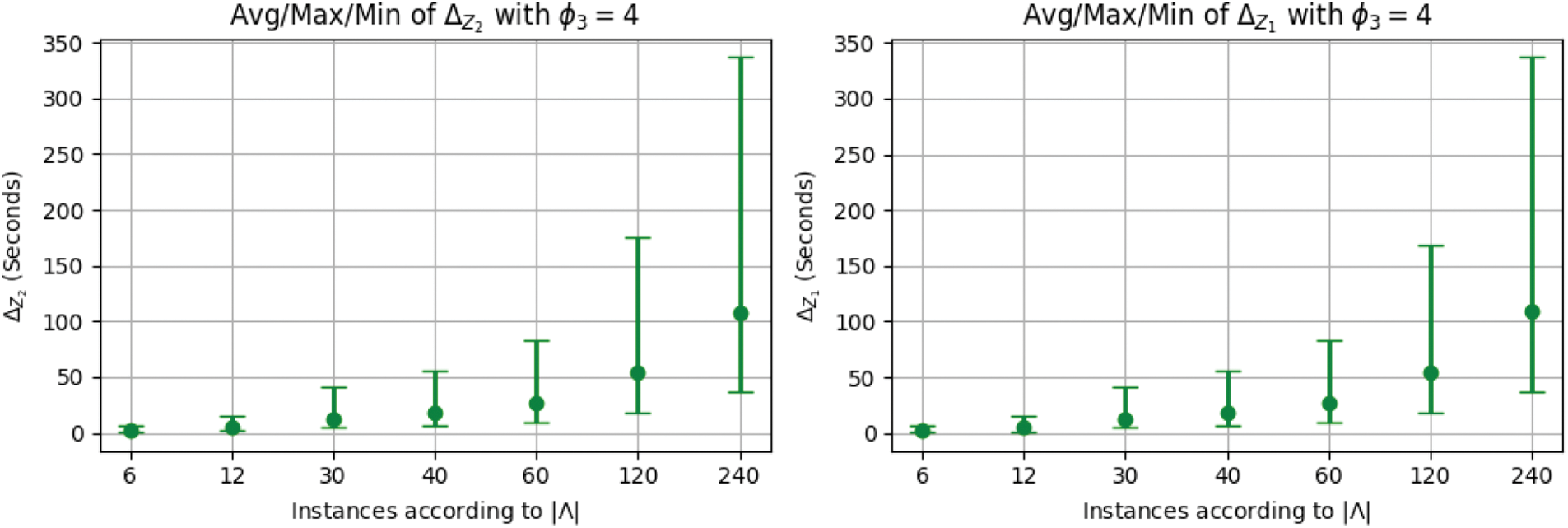
Figure 9: CPU-time consumption Δ of PCTs solver for instances where Ψ=|Λ|

4.3 Objective Functions Sensitivity Analysis

The initial investment in the infrastructure of a given CMA system in terms of UAVs and CSs is very important to be able to provide a high QoS level. Also, it determines its competitiveness level in the market. The two major considered criteria to evaluate a CMA performance are its dissipated energy and its response time for any request. The response time criteria can be evaluated by the time consumed by a solver to provide new distribution/assignment of UAVs over the OCA, already discussed in Section 4.2.2, and the time consumed by all UAVs to rejoin their new positions provided by the solver.

The two considered objective functions Z1λ and Z2λ expressed by Eqs. (6) and (7), i.e., minimizing the total time consumed by all UAVs moves and the total energy consumed, are strongly connected. Indeed, the consumed energy by a given UAV is determined by its characteristic and the moves carried out during the OCA life cycle as shown by the energy loss function expressed by Eq. (1). In this section, we assessed the sensitivity analysis of these two objective functions according to the variation of the initial infrastructure in terms of UAVs and CSs. Then, we provided their sensitivity analysis according to the level of instance granularity determined by the intervene frequency of the PCTs solver to achieve a new distribution of the UAVs over the OCA.

4.3.1 UAVs Availability Impact Analysis

Fig. 10, reports on the two objective functions variation Z1 and Z2 according to the variation of UAVs availability determined by the parameter ϕ3 for all instances where Ψ=|λ| (see Table 1). Then, it can be easily concluded that when the UAVs availability increases, the PCTs solver gains in terms of both energy and time. This is explained by the fact that the PCTs solver has more flexibility in terms of UAVs to select those having the characteristics to dissipate less energy and time during their movements. This fact will be further discussed as a new challenge in Section 5 to be able to achieve more optimality in a given CMA system. Indeed, the choice of a UAV fleet should be carefully carried out according to the UAVs characteristics, already discussed in Section 3.2.

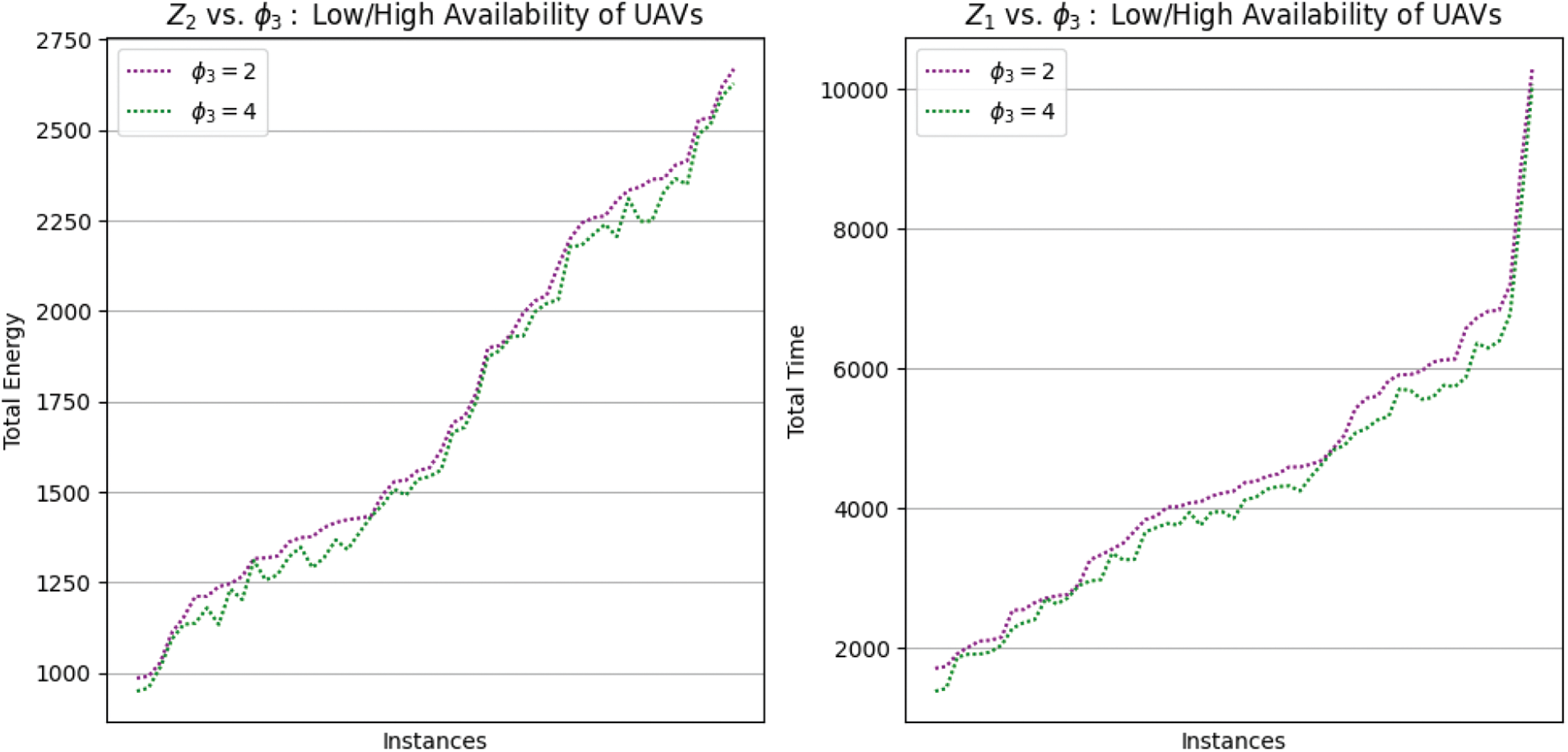
Figure 10: Energy and time sensitivities vs. UAVs availability

4.3.2 CSs Availability Impact Analysis

Fig. 11 reports on the objective function values Z1 and Z2, for instances with fixed parameters ϕ1=8 and ϕ2=2 where Ψ=|λ|, according to different CS numbers (Sλ=p={2,4,6,8}). We can easily notice that for all instances the energy and time decrease when Sλ increases from 2 to 4 and from 4 to 6 but they increase again when Sλ is set to 8. This abnormal behavior has already been noted in Section 4.2.1. Indeed, when the CSs availability is increased, this does not necessarily mean that the UAVs will be closer to the crowds and then the whole CMA consumed energy and time will be reduced. It should be reminded that it depends on the CSs distribution over the OCA and the initial and online assignment of UAVs to Crowds and CSs. This fact will be further discussed in Section 5 and considered as a highly challenging CSs mobility and assignment issue.

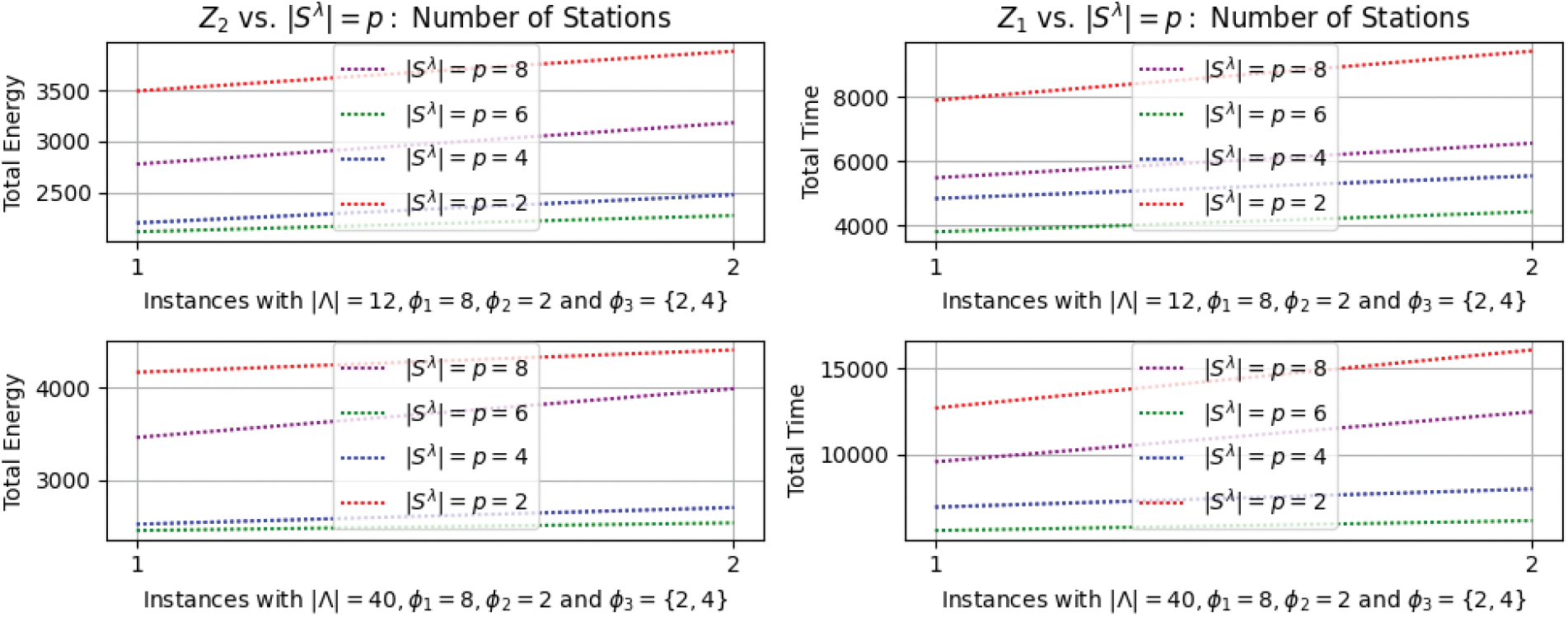
Figure 11: Energy and time sensitivities vs. number of stations

4.3.3 Granularity Level Impact Analysis

Apart from the initial CMA system cost, there is a very important parameter that affects the two objective functions. This parameter is the update frequency of UAVs positions, over the OCA and CSs, provided by the PCTs solver, and noted as granularity level. Fig. 12 shows the objective function values Z1 and Z2, for instances with fixed parameters ϕ3=2 and ϕ3=4 where Ψ=|λ|, for different periods (|λ|={6,12,30,40,60,120,240}). Due to the reduced frequency of the UAVs location change for small |Λ| values, this will logically lead to energy and time increase when |Λ| decreases for all instances. However, it is worth noting that with certain |λ| values, Z1 and Z2 become very close for most of the instances. For example, for |Λ|=120 and |Λ|=240, the consumed energy or time values are very close and sometimes equal. This shows that, for some CMA system contexts, the granularity level can be reduced to optimize energy and time and allow the system to be more competitive in terms of service pricing, without decreasing the QoS level. This observation was further discussed in Section 5.

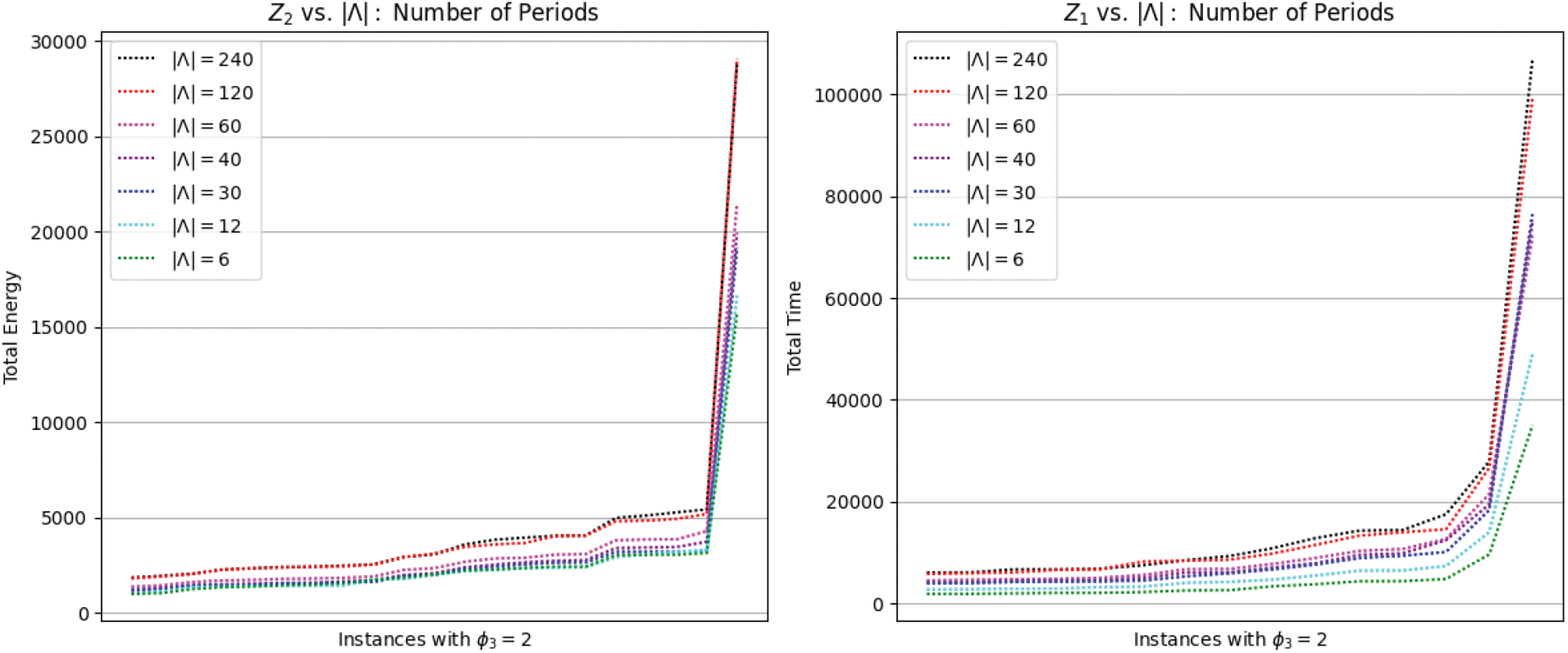
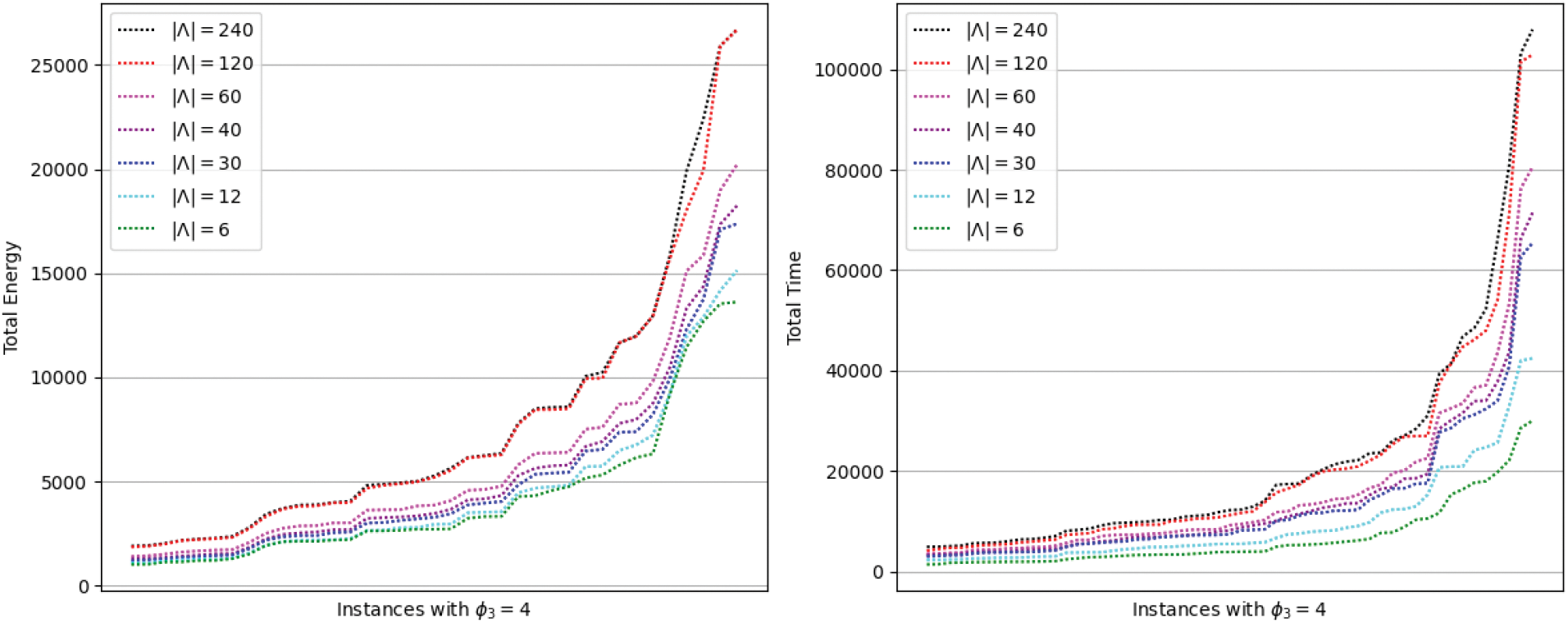
Figure 12: Energy and time sensitivities vs. granularity level (number of periods)

5  Future Challenges

With a certain abstraction level in the context of CMA applications, we suggested the first attempt to formally model and optimally solve the PCT problem using drones. In order to study and analyze the PCTs solversensitivity, we defined a set of greatly important parameters in achieving optimality in terms of CMA infrastructure investment and maintenance, its QoS, service pricing, market competitiveness, among others. By simulating the PCTs solver on a set of diverse instances and then analyzing the obtained results, this section was devoted to enumerating a set of challenges to improve its optimality. In the sequel, we categorized these challenges according to the effective and influential aspects whose impact on PCT optimality had already been proven.

5.1 UAVs-Related Challenges

In the previous section, we referred to the important impact of UAVs availability and characteristics on the PCTs solver in terms of coverage ability, consumed CPU-time, and obtained objective function value. According to these issues, we can report the following challenges:

•   The UAVs availability has an important impact on the PCTs solver coverage ability. In fact, providing a huge number of UAVs would not be a good idea since it would affect the CPU solving-time as well as the CMA initial investment in terms of infrastructure. Consequently, studying the optimal UAVs number in the initial fleet might be a challenge to allow facing this drawback. This type of issues has already been widely investigated in the literature in the context of Vehicle Routing Problem (VRP) [87]. The main specificity that characterizes the PCT problem from that of the VRP is that the characteristics and behavior of crowds are unpredictable which affects the UAVs need. However, the literature involves many proposed methods that can be used to predict crowds characteristics and behavior based on machine learning techniques [35,43,53,57,60–62,67,68].

•   Even if the UAVs availability and characteristics are initially studied based on crowds prediction, the PCTs solver can not cover all the OCA periods. Indeed, by solving the BLP-PCTλ at each period λ∈Λ, only the current OCA state, and CMA available infrastructure are considered. This drawback may involve a PCTs solver coverage inability during future periods. This can be due to the exhaustion of some potential UAVs that might answer a future coverage need. We call this disadvantage the “PCTs solver myopia”. To improve the PCTs perspicacity solver, we can propose to preliminary solve all PCTλ, ∀λ∈Λ, using only one improved BLP. There are many homologous optimization problems that have already been treated in many fields namely the multi-periodic production scheduling where we can cite the Multiple Knapsack Problem with Setup (MKPS) [88]. Some prediction techniques should necessarily be considered like those suggested in the previous challenge. Solving the whole PCTλ, ∀λ∈Λ, relying only on solving one BLP, involves an increasing number of constraints and decision variables and might then result a CPU-time overhead. This issue is due to the fact that the solution process is performed in advance (offline).

•   Balancing the UAVs use can be also considered as an additional challenge to the improved BLP since it involves a set of special objectives or constraints. Indeed, focusing only on the use of a specified kind of UAVs while others, may cause some UAVs maintenance extra cost. Many balancing optimization techniques have already been used in the literature to balance the resources use when solving optimization problems [89–91].

5.2 CSs-Related Challenges

We have already shown that the CSs availability has an impact on the UAVs energy and time consumption. In some cases, the CSs availability and location affect both energy and time consumption. To avoid such an issue, we propose investigating the following challenges:

•   Studying the CSs initial locations tacking into account the crowds behavior and characteristics focusing on a better initial and future UAVs distribution over CSs. Some machine learning techniques, proposed in UAVs related challenges, can be used to achieve this objective. Many analog works in the literature related to the optimization of the Facility Location Problem (FLP) [92–94] can be considered while dealing with this issue.

•   Fixed CSs locations may cause UAVs to consume a lot of energy and time during the whole OCA coverage process. Mobile CSs, can be a very interesting study issue to reduce energy and time consumption and decrease the initial CMA infrastructure costs by controlling the number of UAVs and CSs. Some research works have already tried to propose a system with mobile CSs, no such a formal optimal model has been conceived [63,95]. This is an additional issue to the other UAVs-related challenges in order to efficiently optimize the UAVs online distribution and then their future availability.

•   The BLP improvement challenge, suggested in the previous section, can also be enhanced by the CSs mobile location to ensure UAVs the availability.

5.3 Granularity Level-Related Challenges

The granularity level impact analysis, performed in Section 4.3.3, proves that the update frequency of UAVs locations has a very important impact on energy and time consumption. We also noticed that the increasing of this frequency does not necessarily imply an increase in UAVs energy and time consumption. Therefore, we suggested an open challenge that consists of a technique that minimizes the granularity level (reduce the update frequency) in order to reduce the energy and time consumption without losing the QoS provided by a CMA system. This challenge aims to reduce the service pricing and increase the competitiveness of the system over the market. On the other hand, reducing the number of periods |Λ| makes the improved BLP, proposed as a challenge in the previous sections, easier to solve due to the reduction of the constraints and decision variables numbers.

6  Conclusion

In this paper, a PCTs solver was proposed to periodically solve the PCT using UAVs. This can be embedded in a CMA system using UAVs to provide a crowd-tracking service while ensuring an adequate QoS. The review of the literature allowed us to recognize that all the related works, in the field of crowd tracking, consider only a specified application of the crowd monitoring and analysis systems. In addition, we also diagnosed another gap that consists of a lack of formal and generic models to solve the crowd tracking problem. Consequently, we proposed a BLP to optimally solve the PCT. This model is based on several assumptions and parameters that were thoroughly defined and studied. To assess the performance of the PCTs solver, we provided a set of 840 diversified PCTs instances. The computational results, obtained by the simulation of the PCTs solver on these instances, led us to evaluate the first attempt to formally model the PCT and periodically solve it. Furthermore, we suggested a set of open challenges to enhance its solving capabilities. These potential new challenges were recognized based on many criteria related to the OCA characteristics and the initial infrastructure cost of such a CMA system using UAVs.

Acknowledgement: The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work. They also thank the editor and the anonymous referees who have provided valuable comments on an earlier version of this paper. They would also like to show their gratitude to Dr. Jamel Mtawaa (English Faculty Member at the University of Jeddah, KSA) for the English proofreading of the last version of this paper.

Funding Statement: This work was supported by the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia under Grant No. MoE-IF-G-20-08.

Author Contributions: Kalil Chebil: Methodology, Data Curation, Software, Validation, Writing-Review & Editing. Skander Htiouech: Investigation, Data Curation, Visualization, Supervision, Project administration, Funding Acquisition, Writing-Review & Editing. Mahdi Khemakhem: Conceptualization, Methodology, Formal Analysis, Writing-Original Draft.

Availability of Data and Materials: The detailed PCTs solver simulation results and solutions on the generated 840-instances set are available via https://shortest.link/38ZH.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1According to the Saudi General Authority for Statistics https://www.stats.gov.sa/sites/default/files/haj_40_en.pdf.

2https://www.gnu.org/software/glpk/.

3https://www.ibm.com/sa-en/analytics/cplex-optimizer.

4https://www.gurobi.com/.

5https://www.gams.com/products/solvers/.

6The PCTs 840-instances set is available via https://shortest.link/38ZH.

7https://www.ibm.com/docs/en/icos/12.9.0?topic=cplex-list-parameters.

8The global and detailed PCTs solver simulation results and solutions on the 840-instances set are available via https://shortest.link/38ZH.

References

1. Valavanis, K. P., Vachtsevanos, G. J. (2015). Handbook of unmanned aerial vehicles. Dordrecht: Springer Netherlands. [Google Scholar]

2. Cupp, C. M., Levine, P. (1998). The DTIC review. Unmanned aerial vehicles, vol. 4, no. 2, 19980826172. Defense Technical Information Center Fort Belvoir Va. [Google Scholar]

3. Chen, L., Liu, W. -L., Zhong, J. (2022). An efficient multi-objective ant colony optimization for task allocation of heterogeneous unmanned aerial vehicles. Journal of Computational Science, 58(21), 101545. https://doi.org/10.1016/j.jocs.2021.101545 [Google Scholar] [CrossRef]

4. Akbari, Y., Almaadeed, N., Al-maadeed, S., Elharrouss, O. (2021). Applications, databases and open computer vision research from drone videos and images: A survey. Artificial Intelligence Review, 54(5), 3887–3938. https://doi.org/10.1007/s10462-020-09943-1 [Google Scholar] [CrossRef]

5. Li, X., Savkin, A. V. (2021). Networked unmanned aerial vehicles for surveillance and monitoring: A survey. Future Internet, 13(7), 174. https://doi.org/10.3390/fi13070174 [Google Scholar] [CrossRef]

6. Kakaletsis, E., Symeonidis, C., Tzelepi, M., Mademlis, I., Tefas, A. et al. (2021). Computer vision for autonomous UAV flight safety: An overview and a vision-based safe landing pipeline example. ACM Computing Surveys, 54(9), 1–37. [Google Scholar]

7. Dilshad, N., Hwang, J., Song, J., Sung, N. (2020). Applications and challenges in video surveillance via drone: A brief survey. Proceedings of the 11th International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Korea. [Google Scholar]

8. Alladi, T., Chamola, V., Sahu, N., Guizani, M. (2020). Applications of blockchain in unmanned aerial vehicles: A review. Vehicular Communications, 23(2), 100249. https://doi.org/10.1016/j.vehcom.2020.100249 [Google Scholar] [CrossRef]

9. Gupta, A., Afrin, T., Scully, E., Yodo, N. (2021). Advances of UAVs toward future transportation: The state-of-the-art, challenges, and opportunities. Future Transportation, 1(2), 326–350. https://doi.org/10.3390/futuretransp1020019 [Google Scholar] [CrossRef]

10. Rojas Viloria, D., Solano-Charris, E. L., Muñoz-Villamizar, A., Montoya-Torres, J. R. (2021). Unmanned aerial vehicles/drones in vehicle routing problems: A literature review. International Transactions in Operational Research, 28(4), 1626–1657. https://doi.org/10.1111/itor.12783 [Google Scholar] [CrossRef]

11. Outay, F., Mengash, H. A., Adnan, M. (2020). Applications of unmanned aerial vehicle (UAV) in road safety, traffic and highway infrastructure management: Recent advances and challenges. Transportation Research Part A: Policy and Practice, 141(3), 116–129. https://doi.org/10.1016/j.tra.2020.09.018 [Google Scholar] [PubMed] [CrossRef]

12. Alsamhi, S. H., Afghah, F., Sahal, R., Hawbani, A., Al-qaness, A. et al. (2021). Green internet of things using UAVs in B5G networks: A review of applications and strategies. Ad Hoc Networks, 117(2), 102505. https://doi.org/10.1016/j.adhoc.2021.102505 [Google Scholar] [CrossRef]

13. Alzahrani, B., Oubbati, O. S., Barnawi, A., Atiquzzaman, M., Alghazzawi, D. (2020). UAV assistance paradigm: State-of-the-art in applications and challenges. Journal of Network and Computer Applications, 166(1), 102706. https://doi.org/10.1016/j.jnca.2020.102706 [Google Scholar] [CrossRef]

14. Rejeb, A., Rejeb, K., Simske, S., Treiblmaier, H. (2021). Humanitarian drones: A review and research agenda. Internet of Things, 16(1), 100434. https://doi.org/10.1016/j.iot.2021.100434 [Google Scholar] [CrossRef]

15. Panday, U. S., Pratihast, A. K., Aryal, J., Kayastha, R. B. (2020). A review on drone-based data solutions for cereal crops. Drones, 4(3), 41. https://doi.org/10.3390/drones4030041 [Google Scholar] [CrossRef]

16. Boursianis, A. D., Papadopoulou, M. S., Diamantoulakis, P., Liopa-Tsakalidi, A., Barouchas, P. et al. (2020). Internet of Things (IoT) and agricultural unmanned aerial vehicles (UAVs) in smart farming: A comprehensive review. Internet of Things, 18, 100187. [Google Scholar]

17. Saraf, V., Senapati, L., Swarnkar, T. (2021). Application and progress of drone technology in the COVID-19 pandemic: A comprehensive review. In: Computational modeling and data analysis in COVID-19 research, vol. 1, pp. 47–66. [Google Scholar]

18. Hiebert, B., Nouvet, E., Jeyabalan, V., Donelle, L. (2020). The application of drones in healthcare and health-related services in North America: A scoping review. Drones, 4(3), 30. https://doi.org/10.3390/drones4030030 [Google Scholar] [CrossRef]

19. Devi, G., Sowmiya, N., Yasoda, K., Muthulakshmi, K., Balasubramanian, K. (2020). Review on application of drones for crop health monitoring and spraying pesticides and fertilizer. Journal of Critical Reviews, 7, 667–672. [Google Scholar]

20. Park, S., Choi, Y. (2020). Applications of unmanned aerial vehicles in mining from exploration to reclamation: A review. Minerals, 10(8), 663. https://doi.org/10.3390/min10080663 [Google Scholar] [CrossRef]

21. Husman, M. A., Albattah, W., Abidin, Z. Z., Mustafah, Y. M., Kadir, K. et al. (2021). Unmanned aerial vehicles for crowd monitoring and analysis. Electronics, 10(23), 2974. https://doi.org/10.3390/electronics10232974 [Google Scholar] [CrossRef]

22. Hassanalian, M., Abdelkefi, A. (2017). Classifications, applications, and design challenges of drones: A review. Progress in Aerospace Sciences, 91(4), 99–131. https://doi.org/10.1016/j.paerosci.2017.04.003 [Google Scholar] [CrossRef]

23. Patil, V., Potphode, V., Potdukhe, U., Badgujar, V., Upadhyaya, K. (2022). Smart UAV framework for multi-assistance. In: ICT with intelligent applications, pp. 241–249. Singapore: Springer. [Google Scholar]

24. Kumar, A. (2021). Crowd behavior monitoring and analysis in surveillance applications: A survey. Turkish Journal of Computer and Mathematics Education (TURCOMAT), 12(7), 2322–2336. [Google Scholar]

25. Sindagi, V. A., Patel, V. M. (2018). A survey of recent advances in CNN-based single image crowd counting and density estimation. Pattern Recognition Letters, 107(3), 3–16. https://doi.org/10.1016/j.patrec.2017.07.007 [Google Scholar] [CrossRef]

26. Loy, C. C., Chen, K., Gong, S., Xiang, T. (2013). Crowd counting and profiling: Methodology and evaluation. In: Modeling, simulation and visual analysis of crowds, pp. 347–382. Princeton: Springer. [Google Scholar]

27. Mishra, A. K., Singh, P. (2022). Agile-LSTM: Acclimatizing convolution neural network for crowd behaviour analysis. In: Soft computing and signal processing, pp. 327–337. Singapore: Springer. [Google Scholar]

28. Khan, A., Aslam, S., Aurangzeb, K., Alhussein, M., Javaid, N. (2022). Multiscale modeling in smart cities: A survey on applications, current trends, and challenges. Sustainable Cities and Society, 78(2), 103517. https://doi.org/10.1016/j.scs.2021.103517 [Google Scholar] [CrossRef]

29. Ilgi, G. S., Ever, Y. K. (2020). Critical analysis of security and privacy challenges for the internet of drones: A survey. In: Drones in smart-cities, pp. 207–214. Mersin: Elsevier. [Google Scholar]

30. Mishra, B., Garg, D., Narang, P., Mishra, V. (2020). Drone-surveillance for search and rescue in natural disaster. Computer Communications, 156(2), 1–10. https://doi.org/10.1016/j.comcom.2020.03.012 [Google Scholar] [CrossRef]

31. Felemban, E., Sheikh, A. A., Naseer, A. (2021). Improving response time for crowd management in Hajj. Computers, 10(4), 46. https://doi.org/10.3390/computers10040046 [Google Scholar] [CrossRef]

32. Faragallah, O. S., Alshamrani, S. S., El-Hoseny, H. M., AlZain, M. A., Jaha, E. S. et al. (2022). Utilization of deep learning-based crowd analysis for safety surveillance and spread control of COVID-19 pandemic. Intelligent Automation and Soft Computing, 31(3), 1483–1497. https://doi.org/10.32604/iasc.2022.020330 [Google Scholar] [CrossRef]

33. Al-Sad, M., Kiranyaz, S., Ahmad, I., Sundell, C., Vakkuri, M. et al. (2022). A social distance estimation and crowd monitoring system for surveillance cameras. Sensors, 22(2), 418. https://doi.org/10.3390/s22020418 [Google Scholar] [PubMed] [CrossRef]

34. Masmoudi, N., Jaafar, W., Cherif, S., Abderrazak, J. B., Yanikomeroglu, H. (2021). UAV-based crowd surveillance in post COVID-19 era. IEEE Access, 9, 162276–162290. https://doi.org/10.1109/ACCESS.2021.3133796 [Google Scholar] [CrossRef]

35. Bouhlel, F., Mliki, H., Hammami, M. (2021). Crowd behavior analysis based on convolutional neural network: Social distancing control COVID-19. Proceedings of 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP), Setubal-Portugal. [Google Scholar]

36. Alabdulkarim, L., Alrajhi, W., Aloboud, E. (2016). Urban analytics in crowd management in the context of Hajj. Proceedings of 8th International Conference on Social Computing and Social Media (SCSM), Toronto, Canada. [Google Scholar]

37. Jiang, Y., Miao, Y., Alzahrani, B., Barnawi, A., Alotaibi, R. et al. (2021). Ultra large-scale crowd monitoring system architecture and design issues. IEEE Internet of Things Journal, 8(13), 10356–10366. https://doi.org/10.1109/JIOT.2021.3076257 [Google Scholar] [CrossRef]

38. Al-Sheary, A., Almagbile, A. (2017). Crowd monitoring system using unmanned aerial vehicle (UAV). Journal of Civil Engineering and Architecture, 11(11), 1014–1024. https://doi.org/10.17265/1934-7359/2017.11.004 [Google Scholar] [CrossRef]

39. Poon, K. H., Wong, P. K. Y., Cheng, J. C. (2022). Long-time gap crowd prediction using time series deep learning models with two-dimensional single attribute inputs. Advanced Engineering Informatics, 51(1), 101482. https://doi.org/10.1016/j.aei.2021.101482 [Google Scholar] [CrossRef]

40. Xu, J., Zhao, H., Min, W., Zou, Y., Fu, Q. (2022). DGG: A novel framework for crowd gathering detection. Electronics, 11(1), 31. https://doi.org/10.3390/electronics11010031 [Google Scholar] [CrossRef]

41. Papaioannidis, C., Mademlis, I., Pitas, I. (2021). Autonomous UAV safety by visual human crowd detection using multi-task deep neural networks. Proceedings of 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China. [Google Scholar]

42. Kakaletsis, E., Mademlis, I., Nikolaidis, N., Pitas, I. (2021). Multiview vision-based human crowd localization for UAV fleet flight safety. Signal Processing: Image Communication, 99, 116484. [Google Scholar]

43. Almagbil, A. (2019). Detecting and estimating the levels of crowd density from UAV imagery. Dirasat, Human and Social Sciences, 46(1), 294–309. [Google Scholar]

44. Tzelepi, M., Tefas, A. (2019). Graph embedded convolutional neural networks in human crowd detection for drone flight safety. IEEE Transactions on Emerging Topics in Computational Intelligence, 5(2), 191–204. https://doi.org/10.1109/TETCI.2019.2897815 [Google Scholar] [CrossRef]

45. Küchhold, M., Simon, M., Eiselein, V., Sikora, T. (2018). Scale-adaptive real-time crowd detection and counting for drone images. Proceedings of 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece. [Google Scholar]

46. Xiao, Y. H., Zhen, H. (2017). Pedestrian crowd detection based unmanned aerial vehicle infrared imagery. Proceedings of 4th International Conference on Advanced Materials, Structures and Mechanical Engineering (ICAMSME), Incheon, South Korea. [Google Scholar]

47. Schulte, S., Hillen, F., Prinz, T. (2017). Analysis of combined UAV-based RGB and thermal remote sensing data: A new approach to crowd monitoring. The International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, 42, 347–354. https://doi.org/10.5194/isprs-archives-XLII-2-W6-347-2017 [Google Scholar] [CrossRef]

48. Xiao, Y., Zheng, H., Yu, W. (2017). Automatic crowd detection based on unmanned aerial vehicle thermal imagery. Proceedings of the 11th International Conference on Mechatronics and Intelligent Robotics (ICMIR), Kunming, China. [Google Scholar]

49. Wang, Z., Li, M., Khaleghi, A. M., Xu, D., Lobos, A. et al. (2013). DDDAMS-based crowd control via UAVs and UGVs. Procedia Computer Science, 18(5), 2028–2035. https://doi.org/10.1016/j.procs.2013.05.372 [Google Scholar] [CrossRef]

50. Wang, Q., Breckon, T. P. (2022). Crowd counting via segmentation guided attention networks and curriculum loss. IEEE Transactions on Intelligent Transportation Systems, 23(9), 15233–15243. https://doi.org/10.1109/TITS.2021.3138896 [Google Scholar] [CrossRef]

51. Delussu, R., Putzu, L., Fumera, G. (2022). Scene-specific crowd counting using synthetic training images. Pattern Recognition, 124(5), 108484. https://doi.org/10.1016/j.patcog.2021.108484 [Google Scholar] [CrossRef]

52. Kurnaz, O., Hanilçi, C. (2022). Multi-image crowd counting using multi-column convolutional neural network. Proceedings of 6th International Congress on Information and Communication Technology, London, UK. [Google Scholar]

53. Gouiaa, R., Akhloufi, M. A., Shahbazi, M. (2021). Advances in convolution neural networks based crowd counting and density estimation. Big Data and Cognitive Computing, 5(4), 50. https://doi.org/10.3390/bdcc5040050 [Google Scholar] [CrossRef]

54. Hu, Z., Cao, W., Wu, F., Zhang, Z., Dong, C. et al. (2021). A real-time UAV crowd counting system based on edge computing. Proceedings of 13th International Conference on Wireless Communications and Signal Processing (WCSP), Jiangsu, China. [Google Scholar]

55. Zhang, B., Du, Y., Zhao, Y., Wan, J., Tong, Z. (2021). I-MMCCN: Improved MMCCN for RGB-T crowd counting of drone images. Proceedings of 7th IEEE International Conference on Network Intelligence and Digital Content (IC-NIDC), Beijing, China. [Google Scholar]

56. Castellano, G., Castiello, C., Cianciotta, M., Mencar, C., Vessio, G. (2020). Multi-view convolutional network for crowd counting in drone-captured images. Proceedings of European Conference on Computer Vision (ECCV), Edinburgh, UK. [Google Scholar]

57. Liu, W., Lis, K., Salzmann, M., Fua, P. (2019). Geometric and physical constraints for drone-based head plane crowd density estimation. Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China. [Google Scholar]

58. Balbin, J. R., Garcia, R. G., Fernandez, K. E. D., Golosinda, N. P. G., Magpayo, K. D. G. et al. (2018). Crowd counting system by facial recognition using histogram of oriented gradients, completed local binary pattern, gray-level co-occurrence matrix and unmanned aerial vehicle. Proceedings of 3rd International Workshop on Pattern Recognition (WPR), Jinan, China. [Google Scholar]

59. Choi-Fitzpatrick, A., Juskauskas, T. (2015). Up in the air: Applying the Jacobs crowd formula to drone imagery. Procedia Engineering, 107, 273–281. https://doi.org/10.1016/j.proeng.2015.06.082 [Google Scholar] [CrossRef]

60. Saif, A., Mahayuddin, Z. R. (2021). Crowd density estimation from autonomous drones using deep learning: Challenges and applications. Journal of Engineering and Science Research, 5(6), 1–6. https://doi.org/10.26666/rmp.jesr.2021.6.1 [Google Scholar] [CrossRef]

61. Bouhlel, F., Mliki, H., Hammami, M. (2021). Abnormal crowd density estimation in aerial images based on the deep and handcrafted features fusion. Expert Systems with Applications, 173, 114656. https://doi.org/10.1016/j.eswa.2021.114656 [Google Scholar] [CrossRef]

62. Nafea, I. T. (2021). Simulation of crowd management using deep learning algorithm. International Journal of Web Information Systems, 17(4), 321–332. https://doi.org/10.1108/IJWIS-04-2021-0045 [Google Scholar] [CrossRef]

63. Trotta, A., Muncuk, U., di Felice, M., Chowdhury, K. R. (2020). Persistent crowd tracking using unmanned aerial vehicle swarms: A novel framework for energy and mobility management. IEEE Vehicular Technology Magazine, 15(2), 96–103. https://doi.org/10.1109/MVT.2020.2982244 [Google Scholar] [CrossRef]

64. de Moraes, R. S., de Freitas, E. P. (2019). Multi-UAV based crowd monitoring system. IEEE Transactions on Aerospace and Electronic Systems, 56(2), 1332–1345. https://doi.org/10.1109/TAES.2019.2952420 [Google Scholar] [CrossRef]

65. Yuan, Y., Wang, Z., Li, M., Son, Y. J., Liu, J. (2015). DDDAS-based information-aggregation for crowd dynamics modeling with UAVs and UGVs. Frontiers in Robotics and AI, 2, 8. https://doi.org/10.3389/frobt.2015.00008 [Google Scholar] [CrossRef]

66. Müller, T., Müller, M. (2011). Vision-based drone flight control and crowd or riot analysis with efficient color histogram based tracking. Proceedings of Airborne Intelligence, Surveillance, Reconnaissance (ISR), Orlando, Florida, USA. [Google Scholar]

67. Shao, Y., Li, W., Chu, H., Chang, Z., Zhang, X. et al. (2020). A multitask cascading CNN with multiscale infrared optical flow feature fusion-based abnormal crowd behavior monitoring UAV. Sensors, 20(19), 5550. https://doi.org/10.3390/s20195550 [Google Scholar] [PubMed] [CrossRef]

68. Singh, A., Patil, D., Omkar, S. (2018). Eye in the sky: Real-time drone surveillance system (DSS) for violent individuals identification using scatternet hybrid deep learning network. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, USA. [Google Scholar]

69. Alotaibi, M., Clarke, G., Malleson, N. (2020). Optimal service planning in a temporary city. Journal of Service Science and Management, 13(5), 709–728. https://doi.org/10.4236/jssm.2020.135045 [Google Scholar] [CrossRef]

70. Shambour, M. K., Gutub, A. (2021). Progress of IoT research technologies and applications serving Hajj and Umrah. Arabian Journal for Science and Engineering, 47, 1253–1273. [Google Scholar] [PubMed]

71. Felemban, E. A., Rehman, F. U., Biabani, S. A. A., Ahmad, A., Naseer, A. et al. (2020). Digital revolution for Hajj crowd management: A technology survey. IEEE Access, 8, 208583–208609. https://doi.org/10.1109/ACCESS.2020.3037396 [Google Scholar] [CrossRef]

72. Sharma, D., Bhondekar, A. P., Shukla, A., Ghanshyam, C. (2018). A review on technological advancements in crowd management. Journal of Ambient Intelligence and Humanized Computing, 9(3), 485–495. https://doi.org/10.1007/s12652-016-0432-x [Google Scholar] [CrossRef]

73. Yamin, M., Basahel, A. M., Abi Sen, A. A. (2018). Managing crowds with wireless and mobile technologies. Wireless Communications and Mobile Computing, 2018(3), 1–15. https://doi.org/10.1155/2018/7361597 [Google Scholar] [CrossRef]

74. Kurdi, O. (2017). Crowd modelling and simulation (Ph.D. Thesis). University of Sheffield, UK. [Google Scholar]

75. Al-Salhie, L., Al-Zuhair, M., Al-Wabil, A. (2014). Multimedia surveillance in event detection: Crowd analytics in Hajj. Proceedings of 3rd International Conference of Design, User Experience, and Usability (DUXU), Crete, Greece. [Google Scholar]

76. Alaska, Y. A., Aldawas, A. D., Aljerian, N. A., Memish, Z. A., Suner, S. (2017). The impact of crowd control measures on the occurrence of stampedes during mass gatherings: The Hajj experience. Travel Medicine and Infectious Disease, 15(5), 67–70. https://doi.org/10.1016/j.tmaid.2016.09.002 [Google Scholar] [PubMed] [CrossRef]

77. Illiyas, F. T., Mani, S. K., Pradeepkumar, A., Mohan, K. (2013). Human stampedes during religious festivals: A comparative review of mass gathering emergencies in India. International Journal of Disaster Risk Reduction, 5, 10–18. https://doi.org/10.1016/j.ijdrr.2013.09.003 [Google Scholar] [CrossRef]

78. Hutchins, B., Andrejevcic, M. (2021). Olympian surveillance: Sports stadiums and the normalization of biometric monitoring. International Journal of Communication, 15, 20. [Google Scholar]

79. Robakowska, M., Tyranska-Fobke, A., Nowak, J., Slezak, D., Zuratynski, P. et al. (2017). The use of drones during mass events. Disaster and Emergency Medicine Journal, 2(3), 129–134. https://doi.org/10.5603/DEMJ.2017.0028 [Google Scholar] [CrossRef]

80. Birtchnell, T., Gibson, C. (2015). Less talk more drone: Social research with UAVs. Journal of Geography in Higher Education, 39(1), 182–189. https://doi.org/10.1080/03098265.2014.1003799 [Google Scholar] [CrossRef]

81. Meinhold, R. J., Singpurwalla, N. D. (1983). Understanding the Kalman filter. The American Statistician, 37(2), 123–127. [Google Scholar]

82. Arulampalam, M. S., Maskell, S., Gordon, N., Clapp, T. (2002). A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Transactions on Signal Processing, 50(2), 174–188. https://doi.org/10.1109/78.978374 [Google Scholar] [CrossRef]

83. Silbert, M., Mazzuchi, T., Sarkani, S. (2011). Comparison of a grid-based filter to a Kalman filter for the state estimation of a maneuvering target. Proceedings of Signal and Data Processing of Small Targets (SDPST), San Diego, California, USA. [Google Scholar]

84. Weidmann, U. (1993). Dimensionierung von Fussgängeranlagen. In: Transporttechnik der fussgänger, vol. 90, pp. 55–84. Zurich: Schriftenreihe des IVT. [Google Scholar]

85. Helbing, D. (2009). Derivation of a fundamental diagram for urban traffic flow. The European Physical Journal B, 70(2), 229–241. https://doi.org/10.1140/epjb/e2009-00093-7 [Google Scholar] [CrossRef]

86. Wirz, M., Franke, T., Roggen, D., Mitleton-Kelly, E., Lukowicz, P. et al. (2013). Probing crowd density through smartphones in city-scale mass gatherings. EPJ Data Science, 2(1), 1–24. https://doi.org/10.1140/epjds17 [Google Scholar] [CrossRef]

87. Vargas, A. P., Díaz, D., Jaramillo, S., Rangel, F., Villa, D. et al. (2022). Improving the tactical planning of solid waste collection with prescriptive analytics: A case study. Production, 32(8). https://doi.org/10.1590/0103-6513.20210037 [Google Scholar] [CrossRef]

88. Lahyani, R., Chebil, K., Khemakhem, M., Coelho, L. C. (2019). Matheuristics for solving the multiple knapsack problem with setup. Computers & Industrial Engineering, 129(3), 76–89. https://doi.org/10.1016/j.cie.2019.01.010 [Google Scholar] [CrossRef]

89. Haddar, B., Khemakhem, M., Hanafi, S., Wilbaut, C. (2015). A hybrid heuristic for the 0–1 knapsack sharing problem. Expert systems with Applications, 42(10), 4653–4666.https://doi.org/10.1016/j.eswa.2015.01.049 [Google Scholar] [CrossRef]

90. Haddar, B., Khemakhem, M., Rhimi, H., Chabchoub, H. (2016). A quantum particle swarm optimization for the 0–1 generalized knapsack sharing problem. Natural Computing, 15(1), 153–164. https://doi.org/10.1007/s11047-014-9470-5 [Google Scholar] [CrossRef]

91. Hbaieb, A., Khemakhem, M., Ben Jemaa, M. (2021). Virtual machine placement with disk anti-colocation constraints using variable neighborhood search heuristic. Information Systems Frontiers, 23(5), 1245–1271. https://doi.org/10.1007/s10796-020-10025-4 [Google Scholar] [CrossRef]

92. Zhu, T., Boyles, S. D., Unnikrishnan, A. (2022). Two-stage robust facility location problem with drones. Transportation Research Part C: Emerging Technologies, 137(4), 103563. https://doi.org/10.1016/j.trc.2022.103563 [Google Scholar] [CrossRef]

93. Omidi, S., Fathali, J. (2022). Inverse single facility location problem on a tree with balancing on the distance of server to clients. Journal of Industrial & Management Optimization, 18(2), 1247–1259. https://doi.org/10.3934/jimo.2021017 [Google Scholar] [CrossRef]

94. Ryu, J., Park, S. (2022). A branch-and-price algorithm for the robust single-source capacitated facility location problem under demand uncertainty. EURO Journal on Transportation and Logistics, 11(6), 100069. https://doi.org/10.1016/j.ejtl.2021.100069 [Google Scholar] [CrossRef]

95. Qin, W., Shi, Z., Li, W., Li, K., Zhang, T. et al. (2021). Multiobjective routing optimization of mobile charging vehicles for UAV power supply guarantees. Computers & Industrial Engineering, 162(2), 107714. https://doi.org/10.1016/j.cie.2021.107714 [Google Scholar] [CrossRef]