Many-Objective Optimization-Based Task Scheduling in Hybrid Cloud Environments

1  Introduction

As the main pattern and development direction of cloud computing in recent years, hybrid cloud architecture [1] can provide more flexible cloud service solutions which are favored by more and more enterprise users. The hybrid cloud architecture is constructed by different numbers of private and public clouds [2]. The private cloud is a cloud service used for one user and therefore provides the most effective control over data privacy, security, and quality of service. The public cloud is a shared cloud service built by third-party providers and has the advantage of virtually unlimited resources. Meanwhile, public clouds pay on demand, thus enabling effective cost control. However, it has become an important requirement for business users to expand resources at low cost while protecting critical private data. When private or public clouds alone are not up to the task, hybrid cloud architectures make it possible to address these needs simultaneously [1]. And the problem is that the flexible features and diverse requirements also make using a hybrid cloud architecture more complex. Therefore, how to use the unique advantages of hybrid cloud and reasonably schedule the resources of public and private clouds to meet various requirements of enterprises, such as low cost and high efficiency, are the key problems of hybrid cloud [3]. Similarly, ensuring the security privacy of enterprise information and improving the resource utilization of cloud services during hybrid cloud task scheduling are also key challenges [4].

Many different task scheduling approaches have been proposed by scholars in hybrid cloud environments. Li et al. [5] proposed a market-based local and global two-level scheduling scheme. By optimizing the Qos satisfy rate and task assignment efficiency makes the benefit of task transfer to public cloud maximized. In order to minimize the cost of private clouds during scheduling, Yuan et al. [6] constructed a mixed integer linear model and proposed a temporal task scheduling algorithm (TTSA). In [7,8], a hybrid cloud task scheduling optimization using BP neural networks was proposed. By using cost and task lifetime as constraints, the quality of cloud services is improved while maximizing resource utilization in a private cloud. To balance time and cost in the hybrid cloud task scheduling process, a queuing theory-based hybrid cloud task scheduling method was proposed by Chunlin et al. [9], thus the non-sensitive tasks are transferred to the public cloud for execution. Yuan et al. [10] studied the problem of maximizing the profit of hybrid cloud task scheduling, and a profit maximization algorithm (PMA) based on price variation over time in hybrid clouds was proposed. And the problem is well solved by simulated annealing particle swarm optimization (SAPSO).

However, these approaches focus on the performance or profitability problems of using public cloud extension resources when private cloud resources are insufficient. They ignore the privacy and security risks that may arise when scheduling cloud tasks to the public cloud. This is because some of the tasks may involve large amounts of user information, including company data, personal health, and other private information. Privacy information and data are at risk of being compromised if they are performed on a public cloud with a lower trust level. Therefore, it is critical to consider the security and privacy of task data in hybrid cloud task scheduling.

In [11], the authors proposed a SCAS algorithm for security and cost problems of heterogeneous tasks in cloud services. The algorithm uses deadlines and risk rates as constraints to optimize the cost of task execution. Meanwhile, to counter the danger of third-party cloud services exposing private data, a new SaaS scheduling agent is proposed to protect privacy while satisfying task deadlines [12]. Based on the restriction of sensitive and private data to private clouds, Wen et al. [13] proposed a MOPA algorithm to optimize the time and cost of scheduling. Sharif et al. [14] proposed two algorithms, OMPHC-PCPR and OPHC-TR. This approach enables dynamic scheduling of multiple workflow tasks under the constraints of deadlines and privacy.

However, most of these works classify cloud task data based on privacy levels, and tasks with higher privacy levels are assigned to private clouds for execution, while tasks with lower privacy levels can be assigned to private or public clouds for execution. But real-life cloud tasks are not simple binary decisions. For example, some tasks have both deadlines and privacy requirements, and if they are performed in a private cloud based on privacy requirements. Then the deadline may be exceeded, thus causing loss to the user. Therefore, a more comprehensive scheduling strategy can only be obtained by balancing different requirements, thus improving the service satisfaction of users.

In other words, multiple objectives need to be considered simultaneously during hybrid cloud task scheduling [15,16]. As an important research direction, scholars have done many researches on the construction and solving of many-objective optimization models [17–19], and applied them to many practical engineering fields [20]. For example, resource allocation [21–23], model Prediction [24,25], shop floor scheduling [26], and disease diagnosis [27] which have produced great practical values. In the cloud computing scheduling problem, Xu et al. [28] constructed a fully optimized many-objective model considering task, system, and user characteristics, and used normal distribution to improve the environment selection process of RVEA algorithm with good results. Dubey et al. [29] used task deadline as a constraint to optimize cost, energy consumption and makespan to obtain a high-quality task scheduling policy. In a multi-cloud environment, considering the benefits of users and service providers separately, Cai et al. [30] proposed a many-objective scheduling model for multiple clouds and designed an subgenerational many-objective optimization algorithm for solving it. All these methods provide a basis for many-objective task scheduling research in hybrid clouds. Zade et al. [31] proposed a fuzzy improved red fox optimization algorithm (FIRFO). The algorithm uses QOBL, Levy flight, spiral motion and fuzzy control system to improve the search process. In addition, based on game theory and FIRFO, a novel task scheduling algorithm that balances four objectives is proposed. In addition, a two-stage scheduler considering four conflicting objectives is proposed by Zade et al. [32] and a new caledonian crow learning algorithm (NCCLA) is designed for model solving based on reinforcement learning (RL) and NCCLA.

Table 1 summarizes the basic work related to hybrid cloud scheduling. Most of the previous studies consider only some of the metrics in the hybrid cloud task scheduling process. Especially, the conflict between its data security and other requirements is ignored. On the foundation of the above problems, this work further explores the research methods of many-objective optimization problems. In order to exploit the unique advantages of hybrid cloud architecture, this paper investigates methods to construct and solve scheduling models in hybrid cloud environments.

(1)   Considering the characteristics of hybrid cloud and different cloud task types, a many-objective hybrid cloud task scheduling optimization (HCTSO) model is constructed, which simultaneously optimizes the risk rate, task completion time, total cost and resource utilization.

(2)   To address this model, an opposition-based learning knee driven evolutionary algorithm (OBL-KnEA) is proposed. The algorithm uses the idea of opposition learning to make the initial population uniformly distributed, and designs a perturbation-based crossover operator and a dynamic scale variation operator.

The rest of this paper is organized as follows: Section 2 constructs the hybrid cloud task scheduling optimization model. The OBL-KnEA algorithm is introduced in Section 3. Section 4 designs the related simulation experiments. Section 5 summarizes the paper.

2  Hybrid Cloud Task Scheduling Problem

2.1 Problem Description

Hybrid clouds are an efficient architectural approach that can combine the respective benefits of public and private clouds, which is attracting more and more enterprises to deploy system programs using hybrid cloud technology. Thus, it is a key problem to design a reasonable and effective scheduling strategy to take advantage of the hybrid cloud. Fig. 1 shows the overall flow of hybrid cloud task scheduling. Customers rent public clouds through different cloud service providers, and these cloud resources only provide performance parameters and command interfaces. Private clouds have virtual resources such as CPU, network, memory and storage provided through local physical machines, which can be controlled more effectively. During the scheduling process, the monitoring component is used to monitor the resource pools of the private cloud. And updates the information to the task scheduling component. On the contrary, the public cloud provides the parameter information directly to the task scheduling component. Also, the scheduler component will accept all the information of the task queue submitted by users including the number of tasks, task size. The task scheduler component consolidates all task information and virtual resource information, and assigns the appropriate virtual machine for each task. Due to the architectural differences and charging models and other influencing factors, public and private cloud resources have significantly different features. As shown in Table 2, public clouds offer significant advantages in terms of price/performance, elasticity and amount of resources, while private clouds offer better performance control and security. On the other hand, different tasks also have different attributes such as size and privacy levels between them. As a result, there are inevitably conflicting relationships between multiple user requirements.

Figure 1: The overall flow of hybrid cloud task scheduling

In the field of intelligent optimization, scholars refer to optimization problems with four or more objectives with conflicting relationships as many-objective optimization problems (MaOP). It can be formulated as follows:

{ minimizeF(x)=(f1(x),fx(x),…,fm(x))subject to x∈X (1)

where x is the decision variable, X is the decision space, and m is the number of objectives. In the hybrid cloud task scheduling process, if the task completion time is diminished, it will inevitably add some cost. Assigning all tasks to a cloud service with a higher trust level in order to reduce the risk rate will definitely increase the task completion time and cost. Further, the above factors need to be ensured while also increasing resource utilization as much as possible. Therefore, in order to more get a better scheduling strategy, this paper defines hybrid cloud scheduling as a MaOP. Unlike single-objective optimization, the conflicting nature among multiple objectives makes it impossible to obtain a solution where all objectives are optimal. Instead, it is possible to obtain a set of compromise solutions that optimize as many objectives as possible simultaneously and yield different biases. These tradeoffs are called Pareto optimal solutions, the set of all Pareto optimal solutions is called the Pareto optimal set (PS), and the projected image of the PS in the objective space is called the Pareto optimal front (PF).

In summary, the hybrid cloud task scheduling model in this study includes four optimization objectives of task completion time, cost, risk rate, and resource utilization. In addition, the scheduling process occurs within specific time slice and there are no priorities and dependencies between tasks. Also, the tasks are executed serially on the resource nodes of the cloud service, and the case of cloud service failure is not considered.

2.2 Task Type Description

In the actual business process, there are many interrelated business relationships. For example, In a large-scale entity enterprise, although the products of each department are different, the mining and analysis for market user information can be shared or overlapped. Therefore, in order to better simulate the actual enterprise business process, except for independent random tasks, this paper also considers the reusability of user tasks and designs specific task transmission and execution methods to improve task completion efficiency and reduce task execution and transmission costs.

The privacy level of reusable tasks is kept consistent due to the presence of duplicate data for the tasks. Two types of reusable tasks are given in Fig. 2, and the over-lapping parts are shaded. As shown in Fig. 2a, when there is a partial overlap between Task1 and Task2, Task1 is uploaded and executed as a complete task, while Task2 omits the overlapping part. When downloading the task execution result, Task2 needs to download the overlapped part from the VM node of Task1. As shown in Fig. 2b, when Task1 completely covers Task2, only Task1 needs to be uploaded and executed, ignoring Task2. After execution, Task1 and Task2 download their respective task execution results.

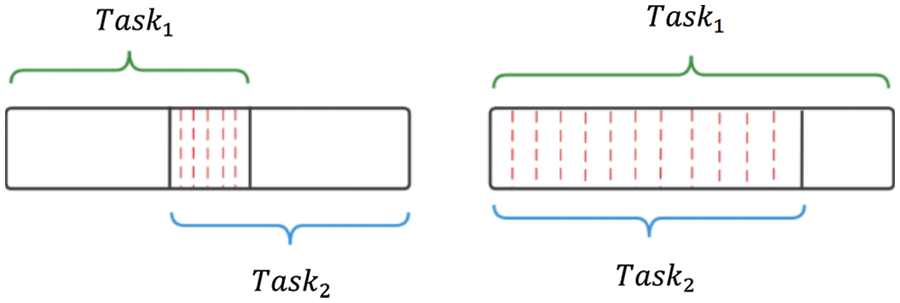
Figure 2: Two types of tasks

2.3 Objective Functions

The purpose of the hybrid cloud task scheduling problem is to find a reasonable mapping relationship between task and resource node VMs. For better model construction, the set of VM nodes of different cloud services is denoted as VM={VM1,VM2,…,VMM}. VMm means the m-th VMs and the number of VMs is M. Furthermore, Task={T1,T2,…,TK} is the set of cloud tasks, Tk means the k-th cloud task and the number of tasks is K.

Tables 3 and 4 describe the parameters of cloud tasks and VMs and their meanings. Combined with the characteristics of the hybrid cloud, the model decision variables are encoded as shown in Table 5, where P={P1,P2,P3,…,PN} denotes the population, D denotes the decision variable dimension, and the x1 value is 2 indicating that the first task will be executed on the 2-th VM.

2.3.1 Risk Rate

The risk rate will evaluate the overall risk of the tasks to be performed on the hybrid cloud resources. For this purpose, a privacy level is assigned to the task data and a trust level is assigned to the cloud service. Moreover, the task privacy level and cloud service trust level are mapped to probability values of [0, 1]. In the calculation, the task privacy level is interpreted as the probability that the task will be attacked when executed on the cloud, and the higher its value, the more vulnerable it is to attack. The cloud service trust level is interpreted as the probability that the cloud service can be unable to protect the task data when it is attacked, and the lower its value, the more unable it is to protect the task data. Finally, the probability of two events occurring simultaneously is obtained by joint probability, which is interpreted as the probability that the cloud task is attacked and the data is corrupted. It is calculated as Eq. (2).

The privacy level is based on the categories and levels of data based on factors such as sensitive attributes and security protection requirements. Referring to [33], according to the requirements of the Data Security Law of the People’s Republic of China, the data privacy level mainly depends on the factors such as the subject, breadth and depth of impact after data leakage, tampering, loss, or misuse. The classification of cloud service trust level is obtained by evaluating the security and reliability of each cloud service.

R=1K∑i=1kP(Tk)P(Vc|Tk)(2)

where K is the number of tasks, Tk represents the k-th task, and Vc represents the c-th cloud service. P(Tk) is the probability value of task Tk privacy level and P(Vc|Tk) is the probability value of cloud service Vc trust level.

2.3.2 Task Completion Time

Task completion time is a key problem in the cloud task scheduling process. It represents the time span between when a user submits a task and when the execution result is received. Task completion time in public clouds consists of execution time, waiting time, and transfer time. Since private clouds are built locally thus do not require task transfer, private cloud task completion time consists of execution time and wait time. The execution time is calculated based on the Mips of the VM and the length of the task, while the transfer time is calculated based on the task data amount and bandwidth. The waiting time includes the VM startup time and the waiting execution time. In addition, multiple clouds in the hybrid cloud environment execute tasks in parallel, so the cloud service with the longest running time is taken as the completion time of the whole scheduling process. The task completion time is calculated as shown in Eq. (3).

T=Mi=1axC(Ti)(3)

Tipu=Tie+Tit+Tiw(4)

Tipr=Tei+Twi(5)

Tei={∑s=1SLsMips,if Tasks is independent task or reusable task1.∑s=1SLs−L′Mips,if Tasks is the reusable task2.(6)

Tti={∑s=1SLsMips,if Tasks is independent task or reusable task1.∑s=1SIs−I′Us+OsDs,if Tasks is the reusable task2.(7)

where T is the total task completion time, C is the number of cloud services. Ti is the task completion time of the i-th cloud service, where Tipu and Tipr correspond to the task completion time of public and private clouds, respectively. And Tei, Tti and Twi are the execution time, transfer time and wait time of the i-th cloud service. Further, S is the number of tasks assigned to the i-th cloud service. Ls, Is and Os are the execution length, upload size and download size of task s on the i-th cloud service. Mipss, Us and Ds are the execution speed, upload band-width and download bandwidth of the VM executing the s-th task, respectively. Finally, L′ and I′ are the execution length and upload size of the overlapping part of task s, respectively.

2.3.3 Task Cost

Task cost indicates the total cost of performing all tasks. In this study, the charging model of public cloud is on-demand. That is, the customer is charged according to the time of use. The higher the performance of the virtual machine, the more expensive it is to use, but the less time it takes to perform the task. The public cloud cost is obtained by combining the computational price per unit of time and the transfer price of the public cloud. In contrast, private clouds are built without additional charges, so their costs are calculated only for energy consumption. Combining the running and idle energy consumption per unit time and the electricity price, the private cloud cost is obtained. The cost of a task is calculated as shown in Eq. (8).

E=∑i=1CEi(8)

Eipu=Tie×Ei+Tiw×Wi(9)

Eipr=Tie×Qi×q+(Ti−Tie)×Gi×q.(10)

where E is the total cost of performing the tasks. Ei is the cost of the i-th cloud service, where Eipu and Eipr are the costs of public and private clouds, respectively. Ei and Wi represent the execution cost and transmission cost of the i-th public cloud per unit of time. Qi and Gi are the execution energy value and idle energy value per unit time of the i-th private cloud. q represents the energy reference price.

2.3.4 Cloud Resource Utilization

Resource utilization indicates how resources are actually used in the cloud service, and in fact, there is a positive correlation between resource utilization and efficiency. Higher resource utilization represents lower demand for renting virtual machines and lower cost. The resource utilization for each cloud service was obtained by the ratio of effective execution time to total time, and the degree of dispersion of the actual situation from 100% utilization is evaluated. Smaller values represent higher resource utilization.

U=1C∑i=1C(1−Ui)2(11)

Ui=TieTi(12)

where Ui is the resource utilization of the i-th cloud service and Ti is the completion time of the i-th cloud service.

By considering the important factors in the whole scheduling process, a many-objective HCTSO model is proposed to demonstrate in Eq. (13).

{minimize F(X)=(R(X),T(X),E(X),U(X))Tsubject to x∈Ω(13)

3  Proposed OBL-KnEA Algorithm

3.1 OBL-KnEA Algorithm Framework

Evolutionary algorithms [34,35] have been proved to be an effective method for solving many-objective problems. It has wide applicability and has better results for complex problems. In the evolutionary algorithm, KnEA [36] enhances the selection pressure on offspring by combining the knee point of the current population’s non-dominated frontier with the traditional Pareto domination. It allows for more accurate selection of individuals so that the population can converge to the PF more quickly. Besides being able to maintain the diversity of candidate solution sets without introducing additional diversity maintenance mechanisms, it significantly reduces the computational complexity. Therefore, the KnEA algorithm has significant advantages in dealing with many-objective problems.

To further enhance the performance on the HCTSO model, this paper analyzes the model characteristics and proposes the OBL-KnEA algorithm. On the one hand, based on economic and efficiency considerations, the ability of all resource nodes to be adequately utilized has a critical impact on the outcome of task execution. The initial solution with more uniform distribution is conducive to maximize the use of all the hybrid cloud resource nodes to improve the quality of the initial population, so as to accelerate the convergence speed [37]. However, the initial population of traditional KnEA is randomly generated, and it does not perform well for large-scale problems with high dimensionality of decision variables. So this paper uses the idea of opposition learning [38] to optimize the initial population. Since different cloud services have different performance, it not only allows the initial solution to be distributed evenly to fully utilize the node resources. It can also enhance population diversity by allocating tasks to different cloud services as much as possible and thus generating solutions of different quality. On the other hand, the traditional crossover-mutation operators of KnEA are all encoded as real numbers, which cannot be well applied to the solution of HCTSO model. Moreover, other integer-coded operators do not fit the characteristics of the resource distribution of the HCTSO model well. Therefore, this paper proposes the Perturbation multipoint crossover and dynamic scale mutation operator to improve the ability of the algorithm to search for the optimal solution in HCTSO model.

The framework of the OBL-KnEA algorithm can be seen in Algorithm 1. First, the initialized population P of size N is generated by an opposition-based learning strategy, where each P contains decision variables and four objective values. The decision variables represent the task assignment strategy and the objective values represent the values of task completion time, cost, risk rate and resource utilization under this assignment strategy. Subsequently, parents were selected in the population, and then individuals P′ were generated by perturbing multipoint crossover and dynamic scale mutation. Afterwards, all previous individuals P and P′ are combined and environmental selection is performed by non-dominance ranking and knee point dominance relationships. Then, the selected individuals constitute a new generation of population Pt+1. Finally, the algorithm is iterated until the maximum number of generations is reached.

3.2 Opposition-Based Learning (OBL) for Population Initialization

The general optimization algorithms initialize the population with a random distribution, which leads to a high randomness and unstable performance [39]. These algorithm takes more time to find the optimal solution and even cannot reach the optimal solution, which makes the algorithms to find only a local optimum. This paper is designed to initialize the population based on the idea of opposition learning by combining the model characteristics. Opposites drive things to move, change and develop, and exist every-where in our lives. In intelligent optimization algorithms, opposition-based learning (OBL) [40] is formulated as a set of candidate solutions with opposite relationships. That is, the candidate solution set is composed of candidate solutions with opposite directions in the decision space, and each candidate solution in the solution set finds its corresponding candidate solution in the opposite direction of the decision space. However, instead of using individuals with opposite relationships in the decision space, genes with opposite relationships comprising individuals are used in this paper. In this way, a more uniform distribution of genes among individuals can be achieved, thus to making adequate use of virtual machine nodes. Opposite-based learning (OBL) makes the initial population more uniformly distributed, expands the range of the solution set, increases the chance of good candidate solutions, and improves the convergence speed of the algorithm.

In this paper, the initial populations are generated using the opposite and quasi-opposite numbers in turn. Suppose P={p1,p2,p3,…,pn} is an n-dimensional vector. pi∈[a,b], i=1,2,…,n. Its opposite, p′ is defined as

pi′=a+b−pi(14)

Further, its quasi-opposite value pi″ is defined as follows:

pi″=rand(pi′,a+b2)(15)

Algorithm 2 shows the pseudo-code to generate the initial population. Firstly, the gene values with dimension D/4 are randomly initialized, and subsequently their opposition values are calculated using Eq. (13). Since Ergezer et al. [41] mathematically proved that the quasi-opposite number has the highest expected probability of approaching the solution of the problem among all OBL methods. There-fore, the quasi-opposite values were finally calculated using Eq. (14) and combined into complete individuals. Finally, the complete population is generated by continuous iteration.

3.3 Perturbation Multi-Point Crossover and Dynamic Scale Variation

3.3.1 Perturbation Multi-Point Crossover

The crossover operator is mainly designed to retain the parent genes and combine them to produce new individuals [42]. It is fast and efficient for searching in the solution space, and has the ability to globally search for optimal solutions. Most of the existing multi-objective optimization algorithms use simulated binary crossover operators. This operator is mostly applied to real number encoding, and the generated offspring can inherit the parents’ genes well, so the offspring is closer to the parents. However, for the hybrid cloud task scheduling optimization model (HCTSO). Simulating the binary crossover operator has a small variation of child genes compared to parent genes due to real number encoding. It cannot produce a better solution quickly. Therefore, a more flexible crossover operator is needed to help extend the search and better find the global optimal solution.

In particular, if the genes are perturbed up and down during the crossover, not only the search space of the operator can be extended, but also the excellent genes of the parents can still be maintained. Taking advantage of this feature, this paper adds the up-and-down perturbation mechanism of genes to the multipoint crossover operator and designs a perturbation-based multipoint crossover operator.

Fig. 3 shows the individuals before and after the crossover. The parent genes are selected for the crossover operation according to the crossover probability, and the offspring genes take values in the range [xi−1,xi+1], with xi being the value of the selected parent gene. Due to the consistent performance of the virtual machines in each cloud service provider, the child genes are perturbed within a certain range not only to preserve the performance of the parent genes. It can also expand the search range and help the algorithm search for the optimal value faster.

Figure 3: Process diagram of perturbation multi-point crossover

3.3.2 Dynamic Range Mutation Operator

The precondition for the global optimal solution to be found is the genetic diversity of the population. Although the above crossover operator can improve the diversity of the population when perturbed, it is not sufficient to help the population find the optimal solution. Therefore, an effective mutation operator is essential. In the HCTSO model, the performance of virtual machines is consistent for each cloud service provider. In this paper, a dynamic scale mutation operator is designed and genes change in different cloud services when mutations occur. In the early stages, a large range of variations is employed to increase the diversity of the solution set in order to find the region of the best solution. In the later stages, the variation range is reduced to enhance local finetuning. By dynamically adjusting the mutation operator, the search speed of the algorithm is accelerated. Its calculation formula is shown in (15).

xi=rand(xi−(a∗Site),xi+(a∗Site))(16)

Site=(1−(GgGmax))b(17)

where Gg is the current evolutionary generation, Gmax is the maximum evolutionary generation, a is the number of VMs in each cloud, and b is a parameter, which takes the value of 2 in this paper.

3.4 OBL-KnEA Complexity Analysis

Based on KnEA, initializing populations and crossover variants are improved by OBL-KnEA. Initializing populations requires transformations for each individual gene and therefore requiresO(DN) time, and D is the dimensions of the decision variable. Similarly, crossover mutations require an O (DN) runtime to produce N offspring by performing them on each gene of the parent individuals. Moreover, the time complexity of the traditional KnEA algorithm is O (MN2), so the running time of OBL-KnEA is also O (MN2), which is computationally very efficient compared to most popular MOEAs.

4  Experiments

To test the performance of the proposed OBL-KnEA on HCTSO model, this section selects some excellent many-objective algorithms, including KnEA [36], NSGA-III [43], GrEA [44], hpaEA [45] and RVEA-NDAPD [28], and compares them in detail in terms of evaluation metrics, initial populations and model optimization effects.

4.1 Experimental Setup and Evaluation Index

The setup of the experimental environment is crucial to validate the performance of the method [46,47]. The experiments were simulated under the Cloudsim framework [48] for Windows 10 operating system with a CPU of inter (R) Xeon (R) Gold 5222 @3.80 GHz, 64 G RAM, IntelliJ IDEA 2020 and Matlab 2018 programming platform, and JDK version 1.8. The simulation hybrid cloud environment is constructed by Cloudsim framework, including one private cloud data center and three public cloud data centers. Four hosts are placed in each data center, and each host contains four virtual machines. The performance of the virtual machines in each data center is kept consistent, and detailed attributes can be referred to Table 6. The parameter values of tasks are obtained in the interval, while the task types represent standalone task, reusable task1 and reusable task2, and the specific attributes can be referred to Table 7. Meanwhile, the privacy level and trust level will be uniformly mapped to [0, 1]. In the experimental environment, the VM and task attributes remain unchanged after being set.

In addition, Table 8 shows the parameter settings of the algorithm, and the parameter settings of the many-objective optimization algorithms compared in the experiments are all the same as those in the original paper. The crossover and mutation probabilities of OBL-KnEA were obtained according to the experimental verification in Table 9. In order to prevent falling into stochastic optimization, the crossover and mutation probabilities within a reasonable range are transformed, and the optimal results are selected as the crossover and mutation probabilities of subsequent experiments.

In this paper, three metrics Coverage, Spacing and HV [49] are used to evaluate the performance of the algorithm and they are described as follows:

(1)   Coverage (C-metric)

Coverage evaluates the convergence by comparing the approximation of the true PF and the set of solutions. C(A,B) denotes the proportion of solution set A that dominates at least one individual in solution set B.

C(A,B)=|{b∈B|∃a∈A:a≻b}||B|(18)

The Coverage relies on the dominance relationship of individuals. However, with the increase in the number of objectives, there are more non-dominated solutions in the solution set and it can not be possible to measure the convergence of the solution set.

(2)   Spacing (SP)

The distribution of the PF approximate solution set in the objective space can be evaluated using Spacing. The formula is shown in (18).

SP=1PF∑i=1PF(di−d¯)2(19)

where PF represents the number of non-dominated solutions, di is the Euclidean distance of two consecutive vectors on the non-dominated boundary in the solution set, and d¯ denotes the mean of the distances.

(3)   Hypervolume (HV)

The HV value is expressed as the volume of the space enclosed by the reference point and the non-dominated solution, which is defined as shown in Eq. (19).

HV(S)=VOL(∪x∈S[f1(x),r1∗]×…[fm(x),rm∗])(20)

where r∗=(r1∗,r2∗,…,rm∗) is the reference point of the objective space. S is the set of solutions obtained by the algorithm. VOL(∗) denotes the Leberger measure and a larger value of HV indicates that S is more approximate to the entire PF. In summary, HV can measure both convergence and diversity.

4.2 Results and Analysis

4.2.1 Comparison of Initialized Populations

To verify the effectiveness of the opposition-based learning initialization method, KnEA generates two populations using both random initialization and opposition-based learning initialization methods, with other parameters and steps held constant. Box plots were used to reflect the characteristics of the distribution of the solution sets of the two initial populations and to compare the solution sets. From Fig. 4, the average risk rate for random initialization is 17.7%, while the average risk rate for opposition learning initialization is 6.75%. In terms of task completion time, the mean values of random and opposition learning initialization are 1221.05 and 735.55 s, respectively. In terms of cost, the mean values of random and opposition learning initialization are $10707.02 and $5657.68, respectively. Finally, in terms of resource utilization, random initialization takes the mean value of 0.24 and opposition learning initialization takes the mean value of 0.23. Obviously, the task completion time, total cost and risk rate are significantly higher for the initial set of solutions based on opposition learning. For resource utilization, the best, mean and worst values all outperformed the random population, although not as significantly as the other three objectives. This demonstrates that for the HCTSO model proposed in this paper, the opposition-based learning population initialization strategy can produce with good results. Each objective of the opposition-based learning initialization population is enhanced, which allows the algorithm to find the optimal solution faster.

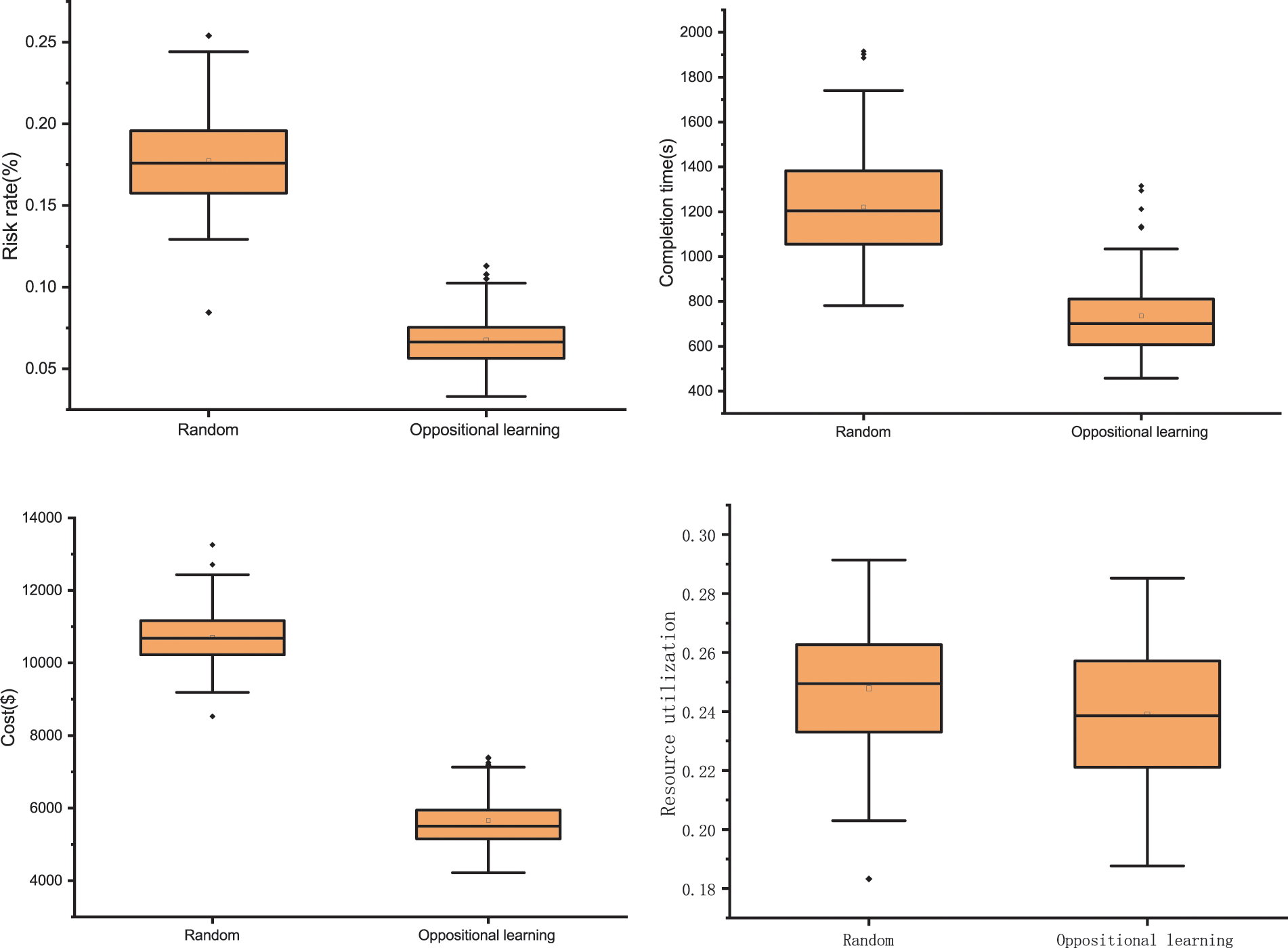
Figure 4: Comparison of random initialization and opposition-based learning for initializing populations

4.2.2 Comparison of Performance Metrics

To accurately evaluate the performance of the algorithms, Table 10 shows the Coverage, Spacing and HV values for OBL-KnEA and the other algorithms on the hybrid cloud task scheduling optimization model (HCTSO). To ensure the generality and universality of the experiments, each algorithm was run for 15 times independently, and the number of evaluations per run was 11000. In the table, the optimal value for each metric is marked in blue font, and “+”, “−”, “=” indicate the degree of superiority of other algorithms compared to OBL-KnEA. The OBL-KnEA algorithm achieves the best results for both the Coverage and HV metrics. However, OBL-KnEA does not perform as well on the Spacing metric. This may be because the opposing initial populations improve the convergence speed while making the solution set more aggregated and discarding some diversity. But overall it can be seen that the OBL-KnEA algorithm outperforms the other algorithms on the HCTSO model.

4.2.3 Comparison of Optimization Results for Different Number of Tasks

Fig. 5 shows the optimization results of each objective function after 1000 iterations of 150 tasks in the HCTSO model. It can be seen that the overall distributions of OBL-KnEA are all relatively aggregated, and the optimal results are obtained for both the risk rate and cost objectives. The mean and minimum values of risk rate are 0.007 and 0.003, and the minimum and mean values of cost are 155.85 and 211.29, respectively. Due to the conflicting objectives, the task completion time and resource utilization are not optimal, but the results are still similar to those of other good algorithms.

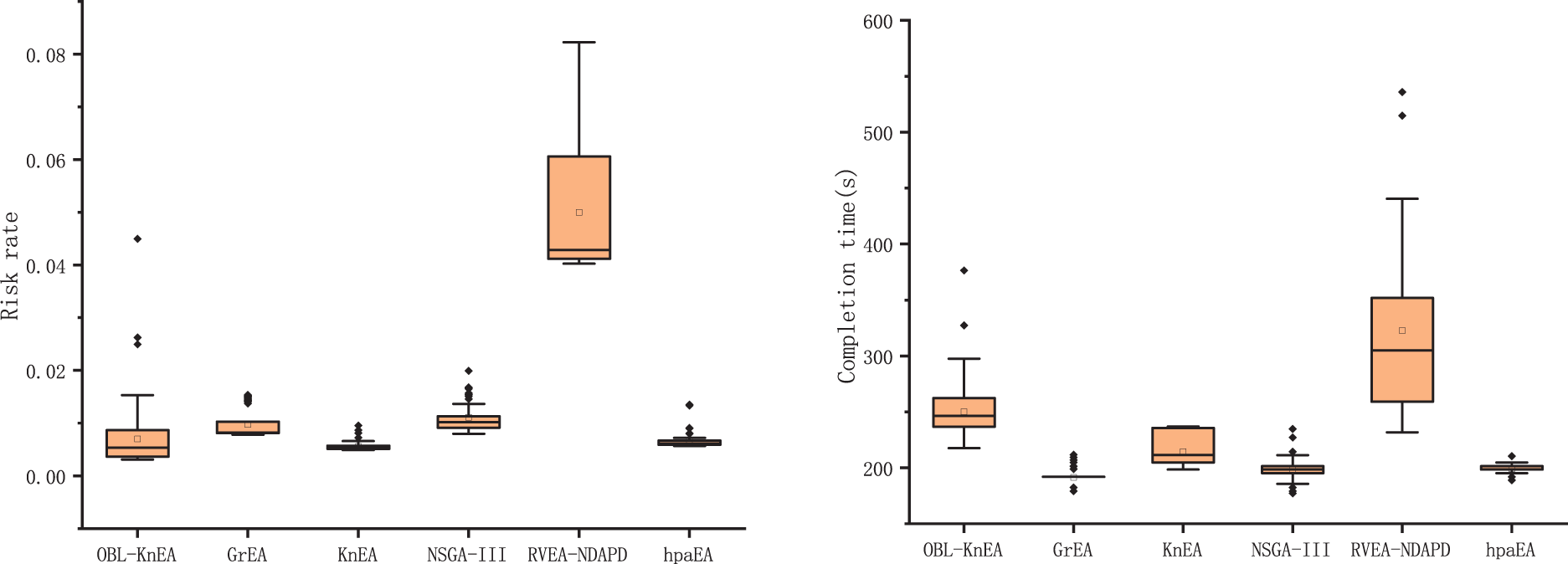
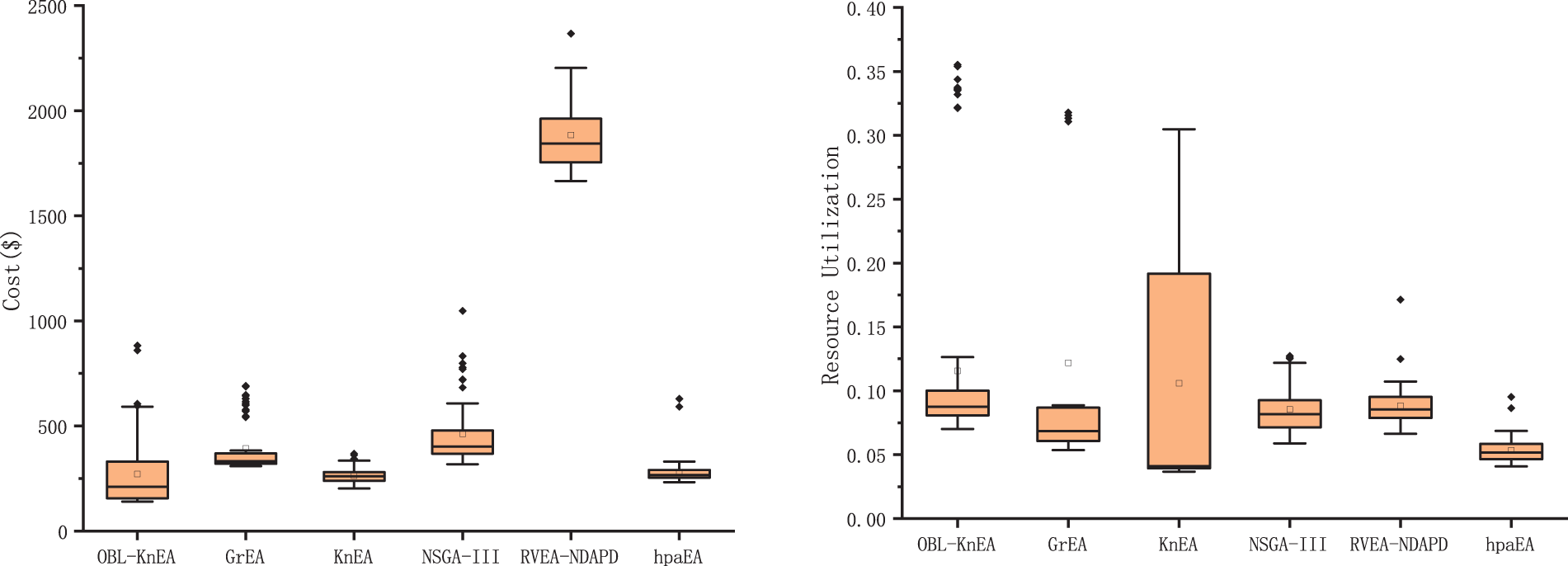
Figure 5: The optimization results of 150 tasks

Fig. 6 shows the optimization results of each objective function after 1000 iterations of 300 tasks in the HCTSO model. The risk rate and cost of OBL-KnEA have a significant advantage over other algorithms, with the best minimum and average values. The risk rate reaches 0.295% and 0.517%, respectively. And the costs reached $248.0 and $478.7, respectively. Their boxes are relatively small, indicating a high degree of data aggregation. For the resource utilization, despite the slightly larger boxes, they also have a significant advantage over the other algorithms in terms of optimization effectiveness, with their mean value reaching 0.09. Due to the conflict between the objective functions optimized in this work, the task completion time does not perform as well as the other algorithms when the other three objectives get better results. Overall, the OBL-KnEA algorithm is able to achieve better performance on different tasks of the hybrid cloud task model.

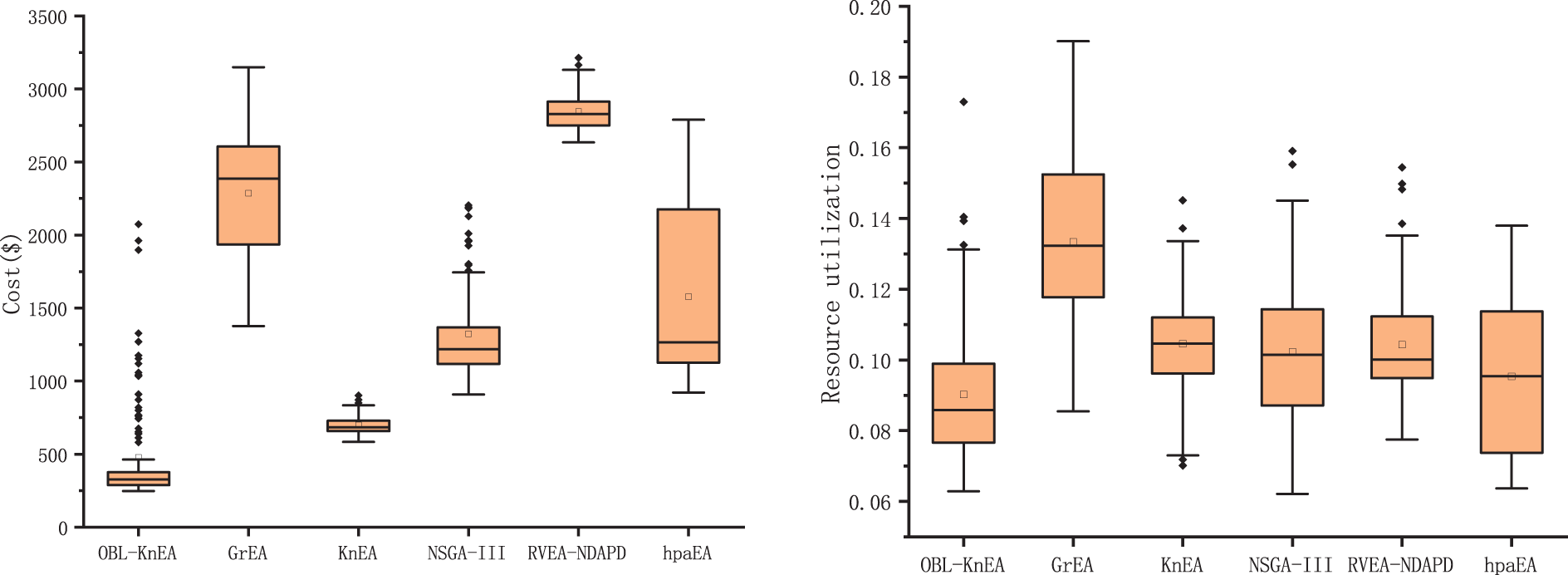
Figure 6: The optimization results of 300 tasks

4.2.4 Comparison of Optimization Process

Fig. 7 shows the optimization process for 1000 iterations of the algorithm for a 300 task. In the first 100 generations, all algorithms converge quickly and find some better solutions. The convergence speed becomes significantly slower when the number of iterations is 100–400. After 400 iterations, the algorithm tends to stabilize. Consistent with the box plot above, OBL-KnEA does not perform as well as the other algorithms in terms of task completion time due to the many-objective conflict. However, the OBL-KnEA performs the best in terms of cost and risk rate, not only converging faster but also being more sufficient to get better objecctive values. In terms of resource utilization, the RVEA-NDAPD gets better results until 400 generations, and the OBL-KnEA, hpaEA and RVEA-NDAPD have equal results in 400–600 generations. When the number of iterations is greater than 600, OBL-KnEA gives the best results. To sum up, it can be shown that OBL-KnEA is efficient and accurate in solving the hybrid cloud task scheduling problem.

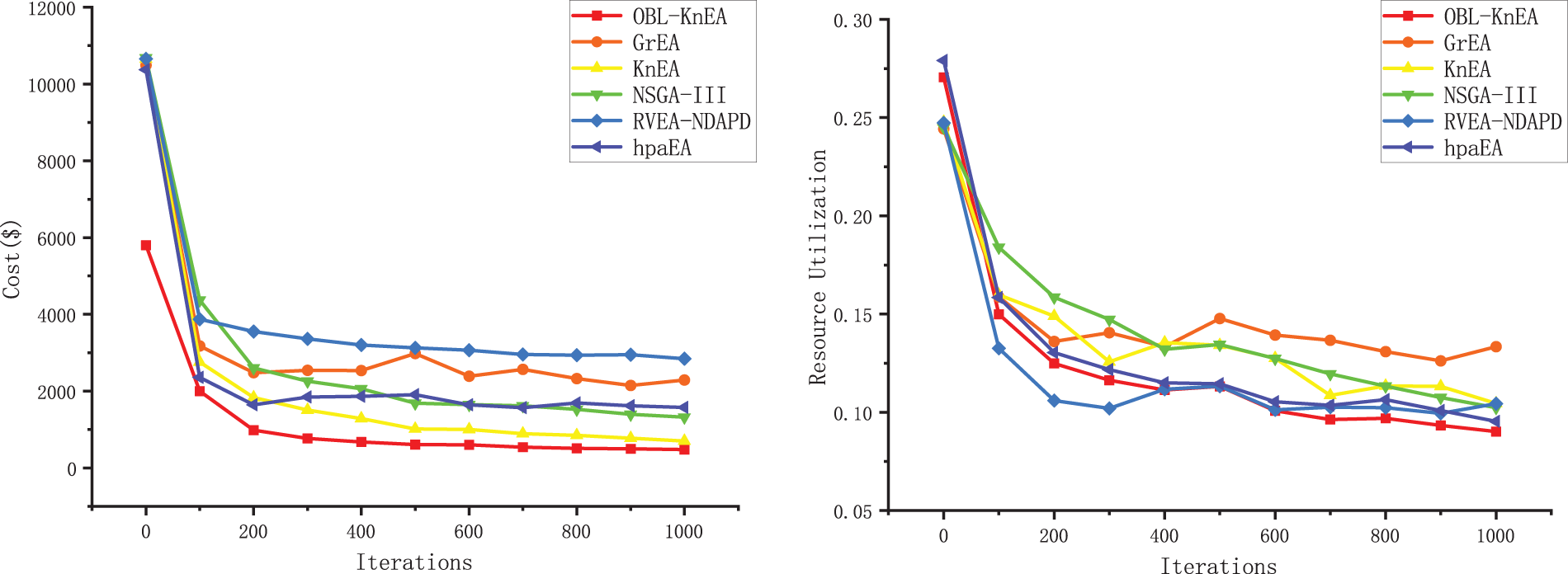
Figure 7: Optimization of different algorithms for 1000 iterations

4.2.5 Comparison of Objective Preference Selection

Since the many-objective algorithm solves the model to obtain a set of compromise solutions. Therefore, the decision maker can choose the scheduling strategy according to different preferences. Table 9 shows the performance of each algorithm under different objective function preferences. For single objective function preference, the minimum value is chosen as the result. For balanced consideration, the result is obtained by normalizing the objective values of different scales and averaging them after adding the same weights. As can be seen from Table 11, when preference is given to task completion time, the RVEA-NDAPD algorithm obtains the smallest value and OBL-KnEA ranks 5 out of the six algorithms. In addition, the OBL-KnEA algorithm is able to obtain the best results regardless of the balance consideration, preference for risk rate, cost, and resource utilization. Therefore, the OBL-KnEA algorithm can better help the decision maker to choose the scheduling strategy from all dimensions.

In summary, OBL-KnEA has better performance and better convergence than other algorithms, and shows good results for solving the HCTSO model pro-posed in this paper, which can provide higher quality and more comprehensive task scheduling solutions for decision makers.

5  Conclusion

In this paper, we delved into the characteristics of hybrid cloud architectures and analyzed the growing user requirements. A hybrid cloud task scheduling optimization model (HCTSO) is constructed by considering reusable task types and combining risk rate, resource utilization, total cost, and task completion time. In addition, an opposition-based learning knee-point-driven evolutionary algorithm (OBL-KnEA) is proposed based on the model characteristics. The algorithm improves the population initialization strategy and the cross-variance operator to accelerate the convergence speed. Simulation experiments show that the initial population generated by OBL-KnEA has a significant advantage over the randomly generated population. Meanwhile, OBL-KnEA achieves the best values in both coverage and HV metrics, indicating that it has the best convergence and diversity. Finally, after comparing the optimization results for different number of tasks and different preferred policy choices, OBL-KnEA is able to get the best scheduling policy to meet the customer’s requirements. In future work, we will consider the dependency between cloud tasks while ensuring security and privacy.

Funding Statement: This work was supported by National Natural Science Foundation of China (Grant No. 61806138), the Central Government Guides Local Science and Technology Development Funds (Grant No. YDZJSX2021A038), Key RD Program of Shanxi Province (International Cooperation) under Grant No. 201903D421048, Outstanding Innovation Project for Graduate Students of Taiyuan University of Science and Technology (Project No. XCX211004), China University Industry-University-Research Collaborative Innovation Fund (Future Network Innovation Research and Application Project) (Grant 2021FNA04014).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Wang, B., Wang, C. H., Song, Y., Cao, J., Cui, X. et al. (2020). A survey and taxonomy on workload scheduling and resource provisioning in hybrid clouds. Cluster Computing—The Journal of Networks Software Tools and Applications, 23(4), 2809–2834. https://doi.org/10.1007/s10586-020-03048-8 [Google Scholar] [CrossRef]

2. Li, C. L., Li, L. Y. (2017). Optimal scheduling across public and private clouds in complex hybrid cloud environment. Information Systems Frontiers, 19(1), 1–12. https://doi.org/10.1007/s10796-015-9581-2 [Google Scholar] [CrossRef]

3. van den Bossche, R., Vanmechelen, K., Broeckhove, J. (2013). Online cost-efficient scheduling of deadline-constrained workloads on hybrid clouds. Future Generation Computer Systems, 29(4), 973–985. https://doi.org/10.1016/j.future.2012.12.012 [Google Scholar] [CrossRef]

4. Zhou, J., Wang, T., Cong, P., Lu, P., Wei, T. et al. (2019). Cost and makespan-aware workflow scheduling in hybrid clouds. Journal of Systems Architecture, 100, 101631. https://doi.org/10.1016/j.sysarc.2019.08.004 [Google Scholar] [CrossRef]

5. Li, C. L., Li, L. Y. (2015). Efficient market strategy based optimal scheduling in hybrid cloud environments. Wireless Personal Communications, 83(1), 581–602. https://doi.org/10.1007/s11277-015-2410-6 [Google Scholar] [CrossRef]

6. Yuan, H. T., Bi, J., Tan, W., Zhou, M. C., Li, B. H. et al. (2017). TTSA: An effective scheduling approach for delay bounded tasks in hybrid clouds. IEEE Transactions on Cybernetics, 47(11), 3658–3668. https://doi.org/10.1109/TCYB.2016.2574766 [Google Scholar] [PubMed] [CrossRef]

7. Li, C., Tang, J., Luo, Y. (2019). Cost-aware scheduling for ensuring software performance and reliability under heterogeneous workloads of hybrid cloud. Automated Software Engineering, 26(1), 125–159. https://doi.org/10.1007/s10515-019-00252-8 [Google Scholar] [CrossRef]

8. Li, C. L., Tang, J. H., Luo, Y. L. (2019). Hybrid cloud adaptive scheduling strategy for heterogeneous workloads. Journal of Grid Computing, 17(3), 419–446. https://doi.org/10.1007/s10723-019-09481-3 [Google Scholar] [CrossRef]

9. Li, C., Tang, J., Luo, Y. (2018). Towards operational cost minimization for cloud bursting with deadline constraints in hybrid clouds. Cluster Computing, 21(4), 2013–2029. [Google Scholar]

10. Yuan, H. T., Bi, J., Tan, W., Li, B. H. (2017). Temporal task scheduling with constrained service delay for profit maximization in hybrid clouds. IEEE Transactions on Automation Science and Engineering, 14(1), 337–348. https://doi.org/10.1109/TASE.2016.2526781 [Google Scholar] [CrossRef]

11. Li, Z. J., Ge, J. D., Yang, H. J., Huang, L. G., Hu, H. Y. et al. (2016). A security and cost aware scheduling algorithm for heterogeneous tasks of scientific workflow in clouds. Future Generation Computer Systems-The International Journal of Escience, 65, 140–152. https://doi.org/10.1016/j.future.2015.12.014 [Google Scholar] [CrossRef]

12. Sharif, S., Watson, P., Taheri, J., Nepal, S., Zomaya, A. Y. (2017). Privacy-aware scheduling saas in high performance computing environments. IEEE Transactions on Parallel and Distributed Systems, 28(4), 1176–1188. https://doi.org/10.1109/TPDS.2016.2603153 [Google Scholar] [CrossRef]

13. Wen, Y. P., Liu, J. X., Dou, W. C., Xu, X. L., Cao, B. Q. et al. (2020). Scheduling workflows with privacy protection constraints for big data applications on cloud. Future Generation Computer Systems—The International Journal of Escience, 108, 1084–1091. https://doi.org/10.1016/j.future.2018.03.028 [Google Scholar] [CrossRef]

14. Sharif, S., Taheri, J., Zomaya, A. Y., Nepal, S. (2014). Online multiple workflow scheduling under privacy and deadline in hybrid cloud environment. 2014 IEEE 6th International Conference on Cloud Computing Technology and Science, pp. 455–462. Singapore. [Google Scholar]

15. Xue, F., Hai, Q., Gong, Y., You, S., Cao, Y. et al. (2022). RVEA-based multi-objective workflow scheduling in cloud environments. International Journal of Bio-Inspired Computation, 20(1), 49–57. [Google Scholar]

16. Yang, W., Chen, L., Li, Y., Abid, F. (2022). A many-objective particle swarm optimisation algorithm based on convergence assistant strategy. International Journal of Bio-Inspired Computation, 20(2), 104–118. [Google Scholar]

17. Cao, Y., Zhou, L., Xue, F. (2021). An improved NSGA-II with dimension perturbation and density estimation for multi-objective DV-Hop localisation algorithm. International Journal of Bio-Inspired Computation, 17(2), 121–130. https://doi.org/10.1504/IJBIC.2021.114081 [Google Scholar] [CrossRef]

18. Cai, X. J., Hu, Z. M., Chen, J. J. (2020). A many-objective optimization recommendation algorithm based on knowledge mining. Information Sciences, 537, 148–161. https://doi.org/10.1016/j.ins.2020.05.067 [Google Scholar] [CrossRef]

19. Cui, Z. H., Zhang, J. J., Wu, D., Cai, X. J., Wang, H. et al. (2020). Hybrid many-objective particle swarm optimization algorithm for green coal production problem. Information Sciences, 518, 256–271. https://doi.org/10.1016/j.ins.2020.01.018 [Google Scholar] [CrossRef]

20. Rather, S. A., Bala, P. S. (2021). Application of constriction coefficient-based particle swarm optimisation and gravitational search algorithm for solving practical engineering design problems. International Journal of Bio-Inspired Computation, 17(4), 246–259. https://doi.org/10.1504/IJBIC.2021.116617 [Google Scholar] [CrossRef]

21. Saeedi, S., Khorsand, R., Bidgoli, S. G., Ramezanpour, M. (2020). Improved many-objective particle swarm optimization algorithm for scientific workflow scheduling in cloud computing. Computers & Industrial Engineering, 147, 106649. https://doi.org/10.1016/j.cie.2020.106649 [Google Scholar] [CrossRef]

22. Chen, H., Wu, G., Pedrycz, W., Suganthan, P. N., Xing, L. et al. (2021). An adaptive resource allocation strategy for objective space partition-based multiobjective optimization. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 51(3), 1507–1522. [Google Scholar]

23. Wang, X., Zhang, L., Liu, Y., Li, F., Chen, Z. et al. (2022). Dynamic scheduling of tasks in cloud manufacturing with multi-agent reinforcement learning. Journal of Manufacturing Systems, 65, 130–145. https://doi.org/10.1016/j.jmsy.2022.08.004 [Google Scholar] [CrossRef]

24. Cai, X. J., Zhang, J. J., Ning, Z. H., Cui, Z. H., Chen, J. J. (2021). A many-objective multistage optimization-based fuzzy decision-making model for coal production prediction. IEEE Transactions on Fuzzy Systems, 29(12), 3665–3675. https://doi.org/10.1109/TFUZZ.2021.3089230 [Google Scholar] [CrossRef]

25. Rong, M., Gong, D., Pedrycz, W., Wang, L. (2020). A multimodel prediction method for dynamic multiobjective evolutionary optimization. IEEE Transactions on Evolutionary Computation, 24(2), 290–304. https://doi.org/10.1109/TEVC.4235 [Google Scholar] [CrossRef]

26. Wu, X., Shen, X., Zhao, N., Wu, S. (2020). An improved discrete pigeon-inspired optimisation algorithm for flexible job shop scheduling problem. International Journal of Bio-Inspired Computation, 16(3), 181–194. https://doi.org/10.1504/IJBIC.2020.111278 [Google Scholar] [CrossRef]

27. Zhang, X., Onieva, E., Perallos, A., Osaba, E. (2020). Genetic optimised serial hierarchical fuzzy classifier for breast cancer diagnosis. International Journal of Bio-Inspired Computation, 15(3), 194–205. https://doi.org/10.1504/IJBIC.2020.107490 [Google Scholar] [CrossRef]

28. Xu, J., Zhang, Z., Hu, Z., Du, L., Cai, X. (2021). A many-objective optimized task allocation scheduling model in cloud computing. Applied Intelligence, 51(6), 3293–3310. https://doi.org/10.1007/s10489-020-01887-x [Google Scholar] [CrossRef]

29. Dubey, K., Sharma, S. C. (2021). A novel multi-objective CR-PSO task scheduling algorithm with deadline constraint in cloud computing. Sustainable Computing-Informatics & Systems, 32. https://doi.org/10.1016/j.suscom.2021.100605 [Google Scholar] [CrossRef]

30. Cai, X. J., Geng, S. J., Wu, D., Cai, J. H., Chen, J. J. (2021). A multicloud-model-based many-objective intelligent algorithm for efficient task scheduling in internet of things. IEEE Internet of Things Journal, 8(12), 9645–9653. https://doi.org/10.1109/JIOT.2020.3040019 [Google Scholar] [CrossRef]

31. Zade, B. M. H., Mansouri, N. (2022). Improved red fox optimizer with fuzzy theory and game theory for task scheduling in cloud environment. Journal of Computational Science, 63, 101805. https://doi.org/10.1016/j.jocs.2022.101805 [Google Scholar] [CrossRef]

32. Zade, M. H., Mansouri, N., Javidi, M. M. (2022). A two-stage scheduler based on new caledonian crow learning algorithm and reinforcement learning strategy for cloud environment. Journal of Network and Computer Applications, 202, 103385. https://doi.org/10.1016/j.jnca.2022.103385. [Google Scholar] [CrossRef]

33. Gao, L., Zhao, Z., Lin, Y. (2021). Research on data classification and grading method based on data security law. Journal of Information Securyity Research, 7(10), 933–940. [Google Scholar]

34. Deng, Q., Kang, Q., Zhang, L., Zhou, M. C., An, J. (2022). Objective space-based population generation to accelerate evolutionary algorithms for large-scale many-objective optimization. IEEE Transactions on Evolutionary Computation, 1. https://doi.org/10.1109/TEVC.2022.3166815 [Google Scholar] [CrossRef]

35. Kang, Q., Song, X., Zhou, M., Li, L. (2019). A collaborative resource allocation strategy for decomposition-based multiobjective evolutionary algorithms. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 49(12), 2416–2423. https://doi.org/10.1109/TSMC.6221021 [Google Scholar] [CrossRef]

36. Zhang, X., Tian, Y., Jin, Y. (2015). A knee point-driven evolutionary algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation, 19(6), 761–776. https://doi.org/10.1109/TEVC.2014.2378512 [Google Scholar] [CrossRef]

37. Zhang, L., Wang, K. F., Xu, L. Y., Sheng, W. J., Kang, Q. (2022). Evolving ensembles using multi-objective genetic programming for imbalanced classification. Knowledge-Based Systems, 255. https://doi.org/10.1016/j.knosys.2022.109611 [Google Scholar] [CrossRef]

38. Tizhoosh, H. R. (2005). Opposition-based learning: A new scheme for machine intelligence. International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), vol. 1. Vienna, Austria. https://doi.org/10.1109/CIMCA.2005.1631345 [Google Scholar] [CrossRef]

39. Wei, W. H., Zhou, J. L., Chen, F., Yuan, H. Q. (2016). Constrained differential evolution using generalized opposition-based learning. Soft Computing, 20(11), 4413–4437. https://doi.org/10.1007/s00500-015-2001-1 [Google Scholar] [CrossRef]

40. Mandavi, S., Rahnamayan, S., Deb, K. (2018). Opposition based learning: A literature review. Swarm and Evolutionary Computation, 39, 1–23. https://doi.org/10.1016/j.swevo.2017.09.010 [Google Scholar] [CrossRef]

41. Ergezer, M., Simon, D., Du, D. (2009). Oppositional biogeography-based optimization. 2009 IEEE International Conference on Systems, Man and Cybernetics, pp. 1009–1014. San Antonio, TX, USA. [Google Scholar]

42. Mc Ginley, B., Maher, J., O’Riordan, C., Morgan, F. (2011). Maintaining healthy population diversity using adaptive crossover, mutation, and selection. IEEE Transactions on Evolutionary Computation, 15(5), 692–714. https://doi.org/10.1109/TEVC.4235 [Google Scholar] [CrossRef]

43. Deb, K., Jain, H. (2014). An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints. IEEE Transactions on Evolutionary Computation, 18(4), 577–601. https://doi.org/10.1109/TEVC.2013.2281535 [Google Scholar] [CrossRef]

44. Yang, S., Li, M., Liu, X., Zheng, J. (2013). A grid-based evolutionary algorithm for many-objective optimization. IEEE Transactions on Evolutionary Computation, 17(5), 721–736. https://doi.org/10.1109/TEVC.2012.2227145 [Google Scholar] [CrossRef]

45. Chen, H. K., Tian, Y., Pedrycz, W., Wu, G. H., Wang, R. et al. (2020). Hyperplane assisted evolutionary algorithm for many-objective optimization problems. IEEE Transactions on Cybernetics, 50(7), 3367–3380. https://doi.org/10.1109/TCYB.6221036 [Google Scholar] [CrossRef]

46. Shukla, S., Gupta, V., Joshi, K., Gupta, A., Mukesh, K. et al. (2022). Self-aware execution environment model (SAE2) for the performance improvement of multicore systems. International Journal of Modern Research, 2(1), 17–27. [Google Scholar]

47. Gupta, V., Shukla, S., Rawat, R. (2022). Crime tracking system and people’s safety in India using machine learning approaches. International Journal of Modern Research, 2(1), 1–7. [Google Scholar]

48. Calheiros, R. N., Ranjan, R., Beloglazov, A., de Rose, C. A. F., Buyya, R. (2011). CloudSim: A toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms. Software-Practice & Experience, 41(1), 23–50. https://doi.org/10.1002/spe.995 [Google Scholar] [CrossRef]

49. Zhang, Z., Zhao, M., Wang, H., Cui, Z., Zhang, W. (2022). An efficient interval many-objective evolutionary algorithm for cloud task scheduling problem under uncertainty. Information Sciences, 583, 56–72. https://doi.org/10.1016/j.ins.2021.11.027 [Google Scholar] [CrossRef]