Energy-Efficient UAVs Coverage Path Planning Approach

1  Introduction

Unmanned aerial vehicles (UAVs) have been widely adopted in civilian and military application domains [1] ranging from transportation to detecting illegal ground activities [2], search and rescue, surveillance, inspection [3,4], and precision agriculture [5]. Due to the unique features of UAVs such as flexibility, mobility, and quick deployment, they can be utilized as human assistance to accomplish several tasks, especially, in severe application conditions, in which humans cannot access [6]. In the above-mentioned applications, ensuring the collecting of the maximum amount of information over a large geographical region is the key purpose of UAV missions.

The terrain coverage is one of the most essential tasks of drones, which has been engaged in many applications, such as disaster management, photography, and intelligent agriculture [7,8]. The determination of a trajectory that covers the whole region by passing through all points of the area of interest (AOI) while avoiding obstacles is called coverage path planning (CPP) [9]. Furthermore, CPP algorithms should be aware of existing obstacles or forbidden zones, known non-flying zones (NFZs). These zones are territories over which the UAVs are not allowed to fly, such as, zones alongside sensitive areas, air terminals, unessential structures, areas next to airports, or irrelevant buildings. These zones are areas that UAVs must not cover or pass over it. When the UAV passes through the point containing the NFZ, it needs to fly around it [10].

The goal of the CPP mechanism is to seek an optimal collision-free flight path so that full coverage of a given region is guaranteed under specific constraint conditions, which is considered as a complicated global optimum problem. It is noteworthy mentioning that the quality of area coverage alone is not the exact metric for achieving high-quality missions. Instead, several operational objective goals, constraints, and restrictions have to be jointly optimized. The constraints and objectives are the two aspects that underpin any mission planning. The overall outputs quality from a mission mainly depends on optimizing final planning to account for both constraints and objectives. These constraints and objectives are required in mission planning for deriving a detailed agenda for a drone in terms of how it should be traveling through an ROI.

Despite UAVs’ ample applications, the onboard energy has fundamentally limited UAV performance and endurance, which is practically finite [11]. Several works in the literature have presented the area coverage using a single UAV, whereby a simple task is done by only one autonomous UAV in small areas such as room cleaning. However, in outdoor like broader area coverage, a UAV may not complete the mission due to battery drainage, and it should stop for refueling. For this reason, the best coverage trajectory for UAV should be obtained such that the energy cost is reduced as much as possible when the optimal coverage path is obtained. Hence, energy-efficient system coverage path planning for maximizing the coverage of a target region is of paramount importance.

Several applications have outgrown the capability of a single drone. Thus, coverage efficiency has been significantly improved by deploying multiple UAVs. This is because multi-UAV provides more significant advantages over a single UAV in CPP robustness enhancing and operational time minimization [12]. Furthermore, in large-scale real-time and distributed collaborative systems, there is an increasing tendency to adopt multiple UAVs for detecting or searching missions. For example, in an agriculture domain, multiple UAVs cooperate for monitoring the weed, and vegetation growth terraces. It is noteworthy mentioning that adapting multiple UAVs has dramatically improved the overall performance and energy conservation. It can be employed when the region size is too large to be covered by a single UAV, which in turn reduces the completion time.

Although adapting the swarm of drones in coverage path planning achieves flexibility enhancement and cost reduction in practical applications development, carrying out their path planning in a complex and large-scale environment increases the complexity of collaborative control and decision-making systems [13]. Such strategies have a significant impact on coverage problem efficiency because generating trajectories require several constraints and high levels of coordination, which are highly dependent on the positions of UAVs.

For handling multiple constraints, many approaches in the literature have formulated the CPP problem based on mixed-integer linear programming (MILP) [14–16]. Exact optimization approaches, such as dynamic programming, branch-and-bound, and constraint satisfaction, have been used to solve the problem via an MILP formulation for optimality using standard solvers in [14,15]. Nevertheless, they are computationally intensive or intractable with hard constraints. Besides, for large-scale problem size, the exact solver fails to obtain the optimal path in a reasonable time. The sophisticated solution is to use a meta-heuristic algorithm where the optimal solution can be obtained in traceable time [17,18].

To handle this issue in a tractable manner, we propose a coverage path planning algorithm that aims to achieve full coverage of the ROI. To this end, in a large-scale problem size in which the exact solution fails to find a solution in a reasonable time, a heuristic approach is implemented to address a large-scale problem in a reasonable time. Most research has focused on obtaining the shortest path coverage and neglected the energy consumption, which depends mainly on acceleration, deceleration, distance, and speed of the drone. To fill this gap, a more accurate model with energy consumption constraints is provided to calculate the energy-efficient optimization trajectory. The problem is formulated as a MILP based optimization problem. The proposed approach composes of two phases. In the first phase, the AOI is decomposed into small cells, known as Point of Interests (PoIs), where the centers of these cells are called waypoints. The cells that constitute the ROI are covered in the second phase when a UAV passes through their centers.

The contribution of this work can be summarized as follows:

•   We develop an optimization formulation of single and multi-UAVs coverage path planning. Mixed-integer linear programming is utilized to formulate the CPP problem as a minimization problem, where the energy consumption is used as the objective to be minimized. The proposed approach can reduce energy consumption which in turn reduces the required number of drones to cover the ROI. Since the turns have a significant effect on energy conservation, the number of turns is included in the objective function to be minimized.

•   The collision avoidance mechanism is proposed to avoid collision with terrain obstacles by designing the required constraints in the proposed formulation. As a result, the proposed CPP approach not only determines the optimal flight path for UAVs but also avoids collision with region obstacles that guarantee to complete the task safely. The proposed CPP problem is solved using the exact approach, i.e., CPLEX solver, and a heuristic approach, i.e., simulated annealing and greedy approaches. The results are analyzed and compared.

•   The proposed approach considers small and large ROI and uses single and multiple drones. In a single UAV scenario, the proposed approach provides multiple trips for a large regional area. Particularly, if the energy of the UAV is not sufficient to cover the whole region, the UAV is allowed to return to the depot and recharges its battery to start the next trip till completing the coverage mission. For multiple UAVs, the proposed approach provides a decomposition mechanism to decompose the region into sub-regions and allocate the sub-regions to the available UAVs. The region allocation aims to balance the energy consumption and reduce the completion time. The sub-regions are created to minimize the overall energy consumption for coverage. For UAV safety, the proposed CPP approach provides an energy calculation or constraint so that the drone can safely return to the depot for recharging.

The remainder of this paper is structured as follow: Section 2 presents the state of the art in the field of coverage path planning. In Section 3, the model of energy consumption is introduced. The proposed Energy-Efficient Coverage Path Planning Approach (EECPPA) is explained in detail in Section 4. The optimization problem is formulated, discussed, and analyzed. The heuristic approaches and their implementations are explained in Section 5. The results and the corresponding discussions are shown in Section 6. Finally, the work is concluded in Section 7.

2  Literature Review

UAV’s coverage path planning problem has been studied extensively in the literature, including energy consumption, terrain shape, and internal obstacles. The optimization solutions for the energy-efficient coverage path planning problem aim to develop new control algorithms that reduce the UAV’s energy consumption during its mission. The flight time is extended, and the energy consumption is minimized through minimum-energy paths design followed by aerial vehicles. For real situations, it is specifically important to realize that UAV operates under a battery-powered limitation [19]. In such situation, a UAV might need to recharge multiple times, especially, for a large region.

In [20], a coverage path planning algorithm was proposed for a single UAV, where the speed-energy model for the drone was used for energy calculation. In [10], the AOI was covered using one rotary-wing drone. The proposed approach worked offine and used an approximate cell decomposition with the grid base technique. Each cell was assigned a positive number that represented the percentage of area. It tried to obtain the shortest path and the least number of turns to reduce energy consumption. In [21], the best path for data collection was studied where the flight time and data collection time were considered. Further, brute force, and two heuristic algorithms, were proposed to solve the CPP problem. Moreover, various decomposition approaches were introduced in [22], such as graph, cellular, and grid-based approaches for UAV CPP. The decomposition approaches as mentioned above were utilized to segment the AOI into sub-areas to obtain the sub-optimal coverage path for a drone.

In [23], an energy-aware CPP algorithm for drones was proposed. The energy model for UAV was derived by carrying out a set of experiments at different conditions of operation such as acceleration, deceleration, and constant speed. The AOI is divided into cells and the drone flied through a grid center to cover it. A zigzag pattern was proposed to reduce the number of turns, which reduces the mission consumption energy. However, obstacles collision avoidance was not considered. Additionally, a CPP problem was formulated as a traveling salesman problem in [24], where the optimal path was obtained to minimize the path length and time windows for multiple salesman problems. In [25], an online CPP algorithm was suggested by utilizing dynamic programming (DP) to enhance performance in terms of energy efficiency and adaptability. The limitation of this work is that the region was decomposed into big cells, and the cells that include any obstacle are completely avoided. In [26], an inspection of the 3D structure approach was proposed using multi-objective optimization. The energy consumption and coverage were considered in the objective function. The main drawback is that energy saving can be achieved for partial coverage.

An energy-aware coverage path planning mechanism was proposed in [27]. The 2D grid partitioning was utilized for region decomposition. Moreover, different irregular and regular regions were considered and covered by one drone. The start point, turning positions, and scan direction were determined. The trajectory was planned in an offline mode and the area coverage, completion time, and energy-saving were studied. However, the collision avoidance of obstacles in the areas of interest was not considered.

The work in [28] included studying full exploration with an energy cost. A method of linear programming to determine a collision-free path was proposed in [12,29]. The points between the start and endpoints were continuously adjusted to build the path. The main limitation of the work is that forbidden zones were not considered in the design.

The heuristic mechanisms are widely studied in the literature for coverage path planning problems, such as particle swarm optimization [30,31], Tabu search [32], simulated annealing [33], and genetic algorithm [34,35]. Such approximation methods are utilized specially for large problem sizes.

In [36], a genetic algorithm was proposed to solve the CPP problem. The objective was to minimize the UAV energy consumption to complete a mission. Reducing the number of turns was proposed to allow the UAV to optimize the flight path and minimize the energy consumption. However, collision avoidance was not considered. In [37], coverage path planning was proposed using a multi-population genetic algorithm, where the problem was formulated as a traveling salesman problem. The drone was tasked to cover multiple regions and came back to the depot following the shortest path. However, the number of UAVs is only one, and they cannot be adapted to regions with multiple UAVs. In [5], the genetic algorithm with a near-optimal sequence of CPP was implemented. To reduce the energy consumption of the robot, the fitness function computed the efficiency of the chromosome, i.e., trajectory. Further, the authors in [38] implemented a genetic algorithm and simulated annealing algorithm to generate multiple local-global coverage trajectories. To reduce the computation cost, both algorithms were processed in parallel. The particle population movements, swarm intelligence algorithm, are utilized in CPP for finding the shortest path or providing the optimal coverage solution. The Particle Swarm Optimization (PSO) is a population meta-heuristic approach, inspired by the social behavior of the natural population swarming [39]. In [40], the smooth CPP trajectory was generated using an online manner based on PSO in a high-resolution grid map.

In most research, the authors have focused on obtaining the shortest path coverage and neglected the energy consumption, which depends mainly on acceleration, deceleration, distance, and speed of the drone. Some literature works achieved enhancement in the performance of region coverage, such as completion time, region coverage maximization, and energy consumption. However, the optimization of energy consumption is not fully addressed. Although fewer works consider the energy consumption, they neglect considering many aspects such as a swarm of UAVs, the number of turns in energy optimization objective, or collision avoidance. It is worth emphasizing that collision avoidance has a significant impact on energy consumption and might increase the number of turns to avoid colliding with the target obstacles. To fill these gaps, we propose an energy-efficient coverage path planning approach to fully cover the target region considering single and multiple drones with minimum energy consumption. To do so, a more accurate model with energy consumption constraints is provided to calculate the energy-efficient optimization collision-free trajectory. To further optimize the flight path and minimize energy consumption, the sub-region allocation is proposed to optimize the allocated sub-regions to the available drones so that the overall energy consumption is minimized.

3  Energy Model for UAV Coverage Path Planning

In spite of significant features of UAVs, the full potential of their applications is still hindered. The limited lifetime of drones due to onboard battery-powered is considered the main limitation [41,42], which causes incomplete missions in some applications. The coverage path planning mission should be done with minimum energy consumption to cope with such limitations. To this end, the CPP problem is formulated and optimized as a minimization problem. The objective function involves energy consumption which is minimized by the optimization approach. That is, the optimal coverage path is selected to fully cover the target area with minimum energy consumption. It has to be stressed once again that the number of turns has a significant impact on energy consumption. Hence, to further optimize the energy consumption of the coverage path, the number of turns is included in the objective function to be reduced.

The energy model for a quadrotor drone in [20] is utilized in our work to calculate the energy consumption during a drone flight mission. The energy model was derived from real measurements where the effect of different factors on energy consumption was studied. Besides, different maneuvering activitie were considered in the real experiments like flying vertically up and down, flying horizontally, hovering, and turning. The energy consumption was obtained as a function of speed. The power consumption (P) was measured during such operations, and the fitting curves were estimated and plotted in [20]. In path planning, we focus on the impact of movement (such as hovering, horizontal movement, vertical movement, and turning) on energy consumption. Thus, the energy consumption for each operation is obtained in [20] as follows:

The flying vertically up or climbing energy for Δh distance with velocity vclimb is given by

Eclimb(Δh)=PclimbΔhvclimb.(1)

The flying vertically down or descent energy for Δh distance with velocity vdesc is given by

Edesc(Δh)=PdescΔhvdesc.(2)

The hovering in place energy from time t1 to time t2 is given by

Ehover=Phover(t2−t1).(3)

The flying horizontally is given as a function of velocity and can be expressed as follows:

Ehoriz=Pvdv,(4)

where d is the horizontal distance, and v is the horizontal speed.

The power and the time needed during rotations were measured. Besides, the angular speed ωturn was assumed to be ωturn (2.1 rad/s) and the corresponding power Pturn (225 W/s) which is considered to be constant during rotations. Then, the energy required to cover an angle θ can be computed as

Eturn=PturnΔθωturn.(5)

Therefore, the energy can be written as follows:

E=Eclimb+Edesc+Ehover+Ehoriz+Eturn.(6)

The total energy of a drone can be simply obtained as E_Total=Vn∗IH∗3600∗P%, where P% is the maximum percentage of energy that a drone can use (particularly 70%) to avoid battery or drone damage [20].

4  Energy-Efficient UAVs Coverage Path Planning Approach Description

The coverage path planning algorithm needs to find the optimal coverage path from a base station, i.e., depot, covering the target region and then returning to the depot. Specifically, the best order of the path waypoints is determined. To do so, the proposed coverage path planning approach composes of two stages. In the first stage, the ROI is decomposed into small cells, which need to be surveyed by UAV. Then the problem is formulated and solved using both exact and heuristic solvers in the second stage. The proposed coverage path planning framework is shown in Fig. 1, and illustrated in Algorithm 1.

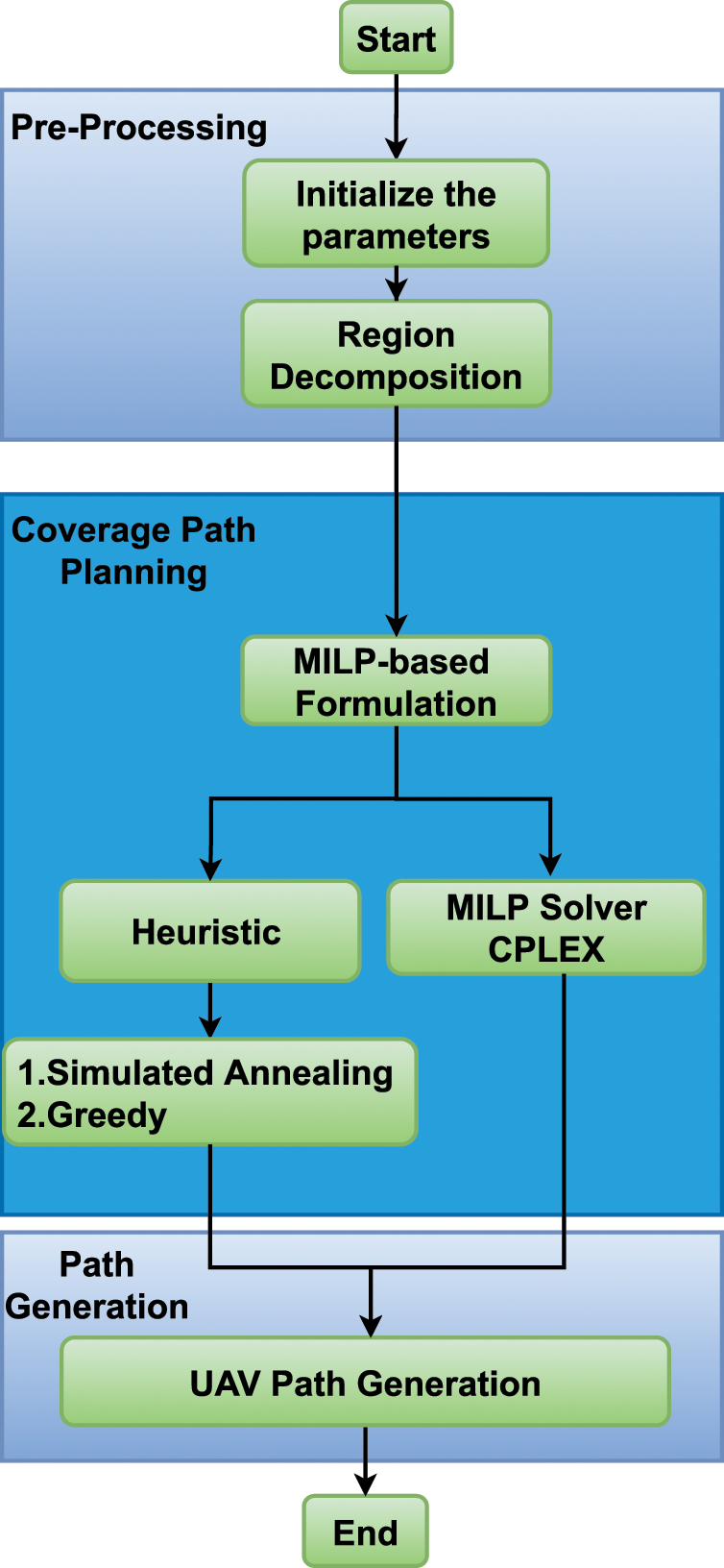
Figure 1: Two phases energy-efficient coverage path planning approach

In the first stage, the proposed approach decomposes the target region into cells, called PoIs, based on the drone camera footprint. Then, the path is planned in the coverage path planning stage, i.e., second stage, where the problem is formulated based on MILP and solved by both exact and heuristic approaches. Due to the complexity of the exact solver, the maximum CPU time is set to a reasonable time, and the best solution of all (exact and heuristic) is selected. The output ofthe algorithm is a collision-free path that guarantees covering the target region. The pseudo-code of the proposed approach is described in Algorithm 1. It starts with the initialization part that receives the region boundaries and uses a decomposition strategy to generate the waypoints of the path, and then obtains the energy matrix. In the second stage, as shown in Fig. 1, MILP formulation for energy efficient coverage path planning is derived and solved using exact solution, i.e., CPLEX, and heuristic approaches. The best solution of exact and heuristic is selected as the optimal solution. The proposed strategy can reduce the energy consumption required to fully cover the ROI as much as possible. This section will explain the parts of the proposed approach in detail.

:

4.1 Region Decomposition

To achieve a better coverage, the ROI is decomposed into cells. The cell size is determined by UAV’s camera footprint and can be fully covered when a UAV is passing through its center, as illustrated in Fig. 2.

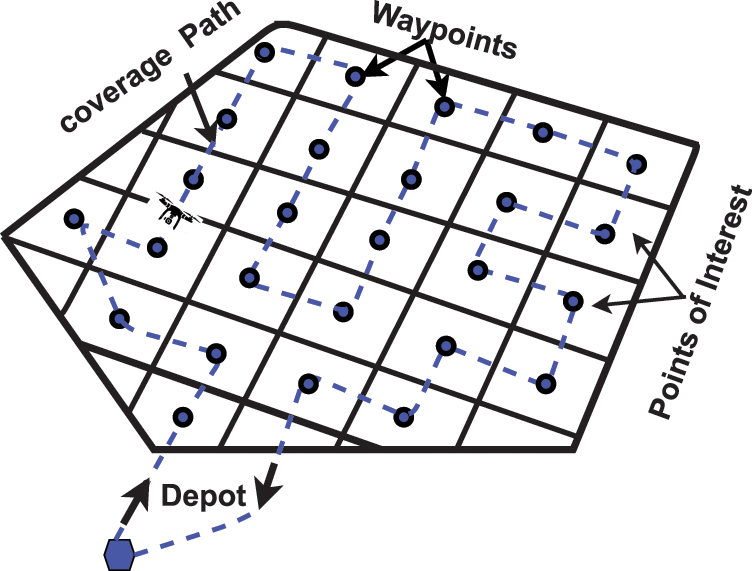
Figure 2: Region decomposed and covered by covering a set of waypoints and returning to the depot

4.2 Problem Description and Formulation

Given a ROI, depot, and UAVs, the aim is to minimize the energy consumption and maximize the coverage region simultaneously. The output of the proposed path planning algorithm is the optimal collision-free flight path with minimum energy consumption for all drones with the following requirements: UAVs can refuel at a depot, i.e., base station. Moreover, the UAVs take off and land at the depot. To this end, the following assumptions are made:

•   The flight trajectory for UAV is planned in a static manner. In other words, the path of a UAV is planned in advance, i.e., before the beginning of a mission.

•   The drone is equipped with a download-facing camera with its coverage capacity known in advance.

•   The drone flies at a fixed altitude, and thus, the problem has been simplified into 2D CPP problem.

•   The ROI can be any shape, squire, circle, polygon, etc.

The objective is to fully cover the ROI with minimum energy consumption. Hence the objective function is a minimization problem. Moreover, the decision variables are inspired by the classical MILP formulation.

Let N is a number of positions or waypoints (1-depot, 2,…, N) in the ROI that are required to be covered by Nd drones, dij is a distance from positioni to positionj, Eu is the available energy of a drone u, Eij is the energy consumed to fly from positioni to positionj, OCij is the cost due to terrain obstacles and can be formulated as follows:

OCij={infif the path from positioni and positionj goes through an obstacle,0Otherwise.

The decision variable xuij can be represented as follows:

xuij={1if a drone u flies from positioni to positionj,0Otherwise.

The objective of these constraints is to generate a collision-free path so that the ROI is fully covered with minimum energy consumption, i.e., minimization problem. Thus, the objective function considers both coverage and drone’s safety mission, i.e., collision avoidance with terrain obstacles.

With this definition, the formulations of MILP are listed below.

The objective function is a minimization problem and can be formulated as

minΓ=∑i=1N∑j=1N(Eij∗xuij+OCij∗xuij),u∈[1,Nd].(7)

Subject to the following constraints:

∑j=1Nxuij=1 ∀i=2,….,N, ∀u=1,…,Nd.(8)

∑j=1Nxu1j=∑j=2Nxuj1=u, ∀u=1,…,Nd.(9)

∑j=1NEij−∑j=1NEji=0, ∀i=2,…,N.(10)

∑i=1N∑j=1NEij∗xuij≤Eu.(11)

0<Eij∗xuij+Ej1≤Eu∀i,j=1,…,N,u=1,…,Nd.(12)

∑u=1Nd∑j=1Nxuij=1 ∀i=1,…,N.(13)

xuij∈[0,1] ∀i,j=1,…,N.(14)

The objective function in Eq. (7) minimizes the total traveling energy consumption across all waypoints inside the ROI. The first part of the objective function is energy calculation for traveling across all waypoints while the second part adds a penalty, i.e., cost, if the path from waypointi to waypointj is passing through an obstacle that prevents collision with terrain obstacles. The constraint in Eq. (8) indicates that each position is preceded and preceded by exactly one another position except the depot (unique sequence of the UAV path). The constraint in Eq. (9) indicates that each UAV departs from the depot and returns to the depot, i.e., the initial location of the drone or base station. Eq. (10) presents the constraint that flying from waypointi to waypointj or from waypointj to waypointi consumes the same energy. The constraint presented in Eq. (11) indicates that the required energy to accomplish the trip by drone u should be less than the available energy of the drone. For large regions in which the available energy of the drone is not sufficient to cover the region, the drone will return to the base station for recharging and complete region coverage. The constraint in Eq. (12) explains that the drone cannot fly from waypointi to waypointj unless its available energy to travel from waypointi to waypointj and from waypointj to the depot is sufficient. This constraint guarantees a safe return to the depot. For multi-UAV, constraint in Eq. (13) ensures that only one UAV flies from waypointi to waypointj and only once. Finally, Eq. (14) shows that xuij is a binary variable.

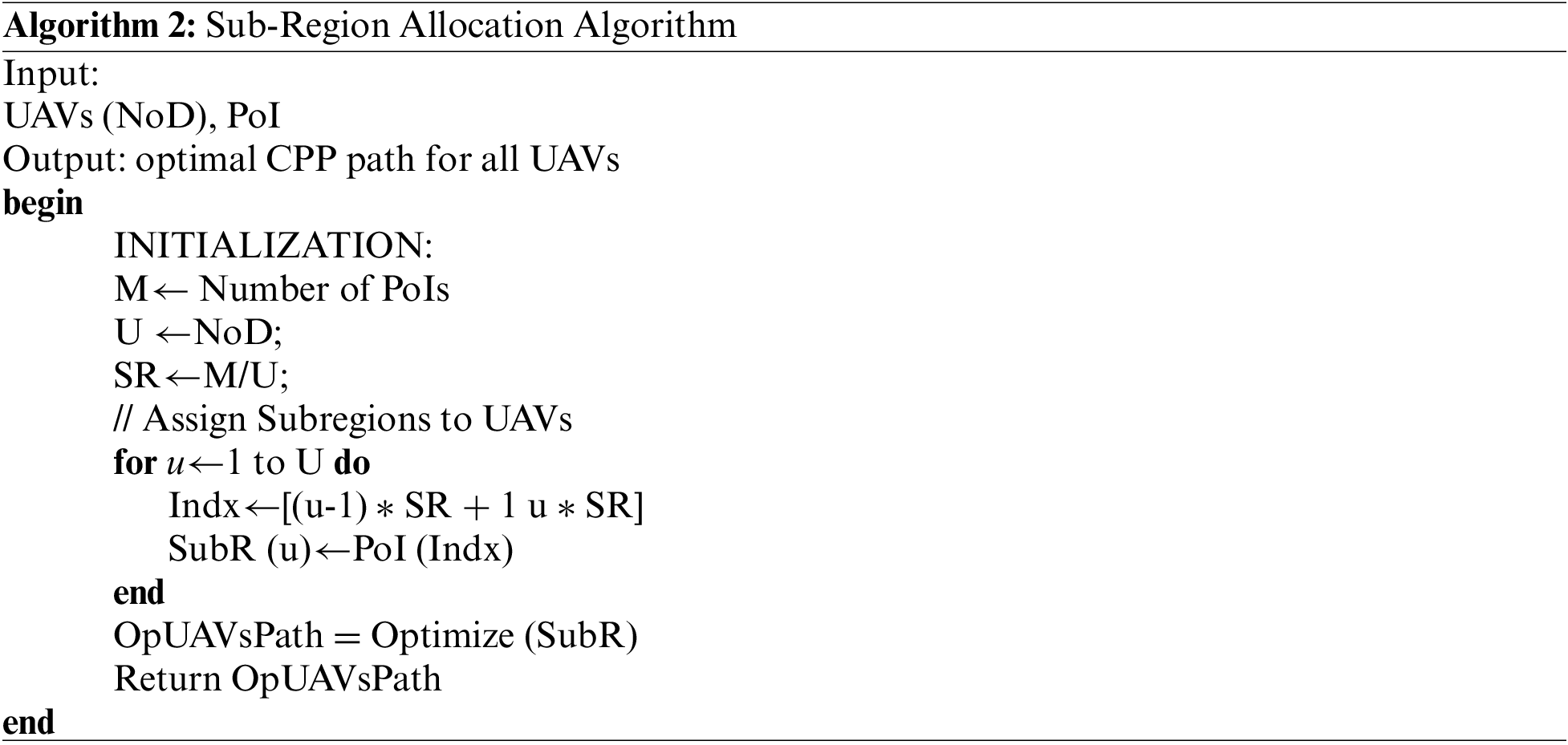
4.3 Sub-Region Allocation to Multiple UAVs

In multiple UAVs, the large region is decomposed depending on the available number of drones. This step aims to prevent drones from intra-collision and balance the energy consumption for different drones. To do so, the region is decomposed into M cells, which are grouped into N groups, i.e., N sub-regions, where the number of sub-regions is equal to the number of drones. The allocation algorithm is illustrated in Algorithm 2. The algorithm receives the region coordinates and the available number of drones, and return the optimal allocation of sub-region to the available UAVs. Without loss of generality, the sub-regions or groups are created as follows:

iSubRegioni=[M/N∗(i−1)+1 toM/N∗i].(15)

To elaborate, assume that two UAVs are available. The whole region is divided into two groups that are determined with different colors, as illustrated in Fig. 3.

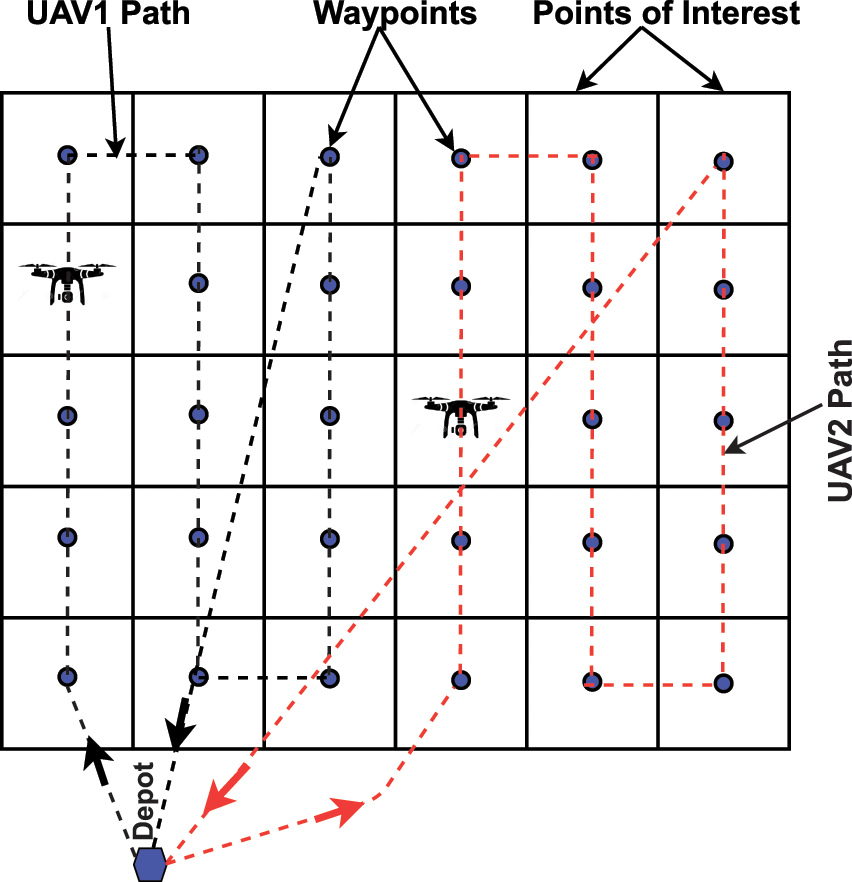
Figure 3: Region decomposed and allocated between two UAVs starting from the same depot

For further optimizing the energy consumption, we further optimize the assigned group to UAVs. To clarify, the waypoints in different positions are swapped and the crossover between different groups is done so that the overall energy cost is minimized as explained in Algorithm 2 (Optimize (SubR)). It has to be stressed that in multiple UAVs starting from the same depot as shown in Fig. 3, when the drone returns to the depot, it follows the shortest collision-free path. To avoid drones collision, a safety distance is maintained between them (2 m safety distance is considered in our work). Thus, even if the trajectories of the two UAVs cross at the same time, the drone safety is guaranteed.

:

5  Heuristic Optimization Solution

The problem formulation of the proposed coverage path planning approach is similar to Vehicle Routing Problem (VRP) which is an NP-Hard problem. The aim is to fully cover the ROI by passing through all waypoints, and minimizing energy consumption.

The exact solution will achieve the best trajectory for drones by completely exploring the solution space if no time limit is set. For small-scale problems, the solution can be obtained within acceptable time consumption. Unfortunately, the solution space is significantly exploding for large-scale and complex system problems, resulting in an inefficient application of such formulation due to the required time consumption. Therefore, the linear programming-based formulation efficiency is unacceptable, especially in large-scale cooperative real path planning. To handle this issue in a tractable manner, we propose implementing simulated annealing [33] and greedy search [43].

This section, will explain these meta-heuristic approaches to solve the formulated CPP problem.

5.1 Simulated Annealing Solution for Coverage Path Planning Problem

One approximation approach for solving the large-scale coverage path planning is simulated annealing. The SA [44–46] is a single-solution meta-heuristic based on the concept of the neighborhood to improve the quality of the current solution. The SA, inspired by physical annealing process used in metallurgy, begins the search with a single initial solution. Then, the initial solution is updated through a series of modifications depending on its neighborhood. The purpose of these local changes is to explore the neighborhood of the solution to gradually improve its quality during the iterations. The quality of the final solution especially depends on the modifications made by the neighborhood operators. The pseudo-code of the algorithm is shown in the Algorithm 3.

:

The SA starts with an initial part that is responsible for initializing the algorithm’s parameters such as initial temperature, stop temperature, and damping rate of the temperature. The initialization part is also responsible to create the initial path, i.e., sequence of waypoints to be followed. It receives parameters and constraints and the best path that achieves the full coverage of ROI with minimum energy consumption is returned. For each iteration, a new solution, i.e., path, is generated from the current solution neighborhood, and the feasibility of the new solution is checked for ensuring that no constraint is violated. Then, the feasible solution is assessed by the objective function and the best solution so far will be stored with the corresponding fitness, i.e., energy consumption. Otherwise, the feasible solution will be accepted as a new solution with probability P, called acceptance probability function, which can be calculated as:

P={1ifthecostofcurrentsolution<=minCost,e−δ/Tifthecostofcurrentsolution>minCost,

where δ is the difference between the fitness value of the current solution and the best solution. The current solution can be accepted if P = 1, i.e., δ<1, or the random number generated (rn) is less than P. Note that the objective function receives the path and calculates the energy required by the drone to follow that path, i.e., flying energy and turning energy.

It has to be stressed that the order of two cells’ positions is randomly exchanged to generate a new solution. Then the transition will occur if the quality of the current solution, i.e., the energy consumption of the new path, is better than the best solution. In the Metropolis criterion, the iteration process is controlled by the temperature T, which controls the whole algorithm. Once all iterations finish, the current temperature is gradually reduced. In this stage, the current temperature is multiplied by the cooling rate (r) to obtain the next temperature (T = T * r) and the iteration starts again. This process is terminated when the temperature reaches stop temperature criteria, and the best path so far for UAV is returned.

5.2 Greedy Approach Solution for CPP

The greedy algorithm is an iterative heuristic that obtains a local optimum at each iteration. It is used to address optimization problems, where a solution is constructed through a sequence of available choices. At every step, once the choice is made, subsequent steps are not changed [47]. The global optimum solution is not always obtained. Instead, an optimal local solution is obtained in less time. The process of calculating the minimum energy consumption in greedy is the same as simulated annealing without temperature damping. For this reason, it cannot always find a globally optimal solution. The greedy algorithm is easy to implement due to its simplicity and it is generally faster. However, finding the globally optimal solution is not guaranteed due to the short-term solution [18]. The pseudo-code of the greedy algorithm for CPP is explained in Algorithm 4.

:

6  Simulation Results and Discussion

In this section, the correctness and efficiency of the proposed approach are verified. The exact solution is compared against heuristic approaches, i.e., SA and greedy. The comparison includes execution time and energy consumption, important metrics in coverage path planning, for a different number of waypoints.

6.1 Execution Time Evaluation

To investigate the ability of the three methods used in the proposed approach in finding the optimal solution of the coverage path planning problem, the execution time that represents a key factor for evaluating the performance, is tested. The average execution time for 10 replications is illustrated in Fig. 4.

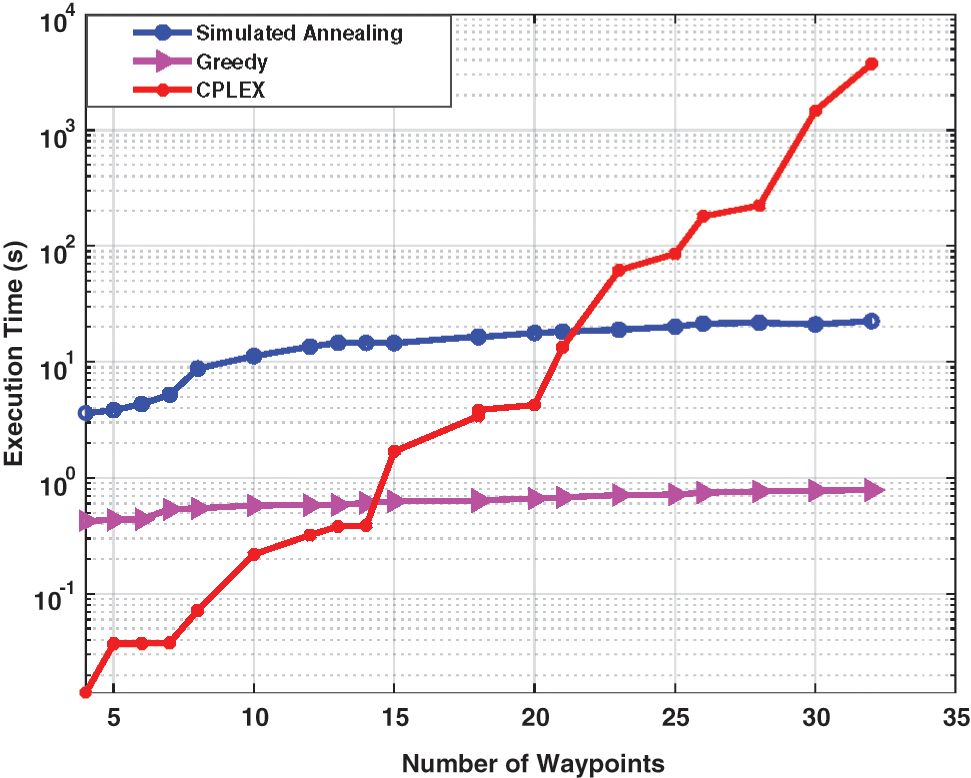
Figure 4: The average execution time with respect to number of waypoints for the three approaches, SA, greedy, and CPLEX solver

It can be observed that the execution time of the three methods goes up simultaneously as the ROI size increases, demonstrating the effect of problem size on execution time. It is worth emphasizing that the greedy obtains a locally optimal solution by looking for the best solution to find a globally optimal solution. Consequently, it needs a shorter time to generate the solution. On the other hand, the exact solution obtains the best solution for drones by thoroughly exploring the solution space.

For small-scale problems, the exact solution can be obtained within acceptable time consumption, while in large-scale and complex system problems, the solution space is significantly exploding, resulting in an inefficient application of such formulation due to the required time consumption to find the exact solution. This fact is depicted in Fig. 4. As the number of waypoints increases, this trend increases, demonstrating the impact of problem size on the exact solution’s execution time. When the number of waypoints exceeded 30, the execution time of the CPLEX solver is significantly increasing, while the execution time shown by SA and greedy are around 25 and 0.8 s, respectively. When the region size is enlarged, the proposed exact solution model is unable to provide a solution. However, the heuristic approaches obtain the results within reasonable computation times. The results show the ability of the proposed approach in obtaining the solution for different problem sizes by an appropriate solver.

6.2 Energy Consumption Evaluation

Energy consumption is recognized as an essential metric for evaluating the performance of algorithms. It reflects the ability of the proposed approach to generate an efficient collision-free path. The drone flies from the depot covering every waypoint and returns. The visited sequence of waypoints is selected so that the overall energy consumption is minimized while avoiding obstacles’ collision and intra-swarm collision (in the case of multi-UAVs). Firstly, we show how the proposed approach contributes in maximizing energy saving. The CPP problem is formulated as a minimization optimization problem where energy consumption is used as the objective to be minimized. Therefore, the proposed approach minimizes the energy consumption, i.e., maximizes the energy saving of drone, during iterations. At the end of the last iteration, the generated path guarantees minimum energy consumption. This claim is proved in Fig. 5a. The figure shows the normalized energy saving at each iteration where the energy saving is normalized to unity by dividing the energy saving for each iteration over the energy saving of the first iteration, i.e., the first generated solution.

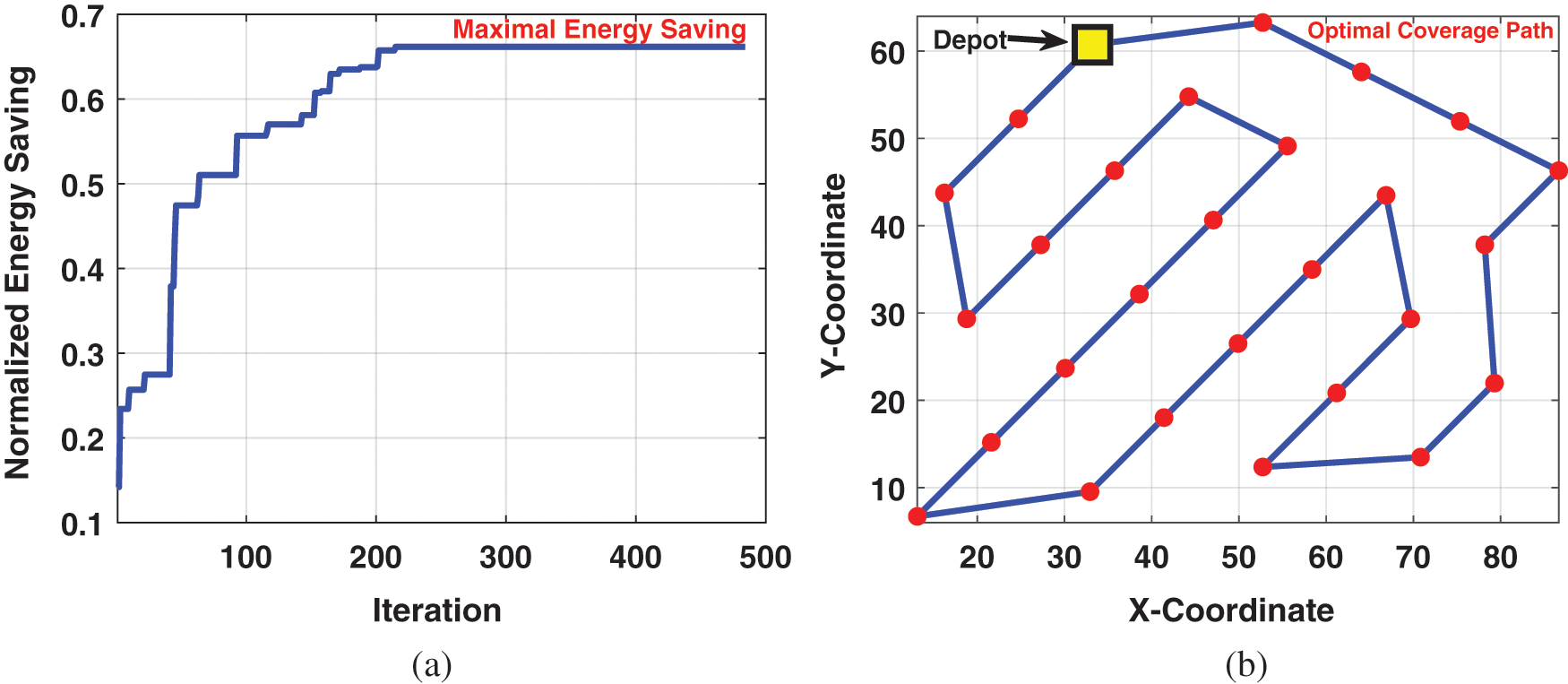
Figure 5: (a) The normalized energy saving with respect to number of iterations, and (b) The optimal coverage path generated by the algorithm

As can be clearly seen in Fig. 5a, at the end of the last iteration, the energy saving reaches to the maximal and the corresponding coverage path is the optimal path as exhibited in Fig. 5b.

To analyze the optimal solution of the proposed model, the average energy consumption of 10 replications is shown in Fig. 6. The energy consumption of the three methods goes up simultaneously with an increase in the number of waypoints, i.e., region size, demonstrating the effect of problem size on energy consumption. From Fig. 6, we can observe that the proposed approach shows lower energy consumption by CPLEX solver than heuristic, while greedy shows the highest energy consumption. This gap increases as the number of waypoints increases. The reason is that the greedy obtains a locally optimal solution by looking for the best solution to find a global optimal solution, and due to the short-term solution, it generates a poorer solution and does not guarantee to find the globally optimal solution. The CPLEX solver will achieve the best solution for drones by completely exploring the solution space. However, for large-scale and complex system problems, the solution space is significantly exploding, resulting in inefficient application due to the required time consumption as discussed before.

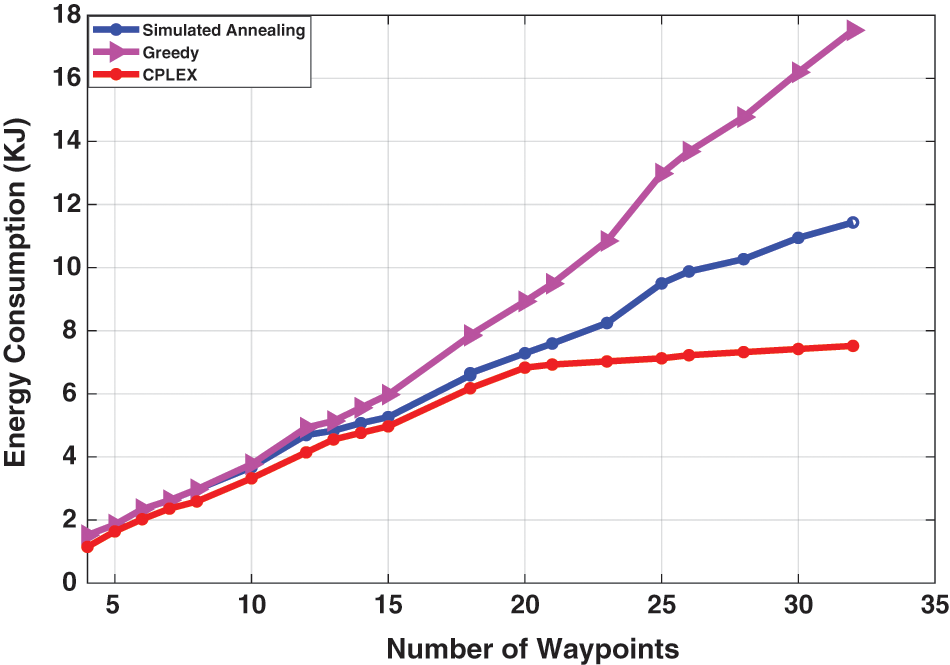
Figure 6: The average energy consumption with respect to number of waypoints for the three strategies, SA, greedy, and CPLEX solver

For further analyzing the optimal solution of the proposed model, the optimality gaps between CPLEX solver and heuristics are calculated and the results are recorded in Table 1. The Gap% represents the gap between CPLEX solver and heuristic approaches, respectively, and can be obtained by

SAGap=SAEn−CPLEXEnCPLEXEn∗100.(16)

GreedyGap=GreedyEn−CPLEXEnCPLEXEn∗100.(17)

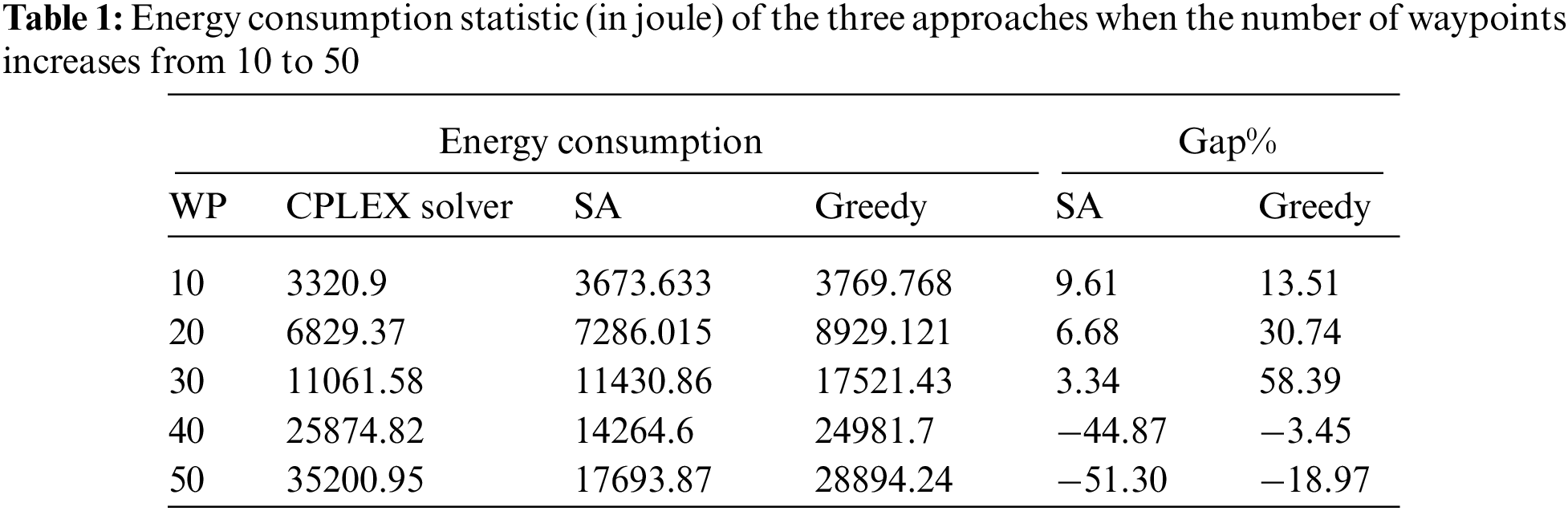
Owing to the complexity of the CPLEX solver, i.e., exact solution model, the maximum CPU time is set to 3600 s. The average optimal solutions of 10, 20, 30, 40, and 50 waypoints are shown. Both greedy and SA could achieve the optimal solutions in a significantly shorter time than the CPLEX solver. For large scenarios where number of waypoints is greater than 30 waypoints, i.e., 40, 50 waypoints, the CPLEX solver cannot solve for optimality in reasonable time while heuristic approaches yield a solution with a gap of (44.8707% and 51.308%) for SA and (3.45% and 18.97%), for greedy. The percentage gap shows that in a small number of waypoints, i.e., small region, the CPLEX solver achieves a better solution than heuristics. The negative sign of Gap% indicates poor solution by CPLEX solver, when the number of waypoints exceeded 30 waypoints.

To further illustrate the impact of execution time on the quality of energy consumption, we plot the energy consumption with respect to number of waypoints, 10 to 50 waypoints, and the result is highlighted in Fig. 7. The result emphasizes that the CPLEX fails to obtain the optimal solution in a reasonable time for the large-scale problem. It also shows the advantage of heuristic approaches in solving large-scale problems in a shorter time.

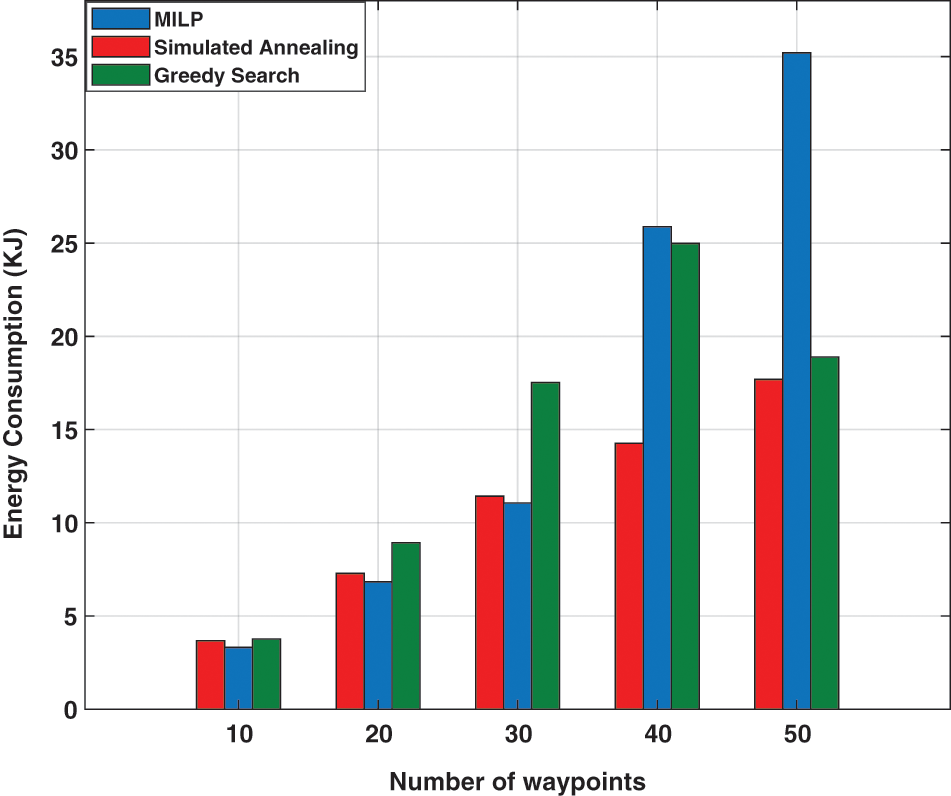
Figure 7: The energy consumption with respect to number of five region sizes, 10 to 50 waypoints, for the three approaches, SA, greedy, and CPLEX solver

6.3 Collision Avoidance Evaluation

In this subsection, the terrain involves two static obstacles. The proposed approach generates a feasible collision-free path, which achieves the objective and satisfies all constraints. The generated collision-free path covers the whole region with minimum energy consumption, as illustrated in two-dimensional views in Fig. 8. It can be clearly seen that no collision is detected with static obstacles in all approaches, and the drones can weave around obstacles efficiently.

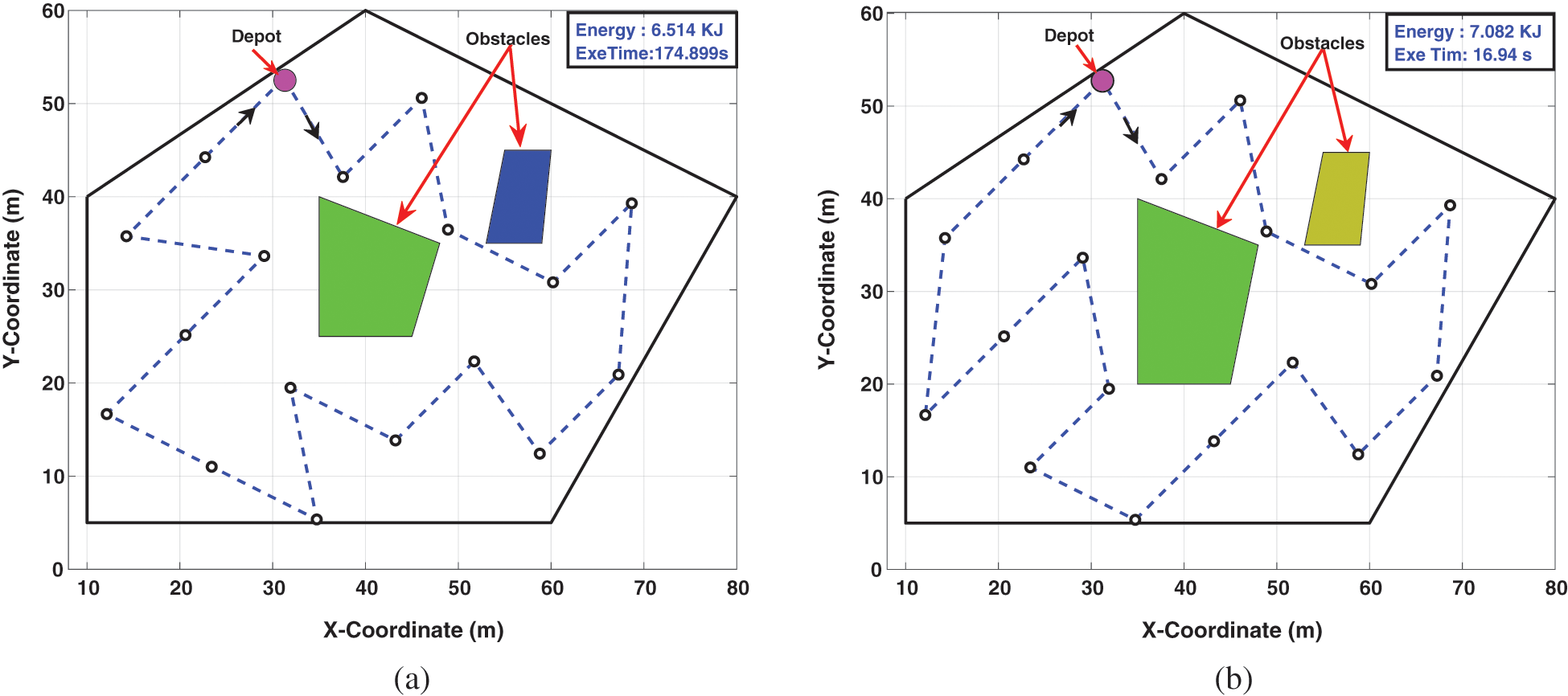
Figure 8: Two-dimensional view for coverage path planning with 2 static obstacles environment. (a) CPLEX solver collision-free path and (b) Simulated annealing collision-free path

It is worth noting that considering the collision avoidance with obstacles impacts the drone’s energy consumption and might increase the number of turns to avoid colliding with terrain obstacles. This fact can be easily seen in Fig. 9. The figure shows the energy consumption for different waypoints with and without collision avoidance considerations. The drone needs more energy to avoid colliding with obstacles which basically reflects more practical results.

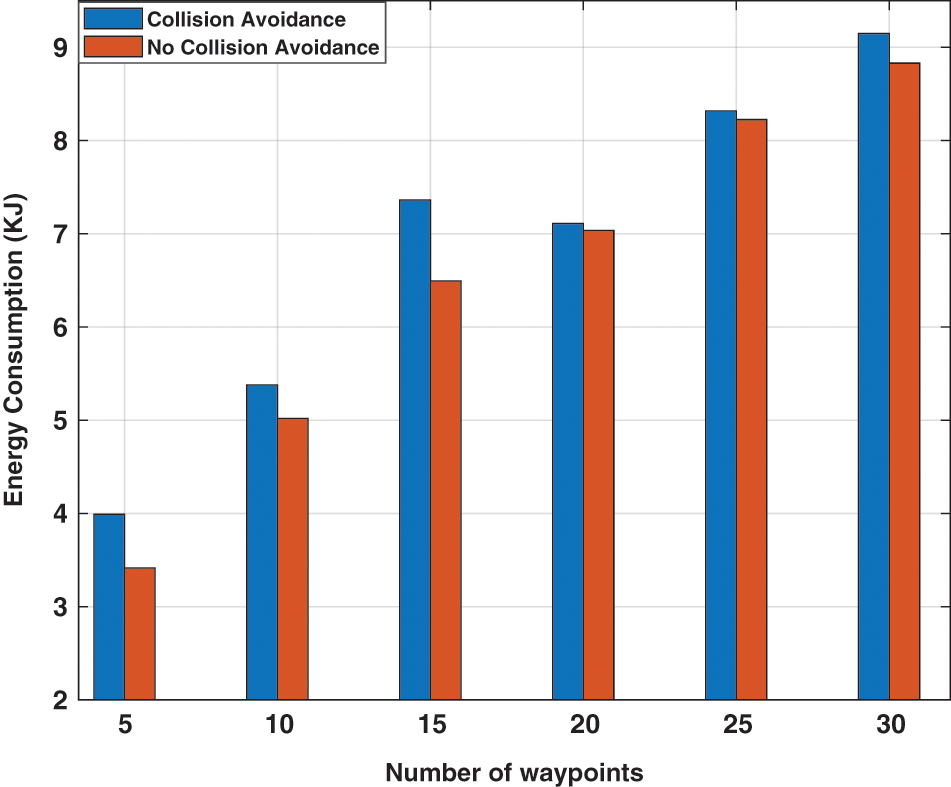
Figure 9: The energy consumption with respect to five region size, 10 to 50 waypoints, with and without considering the effect of obstacles on energy

6.4 Effect of Sub-Region Allocation Optimizing on Performance

To further analyze the effectiveness of the proposed region allocation approach on energy conservation, we discuss the impact of region allocation on reducing the energy consumption to cover the ROI. The optimal solutions of different region sizes are obtained and recorded in Table 2 where the percentage of the average improvement gap of the proposed region allocation is calculated.

6.5 Trajectory Optimization of UAV in Small and Large Region

To show the performance of the proposed approach in addressing small and large region areas, different scenarios involving single UAV and multi-UAV with the small and large region are presented.

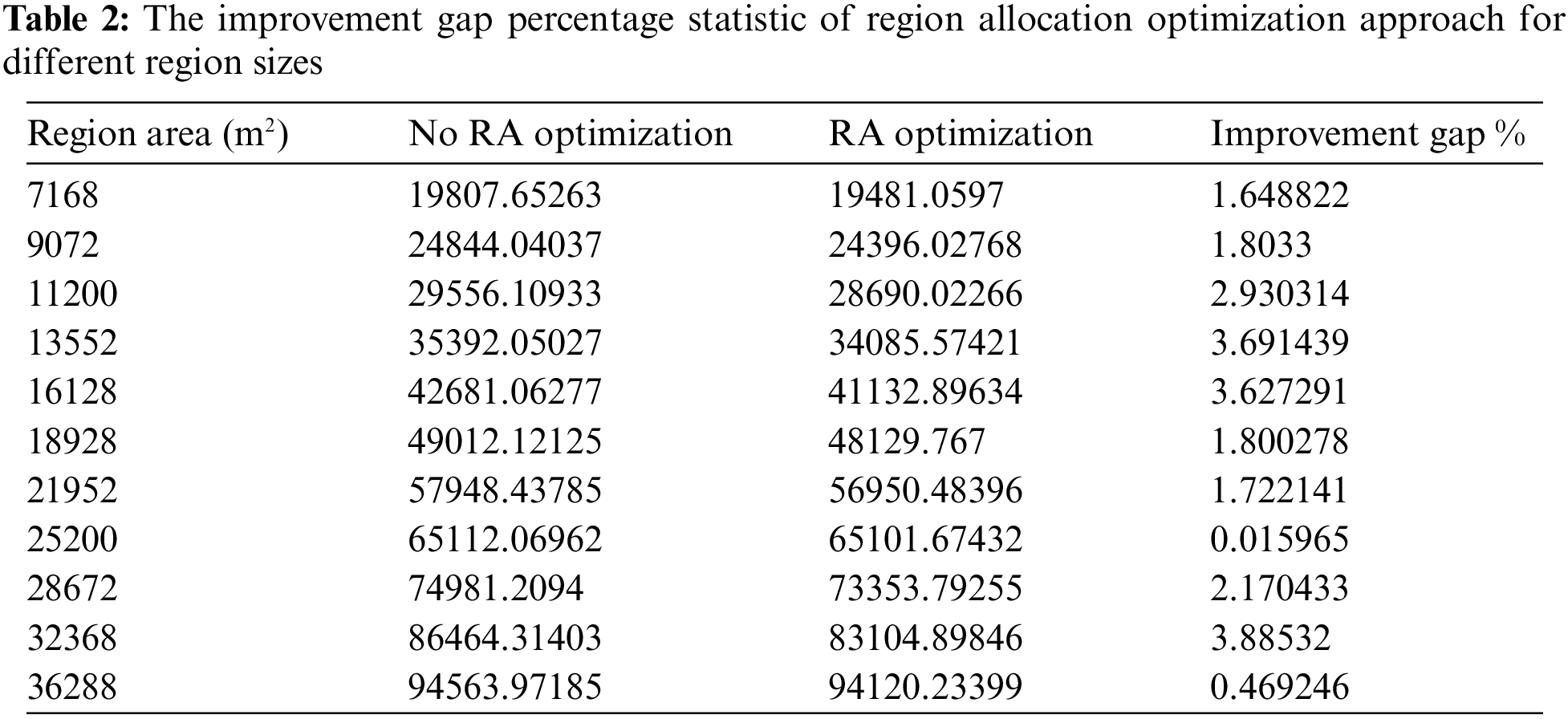
•   Single UAV coverage path planning performance evaluation. In this scenario, the drone is flying from the depot (we consider the starting waypoint of the coverage path as the depot), covering all waypoints, and then returns to the depot, i.e., the region is covered in one trip, as illustrated in Fig. 10. The figure shows the coverage path planning for the three approaches used in the proposed algorithm, where 20 waypoints are covered. As discussed in Section 3, the number of turns has a significant effect on energy consumption due to deceleration and acceleration operation to take a turn that consumes significant energy. In Fig. 10, the SA trajectory requires less energy consumption than greedy but is still greater than the CPLEX solver, which shows the lowest energy consumption. On the other hand, greedy approach shows the fastest execution time while the CPLEX solver shows the slowest execution time. If the region cannot be completely covered by one trip due to insufficient energy, the drone needs to return to the base station or depot and recharges its battery to continue covering the region. To do so, we provide a remaining energy calculation that guarantees the safety of the drone to come back to the base station. The remind energy is calculated as follows: the drone is allowed to fly from positioni to positionj if its available energy is sufficient to fly from positioni to positionj and from positionj to the depot. This constraint is formulated in Eq. (12), and it allows generating the safety path with minimum energy consumption, as shown in Fig. 11. The UAV needs two trips to cover the region. Thus, the proposed approach generates two paths for two trips. It is noteworthy mentioning that the proposed algorithm avoids previously explored covered waypoints, as illustrated in Fig. 11. In this figure, the returning path is also exploited to scan the waypoints in the path toward the depot. The offline failsafe measure is proposed to verify if the UAV has sufficient energy to execute the mission.

•   Multi-UAV coverage path planning performance evaluation. In this scenario, three UAVs are assumed to be available. Thus, the ROI is divided into three parts, and each drone is tasked to cover a set of waypoints as explained above in Section 4.3. The multi-UAVs can be employed when the region size is too large and can not be covered by a single UAV. Thus, the region is split into sub-regions that are assigned among UAVs. The paths generation is shown in Fig. 12. It can be clearly seen that inter-collision is addressed, and the successful collision-free paths are generated for all UAVs.

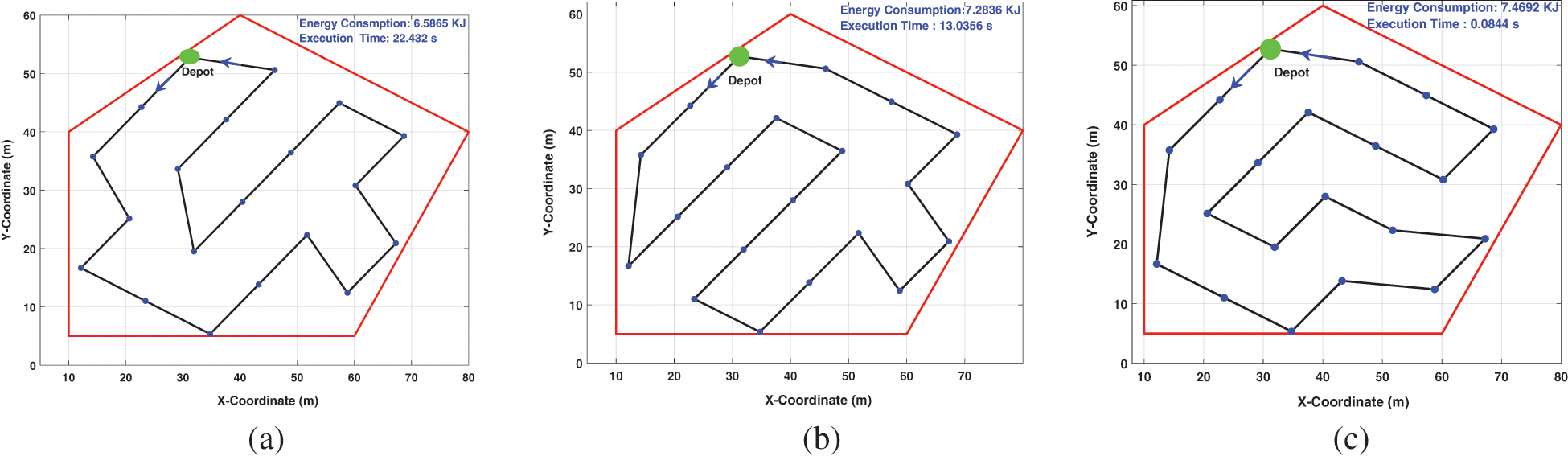
Figure 10: Two-dimensional view for coverage path planning for the three approaches, (a) CPLEX solver, (b) SA, and (c) Greedy. The drone flies from the depot, covering the region, and returns to the depot position

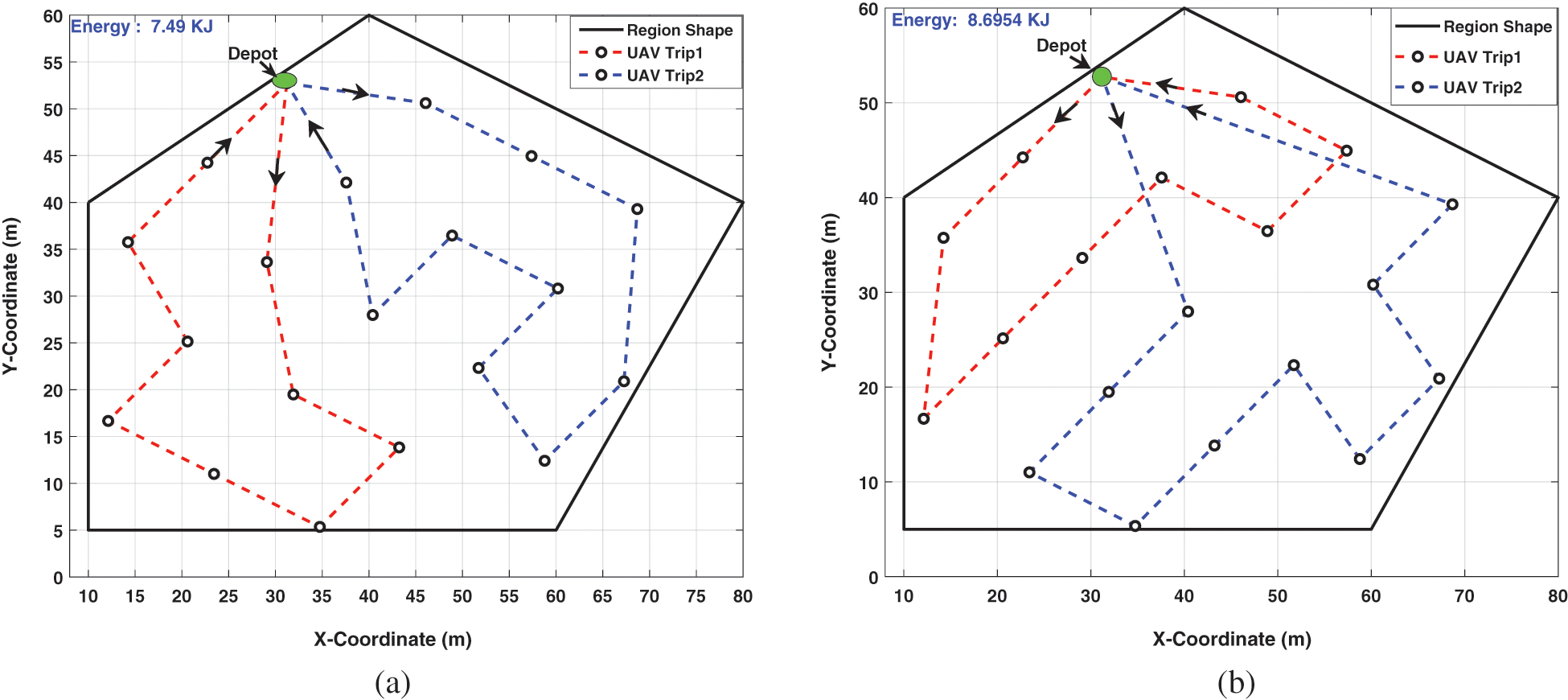
Figure 11: Two-dimensional view for multiple trips coverage path planning when available energy consumption of drone is not sufficient to cover the region by one trip. (a) CPLEX solver and (b) Simulated annealing

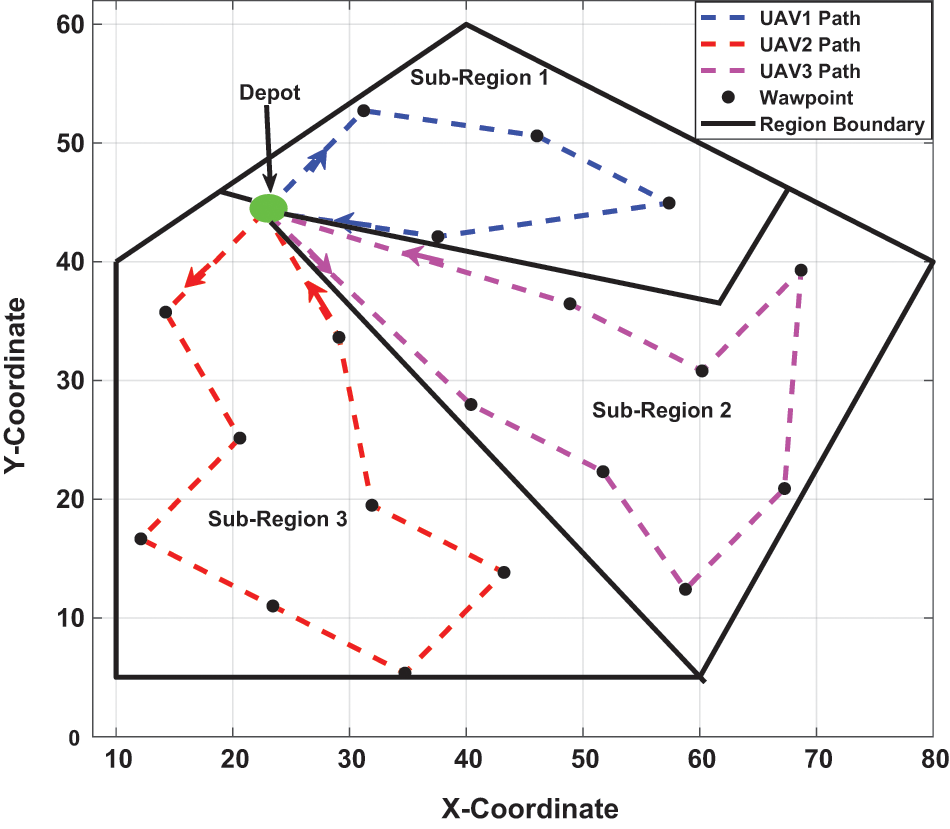
Figure 12: Two-dimensional view of coverage path planning for three UAVs

7  Conclusion

In this paper, we developed an energy-efficient coverage path planning approach that considered different region sizes. Firstly, an optimization formulation of single and multi-UAVs coverage path planning was formulated as a minimization problem, where energy consumption was used as the objective to be minimized. The number of turns was included in the objective function for further minimizing energy consumption. Furthermore, the collision avoidance mechanism was proposed to avoid collision with terrain obstacles by designing the required constraints in the proposed formulation. The exact formulation for CPP was proposed based on MILP to seek the optimal trajectories for drones so that the generated path minimizes the energy consumption and satisfies all constraints during the mission. The proposed approach was able to efficiently decompose the ROI into sub-regions. The proposed sub-regions allocation strategy contributed in reducing energy consumption. The MILP-based formulation was solved using CPLEX solver and heuristic approaches, i.e., simulated annealing and greedy algorithms. Several scenarios were studied to verify the correctness of the proposed approach. The results showed that in small problem sizes, both exact and heuristic approaches were able to generate collision-free paths for UAVs, and the CPLEX solver outperformed the heuristic approaches. However, in large-scale problems, the CPLEX failed to generate the optimal solution in a tractable time. Additionally, the results showed that simulated annealing with energy optimization used less energy consumption than the greedy mechanism. Furthermore, the results illustrated that energy conservation was more prominent as the region size increased.

In future work, the proposed model will be extended by considering multiple separated regions and different depot locations.

Acknowledgement: The authors would like to acknowledge the support of the Interdisciplinary Center of Smart Mobility and Logistics, and the Department of Computer Engineering at King Fahd University of Petroleum and Minerals for the support of this research.

Funding Statement: This research was funded by Project Number INML2104 under the InterdisciPlinary Center of Smart Mobility and Logistics, KFUPM.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Zhao, L., Yang, K., Tan, Z., Li, X., Sharma, S. et al. (2020). A novel cost optimization strategy for sdn-enabled UAV-assisted vehicular computation offloading. IEEE Transactions on Intelligent Transportation Systems, 22(6), 3664–3674. https://doi.org/10.1109/TITS.2020.3024186 [Google Scholar] [CrossRef]

2. Dempsey, M. (2014). Intelligence, surveillance, and reconnaissance joint force 2020 white paper. US Army, Washington, DC, USA. [Google Scholar]

3. Ahmed, G., Sheltami, T., Mahmoud, A., Yasar, A. (2020). Iod swarms collision avoidance via improved particle swarm optimization. Transportation Research Part A: Policy and Practice, 142, 260–278. https://doi.org/10.1016/j.tra.2020.09.005 [Google Scholar] [CrossRef]

4. Peng, C., Isler, V. (2020). Visual coverage path planning for urban environments. IEEE Robotics and Automation Letters, 5(4), 5961–5968. https://doi.org/10.1109/LRA.2020.3010745 [Google Scholar] [CrossRef]

5. Hameed, I. A. (2014). Intelligent coverage path planning for agricultural robots and autonomous machines on three-dimensional terrain. Journal of Intelligent & Robotic Systems, 74(3), 965–983. https://doi.org/10.1007/s10846-013-9834-6 [Google Scholar] [CrossRef]

6. Ahmed, G. A., Sheltami, T. R., Mahmoud, A. S., Imran, M., Shoaib, M. (2021). A novel collaborative iod-assisted vanet approach for coverage area maximization. IEEE Access, 9, 61211–61223. https://doi.org/10.1109/ACCESS.2021.3072431 [Google Scholar] [CrossRef]

7. Melo, A. G., Pinto, M. F., Marcato, A. L., Honório, L. M., Coelho, F. O. (2021). Dynamic optimization and heuristics based online coverage path planning in 3D environment for UAVs. Sensors, 21(4), 1108. https://doi.org/10.3390/s21041108 [Google Scholar] [PubMed] [CrossRef]

8. Cho, S. W., Park, H. J., Lee, H., Shim, D. H., Kim, S. Y. (2021). Coverage path planning for multiple unmanned aerial vehicles in maritime search and rescue operations. Computers & Industrial Engineering, 161, 107612. https://doi.org/10.1016/j.cie.2021.107612 [Google Scholar] [CrossRef]

9. Tan, C. S., Mohd-Mokhtar, R., Arshad, M. R. (2021). A comprehensive review of coverage path planning in robotics using classical and heuristic algorithms. IEEE Access. https://doi.org/10.1109/ACCESS.2021.3108177 [Google Scholar] [CrossRef]

10. Ghaddar, A., Merei, A., Natalizio, E. (2020). PPS: Energy-aware grid-based coverage path planning for uavs using area partitioning in the presence of NFZs. Sensors, 20(13), 3742. https://doi.org/10.3390/s20133742 [Google Scholar] [PubMed] [CrossRef]

11. Li, M., Cheng, N., Gao, J., Wang, Y., Zhao, L. et al. (2020). Energy-efficient uav-assisted mobile edge computing: Resource allocation and trajectory optimization. IEEE Transactions on Vehicular Technology, 69(3), 3424–3438. https://doi.org/10.1109/TVT.25 [Google Scholar] [CrossRef]

12. Zuo, Y., Tharmarasa, R., Jassemi-Zargani, R., Kashyap, N., Thiyagalingam, J. et al. (2020). Milp formulation for aircraft path planning in persistent surveillance. IEEE Transactions on Aerospace and Electronic Systems, 56(5), 3796–3811. https://doi.org/10.1109/TAES.7 [Google Scholar] [CrossRef]

13. Maza, I., Ollero, A. (2007). Multiple UAV cooperative searching operation using polygon area decomposition and efficient coverage algorithms. In: Distributed autonomous robotic systems 6, pp. 221–230. Tokyo: Springer. [Google Scholar]

14. Alidaee, B., Wang, H., Landram, F. (2009). A note on integer programming formulations of the real-time optimal scheduling and flight path selection of UAVs. IEEE Transactions on Control Systems Technology, 17(4), 839–843. https://doi.org/10.1109/TCST.2008.2002265 [Google Scholar] [CrossRef]

15. Nigam, N., Bieniawski, S., Kroo, I., Vian, J. (2011). Control of multiple UAVs for persistent surveillance: Algorithm and flight test results. IEEE Transactions on Control Systems Technology, 20(5), 1236–1251. https://doi.org/10.1109/TCST.2011.2167331 [Google Scholar] [CrossRef]

16. Song, B. D., Kim, J., Morrison, J. R. (2016). Rolling horizon path planning of an autonomous system of UAVs for persistent cooperative service: Milp formulation and efficient heuristics. Journal of Intelligent & Robotic Systems, 84(1–4), 241–258. https://doi.org/10.1007/s10846-015-0280-5 [Google Scholar] [CrossRef]

17. Zhao, L., Saif, M. B., Hawbani, A., Min, G., Peng, S. et al. (2021). A novel improved artificial bee colony and blockchain-based secure clustering routing scheme for fanet. China Communications, 18(7), 103–116. https://doi.org/10.23919/JCC.2021.07.009 [Google Scholar] [CrossRef]

18. Joshi, P. (2017). Artificial intelligence with python. Packt Publishing, Ltd. [Google Scholar]

19. Lin, H. Y., Yao, C. W., Cheng, K. S., Tran, V. L. (2018). Topological map construction and scene recognition for vehicle localization. Autonomous Robots, 42(1), 65–81. https://doi.org/10.1007/s10514-017-9638-9 [Google Scholar] [CrossRef]

20. di Franco, C., Buttazzo, G. (2016). Coverage path planning for UAVs photogrammetry with energy and resolution constraints. Journal of Intelligent & Robotic Systems, 83(3), 445–462. https://doi.org/10.1007/s10846-016-0348-x [Google Scholar] [CrossRef]

21. da Silva, R. I., Nascimento, M. A. (2016). On best drone tour plans for data collection in wireless sensor network. Proceedings of the 31st Annual ACM Symposium on Applied Computing, pp. 703–708. Italy, University of Pisa. [Google Scholar]

22. Galceran, E., Carreras, M. (2013). A survey on coverage path planning for robotics. Robotics and Autonomous Systems, 61(12), 1258–1276. https://doi.org/10.1016/j.robot.2013.09.004 [Google Scholar] [CrossRef]

23. Di Franco, C., Buttazzo, G. (2015). Energy-aware coverage path planning of UAVs. 2015 IEEE International Conference on Autonomous Robot Systems and Competitions, pp. 11–117. Vila Real, Portugal, IEEE, University of Tras-os-Montes e Alto-Douro (UTAD). [Google Scholar]

24. Király, A., Abonyi, J. (2015). Redesign of the supply of mobile mechanics based on a novel genetic optimization algorithm using google maps API. Engineering Applications of Artificial Intelligence, 38, 122–130. https://doi.org/10.1016/j.engappai.2014.10.015 [Google Scholar] [CrossRef]

25. Ghaddar, A., Merei, A. (2020). EAOA: Energy-aware grid-based 3D-obstacle avoidance in coverage path planning for UAVs. Future Internet, 12(2), 29. https://doi.org/10.3390/fi12020029 [Google Scholar] [CrossRef]

26. Valente, J., Barrientos Cruz, A., del Cerro, J., Sanz Muñoz, D. (2011). A waypoint-based mission planner for a farmland coverage with an aerial robot-A precision farming tool. Proceedings of Precision Agriculture 2011, 427–436. [Google Scholar]

27. Ghaddar, A., Merei, A. (2019). Energy-aware grid based coverage path planning for UAVs. Proceedings of the Thirteenth International Conference on Sensor Technologies and Applications, pp. 34–45. Nice, France. [Google Scholar]

28. Shnaps, I., Rimon, E. (2016). Online coverage of planar environments by a battery powered autonomous mobile robot. IEEE Transactions on Automation Science and Engineering, 13(2), 425–436. https://doi.org/10.1109/TASE.2016.2515165 [Google Scholar] [CrossRef]

29. Afonso, R. J., Maximo, M. R., Galvão, R. K. (2020). Task allocation and trajectory planning for multiple agents in the presence of obstacle and connectivity constraints with mixed-integer linear programming. International Journal of Robust and Nonlinear Control, 30(14), 5464–5491. https://doi.org/10.1002/rnc.5092 [Google Scholar] [CrossRef]

30. Wang, G., Li, Q., Guo, L. (2010). Multiple UAVs routes planning based on particle swarm optimization algorithm. 2010 2nd International Symposium on Information Engineering and Electronic Commerce, pp. 1–5. IEEE. [Google Scholar]

31. Tong, H., Chao, W. W., Qiang, H. C., Bo, X. Y. (2012). Path planning of UAV based on voronoi diagram and DPSO. Procedia Engineering, 29, 4198–4203. https://doi.org/10.1016/j.proeng.2012.01.643 [Google Scholar] [CrossRef]

32. Wang, Z., Liu, Q. Q., Tao, H. T., Li, J. X. (2014). Multiple task planning based on ts algorithm for multiple heterogeneous unmanned aerial vehicles. Proceedings of 2014 IEEE Chinese Guidance, Navigation and Control Conference, pp. 630–635. Yantai, China, IEEE. [Google Scholar]

33. Turker, T., Sahingoz, O. K., Yilmaz, G. (2015). 2D path planning for UAVs in radar threatening environment using simulated annealing algorithm. 2015 International Conference on Unmanned Aircraft Systems (ICUAS), pp. 56–61. Denver, Colorado, USA, IEEE. [Google Scholar]

34. Roberge, V., Tarbouchi, M., Labonté, G. (2012). Comparison of parallel genetic algorithm and particle swarm optimization for real-time UAV path planning. IEEE Transactions on Industrial Informatics, 9(1), 132–141. https://doi.org/10.1109/TII.2012.2198665 [Google Scholar] [CrossRef]

35. Sonmez, A., Kocyigit, E., Kugu, E. (2015). Optimal path planning for UAVs using genetic algorithm. 2015 International Conference on Unmanned Aircraft Systems (ICUAS), pp. 50–55. Denver, Colorado, USA, IEEE. [Google Scholar]

36. Shivgan, R., Dong, Z. (2020). Energy-efficient drone coverage path planning using genetic algorithm. 2020 IEEE 21st International Conference on High Performance Switching and Routing (HPSR), pp. 1–6. IEEE. [Google Scholar]

37. Zhao, C., Liu, Y., Zhao, J. (2014). Path planning method of UAV area coverage searching based on PEGA. Science and Technology Review, 32(22), 85–90. [Google Scholar]

38. Hu, X., Lin, Z. (2019). Coverage path planning of Penaeus vannamei feeding based on global and multiple local areas. International Conference on Data Service. Springer. [Google Scholar]

39. Kennedy, J. (1997). The particle swarm: Social adaptation of knowledge. Proceedings of 1997 IEEE International Conference on Evolutionary Computation (ICEC’97), pp. 303–308. Karachi, IEEE. [Google Scholar]

40. Lee, T. K., Baek, S. H., Choi, Y. H., Oh, S. Y. (2011). Smooth coverage path planning and control of mobile robots based on high-resolution grid map representation. Robotics and Autonomous Systems, 59(10), 801–812. https://doi.org/10.1016/j.robot.2011.06.002 [Google Scholar] [CrossRef]

41. Ahmed, G., Sheltami, T., Deriche, M., Yasar, A. (2021). An energy efficient IoD static and dynamic collision avoidance approach based on gradient optimization. Ad Hoc Networks, 118, 102519. https://doi.org/10.1016/j.adhoc.2021.102519 [Google Scholar] [CrossRef]

42. Tseng, C. M., Chau, C. K., Elbassioni, K., Khonji, M. (2017). Autonomous recharging and flight mission planning for battery-operated autonomous drones. arXiv preprint arXiv:1703.10049. [Google Scholar]

43. Feo, T. A., Resende, M. G. (1995). Greedy randomized adaptive search procedures. Journal of Global Optimization, 6(2), 109–133. https://doi.org/10.1007/BF01096763 [Google Scholar] [CrossRef]

44. Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., Teller, E. (1953). Equation of state calculations by fast computing machines. The Journal of Chemical Physics, 21(6), 1087–1092. https://doi.org/10.1063/1.1699114 [Google Scholar] [CrossRef]

45. Kirkpatrick, S., Gelatt, C. D., Vecchi, M. P. (1983). Optimization by simulated annealing. Science, 220(4598), 671–680. https://doi.org/10.1126/science.220.4598.671 [Google Scholar] [PubMed] [CrossRef]

46. Eglese, R. W. (1990). Simulated annealing: A tool for operational research. European Journal of Operational Research, 46(3), 271–281. https://doi.org/10.1016/0377-2217(90)90001-R [Google Scholar] [CrossRef]

47. Wu, Y., Wang, J. (2018). Algorithm design practice for collegiate programming contests and education, pp. 706. CRC Press. [Google Scholar]