Open Access

ARTICLE

New Perspective to Isogeometric Analysis: Solving Isogeometric Analysis Problem by Fitting Load Function

Jingwen Ren¹, Hongwei Lin^1,2,*

1 School of Mathematical Sciences, Zhejiang University, Hangzhou, 310058, China
2 State Key Lab. of CAD&CG, Zhejiang University, Hangzhou, 310058, China

* Corresponding Author: Hongwei Lin. Email:

(This article belongs to the Special Issue: Integration of Geometric Modeling and Numerical Simulation)

Computer Modeling in Engineering & Sciences 2023, 136(3), 2957-2984. https://doi.org/10.32604/cmes.2023.025983

Received 08 August 2022; Accepted 20 October 2022; Issue published 09 March 2023

Abstract

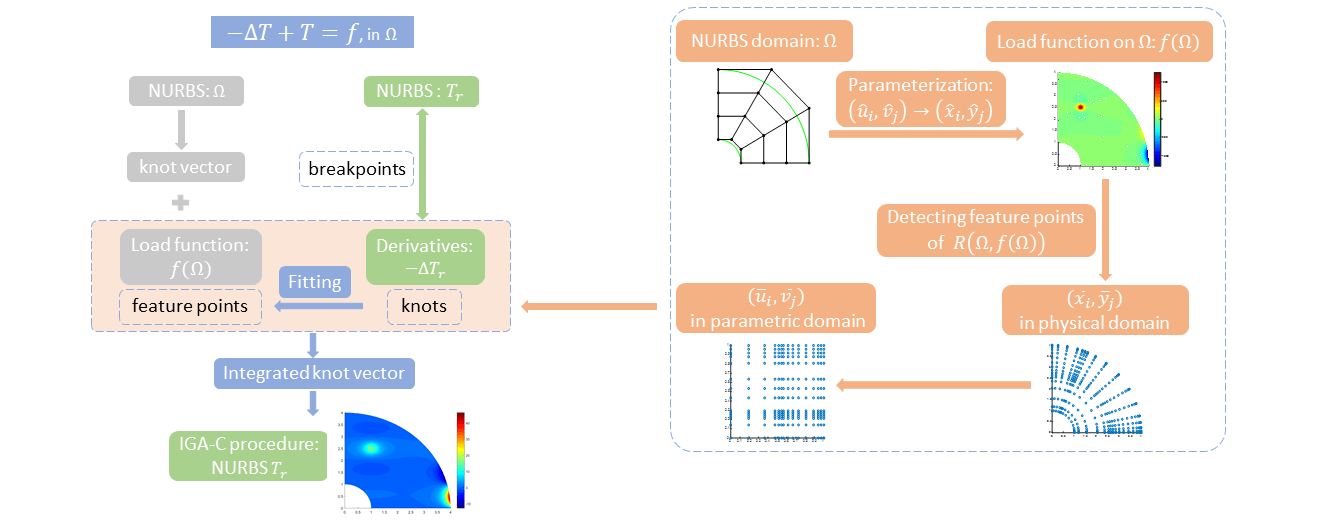
Isogeometric analysis (IGA) is introduced to establish the direct link between computer-aided design and analysis. It is commonly implemented by Galerkin formulations (isogeometric Galerkin, IGA-G) through the use of nonuniform rational B-splines (NURBS) basis functions for geometric design and analysis. Another promising approach, isogeometric collocation (IGA-C), working directly with the strong form of the partial differential equation (PDE) over the physical domain defined by NURBS geometry, calculates the derivatives of the numerical solution at the chosen collocation points. In a typical IGA, the knot vector of the NURBS numerical solution is only determined by the physical domain. A new perspective on the IGA method is proposed in this study to improve the accuracy and convergence of the solution. Solving the PDE with IGA can be regarded as fitting the load function defined on the NURBS geometry (right-hand side) with derivatives of the NURBS numerical solution (left-hand side). Moreover, the design of the knot vector has a close relationship to the NURBS functions to be fitted in the area of data fitting in geometric design. Therefore, the detected feature points of the load function are integrated into the initial knot vector of the physical domain to construct the new knot vector of the numerical solution. Then, they are connected seamlessly with the IGA-C framework for its great potential combining the accuracy and smoothness merits with the computational efficiency, which we call isogeometric collocation by fitting load function (IGA-CL). In numerical experiments, we implement our method to solve 1D, 2D, and 3D PDEs and demonstrate the improvement in accuracy by comparing it with the standard IGA-C method. We also verify the superiority in the accuracy of our knot selection scheme when employed in the IGA-G method, which we call isogeometric Galerkin by fitting load function (IGA-GL).

---

Graphic Abstract

---

Keywords

---