MAQMC: Multi-Agent Deep Q-Network for Multi-Zone Residential HVAC Control

1  Introduction

Nowadays, building energy consumption accounts for 40% of total energy consumption [1], of which HVAC energy consumption takes up 50%, and 30% of all CO2 emissions [2]. The HVAC system, which is the main facility to regulate thermal comfort, is now essential in buildings. It is necessary to study a control strategy to save energy while keeping thermal comfort.

The typical goal in HVAC optimal control is to save energy while maintaining thermal comfort. In the literature, there has been a great deal of research on optimal control strategies for HVAC to achieve the above goal. In HVAC systems, rule-based control (RBC) is an easy-to-implement control method and based on engineer experience. However, RBC cannot learn critical knowledge from historical data to adapt itself. Model predictive control (MPC), a model-based method, has been proposed to deal with the problem of RBC. In [3], the HVAC system is modelled by a grey-box RC-equivalent approach and identified parameters using measurement data extracted directly from the Building Management System, where MPC is used to minimize total cooling effort and energy is saved by 21%. Kumar et al. [4] proposed a stochastic MPC framework for HVAC plants and experimental results showed that stochastic MPC provides a more systematic approach to mitigate uncertainties and that this can save energy by 7.5%. An Artificial Neural Network (ANN) based MPC optimization method was presented in [5] and this method compared with the fixed set-point can save operating cost between 6% and 73% depending on the season.

Model-based methods such as MPC mentioned above need to build an accurate dynamic thermal model of the HVAC to solve the optimal control problem. Accurate modeling requires a large amount of historical data as well as data from sensors collected in real time. Model-based methods inevitably suffer from modeling errors and poor portability to specific models. The above issues are great challenges for the further development of model-based methods.

In recent years, the great progress in computing hardware has led to the development of machine learning techniques such as deep learning and reinforcement learning (RL). Wang et al. [6] proposed a ventilation monitoring and control method based on metabolism to reduce the risk of COVID-19 infection. In [7], Yin et al. applied the deep reinforcement learning method to build an intelligent dynamic pricing system. Wu et al. [8,9] used neural network algorithms to optimize transportation problems. In [10], a rule-based HVAC system uses deep learning to estimate dynamic preconditioning time in residential buildings and the proposed system demonstrates effectiveness over conventional rule-based control. In the power systems field, an intelligent multi-microgrid (MMG) energy management method [11] was proposed based on deep neural network (DNN) and model-free reinforcement learning and this method compared with conventional model-based methods shows the effectiveness in solving power system problems with partial or uncertain information. In [12], an event-driven strategy was proposed to improve the optimal control of HVAC systems. Fu et al. [13] reviewed in detail the application of reinforcement learning in building energy efficiency. Meanwhile, more specifically, model-free deep reinforcement learning (DRL) combining deep learning and reinforcement learning has received tremendous attention in the HVAC optimal control problem. In contrast to model-based methods, model-free DRL requires only the training data generated by the environment, not the exact model. Another advantage of model-free DRL is that it does not require much a priori knowledge, which can be learned from the training data. And the computational cost of DRL is much lower than that of model-based methods. Fu et al. [14] presented a DQN method based on deep-forest to predict building energy consumption. In [15], Gao et al. proposed a DRL based framework, DeepComfort, for thermal comfort control and the proposed method can reduce the energy consumption of HVAC by 4.31% while improving the occupants’ thermal comfort by 13.6%. However, they still focus on single-zone HVAC control and use a single agent to accommodate multiple setpoints. Although the DRL approach has many advantages, for multi-zone residential HVAC control, single-agent DRL may present the following problems. A single agent to control setpoints in multiple zones not only increases the computational cost, but also has the potential for non-convergence.

Motivated by the above issues, this study applies MAQMC (Multi-Agent deep Q-network for Multi-zone residential HVAC Control) to optimize the thermal comfort control of the multi-zone HVAC combination of temperature and humidity. It aims to minimize energy consumption under the condition of satisfying occupants’ thermal comfort requirements in multi-zone HVAC systems. Our proposed approach also provides the theory and technology to reduce carbon emissions in terms of energy efficiency and comfort in buildings. The main contributions of this paper are summarized as follows:

(1)   We apply multi-agent reinforcement learning to optimize multi-zone residential HVAC control. Since multi-zone HVAC has complex thermal dynamics, personnel occupancy changes, and a high-dimensional action space, we use the proposed MAQMC to solve the above problems. Then, we formulate the multi-zone residential HVAC control problem as the RL problem including state, action, and reward function.

(2)   We compare MAQMC and single-agent DQN to demonstrate the effectiveness of MAQMC in multi-zone HVAC control with a high-dimensional action space; we also compare the performance of MAQMC2 (MAQMC with two agents) and MAQMC3 (MAQMC with three agents) as well as design benchmark cases without RL and compare them, experimentally showing that MAQMC3 has a faster convergence speed and slightly higher performance than MAQMC2 and MAQMC can get more energy saving while maintaining thermal comfort compared with benchmark cases.

(3)   We verify that the well-trained MAQMC has high adaptability as well as robustness under different regional weather.

The rest of the paper is organized as follows. Section 2 surveys the related works. Section 3 introduces the theoretical background of RL and multi-agent RL; the HVAC control problem formulation is introduced in Section 4; details of simulation implementation and the simulation results of the MAQMC are presented in Section 5, plus a comparison with the single-agnet DQN and benchmark cases; finally, Section 6 concludes the paper.

2  Related Works

There has been pioneering work using DRL methods applied to HVAC systems. In [16], DRL is applied to optimize the problem of the supply water temperature setpoint in a heating system and the well-trained agent can save energy between 5% and 12%. Achieving energy savings from optimizing HVAC control equates to cost savings. Jiang et al. [17] proposed Deep Q-network (DQN) with an action processor, saving close to 6% of the total cost with demand charges, while close to 8% without demand charges. Du et al. [18] implemented DRL methods to address the issue of 2-zone residential HVAC control strategies that allow for the lower bound of the user comfort level (temperature) with energy savings. In [19], performance-based thermal comfort control (PTCC) based on DQN was proposed to minimize energy consumption while satisfying thermal comfort conditions. In [20], Zhang et al. proposed a practical control framework (named BEM-DRL) based on deep reinforcement learning and the proposed BEM-DRL can reduce the energy consumption of HVAC by 16.7% with more than 95% probability compared to the old rule-based control.

All of the above research work demonstrates the effectiveness of DRL approaches compared with the benchmarks they have designed for HVAC optimal control. Although Du et al. [18] have addressed the multi-zone HVAC control problem, their control object is only the set-point of temperature. In [21], Nagarathinam et al. use a multi-agent deep reinforcement learning method to control air-handling-units (AHUs) and chillers. They mainly consider the cooling side to save energy and maintain comfort. Kurte et al. [22] used Deep Q-Network (DQN) to meet residential demand response and compared it to the model-based HVAC approach. Fu et al. [23] proposed a distributed multi-agent DQN to optimise HVAC systems. Cicirelli et al. [24] used DQN to balance energy consumption and thermal comfort. Kurte et al. [25,26] applied DRL in residential HVAC control to save costs and maintain comfort.

In summary, DRL methods have been heavily applied in HVAC control in recent years. However, multi-agent reinforcement learning (MARL) was less studied in the optimal control of multi-zone residential HVAC, and we take this opportunity to discuss the robustness and adaptability of related techniques in this area.

3  Theoretical Background of RL and Multi-Agent RL

3.1 Reinforcement Learning (RL)

RL is trial-and-error learning by interacting with the environment [27]. From Fig. 1, The agent gets the current state from the environment and then it takes actions to influence the environment. The environment gives the agent the reward. The goal of RL is to maximize the cumulative reward in the environment interaction. The RL problem can be formulated as a Markov Decision Process (MDP), which includes a quintuple ⟨𝒮,𝒜,ℛ,𝒫,γ⟩. MDP is shown in Fig. 2.

(1)   𝒮 represents the state space, st∈𝒮 indicates the state of the agent at time t.

(2)   𝒜 is the action space, at∈𝒜 represents the action taken by the agent at time t.

(3)   ℛ: 𝒮×𝒜→R is the reward function, rt indicates the immediate reward value obtained by the agent executing the action at in the state st.

(4)   𝒫: 𝒮×𝒮×𝒜→[0,1] is state transition probability distribution function satisfying the Markov property p(st+1|s1,a1,…,sT,aT)=p(st+1|st,at).

(5)   γ is the discounted factor. γ is used to weighten the impact of the future reward.

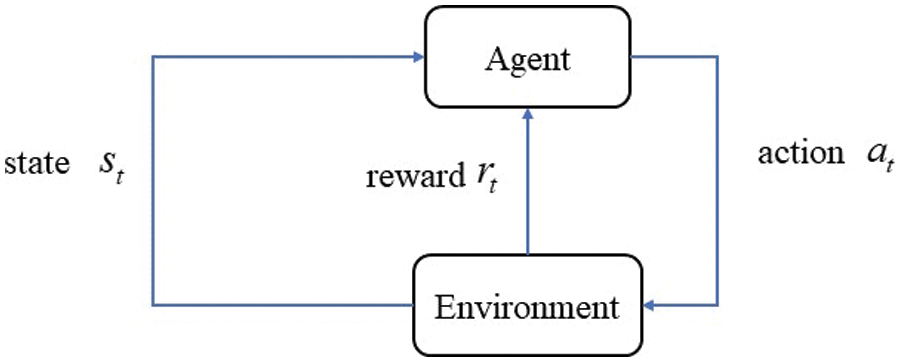
Figure 1: RL agent-environment interaction

Figure 2: Model structure diagram of an MDP

In the MDP model, a RL agent decides which action to take, and this action follows a policy that is π:𝒮×𝒜→[0,1]. π(at|st) represents the probability of selecting at in st. The return Gt is the total discounted reward from time-step t: Gt=∑k=tTγk−trk. The state value function and the state action value function are defined as Vπ(s)=E[Gt|St=s;π] and Qπ(s,a)=E[Gt|St=s,At=a;π].

3.2 Deep Q-Network (DQN)

DQN is a typical DRL method based on value function. Volodymyr et al. [28] combined the convolution neural network with traditional Q-learning and proposed a deep Q-network model to handle high-dimensional state inputs. Convolutional neural networks can also be replaced by deep neural networks. In DQN, the input is current state and the output is Q-value for each potential action at the current state. DQN parameterizes the state action value function Qπ(s,a) by a nonlinear neural network, and updates the neural network parameters to approximate the optimal state action value function Q∗(s,a). We use Q(s,a;ω), where ω repesents the estimated parameters, to denote the parameterized value function. However, it is usually not convergent to use a nonlinear function approximation for the value function in RL. To address the above issues, experience replay mechanism and two neural networks are used in the DQN. One is the target network Q(s,a;ω′) and the other is the online network Q(s,a;ω). Yj=r+maxa′Q(s′,a′;ω′) is used to approximately represent the optimization objective of the value function. The loss function is as follows:

L(ω)=Es,a,r,s′[(Yj−Q(s,a;ω))2].(1)

The online network Q(s,a;ω) is updated in real time. The target network Q(s,a;ω′) can be copied from the online network Q(s,a;ω) after N rounds. We can differentiate ω in Eq. (1), and the gradient is as follows:

∇ωL(ω)=Es,a,r,s′[(Yj−Q(s,a;ω))∇ωQ(s,a;ω)].(2)

3.3 Multi-Agent Reinforcement Learning (MARL)

As the name implies, there are multiple agents interacting with the environment together, and these agents work together to learn the optimal policy. A multi-agent MDP is composed of the tuples <N,𝒮,𝒜ii∈N,ℛii∈N,𝒫,γ>, where N represents the number of agents, 𝒮 is the environment state,𝒜i represents the set of actions of agent i, 𝒫 is the state transition probability distribution function, ℛi is the reward function of agent i, and γ is the discount factor.

Generating an optimal joint strategy for MARL is difficult when multiple agents are learning in a non-stationary environment. There is a large amount of MARL research today to address such problems. In this study, we use a distributed MARL with cooperation mechanism [29]. In a distributed cooperative multi-agent, agents share rewards among them, i.e., r1=r2=⋯=rN. The structure of a distributed MARL with cooperation mechanism is shown in Fig. 3.

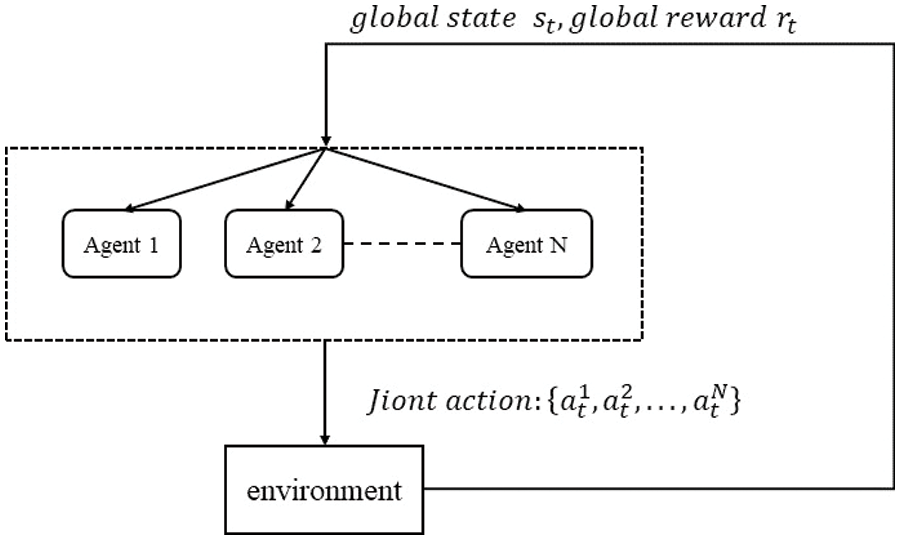
Figure 3: MARL

4  Multi-Zone Residential HVAC System Control Problem Formulation

4.1 Optimization Control Problem

In this study, we consider a residential apartment with multiple zones. Firstly, we give a brief introduction of multi-zone residential HVAC system control problem. The goal of the HVAC control is to minimize energy consumption while keeping thermal comfort within the comfort band. When there is a difference between indoor temperature and humidity and the set point, the HVAC system will be turned on to push the indoor temperature and humidity closer to the set point to meet the comfort level of the user. In this paper, we consider HVAC systems being utilized for cooling without loss of generality.

In optimization control problems, we need to consider not only the energy consumption but also the thermal comfort of the user. Thermal comfort is usually influenced by many factors such as temperature, humidity, wind speed, thermal radiation and clothing. Generally speaking, temperature and humidity are two factors that are easier to consider and measure in real time. Fanger [30] proposed a Predicted Mean Vote-Predicted Percentage Dissatisfied (PMV-PPD) thermal comfort model to express people’s satisfaction with the environment. The value of PPD ≤10 is considered acceptable according to the ASHRAE 55-2017 [31]. The range of PMV is [−3,3], where −3 stands for cold, 3 for hot, and 0 for moderate. In this work, we use a Python package in [32] to calculate PMV and PPD. We consider PMV and PPD together to maintain thermal comfort of the occupants. We use the PMV-PPD model that takes as inputs room temperature, room humidity, average air velocity, metabolic rate, and clothing insulation, and outputs the PMV-PPD values. The average air velocity, metabolic rate and clothing insulation are set to general default values of 0.1, 1.1 and 0.5.

4.2 Mapping Multi-Zone Residential HVAC Control Problem into Markov Decision Process (MDP)

In this section, we formulate the multi-zone residential HVAC control problem as an MDP which can be solved by deep RL algorithms. Because of the complex thermal dynamics of HVAC, it is difficult to obtain the state transition probability 𝒫. As a result, we need model-free DRL methods to solve the optimal control problem. The model-free DRL method does not require any prior knowledge of the environment or 𝒫 in advance. If 𝒫 is known, we can solve it using model-based RL methods such as dynamic programming, which becomes a planning problem. In this paper, an MDP mainly includes state, action and reward functions, which can be defined as follows:

1)   State space

The state space includes: 1) current outdoor temperature Tout(t); 2) current outdoor relative humidity RHout(t); 3) current indoor temperature Tin,Roomk(t) for Room1, Room3 and Room5; 4) humidity ratio Hrin,Roomk(t) for Room1, Room3 and Room5; 5) the lower bound of the comfort |PMVRoomk(t)| and PPDRoomk(t) for Room1, Room3 and Room5; 6) current electricity price price(t), where t is the current time step.

Note that the state space includes the lower bound of the comfort |PMVRoomk(t)| and PPDRoomk(t), which change with time. This is reasonable when the room is occupied, the indoor comfort needs to be maintained at a higher level than when the room is not occupied. It is necessary to lower the range of user comfort to save energy during working hours. The state space also includes the current electricity price price(t). It is also necessary to reduce the cost while meeting the lower bound of comfort.

2)   Action space

The action space shown in Table 1 includes temperature set-points and relative humidity set-points in Room1, Room3 and Room5. In DQN, the action space is discrete, so this study discretizes the range of temperature setpoints and relative humidity set-points respectively with a step size of 0.5∘C and 5%. If there is only one agent, there will be 157464 action combinations. Using a single agent DQN algorithm is difficult to converge due to the above 157464 action combinations.

3)   Reward function

To minimize energy consumption under the condition of satisfying thermal comfort requirements, we define the reward function as:

rewardRoom1(t)={α∗(|PMVRoom1|+PPDRoom1)+β∗QtRoom1,ifPMVandPPDmeetcurrentpenalty,requirements,otherwise(3)

rewardRoom3(t)={α∗(|PMVRoom3|+PPDRoom3)+β∗QtRoom3,ifPMVandPPDmeetcurrentpenalty,requirements,otherwise(4)

rewardRoom5(t)={α∗(|PMVRoom5|+PPDRoom5)+β∗QtRoom5,ifPMVandPPDmeetcurrentpenalty,requirements,otherwise(5)

rt=−(rewardRoom1(t)+rewardRoom3(t)+rewardRoom5(t))/153,(6)

where rewardRoom1(t), rewardRoom3(t), and rewardRoom5(t) respectively represent the rewards obtained by agents from Room1, Room3 and Room5 at time t. QtRoomk represents the cost spent at time t. 153 represents the number of days of training. The reward function is closely related to thermal comfort and energy consumption. The thermal comfort we represent by considering PMV and PPD together. Taking into account the occupancy, we set weighting coefficients α and β to reflect whether to focus on considering thermal comfort or energy consumption. penalty we set is 50. Also taking into account the occupancy in a room, we set different ranges for PMV and PPD in three rooms. The higher the comfort, the closer the absolute value of PMV is to 0, and the smaller the value of PPD.

4.3 MAQMC-Based Control Strategy for Multi-Zone HVAC System

In this section, we detail the proposed MAQMC algorithm. MAQMC follows a similar process to that of the DQN. MAQMC can be divided into MAQMC2 and MAQMC3 as shown in Algorithm 1. These two algorithms are further explained as follows:

:

MAQMC2: In the MAQMC2, we use two agents: one to control the temperature set-points in three zones and the other to control the humidity setpoints. First, the online network Qn is randomly initialized for each agentn, and their corresponding target networks Qn′ are initialized with the same parameters, as shown in lines 1–3. In line 4, replay buffer Dn is also initialized. Starting from line 6, for each episode, the agents can obtain the initial state s0(Tout(0),RHout(0),Tin,Roomk(0),Hrin,Roomk(0),|PMVRoomk(t)|,PPDRoomk(t),price(t)), then HVAC control action, i.e., set-points of the temperature and humidity, is chosen based on the online network Qn by ε−greedy policy, as shown by lines 9 and 10. Next, in line 11, the selected action is executed in the environment so that RL agents get the reward rt from the reward function we set as well as the next state st+1. The transition (st,atn,rt,st+1) is stored in replay buffer Dn. When the number of transitions reaches the limit we set, a small-batch of transitions is randomly selected to calculate Yjn, as shown in lines 13 and 14. Randomly selected transitions can break the temporal correlation, making it possible to satisfy the condition that the data for machine learning obeys independent identical distribution. The parameters of the online network Qn are updated by the mean square error of Yjn with respect to the Q value of the online network in line 15. After C steps, the parameters of the online network Qn are copied to the target network Qn′, as shown by line 16.

MAQMC3: In the MAQMC3, we use three agents: the agent, which controls the temperature setpoint and humidity setpoint, is deployed in each zone. The training process of MAQMC3 is similar to the that of MAQMC2. It mainly differs from MAQMC2 in that the joint action of the agents is different.

The control interval of RL agents is one hour. Since we only focus on the HVAC cooling, the weather data from May to September in Changsha is used as the training data. During the training period, May to September is defined as an episode. In 50 episodes are simulated for RL agents to learn. After training, we use weather data from two different regions as test data to verify the adaptability and robustness of the proposed MAQMC.

5  Case Study

In this section, a multi-zone residential HVAC model is used to demonstrate the effectiveness of the applied MAQMC-based control method, as well as by comparison with the single-DQN-based control method and the benchmark cases, to fully verify the advantages of the MAQMC method.

5.1 Simulation Environment

In this study, we use a multi-zone residential HVAC model [33] with real-world weather data [34] to train and test the proposed MAQMC. The plain layout of the residential HVAC model which has five zones and three occupants is shown Fig. 4. The layout of the residential apartment is identified from multi-level residential buildings in Chongqing, China.

Figure 4: Plain layout of the 3-occupant apartment

Considering whether the room is occupied and how many occupants there are at different moments, the specific schedule is shown in Table 2. As the toilet and kitchen are occupied only under specific circumstances, these two rooms are not considered for the time being. When Room1, Room3 and Room5 are occupied, there are 2 occupants, 1 occupant and 3 occupants, respectively. Agents control the set points of temperature and humidity in each room, so that when the room is occupied, it can save energy while maintaining thermal comfort, and pay more attention to energy saving when it is unoccupied. The specific simulation process is shown in Fig. 5. Firstly, the PMV and PPD of the three rooms are calculated by the indoor temperature and relative humidity. Then, judge whether rooms are occupied and whether PMV and PPD are within the set range to get the reward. Agents get the state and the reward to learn continuously, and finally get the optimal strategy.

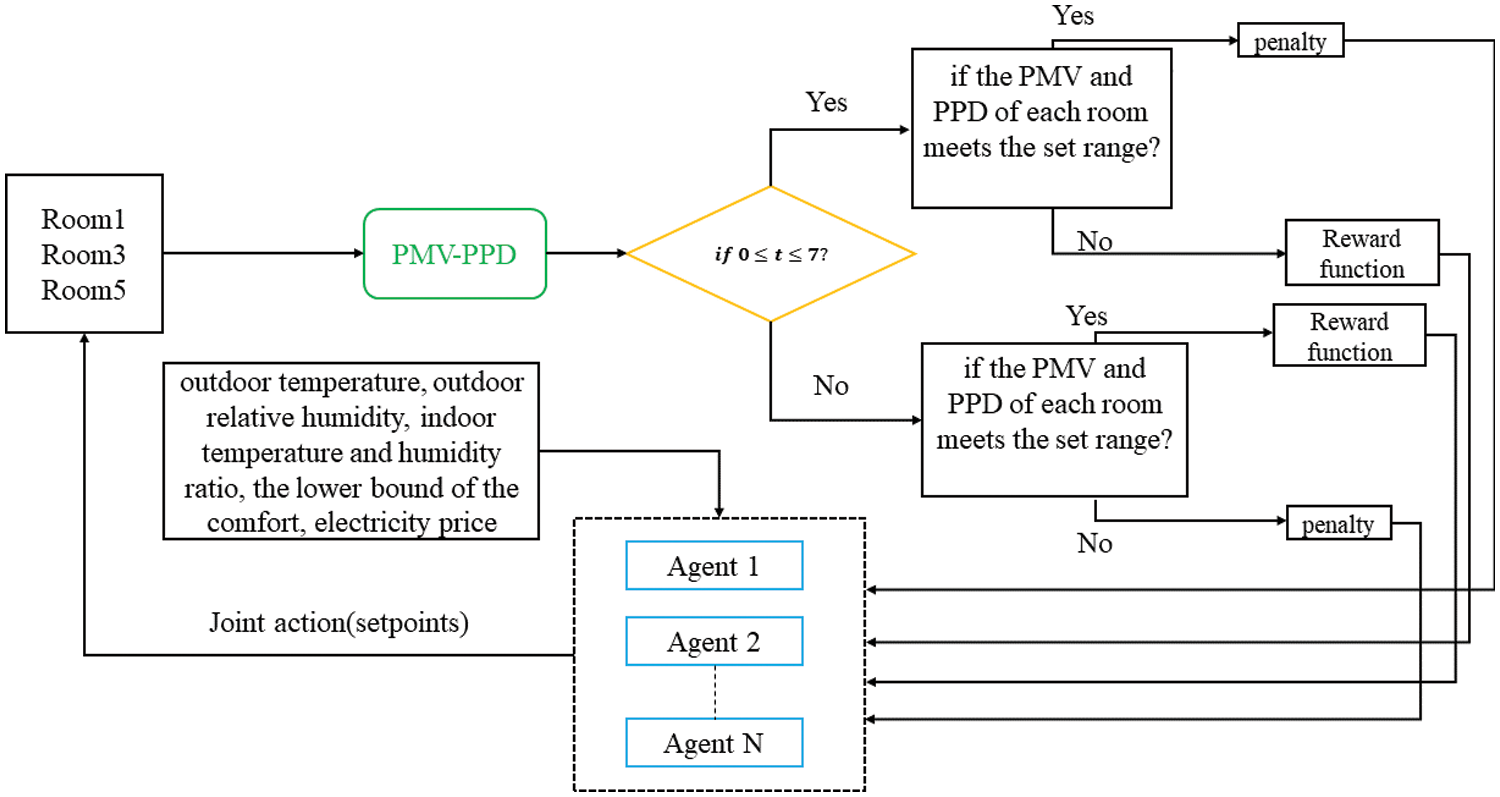
Figure 5: The simulation process

5.2 Implementation Details

The detailed design of networks and hyperparameters in the MAQMC are shown in Table 3. The design of the DQN is also listed for comparison. The input of MAQMC and DQN is a vector containing state variables. Since the DQN requires a discrete action space, we discretize the range of temperature setpoints and relative humidity set-points respectively with a step size of 0.5∘C and 5%. Therefore, there are 54 actions for each zone and 157464 combinations of actions for the 3-zone HVAC. In MAQMC2, agent 1 contains 729 actions of temperature and agent 2 contains 216 actions of humidity. As a result, the outputs of agent 1 and agent 2 in MAQMC2 are vectors respectively containing 729 Q values and 216 Q values. In MAQMC3, the agent in each zone contains 54 actions of temperature and humidity. The output of each agent in MAQMC3 is a vector containing 54 Q values.

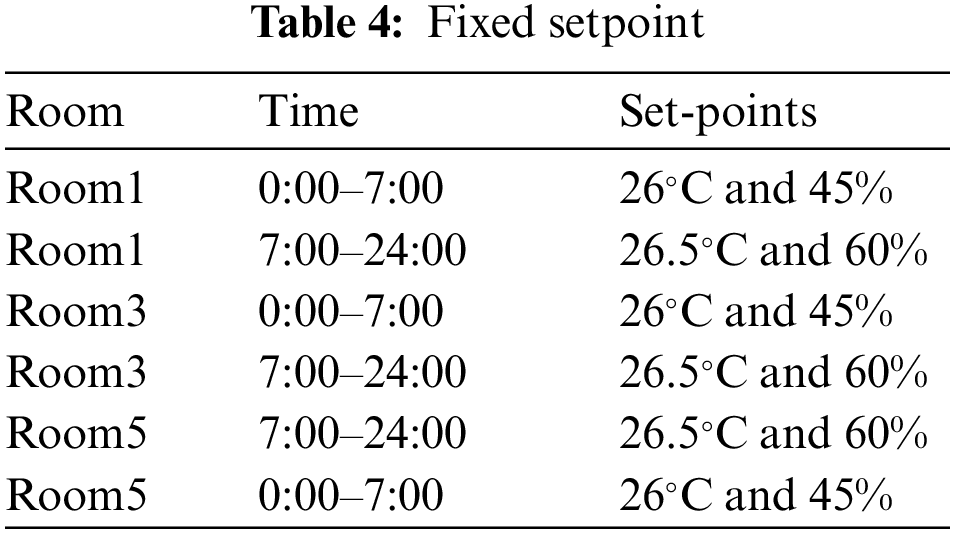
In this study, we similarly design two benchmark cases without the RL agent described as follows: (1) Fixed setpoint case is shown in Table 4. The setpoints are set at values that more comfort-oriented values; (2) Rule-based case is shown in Table 5. The setpoints are set at values that favor energy efficiency at peak price hours, and more comfort-oriented values at non-peak price hours.

5.3 Performance of the MAQMC

5.3.1 Convergence of the MAQMC

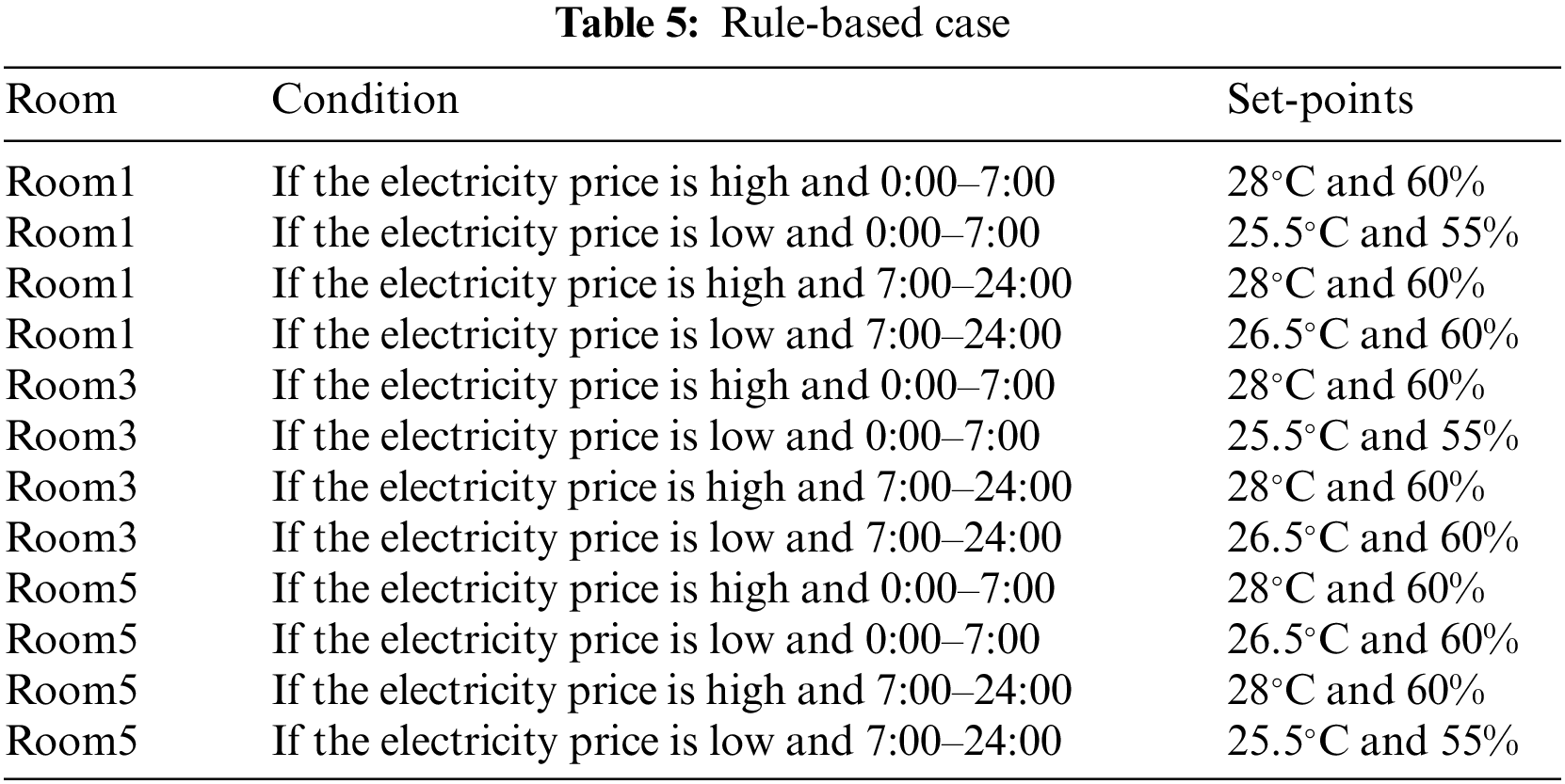
The rewards obtained after each episode for MAQMC2, MAQMC3 and single-DQN are presented in Fig. 6 during training. We conduct five independent experiments on MAQMC2 and MAQMC3, respectively. We take the months of May to September as a training episode. Notice that the reward for single-DQN is not convergent and the rewards for both MAQMC2 and MAQMC3 converge. This is because it is difficult for single-DQN to select the optimal action among 157464 action combinations in a limited amount of time. MAQMC can then greatly reduce the space of action combinations, allowing for collaborative cooperation among each agent to solve complex control problems. From Fig. 6, MAQMC3 converges faster than MAQMC2, and its reward is somewhat higher than that of MAQMC2. The reward of MAQMC3 tends to converge after 7 episodes, while that of MAQMC2 begins to converge after 10 episodes. In MAQMC3, there are three agents such that the action space of each agent will be smaller than that of the two agents in MAQMC2. Therefore, MAQMC3 will learn faster than MAQMC2. The reward of MAQMC3 is higher than that of MAQMC2 because some of the selected actions in MAQMC2 may be suboptimal while learning.

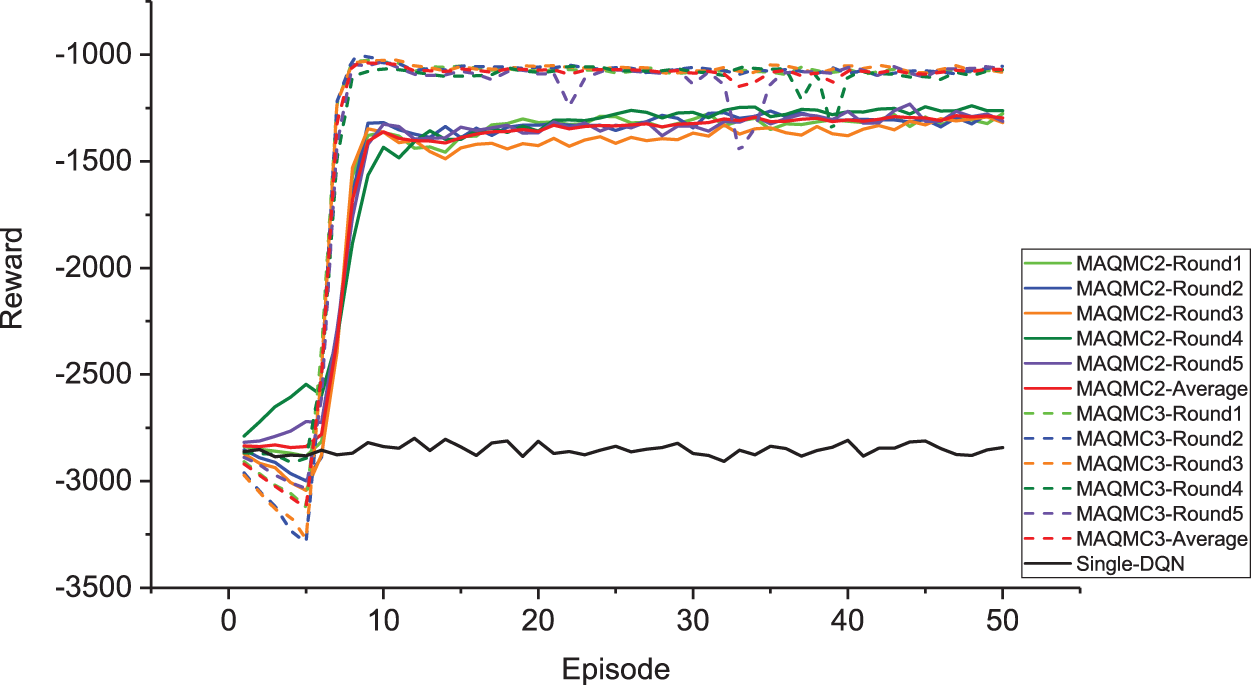
Figure 6: The rewards of MAQMC2, MAQMC3 and single-DQN

5.3.2 Computational Efficiency

In both the training process and the testing process, the code is written in Python 3.7 with the open source deep learning platform pytorch 1.6 [35]. The time cost is around a few minutes for testing, which is highly time-efficient. The hardware environment is a desktop with an Intel(R) Core(TM) i5-10400F 2.9 GHz CPU and 8.00 GM RAM.

5.3.3 Comparison of the MAQMC with the Benchmark Cases under Different Weather Data

a)   Overall evaluation of energy consumption, cost and thermal comfort of the four methods

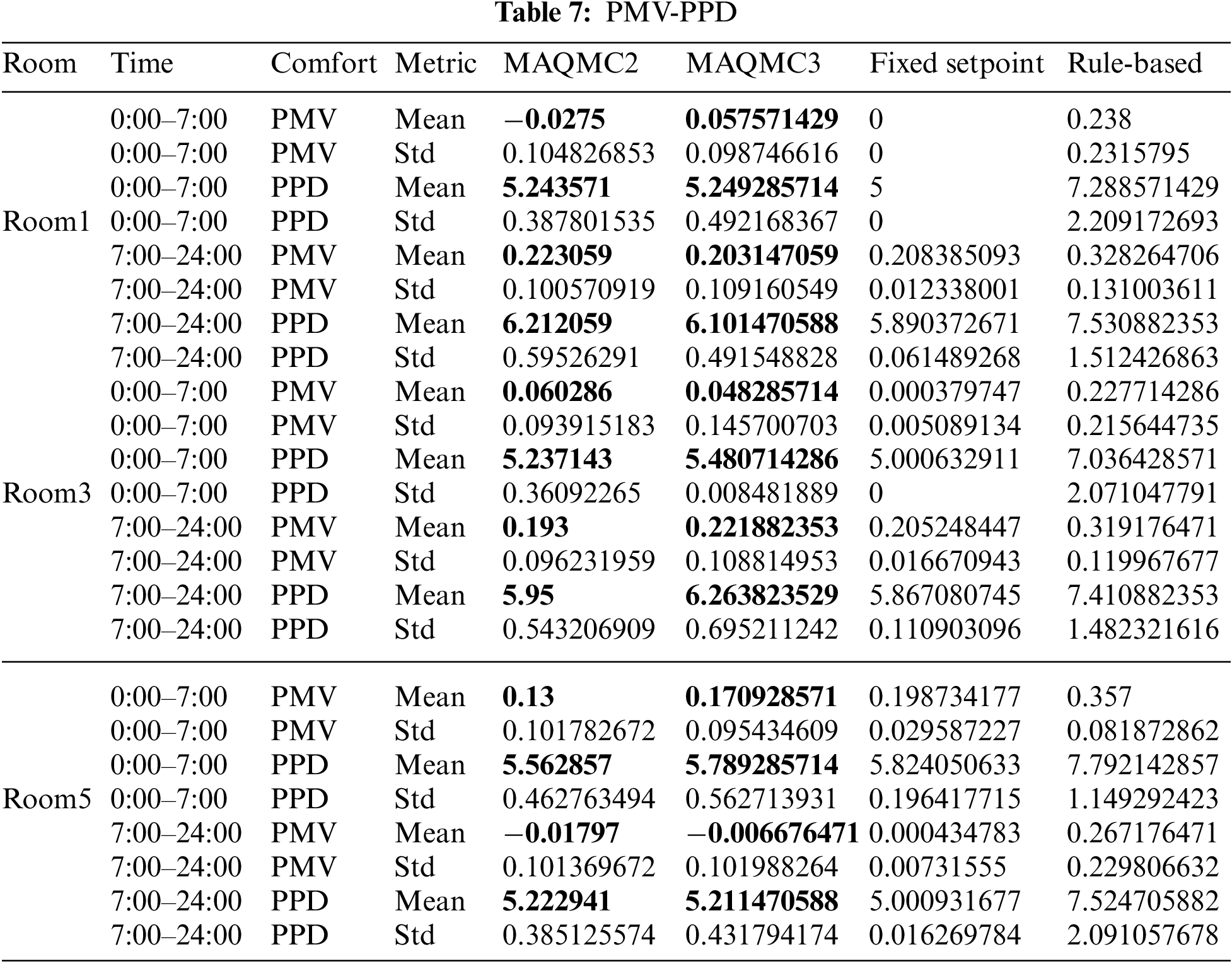
In this work, the well-trained RL agents from MAQMC2 and MAQMC3 are applied in new test days to verify their learning performance and adaptability. We compare MAQMC with benchmark cases in terms of energy consumption and thermal comfort. The final optimized test results of the MAQMC and the benchmark cases are shown in Table 6. Energy consumption and total cost are further shown in Fig. 7. In Table 6, the well-trained RL agents from MAQMC2 and MAQMC3 are applied to generate the HVAC control strategies for the test 20 days from July 01 to July 20 in Chongqing. The weather conditions on the test days are different from those on the training days, because the outdoor temperature in Chongqing is higher than that in Changsha in summer. Energy consumption in the table represents the total energy consumption on the test day, and the total cost involves the total energy cost over the 20 days. Average comfort violation in a day indicates on the average number of hours per day in violation of thermal comfort. As shown in the table, the control strategy generated by MAQMC3 has less energy consumption, lower cost and fewer average comfort violation than those of MAQMC2. With respect to benchmark cases, in the fixed setpoint case, the setpoints are always set to be biased towards comfort to avoid any comfort violation. However, the fixed setpoint case has the highest energy consumption and total cost. In the rule-based case, because it follows the electricity price structure, it has the lowest energy consumption and total cost among the four methods. Since the setpoints are always set in favor of energy saving at peak price hours, its comfort violation is the highest. The indoor temperature and humidity ratios of the three zones are shown in Figs. 8–13. PMV-PPD in each zone is further illustrated in Figs. 14–16.

b)   Control performance of MAQMC for PMV-PPD in three rooms under price signals

From Figs. 8–13, the indoor temperature and humidity ratio change at a daily cycle. From Figs. 8 and 14, indoor temperature in Room1 is basically controlled between 25∘C and 27.5∘C based on the MAQMC. From 0:00 to 7:00, PMV in Room1 is more biased towards the positive interval based on MAQMC3. However, based on MAQMC2 is more biased towards the negative interval. Therefore, MAQMC3 is better than MAQMC2 in reducing energy costs. From 7:00 to 24:00, PMV at some moments violates the comfort range we set, which may be due to the fact that MAQMC makes the setpoint more biased towards better comfort at off-peak price hours. Throughout the day, PPD in Room1 remains within the comfort range based on the MAQMC. In the rule-based case, since the rule-based control is with the price structure, if the electricity price is high at this moment and the outdoor temperature is high, which can lead to severe comfort violation, as shown in Fig. 14. Finally, in the fixed setpoint case, since the setpoint is always biased towards comfort, the comfort level in the room is kept at the highest level in the four cases. However, this fixed setpoint case leads to the highest energy consumption and cost.

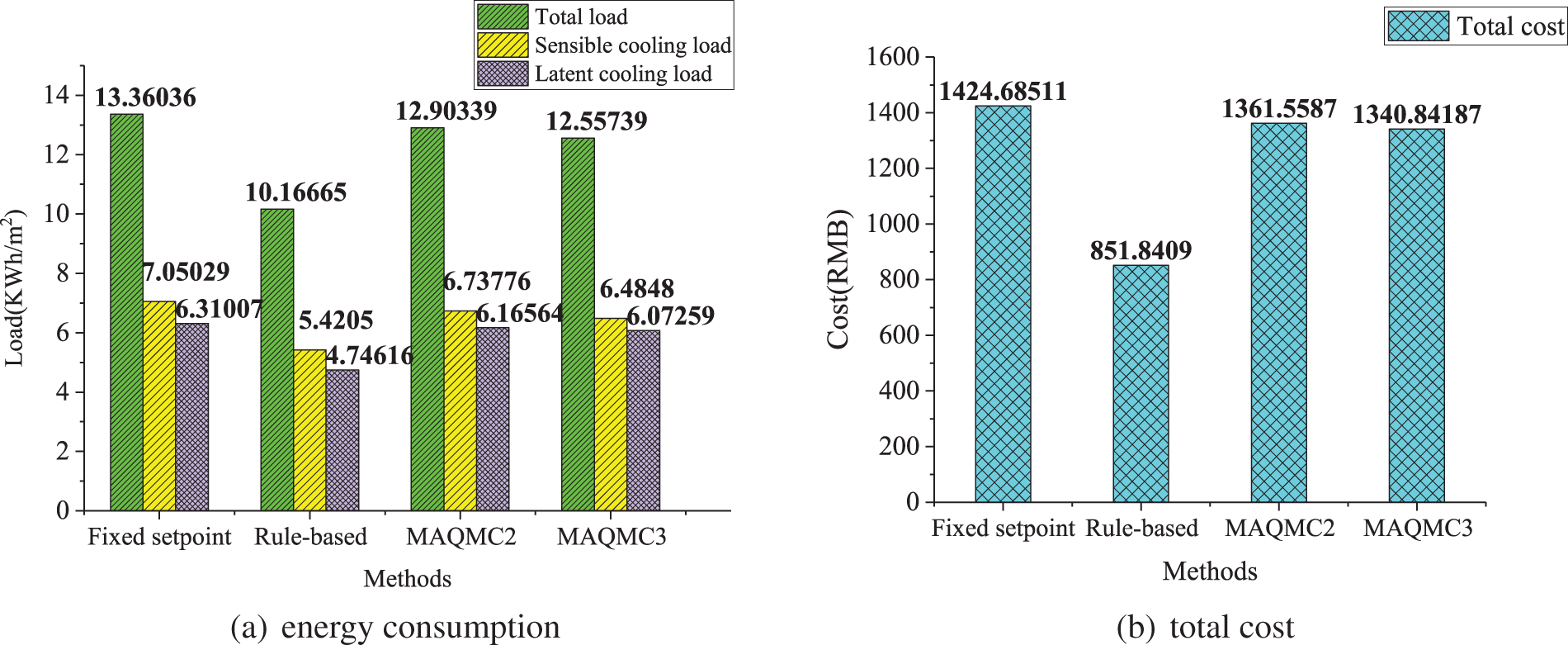
Figure 7: Comparison of energy consumption and cost

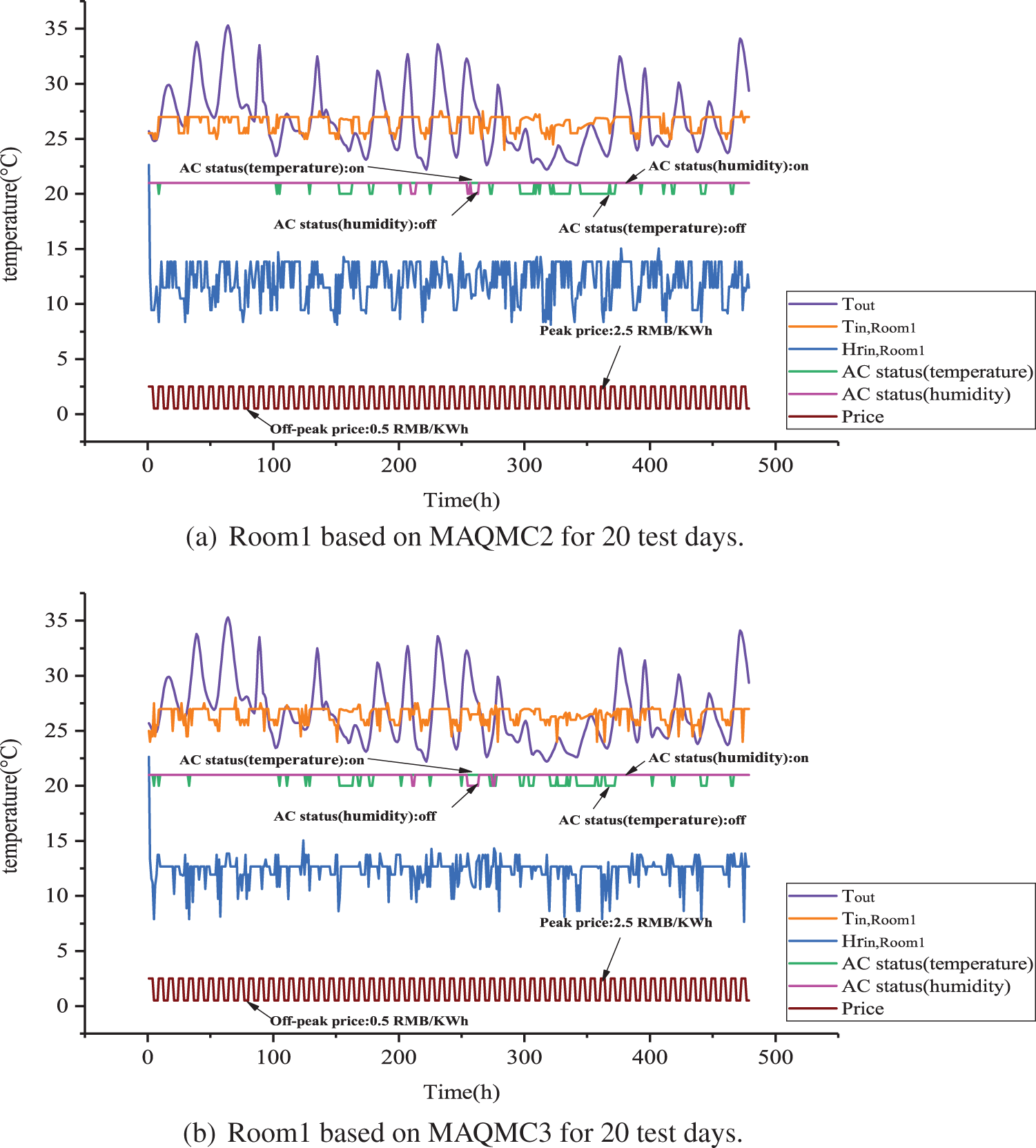
Figure 8: Room1 based on MAQMC and benchmark cases for 20 test days

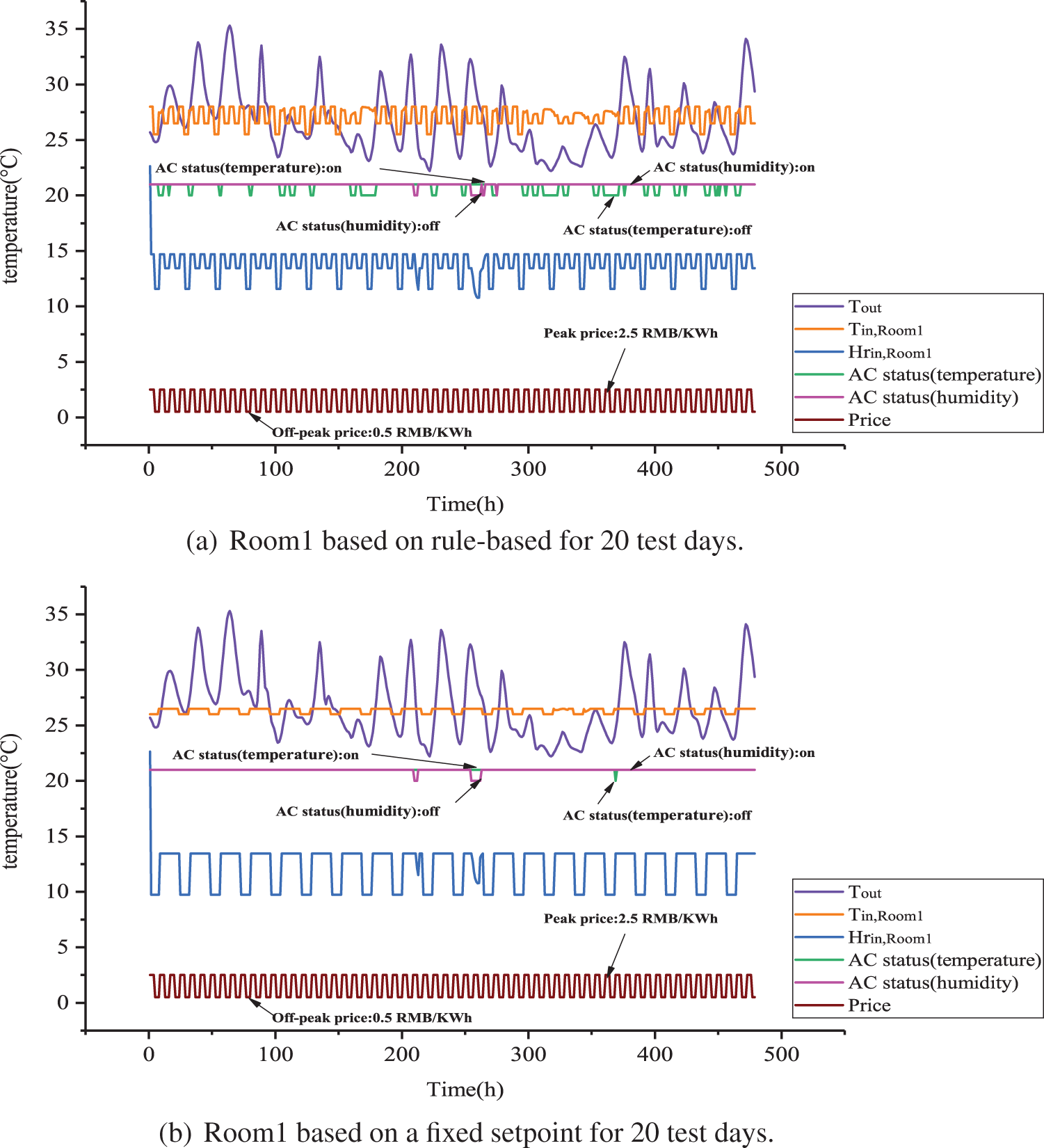
Figure 9: Room1 based on MAQMC and benchmark cases for 20 test days

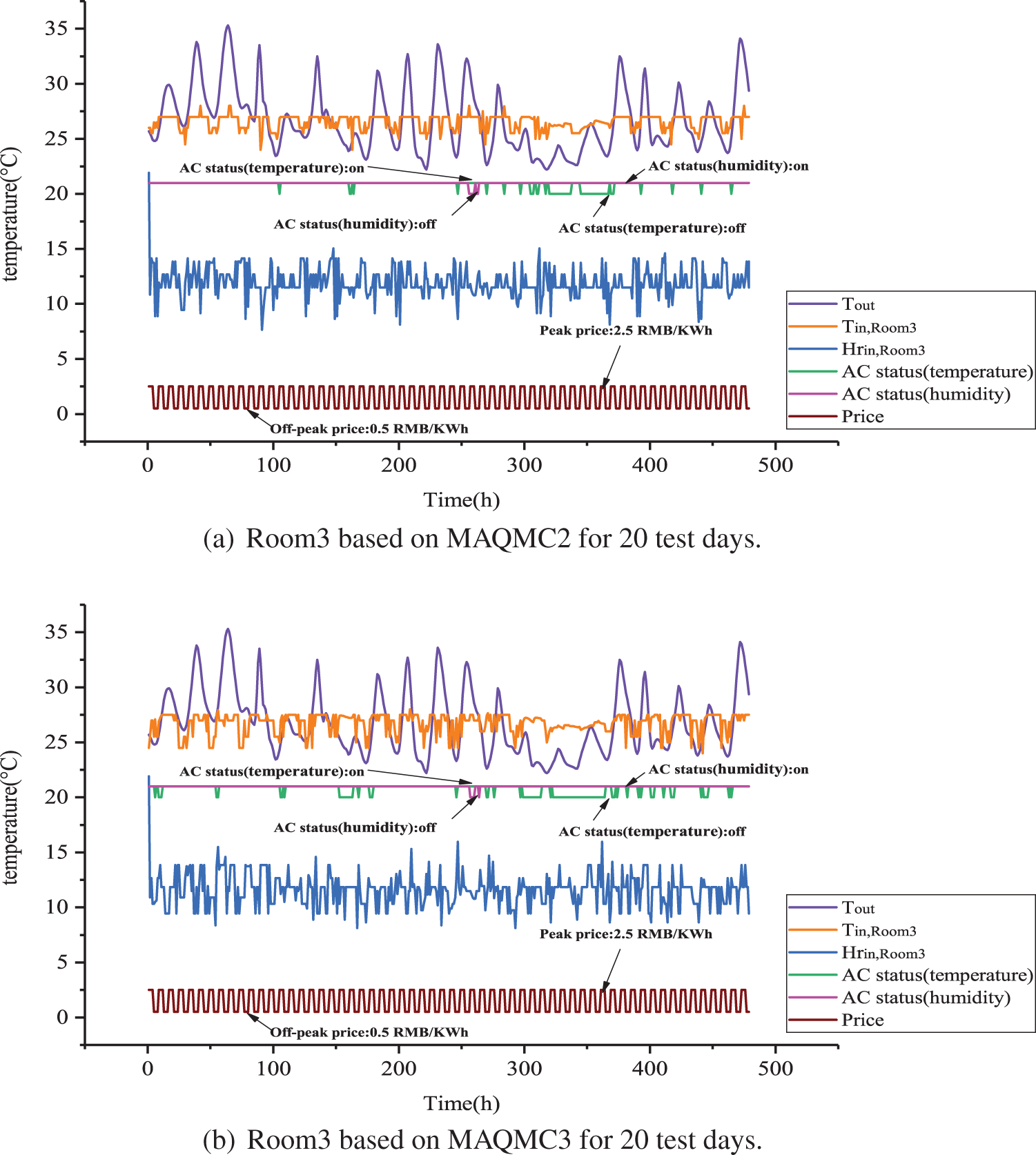
Figure 10: Room3 based on MAQMC and benchmark cases for 20 test days

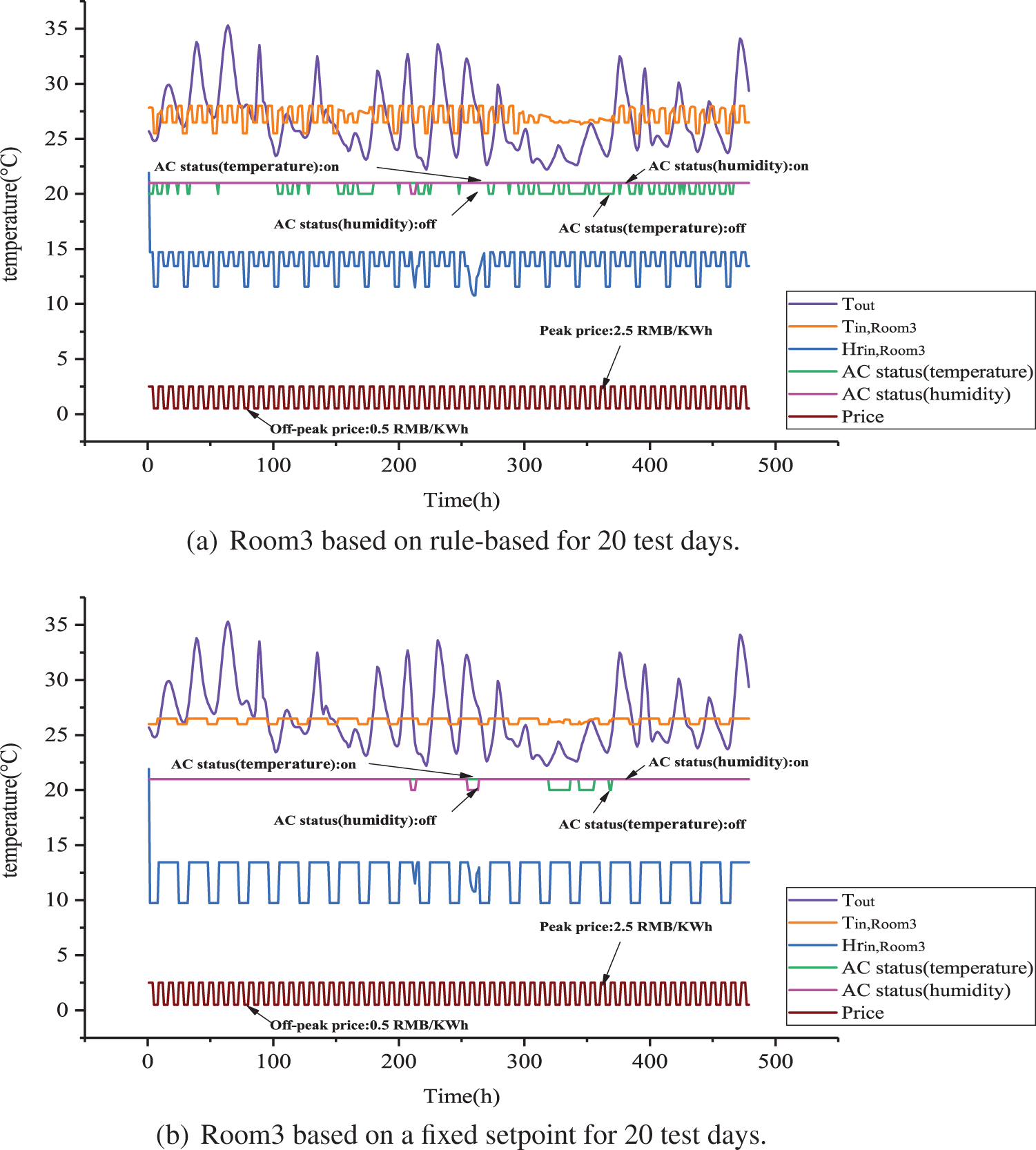
Figure 11: Room3 based on MAQMC and benchmark cases for 20 test days

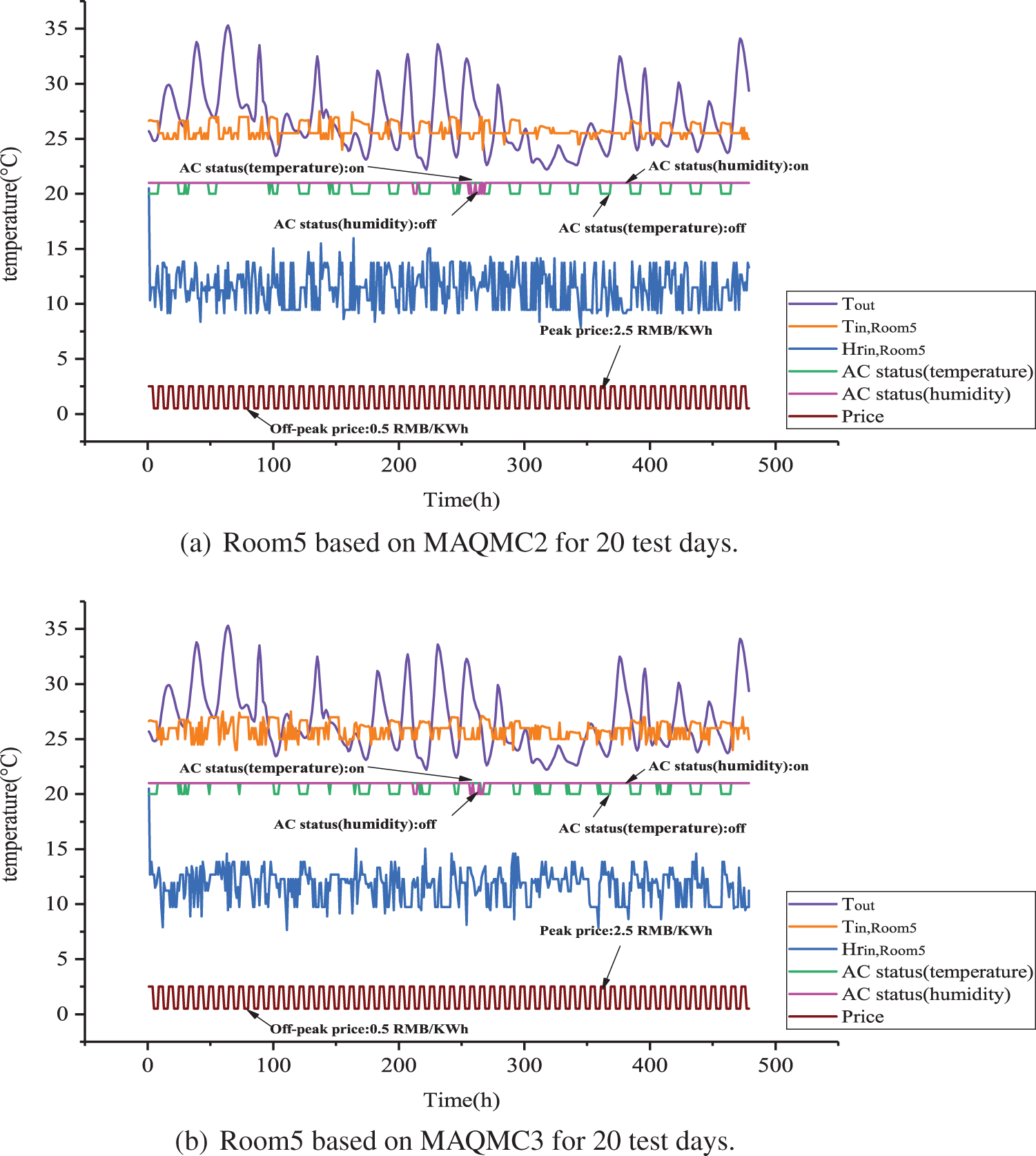
Figure 12: Room5 based on MAQMC and benchmark cases for 20 test days

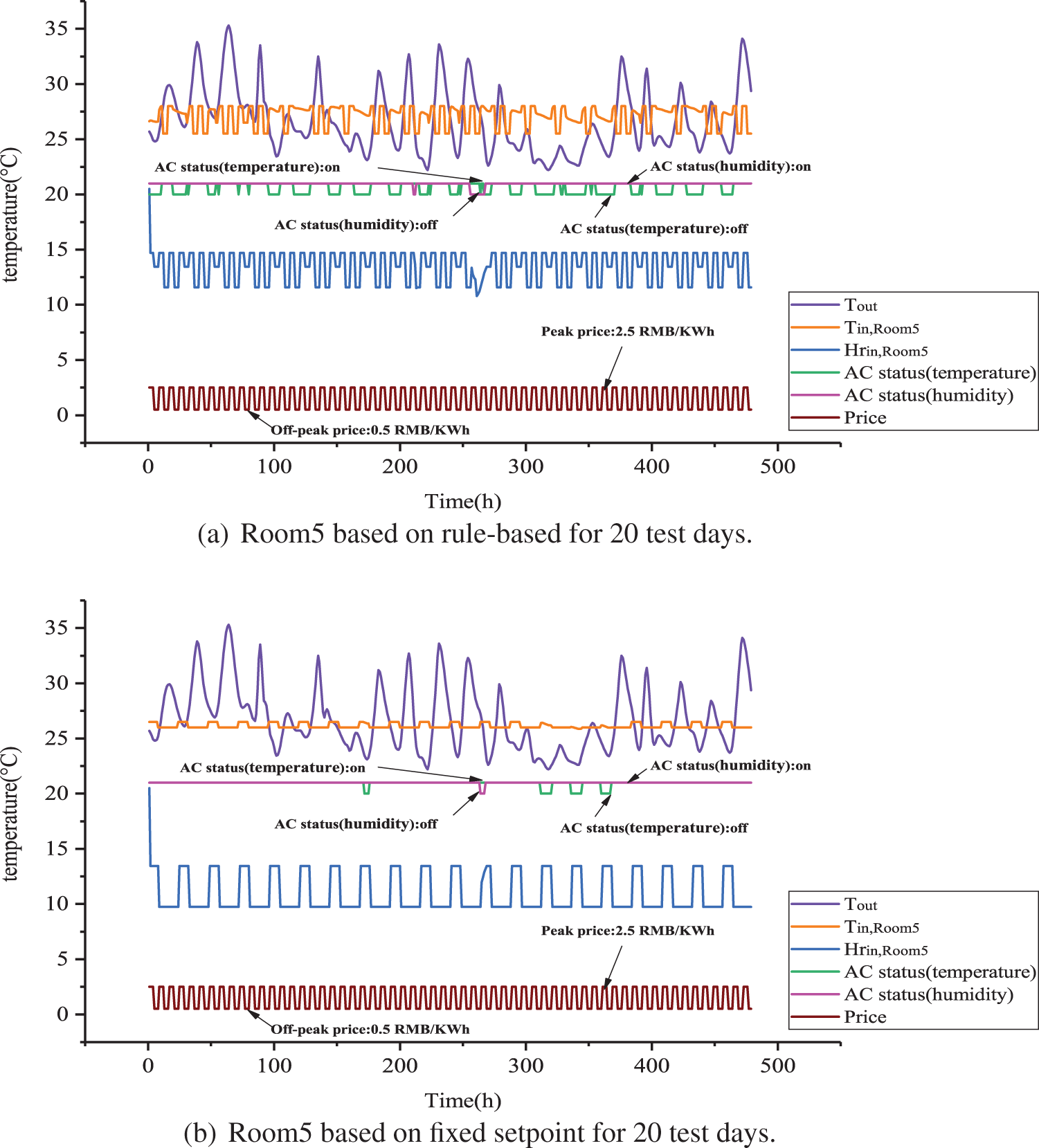
Figure 13: Room5 based on MAQMC and benchmark cases for 20 test days

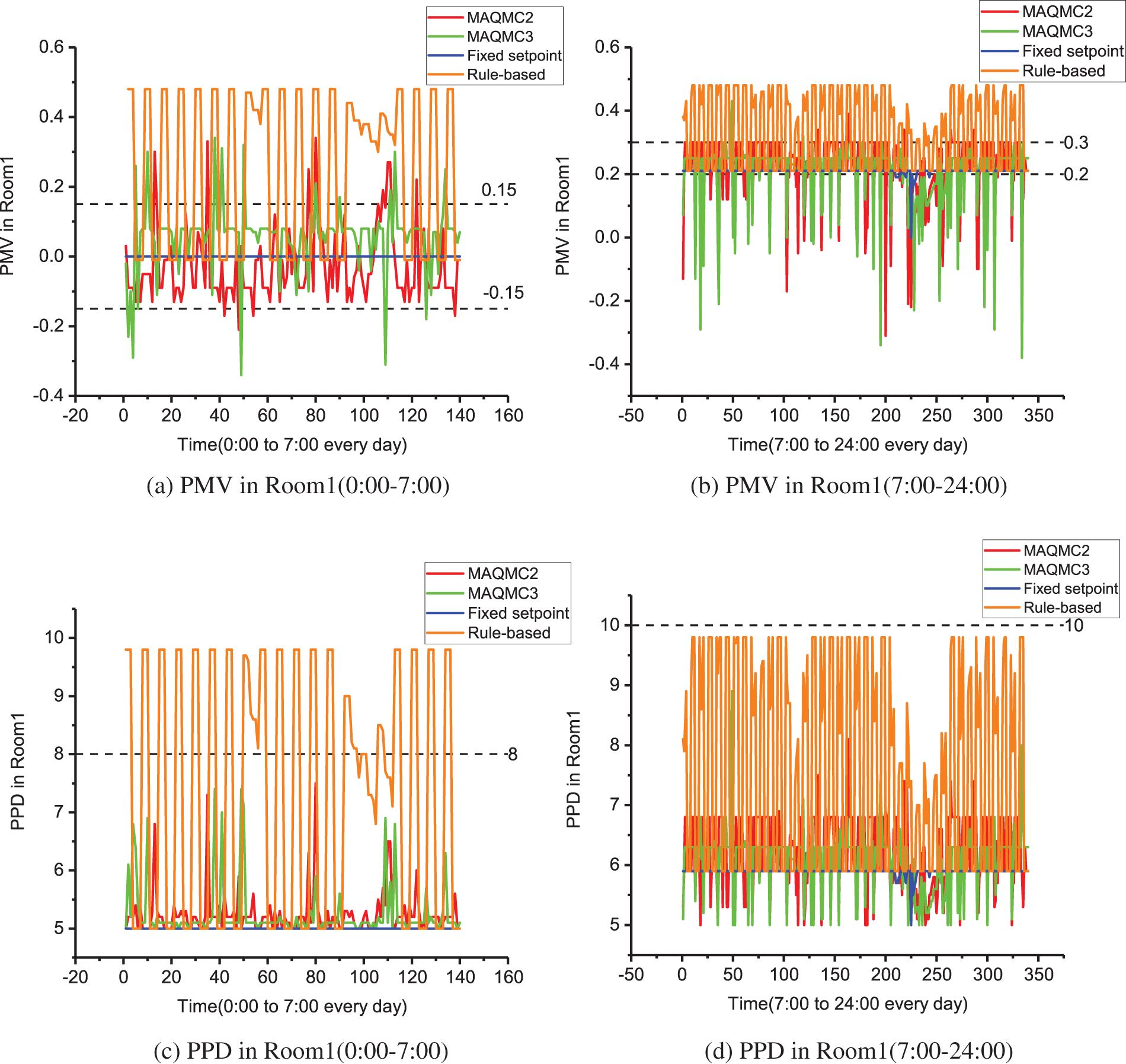
Figure 14: Comparison of energy consumption and cost

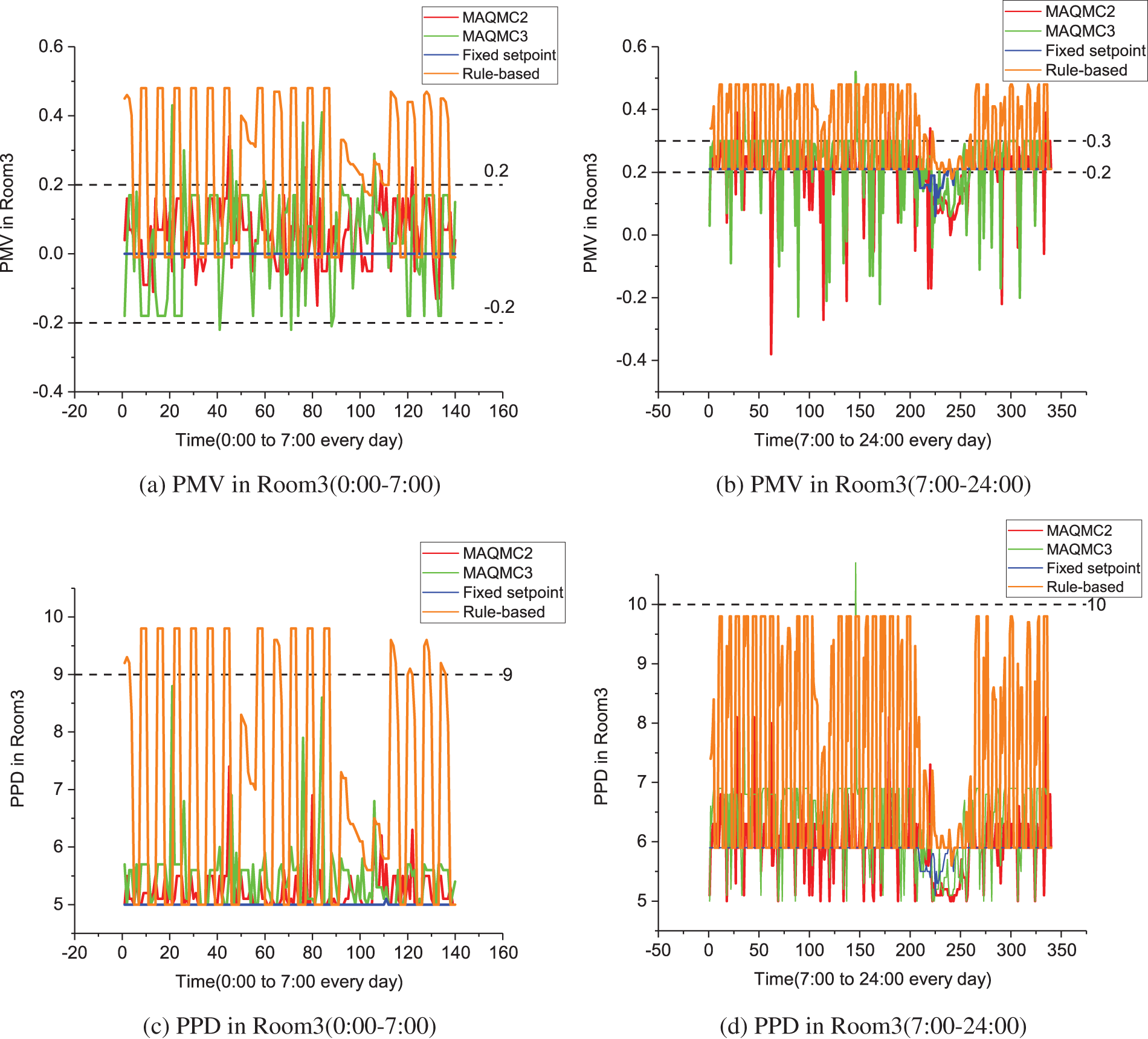
Figure 15: Comparison of energy consumption and cost

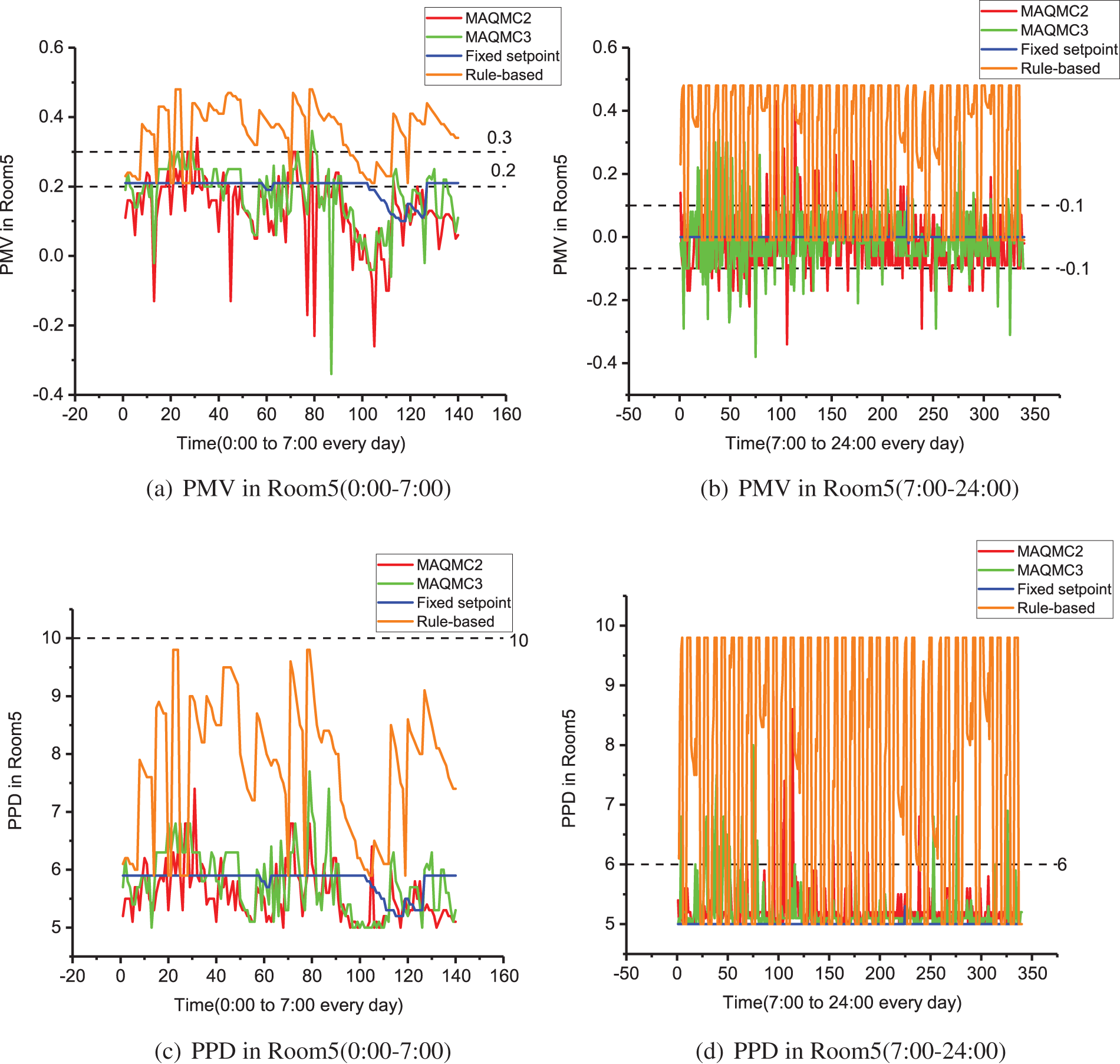
Figure 16: Comparison of energy consumption and cost

Indoor temperature, humidity ratio and PMV-PPD in Room3 are shown in Figs. 10 and 15. From Fig. 15, PMV in Room3 based on MAQMC2 and MAQMC3 basically remained in [−0.2, 0.2] in 0:00 to 7:00. However, between 7:00 and 24:00, PMV violates the set range based on MAQMC at some moments. PPD in Room3 based on MAQMC are kept above the lower bound of PPD and the value of PPD is almost below 7. Similarly, the rule-based case with the highest level of comfort violation but it has the lowest energy cost.

In Figs. 12 and 16, the details of Room5 are presented. From 0:00 to 7:00, PMV in Room5 based on MAQMC violation moments are more. This is also partly due to the fact that the HVAC system is not fully activated, for example, only the humidity regulation system is turned on and the temperature regulation system is not turned on. Between 7:00 and 24:00, only a few moments violate the comfort level in terms of PMV. For PPD, only at 7:00 to 24:00 very few moments have slight comfort violation. Again, the rule-based case is the control method that has the highest comfort level violations and the fixed setpoint is the method that has the least violations.

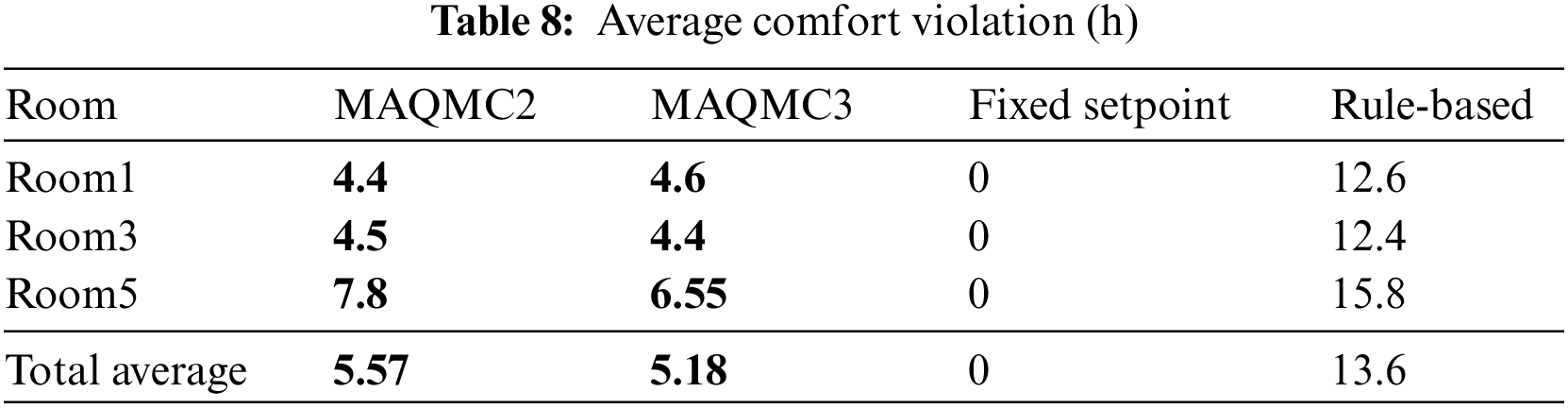
Table 7 presents the average PMV and PPD value for all three zones In July 1st to July 20th under Chongqing weather data. MAQMC2 and MAQMC3 can maintain the PMV and PPD value in the set range for most of the time. The average value of PMV in Room3 from 7:00 to 24:00 is slightly less than 0.2 based on MAQMC2, so there is a slight comfort violation in this time period. And the average value of PMV in Room5 from 0:00 to 24:00 is also less than 0.2 based on MAQMC2 and MAQMC3. However, the average PMV value of MAQMC3 is higher than that of MAQMC2. Therefore, the energy consumption of MAQMC2 is slightly higher than that of MAQMC3. The average values of PPD are kept within the set range based on MAQMC2 and MAQMC3. The rule-based control method has the most comfort violations and the fixed setpoint method has the least comfort violations. The average comfort violation in the three rooms on the test days is shown in Table 8. Except for the fixed setpoint, MAQMC3 has the smallest average comfort violation, MAQMC2 is the second, and rule-based control is the worst. The total average comfort violation for MAQMC was less than half of the rule-based.

In summary, both MAQMC2 and MAQMC3 can learn from outdoor temperature and humidity, indoor conditions and electricity price signals to learn better control strategies. Of course, MAQMC also performs average at some time, but overall performs well.

6  Conclusion

In this paper, we propose a MAQMC method that is applied to control the multi-zone HVAC system to minimize energy consumption while maintaining occpants’ comfort. The simulation results show that the trained RL agents of MAQMC are able to save energy while maintaining comfort and have the adaptability to different environments. MAQMC is more energy efficient than fixed-point and better than rule-based to maintain comfort. And The performance of MAQMC3 is better than that of MAQMC2. On the one hand, the action space for each intelligence in MAQMC3 is much smaller than that of MAQMC2, so MAQMC3 is able to explore more space to get a better strategy. On the other hand, MAQMC3’s agents (one agent controls the temperature and humidity of a room) are more coordinated than MAQMC2’s agents (one agent controls the temperature and the other the humidity). MAQMC3 and MAQMC2 can reduce energy consumption by 6.27% and 43.73%, respectively, compared with to the fixed point. Compared with the rule-based, MAQMC3 and MAQMC2 can reduce the comfort violation by 61.89% and 59.07%, respectively.

For future work, we focus on both the cooling and heating seasons. Being able to develop RL agents that can adapt to both heating and cooling on a year-round basis. The agents can make optimal decisions while maintaining thermal comfort and saving energy.

Funding Statement: This work was financially supported by Primary Research and Development Plan of China (No. 2020YFC2006602), National Natural Science Foundation of China (Nos. 62072324, 61876217, 61876121, 61772357), University Natural Science Foundation of Jiangsu Province (No. 21KJA520005), Primary Research and Development Plan of Jiangsu Province (No. BE2020026), Natural Science Foundation of Jiangsu Province (No. BK20190942).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Pérez-Lombard, L., Ortiz, J., Pout, C. (2008). A review on buildings energy consumption information. Energy and Buildings, 40(3), 394–398. https://www.sciencedirect.com/science/article/pii/S0378778807001016 [Google Scholar]

2. Costa, A., Keane, M. M., Torrens, J. I., Corry, E. (2013). Building operation and energy performance: Monitoring, analysis and optimisation toolkit. Applied Energy, 101, 310–316. https://www.sciencedirect.com/science/article/pii/S030626191100691X [Google Scholar]

3. Petersen, J. B., Bendtsen, J. D., Stoustrup, J. (2019). Nonlinear model predictive control for energy efficient cooling in shopping center HVAC. 2019 IEEE Conference on Control Technology and Applications (CCTA). Hong Kong, China. [Google Scholar]

4. Kumar, R., Wenzel, M. J., Elbsat, M. N., Risbeck, M. J., Zavala, V. M. (2020). Stochastic model predictive control for central HVAC plants. Journal of Process Control, 90, 1–17. https://www.sciencedirect.com/science/article/pii/S0959152420301943 [Google Scholar]

5. Afram, A., Janabi-Sharifi, F., Fung, A. S., Raahemifar, K. (2017). Artificial neural network (ANN) based model predictive control (MPC) and optimization of HVAC systems: A state of the art review and case study of a residential HVAC system. Energy & Buildings, 141, 96–113. https://doi.org/10.1016/j.enbuild.2017.02.012 [Google Scholar] [CrossRef]

6. Wang, J., Huang, J., Fu, Q., Gao, E., Chen, J. (2022). Metabolism-based ventilation monitoring and control method for COVID-19 risk mitigation in gymnasiums and alike places. Sustainable Cities and Society, 80, 103719. [Google Scholar] [PubMed]

7. Yin, C. L., Han, J. L. (2021). Dynamic pricing model of e-commerce platforms based on deep reinforcement learning. Computer Modeling in Engineering & Sciences, 127(1), 291–307. https://doi.org/10.32604/cmes.2021.014347 [Google Scholar] [CrossRef]

8. Wu, Z., Karimi, H. R., Dang, C. (2020). A deterministic annealing neural network algorithm for the minimum concave cost transportation problem. IEEE Transactions on Neural Networks and Learning Systems, 31(10), 4354–4366. https://doi.org/10.1109/TNNLS.5962385 [Google Scholar] [CrossRef]

9. Wu, Z., Gao, Q., Jiang, B., Karimi, H. R. (2021). Solving the production transportation problem via a deterministic annealing neural network method. Applied Mathematics and Computation, 411, 126518. https://www.sciencedirect.com/science/article/pii/S009630032100607X [Google Scholar]

10. Esrafilian-Najafabadi, M., Haghighat, F. (2021). Occupancy-based HVAC control using deep learning algorithms for estimating online preconditioning time in residential buildings. Energy and Buildings, 252, 111377. https://doi.org/10.1016/j.enbuild.2021.111377 [Google Scholar] [CrossRef]

11. Du, Y., Li, F. (2020). Intelligent multi-microgrid energy management based on deep neural network and model-free reinforcement learning. IEEE Transactions on Smart Grid, 11(2), 1066–1076. https://doi.org/10.1109/TSG.5165411 [Google Scholar] [CrossRef]

12. Wang, J., Hou, J., Chen, J., Fu, Q., Huang, G. (2021). Data mining approach for improving the optimal control of HVAC systems: An event-driven strategy. Journal of Building Engineering, 39, 102246. https://www.sciencedirect.com/science/article/pii/S2352710221001029 [Google Scholar]

13. Fu, Q., Han, Z., Chen, J., Lu, Y., Wu, H. et al. (2022). Applications of reinforcement learning for building energy efficiency control: A review. Journal of Building Engineering, 50, 104165. https://www.sciencedirect.com/science/article/pii/S2352710222001784 [Google Scholar]

14. Fu, Q., Li, K., Chen, J., Wang, J., Lu, Y. et al. (2022). Building energy consumption prediction using a deep-forest-based DQN method. Buildings, 12(2), 131. https://www.mdpi.com/2075-5309/12/2/131 [Google Scholar]

15. Gao, G., Li, J., Wen, Y. (2020). Deepcomfort: Energy-efficient thermal comfort control in buildings via reinforcement learning. IEEE Internet of Things Journal, 7(9), 8472–8484. https://doi.org/10.1109/JIoT.6488907 [Google Scholar] [CrossRef]

16. Brandi, S., Piscitelli, M. S., Martellacci, M., Capozzoli, A. (2020). Deep reinforcement learning to optimise indoor temperature control and heating energy consumption in buildings. Energy and Buildings, 224, 110225. https://www.sciencedirect.com/science/article/pii/S0378778820308963 [Google Scholar]

17. Jiang, Z., Risbeck, M. J., Ramamurti, V., Murugesan, S., Amores, J. et al. (2021). Building HVAC control with reinforcement learning for reduction of energy cost and demand charge. Energy and Buildings, 239, 110833. https://www.sciencedirect.com/science/article/pii/S0378778821001171 [Google Scholar]

18. Du, Y., Zandi, H., Kotevska, O., Kurte, K., Munk, J. et al. (2021). Intelligent multi-zone residential HVAC control strategy based on deep reinforcement learning. Applied Energy, 281, 116117. https://www.sciencedirect.com/science/article/pii/S030626192031535X [Google Scholar]

19. Yoon, Y. R., Moon, H. J. (2019). Performance based thermal comfort control (PTCC) using deep reinforcement learning for space cooling. Energy and Buildings, 203, 109420. https://www.sciencedirect.com/science/article/pii/S0378778819310692 [Google Scholar]

20. Zhang, Z., Chong, A., Pan, Y., Zhang, C., Lam, K. P. (2019). Whole building energy model for HVAC optimal control: A practical framework based on deep reinforcement learning. Energy and Buildings, 199, 472–490. https://www.sciencedirect.com/science/article/pii/S0378778818330858 [Google Scholar]

21. Nagarathinam, S., Menon, V., Vasan, A., Sivasubramaniam, A. (2020). Marco-multi-agent reinforcement learning based control of building HVAC systems. Proceedings of the Eleventh ACM International Conference on Future Energy Systems. New York, NY, USA, Association for Computing Machinery. https://doi.org/10.1145/3396851.3397694 [Google Scholar] [CrossRef]

22. Kurte, K., Amasyali, K., Munk, J., Zandi, H. (2021). Comparative analysis of model-free and model-based HVAC control for residential demand response. Proceedings of the 8th ACM International Conference on Systems for Energy-Efficient Buildings, Cities, and Transportation, New York, NY, USA, Association for Computing Machinery. https://doi.org/10.1145/3486611.3488727 [Google Scholar] [CrossRef]

23. Fu, Q., Chen, X., Ma, S., Fang, N., Xing, B. et al. (2022). Optimal control method of HVAC based on multi-agent deep reinforcement learning. Energy and Buildings, 270, 112284. https://www.sciencedirect.com/science/article/pii/S0378778822004558 [Google Scholar]

24. Cicirelli, F., Guerrieri, A., Mastroianni, C., Scarcello, L., Spezzano, G. et al. (2021). Balancing energy consumption and thermal comfort with deep reinforcement learning. 2021 IEEE 2nd International Conference on Human-Machine Systems (ICHMS), Magdeburg, Germany. [Google Scholar]

25. Kurte, K., Munk, J., Kotevska, O., Amasyali, K., Smith, R. et al. (2020). Evaluating the adaptability of reinforcement learning based HVAC control for residential houses. Sustainability, 12(18). https://www.mdpi.com/2071-1050/12/18/7727 [Google Scholar]

26. Kurte, K., Munk, J., Amasyali, K., Kotevska, O., Cui, B. et al. (2020). Electricity pricing aware deep reinforcement learning based intelligent HVAC control. Proceedings of the 1st International Workshop on Reinforcement Learning for Energy Management in Buildings & Cities, New York, NY, USA, Association for Computing Machinery. https://doi.org/10.1145/3427773.3427866 [Google Scholar] [CrossRef]

27. Montague, P. (1999). Reinforcement learning: An introduction, by sutton, R.S. and barto, A.G. Trends in Cognitive Sciences, 3(9), 360. https://www.sciencedirect.com/science/article/pii/S1364661399013315 [Google Scholar]

28. Volodymyr, M., Koray, K., David, S., Rusu, A. A., Joel, V. et al. (2019). Human-level control through deep reinforcement learning. Nature, 518(7540), 529–533. [Google Scholar]

29. Lauer, M. (2000). An algorithm for distributed reinforcement learning in cooperative multiagent systems. Proceeding 17th International Conference on Machine Learning, Stanford, USA. [Google Scholar]

30. Fanger, P. O. (1972). Thermal comfort: Analysis and applications in environmental engineering. Applied Ergonomics, 3(3), 181. https://www.sciencedirect.com/science/article/pii/S0003687072800747 [Google Scholar]

31. Standard, A. (2017). Standard 55–2017 thermal environmental conditions for human occupancy. Atlanta, GA, USA: Ashrae. [Google Scholar]

32. Tartarini, F., Schiavon, S. (2020). Pythermal comfort: A Python package for thermal comfort research. SoftwareX, 12, 100578. https://www.sciencedirect.com/science/article/pii/S2352711020302910 [Google Scholar]

33. Deng, J., Yao, R., Yu, W., Zhang, Q., Li, B. (2019). Effectiveness of the thermal mass of external walls on residential buildings for part-time part-space heating and cooling using the state-space method. Energy and Buildings, 190, 155–171. https://www.sciencedirect.com/science/article/pii/S0378778818329219 [Google Scholar]

34. China Meteorological Bureau, Climate Information Center, C. D. O., Tsinghua University, D. O. B. S., Technology (2005). China standard weather data for analyzing building thermal conditions. China: China Building Industry Publishing House Beijing, China. [Google Scholar]

35. Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J. et al. (2019). Pytorch: An imperative style, high-performance deep learning library. In: Wallach, H., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E. et al. (Eds.Advances in neural information processing systems, vol. 32, pp. 8024–8035. Curran Associates, Inc. http://papers.neurips.cc/paper/9015-pytorch-an-imperative-style-high-performance-deep-learning-library.pdf [Google Scholar]