 Open Access
Open Access
ARTICLE
Novel Decision Making Methodology under Pythagorean Probabilistic Hesitant Fuzzy Einstein Aggregation Information
1
Institute of Mathematics, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, 64200, Pakistan
2
Department of Mathematics, University of Sargodha, Sargodha, 40100, Pakistan
3
Department of Mathematics, Deanship of Applied Sciences, Umm Al-Qura University, Makkah, 24382, Saudi Arabia
* Corresponding Author: Muhammad Naeem. Email:
(This article belongs to the Special Issue: Decision making Modeling, Methods and Applications of Advanced Fuzzy Theory in Engineering and Science)
Computer Modeling in Engineering & Sciences 2023, 136(2), 1785-1811. https://doi.org/10.32604/cmes.2023.024851
Received 09 June 2022; Accepted 19 October 2022; Issue published 06 February 2023
Abstract
This research proposes multicriteria decision-making (MCDM)-based real-time Mesenchymal stem cells (MSC) transfusion framework. The testing phase of the methodology denotes the ability to stick to plastic surfaces, the upregulation and downregulation of certain surface protein markers, and lastly, the ability to differentiate into various cell types. First, two scenarios of an enhanced dataset based on a medical perspective were created in the development phase to produce varying levels of emergency. Second, for real-time monitoring of COVID-19 patients with different emergency levels (i.e., mild, moderate, severe, and critical), an automated triage algorithm based on a formal medical guideline is proposed, taking into account the improvement and deterioration procedures from one level to the next. For this strategy, Einstein aggregation information under the Pythagorean probabilistic hesitant fuzzy environment (PyPHFE) is developed. Einstein operations on PyPHFE such as Einstein sum, product, scalar multiplication, and their properties are investigated. Then, several Pythagorean probabilistic hesitant fuzzy Einstein aggregation operators, namely the Pythagorean probabilistic hesitant fuzzy weighted average (PyPHFWA) operator, Pythagorean probabilistic hesitant fuzzy Einstein weighted geometric (PyPHFEWG) operator, Pythagorean probabilistic hesitant fuzzy Einstein ordered weighted average (PyPHFEOWA) operator, Pythagorean probabilistic hesitant fuzzy Einstein ordered weighted geometric (PyPHFEOWG) operator, Pythagorean probabilistic hesitant fuzzy Einstein hybrid average (PyPHFEHA) operator and Pythagorean probabilistic hesitant fuzzy Einstein hybrid geometric (PyPHFEHG) operator are investigated. All the above-mentioned operators are helpful in design the algorithm to tackle uncertainty in decision making problems. In last, a numerical case study of decision making is presented to demonstrate the applicability and validity of the proposed technique. Besides, the comparison of the existing and the proposed technique is established to show the effectiveness and validity of the established technique.Keywords
Coronavirus disease 2019 (COVID-19) is a highly contagious sickness that can range from mild to severe. Fever, cough, and shortness of breath are common symptoms of COVID-19, which can escalate to acute respiratory distress syndrome, which causes breathing problems, a low ratio of the partial pressure arterial oxygen to the fraction of inspired oxygen (PaO2/FiO2), and multi-organ failure [1,2]. MSCs were first found in the bone marrow in 1991, but they can now be extracted from a variety of tissues, including the umbilical cord and adipose tissue [3]. MSCs have anti-inflammatory characteristics due to their ability to modify cellular immune responses. MSCs can be used to treat a variety of disorders due to their regeneration capabilities and immunoregulatory function [4]. Finding and testing acceptable MSC methods with effective utilization may be difficult since MSCs must first meet the selection and general requirements. Additionally, dealing with very precious MSCs and a huge number of patients needs an intelligent transfusion approach for COVID-19 patients with varying degrees of sickness severity, making prioritization problematic. This method falls under a multicriteria decision making (MCDM) problem since the needs in the second stage should follow the ranking of emergency COVID-19 patients in each severity level according to the evaluation criteria. As a result, choosing the finest MSC preparation process that conforms with national health laws, as well as selecting the most suited patients for the treatment, is critical for delivering effective cell-based therapy. To assist medical teams in solving the complicated obstacles outlined above, intelligent computing concerns should be addressed in order to present a fully intelligent real-time MSC transfusion framework based on the emergency severity of COVID-19 patients. Triage and prioritization are used in the medical field to either classify patients into distinct emergency categories or to prioritize them in the hereafter. Triage is an emergency medical procedure that classifies the severity of a patient’s condition and defines the treatment sequence. Automating this task could considerably enhance the quality of patient treatment and hospitalization, allowing for the greatest number of lives to be saved. Patients with chronic heart disease were previously classified into distinct emergency levels using an automated triage approach.
In fact, a system’s complexity grows more and more, making it impossible for DMs to select the best option among a wide range of viable options. It is difficult to put into words how challenging achieving a single objective is, yet it is not unattainable. Several corporations are faced with encouraging workers, identifying aims, and creating viewpoint. As a result, whether affecting individuals or panels, organizational decisions must consider a number of goals simultaneously. In this context, each DM should be restricted to finding the optimum solution for each factor associated with real problems, based on criteria that can be handled consciously. For decision-makers, establishing suitable ways for deciding on the appropriate option has become increasingly vital.
Classic or crisp procedures may not necessarily be the most successful when dealing with unstructured situations in decision-making circumstances. Zadeh [5] developed fuzzy sets (FS) in 1965 as a technique to manage such inconsistency. In FSs, Zadeh assigns membership grades to a set of components in the interval [0,1]. Zadeh’s work on this topic is notable since many of the set theoretic elements of crisp circumstances were described for fuzzy sets and it plays an important role in decision making [6,7].
Atanassov [8] investigated the intuitionistic fuzzy set (IFS), a better variation of the fuzzy set (FS) that includes both membership and non-membership degrees. IFSs have been shown to be useful and commonly used by researchers to evaluate uncertainty and instability in data throughout the previous few decades. Several researchers work on it, such as Yue [9] proposed the bilateral matching decision-making for knowledge innovation management taking into account matching willingness by using the intuitionistic fuzzy set environment, group decision making [10], aggregation operators [11], geometric aggregation operators [12], etc.
Wherever the MG and NMG numbers are more than one, the DMs are frequently confronted with certain qualities. In that circumstance, IFSs have little chance of producing a satisfactory result. To handle such a circumstance, Yager [13] proposed the Pythagorean fuzzy set (PyFS), which is a broad form of IFS. For PyFS, the sum of the squares of MG and NMG equals one. Wan et al. [14] introduced a three-step process for managing haze using the Pythagorean fuzzy multi-attribute group decision making, Yager et al. [15,16] also presented decision making procedures by using PyFS, Peng et al. [17] proposed some PyFS results. Torra [18] created the hesitant fuzzy set (HFS) to demonstrate the FS more firmly than the previous classical fuzzy set modifications, which needed the membership to have a set of specific values. Yue et al. [19] introduced the methodology for matching two-sided under hesitant fuzzy information and discussed their application related to smart intelligence, Xia et al. [20] presented hesitant fuzzy aggregation information, Liu et al. [21] introduced generalized power aggregation operator, Yu et al. [22] presented the MCDM under choquet integral based on HFS, Zhang [23] introduced the power aggregation operator, Liao et al. [24,25] introduced the hybrid and extended hybrid weighted aggregation operator on HFS, Joshi et al. [26] introduced TOPSIS method based on interval valued IHF choquet integral and similarly many other researchers also worked on HFS.
The concept of Pythagorean HFS (PyHFS) was suggested by Khan et al. [27]. They developed operators to aggregate the data and proposed a comparison mechanism. Wan et al. [28,29] presented the decision methodologies under Pythagorean fuzzy information and Garg [30] presented hesitant PyF (HPyF) maclaurin symmetric mean operator, Garg et al. [31,32] introduced aggregation operators on HPyFS and Khan et al. [33] introduced hybrid aggregation operators on PyHFS. Zulqarnain et al. [34] developed some aggregation operators under interval-valued Pythagorean fuzzy soft information. Batool et al. [35] proposed the notion of a Pythagorean probabilistic hesitant fuzzy set and investigated its application in decision-making approaches. PyPHFS has both positive and negative hesitant membership degrees with the restriction that the square sum of the positive and negative hesitant membership degrees is either less than or equal to one. The DMs in PHFS is constrained to a single domain and are unaware of the negative membership degree or its possible occurrence probabilities. Each hesitantly negative membership level also has a preference over others. If one DM includes values 0.3, 0.4, and 0.6 for positive membership degree with their associated preference values 0.1 and 0.9, other DM may reject. As an example, the DMs may offer their opinions on DM difficulties in the form of multiple alternative values. Under the PyPHFS idea, the possibility of rejection level with hesitation is taken into account. Despite HFSs and PHFSs, the information about chances will reduce. The probability of occurrence with positive and negative membership degrees provides extra information on the degree of disagreement among the DMs. Batool et al. [35] also used its application for Fog-Haze Factor Assessment Problem.
Different priority levels are frequently assigned to each criterion in each emergency situation, adding to the task’s complexity. Ultimately, a COVID-19 patient prioritization process inside each emergency/triage situation necessitates a synchronized evaluation of the inverse relationship among the criteria, resulting in a trade-off. To address the first issue, an accurate automated triage guideline must be developed and implemented into the proposed MSC transfusion system. By prioritizing COVID-19 patients within each triage level, MCDM approaches are critical for overcoming the aforementioned problems. MCDM is a multi-objective decision model that is an extension of decision theory. It can address multi-criteria decision-making problems by constructing a decision matrix based on the intersection of each triage level’s evaluation criteria. The fundamental purpose of the MCDM is to rank/prioritize a group of alternatives based on a variety of evaluation criteria. For the MCDM technique Pythagorean Probabilistic Hesitant Fuzzy Information Aggregation when dealing with difficulties like this, Einstein Operations can be quite useful.
In this research work, we administered the Einstein aggregation operators (AOs) to PyPHFS environment, i.e., PyPHFEWA, PyPHFEOWA, PyPHFEHWA, PyPHFEWG, PyPHFEOWG and PyPHFEHWG operator. Idempotency, boundedness, and monotonicity are among the properties of the recommended operators that are established. The PyPHF AOs are taken into consideration by such operators in probabilistic scenarios, which is their main benefit. In the case of probabilistic material, the lack of PyPHFE AOs could lead to a scarcity of probabilistic information.
The paper is arranged in the prescribed manner. Section 2 contains the definition of FSs, IFSs, PyFSs, HFSs, and PyHFSs, PyPHFSs as well as PyPHFE aggregation operators. Section 3 is comprised of the PyPHFEWA, PyPHFEOWA, PyPHFEHWA, PyPHFEWG, PyPHFEOWG, and PyPHFEHWG operators, as well as their features such as monotonicity, idempotency, and boundedness. Section 4 presents how to use the MCDM technique. Section 5 contains the conclusion and discussion of the study.
In this section, let’s review the fundamentals of fuzzy sets, intuitionistic fuzzy sets, and Pythagorean fuzzy sets. These concepts will be used here when they have been reviewed.
Definition 2.1.[5] For a fixed set
for each
Definition 2.2.[8] For a fixed set
for each
Definition 2.3.[10] For a fixed set
for each
In what follows, we symbolize by
Definition 2.4.[10] Let
(1)
(2)
(3)
(4)
Definition 2.5.[18] For a fixed set
where
Definition 2.6.[18] Let
(1)
(2)
(3)
Definition 2.7.[32] For a fixed set
for each
Definition 2.8.[32] Let
(1)
(2)
(3)
Definition 2.9.[36] For a fixed set
where
2.1 Pythagorean Probabilistic Hesitant Fuzzy Set
Definition 2.10.For a fixed set
for all
Definition 2.11.Let
(1)
(2)
(3)
Definition 2.12.Let
(1)
(2)
(3)
(4)
Definition 2.13.For any PyPHFN
where
Definition 2.14.For any PyPHFN
where
Definition 2.15.Let
(1) If
(2) If
Definition 2.16.Let
(1) the PyPHFWA operator can be described as
(2) the PyPHFWG operator can be described as
Definition 2.17.Let
(1) PyPHFOWA operator can be described as
(2) PyPHFOWG operator can be described as
Definition 2.18.Let
(1) PyPHFHWA operator
(2) PyPHFHWG operator can be described as
2.2 Einstein Operational Laws Based on PyPHFEs
The application of t-norms in FS theory at the intersection of two FSs is widely recognized. T-conorms are being used to model disjunction or union. These are a straightforward explanation of the conjunction and disjunction in mathematical fuzzy logic syntax, and they are utilized in MCDM to combine criteria.
The Einstein sum (
Based on the above Einstein operations, we give the following new operations on PyPHFEs.
Definition 2.19.Let
(1)
(2)
(3)
(4)
3 PyPHF Einstein Aggregation Operators
In this section, we develop several new Einstein operators for PyPHFNs, namely the Pythagorean probabilistic hesitant fuzzy Einstein weighted averaging (PyPHFEWA) operator, the Pythagorean probabilistic hesitant fuzzy Einstein ordered weighted averaging (PyPHFEOWA) operator, the Pythagorean probabilistic hesitant fuzzy Einstein weighted geometric (PyPHFEWG) operator, and the Pythagorean probabilistic hesitant fuzzy Einstein ordered weighted geometric (PyPHFEOWG) operator.
3.1 Pythagorean Probabilistic Hesitant Fuzzy Einstein Weighted Averaging Operators
Definition 3.1.Let
is called the Pythagorean probabilistic hesitant fuzzy Einstein weighted averaging operator.
Theorem 3.1.Let
where
Proof. We will demonstrate the theorem by mathematical induction. For
Since both
Then
Thus, the result holds for
Assume that the results holds for
Now we will prove for
Thus
There are some properties which are fulfilled by the PyPHFEWA as follows:
Theorem 3.2.Let
(1) Boundary:
where
(2) Monotonicity: Let
Proof. (1) Let
Since
Thus,
Consider
Then
Let,
and
Let
Definition 3.2.Let
is called the Pythagorean probabilistic hesitant fuzzy Einstein weighted geometric operator.
Theorem 3.3.Let
where
There are some properties which are fulfilled by the PyPHFEWG as follows:
Theorem 3.4. Let
(1) Boundary:
where
(2) Monotonicity: Let
We developed the following ordered weighted operators based on PyPHFNs.
Definition 3.3.(1) Let
where
(2) Let
where
Step 1 Normalization of the Expert information in Pythagorean probabilistic hesitant fuzzy information.
Step 2 We determine the weight vectors by using the Pythagorean probabilistic hesitant fuzzy entropy measure, entropy of the criteria is defined as
Step 3 By exploiting the proposed PyPHFWA operator/PyPHFWG operator, the overall preference values
and
Step 4 Find out the score values for each given alternative using the following formula:
Step 5 Rank the alternative in ascending order. The alternative having large score value are the best alternative among the consider alternatives.
Flow chart of the proposed decision making methodology is given in Fig. 1.
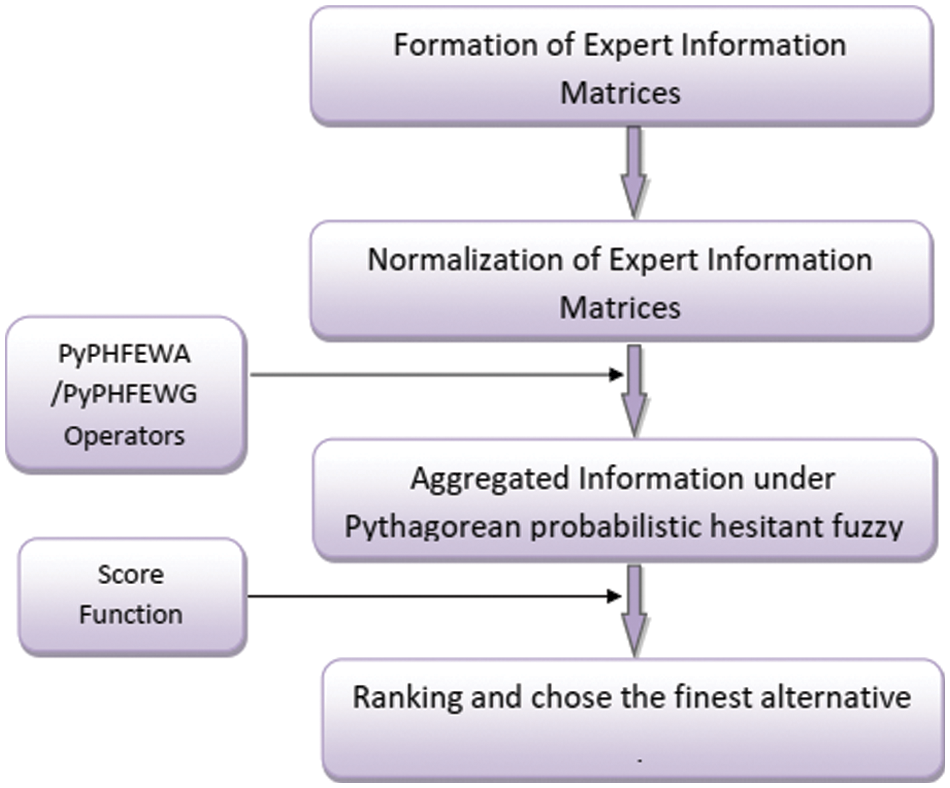
Figure 1: Steps of algorithm for MCDM by using pythagorean probabilistic hesitant fuzzy einstein aggregation operators
The Emergency Decision Making for COVID-19’s emergency circumstance is discussed in this part. Several researchers made decisions to minimize the influence of COVID-19 [37–40].
Case Study: We present a real specific example of an emergency caused by a novel coronavirus outbreak (NCoViD-2019) that occurred in China to demonstrate the objectivity and operation of the suggested methodology. NCoViD-2019 is a brand-new virus that has infected thousands of people in just a few weeks. The virus has killed about 3,000 people in China, and it has afflicted more than 80,000 people around the world. Due to the nature of the emergency, the DMs must act quickly and rescue those who are in danger in order to effectively control the situation and prevent further deaths. There are three important factors to communicating emergency response requirements:
(1)
(2)
(3)
To combat NCoViD-2019, there are four emergency options:
Step 1 Because the attributes are uniform so there are no need to normalized.
Step 2 The weight vector in this case study is known
Step 3 By exploiting the proposed PyPHFWA operator, we achieve the overall preference values
Similarly for other alternatives
Step 4 The score values are obtained as
Step 5
Therefore
The best choice is
Step 3 By exploiting the proposed PyPHFWG operator, we achieve the overall preference values
Step 4 The score values are obtained as
Step 5
Therefore
The best choice is
To show the applicability and appropriateness of the established Pythagorean probabilistic hesitant fuzzy Einstein operators-based methodology, we compared the approach based on the suggested operator in accordance with the existing decision assistance approach to validate the advantages and stability of the developed methodology.
Comparison with Batool et al. [41]:
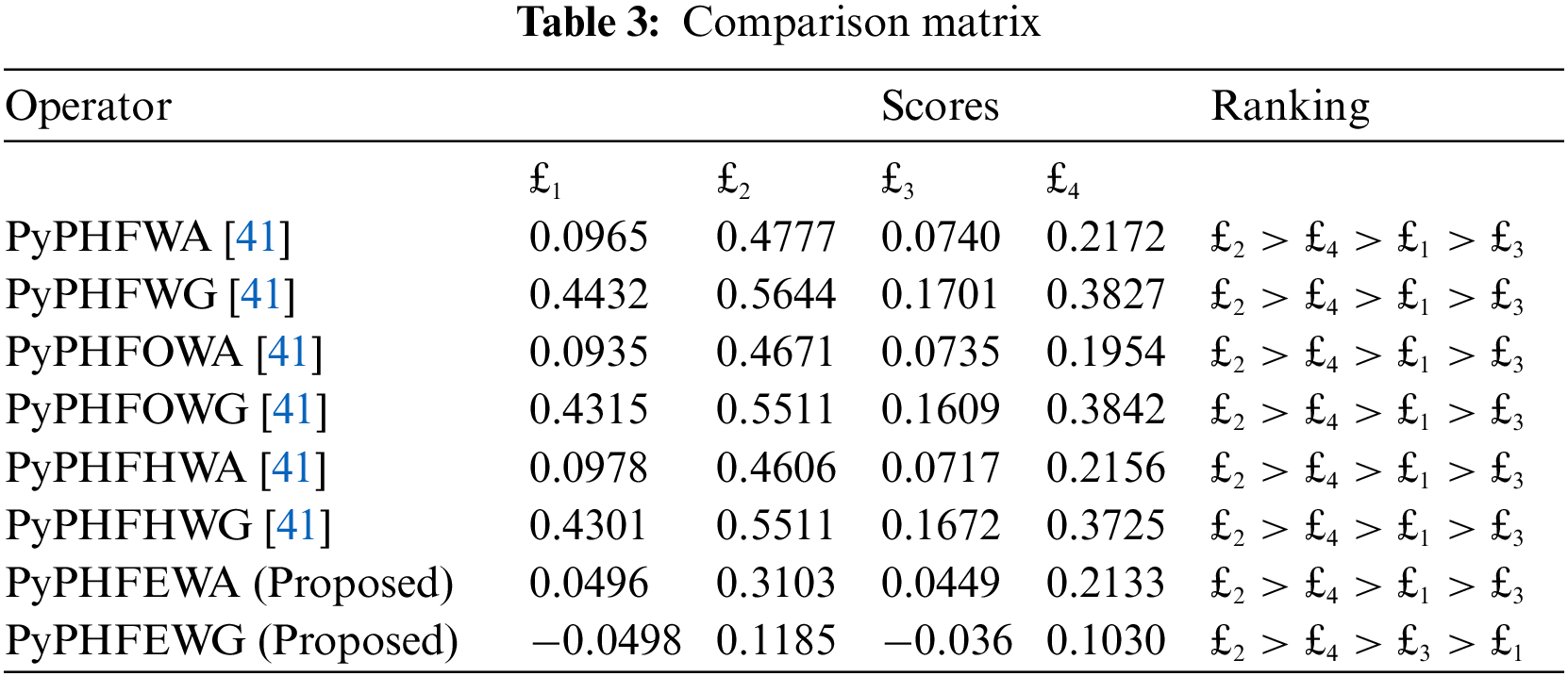
Batool et al. [41] evolved novel Algebraic aggregation operators under Pythagorean probabilistic hesitant fuzzy information to sort out the best alternative. Table 3 gives the comparison findings and shows that the PyPHFWA, PyPHFOWA, PyPHFHWA, PyPHFWG, PyPHFOWG and PyPHFHWG operators are special instances of our developed Einstein aggregation operators.
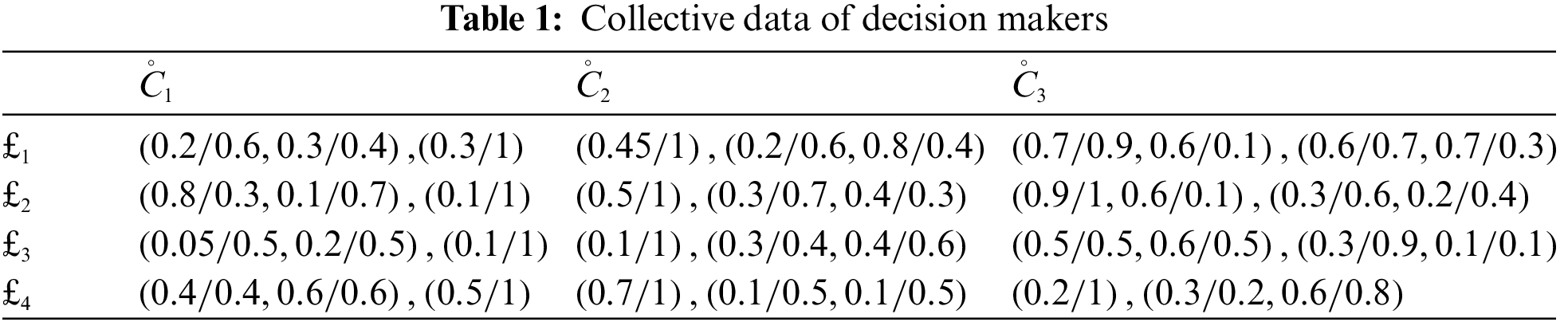
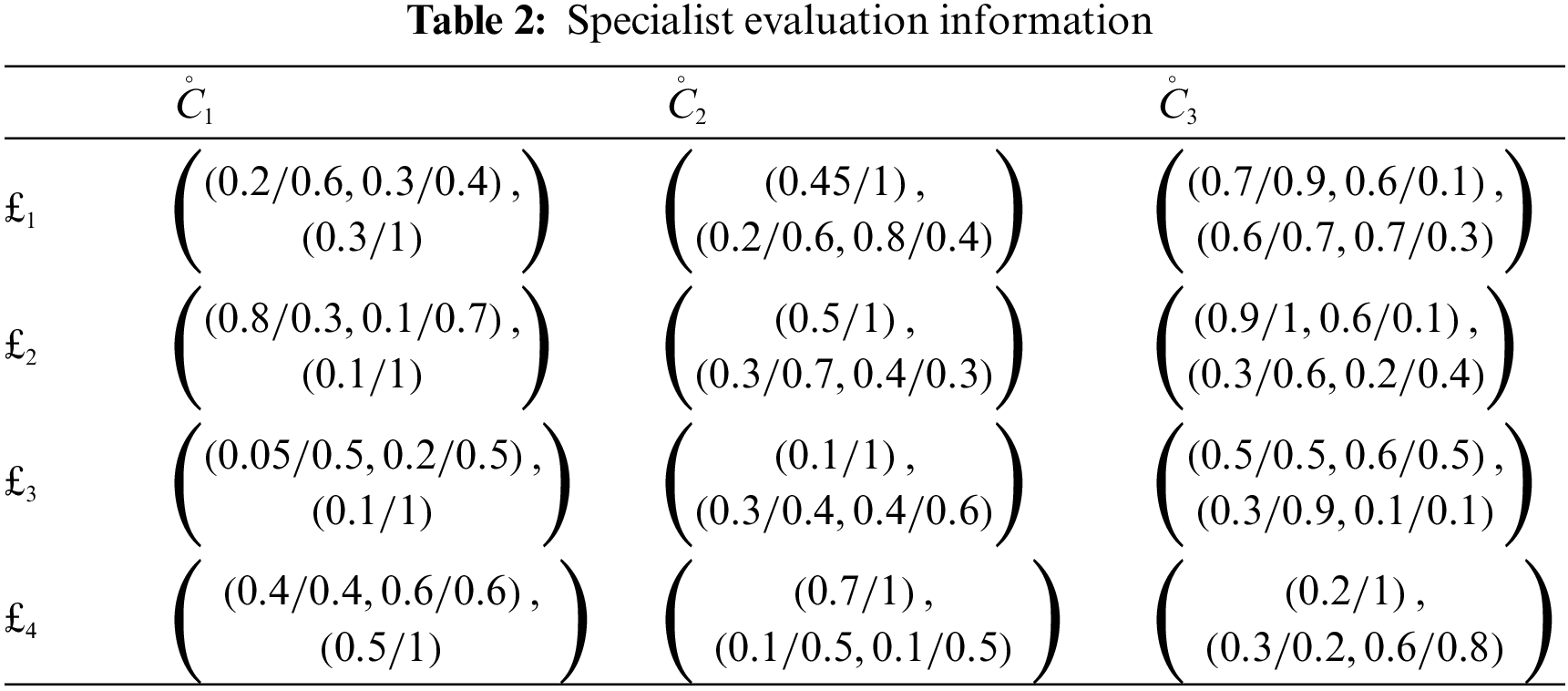
In a nutshell, our suggested solutions are expected to become more extensive and flexible than a few existing strategies for addressing MADM problems. Collected specialist data [41] is listed in Table 2.
Given weight vector is
Comparative studies with collected specialist data by [41] is enclosed in Table 3.
Table 3 shows a comparison between the existing technique and the results obtained by the proposed methodology along with the final ranking order of the alternatives. The operators in the considered existing theories are: PyPHFWA, PyPHFOWA, PyPHFHWA, PyPHFWG, PyPHFOWG and PyPHFHWG aggregation operators by Batool et al. [41]. Thus, the proposed operators are an enhanced and generalized form of the existing operators because it remains unchanged on the same output ranking for different operators. Moreover, the best alternative chosen by the proposed operators remains the same as that with that of the existing operator signifies that the established operators are an enhanced version and generalized over the existing operator in the literature.
We conducted a thorough investigation into PyPHF aggregation operators in this paper. First, we have defined certain operational guidelines based on Einstein operations for PyPHFS. The weighted averaging and geometric Einstein aggregation operators have also been intended to deal with PyPHF data, such as Pythagorean probabilistic hesitant fuzzy averaging (PyPHFA) and Pythagorean probabilistic hesitant fuzzy geometric (PyPHFG) aggregation data in decision-making issues, due to the importance of operating procedures and a number of useful characteristics have been shown on them. To explain the usage, adaptability, and effectiveness of the procedure, we created a Healthcare framework and employed specified aggregation material to solve this problem.
We will examine the conceptual framework of Pythagorean probabilistic hesitant fuzzy sets for Einstein operations in future work using innovative decision-making approaches like as TOPSIS, VIKOR, EDAS and how these techniques are used in domains including analytical thinking, intelligent systems, soft computing, etc.
Acknowledgement: The authors would like to thank the Deanship of Scientific Research at Umm Al-Qura University for supporting this work by Grant Code: 22UQU4310396DSR32.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Albahri, A. S., Hamid, R. A., Al-qays, Z. T., Zaidan, A. A., Zaidan, B. B. et al. (2020). Role of biological data mining and machine learning techniques in detecting and diagnosing the novel coronavirus (COVID-19A systematic review. Journal of Medical Systems, 44(7), 1–11. DOI 10.1007/s10916-020-01582-x. [Google Scholar] [CrossRef]
2. Asmundson, G. J., Taylor, S. (2020). Coronaphobia: Fear and the 2019-nCoV outbreak. Journal of Anxiety Disorders, 70, 102196. DOI 10.1016/j.janxdis.2020.102196. [Google Scholar] [CrossRef]
3. Marino, L., Castaldi, M. A., Rosamilio, R., Ragni, E., Vitolo, R. et al. (2019). Mesenchymal stem cells from the Wharton’s jelly of the human umbilical cord: Biological properties and therapeutic potential. International Journal of Stem Cells, 12(2), 218–226. DOI 10.15283/ijsc18034. [Google Scholar] [CrossRef]
4. Wang, M., Yuan, Q., Xie, L. (2018). Mesenchymal stem cell-based immunomodulation: Properties and clinical application. Stem Cells International, 2018(1–2), 1–12. DOI 10.1155/2018/3057624. [Google Scholar] [CrossRef]
5. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8, 338–353. [Google Scholar]
6. Deveci, M., Canıtez, F., Gökaşar, I. (2018). WASPAS and TOPSIS based interval type-2 fuzzy MCDM method for a selection of a car sharing station. Sustainable Cities and Society, 41(1), 777–791. DOI 10.1016/j.scs.2018.05.034. [Google Scholar] [CrossRef]
7. Fu, J., Ye, J., Xie, L. (2022). Group decision-making model of renal cancer surgery options using entropy fuzzy element aczel-alsina weighted aggregation operators under the environment of fuzzy multi-sets. Computer Modeling in Engineering & Sciences, 130(3), 1751–1769. DOI 10.32604/cmes.2022.018739. [Google Scholar] [CrossRef]
8. Atanassov, K. T. (1999). Intuitionistic fuzzy sets. In: Intuitionistic fuzzy sets, pp. 1–137. Heidelberg: Physica. [Google Scholar]
9. Yue, Q. (2022). Bilateral matching decision-making for knowledge innovation management considering matching willingness in an interval intuitionistic fuzzy set environment. Journal of Innovation and Knowledge, 7(3), 100209. DOI 10.1016/j.jik.2022.100209. [Google Scholar] [CrossRef]
10. Chen, S. M., Cheng, S. H., Chiou, C. H. (2016). Fuzzy multiattribute group decision making based on intuitionistic fuzzy sets and evidential reasoning methodology. Information Fusion, 27(1), 215–227. DOI 10.1016/j.inffus.2015.03.002. [Google Scholar] [CrossRef]
11. Xu, Z. (2007). Intuitionistic fuzzy aggregation operators. IEEE Transactions on Fuzzy Systems, 15(6), 1179–1187. DOI 10.1109/TFUZZ.2006.890678. [Google Scholar] [CrossRef]
12. Xu, Z., Yager, R. R. (2006). Some geometric aggregation operators based on intuitionistic fuzzy sets. International Journal of General Systems, 35(4), 417–433. DOI 10.1080/03081070600574353. [Google Scholar] [CrossRef]
13. Yager, R. R. (2013). Pythagorean membership grades in multicriteria decision making. IEEE Transactions on Fuzzy Systems, 22(4), 958–965. [Google Scholar]
14. Wan, S. P., Li, S. Q., Dong, J. Y. (2018). A three-phase method for Pythagorean fuzzy multi-attribute group decision making and application to haze management. Computers and Industrial Engineering, 123(1), 348–363. DOI 10.1016/j.cie.2018.07.005. [Google Scholar] [CrossRef]
15. Yager, R. R., Abbasov, A. M. (2013). Pythagorean membership grades, complex numbers, and decision making. International Journal of Intelligent Systems, 28(5), 436–452. DOI 10.1002/int.21584. [Google Scholar] [CrossRef]
16. Yager, R. R. (2013). Pythagorean membership grades in multicriteria decision making. IEEE Transactions on Fuzzy Systems, 22(4), 958–965. DOI 10.1109/TFUZZ.2013.2278989. [Google Scholar] [CrossRef]
17. Peng, X., Yang, Y. (2015). Some results for Pythagorean fuzzy sets. International Journal of Intelligent Systems, 30(11), 1133–1160. DOI 10.1002/int.21738. [Google Scholar] [CrossRef]
18. Torra, V. (2010). Hesitant fuzzy sets. International Journal of Intelligent Systems, 25(6), 529–539. DOI 10.1002/int.20418. [Google Scholar] [CrossRef]
19. Yue, Q., Zhang, L. (2020). Two-sided matching for hesitant fuzzy numbers in smart intelligent technique transfer. Mechanical Systems and Signal Processing, 139(5), 106643. DOI 10.1016/j.ymssp.2020.106643. [Google Scholar] [CrossRef]
20. Xia, M., Xu, Z. (2011). Hesitant fuzzy information aggregation in decision making. International Journal of Approximate Reasoning, 52(3), 395–407. DOI 10.1016/j.ijar.2010.09.002. [Google Scholar] [CrossRef]
21. Liu, J., Sun, M. (2013). Generalized power average operator of hesitant fuzzy numbers and its application in multiple attribute decision making. Journal of Computational Information Systems, 9(8), 3051–3058. [Google Scholar]
22. Yu, D., Wu, Y., Zhou, W. (2011). Multi-criteria decision making based on Choquet integral under hesitant fuzzy environment. Journal of Computational Information Systems, 7(12), 4506–4513. [Google Scholar]
23. Zhang, Z. (2013). Hesitant fuzzy power aggregation operators and their application to multiple attribute group decision making. Information Sciences, 234(5), 150–181. DOI 10.1016/j.ins.2013.01.002. [Google Scholar] [CrossRef]
24. Liao, H., Xu, Z. (2014). Some new hybrid weighted aggregation operators under hesitant fuzzy multi-criteria decision making environment. Journal of Intelligent & Fuzzy Systems, 26(4), 1601–1617. DOI 10.3233/IFS-130841. [Google Scholar] [CrossRef]
25. Liao, H., Xu, Z. (2015). Extended hesitant fuzzy hybrid weighted aggregation operators and their application in decision making. Soft Computing, 19(9), 2551–2564. DOI 10.1007/s00500-014-1422-6. [Google Scholar] [CrossRef]
26. Joshi, D., Kumar, S. (2016). Interval-valued intuitionistic hesitant fuzzy Choquet integral based TOPSIS method for multi-criteria group decision making. European Journal of Operational Research, 248(1), 183–191. DOI 10.1016/j.ejor.2015.06.047. [Google Scholar] [CrossRef]
27. Khan, M. S. A., Abdullah, S., Ali, A., Siddiqui, N., Amin, F. (2017). Pythagorean hesitant fuzzy sets and their application to group decision making with incomplete weight information. Journal of Intelligent & Fuzzy Systems, 33(6), 3971–3985. DOI 10.3233/JIFS-17811. [Google Scholar] [CrossRef]
28. Wan, S. P., Jin, Z., Dong, J. Y. (2018). Pythagorean fuzzy mathematical programming method for multi-attribute group decision making with Pythagorean fuzzy truth degrees. Knowledge and Information Systems, 55(2), 437–466. DOI 10.1007/s10115-017-1085-6. [Google Scholar] [CrossRef]
29. Wan, S. P., Jin, Z., Dong, J. Y. (2020). A new order relation for Pythagorean fuzzy numbers and application to multi-attribute group decision making. Knowledge and Information Systems, 62(2), 751–785. DOI 10.1007/s10115-019-01369-8. [Google Scholar] [CrossRef]
30. Garg, H. (2019). Hesitant Pythagorean fuzzy Maclaurin symmetric mean operators and its applications to multiattribute decision-making process. International Journal of Intelligent Systems, 34(4), 601–626. DOI 10.1002/int.22067. [Google Scholar] [CrossRef]
31. Garg, H. (2018). Hesitant Pythagorean fuzzy sets and their aggregation operators in multiple attribute decision-making. International Journal for Uncertainty Quantification, 8(3), 267–289. DOI 10.1615/Int.J.UncertaintyQuantification.2018020979. [Google Scholar] [CrossRef]
32. Khan, M. S. A., Abdullah, S., Ali, A., Rahman, K. (2020). Pythagorean hesitant fuzzy information aggregation and their application to multi-attribute group decision-making problems. Journal of Intelligent Systems, 29(1), 154–171. DOI 10.1515/jisys-2017-0231. [Google Scholar] [CrossRef]
33. Khan, M. S. A., Abdullah, S., Ali, A., Amin, F., Rahman, K. (2019). Hybrid aggregation operators based on Pythagorean hesitant fuzzy sets and their application to group decision making. Granular Computing, 4(3), 469–482. DOI 10.1007/s41066-018-0107-4. [Google Scholar] [CrossRef]
34. Zulqarnain, R. M., Siddique, I., Iampan, A., Baleanu, D. (2022). Aggregation operators for interval-valued pythagorean fuzzy so set with their application to solve multi-attribute group decision making problem. Computer Modeling in Engineering & Sciences, 131(3), 1717–1750. DOI 10.32604/cmes.2022.019408. [Google Scholar] [CrossRef]
35. Batool, B., Ahmad, M., Abdullah, S., Ashraf, S., Chinram, R. (2020). Entropy based pythagorean probabilistic hesitant fuzzy decision making technique and its application for fog-haze factor assessment problem. Entropy, 22(3), 318. DOI 10.3390/e22030318. [Google Scholar] [CrossRef]
36. Xu, Z., Zhou, W. (2017). Consensus building with a group of decision makers under the hesitant probabilistic fuzzy environment. Fuzzy Optimization and Decision Making, 16(4), 481–503. DOI 10.1007/s10700-016-9257-5. [Google Scholar] [CrossRef]
37. Ashraf, S., Abdullah, S. (2020). Emergency decision support modeling for COVID-19 based on spherical fuzzy information. International Journal of Intelligent Systems, 35(11), 1601–1645. DOI 10.1002/int.22262. [Google Scholar] [CrossRef]
38. Ashraf, S., Abdullah, S., Almagrabi, A. O. (2020). A new emergency response of spherical intelligent fuzzy decision process to diagnose of COVID19. Soft Computing. DOI 10.1007/s00500-020-05287-8. [Google Scholar] [CrossRef]
39. Khan, A., Abosuliman, S. S., Ashraf, S., Abdullah, S. (2021). Hospital admission and care of COVID-19 patients problem based on spherical hesitant fuzzy decision support system. International Journal of Intelligent Systems, 36(8), 4167–4209. DOI 10.1002/int.22455. [Google Scholar] [CrossRef]
40. Ashraf, S., Abdullah, S., Chinram, R. (2022). Emergency decision support modeling under generalized spherical fuzzy Einstein aggregation information. Journal of Ambient Intelligence and Humanized Computing, 13(4), 2091–2117. DOI 10.1007/s12652-021-03493-2. [Google Scholar] [CrossRef]
41. Batool, B., Abdullah, S., Ashraf, S., Ahmad, M. (2021). Pythagorean probabilistic hesitant fuzzy aggregation operators and their application in decision-making. Kybernetes, 51(4), 1626–1652. DOI 10.1108/K-11-2020-0747. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools