 Open Access
Open Access
ARTICLE
Language Education Optimization: A New Human-Based Metaheuristic Algorithm for Solving Optimization Problems
1
Department of Mathematics, Faculty of Science, University of Hradec Králové, Hradec Králové, 500 03, Czech Republic
2
Department of Applied Cybernetics, Faculty of Science, University of Hradec Králové, Hradec Králové, 500 03, Czech Republic
* Corresponding Author: Pavel Trojovský. Email:
(This article belongs to the Special Issue: Computational Intelligent Systems for Solving Complex Engineering Problems: Principles and Applications)
Computer Modeling in Engineering & Sciences 2023, 136(2), 1527-1573. https://doi.org/10.32604/cmes.2023.025908
Received 05 August 2022; Accepted 19 October 2022; Issue published 06 February 2023
Abstract
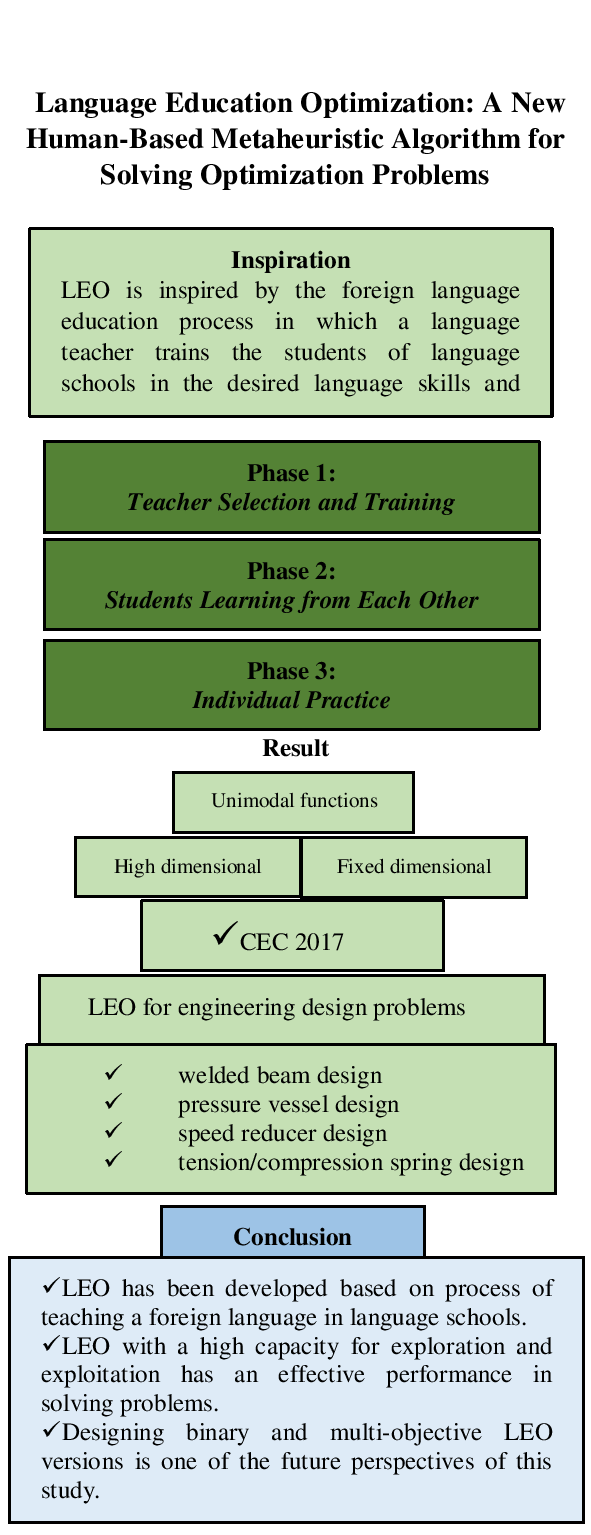
In this paper, based on the concept of the NFL theorem, that there is no unique algorithm that has the best performance for all optimization problems, a new human-based metaheuristic algorithm called Language Education Optimization (LEO) is introduced, which is used to solve optimization problems. LEO is inspired by the foreign language education process in which a language teacher trains the students of language schools in the desired language skills and rules. LEO is mathematically modeled in three phases: (i) students selecting their teacher, (ii) students learning from each other, and (iii) individual practice, considering exploration in local search and exploitation in local search. The performance of LEO in optimization tasks has been challenged against fifty-two benchmark functions of a variety of unimodal, multimodal types and the CEC 2017 test suite. The optimization results show that LEO, with its acceptable ability in exploration, exploitation, and maintaining a balance between them, has efficient performance in optimization applications and solution presentation. LEO efficiency in optimization tasks is compared with ten well-known metaheuristic algorithms. Analyses of the simulation results show that LEO has effective performance in dealing with optimization tasks and is significantly superior and more competitive in combating the compared algorithms. The implementation results of the proposed approach to four engineering design problems show the effectiveness of LEO in solving real-world optimization applications.Graphic Abstract
Keywords
Numerous challenges in various sciences face several possible solutions. Such challenges are known as optimization issues. Hence, the operation of finding the best solution to such problems is called optimization [1]. In order to deal with optimization problems, these problems must be modeled mathematically. This modeling defines the optimization challenge based on the three main parts of decision variables, constraints, and objective function [2].
Optimization techniques fall into two groups: deterministic and stochastic methods. Deterministic methods are efficient on optimization topics that have a linear, convex, continuous, differentiable objective function, and a continuous search space. However, as optimization problems become more complex, deterministic approaches lose their ability in real-world applications that have features, such as non-convex, discrete, nonlinear, non-differentiable objective functions, discrete search space, and high-dimensions [3]. Such difficulties in deterministic approaches have led scientists to efforts to introduce random methods that have effective performance in solving complex optimization problems. Metaheuristic algorithms, as a sub-group of stochastic methods, are efficient tools that rely on random search in the problem-solving space [4]. Metaheuristic algorithms have become very popular thanks to the following advantages: easy implementation, simple concepts, efficiency in discrete search spaces and efficiency in nonlinear, non-convex, and NP-hard problems [5].
The two most important factors influencing the performance of metaheuristic algorithms are exploration and exploitation. Exploration represents the power of the algorithm in the global search, and exploitation represents the power of the algorithm in the local search [6]. Due to the nature of random search in metaheuristic algorithms, the solutions obtained from these methods are not guaranteed to be the best solution to the problem. However, because these solutions are close to the global optimal, they can be accepted as searched solutions to optimization problems. In fact, what has prompted researchers to develop numerous metaheuristic algorithms has been the pursuit of solutions closer to the global optimal.
Natural phenomena, the behaviors of living things in nature, the laws of physics, the concepts of biology, and other evolutionary processes have been the sources of inspiration for the design of metaheuristic algorithms. The Genetic Algorithm (GA) [7], which is inspired by concepts of biology, the Particle Swarm Optimization (PSO) [8], which is inspired by bird life, the Artificial Bee Colony (ABC) [9], which is inspired by bee colony behaviors, and the Ant Colony Optimization (ACO) [10], which is inspired by ant swarm activities, are the widely used and most famous metaheuristic algorithms.
The main research question is: Despite the numerous metaheuristic algorithms introduced till now, is there still any necessity for designing newer metaheuristic algorithms? The No-Free-Lunch Theorem (NFL) [11] answers the question because it says that there is no guarantee that an algorithm with good results in solving some optimization problems will work well in solving other optimization problems. The NFL theorem is the main incentive for researchers to introduce new metaheuristic algorithms to be able to provide better solutions for optimization tasks.
The aspects of novelty and innovation of this study are in the introduction of a new human-based metaheuristic algorithm called Language Education Optimization (LEO) that is efficient in optimization tasks. The key contributions of this paper are as follows:
• LEO is introduced based on the simulation of the foreign language education process.
• The fundamental inspiration of LEO is to train students in language schools in language skills and rules.
• The LEO theory is described and then mathematically modeled in three phases.
• The performance of LEO in optimization tasks is assessed in dealing with fifty-two standard benchmark functions.
• The results of LEO are compared with the performance of ten well-known metaheuristic algorithms.
• The effectiveness of LEO in handling real-world applications is evaluated in the optimization of four engineering design problems.
The paper consists of the following sections: a literature review is provided in the section “Literature Review.’’ The proposed Language Education Optimization (LEO) approach is introduced and modeled in the section “Language Education Optimization.’’ LEO simulation and evaluation studies on the handling of optimization tasks are presented in the section “Simulation Studies and Results’’. A discussion of the results is provided in the section “Discussion.’’ The study evaluating the ability of the proposed LEO approach in CEC 2017 test suite optimization is presented in the section “Evaluation CEC 2017 Test Suite.” The analysis of LEO capabilities in real-world applications is presented in the section “LEO for Real-World Applications.” Conclusions and suggestions for further studies are expressed in the section “Conclusions and Future Researches.’’
Metaheuristic algorithms have been developed based on mathematical simulations of various phenomena, such as genetics and biology, swarm intelligences in the life of living organisms, physical phenomena, rules of games, human activities, etc. According to the main source of inspiration resulting in the design, metaheuristic algorithms fall into the following five groups: (i) swarm-based, (ii) evolutionary-based, (iii) physics-based, (iv) human-based, and (v) game-based methods.
Modeling the swarming behaviors and social and individual lives of living organisms (birds, aquatic animals, insects, animals, etc.) has led to the development of swarm-based metaheuristic algorithms. The major algorithms belonging to this group are PSO, ABC, and ACO. PSO is based on modeling the behavior of swarm movement of groups of fish and birds in which two factors, individuals' experience and group experience, affect the population displacement of the algorithm. ABC is based on simulating the social life of bees seeking food sources and extracting nectar from these food sources. ACO is based on the behavior of the ant colony searching the optimal path between the nest and the food sources. Artificial Hummingbird Algorithm (AHA) is a swarm-based method based on the simulation of intelligent foraging strategies and special flight skills of hummingbirds in nature [12]. Beluga Whale Optimization (BWO) is a swarm-based metaheuristic algorithm based on beluga whales’ behaviors, including pair swim, prey, and whale fall [13]. Starling Murmuration Optimizer (SMO) is a bio-inspired metaheuristic algorithm that is based on starlings’ behaviors during their stunning murmuration [14]. Rat Swarm Optimizer (RSO) is a bio-inspired optimizer that is proposed based on the chasing and attacking behaviors of rats in nature [15]. Sooty Tern Optimization Algorithm (STOA) is a bio-inspired metaheuristic algorithm that is introduced based on the simulation of attacking and migration behaviors of sea bird sooty tern in nature [16]. Emperor Penguin Optimizer (EPO) is proposed based on huddling behavior of emperor penguins in nature [17]. Orca Predation Algorithm (OPA) is introduced based on the hunting behavior of orcas, including driving, encircling, and attacking prey [18]. The activities of living organisms in nature, such as a search for food resources, foraging, and feeding through hunting effectively, have inspired the design of well-known metaheuristic algorithms, such as Whale Optimization Algorithm (WOA) [19], African Vultures Optimization Algorithm (AVOA) [20], Marine Predator Algorithm (MPA) [21], Golden Jackal Optimization (GJO) [22], Gray Wolf Optimizer (GWO) [23], Reptile Search Algorithm (RSA) [24], Honey Badger Algorithm (HBA) [25], Spotted Hyena Optimizer (SHO) [26], and Tunicate Swarm Algorithm (TSA) [27].
Modeling of genetics and biology concepts has been the main source for evolutionary-based metaheuristic algorithms development. The reproduction process simulation, based on the concepts of Darwin’s theory of evolution and natural selection, has been the main source in the design of Differential Evolution (DE) [28] and GA.
Modeling of the physical laws and phenomena has been used in the physics-based metaheuristic algorithms development. Material engineers use the annealing method to achieve a state in which the solid is well organized, and its energy is minimized. This method involves placing the material in a high-temperature environment and following a gradual lowering of the temperature. The Simulated Annealing (SA) method simulates this solid-state annealing process to solve the optimization problem [29]. Lichtenberg Algorithm (LA) is a physics-based optimization algorithm inspired by the Lichtenberg figures patterns and the physical phenomenon of radial intra-cloud lightning [30]. Henry Gas Solubility Optimization (HGSO) is a physics-based metaheuristic algorithm that is based on imitation of the behavior governed by Henry’s law [31]. Mathematical modeling of gravitational force and Newton’s laws of motion [32] is used in the Gravitational Search Algorithm (GSA) design. The development of Water Cycle Algorithm (WCA) [33] is based on the natural water cycle physical phenomenon. Archimedes Optimization Algorithm (AOA) [34], Spring Search Algorithm (SSA) [35], Multi-Verse Optimizer (MVO) [36], Equilibrium Optimizer (EO) [37], and Momentum Search Algorithm (MSA) [38] are other physics-based metaheuristic algorithms.
Modeling of human activities and interactions existing in society and individuals' life has led to the emergence of human-based metaheuristic algorithms. The educational environment of the classroom and the exchange of knowledge between the teacher and the students and also among students, have been a good inspiration source for Teaching-Learning Based Optimization (TLBO) [39]. Collaboration between members of a team and presenting teamwork applied with the aim to achieve the assigned goal set to the team is the main idea of the Teamwork Optimization Algorithm (TOA) [40]. Election Based Optimization Algorithm (EBOA) is developed based on the simulation of the election and voting process in society [41]. The War Strategy Optimization (WSO) [42] is based on the strategic movement of army troops during the war. Following Optimization Algorithm (FOA) is a human-based approach based on the simulation of the impressionability of the people of the society from the most successful person in the society who is known as the leader [43]. Human Mental Search (HMS) is a human-based method that is inspired by exploration strategies of the bid space in online auctions [44]. Examples of well-established and recently developed human-based metaheuristic algorithms are: Driving Training-Based Optimization (DTBO) [45], Chef-based Optimization Algorithm (CBOA) [46], and Poor and Rich Optimization (PRO) [47].
Modeling the game rules and behavior of players, referees, and coaches brings tremendous inspiration to game-based metaheuristic algorithms development. Football League simulations and club performances resulted in the Football Game Based Optimization (FGBO) [48], and the simulation of volleyball league matches is utilized in the Volleyball Premier League Algorithm (VPL) [49]. The Tug of war game inspired the Tug of War Optimization (TWO) [50]. Archer’s strategy in shooting inspired the Archery Algorithm (AA) [51], the players’ attempt to solve the puzzle inspired the Puzzle Optimization Algorithm (POA) [52], and the players’ skill in throwing darts inspired the Darts Game Optimizer (DGO) [53]. Some other game-based metaheuristic algorithms are Ring Toss Game-Based Optimization (RTGBO) [54], Dice Game Optimizer (DGO) [55], and Orientation Search Algorithm (OSA) [56].
We have not found any metaheuristic algorithms simulating a foreign language education process in language schools. However, the process of teaching language skills decided by the teacher and applied to the learners is an intelligent structure with remarkable potential to be used in designing a new optimizer. In order to complete this research gap, a new human-based metaheuristic algorithm based on a simulation of the foreign language teaching process and the interactions of the people involved in it is designed and presented in this paper.
3 Language Education Optimization
In this section, the metaheuristic algorithm LEO and its mathematical model based on the simulation of human activity in foreign language education is presented.
One of the most important ways human beings communicate with each other is by using their ability to speak. First, human beings acquire and empirically learn the official language of their society and country. With the advancement of societies and technology, communication between different nations has increased. This reality has led to the increasing importance of learning not only the native language if people are to be able to communicate with people living in other countries. As a consequence, foreign language schools have been established.
When a person decides to learn other languages, she/he has several options for choosing a school or language teacher. Choosing the appropriate school and teacher is one of the essential steps which has a great impact on the person’s success in the language learning process. After the learner chooses the language teacher, she/he also communicates with other students in the classroom environment. These learners make efforts to learn language skills from the teacher training them in the given classroom environment. Additionally, to improve their skills, the students talk and practice with each other. These interactions between students improve their level of language learning. In addition, each student improves foreign language skills by doing homework and individual practice.
There are three important phases in this intelligent process, which represent the basic specifics of human activity in foreign language teaching, which must be considered into account in the new design of the metaheuristic algorithm. These three phases are (see Figs. 1 to 3): (i) students selecting their teacher, (ii) students learning from each other, and (iii) individual practice. Mathematical modeling of foreign language education based on these three phases is utilized in the design of LEO.
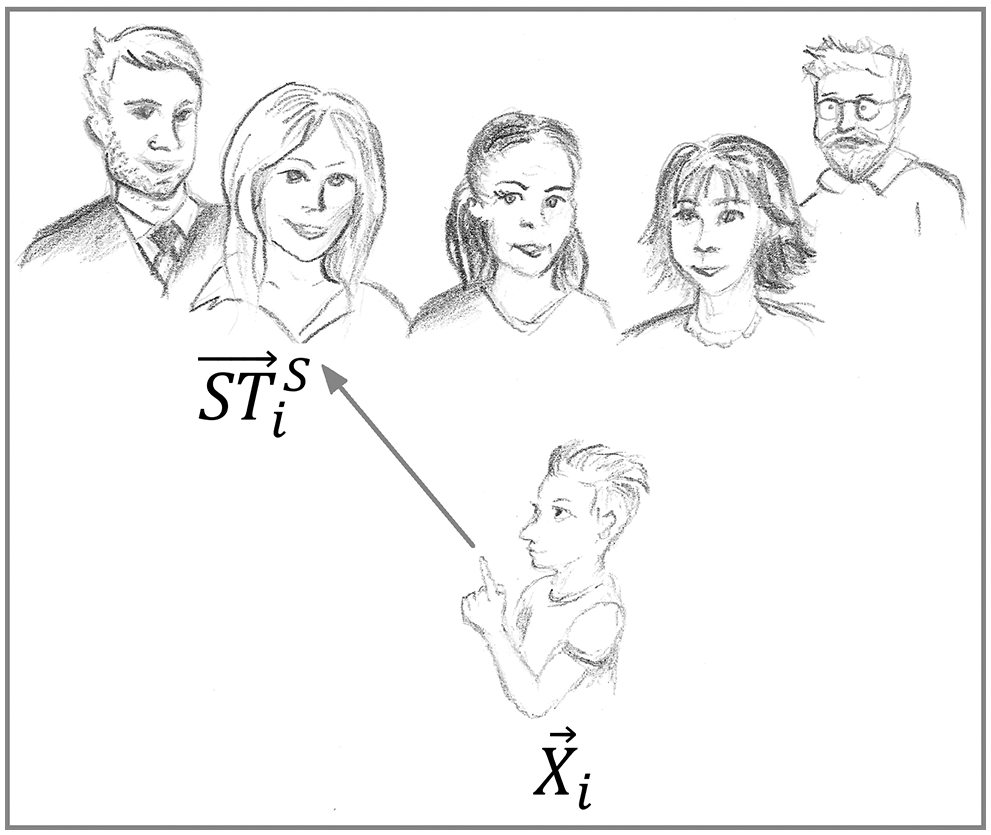
Figure 1: The first phase: Selection of a teacher

Figure 2: The second phase: Students learning in pairs
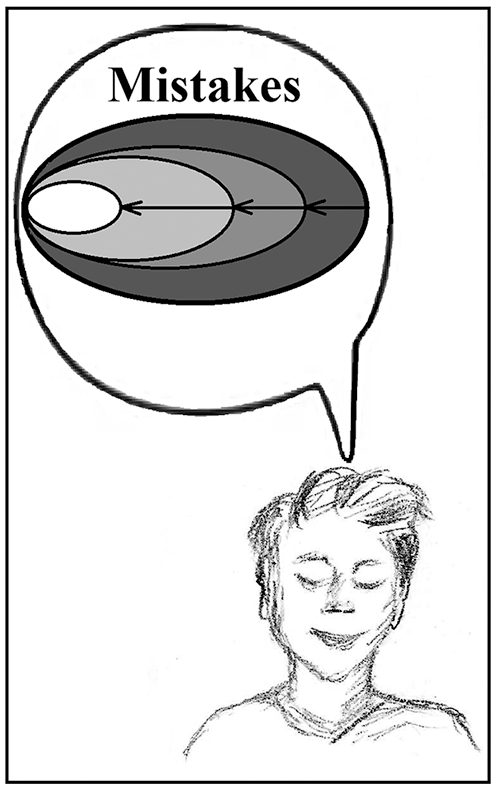
Figure 3: The third phase: Individual practice
LEO is a population-based approach that is able to provide the problem-solving process for an optimization task in an iteration-based procedure. Each member of LEO is a candidate solution of the optimization problem that proposes values for decision variables. From a mathematical point of view, each LEO member can be modeled using a vector, and the population of LEO members using a matrix according to the Eq. (1).
where
The initial positions of all LEO members in the search space are randomly set-up by the Eq. (2).
where r is a random number from the interval
where
As the value of the objective function is the main criterion for measuring the goodness of a candidate solution, the minimal value in the set of values of objective function
3.3 Mathematical Modelling of LEO
By initializing the algorithm, candidate solutions are generated and evaluated. These candidate solutions in LEO are updated in three different phases to improve their quality.
3.3.1 Teacher Selection and Training
Each person can choose one of the available teachers in order to learn a foreign language. In LEO, for each member of the population, members who have a better objective function value than that member are considered as suggested teachers. One of these suggested teachers is randomly selected for language teaching whose schematic is shown in Fig. 1.
This strategy leads LEO members to move to different areas of the search space, which demonstrates the global search power of LEO in exploration. In order to mathematically model this phase, the set of suggested teachers for each member of LEO, thus, for the
where
Similar to the decision of the student in language school, who chooses a teacher from among the teachers who teach in the school, in the design of LEO, this concept has also been selected for choosing a teacher. Therefore, one teacher is randomly selected among the members who have been identified as possible teachers to teach the
In language school, the teacher tries to make positive changes in the student’s foreign language skill level by teaching the student. Inspired by this process, in the design of LEO, the number of changes in the position of the population members has been calculated based on the subtraction of the position of the teacher and the student to improve the position of the population members in the search space. According to this, new components of each LEO member are generated for
where
where
3.3.2 Students Learning from Each Other
In the second phase of LEO, population members of LEO are updated based on modeling skills exchange between students. Students try to improve their skills based on their interactions with each other whose schematic is shown in Fig. 2.
This affects the ability of LEO exploration to scan the search space. In language schools, students usually practice with each other and improve their skills. In this exercise, the student who has more skills tries to increase the scientific level of that student by teaching another student. Inspired by this interaction in language school, in LEO design, another member of the population is randomly selected for each member of the population. Then, based on the subtraction of the difference in the position of the two members, the changes in the displacement of the corresponding member are calculated. To mathematically model these interactions, for each LEO member another member of the population is randomly selected, and it is used for recomputing of its components. Thus, the new components of each member of LEO are calculated for
where
The third phase of LEO is motivated by learning approaches that are commonly called self-learning. This is how the students make efforts to identify their own learning needs. Set learning goals, find the additional study literature and self-study online platforms. In this phase of LEO, members of LEO are updated based on simulations of individual students’ practices to improve the skills they have acquired from the teacher in the first phase whose schematic is shown in Fig. 3.
In fact, LEO scans the search space around members based on local search, seeking better solutions. A student who goes to a language school, after participating in the class and practicing with her/his classmates, tries to improve his skills as much as possible with individual practice, which leads to small but useful changes in the student’s language skills. Inspired by this student’s behavior in the language learning process, in the design of LEO, the students’ individual practice is modeled by making small changes in their position. To model the concepts of this LEO phase mathematically, a random position near each member is first generated using Eq. (9).
where
Subsequently, a decision is made whether to update each LEO member
where
3.3.4 Repetition Process, Pseudocode, and Flowchart of LEO
After updating all members of LEO based on all three phases, an iteration of the algorithm is completed. At the end of each iteration, the best candidate solution is updated. The iterative process of the algorithm based on Eqs. (4) to (10) continues until the end of the LEO implementation. After the LEO implementation is completed, the best candidate solution obtained during the iteration of the algorithm for the given problem is presented. The LEO pseudocode is presented in Algorithm 1 and the flowchart of its implementation is presented in Fig. 4.

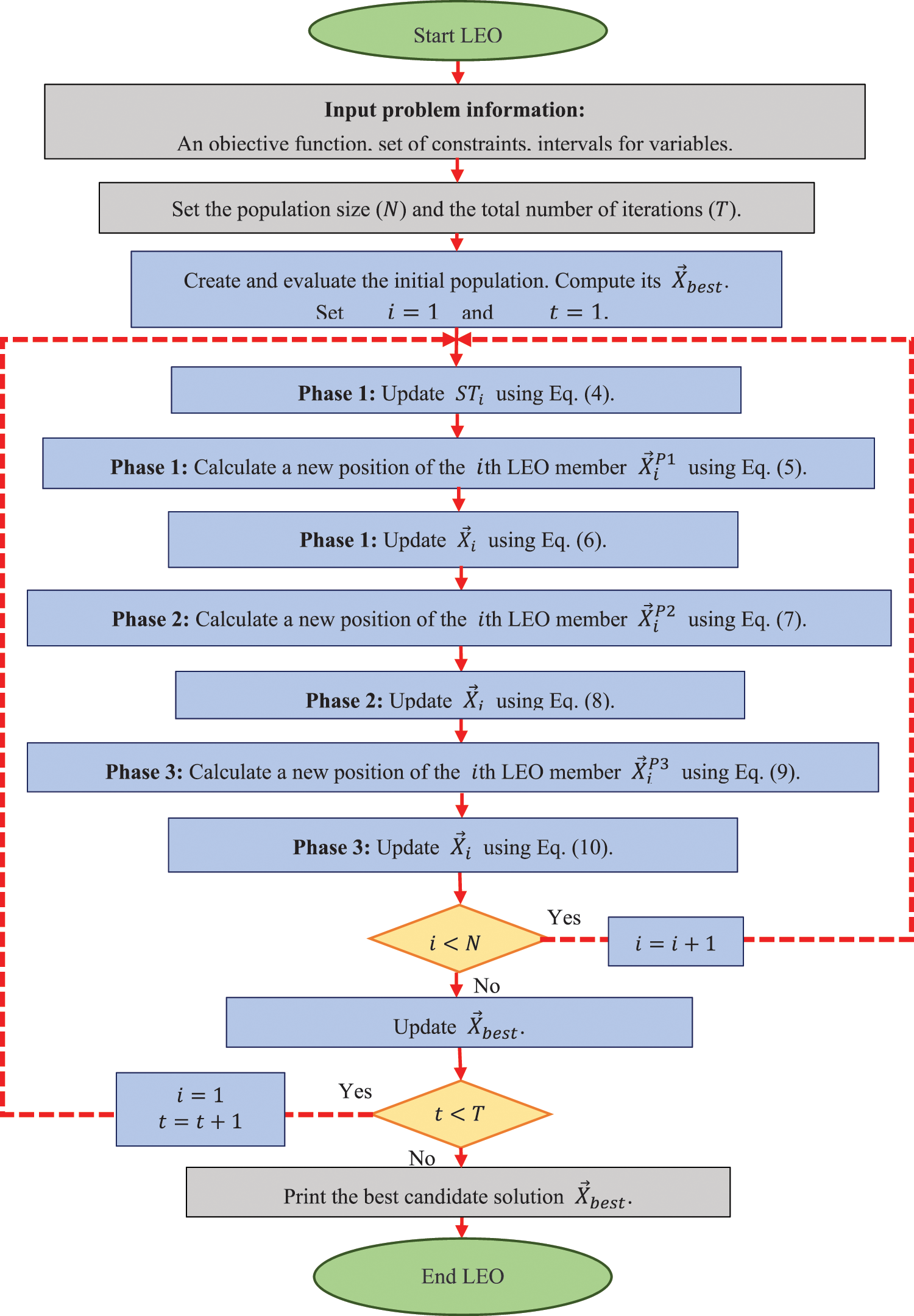
Figure 4: Flowchart of LEO
3.4 Computational Complexity of LEO
The computational complexity of LEO is analyzed in this subsection. LEO initialization has a computational complexity equal to
The TLBO algorithm updates the population members of the algorithm in two phases, teacher and student. On the other hand, the proposed LEO approach updates the population members in three stages: teacher selection and training, students learning from each other, and individual practice.
In the teacher’s phase of the TLBO algorithm, the best member is considered a teacher for the entire population, and the other members are considered students. But in LEO, for each member of the population, all the members with better fitness compared to that member are considered candidate teachers for the corresponding member. Among them, the teacher is randomly selected to train the corresponding member. Also, in the population update equation in TLBO, subtracting the teacher’s position from the average of the entire population is used. But in the population update equation in LEO, the difference between the selected teacher’s position and the corresponding member’s position. In the student phase of the TLBO algorithm, the update equation is modeled based on the subtraction of the position of two students. But in the design of LEO, the subtraction of the member with better fitness than the other member multiplied by the I index is used.
Also, compared to TLBO, which only has two phases of population update, in LEO design, to increase the exploitation ability in local search, the third phase of an update called individual exercise is used.
4 Simulation Studies and Results
In this section, the capability of the proposed LEO algorithm in optimization applications is studied. A set of twenty-three objective functions including seven unimodal functions, six multimodal functions, and ten fixed-dimensional multimodal functions have been utilized to analyze LEO performance. Details and full description of these benchmark functions are provided in [57]. The reasons for selecting these benchmark functions are explained below. Unimodal functions, including F1 to F7, have only one extremum in their search space and, therefore, lack local optimal solutions. The purpose of optimizing these types of functions is to test the exploitation power of the metaheuristic algorithm in the local search and to get as close to the global optimal as possible. multimodal functions, including F8 to F13, have a number of extremums, of which only one is the main extremum and the rest are local extremums. The main purpose of optimizing this type of functions is to test the exploration power of the metaheuristic algorithm in the global search to achieve the main extremum and not get stuck in other local extremums. Multimodal functions including F14 to F23 have smaller dimensions, as well as fewer local extremums, compared to multimodal functions F8 to F13. The purpose of optimizing these functions is to simultaneously test the exploration and exploitation of the metaheuristic algorithm in local and global searches. In fact, the purpose of selecting these functions is to benchmark the ability of the metaheuristic algorithm to strike a balance between exploitation and exploration. Details of these functions are provided in Tables 1–3 [57].



LEO’s ability in optimization applications is compared with the performance of ten well-known metaheuristic algorithms. The reasons for choosing these competitor algorithms are explained below. The first group includes the widely used and well-known GA and PSO algorithms. The second group includes highly cited algorithms TLBO, MVO, GSA, GWO, and WOA, which have been employed by researchers in many optimization applications. The third group includes MPA, RSA, and TSA algorithms that have recently been published and have received a lot of attention. The control parameters of the competitor algorithms are set according to Table 4.
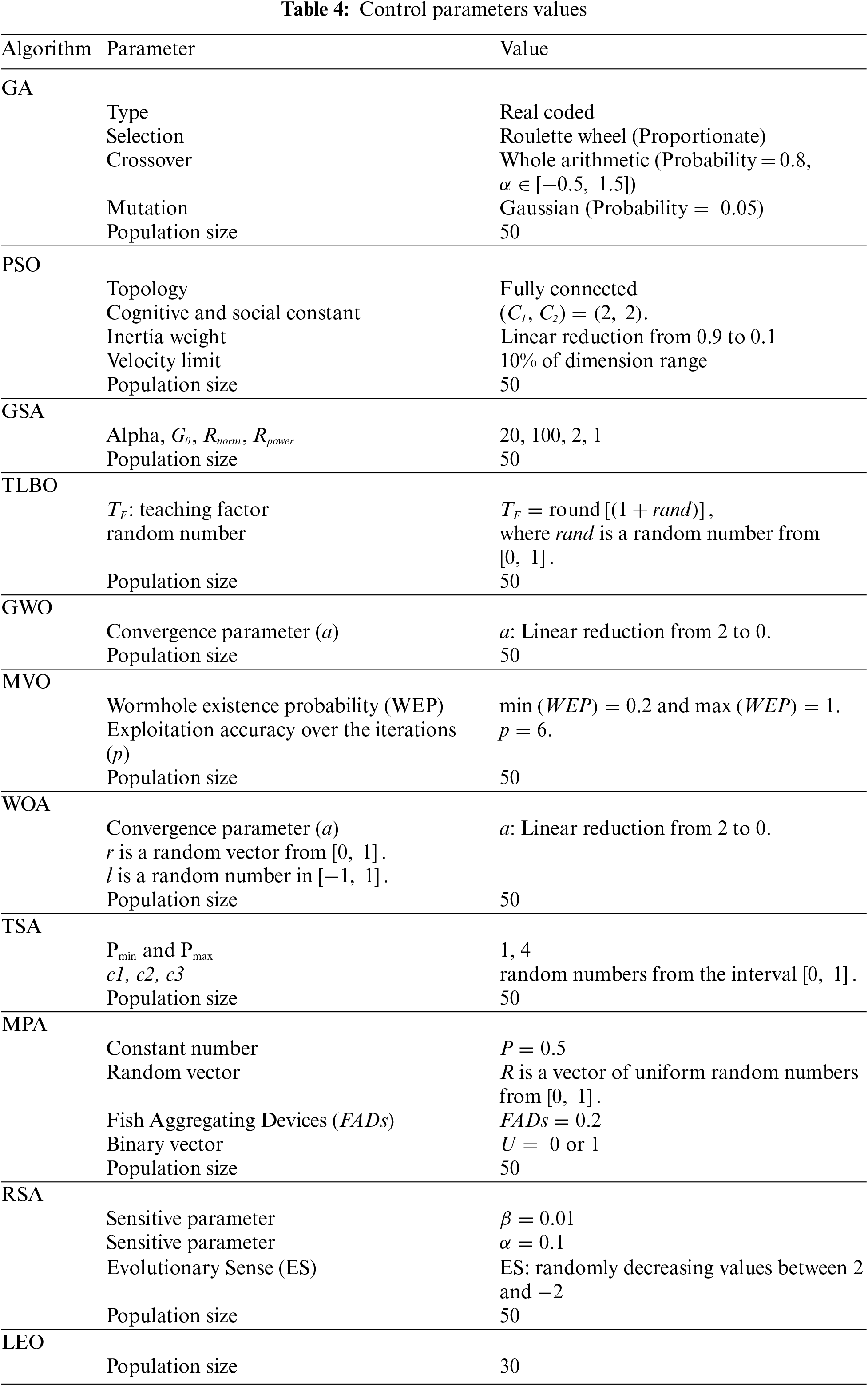
The LEO method and ten competing algorithms are each employed in twenty independent executions, while each execution contains 1000 iterations to optimize the objective functions. The results of these simulations are reported using indicators: best, mean, median, standard deviation (std), execution time (ET), and rank.
4.1 Evaluation Unimodal Objective Function
The results of recruiting LEO and competitor algorithms to handle the benchmark functions F1 to F7 are reported in Table 5. Based on the optimization results, it is inferred that LEO with a high local search capability has been able to converge to the global optimal in handling the functions of F1, F2, F3, F4, F5, and F6. Additionally, in handling F7, the proposed LEO approach ranks first as the best optimizer for this function compared to competitor algorithms. What can be deduced from the analysis of the simulation results is that LEO has a superior performance in handling the unimodal functions of F1 to F7 compared to ten competitor algorithms, by presenting much better and more competitive results.
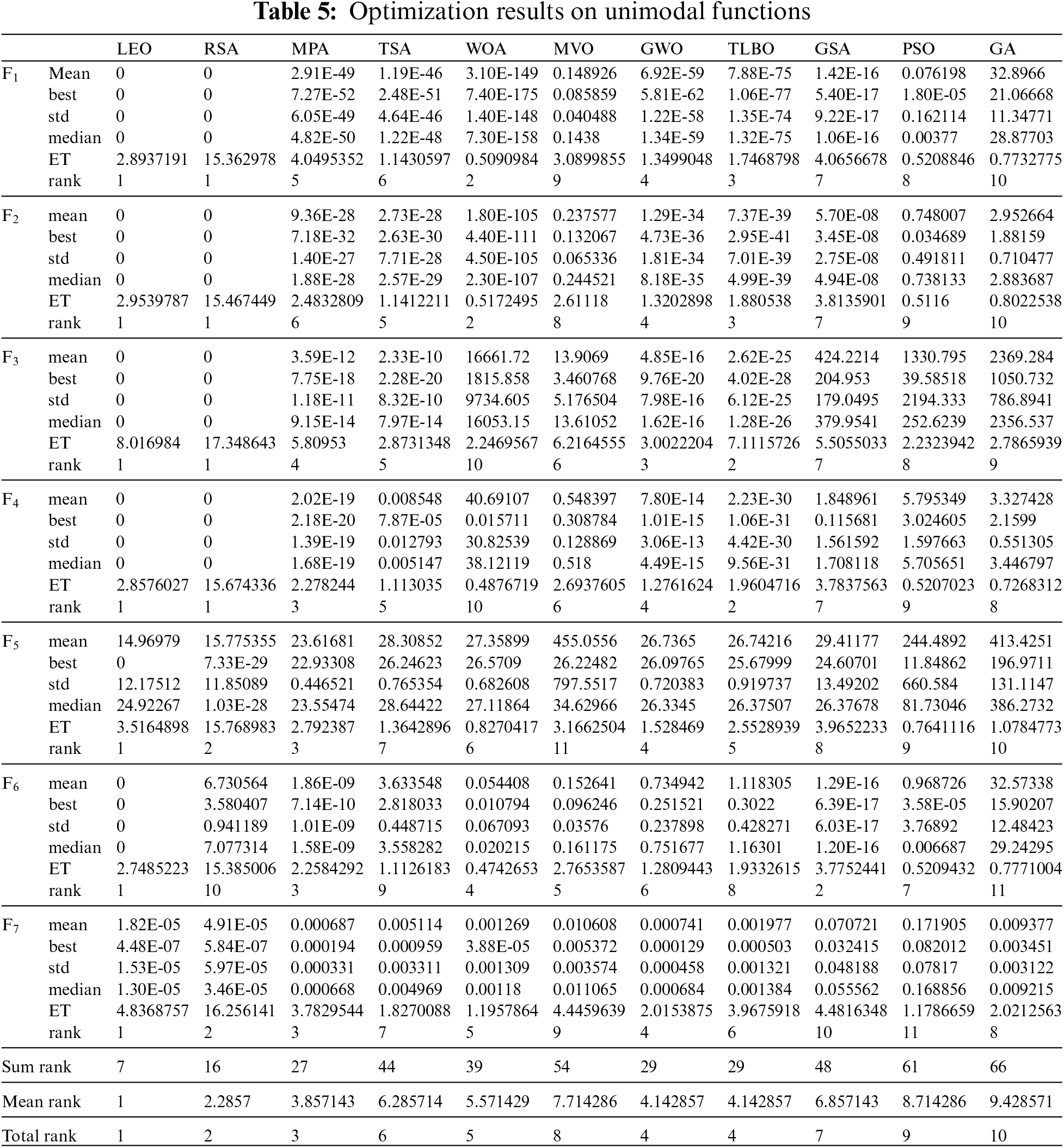
4.2 Evaluation Multimodal Objective Function
The optimization results for the multimodal functions F8 to F13 using LEO and competitor algorithms are released in Table 6. The simulation results show the high global search power of LEO in identifying the main optimal area in the search space and providing the global optima for functions F9 and F11. In tackling the functions F10, F12, and F13, the LEO approach ranks first as the best optimizer against ten competitor algorithms. In handling F8, the proposed LEO approach is the second-best optimizer for this function after GA. Analysis of simulation results shows that LEO has an effective capability in global search and has outperformed competitor algorithms in handling functions F8 to F13.
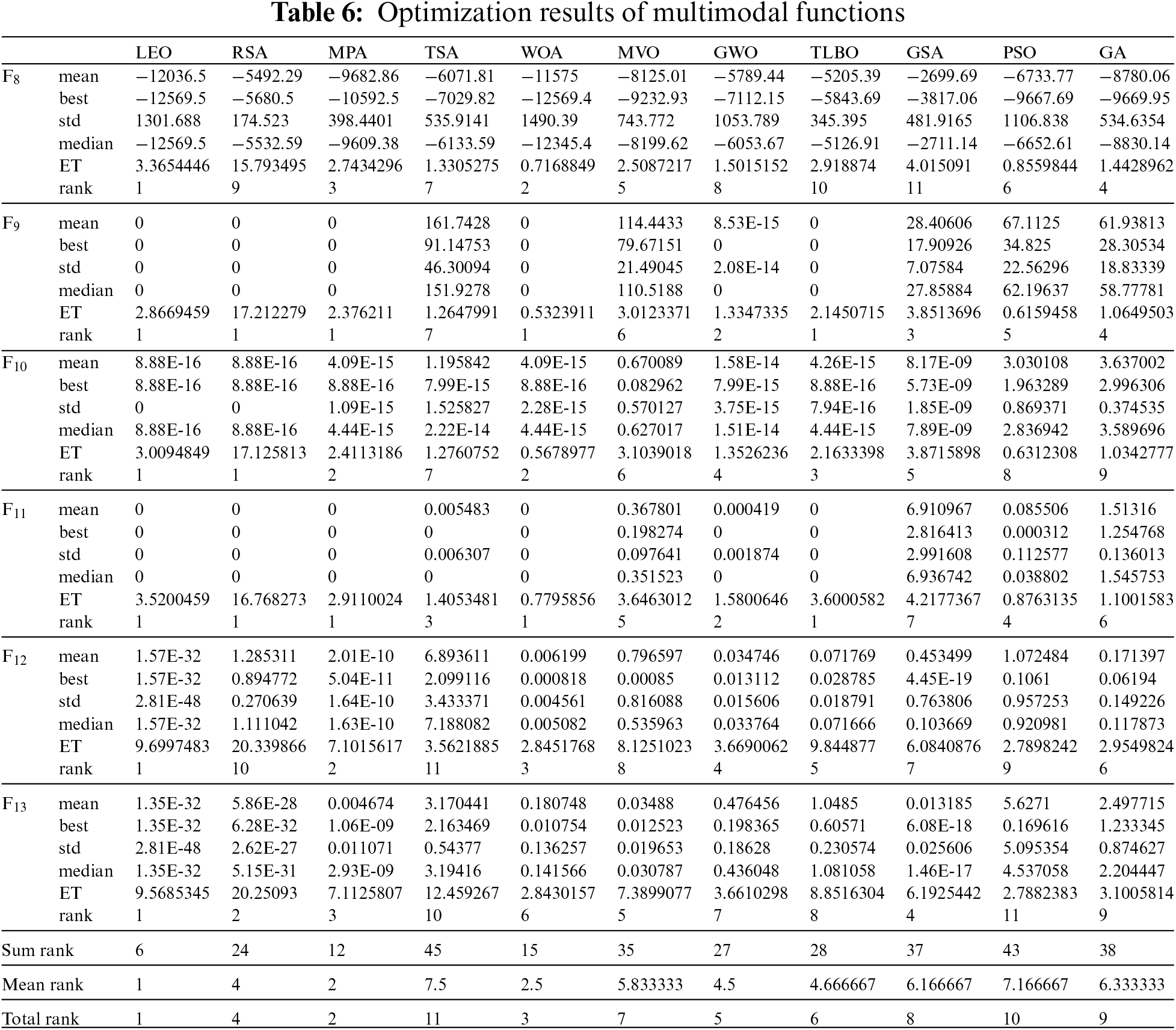
4.3 Evaluation Fixed-Dimensional Multimodal Objective Function
The results of recruiting LEO and ten competitor algorithms to tackle fixed-dimensional multimodal functions F14 to F23 are reported in Table 7. The optimization results show that LEO is the best optimizer in handling functions F14, F19, and F20 against ten competitor algorithms. In functions where LEO has a performance similar to some of the competitor algorithms in presenting the “mean” index, it can be seen that the proposed algorithm has provided more efficient performance in handling the relevant functions by providing better values for the ‘‘std’’ index. What can be deduced from the analysis of the simulation results is that LEO has a superior performance compared to competitor algorithms by having the suitable ability to search globally and locally, as well as maintaining a balance between exploration and exploitation.
Boxplot diagrams of the proposed LEO and competitor algorithms to handle the functions F1 to F23 are shown in Fig. 5.
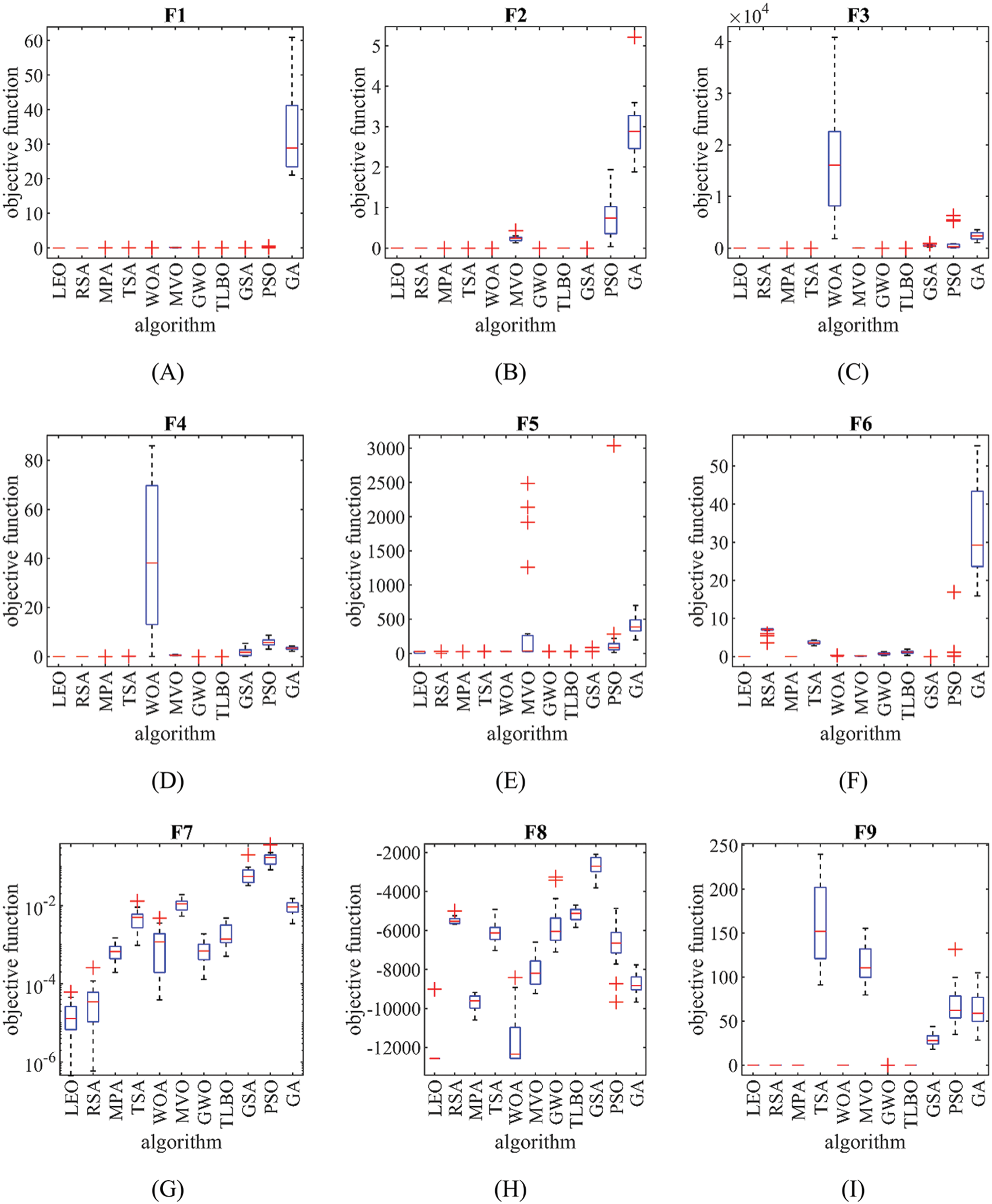
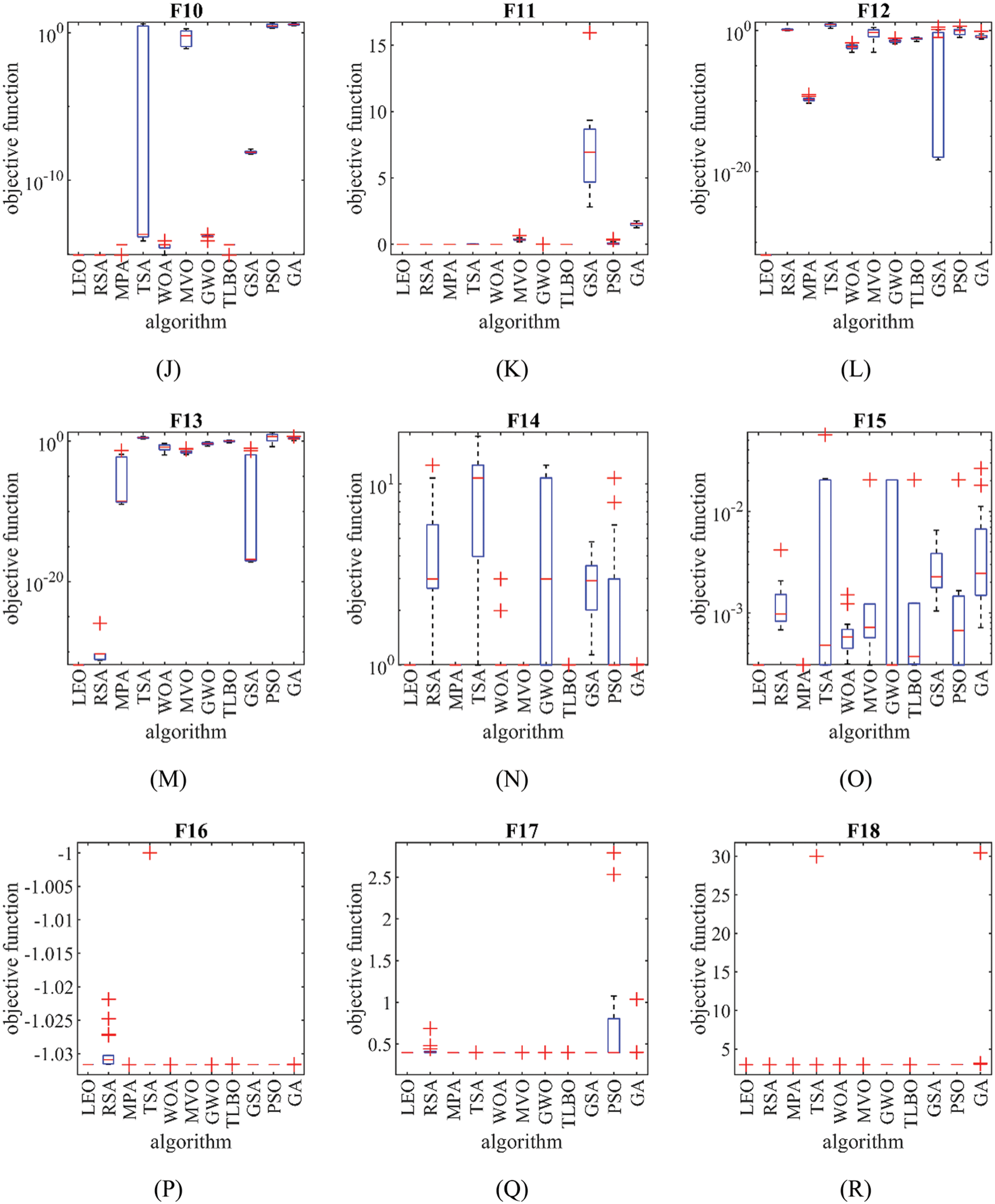
Figure 5: Boxplot diagrams of LEO and competitor algorithms performances on F1 to F23
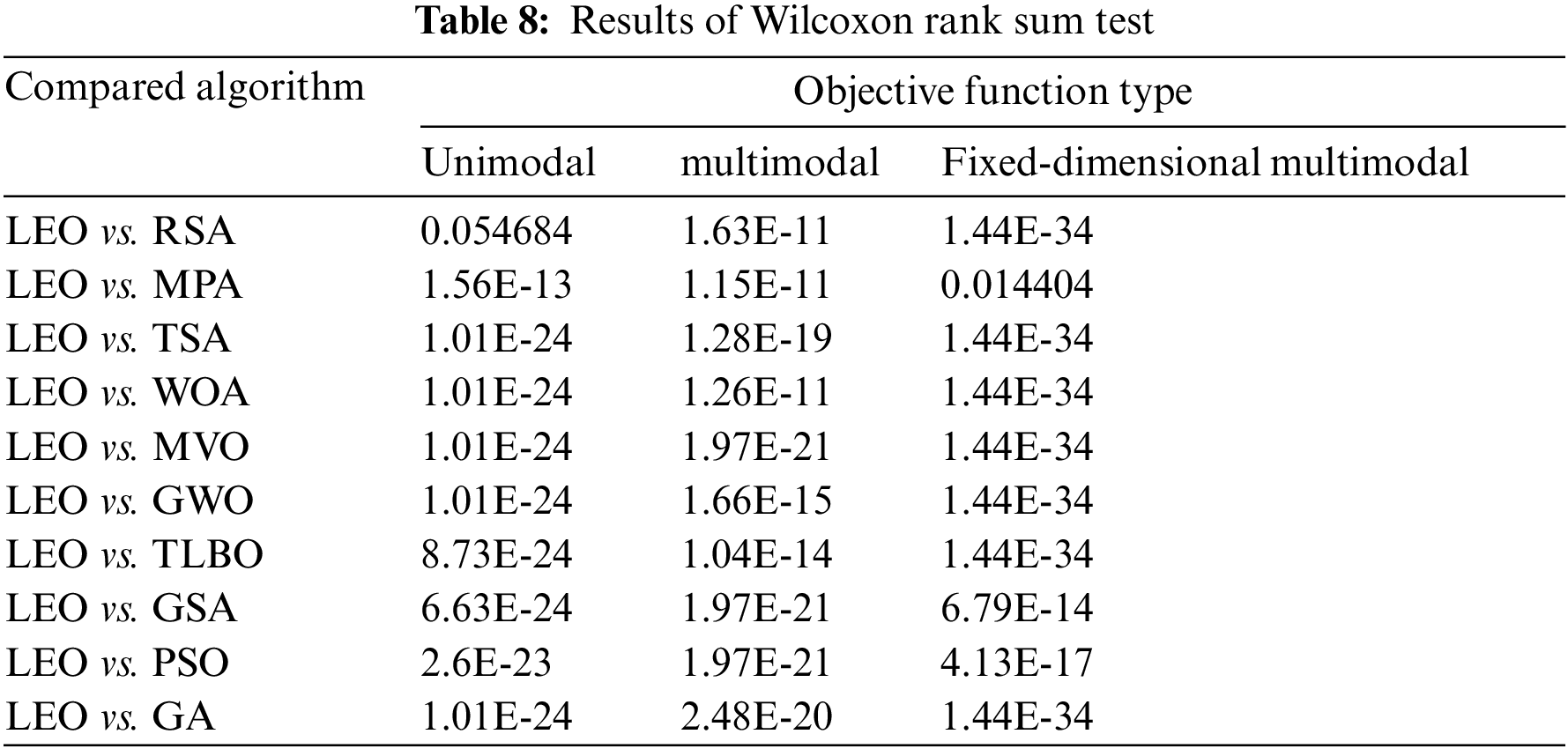
This subsection is devoted to statistical analysis to determine whether LEO has a statistically significant superiority over competitor algorithms. To this end, the non-parametric Wilcoxon rank sum test is utilized to determine this issue [58]. As usual, a “
The results obtained from the statistical analysis using the Wilcoxon rank sum test of the performance of the LEO and competitor algorithms are presented in Table 8. What can be deduced from the results of statistical analysis is that in cases where the p-value is less than 0.05, LEO has a significant statistical superiority over the compared algorithm. Consequently, it is observed that LEO has a statistically significant advantage over all competitor algorithms.
The LEO method performs the optimization process using a random search of its population members in the problem-solving space in an iteration-based procedure. As a result, the LEO population size (
In the first analysis, the sensitivity of the LEO to the parameter N is evaluated. For this purpose, LEO is used for different values of the parameter N equal to 20, 30, 50, and 100 to handle the benchmark functions F1 to F23. The results of this simulation are published in Table 9 and the LEO convergence curves under this study are plotted in Fig. 6. What can be deduced from the LEO sensitivity analysis to the parameter N is that increasing the set values for the parameter N increases the algorithm’s search power to achieve better solutions, and as a result, the objective function values decrease.
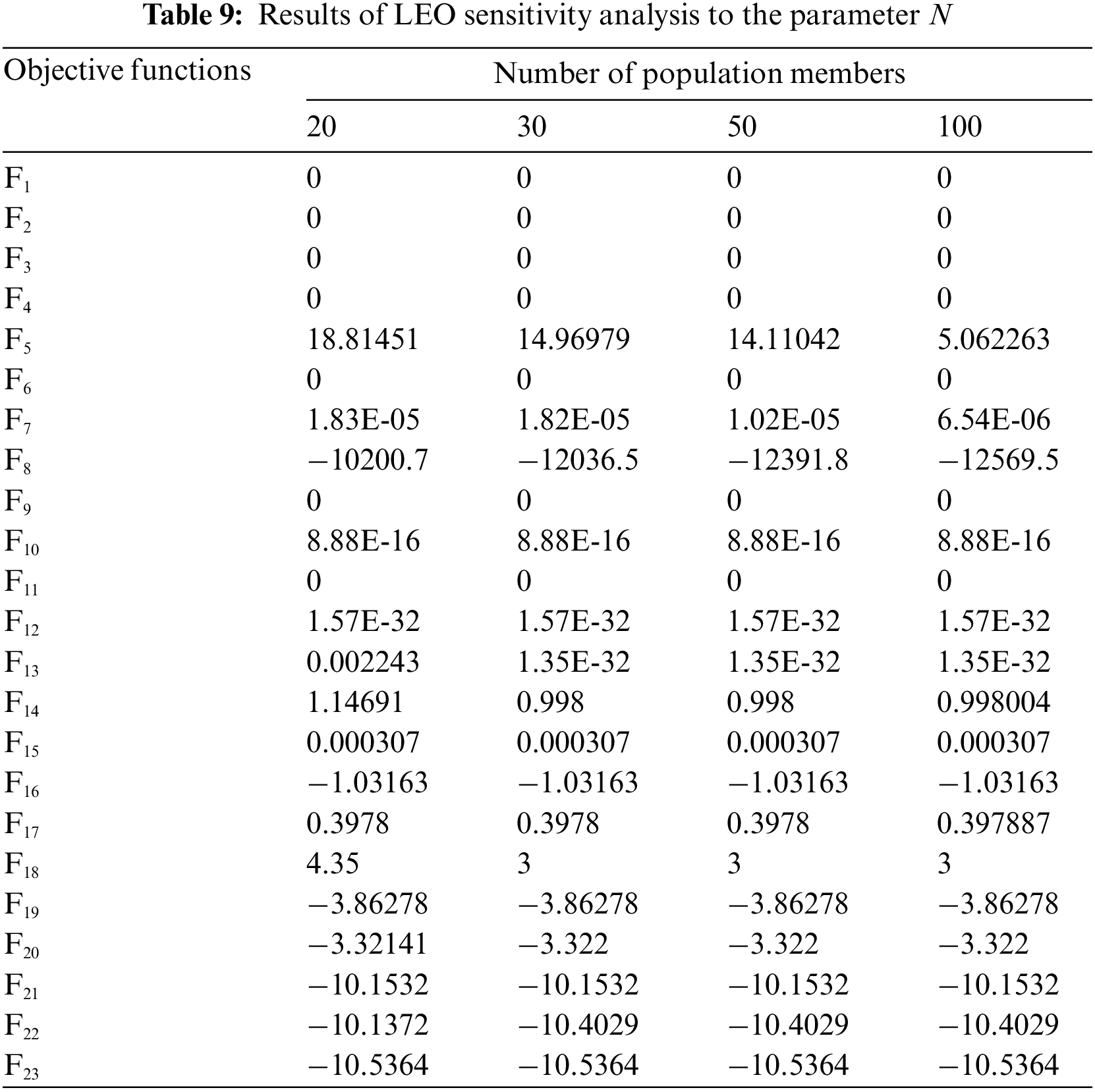
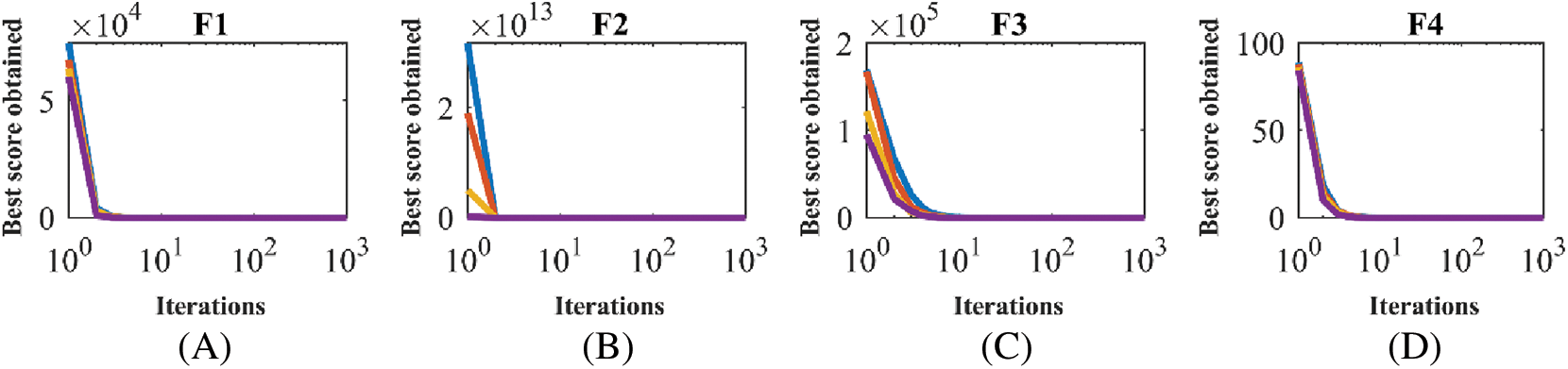
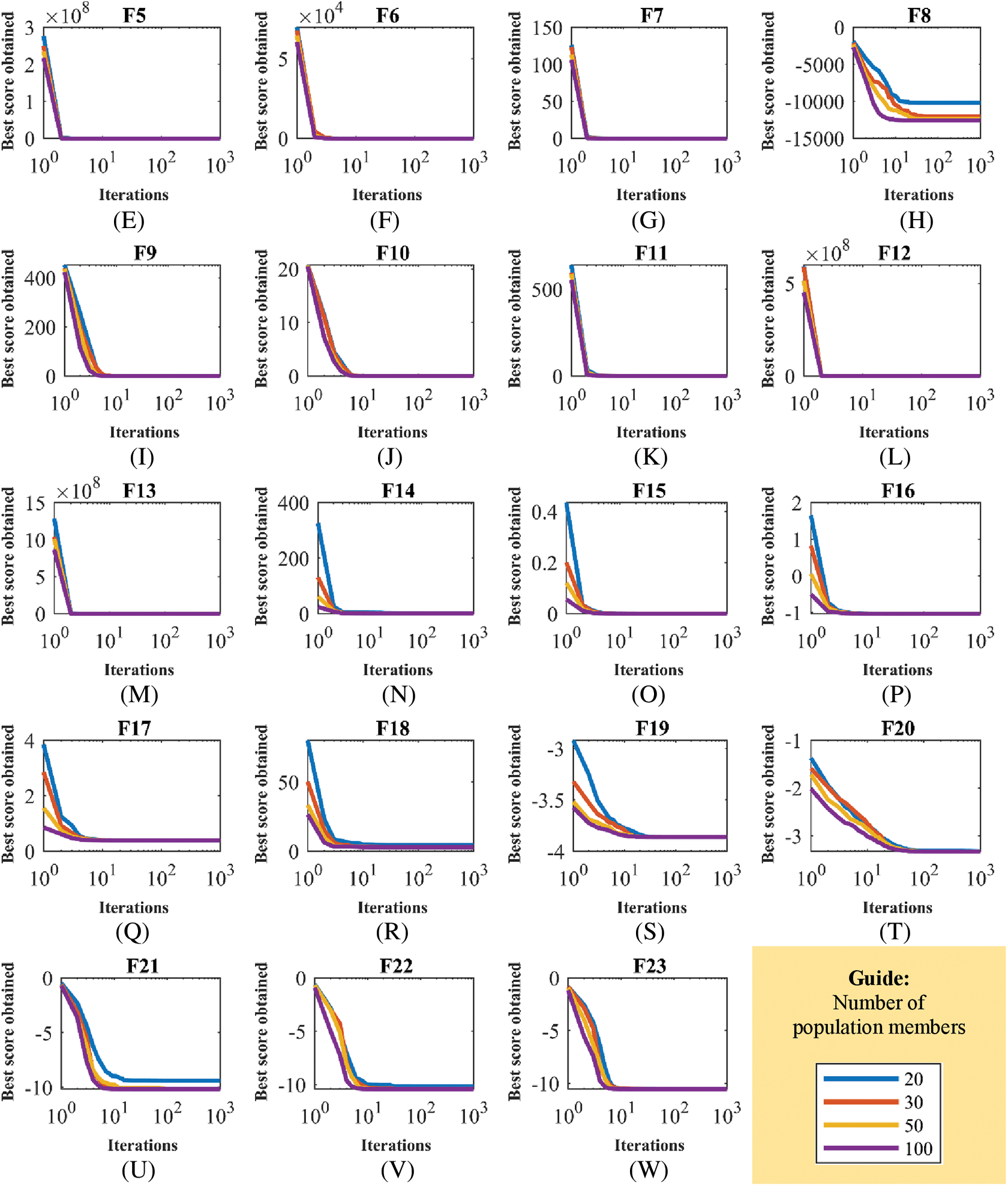
Figure 6: LEO convergence curves in the study of sensitivity analysis to the parameter
In the analysis, the sensitivity of LEO to the T parameter is evaluated. For this purpose, LEO is utilized for different values of the T parameter equal to 200, 500, 800, and 1000 to tackle the F1 to F23 benchmark functions. The results of this simulation are released in Table 10 and the LEO convergence curves of this study are plotted in Fig. 7. Based on the simulation results obtained from the LEO sensitivity analysis to the parameter T, it is observed that by increasing the values of the parameter T, the proposed approach has converged to better results, and as a result the values of the objective function have decreased.
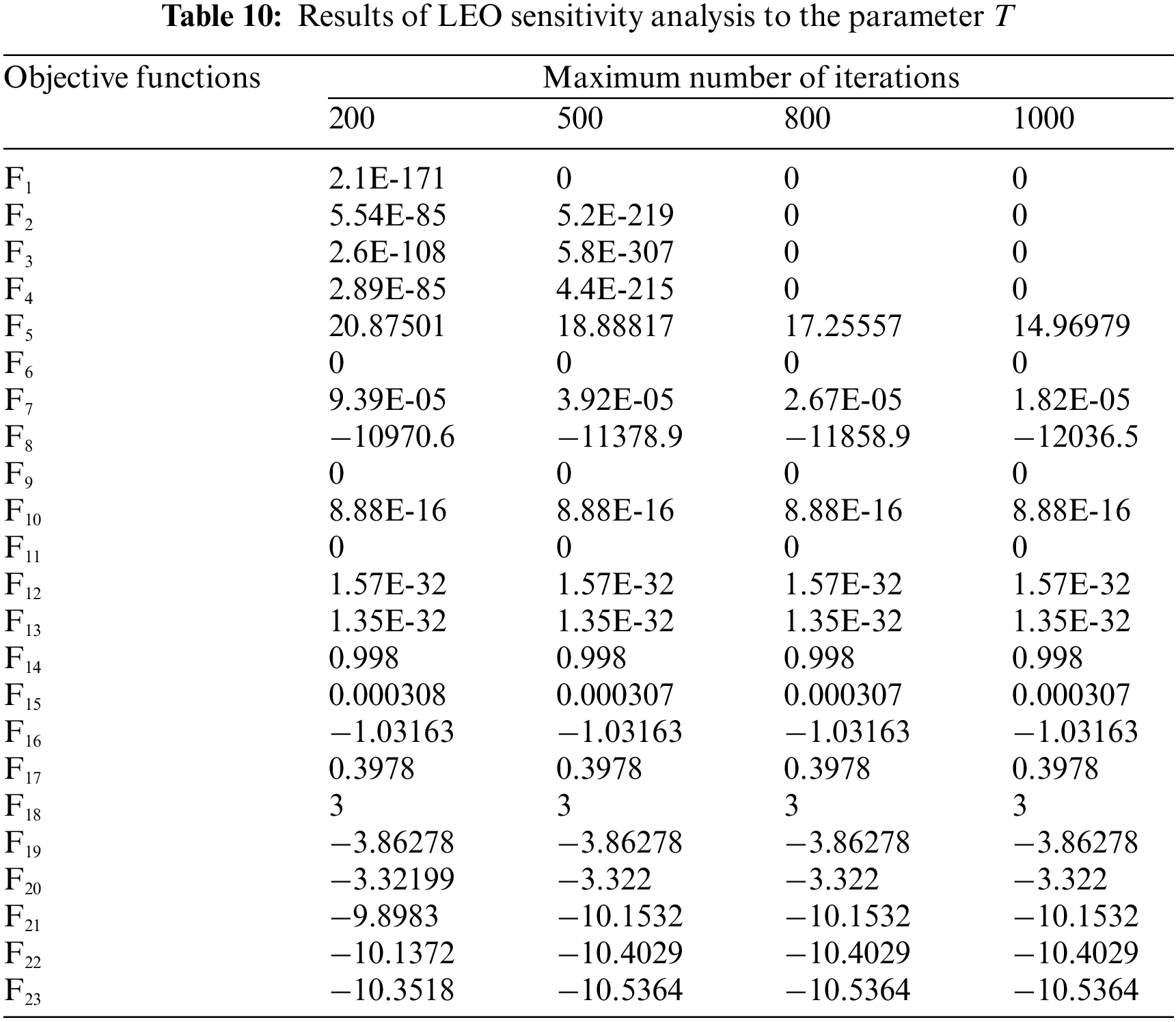
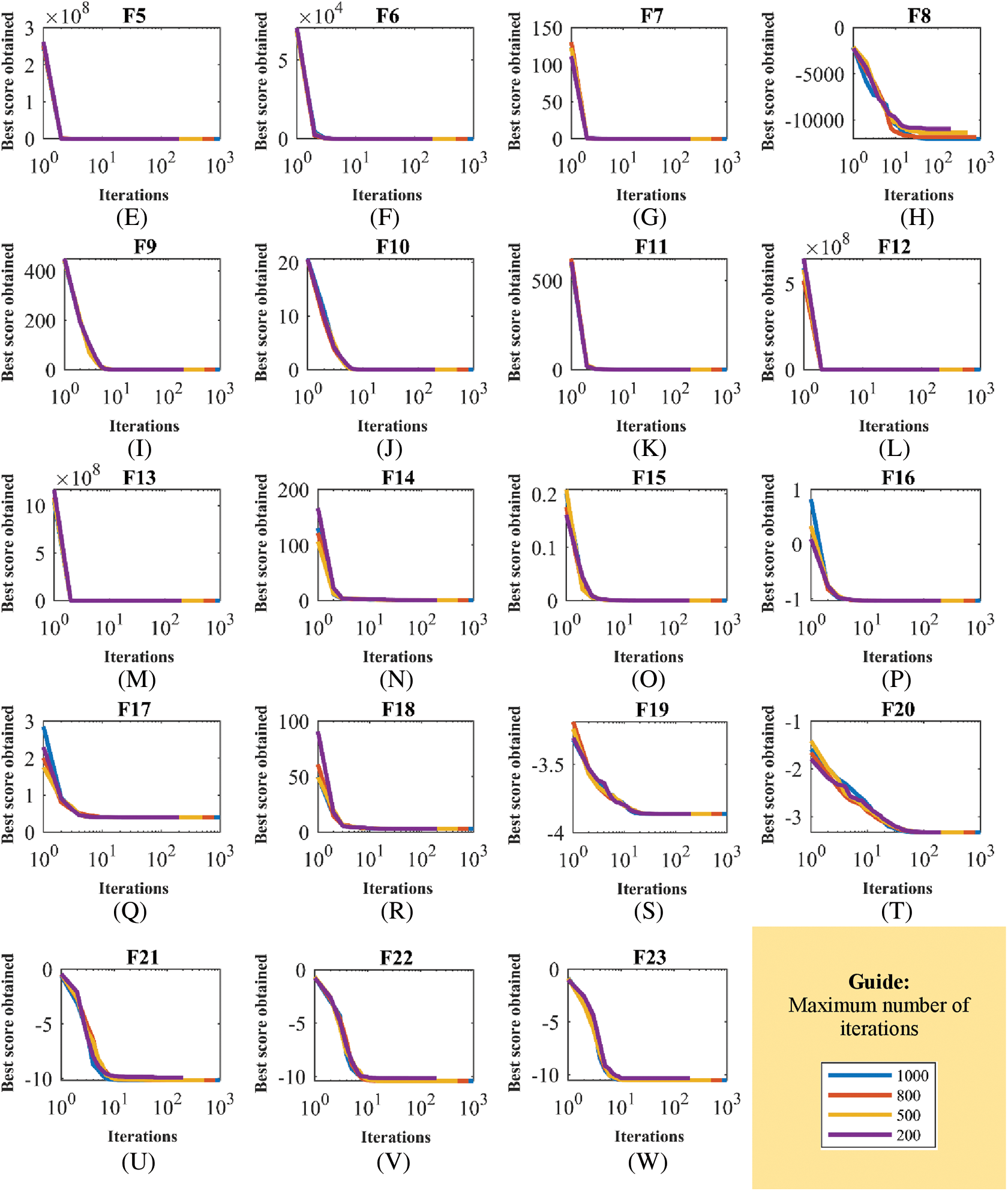
Figure 7: LEO convergence curves in the study of sensitivity analysis to the parameter
Metaheuristic algorithms provide an optimization process based on a random search in the problem-solving space. The optimization operation will be successful when, first, the problem-solving space is scanned well at the global level, and second, it is scanned around the solutions discovered at the local level.
Metaheuristic algorithms based on local search, which indicates the exploitation ability of an algorithm, scan around existing solutions to achieve a better possible solution. Exploitation gives this capability to the metaheuristic algorithm to be able to converge towards the global optimal. The exploitation power of a metaheuristic algorithm in local search is well measured in unimodal problems. These types of issues have only one optimal solution, and the goal of optimizing them is to get as close as possible to the global optimal based on the power of exploitation. The results obtained from LEO on the unimodal functions of F1 to F7 indicate the exploitation capability of the proposed method in converging towards global optimal. This ability is especially evident in handling the functions F1, F2, F3, F4, F5, and F6, as LEO is converged precisely to the global optimum. Therefore, the simulation finding of unimodal functions is the high exploitation capability of LEO in local search.
Metaheuristic algorithms based on global search, which indicates the exploration ability of the algorithm, scan different parts of the problem-solving space with the aim of identifying the main optimal area without getting caught up in local solutions. In fact, exploration gives this metaheuristic algorithm the ability to break out of local optimal solutions. The exploitation power of a metaheuristic algorithm in global search is well measured in multimodal problems. In addition to the main solution, these types of problem have several local solutions, and the purpose of optimizing them is to identify the area related to the main optimal solution based on the power of exploration. The results obtained from the use of LEO in the multimodal functions of F8 to F13 indicate the exploration ability of the proposed method in identifying the main optimal region and not getting caught in local solutions. This ability is especially evident in the handling of the functions F9 and F11, as LEO has been able to both discover the local optimal region well and converge precisely to the global optimal of these functions. Thus, the finding that simulates multimodal functions is the high exploration capability of LEO in the global search.
Although exploration and exploitation capabilities are crucial to the performance of metaheuristic algorithms, a more successful algorithm can balance these two capabilities during the optimization process. Creating this balance will lead to: first, the algorithm being able to discover the main optimal region based on exploration, and second, to converge towards the global optimal based on exploitation. The ability of a metaheuristic algorithm to strike a balance between exploration and exploitation is well measured in fixed-dimensional multimodal problems. The results obtained from the implementation of LEO on fixed-dimensional multimodal functions from F14 to F23 indicate the ability of the proposed method to strike a balance between exploration and exploitation. In addition, LEO showed the capability to explore the main optimal region and converge towards the global optimal. Therefore, the simulation finding of fixed-dimensional multimodal functions is a high capability of LEO in balancing exploration and exploitation.
6 Evaluation the CEC 2017 Test Suite
In this section, the performance of the proposed LEO approach in optimization tasks is evaluated on the CEC 2017 test suite. This set has thirty standard benchmark functions, including three unimodal functions C17-F1 to C17-F3, seven multimodal functions C17-F4 to C17-F10, ten hybrid functions C17-F11 to C17-F20, and ten composition functions C17-F21 to C17-F30. Full details of the CEC 2017 test suite are explained in [59].
The proposed LEO approach and competitor algorithms are employed in handling the CEC 2017 test suite. The simulation results are reported in Table 11. The resulting boxplots of the performance of the proposed LEO and competitor algorithms in the optimization of the CEC 2017 test suite are drawn in Fig. 8. The results show that LEO is the best optimizer for C17-F1, C17-F4 to C17-F6, C17-F8, C17-F10 to C17-F21, C17-F23 to C17-F25, and C17-F28 to C17-F30 functions. In optimizing C17-F2 and C17-F26, the proposed LEO approach is the second best optimizer for these functions after PSO. The proposed LEO approach is the second best optimizer after GSA for the functions C17-F7, C17-F9, and C17-F22. The analysis of the simulation results shows that the proposed LEO approach has provided better results in most of the benchmark functions and superior performance in the optimization of the CEC 2017 test suite compared to the competitor algorithms. Also, referring to the values obtained for the “p-value” index from the Wilcoxon rank sum statistical test shows that the superiority of LEO against competitor algorithms is significant from a statistical point of view.
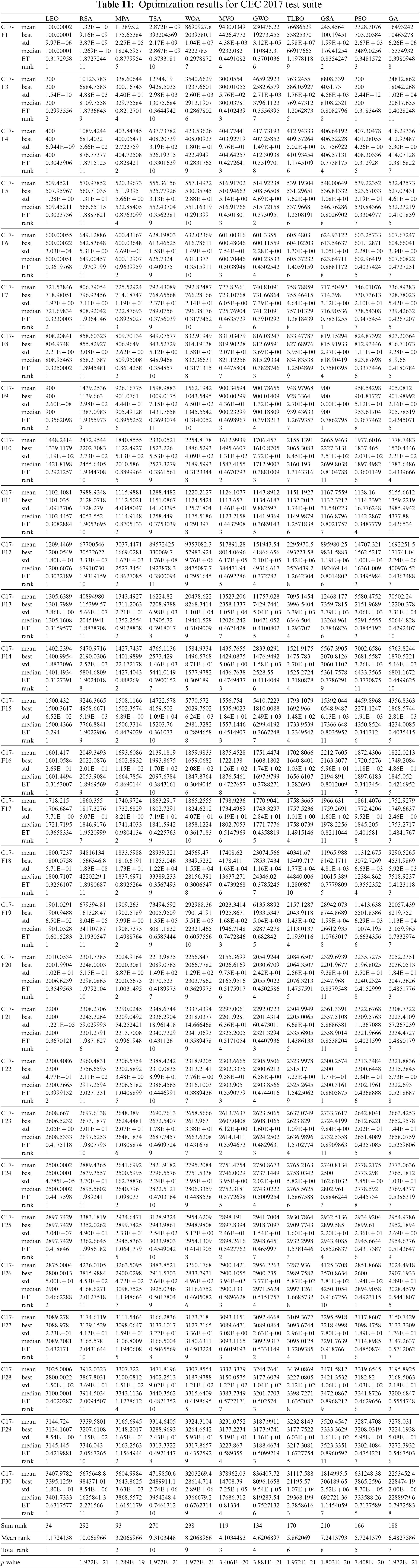
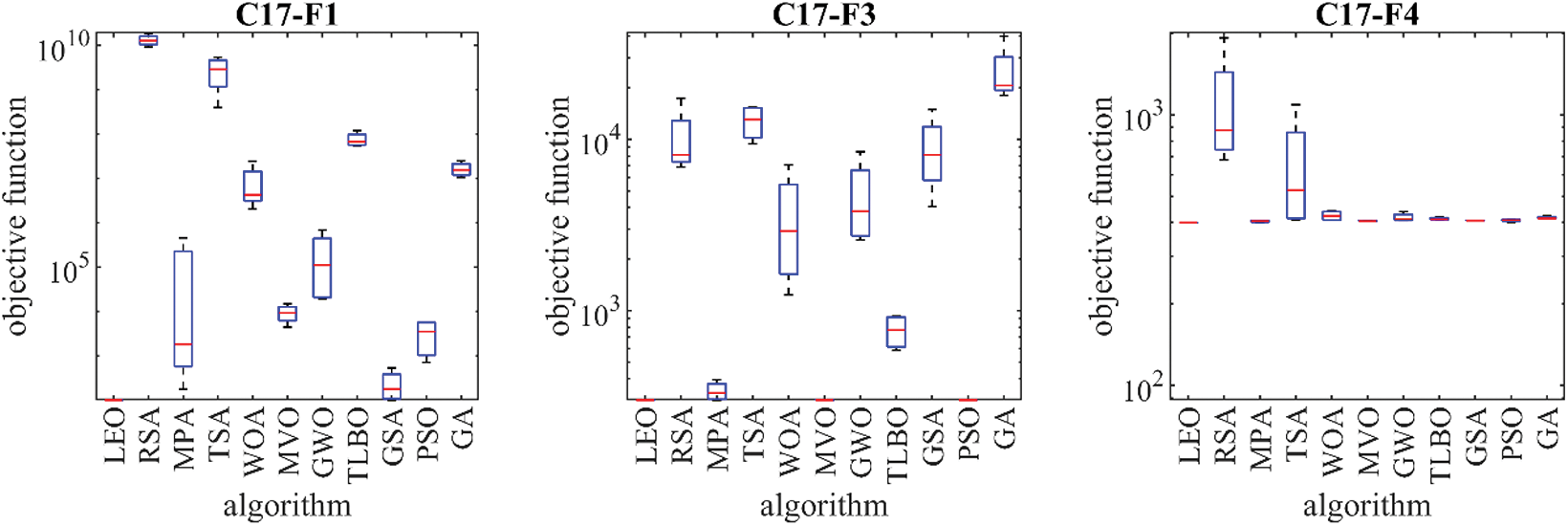
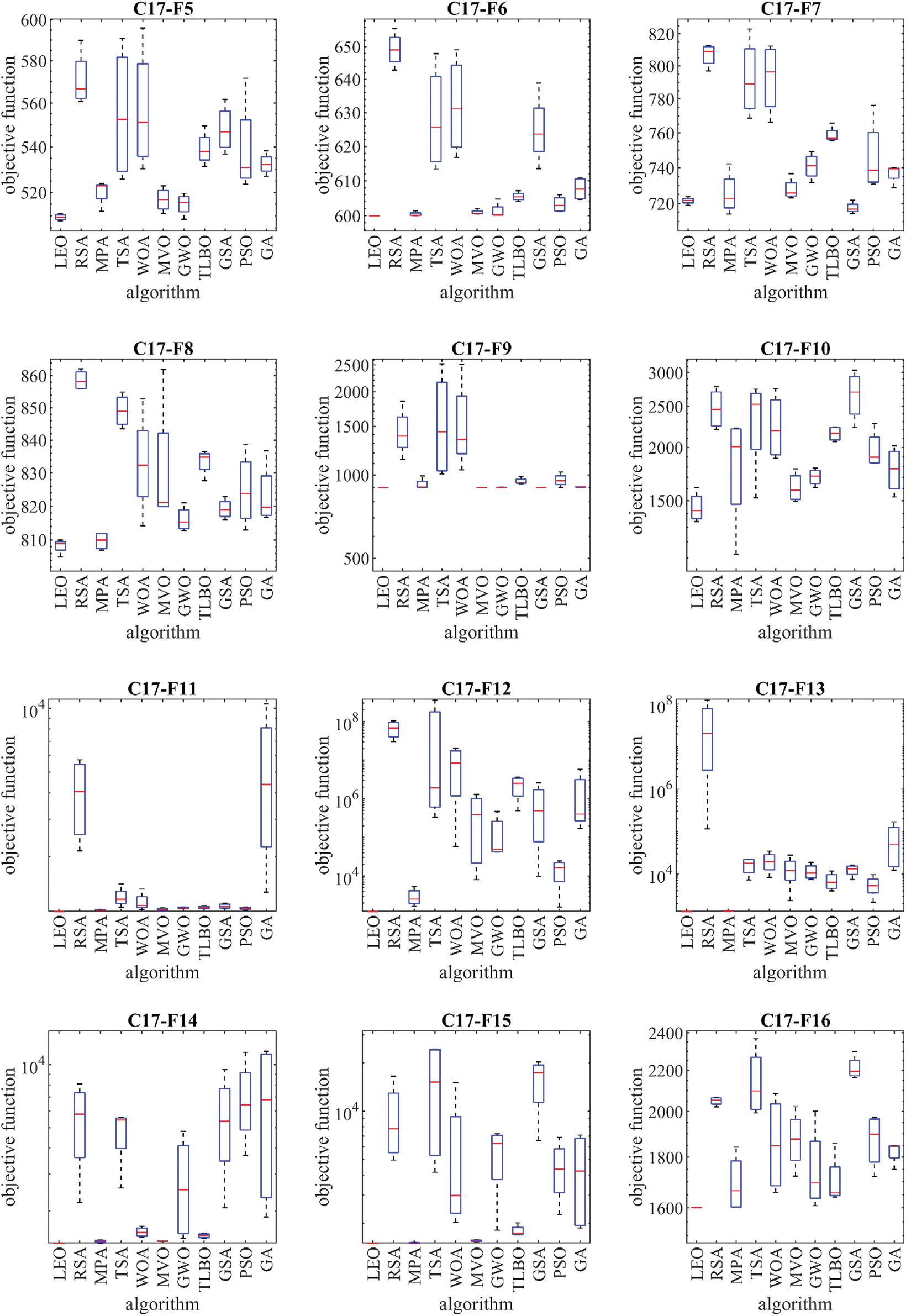
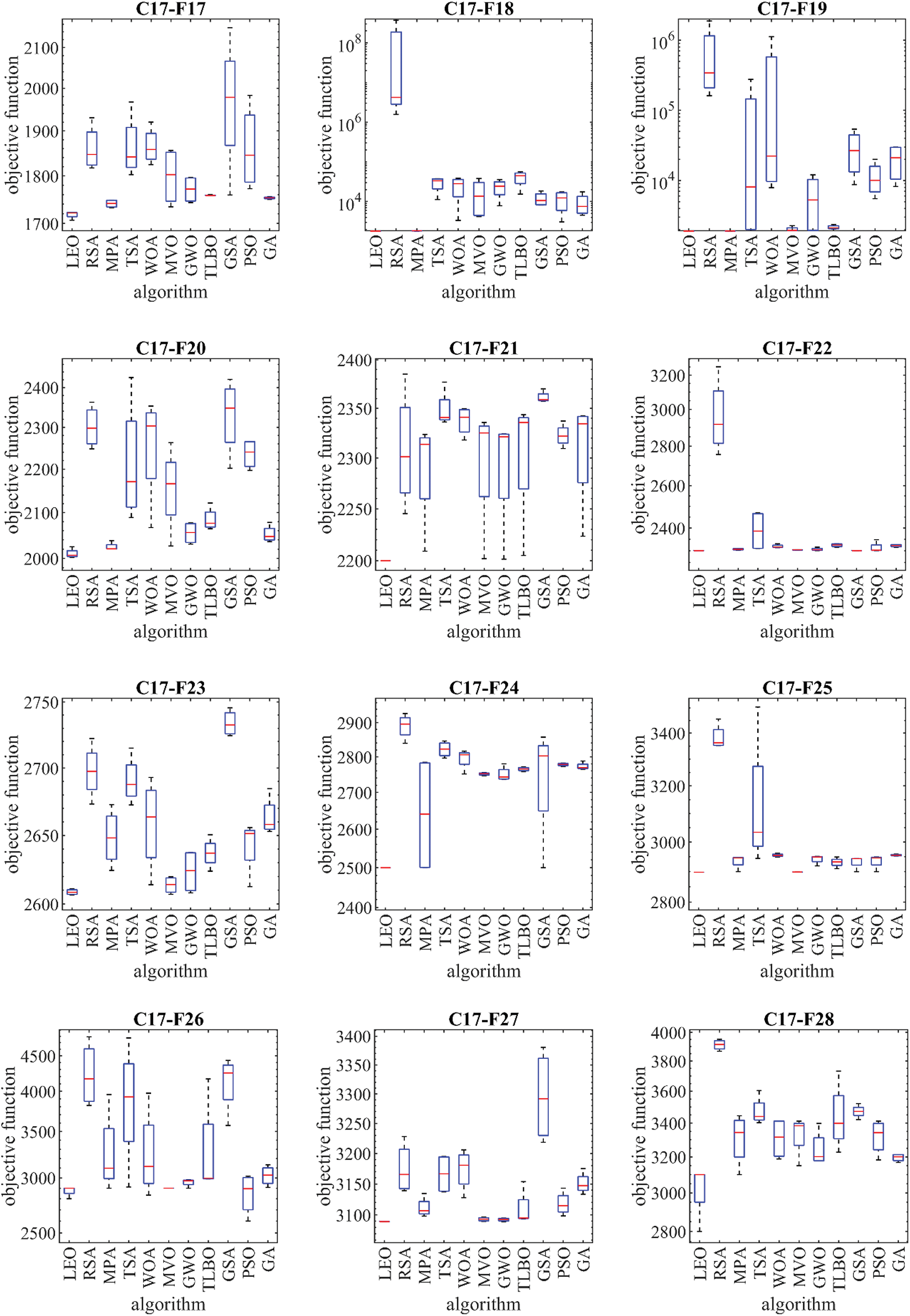
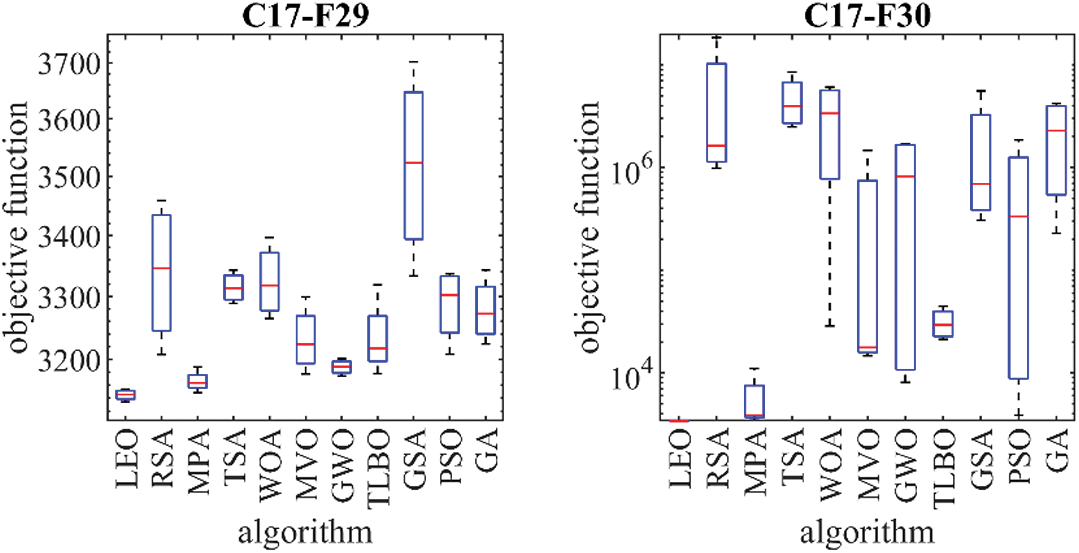
Figure 8: Boxplot diagrams of LEO and competitor algorithms performances on the CEC 2017 test suite
7 LEO for Real-World Applications
In this section, LEO’s ability to solve real-world optimization applications is evaluated.
7.1 Tension/Compression Spring Design Optimization Problem
The tension/compression spring problem is a design challenge in real-world applications, the goal of which is to minimize the weight of the tension/compression spring. The schematic of this design is shown in Fig. 9. The mathematical model of tension/compression spring design is as follows [19]:
Figure 9: Schematic view of the tension/compression spring problem
Consider:
Minimize:
Subject to:
with
The results of the implementation of LEO and competitor algorithms in the optimization of tension/compression spring design are reported in Tables 12 and 13. The simulation results show that LEO has provided the optimal solution to this problem with the values of design variables equal to
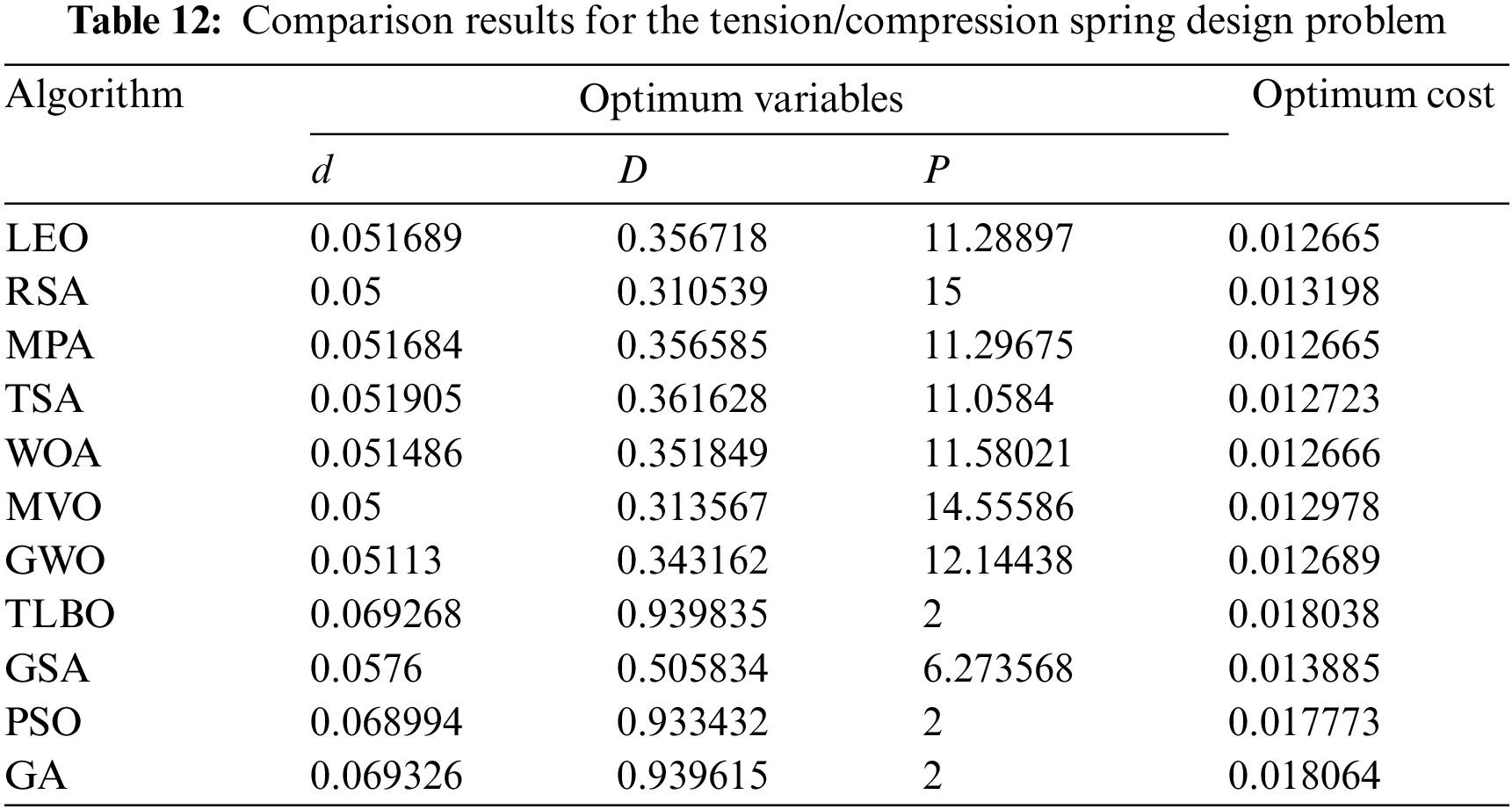
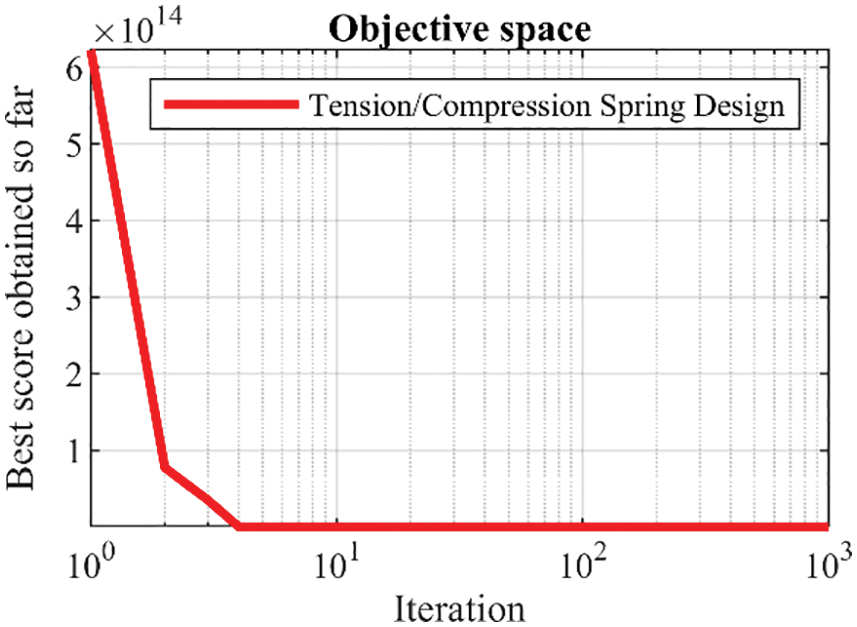
Figure 10: Convergence analysis of the LEO for the tension/compression spring design optimization problem
7.2 Welded Beam Design Optimization Problem
The welded beam design problem is an engineering issue in real-world applications to minimize the fabrication cost of the welded beam. The schematic of this design is shown in Fig. 11. The mathematical model of welded beam design is as follows [19]:
Figure 11: Schematic view of the welded beam design problem
Consider:
Minimize:
Subject to:
where
with
The results of welding beam design optimization using LEO and competitor algorithms are reported in Tables 14 and 15. The simulation results show that LEO has provided the optimal solution to this problem with the values of design variables equal to (0.20573, 3.470489, 9.036624, 0.20573) and the value of the objective function equal to (1.724852). Based on the optimization results, the proposed LEO approach has provided superior performance in handling the welded beam design problem compared to competitor algorithms. The convergence curve of LEO while achieving the solution for welded beam design is plotted in Fig. 12.
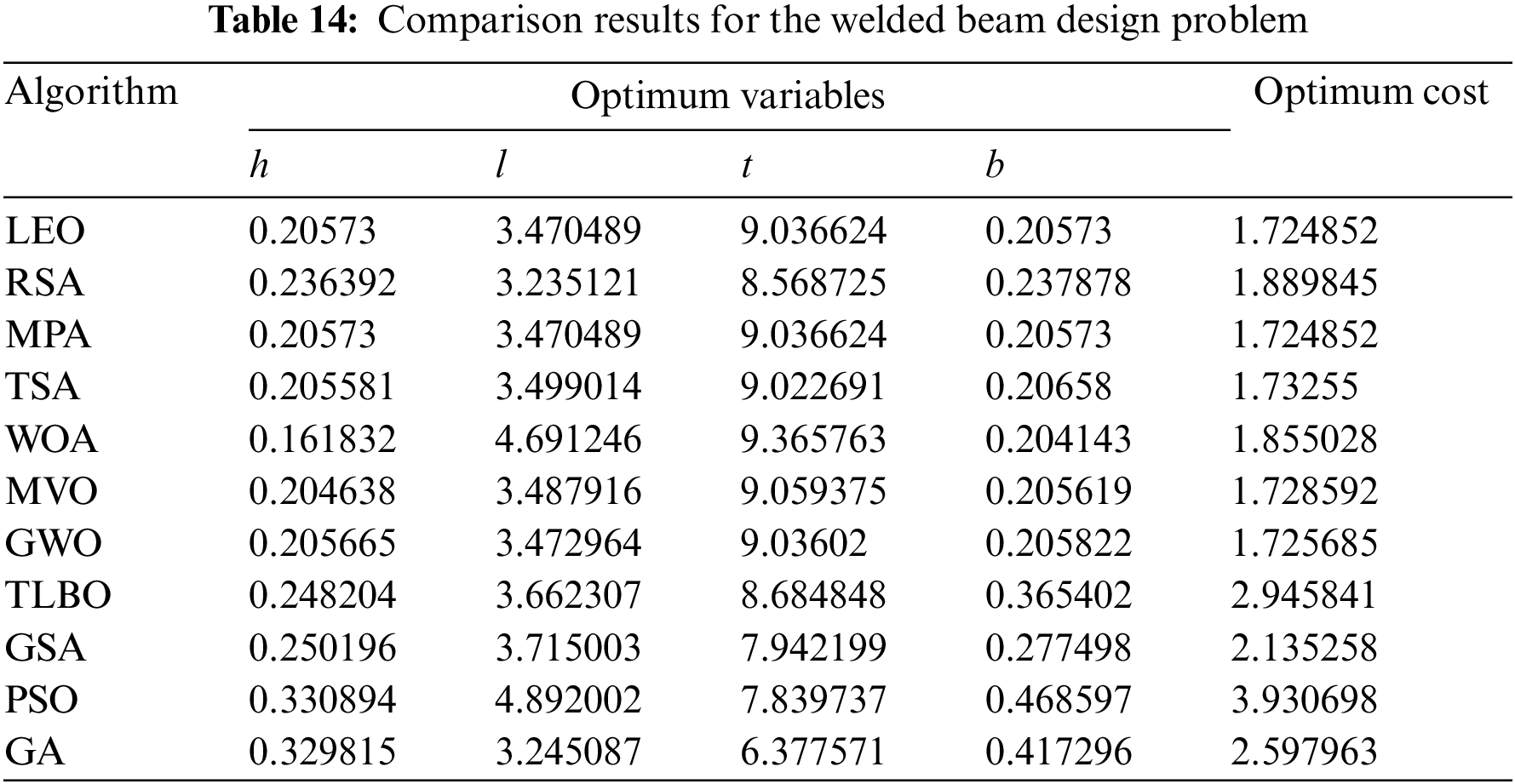
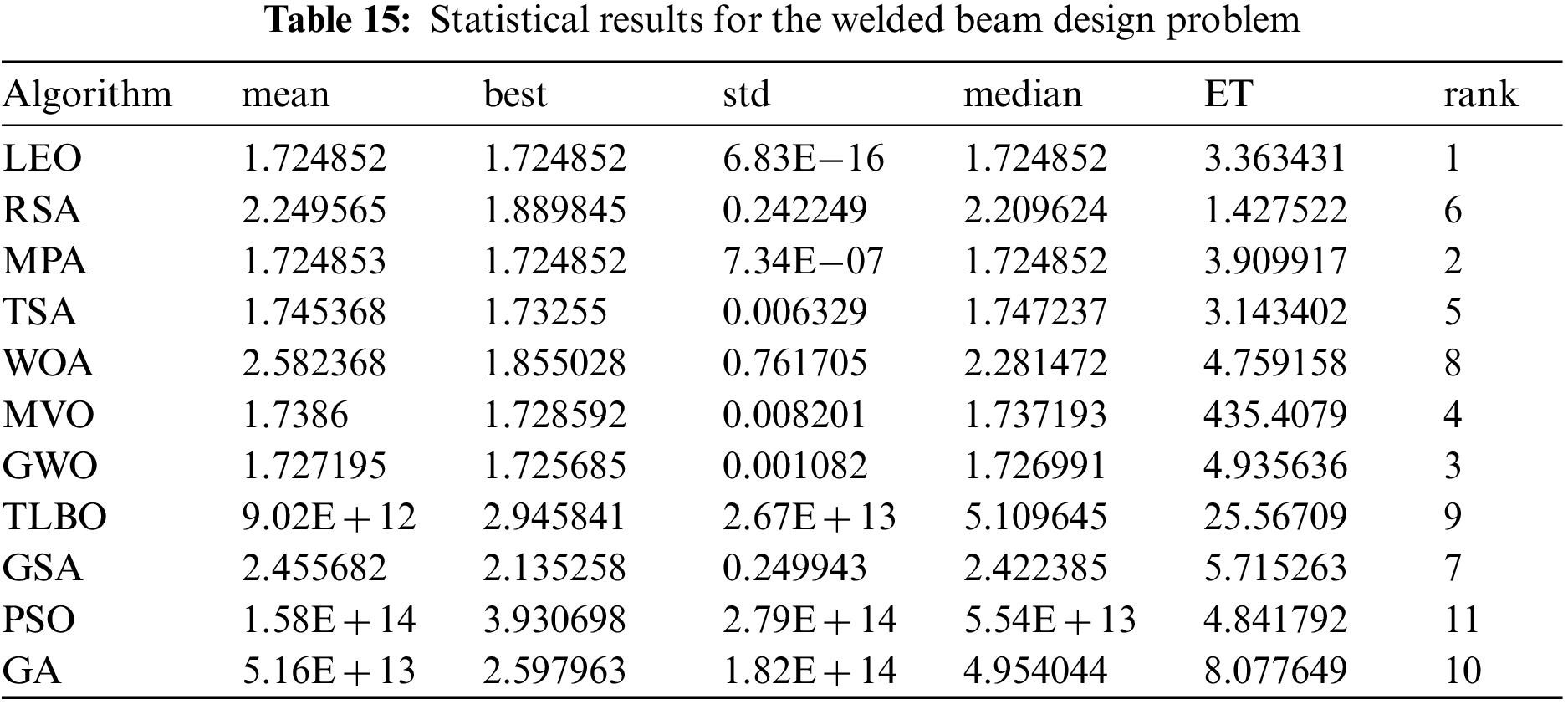
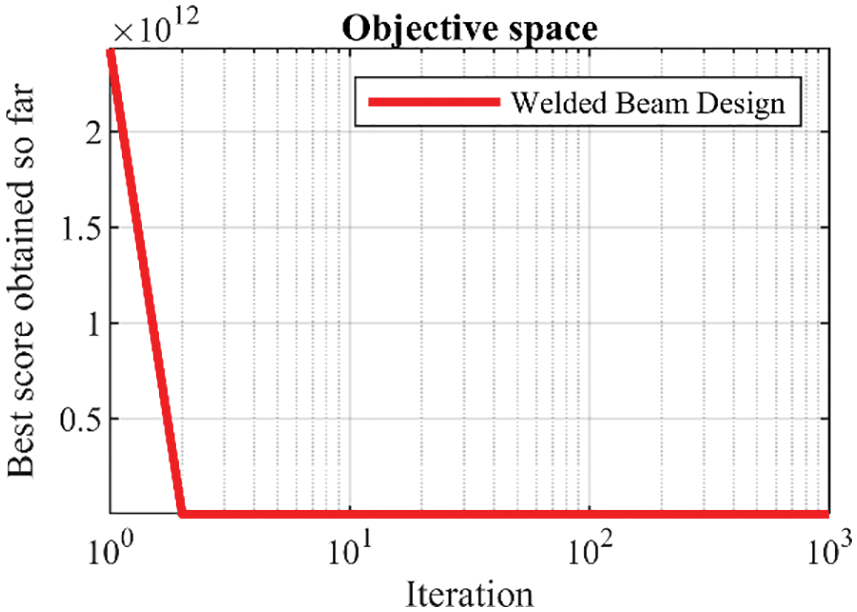
Figure 12: Convergence analysis of the proposed LEO for the welded beam design optimization problem
7.3 Speed Reducer Design Optimization Problem
The speed reducer design problem is a real-world application in engineering studies with the aim of minimizing the weight of the speed reducer. The schematic of this design is shown in Fig. 13. The mathematical model of speed reducer design is as follows [60,61]:
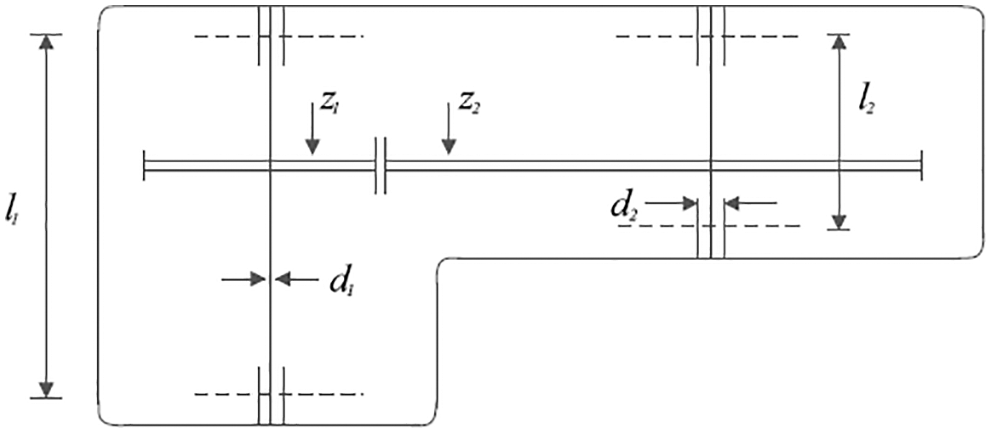
Figure 13: Schematic view of speed reducer design problem
Consider:
Minimize:
Subject to:
with
The results of using LEO and competitor algorithms in optimizing of speed reducer design are released in Tables 16 and 17. The simulation results show that LEO has provided the optimal solution to this problem with the values of design variables equal to
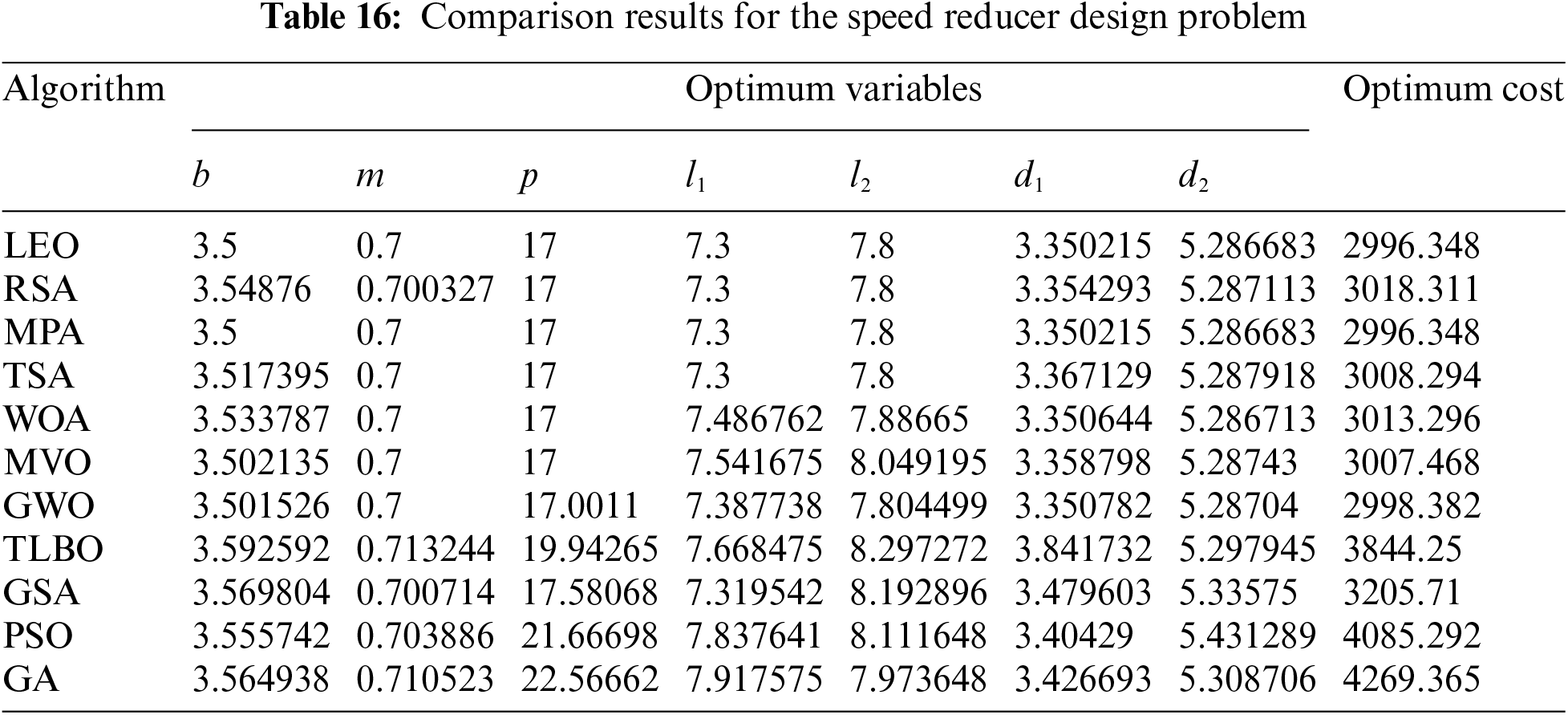
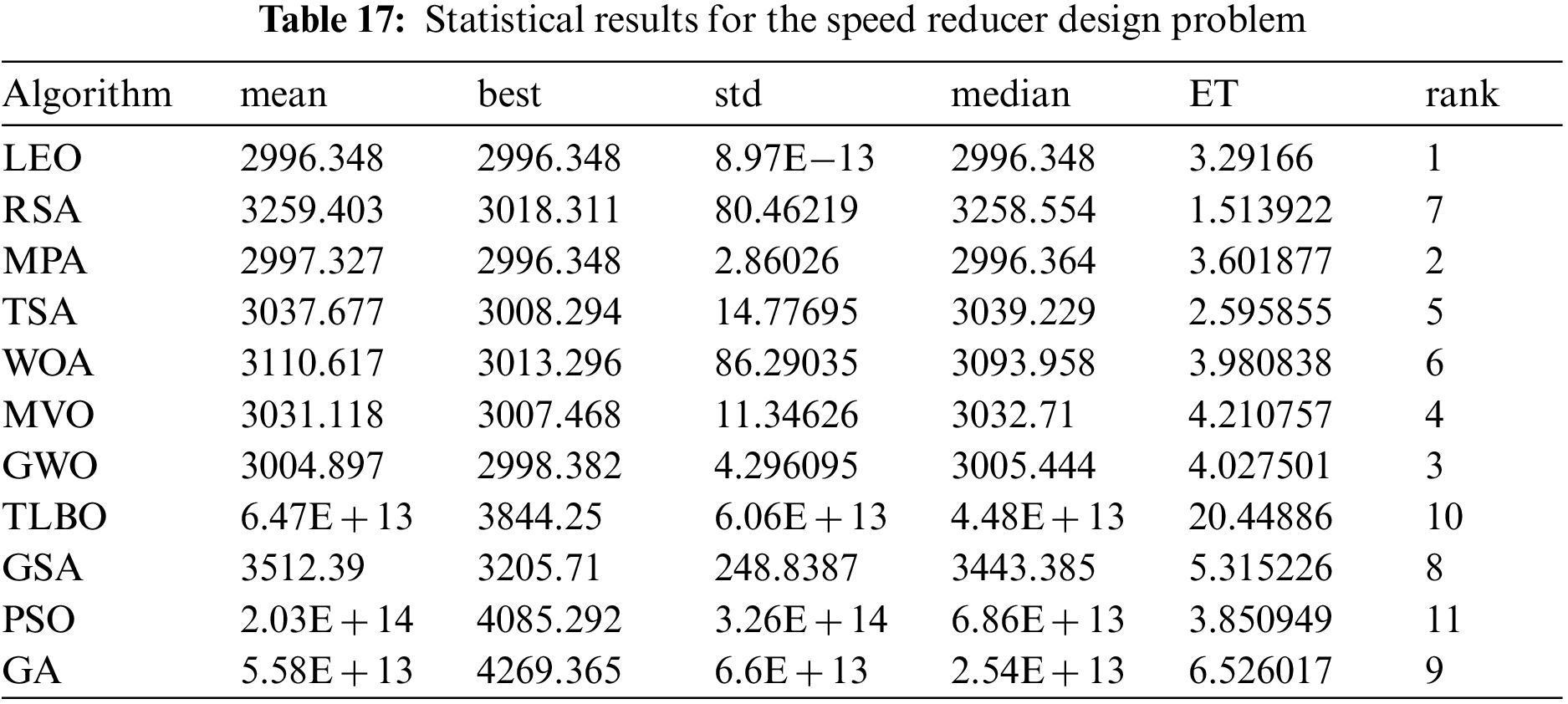
Figure 14: Convergence analysis of the LEO for the speed reducer design optimization problem
7.4 Pressure Vessel Design Optimization Problem
The pressure vessel design problem is an optimization challenge in real-world applications to minimize the design cost. The schematic of this design is shown in Fig. 15. The mathematical model of pressure vessel design is as follows [62]:
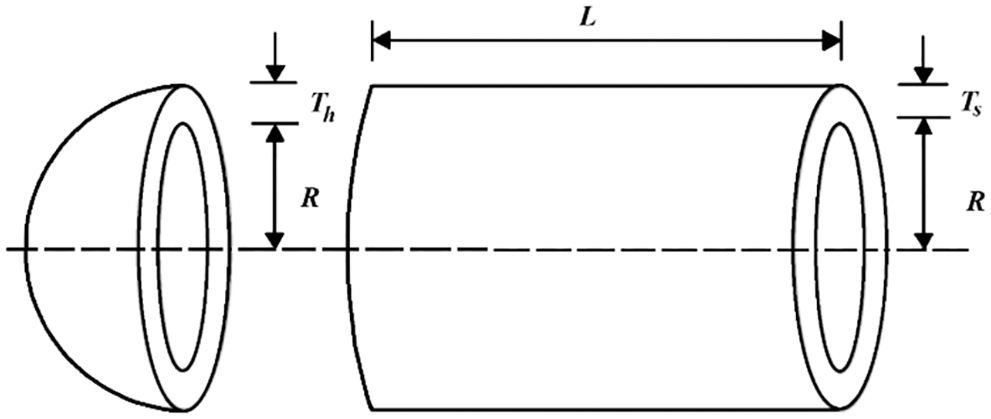
Figure 15: Schematic view of the pressure vessel design problem
Consider:
Minimize:
Subject to:
with
The results obtained from the implementation of LEO and competitor algorithms on the pressure vessel design problem are reported in Tables 18 and 19. The simulation results show that LEO has the optimal solution to this problem with the values of design variables equal to
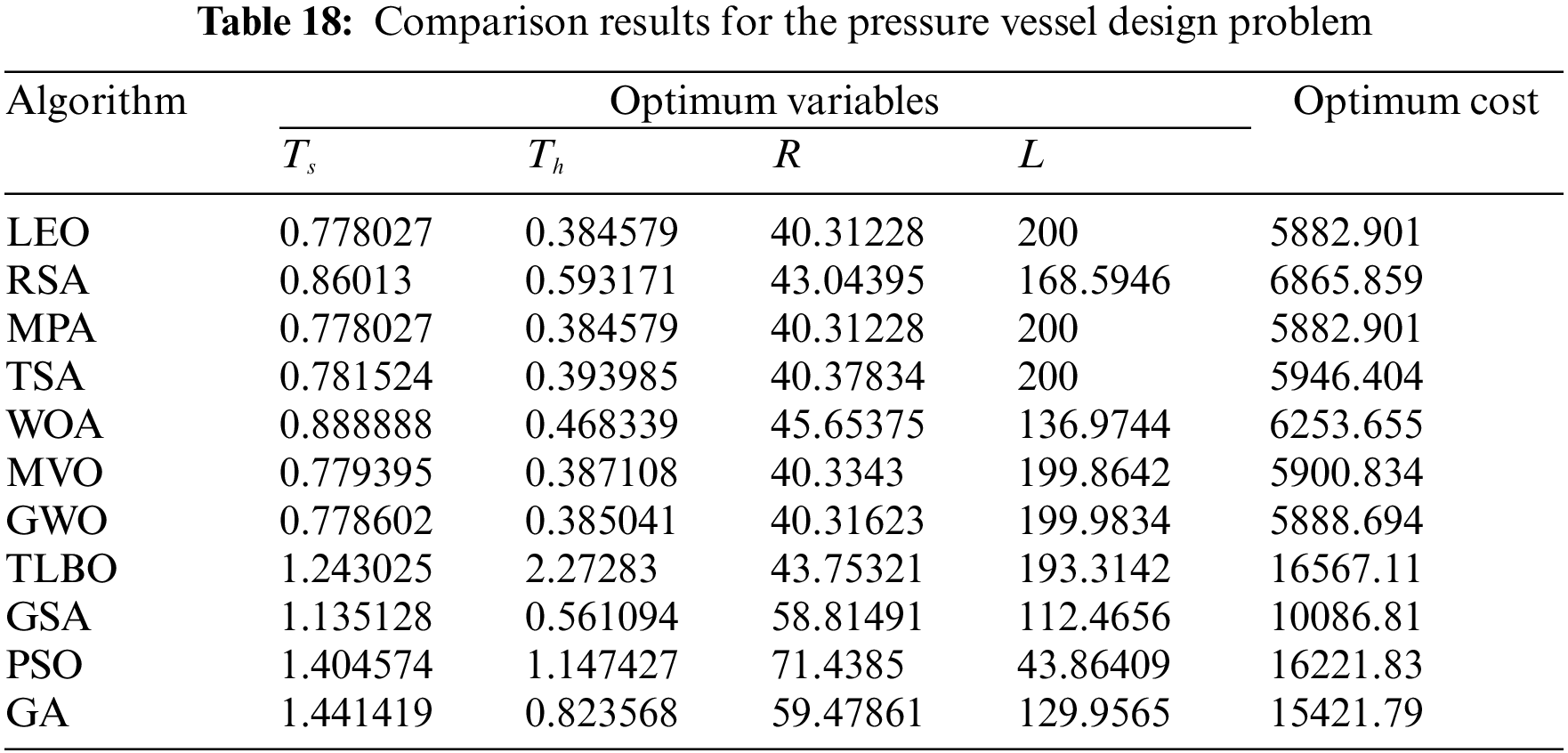
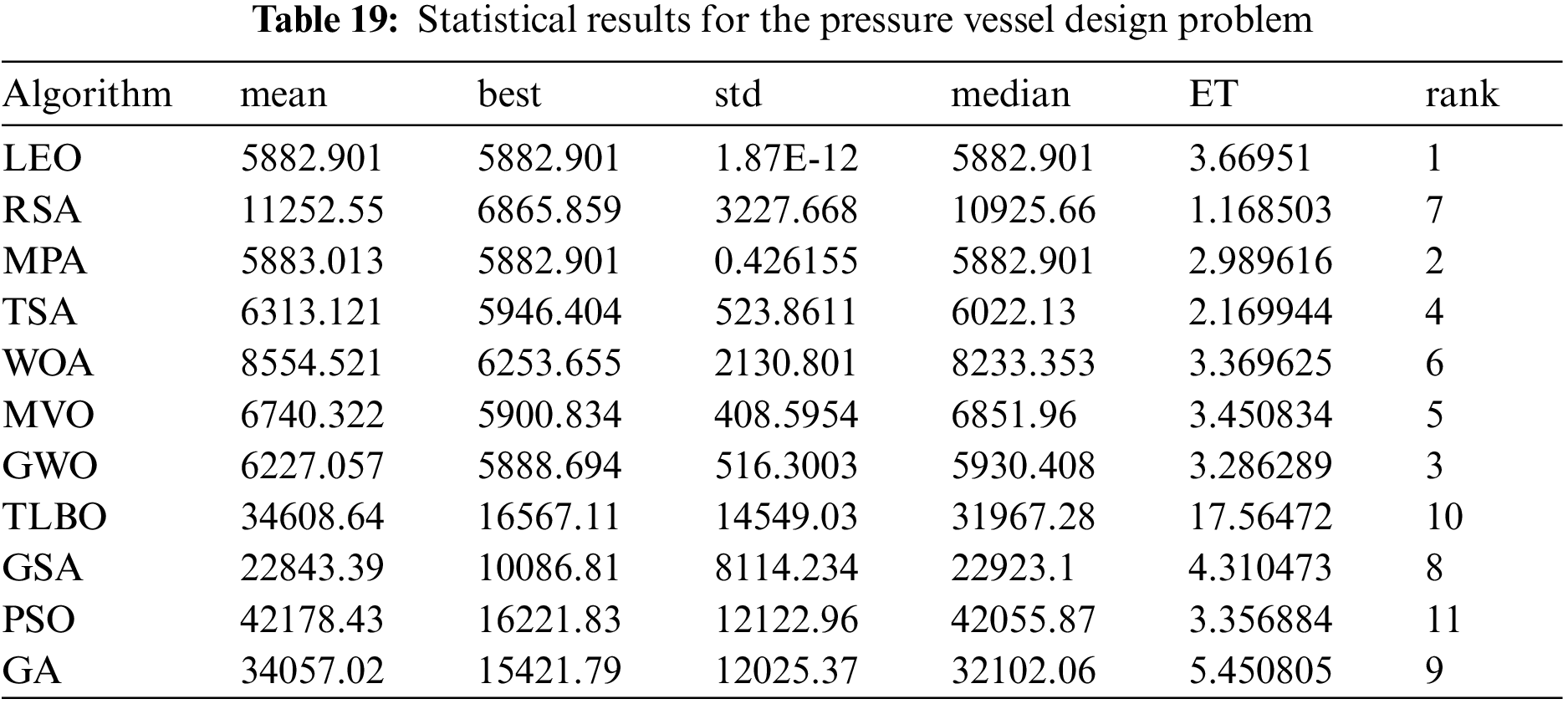
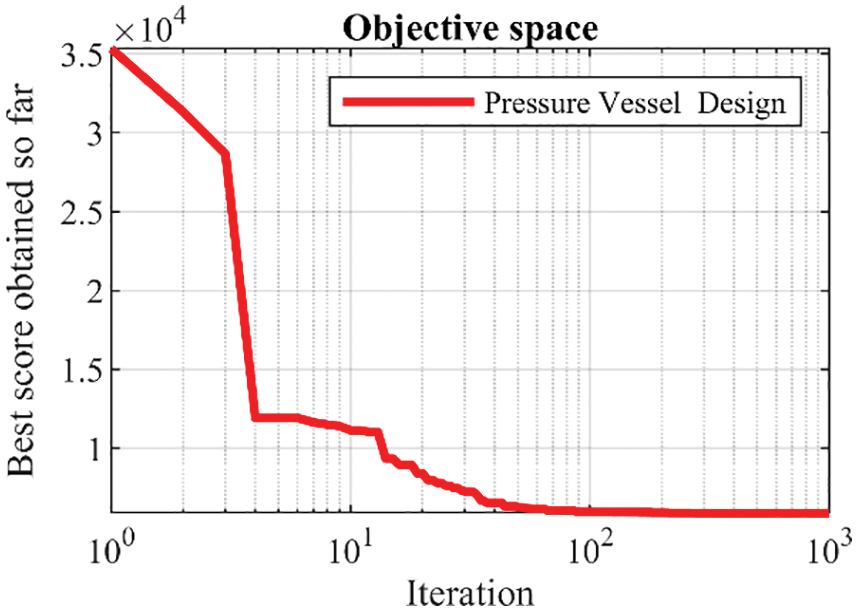
Figure 16: Convergence analysis of the LEO for the pressure vessel design optimization problem
7.5 The Effectiveness of the LEO in Solving Real-Time Applications
Real-Time Applications (RTAs) are applications that operate in specific time frames that users sense as current or immediate. Typically, RTAs are employed to process streaming data. Without ingesting and storing the data in a back-end database, real-time software should be able to sense, analyze and act on streaming data as it enters the system. RTAs usually use event-driven architecture to handle streaming data [63] asynchronously. RTAs include clustering applications, Internet of Things (IoT) applications, systems that control scientific experiments, medical imaging systems, industrial control systems, and certain monitoring systems.
Metaheuristic algorithms, including the proposed LEO approach, are effective tools for managing real-time applications. In many RTAs, a combination of metaheuristic algorithms and neural networks have been employed to optimize the performance of real-time systems. The proposed LEO approach has applications in various fields of RTAs, including sensor networks, medical applications, IoT systems, military applications, electric vehicle control, fuel injection system control, robotics applications, clustering, etc.
8 Conclusions and Future Research
This paper introduced a new human-based metaheuristic algorithm called Language Education Optimization (LEO), which has applications in optimization tasks. The fundamental inspiration behind LEO design is the process of teaching a foreign language in language schools where the teacher teaches skills to students. According to exploration and exploitation abilities, LEO was mathematically modeled in three phases (i) teacher selection, (ii) students learning from each other, and (iii) individual practice. The performance of LEO in optimization applications was tested on fifty-two benchmark functions of unimodal, multimodal, fixed-dimensional multimodal types and the CEC 2017 test suite. The optimization results showed that LEO, with its high power of exploration and exploitation, and its ability to balance exploration and exploitation, has a compelling performance in solving optimization problems. Ten well-known metaheuristic algorithms were employed to compare the results of the LEO implementation. The analysis of the simulation results showed that LEO has an effective performance in handling optimization tasks and providing solutions, and is far superior and more competitive than the competitor algorithms. The implementation results of the proposed LEO approach on four engineering design problems showed the high ability of LEO in optimizing real-world applications.
The most special advantage of the proposed LEO approach is that it does not have any control parameters and therefore does not need a parameter adjustment process. The high ability in exploration and exploitation and balancing them during the search process is another advantage of the proposed LEO. However, LEO also has limitations and disadvantages. First, as with all metaheuristic algorithms, there is no claim that LEO is the best optimizer for all optimization problems. The second disadvantage of LEO is that there is always a possibility that newer algorithms will be designed that perform better in solving optimization problems compared to the proposed approach. The third disadvantage of LEO is that, similar to other stochastic approaches. It does not provide any guarantee to provide the global optima for all optimization problems.
Following the design of LEO, several research tasks are activated for future work, the most important of which is the design of binary and multimodal versions of LEO. Employing LEO in optimization tasks in various sciences, real-time applications, and implementing LEO in real-world applications are other research suggestions of this study.
Acknowledgement: The authors thank Dušan Bednařík from the University of Hradec Kralove for our fruitful and informative discussions.
Funding Statement: The research was supported by the Project of Specific Research PřF UHK No. 2104/2022–2023, University of Hradec Kralove, Czech Republic.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Dhiman, G. (2021). SSC: A hybrid nature-inspired meta-heuristic optimization algorithm for engineering applications. Knowledge-Based Systems, 222, 106926. DOI 10.1016/j.knosys.2021.106926. [Google Scholar] [CrossRef]
2. Zeidabadi, F. A., Dehghani, A., Dehghani, M., Montazeri, Z., Hubálovský. et al. (2022). SSABA: Search step adjustment based algorithm. Computers, Materials & Continua, 71(2), 4237–4256. DOI 10.32604/cmc.2022.023682. [Google Scholar] [CrossRef]
3. Mohammadi-Balani, A., Nayeri, M. D., Azar, A., Taghizadeh-Yazdi, M. (2021). Golden eagle optimizer: A nature-inspired metaheuristic algorithm. Computers Industrial Engineering, 152, 107050. DOI 10.1016/j.cie.2020.107050. [Google Scholar] [CrossRef]
4. Cavazzuti, M. (2013). Deterministic optimization. In: Optimization methods: From theory to design scientific and technological aspects in mechanics, pp. 77–102. Berlin, Heidelberg: Springer. [Google Scholar]
5. Gonzalez, M., López-Espín, J. J., Aparicio, J., Talbi, E. G. (2022). A hyper-matheuristic approach for solving mixed integer linear optimization models in the context of data envelopment analysis. PeerJ Computer Science, 8, e828. DOI 10.7717/peerj-cs.828. [Google Scholar] [CrossRef]
6. Črepinšek, M., Liu, S. H., Mernik, M. (2013). Exploration and exploitation in evolutionary algorithms: A survey. ACM Computing Surveys (CSUR), 45(3), 1–33. DOI 10.1145/2480741.2480752. [Google Scholar] [CrossRef]
7. Goldberg, D. E., Holland, J. H. (1988). Genetic algorithms and machine learning. Machine Learning, 3(2), 95–99. [Google Scholar]
8. Kennedy, J., Eberhart, R. (1995). Particle swarm optimization. Proceedings of ICNN’95-International Conference on Neural Networks, pp. 1942–1948. Perth, WA, Australia. [Google Scholar]
9. Karaboga, D., Basturk, B. (2007). Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems. In: Foundations of fuzzy logic and soft computing. IFSA 2007. Lecture notes in Computer Science, pp. 789–798. Berlin, Heidelberg, Springer. [Google Scholar]
10. Dorigo, M., Maniezzo, V., Colorni, A. (1996). Ant system: Optimization by a colony of cooperating agents. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 26(1), 29–41. [Google Scholar]
11. Wolpert, D. H., Macready, W. G. (1997). No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1(1), 67–82. DOI 10.1109/4235.585893. [Google Scholar] [CrossRef]
12. Zhao, W., Wang, L., Mirjalili, S. (2022). Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications. Computer Methods in Applied Mechanics and Engineering, 388, 114194. DOI 10.1016/j.cma.2021.114194. [Google Scholar] [CrossRef]
13. Zhong, C., Li, G., Meng, Z. (2022). Beluga whale optimization: A novel nature-inspired metaheuristic algorithm. Knowledge-Based Systems, 251(5), 109215. DOI 10.1016/j.knosys.2022.109215. [Google Scholar] [CrossRef]
14. Zamani, H., Nadimi-Shahraki, M. H., Gandomi, A. H. (2022). Starling murmuration optimizer: A novel bio-inspired algorithm for global and engineering optimization. Computer Methods in Applied Mechanics and Engineering, 392, 114616. DOI 10.1016/j.cma.2022.114616. [Google Scholar] [CrossRef]
15. Dhiman, G., Garg, M., Nagar, A., Kumar, V., Dehghani, M. (2020). A novel algorithm for global optimization: Rat swarm optimizer. Journal of Ambient Intelligence and Humanized Computing, 12, 1–26. [Google Scholar]
16. Dhiman, G., Kaur, A. (2019). STOA: A bio-inspired based optimization algorithm for industrial engineering problems. Engineering Applications of Artificial Intelligence, 82, 148–174. DOI 10.1016/j.engappai.2019.03.021. [Google Scholar] [CrossRef]
17. Dhiman, G., Kumar, V. (2018). Emperor penguin optimizer: A bio-inspired algorithm for engineering problems. Knowledge-Based Systems, 159, 20–50. DOI 10.1016/j.knosys.2018.06.001. [Google Scholar] [CrossRef]
18. Jiang, Y., Wu, Q., Zhu, S., Zhang, L. (2022). Orca predation algorithm: A novel bio-inspired algorithm for global optimization problems. Expert Systems with Applications, 188, 116026. DOI 10.1016/j.eswa.2021.116026. [Google Scholar] [CrossRef]
19. Mirjalili, S., Lewis, A. (2016). The whale optimization algorithm. Advances in Engineering Software, 95, 51–67. DOI 10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]
20. Abdollahzadeh, B., Gharehchopogh, F. S., Mirjalili, S. (2021). African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems. Computers Industrial Engineering, 158, 107408. DOI 10.1016/j.cie.2021.107408. [Google Scholar] [CrossRef]
21. Faramarzi, A., Heidarinejad, M., Mirjalili, S., Gandomi, A. H. (2020). Marine predators algorithm: A nature-inspired metaheuristic. Expert Systems with Applications, 152, 113377. DOI 10.1016/j.eswa.2020.113377. [Google Scholar] [CrossRef]
22. Chopra, N., Ansari, M. M. (2022). Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Systems with Applications, 198, 116924. DOI 10.1016/j.eswa.2022.116924. [Google Scholar] [CrossRef]
23. Mirjalili, S., Mirjalili, S. M., Lewis, A. (2014). Grey wolf optimizer. Advances in Engineering Software, 69, 46–61. DOI 10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]
24. Abualigah, L., Abd Elaziz, M., Sumari, P., Geem, Z. W., Gandomi, A. H. (2022). Reptile search algorithm (RSAA nature-inspired meta-heuristic optimizer. Expert Systems with Applications, 191, 116158. DOI 10.1016/j.eswa.2021.116158. [Google Scholar] [CrossRef]
25. Hashim, F. A., Houssein, E. H., Hussain, K., Mabrouk, M. S., Al-Atabany, W. (2022). Honey badger algorithm: New metaheuristic algorithm for solving optimization problems. Mathematics and Computers in Simulation, 192, 84–110. DOI 10.1016/j.matcom.2021.08.013. [Google Scholar] [CrossRef]
26. Dhiman, G., Kumar, V. (2017). Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications. Advances in Engineering Software, 114, 48–70. DOI 10.1016/j.advengsoft.2017.05.014. [Google Scholar] [CrossRef]
27. Kaur, S., Awasthi, L. K., Sangal, A. L., Dhiman, G. (2020). Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Engineering Applications of Artificial Intelligence, 90, 103541. DOI 10.1016/j.engappai.2020.103541. [Google Scholar] [CrossRef]
28. Storn, R., Price, K. (1997). Differential evolution–A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 11(4), 341–359. DOI 10.1023/A:1008202821328. [Google Scholar] [CrossRef]
29. Kirkpatrick, S., Gelatt, C. D., Vecchi, M. P. (1983). Optimization by simulated annealing. Science, 220(4598), 671–680. DOI 10.1126/science.220.4598.671. [Google Scholar] [CrossRef]
30. Pereira, J. L. J., Francisco, M. B., Diniz, C. A., Oliver, G. A., Cunha Jr, S. S. et al. (2021). Lichtenberg algorithm: A novel hybrid physics-based meta-heuristic for global optimization. Expert Systems with Applications, 170, 114522. DOI 10.1016/j.eswa.2020.114522. [Google Scholar] [CrossRef]
31. Hashim, F. A., Houssein, E. H., Mabrouk, M. S., Al-Atabany, W., Mirjalili, S. (2019). Henry gas solubility optimization: A novel physics-based algorithm. Future Generation Computer Systems, 101, 646–667. DOI 10.1016/j.future.2019.07.015. [Google Scholar] [CrossRef]
32. Rashedi, E., Nezamabadi-Pour, H., Saryazdi, S. (2009). GSA: A gravitational search algorithm. Information Sciences, 179(13), 2232–2248. DOI 10.1016/j.ins.2009.03.004. [Google Scholar] [CrossRef]
33. Eskandar, H., Sadollah, A., Bahreininejad, A., Hamdi, M. (2012). Water cycle algorithm–A novel metaheuristic optimization method for solving constrained engineering optimization problems. Computers Structures, 110, 151–166. DOI 10.1016/j.compstruc.2012.07.010. [Google Scholar] [CrossRef]
34. Hashim, F. A., Hussain, K., Houssein, E. H., Mabrouk, M. S., Al-Atabany, W. (2021). Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems. Applied Intelligence, 51(3), 1531–1551. DOI 10.1007/s10489-020-01893-z. [Google Scholar] [CrossRef]
35. Dehghani, M., Montazeri, Z., Dhiman, G., Malik, O., Morales-Menendez, R. et al. (2020). A spring search algorithm applied to engineering optimization problems. Applied Sciences, 10(18), 6173. DOI 10.3390/app10186173. [Google Scholar] [CrossRef]
36. Mirjalili, S., Mirjalili, S. M., Hatamlou, A. (2016). Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Computing and Applications, 27(2), 495–513. DOI 10.1007/s00521-015-1870-7. [Google Scholar] [CrossRef]
37. Faramarzi, A., Heidarinejad, M., Stephens, B., Mirjalili, S. (2020). Equilibrium optimizer: A novel optimization algorithm. Knowledge-Based Systems, 191, 105190. DOI 10.1016/j.knosys.2019.105190. [Google Scholar] [CrossRef]
38. Dehghani, M., Samet, H. (2020). Momentum search algorithm: A new meta-heuristic optimization algorithm inspired by momentum conservation law. SN Applied Sciences, 2(10), 1–15. DOI 10.1007/s42452-020-03511-6. [Google Scholar] [CrossRef]
39. Rao, R. V., Savsani, V. J., Vakharia, D. (2011). Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Computer-Aided Design, 43(3), 303–315. DOI 10.1016/j.cad.2010.12.015. [Google Scholar] [CrossRef]
40. Dehghani, M., Trojovský, P. (2021). Teamwork optimization algorithm: A new optimization approach for function minimization/maximization. Sensors, 21(13), 4567. DOI 10.3390/s21134567. [Google Scholar] [CrossRef]
41. Trojovský, P., Dehghani, M. (2022). A new optimization algorithm based on mimicking the voting process for leader selection. PeerJ Computer Science, 2, cs976. DOI 10.7717/peerj-cs.976. [Google Scholar] [CrossRef]
42. Ayyarao, T. L., RamaKrishna, N., Elavarasam, R. M., Polumahanthi, N., Rambabu, M. et al. (2022). War strategy optimization algorithm: A new effective metaheuristic algorithm for global optimization. IEEE Access, 10, 25073–25105. DOI 10.1109/ACCESS.2022.3153493. [Google Scholar] [CrossRef]
43. Dehghani, M., Mardaneh, M., Malik, O. (2020). FOA: ‘Following’ optimization algorithm for solving power engineering optimization problems. Journal of Operation and Automation in Power Engineering, 8(1), 57–64. [Google Scholar]
44. Mousavirad, S. J., Ebrahimpour-Komleh, H. (2017). Human mental search: A new population-based metaheuristic optimization algorithm. Applied Intelligence, 47(3), 850–887. DOI 10.1007/s10489-017-0903-6. [Google Scholar] [CrossRef]
45. Dehghani, M., Trojovská, E., Trojovský, P. (2022). A new human-based metaheuristic algorithm for solving optimization problems on the base of simulation of driving training process. Scientific Reports, 12(1), 9924. DOI 10.1038/s41598-022-14225-7. [Google Scholar] [CrossRef]
46. Trojovská, E., Dehghani, M. (2022). A new human-based metahurestic optimization method based on mimicking cooking training. Scientific Reports, 12(1), 1–24. DOI 10.1038/s41598-022-19313-2. [Google Scholar] [CrossRef]
47. Moosavi, S. H. S., Bardsiri, V. K. (2019). Poor and rich optimization algorithm: A new human-based and multi populations algorithm. Engineering Applications of Artificial Intelligence, 86, 165–181. DOI 10.1016/j.engappai.2019.08.025. [Google Scholar] [CrossRef]
48. Dehghani, M., Mardaneh, M., Guerrero, J. M., Malik, O., Kumar, V. (2020). Football game based optimization: An application to solve energy commitment problem. International Journal of Intelligent Engineering and Systems, 13, 514–523. DOI 10.22266/ijies. [Google Scholar] [CrossRef]
49. Moghdani, R., Salimifard, K. (2018). Volleyball premier league algorithm. Applied Soft Computing, 64, 161–185. DOI 10.1016/j.asoc.2017.11.043. [Google Scholar] [CrossRef]
50. Kaveh, A., Zolghadr, A. (2016). A novel meta-heuristic algorithm: Tug of war optimization. International Journal of Optimization in Civil Engineering, 6(4), 469–492. [Google Scholar]
51. Zeidabadi, F. A., Dehghani, M., Trojovský, P., Hubálovský, Š, Leiva, V. et al. (2022). Archery algorithm: A novel stochastic optimization algorithm for solving optimization problems. Computers, Materials & Continua, 72(1), 399–416. DOI 10.32604/cmc.2022.024736. [Google Scholar] [CrossRef]
52. Zeidabadi, F. A., Dehghani, M. (2022). POA: Puzzle optimization algorithm. International Journal of Intelligent Engineering and Systems, 15(1), 273–281. [Google Scholar]
53. Dehghani, M., Montazeri, Z., Givi, H., Guerrero, J. M., Dhiman, G. (2020). Darts game optimizer: A new optimization technique based on darts game. International Journal of Intelligent Engineering and Systems, 13, 286–294. [Google Scholar]
54. Doumari, S. A., Givi, H., Dehghani, M., Malik, O. P. (2021). Ring toss game-based optimization algorithm for solving various optimization problems. International Journal of Intelligent Engineering and Systems, 14(3), 545–554. [Google Scholar]
55. Dehghani, M., Montazeri, Z., Malik, O. P. (2019). DGO: Dice game optimizer. Gazi University Journal of Science, 32(3), 871–882. DOI 10.35378/gujs.484643. [Google Scholar] [CrossRef]
56. Dehghani, M., Montazeri, Z., Malik, O. P., Ehsanifar, A., Dehghani, A. (2019). OSA: Orientation search algorithm. International Journal of Industrial Electronics, Control and Optimization, 2(2), 99–112. [Google Scholar]
57. Yao, X., Liu, Y., Lin, G. (1999). Evolutionary programming made faster. IEEE Transactions on Evolutionary Computation, 3(2), 82–102. DOI 10.1109/4235.771163. [Google Scholar] [CrossRef]
58. Wilcoxon, F. (1945). Individual comparisons by ranking methods. Biometrics Bulletin, 1, 80–83. DOI 10.2307/3001968. [Google Scholar] [CrossRef]
59. Awad, N., Ali, M., Liang, J., Qu, B., Suganthan, P. et al. (2016). Evaluation criteria for the CEC 2017 special session and competition on single objective real-parameter numerical optimization. Technology Report. DOI 10.13140/RG.2.2.12568.70403. [Google Scholar] [CrossRef]
60. Gandomi, A. H., Yang, X. S. (2011). Benchmark problems in structural optimization. In: Koziel, S., Yang, X. S. (Eds.Computational optimization, methods and algorithms. studies in computational intelligence, vol. 356. Berlin, Heidelberg: Springer. [Google Scholar]
61. Mezura-Montes, E., Coello, C. A. C. (2005). Useful infeasible solutions in engineering optimization with evolutionary algorithms. In: Gelbukh, A., de Albornoz, Á., Terashima-Marín, H. (Eds.MICAI 2005: Advances in artificial intelligence, pp. 652–662, vol. 3789. Berlin, Heidelberg: Springer. [Google Scholar]
62. Kannan, B., Kramer, S. N. (1994). An augmented lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design. Journal of Mechanical Design, 116(2), 405–411. DOI 10.1115/1.2919393. [Google Scholar] [CrossRef]
63. Rao, A. S., Radanovic, M., Liu, Y., Hu, S., Fang, Y. et al. (2022). Real-time monitoring of construction sites: Sensors, methods, and applications. Automation in Construction, 136, 104099. DOI 10.1016/j.autcon.2021.104099. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools