A Large-Scale Scheduling Method for Multiple Agile Optical Satellites

1  Introduction

Agile optical satellites (AOSs) are a new generation of imaging platforms that can take pictures of ground targets through optical payloads. A ground target means an observation task. Over the past decades, the Agile Earth Observation Satellite (AEOS), represented by the AOS, has played a significant role in many fields, such as resource exploration, environmental monitoring, disaster control, city planning, and military reconnaissance [1,2]. With the rapid growth in observation requests and the number of in-orbit AOSs, the scheduling of multiple AOSs for large-scale tasks has become an important issue.

Compared with traditional satellites, the AOSs have three degrees of freedom, which can adjust the attitude by rolling, pitching, and yawing. In this study, the AOSs adopt the push-broom observation mode, so only two ways of attitude adjustment, rolling and pitching, are taken into consideration. The visible time window (VTW) is the period during which the ground target is visible to the satellite. The observation window (OW) is the period during which the satellite continuously observes the target. The multi-AOS scheduling problem has proven to be an NP-hard combinatorial optimization problem [3]. The scheduling of satellites does not only involve the selection of appropriate VTWs for targets but also the determination of OWs and observation angles. Therefore, the complexity of this problem comprises two main aspects. First, several VTWs exist in different orbits for a target, and it is difficult to select the appropriate VTWs for all targets. As the problem scale expands, the solution space exhibits the characteristics of a combinatorial explosion. Second, it is difficult to determine the OWs of the targets. As shown in Fig. 1, the AOS has a relatively longer VTW than the traditional satellite because of its agility. The OW can start at any time within the VTW. Thus, a longer VTW indicates more possibilities for determining the OW. In addition, the observation start time is determined by the pitch angle and can further impact the transition time between a current target and a previous one, whereas the transition time is needed for a satellite to adjust its attitude. This characteristic is a time-dependent characteristic [4], which makes the OW more difficult to be determined. Because of these features, the multi-AOS scheduling problem is complex and difficult to solve.

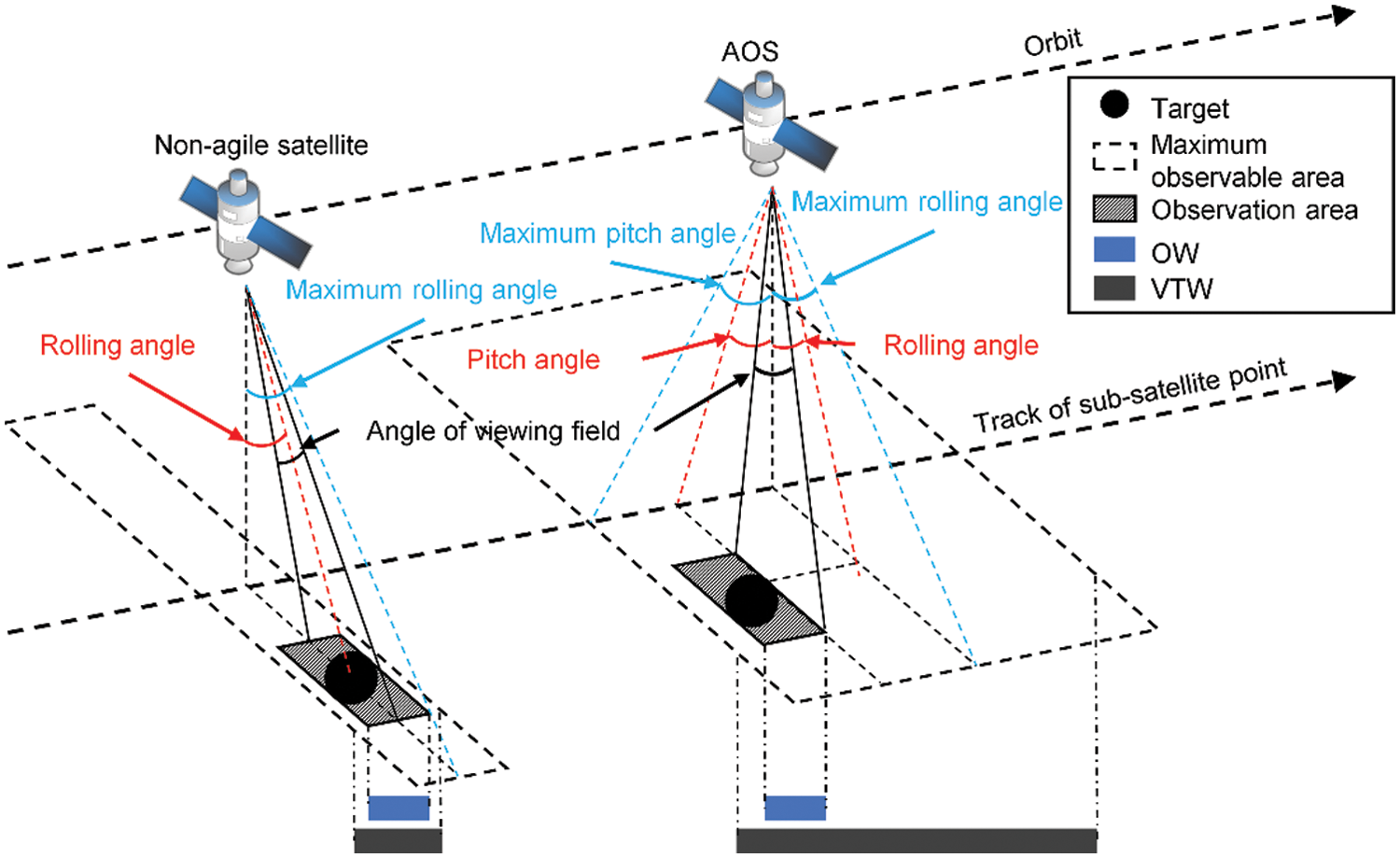
Figure 1: Observation process of a traditional satellite and an AOS

Exact algorithms and heuristic algorithms have been widely applied to solve this problem. Because of the NP-hard characteristic, exact algorithms are only adopted for small-scale single-orbit scheduling or single-satellite scheduling. Heuristic algorithms are the better choice to solve the scheduling problem of multiple AOSs. Several constructive heuristic algorithms [5–8] have been designed according to the characteristics of the problem and have achieved relatively good results. Meta-heuristic algorithms have also been widely used to solve this problem. In particular, evolutionary algorithms have been extensively applied owing to their simplicity and efficiency [9]. Li et al. [10] proposed a combination of genetic algorithm (GA) and simulated annealing (SA) algorithm for the single-orbit scheduling of an agile satellite. Yuan et al. [11] attempted to adopt GA to obtain a high-quality solution by improving the initialization. Chatterjee et al. [12] proposed an elitist mixed coded genetic algorithm (EMCGA) for satellite scheduling, and further improved the algorithm by combining it with a hill-climber mechanism to obtain better initialization. Zhi et al. [13] presented a variable observation duration scheduling method based on the quantum genetic algorithm for the scheduling of multiple agile satellites. Zhang et al. [14] developed a hybrid discrete particle swarm optimization (PSO) algorithm for the daily scheduling problem of the SPOT5 satellite. Yan et al. [15] presented a combination of PSO and the multiplicative MOORA (Multi Objective Optimization on the basis of Ratio Analysis) method for the emergency scheduling of multiple satellites. He et al. [16] proposed a hierarchical scheduling method based on ant colony algorithm for the real-time scheduling of agile satellites. Luo [17] proposed a hybrid binary artificial bee colony (BABC) algorithm for the satellite scheduling problem. The algorithm integrated the operators of crossover and mutation and a two-phase repair operator into the framework of an artificial bee colony. In addition to these evolutionary algorithms, other heuristic algorithms have been proposed. Wei et al. [18] considered the failure rate and the load balance degree as the two optimization objectives and proposed a multi-objective memetic approach. Besides, Wang et al. [19] introduced the complex network theory into the agile satellite scheduling problem and obtained effective scheduling results. Most of the abovementioned studies focus on the single-satellite scheduling or the scheduling of multiple satellites for dozens of tasks. With a further increase in the problem scale, these algorithms, including the abovementioned evolutionary algorithms, can hardly search for the optimal solution from a large solution space. Therefore, an effective scheduling method is required to obtain a good solution with the maximum given objective function.

In order to improve the satellite observation efficiency, task merging or task clustering is an effective way to process tasks. When a satellite moves in an orbit, an observation strip can be formed on the ground, and different observation angles lead to different strips. If two adjacent targets can be covered by the same observation strip, they can be merged. By merging multiple tasks into a whole task, a satellite can observe more targets with fewer observation times. In fact, ground targets tend to be concentrated in hot areas, and large-scale targets are usually densely distributed. In conventional methods without task merging, targets can only be observed individually, which results in conflicts among adjacent targets and inefficiency. As shown in Fig. 2a, adjacent targets compete for an observation opportunity, and only one of them can be observed. However, more adjacent targets can be observed through one observation action via task merging, as shown in Fig. 2b. In this way, the observation strips can cover two or more targets simultaneously. Many task merging methods have been proposed to address the traditional satellite scheduling problem [20–24]. Task merging of agile satellites is difficult to realize because of the time-dependent characteristic. A few researchers have achieved preliminary achievements. Zhao et al. [25] clustered target points according to the distance condition in the preprocessing stage. Chang et al. [26] developed a task clustering method that clustered two adjacent targets according to the maximum interval time and the true interval time between them. Long et al. [27] introduced a task merging mechanism to the stage of single-orbit scheduling. They proposed four kinds of task clustering constraints, including roll angle constraint, time-window related constraint, free time constraint of imaging, and transitive constraint, built a task clustering graph model, and realized the clustering of dozens of tasks with two satellites. However, the abovementioned merging methods have three deficiencies: first, the time-dependent characteristic is not sufficiently considered; second, these methods only apply to the small-scale scheduling of dozens of tasks; and finally, these methods may result in redundant observations which lead to a waste of memory and energy.

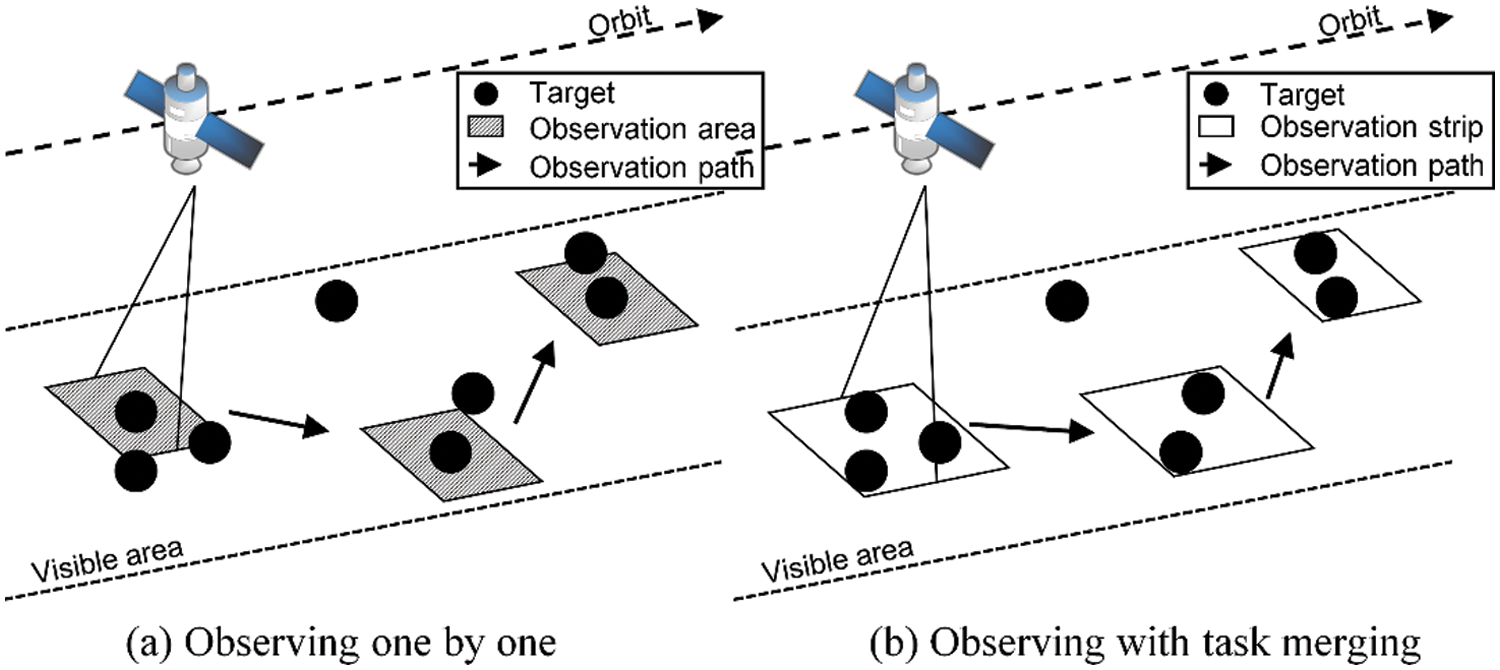
Figure 2: Illustration of two observation ways

In this study, we focus on the multi-AOS scheduling problem with large-scale tasks and propose a scheduling method with task merging. The main contributions are fourfold: (i) We take the time-dependent characteristic into full consideration and build the multi-AOS scheduling model with task merging constraints and observation action constraints; (ii) An improved sine and cosine algorithm (ISCA) is proposed for searching the optimal solution; (iii) A task merging method with a task reallocation mechanism (MR) is presented to improve the preliminary solution; (iv) Extensive experimental results prove the effectiveness of the proposed algorithm and test the effect of its parameters.

The remainder of this paper is organized as follows. In Section 2, we describe the multi-AOS scheduling problem in detail and model it. Section 3 presents a multi-AOS scheduling method based on an improved sine and cosine algorithm and a task merging method with a task reallocation mechanism. Section 4 presents the experimental results, and Section 5 presents the conclusions of the study with a summary and directions for future work.

2  Problem Description and Modeling

The process of multi-AOS scheduling through task merging is to select appropriate VTWs for tasks, merge multiple tasks into a whole task, and determine the corresponding observation actions of AOSs, satisfying all constraints. The whole task is called the merged task. For the tasks, sets of candidate VTWs are acquired according to the orbit parameters of the AOSs, their location, and the imaging requirements, which are the inputs of the problem. The VTWs in the solar shadow period are eliminated in consideration of the characteristics of the optical sensors. Furthermore, the outputs of the problem are the observation actions of the AOSs, including observation start time, observation end time, roll angle, and pitch angle.

2.1 Assumptions

The practical scheduling of AOSs is a complicated process, and many complex constraints must be satisfied. To simplify this problem, the following assumptions are made:

•   The data transmission process is not considered;

•   Every task is a point target or a small area that can be observed in one pass;

•   Each AOS has only one optical sensor;

•   For each AOS, the memory space is completely released and the energy is full at the initial moment of each orbital cycle.

2.2 Notations and Variables

The orbits of different AOSs can be equally treated as resources of the same type. Thus, the multi-AOS scheduling problem can be transformed into a multi-orbit scheduling problem. All orbits are put together in an orbit set. The set of orbits is denoted as O={oj|j=1,2,…,|O|}, where |O| is the number of orbits. The set of tasks is denoted as T={ti|i=1,2,…,|T|}, where |T| is the number of tasks. The VTW set of the task ti is denoted by VTWi, and |VTWi| is the number of VTWs. MTj={mtjk|k=1,2,…,|MTj|} is the set of merged tasks in the orbit oj, and |MTj| is the number of merged tasks. In order to describe all tasks in a uniform way, the task executed without merging is also denoted as mtjk. Aj={ajk|k=1,2,…,|Aj|} is the observation action sequence in the orbit oj, where |Aj| is the number of observation actions, and |Aj|=|MTj|. An observation action ajk accomplishes a merged task mtjk.

In addition, some notions are defined as follows:

•   vtwij=[estij,lstij] is the selected VTW for the task ti in the orbit oj, where estij is the earliest start time of the VTW and lstij is the latest start time; vtwij∈VTWi.

•   Rij is the roll angle range of the AOS corresponding the VTW vtwij.

•   di is the requested observation duration of ti.

•   pi is the priority of ti, representing the task profit.

•   owi=[sti,eti] is the observation window of ti. sti∈vtwij, eti=sti+di.

•   ajk={astjk,aetjk,arjk,apjk} is an observation action, where astjk is the observation start time, aetjk is the observation end time, arjk is the observation roll angle, and apjk is the observation pitch angle.

•   M is the maximum memory capacity in every orbit.

•   m is the memory consumption rate when the AOS observes.

•   E is the maximum energy in every orbit.

•   eo is the energy consumption rate when the AOS observes.

•   ea is the energy consumption rate when the AOS adjusts its attitude angle. ω is the angular velocity when the AOS adjusts its attitude angle.

•   pa is the pitch angle of the AOS. pa∈[pl,pu].

•   ra is the roll angle of the AOS. ra∈[rl,ru].

The 2-tuple (xi,yi) is used as the decision variable. xi is the serial number of the VTW selected for the task ti, and xi∈{0,1,2,|VTWi|}. xi=0 indicates that no VTWs are selected for ti. yi indicates whether the task ti can be successfully completed. If ti is successfully arranged in the selected VTW, yn=1; otherwise, yn=0. The two decision variables ensure that each task can be executed at most once.

2.3 Optimization Objective

The optimization objective of the multi-AOS scheduling problem is to maximize the profit ratio of the accomplished tasks. The objective function is expressed as below:

Maximizef=∑n=1|T|(pn⋅yn)∑n=1|T|pn(1)

2.4 Constraints

Practical multi-AOS scheduling is a complicated process, and a few complex constraints must be satisfied. Two types of constraints must be considered. First, the task merging constraints should be examined before merging multiple tasks. Second, the observation action constraints should be checked to determine whether the observation action can be executed.

2.4.1 Task Merging Constraints

If two or more tasks can be observed through one observation action, they can be merged into one merged task. The observation action is determined through the roll angle, the pitch angle, the observation start time, and the observation end time. On account of the time-dependent characteristic, the observation start time is determined through the pitch angle. Hence, the task merging constraints contain the roll angle constraint and the pitch angle constraint.

Assuming that (1) tasks t1, t2,…, tn are sorted by the earliest start time of their VTWs, (2) they are merged into the merged task mtjk, and (3) the observation action is ajk, the task merging constraints are described as follows.

(1)   Roll angle constraint

These tasks should satisfy the roll angle constraint.

R1∩R2∩⋯∩Rn≠∅(2)

If the roll constraint is satisfied, the lower bound of the roll angle range will be denoted as lrjk, and the upper bound will be denoted as urjk.

(2)   Pitch angle constraint

The pitch angle is related to the observation start time because of the time-dependent characteristic of the AOS. Liu et al. [4] adopted a linear function to describe the relationship between the pitch angle and the observation start time. For ti, the functional relationship between the pitch angle pa and the start time of its observation window sti is described as below:

pa=αij⋅sti+βij,estij≤sti≤lstij{ αij=pu−plestij−lstijβij=pu⋅estij−pl⋅lstijestij−lstij (3)

The pitch constraint must be sequentially examined in pairs. Tasks tu and tv are taken for examples. The linear relationship function curves of vtwuj and vtwvj are shown in Fig. 3. Using Eq. (3), the relationship among pa, stu and stv is described in Eq. (4). In order to observe the two tasks with a nonredundant observation, the conditions should be satisfied in Eq. (5).

pa=αuj⋅stu+βuj=αvj⋅stv+βvj(4)

stu+du≥stv(5)

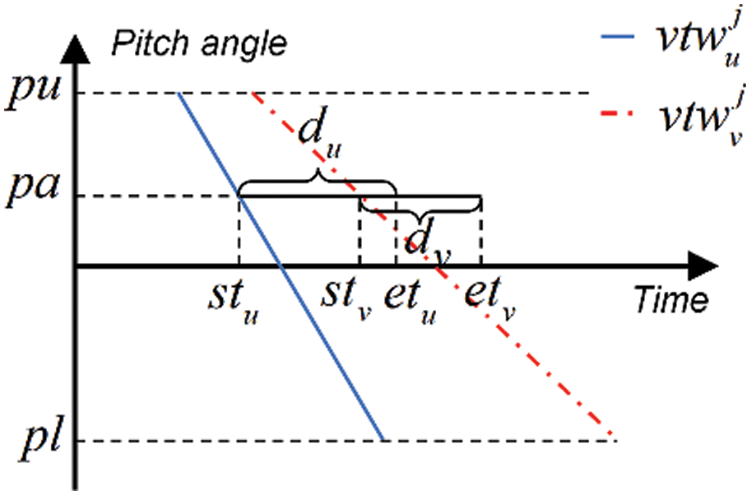
Figure 3: Linear relation function curves of two VTWs

The pitch angle range is denoted as P(tu,tv). Substituting Eq. (4) into Eq. (5), P(tu,tv) can be obtained. When tu and tv are merged, the pitch constraint is described by Eq. (6). The tasks t1, t2,…, tn should satisfy the constraint in Eq. (7), if they succeed in merging. The upper bound of the pitch angle range is denoted as upjk.

P(tu,tv)≠∅(6)

P(t1,t2)∩P(t2,t3)∩⋯∩P(tn−1,tn)≠∅(7)

After both the roll angle constraint and the pitch angle constraint are met, the observation action ajk can be obtained. The intermediate value of R1∩R2∩⋯∩Rn is taken as the roll angle on account of the observation quality, as expressed in Eq. (8). upjk is taken as the pitch angle to accomplish the merged task as early as possible, as shown in Eq. (9). Once the pitch angle is obtained, the start time of the OWs of these tasks can be calculated according to Eq. (3). Then, the duration of the observation action ajk is obtained through Eq. (10). Thus, the observation action of the merged task is determined.

arjk=lrjk+urjk2(8)

apjk=upjk(9)

[astjk,aetjk]=ow1∪ow2∪⋯∪own(10)

2.4.2 Observation Action Constraints

Several observation action constraints must be satisfied to ensure that the observation action is executed successfully.

(1)   Transition time constraint

Sufficient transition time is required for the adjustment from the previous attitude to the succeeding one. The attitude adjustment includes the adjustment of the pitch and roll angles. The transition time constraint is expressed as follows:

∀k∈{0,1,…,|Aj|−1},|apjk+1−apjk|+|arjk+1−arjk|ω≤astjk+1−aetjk(11)

where k=0 indicates the initial state of the AOS in the orbit oj.

Any two adjacent observation actions must satisfy this constraint. If the constraint cannot be satisfied, the succeeding observation action cannot be executed, and the corresponding merged task will be given up. In addition, the succeeding observation action is influenced by the previous action. Therefore, the observation actions can only be determined individually.

(2)   Memory capacity constraint

The observation data cannot exceed the maximum memory capacity:

∑k=1|Aj|[m⋅(aetjk−astjk)]≤M(12)

(3)   Energy constraint

The energy consumed for observation and attitude adjustment cannot exceed the maximum value:

∑k=1|Aj|[eo⋅(aetjk−astjk)]+∑k=0|Aj|−1[ea⋅(|apjk+1−apjk|+|arjk+1−arjk|)]≤E(13)

3  Multi-AOS Scheduling Method

In this section, an improved sine and cosine algorithm (ISCA) is proposed to allocate tasks to different orbits. An adaptive factor and an adaptive greedy degree are adopted to improve the search ability of the algorithm. Furthermore, a task merging method is developed to complete the scheduling of each orbit and a reallocation mechanism is adopted to improve the scheduling result. Eventually, the entire framework of the multi-AOS scheduling algorithm is introduced and the pseudocode is provided.

3.1 Improved Sine and Cosine Algorithm

Sine and cosine algorithm (SCA) [28] is a novel population-based heuristic algorithm. It was proposed by Mirjalili in 2016. The algorithm utilizes the mathematical properties of sine and cosine functions to search for an optimal solution. It can balance the global exploitation capacity and the local exploration capacity by changing the amplitude of sine and cosine functions. SCA has the advantages of few parameters and fast convergence.

Its core formulae for population update are described as below:

xhiiter+1=xhiiter+Δx(14)

Δx={xhiiter+r1⋅sin⁡r2⋅|r3⋅biiter−xhiiter|,r4<0.5xhiiter+r1⋅cos⁡r2⋅|r3⋅biiter−xhiiter|,r4≥0.5(15)

where xhiiter is the value in the ith dimension of the hth individual in the iterth iteration, biiter is the target value, r1 is a linear adaptive parameter, and r2, r3 and r4 are random numbers subject to a uniform distribution (r2∈[0,2π], r3∈[0,2], and r4∈[0,1]).

The multi-AOS scheduling problem is a discrete optimization problem, and thus, Δx needs to be rounded. Furthermore, the number of VTWs for each task is not large, and the range of xhiiter is small. To prevent xhiiter from exceeding its range, we adopt a mapping function to map Δx to a small range. The improved formulae are described below:

Δx′=round(21+exp⁡(−Δx)−1)(16)

xhiiter+1=xhiiter+Δx′(17)

In the original SCA, r1 is a linear factor. In order to further improve the search and convergence capability, a cosine factor is adopted as the adaptive parameter, as shown in Eq. (18).

r1=[cos⁡(π⋅iterMaxIter)+1]2(18)

where MaxIter is the maximum number of iterations.

Besides, the original algorithm adopts the global optimal solution as the target value to guide the evolution of the population. We propose an adaptive greedy factor δ to select the optimal solution or the local optimal solution of the previous iteration, as shown in Eq. (19).

biiter={gbi,r5≤δpbi,r5>δδ=iterMaxIter(19)

where gbi is the value in the ith dimension of the global optimal solution, pbi is the value in the ith dimension of the local optimal solution, and r5 is a random number (r5∈[0,1]).

Before the algorithm is used to solve the problem, appropriate encoding and decoding rules should be made to clarify the corresponding relationship between the actual problem and the solution obtained by the algorithm. An individual solution is merely a preliminary solution in encoding form. The code xhiiter corresponds to the series number of the VTW selected for the task ti. The decoding process allocates tasks to different orbits according to the selected VTWs.

3.2 Task Merging Method

After tasks are allocated to different orbits, a directed acyclic graph model is proposed to describe the merging relation among tasks in an orbit. As illustrated in Fig. 4a, Gj=(Vj,Ej) denotes the task merging model for the orbit oj, where Vj is a vertex set and Ej is an edge set. Vj is matched with the set of tasks allocated to the orbit oj. A vertex v represents a task. The tasks in Vj are sorted by the earliest start time of their selected VTWs. The numbers in the picture are the serial numbers of the vertices after sorting. An edge represents the merging relation between two vertices. If the relation between two vertices meets the task merging constraints, they will be linked by a directed edge which directs from the previous vertex to the succeeding one. N(v) is the neighbor set of the vertex v. The neighbors are the vertices which v points to. They are also the potential vertices that v can get merged with.

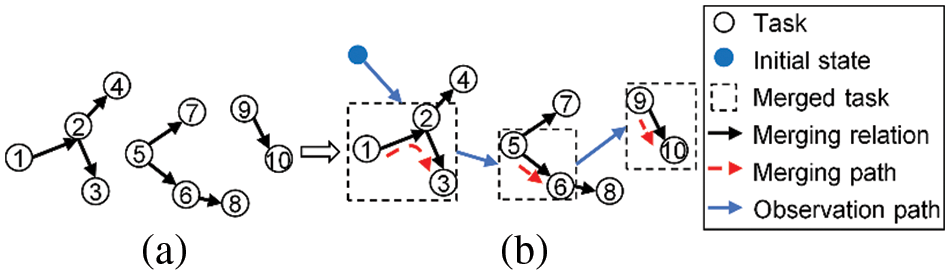
Figure 4: Directed acyclic graph model

The process of task merging is similar to that of path searching. First Come First Service (FCFS) strategy is adopted for rapid searching. As illustrated in Fig. 4b, the first vertex is selected as the starting point of the merging path. Next, a vertex in its neighbor set is selected as the second point. The third vertex is the neighbor of the second vertex. The merging path search does not stop until the final selected vertex has no neighbors or its neighbors cannot merge with the previous vertices. In this manner, a merged task can be obtained, and its observation action can be determined. The observation path starts from the initial state. If the observation action satisfies the observation action constraints, it will become the following point in the observation path. The removed vertices represent tasks that cannot be executed. A reallocation mechanism is adopted to improve the preliminary allocation. The reallocation process selects the next candidate VTW for every removed task. According to the selected VTWs, the removed tasks are reallocated to the feasible orbits. The tasks without VTW candidates are removed completely. The task merging method with the task reallocation mechanism (MR) is described in Table 1.

3.3 Improved Sine and Cosine Algorithm with Merging and Reallocation

In this subsection, the improved sine and cosine algorithm with merging and reallocation (ISCA-MR), which is a combination of ISCA and MR algorithm, is introduced. The main parts of ISCA-MR include population initialization, termination criteria, and population update. A random population is adopted as the initialization method. The algorithm terminates when the maximum number of iterations is reached or the objective function of the best individual remains unchanged for subsequent generations. In the process of the population update, every individual must follow four steps. Firstly, an individual is updated according to Eqs. (15)–(17). Secondly, the individual is converted into an allocation result by decoding. Thirdly, the MR algorithm is used to complete the scheduling of each orbit. Through the second and third steps, an individual solution is converted into a scheduling scheme, that contains the final allocation scheme and the observation action sequence of every AOS. The transformation process is illustrated in Fig. 5. Finally, the objective function of the individual is calculated according to Eq. (1). After updating the population, the local and global optimal solutions are obtained through comparison. The flow chart of the ISCA-MR is shown in Fig. 6, and the pseudocode is presented in Table 2.

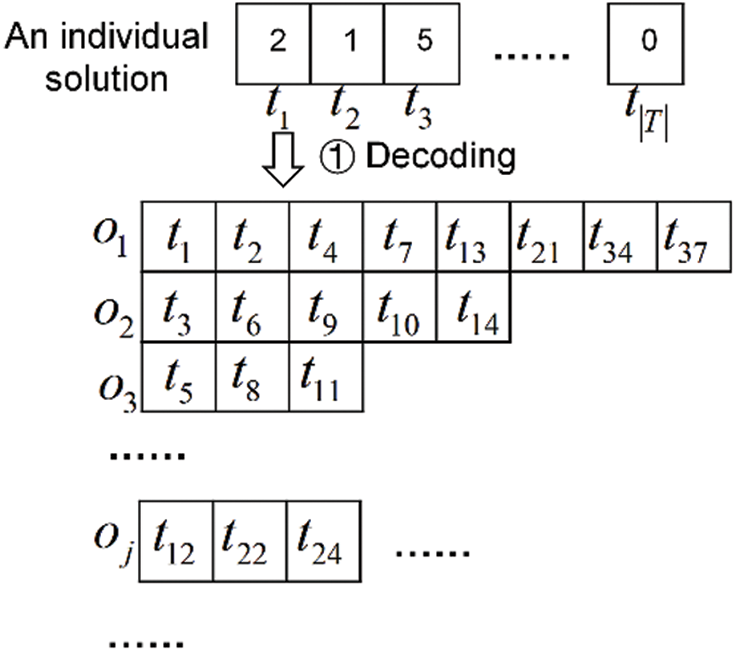
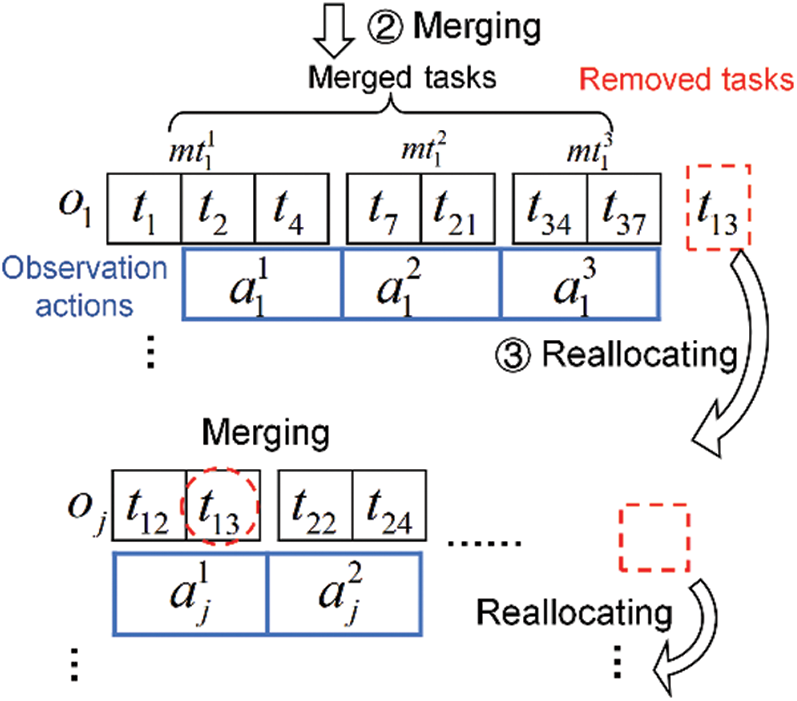
Figure 5: The transformation process of an individual solution

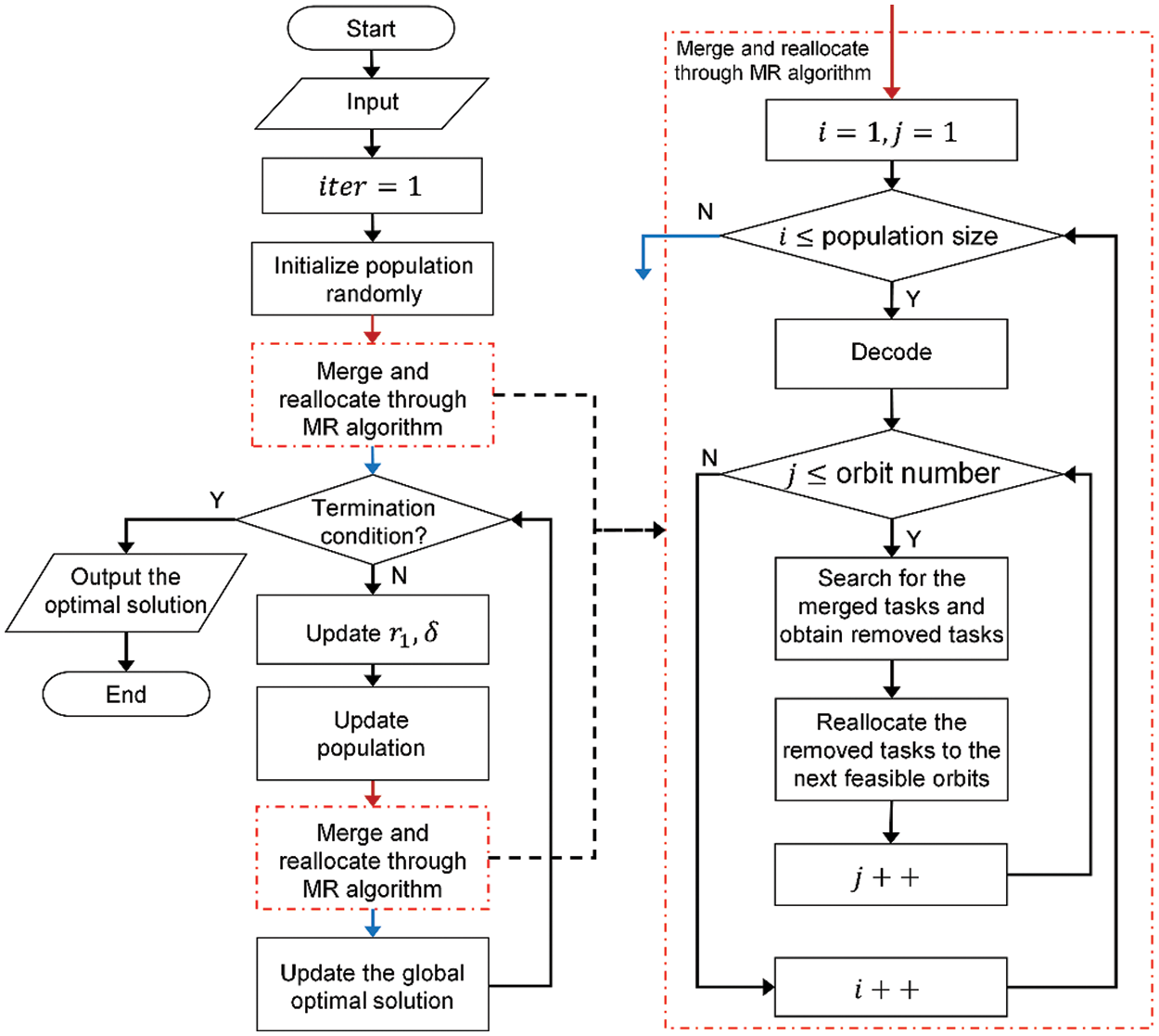
Figure 6: Flow chart of ISCA-MR

4  Computational Experiments

In this section, sufficient experiments are designed to verify the effectiveness of the proposed algorithm. The main aspects of the validation include the effect of task merging, the solving ability of the ISCA-MR in scenarios with large-scale tasks, and the influence of relevant parameters.

4.1 Scenario Design

The algorithm is coded by MATLAB R2016b, and the experiments are conducted on a laptop computer with Intel (R) Core (TM) i7-8565U CPU @ 1.80 GHz.

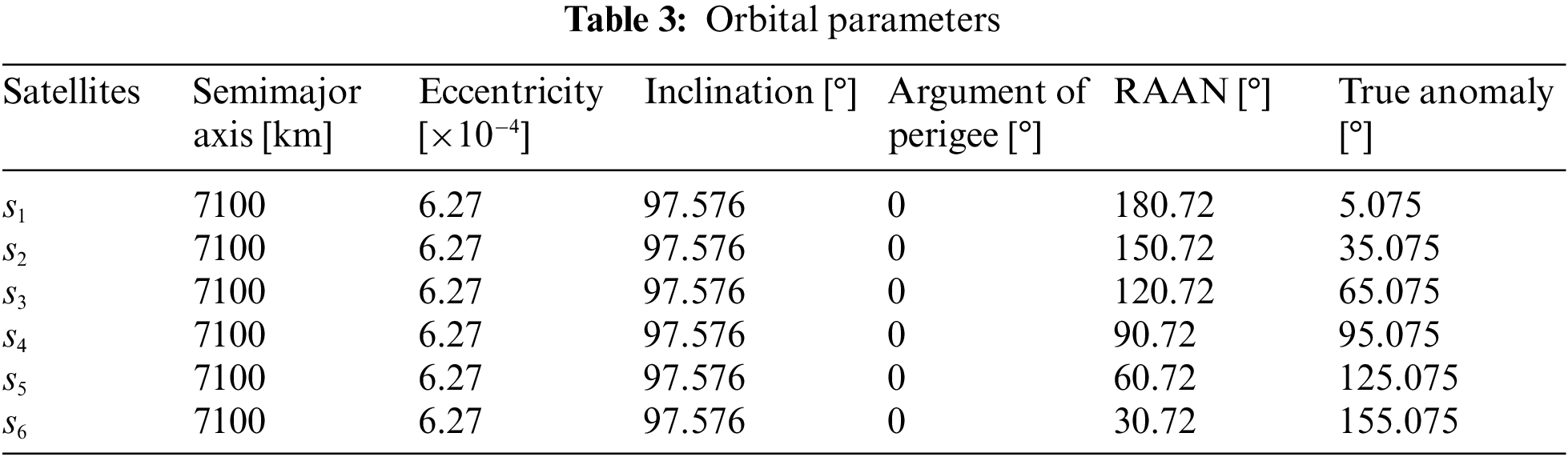
The design of the scenarios refers to reference [4]. A large number of point targets, densely distributed in the region, are set as tasks. The region is an area with the latitude from 0° N to 50° N and the longitude from 70° E to 130° E. The tasks are randomly distributed in this region. The number of tasks varies from 300 to 1000, with an increment step of 100, which generates eight scenarios. For each task, the requested observation duration is a random integer between 15 and 30, and the priority is a random integer between 1 and 10. Each scenario has six AOSs, and their orbital parameters are listed in Table 3. All satellites have the same attribute parameters. The roll angle is within [−45,45], and the pitch angle is also within [−45,45]. The other attribute parameters are listed in Table 4. The scheduling time horizon is from January 01, 2022, 00:00:00, to January 01, 2022, 24:00:00.

4.2 Results of Task Merging

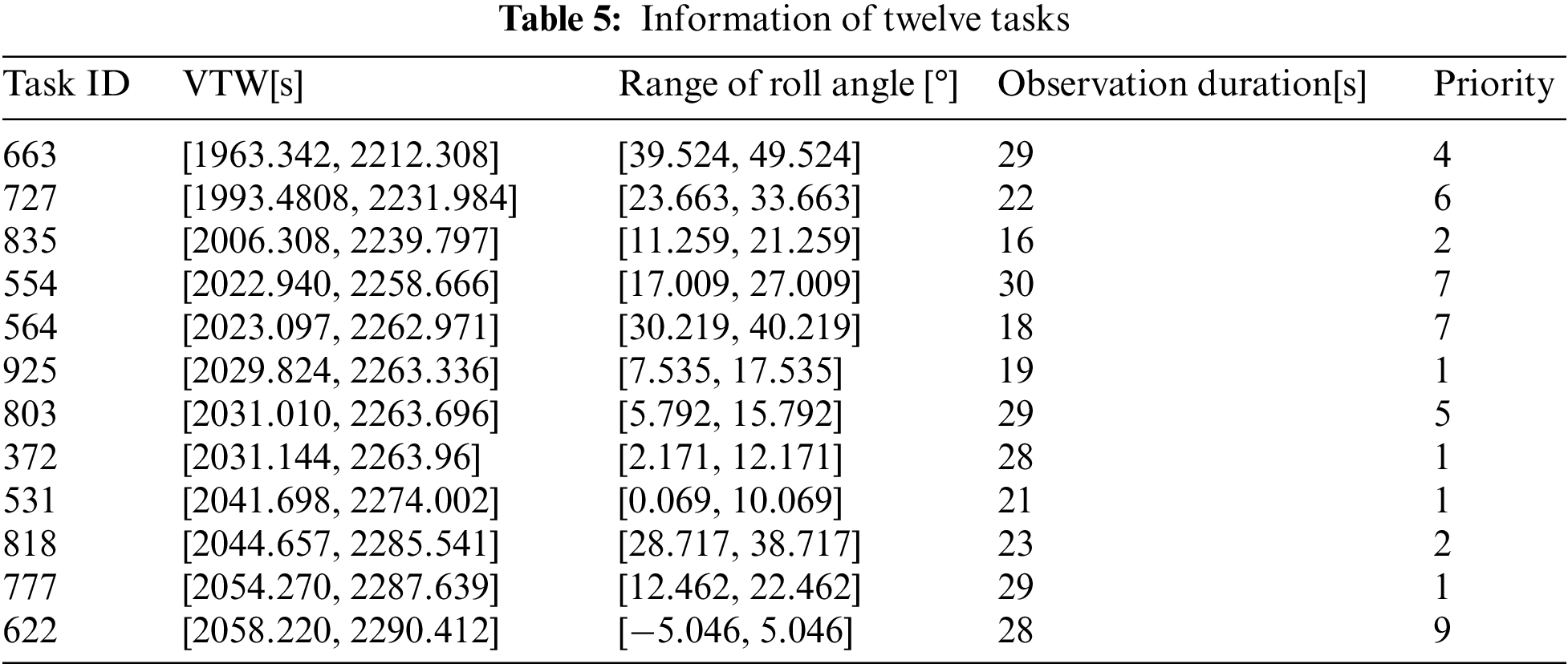
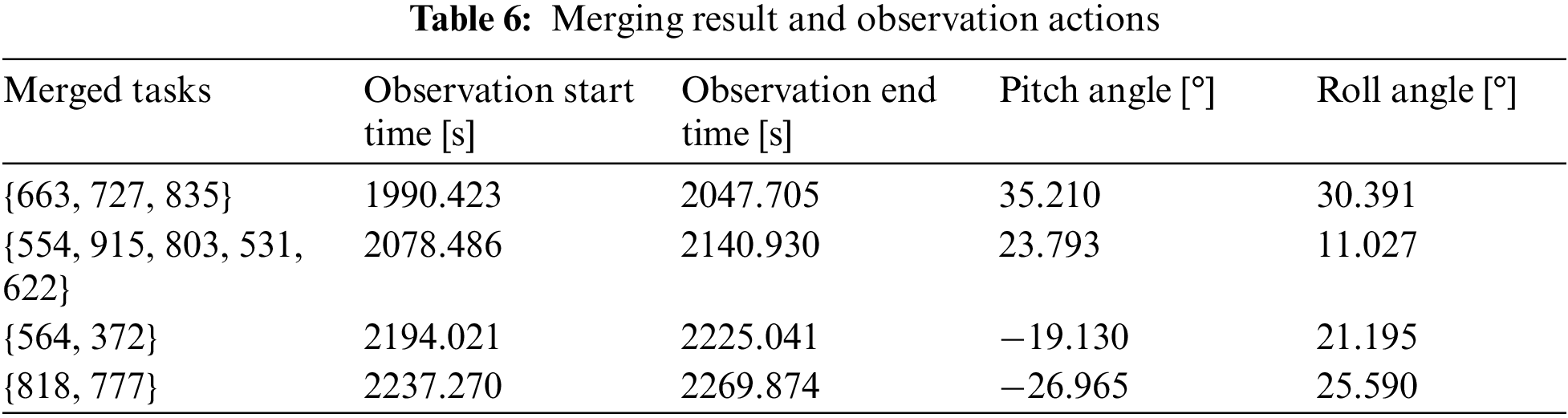
In order to better reflect the task merging effect, this subsection presents the partial scheduling result in one orbit in the scenario with 1000 tasks. 48 tasks are allocated to this orbit. These tasks are merged into 22 merged tasks. The first twelve tasks are selected to present the merging effect. Detailed information on these tasks is provided in Table 5, and they are sorted by the earliest start time of the VTWs. As shown in Table 6, the 12 tasks merge into 4 merged tasks, which can be completed through four observation actions. The time presented in the two tables is the number of seconds from the start of scheduling. Hence, the task merging result indicates that the proposed task merging method can improve the efficiency of the satellite observation.

4.3 Comparison with Other Meta-Heuristics

In this subsection, we compare the results of the proposed ISCA-MR algorithm with those of other meta-heuristics, including the improved sine and cosine algorithm with only reallocation (ISCA-R), the original sine and cosine algorithm (SCA), the aquila optimizer (AO) [29], the aquila optimizer with merging (AO-M), the tunicate swarm algorithm (TSA) [30] and the tunicate swarm algorithm with merging (TSA-M). For the sake of fairness, the ISCA-MR and the comparison meta-heuristics are terminated when the number of iterations reaches 100, and their population size is 10. The other parameters of AO and TSA are listed in Table 7. These algorithms are run once in the eight scenarios, and their convergence curves are obtained.

Fig. 7 illustrates the objective function curves of these eight algorithms. The horizontal axis represents the number of iterations, and the vertical axis represents the value of the objective function, which is the profit ratio. The comparison results are presented as follows:

(1)   In general, ISCA-MR outperforms all other algorithms in eight scenarios. In the first four scenarios, the number of tasks is less than 600, and the ISCA-MR can obtain the optimal solution. With an increase in the number of tasks, the curves of the other algorithms tend to flatten more easily, indicating that these algorithms easily fall into local optimization. However, ISCA-MR can still obtain a better solution, demonstrating that it is more applicable to the multi-AOS scheduling problem with large-scale tasks.

(2)   ISCA-MR performs best among the meta-heuristics with task merging, and similarly, ISCA-R performs best among the meta-heuristics without task merging. It is difficult for SCA-M, SCA, TSA-M, and TSA to optimize the population. Especially, TSA-M and TSA easily fall into local optimization at the beginning. Although the exploitation mechanism helps the further optimization of AO-M and AO at the end, they fail to obtain a high-quality solution. On the contrary, ISCA-MR and ISCA-R can obtain better solutions through iterative updates, indicating that they have better exploitation and exploration capabilities.

(3)   The meta-heuristic algorithms with task merging are apparently better than those without task merging. Especially, when the number of tasks exceeds 600, all algorithms with task merging obtain better solutions than those without task merging. Besides, the algorithms with task reallocation perform better than those without task reallocation. These prove that task merging and reallocation can effectively improve multi-AOS scheduling.

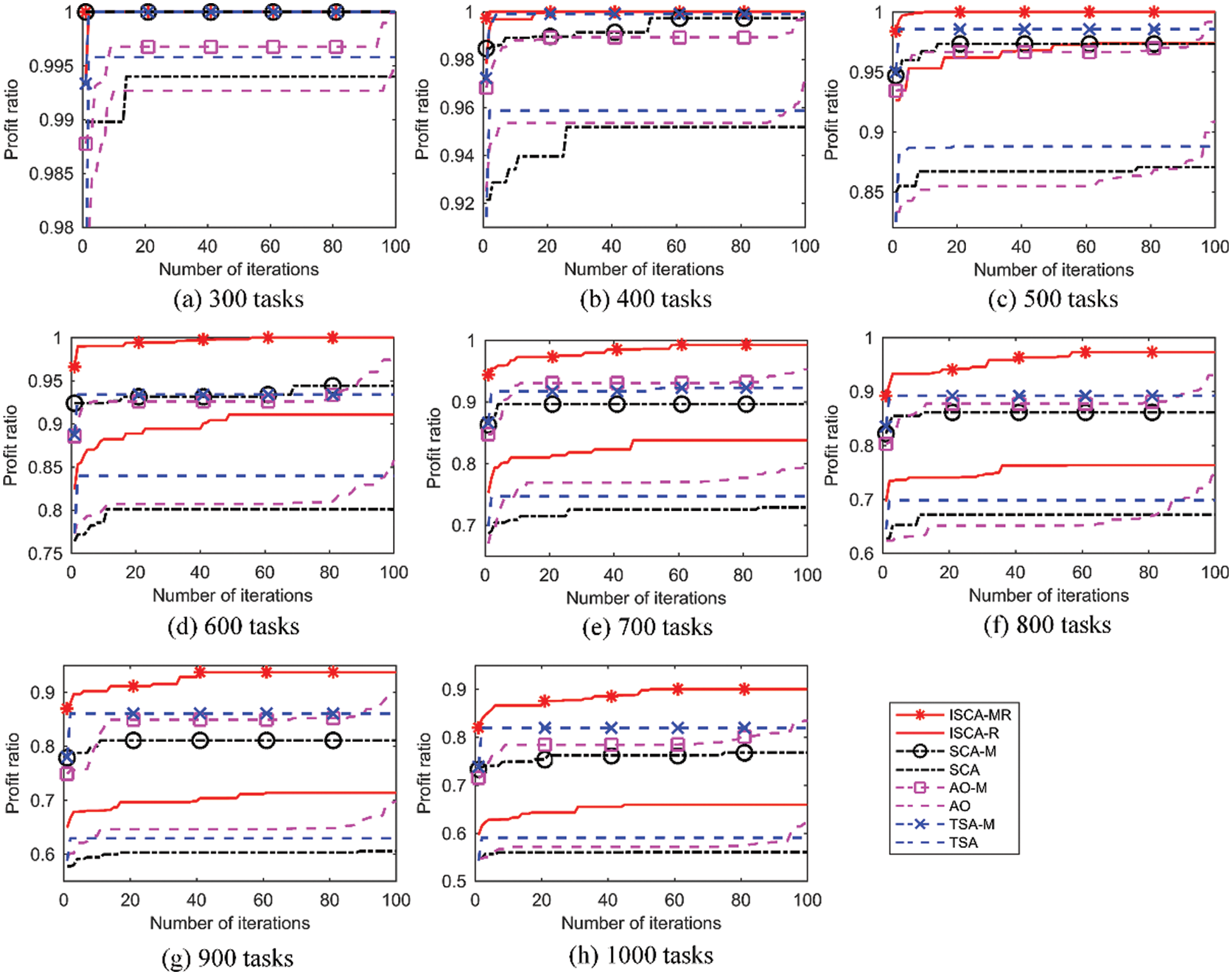
Figure 7: Objective function curves of different meta-heuristics

Therefore, we can draw two conclusions: (1) ISCA-MR is a competitive heuristic algorithm for solving the multi-AOS scheduling problem with large-scale tasks; (2) The task merging algorithm and the task reallocation mechanism can significantly improve scheduling efficiency.

4.4 Comparison with the State-of-the-Art Heuristics for Satellite Scheduling

To further verify the effect of ISCA-MR, we compare it with the state-of-the-art heuristics for satellite scheduling. In the eight scenarios, an elitist mixed coded hybrid genetic algorithm with a hill-climber mechanism (EMCHGA) [12] and a hybrid binary artificial bee colony algorithm (BABC) [17] are compared with the proposed algorithm. The population size of ISCA-MR, EMCHGA, and BABC is 10. These algorithms terminate when the number of iterations reaches 1000 or the objective function of the best individual remains unchanged for 100 consecutive iterations. These algorithms are run 10 times in every scenario, and the average profit ratio and the average CPU time are calculated, which are listed in Table 8.

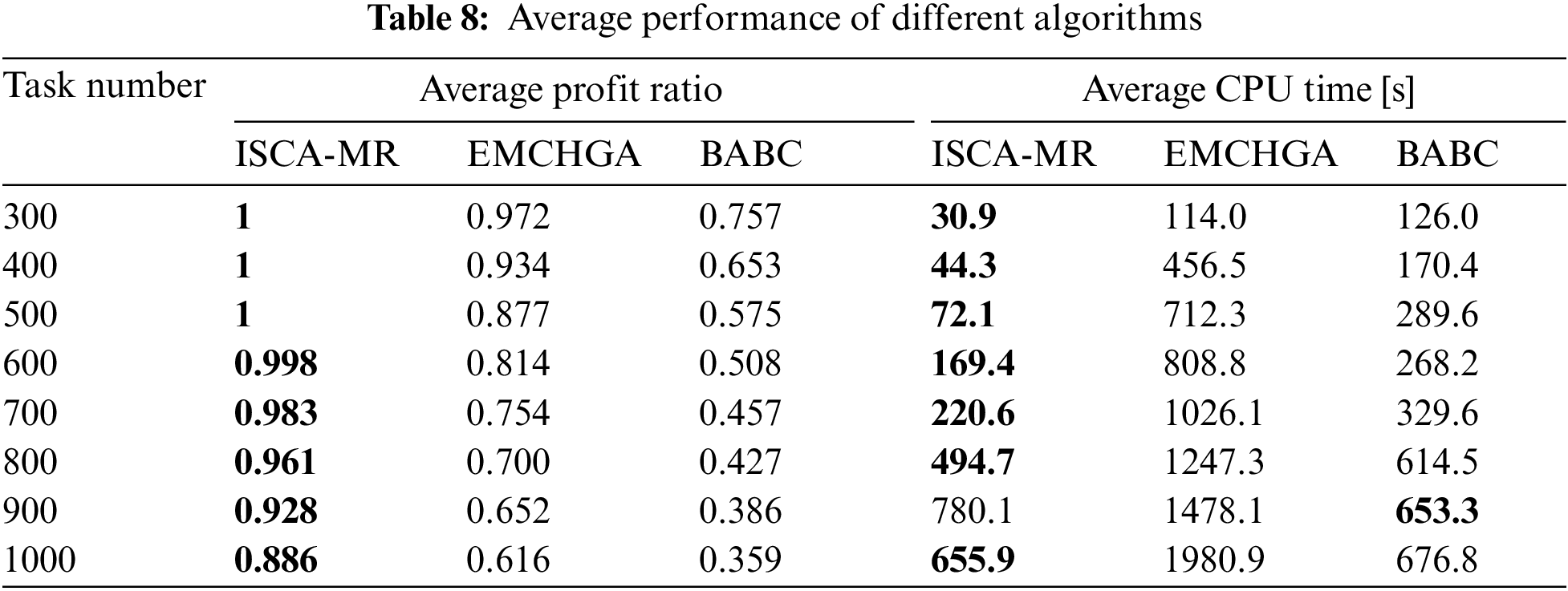
Table 8 reveals the performance of different algorithms for satellite scheduling, where the best results are in bold. The comparison results are given as follows:

(1)   Comparing the average profit ratio, ISCA-MR obtains the highest profit ratio among these three algorithms. When the number of tasks is less than 400, EMCHGA is close to ISCA-MR. Nevertheless, the gap between them is widening with the increase of the task number. BABC performs worst, indicating that BABC can hardly deal with large-scale tasks.

(2)   Comparing the average CPU time, ISCA-MR is far faster than the other two algorithms in most scenarios. The CPU time of EMCHGA increases most rapidly, and it reaches a high level when the number of tasks increases to 1000. The CPU time consumed by BABC is slightly less than that of ISCA-MR only in the scenario with 900 tasks, whereas it is a little more than that of ISCA-MR in the other scenarios.

(3)   Comparing the comprehensive performance of these algorithms, we can find that ISCA-MR can obtain the best solution with the minimum time cost. EMCHGA cannot get a good solution, and it needs a long CPU time. BABC obtains the worst solution in a short time, proving that it is easy to converge to a local optimum when the problem scale is large. The comparison results further prove that ISCA-MR is a competitive and efficient heuristic for satellite scheduling, and it is extremely applicable to the large-scale scheduling problem of multiple AOSs.

4.5 Parameter Sensitivity Analysis

In this subsection, we take the scenario with 1000 tasks as an example to test the influence of the size of population and the number of iterations on ISCA-MR. Two separate groups of experiments are set up. In the first set of experiments, the size of the population varies from 10 to 100, with an increment step of 10, and the number of iterations is still 100. In the second set, the number of iterations varies from 100 to 1000, with an increment step of 100, and the size of the population is 10. All results are obtained from the independent runs of the algorithm.

As shown in Fig. 8, the difference in the solution quality remains small when the population size is increased from 10 to 100. However, every time the population size increases by 10, the consumed CPU time increases by approximately 320 s. This indicates that the population size has a slight influence on the solution quality of ISCA-MR, and a small population size can lead to an acceptable solution within a relatively short time. Therefore, it is appropriate to set the population size to 10. Fig. 9 illustrates the effect of the number of iterations on the algorithm. As the number of iterations increases from 100 to 500, the solutions continue to improve. However, the change in the profit ratio is small when the number of iterations exceeds 500. Unsurprisingly, the consumed CPU time increases quickly. It increases to 1667 s when the number of iterations is 500. The results suggest that ISCA-MR can further improve the solution when the number of iterations is more than 100, and it finally converges to a satisfactory solution within 500 iterations.

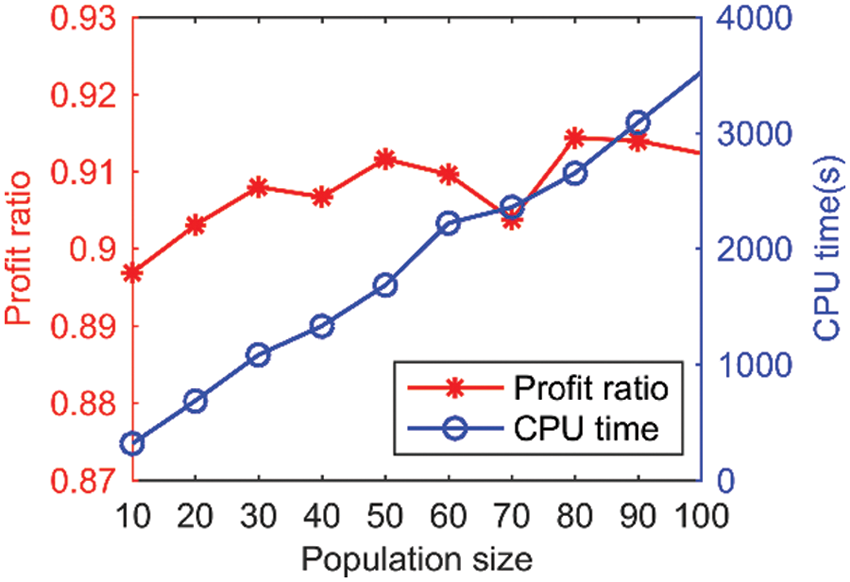
Figure 8: Results of ISCA-MR with different population sizes

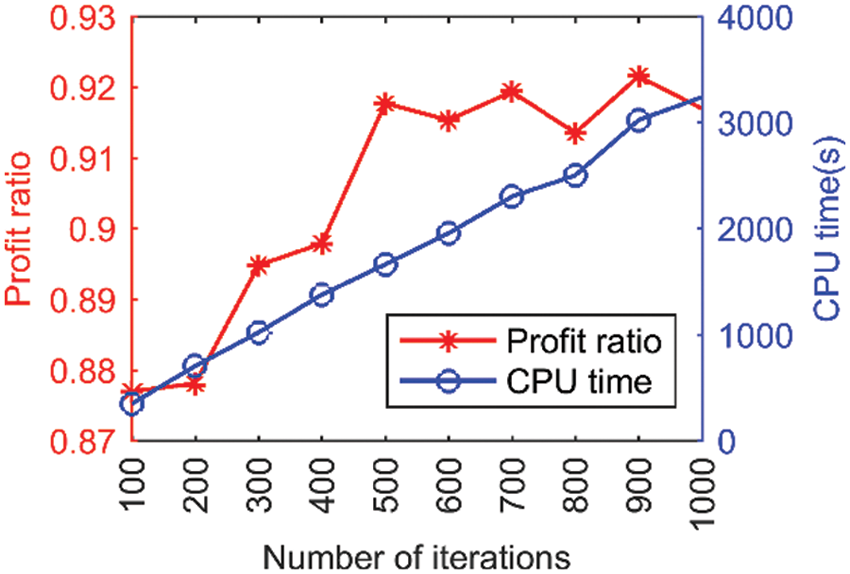
Figure 9: Results of ISCA-MR with different iteration numbers

5  Conclusion and Future Work

In this study, we investigate the multi-AOS scheduling problem with large-scale tasks and provide a scheduling method based on an improved sine and cosine algorithm and a task merging method. Firstly, we set up an optimization model for this problem with task merging constraints and observation action constraints. The time-dependent characteristic and the nonredundant observation are taken into consideration. Then, we propose the ISCA-MR heuristic algorithm to solve this problem. In the algorithm, an adaptive factor and an adaptive greedy factor are adopted to enhance the searching ability, and a task merging algorithm with a reallocation mechanism is developed to increase scheduling efficiency.

Furthermore, numerous experiments are designed to verify the effectiveness of the proposed ISCA-MR algorithm. The partial task merging results verify the effectiveness of the task merging method. Several algorithms are compared with the proposed algorithm. The influence of relevant parameters is analyzed. The results show that the proposed algorithm considerably outperforms the comparison algorithms, particularly for large-scale problems. Moreover, the task merging method and the task reallocation mechanism dramatically improve scheduling efficiency.

Future work will focus on autonomous scheduling of multiple AOSs. The attitude planning model of agile satellites should be considered. A multi-AOS coordination mechanism will be studied to enhance the collaborative scheduling capability. In addition, data transmission should be considered and an integrated scheduling model for observation and data transmission should be investigated.

Funding Statement: This research was supported by Science and Technology on Complex Electronic System Simulation Laboratory (Funding No. 6142401003022109).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Wu, G., Pedrycz, W., Li, H., Ma, M., Liu, J. (2015). Coordinated planning of heterogeneous earth observation resources. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 46(1), 109–125. DOI 10.1109/TSMC.2015.2431643. [Google Scholar] [CrossRef]

    2. Berger, J., Lo, N., Noël, M., Noutegne, L. (2020). Dynaquest: A new approach to the dynamic multi-satellite scheduling problem. Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES), pp. 194–201. Valletta, Malta. [Google Scholar]

    3. Lemaıtre, M., Verfaillie, G., Jouhaud, F., Lachiver, J. M., Bataille, N. (2002). Selecting and scheduling observations of agile satellites. Aerospace Science and Technology, 6(5), 367–381. DOI 10.1016/S1270-9638(02)01173-2. [Google Scholar] [CrossRef]

    4. Liu, X., Laporte, G., Chen, Y., He, R. (2017). An adaptive large neighborhood search metaheuristic for agile satellite scheduling with time-dependent transition time. Computers & Operations Research, 86, 41–53. DOI 10.1016/j.cor.2017.04.006. [Google Scholar] [CrossRef]

    5. Xu, R., Chen, H., Liang, X., Wang, H. (2016). Priority-based constructive algorithms for scheduling agile earth observation satellites with total priority maximization. Expert Systems with Applications, 51, 195–206. DOI 10.1016/j.eswa.2015.12.039. [Google Scholar] [CrossRef]

    6. Cho, D. H., Kim, J. H., Choi, H. L., Ahn, J. (2018). Optimization-based scheduling method for agile earth-observing satellite constellation. Journal of Aerospace Information Systems, 15(11), 611–626. DOI 10.2514/1.I010620. [Google Scholar] [CrossRef]

    7. He, Y., Chen, Y., Lu, J., Chen, C., Wu, G. (2019). Scheduling multiple agile earth observation satellites with an edge computing framework and a constructive heuristic algorithm. Journal of Systems Architecture, 95, 55–66. DOI 10.1016/j.sysarc.2019.03.005. [Google Scholar] [CrossRef]

    8. Kim, J., Ahn, J., Choi, H. L., Cho, D. H. (2020). Task scheduling of agile satellites with transition time and stereoscopic imaging constraints. Journal of Aerospace Information Systems, 17(6), 285–293. DOI 10.2514/1.I010775. [Google Scholar] [CrossRef]

    9. Wang, X., Wu, G., Xing, L., Pedrycz, W. (2020). Agile earth observation satellite scheduling over 20 years: Formulations, methods, and future directions. IEEE Systems Journal, 15(3), 3881–3892. DOI 10.1109/JSYST.2020.2997050. [Google Scholar] [CrossRef]

  10. Li, Y., Xu, M., Wang, R. (2007). Scheduling observations of agile satellites with combined genetic algorithm. Proceedings of the 3rd International Conference on Natural Computation (ICNC), pp. 29–33. Haikou, China. [Google Scholar]

  11. Yuan, Z., Chen, Y., He, R. (2014). Agile earth observing satellites mission planning using genetic algorithm based on high quality initial solutions. 2014 IEEE Congress on Evolutionary Computation (CEC), pp. 603–609. Beijing, China. [Google Scholar]

  12. Chatterjee, A., Tharmarasa, R. (2022). Reward factor-based multiple agile satellites scheduling with energy and memory constraints. IEEE Transactions on Aerospace and Electronic Systems, 58(4), 3090–3103. DOI 10.1109/TAES.2022.3146115. [Google Scholar] [CrossRef]

  13. Zhi, H., Liang, W., Han, P., Guo, Y., Li, C. (2021). Variable observation duration scheduling problem for agile earth observation satellite based on quantum genetic algorithm. 2021 40th Chinese Control Conference (CCC), pp. 1715–1720. Beijing, China. [Google Scholar]

  14. Zhang, D., Guo, L., Cai, B., Sun, N., Wang, Q. (2013). A hybrid discrete particle swarm optimization for satellite scheduling problem. 2011 IEEE International Conference on Intelligent Computingand Integrated Systems (ICISS), Guilin, China. DOI 10.1109/ANTHOLOGY.2013.6784716. [Google Scholar] [CrossRef]

  15. Yan, B., Wang, Y., Xia, W., Hu, X., Ma, H. et al. (2022). An improved method for satellite emergency mission scheduling scheme group decision-making incorporating PSO and MULTIMOORA. Journal of Intelligent & Fuzzy Systems: Applications in Engineering and Technology, 42(4), 3837–3853. DOI 10.3233/JIFS-212034. [Google Scholar] [CrossRef]

  16. He, L., Liu, X. L., Chen, Y. W., Xing, L. N., Liu, K. (2019). Hierarchical scheduling for real-time agile satellite task scheduling in a dynamic environment. Advances in Space Research, 63(2), 897–912. DOI 10.1016/j.asr.2018.10.007. [Google Scholar] [CrossRef]

  17. Luo, K. (2020). A hybrid binary artificial bee colony algorithm for the satellite photograph scheduling problem. Engineering Optimization, 52(8), 1421–1440. DOI 10.1080/0305215X.2019.1657113. [Google Scholar] [CrossRef]

  18. Wei, L., Xing, L., Wan, Q., Song, Y., Chen, Y. (2021). A multi-objective memetic approach for time-dependent agile earth observation satellite scheduling problem. Computers & Industrial Engineering, 159, 107530. DOI 10.1016/j.cie.2021.107530. [Google Scholar] [CrossRef]

  19. Wang, X. W., Chen, Z., Han, C. (2016). Scheduling for single agile satellite, redundant targets problem using complex networks theory. Chaos, Solitons & Fractals, 83, 125–132. DOI 10.1016/j.chaos.2015.12.003. [Google Scholar] [CrossRef]

  20. Wu, G., Liu, J., Ma, M., Qiu, D. (2013). A two-phase scheduling method with the consideration of task clustering for earth observing satellites. Computers & Operations Research, 40(7), 1884–1894. DOI 10.1016/j.cor.2013.02.009. [Google Scholar] [CrossRef]

  21. Wang, J., Zhu, X., Qiu, D., Yang, L. T. (2013). Dynamic scheduling for emergency tasks on distributed imaging satellites with task merging. IEEE Transactions on Parallel and Distributed Systems, 25(9), 2275–2285. DOI 10.1109/TPDS.2013.156. [Google Scholar] [CrossRef]

  22. Liu, X. L., Bai, B. C., Chen, Y. W., Yao, F. (2014). Multi satellites scheduling algorithm based on task merging mechanism. Applied Mathematics and Computation, 230, 687–700. DOI 10.1016/j.amc.2013.12.109. [Google Scholar] [CrossRef]

  23. Wu, G., Wang, H., Pedrycz, W., Li, H., Wang, L. (2017). Satellite observation scheduling with a novel adaptive simulated annealing algorithm and a dynamic task clustering strategy. Computers & Industrial Engineering, 113, 576–588. DOI 10.1016/j.cie.2017.09.050. [Google Scholar] [CrossRef]

  24. Du, B., Li, S. (2019). A new multi-satellite autonomous mission allocation and planning method. Acta Astronautica, 163, 287–298. DOI 10.1016/j.actaastro.2018.11.001. [Google Scholar] [CrossRef]

  25. Zhao, Y., Du, B., Li, S. (2020). Agile satellite mission planning via task clustering and double-layer tabu algorithm. Computer Modeling in Engineering & Sciences, 122(1), 235–257. DOI 10.32604/cmes.2020.08070. [Google Scholar] [CrossRef]

  26. Chang, Z. X., Zhou, Z. B., Yao, F., Liu, X. L. (2021). Observation scheduling problem for AEOS with a comprehensive task clustering. Journal of Systems Engineering and Electronics, 32(2), 347–364. DOI 10.23919/JSEE.2021.000029. [Google Scholar] [CrossRef]

  27. Long, J., Chen, S., Li, C., Liu, J. (2018). A task clustering method for multi agile satellite based on clique partition. 2018 11th International Conference on Intelligent Computation Technology and Automation (ICICTA), pp. 332–336. Changsha, China. [Google Scholar]

  28. Mirjalili, S. (2016). SCA: A sine cosine algorithm for solving optimization problems. Knowledge-Based Systems, 96, 120–133. DOI 10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]

  29. Abualigah, L., Yousri, D., Abd Elaziz, M., Ewees, A. A., Al-Qaness, M. A. et al. (2021). Aquila optimizer: A novel meta-heuristic optimization algorithm. Computers & Industrial Engineering, 157, 107250. DOI 10.1016/j.cie.2021.107250. [Google Scholar] [CrossRef]

  30. Kaur, S., Awasthi, L. K., Sangal, A., Dhiman, G. (2020). Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization. Engineering Applications of Artificial Intelligence, 90, 103541. DOI 10.1016/j.engappai.2020.103541. [Google Scholar] [CrossRef]