Safety Risk Assessment of Overturning Construction of Towering Structure Based on Cloud Matter–Element Coupled Model

1  Introduction

The concept of risk and risk assessment has a long history; as early as more than 2400 years ago, the Athenians suggested that they could assess risk before making decisions [1]. In the 1930s, risk assessment emerged in the United States, and the U.S. Insurance Management Association first introduced risk assessment into education in the 1960s, which meant that risk assessment became a new discipline [2]. Since then, many scholars have conducted extensive and in-depth research on the types, characteristics, causes, and management of risks in various industries. In the construction process of large and complex structural systems such as towering buildings, various risk factors can interact and couple with each other, leading to safety accidents. The turnover formwork construction is a modern evolution of traditional climbing technology; its relatively unique process and technology can effectively adapt to the diversified variable section construction. This technology has been widely used in barrel, rectangular, and other engineering practices in recent years [3–5]. However, the complexity and uncertainty of the turnover formwork construction plan are still considerably due to the complexity of the structure system, the number of related processes involved, the high technical requirements, and the imperfect research on its safety [6]. Such difficulty leads to serious losses once the safety production accidents of the turnover formwork construction occur. Thus, in order to improve the effectiveness of safety risk assessment in the construction of towering buildings with overturned forms, it is important to combine traditional construction processes with information calculation models for systematic analysis of risks in the construction phase of projects.

In terms of risk assessment methods, existing studies have made important contributions to the safety risk assessment of overturning construction of towering structures. Literature [7] first proposed a new method of accident tree embedding artificial neural network based on the traditional accident tree analysis method through fuzzy set theory and hierarchical analysis. Literature [8] proposed a newly developed hierarchical distributed agent model for network risk assessment inspired by deep learning neural network theory. Literature [9,10] both incorporated the original analytic hierarchy process (AHP) and triangular fuzzy number-based AHP (TFN-AHP) into a geographic information system (GIS) to assess the risk of flood. The purpose of TFN-AHP is to effectively address complex situations where a significant number of experts have a high degree of preference variation. Literature [11] proposed a gray fuzzy material element theory construction risk assessment method based on Delphi method to improve the scientific aspect and effectiveness of construction risk source determination and increase the accuracy of construction risk factor analysis. Literature [12] introduced for the first time a new method of multi-indicator assessment of risk level based on entropy weight normal cloud model to address the situation that the assessment indexes will be affected by multiple factors when the construction risk assessment object itself has great complexity and ambiguity. Literature [13] first developed a stepwise process of fuzzy affiliation function based on the improved fuzzy set theory to determine risk variables, which provides a solution to the lack of historical data and reliance on expert opinions when assessing construction risk. Literature [14] identified the most important factors influencing the formwork systems by applying the relative importance index method through questionnaires and interviews with experts. Literature [15] addressed the problem of insufficient quantitative assessment of tall formwork construction risks based on the improved LEC method (operational conditions hazard rating method) for risk assessment indicators of tall formwork considering the influence of the formwork system itself and human factors.

Through the summary and analysis of the relevant risk assessment methods, it can be found that the commonly used assessment methods can be divided into subjective and objective evaluation methods. Subjective evaluation methods include Delphi method, hierarchical analysis, etc.; the objective ones include gray system evaluation, matter-element extension method [16,17], cloud model, artificial neural network, etc. In complex building construction safety risk assessment, analysis and decision-making are affected by various factors, making the information often present a certain degree of ambiguity and randomness [18,19]. Moreover, the building construction risk assessment is affected by various factors, and the relationship between them is difficult to express quantitatively. Therefore, considering these factors comprehensively is difficult for a single evaluation method. Hierarchical analysis is often used in the evaluation process to quantify the index weights [20]. However, this approach is also inclined to depend on expert opinions, and the fuzziness and incompatibility between evaluation indexes contribute to certain limitations of the above evaluation methods. Cloud model has attracted the attention of many scholars because of their ability to express the ambiguity and randomness of assessment information [21], the advantage of the widely used matter–element theory in recent years lies in its scientific solving of the incompatibility problem of evaluation objects. With the continuous development of theoretical methods, both cloud model and matter-element theory are gradually applied to practical problems, such as fuzzy evaluation, multi-attribute decision making and risk assessment [22]. In the field of uncertain information processing, seeking scientific and reasonable combination assessment methods to analyze and deal with various uncertainties in the process of security risk assessment is the direction and difficulty of scientific assessment.

Therefore, this paper proposed a novel risk assessment method for overturning construction of towering structures. The main contributions of this paper are as follows. (1) An index system for overturning construction of towering structures is established on the basis of overturning construction process to deal with the problem of complex formwork construction technology and numerous construction projects. (2) The cloud model is used to improve the hierarchical analysis method to determine the index weights and avoid the adverse impact of over-reliance on expert opinions. (3) The risk assessment of overturning construction of towering structures is conducted by the cloud matter–element coupled model to estimate the uncertainty of different evaluation indexes scientifically. (4) A specific project in Xinjiang Province, China, is selected for the case study, and the research results provide new ideas for the safety risk assessment of similar projects.

This paper consists of five sections. Section 1 introduces the present situation of the study and highlights the need of the study. Section 2 describes the establishment of the construction risk evaluation index system of overturning construction of towering structure, and presents the novel construction risk assessment method based on cloud matter-element coupled model. Section 3 presents the case study of the overturning construction project of Turpan area in Xinjiang Province, China. Section 4 presents the discussion of the study and the last section presents the conclusions made from this study.

2  Risk Assessment Model for Overturning Construction of Towering Structures

The purpose of this section is to establish a safety risk assessment model for turnover form-work construction of towering structures. This section contains five aspects: (1) Establishment of construction safety risk assessment index system by risk identification; (2) Grading of assessment indexes and safety risk metrics; (3) Determination of risk assessment index weights; (4) Introduction of the basic idea of cloud matter–element coupling model; (5) Creation of the construction safety risk assessment model based on the first four parts. The specific evaluation process is shown in Fig. 1.

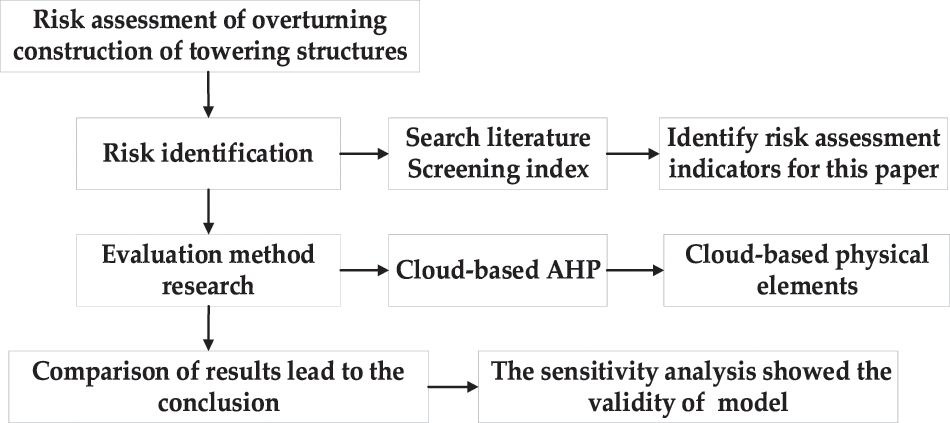
Figure 1: Evaluation flow chart

2.1 Establishment of Security Risk Assessment Index System

The first step of risk assessment is to identify risk factors [23]. Based on the “Standard for Safety Inspection of Building Construction” (JGJ 59-2011) [24], this paper started from the perspective of the technique and process of overturning construction and referred to the engineering geological survey report, project design drawings, national standards and local codes. Combined with a large number of engineering practice and theoretical research of many experts, the risk assessment index system was constructed by selecting the indexes that play an important role in overturning construction.

2.1.1 Risk Indicators for the Formwork Design and Installation Stage

The factors affecting the installation of formwork include wind load calculation [25], pressure calculation of the main beam [26], pull-out test computation of buried parts, and permissible deviation of verticality of formwork installation [27]. The installation stage of the formwork should consider the load-bearing capacity requirements of the formwork in the design stage and the installation error of the formwork in the construction process on site.

2.1.2 Risk Indicators for Concrete Pouring Phase

For the construction of towering structures with turnover formwork on site, the risks involved in concrete placement operations cannot be ignored. During the pouring process, considering the influence of concrete slump, newly poured concrete lateral pressure [28], and concrete pouring speed under the influence of wind load [29] is important.

2.1.3 Risk Indicators for the Template Upgrading Phase

Factors, such as the strength of the concrete before the formwork is lifted, the test hoisting, and the wind load factors at high altitude, are all important influencing features that constitute the construction risk during the turnover formwork upgrading stage [30].

2.1.4 Formwork Removal Stage Risk Indicators

The risk factors influencing the removal of turnover formwork [31,32] include the location of the center of gravity of the formwork, the percentage of concrete design strength achieved, the order of formwork removal, and falling objects from height.

The resulting hierarchy of risk indicators for overturning the construction of towering structures is shown in Fig. 2.

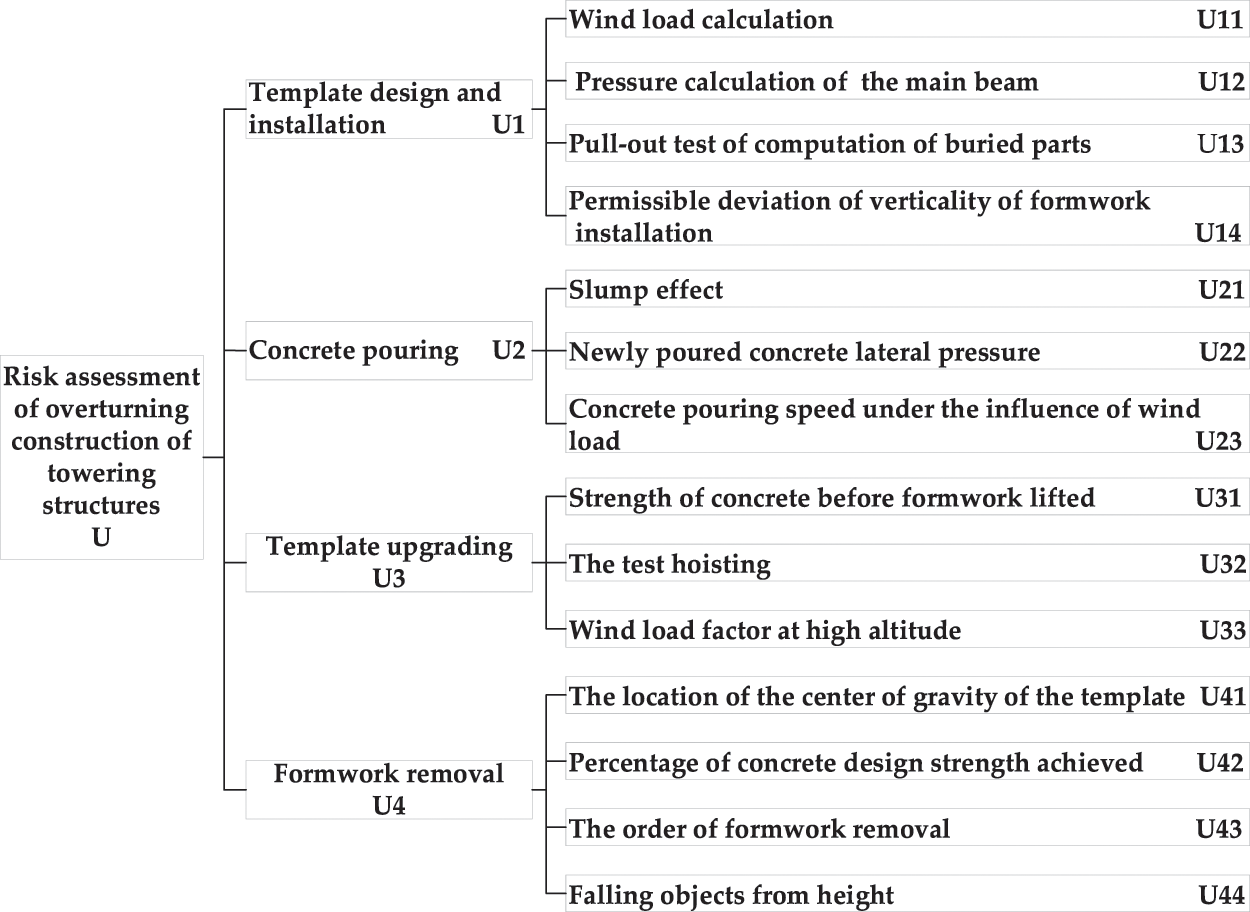
Figure 2: The hierarchical model of risk causes in overturning construction of towering structures

2.2 Grading of Assessment Indicators and Security Risk Metrics

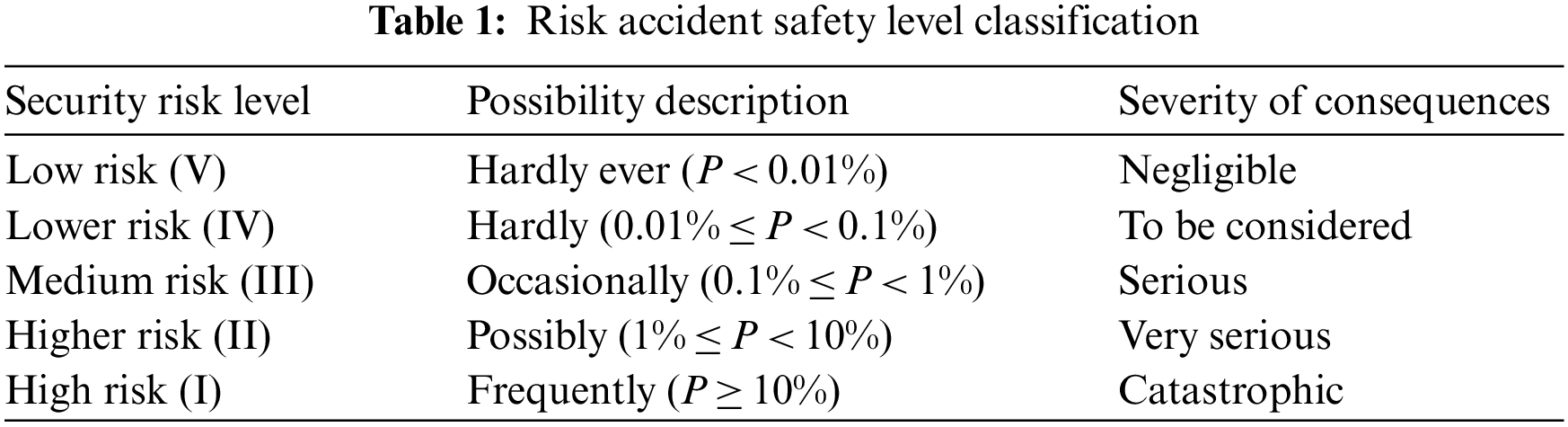
The selected evaluation indexes must first be judged for the safety status to evaluate the safety risk status of the overturning construction of towering structures based on the published and implemented “Technical Regulations for Concrete in Tall Buildings” (JGJ3-2010) [33], “Safety Technical Specification for Building Construction Formwork” (JGJ162-2008) [34], “The Code for Structural Loading of Buildings” (GB 50009-2012) [35], and “Pressure of freshly cast concrete on vertical formwork” (DIN18218-2010) [36]. By combining the research results of relevant literature and other relevant codes, the severity of safety risk of overturning construction of towering structures was divided into five levels: high risk, higher risk, medium risk, lower risk, and low risk, which were indicated by I–V as shown in Table 1.

2.3 Methods for Determining the Weight of Evaluation Indicators

The commonly used weight determination methods are gray correlation, hierarchical analysis, and fuzzy evaluation. Among these methods, hierarchical analysis is widely used because of its simple operation and concise system. However, the hierarchical analysis method also has the following disadvantages: failure to solve the conflicts of multiple decision making during comprehensive evaluation and incomprehensive and subjective constructed judgment matrix. Simultaneously considering the fuzziness and randomness of the problem is also difficult. Therefore, this paper aims to improve the traditional hierarchical analysis method by using the cloud model to overcome the shortcomings of excessive dependence on subjective experience to determine the index weights.

2.4 Theoretical Preparation

2.4.1 Cloud Model

Based on the concept of fuzzy set theory and probability statistics, the cloud model theory was developed by a Chinese scholar, Academician Li et al. [37]. This theory, which effectively combines the randomness and fuzziness of objective things by a unified mathematical expression, was first proposed in 1995; thus, the cloud model has been widely used in fuzzy evaluation, multi-attribute decision making, and risk assessment [38,39]. The detailed theoretical content of cloud models can be found in reference [37].

2.4.2 Matter–Element Extension Theory

The matter–element extension theory is a novel creation of Chinese scholar Cai in 1983 [40,41]. This theory incorporates the core ideas of the matter–element theory into topology by using the matter–element as the basic component to describe the thing. Thus, an ordered triad denoted as R = (N, C, V) is formed, where N is the name of the one described, C is the feature of the thing, and V is the characteristic value of the object. The topological evaluation method can determine the classical and node domains by changing the topology of the evaluated thing and calculating the correlation function and affiliation degree to perform the evaluation process combining quantitative and qualitative, which can effectively solve the uncertainty and contradiction problem.

2.5 Cloud-Based Coupled Matter–Element Model

2.5.1 Improved AHP Empowerment Method Based on Cloud Model

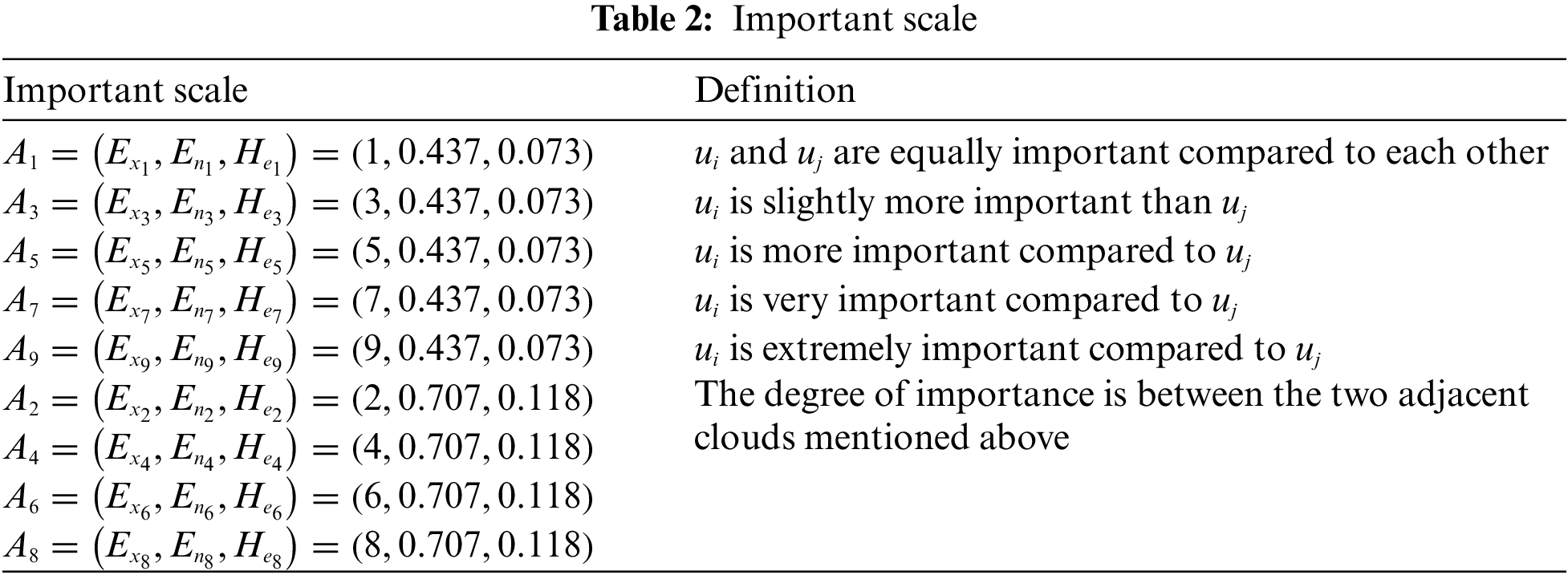
The cloud model was used in this study to transform the judgment matrix in AHP. The numerical judgment matrix was utilized to express the decision information quantitatively through the 1–9 scaling method. Assuming the existence of the theoretical domain U={i},i=1,2,3,⋯,9, Ai is defined as the nine-cloud model with the structure Ai=(Exi,Eni,Hei), where Exi,Eni,Hei respectively denote the expectation, entropy, and hyperentropy. In reference [42], the golden section method was used to calculate [42] the above Ai parameters, as shown in Eq. (1).

{Exi=1,2,3…9,i=1,2,3…9,Exi∈ZEn1=En3=En5=En7=En9=0.382α(xmax−xmin)/6=0.437En2=En1/0.618,En4=En3/0.618,En6=En5/0.618,En8=En7/0.618He1=He3=He5=He7=He9=0.382α(xmax−xmin)/36=0.073He2=He1/0.618,He4=He3/0.618,He6=He5/0.618,He8=He7/0.618(1)

where xmax=9,xmin=1 and α are the adjustment factors, generally taking 0.858.

The final numerical characteristics of the critical scale cloud model are shown in Table 2. The table shows that a large expected Exi value indicates its high importance.

According to the above decision method, the cloud model scalar judgment matrix for the clouded hierarchical analysis was established in the form of Eq. (2).

[a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮an1an2⋯ann]=[A11A12⋯A1nA21A22⋯A2n⋮⋮⋮⋮An1An2⋯Ann](2)

The entropy and hyperentropy of the elements on the diagonal in the above equation were 0 and the expectation was 1; n is the number of evaluation indicators. When the indicators were compared two by two, the aji=1aij,Aji=1Aij=(1Ex,En(Ex)2,He(Ex)2).

The obtained evaluation results of the experts were aggregated, and the average value was taken. The aggregation formula is shown in Eqs. (3)–(5) as follows:

Ex¯=1n(∑i=1nExi)(3)

En¯=1n(∑i=1nEni2)1/2(4)

He¯=1n(∑i=1nHei2)1/2(5)

The matrix was normalized and the multiplication calculation was introduced in cloud computing, and the relative weights AWi¯(Exi′,Eni′,Hei′) of expectation, ambiguity, and randomness of the elements are calculated using the square root method. Expression of the parameters are shown in Eqs. (6)–(8):

Exi′=Exi∑Exi=(∏j=1nExij)1/n∑i=1n(∏j=1nExij)1/n(6)

Eni′=Eni∑Eni=((∏j=1nExij)∑j=1n(EnijExij)2)1/n∑i=1n((∏j=1nExij)∑j=1n(EnijExij)2)1/n(7)

Hei′=Hei∑Hei=((∏j=1nExij)∑j=1n(HeijExij)2)1/n∑i=1n((∏j=1nExij)∑j=1n(HeijExij)2)1/n(8)

The expected consistency test was performed by consistency metrics C and R. This test required satisfying Eq. (9), where C=λmax−nn−1, λmax≈1n∑i=1n(∑j=1nExijAWiAWi), and R are the average of the consistency metrics of the same order random judgment matrix. The consistency ratio I is calculated as follows:

I=CR<0.1(9)

2.5.2 Improved Cloud-Based Model for Matter–Element Risk Assessment

The cloud matter–element was used in this paper to utilize the cloud model to redefine and construct the matter–element extension theory and to employ the general steps of extension evaluation to describe and evaluate things. The cloud matter–element [43] replaced the specific values V in the ordered triple R=(N,C,V) in the matter–element theory with (Ex,En,He) in the normal cloud model to realize the description of the randomness and fuzziness in the evaluation process. The cloud matter–element model is expressed as:

R=(NC1(Ex1,En1,He1)NC2(Ex1,En1,He1)⋮⋮⋮NCn(Ex1,En1,He1))(10)

where expectation Exi indicates the center of the cloud distribution, which is the point value that best reflects the attribute concept; entropy En indicates the degree of uncertainty: a large entropy value leads to high uncertainty of the indicator; hyperentropy He is a measure of the degree of entropy uncertainty: a large hyperentropy leads to large ambiguity and uncertainty of entropy En and large thickness of cloud drops on the cloud map. The cloud model is an overall reflection of the quantitative characteristics of the qualitative concept by the three numerical characteristics.

2.5.3 Calculation of Cloud Model Parameters

In the cloud matter–clement model, when dividing the interval of safety risk level for the overturning construction of towering structures, the fuzzy and random nature of the cloud model was used to fuzzy the interval boundary values of the traditional matter–element model. That is to say, the hierarchical boundary of the classification level boundary of each evaluation index for the safety risk of turnover formwork construction of towering structures can help obtain the expectation Ex, entropy En, and hyperentropy He.

Ex=(Cmin+Cmax)2(11)

En(1)=(Cmax−Cmin)6(12)

En(2)=(Cmax−Cmin)2.3548(13)

He=s(14)

At present, the evaluation of indicators has two main methods of cloud entropy calculation: formula (12) is used for the classification of levels with clear boundaries, such as low-risk level, and formula (13) is used to classify various hazard levels other than low-risk level. Cmin,Cmax are the minimum and maximum values of the classification level interval of the evaluation indicators, respectively; s is a constant, which can be adjusted in combination with the ambiguity and randomness of the risk assessment indicators of turnover formwork construction. This paper takes s=0.08 [44].

2.5.4 Correlation Calculation of Cloud Matter–Element Model

The introduction of clouds has changed the ambiguity and randomness of the traditional matter–element theory in determining the grade boundaries. Thus, the calculation of the correlation degree of the matter–element model combined with the cloud model has also changed. If each assessed value of the turnover formwork construction to be evaluated x is regarded as a cloud droplet, then the correlation degree for calculating the cloud droplet x belonging to a specific grade is calculated by the following equation:

k=exp⁡(−(x−Ex)22(En′)2)(15)

where En′ is the normal random number generated from the entropy En and the hyperentropy He.

According to Eq. (15), the cloud correlation between each index to be evaluated and the standard normal cloud of security risk level was calculated, and the cloud correlation matrix K was obtained, which was in the form of Eq. (16).

K=[k11k12k13k14k15k21k22k23k24k25⋮⋮⋮⋮⋮kn1kn2kn3kn4kn5](16)

where kij is the cloud correlation between the evaluation index i and the security risk level j; i(i=1,2,⋯,n) is the number of evaluation index (in this paper, n is 14); j is the security risk level number (in this paper, j is the integer of 1∼4).

2.5.5 Determination of the Security Risk Level

The integrated evaluation vector B was obtained by multiplying the weight coefficient AWi¯ with the cloud correlation matrix K, and the formula is shown in (17).

B=AWi¯⋅K(17)

where the evaluation index weight vector AWi¯ comprises the weights of each evaluation index.

A weighted average method was applied to the composite assessment vector B to derive the composite assessment score r [45] as in Eq. (18).

r=∑i=15bifi∑i=15bi(18)

where bi is the component of vector B; fi is the score of the i level, which corresponds to the scores of 5, 4, 3, 2, and 1 for the judgment levels I to V.

When calculating the correlation degree, the presence of normal random numbers produced common calculation results. Therefore, the combined evaluation score of expectation Erx and entropy Ern after multiple simulations must be calculated to reduce the influence of random factors. The calculation equations are shown in Eqs. (19) and (20).

Erx=r1(x)+r2(x)+⋯+rm(x)m(19)

Ern=1m∑h=1m(rh(x)−Erx)2(20)

where m is the number of simulation calculations, which was taken as 100 in this paper; rh(x) is the comprehensive evaluation score of the h−th simulation calculation. The final expected value is the evaluation score that best represents the level of risk in the construction of overturned forms of towering structures; when the score is close to the value, the safety risk level is judged as the level corresponding to that value. The entropy is the measure of the variance of the evaluation result, and as the value becomes larger, the evaluation result is distributed. Meanwhile, the confidence factor θ [46] is defined as Eq. (21).

θ=ErnErx(21)

A large θ value in the formula indicates the large variance and the low credibility of the evaluation results; otherwise, the credibility of the evaluation results is high. The process of the specific evaluation method is shown in Fig. 3.

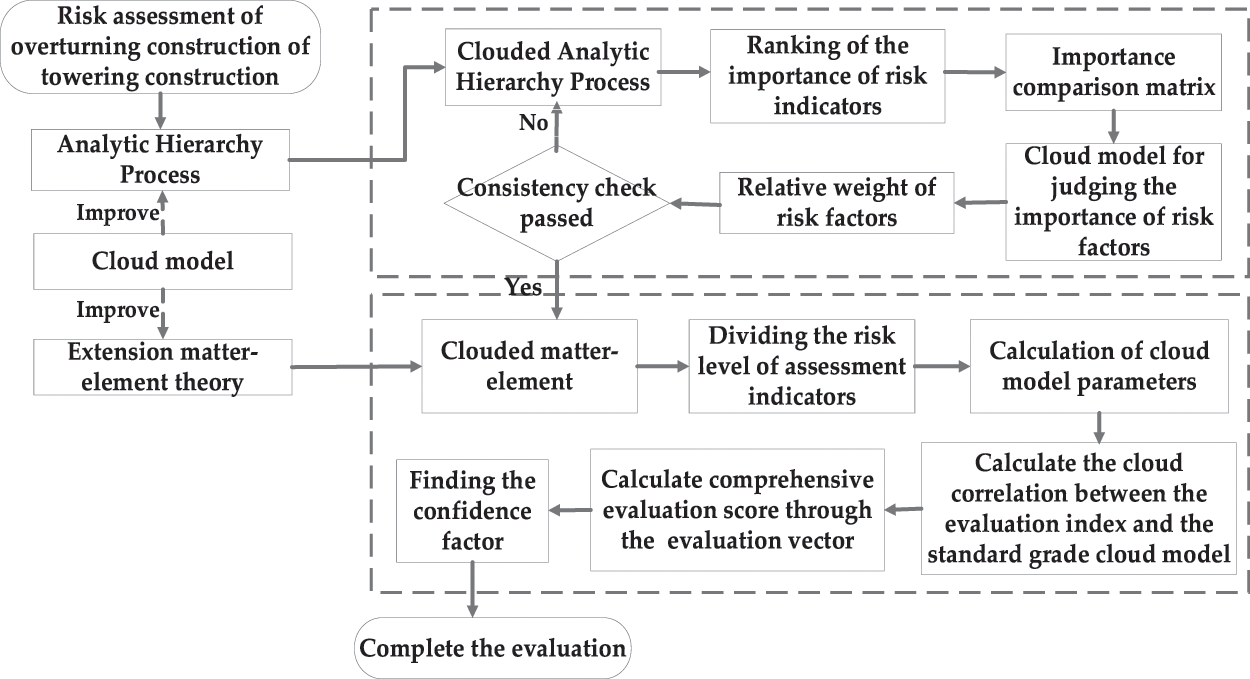
Figure 3: Flow chart of evaluation method

3  Empirical Analysis

3.1 Project Background

The project is located in Turpan City, Xinjiang, China. The climatic conditions of the project location are remarkably extreme, with frequent windy weather in summer belonging to the continental monsoon climate and four indistinguishable seasons. Thus, the impact of the natural environment on construction cannot be ignored. The structure of the project is a reinforced concrete cylindrical tower structure with a building height of 149.85m, 28 floors above ground, and 2 floors underground. The radius of the structure is 10.5m, and the span of each floor beam support is more than 18m. The concrete wall outer mold adopts cantilevered overturning mold. Among them, the formwork panel adopts an imported Vespa board, wherein the size of the formwork is 5.6m×4.131m (height × width) and its thickness is 18mm; meanwhile, the vertical flute of formwork adopts a woodworking word beam, and the main back flute is double 14# channel steel. The support system comprises a triangle frame, a picket frame, a hanging platform, and an embedded load-bearing device. The formwork structure is shown in Figs. 4 and 5 below.

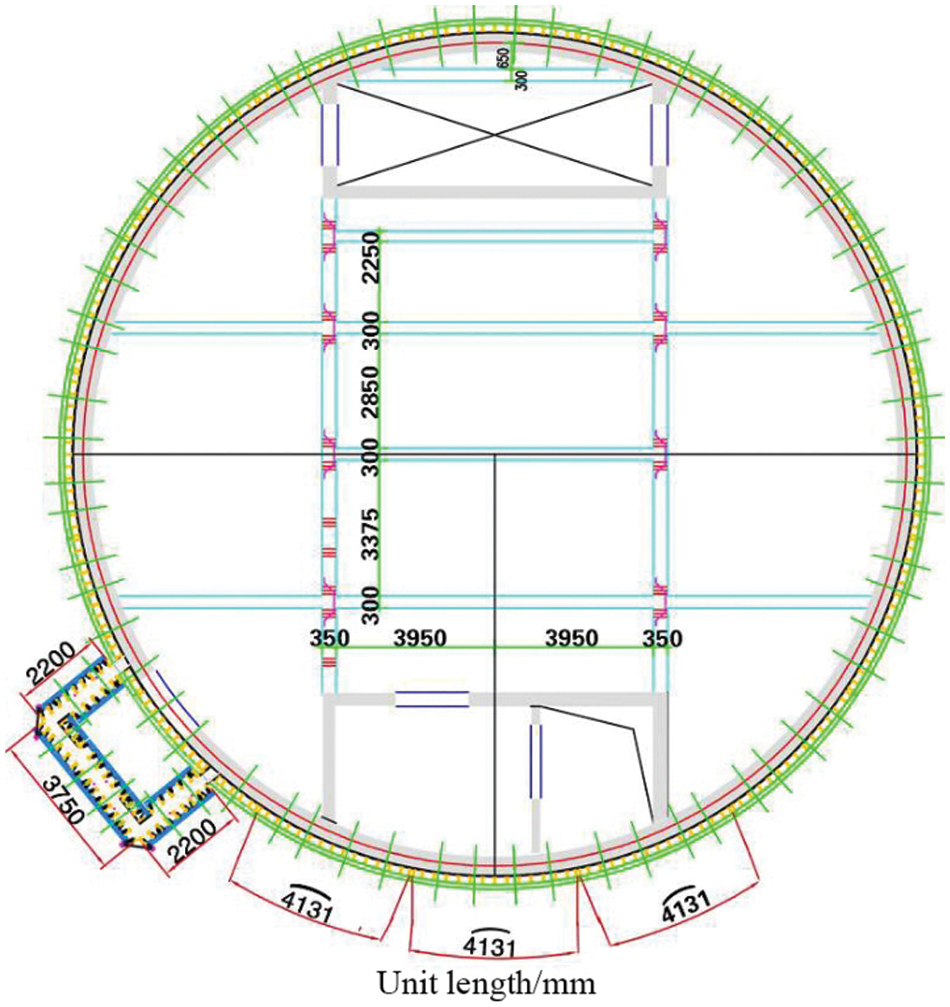
Figure 4: Formwork plan layout

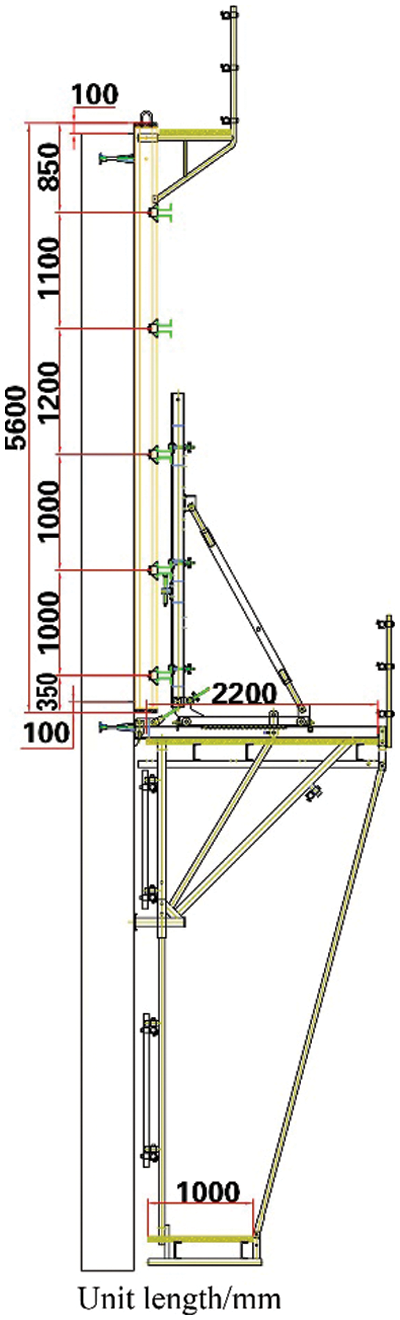
Figure 5: Formwork elevation

3.2 Determination of Index Weights

The importance of risk indicators affecting safety was ranked by familiarizing with relevant project information and consulting with relevant experts. In this paper, 20 experts with a considerable amount of successful experience in the construction and risk control of overturning sites of towering structures were invited to conduct a questionnaire survey. Detailed information is shown in Table 3. Their questionnaire results were randomly selected to compare and analyze the risk factors of overturning construction sequentially, and the flowchart is shown in Fig. 6. The importance ranking of the first-level indicators was obtained as follows. Expert 1 thought the relative importance ranking of four risk factors was U2>U4>U3>U1 and the risk comparison matrix was Q1; Expert 2 believed that the relative importance of the four risk factors was U2>U3>U4>U1 and the risk comparison matrix was Q2; Expert 3 thought that the relative importance of the four risk factors was U2>U4>U3>U1 and the risk comparison matrix was Q3. The summary results of the risk comparison matrix of the first-level indicators are shown in Table 4.

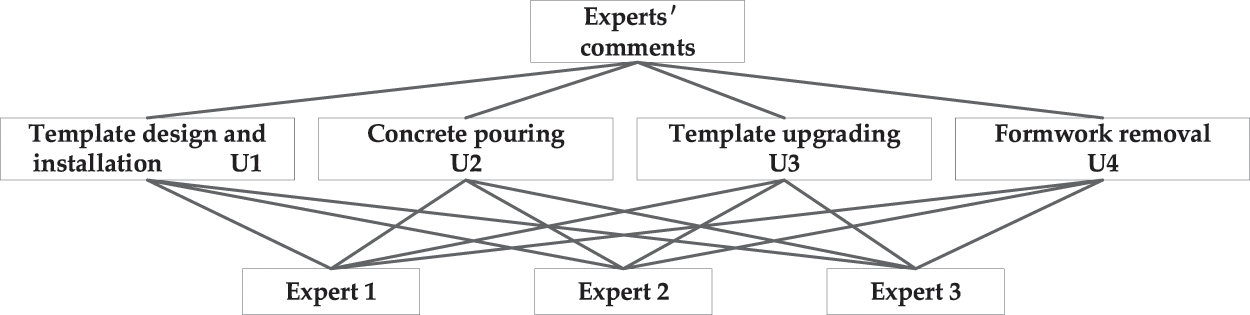
Figure 6: Flow chart of risk evaluation

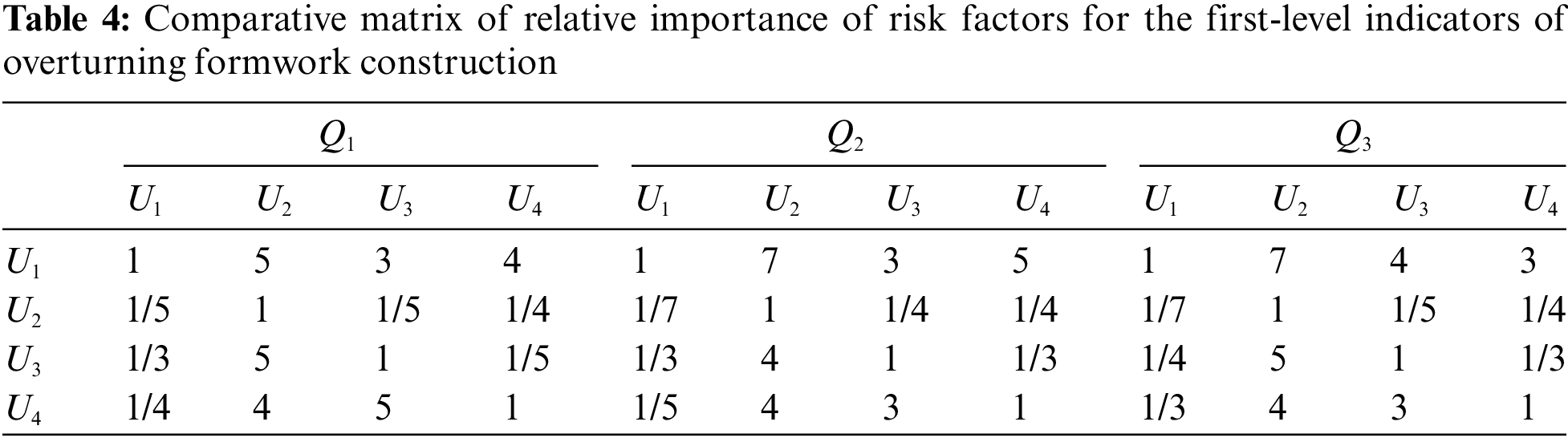
The cloud model-based linguistic judgment scales A12 given by three experts for the importance of two elements U1 and U2 are as follows: Q1(A12)=(5,0.437,0.073), Q2(A12)=(7,0.437,0.073), and Q3(A12)=(7,0.437,0.073). After the aggregation of formulas (3)–(5), the cloud model for the importance judgment of U1 and U2 can be obtained as (3.333,0.313,0.052). In detail, (Ex¯)A12=(5+7+7)1/3=6.333, (En¯)A12=13(0.4372+0.4372+0.4372)=0.252(He¯)A12=13(0.0732+0.0732+0.0732)=0.042. Similarly, the cloud model of importance judgment of other risk factors obtained by the same method is summarized in Table 5.

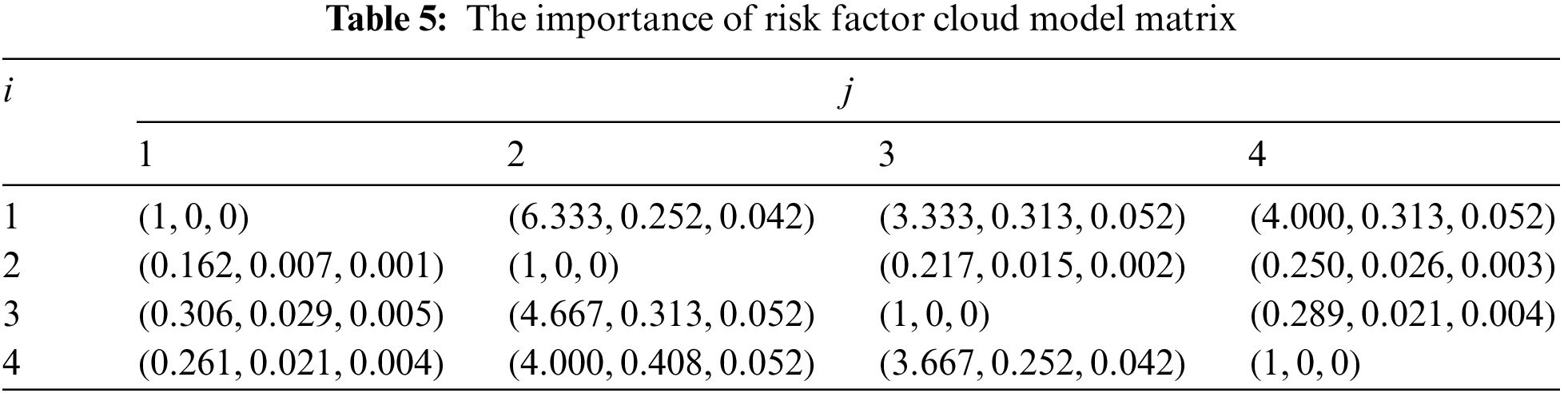
The relative weights calculated by Eqs. (6)–(8) are shown in Table 6. In detail, Ex1=(1×6.333×3.333×4)14=3.031, similarly, Ex2=0.306,Ex3=0.801,Ex4=1.399.

Ex1′=3.031/(3.031+0.306+0.801+1.399)=0.547, similarly, Ex2′=0.055,Ex3′=0.145,Ex4′=0.253.

En1={(1×6.333×3.333×4)[0+(0.2526.333)2+(0.3133.333)2+(0.3134.000)2]1/2}1/4=1.185, similarly, En2=0.183,En3=0.488,

En4=0.867. En1′=1.185/(1.185+0.183+0.488+0.867)=0.541, similarly, En2′=0.055,En3′=0.146,En4′=0.259.He1={(1×6.333×3.333×4)[0+(0.0426.333)2+(0.0523.333)2+(0.0524.000)2]1/2}1/4=1.160, similarly,

He2=0.113,He3=0.312,He4=0.539.He1′=1.16/(1.16+0.113+0.312+0.539)=0.546,He2′=0.053,He3′=0.147,He4′=0.254.

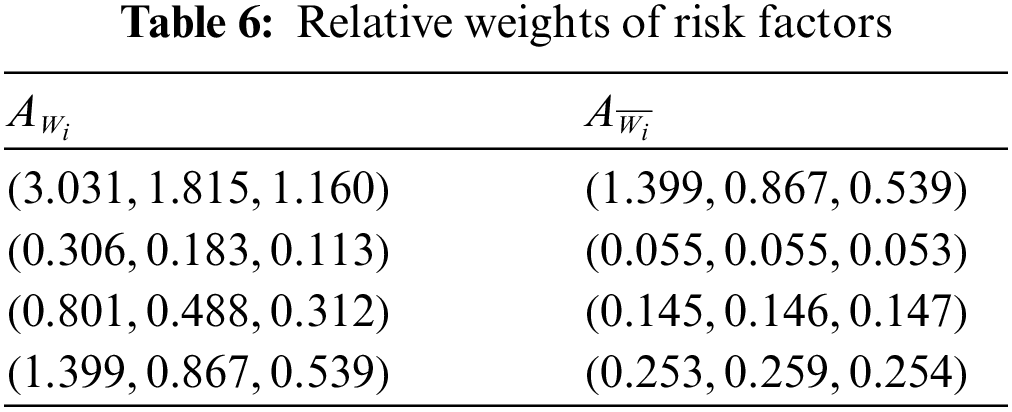
The consistency test was performed by Eq. (10) to obtain I=0.052<0.1. In detail,

[ 16.3333.33340.16210.2170.250.3064.66710.2890.26143.6671 ][ 3.0310.3060.8011.399 ]=[ 13.2361.3203.5606.352 ],λmax≈14( 13.2363.031+1.320.306+ 3.560.801+6.3521.399 )=4.175,C=λmax−nn−1=4.175−44−1=0.058,I=CR=0.0580.89=0.065 . Therefore, the first-level indicators of template design and installation U1, concrete pouring U2, template upgrading U3, and formwork removal U4 had a weight vector of w=(0.547,0.055,0.145,0.253), respectively.

For the second-level indicators under the risk of template design and installation, Expert 1 believed that the relative importance of the four risk factors was ranked as U1−3>U1−4>U1−2>U1−1 and the risk comparison matrix was Q1−1; Expert 2 believed that the relative importance of the four risk factors was ranked as U1−3>U1−4=U1−2>U1−1 and the risk comparison matrix was Q1−2; Expert 3 believed that the relative importance of the four risk factors was U1−3>U1−4>U1−2>U1−1 and the risk comparison matrix was Q1−3.

For the second-level indicators under the risk of concrete pouring, Expert 1 believed that the relative importance of the three risk factors was ranked as U2−2>U2−3>U2−1 and the risk comparison matrix was Q2−1; Expert 2 believed that the relative importance of the three risk factors was ranked as U2−2>U2−3>U2−1 and the risk comparison matrix was Q2−2; Expert 3 believed that the relative importance of the three risk factors was ranked as U2−2>U2−3>U2−1 and the risk comparison matrix was Q2−3.

For the second-level indicators under the risk of template upgrading, Expert 1 believed that the relative importance of the three risk factors was ranked as U3−2>U3−3>U3−1 and the risk comparison matrix was Q3−1; Expert 2 believed that the relative importance of the three risk factors was ranked as U3−2>U3−3>U3−1 and the risk comparison matrix was Q3−2; Expert 3 believed that the relative importance of the three risk factors was ranked as U3−2>U3−3>U3−1 and the risk comparison matrix was Q3−3.

For the second-level indicators under the risk of formwork removal, Expert 1 believed that the relative importance of the four risk factors was ranked as U4−2>U4−4>U4−1=U4−3 and the risk comparison matrix was Q4−1; Expert 2 believed that the relative importance of the four risk factors was ranked as U4−2>U4−4>U4−3>U4−1 and the risk comparison matrix was Q4−2; Expert 3 believed that the relative importance of the four risk factors was U4−2>U4−4>U4−3>U4−1 and the risk comparison matrix was Q4−3. The summary comparison matrix of all levels of indicators is shown in Tables 7–10.

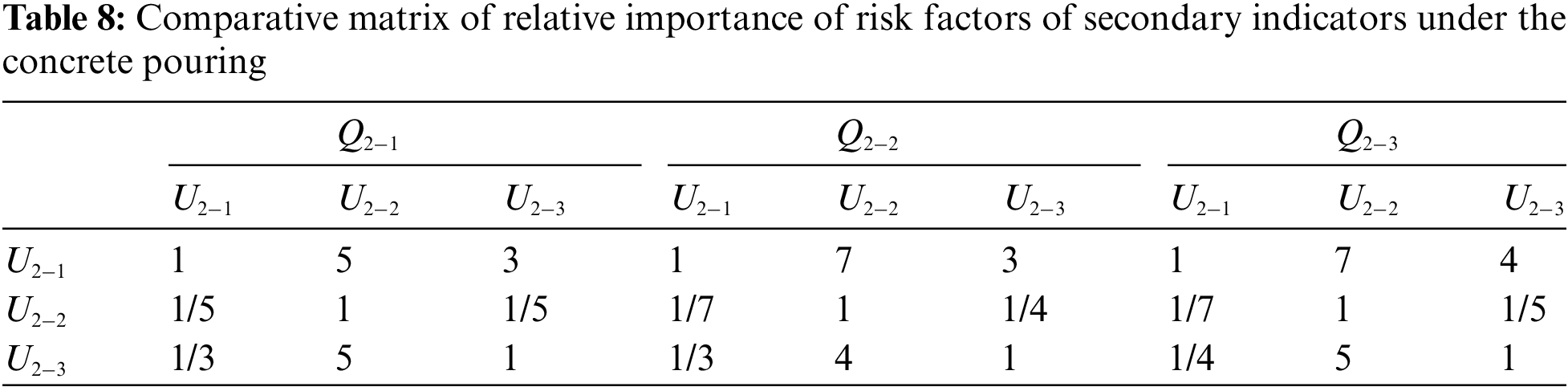
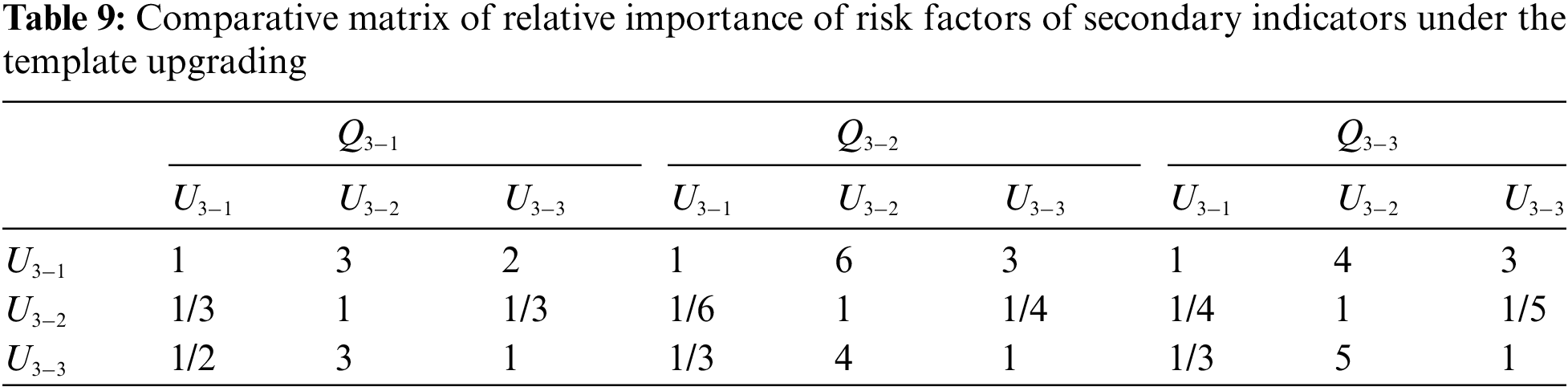
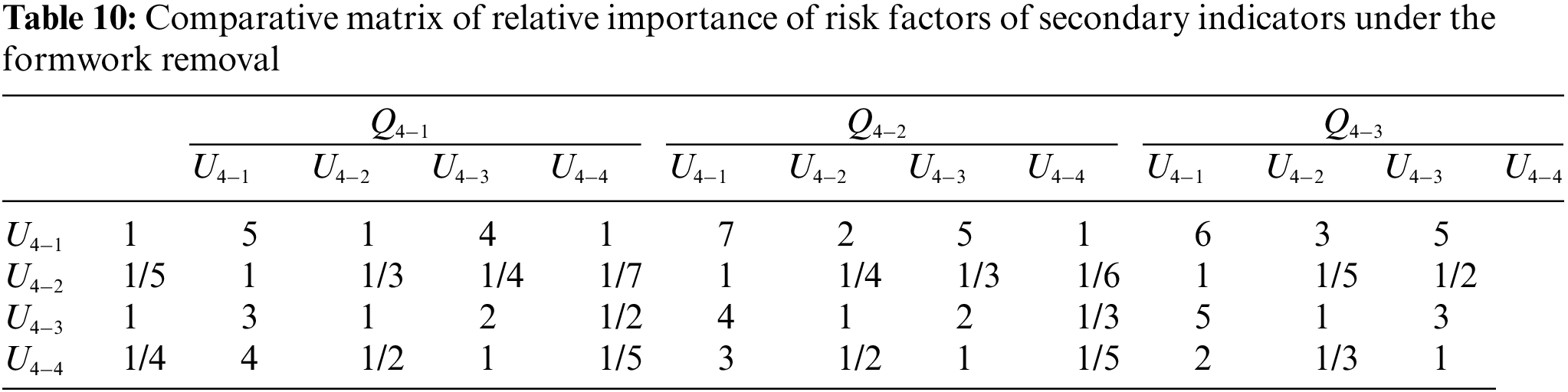
The same method was used to calculate the weights under different indicators in turn. With the inclusion of the second-level index, the weight vectors of the template design and installation, concrete pouring, template upgrading, and formwork removal were {0.553,0.225,0.067,0.155}, {0.655,0.078,0.267}, {0.592,0.105,0.303}, and {0.509,0.066,0.288,0.137}, respectively. The consistency test met the requirements, and the final comprehensive weight is shown in Table 11.

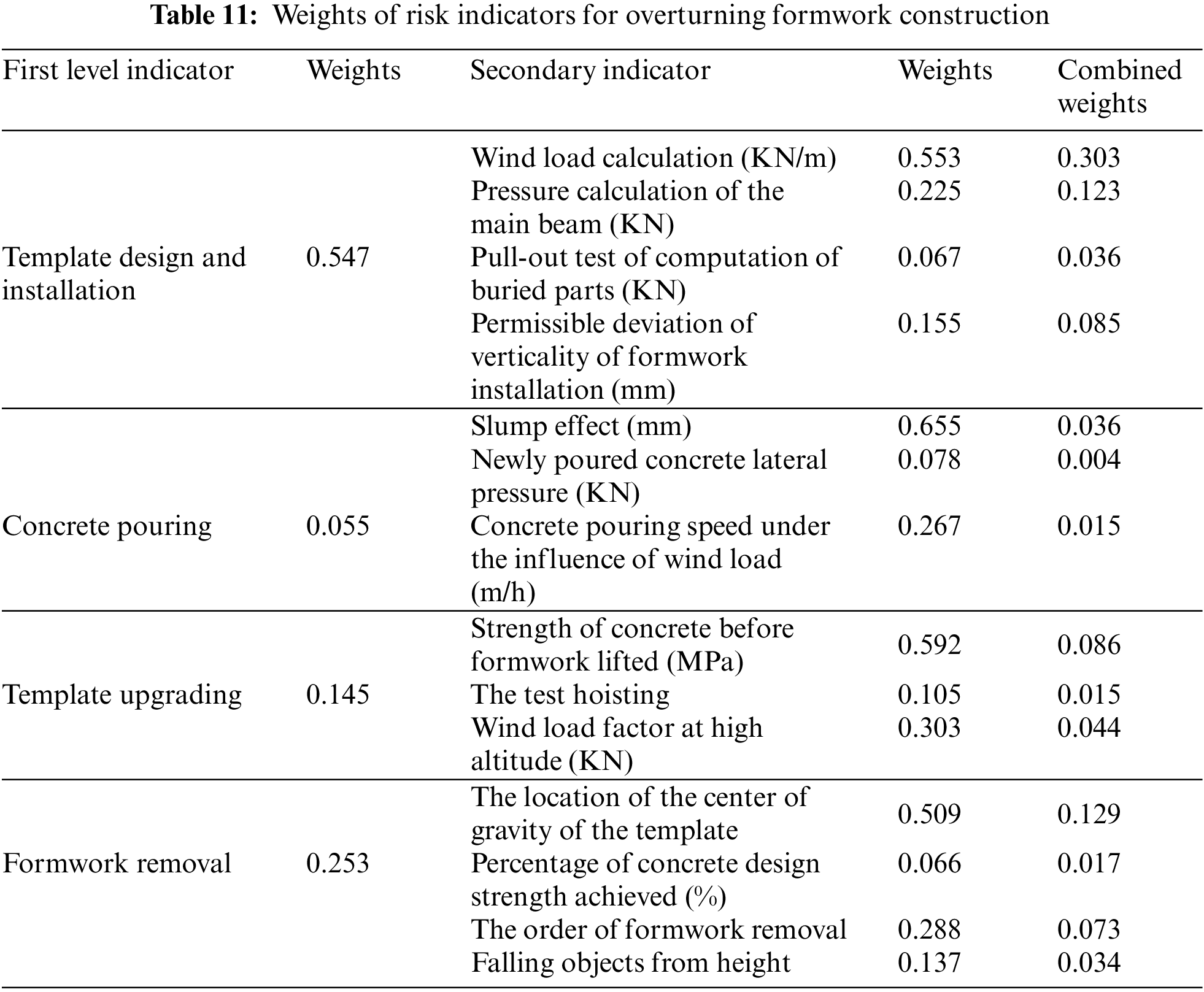
3.3 Cloud-Based Risk Assessment

The index system contained 4 qualitative indicators and 10 quantitative indicators. For quantitative indicators, the data from public sources, such as statistical yearbooks and design specifications, are used for the interval division criteria; for qualitative indicators, levels I, II, III, IV, and V were respectively assigned 2, 4, 6, 8, and 10, as shown in Table 12.

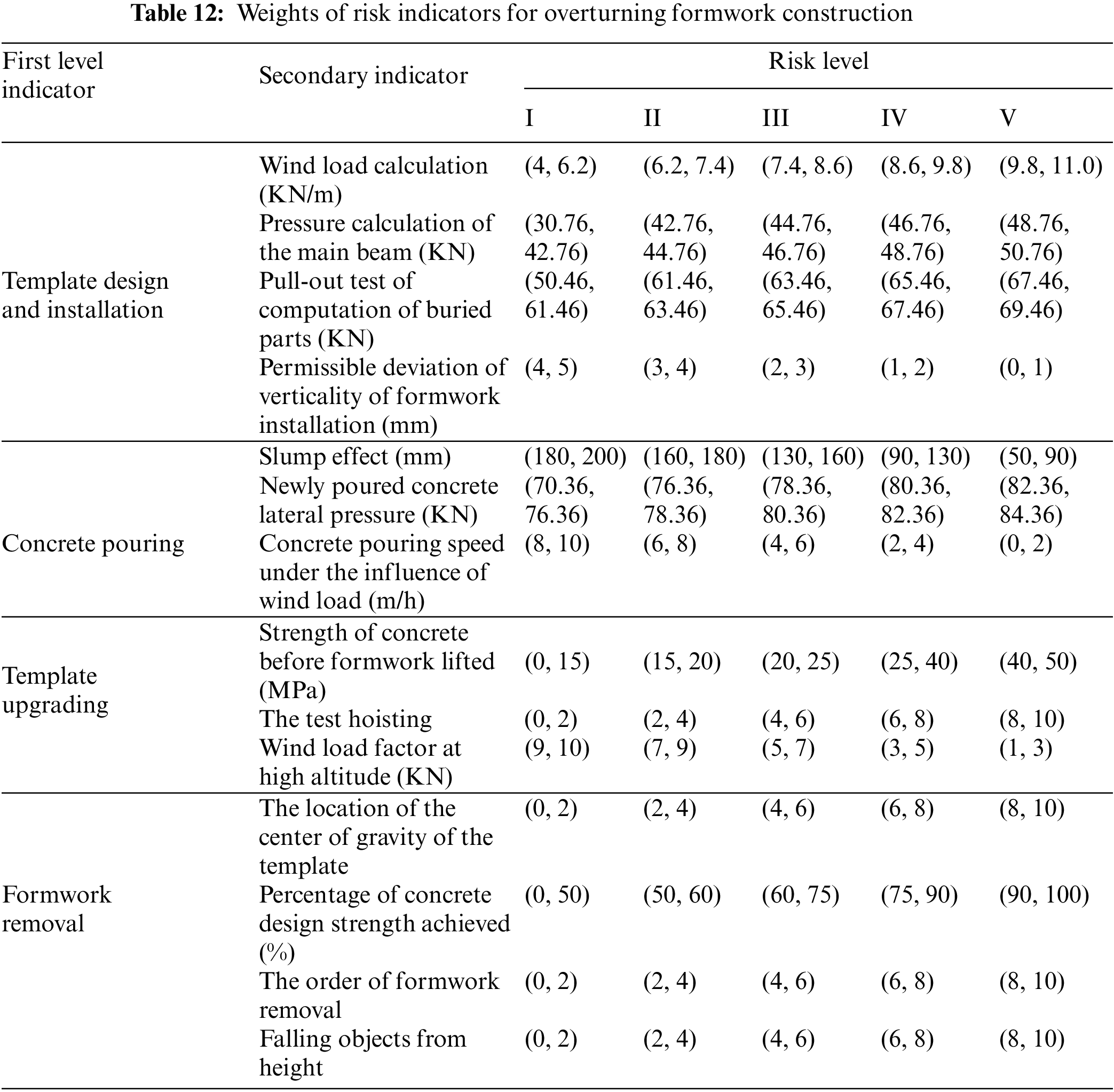
After obtaining the grade division index, the standard cloud model of each secondary index was calculated by the method of determining the cloud model parameters. The specific numerical calculation results are shown in Table 13.

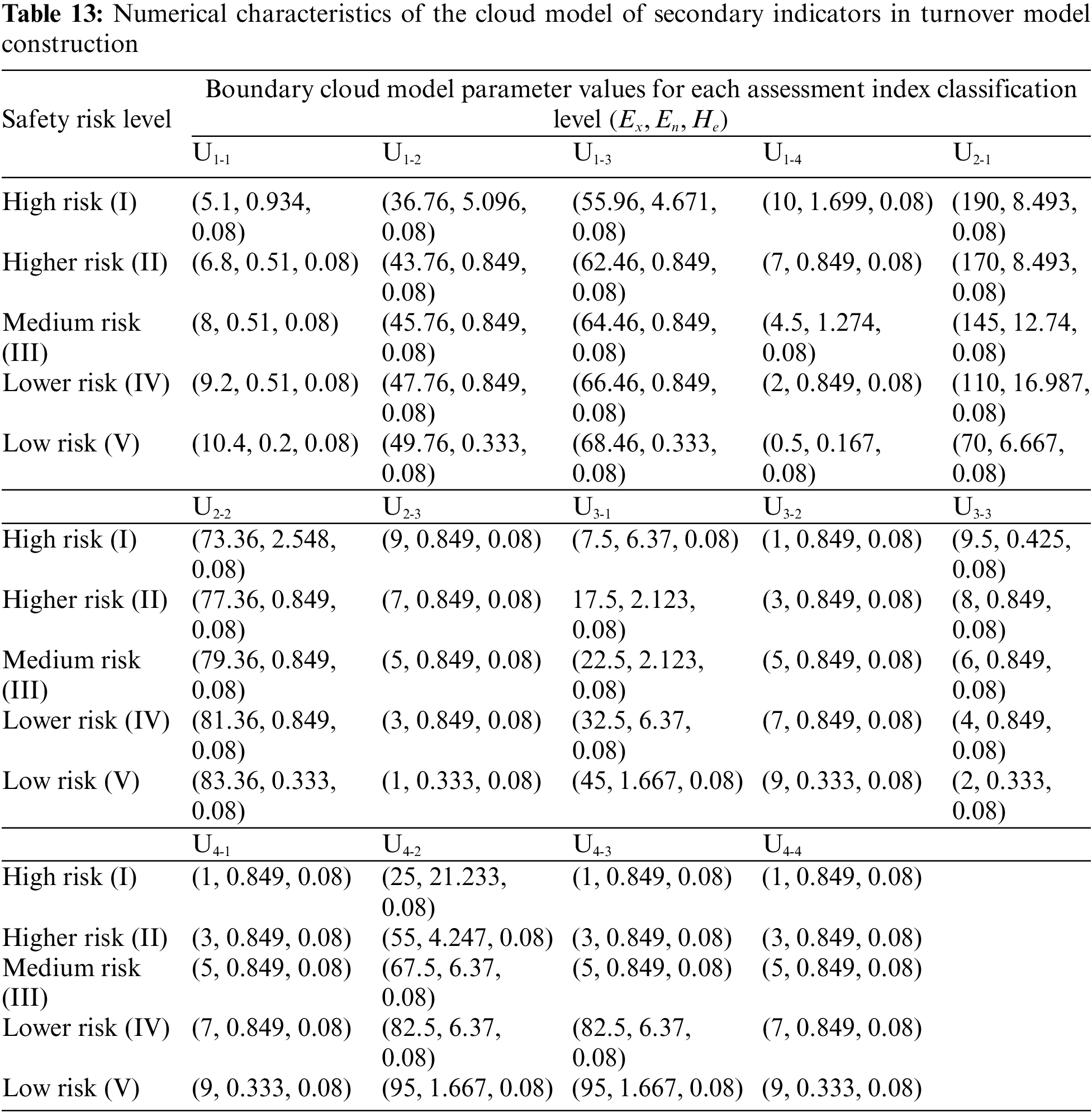
The MATLAB program was prepared in accordance with the three numerical characteristics of the cloud model of the classification level boundaries of each assessment index in Table 13. Therefore, each safety risk level corresponded to a cloud, and five normal clouds were generated using the normal cloud generator. Among them, the standard cloud diagram of the risk factor of wind load is shown in Fig. 7. The standard cloud diagrams of other risk factors were not comprehensively described in the paper due to space limitation.

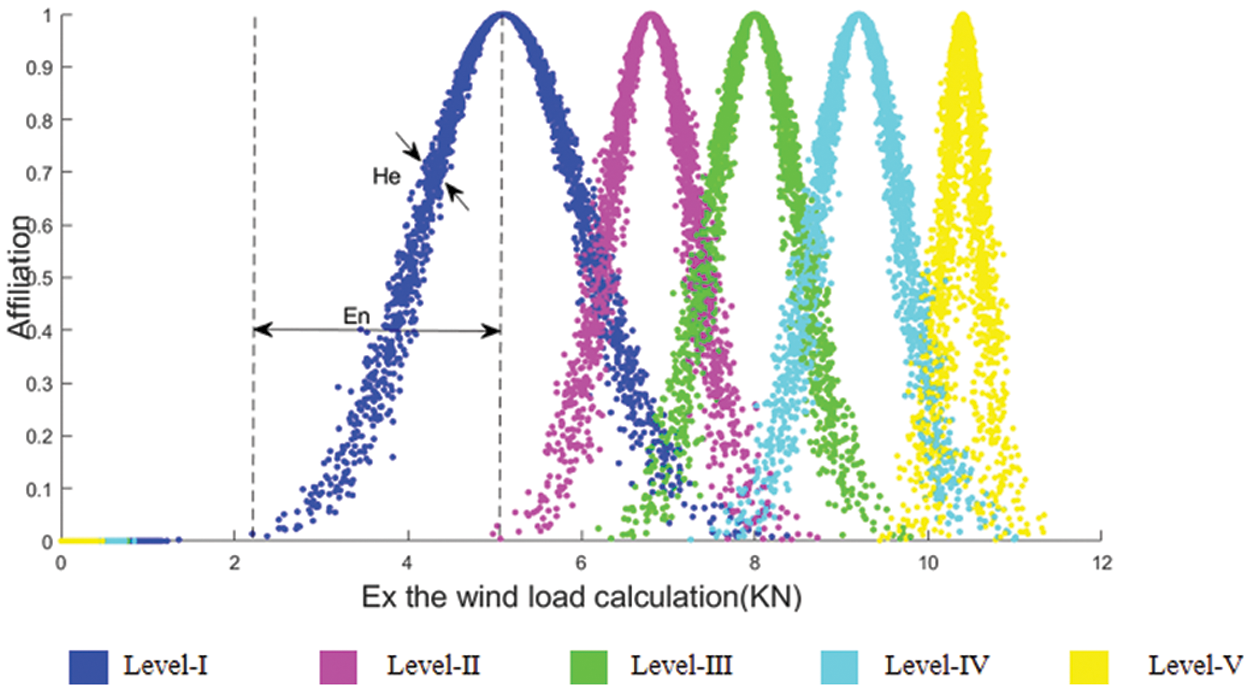
Figure 7: Standard cloud diagram of risk factors

By investigating the field situation and schedule of the construction site, three groups of working conditions with different orientations of the same construction height were selected in this study. The actual measured or score values of the 13 evaluation indicators in were inputted in Table 14, and the cloud correlation degree between each evaluation indicator and the normal cloud of the security risk level standard was calculated in accordance with Eq. (15). Taking working condition one as an example, the cloud correlation matrix K was calculated as follows:

K=[0.00010.00010.00170.49890.01080.99980.00010.00010.00010.00010.04790.00010.00190.49950.01090.49880.49950.02290.00010.00010.00010.00010.14580.84080.00010.00190.00010.00190.49860.01090.00010.00010.01280.83860.00010.00200.00010.00190.92580.00010.06171.00000.06080.00010.00010.00010.00010.20850.83860.00010.06051.00000.05990.00010.00010.00920.00010.00190.49950.01110.00010.05991.00000.06090.00010.00180.49850.49870.00180.0001]

The sample evaluation vector B={0.1765,0.2079,0.1159,0.3432,0.0040} can be calculated in accordance with Eq. (15), and the weighted average evaluation score r was 3.2475. In detail, r=0.1765×5+0.2079×4+0.1159×3+0.3432×2+0.004×10.1765+0.2079+0.1159+0.3423+0.004=3.2475. The above steps are repeated 100 times to reduce the effect of random factors. Eqs. (19) and (20) indicate that the mean and standard deviation of the comprehensive evaluation scores were 3.246 and 0.0134, respectively. Finally, the confidence factor was found to be 0.0041 according to formula (21). A small factor leads to a small dispersion of the evaluation results but produces reliable evaluation results. The correlation of the ranks is determined using the Spearman’s correlation coefficient rs.

Meanwhile, the evaluation results were compared with the conventional matter–element method and cloud model to verify the effectiveness of the method in this paper. The results of the final evaluation are shown in Table 15.

3.4 Cloud-Based Risk Assessment

Sensitivity Analysis is performed based on the risks index system of overturning construction of towering structure. When the weights of risk index in Table 11 changed by ±0.1, ±0.05, +0.2, +0.3, we obtained the result shown in Fig. 8.

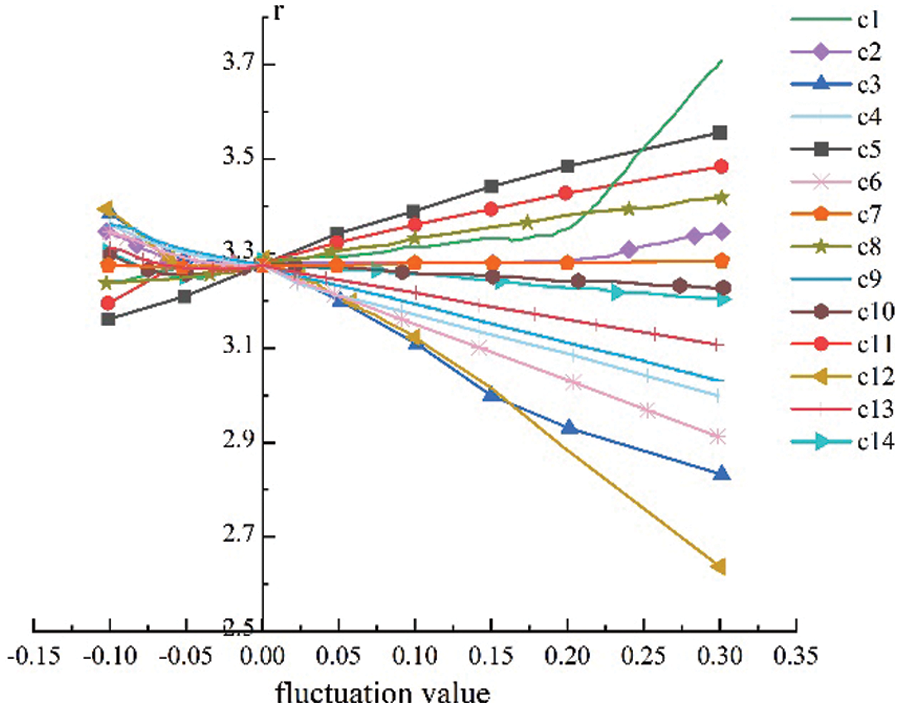
Figure 8: Sensitivity analysis of the weights of risk index

As we can see from Fig. 8, with the weight of the risk indexes c1,c5,c11 increasing, the whole risk level deviates from the medium level to larger level gradually and the weight of c1 is the most sensitive. With the weight of the risk indexes c12,c3,c6 increasing, the whole risk level deviates from the medium level to smaller level gradually and the weight of c12 is the most sensitive. The weights change of risk index c7,c10,c14 have little effect on the risk level, so their sensitivities are weak.

From above sensitivity analysis, we can make a conclusion that c1,c12 are sensitive factors in the safety risk assessment of overturning construction of towering structure. They are the wind load calculation and the percentage of concrete design strength achieved. In the construction risk management process, these indexes should be analyzed mainly in order to make a better risk aversion measure and reduce the risk of overturning construction of towering structure.

4  Discussion

Table 15 shows that the evaluation results obtained by the evaluation methods in this paper were consistent and the confidence factors were all less than 0.05, indicating that the cloud matter–element coupled model evaluation method for the safety risk assessment of overturning construction of towering structures had a high confidence level. The Spearman’s rank test for correlation between the weighted average evaluation score r and level III, the mean value of rs was 0.979, which indicates an extremely large correlation of level III. In addition, the weight calculation in this paper combined the decision results of all experts. Thus, the proposed evaluation model considered the randomness and fuzziness among the risk factors in construction risk assessment. The final result of the risk assessment for the construction of towering structure overturning was level III (medium risk level), which is consistent with the actual situation of the project.

The evaluation results of the cloud-based matter–element coupled model in this paper had high similarity individually compared with the two other commonly used methods. Among them, the assessment results of the proposed method in this paper were consistent with 100% compared with the traditional matter–element method, and two-thirds of the assessment results were consistent compared with the cloud model method. In the two other methods, the proportion of level III was 83.3%. Thus, the assessment results of the cloud matter–element coupled model were representative.

In addition, the cloud matter-coupled model defined the safety risk level by using a comprehensive assessment score mean Ex,r, which can provide more integrated information on the assessment cases compared with other methods. For example, the assessment results of cases 1 and 2 were III. However, the comprehensive assessment score mean of case 1 was 3.275 higher than that of case 2, which indicated that the risk of case 1 was higher than that of case 2. The evaluation method in this paper retains the advantages of traditional matter–element theory in dealing with the incompatibility problem among evaluation indicators. Thus, the introduction of the cloud model can quantitatively convert the ambiguity and randomness in the process of risk assessment of overturning construction to reflect its uncertainty characteristics accurately. Therefore, compared with other evaluation methods, the proposed evaluation method in this paper was comprehensive to evaluate the safety risk level of the overturning construction of towering structures.

5  Conclusion

This paper first adopted the cloud matter–element coupled model to solve the complex uncertainty problem of safety risk assessment of overturning construction of towering structures effectively. This model maximized the advantages of matter–element theory and cloud model to deal with the fuzziness and randomness in the safety risk assessment of the overturning the construction of towering structures. The improved hierarchical analysis method was then employed on the basis of the cloud model through the aggregation algorithm of the cloud model to bring all the assignments of multi-person decision making into the calculation formula. The determination of the weights of various construction risk indicators was more objective and reliable. Finally, a reinforced concrete cylindrical tower structure overturning construction safety risk assessment was taken as a case to describe the application steps of the proposed method. The evaluation results of the proposed method are also compared with those of the traditional matter–element and cloud model methods to test the application effect of the proposed method. The findings showed that the assessment results of the cloud matter–element coupled model method were consistent with those of two other common methods. Moreover, the confidence factor of each assessment case was less than 0.05, which indicated that the proposed method in this paper was effective in the safety risk assessment of overturning the construction of towering structures. The proposed model in this paper used a comprehensive assessment score mean to determine the safety risk level, which can provide more integrated information regarding the assessment cases compared with other assessment methods, and reflect the uncertain relationship among evaluation indexes more comprehensively compared with other evaluation methods, thus increasing the reliability of the evaluation results.

However, in the process of safety risk assessment of towering structure overturning construction, the classification criteria of the safety risk level of each assessment index are not constant, and the scoring value of the assessment index is susceptible to subjective factors, both of which have an impact on the reasonableness of the assessment results. Therefore, further supplementing and improving the safety risk assessment index system of towering structure overturning construction is necessary for the subsequent research. Moreover, the issues, such as the scoring value of the assessment index and its safety risk classification criteria, should be investigated further to improve the scientificity of the assessment index system and enhance the comprehensiveness and objectivity of the assessment results.

Funding Statement: This research was funded by China Railway No. 21 Bureau Group No. 1 Engineering Co., Ltd., Grant No. 202209140002.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Bernstein, P. L. (1996). Against the gods: The remarkable story of risk. New York, USA: John Wiley & Sons. [Google Scholar]

    2. Aven, T. (2016). Risk assessment and risk management: Review of recent advances on their foundation. European Journal of Operational Research, 253(1), 1–13. DOI 10.1016/j.ejor.2015.12.023. [Google Scholar] [CrossRef]

    3. Xu, X. Z., Wang, B., Liu, B. (2016). Factors affecting verticality and pre-control measures for construction of hollow thin-walled high piers without brackets in mountainous areas. Highway, 61(6), 180–183. [Google Scholar]

    4. Pallarés, F. J., Ivorra, S., Pallarés, L., Adam, J. M. (2011). State of the art of industrial masonry chimneys: A review from construction to strengthening. Construction and Building Materials, 25(12), 4351–4361. DOI 10.1016/j.conbuildmat.2011.02.004. [Google Scholar] [CrossRef]

    5. Zhao, P. B., Zhang, W. H., Zhu, H. (2011). Discussion about concrete construction of the discharge tunnel intake tower in the right bank of Xiluodu hydropower station. Concrete, (4), 121–123. DOI 10.3969/j.issn.1002-3550.2011.04.034. [Google Scholar] [CrossRef]

    6. Ghaleb, H., Alhajlah, H. H., Bin Abdullah, A. A., Kassem, M. A., Al-Sharafi, M. A. (2022). A scientometric analysis and systematic literature review for construction project complexity. Buildings, 12(4), 482. DOI 10.3390/buildings12040482. [Google Scholar] [CrossRef]

    7. Qiao, W. L., Liu, Y., Zhou, Q., Ma, X. X. (2021). A risk assessment model based on the fuzzy artificial neural network (FANN). Journal of Safety and Environment, 21(4), 1405–1411. DOI 10.13637/j.issn.1009-6094.2020.0341. [Google Scholar] [CrossRef]

    8. Yang, J., Li, T., Liang, G., He, W., Zhao, Y. (2019). A hierarchy distributed-agents model for network risk evaluation based on deep learning. Computer Modeling in Engineering & Sciences, 120(1), 1–23. DOI 10.32604/cmes.2019.04727. [Google Scholar] [CrossRef]

    9. Lyu, H. M., Zhou, W. H., Shen, S. L., Zhou, A. N. (2020). Inundation risk assessment of metro system using AHP and TFN-AHP in Shenzhen. Sustainable Cities and Society, 56, 102103. DOI 10.1016/j.scs.2020.102103. [Google Scholar] [CrossRef]

  10. Cai, S., Fan, J., Yang, W. (2020). Flooding risk assessment and analysis based on GIS and the TFN-AHP method: A case study of Chongqing, China. Atmosphere, 12(5), 623. DOI 10.3390/atmos12050623. [Google Scholar] [CrossRef]

  11. Zhang, H., Zhu, Q. Q. (2021). Construction risk assessment of medium-bearing tied-arch bridges based on grey fuzzy physical element theory. Highway, 66(5), 229–233. [Google Scholar]

  12. Gu, X. B., Wu, S. T., Ji, X. J., Zhu, Y. H. (2021). The risk assessment of debris flow hazards in banshanmen gully based on the entropy weight-normal cloud method. Advances in Civil Engineering, 2021, 8841310. DOI 10.1155/2021/8841310. [Google Scholar] [CrossRef]

  13. Nguyen, L. D., Tran, D. Q. (2021). Measurement of fuzzy membership functions in construction risk assessment. Journal of Construction Engineering and Management, 147(4), 04021005. DOI 10.1061/(ASCE)CO.1943-7862.0002015. [Google Scholar] [CrossRef]

  14. Rajeshkumar, V., Sreevidya, V. (2019). Performance evaluation on selection of formwork systems in high rise buildings using regression analysis and their impacts on project success. Archives of Civil Engineering, 65(2), 209–222. DOI 10.2478/ace-2019-0029. [Google Scholar] [CrossRef]

  15. Wang, J. M. (2020). Study on safety risk assessment and countermeasures of lofty formwork construction. Scientific Reports, 42, 1797–1799. DOI 10.14144/j.cnki.jzsg.2020.09.065. [Google Scholar] [CrossRef]

  16. He, Y. X., Dai, A. Y., Zhu, J., He, H. Y., Li, F. (2011). Risk assessment of urban network planning in China based on the matter-element model and extension analysis. International Journal of Electrical Power & Energy Systems, 33(3), 775–782. DOI 10.1016/j.ijepes.2010.12.037. [Google Scholar] [CrossRef]

  17. Yan, Q., Dong, H., Zhang, M. (2021). Service evaluation of electric vehicle charging station: An application of improved matter-element extension method. Sustainability, 13(14), 7910. DOI 10.3390/su13147910. [Google Scholar] [CrossRef]

  18. Du, C., Ye, J. (2021). Weighted parameterized correlation coefficients of indeterminacy fuzzy multisets and their multicriteria group decision making method with different decision risks. Computer Modeling in Engineering & Sciences, 129(1), 341–354. DOI 10.32604/cmes.2021.016758. [Google Scholar] [CrossRef]

  19. Barghi, B., Shadrokh, S. (2020). Qualitative and quantitative project risk assessment using a hybrid PMBOK model developed under uncertainty conditions. Heliyon, 6(1), e03097. DOI 10.1016/j.heliyon.2019.e03097. [Google Scholar] [CrossRef]

  20. Alosta, A., Elmansuri, O., Badi, I. (2021). Resolving a location selection problem by means of an integrated AHP-RAFSI approach. Reports in Mechanical Engineering, 2(1), 135–142. DOI 10.31181/rme200102135a. [Google Scholar] [CrossRef]

  21. Han, F., Liu, Z., Li, L., Yin, W., Wu, J. (2022). Study on ecological risk evaluation and optimum selection of desert expressway schemes based on the two-dimensional cloud model. Mathematical Problems in Engineering, 2022, 1361861. DOI 10.1155/2022/1361861. [Google Scholar] [CrossRef]

  22. Cao, W., Deng, J., Yang, Y., Zeng, Y., Liu, L. (2022). Water carrying capacity evaluation method based on cloud model theory and an evidential reasoning approach. Mathematics, 10(2), 266. DOI 10.3390/math10020266. [Google Scholar] [CrossRef]

  23. Yan, H. Y., Gao, C., Elzarka, H., Mostafa, K., Tang, W. B. (2019). Risk assessment for construction of urban rail transit projects. Safety Science, 118, 583–594. DOI 10.1016/j.ssci.2019.05.042. [Google Scholar] [CrossRef]

  24. Housing and Urban-Rural Development (2012). JGJ 59-2011, Building construction safety inspection standards. Beijing: China Building Industry Press. [Google Scholar]

  25. Karshenas, S., Ayoub, H. (1994). Construction live loads on slab formworks before concrete placement. Structural Safety, 14(3), 155–172. DOI 10.1016/0167-4730(94)90082-5. [Google Scholar] [CrossRef]

  26. Lv, L. X., Ren, H. B. (2013). Application study on steel platform with removable climbing formwork. Construction Technology, 42, 108–110. [Google Scholar]

  27. Yang, J. K., Gao, J., Qiang, A. L. (2017). Application of tripod rollover mold system for cooling towers to chimney wall construction. Engineering Journal of Wuhan University, 1, 461–464. [Google Scholar]

  28. Zhang, W. X., Huang, J., Li, Z. Y., Huang, C. (2016). An experimental study on the lateral pressure of fresh concrete in formwork. Construction and Building Materials, 111, 450–460. DOI 10.1016/j.conbuildmat.2016.02.067. [Google Scholar] [CrossRef]

  29. Sun, H. X., Duan, X. P., Xu, J. P., He, X., Wang, P. F. (2019). Application of hydraulic self-climbing cantilever formwork in concrete construction of inlet tower: Taking baihetan hydropower station as an example. Yangtze River, 50, 148–155. DOI 10.16232/j.cnki.1001-4179.2019.06.027. [Google Scholar] [CrossRef]

  30. Zhang, L. R., Gan, L. H. (2017). The key technology of high pier self-lifting without tower crane inward slip and valgus construction. Highway, 62(6), 138–142. [Google Scholar]

  31. Qiu, P. Z., Ye, J. B. (2016). Research on the safety protection of high working places in the construction of high pier overturning formwork. Construction Technology, 45(s2), 643–645. [Google Scholar]

  32. Zhang, Y., Chen, G., Li, Y. P. (2016). Application of key technology of high pier overturning construction and safety protection. Highway, 61(6), 130–133. [Google Scholar]

  33. Housing and Urban-Rural Development (2011). JGJ 3-2010, Technieal specifiation for concrete structures of tall building. Beijing: China Building Industry Press. [Google Scholar]

  34. Housing and Urban-Rural Development (2008). JGJ 162-2008, Technical code for safety of forms in construction. Beijing: China Building Industry Press. [Google Scholar]

  35. Housing and Urban-Rural Development (2012). GB 50009-2012, Load code for the design of building structures. Beijing: China Building Industry Press. [Google Scholar]

  36. German Institute for Standardization (2010). DIN 18218-2010, Pesue of fesh cncete on vetical fomwonk. Germany German Institute for Standardization. [Google Scholar]

  37. Li, D. Y., Meng, H. J., Shi, X. M. (1995). Affiliated cloud and affiliated cloud generator. Computer Research and Development, 32(6), 15–20. [Google Scholar]

  38. Yang, Z., Wang, Y. (2020). The cloud model based stochastic multi-criteria decision making technology for river health assessment under multiple uncertainties. Journal of Hydrology, 581, 124437. DOI 10.1016/j.jhydrol.2019.124437. [Google Scholar] [CrossRef]

  39. Yan, L. P., Hong, W. C. (2021). Evaluation and forecasting of wind energy investment risk along the belt and road based on a novel hybrid intelligent model. Computer Modeling in Engineering & Sciences, 128(3), 1069–1102. DOI 10.32604/CMES.2021.016499. [Google Scholar] [CrossRef]

  40. Cai, W. (1992). New discipline “physical element analysis”. Journal of Guangdong Institution Technology, 1, 105–108. [Google Scholar]

  41. Cai, W. (1998). Introduction of extenics. Systems Engineering-Theory & Practice, 1, 76–84. [Google Scholar]

  42. Jia, X. L., Xu, J. L. (2014). Cloud model-based seismic risk assessment of road in earthquake region. Journal of Tongji University (Natural Science), 42, 1352–1358. DOI 10.3969/j.issn.0253-374x.2014.09.008. [Google Scholar] [CrossRef]

  43. Tu, S. W., Zhao, Z. H., Deng, M. X., Wang, B. (2021). Safety risk assessment of blasting construction in rock high slope engineering based on the cloud matter-element model. Safety and Environmental Engineering, 28(2), 102–108. DOI 10.13578/j.cnki.issn.1671-1556.2021.02.014. [Google Scholar] [CrossRef]

  44. Yue, K. W. (2012). The study of a comprehensive power quality evaluation model based on cloud matter element theory and its application (Master′s Thesis). Beijing Jiaotong University, Beijing, China. [Google Scholar]

  45. Gao, S., Teng, K., Chen, J., Su, N. Y. (2020). Effectiveness evaluation of equipment system of system based on MCM-extension cloud. Journal of Ordnance Equipment Engineering, 41, 20–24. DOI 10.11809/bqzbgcxb2020.02.005. [Google Scholar] [CrossRef]

  46. Wang, X. L., Dai, L. H., Lu, P., Wang, C., Cheng, Z. F. (2019). Study on comprehensive evaluation model of seepage safety based on DSR-extension cloud. Journal of Tianjin University, 52, 52–61. DOI 10.11784/tdxbz201802022. [Google Scholar] [CrossRef]