 Open Access
Open Access
ARTICLE
A Linear Homomorphic Proxy Signature Scheme Based on Blockchain for Internet of Things
1 College of Big Data and Internet, Shenzhen Technology University, Shenzhen, 518118, China
2 School of Electronic and Information Engineering, Lanzhou Jiaotong University, Lanzhou, 730070, China
* Corresponding Author: Caifen Wang. Email:
(This article belongs to the Special Issue: Emerging Trends on Blockchain: Architecture and Dapp Ecosystem)
Computer Modeling in Engineering & Sciences 2023, 136(2), 1857-1878. https://doi.org/10.32604/cmes.2023.026153
Received 19 August 2022; Accepted 14 October 2022; Issue published 06 February 2023
Abstract
The mushroom growth of IoT has been accompanied by the generation of massive amounts of data. Subject to the limited storage and computing capabilities of most IoT devices, a growing number of institutions and organizations outsource their data computing tasks to cloud servers to obtain efficient and accurate computation while avoiding the cost of local data computing. One of the most important challenges facing outsourcing computing is how to ensure the correctness of computation results. Linearly homomorphic proxy signature (LHPS) is a desirable solution to ensure the reliability of outsourcing computing in the case of authorized signing right. Blockchain has the characteristics of tamper-proof and traceability, and is a new technology to solve data security. However, as far as we know, constructions of LHPS have been few and far between. In addition, the existing LHPS scheme does not focus on homomorphic unforgeability and does not use blockchain technology. Herein, we improve the security model of the LHPS scheme, and the usual existential forgery and homomorphic existential forgery of two types of adversaries are considered. Under the new model, we present a blockchain-based LHPS scheme. The security analysis shows that under the adaptive chosen message attack, the unforgeability of the proposed scheme can be reduced to the CDH hard assumption, while achieving the usual and homomorphic existential unforgeability. Moreover, compared with the previous LHPS scheme, the performance analysis shows that our scheme has the same key size and comparable computational overhead, but has higher security.Keywords
In the past decade, the way of data collection and dissemination have inspired the rapid development of the Internet of Things (IoT) [1,2]. The IoT has opened up new avenues for technical support and business upgrades in the fields of industry, healthcare, transportation, military target tracking, smart homes and food traceability, among which mobile healthcare systems (MHSs) and the industrial Internet of Things (IIoT) are the most successful applications.
The IIoT continuously integrates all kinds of acquisition, sensors or controllers with sensing abilities, as well as mobile communication technology, into all aspects of industrial production, to improve production efficiency, reduce costs, and ultimately realize the conversion of traditional industry to smart industry [3]. MHSs provide services and applications [4,5], including mobile telemedicine and electronic monitoring systems based on wireless sensors. In this system, sensors (wearable or implanted) are connected to the bodies of remote patients to collect medical data, including body temperature, blood pressure, pH-value etc., and transmit these data through nodes to a medical server, which distributes the relevant data to professional medical personnel.
The rapid development of IIoT and MHSs, along with the generation of massive medical and industrial data, has led to increasing computing overhead and resource consumption, which makes traditional local computing model (most IoT devices have limited processing and computing power and are not economical to calculate) unable to meet the application requirements. Fortunately, due to the convenience and rapidity of cloud computing, many users migrate local data to cloud servers to meet the above challenge. Fig. 1 shows a typical cloud-based network architecture. Outsourcing data to cloud servers to obtain and accurate computation or analysis results have become preferential.
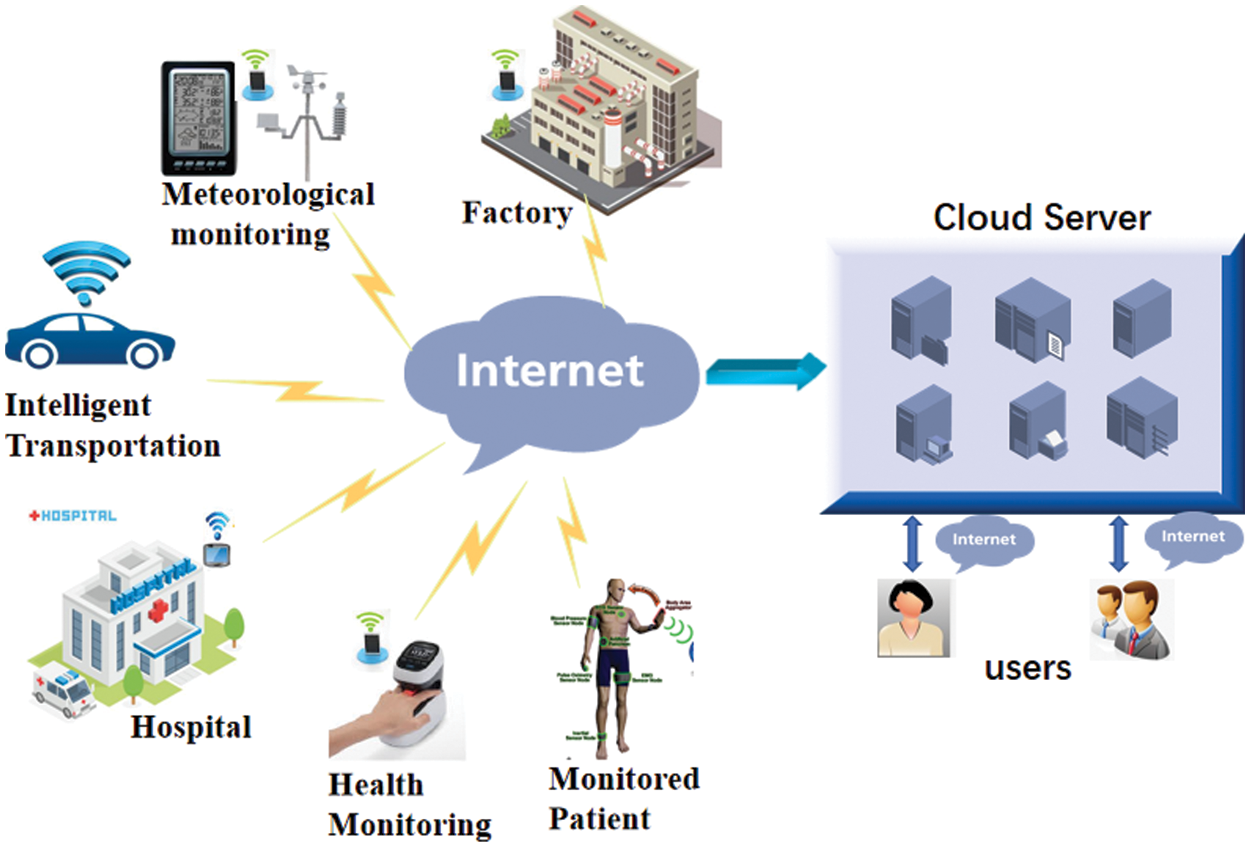
Figure 1: A typical architecture of cloud-based network
However, as an unsecure third party, cloud servers may return incomplete or wrong calculation results due to software and hardware errors and commercial interest inducement. Homomorphic signature (HS) provides a natural method for verifying outsourced computing, which can effectively solve the above problems. HS can enable untrusted servers to run calculations on outsourced data and generate a short signature to ensure the integrity and correctness of the calculation results. In recent years, HS has been extensively studied and developed [6–10].
Furthermore, consider such an application scenario: a hospital authorizes a sensor to sign data and communicate with the cloud server. The cloud server first confirms the authenticity of the sender (i.e., the sensor connected to the bodies of remote patients) and then sends the data calculation result and the derived signature to the hospital or research institution to verify its correctness. In an IIoT environment, an executive officer issues instructions to subordinates (such as the plant manager) to perform communication tasks. Thus, the data signature was often carried out by the subordinate on behalf of the superior organization. To realize this kind of authentication mechanism, it is necessary to authorize the signing right. In order to implement such kind of authentication mechanism, signature rights need to be authorized. Mambo et al. [11] realized this delegation authorization relationship with the concept of proxy signature (PS). In the PS scheme, the original signer (all represented by Alice) delegates its signing power to the proxy signer (all represented by Bob). Bob can generate valid proxy signatures in the name of Alice, and the verifier accepts the authorization protocol.
Naturally, to ensure the reliability of outsourced computing in the case of authorized signing rights, constructing a PS scheme with the homomorphism is interesting, which combines the delegation characteristics and homomorphism in the authentication method. In this type of scheme, Alice can authorize Bob, and Bob can create a proxy signature with homomorphic properties. However, as far as we know, constructions of linearly homomorphic proxy signature (LHPS) have been few and far between; in addition, the existing LHPS scheme [12] is only proven to be usually existential unforgeable (EUF) against adaptive chosen-message attacks (CMA). This security concept only guarantees that an adversary cannot forge a signature of any new message under the unqueried data identifier; it does not ensures that the adversary generates a valid signature for the data sets that have been queried for signatures (i.e., homomorphic existential forgery). In detail, for the security of a signature with homomorphic properties, there are two meanings of existential unforgeability, a verifiable forgery
To overcome this security flaw, we improve the security definition for LHPS and construct a new LHPS scheme for IoT environments, and makes the following main contributions in this paper:
1. The security model for LHPS is improved. For the two types of adversaries, considering the situation of an adversary’s output of a homomorphic existential forgery, the types of forgeries are more comprehensive, so the model security standard is higher.
2. We construct a blockchain-based LHPS scheme and prove that this scheme is secure against existentially forgery (including the usual existential forgery and homomorphic existential forgery) on adaptive CMA based on the CDH assumption under two types of adversaries.
3. The performance of the new LHPS is analyzed in detail. The discussion shows that our scheme has the same key size and comparable computational overhead as Lin et al.’s LHPS scheme [12], but it has higher security. Therefore, it is feasible to deploy and implement our LHPS scheme in cloud-based IoT environments.
The concept of HS scheme was first proposed by Goldwasser et al. [13] in 2000. Johnson et al. [14] first introduced the formal definition and overall framework of HS. Until 2009, Boneh et al. [15] proposed the first secure and practical LHS scheme, which can be regarded as a milestone of LHS scheme. Utilizing the k-SIS hardness assumption, reference [9] proposed the first scheme that can against quantum attacks. In order to be independent of certificate management, scholars proposed identity-based LHS schemes [16–19]. Although certificate management is simplified, key escrow issues are introduced. In response to this problem, researchers have successively proposed certificateless LHS [20,21]. Recently, multi-key HS has attracted attention [22–29]. For datasets involving inputs authenticated by different clients, multiple-key support is required, Chen et al. [27,28] successively proposed two multi-key LHS schemes, supporting three-layer and multi-layer routing networks respectively. Lai et al. [29] proposed an unforgeable multi-key HS under internal corruption based on adaptive zero-knowledge non-interactive knowledge demonstration. The public verifiability of HS makes them studied in other application scenarios. For example, the verifiable encryption HS scheme proposed by Seo et al. [30] has been successfully applied to cumulative optimistic fair exchange, and the homomorphic signcryption scheme proposed by Fan et al. [31] has been successfully applied to electronic voting, for voters, the use of homomorphic signcryption can complete the encryption and signature of votes in one step. In 2021, Li et al. [32] proposed a homomorphic signcryption scheme with verifiable public plaintext results, allowing the evaluation of arbitrary functions on signcrypted data, and allowing anyone to publicly test whether a given ciphertext is a signcrypted file for a message under a key.
Since Mambo et al. [11] proposed the concept of PS in 1996, many variants of PS have been proposed by other researchers successively, including proxy multi-signatur, multi-PS, proxy blind signature, certificate-based proxy signature and designated verifier proxy signature [33–38]. In 2003, Lee et al. [39] believed that proxy signature does not necessarily require a secure channel. In terms of the security model, Cao et al. [40] and Wang et al. [41] presented the model of a multi-proxy signature scheme. However, as Schuldt et al. [42] pointed out, the structure of the model is complex and incomplete. In 2012, Boldyreva et al. [43] improved its early security model by clearly defining the security attributes of proxy signatures and formalizing the definition of adversary behavior.
Blockchain is a new type of decentralized protocol that can securely store Bitcoin transactions or other data. The information cannot be forged or tampered with, and smart contracts can be automatically executed without the audit of any centralized organization [44,45]. Transactions can be digital currencies such as Bitcoin or digital assets such as debt, equity, copyright, etc. Blockchain technology solves the Byzantine general problem, greatly reduces the cost of trust and accounting in the real economy, and redefines the property right system in the Internet era. The introduction of blockchain technology in the proxy signature mechanism can realize the delegation of digital signature rights under the premise of safety and reliability, and support traceability and tamper-proof modification [46]. Additionally, blockchain-based proxy signatures enable anonymity of authentication while ensuring traceability of misconduct [47].
3 Architecture of Sign Delegation and Authentication Computing in a Cloud-Based IoT Environment
In the architecture of a cloud-based IoT environment using delegation and authentication computing, five entities are involved: CA, data owner, cloud server, end user and blockchain, as shown in Fig. 2. The specific functions are as follows (In this paper, Alice/Bob always represents the original/proxy signer):
• CA: It generates system parameters and generates certificates for users according to the identity and public key provided by each user.
• Data owner: It is composed of industry officials (e.g., system administrators, executive officers, etc.) and intelligent devices (embedded sensors). In our LHPS scheme, the superior is the Alice, and the subordinate is the Bob. For smart machines, the deployment agency/supervisor acts as the Alice, and the sensor will act as the Bob. Therefore, the superior (or supervisor) delegates its signature right to the subordinate (or smart machine).
• Cloud server: The cloud server can use the homomorphic signature to perform various calculations on the authentication data, and then sends the calculation results and the derived signatures to the end user, which can be done with minimal interaction and communication.
• End user: The end user may be a hospital, a research institution, or an intelligent machine (depending on the scenario). It receives the calculation result and the corresponding signature and uses the public key of the two signers for verification.
• Blockchain: The blockchain mainly stores the warrant from the original signer to the proxy signer so that other entities can download and verify the validity of the warrant.
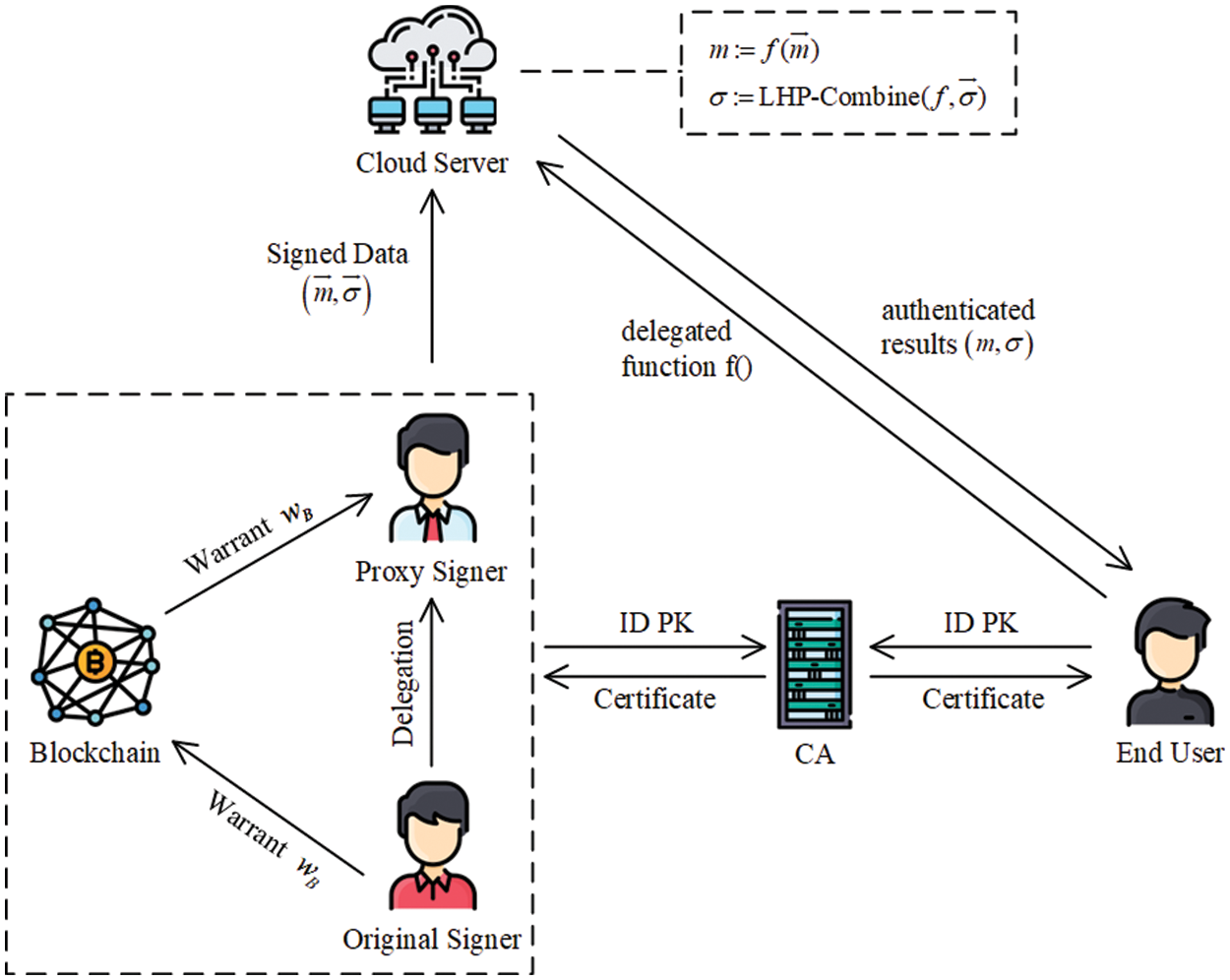
Figure 2: Architecture for IoT environment based on LHPS, blockchain and cloud computing
4 Definitions and Security Model
4.1 Linearly Homomorphic Proxy Signature
A LHPS scheme proposed in this paper includes seven polynomial-time algorithms (Setup, UserKGen, Delegation, DeleVerify, LHP-Sign, LHP-Combine, LHP-Verify):
• Setup: On input a security parameter
• UserKGen: On input params, it output a public/private key pair (
• Delegation: Given params, the private key
• DeleVerify: For the input params, public key of Alice, delegation and warrant, it outputs 0 or 1 according to reject or accept.
• LHP-Sign: Bob greats a proxy signature
• LHP-Combine: Takes a file identifier
• LHP-Verify: Takes as input public keys of both signer,
Correctness. The requirement is that for any output
(1) For any
(2) For all
We consider two type of adversaries, and denoted by
Type-I adversary (
Type II adversary (
We use the following game between challenger
Game 1. (Security against adversary
• Setup:
• Queries: Adversary
– Key Registration Queries: Given a key pair
– Signing Queries: Given a tuple
Output:
(1) For any
(2) For a
Game 2. (Security against adversary
• Setup:
• Queries: Adversary
– Key Registration Queries: Given a key pair
– Delegate Queries: Given public key
– Signing Queries: Given public key
• Output:
(1) For any
(2) For a
The advantage of adversary
Definition 4.1. Our proposed LHPS scheme is said to be unforgeable against the adversaries
Our proposed LHPS scheme is described in detail as follows:
• Setup: Takes a security parameter
(1) Choose two groups
(2) Selects different hash functions
• UserKGen: Each user chooses
• Delegation: Alice generates a warrant
• DeleVerify: Bob checks
• LHP-Sign: Suppose that this algorithm has stored an initially empty list L containing information about all identifiers
(1) Retrieve the relevant
(2) Otherwise, it chooses a random number
(3) Calculate hash values
(4) Choose a random number
(5) Output
LHP-Combine: On input
LHP-Verify: Given a tuple
Correctness
(1) Given a tuple
(2) Given a tuple
Therefore, for the LHP-Combine algorithm, the LHP-Verify algorithm is correct.
This section presents the security analysis of our LHPS scheme. In this section,
Theorem 6.1. If there is an adversary
Proof. For any PPT adversary
Case 1 (usual existential-forgery.)
• Setup:
• Queries:
– Key Registration Queries: When
– H Queries: On a requested
–
–
– Signing Queries: Given
(1) Randomly choose numbers
(2) Define the hash values of
(3) Recover
(4) Finally,
• Output: Finally,
Therefore, we have
The CDH problem can be solved by calculating the following equation:
Next we calculate the probability of
We only need to analyze the probability of
Case 2 (homomorphic existential-forgery):
• Setup:
• Queries:
– Key Registration Queries: When
– H Queries: On a requested
–
–
– Signing Queries: Given
(1) If list L does not contain
(2)
and returns the signature
• Output: Finally,
Therefore, we have
If
Now, we show that
Moreover, according to the definition of type 2 forgery,
Assume
Note that
From Gramer criterion,
Theorem 6.2. If there is an adversary
Proof. For any PPT adversary
Case 1 (usual existential-forgery):
• Setup:
• Queries:
– Key Registration Queries: As in the query/response in the proof of case 1 in Theorem 1, it is omitted here.
Suppose that
–
–
– Delegation Queries: Given a warrant
– Signing Queries: Given
If
Otherwise,
Output:
Further, we have
Next,
Then the CDH problem has been solved.
It is not difficult to see that the probability of not aborting in delegation queries, signing queries and forgery stage is at least
Case 2 (homomorphic existential-forgery):
• Setup:
• Queries:
– Key Registration Queries, H (
–
– Delegation Queries: Given a warrant
– Signing Queries: Given
If
If
• Output: Finally,
Therefore, we have
If
Now, we need to show that
7 Analysis of Security and Efficiency
We compare our scheme with the only LHPS scheme proposed by Lin et al. [12]. For convenience, we abbreviate this scheme as Lin-LHPS. Specifically, Tables 1 and 2 compare the proposed LHPS scheme with the Lin-LHPS scheme in terms of security, communication overhead and delegation overhead. Two main operations are listed: “E” represents the exponential operation on
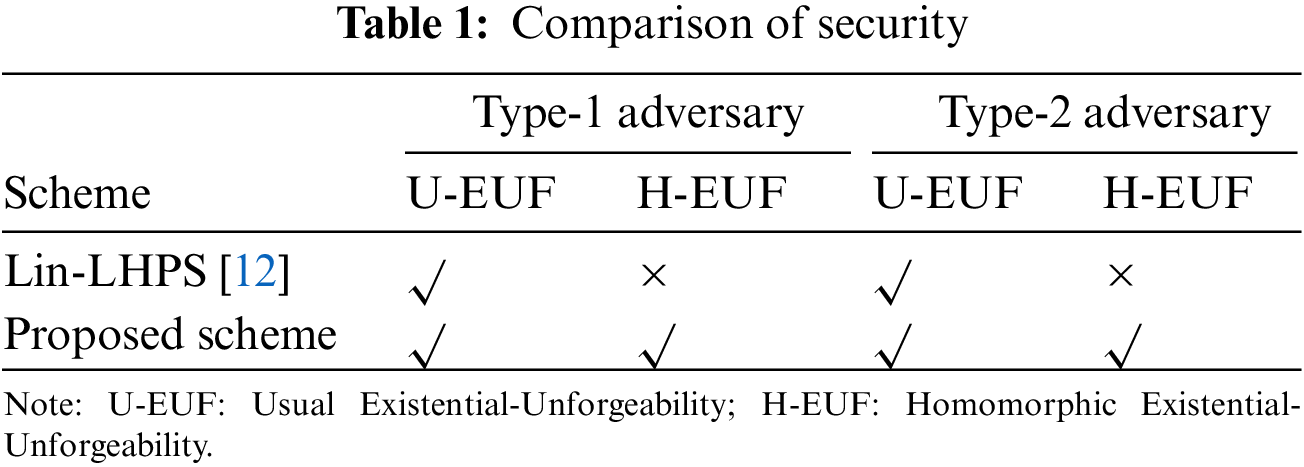

As seen in Table 1, our scheme satisfies both the usual and homomorphic existential unforgeability, while the Lin-LHPS scheme only satisfies the usual existential unforgeability. In the outsourced computation of authentication data, homomorphic existential unforgeability can prevent untrusted cloud servers from authenticating the wrong computing or analysis results and returning them to the receiver. In Table 2, DeleSize and SigSize represent the size of the delegation and the proxy signature, respectively. The two columns, DeleGen and DeleVer, show the computational cost of generating the delegation signature and delegation verification, respectively. Table 2 shows that the signature size of the proposed scheme is larger than that of the Lin-LHPS scheme; whereas the size of delegation, the computational cost of generating the delegation signature and delegation verification in our scheme are the same as those in the Lin-LHPS scheme. However, our scheme provides stronger security. We implement our LHPS scheme and Lin-LHPS in the experiments. The experiment was run on a laptop equipped with a 3.10-GHz Intel i5 CPU, 128 GB memory, and the Ubuntu Linux operating system.
As shown in Figs. 3 and 4, the computational cost of signature generation and signature verification in our scheme is slightly higher than that in the Lin-LHPS. It is a natural result because our scheme provides provably secure homomorphic existential unforgeability.
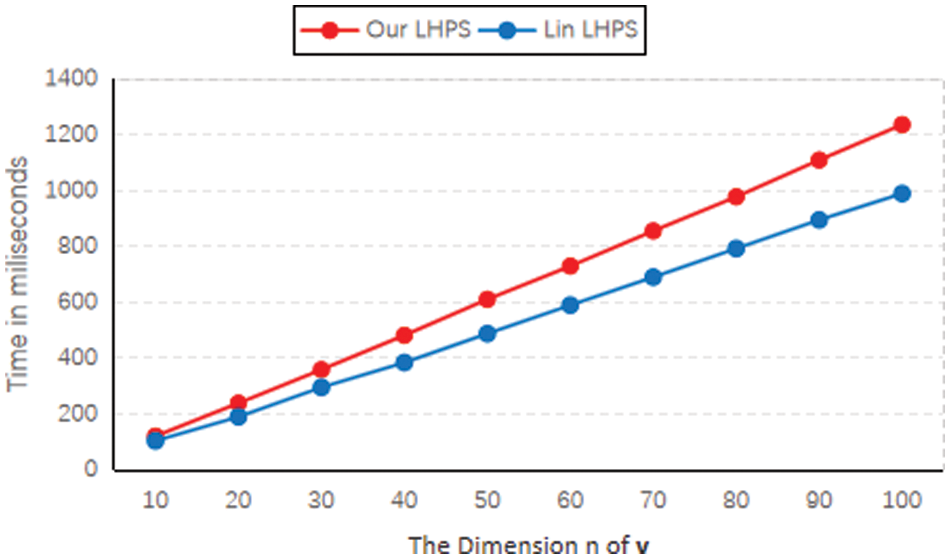
Figure 3: A comparison of the signature generation cost
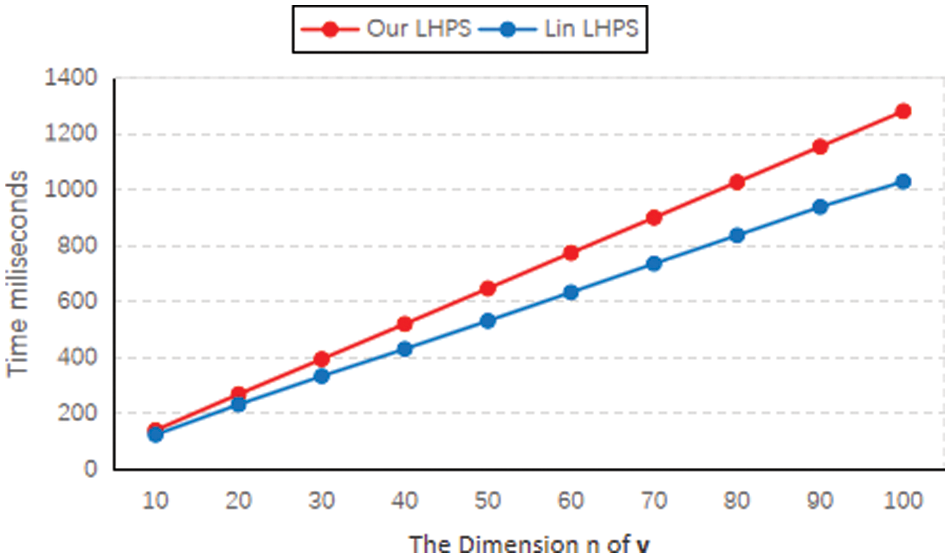
Figure 4: A comparison of the signature verification cost
In this paper, we improve the security model of the LHPS for the two types of adversaries, considering the situation in which adversaries output homomorphic existential forgeries. Under the new model, we present a blockchain-based LHPS scheme and prove that this scheme is secure against existential forgery (including the usual existential forgery and homomorphic existential forgery) under adaptive CMA based on the CDH assumption. The tamper-proof modification of the blockchain ensures the validity of the original signer’s warrant, which prevents problems such as the abuse of proxy signing rights. Moreover, the performance analysis shows that this new scheme has the same key size and comparable computing cost as Lin et al.’s LHPS scheme [12], and it has higher security. Therefore, our LHPS scheme is suitable for deployment and implementation in cloud-based IoT environments. However, the proposed scheme cannot resist quantum computing attacks. The next task is to design a secure and efficient LHPS scheme on lattice.
Funding Statement: This research is funded by the Special Innovation Project for General Colleges and Universities in Guangdong Province (Grant No. 2020KTSCX126).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Atzori, L., Iera, A., Morabito, G. (2010). The Internet of Things: A survey. Computer Networks, 54, 2787–2805. DOI 10.1016/j.comnet.2010.05.010. [Google Scholar] [CrossRef]
2. Ray, P. P. (2018). A survey on Internet of Things architectures. Journal of King Saud University-Computer and Information Sciences, 30(3), 291–319. DOI 10.1016/j.jksuci.2016.10.003. [Google Scholar] [CrossRef]
3. Xu, L., He, W., Li, S. (2014). Internet of Things in industries: A survey. IEEE Transactions on Industrial Informatics, 10(4), 2233–2243. DOI 10.1109/TII.2014.2300753. [Google Scholar] [CrossRef]
4. Doukas, C., Pliakas, T., Maglogiannis, I. (2010). Mobile healthcare information management utilizing cloud computing and android OS. Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos, Aires, Argentina. DOI 10.1109/IEMBS.2010.5628061. [Google Scholar] [CrossRef]
5. Li, X., Huang, X., Li, C., Yu, R., Shu, L. (2019). EdgeCare: Leveraging edge computing for collaborative data management in mobile healthcare systems. IEEE Access, 7, 22011–22025. DOI 10.1109/ACCESS.2019.2898265. [Google Scholar] [CrossRef]
6. Hu, X., Zheng, S., Gong, J., Cheng, G., Zhang, G. et al. (2019). Enabling linearly homomorphic signatures in network coding-based named data networking. Proceedings of the 14th International Conference on Future Internet Technologies, New York, USA. DOI 10.1145/3341188.3341191. [Google Scholar] [CrossRef]
7. Schabhüser, L., Buchmann, J., Struck, P. (2017). A linearly homomorphic signature scheme from weaker assumptions. IMA International Conference on Cryptography and Coding, Oxford, UK. DOI 10.1007/978-3-319-71045-7_14. [Google Scholar] [CrossRef]
8. Luo, F., Wang, F., Wang, K., Chen, K. (2019). A more efficient leveled strongly-unforgeable fully homomorphic signature scheme. Information Sciences, 480, 70–89. DOI 10.1016/j.ins.2018.12.025. [Google Scholar] [CrossRef]
9. Boneh, D., Freeman, D. M. (2011). Linearly homomorphic signatures over binary fields and new tools for lattice-based signatures. International Workshop on Public Key Cryptography, Taormina, Italy. DOI 10.1007/978-3-642-19379-8_1. [Google Scholar] [CrossRef]
10. Wang, F., Shi, S., Wang, C. (2019). Leveled lattice-based linearly homomorphic signature scheme in the standard model for network coding. International Conference on Frontiers in Cyber Security, Xi’an, China. DOI 10.1007/978-981-15-0818-9_6. [Google Scholar] [CrossRef]
11. Mambo, M., Usuda, K., Okamoto, E. (1996). Proxy signatures: Delegation of the power to sign messages. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 79(9), 1338–1354. CRID 1570009752558013440. [Google Scholar]
12. Lin, Q., Li, J., Huang, Z., Chen, W., Shen, J. (2018). A short linearly homomorphic proxy signature scheme. IEEE Access, 6, 12966–12972. DOI 10.1109/ACCESS.2018.2809684. [Google Scholar] [CrossRef]
13. Goldwasser, S., Micali, S., Rivest, R. L. (1988). A digital signature scheme secure against adaptive chosen-message attacks. SIAM Journal on Computing, 17(2), 281–308. DOI 10.1137/0217017. [Google Scholar] [CrossRef]
14. Johnson, R., Molnar, D., Song, D., Wagner, D. (2002). Homomorphic signature schemes. Cryptographers
15. Boneh, D., Freeman, D., Katz, J., Waters, B. (2009). Signing a linear subspace: Signature schemes for network coding. Proceedings of International Workshop on Public Key Cryptography, Irvine, CA, USA. DOI 10.1007/978-3-642-00468-1_5. [Google Scholar] [CrossRef]
16. Zhang, Y., Jiang, Y., Li, B., Zhang, M. (2017). An efficient identity-based homomorphic signature scheme for network coding. International Conference on Emerging Internetworking, Data and Web Technologies, Wuhan, China. DOI 10.1007/978-3-319-59463-7_52. [Google Scholar] [CrossRef]
17. SadrHaghighi, S., Khorsandi, S. (2016). An identity-based digital signature scheme to detect pollution attacks in intra-session network coding. 2016 13th International Iranian Society of Cryptology Conference on Information Security and Cryptology, Tehran, Iran. DOI 10.1109/iscisc.2016.7736444. [Google Scholar] [CrossRef]
18. Lin, Q., Yan, H., Huang, Z., Chen, W., Shen, J. et al. (2018). An ID-based linearly homomorphic signature scheme and its application in blockchain. IEEE Access, 6, 20632–20640. DOI 10.1109/ACCESS.2018.2809426. [Google Scholar] [CrossRef]
19. Chang, J., Ma, H., Zhang, A., Xu, M., Xue, R. (2019). RKA security of identity-based homomorphic signature scheme. IEEE Access, 7, 50858–50868. DOI 10.1109/ACCESS.2019.2908244. [Google Scholar] [CrossRef]
20. Chang, J., Ji, Y., Shao, B., Xu, M., Xue, R. (2020). Certificateless homomorphic signature scheme for network coding. IEEE/ACM Transactions on Networking, 28(6), 2615–2628. DOI 10.1109/TNET.2020.3013902. [Google Scholar] [CrossRef]
21. Li, Y., Zhang, F., Sun, Y. (2021). Lightweight certificateless linearly homomorphic network coding signature scheme for electronic health system. IET Information Security, 15(1), 131–146. DOI 10.1049/ise2.12011. [Google Scholar] [CrossRef]
22. Wang, F., Wang, K., Li, B., Gao, Y. (2015). Leveled strongly-unforgeable identity-based fully homomorphic signatures. International Conference on Information Security, Trondheim, Norway. DOI 10.1007/978-3-319-23318-5_3. [Google Scholar] [CrossRef]
23. Fiore, D., Mitrokotsa, A., Nizzardo, L., Pagnin, E. (2016). Multi-key homomorphic authenticators. International Conference on the Theory and Application of Cryptology and Information Security, Hanoi, Vietnam. DOI 10.1007/978-3-662-53890-6_17. [Google Scholar] [CrossRef]
24. Samarin, S. D., Fiore, D., Venturi, D., Amini, M. (2021). A compiler for multi-key homomorphic signatures for turing machines. Theoretical Computer Science, 889, 145–170. DOI 10.1016/j.tcs.2021.08.002. [Google Scholar] [CrossRef]
25. Aranha, D. F., Pagnin, E. (2019). The simplest multi-key linearly homomorphic signature scheme. International Conference on Cryptology and Information Security in Latin America, Bogota, Colombia. DOI 10.1007/978-3-030-30530-7_114. [Google Scholar] [CrossRef]
26. Schabhüser, L., Butin, D., Buchmann, J. (2019). Context hiding multi-key linearly homomorphic authenticators. Cryptographers
27. Chen, W., Lei, H., Li, J., Gao, C., Li, F. et al. (2017). A multi-source homomorphic network coding signature in the standard model. International Conference on Green, Pervasive, and Cloud Computing, Xi’an, China. DOI 10.1007/978-3-319-57186-7_6. [Google Scholar] [CrossRef]
28. Li, T., Chen, W., Tang, Y., Yan, H. (2018). A homomorphic network coding signature scheme for multiple sources and its application in IoT. Security and Communication Networks, 2018, 9641273. DOI 10.1155/2018/9641273. [Google Scholar] [CrossRef]
29. Lai, R. W., Tai, R. K., Wong, H. W., Chow, S. S. (2018). Multi-key homomorphic signatures unforgeable under insider corruption. International Conference on the Theory and Application of Cryptology and Information Security, Brisbane, QLD, Australia. DOI 10.1007/978-3-030-03329-3_16. [Google Scholar] [CrossRef]
30. Seo, J. H., Emura, K., Xagawa, K., Yoneyama, K. (2018). Accumulable optimistic fair exchange from verifiably encrypted homomorphic signatures. International Journal of Information Security, 17(2), 193–220. DOI 10.1007/s10207-017-0367-z. [Google Scholar] [CrossRef]
31. Fan, X., Wu, T., Zheng, Q., Chen, Y., Alam, M. et al. (2020). HSE-voting: A secure high-efficiency electronic voting scheme based on homomorphic signcryption. Future Generation Computer Systems, 111, 754–762. DOI 10.1016/j.future.2019.10.016. [Google Scholar] [CrossRef]
32. Li, S., Liang, B., Mitrokotsa, A., Xue, R. (2021). Homomorphic signcryption with public plaintext-result checkability. IET Information Security, 15(5), 333–350. DOI 10.1049/ise2.12026. [Google Scholar] [CrossRef]
33. Gu, K., Jia, W., Li, C., Chen, R. (2013). Identity-based group proxy signature scheme in the standard model. Journal of Computer Research and Development, 40(7), 1370–1386. DOI 10.1016/j.mejo.2013.01.001. [Google Scholar] [CrossRef]
34. Chen, M., Yuan, S. (2016). Provably secure identity-based multi-proxy signature scheme in standard model. Journal of Computer Research and Development, 54(8), 1879–1892. DOI 10.7544/issn1000-1239.2016.20150197. [Google Scholar] [CrossRef]
35. Verma, G. K., Singh, B. B. (2017). Efficient message recovery proxy blind signature scheme from pairings. Transaction on Emerging Telecommunication Technologies, 28(11), e3167. DOI 10.1002/ett.3167. [Google Scholar] [CrossRef]
36. Verma, G. K., Singh, B. B., Singh, H. (2018). Bandwidth efficient designated verifier proxy signature scheme for healthcare wireless sensor networks. Ad Hoc Networks, 81, 100–108. DOI 10.1016/j.adhoc.2018.07.026. [Google Scholar] [CrossRef]
37. Verma, G. K., Singh, B. B., Singh, H. (2018). Provably secure certificate-based proxy blind signature scheme from pairings. Information Sciences, 468, 1–13. DOI 10.1016/j.ins.2018.08.031. [Google Scholar] [CrossRef]
38. Verma, G. K., Singh, B. B., Kumar, N., Obaidat, M. S., He, D. et al. (2020). An efficient and provable certificate-based proxy signature scheme for IIoT environment. Information Sciences, 518, 142–156. DOI 10.1016/j.ins.2020.01.006. [Google Scholar] [CrossRef]
39. Lee, J. Y., Cheon, J. H., Kim, S. (2003). An analysis of proxy signatures: Is a secure channel necessary? Cryptographers
40. Cao, F., Cao, Z. (2009). A secure identity-based multi-proxy signature scheme. Computers and Electrical Engineering, 35(1), 86–95. DOI 10.1016/j.compeleceng.2008.05.005. [Google Scholar] [CrossRef]
41. Wang, Q., Cao, Z., Wang, S. (2005). Formalized security model of multi-proxy signature schemes. The Fifth International Conference on Computer and Information Technology, Shanghai, China. DOI 10.1109/CIT.2005.119. [Google Scholar] [CrossRef]
42. Schuldt, J. C., Matsuura, K., Paterson, K. G. (2008). Proxy signatures secure against proxy key exposure. International Workshop on Public Key Cryptography, Barcelona, Spain. DOI 10.1007/978-3-540-78440-1_9. [Google Scholar] [CrossRef]
43. Boldyreva, A., Palacio, A., Warinschi, B. (2012). Secure proxy signature schemes for delegation of signing rights. Journal of Cryptology, 25(1), 57–115. DOI 10.1007/s00145-010-9082-x. [Google Scholar] [CrossRef]
44. Han, D., Chen, J., Zhang, L., Shen, Y., Gao, Y. et al. (2021). A deletable and modifiable blockchain scheme based on record verification trees and the multisignature mechanism. Computer Modeling in Engineering & Sciences, 128(1), 223–245. DOI 10.32604/cmes.2021.016000. [Google Scholar] [CrossRef]
45. Hu, N., Teng, Y., Zhao, Y., Yin, S., Zhao, Y. (2021). IDV: Internet domain name verification based on blockchain. Computer Modeling in Engineering & Sciences, 129(1), 299–322. DOI 10.32604/cmes.2021.016839. [Google Scholar] [CrossRef]
46. Wang, Y., Qiu, W., Dong, L., Zhou, W., Pei, Y. et al. (2020). Proxy signature-based management model of sharing energy storage in blockchain environment. Applied Sciences, 10(21), 7502. DOI 10.3390/app10217502. [Google Scholar] [CrossRef]
47. Zou, H., Liu, X., Ren, W., Zhu, T. (2022). A decentralized electronic reporting scheme with privacy protection based on proxy signature and blockchain. Security and Communication Networks, 2022, 5424395. DOI 10.1155/2022/5424395. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools