Distributionally Robust Newsvendor Model for Fresh Products under Cap-and-Offset Regulation

1  Introduction

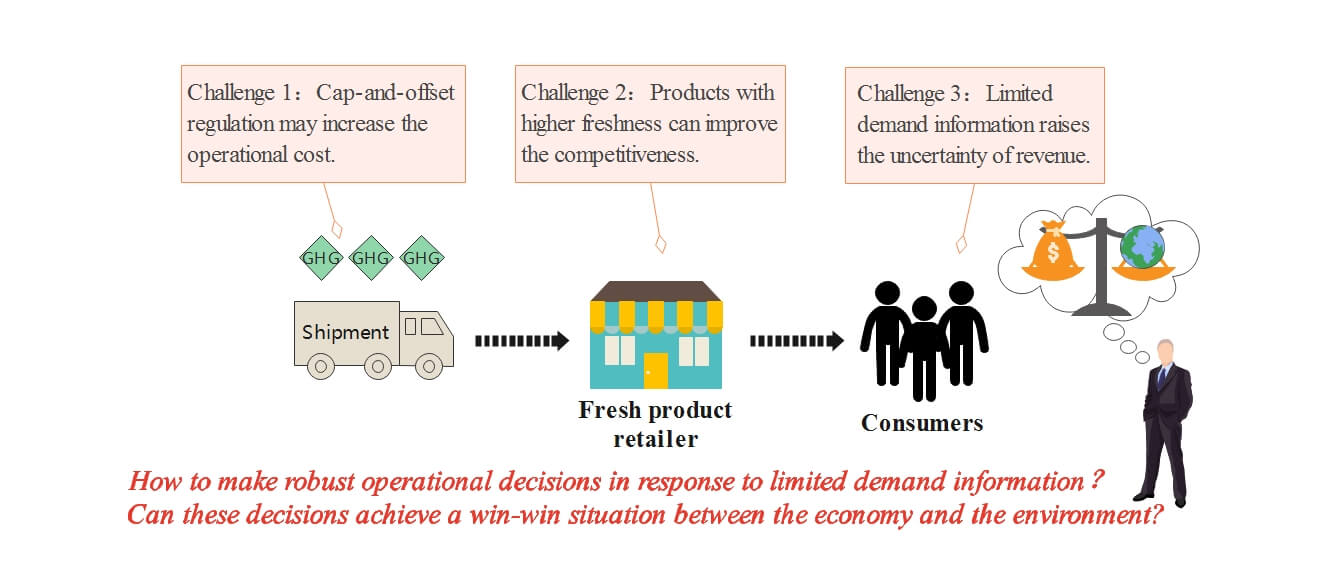
With the intensification of climate warming and enhancement of sustainable awareness, carbon emissions reduction has become one of the critical issues in the world. Carbon dioxide is a major contributor to global warming. Many countries and regions have set short-term and long-term targets to lessen emissions. In September 2020, the Chinese government promised to lower carbon emissions, and successively released a series of supporting measures to achieve carbon peaking and carbon neutrality goals. Great efforts, such as implementing carbon regulations, have been made to achieve the goal of sustainable development [1,2]. The carbon tax, carbon trading and cap-and-offset regulations are most frequently adopted and researched [3–5]. In this paper, we assume that a fresh product retailer operates under the cap-and-offset regulation. Under cap-and-offset regulation, a certain threshold on carbon emissions is allocated to the retailer. The retailer can emit more than the threshold but will be penalized for the emissions exceeding the threshold.

In this context, the operational objective of the retailer has been changed to pursue economic benefits and protect environment simultaneously. Many enterprises take active measures to protect the environment. For example, WalMart, the largest department store in the United States, actively adopted new technologies to save energy and has built a low-carbon distribution center and a low-carbon supermarket. The development of cold chain market urges retailers to concentrate on the operational management of fresh products. The fresh products have perishable physical properties and are preserved in special temperature-controlled equipment that generates higher carbon emissions. Lekkerland, a famous retailer in Germany, implemented a “multi-temperature logistics” distribution strategy to sell perishable products. However, using such special multi-temperature equipment leads Lekkerland to produce much greenhouse gases compared with standard warehousing and logistics systems [6]. In this scenario, new challenges have been brought and raised our research interest in studying the influences of cap-and-offset regulation on retailer management strategies.

Affected by market fluctuations and uncertainties, it is more difficult for fresh product retailers to forecast the full distribution information of demand [7–9]. Partial distribution information of the demand is easier to specified accurately. In this scenario, when carbon emission reduction is considered in the operational management of fresh product retailers, the following issues arise. (i) How do fresh product retailers make robust strategies to pursue maximum economic benefits under cap-and-offset policy? (ii) How does the implementation of cap-and-offset affect the economic benefits and environmental performance of fresh product retailers? (iii) With incomplete distribution information of consumer demand, how can retailers achieve a win-win situation between the economy and the environment?

To address the major issues mentioned above, we consider the operational strategy of a fresh product retailer under cap-and-offset regulation. The retailer has to decide whether to invest in sustainable technology to lessen greenhouse gas emissions and find the optimal order quantity only according to the mean and variance of the stochastic demand. In order to give valuable suggestions to the retailer, we construct a distributionally robust optimization model and work out the analytic formula of joint order quantity and low-carbon technology investment. We further explore the situation without technology investment and compare two distributionally robust optimization models. Finally, some computational studies are conducted to validate the impact of principal factors on the robustness of operational decisions.

Our work has the following research contributions. First, we consider limited distribution information of stochastic demand and low-carbon technology investment in operational decisions of the fresh product retailer. We use a distributionally robust newsvendor method to work out the analytic formula of joint order quantity and sustainable technology investment. Second, we theoretically and numerically provide some conditions where investing in sustainable technology leads the fresh product retailer to gain higher expected profit and emit lower greenhouse gases under cap-and-offset regulation. Finally, we numerically investigate how carbon parameters affect the robustness of the optimal joint strategies on order quantity and sustainable technology investment.

The reminders of this paper are arranged as follows. Section 2 reviews the relevant literature and shows the research gap. Section 3 interprets the considered problem and relevant notations, and constructs two distributionally robust models. Section 4 contains some numerical studies to illustrate and complement the theoretical outcomes. Conclusions and implications are revealed in the last section.

2  Literature Review

Two research branches are connected with the considered topic. Operational decisions of the fresh product retailer and robust decisions of the retailer under carbon regulations.

The first branch of research concentrates on operational decisions of the fresh product retailer. This topic has received extensive attentions. In this context, Cai et al. [10] characterized a continuous variable to affect the fresh quality and survival quantity of fresh products. The fresh quality impacts the price-dependent stochastic demand with a complete probability distribution function. This system is coordinated with price discount scheme and compensation scheme. On this foundation, Cai et al. [11] developed the impact of transportation time on the perishability of quantity and quality of fresh products by simplifying the influence of random factors. In addition, a new mechanism is proposed to promote the cooperation between producer and distributor. Wu et al. [12] investigated how the channel power structure affects the decision-making behavior of managers in the game. The authors deem that logistics service level and pricing standard affect the sales demand of fresh products. Ma et al. [13] argued that asymmetric demand messages can cause the loss of profit in decentralized system. Combined with the particularity of agricultural products, the authors propose a new mechanism to promote cooperation and make up for system losses. Wu et al. [14] explored the impact of adopting blockchain technology on optimal strategies for e-sales of fresh products. The authors design an incentive mechanism to realize the overall optimization of the supply chain. Other literature on fresh products includes Chen et al. [15], Xu et al. [16], Duan et al. [17].

The articles mentioned above do not consider the impact of carbon emission reduction on developing models for different types of supply chains with fresh products. However, how to lessen carbon emissions has become a major issue in optimizing the fresh product supply chain. It is due to the fact that employing special packaging, cryogenic devices and other equipment may release more greenhouse gases. Bai et al. [18] integrated emission trading policy in a manufacturer-retailer supply chain for perishable items. The authors construct some optimization system models and coordinated mechanisms. Wang et al. [19] put forward pricing strategies of fresh foods and proclaim the relationship between carbon trading and cold logistics services. Wang et al. [20] proposed three replenishment scenarios to solve the optimal scheme between a supplier and several retailers under cap-and-trade policy. Ma et al. [21] considered the impact of freshness-keeping efforts on a three-tier cold chain under cap-and-trade policy. The authors propose a coordinated scheme to improve the profit of the whole system. Although these scholars introduce cap-and-trade regulation into the fresh product system, they assume that market demand is deterministic or stochastic with full distribution information. Many scholars assume that full information of the demand distribution is known and use a newsvendor mechanism to work out the optimal tactics under different types of carbon regulations [22–25]. Unlike them, in this paper, we integrate cap-and-offset regulation and limited distribution information of the demand into the decision-making background of a fresh product retailer. We utilize a distributionally robust optimization mechanism to work out the optimal joint strategies on the order quantity and sustainable technology investment.

The second branch of research concentrates on frims’ robust decisions under carbon regulations. This topic is popular in the operational management field. Due to the difficulties of acquiring full information of demand distribution, distributionally robust optimization approach is proposed to work out the optimal tactics with limited distribution information [26–29]. Recently, Liu et al. [30] extend the newsvendor problem to an independent remanufacturing structure under three different kinds of carbon regulations. The authors assume that only the mean and variance of stochastic demand are specified. And they work out the optimal robust remanufacturing quantity. Bai et al. [31] exploited a distributionally robust newsvendor model to work out the optimal order tactic on dual sources when the firm is regulated by carbon tax and carbon trading schemes. Xu et al. [32] studied and compare the impacts of carbon cap and carbon trading schemes on the firms’ robust order tactics with limited distribution information of the demand. Bai et al. [33] considered a remanufacturing structure under carbon trading scheme and develop a distributionally robust newsvendor model to find out the optimal decisions on collection and production quantities. Bai et al. [34] combined robust optimization method and Hurwicz-decision theory to solve the optimal decision of the sustainable manufacturer. The authors comparatively analyze the impact of carbon tax and mandatory carbon quota on decision-making. Although these scholars relax the information of demand distribution, they do not take the carbon policies into account in the operational decisions for fresh products. However, in this paper, we exploit a distributionally robust optimization model under cap-and-offset regulation for the fresh product retailer. We emphasize the impacts of both cap-and-offset regulation and limited distribution information on the optimal joint order quantity and low-carbon technology investment.

3  The Model

3.1 Problem Description and Hypothesis

The retailer purchases q units of a kind of fresh products at a unit order cost c1, and sells them at the unit price p to fulfill the random consumption demand. Referencing to Bai et al. [18], the transportation time can be standardized to 1 and the unit transportation cost is c2. Due to the perishable property of fresh products, referring to Cai et al. [10], we characterize surviving index τ and freshness index ϑ, where τ is defined over (0,1], τ=1 indicates that all products survive during transportation. The survival quantity reaching the market that is available for sale becomes qτ with qτ>0. ϑ is defined over (0,1], and ϑ=1 represents the products are completely fresh before the sales period. In addition, ε represents the other influence factors of demand that is random variable. Consequently, the demand function can be expressed as

D(ϑ,p,ε)=y0ϑp−k0ε(1)

In Eq. (1), y0 is the potential sales scale, k0 is the price elasticity of demand, and ε represents the random demand fluctuation.

If actual demand D during selling period does not exceed qτ, then the revenue is pD. Due to the perishability of fresh products over time, its salvage value is not considered temporarily. Alternatively, if demand D exceeds qτ, then the revenue is pqτ, and the D(ϑ,p,ε)−qτ shortages is assessed by the per-unit penalty cost s. The expected profit is expressed as

Π0(q)=pEε[min(D(ϑ,p,ε),qτ))]−(c1+c2)q−sEε[(D(ϑ,p,ε)−qτ)+](2)

In Eq. (2), the first item indicates expected income, the second item indicates the order and transportation cost, and the third item indicates the expected shortage cost.

The transportation is the main link to emit greenhouse gases. The retailer can reduce carbon emissions by investing in sustainable technologies, equipments or machineries. The marginal reduction amount of carbon emissions deceases as the increment of the investment cost that identifies with the principle of “Increasing Marginal Cost” in economics. Referring to Huang et al. [35] and Toptal et al. [36], if the retailer invests in technologies, then the carbon emissions can be cut down by amount of aR−bR2 as the return on investment of R currency per year (0≤R≤a2b). Here, a reflects the efficacy of sustainable technology in decreasing emissions, and b is the decreasing return coefficient. Let e be the carbon emissions per unit product before investment. The carbon emissions are eq if the retailer does not invest in technologies. Consequently, the total carbon emissions are expressed as

Y(q,R)=eq−aR+bR2(3)

Considering the fact that the carbon emissions cannot be completely lessened to 0 even if investing in sustainable technologies, we assume that carbon emissions satisfies Y(q,R)>0 in Eq. (3). The relevant notations involved in the paper are summarized in Table 1.

3.2 Robust Optimization Strategies under Cap-and-Offset Policy

This subsection utilizes the distributionally robust optimization approach to analyze the optimal joint strategies on order quantity and sustainable technology investment. The fresh product retailer faces the fact that the probability distribution of demand is difficult to acquire and operation management is constrained by cap-and-offset regulation.

Referring to Chen et al. [5], under the cap-and-offset regulation, the government allocates the fixed number of carbon emission permits to the retailer, that is denoted by carbon cap K. When the total carbon emissions Y (q,R) exceed the carbon cap, the retailer needs to pay c3[Y(q,R)−K] for excess emissions where c3 is carbon tax charged on unit redundant carbon emissions. Otherwise, the retailer does not need to pay carbon tax.

Based on historical data information, the retailer can only acquire the mean μ and variance σ2 of the random factor but cannot obtain the complete distribution function G. Let Ψ represent the set of distribution functions whose mean and variance is μ and σ2, respectively. That is, G∈Ψ. Using Eqs. (2) and (3), we establish the distributionally robust optimization model for the fresh product retailer under cap-and-offset regulation as follows:

(M1)maxq,RminG∈ΨΠ1(q,R)=Π0(q)−R−c3(Y(q,R)−K)+s.t.q≥0,R≥0(4)

Here, x+=max{x,0}. According to characteristic of Eq. (4), we first solve the following two sub-models M11 and M12 before solving model M1.

(M11)maxq,RminG∈ΨΠ11(q,R)=Π0(q)−R−c3(Y(q,R)−K)(5)

s.t.        {Y(q,R)≥Kq≥0,R≥0(6)

(M12)maxq,RminG∈ΨΠ12(q,R)=Π0(q)−R(7)

s.t. ​​​    { Y(q,R)≤Kq≥0,R≥0(8)

We solve the distributionally robust optimization models M11 and M12 with a two-stage optimization approach. That is, first we focus on the expected profit in the worst demand scenario, namely minG∈ΨΠ(q,R). Then we maximize the profit function minG∈ΨΠ(q,R) to obtain the optimal joint strategies on order quantity and sustainable technology investment.

Referring to Gallego et al. [27], the following lemma is given to show the relevant properties of the distribution function of stochastic demand.

Lemma 3.1. If the distribution function G belongs to set Ψ on [0,+∞) satisfied E(ε)=μ and Var(ε)=σ2, then the following inequality holds.

E(ε−z)+≤σ2+(z−μ)2−(z−μ)2.(9)

And there exists a distribution function G∗∈Ψ that makes Eq. (9) holds with equality.

For the convenience of solving the model, set A0=y0ϑp−k0τ and let z=qA0 represent the stock factor [37]. Combined with Lemma 3.1 to solve model M11, there exists a two-point cumulative distribution function G∗∈Ψ to minimize Π11(q,R). The expected profit function is further simplified as

minG∗∈ΨΠ11(z,R)=A0{τ(p+s)[(z+μ)−σ2+(z−μ)2]2−sμτ−(c1+c2+c3e)z}−R(1−ac3+bc3R)+c3K(10)

To ensure the feasibility of the solution, we assume that p>(c1+c2+c3e+ea)1τ. For simplicity, we define two parameters zα and zβ.

zα=μ+σ2[(p+s)τ−(c1+c2+c3e)c1+c2+c3e−c1+c2+c3e(p+s)τ−(c1+c2+c3e)],(11)

zβ=μ+σ2[a(p+s)τ−(ac1+ac2+e)ac1+ac2+e−ac1+ac2+ea(p+s)τ−(a1+ac2+e)].(12)

Using Eqs. (6), (10)–(12), the following theorem can be obtained by solving the model M11.

Theorem 3.1. For model M11, there exists the only optimal stock factor z11∗ and sustainable technology investment R11∗ to maximize expected profit. They can be expressed as

(z11∗,R11∗)={(zα,0),0<K≤ezαA0and0<c3<1a;(KeA0,0),K>ezαA0and0<c3<1aorK>ezβA0andc3≥1a;(z11,R11),ezαA0−a24b+14bc32<K≤ezβA0andc3≥1a;arg⁡maxz,R{Π11G(zα,ac3−12bc3),Π11G(z11,R11)},ezαA0−a24b<K≤ezαA0−a24b+14bc32andc3≥1a;(zα,ac3−12bc3),0<K≤ezαA0−a24bandc3≥1a.(13)

where

z11=u+σ2{(a−2bR11)(p+s)τ−[(a−2bR11)(c1+c2)+e](a−2bR11)(c1+c2)+e−(a−2bR11)(c1+c2)+e(a−2bR11)(p+s)τ−[(a−2bR11)(c1+c2)+e]}

and

R11=a−a2−4b(ez11A0−K)2b.

Please refer to Appendix A for the specific certification process. It can be seen that the optimal solution depends on the parameters of cap-and-offset regulation. Particularly, when ezαA0−a24b+14bc32<K≤ezβA0 and c3≥1a, the optimal joint strategies of model M11 is (z11∗,R11∗)=(z11,R11). When 0<K≤ezαA0−a24b and c3≥1a, the optimal joint strategies of model M11 can be expressed as (z11∗,R11∗)=(zα,ac3−12bc3). In the overlapping interval ezαA0−a24b<K≤ezαA0−a24b+14bc32, we choose the solution that maximizes the objective function as the optimal solution.

From the proof of Theorem 3.1, we can also draw the following corollary that reflects the conditions of investment and relation between the total carbon emissions and carbon cap for model M11.

Corollary 3.1. For the model M11, the following conclusions hold.

(i)   When K>ezαA0 and 0<c3<1a, or K>ezβA0 and c3≥1a, or 0<K≤ezαA0 and 0<c3<1a, the fresh product retailer does n’t invest in low-carbon technology, i.e., R11∗=0.

(ii)   When K>ezαA0 and 0<c3<1a, or K>ezβA0 and c3≥1a, or ezαA0−a24b+14bc32<K≤ezβA0 and c3≥1a, the carbon emissions generated by the retailer are equal to the carbon cap, i.e., Y(q11∗(z11∗),R11∗)=K.

(iii)   When ezαA0−a24b<K≤ezαA0−a24b+14bc32 and c3≥1a, if Π11G(zα,ac3−12bc3)<Π11G(z11,R11) is true, then Y(q11∗(z11∗),R11∗)=K; otherwise, Y(q11∗(z11∗),R11∗)>K.

Next, we solve the distributionally robust optimization model M12. Similar to the analysis of model M11, using Lemma 3.1 and Eq. (7), the expected profit can be expressed as

minG∗∈ΨΠ12(z,R)=A0{τ(p+s)[(z+μ)−σ2+(z−μ)2]2−sμτ−(c1+c2)z}−R.(14)

Defined z0 as

z0=μ+σ2[(p+s)τ−(c1+c2)c1+c2−c1+c2(p+s)τ−(c1+c2)].(15)

Using Eqs. (8), (12), (14) and (15), we can draw the following theorem by solving model M12.

Theorem 3.2. For model M12, there exists the only optimal stock factor z12∗ and sustainable technology investment R12∗ to maximize expected profit under the condition of K>ezβA0−a24b. They can be expressed as

(z12∗,R12∗)={(z0,0),K≥ez0A0;(KeA0,0),ezβA0<K<ez0A0;(z11,R11),ezβA0−a24b<K≤ezβA0.(16)

Otherwise, there does not exist optimal solutions.

Above theorem indicates that when carbon emissions are restricted by carbon cap, the optimal joint strategy is easier to determine than in the case where carbon emissions exceed carbon cap. Additionally, the selection of optimal solution only depends on carbon cap K. However, in Theorem 3.1, the selection of optimal solution depends on both carbon cap K and carbon tax c3.

According to Theorem 3.2, we can also draw the following corollary that reflects the conditions of investment and relation between the total carbon emissions and carbon cap for model M12.

Corollary 3.2. For model M12, the following conclusions hold.

(i)   When K≥ezβA0 holds, the fresh product retailer does not invest in low-carbon technology, i.e., R12∗=0.

(ii)   When ezβA0−a24b<K<ez0A0 holds, the carbon emissions generated by the retailer are equal to the carbon cap, i.e., Y(q12∗(z12∗),R12∗)=K.

Combining with Theorem 3.1 and Theorem 3.2, we can get Theorem 3.3.

Theorem 3.3. For model M1, there exists the only optimal stock factor z1∗ and sustainable technology investment R1∗ that maximizes expected profit function. They can be expressed as

(z1∗,R1∗)=arg⁡maxz,R{Π11G(z11∗,R11∗),Π12G(z12∗,R12∗)}(17)

Theorem 3.3 shows that the fresh product retailer can make the distributionally robust optimal decisions to maximize expected profit function when the random demand information is limited to know.

3.3 Performance Analysis

This subsection constructs another distributionally robust optimization model, denoted as M2. M2 represents the situation where the retailer doesn’t invest in sustainable technology under cap-and-offset regulation. By comparing M1 and M2, we can further explore the impact of cap-and-offset regulation and emission reduction technology investment on operational decisions of the retailer.

Similar to model M1, model M2 can be expressed as Eq. (18).

(M2)maxqminG∈ΨΠ2(q)=Π0(q)−c3(Y(q,0)−K)+s.t.q≥0.(18)

Without investing in sustainable technology, M21 represents the robust optimization model when the emissions exceed carbon cap. M22 represents the robust optimization model when the emissions are no more than carbon cap. Similar to the previous proof, Theorem 3.4 can be obtained by solving model M21 and model M22 using Eq. (18).

Theorem 3.4. When the fresh product retailer does not invest in sustainable technology, the following conclusions hold.

(i)   For Model M21, there exists the only optimal stock factor z21∗=max{zα,KeA0} to maximize the target profit Π21G(z).

(ii)   For Model M22, there exists the only optimal stock factor z22∗=min{z0,KeA0} to maximize the target profit Π22G(z).

(iii)   For Model M2, there exists the only optimal stock factor z2∗=arg⁡maxz{Π21G(z21∗),Π22G(z22∗)} to maximize the target profit Π2G(z).

Theorem 3.4 solves the analytic formula for the optimal solution of M21, M22 and M2. This shows that there exists the only optimal order strategy for the retailer without investing in sustainable technology under cap-and-offset regulation.

According to Theorem 3.3 and Theorem 3.4, we can obtain the following theorem.

Theorem 3.5. Comparing with M1 and M2, the following conclusions hold:

(i)   Π1G(z1∗,R1∗)≥Π2G(z2∗) and Y(z12∗,R12∗)=Y(z22∗,0)≤K;

(ii)   If (z11∗,R11∗)=(KeA0,0) or (z11,R11), then K=Y(z11∗,R11∗)≤Y(z21∗,0);

If (z11∗,R11∗)=(zα,ac3−12bc3) and z21∗=zα, then K≤Y(z11∗,R11∗)≤Y(z21∗,0);

If (z11∗,R11∗)=(zα,0) and z21∗=zα, then K≤Y(z11∗,R11∗)=Y(z21∗,0).

Theorem 3.5 compares the expected profits and carbon emissions between models M1 and M2. Compared with the case of not investing in sustainable technology, the retailer will earn more profits and generate lower carbon emissions. This may be due to the fact that investing in low-carbon technology promotes an increase of order quantity under cap-and-offset regulation. Thereby the fresh product retailer can achieve the target of reducing carbon emissions while increasing expected profits. It is conducive to achieve sustainable development for the fresh product retailer.

4  Computational Studies

In this subsection, the computational examples are reported. We explore the impact of some critical parameters, such as carbon cap K, unit carbon tax c3, surviving index τ and freshness index ϑ, on the joint order quantity and sustainable technology investment strategies. The basic parameters are chosen as: c1=5, c2=2, p=15, y0=600, k0=2.32, s=2, e=6, a=5, b=0.01, τ=0.8639, ϑ=0.8930, c3=0.34, K=3800, μ=600, σ=100.

Based on the above situation, we solved the expected profits and carbon emissions of the retailer with only acquiring the mean and variance of stochastic demand. The calculation results are shown in Table 2.

From Table 2, the following observations can be made.

From the aspect of emissions, if the retailer decides to invest in sustainable technology under cap-and-offset regulation with limited distribution information, the optimal sustainable technology investments are 57.62, and the carbon emissions are 3800, which are equivalent to the carbon cap stipulated by authorities. When the retailer does not invest in sustainable technology, the carbon emissions are 4006.54 that exceed the carbon cap. It shows that investing in sustainable technologies can effectively lessen releasing greenhouse gases.

Moreover, the expected profits in the case of investing in sustainable technology increase by 0.8% and the carbon emissions decrease by 8.2% compared with the case of no investment. It demonstrates that under the cap-and-offset regulation, investing in sustainable technology is more conducive for the retailer to achieving higher expected profits and lower carbon emissions.

We further analyze the sensitivity effects of carbon cap K and carbon tax c3 on the retailer’s operational decisions. The corresponding changes are shown in Figs. 1 and 2.

Figure 1: The impact of K on the retailer’s operational decisions

Figure 2: The impact of c3 on the retailer’s operational decisions

Fig. 1 depicts the impact of carbon cap K on the retailer’s optimal strategies and operational effectiveness. It can be seen that, with the increase of K, the change trend of optimal order quantity and carbon emissions will firstly remain unchanged, then increase, and finally remain unchanged; the change trend of sustainable technology investments will firstly remain unchanged, then decrease, and finally remain unchanged; the change trend of expected profits will firstly increase and then remain unchanged. The change trend of the corresponding indicators in the cases of with and without investing in sustainable technology is similar. Moreover, when K<4000, even if the retailer invests in sustainable technology, its expected profits still exceed that without investment, and its carbon emissions are lower than that without investment. However, when K>4000, the retailer’s expected profits and carbon emissions are equivalent in the both cases. This suggests that if the carbon cap is set too high, the restrictive efficacy of the cap-and-offset regulation on the retailer will be lost.

Fig. 2 depicts the impact of carbon tax c3 on the retailer’s optimal strategies and operational effectiveness. It can be seen that, with the increase of c3, the change trend of optimal order quantity and carbon emissions will firstly decrease, and finally remain unchanged; the change trend of sustainable technology investment will firstly remain unchanged, then increase, and finally remain unchanged; the change trend of expected profits will firstly decrease and then remain unchanged. The change trend of the corresponding indicators in the cases of with and without investing in sustainable technology is similar. Moreover, when c3<0.65, the carbon emissions after investment are significantly lower than that without investment. When c3>0.65, the carbon emissions of investing and not investing in sustainable technology are equivalent and remain unchanged. This indicates that when c3 is set too high, it is not only unfavorable to reduce carbon emissions, but also increases the heavy tax burden of retailers.

According to the above discussion, the increase of carbon cap could encourage retailer to order and increase operating profit. But the increase of carbon tax could restrict the retailer to ordering less products and lessen operating profit. Under the cap-and-offset regulation, the optimal order quantity and expected profits after investment are always no less than that without investment. As well as the carbon emissions are always no more than that without investment. This suggests that the cap-and-offset regulation can effectively promote the retailer to invest in sustainable technology. It is beneficial for the retailer to achieve the target of higher expected profits and lower carbon emissions.

Next, we analyze the impact of surviving index τ and freshness index ϑ on optimal strategies and operational effectiveness. The results are shown in Figs. 3 and 4.

Figure 3: The impact of τ on the retailer’s operational decisions

Figure 4: The impact of ϑ on the retailer’s operational decisions

Fig. 3 depicts the impact of surviving index τ on optimal strategies. When the product has a high survivability and is not easy to decay, the fresh product retailer does not need to maintain a high inventory. So it will appropriately reduce the order quantity and will not invest too much capital in sustainable technology. Thus, the order cost, inventory cost and investment cost of the retailer are reduced. The retailer can obtain higher expected profits and release fewer emissions. If the survival rate of the product is too low, for example, when τ<0.6, the retailer cannot gain positive profit because the output cost is higher than the income.

Fig. 4 depicts the impact of freshness index ϑ on optimal strategies that have a great difference from the impact of τ. This is because the freshness index affects the demand of consumers. When the product has a high freshness level, it stimulates the increase in consumer demand which further promotes the retailer to expand order quantity. At the same time, the retailer will increase its investment in sustainable technologies and achieve higher expected profits.

In addition, we can also find that no matter how the survival and freshness of products affect business operations, investing in sustainable technologies is more profitable and emits fewer emissions than that without investment under the cap-and-offset policy.

5  Conclusions

With the enhancement of environmental awareness, the sustainable management concept brings new opportunities and challenges to the operation of fresh product retailers. Based on this background, we combine cap-and-offset regulation to research the optimal decisions of the fresh product retailer. Firstly, we construct distributionally robust newsvendor models where the information of stochastic factors in the market demand is limited to the mean and variance. We propose the analytic formula of joint decisions on order quantity and low-carbon technology investment by KKT conditions. A further comparison between the problems with investment and without investment is revealed. Finally, numerical studies are carried out to verify the impact of the critical carbon factors on the robustness of operational tactics. The results show that the cap-and-offset regulation can effectively encourage the retailer to invest in sustainable technologies and lead to higher expected profits and lower carbon emissions. This is consistent with the retailer’s long-term goals and is conducive to achieving sustainable development. This paper mainly studies the optimal strategies from the angle of a single fresh product retailer. Further research can be conducted from the angle of the whole supply chain with fresh products in the future.

Funding Statement: This study is financially supported by the National Natural Science Foundation of China (Grant No. 71702087), the Youth Innovation Science and Technology Support Program of Shandong Province Higher Education (Grant No. 2021RW024), and the Special Funds for Taishan Scholars, Shandong (Grant No. tsqn202103063).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Sheng, D., Li, Z. C., Fu, X. W., Gillen, D. (2017). Modeling the effects of unilateral and uniform emission regulations under shipping company and port competition. Transportation Research Part E: Logistics and Transportation Review, 101, 99–114. DOI 10.1016/j.tre.2017.03.004. [Google Scholar] [CrossRef]

    2. Sheng, D., Meng, Q., Li, Z. C. (2019). Optimal vessel speed and fleet size for industrial shipping services under the emission control area regulation. Transportation Research Part C: Emerging Technologies, 105, 37–53. DOI 10.1016/j.trc.2019.05.038. [Google Scholar] [CrossRef]

    3. Konstantaras, I., Skouri, K., Benkherouf, L. (2021). Optimizing inventory decisions for a closed-loop supply chain model under a carbon tax regulatory mechanism. International Journal of Production Economics, 239, 108185. DOI 10.1016/j.ijpe.2021.108185. [Google Scholar] [CrossRef]

    4. Linghu, D., Wu, X., Lai, K. H., Ye, F., Kumar, A. et al. (2022). Implementation strategy and emission reduction effectiveness of carbon cap-and-trade in heterogeneous enterprises. International Journal of Production Economics, 248, 108501. DOI 10.1016/j.ijpe.2022.108501. [Google Scholar] [CrossRef]

    5. Chen, X., Benjaafar, S., Elomri, A. (2013). The carbon-constrained EOQ. Operations Research Letters, 41(2), 172–179. DOI 10.1016/j.orl.2012.12.003. [Google Scholar] [CrossRef]

    6. Bai, Q. G., Gong, Y. Y., Jin, M. Z., Xu, X. H. (2019). Effects of carbon emission reduction on supply chain coordination with vendor-managed deteriorating product inventory. International Journal of Production Economics, 208, 83–99. DOI 10.1016/j.ijpe.2018.11.008. [Google Scholar] [CrossRef]

    7. Qu, S., Meng, D., Dai, Y. (2017). Distributionally robust games with an application to supply chain. Journal of Intelligent & Fuzzy Systems, 33(5), 2749–2762. DOI 10.3233/JIFS-169324. [Google Scholar] [CrossRef]

    8. Qu, S., Han, Y., Wu, Z., Raza, H. (2021). Consensus modeling with asymmetric cost based on data-driven robust optimization. Group Decision and Negotiation, 33, 1395–1432. DOI 10.1007/s10726-020-09707-w. [Google Scholar] [CrossRef]

    9. Ji, Y., Jin, X., Xu, Z., Qu, S. (2021). A mixed 0–1 programming approach for multiple attribute strategic weight manipulation based on uncertainty theory. Journal of Intelligent & Fuzzy Systems, 41(6), 6739–6754. DOI 10.3233/JIFS-210650. [Google Scholar] [CrossRef]

  10. Cai, X., Chen, J., Xiao, Y., Xu, X. (2010). Optimization and coordination of fresh product supply chains with freshness-keeping effort. Production and Operation Management, 19(3), 261–278. DOI 10.1111/j.1937-5956.2009.01096.x. [Google Scholar] [CrossRef]

  11. Cai, X., Chen, J., Xiao, Y., Xu, X. (2013). Fresh-product supply chain management with logistics outsourcing. Omega, 41(4), 752–765. DOI 10.1016/j.omega.2012.09.004. [Google Scholar] [CrossRef]

  12. Wu, Q., Mu, Y., Feng, Y. (2015). Coordinating contracts for fresh product outsourcing logistics channels with power structures. International Journal of Production Economics, 160, 94–105. DOI 10.1016/j.ijpe.2014.10.007. [Google Scholar] [CrossRef]

  13. Ma, X. L., Wang, S. Y., Islam, S. M. N., Liu, X. B. (2019). Coordinating a three-echelon fresh agricultural products supply chain considering freshness-keeping effort with asymmetric information. Applied Mathematical Modelling, 67, 337–356. DOI 10.1016/j.apm.2018.10.028. [Google Scholar] [CrossRef]

  14. Wu, X. Y., Fan, Z. P., Cao, B. B. (2021). An analysis of strategies for adopting blockchain technology in the fresh product supply chain. International Journal of Production Research. DOI 10.1080/00207543.2021.1894497. [Google Scholar] [CrossRef]

  15. Chen, J., Tian, Z. W., Hang, W. (2020). Optimal ordering and pricing policies in managing perishable products with quality deterioration. International Journal of Production Research, 59(15), 4472–4494. DOI 10.1080/00207543.2020.1766715. [Google Scholar] [CrossRef]

  16. Xu, C., Fan, T. J., Zheng, Q., Song, Y. (2020). Contract selection for fresh produce suppliers cooperating with a platform under a markdown-pricing policy. International Journal of Production Research. DOI 10.1080/00207543.2021.1987548. [Google Scholar] [CrossRef]

  17. Duan, Y. R., Liu, J. J. (2019). Optimal dynamic pricing for perishable foods with quality and quantity deteriorating simultaneously under reference price effects. International Journal of Systems Science: Operations & Logistics, 6(4), 346–355. [Google Scholar]

  18. Bai, Q. G., Chen, M. Y., Xu, L. (2017). Revenue and promotional cost-sharing contract versus two-part tariff contract in coordinating sustainable supply chain systems with deteriorating items. International Journal of Production Economics, 187, 85–101. DOI 10.1016/j.ijpe.2017.02.012. [Google Scholar] [CrossRef]

  19. Wang, M., Zhao, L. D., Herty, M. (2018). Modelling carbon trading and refrigerated logistics services within a fresh food supply chain under carbon cap-and-trade regulation. International Journal of Production Research, 56(12), 4207–4225. DOI 10.1080/00207543.2018.1430904. [Google Scholar] [CrossRef]

  20. Wang, M., Zhao, L. D., Herty, M. (2019). Joint replenishment and carbon trading in fresh food supply chains. European Journal of Operational Research, 277(2), 561–573. DOI 10.1016/j.ejor.2019.03.004. [Google Scholar] [CrossRef]

  21. Ma, X. L., Wang, J., Bai, Q. G., Wang, S. Y. (2020). Optimization of a three-echelon cold chain considering freshness-keeping efforts under cap-and-trade regulation in Industry 4.0. International Journal of Production Economics, 220, 107457. DOI 10.1016/j.ijpe.2019.07.030. [Google Scholar] [CrossRef]

  22. Chen, X., Wang, X. J. (2016). Effects of carbon emission reduction policies on transportation mode selections with stochastic demand. Transportation Research Part E: Logistics and Transportation Review, 90, 196–205. DOI 10.1016/j.tre.2015.11.008. [Google Scholar] [CrossRef]

  23. Qu, S., Zhou, Y., Zhang, Y., Wahab, M. I. M., Zhang, G. et al. (2019). Optimal strategy for a green supply chain considering shipping policy and default risk. Computers & Industrial Engineering, 131, 172–186. DOI 10.1016/j.cie.2019.03.042. [Google Scholar] [CrossRef]

  24. Qu, S., Jiang, G., Ji, Y., Zhang, G., Mohamed, N. (2021). Newsvendor’s optimal decisions under stochastic demand and cap-and-trade regulation. Environment, Development and Sustainability, 23, 17764–17787. DOI 10.1007/s10668-021-01411-2. [Google Scholar] [CrossRef]

  25. Qi, Q., Zhang, R. Q., Bai, Q. G. (2021). Joint decisions on emission reduction and order quantity by a risk-averse firm under cap-and-trade regulation. Computers & Industrial Engineering, 162, 107783. DOI 10.1016/j.cie.2021.107783. [Google Scholar] [CrossRef]

  26. Scarf, H. E. (1958). A min-max solution of an inventory problem. In: Arrow, K. J., Karlin, S., Scarf, H. E. (eds.Studies in the mathematical theory of inventory and production, pp. 201–209. California, USA: Stanford University Press. [Google Scholar]

  27. Gallego, G., Moon, I. (1993). The distribution free newsboy problem: Review and extensions. Journal of the Operational Research Society, 44(8), 825–834. DOI 10.1057/jors.1993.141. [Google Scholar] [CrossRef]

  28. Han, Q., Du, D., Zuluaga, L. F. (2014). A risk and ambiguity-averse extension of the max-min newsvendor order formula. Operations Research, 62(3), 535–542. DOI 10.1287/opre.2014.1262. [Google Scholar] [CrossRef]

  29. Zhang, H. J., Ji, Y., Qu, S. J., Li, H. H., Huang, R. P. (2022). The robust minimum cost consensus model with risk aversion. Information Sciences, 587, 283–299. DOI 10.1016/j.ins.2021.12.023. [Google Scholar] [CrossRef]

  30. Liu, B., Holmbom, M., Segerstedt, A., Chen, W. (2015). Effects of carbon emission regulations on remanufacturing decisions with limited information of demand distribution. International Journal of Production Research, 53(2), 532–548. DOI 10.1080/00207543.2014.957875. [Google Scholar] [CrossRef]

  31. Bai, Q. G., Chen, M. Y. (2016). The distributionally robust newsvendor problem with dual sourcing under carbon tax and cap-and-trade regulations. Computers & Industrial Engineering, 98, 260–274. DOI 10.1016/j.cie.2016.05.042. [Google Scholar] [CrossRef]

  32. Xu, J. T., Bai, Q. G., Xu, L., Hu, T. T. (2018). Effects of emission reduction and partial demand information on operational decisions of a newsvendor problem. Journal of Cleaner Production, 188, 825–839. DOI 10.1016/j.jclepro.2018.04.027. [Google Scholar] [CrossRef]

  33. Bai, Q. G., Xu, J. T., Zhang, Y. (2022). The distributionally robust optimization model for a remanufacturing system under cap-and-trade policy: A newsvendor approach. Annals of Operations Research, 309, 731–760. DOI 10.1007/s10479-020-03642-4. [Google Scholar] [CrossRef]

  34. Bai, Q. G., Xu, J. T., Gong, Y. M., Chauhan, S. S. (2022). Robust decisions for regulated sustainable manufacturing with partial demand information: Mandatory emission capacity versus emission tax. European Journal of Operational Research, 298(3), 874–893. DOI 10.1016/j.ejor.2021.06.011. [Google Scholar] [CrossRef]

  35. Huang, M. H., Rust, R. T. (2011). Sustainability and consumption. Journal of the Academy of Marketing Science, 39(1), 40–54. DOI 10.1007/s11747-010-0193-6. [Google Scholar] [CrossRef]

  36. Toptal, A., Özlü, H., Knour, D. (2014). Joint decisions on inventory replenishment and emission reduction investment under different emission regulations. International Journal of Production Research, 52(1), 243–269. DOI 10.1080/00207543.2013.836615. [Google Scholar] [CrossRef]

  37. Petruzzi, N. C., Dada, M. (1999). Pricing and the newsvendor problem: A review with extensions. Operations Research, 47(2), 183–194. DOI 10.1287/opre.47.2.183. [Google Scholar] [CrossRef]

Appendix A.

Proof of Theorem 3.1.

Let Π11G(z,R)=minG∗∈ΨΠ11(z,R). Taking the second partial derivative of Π11G(z,R) with respect to z and R, we have ∂2Π11G(z,R)∂R2=−2bc3<0, ∂2Π11G(z,R)∂z2=−(p+s)τA0σ22[σ2+(z−μ)2]32<0, and ∂2Π11G(z,R)∂z∂R=0. As a result, it can be seen that Hessian matrix is a negative definite matrix and Π11G(z,R) is strictly concave with respect to z and R.

Using Eqs. (3), (6) and (10), the Lagrange function of the model M11 is constructed as

L1(z,R,λ,u1,u2)=A0{τ(p+s)[(z+μ)−σ2+(z−μ)2]2−sμτ−(c1+c2+c3e)z}+c3K−R(1−ac3+bc3R)+λ(ezA0−aR+bR2−K)+u1z+u2R.(19)

KKT conditions are as follows:

A0{(p+s)τ2[1−z−μσ2+(z−μ)2]−(c1+c2+c3e)}+λeA0+u1=0(20)

−1+ac3−2bc3R−aλ+2bλR+u2=0(21)

λ(ezA0−aR+bR2−K)=0(22)

u1z=0(23)

u2R=0(24)

ezA0−aR+bR2≥K(25)

z≥0,R≥0,λ≥0,u1≥0,u2≥0(26)

In actual operation, the retailer pursues profit maximization, and the stock factor satisfies the condition z>0. According to Eq. (23), it is easy to get u1=0. Therefore, we solve the model M11 by analyzing the following cases.

Case 1. λ=0,u1=0,u2>0. According to Eq. (24), it is easy to get R=0. Further putting λ=0 and R=0 into Eq. (21) obtains u2=1−ac3>0, i.e., 0<c3<1a. Using λ=0 and u1=0 to simplify Eq. (20), we can get z=zα. Combined with R=0, Eq. (25) can be simplified to K≤ezαA0. Thus, when 0<K≤ezαA0 and 0<c3<1a, the optimal joint strategy of model M11 is (z11∗,R11∗)=(zα,0).

Case 2. λ>0,u1=0,u2>0. In this case, R=0 still holds. Further using λ>0 and Eq. (22), we can get z=KeA0. Using R=0 to simplify Eq. (21), we obtain u2=1+aλ−ac3. Because of u2>0, we have λ>c3−1a. Using u1=0 to simplify Eq. (20), we can get the following formula:

λ=c1+c2+c3ee−(p+s)τ2e[1−z−uσ2+(z−u)2].(27)

Since dλdz=(p+s)τσ2[σ2+(z−u)2]−322e>0, λ is an increasing function of z.

If c3<1a is true, then λ satisfies the condition λ>0. Combined with Eq. (27), we can get z>zα, i.e., KeA0>zα. On the other hand, if c3≥1a is true, then λ satisfies the condition λ>c3−1a≥0. Combined with Eq. (27), we have z>zβ, i.e., KeA0>zβ. Thus, when K>eA0zα and 0<c3<1a, or K>eA0zβ and c3≥1a, the optimal joint strategy of model M11 is (z11∗,R11∗)=(KeA0,0).

Case 3. λ>0,u1=0,u2=0. Substituting u2=0 into Eq. (21) deduces the analytical formula of λ.

λ=c3−1a−2bR(28)

Substituting Eqs. (28) into (20), the optimal stock factor of model M11 can be expressed as z11∗=z11. Combined with 0≤R≤a2b, we have a−2bR>0 and 0<λ≤c3−1a, i.e., c3≥1a. Using Eq. (27), we know that λ is an increasing function of z. Thus, when 0<λ≤c3−1a, zα<z11≤zβ holds. Otherwise, when λ>0, using z11 to simplify Eq. (22), we obtain ez11A0−aR+bR2=K. When K<ezαA0−a24b, there does not exist any feasible solution of sustainable technology investment. When K>ezαA0−a24b, combined with 0≤R<a2b, the optimal sustainable technology investment of model M11 is R11∗=R11=a−a2−4b(ez11A0−K)2b. In this case, K≤ezβA0 holds. If not, the above equation yields e(z11−zβ)A0>aR11−bR112≥0. Thereby, z11>zβ holds, which contradicts zα<z11≤zβ. Thus, when ezαA0−a24b<K≤ezβA0 and c3≥1a, the optimal joint strategy of model M11 is (z11∗,R11∗)=(z11,R11).

Case 4. λ=0,u1=0,u2=0. Substituting λ=0 and u1=0 into Eq. (20) obtains z=zα. Substitute λ=0 and u2=0 into Eq. (21), we have R=ac3−12bc3<a2b. According to the non-negativity of sustainable technology investment, c3≥1a holds. Using R=ac3−12bc3 and z=zα to simplify Eq. (25), we get K≤ezαA0−a24b+14bc32. Thus, when 0<K≤ezαA0−a24b+14bc32 and c3≥1a, the optimal joint strategy of model M11 is (z11∗,R11∗)=(zα,ac3−12bc3).

Case 5. Combining with Case 3 and Case 4 in the overlapping interval ezαA0−a24b<K≤ezαA0−a24b+14bc32, we choose the solution that maximizes the objective function as the optimal solution.

Proof of Theorem 3.2.

Let Π12G(z,R)=minG∗∈ΨΠ12(z,R). Taking the second order partial derivative on Π12G(z,R) with respect to z and R, we have ∂2Π12G(z,R)∂z2=−(p+s)τA0σ22[σ2+(z−μ)2]32<0, ∂2Π12G(z,R)∂R2=0, and ∂2Π12G(z,R)∂z∂R=0. As a result, it can be seen that Π12G(z,R) is a concave function of z and R.

Using Eqs. (3), (8) and (14), the Lagrange function of the model M12 is constructed as

L2(z,R,λ,u1,u2)=A0{τ(p+s)[(z+μ)−σ2+(z−μ)2]2−sμτ−(c1+c2)z}−R+λ(K−ezA0+aR−bR2)+u1z+u2R(29)

KKT conditions are as follows:

A0{(p+s)τ2[1−z−μσ2+(z−μ)2]−(c1+c2)}−λeA0+u1=0(30)

−1+aλ−2bλR+u2=0(31)

λ(K−ezA0+aR−bR2)=0(32)

u1z=0(33)

u2R=0(34)

ezA0−aR+bR2≤K(35)

z≥0,R≥0,λ≥0,u1≥0,u2≥0.(36)

Similar to the proof of Theorem 3.1, we assume the stock factor satisfies z>0. According to Eq. (33), it is easy to get u1=0. Therefore, we solve the model M12 by analyzing the following four cases.

Case 1. λ=0,u1=0,u2>0. According to Eqs. (34) and (31), it is easy to get R=0 and u2=1. Further putting λ=0 and u1=0 into Eq. (30), we can obtain z=z0. Combined with Eq. (35), when K≥ez0A0, the optimal joint strategy of model M12 can be expressed as (z12∗,R12∗)=(z0,0).

Case 2. λ>0,u1=0,u2>0. According to Eq. (34), it is easy to get R=0. Simplify Eq. (31), we can obtain u2=1−aλ and λ<1a. Further using λ>0 and Eq. (32), we have z=KeA0. Substitute u1=0 into Eq. (30), we obtain

λ=(p+s)τ2e[1−z−uσ2+(z−u)2]−(c1+c2)e.(37)

Taking the first derivative on λ with respect to z, we get dλdz=−(p+s)τσ2[σ2+(z−u)2]−322e<0, and λ is a decreasing function of z. Combined with 0<λ<1a, the value range of z is zβ<z<z0. Thus, when ezβA0<K<ez0A0, the optimal joint strategy of model M12 is (z12∗,R12∗)=(KeA0,0).

Case 3. λ>0,u1=0,u2=0. Using u2=0 and Eq. (31), we can get λ=1a−2bR. Combined with 0≤R<a2b, it is easy to know λ≥1a. Substitute it into Eq. (30), we have z12∗=z11. According to Eq. (37), we know that λ is a decreasing function of z. Because of λ≥1a, the formula of z≤zβ holds.

From Eq. (32), we can deduce K−ezA0+aR−bR2=0. It is easy to verify when K<ezβA0−a24b, there doesn’t exist any feasible solution to optimize the objective function. When K>ezβA0−a24b, according to 0≤R<a2b, the optimal sustainable technology investment of model M12 is R12∗=R11. In this case, K≤ezβA0 holds. If not, the above equation yields ezA0−aR+bR2>ezβA0, i.e., eA0(z−zβ)>aR−bR2≥0. It is in contradiction with z≤zβ. Thus, when ezβA0−a24b<K≤ezβA0, the optimal joint strategy of model M12 is (z12∗,R12∗)=(z11,R11).

Case 4. λ=0,u1=0,u2=0. Substituting λ=0 and u2=0 into Eq. (31) shows that there doesn’t exist any feasible solution to optimize the objective function.

Proof of Theorem 3.5.

(i) Using Eqs. (5) and (18), we have Π11(q,R)=Π21(q)−R+c3(aR−bR2) or Π11(z,R)=Π21(z)−R+c3(aR−bR2). Since the optimal solution (z21∗,0) of model M21 is the feasible solution of model M11, we obtain Π11G(z11∗,R11∗)≥Π11G(z21∗,0)=Π21G(z21∗). Similarly, Π12(q,R)=Π22(q)−R or Π12(z,R)=Π22(z)−R can be deduced from Eqs. (7) and (18). Since the optimal solution (z22∗,0) of model M22 is the feasible solution of model M12, we have Π12G(z12∗,R12∗)≥Π12G(z22∗,0)=Π22G(z22∗). Due to the fact that Π1G(z1∗,R1∗)=max{Π11G(z11∗,R11∗),Π12G(z12∗,R12∗)} and Π2G(z2∗)=max{Π21G(z21∗),Π22G(z22∗)}, the relationship between the expected profits of M1 and M2 is Π1G(z1∗,R1∗)≥Π2G(z2∗).

According to the aforementioned proof, we know that if K≥ez0A0, then (z12∗,R12∗)=(z0,0) and z22∗=z0. Substitute them into Eq. (3), we get Y(z12∗,R12∗)=Y(z22∗,0)≤K. If K<ez0A0, then (z12∗,R12∗)=(KeA0,0) or (z12∗,R12∗)=(z11,R11) and z22∗=KeA0. Thus, Y(z12∗,R12∗)=Y(z22∗,0)=K is obtained. The relationship between carbon emissions of M1 and M2 is Y(z12∗,R12∗)=Y(z22∗,0)≤K.