Automatic Extraction of the Sparse Prior Correspondences for Non-Rigid Point Cloud Registration

1  Introduction

Non-rigid point cloud registration [1], which is the surface registration of multiple non-rigid 3D point clouds optimally together into a common coordinate system, is important for 3D vision and graphics related areas, such as medical imaging, virtual reality and robotics. The widespread usage of low-cost 3D scanning devices, such as Microsoft Kinect, further promotes it. Non-rigid registration is more challenging than the registration of rigid surface clouds (rigid registration) because it faces a much bigger solution space brought by its local deformations, especially when the deformations between the clouds are large. This paper tries to overcome this difficulty with a novel prior correspondences based solution.

As an ill-posed problem, non-rigid point cloud registration often takes different prior assumptions to obtain a robust solution [2–5]. Among them is the sparse initial-correspondence assumption [6], which can impose strong constraints on the relationship between the clouds and thus greatly help the registration. However, existing methods to obtain the prior correspondences are often either manually specified [6,7], or based on some locally direct [6,8,9] and indirect (transformational) [10,11] distance measurements. Locally computing the initial correspondences is unstable for large deformation clouds, considering that there are many points visually similar but from geometrically different object parts (Fig. 1b).

Figure 1: Demonstration of the proposed registration process. The initial matches (b) for registering the source (red) to the target (blue) (a) are globally refined by region correspondences (c) and further locally refined by the local isometric and structural consistencies (d) for the final registration (e). Note: The matches inside each black rectangle are zoomed in on the right of their corresponding clouds for a clear view

Therefore, a natural idea is to consider more global cues to filter out those inconsistent correspondences whose matching points are from different object parts. Directly separating semantically effective object parts is difficult because of the ambiguity in specifying their boundaries. However, the structures of the object are generally kept across different deformations, especially for the articulated objects (Fig. 1a). The structure associates closely with the appearance of body parts, no matter what the deformations are. Therefore, the structure can be utilized as the global constraint to work around the ambiguity of parts. Consequently, the effective idea is to match points only from the same regions by just segmenting the clouds into different regions according to their global structures. This method can drastically reduce the error matches across different regions (Fig. 1c) and ensure the global consistency of prior computation.

Further, a more effective local-matching strategy is proposed so that globally consistent matches with strict local similarities can finally be taken as correct prior matches. Existing methods can be summarized as based on spatial (e.g., the Euclidean distance) or transformational (e.g., the descriptor similarity) proximity. However, these methods are good at slightly deformed regions and cannot cope with the largely deformed local ones. Therefore, a novel combined strategy with two local metrics (isometric consistency and structural consistency) are introduced to obtain the rich prior matches in different clouds (Fig. 1d). Especially, for the largely deformed clouds, we explicitly estimate the local structure similarity of the two putative correspondences with the Linear Embedding Technique (LLE) [12], so that two points with similar local neighborhood relationships are considered as the correct match.

The global and local combined strategy leads to sparse but strong prior correspondences for further registration. The robust Coherent Point Drift (CPD) [13] framework is taken with two additional constraints to better utilized the supervision of the priors: spatial proximity constraint and locally structural consistency constraint. Thanks to the robust prior matches distributed all over the point clouds, our method can obtain more stable results than previous methods [14,15] without such supervised constraints (Fig. 1e). Our work is also different from the previous prior correspondence based work, such as the Extended Coherent Point Drift (ECPD) [6], which cannot automatically build the priors and thus take the supervised constraints as we do.

In addition, in comparison with the recent developments in deep neural networks based ideas [16–19], our method belongs to the traditionally artificial feature based methods which is easier and more stable to apply without a big training set and tedious parametric tuning.

Consequently, our contributions are the following:

•   A novel global and local combined strategy to automatically estimate the robust prior matches for large deformed cloud pairs. Globally, a structure guided global matches are first obtained, so that correspondences not from the same regions are filtered out. Locally, a refinement strategy combining isometric consistency and structural consistency is proposed, so that effective prior correspondences with different degrees of deformation can be efficiently localized.

•   An improved CPD method with two additional supervised constraints from the estimated prior correspondences. The spatial proximity and local structural consistency constraints impose the spatial closeness and the local structure similarity of the priors, and their supervisions help make the registration successfully converge for large deformed clouds.

2  Related Work

Generally, there are two types of registration, rigid and non-rigid. The former assumes a globally consistent rigid transformation between two clouds with the latter allowing local deformations between them. The non-rigid registration is more challenging than the rigid registration because it deals with a much larger solution space brought by the extra deformations. The related work on non-rigid point cloud registration is our main focus here. For more work on other work, such as the rigid ones, please refer to [4,20]. Note that the geometrical deformation is perhaps the main cause of the difficulty of non-rigid registration when compared with the rigid registration. This deformation is also common in other areas, such as medical imaging [21], additive manufacturing [22] and even traffic safety [23].

In the following, we will first show the general development of non-rigid registration and then focus on the sparse prior correspondences related work. Note that there are also some studies on building dense shape correspondences [24,25]. However, they do not consider the non-rigid registration of the two point sets with suitable transformations as we do.

2.1 Non-Rigid Registration

Traditional methods can be roughly classified into three types [26]: Nearest-neighbor search, probabilistic and physics based methods. The nearest-neighbor search based methods define a distance error metric to optimize for either the deformation or displacement field. Probabilistic methods adopt different probabilistic principles to softly assign the correspondences according to some probability model. Physics based methods consider the registration as a nature and physical phenomenon.

Each type can be further classified with different standards, such as optimization technique [27], displacement regularizer [13], probabilistic model [28], acceleration technique [29], and type of physical law [30]. Most researches, as far as we know, are either nearest-neighbor search based [9,14,31] or probabilistic based [32,33]. The former ones are generally the variants of the rigid registration oriented Iterative Closest Point method (ICP) [34,35]. However, these ICP based studies are sensitive to outliers, like their rigid counterparts.

For the probabilistic based approaches, perhaps the most popular probabilistic method is the Coherent Point Drift method (CPD) [13] which employs an EM algorithm with a motion coherence based global regularization to optimize the GMM. It can fulfill superior accuracy and stability with outliers and thus receive a lot of attentions with various improvements [20], such as incorporating color information for registering colored point clouds [36], reformulating by a more general Bayesian setting for a more unified and stable solution [37] and hybrid modeling of position and orientation components of the point sets [38], etc. Dai et al. [39] combined both ICP and CPD for a more stable and accurate correspondences.

One of the interesting extension to CPD is the Extended CPD (ECPD) method [6] which embeds prior matches for robust registration by adopting the constraint of distance errors of these prior matches. Similar prior matches based methods [40] are also proposed. However, all these studies do not elaborate on how to obtain the robust initial correspondences: They simply recruit previous methods or heuristic ways to specify the correspondences directly.

Local smooth regularizers have also been widely adopted [2,14,15], where neighboring points are assumed to share similar transformations. For example, Zhang et al. [2] extended CPD with two features, the point-wise Euclidean distance and the local structure descriptor, to estimated the reliable correspondence and local regularizer for local structural consistency during the transformation estimation. We, however, propose to incorporate the local smooth constraint from the prior correspondences and thus fulfill a supervised local regularizer.

Recently, deep learning based methods also attract attentions [16–19,41]. For example, Shimada et al. [19] predicted the displacement fields on a voxel grid by the Displacements on Voxels Networks (DispVoxNets); Feng et al. [17] represented the non-rigid transformation with a combination of K rigid transformations and, accordingly, proposed a GRU-based framework. However, deep learning studies rely on large training datasets and may not obtain fine registration for different types of testing data.

2.2 Sparse Correspondences Computation

Existing methods for computing the prior correspondences can be roughly separate into three types: Manual specification, direct similarity and indirect similarity. Manual method relies on user specification [6] or an assistant input tool [7]. Apparently, the manual methods are inconvenient to apply in practice.

Existing methods often resort directly to some spatial distance metrics. Some studies [8,42] used geodesic distance by assuming the isometric property of deformed clouds. However, they assume (near) isometric deformation and thus still cannot cope with the relatively large deformation in the real scene. Recently, Dyke et al. [9] adopted an additional anisotropic geodesic measure [43] based on a new local anisotropy metric to further prune the landmarks for globally consistent correspondences.

Some studies estimate the similarity of points with some description [6], transformation of them [44] or a combined way [10]. However, these methods still focus on local properties of rigid objects and thus also are unstable for deformed clouds.

Recently, Li et al. [11] registered the point sets by an EM-like algorithm with a clustering projection between the cluster centers and all the points in the clusters. Similar method is proposed by Lachinov et al. [45] where CPD is extended with the known correspondences between the known clusters of different sets. However, the cluster correspondences can be difficult to obtain. In addition, these methods are still local without considering the global structure. Our method builds a cluster around each point of the global-consistent putative matches and uses the similarity of the local structures between the peers to filter out wrong correspondences.

2.3 Other Related Work

Global structure we consider has also been taken for registering articulated objects [46,47], where essentially a piecewise rigid transformation model is used. They cannot process the large and whole body deformations we considered. Similar methods are also proposed by Huang et al. [42]. We build the region level correspondences automatically according to the global structure without the burden of separating the rigid and non-rigid parts.

Recently, Kleiman et al. [48] computed the region correspondences using the estimated shape graphs which facilitate the global similarity computation between regions without the affection of its local geometrical details. We apply this idea to segment the clouds into different matching regions for the global filter of incorrect correspondences.

3  Overview of the Proposed Method

The proposed registration method (Fig. 2) consists of two main steps: Estimating the prior correspondences and registering the clouds. In the first step, the prior correspondences are robustly estimated through a global and local combined strategy. Globally, the region correspondences between two clouds are computed first via the graph structures of the clouds and then refined to be global matches. Locally, global matches are refined again by locally checking both the isometric and structural consistencies and thus the robust prior matches in different deformations are obtained. In the second step, the clouds are registered based the CPD framework, where supervised spatial proximity and structural consistency constraints from the priors are additionally imposed. The details about the two steps are presented as follows.

Figure 2: The pipeline of the proposed method. The modules whose names are in red are the main contributions

4  Automatic Establishment of Prior Correspondences

We first show how the initial putative matches are computed and then describe the global and local combined prior estimation idea.

4.1 Initialization of the Putative Matches

The initial matches are created based on a feature signature of each point. The Heat Kernel Signature (HKS) [49] is invariant under local deformations and can capture the intrinsic shape geometry in an efficient and multi-scale way. Simply put, HKS is based on the heat diffusion on Riemannian manifolds, which is defined with heat kernel, kτ(x,y), representing the amount of heat that is transferred from x to y in time τ, given a unit heat source at x.

kτ(x,y)=∑i=0∞e−λiτϕi(x)ϕi(y),(1)

where λi and ϕi are the i-th eigenvalue and eigenfunction of the Laplace-Beltrami operator ∇, respectively.

∇ϕi=λiϕi.(2)

When used as a feature descriptor, HKS restricts the heat kernel only to the temporal domain,

kτ(x,x)=∑i=0∞e−λiτϕi2(x).(3)

HKS is stable against noise and topology changes to some degree and also insensitive to the order of the eigenfunctions.

HKS can be adopted for multi-scale matching with the predefined time interval, which can be explained as that the heat distributes to the surface by that interval. Consequently, it can be extended as the feature descriptor of each point by sampling it into discrete function values according to different times. If that, the comparison between two points x and x′, d(x,x′), can then be described as the Euclidean distance between two HKS based feature descriptors,

d(x,x′)=∑i=1Γτ(kτi(x,x)−kτi(x′,x′))2,(4)

where τi+1−τi is set to a constant.

In our method, the multi-scale signature of each point in both source and target clouds is computed. Experimentally, we set the set the time interval to be 15, i.e., Γτ=15 in Eq. (4) and the minimal and maximal times are set to 0.03 and 0.25, respectively.

Fig. 3 demonstrates the initial matches estimated by HKS. They are dense but some of them are incorrect due to their matching points from different body regions. Therefore, it is necessary and possible to first remove those matches using region correspondences.

Figure 3: The initial matches estimated by HKS. The source and target clouds are shown in red and blue, respectively. Note: The matches inside the black rectangle of (b) are zoomed in on the right for a clear view

4.2 Global Estimation of the Prior Correspondences

As shown in Fig. 3b, mismatched points often have similar local distributions but actually can from different object parts. Generally, non-rigid objects have some unique global skeleton-like structure controlling the surface deformations: Same surface regions will always associate with the same structure parts, no matter what deformations the object may take. Therefore, the uniqueness of object structure can be used to guide the segmentation of the two differently deformed object surfaces and help obtain the same spatial distribution of surface regions. Consequently, the regional correspondences between the clouds can be built. Accordingly, putative matches with matching points from different parts can then be removed if they are not from the matched regions.

We compute the region correspondences by the structure-based method [48] so that co-segmentation of the cloud pairs is then applied to filter out wrong matches. It first jointly segments the cloud pairs and constructs the shape graphs of them with the HKS based shape descriptor. Then the corresponding regions are obtained by a two-step strategy that first computes the symmetric correspondences between regions and then breaks the symmetries. The k-means clustering and the Mapper graphs [50] are adopted for obtaining the segmentation and creating the shape graph, while the subspace-based spectral matching [51] and heuristic method are used to compute the symmetric correspondence and further one-to-one region correspondences, respectively.

As shown in Fig. 4a, the regions capture different local areas consistently across two clouds, thanks to the similarities of the shape graphs (structures), with some object parts possibly having multiple regions (such as the regions of the arm). These corresponding regions can be used to globally filter the initial matches whose points are from different parts.

Figure 4: Demonstration of estimating the global matches (b) from the initial matches for the two clouds in Fig. 3a by the estimated region correspondences (a). Note: The matches inside the black rectangle of (b) are zoomed in on the right for a clear view

Fig. 5 shows the idea of using the region correspondence to obtain the global matches. For the initial matches (s1,t1), (s1,t2) and (s1,t3), only s1 and t2 are from the corresponding regions and thus only (s1,t2) is kept as a global match with the other two dropped. The same idea applies to the matches of s2 whose correct global match being (s2,t3). This structure-guided global matching is important for large deformed clouds of an articulated object (Fig. 4b). Global matches are then taken for further local evaluation as discussed below.

Figure 5: Principle of refining initial matches for global ones. Note: 1) Corresponding regions shown in the same way as Fig. 4a; 2) lines representing the initial matches, with blue lines being the selected global ones

4.3 Local Refinement to Obtain the Robust Sparse Prior Correspondences

Matches may be from the small or large deformed areas, which calls for different metrics to refine them from different deformed parts, so that a rich and evenly distributed matches can be obtained. For the small deformed areas, isometric consistency can be utilized to find matches, while for the large deformed areas, the structural consistency is more relaxed and can be adopted. Consequently, we take a combined local strategy where both the isometric and the structural consistencies are adopted.

4.3.1 Isometric Consistency Constraint

Correspondences in the small-deformed areas generally share the same geodesic distances and thus isometric consistency can be used locally to filter out those significant from others. Here, the spectral pruning [51,8] is taken to estimate the isometric similarities between correspondences. The original pruning method builds a matrix L for all putative correspondences and takes its largest eigenvector as a confidence value on consistency of each correspondence belonging to a single consistent cluster. This can be extended as the similarity metric between correspondences for eliminating the incorrect matches.

Assume two correspondences a=(si,tu) and b=(sj,tv). The isometric consistency of a and b, lab, measures the isometric agreement between the end-points of the two corresponding pairs by the ratio of their geodesic distances dg(si,sj) and dg(tu,tv) as

lab=min(dg(si,sj)dg(tu,tv),dg(tu,tv)dg(si,sj)),(5)

lab≥c0,(6)

where c0(0<c0<1) is the lower bound for isometric consistency so that those correspondences with smaller values are unrelated.

In addition, both points of the related correspondences must also fall into the local geodesic discs around them. Assume the geodesic of si as Gsiδ with δ controlling the size of the disc. We obtain

sj∈Gsiδ and tv∈Gtuδ,(7)

Consequently, the consistency for a and b, L(a, b), can be computed as

L(a,b)={ lab−c01−c0,if a≠b, and both Eqs. (6) and (7) are satisfied;0,otherwise.(8)

which is also a confidence score of each correspondence a. Those with higher scores can then be chosen as the correct matches for further refinement (Fig. 7a). The score is computed by the Markov principle according to the diffusion method [52].

Isometric is good for small deformed areas but may fail for large deformed areas. Therefore, a more relaxed filter is required so that matches with large deformations can be selected as priors. Here, we take the idea of LLE as the structural consistency measure, which is good at deformation measurement to compute the similarities between two points by their neighbors.

4.3.2 Structural Consistency Constraint

This consistency requires to first build a local area for computing the local structure relationship, which is fulfilled by first down sampling the source cloud and then taking each point as the center of each local area. Consequently, structural consistency for all matches starting from this central point is evaluated for finding the correct matches.

For a correspondence a=(si,tu), the closest Γc points surrounding each end within the radius r, {siq}q=1Γc and {tuq}q=1Γc is computed first, where

‖si−siq‖<r and ‖tu−tuq‖<r.(9)

Then si can be formulated as the weighted sum of its Γc closest neighbors as

si=∑q=1Γcwqsiq.(10)

where

w=(w1,w2,…,wΓc)Ts.t.∑q=1Γcwq=1(11)

is the affine coefficient vector consisting of the weights from each of the Γc neighbors. Similarly, tu can also be formulated as the affine vector weighted sum of its Γc closest neighbors, with the weight vector defined as

w′=(w1′,w2′,…,wΓc′)Ts.t.∑q=1Γcwq′=1.(12)

There is a problem with above Γc-closest neighboring points, i.e., they may not represent the really closest Γc points considering the spatial distribution of points without topological information. Therefore, we propose to use the centers of the top-Γc closest surrounding areas as the closest points. Fig. 6 shows how to obtain the Γc (Γc=2 in this example) surrounding areas for the center point sb. First, the 10 closest points of sb is located as the initial cluster. Then, the 10 closest points for each point in the initial cluster is located as the spreading cluster. The overlapped points between the initial cluster and each spreading cluster are counted to show the closeness of (the center of ) each spreading cluster to (the center, sb, of ) the initial cluster. Finally, those centers from the spreading clusters sharing the maximal points with the initial cluster are chosen as the closest neighboring points (sr and sg) to the center (sb).

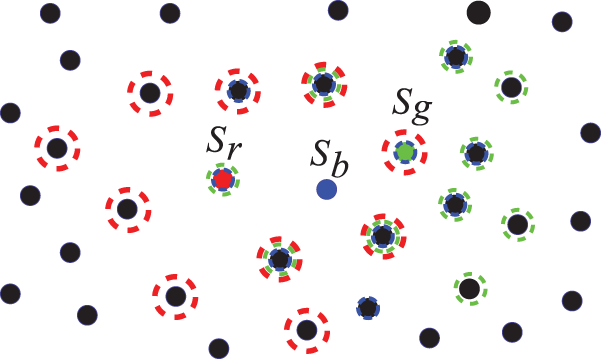
Figure 6: Computation of the two nearest neighbors (sr and sg) for sb. The dashed circle shows the closest points to the central point of the same color, while the point with multiple circles is one of the 10-closest points to the centers of those colors

Another problem is the formation of the weight vector. w (Eq. (11)) and w′ (Eq. (12)) depict the local geometrical properties surrounding the two matching points and, therefore, can represent them. However, w and w′ of a true match may be quite different with different element orders caused by the deformation, even though they may depicts the same set of closest points on the object. Therefore, directly comparing their distances may not reflect the true similarity of them and lead to wrong decision. However, the matched points should be close to each other. Therefore, a heuristic method is adopted so that the close matches are taken as valid.

In this method, one of the two vectors fixes while the other varies. The Euclidean distance of the fixed vector to each permuted vector is computed and the smallest distance is finally obtained among all permutations. Fig. 7b gives the matches obtained from Fig. 4b after applying the structural consistency constaint.

4.3.3 Merging the Matches

After obtaining the matches according to both the isometric and structural consistencies, we can merge them to obtain the final prior matches. However, the structural consistency is more loose due to relaxed structure similarity for large deformation and thus may obtain more matches than the isometric consistency, as shown in Figs. 7a and 7b. Consequently, it may include the wrong matches. Therefore, when mixing the refined matches from both steps, the matches from the isometric consistency retain higher priorities than those from the structural consistency, i.e., only the matches obtained by the isometric consistency are kept with the same source, which are further refined by both the isometric and the structural consistencies (Fig. 7c).

Figure 7: Demonstration of the local refinement process for prior matches from the global matches shown in Fig. 4b. The final prior matches (c) are obtained by combing the matches refined by the isometric consistency (a) and the structural consistency (b). Note: The matches inside each black rectangle are zoomed in on the right of their corresponding clouds for a clear view

5  Registration with Supervised Local Smoothness Constraints from the Priors

The prior matches obtained with above idea can be used to supervise the CPD registration. Assume two D-dimensional point sets XN×D=(x1,…,xN)T and YM×D=(y1,…,yM)T. CPD models their alignment as a probability density estimation problem where one point set represents the GMM centroids YM×D with the other one being the data points XN×D. The alignment can be obtained by maximizing the GMM posterior probability for a given data point through forcing the GMM centroids to move coherently as a group to preserve the topological structure of the point sets.

5.1 The Energy Model

The energy model of our supervision based method consists of not only the traditionally whole cloud similarity term (data term) and motion coherent term from CPD but also the additional constraint brought by the prior correspondences.

E(θ,σ2)=λDED(θ,σ2)+λθEθ(θ,σ2)+λpEp(θ,σ2),(13)

where: 1) θ and σ2 are two parameters to be estimated: the set of motion parameters and the equal isotropic covariances of all GMM components; and 2) λD, λθ and λp are the coefficients for the three energy terms respectively, namely data term, motion coherent term and prior constraint term.

We now discuss the three energy terms. The data term and motion coherent term are brought from ECPD, and thus are reviewed first briefly.

5.2 Data Term and Motion Coherent Term

The overall process of the registration process in CPD can be formulated by the following energy function:

ED(θ,σ2)=−∑n=1Nlog∑m=1M+1P(m)p(xn|m).(14)

where: 1) P(m) is the prior probability of the Gaussian component centering at m; 2) p(x|m) is the posterior density of a point x given. Formally,

p(x)=w1N+(1−w)∑m=1MP(m)p(x|m),(15)

where 0≤w≤1 and

p(x|m)=1(2πσ2)D/2exp(−‖x−R(yk,θ)‖22σ2).(16)

Here R(yk,θ) is a transformation applied to Y and defined as

R(Y,v)=Y+v(Y)(17)

The motion coherent term can be reformulated as

Eθ(θ,σ2)=‖ℒv‖2,(18)

where ℒ is the high-pass filter to obtain the high frequency content for the regularization. The function v to minimize must satisfy the Euler-Lagrange differential equation for all vectors z and be deduced as

v(z)=∑m=1MwmG(z,ym),(19)

where: wm=1σ2λ∑n=1NPold(m|xn)(xn−(ym+v(ym))) and G(s)=exp(−‖sβ‖2) which is kernel function that approaches zero as ‖s‖→∞.

Consequently, Eq. (17) can also be reformulated as

R(Y,W)=Y+GW(20)

5.3 The Prior Constraint

Two aspects are considered for the supervision of the prior correspondences: spatial proximity and neighboring structural consistency. The former can be formulated as the minimization of the point-to-point distances of the correspondences, while the latter can be represented by the similarities of transformations among the neighbors.

Spatial proximity The spatial proximity constraint is formulated as minimizing the point-to-point distances in the set of the matching correspondences, Nc,

Es(θ,σ2)=∑(j,k)∈Nc‖Xj−(Yk+G(k,⋅)W)‖2,(21)

where G(j,⋅) is the j−th row of G.

Structural consistency This constraint is similar to the idea of structural consistency for prior estimation, i.e., points in the local area should keep the similar structures. Here, the constraint is formulated by the weighted displacement differences between one correspondence and its nearest neighbors. Assume the Γc neighbors of xi of each prior correspondences in Nc, NiΓc. If taking the correspondences from the source cloud as the constraint target, we obtain

Ec(θ,σ2)=∑(i,j)∈Nc‖(G(i,⋅)W−∑q∈NiΓcαi,qG(q,⋅)W‖2(22)

where αi,q is weight uniformly defined as 1Γc.

The nearest neighbors in Eq. (22) only depends on one end of the match and we take the same method as applying the structural consistency to select the robust neighbors.

Putting the space proximity and structural consistency constraints together, we can obtain the following local prior constraint.

Ep(θ,σ2)=μsEs(θ,σ2)+μcEc(θ,σ2),(23)

where both μs and μc are the coefficients.

5.4 Optimization

The optimization follows the basic idea of CPD where EM is adopted for solve the complex energy minimization problem. EM first guesses the values of parameters and uses the Bayes’ theorem to compute a posterior probability distribution Pold(m|xn) of the mixture components (E-step). Then it finds the new parameter values by minimizing the expectation of complete negative log-likelihood function,

QD=−∑n=1N∑m=1M+1Pold(m|xn)log(Pnew(m)Pnew(xn|m)).(24)

with respect to the new parameters (M-step). EM alternates between E- and M-steps until convergence.

The object function in Eq. (24) can be rewritten from the proposed energy model as follows:

Q(W~,σ2)=λDQD(W,σ2)+λθQθ(W,σ2)+λpEp(θ,σ2).(25)

QD(W,σ2) in Eq. (25) corresponds to the data term ED in Eq. (13),

QD(W,σ2)=1σ2∑n=1m∑m=1MPold(m|xn)‖xn−(ym−G(m,⋅)W)‖2+NPDlog⁡σ2.(26)

Qθ(W,σ2) in Eq. (25) corresponds to the motion coherent term Eθ in Eq. (13),

Qθ(W,σ2)=tr(WTGW).(27)

Then, W and σ can be estimated in each iteration by minimizing Q~ and thus computing the partial derivatives of Q~ to them, respectively. For W,

∂Q~D∂W=2G1σ2[d(P1)(Y+GW)−PX]≐2(A+B1W);(28)

∂Q~θ∂W=2GW≐2B2W;(29)

∂Es∂W=∑(j,k)∈Nc2GT(k,⋅)(Xj−Yk)+2∑(j,k)∈NcGT(k,⋅)G(k,⋅)W≐2C+2B3W.(30)

∂Ec∂W=2∑(j,k)∈Ncl∈NjK((GT(j,⋅)−GT(l,⋅))G(j,⋅)(GT(j,⋅)−GT(l,⋅))G(l,⋅))W≐2B4W.(31)

Combining Eqs. (28)–(31) and setting ∂Q~∂W=0, we can obtain

(λDB1+λθB2+λpμsB3+λpμcB4)W=−λpμsC−λDA(32)

The motion field can be obtained according to Eq. (20) after solving ∂Q~∂W=0.

For σ2, similarly we can obtain the solution with Eq. (25) as

σ2=1NPD(tr(XTd(PT1)X))−2tr((PX)T(Y+GW))+tr((Y+GW)Td(P1)(Y+GW))(33)

6  Experimental Results

In this section, both qualitative and quantitative experiments are presented based on the datasets: SCAPE [53], MPI FAUST [54], where both can provide large deformation clouds with dense correspondences. To accelerate the computation, we downsample each testing cloud to have around 3500 points. λD, λθ, λp, μs and μc in Eq. (32) are set to 1, 100, 1, 0.0001 and 2,500,000, respectively.

Three methods are compared with ours in the experiment: CPD [13], GLTP [15] and DispVoxNets [19]. CPD and GLTP are optimization based methods where GLTP combines CPD with an additional local topology preservation constraint. DispVoxNets is a deep neural network based method which regresses the displacements of source cloud directly.

6.1 Qualitative Results

Fig. 8 gives the estimated prior matches and registration results of four pairs computed by our method. Our methods can successfully get robust prior matches and thus accurately register the clouds, even though there are large deformations between the clouds.

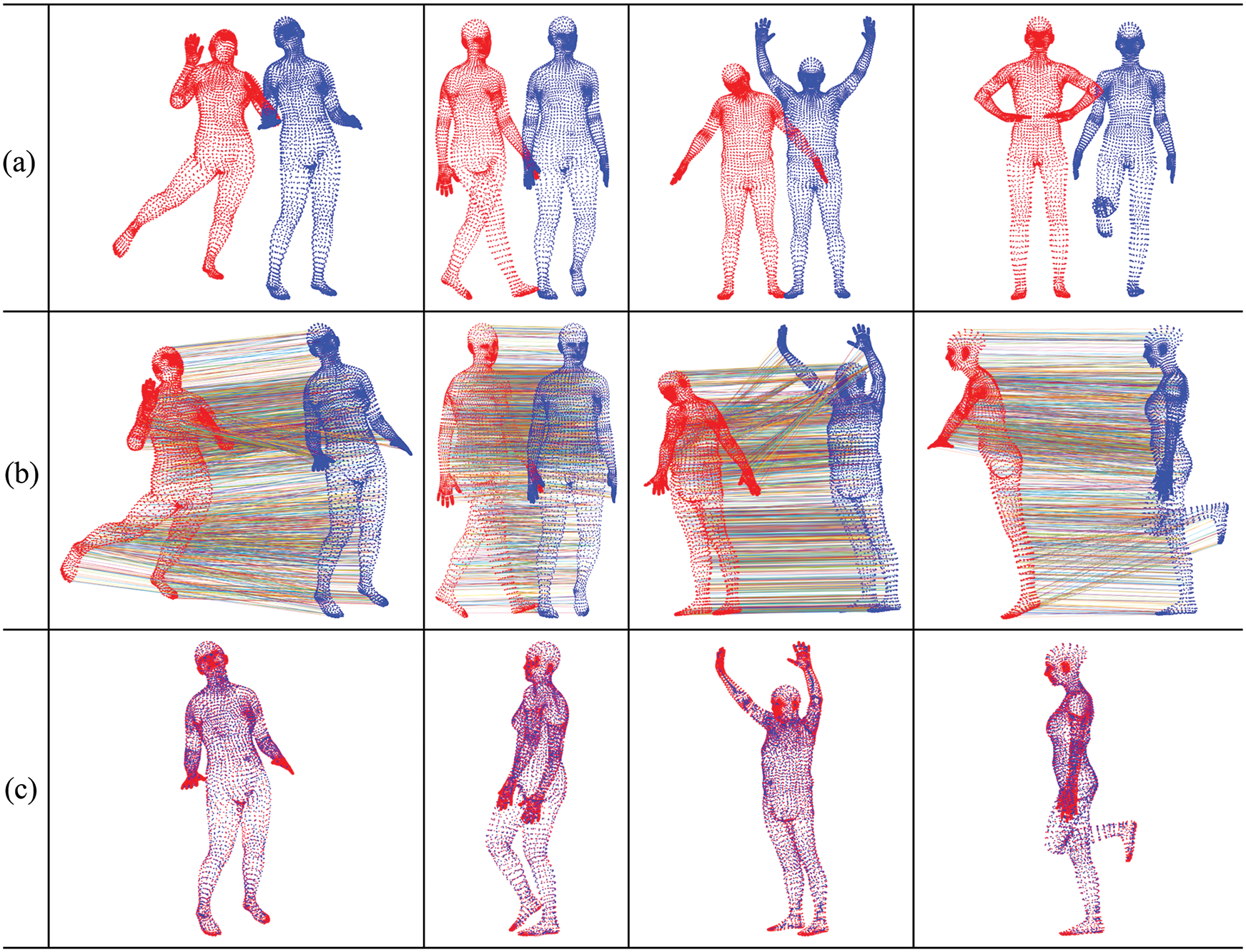
Figure 8: Four registration results by our method. The clouds are colored in the same way as Fig. 1. (a): The cloud pair to be registered; (b): estimated prior matches; and (c): the registration result

Fig. 9 shows the performance comparison among different methods. DispVoxNets and CPD have apparent errors, while GTLP always associates some points for all the eight cloud pairs. However, our method shows no mis-registraton artifacts. DispVoxNets relies on the training set and cannot effectively process large deformations, while CPD only considers the global registration. GLTP takes a global and local incorporated idea and thus obtains better results than DispVoxNets and CPD. Our method adopts the similar merits of global-local collaboration in GLTP, but further incorporates the robust prior matches for an effective supervision of the registration process. Thus, our method obtains the best performances among the four methods.

Figure 9: Qualitative comparisons among different methods. The clouds are colored in the same way as Fig. 1. (a): Cloud pair; (b) DispVoxNets; (c) CPD; (d) GLTP; and (e) our method

6.2 Quantitative Results

The quantitative experiments are applied to 20 cloud pairs with different deformations (Fig. 10). Indexed from 1 to 20, these clouds have different degrees of deformation with generally the higher index representing the smaller deformation in arms and legs.

Figure 10: The example cloud pairs used for quantitative experiments with their indexes shown below. The clouds are colored in the same way as Fig. 1 and the degree of deformation lows gradually from left to right

Fig. 11 shows the variation of matches according to different refinement stages. 27.33% matches are removed after estimating the global matches. Then at most 2.37% of global matches (#17 pair) are detected as valid after checking the isometric consistency and 5.87% (#8 pair) are valid after checking the structural consistency. Combining these valid matches by removing the duplicated ones while keeping the corresponding isometrically consistent ones, we can obtain maximally 1728 matches (for #3 pair) at last as prior correspondences for the 20 cloud pairs. Totally, only 4.27% and 5.87% matches are kept as prior matches in comparison with the initial and global ones respectively, with average 1,456.8 matches kept for each pair. This experiment shows effectiveness of our sparse prior matching idea in reducing the wrong matches.

Figure 11: Statistical comparisons of the varying matches after applying different refinement stages

The overall sparsity of the prior matches can also be seen from Table 1. Generally, less than 5% of the initial matches are finally utilized as priors which, however, greatly improve the registration efficiency as the following performance statistics show.

The registration performance are experimented based on two metrics. One is matching accuracy A~m which is computed by the ratio of correct matches (C~m) among all detected matches (D~m),

A~m=C~mD~m.(34)

The other, average registration error E~r, is computed by averaging the distances of the matching set Nm after registration,

E~r=1S~∑(i,j)∈Nm(yi−xj)2,(35)

where (xi,yj)∈Nm represents one of its total S~ matches in the clouds. DispVoxNets is not considered in this experiment because it cannot directly obtain the closest correspondence for each point.

Figs. 12a and 12b gave the statistical results of different methods. Here our method is transformed into two versions for evaluating the importance of prior matches. One is our full method. The other is our full method without taking the two constraints of the prior matches. It can be seen that the accuracy increases and the mean error decreases as the deformation increases for all method. However, our full method always obtains the highest accuracies and smallest average registration errors for all cloud pairs among all methods. If comparing our full method with CPD, the average accuracies and registration errors for all pairs are 17.34% and 22.42% for our method, while they are 9.13% and 25.34% respectively for CPD. On the other hand, our method without the prior constraint can be barely better than CPD in matching accuracy and almost the worst among all methods in mean error. This is in stark contrast with the performances of our full method, which shows the necessity of the prior constraints for better performances.

Figure 12: Statistical comparisons of different methods with 20 cloud pairs in different deformations. Note: DispVoxNets is not considered because it cannot output the closest correspondence for each point

7  Conclusions

This paper proposed a novel method to automatically extract the sparse prior matches from global and local points. Globally, the region correspondences are created first to filter out matches whose points are from different object regions and obtain the global matches. Locally, isometric and structural consistencies are both considered to obtain rich prior matches in different deformations from the global ones. Then, a new prior-match based non-registration method is proposed where the prior correspondences are adopted into spatial proximity and neighboring structural consistency constraints to supervise the optimization of CPD. Experimental results demonstrate the advantages of the method.

Region matching is important for the extraction of local matches. However, our adopted region matching method is general and thus may not fit well with specifically deformed objects, such as stretch deformed ones. This matching method may also fall when there are highly symmetrical and drastically deformed clouds, such as human bodies rigged face to face. In the future, we will study more robust region matching methods or try other types of region corresponding methods [55,56]. Our current method is also slow without accelerating the optimization. We will take GPU and faster optimization into consideration in the future work. In addition, our current work mainly focuses on the efficient registration of clean clouds. It does not consider the noise which may ruin the proposed method. How to cope with the noisy clouds is also one of our future directions.

Funding Statement: This work is supported by Natural Science Foundation of Anhui Province (2108085MF210, 1908085MF187), Key Natural Science Fund of Department of Eduction of Anhui Province (KJ2021A0042) and Natural Social Science Foundation of China (19BTY091).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Deng, B., Yao, Y., Dyke, R. M., Zhang, J. (2022). A survey of non-rigid 3D registration. arXiv preprint arXiv:2203.07858. DOI 10.1111/cgf.14502. [Google Scholar] [CrossRef]

    2. Zhang, S., Yang, K., Yang, Y., Luo, Y., Wei, Z. (2018). Non-rigid point set registration using dual-feature finite mixture model and global-local structural preservation. Pattern Recognition, 80, 183–195. DOI 10.1016/j.patcog.2018.03.004. [Google Scholar] [CrossRef]

    3. Tam, G. K. L., Cheng, Z. Q., Lai, Y. K., Langbein, F. C., Liu, Y. et al. (2013). Registration of 3D point clouds and meshes: A survey from rigid to nonrigid. IEEE Transactions on Visualization and Computer Graphics, 19(7), 1199–1217. DOI 10.1109/TVCG.2012.310. [Google Scholar] [CrossRef]

    4. Sahillioğlu, Y. (2020). Recent advances in shape correspondence. The Visual Computer, 36(8), 1705–1721. DOI 10.1007/s00371-019-01760-0. [Google Scholar] [CrossRef]

    5. Pai, G., Ren, J., Melzi, S., Wonka, P., Ovsjanikov, M. (2021). Fast sinkhorn filters: Using matrix scaling for non-rigid shape correspondence with functional maps. Proccedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 384–393. Virtual. [Google Scholar]

    6. Golyanik, V., Taetz, B., Reis, G., Stricker, D. (2016). Extended coherent point drift algorithm with correspondence priors and optimal subsampling. Proceedings of IEEE Winter Conference on Applications of Computer Vision, pp. 1–9. Lake Placid, NY, USA. [Google Scholar]

    7. Allen, B., Curless, B., Popović, Z. (2002). Articulated body deformation from range scan data. ACM Transactions on Graphics, 21(3), 612–619. DOI 10.1145/566654.566626. [Google Scholar] [CrossRef]

    8. Tam, G. K. L., Martin, R. R., Rosin, P. L., Lai, Y. K. (2014). Diffusion pruning for rapidly and robustly selecting global correspondences using local isometry. ACM Transactions on Graphics, 33(1), 1–17. DOI 10.1145/2517967. [Google Scholar] [CrossRef]

    9. Dyke, R. M., Lai, Y. K., Rosin, P. L., Tam, G. K. (2019). Non-rigid registration under anisotropic deformations. Computer Aided Geometric Design, 71, 142–156. DOI 10.1016/j.cagd.2019.04.014. [Google Scholar] [CrossRef]

  10. Theiler, P. W., Wegner, J. D., Schindler, K. (2014). Keypoint-based 4-points congruent sets–automated marker-less registration of laser scans. ISPRS Journal of Photogrammetry and Remote Sensing, 96, 149–163. DOI 10.1016/j.isprsjprs.2014.06.015. [Google Scholar] [CrossRef]

  11. Li, M., Xu, R. Y., Xin, J., Zhang, K., Jing, J. (2020). Fast non-rigid points registration with cluster correspondences projection. Signal Processing, 170, 107425. DOI 10.1016/j.sigpro.2019.107425. [Google Scholar] [CrossRef]

  12. Roweis, S. T. (2000). Nonlinear dimensionality reduction by locally linear embedding. Science, 290(5500), 2323–2326. DOI 10.1126/science.290.5500.2323. [Google Scholar] [CrossRef]

  13. Myronenko, A., Song, X. (2010). Point set registration: Coherent point drift. IEEE Transactions on Pattern Analysis and Machine Intelligence, 32(12), 2262–2275. DOI 10.1109/TPAMI.2010.46. [Google Scholar] [CrossRef]

  14. Li, K., Yang, J., Lai, Y. K., Guo, D. (2019). Robust non-rigid registration with reweighted position and transformation sparsity. IEEE Transactions on Visualization and Computer Graphics, 25(6), 2255–2269. DOI 10.1109/TVCG.2945. [Google Scholar] [CrossRef]

  15. Ge, S., Fan, G., Ding, M. (2014). Non-rigid point set registration with global-local topology preservation. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition Workshops, pp. 245–251. Columbus, OH, USA. [Google Scholar]

  16. Huang, J., Birdal, T., Gojcic, Z., Guibas, L. J., Hu, S. M. (2022). Multiway non-rigid point cloud registration via learned functional map synchronization. IEEE Transactions on Pattern Analysis and Machine Intelligence. DOI 10.1109/TPAMI.2022.3164653. [Google Scholar] [CrossRef]

  17. Feng, W., Zhang, J., Cai, H., Xu, H., Hou, J. et al. (2021). Recurrent multi-view alignment network for unsupervised surface registration. Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 10297–10307. Virtual. [Google Scholar]

  18. Wang, L., Chen, J., Li, X., Fang, Y. (2019). Non-rigid point set registration networks. http://arxiv.org/abs/1904.01428. [Google Scholar]

  19. Shimada, S., Golyanik, V., Tretschk, E., Stricker, D., Theobalt, C. (2019). Dispvoxnets: Non-rigid point set alignment with supervised learning proxies. Proceedings of International Conference on 3D Vision, pp. 27–36. Québec, Canada. [Google Scholar]

  20. Zhu, H., Guo, B., Zou, K., Li, Y., Yuen, K. V. et al. (2019). A review of point set registration: From pairwise registration to groupwise registration. Sensors, 19(5), 1191. DOI 10.3390/s19051191. [Google Scholar] [CrossRef]

  21. Xu, J., Tao, M., Zhang, S., Jiang, X., Tan, J. (2021). Non-rigid registration of biomedical image for radiotherapy based on adaptive feature density flow. Biomedical Signal Processing and Control, 68, 102691. DOI 10.1016/j.bspc.2021.102691. [Google Scholar] [CrossRef]

  22. Wang, C., Li, S., Zeng, D., Zhu, X. (2021). Quantification and compensation of thermal distortion in additive manufacturing: A computational statistics approach. Computer Methods in Applied Mechanics and Engineering, 375, 113611. DOI 10.1016/j.cma.2020.113611. [Google Scholar] [CrossRef]

  23. Xie, Y., Wu, C., Li, B., Hu, X., Li, S. (2022). A feed-forwarded neural network-based variational Bayesian learning approach for forensic analysis of traffic accident. Computer Methods in Applied Mechanics and Engineering, 397, 115148. DOI 10.1016/j.cma.2022.115148. [Google Scholar] [CrossRef]

  24. Litany, O., Remez, T., Rodola, E., Bronstein, A., Bronstein, M. (2017). Deep functional maps: Structured prediction for dense shape correspondence. Proceedings of IEEE International Conference on Computer Vision, pp. 5660–5668. Venice, Italy. [Google Scholar]

  25. Kirgo, M., Melzi, S., Patane, G., Rodola, E., Ovsjanikov, M. (2021). Wavelet-based heat kernel derivatives: Towards informative localized shape analysis. Computer Graphics Forum, 40(1), 165–179. DOI 10.1111/cgf.14180. [Google Scholar] [CrossRef]

  26. Ali, S. A., Golyanik, V., Stricker, D. (2018). NRGA: Gravitational approach for non-rigid point set registration. Proceedings of International Conference on 3D Vision, pp. 756–765. Verona, Italy. [Google Scholar]

  27. Ma, J., Zhao, J., Jiang, J., Zhou, H. (2017). Non-rigid point set registration with robust transformation estimation under manifold regularization. Proceedings of Thirty-First AAAI Conference on Artificial Intelligence, pp. 4218–4224. San Francisco, California, USA. [Google Scholar]

  28. Wang, G., Wang, Z., Chen, Y., Zhao, W. (2015). A robust non-rigid point set registration method based on asymmetric Gaussian representation. Computer Vision and Image Understanding, 141, 67–80. DOI 10.1016/j.cviu.2015.05.014. [Google Scholar] [CrossRef]

  29. Mourning, C., Nykl, S., Xu, H., Chelberg, D., Liu, J. (2010). GPU acceleration of robust point matching. Proceedings of International Symposium on Visual Computing, pp. 417–426. Las Vegas, NV, USA. [Google Scholar]

  30. Golyanik, V., Ali, S. A., Stricker, D. (2016). Gravitational approach for point set registration. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, pp. 5802–5810. Las Vegas, Nevada, USA. [Google Scholar]

  31. Amberg, B., Romdhani, S., Vetter, T. (2007). Optimal step nonrigid ICP algorithms for surface registration. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, pp. 1–8. Minneapolis, MN, USA. [Google Scholar]

  32. Gold, S., Rangarajan, A., Lu, C. P., Pappu, S., Mjolsness, E. (1998). New algorithms for 2D and 3D point matching: Pose estimation and correspondence. Pattern Recognition, 31(8), 1019–1031. DOI 10.1016/S0031-3203(98)80010-1. [Google Scholar] [CrossRef]

  33. Min, Z., Pan, J., Zhang, A., Meng, M. Q. H. (2019). Robust non-rigid point set registration algorithm considering anisotropic uncertainties based on coherent point drift. Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, pp. 7903–7910. Macau, China. [Google Scholar]

  34. Besl, P., McKay, N. D. (1992). A method for registration of 3-D shapes. IEEE Transactions on Pattern Analysis and Machine Intelligence, 14(2), 239–256. DOI 10.1109/34.121791. [Google Scholar] [CrossRef]

  35. Zhang, Z. (1994). Iterative point matching for registration of free-form curves and surfaces. International Journal of Computer Vision, 13(2), 119–152. DOI 10.1007/BF01427149. [Google Scholar] [CrossRef]

  36. Saval-Calvo, M., Azorin-Lopez, J., Fuster-Guillo, A., Villena-Martinez, V., Fisher, R. B. (2018). 3D non-rigid registration using color: Color coherent point drift. Computer Vision & Image Understanding, 169, 119–135. DOI 10.1016/j.cviu.2018.01.008. [Google Scholar] [CrossRef]

  37. Hirose, O. (2020). A Bayesian formulation of coherent point drift. IEEE Transactions on Pattern Analysis and Machine Intelligence, 43(7), 2269–2286. DOI 10.1109/TPAMI.2020.2971687. [Google Scholar] [CrossRef]

  38. Ravikumar, N., Gooya, A., Frangi, A. F., Taylor, Z. A. (2017). Generalised coherent point drift for group-wise registration of multi-dimensional point sets. Proceedings of International Conference on Medical Image Computing and Computer-Assisted Intervention, pp. 309–316. Québec City, QC, Canada. [Google Scholar]

  39. Dai, H., Pears, N., Smith, W. (2018). Non-rigid 3D shape registration using an adaptive template. Proceedings of European Conference on Computer Vision (ECCV) Workshops, Munich, Germany. [Google Scholar]

  40. Kolesov, I., Lee, J., Sharp, G., Vela, P., Tannenbaum, A. (2016). A stochastic approach to diffeomorphic point set registration with landmark constraints. IEEE Transactions on Pattern Analysis and Machine Intelligence, 38(2), 238–251. DOI 10.1109/TPAMI.2015.2448102. [Google Scholar] [CrossRef]

  41. Wang, L., Li, X., Chen, J., Fang, Y. (2019). Coherent point drift networks: Unsupervised learning of non-rigid point set registration. http://arxiv.org/abs/1906.03039. [Google Scholar]

  42. Huang, Q. X., Adams, B., Wicke, M., Guibas, L. J. (2008). Non-rigid registration under isometric deformations. Computer Graphics Forum, 27(5), 1449–1457. DOI 10.1111/j.1467-8659.2008.01285.x. [Google Scholar] [CrossRef]

  43. Liu, B., Chen, S., Xin, S. Q., He, Y., Liu, Z. et al. (2017). An optimization-driven approach for computing geodesic paths on triangle meshes. Computer-Aided Design, 90, 105–112. DOI 10.1016/j.cad.2017.05.022. [Google Scholar] [CrossRef]

  44. Mellado, N., Dellepiane, M., Scopigno, R. (2016). Relative scale estimation and 3D registration of multi-modal geometry using growing least squares. IEEE Transactions on Visualization and Computer Graphics, 22(9), 2160–2173. DOI 10.1109/TVCG.2015.2505287. [Google Scholar] [CrossRef]

  45. Lachinov, D., Turlapov, V. (2018). The coherent point drift for clustered point sets. arXiv preprint arXiv:1812.05869. [Google Scholar]

  46. Hirshberg, D. A., Loper, M., Rachlin, E., Black, M. J. (2012). Coregistration: Simultaneous alignment and modeling of articulated 3D shape. Proceedings of European Conference on Computer Vision, pp. 242–255. Florence, Italy. [Google Scholar]

  47. Ge, S., Fan, G. (2015). Non-rigid articulated point set registration with local structure preservation. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition Workshops, pp. 126–133. Boston, MA, USA. [Google Scholar]

  48. Kleiman, Y., Ovsjanikov, M. (2018). Robust structure-based shape correspondence. Computer Graphics Forum, 38(1), 7–20. DOI 10.1111/cgf.13389. [Google Scholar] [CrossRef]

  49. Sun, J., Ovsjanikov, M., Guibas, L. (2009). A concise and provably informative multi-scale signature based on heat diffusion. Computer Graphics Forum, 28(5), 1383–1392. DOI 10.1111/j.1467-8659.2009.01515.x. [Google Scholar] [CrossRef]

  50. Singh, G., Mémoli, F., Carlsson, G. E. (2007). Topological methods for the analysis of high dimensional data sets and 3D object recognition. http://diglib.eg.org/bitstream/handle/10.2312/SPBG.SPBG07.091-100/091-100.pdf?sequence=1&isAllowed=y. [Google Scholar]

  51. Leordeanu, M., Hebert, M. (2005). A spectral technique for correspondence problems using pairwise constraints. Proceedings of IEEE International Conference on Computer Vision, vol. 1, pp. 1482–1489. Beijing, China. [Google Scholar]

  52. Coifman, R. R., Lafon, S. (2006). Diffusion maps. Applied and Computational Harmonic Analysis, 21(1), 5–30. DOI 10.1016/j.acha.2006.04.006. [Google Scholar] [CrossRef]

  53. Anguelov, D., Srinivasan, P., Koller, D., Thrun, S., Rodgers, J. et al. (2005). SCAPE: Shape completion and animation of people. ACM Transactions on Graphics, 24(3), 408–416. DOI 10.1145/1073204.1073207. [Google Scholar] [CrossRef]

  54. Bogo, F., Romero, J., Loper, M., Black, M. J. (2014). FAUST: Dataset and evaluation for 3D mesh registration. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, pp. 3794–3801. Columbus, OH, USA. [Google Scholar]

  55. Denitto, M., Melzi, S., Bicego, M., Castellani, U., Farinelli, A. et al. (2017). Region-based correspondence between 3D shapes via spatially smooth biclustering. Proceedings of IEEE International Conference on Computer Vision, pp. 4260–4269. Venice, Italy. [Google Scholar]

  56. Ganapathi-Subramanian, V., Thibert, B., Ovsjanikov, M., Guibas, L. (2016). Stable region correspondences between non-isometric shapes. Computer Graphics Forum, 35(5), 121–133. DOI 10.1111/cgf.12969. [Google Scholar] [CrossRef]