An Edge Computing Algorithm Based on Multi-Level Star Sensor Cloud

1  Introduction

A star sensor obtains the star image through charge coupled device (CCD) cameras, obtains the orientation of the star point on the star image, and then locates the position of the spacecraft [1,2]. The star image has a wide viewing angle and high dynamics, which can intuitively display the distribution of star points [3]. The rapid development of sensor cloud technology enables the data interaction between sensors. Currently, the research on sensor cloud mainly focuses on data storage, data application and data security.

In terms of data storage and application, Sen et al. [4] established a multi-modal mechanism in the face of the response needs of multiple users. Nastic et al. [5] built an intermediate structure between the cloud and the base end to realize data interaction. Villari et al. [6] drew on the idea of internet of things (IoT) to combine cloud computing with sensors. Wind et al. [7] used sensor cloud technology to fuse the remote sensing data. Dinh et al. [8] proposed an on-demand distributed sensor cloud work scheme. Wieland et al. [9] constructed a convolutional neural network to coordinate multiple sensors to achieve cloud shadow segmentation. Liang et al. [10] implemented a low-coupling model based on edge computing. Sangulagi et al. [11] improved the neuro-fuzzy set algorithm to balance the data-carrying status of the sensor cloud. Wang [12] proposed a decoupling scheme based on fog computing. Gong et al. [13] used deep learning and matrix factorization to predict each sensor’s weight. Dwivedi et al. [14] constructed a Gaussian distribution model to analyze abnormal data events. Sun et al. [15] proposed a distributed intelligent processing scheme. Dash et al. [16] analyzed the data in cloud, edge and fog computing to realize data management. Wu et al. [17] analyzed the effectiveness of edge computing from an energy perspective. Peng et al. [18] analyzed the characteristics of IoT computing in cloud computing and optimized the objective function. Qu et al. [19] built a deep meta-reinforcement learning to increase edge computing performance. Lu et al. [20] analyzed the network structure based on mobile data characteristics. Wan et al. [21] analyzed data characteristics and built edge computing structures to enable real-time processing. Mousa et al. [22] used GPU to achieve fast data calculation.

In terms of data security, Saha et al. [23] proposed a data security scheme based on a high-density sensor cloud system. Kamburugamuve et al. [24] proposed a novel network scheme to meet the requirements of fast computation. Dalvi et al. [25] established an adjustment mechanism to meet the needs of different tasks. Wang et al. [26] conducted research on data credibility through fog. Das et al. [27] constructed a sensor cloud energy-saving system. Zhu et al. [28] carried out research on data protection under the condition of big data. Liang et al. [29] analyzed the construction of the sensor cloud and proposed a solution for stability. El Rachkidi et al. [30] studied sensor usage and sharing mechanisms. Zhang et al. [31] combined fog and trust evaluation method to realize sensor cloud security detection. Chakraborty et al. [32] introduced a dynamic mechanism to manage data confidentiality. Kim [33] constructed a game theory model to analyze the effectiveness of sensor networks. Wang et al. [34] implemented data cleaning based on edge computing. Wang et al. [35] proposed to use differential pair data for protection. Mo et al. [36] constructed a simplified neural network to measure the stability of cloud systems. Thabit et al. [37] proposed a lightweight approach to data encryption. Abel et al. [38] used the hybrid algorithm for cloud-based data protection.

To sum up, the main problems faced by the research on star sensor cloud are as follows. 1) The analysis of the imaging characteristics acquired by the sensor is insufficient, resulting in the weak pertinence of the built model. 2) The analysis of image content is insufficient, and the cost of communication and transmission by constructing full information transmission is high. 3) The data encoding and decoding methods in image units have certain limitations, which need further improvement in data privacy.

In response to the above problems, we have conducted in-depth research on the characteristics of star sensor imaging. This paper proposes an edge computing algorithm based on the star sensor cloud. The work of this research is as follows. 1) This research analyzes the composition of star images, builds an exponential entropy model based on fuzzy sets, and accurately extracts the star points. 2) A content and space mapping model is constructed to reduce communication and storage cost. 3) A multi-level data processing model is established and a differential mechanism is built to realize data privacy protection.

2  Algorithm

Star sensors mainly have two roles. 1) Star sensors are a very important component of the satellite attitude control system, providing the satellite attitude data to the system and making correction for gyroscopic drift. Star sensors determine the three-axis attitude of a satellite with respect to the celestial coordinate system by sensitizing it to stellar radiation. 2) Star sensors are the most efficient way of observing cosmic space as they can obtain a wide-area star image, which is of great importance. Besides, autonomous navigation based on star sensors is also very important, as unpredictable targets such as meteorites may appear in the universe. As the acquired star images are 16-bit data with high resolution, it is a great challenge if the data is processed at the star sensor side due to the huge computation amount. To reduce the computation burden on the star sensor side, we propose an edge computing solution that improves the efficiency, stability and scalability of the algorithm and further increases the stability of the system.

With the increase in the frequency of international satellite launches, satellites have formed a network of interaction in space. Accordingly, satellite-to-satellite interactions will become more frequent. We consider the servers contained in individual satellites as local servers, the servers of other satellites and those that interact with ground stations as edge servers for edge computing. Edge computing offers the following advantages. 1) High speed. Instead of data being transferred back to a central server, IoT devices can process data at the edge data center or locally, reducing network latency. 2) High security. Edge computing distributes data processing work between different data centers and devices, eliminating the need to transfer all data back to the main server, therefore reducing the risk of data leakage and increasing the data security. 3) Easy scalability. Edge computing makes it easy to scale infrastructure and extend networks by purchasing IoT devices. 4) High reliability. With all edge data centers and IoT devices located close to the user, the probability of network disruption is very low. If the edge data center is not available, the IoT devices will handle most functions automatically.

To this end, we propose a novel edge computing algorithm, as shown in Fig. 1. The first step is to acquire images from space by star sensors. The fuzzy set-based algorithm is then used to extract star points and construct a content-to-space mapping model to reduce the data dimensionality. Finally, image reconstruction is achieved using an edge-based clustering computational algorithm.

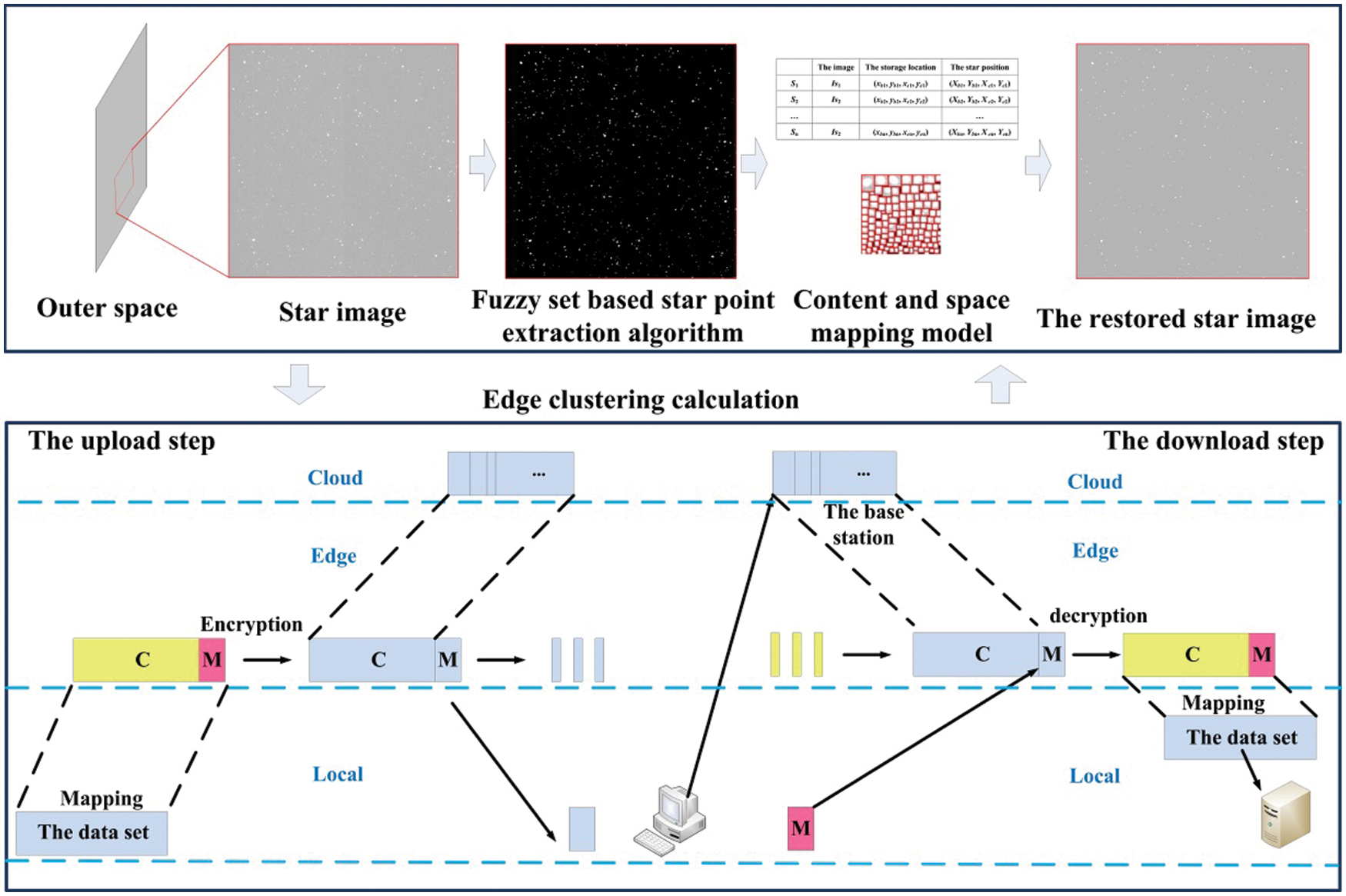
Figure 1: Algorithm flow chart

2.1 Fuzzy Set Based Star Point Extraction Algorithm

A star image is highly dynamic and high-resolution. A star image I can be regarded as the superposition of star point S, noise N, and background B.

I=S+N+B(1)

where S is an important part of the star image, and it is particularly important to the research on star points. The star points are displayed as a set of a few bright pixels in the image, which show a spherical shape. The pixel values of star points are susceptible to noise interference, and the brightness of long-distance star points is weak, resulting in blurred boundaries. However, it is difficult to effectively determine star points and accurately extract star points from the perspective of computer calculation as Fig. 2.

Figure 2: High dynamic star image

Fuzzy set theory is a mathematical means of describing uncertain things and phenomena. This theory is close to human real thinking and decision making [39]. Hassaballah et al. [40] constructed an image quality evaluation mechanism based on fuzzy sets. Ansari et al. [41] combined the fuzzy set and entropy to extract the target boundary in an image. Mardani et al. [42] constructed deep fuzzy sets to classify images. Zhang et al. [43] fused multi-sensor images based on fuzzy set theory. It can be seen that the fuzzy set theory can better simulate the human cognitive process. As the boundaries of the star points and the background have similar grey scale values, it is difficult to distinguish between them. For this reason, we introduce fuzzy sets for analysis to achieve the distinction.

On the basis of fuzzy set theory, it is necessary to determine the appropriate measurement method to achieve the accurate segmentation of image objects. Since the fuzzy set theory is an important way to describe uncertain phenomena, an algorithm that can measure uncertainty should be selected for this purpose. Entropy is a measure of the uncertainty of the probability of an event, which can effectively reflect the information contained in the event.

Therefore, based on the fuzzy set theory, this research constructs the entropy measurement mechanism, and proposes a star point extraction algorithm that conforms to the human cognitive process. Firstly, an image is divided into bright and dark fuzzy sets according to the pixel value of the star point. Then, the entropy is calculated to determine the threshold value to segment the image. Finally, the star points are completely extracted according to the imaging characteristics of the star points.

A fuzzy set is a set whose elements have degrees of membership. It allows for a step-by-step evaluation of the membership of elements in a set.

A=∑i=1nμ(xi)/xixi∈X(2)

where A represents the fuzzy set of X, μ (xi) is the fuzzy membership function, and μ (xi)/xi represents the ambiguity of xi to A.

The probability of fuzzy event A is

P(A)=∑i=0GμA(xi)Px(xi)(3)

Traditional entropy is a probability distribution to measure the randomness of a signal, which is defined as

H=−∑i=0Gpilog⁡(pi)(4)

where pi represents the probability of i appearing, and G represents the included signal level.

On the basis of traditional entropy, texture entropy [44], minimum cross entropy [45] and exponential entropy [46], etc. are derived. The exponential entropy is used for calculation.

H=−∑i=0Gpie1−pi(5)

It can be seen that the randomness strength of the signal is inversely proportional to H. When an image is displayed, the more severe the gray scale change of the image is, the larger the H value is; on the contrary, the more flat the image gray scale change is, the smaller the H value is.

In the star image, S and N are displayed as bright pixels, and B is displayed as dark pixels. According to the fuzzy set analysis, the bright pixel set is ASN, the dark pixel set is AB, and T is the potential segmentation threshold point of the image. It satisfies

P(AB)=∑i=0TμAB(xi)Px(xi)(6)

P(ASN)=∑i=T+1L−1μASN(xi)Px(xi)(7)

P(ASN)+P(AB)=1(8)

where μ(xi) is the membership function, which is used to distinguish the membership of different pixels.

The exponential entropy is used to measure the difference between bright pixels and dark pixels, and the optimal threshold T satisfies

Hmax=arg⁡Max(H(T))(9)

H=−(∑i=0TP(AB)e1−P(AB)+∑i=T+1L−1P(ASN)e1−P(ASN))(10)

Since there is a transition area between ASN and AB, we construct

uAB(xi)={1i≤α1−(i−α)2(γ−α)(β−α)α<i≤β(i−γ)2(γ−α)(γ−β)β<i≤γ0i>γ(11)

uASN(xi)={0i≤α(i−α)2(γ−α)(β−α)α<i≤β1−(i−γ)2(γ−α)(γ−β)β<i≤γ1i>γ(12)

where the parameters satisfy 0 ≤ α < β < γ ≤ 255, β=(α+γ)/2. When Ti is the optimal threshold, H = Hmax, uASN(Ti)=uAB(Ti)=0.5. Then we solve for α, β, γ at this time.

Bright areas and dark areas can be distinguished. It is still impossible to distinguish between S and N. The change of S in the image collected in a short time should be relatively small, while the change of N is random and the change is relatively large. For this reason, we collected 3 frames of images from a fixed camera to determine whether there was a change in bright and dark areas at the same location.

gj(x,y)=∑i=j−1j+1{Ii(x,y)−Ij(x,y)}(x,y)∈S∩N(13)

where Ii (x, y) is the pixel value of the i-th frame image at (x, y). If gj(x, y) < 0, then (x, y) ∈ N; otherwise (x, y) ∈ S. The star points are accurately extracted on the basis of removing noise.

2.2 Content and Space Mapping Model

It is necessary to store and transmit the shooting data of stars efficiently. The star point is the important observation object. S can be regarded as a comprehensive representation of the pixel value V and the location L.

S=V+L(14)

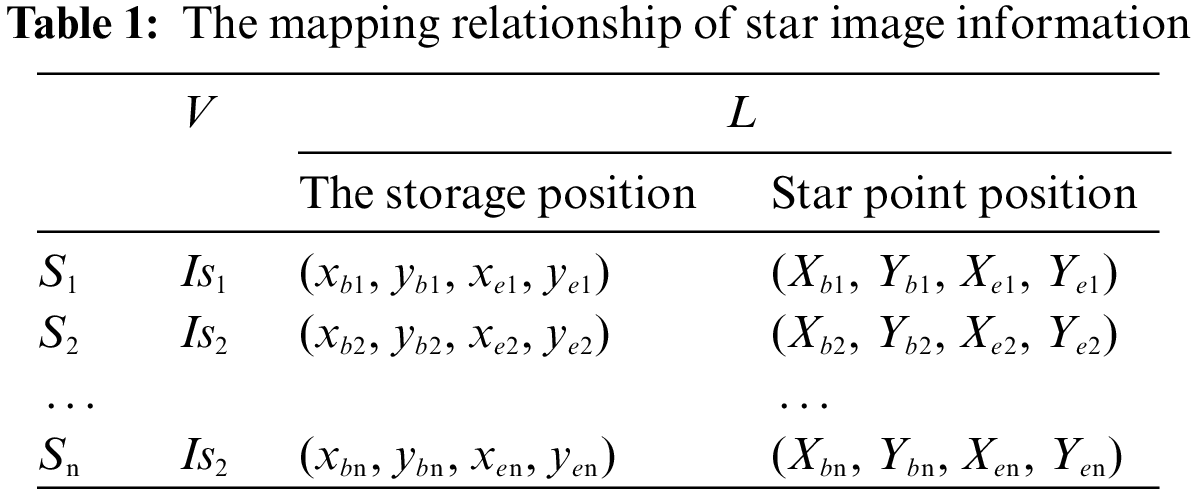
In order to make full use of the storage space, the extracted star points are sorted from large to small according to the number of pixels they occupy, as shown in Table 1. The nth star point is denoted as Sn, and stored in the form of the following table, where Isn is the smallest rectangular area containing the star point image. The storage location is (xbn, ybn, xen, yen), and the original star location is (Xbn, Ybn, Xen, Yen). Notably, (xbn, ybn) and (Xbn, Ybn) are the coordinates of the initial point, and (xen, yen) and (Xen, Yen) are the coordinates of the end point. Isn is extracted in the storage area, and then the area corresponding to the star point is mapped to realize the storage and transmission of the star image.

2.3 Edge Clustering Computing Algorithm

Data processing technology has been widely used in data privacy, data integrity, and data availability [47]. The three layers storage (TLS) framework is arbitrarily divided into three parts and stored, making full use of the data processing capabilities of edge servers to effectively manage cloud servers [48].

Star images need huge computation amount and storage space due to their high resolution. In addition to the current situation where the spacecraft cannot be manually involved in commissioning, edge computing is used to break down the computation so that some of the information is kept between the various sensor nodes to enable collaboration. With the increase in the frequency of international satellite launches, satellites have formed a network of interaction in space. Accordingly, satellite-to-satellite interactions will become more frequent. We consider the servers contained in individual satellites as local servers, the servers of other satellites and those that interact with ground stations as edge servers.

Previous research has shown that the data collected by the sensor follows a rent-free law. Specifically, in a set of data, the data basically fluctuates around a certain value or a certain subset of data sets. To this end, a new type of differential three layers storage (DTLS) with regular data distribution is constructed. When a set of data is collected and processed, the data is split into basic data M and differential data C. Then the complete dataset I can be expressed as

I=M+C(15)

where the selection of M is particularly important, which directly affects the efficiency of hierarchical storage. In addition, the stored data set is divided into k parts in combination with binary coding. The size of each part is l, and k blocks of data are generated into n coding blocks by the coding matrix, then n = k + m, where m is the number of redundant blocks, and each data block is coded and stored in the storage node. When the number of coded block losses is not greater than m, the system can repair all coded data. When fewer than k coding blocks are used, the data cannot be recovered. In DTLS, differential storage of raw data through different algorithms reduces storage costs in cloud servers while improving cloud performance. In this way, user security is guaranteed. The steps of upload and download are described below, as shown in Fig. 3.

Figure 3: Flow chart of edge clustering algorithm

In the upload step, the data is transmitted to the edge server, and the data is divided into three parts for processing. a) The monitoring value is divided into M and C. b) M and C are encrypted. c) The encrypted C is uploaded to the cloud server for storage. The encrypted M is processed according to the Reed-Solomon coding principle. To prevent data recovery, most databases and redundant blocks smaller than k are stored in cloud server. The remaining data will be stored in the edge server and backhauled locally according to user needs, so as to reduce storage cost and protect data security.

In the download step, when the user needs to use the data, he transmits the request to the cloud, and the cloud transmits the separately stored C and part M to the edge layer. Some key data blocks are transmitted locally to the edge layer, and the edge layer decodes C and M respectively to obtain complete data and transmits it back to the local.

The above analysis shows that the selection of M is very important. In the actual starry sky scene, the data collected by the sensor is relatively complex. Here, we introduce the idea of clustering, and divide the data set with many attributes into multiple subsets according to the similarity. This leads to the large intra-class similarity and large inter-class difference.

The dataset is divided into multiple clusters to determine M, so that the distance from the minimized cluster center to the cluster sample is C.

Let the sample set be X = {X1, X2, …, Xi,…, Xn}, and each sample set Xi contains p attributes, Xi={Xi1,Xi2,…,Xip}. The sample set is sampled, and the optimal number of clusters kopt in the range of [kmin, kmax] is selected according to the inter-class and intra-class partition index B. Then, the sample set is divided into X = {T1, T2, …., Tkopt}. The Euclidean distance is sued to measure the spatial location relationship:

d(Xi,Xj)=∑w=1p(Xiw−Xjw)2,i,j∈(1,2…,n)(16)

Then, the corresponding average distance is

D=∑i=1n∑j=1nd(Xi,Xj)n2(17)

The density of the sample Xi is defined as the data object contained in the area with Xi the center and αD as the radius, the defined average density is

E=∑i=1n∑j=1nQ[d(Xi,Xj)]n,Q[d(Xi,Xj)]={1d(Xi,Xj)≤αD0others(18)

High density points are defined as a set of data objects. The specific steps of the algorithm are as follows:

:

3  Experimental Results and Analysis

In order to verify the effectiveness of the algorithm proposed in this paper, we constructed 2 groups of databases for simulation due to the rare availability of space equipment. The first group was carried out for 10 onboard server databases and the second group was carried out for 20 ground-based simulation server databases. The experiment used 4214 frames of 16-bit real star images with a resolution of 1024 × 1024 to form a database. The program was run on FPGA. In order to ensure the stability of data, we maintain 50% data duplication in different nodes and backup the data transmitted to the local station.

3.1 Effects of Star Point Detection and Extraction

A star image consists of star points, noise, and background. The accurate detection of star points is the premise of the future research on star images. The evaluation criteria are listed as Table 2.

Sensitivity (SEN) reflects the detection performance of the algorithm for true star points. Specificity (SPE) reflects the detection performance of the algorithm for false star points. Accuracy (ACC) reflects the ratio of correct detection results to all samples in the detection results. False Positive Fraction (FPF) reflects the ratio of false positive detection results that are diagnosed as true star points [49]. SEN, SPE and ACC are directly proportional to the results, and FPF is inversely proportional to the results.

SEN=TPTP+FN(19)

SPE=TNTN+FP(20)

ACC=TP+TNTP+FP+TN+FN(21)

FPF=1−ACC(22)

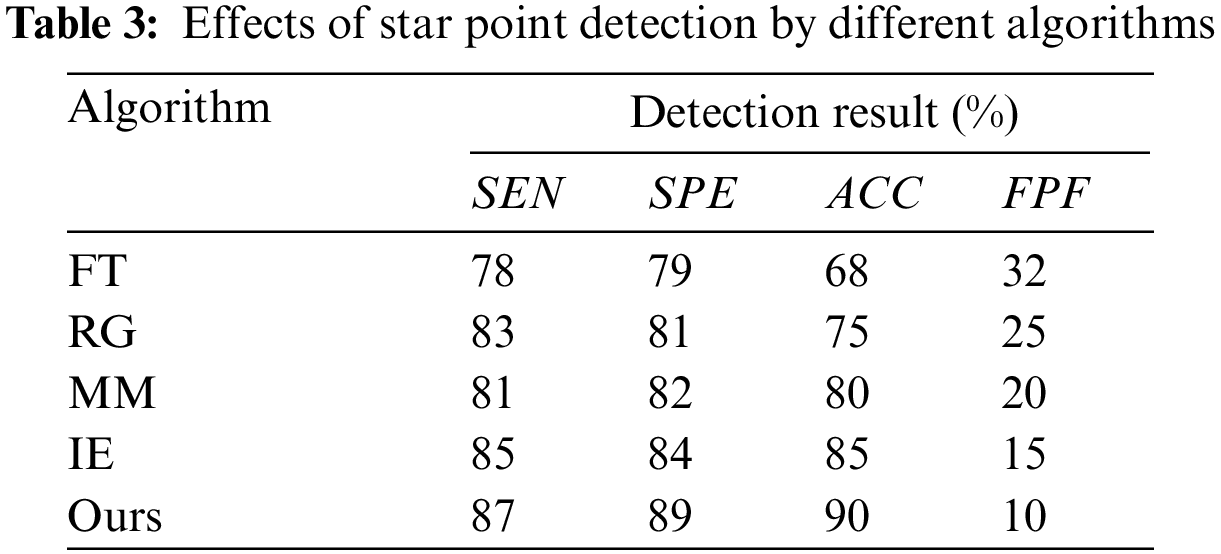
The comparison of star point detection effect by different algorithms is shown in Table 3. The Fixed Threshold (FT) algorithm [50] manually sets the threshold and can extract star points, but does not use the star point features to further discriminate, resulting in many non-star points, and the effect is not good. The Region Growing (RG) [51] algorithm selects the high point of the local gray value as the seed point for regional growth, and the number of extracted star points is higher than that of the FT algorithm. The Mathematical Morphology (MM) algorithm [52] establishes a circular model to extract and discriminate star points. The Image Enhance (IE) algorithm [53] combines gray scale information with morphological information to extract star points with lower gray scale values. The above algorithms all start from the perspective of a single-frame star image, and fail to consider the excessive area between the star point and the background, resulting in an unsatisfactory detection effect. The algorithm proposed in this paper simulates human’s real thinking and decision-making to establish a fuzzy set model. It uses entropy to measure the difference between the star point and the background. Besides, the proposed algorithm considers the information of multiple frames of images comprehensively, so that the noise interference is further reduced and star points are extracted. The detection effect of the proposed algorithm is higher than that of other algorithms.

In order to verify the segmentation effect of the algorithms, on the premise that the segmentation area is a star point, the area overlap measure (AOM) is introduced to evaluate the segmentation effect, which is defined as:

AOM(ξ,φ)=S(ξ∩φ)S(ξ∪φ)×100%(23)

where AOM is the area overlap, ξ is the manually marked star points, φ is the segmentation result map, S (.) represents the number of pixels in the area, and the larger the AOM, the better the segmentation effect.

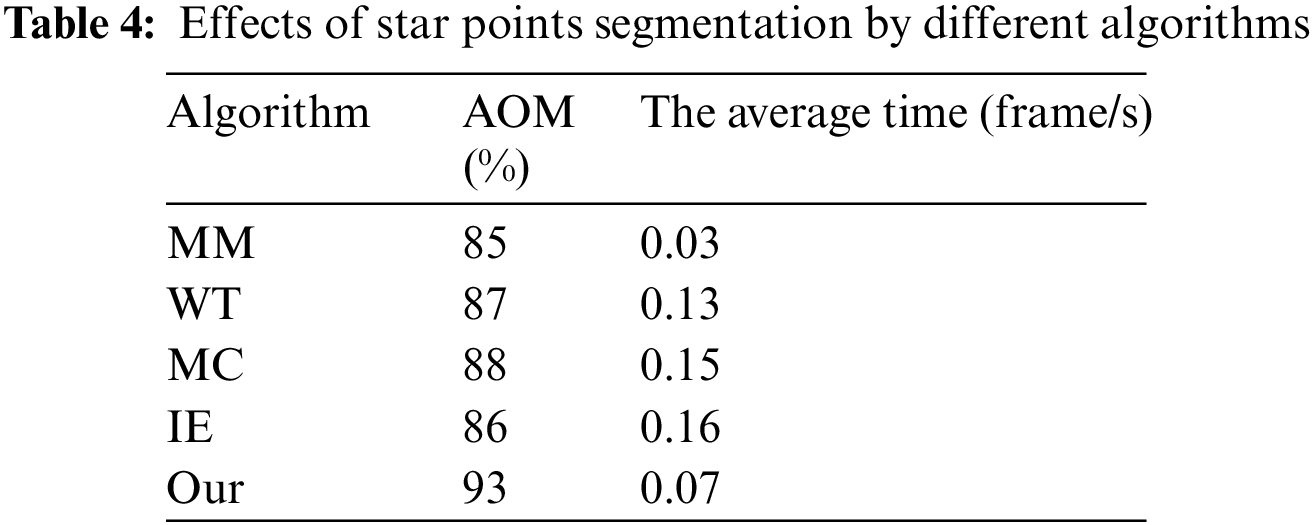
The effect of star point segmentation is shown in Table 4. The MM algorithm establishes a circular model to segment star points, and the segmentation speed is fast. The Wavelet Transform (WT) algorithm [54] builds a model in the frequency domain to segment the star points. The Motion Compensation (MC) algorithm [55] can extract the center of the star point for the motion-blurred star points. The IE algorithm [53] builds an image enhancement model from grayscale and geometric shapes to segment star points, but the algorithm is complex. From the perspective of human cognition, the proposed algorithm establishes an analysis and quantification framework based on fuzzy sets and entropy. Although the processing time of the proposed algorithm is slightly longer to that of the MM algorithm, the segmentation accuracy of the proposed algorithm is the highest.

3.2 Performance Comparison of Edge Computing

Our experiment on a large number of open-source datasets shows that most of the data appear Gaussian distribution over a period of time. The comparison of edge computing performance by different algorithms is shown in Fig. 4. Under the same algorithm, the storage cost is the most significant indicator to evaluate the algorithm’s performance.

Figure 4: Comparison of storage cost by different algorithms effects under different classifications

Through the above analysis, we fixed the expectation on the basis of Gaussian distribution to investigate the performance of the algorithms on the experimental data with different variances. As shown in Fig. 5, with the increase of the standard deviation of the Gaussian distribution, the storage space occupied by the algorithm gradually decreases, and the storage cost tends to be stable. Differential privacy computing (DPC) [42] uses differential to reduce the amount of data to a certain extent. Dynamic trust enforcing (DTE) [32], a dynamic adjustment scheme, operates on the data, and has achieved certain effects. For the clustering-based difference method proposed by us, with the increase of the standard deviation of the Gaussian distribution, it still stores part of the data locally and at the edge, which shows that the proposed algorithm is superior to other algorithms.

Figure 5: Comparison of storage cost by different algorithms under different standard deviations

The efficiency of encryption and decryption in data processing is analyzed, as shown in Fig. 6. The number of redundant blocks is fixed to 3 to show the effects under different data amount. As the number of data blocks increases, both encryption and decryption time show an upward trend. When the number of data blocks is increased to 400, the processing speed becomes even more obvious. The decryption process consumes more time than the encryption process. Since encryption is processed in the cloud, it has certain requirements for processing time. The decryption is performed at the base station, and high-performance equipment can be used to reduce the decryption time.

Figure 6: Comparison of encryption and decryption time

The proposed algorithm not only increases the storage efficiency of the sensor cloud but also reduces the bandwidth consumption of the transmission process, as shown in Fig. 7. In the experiment, the number of redundancy blocks was set to 3 and the data block data size was set to 400. The interactive model (IM) [8] allocates bandwidth based on demand. Deep learning and matrix factorization (DLMF) [13] algorithm allocate the bandwidth. As the amount of data grows, the proposed algorithm consumes less bandwidth compared with the traditional algorithm that adopts the difference and clustering strategies. It shows that the proposed algorithm can make full use of resources to a certain extent and reduce the transmission burden.

Figure 7: Comparison of data transmission bandwidth by different algorithms

3.3 Storage and Reconstruction of Data

According to the algorithm proposed in this paper, the star point data is saved, and a mapping mechanism is established. The star image can be obtained only by transmitting the compressed data and the mapping function, with the effect shown in Fig. 8.

Figure 8: Flow chart of star image information storage algorithm

4  Conclusions

This research focuses on the problem of a large amount of star image data, which is difficult to process, store and keep confidential. In order to improve star sensor performance and give full play to the advantages of fast, secure, reliable and scalable edge computing, we propose the edge computing algorithm based on the star sensor cloud. Starting from the composition of the star image, this paper builds a fuzzy set-based star point extraction model to accurately retain the integrity of its useful information. The proposed content and space mapping model greatly reduces the data storage cost and transmission memory. In addition, an edge clustering framework is proposed to distribute data in the cloud and at the edge, and a differential model is built to protect data privacy. Experiments show that the proposed algorithm has achieved good results on simulated and real datasets. The SEN is 0.87, AOM is 0.93 and the average time is 0.07 frame/s. Due to the special nature of star images, it is not possible to carry out large-scale star image starboard experiments. Subsequently, we will further accumulate data, analyze data components, and improve data utilization efficiency, to realize autonomous spacecraft navigation, expecting to provide data support for space research.

Funding Statement: This work is supported by Science and Technology Rising Star of Shaanxi Youth (No. 2021KJXX-61); The Open Project Program of the State Key Lab of CAD&CG, Zhejiang University (No. A2206).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Sarpotdar, M., Mathew, J., Sreejith, A. G., Ambily, S., Prakash, A. et al. (2017). A software package for evaluating the performance of a star sensor operation. Experimental Astronomy, 43(1), 99–117. DOI 10.1007/s10686-016-9522-1. [Google Scholar] [CrossRef]

    2. Cheng, J., Wang, T., Wang, L., Wang, Z. (2017). A new polar transfer alignment algorithm with the aid of a star sensor and based on an adaptive unscented Kalman filter. Sensors, 17(10), 2417. DOI 10.3390/s17102417. [Google Scholar] [CrossRef]

    3. Yang, H., Wang, J., Liu, H., Sun, H. (2015). An algorithm for fast extraction and identification of star target. Optik, 126(21), 3034–3038. DOI 10.1016/j.ijleo.2015.07.067. [Google Scholar] [CrossRef]

    4. Sen, A., Modekurthy, V. P., Dalvi, R., Madria, S. (2016). A sensor cloud test-bed for multi-model and multi-user sensor applications. 2016 IEEE Wireless Communications and Networking Conference, pp. 1–7. Doha, Qatar, IEEE. DOI 10.1109/WCNC.2016.7564764. [Google Scholar] [CrossRef]

    5. Nastic, S., Truong, H. L., Dustdar, S. (2016). A middleware infrastructure for utility-based provisioning of IoT cloud systems. 2016 IEEE/ACM Symposium on Edge Computing (SEC), pp. 28–40. Washington DC, USA, IEEE. DOI 10.1109/SEC.2016.35. [Google Scholar] [CrossRef]

    6. Villari, M., Al-Anbuky, A., Celesti, A., Moessner, K. (2016). Leveraging the Internet of Things: Integration of sensors and cloud computing systems. International Journal of Distributed Sensor Networks, 12(7), 9764287. DOI 10.1177/155014779764287. [Google Scholar] [CrossRef]

    7. Wind, G., Silva, A. M. D., Norris, P. M., Platnick, S., Mattoo, S. et al. (2016). Multi-sensor cloud and aerosol retrieval simulator and remote sensing from model parameters–Part 2: Aerosols. Geoscientific Model Development, 9(7), 2377–2389. DOI 10.5194/gmd-9-2377-2016. [Google Scholar] [CrossRef]

    8. Dinh, N. T., Kim, Y. (2018). An efficient on-demand latency guaranteed interactive model for sensor-cloud. IEEE Access, 6, 68596–68611. DOI 10.1109/ACCESS.2018.2879811. [Google Scholar] [CrossRef]

    9. Wieland, M., Li, Y., Martinis, S. (2019). Multi-sensor cloud and cloud shadow segmentation with a convolutional neural network. Remote Sensing of Environment, 230, 111203. DOI 10.1016/j.rse.2019.05.022. [Google Scholar] [CrossRef]

  10. Liang, Y., Mei, Y., Yang, Y., Ma, Y., Jia, W. et al. (2020). A low-coupling method in sensor-cloud systems based on edge computing. Journal of Computer Research and Development, 57(3), 639. DOI 10.7544/issn1000-1239.2020.20190588. [Google Scholar] [CrossRef]

  11. Sangulagi, P., Sutagundar, A. (2021). Agent-based improved neuro-fuzzy for load balancing in sensor cloud. International Journal of Energy Optimization and Engineering, 10(1), 16–35. DOI 10.4018/IJEOE.2021010102. [Google Scholar] [CrossRef]

  12. Wang, T., Mei, Y., Jia, W., Zheng, X., Wang, G. et al. (2020). Edge-based differential privacy computing for sensor-cloud systems. Journal of Parallel and Distributed Computing, 136, 75–85. DOI 10.1016/j.jpdc.2019.10.009. [Google Scholar] [CrossRef]

  13. Gong, J., Du, W., Li, H., Li, Q., Zhao, Y. et al. (2020). Score prediction algorithm combining deep learning and matrix factorization in sensor cloud systems. IEEE Access, 9, 47753–47766. DOI 10.1109/ACCESS.2020.3035162. [Google Scholar] [CrossRef]

  14. Dwivedi, R. K., Kumar, R., Buyya, R. (2021). Gaussian distribution-based machine learning scheme for anomaly detection in healthcare sensor cloud. International Journal of Cloud Applications and Computing, 11(1), 52–72. DOI 10.4018/IJCAC.2021010103. [Google Scholar] [CrossRef]

  15. Sun, Z., Li, C., Wei, L., Li, Z., Min, Z. et al. (2019). Intelligent sensor-cloud in fog computer: A novel hierarchical data job scheduling strategy. Sensors, 19(23), 5083. DOI 10.3390/s19235083. [Google Scholar] [CrossRef]

  16. Dash, S., Biswas, S., Banerjee, D., Rahman, A. U. (2019). Edge and fog computing in healthcares–A review. Scalable Computing: Practice and Experience, 20(2), 191–206. DOI 10.12694/scpe.v20i2.1504. [Google Scholar] [CrossRef]

  17. Wu, H., Sun, Y., Wolter, K. (2018). Energy-efficient decision making for mobile cloud offloading. IEEE Transactions on Cloud Computing, 8(2), 570–584. DOI 10.1109/TCC.2018.2789446. [Google Scholar] [CrossRef]

  18. Peng, G., Wu, H., Wu, H., Wolter, K. (2021). Constrained multiobjective optimization for IoT-enabled computation offloading in collaborative edge and cloud computing. IEEE Internet of Things Journal, 8(17), 13723–13736. DOI 10.1109/JIOT.2021.3067732. [Google Scholar] [CrossRef]

  19. Qu, G., Wu, H., Li, R., Jiao, P. (2021). DMRO: A deep meta reinforcement learning-based task offloading framework for edge-cloud computing. IEEE Transactions on Network and Service Management, 18(3), 3448–3459. DOI 10.1109/TNSM.2021.3087258. [Google Scholar] [CrossRef]

  20. Lu, J., Chen, L., Xia, J., Zhu, F., Tang, M. et al. (2022). Analytical offloading design for mobile edge computing-based smart internet of vehicle. EURASIP Journal on Advances in Signal Processing, 2022(1), 1–19. DOI 10.1186/s13634-022-00867-2. [Google Scholar] [CrossRef]

  21. Wan, S., Ding, S., Chen, C. (2022). Edge computing enabled video segmentation for real-time traffic monitoring in internet of vehicles. Pattern Recognition, 121, 108146. DOI 10.1016/j.patcog.2021.108146. [Google Scholar] [CrossRef]

  22. Mousa, M. H., Hussein, M. K. (2022). Efficient UAV-based MEC using GPU-based PSO and voronoi diagrams. Computer Modeling in Engineering & Sciences, 133(2), 413–434. DOI 10.32604/cmes.2022.020639. [Google Scholar] [CrossRef]

  23. Saha, S. (2015). Secure sensor data management model in a sensor-cloud integration environment. 2015 Applications and Innovations in Mobile Computing (AIMoC), pp. 158–163. Kolkata, India, IEEE. DOI 10.1109/AIMOC.2015.7083846. [Google Scholar] [CrossRef]

  24. Kamburugamuve, S., Christiansen, L., Fox, G. (2015). A framework for real time processing of sensor data in the cloud. Journal of Sensors, 2015. DOI 10.1155/2015/468047. [Google Scholar] [CrossRef]

  25. Dalvi, R., Madria, S. K. (2015). Energy efficient scheduling of fine-granularity tasks in a sensor cloud. International Conference on Database Systems for Advanced Applications, pp. 498–513. Cham: Springer. DOI 10.1007/978-3-319-18123-3_30. [Google Scholar] [CrossRef]

  26. Wang, T., Li, Y., Chen, Y., Tian, H., Cai, Y. et al. (2017). Fog-based evaluation approach for trustworthy communication in sensor-cloud system. IEEE Communications Letters, 21(11), 2532–2535. DOI 10.1109/LCOMM.2017.2740279. [Google Scholar] [CrossRef]

  27. Das, K., Das, S., Darji, R. K., Mishra, A. (2017). Energy efficient model for the sensor cloud systems. 2017 2nd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), pp. 373–375. Bangalore, India, IEEE. DOI 10.1109/RTEICT.2017.8256619. [Google Scholar] [CrossRef]

  28. Zhu, C., Shu, L., Leung, V. C., Guo, S., Zhang, Y. et al. (2017). Secure multimedia big data in trust-assisted sensor-cloud for smart city. IEEE Communications Magazine, 55(12), 24–30. DOI 10.1109/MCOM.2017.1700212. [Google Scholar] [CrossRef]

  29. Liang, Y., Wang, T., Bhuiyan, M. Z. A., Liu, A. (2017). Research on coupling reliability problem in sensor-cloud system. International Conference on Security, Privacy and Anonymity in Computation, Communication and Storage, pp. 468–478. Cham, Springer. DOI 10.1007/978-3-319-72395-2_43. [Google Scholar] [CrossRef]

  30. El Rachkidi, E., Agoulmine, N., Chendeb, N., Belaid, D. (2017). Resources optimization and efficient distribution of shared virtual sensors in sensor-cloud. 2017 IEEE International Conference on Communications (ICC), pp. 1–6. Paris, France, IEEE. DOI 10.1109/ICC.2017.7996643. [Google Scholar] [CrossRef]

  31. Zhang, G., Wang, T., Wang, G., Liu, A., Jia, W. (2018). Detection of hidden data attacks combined fog computing and trust evaluation method in sensor-cloud system. Concurrency and Computation: Practice and Experience, e5109. DOI 10.1002/cpe.5109. [Google Scholar] [CrossRef]

  32. Chakraborty, A., Mondal, A., Roy, A., Misra, S. (2018). Dynamic trust enforcing pricing scheme for sensors-as-a-service in sensor-cloud infrastructure. IEEE Transactions on Services Computing, 14(5), 1345–1356. DOI 10.1109/TSC.2018.2873763. [Google Scholar] [CrossRef]

  33. Kim, S. (2018). An effective sensor cloud control scheme based on a two-stage game approach. IEEE Access, 6, 20430–20439. DOI 10.1109/ACCESS.2018.2815578. [Google Scholar] [CrossRef]

  34. Wang, T., Liang, Y., Tian, Y., Bhuiyan, M. Z. A., Liu, A. et al. (2019). Solving coupling security problem for sustainable sensor-cloud systems based on fog computing. IEEE Transactions on Sustainable Computing, 6(1), 43–53. DOI 10.1109/TSUSC.2019.2904651. [Google Scholar] [CrossRef]

  35. Wang, T., Ke, H., Zheng, X., Wang, K., Sangaiah, A. K. et al. (2019). Big data cleaning based on mobile edge computing in industrial sensor-cloud. IEEE Transactions on Industrial Informatics, 16(2), 1321–1329. DOI 10.1109/TII.2019.2938861. [Google Scholar] [CrossRef]

  36. Mo, Y., Liang, M., Xing, L., Liao, J., Liu, X. (2020). Network simplification and K-terminal reliability evaluation of sensor-cloud systems. IEEE Access, 8, 177206–177218. DOI 10.1109/ACCESS.2020.3024964. [Google Scholar] [CrossRef]

  37. Thabit, F., Can, O., Alhomdy, S., Al-Gaphari, G. H., Jagtap, S. (2022). A novel effective lightweight homomorphic cryptographic algorithm for data security in cloud computing. International Journal of Intelligent Networks, 3, 16–30. DOI 10.1016/j.ijin.2022.04.001. [Google Scholar] [CrossRef]

  38. Abel, K. D., Misra, S., Jonathan, O., Agrawal, A., Maskeliunas, R. et al. (2022). Data security in cloud computing using a hybrid algorithm approach. In: Computational intelligence in machine learning, pp. 467–474. Singapore, Springer. DOI 10.1007/978-981-16-8484-5_45. [Google Scholar] [CrossRef]

  39. Qiu, S., Jin, Y., Feng, S., Zhou, T., Li, Y. (2022). Dwarfism computer-aided diagnosis algorithm based on multimodal pyradiomics. Information Fusion, 80, 137–145. DOI 10.1016/j.inffus.2021.11.012. [Google Scholar] [CrossRef]

  40. Hassaballah, M., Ghareeb, A. (2017). A framework for objective image quality measures based on intuitionistic fuzzy sets. Applied Soft Computing, 57, 48–59. DOI 10.1016/j.asoc.2017.03.046. [Google Scholar] [CrossRef]

  41. Ansari, M. D., Mishra, A. R., Ansari, F. T. (2018). New divergence and entropy measures for intuitionistic fuzzy sets on edge detection. International Journal of Fuzzy Systems, 20(2), 474–487. DOI 10.1007/s40815-017-0348-4. [Google Scholar] [CrossRef]

  42. Mardani, A., Hooker, R. E., Ozkul, S., Yifan, S., Nilashi, M. et al. (2019). Application of decision making and fuzzy sets theory to evaluate the healthcare and medical problems: A review of three decades of research with recent developments. Expert Systems with Applications, 137, 202–231. DOI 10.1016/j.eswa.2019.07.002. [Google Scholar] [CrossRef]

  43. Zhang, K., Huang, Y., Yuan, X., Ma, H., Zhao, C. (2020). Infrared and visible image fusion based on intuitionistic fuzzy sets. Infrared Physics & Technology, 105, 103124. DOI 10.1016/j.infrared.2019.103124. [Google Scholar] [CrossRef]

  44. Ma, B., Chen, Y., Zhang, S., Li, X. (2018). Remote sensing extraction method of tailings ponds in ultra-low-grade iron mining area based on spectral characteristics and texture entropy. Entropy, 20(5), 345. DOI 10.3390/e20050345. [Google Scholar] [CrossRef]

  45. Sathya, P. D., Kalyani, R., Sakthivel, V. P. (2021). Color image segmentation using Kapur, Otsu and minimum cross entropy functions based on exchange market algorithm. Expert Systems with Applications, 172, 114636. DOI 10.1016/j.eswa.2021.114636. [Google Scholar] [CrossRef]

  46. Ye, F., Zhang, X. (2016). Non-uniform quantized exponential entropy-based spectrum sensing algorithm in cognitive radio. 2016 Progress in Electromagnetic Research Symposium (PIERS), pp. 2511–2516. Shanghai, China, IEEE. DOI 10.1109/PIERS.2016.7735030. [Google Scholar] [CrossRef]

  47. Acheampong, A., Zhang, Y., Xu, X., Kumah, D. A. (2023). A review of the current task offloading algorithms, strategies and approach in edge computing systems. Computer Modeling in Engineering & Sciences, 134(1), 35–88. DOI 10.32604/cmes.2022.021394. [Google Scholar] [CrossRef]

  48. Yun, S., Chen, Y. (2023). Intelligent traffic scheduling for mobile edge computing in IoT via deep learning. Computer Modeling in Engineering & Sciences, 134, 1815–1835. DOI 10.32604/cmes.2022.022797. [Google Scholar] [CrossRef]

  49. Qiu, S., Luo, J., Yang, S., Zhang, M., Zhang, W. (2019). A moving target extraction algorithm based on the fusion of infrared and visible images. Infrared Physics & Technology, 98, 285–291. DOI 10.1016/j.infrared.2019.03.022. [Google Scholar] [CrossRef]

  50. Yu, X., Zhou, Z., Gao, Q., Li, D., Ríha, K. (2018). Infrared image segmentation using growing immune field and clone threshold. Infrared Physics & Technology, 88, 184–193. DOI 10.1016/j.infrared.2017.11.029. [Google Scholar] [CrossRef]

  51. Ma, J., Du, K., Zhang, L., Zheng, F., Chu, J. et al. (2017). A segmentation method for greenhouse vegetable foliar disease spots images using color information and region growing. Computers and Electronics in Agriculture, 142, 110–117. DOI 10.1016/j.compag.2017.08.023. [Google Scholar] [CrossRef]

  52. Ma, L., Huang, Z., Wang, X., Qin, S. (2016). Mathematical morphology operations applied in star image processing for star trackers. Imaging Systems and Applications, Heidelberg, Germany, Optical Society of America. DOI 10.1364/ISA.2016.IW2F.3. [Google Scholar] [CrossRef]

  53. Zhang, C., Zhao, J., Yu, T., Yuan, H., Li, F. (2017). Fast restoration of star image under dynamic conditions via lp regularized intensity prior. Aerospace Science and Technology, 61, 29–34. DOI 10.1016/j.ast.2016.11.013. [Google Scholar] [CrossRef]

  54. Han, J., Wang, C., Li, B. (2017). A novel optimization method for star-sensor data processing. Optik, 132, 192–202. DOI 10.1016/j.ijleo.2016.12.038. [Google Scholar] [CrossRef]

  55. Jiang, J., Huang, J., Zhang, G. (2016). An accelerated motion blurred star restoration based on single image. IEEE Sensors Journal, 17(5), 1306–1315. DOI 10.1109/JSEN.2016.2645861. [Google Scholar] [CrossRef]