A Drone-Based Blood Donation Approach Using an Ant Colony Optimization Algorithm

1  Introduction and Preliminaries

The lack of blood supply is one of the main causes of mortality in the developing world today. This complaint necessitates abrupt medical dealing and transfusion with appropriate blood products. A blood supply could be upfront in an urban hospital, but within the bleak rural territory of nations like Rwanda, it is getting dreadful. Nowadays, our blood mobiles are ambulances or blood donation camps etc., which are then stuck in traffic and cannot be able to reach the relevant patient in backward underdeveloped areas. Due to no proper roads or links, the mobiles get sucked in rough slums, and ultimately we lose the patient. However, in some areas, we have blood banks, but do not have enough stock for the relevant blood groups or blood components, such as white blood cells, platelets, etc. [1].

Apart from all these facilities of advertisement, we need the shortest path to deliver blood or any blood component. In this article, we use applications of graph theory to find an algorithm that fits in all these circumstances. The graphs are one amongst the major articles of study in discrete mathematics. The graphs are mathematical structures to model pairwise relations between objects [2]. A graphical network is a set of objects called nodes or vertices that are connected with each other. The connections between the nodes are called edges or links/linkage. A telecommunication structure can also be characterized as a linkage. In a complete graph of order n, there is a number of vertices and each vertex is linked with all the other vertices, this forms a complete network. In this article, we have a complete network of blood banks acting as nodes [3]. In graph theory, we have different shortest path problems in which we want to compute the shortest and most feasible paths to succeed in with brief period of time. A number of solutions to our problem can be found in graph theory. Here we consider a closed path connecting all blood banks, such that it forms a complete graph, and now there are many problems in graph theory which may minimally optimize the path and convey the shortest route. In this article, we are using the Traveling Salesman Problem (TSP) along with Ant Colony Optimization (ACO) applied to a network.

The Traveling Salesman Problem (often called TSP) is a definitive algorithmic problem within the subdivision of computing and examination. TSP is demonstrated as an undirected complete graph, where cities are represented as the graph’s vertices, paths are embodied as the graph’s edges, and a path’s distance is characterized as the edge’s weight. It is a minimization problem started and terminated at a specified node after visiting every vertex once. The ideal case may be a complete graph, i.e., individually pair of vertices is connected by an edge. Traveling Salesman Problem (TSP) is defined as, if a salesman starts from a city or a node stops over each city once and then comes back at the initial vertex, then the mandate of the tour is that the entire distance toured should be minimal. A complete graph G=(N,E) is viewed as TSP, where N is the set of cities and E is the set of paths linking all cities. Each edge (i,j)∈E is allotted a cost n, which is the distance among cities i and j [4–6].

Ant Colony Optimization (ACO) is a pattern for designing metaheuristic algorithms for combinatorial optimization problems. The first algorithm which can be classified within this framework was presented in 1991 and, since then, many diverse variants of the basic principle have been reported in the literature. The essential trait of the ACO algorithm is the combination of a priori information about the structure of a promising solution with a posteriori information about the structure of previously obtained good solutions [7].

We describe Ant Colony Optimization (ACO) as capable of solving the traveling salesman problem (TSP). Ants of the artificial colony are able to generate successively shorter feasible tours by using information accumulated in the form of a pheromone trail deposited on the edges of the TSP graph. Computer simulations demonstrate that the artificial ant colony is capable of generating good solutions to both symmetric and asymmetric instances of the TSP. The method is an example, like simulated annealing, neural networks and evolutionary computation of the successful use of a natural metaphor to design an optimization algorithm [8].

The research on a new metaheuristic for optimization is often initially focused on proof-of-concept applications. It is only after experimental work that has shown a practical interest in the method that researchers try to deepen their understanding of the method’s functioning not only through more and more sophisticated experiments but also by means of an effort to build a theory. Tackling questions such as “how and why the method works” is important, because finding an answer may help in improving its applicability. This article provided a survey on theoretical results on ant colony optimization and relations between ant colony optimization algorithms and other approximate methods for optimization [9].

Focused on a variation of the Euclidean traveling salesman problem (ETSP), namely, the generalized traveling salesman problem (GTSP), we can extend Ant Colony Optimization (ASP) method from TSP. By considering the group influence, the method is further improved. To avoid locking into local minima, a mutation process and a local searching technique are also introduced into this method. Numerical results show that the proposed method can deal with the GTSP problems fairly well, and the developed mutation process and local search technique are effective [10].

This work is proposed by combining two approaches, one optimizing TSP by using ACO [11], and the second using aerial drones in health care [12,13]. A preceding article [11] was designed to minimize TSP and find the shortest route by applying Ant System, and modelling forage in ants. So, in this paper, the phenomenon as an applicable approach of minimally optimizing routes is used to get blood delivered via drones. Here drones are acting as an artificial ants to fulfil blood necessitate in underdeveloped areas.

Ant Colony Optimization (ACO) is one of the legion intelligent approaches for answering computational problems, especially in finding the optimal paths through graphs. In history, a flating point is extensively used to represent the pheromone in ACO, therefore taking large quantities of memory to find the optimal results. Quantification-based ACS (QACS) is proposed to reduce the space complexity. New updating rules of pheromone with no decay parameters are also designed in the proposed QACS for simplifying the updating processing of pheromone. Based on the experimental results of the proposed QACS, the confluence rate can be improved with lower memory space for answering Traveling Salesperson Problem (TSP) [14].

The artificial ants are partitioned to several groups. Seven communication approaches for streamlining the pheromone position between groups in ACS are proposed. With similar or better control times than the existing ant colony (ACS) and ant system (AS), the proposed ACS with communication strategies is superior to the existing ant colony (ACS) and ant system (AS) [15].

In the second section, we proposed our methodology. In the third section, we computed our data to acquire our desired results, i.e., a minimized route for a complete network of blood banks to deliver blood or blood components via drones is discussed.

The limitations of this study are very precise. As drones are being used for our blood donation collection and distribution and unmanned products drones are expensive, they need all time maintenance, complete battery timings to reach some places. If GPS does not work properly, our drone will not appear on time and no algorithm will work on it correctly. Delimitations conclude the solutions. If we use big batteries instead of small ones, or we can install charging spots, UPS batteries or solar batteries are also very productive to enhance battery timings. Updated GPS should be installed which can direct the drones according to our optimized algorithm.

2  Methodology and Application of Algorithm

An unmanned aerial vehicle (UAV) transport for collection and distribution of blood will be used. Blood banks should be originated all over the area under consideration nominating by a vertex set B = {β1, β2, β3,…, βn }. Then connect all these blood banks by routes joining them appointed as edge set R = {r1, r2, r3,…, rn }. Those blood banks and the connection or link between them wind up as shaping a complete graph of order n.

After deriving a complete network, Travelling Salesman Problem will be applied on it. The starting vertex will be considered as a flying station, then it will cover all the blood donation centers and donate blood bottles or blood components, and then it will come back to its flying station. In this way, a closed path will be formed. This routing wants Travelling Salesman Problem that can precise a way from a starting point to all blood donation centers and back to where it took off. To succeed the procedure, some parameters such as time, distance, battery consumption will be considered. At this point, for the sake of optimizing all the routes, and ant colony system algorithm will be functional to seek the shortest round-trip to link all blood banks, supported by a group of drones Dn, each constructing one among the probably closed trips along the blood banks, to donate blood.

By using the equation below minimal path will be originated with the least cost.

Pijk=[τij]Γ[ηij]Ω∑allowedk[τij]Γ[ηij]Ω,

where nij is the nearest visibility of edge (i,j), it is value is 1n where n is the distance between blood bank i and blood bank j. Blood bank j is a set of blood banks which remain to be visited when the drone is at blood bank i. Γ and Ω are two adjustable positive parameters that control the relative weights of the pheromone trail that is demand level of blood. If Γ = 0, the closed vertex i more likely to be selected. If Ω = 0, only pheromone (demand level) amplification is at work. This method will lead the system to a stagnation situation, i.e., a situation in which the drone will generate a sub-optimal tour. So the trade-off between edge length and pheromone intensity is necessary. After the drone completes its tour, the pheromone amount on each path will be adjusted according to the equation, (1 − ρ) is the pheromone decay parameter (0 < ρ< 1) where it represents the trail evaporation when the drone chooses a blood bank and decide to move.

Lk is the length of the tour performed by drone at the end. In this application, pheromones can be customized to the demand level. After the drone complete their tour, the pheromone (demand level) is required to be updated using τij (t + 1) = (1 + ρ)τij (t) + Δτij(t),

where Δτij(t) = Σk=1mΔτijk(t) and m represents the number of drones.

TourLength=[1Lkif(i,j)ϵtourk0otherwise].

At each stage, the drones chooses to maneuver from one blood bank to a different consistent with some rules:

1.    Our drone should visit each blood bank accurately once.

2.    A detached blood bank has fewer chance of being selected (the visibility).

3.    The stronger the pheromone (demand level of blood) track rested out on link among two blood banks, link with superior prospect will be preferred.

4.    After each iteration, trails of pheromone (demand level) will be evaporated. A flowchart of methodology is given below (see Fig. 1).

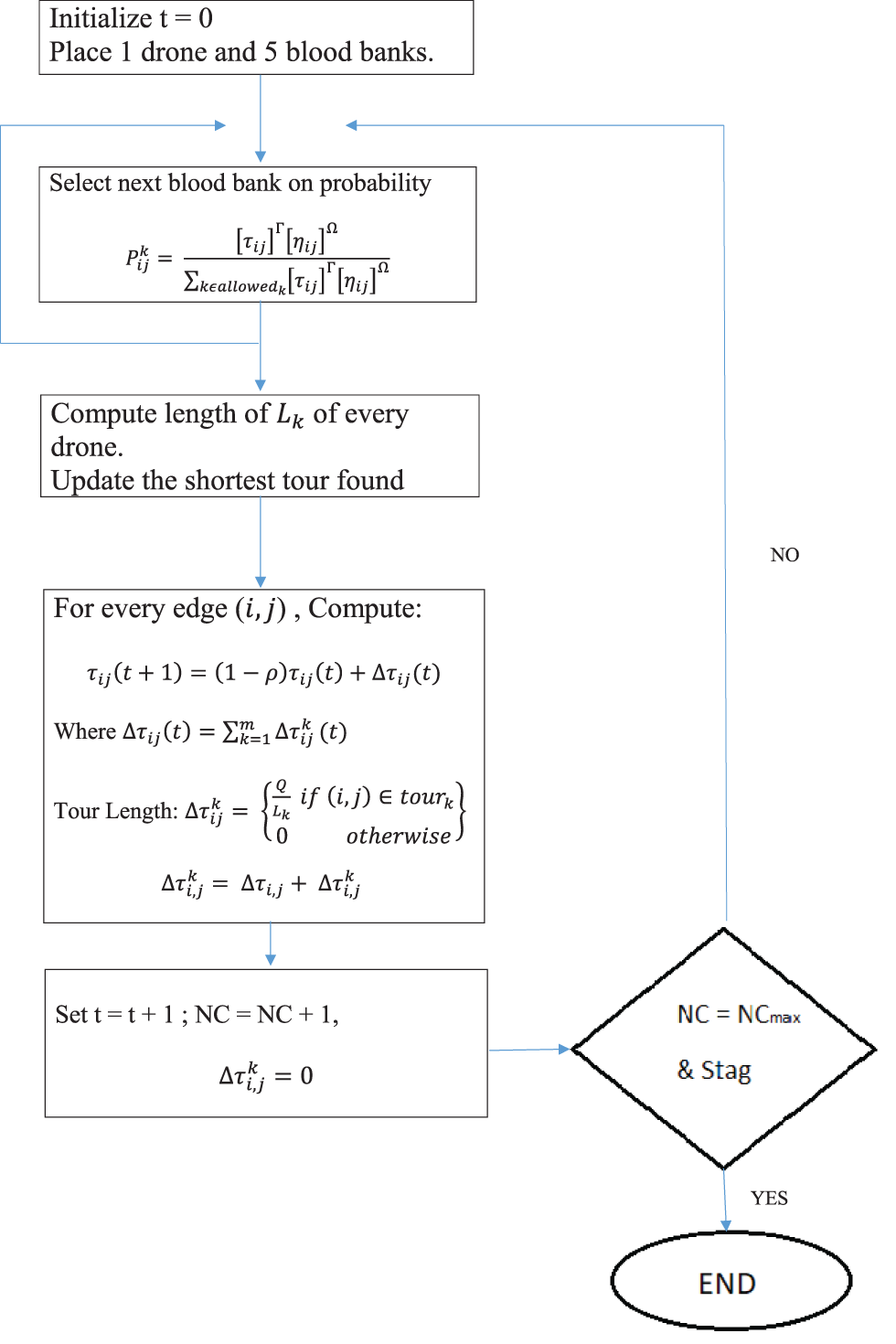
Figure 1: Flowchart to compute shortest route

3  Computation

Originating five blood banks B = {β1, β2, β3, β4, β5}, the routes between them form a complete graph of order n with 1 drone D and Γ = 0.5, Ω = 0.5. In the beginning pheromone (τ), distribution for every route is 1. Table 1 shows the membership values for distance (cost) between the blood banks B = {β1, β2, β3, β4, β5}, and the distance from the vertex to itself is undefined, i.e., it is zero. The drone is not allowed to repeat any vertex and the vertex itself in one rotation.

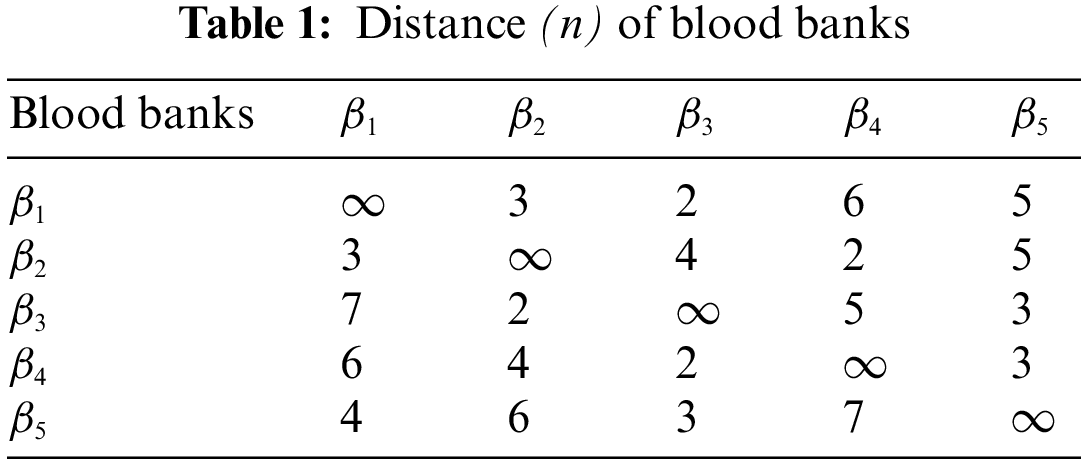
Table 2 is calculating the reciprocals of distances, for respected blood banks by 1n.

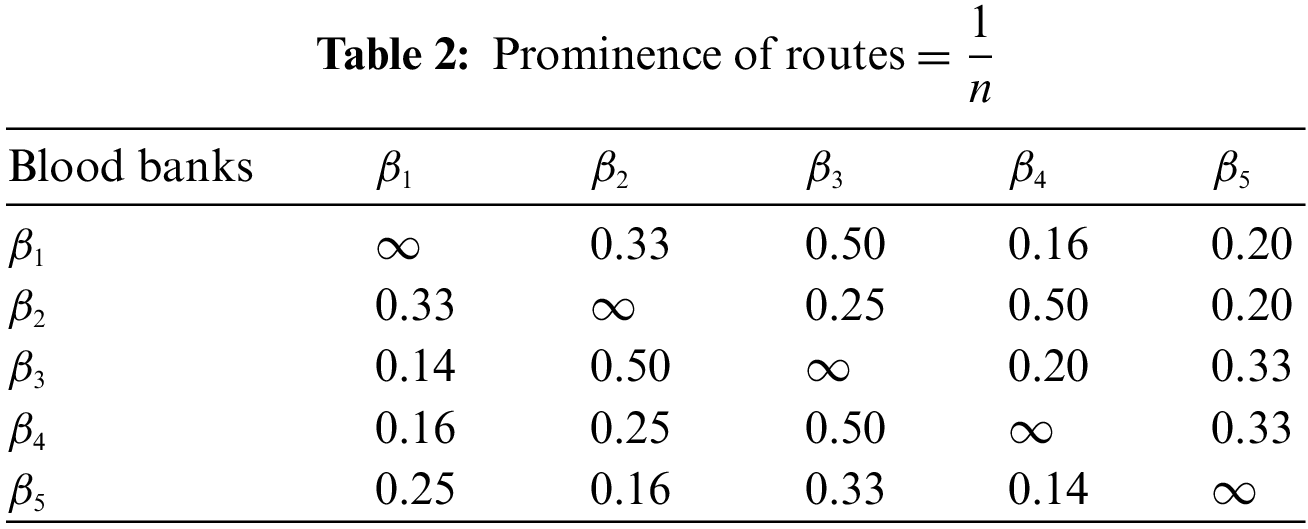
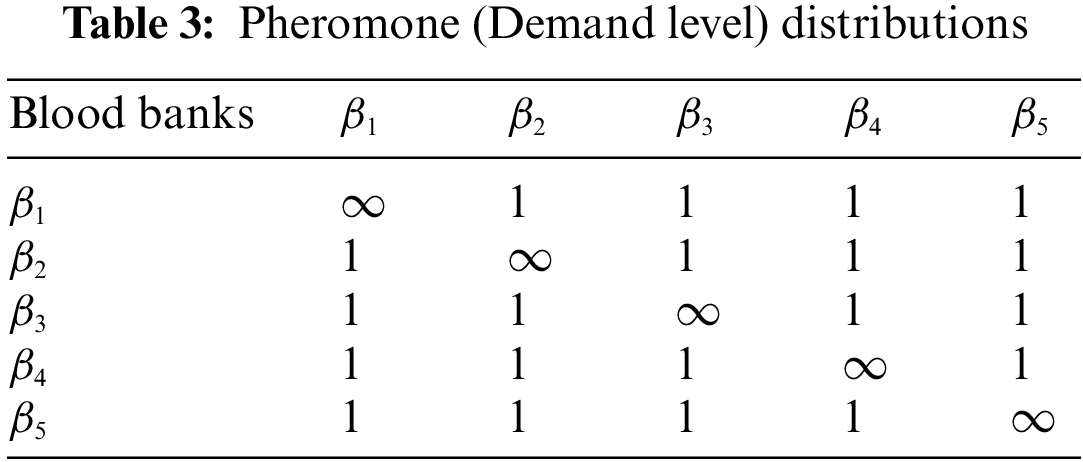
Table 3 expresses the initial pheromone level distribution on edeges/routes between blood banks. And as we are assuming pheromone level as demand of blood in blood banks. Our membership values for pheromone distribution will range between (0 to 1), hence initially it is 1 that means demand is on its extreme. After every drone rotation, the pheromone distribution that is our demand level will be updated. So now we will compute our results.

In Fig. 2, the first route is cleared which is passing through every blood bank delivering blood and then coming back to its starting point. That is, our drone started from blood bank β1 and travelled to β3 then β2 then β4 then β5 then came back to β1, and gave a minimally optimized path with the cost equals to 13. The graphical representation of first route is given in Fig. 3.

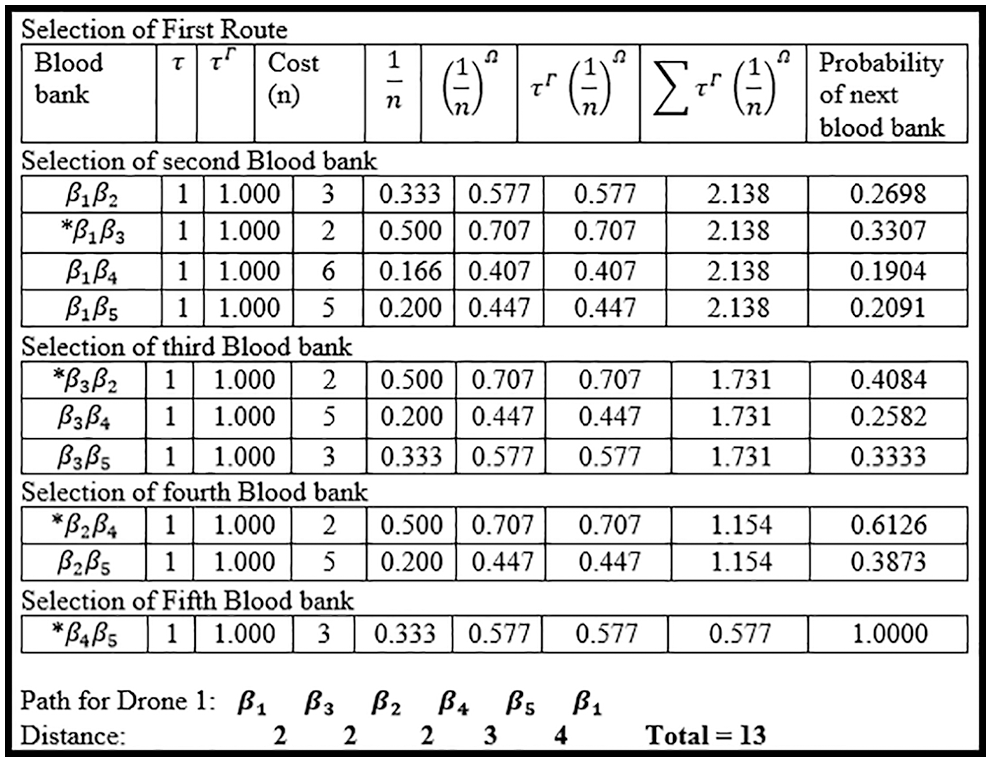
Figure 2: Selection of first route

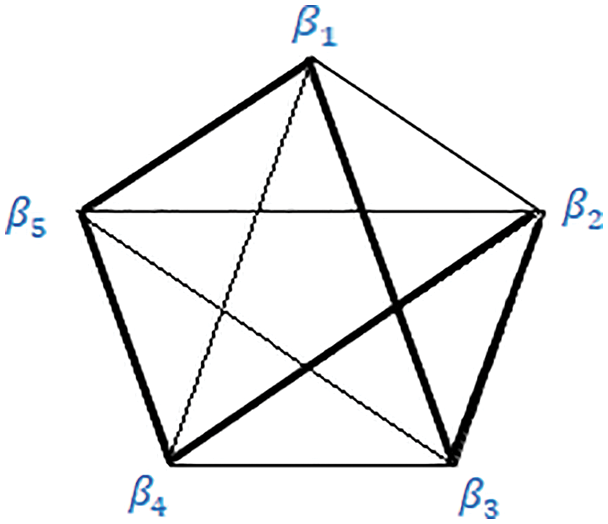
Figure 3: Graph for first route

Table 4 illustrates the membership value of evaporated pheromone that means our fulfilled demand for blood in blood banks ranging between 0 and 1.

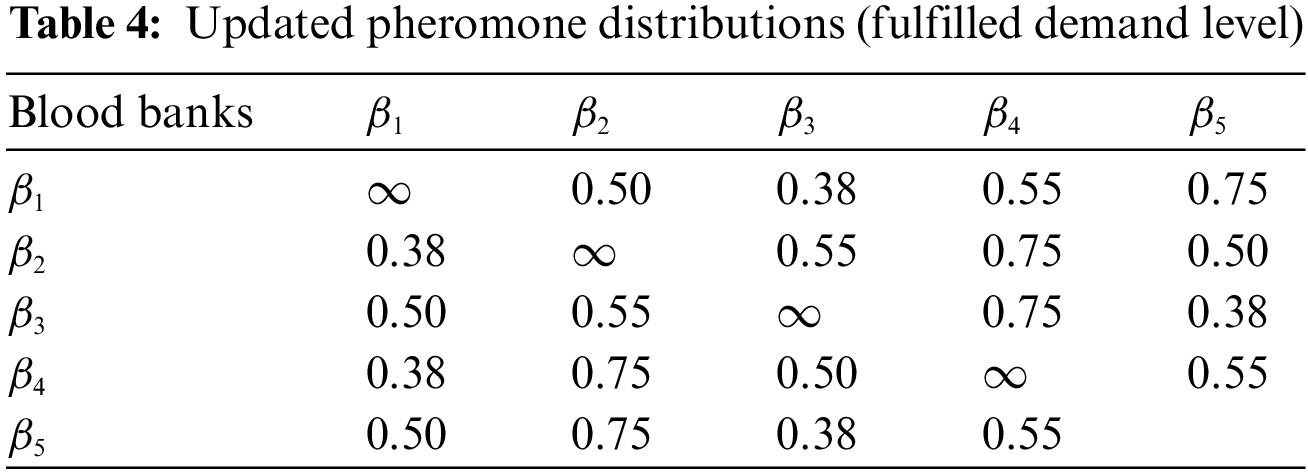
After the first rotation, the pheromone level is updated in Table 5. The value for our update pheromone shows our blood demand to be acquired, given in the membership function between 0 and 1.

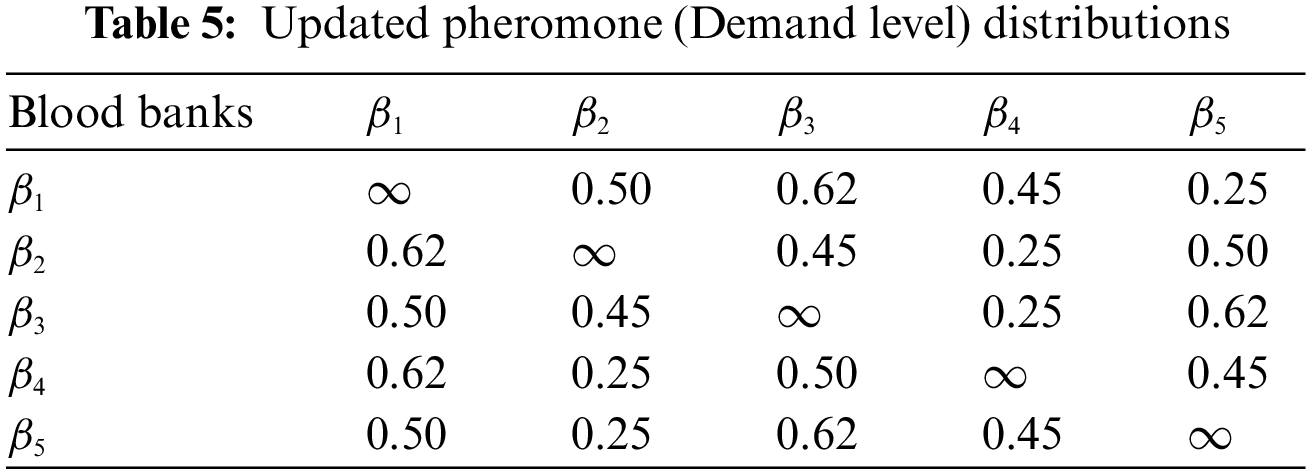
By interpretation of both Tables 4 and 5, we can represent our acquired as well as remaining blood deposition in percentage. Such that from β1 to β2, 50% is acquired and 50% is remaining, From β1 to β3, 38% is acquired and 62% is remaining. From β1 to β4, 55% is acquired and 45% is remaining. From β1 to β5, 75% is acquired and 25% is remaining. From β2 to β3, 55% is acquired and 45% is remaining. From β3 to β4, 75% is acquired and 25% is remaining. From β2 to β5, 50% is acquired and 50% is remaining. From β3 to β4, 75% is acquired and 25% is remaining. From β3 to β5, 38% is acquired and 62% is remaining. From β4 to β5, 55% is acquired and 45% is remaining.

In Fig. 4, the second path is cleared which is passed through every blood bank delivering blood and then comes back to its starting point from blood bank β2 and travels to β1 then β3 then β5 then β4 then travels back to β2, and travels a minimally optimized path with the cost equals to 19. The graphical representation of second route is given in Fig. 5.

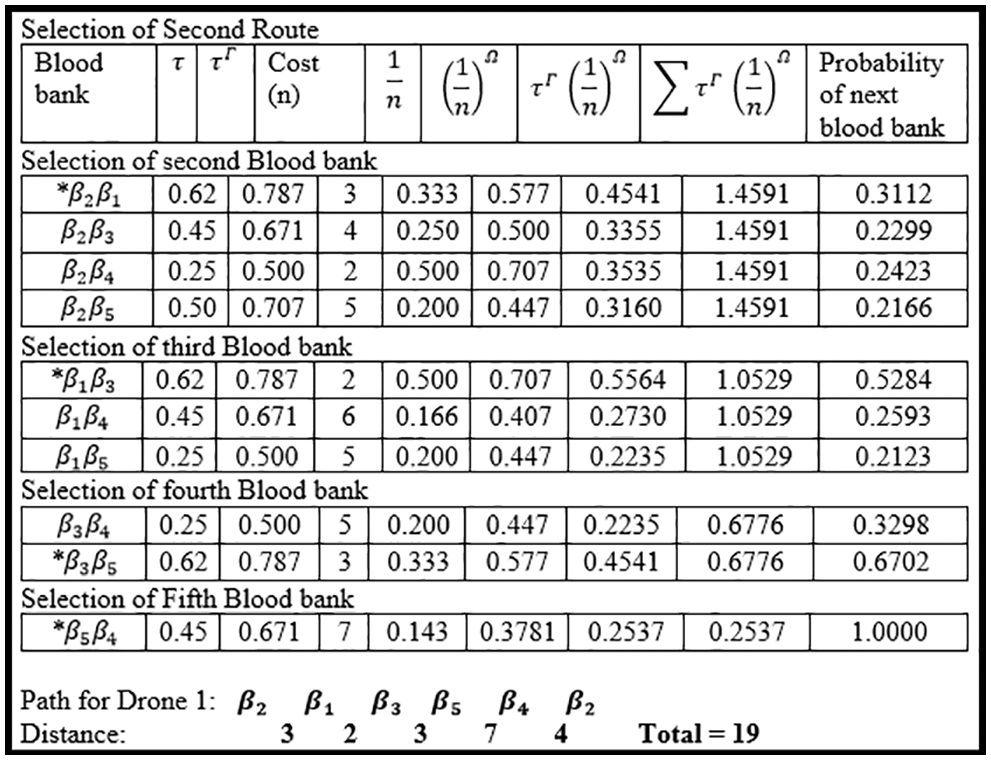
Figure 4: Selection of the second route

Figure 5: Graph for the second route

In Table 6, the membership value of evaporated pheromone is given that is our fulfilled demand.

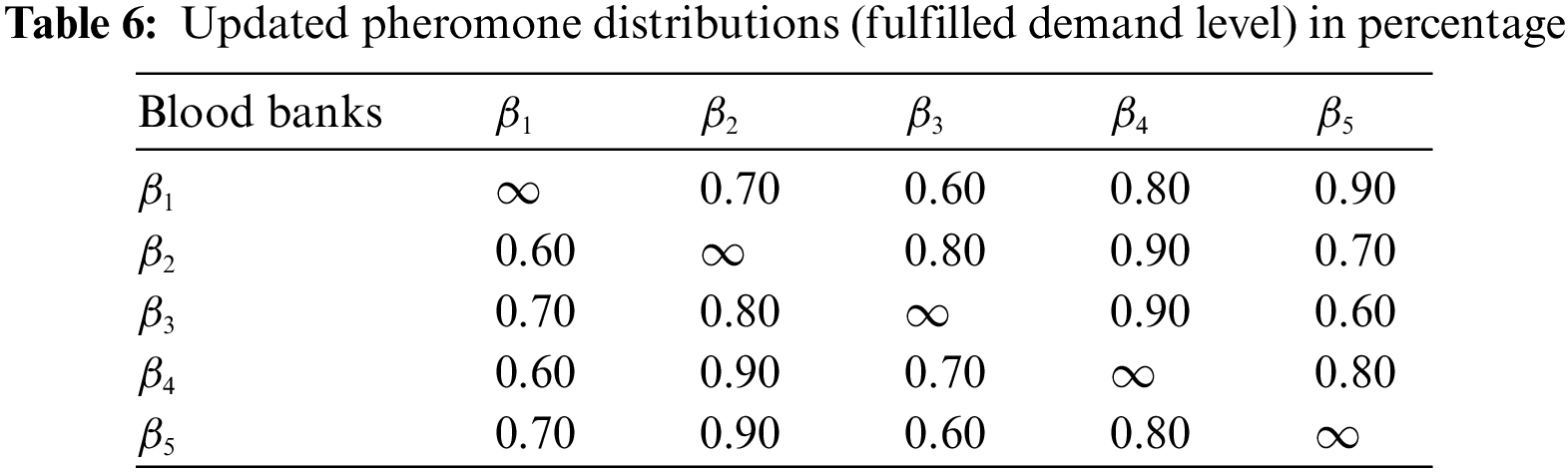
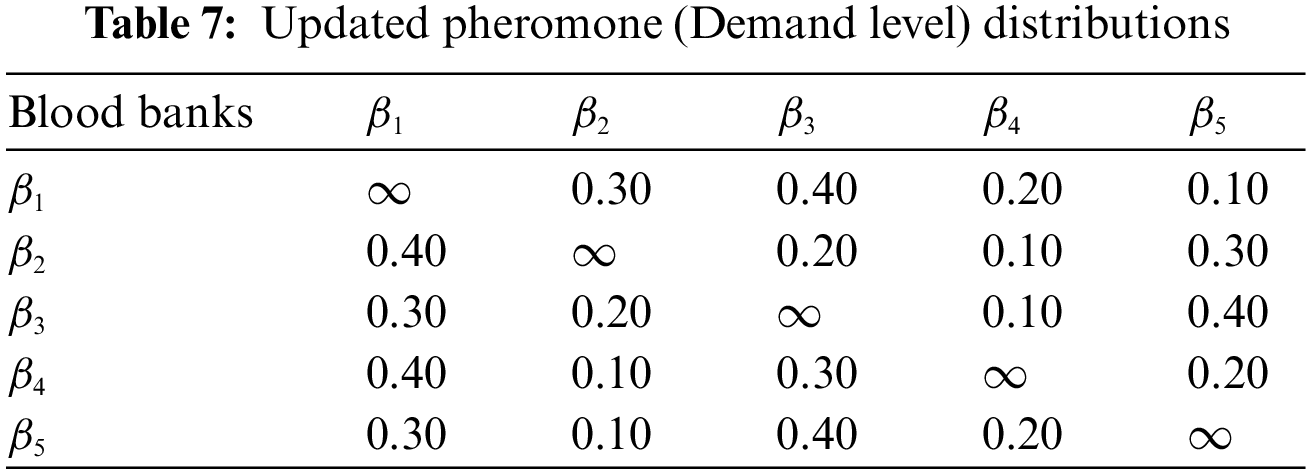
After the second rotation of our drone, the pheromone level is updated in Table 7. That is our left blood necessitate. Here we can also calculate the acquired and remaining blood demand in our blood banks. From β1 to β2, 70% is acquired and 30% is remaining. From β1 to β3, 60% is acquired and 40% is remaining. From β1 to β4, 80% is acquired and 20% is remaining. From β1 to β5, 90% is acquired and 10% is remaining. From β2 to β3, 80% is acquired and 20% is remaining. From β3 to β4, 90% is acquired and 10% is remaining. From β2 to β5, 70% is acquired and 30% is remaining. From β3 to β4, 90% is acquired and 10% is remaining. From β3 to β5, 60% is acquired and 40% is remaining. From β4 to β5, 80% is acquired and 20% is remaining.

In Fig. 6, the third route is cleared, which passes through every blood bank delivering blood and then comes back to its starting point that is our drone starts from blood bank β3 and travelled to β5 then β1 then β2 then β4 then come back to β3, and gives a minimally optimized path with the cost equals to 14. The graphical representation of the third route is given in Fig. 7. In Table 8, the percentage of evaporated pheromone is given that is our fulfilled demand.

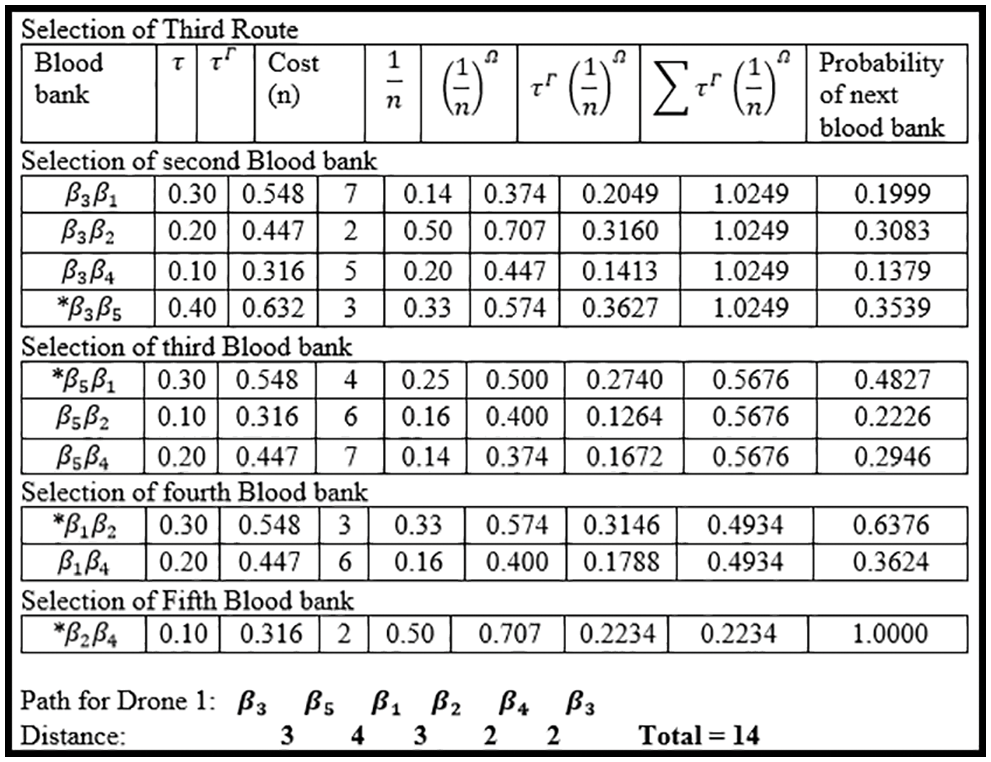
Figure 6: Selection of the third route

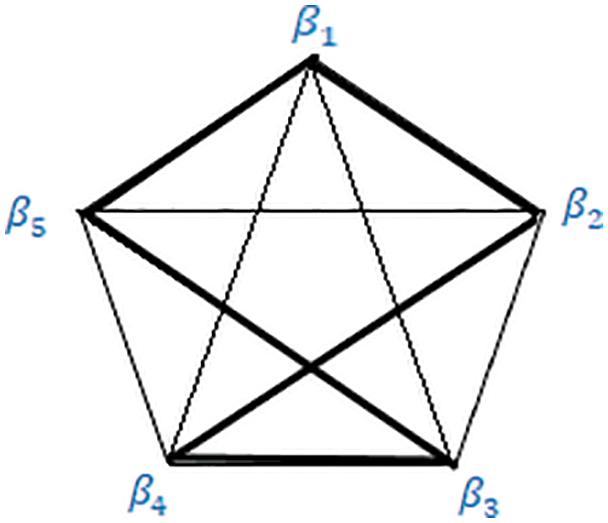
Figure 7: Graph for the third route

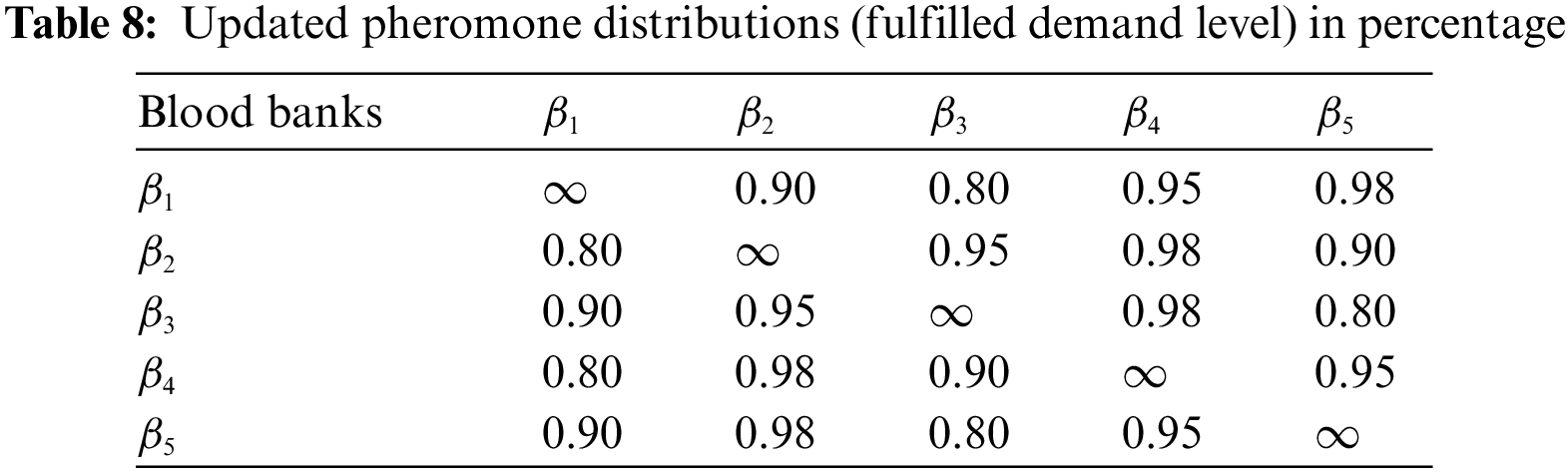
After the third rotation of our drone, the pheromone level is updated in Table 9. That is our left blood necessitate. Here we can also calculate the acquired and remaining blood demand in our blood banks. From β1 to β2, 90% is acquired and 10% is remaining. From β1 to β3, 80% is acquired and 20% is remaining. From β1 to β4, 95% is acquired and 5% is remaining. From β1 to β5, 98% is acquired and 2% is remaining. From β2 to β3, 95% is acquired and 5% is remaining. From β3 to β4, 98% is acquired and 2% is remaining. From β2 to β5, 90% is acquired and 10% is remaining. From β3 to β4, 98% is acquired and 2% is remaining. From β3 to β5, 80% is acquired and 20% is remaining. From β4 to β5, 95% is acquired and 5% is remaining. In Fig. 8, the forth route has been cleared which is passing through every blood bank delivering blood and then coming back to its starting point, i.e., from blood bank β4 and travelling to β3, β5, β1, β2 then coming back to β4, and give a minimally optimized path with the cost equals to 14. The graphical representation of the fourth route is given in Fig. 9.

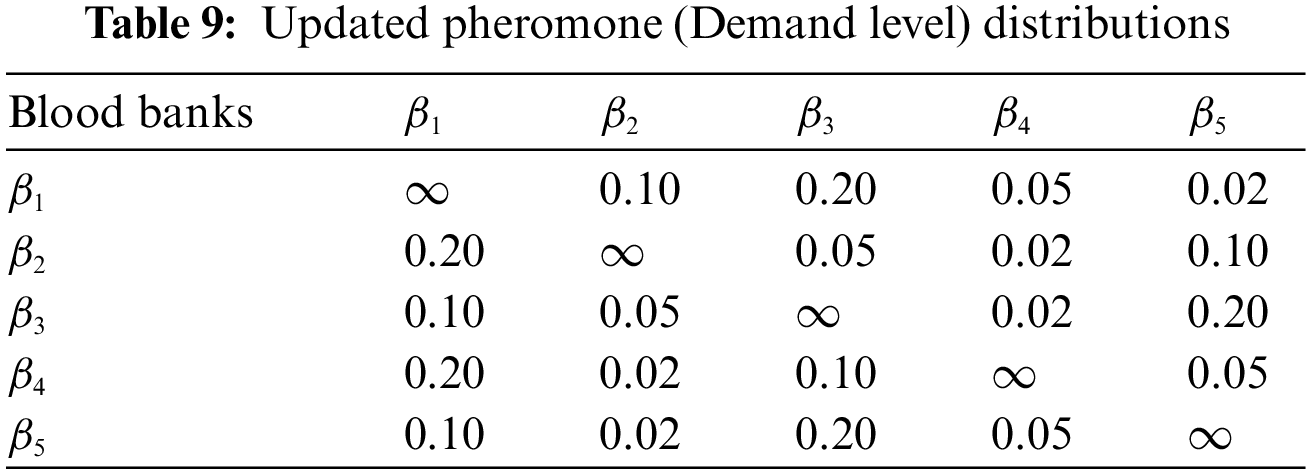
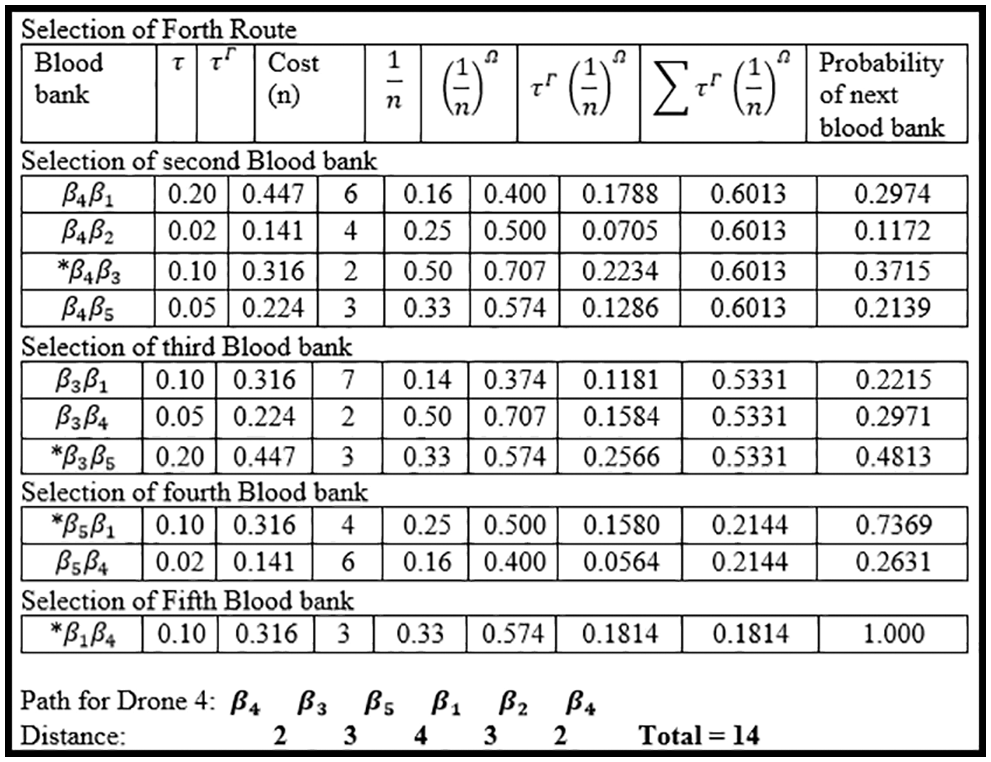
Figure 8: Selection of the fourth route

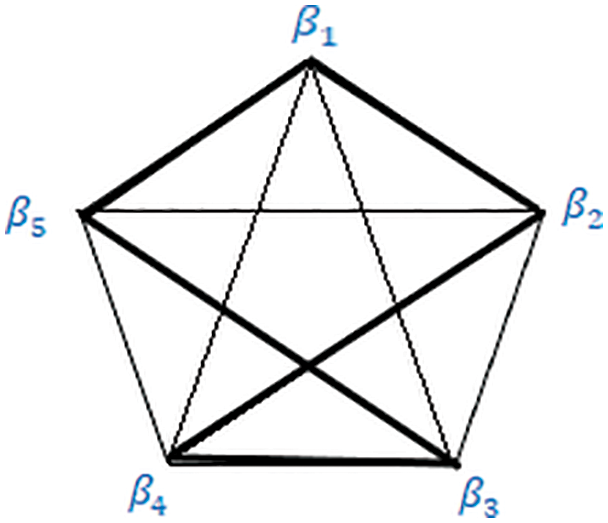
Figure 9: Graph for the fourth route

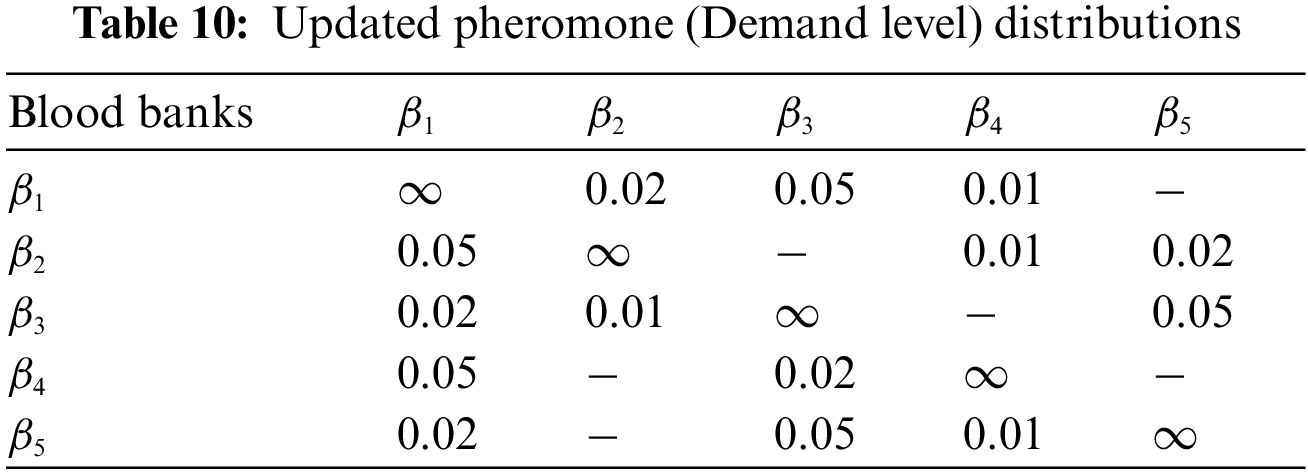
After the fourth rotation, the pheromone level is updated in Table 10, and we define the pheromone level as our demand level for blood.

In Fig. 10, the fifth route has been cleared, which passes through every blood bank delivering blood and then comes back to its starting point that is our Drone 5, it starts from blood bank β5 and travelled to β3 then β2 then β1 then β4 then come back to β5, and give a minimally optimized path with the cost equals to 17. The graphical representation of the fifth route is given in Fig. 11.

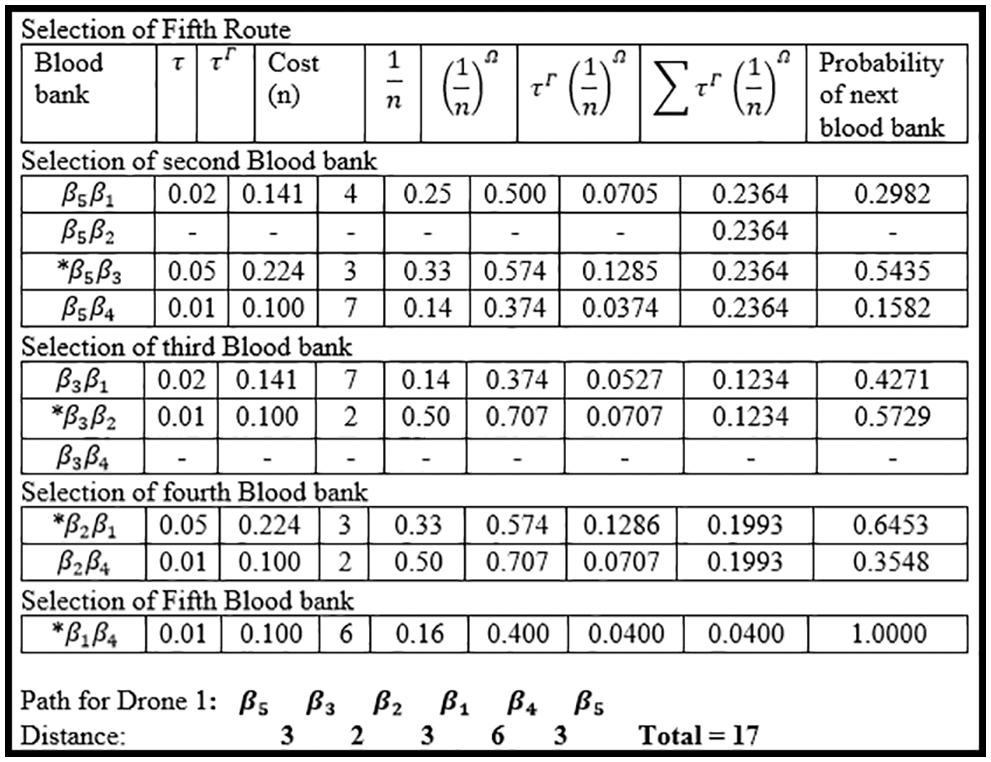
Figure 10: Selection of fifth route

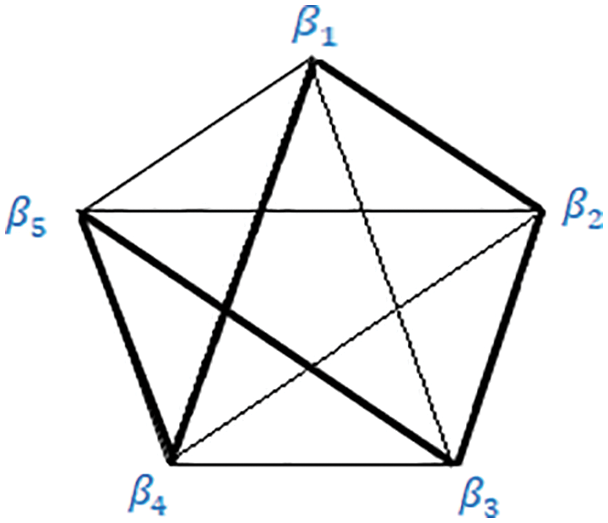
Figure 11: Graph for the fifth route

4  Conclusion

To expedite various aspects of donating blood in a faster way to underdeveloped areas, an optimized transport problem is discussed with the help of the Travelling Salesman Problem by operating the Ant Colony Optimization algorithm in this paper. A closed path is found which covers every blood bank to accommodate the demand level of each blood bank. Route 1, i.e., starting from blood bank β1 to blood bank β3, then to blood bank β2, then towards blood bank β4, then towards blood bank β5 and lastly coming back to blood bank β1 to close the path costing 13. In this way, all the blood demand will be fulfilled.

There are many algorithms to find the shortest paths, e.g., Dijkstra’s algorithm, A* search algorithm. In this research, the Travelling Salesman Problem and ACO for minimally optimizing are used because we want a route that covers every vertex without repeating any edge in a network of the complete graph of order n. After acquiring that path, our blood demand is used as a pheromone density to minimize our path towards our demand and apply ant system.

Acknowledgement: The authors would like to express their sincere gratitude to the anonymous referees for their valuable suggestions, which led to great deal of improvement of the original manuscript.

Funding Statement: The authors received no specific funding for this study.

Availability of Data and Materials: My manuscript has no associated data.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Masser, B. M., White, K. M., Hyde, M. K., Terry, D. J. (2008). The psychology of blood donation: Current research and future directions. Transfusion Medicine Reviews, 22(3), 215–233. DOI 10.1016/j.tmrv.2008.02.005. [Google Scholar] [CrossRef]

    2. Liu, J. B., Zhao, J., He, H., Shao, Z. (2019). Valency-based topological descriptors and structural property of the generalized sierpinski networks. Journal of Statistical Physics, 177, 1131–1147. DOI 10.1007/s10955-019-02412-2. [Google Scholar] [CrossRef]

    3. Chartrand, G., Lesniak, L., Zhang, P. (2016). Graphs and digraphs. 6th edition. USA: Taylor and Francis Group. [Google Scholar]

    4. Laporte, G., Martello, S. (1990). The selective travelling salesman problem. Discrete Applied Mathematics, 26(2–3), 193–207. DOI 10.1016/0166-218X(90)90100-Q. [Google Scholar] [CrossRef]

    5. Laporte, G., Asef-Vaziri, A., Sriskandarajah, C. (1996). Some applications of the generalized travelling salesman problem. Journal of the Operational Research Society, 47(12), 1461–1467. DOI 10.1057/jors.1996.190. [Google Scholar] [CrossRef]

    6. Gavish, B., Graves, S. C. (1978). The travelling salesman problem and related problems and related problems. https://hdl.handle.net/1721.1/5363. [Google Scholar]

    7. Maniezzo, V., Gambardella, L. M., de Luigi, F. (2004). Ant colony optimization. New Optimization Techniques in Engineering, 101–121. DOI 10.1007/978-3-540-39930-85. [Google Scholar] [CrossRef]

    8. Dorigo, M., Gambardella, L. M. (1997). Ant colonies for the travelling salesman problem. Biosystems, 43(2), 73–81. DOI 10.1016/S0303-2647(97)01708-5. [Google Scholar] [CrossRef]

    9. Dorigo, M., Blum, C. (2005). Ant colony optimization theory: A survey. Theoretical Computer Science, 344(2–3), 243–278. DOI 10.1016/j.tcs.2005.05.020. [Google Scholar] [CrossRef]

  10. Yang, J., Shi, X., Marchese, M., Liang, Y. (2008). An ant colony optimization method for generalized TSP. Progress in Natural Science, 18(11), 1417–1422. DOI 10.1016/j.pnsc.2008.03.028. [Google Scholar] [CrossRef]

  11. Raghavendra, B. V. (2015). Solving traveling salesmen problem using ant colony optimization algorithm. Journal of Applied Computational Mathematics, 4(6). DOI 10.4172/2168-9679.1000260. [Google Scholar] [CrossRef]

  12. Hiebert, B., Nouvet, E., Jeyabalan, V., Donelle, L. (2020). The application of drones in healthcare and health-related services in North America: A scoping review. Drones, 4(3), 30. DOI 10.3390/drones4030030. [Google Scholar] [CrossRef]

  13. Ling, G., Draghic, N. (2019). Aerial drones for blood delivery. Transfusion, 59(2), 1608–1611. DOI 10.1111/trf.15195. [Google Scholar] [CrossRef]

  14. Zhao, M., Pan, J. S., Lin, C. W., Yan, L. (2013). Quantification-based ant colony system for TSP. In: Genetic and evolutionary computing, pp. 331–339. [Google Scholar]

  15. Chu, S. C., Roddick, J. F., Pan, J. S. (2004). Ant colony system with communication strategies. Information Sciences, 167(1–4), 63–76. DOI 10.1016/j.ins.2003.10.013. [Google Scholar] [CrossRef]