Strong Tracking Particle Filter Based on the Chi-Square Test for Indoor Positioning

1  Introduction

Accurate location information can greatly facilitate our daily lives, such as shopping guides in supermarkets and car searching in garages. The Global Navigation Satellite System (GNSS) can provide reliable positioning information in outdoor open areas [1]. However, the positioning accuracy of GNSS will be greatly reduced or even invalid in indoor environments because the satellite signal is blocked by the building. Accordingly, researchers are also exploring the indoor positioning potential of wireless signal, such as Wi-Fi [2–6], Bluetooth [7,8], UWB [9,10], ultrasound [11–13], infrared [14], and visible light [15]. Wi-Fi positioning technology has wide coverage and does not require additional equipment. UWB technology has also received extensive attention and research with its centimeter-level positioning accuracy. Wireless technologies, such as ultrasound, infrared [14], and visible light [15], can also provide higher positioning accuracy. However, the wireless signal is seriously affected by the indoor environment, especially in the NLOS environment. The positioning error of wireless indoor positioning will sharply increase when an obstacle exists between the mobile terminal and the positioning base station due to the influence of the multipath effect [16–18].

To solve this problem, some scholars have proposed many methods to identify and mitigate the NLOS effect. In reference [16], the indoor positioning problem is converted to a generalized trust-region subproblem. Then, an estimator based on the squared-range method and the weighted least squares criterion is developed to obtain the exact solution only through the bisection process, thus reducing the influence of NLOS bias on the positioning results. Pak et al. [17] proposed an NLOS mitigation algorithm based on distributed filtering. This algorithm uses the ellipsoidal gating algorithm to identify NLOS and reduces the impact of NLOS through a distributed method. Although these methods can identify and mitigate the impact of NLOS bias, they still cannot eliminate the impact of NLOS because no other sensor information is available to assist. The Geometry-Assisted Location Estimation (GALE) [19] algorithm based on the three TOA measurements estimates the position of the mobile station with reasonable accuracy. The Modified Geometry Aided Location Estimation (MGALE) [20] algorithm considers the intersection of the common chords of the range circles and the geometry of these range circles, rather than relying on the standard deviation of TOA measurements to estimate the position of mobile station. As the MGALE reduces the area of the area where the mobile station is located, it provides better positioning accuracy compared to the GALE in the presence of NLOS errors. However, it only mitigates the effect of NLOS error rather than eliminates the effect of NLOS error completely.

Therefore, some scholars combine wireless indoor positioning algorithms with pedestrian dead reckoning (PDR) algorithms to achieve continuous and accurate indoor positioning [7–8,10,21]. The PDR algorithm can only rely on the IMU sensor embedded in the smartphone to estimate the direction and distance of the movement of the moving target and calculate the location of the moving target [7,22]. Accordingly, PDR cannot be affected by NLOS. However, PDR only provides relative position information, and its error will continue to accumulate with the number of moving steps. The wireless positioning algorithm and the PDR algorithm have their advantages and disadvantages and complementary characteristics. The fusion positioning of the two algorithms is currently the most common and effective way to improve the positioning performance of the indoor positioning system. Currently, the common fusion algorithms include Kalman filter (KF) and particle filter (PF) algorithms. KF algorithm is currently the most widely used information fusion algorithm. For example, Yu et al. proposed a precise dead reckoning algorithm based on Bluetooth and multiple sensors (DRBMs). DRBMs combine the Bluetooth signal strength and the positioning result of the mobile phone IMU sensor through the KF [7]. NI-hybrid positioning system uses KF to identify NLOS environments and mitigate UWB errors through PDR [21]. However, the KF algorithm requires an accurate system model and noise type [23], which is not easy to obtain in practice. Scholars have proposed many solutions to address this problem. These methods can be divided into two categories. The first one is the adaptive KF (AKF), which can estimate and modify the statistical characteristics of the model parameters and noise according to the dynamic characteristics of the system to reduce the actual error of the filter [24]. The other one is the strong tracking filter (STF). STF dynamically adjusts the covariance matrix by introducing a fading factor to constrain the output of the filter [25,26]. The PF algorithm can handle systems with non-Gaussian noise and is relatively easy to implement [17]. Reference [10] proposed a UWB/inertial navigation system (UWB/INS) algorithm. This algorithm calculated the position through the UWB-based joint state estimation PF algorithm and solved the navigation information through the INS-based Zero Velocity Update (ZUPT) algorithm. Finally, the navigation information of the two systems is fused under the framework of the INS error equation. Conventional PF mostly uses the distance between the predicted value of the particle’s observation value and the observation value to determine the weight of the particle. However, the observation value in an indoor environment is severely affected by noise; if it is affected by NLOS, then a large positioning deviation will occur, which affects the result of PF.

To achieve continuous and accurate positioning in a complex indoor environment, this paper proposed a new indoor fusion algorithm, namely the strong tracking PF based on the chi-square test (SPFC). The SPFC algorithm first uses PDR as the reference system and STF as the signal processor. Then, SPFC uses the chi-square test (CST) to detect whether the wireless indoor positioning algorithm is affected by NLOS. Next, the state transition is based on the framework of PF. If the CST does not detect the influence of NLOS, then the states of particles are transferred according to the result of PDR. The result of STF is used as the observation value to obtain the weights of particles. Meanwhile, the result of the PF is calculated based on the weighted average. Otherwise, SPFC only uses the result of PDR for the PF and directly calculates the result of the PF. Finally, the result of PF is used to update the estimated states of PDR and STF. Simulation results show that SPFC can significantly improve the accuracy of indoor positioning in the LOS/NLOS environment.

The main contributions of this paper are as follows: (1) The SPFC determines whether the current wireless indoor positioning result is affected by NLOS by CST; (2) The SPFC uses the result of STF as the observation value to obtain weights of particles and improve the accuracy of PF; (3) When the NLOS deviation is eliminated, the strong tracking ability of STF can quickly restore the positioning and tracking of the moving target.

The structure of this paper is arranged as follows: Section 2 introduces the fusion positioning scheme of wireless indoor positioning and PDR. Section 3 introduces the implementation details of the proposed strong tracking PF based on the CST, and Section 4 illustrates the simulation experiment. Section 5 summarizes the effectiveness of the proposed method.

2  Preliminaries

A wireless indoor positioning system consists of a moving target and no less than three positioning base stations in the 2D plane [17]. The positioning base station can be a wireless signal transmitting device, such as Bluetooth and UWB, and is generally installed in a fixed location to transmit wireless signals. A moving target refers to an object carrying a wireless signal receiving device. In this work, a moving target refers to a pedestrian carrying a smartphone. The smartphone is used not only to receive the wireless signals sent by the positioning base station but also to process the received wireless signals to parse out relevant information and calculate the location of the moving target. The range between the moving target and each positioning base station can be calculated according to the time of arrival (TOA) of the received signal or received signal strength (RSS). When the ranging measurement values of at least three positioning base stations are available, the position of the moving target can be calculated by the trilateral positioning method. Adding positioning base stations can improve the positioning accuracy, but it also increases the computational burden and hardware cost.

To implement the STF and PF, the state and observation equations of the indoor fusion positioning system must be established. The motion model of the moving target is required for the construction of the system state equation. In this work, the moving target is a pedestrian carrying a smartphone. Hence, the PDR algorithm obtains the movement information of the moving target based on the data of the IMU sensors embedded in the smartphone. PDR calculates the pedestrian’s position at the current time instant based on the pedestrian’s previous position, step length, and heading angle. As shown in Fig. 1, assuming that the pedestrian’s previous position is (xk−1,yk−1)T, the forward step length is dk, and heading angle is αk, the current position of the pedestrian can be determined by using formula (1):

xk=xk−1+dk−1cos⁡αk−1yk=yk−1+dk−1sin⁡αk−1.(1)

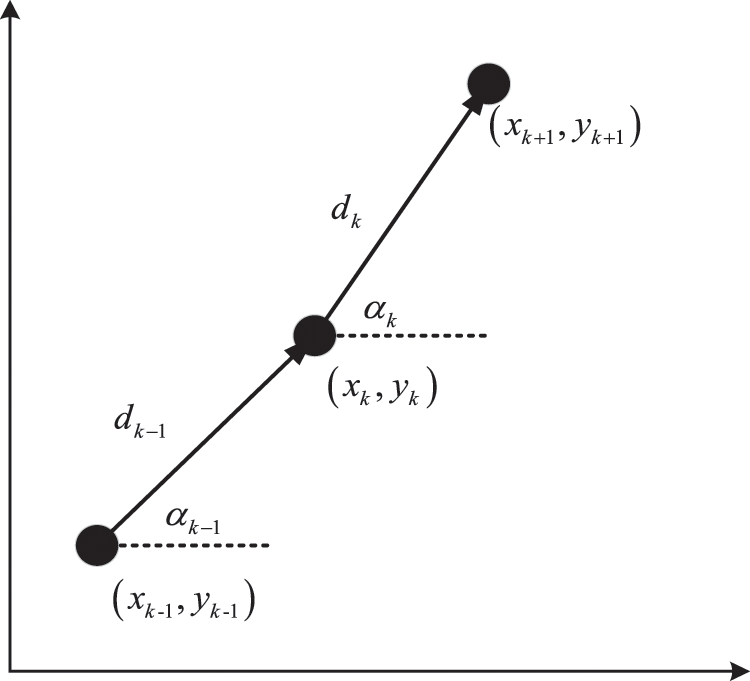
Figure 1: Schematic of the PDR algorithm principle

Accordingly, the state equation of the system is:

Xk=FXk−1+Uk−1+Wk,(2)

where Xk=(xk,yk)T is the system state variable; F is the transition matrix; here it is an identity matrix; Wk−1 is the process noise; and Uk−1=[dk−1cos⁡αk−1dk−1sin⁡αk−1] is the input vector. The process noise covariance is Qk−1=E(Wk−1Wk−1T).

In addition, the observation equation of the system is:

Zk=HXk+Vk,(3)

where Zk is the location vector of the moving target obtained by using a kind of wireless indoor positioning technology. H is the observation matrix because the result of wireless positioning is also horizontal and vertical coordinates of the target. Accordingly, the observation matrix is an identity matrix. Vk is measurement noise, which is the positioning error caused by the ranging noise. The measurement noise covariance is Rk=E(VkVkT).

3  SPFC

SPFC can be divided into three parts, as shown in Fig. 2. First, SPFC uses PDR as the reference system and STF as the signal processor. Next, SPFC uses the CST to detect whether the result of the wireless indoor positioning algorithm is affected by NLOS. Then, the state transition is based on the framework of the PF. The rules for state transition are as follows. If the CST does not detectthe influence of NLOS, then the states of the particles are transferred according to the result of PDR. The result of STF is used as the observation value to obtain the weights of the particles. Meanwhile, the result of the PF is calculated based on the weighted average. Otherwise, SPFC only uses the result of PDR for the PF and directly calculates the result of the PF. Finally, the result of the PF is used to update the estimated states of PDR and STF.

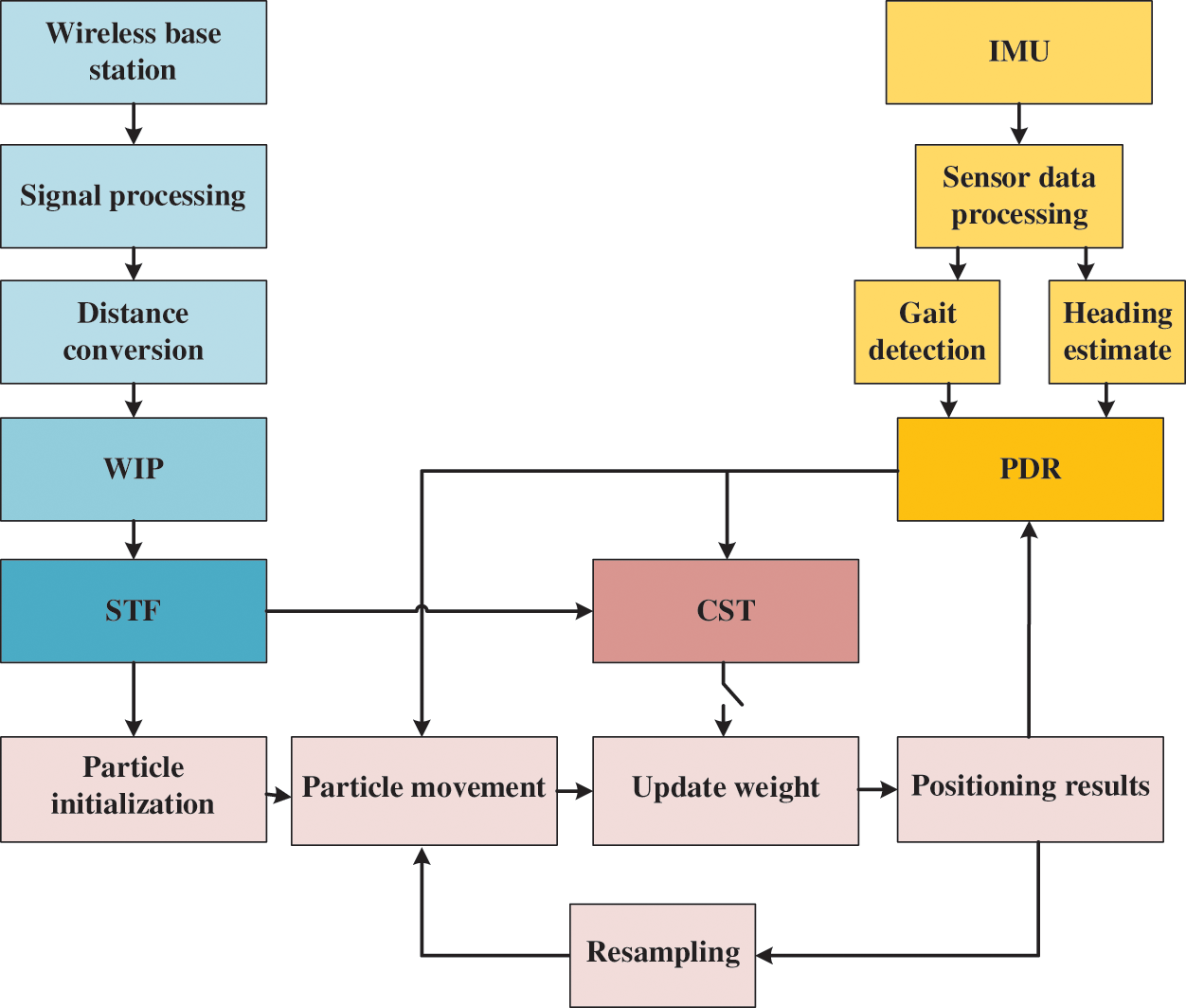
Figure 2: Basic architecture of SPFC

3.1 STF

In the actual application process, an accurate motion model of the moving target is impossible to obtain due to the poor measurement accuracy of the IMU sensors of the smartphone. In addition, the indoor environment is complex and changeable, and the noise parameters of the various wireless positioning technologies are prone to change. Accordingly, this work used the STF algorithm to estimate the current position based on the state equation and observation equation of the indoor fusion positioning system and provided pre-information for the subsequent CST and PF. Given that the STF also adopts the structural framework of the KF, it has the following general structure [25]: uses the state transition matrix to perform one-step prediction to obtain the state prediction:

X^k|k−1=FX^k−1.(4)

Calculates the covariance matrix of the state prediction:

Pk|k−1=λkFPk−1FT+Qk,(5)

Calculates the filter gain:

Kk=Pk|k−1HT(HPk|k−1HT+Rk)−1,(6)

Uses the measurement information to calculate the state estimates:

X^k=X^k|k−1+Kk(Zk−HX^k|k−1),(7)

Calculates the covariance matrix of the state estimation:

Pk=(I−KkH)Pk|k−1,(8)

STF only adds a fading factor when calculating the covariance matrix Pk|k−1 of one-step prediction compared with the conventional KF. The gain matrix Kk can be adjusted by the fading factor to ensure that the output residual satisfies the orthogonality. Therefore, the calculation of the fading factor is the key to STF. The process of obtaining the fading factor is as follows [25]:

V0,k={γ1γ1Tk=1ρV0,k−1+γkγkT1+ρk>1.(9)

Nk=V0,k−HQk−1HT−βRk.(10)

Mk=HFPk−1FTHT.(11)

λ0,k=tr(Nk)tr(Mk).(12)

λk={λ0,kλ0,k≥11λ0,k<1.(13)

where γk is the residual information with γk=Zk−HX^k|k−1. tr(⋅) represents the computing of the trace of the matrix. ρ is the forgetting factor, and its value range is generally 0.95–0.99. β is a weakening factor (β≥1), and its function is to make the values of the state estimation smoother. The value of β is obtained through experience, and no theoretical solution method is available.

3.2 NLOS Detection Based on CST

The focus of this work is to discuss how to eliminate the impact of NLOS deviation in indoor positioning. As previously discussed, STF can adjust the gain matrix by using the residual information of the observation and expected values. Therefore, the STF is more dependent on the result of wireless positioning. In the NLOS environment, the measurement deviation of the wireless signal will sharply increase and may even get the wrong positioning result. This work adopts the CST [23] to detect NLOS deviation. Specifically, this method uses PDR as the reference system and defines its state estimation and covariance matrix based on a prior system model.

X^pdr,k|k−1=FX^pdr,k−1Ppdr,k=FPpdr,k−1FT+Qk.(14)

After the PF fusion, the state of PDR will be updated as follows:

X^pdr,k=X^pf,k,(15)

where X^pf,k is the final result of the PF at the kth time instant. Meanwhile, the state estimation and covariance matrix of the STF can be obtained: X^stf,k and Pstf,k. Then, the difference between the two estimates can be simplified as follows:

rk=X^stf,k−X^pdr,k|k−1.(16)

The difference between the two estimates is a Gaussian random vector with zero mean and covariance of Ck and,

Ck=E[rkrkT]=Pstf,k−Ppdr,k(17)

Then,

ξk=rkTCk−1rk.(18)

ξk satisfies the chi-square distribution of two degrees of freedom [25]. Therefore, the NLOS detection rules can be:

ifξk≥ηNLOSifξk<ηLOS,(19)

where η is the selected decision threshold. In this paper, η is set to 0.211, which is the chi-square value at P = 0.9 in the chi-square test table.

When the wireless indoor positioning is affected by NLOS, it will produce a huge positioning deviation. In this case, if the positioning deviation is not timely isolated, the final positioning result will be worse. The wireless indoor positioning result with a huge deviation will be isolated to ensure the validity of the fusion result. Specifically, the positioning result of STF is not used in the fusion process of PF. However, the states of particles are updated, and the current position is estimated based only on PDR.

3.3 SPFC

According to the results of the CST, if the deviation of the wireless indoor positioning result is considerably large, the states of the particles will be transferred based on PDR only. However, the weights of the particles will not be updated. Otherwise, the states of the particles are transferred based on PDR. The weights of the particles will be updated according to the result of STF. After calculating the position estimation of the moving target based on the states and weights of the particles, the result of the PF is taken as the current position of the moving target. The specific process is as follows.

The first step of the SPFC needs to initialize the particles. This work uses wireless indoor positioning to obtain the initial position of the moving target. Then, SPFC uses the result of PDR to transfer the states of particles according to the following rules:

xk⌊k−1i=xk−1i+dk−1cos⁡αk−1yk⌊k−1i=yk−1i+dk−1sin⁡αk−1,(20)

where dk−1 and αk−1 are the pedestrian movement step length and the angle between the walking direction and the reference coordinate system, respectively.

According to the result of the CST, the weights of all particles are not updated if the positioning result of STF has a huge deviation. We will directly calculate the result and update the result of the STF. Otherwise, the weights of all particles will be updated according to the result of STF. The specific calculation rules are as follows: suppose the output result of the STF is (x^stf,k,y^stf,k)T, the weight of each particle is:

ωk|k−1i¯=12πσk,x2σk,y2e(x^stf,k−xki)2−2σk,x2+(y^stf,k−yki)2−2σk,y2,(21)

ωki¯=ωk−1iωk|k−1i¯.(22)

Then, the weight is normalized to:

ωki=ωki¯∑i=1Nωki¯.(23)

Then, the estimated position of the moving target at kth time instants can be expressed as follows:

{xk=∑i=1Nωkixkiyk=∑i=1Nωkiyki(24)

After this method obtains an estimation result to prevent particle degradation, the particles need to be resampled. The resampling rule in this work is as follows. If the weight of a particle is less than a fixed threshold, then the particle is invalid. This threshold is set to one-tenth of the reciprocal of the total number of particles in this paper. Suppose the number of invalid particles is M. If M is greater than one-third of the total number of all particles, then all particles will be reinitialized according to the result of STF. Otherwise, the invalid particles will be deleted, and the particles with the largest weight will be copied M times. Then, the resampled particles are normalized again.

When the PF obtains the final estimate, the state of the PDR and STF will also be adjusted to the estimated value of the PF. On the one hand, this method can prevent the accumulation of errors in the PDR. On the other hand, this method can prevent the deterioration of the performance of STF due to NLOS, which in turn affects the performance of the CST and the PF.

4  Experimental Design and Result Analysis

This section will verify the effectiveness of the proposed indoor fusion positioning algorithm (SPFC) through simulation experiments. All experiments of this work were conducted on a 64 bit Windows 10 operating system computer using Python (3.7.9). The CPU is Intel (R) Core (TM) i5-6500, the main frequency is 3.20 GHz, and the memory is 16 G. In the simulation experiments, the SPFC algorithm was compared with KF, STF, PF, and STF based on the CST (STFC). The STFC algorithm does not use the PF algorithm to fuse the results of the PDR and STF compared with the SPFC algorithm. Instead, this algorithm decides to use the result of the PDR or the STF directly as the final positioning result based on the result of the CST.

4.1 Experimental Design

The parameters of the simulation experiment in this work were set as follows: The motion model of the moving target [8] was:

L=L0+A+Xσ1θ=θ0+B+Xσ2,(25)

where L0 and θ0 are the real step length and direction of each step of the moving target, respectively; and A and B are constants. A used to simulate the measurement error caused by the IMU sensors. B used to simulate the ranging error caused by the wireless positioning sensors. We set A=0.1m and B=3∘. Xσ1 and Xσ2 are Gaussian noises with zero mean, where σ1 and σ2 are standard deviations, set to σ1=0.1 and σ2=5.87, respectively.

The simulation scene is shown in Fig. 3. The four positioning base stations are arranged at four locations with coordinates (0, 0), (50, 0), (0, 50), and (50, 50), where the unit is meter. The moving target takes the smartphone away from the position (0, 0) and moves clockwise along the rectangular track. The movement speed is v=0.6m/step, and the simulation time is Ts=400 step.

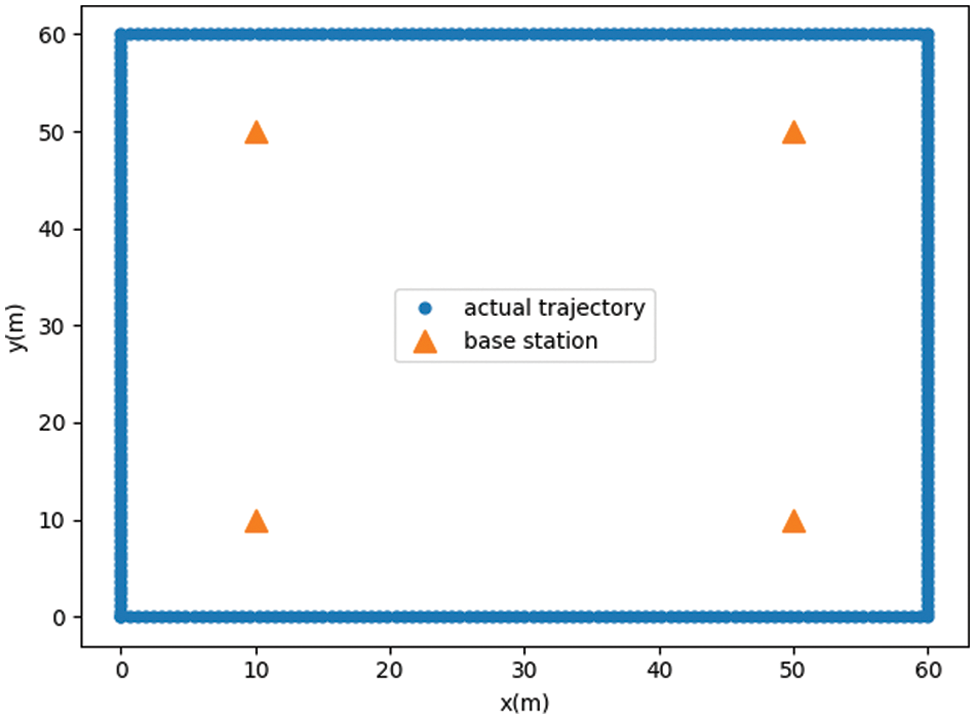
Figure 3: Schematic of the simulation scene. The blue solid line represents the trajectory of the moving target. The yellow triangle indicates the location of the base station

The wireless indoor positioning used the trilateration algorithm based on ranging for positioning. The noise of the distance measurement obeys the Gaussian noise with the mean value of zero and the standard deviation of σ. In addition, the obstacle is assumed to be a cylinder with a radius of r m to simulate the NLOS situation. This assumption simplifies the calculations used to identifythe NLOS situation. Suppose the distance from the center of the obstacle to the straight line between the moving target and the positioning base station is less than the radius of the obstacle. In that case, the moving target and the positioning base station are in the NLOS situation [16]. The specific setting of the ranging model was as follows:

dki=dk,reali+σ×randn()+dk,nlosi,(26)

where dki represents the measured distance obtained by the wireless signal from the moving targetto the ith base station at the kth time instant, dk,reali represents the true distance between the target and the ith base station, and dk,nlosi represents the distance measurement deviation between the target and the ith base station due to NLOS. The NLOS deviation is assumed to be positive and greater than the measurement noise [15,16].

The parameter settings of the various algorithms (KF, STF, STFC, and SPFC) need to specify the initial system covariance matrix P, system noise matrix Q, and measurement noise matrix R. In the process of updating the particle weights of PF and SPFC, standard deviations σx and σy of the particles need to be set. The parameters were set as follows:

P=[250025],Q=[0.11000.11],R=[100010],

σx=5,σy=5.

4.2 Result Analysis

We first set the radius of the obstacle to r=0m to verify the performance of the SPFC fusion positioning algorithm, which means that the test is performed in the LOS environment.

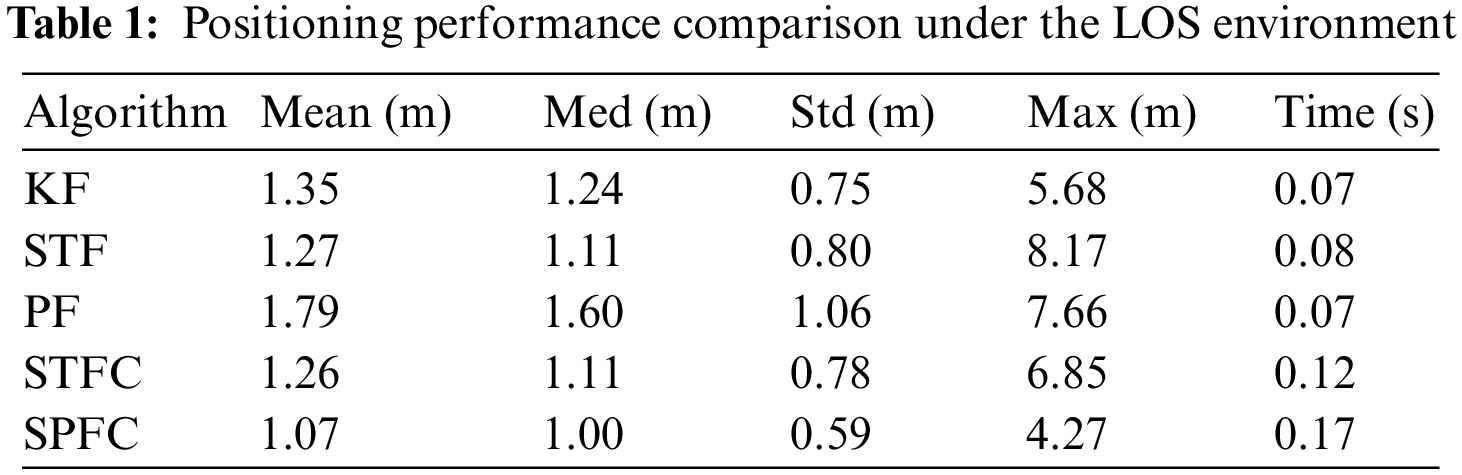
Figs. 4–6 show the simulation results under the LOS environment. Fig. 4 shows the trajectory of the positioning result. Fig. 5 shows the positioning error, and Fig. 6 presents the cumulative distribution function (CDF) of the positioning error. Overall, the five algorithms compared in this work maintain good positioning performance under the LOS environment. In Fig. 6, the curves of CDF of the positioning error of STF and STFC are overlapped. This situation occurs because the STFC hardly detects the NLOS error under the LOS environment. This notion means that the positioning results of STFC and STF are the same. Table 1 shows the positioning error statistics of each algorithm after 10 repeated experiments, including the average, median, standard deviation, and maximum value. The results show that the five fusion positioning algorithms can maintain good positioning results under the LOS environment. Although SPFC is more time-consuming than the other algorithms, its positioning accuracy is better 15.1% than that of STFC, which is the best among the other algorithms.

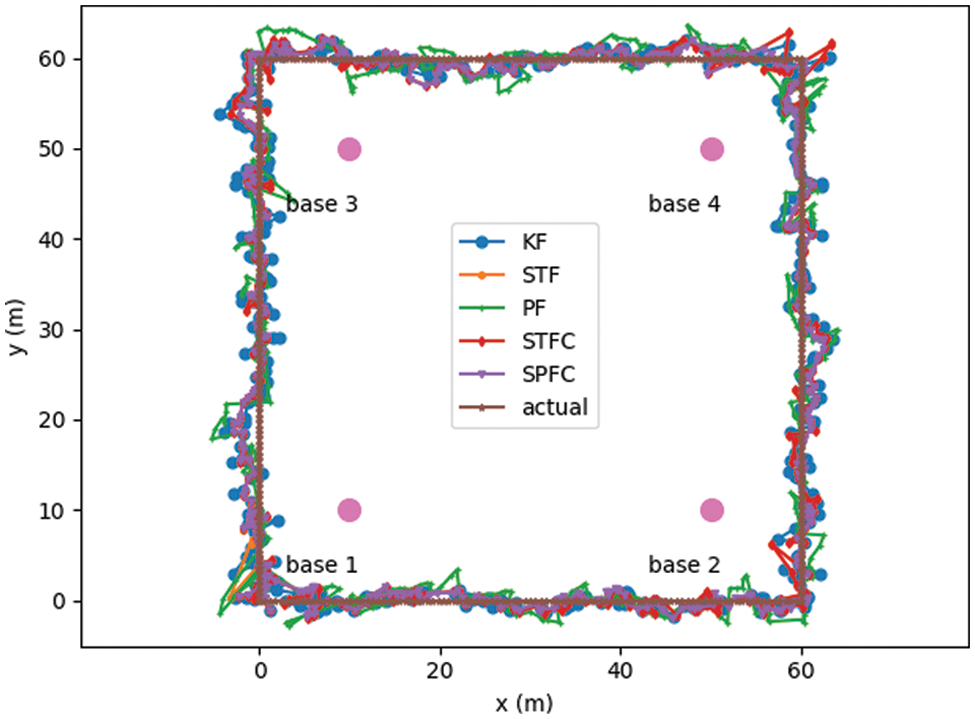
Figure 4: Real and estimated trajectories under the LOS environment

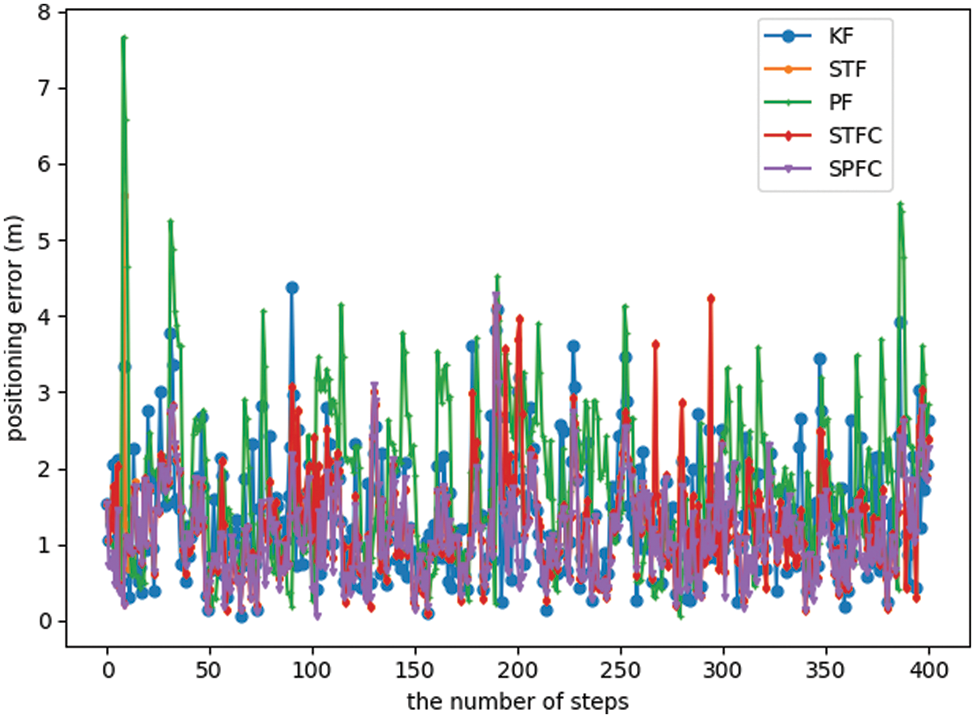
Figure 5: Positioning error under the LOS environment

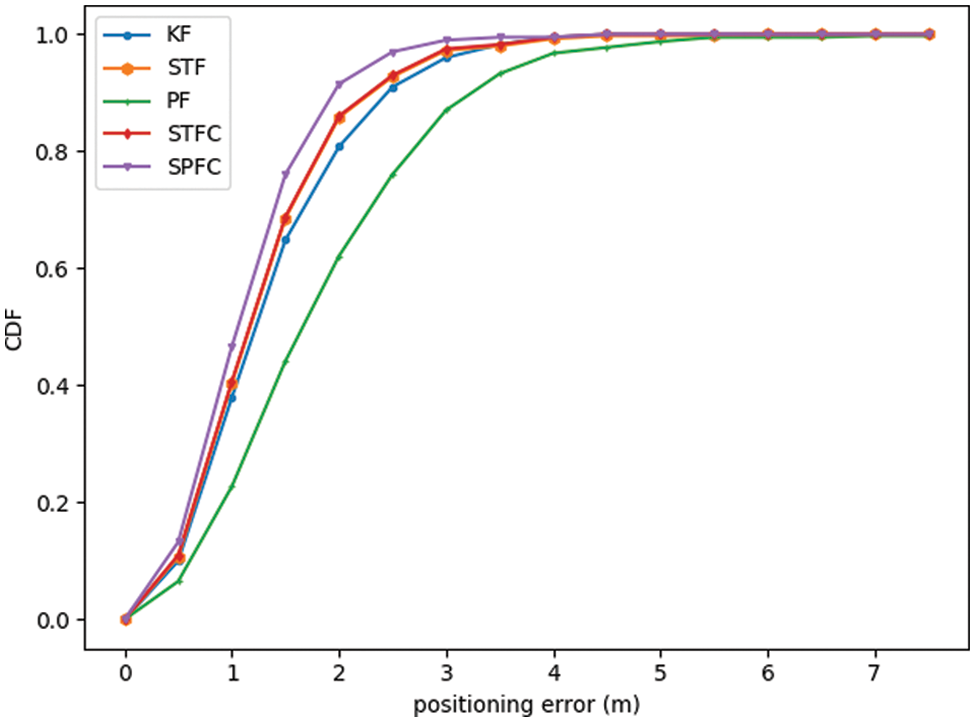
Figure 6: CDF of the positioning error under the LOS environment

This study aims to further verify the characteristics of the SPFC algorithm under the LOS/NLOS environment and its advantages over other indoor fusion algorithms. Accordingly, we set the radius of the obstacle to r = 2 m. Fig. 7 shows that the moving target and the positioning base station 2 are in the NLOS condition due to the obstruction when the moving target moves near positioning base station 3. Meanwhile, the positioning results of KF, STF, and PF greatly differ from the actual position of the moving target. However, the positioning results of STFC and SPFC still move around the target’s actual position. Fig. 10 shows the actual existence and detection result of NLOS during a circular movement around the rectangle through the ON–OFF model (one and zero). In Fig. 9, an obstacle can be observed between the moving target and base station 2 within the time of 88 ≤ k ≤ 110, and STFC and SPFC have detected NLOS through the CST. During this period, the moving target moves near base station 3. Fig. 8 shows that the positioning errors of KF, STF, and PF will immediately increase. However, the STFC and SPFC results do not have much error compared with the actual trajectory. Moreover, the SPFC algorithm can resume the use of observations and quickly reduce the error when k > 110 compared with the KF algorithm, indicating the disappearance of the NLOS. During a period of LOS, the positioning performance of the SPFC is more stable than STFC, and the positioning accuracy is higher. Table 2 shows the statistical results of the positioning errors of the various positioning algorithms after repeated experiments (10 times). Similar to the LOS environment, although SPFC is more time-consuming than the other algorithms, its positioning accuracy is 12.3% higher than that of STFC, the best of other algorithms.

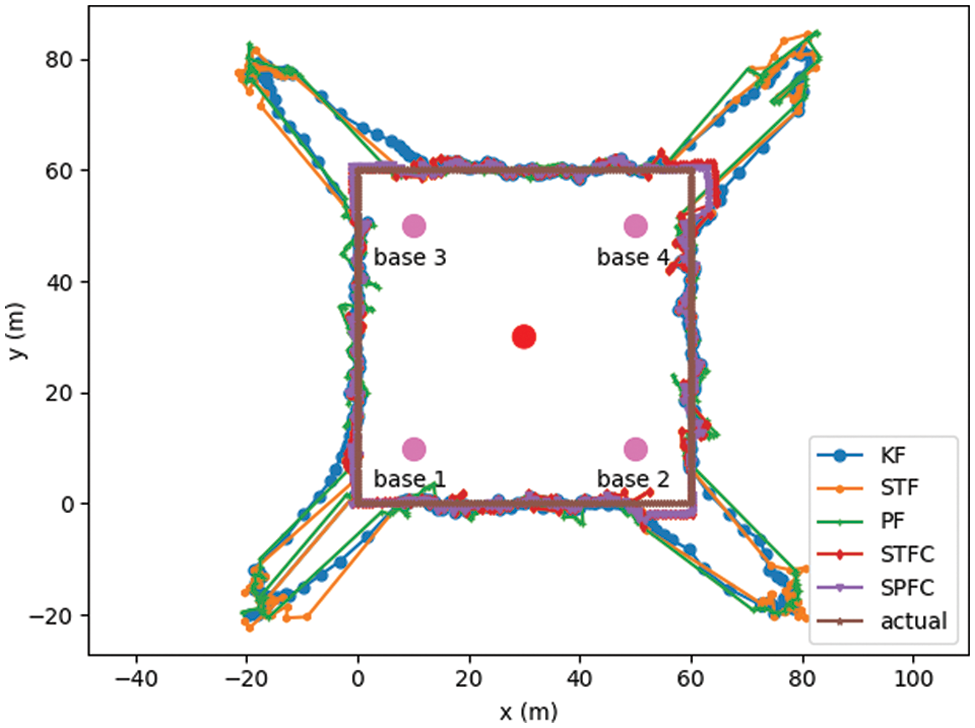
Figure 7: Real and estimated trajectories under the LOS/NLOS environment

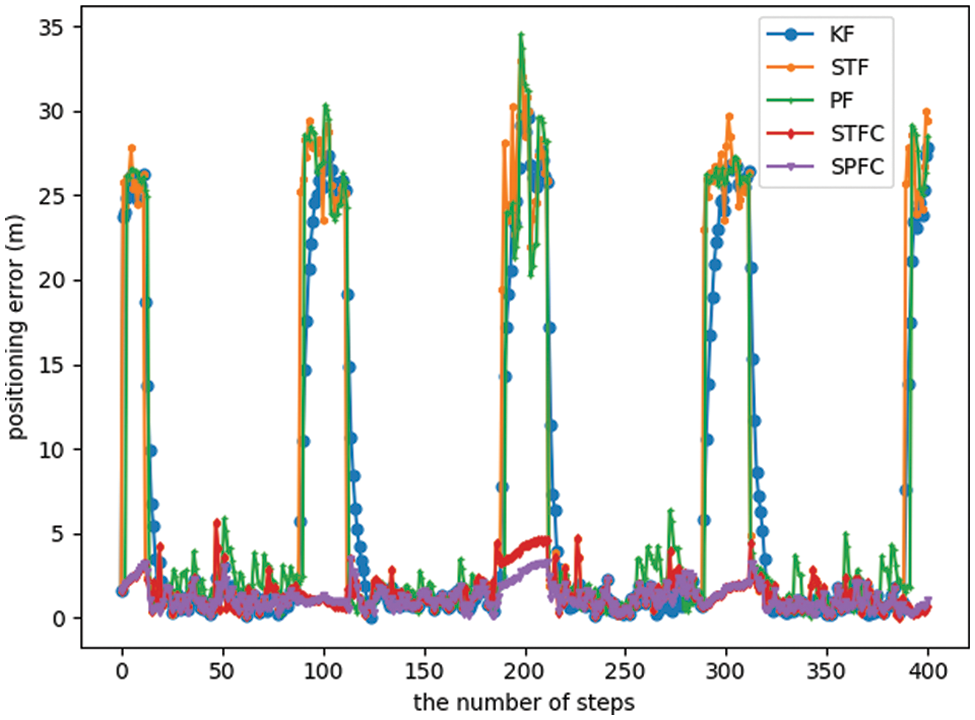
Figure 8: Positioning error under the LOS/NLOS environment

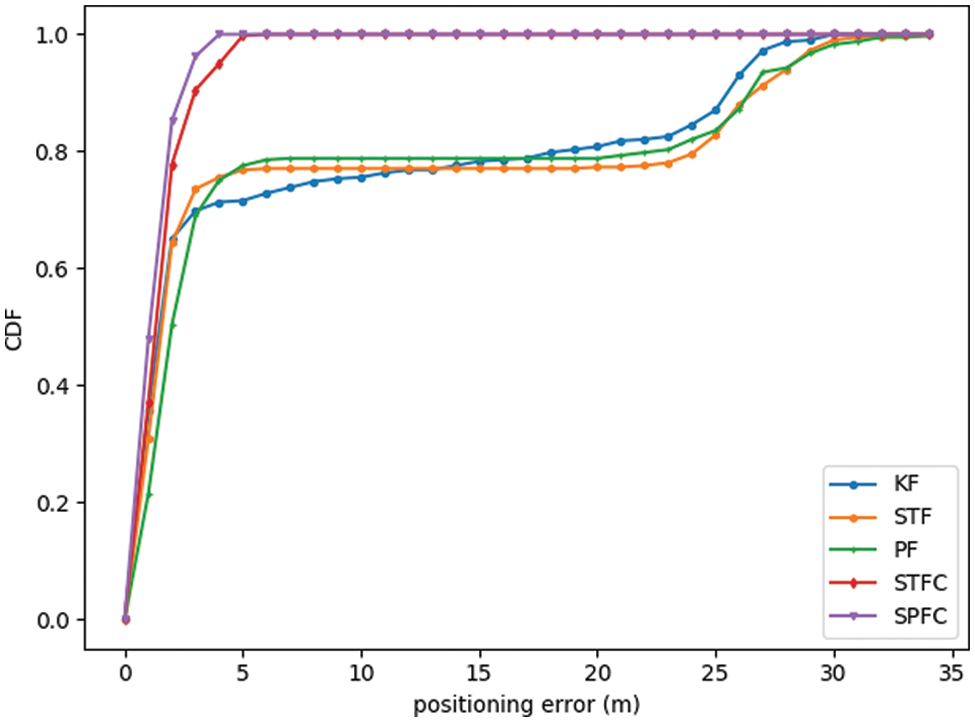
Figure 9: CDF of the positioning error under the LOS/NLOS environment

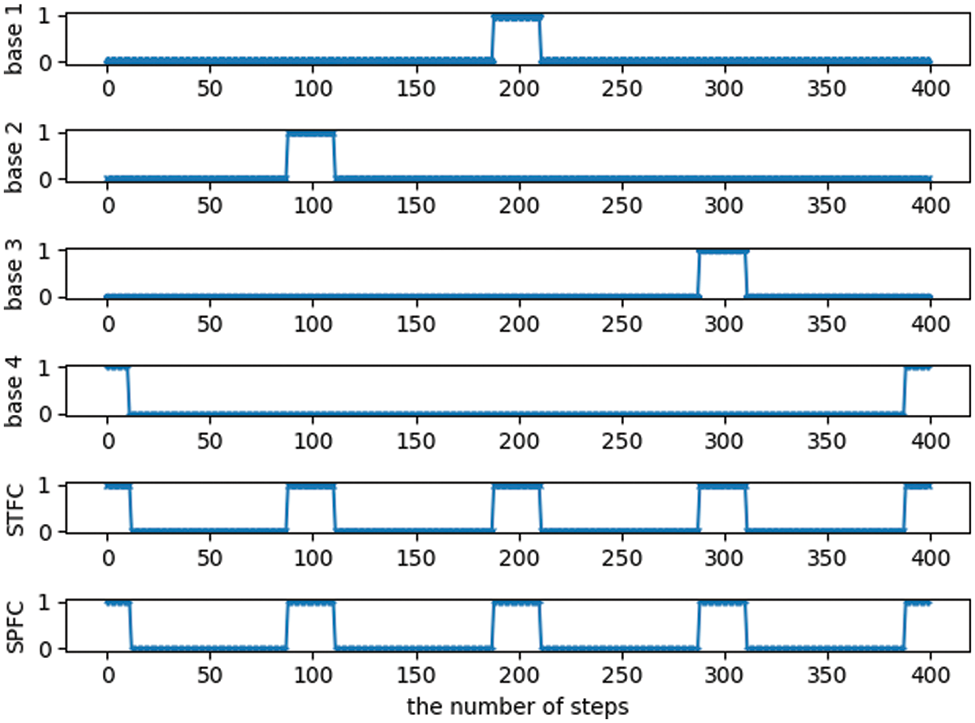
Figure 10: ON–OFF model of the NLOS detection result under the LOS/NLOS environment

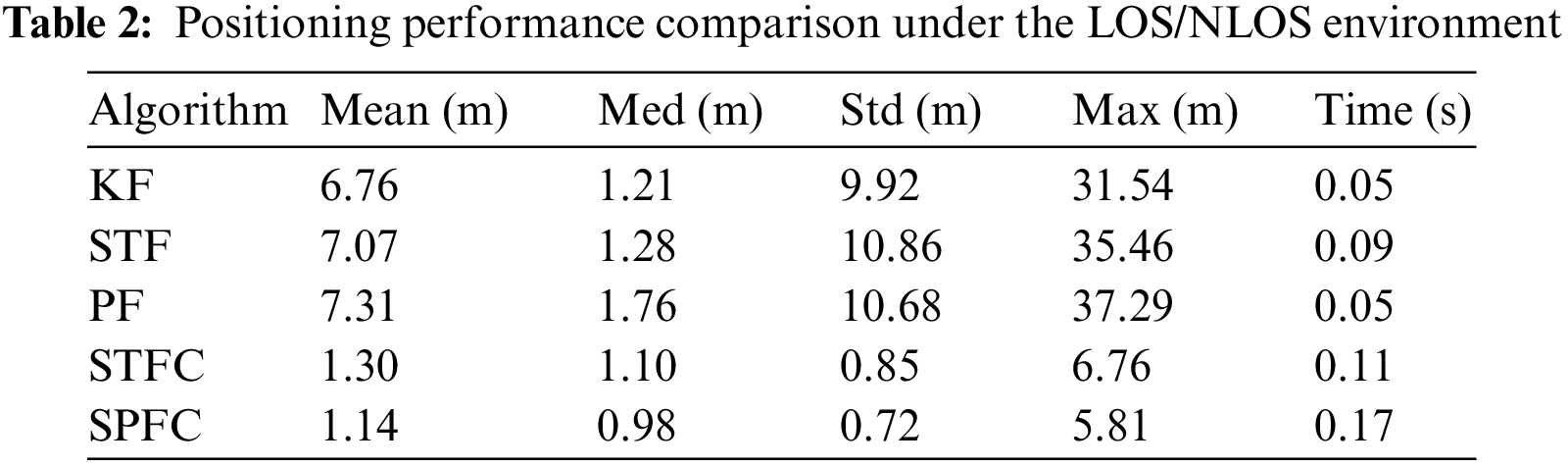
In summary, this work compares the positioning performance and running time of five positioning algorithms in two environments. The results show that SPFC can effectively improve the positioning accuracy at the cost of a certain degree of computational complexity whether in the LOS or LOS/NLOS environments.

5  Conclusion

This study proposes a strong tracking PF based on the CST for the indoor positioning method to obtain real-time and accurate indoor positioning in a complex and changeable indoor environment. The aforementioned method is mainly divided into three parts. The first part is based on mobile phone IMU sensor data using pedestrian dead reckoning and based on wireless signal data using an STF algorithm to initially achieve the indoor positioning of the moving targets. The second part detects whether the wireless positioning result is affected by NLOS based on the CST. The third part is to decide whether to recalculate the particle weight after the state transition according to the result of the CST. The simulation results show that the positioning performance of SPFC in the LOS and NLOS environments is improved by 15.1% and 12.3% compared with the best algorithms among the other algorithms. This notion that the proposed SPFC method can achieve better positioning and tracking performance on moving targets in indoor environments with occlusions. In future work, we hope to obtain more information, such as high-precision indoor maps, to further improve the accuracy of indoor positioning.

Acknowledgement: This work was funded by the project “Design of System Integration Construction Scheme Based on Functions of Each Module” (No. XDHT2020169A) and the project “Development of Indoor Inspection Robot System for Substation” (No. XDHT2019501A).

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Dow, J. M., Neilan, R. E., Rizos, C. (2009). The international GNSS service in a changing landscape of global navigation satellite systems. Journal of Geodesy, 83(3–4), 191–198. DOI 10.1007/s00190-008-0300-3. [Google Scholar] [CrossRef]

    2. Chai, M., Chai, C., Huang, H. (2019). A new indoor positioning algorithm of cellular and Wi-Fi networks. Journal of Navigation, 73(3), 509–529. DOI 10.1017/S0373463319000742. [Google Scholar] [CrossRef]

    3. Wu, C., Zhang, F., Wang, B., Liu, K. J. R. (2020). EasiTrack: Decimeter-level indoor tracking with graph-based particle filtering. IEEE Internet of Things Journal, 7(3), 2397–2411. DOI 10.1109/JIoT.6488907. [Google Scholar] [CrossRef]

    4. Xiao, Z., Wen, H., Markham, A., Trigoni, N., Blunsom, P. et al. (2015). Non-line-of-sight identification and mitigation using received signal strength. IEEE Transactions on Wireless Communications, 14(3), 1689–1702. DOI 10.1109/TWC.7693. [Google Scholar] [CrossRef]

    5. Chen, C., Chen, Y., Han, Y., Lai, H. Q., Liu, K. J. R. (2016). Achieving centimeter accuracy indoor localization on WiFi platforms: A frequency hopping approach. IEEE Internet of Things Journal, 4(1), 111–121. DOI 10.1109/JIOT.2016.2628701. [Google Scholar] [CrossRef]

    6. Si, M., Wang, Y., Seow, C. K., Cao, H., Liu, H. et al. (2022). An adaptive weighted Wi-Fi FTM-based positioning method in an NLOS environment. IEEE Sensors Journal, 22(1), 472–480. DOI 10.1109/JSEN.2021.3124275. [Google Scholar] [CrossRef]

    7. Yu, N., Zhan, X., Zhao, S., Wu, Y., Feng, R. (2018). A precise dead reckoning algorithm based on bluetooth and multiple sensors. IEEE Internet of Things Journal, 5(1), 336–351. DOI 10.1109/JIOT.2017.2784386. [Google Scholar] [CrossRef]

    8. Yao, Y., Bao, Q., Han, Q., Yao, R., Xu, X. et al. (2018). BtPDR: Bluetooth and PDR-based indoor fusion localization using smartphones. KSII Transactions on Internet and Information Systems, 12(8), 3657–3682. [Google Scholar]

    9. Yu, K., Wen, K., Li, Y., Zhang, S., Zhang, K. (2019). A novel NLOS mitigation algorithm for UWB localization in harsh indoor environments. IEEE Transactions on Vehicular Technology, 68(1), 686–699. DOI 10.1109/TVT.2018.2883810. [Google Scholar] [CrossRef]

  10. Zhang, Y., Tan, X., Zhao, C. (2020). UWB/INS integrated pedestrian positioning for robust indoor environments. IEEE Sensors Journal, 20(23), 14401–14409. DOI 10.1109/JSEN.7361. [Google Scholar] [CrossRef]

  11. Piontek, H., Seyffer, M., Kaiser, J. (2006). Improving the accuracy of ultrasound-based localisation systems. Personal and Ubiquitous Computing, 11(6), 439–449. DOI 10.1007/s00779-006-0096-1. [Google Scholar] [CrossRef]

  12. Dang, X., Cheng, Q., Zhu, H. (2019). Indoor multiple sound source localization via multi-dimensional assignment data association. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 27(12), 1944–1956. DOI 10.1109/TASLP.6570655. [Google Scholar] [CrossRef]

  13. Ashhar, K., Noor-A-Rahim, M., Khyam, M. O., Soh, C. B. (2019). A narrowband ultrasonic ranging method for multiple moving sensor nodes. IEEE Sensors Journal, 19(15), 6289–6297. DOI 10.1109/JSEN.7361. [Google Scholar] [CrossRef]

  14. Sayeef, S., Madawala, U. K., Handley, P. G., Santoso, D. (2004). Indoor personnel tracking using infrared beam scanning. Position Location and Navigation Symposium (IEEE Cat. No. 04CH37556), pp. 698–705. Monterey, CA, USA. [Google Scholar]

  15. Khan, L. U. (2017). Visible light communication: Applications, architecture, standardization and research challenges. Digital Communications and Networks, 3(2), 78–88. DOI 10.1016/j.dcan.2016.07.004. [Google Scholar] [CrossRef]

  16. Tomic, S., Beko, M. (2018). A bisection-based approach for exact target localization in NLOS environments. Signal Processing, 143, 328–335. DOI 10.1016/j.sigpro.2017.09.019. [Google Scholar] [CrossRef]

  17. Pak, J. M., Ahn, C. K., Shi, P., Shmaliy, Y. S., Lim, M. T. (2017). Distributed hybrid particle/FIR filtering for mitigating NLOS effects in TOA-based localization using wireless sensor networks. IEEE Transactions on Industrial Electronics, 64(6), 5182–5191. DOI 10.1109/TIE.2016.2608897. [Google Scholar] [CrossRef]

  18. Marano, S., Gifford, W., Wymeersch, H., Win, M. (2010). NLOS identification and mitigation for localization based on UWB experimental data. IEEE Journal on Selected Areas in Communications, 28(7), 1026–1035. DOI 10.1109/JSAC.2010.100907. [Google Scholar] [CrossRef]

  19. Kai Ten, F., Chao Lin, C., Chien Hua, C. (2008). GALE: An enhanced geometry-assisted location estimation algorithm for NLOS environments. IEEE Transactions on Mobile Computing, 7(2), 199–213. DOI 10.1109/TMC.2007.70721. [Google Scholar] [CrossRef]

  20. Sadhukhan, P., Das, P. K. (2009). MGALE: A modified geometry-assisted location estimation algorithm reducing location estimation error in 2D case under NLOS environments. International Workshop on Mobile Entity Localization and Tracking in GPS-Less Environments, pp. 1–18. Berlin, Heidelberg, Springer. [Google Scholar]

  21. Kim, D. H., Pyun, J. Y. (2021). NLOS identification based UWB and PDR hybrid positioning system. IEEE Access, 9, 102917–102929. DOI 10.1109/ACCESS.2021.3098416. [Google Scholar] [CrossRef]

  22. Xu, Y., Li, G., Li, Z., Yu, H., Cui, J. et al. (2022). Smartphone-based unconstrained step detection fusing a variable sliding window and an adaptive threshold. Remote Sensing, 14(12). DOI 10.3390/rs14122926. [Google Scholar] [CrossRef]

  23. Xiong, H., Bian, R., Li, Y., Du, Z., Mai, Z. (2020). Fault-tolerant GNSS/SINS/DVL/CNS integrated navigation and positioning mechanism based on adaptive information sharing factors. IEEE Systems Journal, 14(3), 3744–3754. DOI 10.1109/JSYST.4267003. [Google Scholar] [CrossRef]

  24. Hajiyev, C. (2012). Fault tolerant integrated radar/inertial altimeter based on nonlinear robust adaptive kalman filter. Aerospace Science and Technology, 17(1), 40–49. DOI 10.1016/j.ast.2011.03.005. [Google Scholar] [CrossRef]

  25. Zhou, D. H., Frank, P. M. (1996). Strong tracking filtering of nonlinear time-varying stochastic systems with coloured noise: Application to parameter estimation and empirical robustness analysis. International Journal of Control, 65(2), 295–307. DOI 10.1080/00207179608921698. [Google Scholar] [CrossRef]

  26. Xiong, H., Tang, J., Xu, H., Zhang, W., Du, Z. (2018). A robust single GPS navigation and positioning algorithm based on strong tracking filtering. IEEE Sensors Journal, 18(1), 290–298. DOI 10.1109/JSEN.2017.2767066. [Google Scholar] [CrossRef]