 Open Access
Open Access
ARTICLE
Emerging Trends in Social Networking Systems and Generation Gap with Neutrosophic Crisp Soft Mapping
1 Department of Mathematics, University of the Punjab, Lahore, Pakistan
2 Department of Mathematics, Çankırı Karatekin University, Çankırı, Turkey
3 Department of Mathematics and Science Education, Amasya University, Amasya, Turkey
4 Department of Mathematics, Faculty of Science and Arts, King Khalid University, Muhayl Assir, Saudi Arabia
5 Department of Mathematics and Computer, Faculty of Science, Ibb University, Ibb, Yemen
6 Higher Institute of Engineering and Technology King Marriott, Alexandria, Egypt
7 Faculty of Engineering, Arab Academy for Science & Technology and Maritime Transport (AASTMT), Aswan Branch, Egypt
* Corresponding Author: Mohammed M. Ali Al Shamiri. Email:
(This article belongs to the Special Issue: Decision making Modeling, Methods and Applications of Advanced Fuzzy Theory in Engineering and Science)
Computer Modeling in Engineering & Sciences 2023, 136(2), 1759-1783. https://doi.org/10.32604/cmes.2023.023327
Received 20 April 2022; Accepted 22 August 2022; Issue published 06 February 2023
Abstract
This paper aims to introduce the novel concept of neutrosophic crisp soft set (NCSS), including various types of neutrosophic crisp soft sets (NCSSs) and their fundamental operations. We define NCS-mapping and its inverse NCS-mapping between two NCS-classes. We develop a robust mathematical modeling with the help of NCS-mapping to analyze the emerging trends in social networking systems (SNSs) for our various generations. We investigate the advantages, disadvantages, and natural aspects of SNSs for five generations. With the changing of the generations, it is analyzed that emerging trends and the benefits of SNSs are increasing day by day. The suggested modeling with NCS-mapping is applicable in solving various decision-making problems.Graphic Abstract
Keywords
Fuzzy set theory [1] and soft set theory [2] are independent abstraction of classical set theory to address uncertainties by using membership functions and parameterizations, respectively. These theories have been widely used for solving real-world problems. The researchers extended the fuzzy set theory to develop various new models such as intuitionistic fuzzy sets [3], interval-valued intuitionistic fuzzy sets [4–7], Pythagorean fuzzy sets [8,9], q-rung orthopair fuzzy sets [10], bipolar fuzzy sets [11,12], and m-polar fuzzy sets [13].
These models have been developed by using the membership function and non-membership function to cover the limitations of membership and non-membership grades. In the case of a bipolar fuzzy set, the membership grades are categorized into positive and negative grades to discuss the counter property of objects. Smarandache [14,15] introduced the idea of the neutrosophic set (NSs), which assign three independent grades (truth-membership, indeterminacy, and falsity). Wang et al. [16] introduced single-valued neutrosophic sets as a consequence of NSs. A neutrosophic set is more general than various existing fuzzy sets. Some neutrosophic concepts have been explored by Salama et al. [17,18]. They presented a novel idea of the neutrosophic crisp set (NCS) and neutrosophic crisp relations with the construction of neutrosophic crisp topological spaces. Salama et al. [19] established the novel concepts about NCS theory and developed some applications of this theory in diverse areas. Karaaslan [20] investigated some properties of the neutrosophic soft set (NSS) and presented interesting applications in decision-making problems. Maji [21] presented some significant results on NSSs. Kharal et al. [22] presented several results on the mappings of soft classes. Wardowski [23] presented innovative results on soft mappings and their fixed points.
Information measures (similarity measures, distance measures, inclusion measures, and entropy) proposed by Peng et al. [24]. They developed algorithms and their applications towards medical diagnosis, pattern recognition, and clustering analysis. Akram et al. [25] suggested extension of competition graphs like k-competition graphs and p-competition complex fuzzy graphs under complex fuzzy environment and their application in ecosystem. Akram et al. [26] suggested an implementation of SVN soft hypergraphs on human nervous system. Zhan et al. [27] proposed new decision-making method based on bipolar neutrosophic information. Feng et al. [28] proposed MADM application by using new score function for ranking of alternatives with generalized orthopair fuzzy membership grades. Akram [29] initiated the concept of BFS graphs and Akram et al. [30] suggested a hybrid decision-making framework by using aggregation operators under a complex spherical fuzzy prioritization approach. Alghamdi et al. [31] proposed some MCDM methods in a bipolar fuzzy environment. Yang et al. [32] investigated certain aspects of single valued neutrosophic relations. Yue [33] proposed the idea of interval intuitionistic fuzzy set based bilateral matching decision-making for knowledge innovation management considering matching willingness.
Naeeem et al. [34] proposed the idea of Pythagorean m-polar fuzzy sets with new directions and applications. Thao et al. [35] proposed similarity measures based on new entropy by using single-valued neutrosophic sets with application to select supplier material. Ulucay et al. [36] introduced novel similarity measures of bipolar neutrosophic sets and their application to MCDM. Hashim et al. [37] developed new kinds of similarity measures and their applications for neutrosophic bipolar fuzzy information. They suggested a practical application to hope foundation for planning to build a children hospital under uncertain neutrosophic bipolar fuzzy environment. Garg et al. [38] proposed the idea of hybrid weighted aggregation operators under neutrosophic set information. They suggested an interesting application to MCDM for ranking of feasible objects. Karaaslan et al. [39] developed certain operations on single-valued neutrosophic matrices. They proposed a new method for finding an optimal alternative and ranking of feasible alternatives. Hashmi et al. [40] introduced the idea of m-polar neutrosophic sets and m-polar neutrosophic topology. They proposed novel algorithms for MCDM in clustering analysis and medical diagnosis. Zhang et al. [41] suggested the idea of interval neutrosophic sets and their applications in MCDM. Ye [42] developed a novel MCDM approach for uncertain single-value neutrosophic information and related correlation coefficient. Ye [43] suggested simplified neutrosophic aggregation operators for MCDM and ranking of feasible alternatives in the universe of discourse. Feng et al. [44] proposed certain properties of soft sets, fuzzy sets and rough sets. They suggested soft computing approaches in terms of the possible fusion of fuzzy sets, soft sets, and rough sets. They proposed some significant results related to the extension of Pawlak approximation space, equivalence relation, and granular computing. Pamucar [45] proposed a robust approach for interval grey normalized weighted geometric Dombi Bonferroni mean aggregation operators by using or uncertain MCDM problems. Chen et al. [46] proposed an efficiency-based interval type-2 fuzzy MCGDM technique for makeshift hospital selection. Riaz et al. [47] proposed an innovative bipolar fuzzy sine trigonometric aggregation operators and SIR method for medical tourism supply chain. Hanif et al. [48] suggested the notion of linear Diophantine fuzzy graphs with new decision-making approach. Saeed et al. [49] developed an application of neutrosophic hypersoft mapping to diagnose hepatitis and propose appropriate treatment. Riaz et al. [50] proposed images and inverse images of m-polar neutrosophic soft mappings and their application to mental disorders and multiple personality disorder. Riaz et al. [51] proposed images and inverse images of bipolar fuzzy soft mappings and their application to bipolar disorders. Latreche et al. [52] introduced the concept of single valued neutrosophic mappings defined by single valued neutrosophic relations with applications.
Neutrosophy is a branch of philosophy that investigates the scope, nature, and origin of neutralities, as well as their interactions with various conceptual spectra. Neutrosophy forms the base of neutrosophic science involving the area such as neutrosophic logic, neutrosophic sets, and neutrosophic probability, etc. These have been successfully applied for modeling uncertainties in decision-making problems. Neutrosophic crisp set (NCS) and neutrosophic crisp soft set (NCSS) are strong modeling tools to address vagueness and uncertainties in decision-making problems.
The first objective of this paper is to introduce the novel concept of neutrosophic crisp soft set (NCSS) including various types of neutrosophic crisp soft sets (NCSSs) and their fundamental operations. The second objective is to define the idea of NCS-mapping to investigate images and inverse images of NCS-classes. The third objective is to develop a robust mathematical modeling with the help of NCS-mapping. The fourth objective is to analyze the emerging trends in social networking systems (SNSs) for our various generations. The fifth objective is to derive valid conclusions regarding the advantages, disadvantages, and natural aspects of SNSs for five generations.
The layout of this paper is designed as follows: In Section 2, we first present the notion of NCSS and then we talk about some of its types. We introduce some operations on NCSSs for the dissimilar types of NCSSs. In Section 3, we establish NCS-mapping and inverse NCS-mapping by merging the ideas of soft mapping and NC mapping, then extend the definition with the help of examples. In Section 4, we discuss and construct a model on emerging trends in social networking system (SNS) via NCS-mapping for different generations. In Section 5, we briefly discuss our concepts about this paper and the construction of the articles with the comparison of neutrosophic, fuzzy and soft notions and their hybrid structures. Lastly, judgments are drawn in Section 6.
Some abbreviations used in this paper are as follows:
IFS Intuitionistic fuzzy set
GIFS Generalized intuitionistic fuzzy set
GNS Generalized neutrosophic set
NC Neutrosophic crisp
NSS Neutrosophic soft set
NCS Neutrosophic crisp soft
NCSS Neutrosophic crisp soft set
SNS Social networking system
SNWs Social networking websites
FNS Fuzzy neutrosophic soft
2 Neutrosophic Crisp Soft Sets
In this section, we introduce the notion of neutrosophic crisp soft set (NCSS), different types NCSSs, operations on NCSSs with the help of some illustrations. First, we recall the definition of soft set.
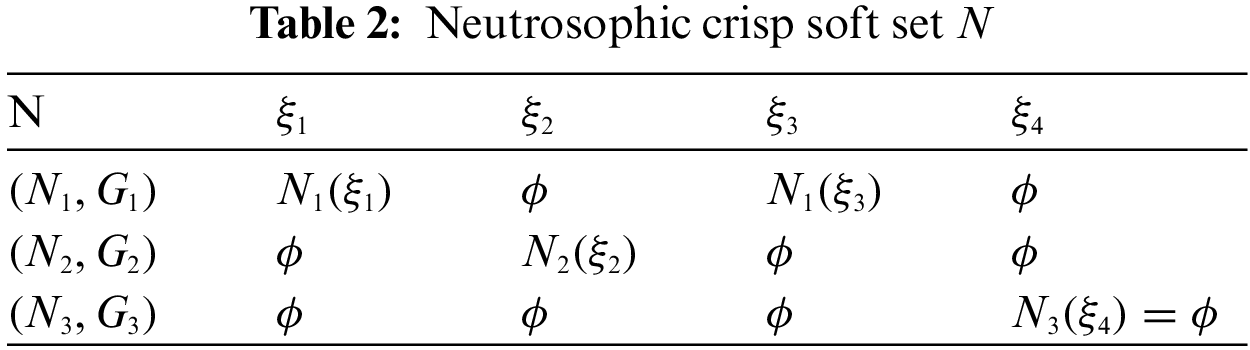
Example 2.1.Let X be the set of non-negative integers and
Consider
where
If
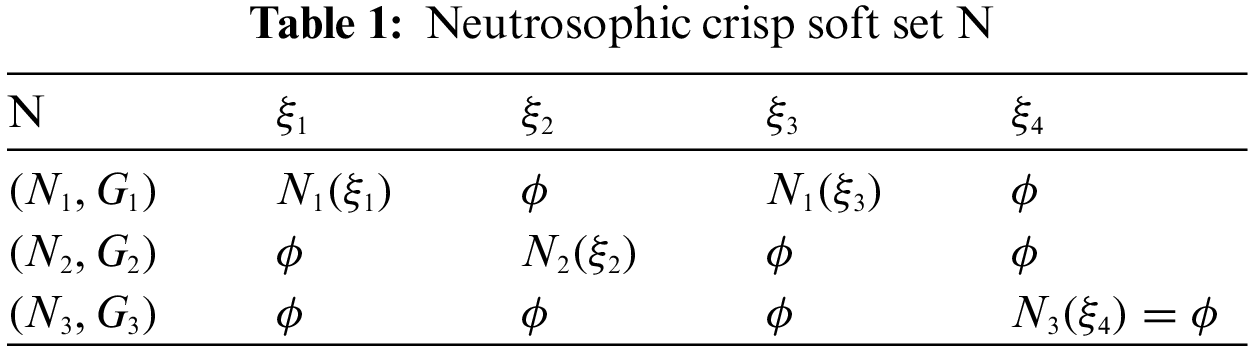
where
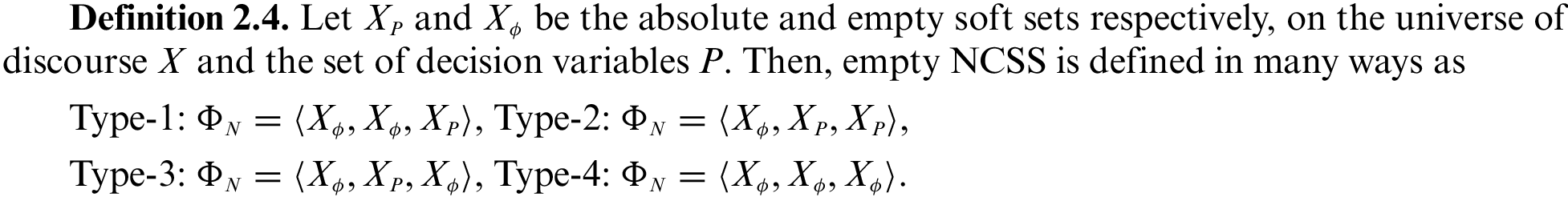
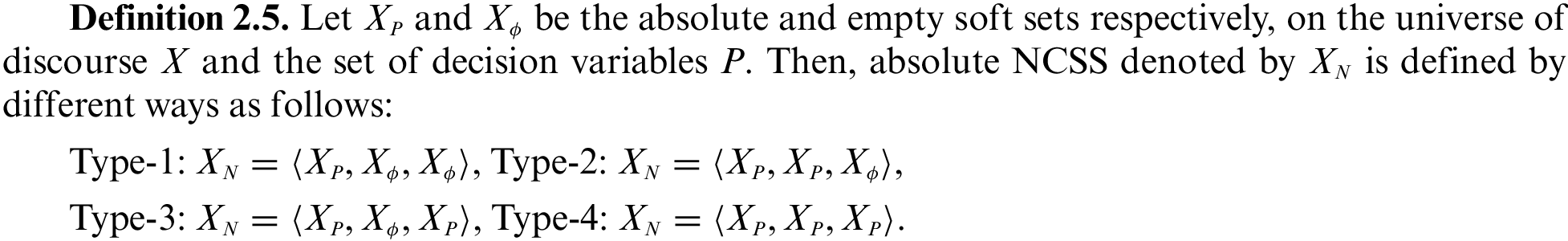
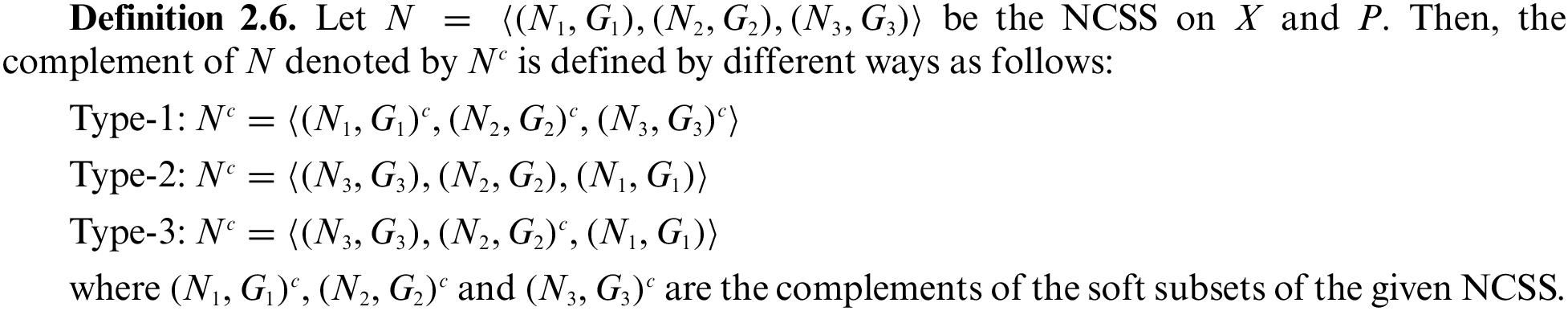
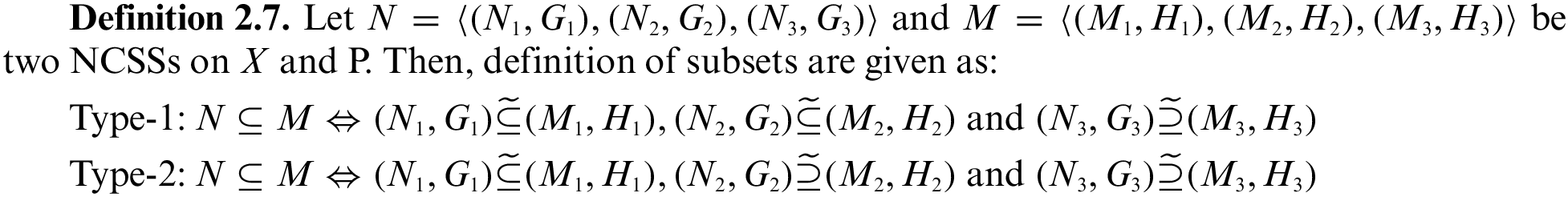

Proof. The proof is obvious. Therefore, it is omitted.
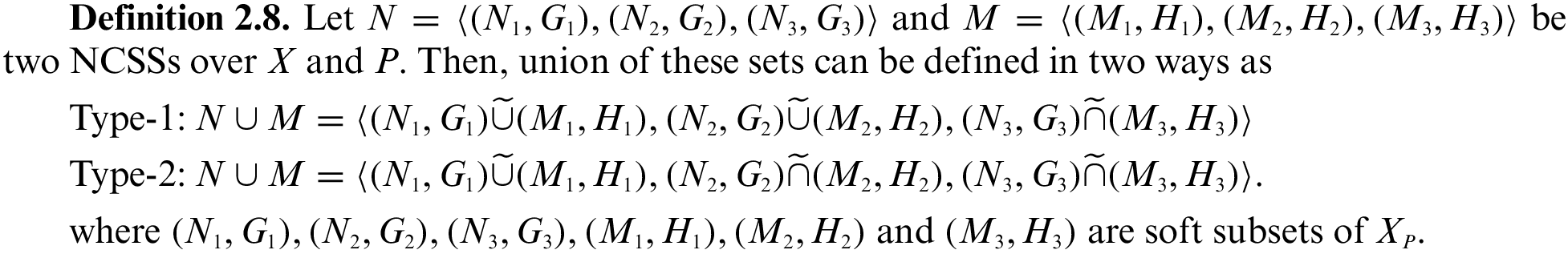
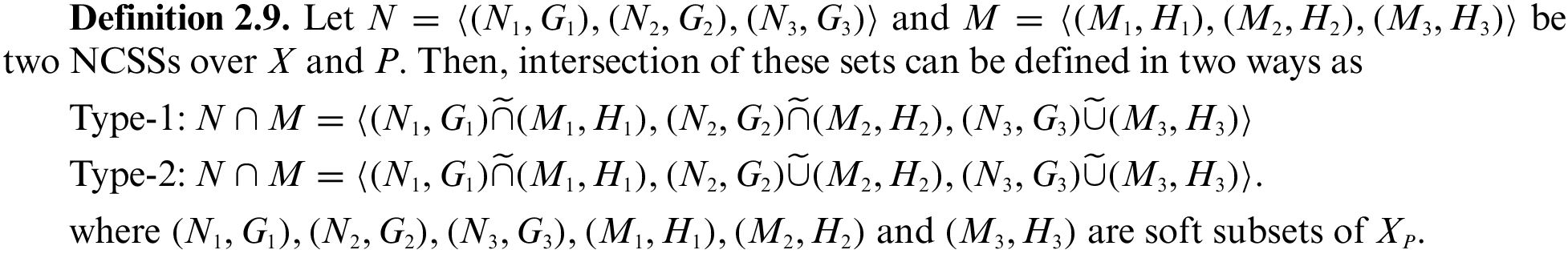
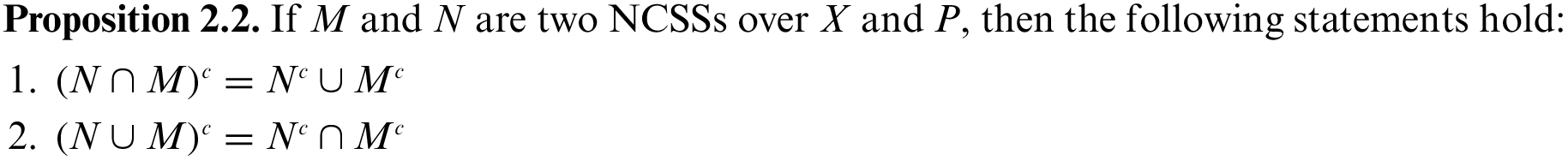
Proof. The proof is obvious. Therefore, it is omitted.

Example 2.2.Let
Let

Union of NCSSs:
Type-1:
Type-2:
By using Definition 2.8, the neutrosophic crisp soft set L and O can be demonstrated in Tables 4 and 5, respectively.
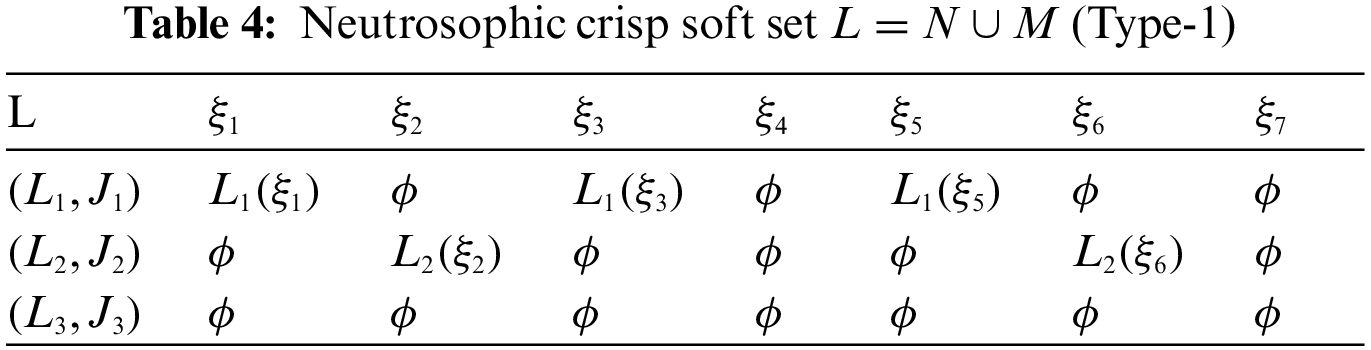
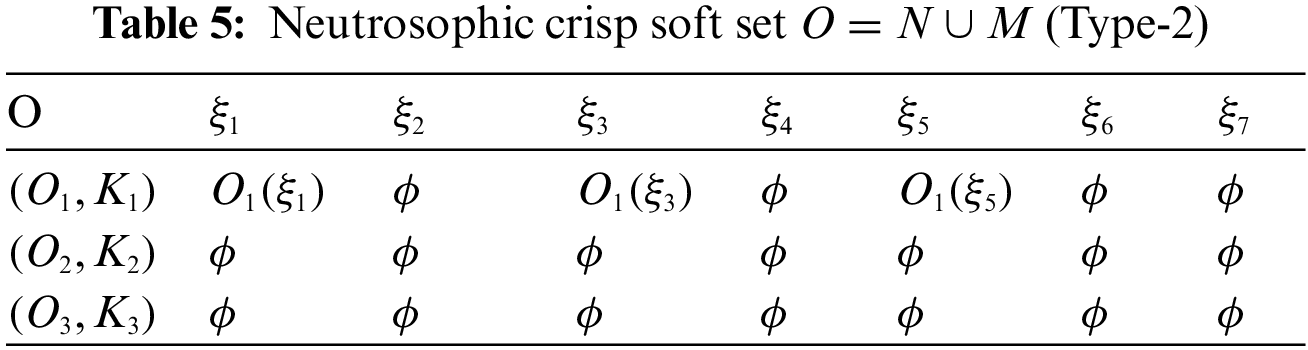
Intersection of NCSSs:
By using Definition 2.9, the intersection of N and M can be expressed in Tables 6 and 7, respectively.
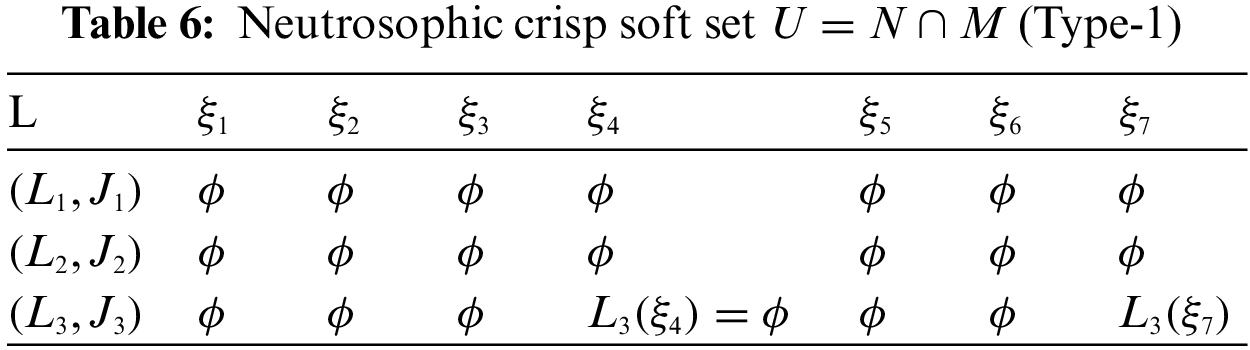
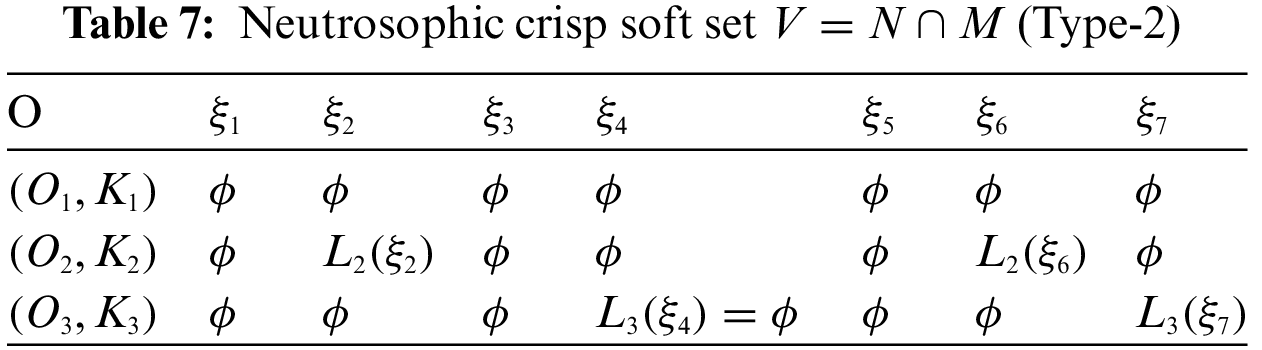

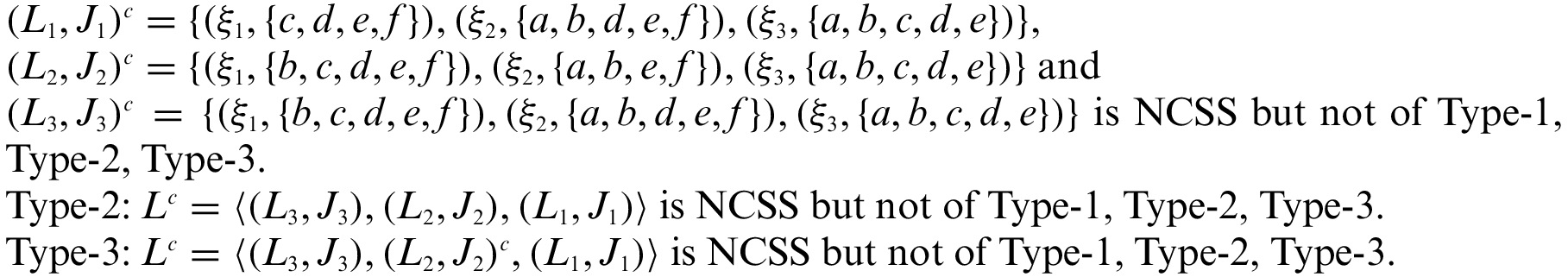
(1) Every NCSS of Type-1, Type-2 and Type-3 are NCSS.
(2) Every NCSS of Type-1 may not be NCSS Type-2 and Type-3.
(3) Every NCSS of Type-2 may not be NCSS Type-1 and Type-3.
(4) Every NCSS of Type-3 may not be NCSS Type-1 and Type-2.
(5) Every soft set is NCSS.
The relationship between different types of NCSSs and soft set are shown in Fig. 1.
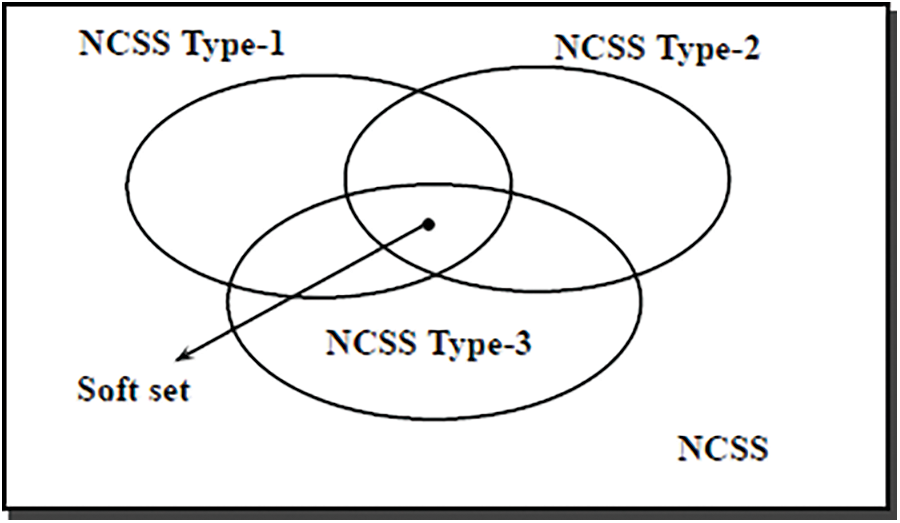
Figure 1: Relationship between different types of NCSSs and soft set
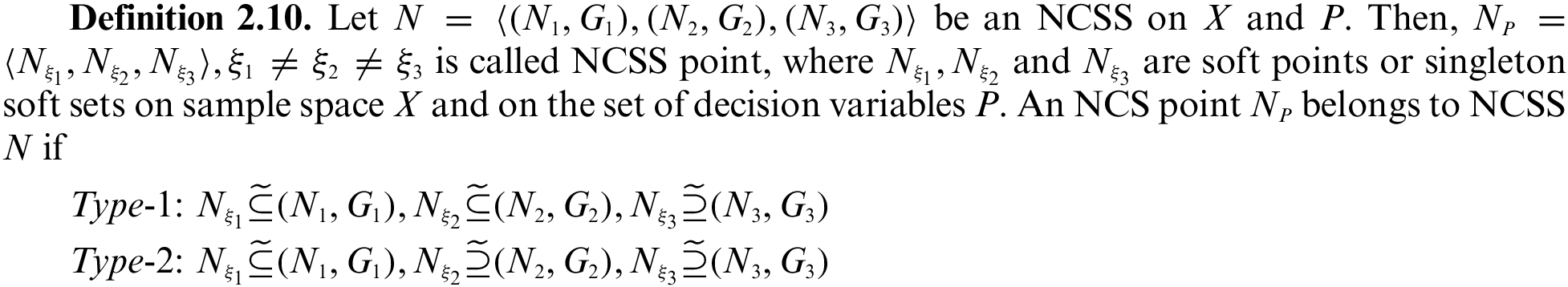
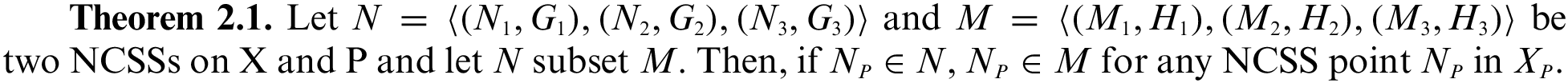
Proof. Let
This shows that

Proof. Proof is obvious.
In this section, we establish NCS-mapping and inverse NCS-mapping by merging the ideas of soft mapping and NC mapping, then explain the definition with the help of examples.




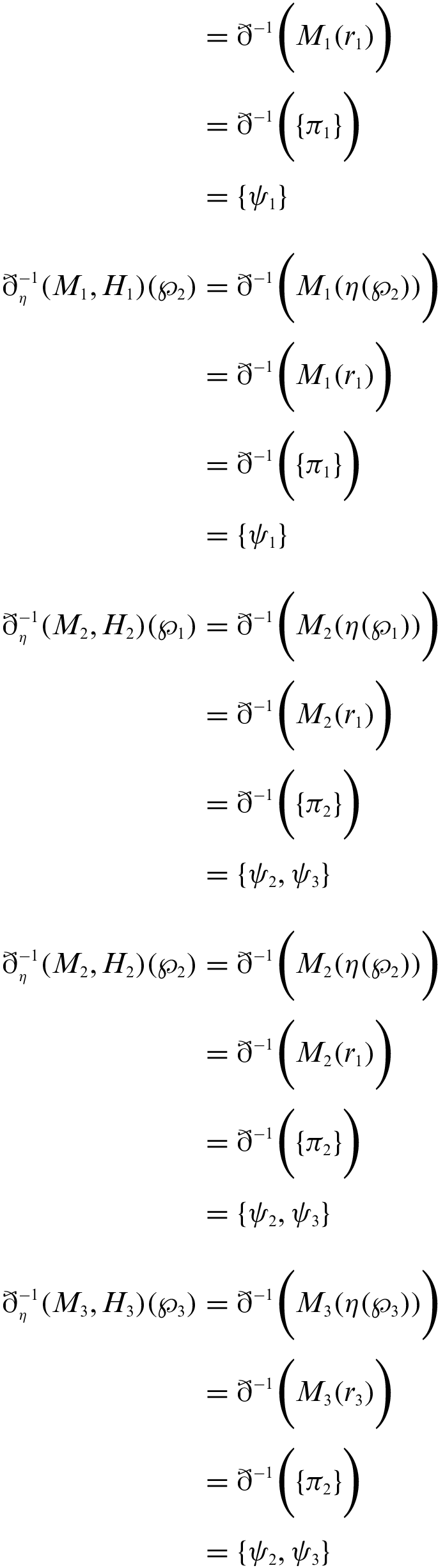
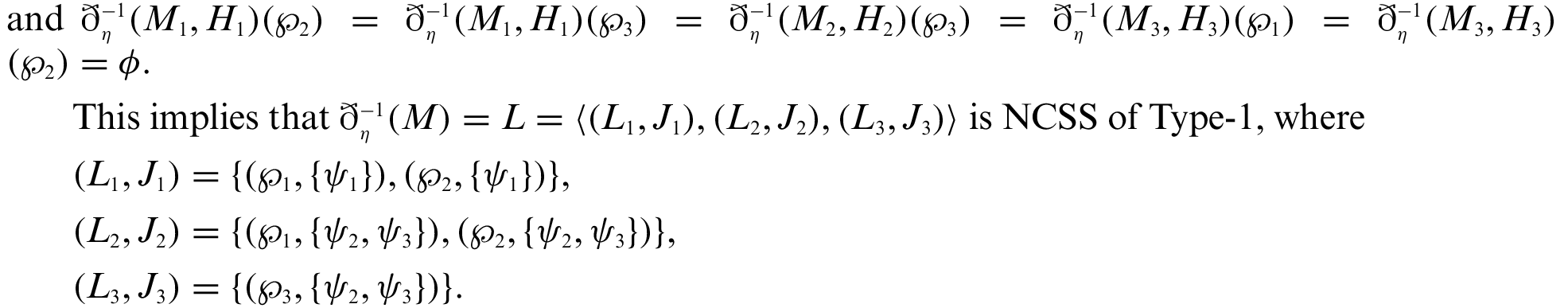
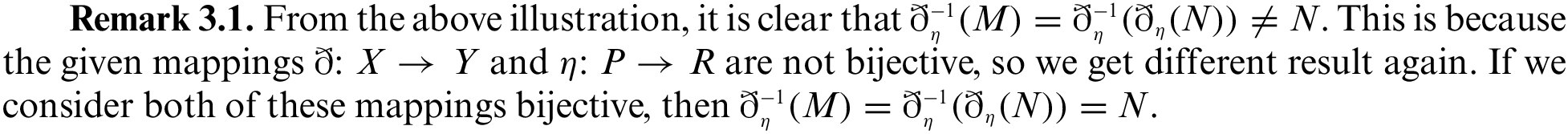

Proof.
1. Proof is obvious.
2. We have to show that
Type-1:
Type-2:
3. We have to show that
Type-1:
Type-2:
4. Type-1: Given is that
From [22],
Type-2: Let
From [22],
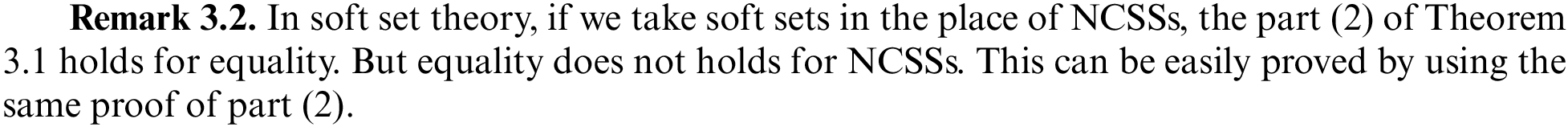

Proof. The proof is obvious by using the same arguments used in the proof of Theorem 3.1.
4 Emerging Trends in SNS via NCS-Mapping with the Generation Gap
An online program utilized by societies to construct social links or social associations with other individuals who partake comparable personal or professional interests, events, experiences or real-life influences is called a social networking service (social networking site, or SNS or social media). In 2015, according to a study, 63 percent of the users of Twitter and Facebook in the USA consider that the major source of entertainment and update is SNS. A survey made in 2015 survey shows that 85 percent of people who are Millennials or of generation Y use SNS for their purchase decision-making.
Early SNS has begun in the form of online websites given as http://www.theglobe.com/ (1995), Geocities (1994) and Tripod.com (1995). Some web sites such as Classmates.com-took a diverse methodology by merely having people refer to one another via email addresses. PlanetAll was initiated in 1996.
In the recent 1990s, user profiles became a central characteristic of SNW. The i-generation uses SNW to boom with the development of SixDegrees.com in 1997, followed by Open Diary in 1998, mixi in 1999, Makeoutclub in 2000, Hub Culture and Friendster in 2002. In 2004, Facebook was launched, became the biggest SNW in the cosmos in early 2009. The term SNS were ushered in and soon became widespread.
Table 8 provides the list of the biggest SNS with the ranking of active users, as of January 2018, as issued by Statista.
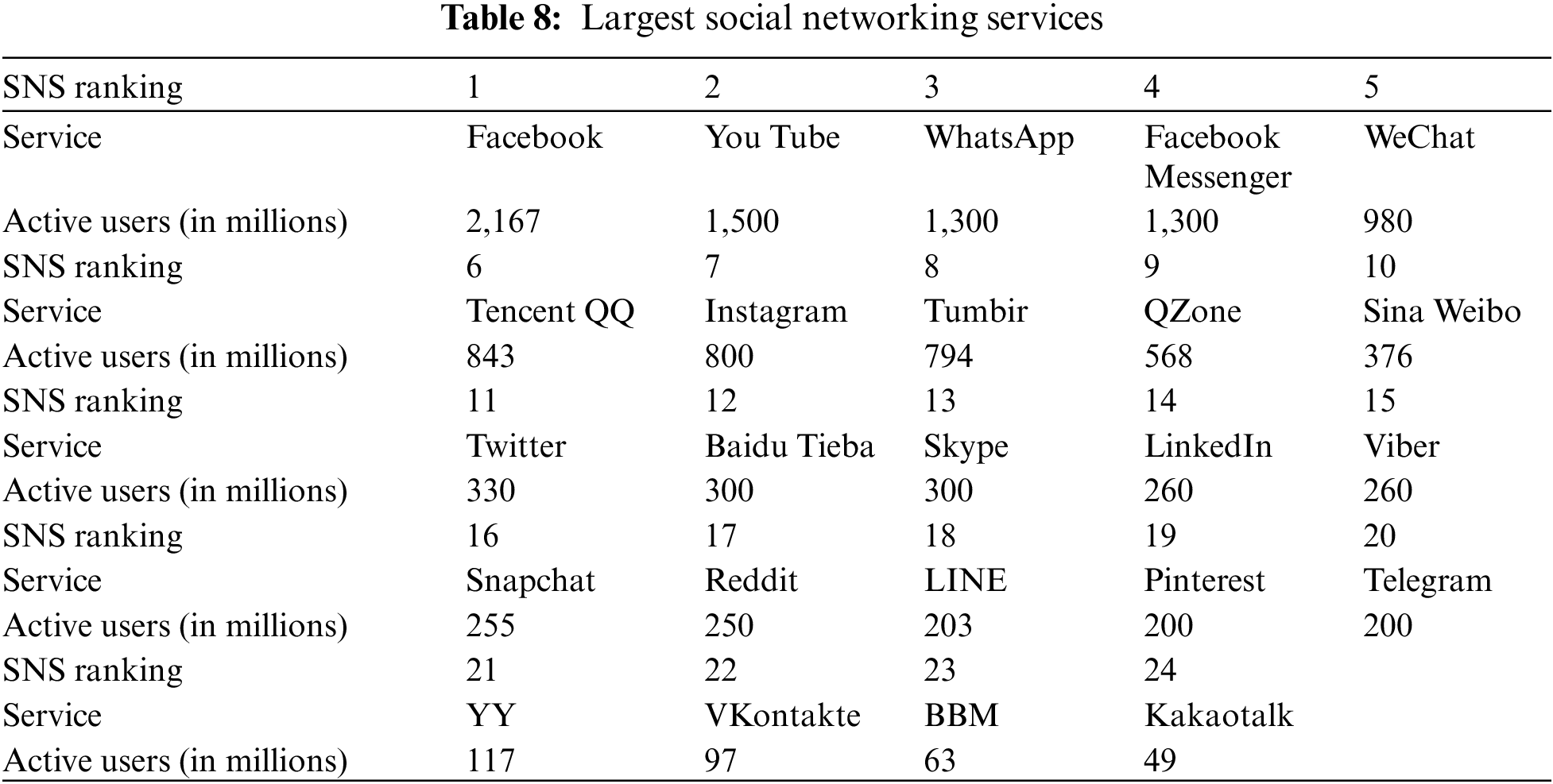
Example 4.1.
We are presenting an application of social networking system (SNS), where we can analysis the emerging trends and issues of SNS for different generations by using the NCSS mapping. We construct a model of NCSS data containing some important purposes of SNS, we can increase the points of features used in SNS according to our requirement. In this example, we choose some specific features and discuss about some specific trends and issues for different generations. Our choice is random and gives us an idea about the trends and issues that how these factors changes with the generation gap.
Algorithm:
Input:
Step-1: Input the sample spaces X and Y with the sets of decision variables P and R.
Step-2: Construct the NCS classes
Step-3: Define appropriate mappings
Step-4: Construct the NCS data for every generation separately. This implies that we can get different NCSSs for every individual generation.
Output:
Step-5: Use Definition 3.1 of NCSS mapping and calculate the image NCSS for every generation.
Step-6: Resulting NCSSs show how the SNS is tending or creating issue with the change of time or with the gap of generation. Basically, this model is used for data collection at a large scale and can be used for checking the results and observing the changings in the collected information with the change of time.
The flow chart diagram of NCSS-algorithm is shown in Fig. 2.
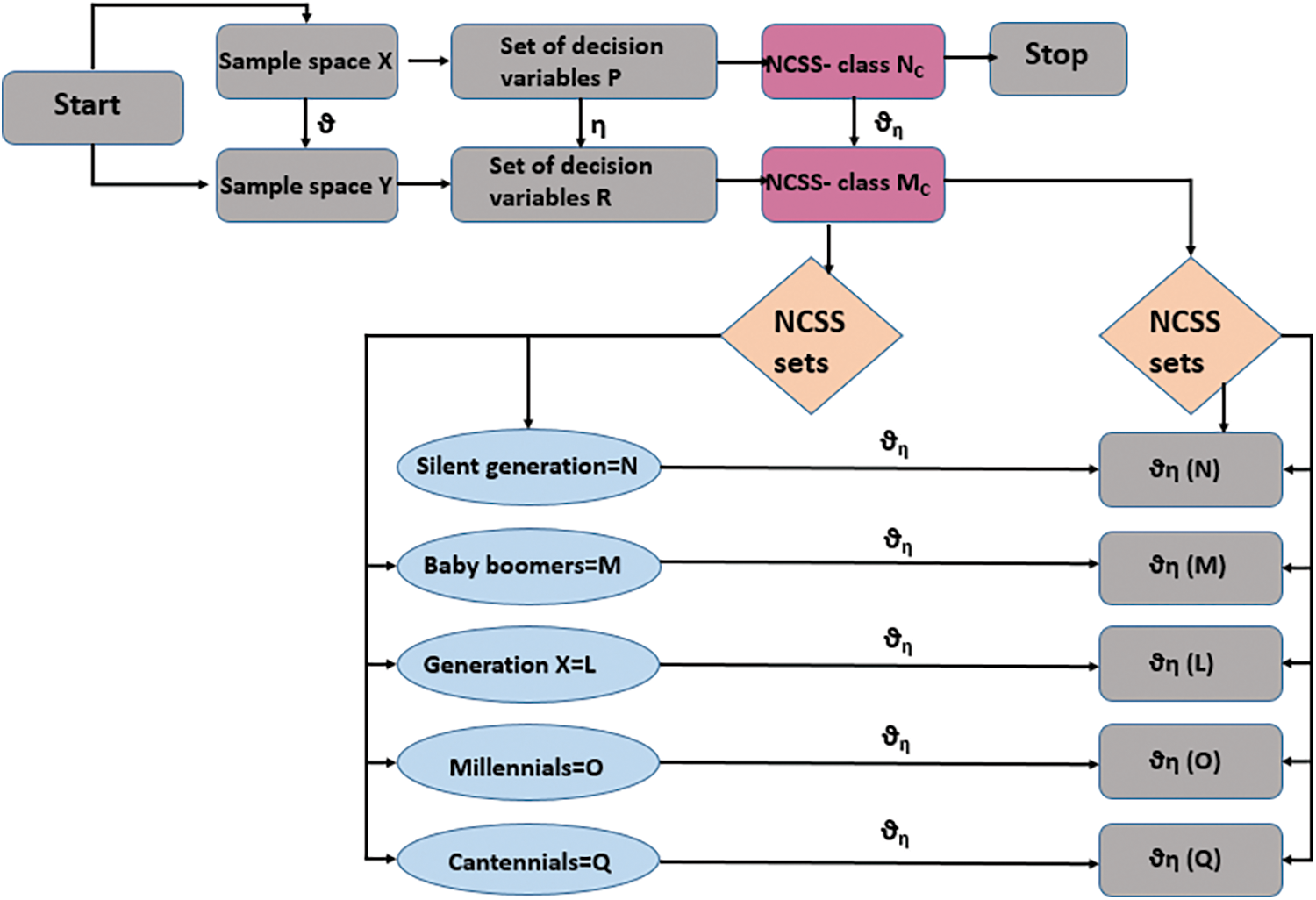
Figure 2: Flow chart diagram of NCSS-algorithm
Construction:
Let we have a sample space
Let sample space
The collection
In this application, we use the age factor for our discussion about SNS and its trends. We consider five generations given as:
(1): Traditional or silent generation: (Born in 1945 and before).
(2): Baby boomers: (Born in 1946 to 1964, roughly 50 to 70 years).
(3): Generation X: (Born in 1965 to 1976, 35–50 years).
(4): Millennials or generation Y: (Born in 1977 to 1995, 18–34 years).
(5): Centennials Generation Z or i-generation: (Born in 1996 and later).
Now, we construct five NCSSs which are N, M, L, O and Q for above five generations.
The tabular representation of
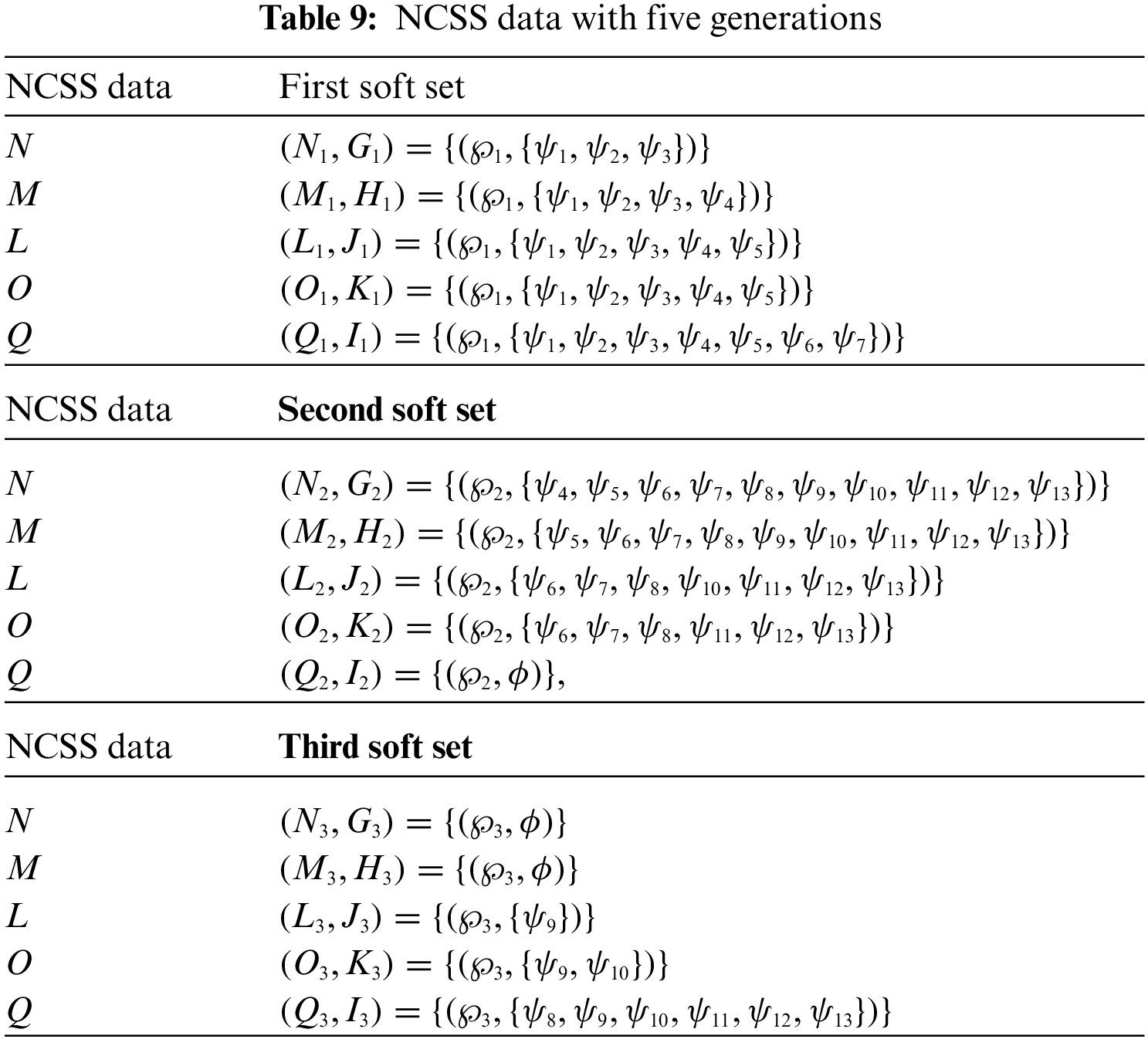
Now, we define appropriate mappings
and
Calculations:
We use Definition 3.1 and calculate the images of N, M, L, O and Q respectively as
The tabular representation of images of
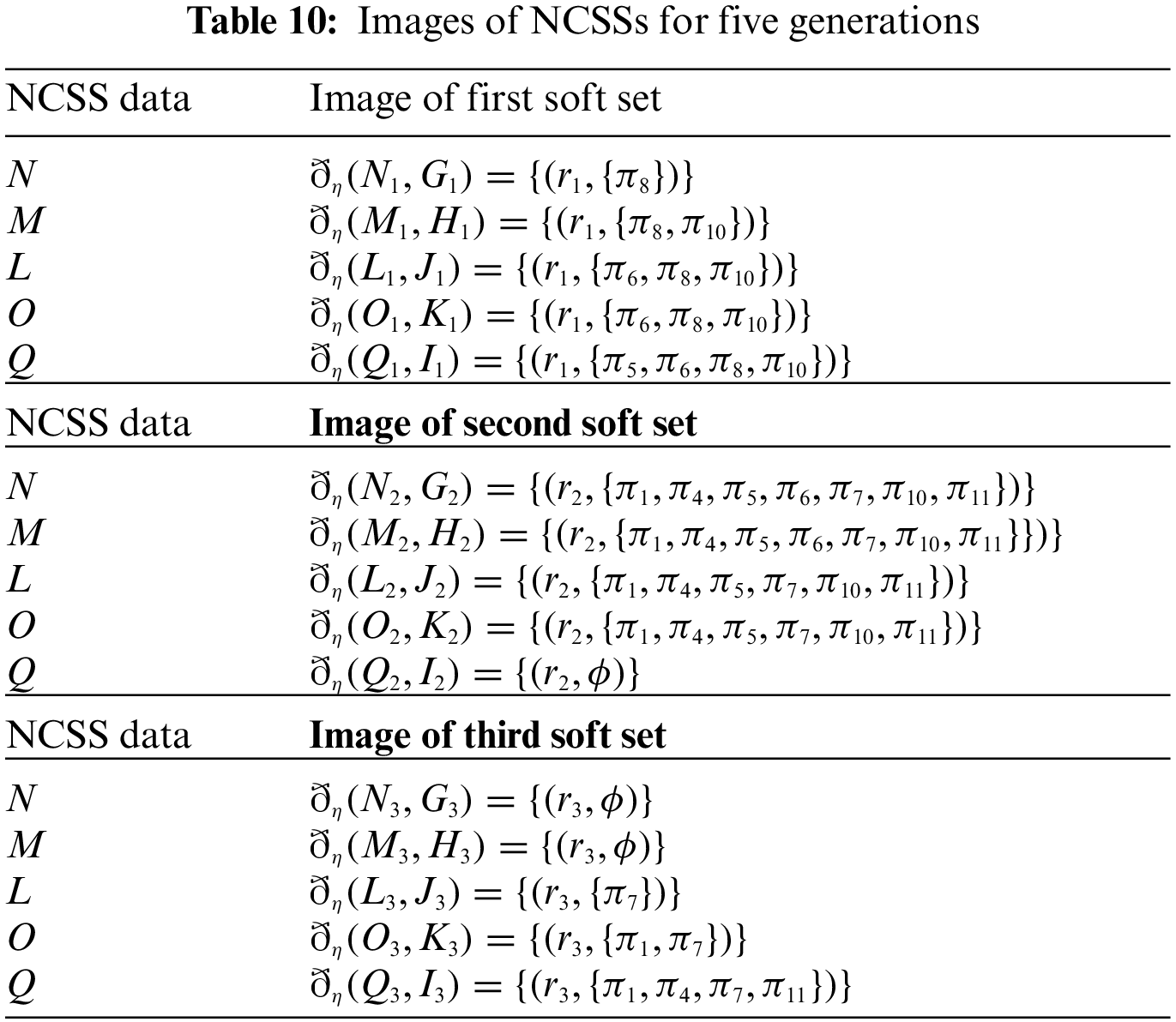
The information of SNS via NCSS data for five generations (Input) and effects of SNS to different generations (Output) is expressed in Tables 9 and 10, respectively.
In the Table 10, five NCSSs show the benefits, drawbacks and unaffected factors of SNS for the five generations. With the change of generation, we can see that emerging trends and benefits of SNS are increasing day by day. Similarly, some drawbacks are also increasing with the very much use of SNS. In the Table 10, the image of first soft set column shows the increase in benefits of SNS with the change of time and image of second soft set column shows that indeterminacy decreases with the generation gap, because people are searching and exploring things and collect information about the facts and easily decide that these features are beneficial or not for themselves. In the same way, the image of third soft set column also increasing which means the drawbacks or bad impacts of SNS are increasing for different generations, because when the use of SNS increases, then its bad impacts also affects the personal and social life of people and create disturbance in many areas of life.
5 A Comparison Analysis and Discussion
In this section, to corroborate the practicability of proposed NCSS and NCS-mapping we compare it with other hybrid structures of soft and fuzzy sets. In this inquiry, we present a new concept of NCSS with different characters and operations and use illustrations to flesh out the concept. Essentially, we construct three parameterized families of subsets of the creation of discourse with the given set of decision variables and the triplet becomes an NCSS. The presented idea of parameters or decision variables in the NC set contributes to the new approach of NCSS and covers the NC set theory as easily.
Resulting NCSSs show how the SNS is tending or creating issue with the change of time or with the gap of generation. Basically, this model is used for data collection at a large scale and can be used for checking the results and observing the changings in the collected information with the change of time.
The relations between neutrosophic hybrid sets and other hybrid structures are shown in Fig. 3.
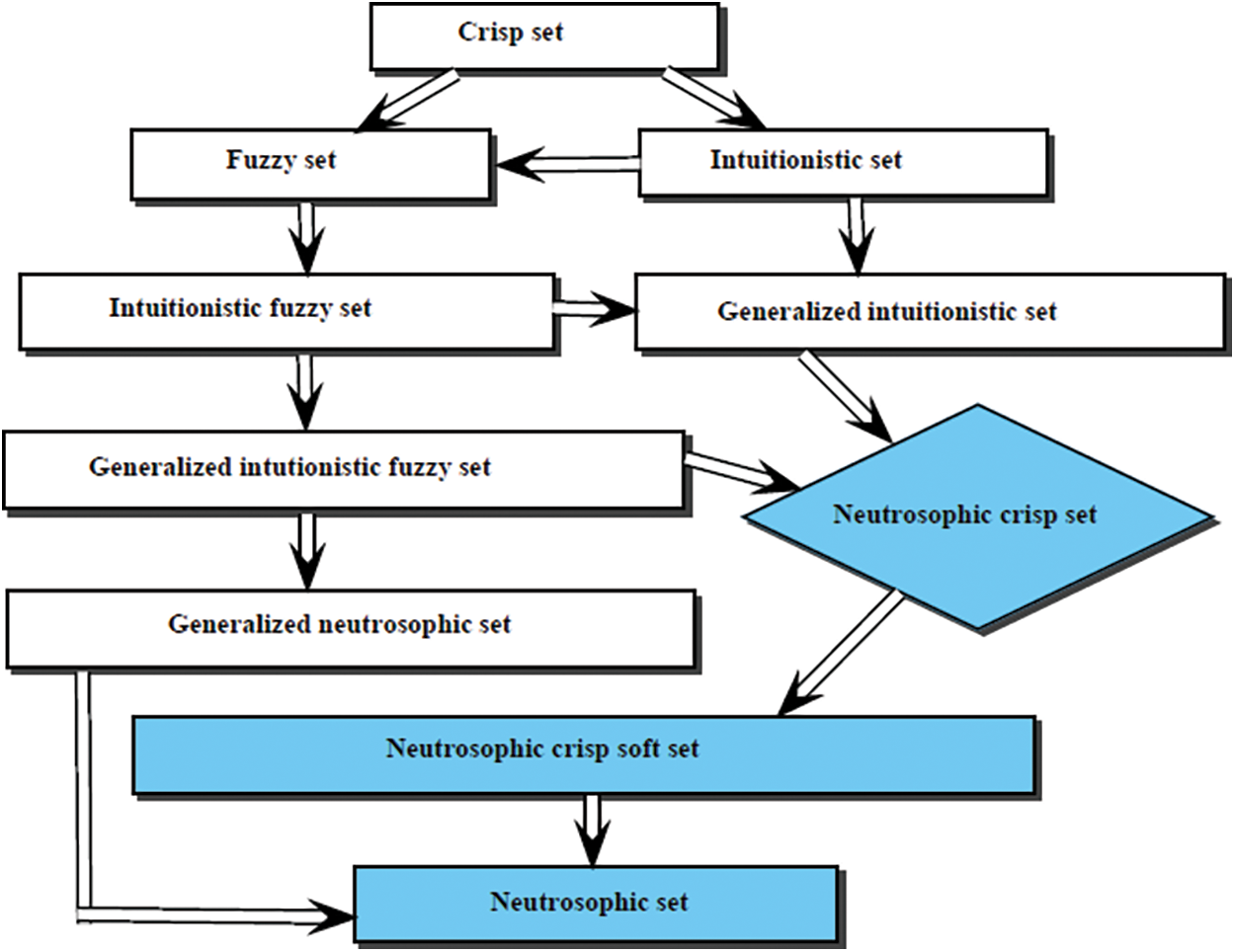
Figure 3: The relations between neutrosophic hybrid sets and other hybrid structures
In previous parts, we establish NCS-mapping of NCS classes and establish some results of mathematical functions which hold in soft set theory but do not hold in NCSS theory. In the application regarding SNS, we can utilize our set and its mapping to develop a robust mathematical modeling, and it can be easily used for data collection at a large scale and for a long time period. This constructed model through NCSSs can be used for discussion about the emerging trends, disadvantages and unpretentious factors of the social networking system for the five generations at the same time. If we examine the hybrid structures of soft and fuzzy sets, then we can well conclude that there is a chain relationship between NCSS and other hybrid structures like fuzzy set, IFS, GIFS, GNS. This relationship can be easily determined through the given flow chart diagram Fig. 3.
We introduced some new concepts of the neutrosophic crisp soft set (NCSS) and established different types of NCSSs. We defined some operations on NCSSs and illustrated these concepts with the help of some examples of NCSSs. We introduced NCS-mapping and developed images and inverse images of NCS classes. We derived some significant results regarding NCS-mapping. We further discussed some consequences of mapping which hold in soft set theory but do not hold in NCSS theory. We used NCS-mapping to develop a robust mathematical modeling to analyze emerging trends in social networking systems and the generation gap. The benefits, disadvantages and unpretentious factors of social networking systems for five generations were investigated. This article is an innovative approach to data science and information fusion at a large scale. Proposed theories and models are more efficient in addressing vagueness and uncertainties in real-life problems. This theory can be extended to various fields like geographical information systems, networking systems, robotics, pattern recognition, computational intelligence, medical diagnosis, etc.
Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through General Research Project under Grant No. R.G.P.2/181/44.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. DOI 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
2. Molodtsov, D. (1999). Soft set theory-first results. Computers and Mathematics with Applications, 37(4–5), 19–31. DOI 10.1016/S0898-1221(99)00056-5. [Google Scholar] [CrossRef]
3. Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87–96. DOI 10.1016/S0165-0114(86)80034-3. [Google Scholar] [CrossRef]
4. Atanassov, K. T. (1999). Interval valued intuitionistic fuzzy sets, In: Intuitionistic fuzzy sets, pp. 139–177. Heidelberg: Physica. [Google Scholar]
5. Bustince, H., Burillo, P. (1995). Correlation of interval-valued intuitionistic fuzzy sets. Fuzzy Sets and Systems, 74(2), 237–244. DOI 10.1016/0165-0114(94)00343-6. [Google Scholar] [CrossRef]
6. Zhang, Q. S., Jiang, S., Jia, B., Luo, S. (2010). Some information measures for interval-valued intuitionistic fuzzy sets. Information Sciences, 180(24), 5130–5145. DOI 10.1016/j.ins.2010.08.038. [Google Scholar] [CrossRef]
7. Wan, S. P., Dong, J. Y. (2020). Decision making theories and methods based on interval-valued intuitionistic fuzzy sets, pp. 1–313. Springer Nature. [Google Scholar]
8. Yager, R. R. (2013). Pythagorean fuzzy subsets. 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), pp. 57–61. Edmonton, AB, Canada, Piscataway, NJ, USA, IEEE. [Google Scholar]
9. Yager, R. R., Abbasov, A. M. (2013). Pythagorean membership grades, complex numbers, and decision making. International Journal of Intelligent Systems, 28(5), 436–452. DOI 10.1002/int.21584. [Google Scholar] [CrossRef]
10. Yager, R. R. (2017). Generalized orthopair fuzzy sets. IEEE Transactions on Fuzzy Systems, 25(5), 1220–1230. DOI 10.1109/TFUZZ.2016.2604005. [Google Scholar] [CrossRef]
11. Zhang, W. R. (1994). Bipolar fuzzy sets and relations: a computational framework for cognitive modeling and multiagent decision analysis. Proceedings of the First International Joint Conference of the North American Fuzzy Information Processing Society Biannual Conference, pp. 305–309. San Antonio, TX, USA. [Google Scholar]
12. Zhang, W. R. (1998). Bipolar fuzzy sets. Proceedings of IEEE International Conference on Fuzzy Systems, pp. 835–840. Anchorage, AK, USA. [Google Scholar]
13. Chen, J., Li, S., Ma, S., Wang, X. (2014). m-polar fuzzy sets: An extension of bipolar fuzzy sets. The Scientific World Journal, 2014(3), 1–8. DOI 10.1155/2014/416530. [Google Scholar] [CrossRef]
14. Smarandache, F. (1998). Neutrosophy: neutrosophic probability, set, and logic: analytic synthesis & synthetic analysis, pp. 1–105. Rehoboth, USA: American Research Press. [Google Scholar]
15. Smarandache, F. (1999). A unifying field in logics. Neutrosophy: Neutrosophic probability, set and logic, pp. 1–141. Rehoboth, DE, USA: American Research Press. [Google Scholar]
16. Wang, H., Smarandache, F., Zhang, Y. Q., Sunderraman, R. (2010). Single valued neutrosophic sets. Multispace and Multistructure, 4, 410–413. [Google Scholar]
17. Salama, A. A., Smarandache, F., Kroumov, V. (2014). Neutrosophic crisp sets and neutrosophic crisp topological spaces. Neutrosophic Sets and Systems, 2, 25–30. [Google Scholar]
18. Salama, A. A., Broumi, S., Smarandache, F. (2014). Some types of neutrosophic crisp sets and neutrosophic crisp relations. In: IJ information engineering and electronic business, pp. 1–9. DOI 10.6084/M9.FIGSHARE.1502624. [Google Scholar] [CrossRef]
19. Salama, A. A., Smarandache, F. (2014). Neutrosophic crisp set theory. Neutrosophic Sets and Systems, 5, 27–35. [Google Scholar]
20. Karaaslan, F. (2015). Neutrosophic soft set with applications in decision making. International Journal ofInformation Science and Intelligent System, 4(2), 1–20. DOI 10.5281/zenodo.23151. [Google Scholar] [CrossRef]
21. Maji, P. K. (2013). Neutrosophic soft set. Annals of Fuzzy Mathematics and Informatics, 5(1), 157–168. [Google Scholar]
22. Kharal, A., Ahmad, B. (2011). Mappings on soft classes. New Mathematics and Natural Computation, 7(3), 471–481. DOI 10.1142/S1793005711002025. [Google Scholar] [CrossRef]
23. Wardowski, D. (2013). On a soft mapping and its fixed points. Fixed Point Theory and Applications, 2013(1), 1–11. DOI 10.1186/1687-1812-2013-182. [Google Scholar] [CrossRef]
24. Peng, X., Liu, L. (2019). Information measures for q-rung orthopair fuzzy sets. International Journal of Intelligent Systems, 34(8), 1795–1834. DOI 10.1002/int.22115. [Google Scholar] [CrossRef]
25. Akram, M., Sattar, A., Karaaslan, F., Samanta, S. (2021). Extension of competition graphs under complex fuzzy environment. Complex & Intelligent Systems, 7(1), 539–558. DOI 10.1007/s40747-020-00217-5. [Google Scholar] [CrossRef]
26. Akram, M., Nawaz, H. S. (2022). Implementation of single-valued neutrosophic soft hypergraphs on human nervous system. Artificial Intelligence Review, 33(2), 1–39. DOI 10.1007/s10462-022-10200-w. [Google Scholar] [CrossRef]
27. Zhan, J., Akram, M., Sitara, M. (2019). Novel decision-making method based on bipolar neutrosophic information. Soft Computing, 23(20), 9955–9977. DOI 10.1007/s00500-018-3552-8. [Google Scholar] [CrossRef]
28. Feng, F., Zheng, Y., Sun, B., Akram, M. (2022). Novel score functions of generalized orthopair fuzzy membership grades with application to multiple attribute decision making. Granular Computing, 7(1), 95–111. DOI 10.1007/s41066-021-00253-7. [Google Scholar] [CrossRef]
29. Akram, M. (2011). Bipolar fuzzy graphs. Information Sciences, 181(24), 5548–5564. DOI 10.1016/j.ins.2011.07.037. [Google Scholar] [CrossRef]
30. Akram, M., Khan, A., Alcantud, J. C. R., Santos-García, G. (2021). A hybrid decision-making framework under complex spherical fuzzy prioritized weighted aggregation operators. Expert Systems, 38(6), 1–24. DOI 10.1111/exsy.12712. [Google Scholar] [CrossRef]
31. Alghamdi, M. A., Alshehri, N. O., Akram, M. (2018). Multi-criteria decision-making methods in bipolar fuzzy environment. International Journal of Fuzzy Systems, 20(6), 2057–2064. DOI 10.1007/s40815-018-0499-y. [Google Scholar] [CrossRef]
32. Yang, H. L., Guo, Z. L., She, Y., Liao, X. (2016). On single valued neutrosophic relations. Journal of Intelligent & Fuzzy Systems, 30(2), 1045–1056. DOI 10.3233/IFS-151827. [Google Scholar] [CrossRef]
33. Yue, Q. (2022). Bilateral matching decision-making for knowledge innovation management considering matching willingness in an interval intuitionistic fuzzy set environment. Journal of Innovation & Knowledge, 7(3), 1–17. DOI 10.1016/j.jik.2022.100209. [Google Scholar] [CrossRef]
34. Naeem, K., Riaz, M., Karaaslan, F. (2021). Some novel features of Pythagorean m-polar fuzzy sets with applications. Complex & Intelligent Systems, 7(1), 459–475. DOI 10.1007/s40747-020-00219-3. [Google Scholar] [CrossRef]
35. Thao, N. X., Smarandache, F. (2020). Apply new entropy based similarity measures of single valued neutrosophic sets to select supplier material. Journal of Intelligent & Fuzzy Systems, 39(1), 1–15. DOI 10.3233/JIFS-191929. [Google Scholar] [CrossRef]
36. Ulucay, V., Deli, I., Sahin, M. (2018). Similarity measures of bipolar neutrosophic sets and their application to multiple criteria decision making. Neural Computing & Applications, 29(3), 739–748. DOI 10.1007/s00521-016-2479-1. [Google Scholar] [CrossRef]
37. Hashim, R. M., Gulistan, M., Smarandache, F. (2018). Applications of neutrosophic bipolar fuzzy sets in hope foundation for planning to build a children hospital with different types of similarity measures. Symmetry, 10(8), 1–26. DOI 10.3390/sym10080331. [Google Scholar] [CrossRef]
38. Garg H., Nancy (2018). Some hybrid weighted aggregation operators under neutrosophic set environment and their applications to multicriteria decision-making. Applied Intelligence, 48(12), 4871–4888. DOI 10.1007/s10489-018-1244-9. [Google Scholar] [CrossRef]
39. Karaaslan, F., Hayat, K. (2018). Some new operations on single-valued neutrosophic matrices and their applications in multi-criteria group decision making. Applied Intelligence, 48(12), 4594–4614. DOI 10.1007/s10489-018-1226-y. [Google Scholar] [CrossRef]
40. Hashmi, M. R., Riaz, M., Smarandache, F. (2020). m-polar neutrosophic topology with applications to multi-criteria decision-making in medical diagnosis and clustering analysis. International Journal of Fuzzy Systems, 22(1), 273–292. DOI 10.1007/s40815-019-00763-2. [Google Scholar] [CrossRef]
41. Zhang, H. Y., Wang, J. Q., Chen, X. H. (2014). Interval neutrosophic sets and their applications in multi-criteria decision making problems. The Scientific World Journal, 1–15. DOI 10.1155/2014/645953. [Google Scholar] [CrossRef]
42. Ye, J. (2013). Multicriteria decision-making method using the correlation coefficient under single-value neutrosophic environment. International Journal of General Systems, 42(4), 386–394. DOI 10.1080/03081079.2012.761609. [Google Scholar] [CrossRef]
43. Ye, J. (2014). A multi-criteria decision-making method using aggregation operators for simplified neutrosophic sets. Journal of Intelligent & Fuzzy Systems, 26(5), 2459–2466. DOI 10.3233/IFS-130916. [Google Scholar] [CrossRef]
44. Feng, F., Li, C., Davvaz, B., Ali, M. I. (2010). Soft sets combined with fuzzy sets and rough sets: A tentative approach. Soft Computing, 14(9), 899–911. DOI 10.1007/s00500-009-0465-6. [Google Scholar] [CrossRef]
45. Pamucar, D. (2020). Normalized weighted geometric Dombi Bonferroni mean operator with interval grey numbers: Application in multicriteria decision making. Reports in Mechanical Engineering, 1(1), 44–52. DOI 10.31181/rme200101044p. [Google Scholar] [CrossRef]
46. Chen, Z. H., Wan, S. P., Dong, J. Y. (2022). An efficiency-based interval type-2 fuzzy multi-criteria group decision making for makeshift hospital selection. Applied Soft Computing, 115, 1–19. DOI 10.1016/j.asoc.2021.108243. [Google Scholar] [CrossRef]
47. Riaz, M., Pamucar, D., Habib, A., Riaz, M. (2022). Innovative bipolar fuzzy sine trigonometric aggregation operators and SIR method for medical tourism supply chain. Mathematical Problems in Engineering, 2022(1), 1–17. DOI 10.1155/2022/4182740. [Google Scholar] [CrossRef]
48. Hanif, M. Z., Yaqoob, N., Riaz, M., Aslam, M. (2022). Linear Diophantine fuzzy graphs with new decision-making approach. AIMS Mathematics, 7(8), 14532–14556. DOI 10.3934/math.2022801. [Google Scholar] [CrossRef]
49. Saeed, M., Ahsan, M., Saeed, M. H., Mehmood, A., Abdeljawad, T. (2021). An application of neutrosophic hypersoft mapping to diagnose hepatitis and propose appropriate treatment. IEEE Access, 9, 70455–70471. DOI 10.1109/ACCESS.2021.3077867. [Google Scholar] [CrossRef]
50. Riaz, M., Hashmi, M. R. (2021). m-polar neutrosophic soft mapping with application to multiple personality disorder and its associated mental disorders. Artificial Intelligence Review, 54(4), 2717–2763. DOI 10.1007/s10462-020-09912-8. [Google Scholar] [CrossRef]
51. Riaz, M., Hashmi, M. R. (2019). Bipolar fuzzy soft mappings with application to bipolar disorders. International Journal of Biomathematics, 12(7), 1–31. DOI 10.1142/S1793524519500803. [Google Scholar] [CrossRef]
52. Latreche, A., Barkat, O., Milles, S., Ismail, F. (2020). Single valued neutrosophic mappings defined by single valued neutrosophic relations with applications. Neutrosophic Sets and Systems, 1, 203–220. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools