Open Access

ARTICLE

2D Minimum Compliance Topology Optimization Based on a Region Partitioning Strategy

Chong Wang¹, Tongxing Zuo^1,2, Haitao Han^1,2, Qianglong Wang^1,2, Han Zhang¹, Zhenyu Liu^1,*

1 Changchun Institute of Optics, Fine Mechanics and Physics (CIOMP), Chinese Academy of Sciences, Changchun, 130000, China
2 School of Optoelectronics, University of Chinese Academy of Science, Beijing, 100049, China

* Corresponding Author: Zhenyu Liu. Email:

(This article belongs to the Special Issue: New Trends in Structural Optimization)

Computer Modeling in Engineering & Sciences 2023, 136(1), 655-683. https://doi.org/10.32604/cmes.2023.025153

Received 24 June 2022; Accepted 21 September 2022; Issue published 05 January 2023

Abstract

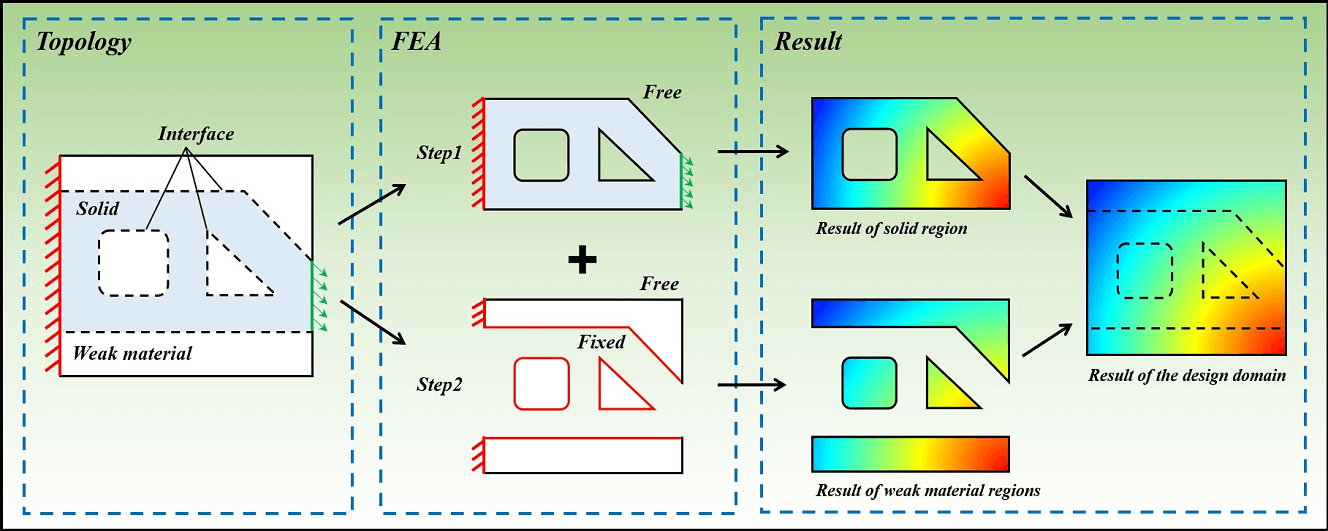
This paper presents an extended sequential element rejection and admission (SERA) topology optimization method with a region partitioning strategy. Based on the partitioning of a design domain into solid regions and weak regions, the proposed optimization method sequentially implements finite element analysis (FEA) in these regions. After standard FEA in the solid regions, the boundary displacement of the weak regions is constrained using the numerical solution of the solid regions as Dirichlet boundary conditions. This treatment can alleviate the negative effect of the material interpolation model of the topology optimization method in the weak regions, such as the condition number of the structural global stiffness matrix. For optimization, in which the forward problem requires nonlinear structural analysis, a linear solver can be applied in weak regions to avoid numerical singularities caused by the over-deformed mesh. To enhance the robustness of the proposed method, the nonmanifold point and island are identified and handled separately. The performance of the proposed method is verified by three 2D minimum compliance examples.

---

Graphic Abstract

---

Keywords

---