Secure Downlink Transmission Strategies against Active Eavesdropping in NOMA Systems: A Zero-Sum Game Approach

1  Introduction

Non-orthogonal multiple access (NOMA) has been envisioned as a potentially promising technology for fifth generation (5G) and beyond 5G (B5G) wireless communication networks for its superior performance over the conventional orthogonal multiple access (OMA) in terms of spectral efficiency, connection density, as well as user fairness [1–4]. However, due to the broadcast nature of wireless communication, the NOMA system is vulnerable to eavesdropping. To secure information transmission against malicious eavesdropping, many countermeasures, such as encryption-based approaches implemented at the higher layers [5] and physical layer security (PLS) [6,7], have been put forward in recent years. PLS, as a promising solution to safeguard confidential transmission from the wireless information-theoretic perspective, exploits the intrinsic randomness of the wireless medium to enhance security, and can provide a secure transmission without keys or sophisticated encryption/decryption algorithms. In addition, the physical layer security techniques can be easily implemented and have the capability to quickly adapt to different wireless scenarios [8].

Recently, the concept of PLS has been applied to NOMA systems for secure transmission, and has attracted significant attention and increasing interest in both academia and industry [9,10]. The existing work generally falls into two categories: the security-oriented system design, and X-assisted security scheme. Specifically, the security-oriented system design approaches enhance security by optimizing the parameters of the NOMA system, such as beamforming matrix and power allocation coefficients. Whilst, in X-assisted security schemes, X denotes artificial signal, relay, cooperative jamming or something additional. The key idea behind the approaches is to deliberately improve the legitimated communication channel and/or degrade the eavesdropping channel.

Nevertheless, most of the existing studies on secure transmission in NOMA are conducted from the perspective of legitimate communicators, and fail to reflect the confrontation relationship between eavesdroppers and legitimate communicators. In other words, they assume the precondition that the eavesdropper keeps wiretapping regardless of the radio environment. As a matter of fact, eavesdroppers may incur more costs than benefits when faced with harsh eavesdropping channel conditions, and have no intent to eavesdrop in this situation, which makes the precondition more conservative. Therefore, it is of great significance to comprehensively study the interaction strategies between the two sides considering the channel conditions. However, the various and variable channel state information in radio environment complicates the dynamic secure transmission and eavesdropping process, and further affects their optimal strategy selection for both sides, which poses a huge challenge to studying the secure transmission in NOMA system from the interaction perspective.

Fortunately, game theory, as a mathematical theory and tool to study competitive or cooperative behaviors, provides a powerful framework with which the optimal strategies for both/all sides under various solution concepts of equilibrium can be found. In the secure transmission strategy selections of NOMA systems, we study the interaction between the legitimate communicators and the eavesdropper based on game theory. Specifically, both sides will pay the cost and receive the corresponding benefits in the light of the strategy profile comprised of strategies they select, respectively. That is to say, one’s gain is influenced not only by his/her strategy, but also by the other’s. The advantage of doing so is that the optimal secure transmission strategy can be selected by analyzing the opponent’s strategy, and its conservativeness can be reduced to some extent.

Motivated by this, for a NOMA system with external eavesdroppers, we focus on two typical security schemes, artificial-signal-assisted scheme (AS scheme) and relay-station-assisted scheme (RS scheme). Specifically, artificial signals are superimposed in the orthogonal subspace of weak users’ transmission directions in AS scheme and relays are employed in weak users’ transmission links in RS scheme, to impair the eavesdropping capability. In both schemes, the external active eavesdropper can impose interference signals while eavesdropping to reduce the quality of legitimate communication. In this paper, we first establish the system models, including channel models and signal models, and formulate the information transmission rate for each legitimate communicator and eavesdropper in AS and RS schemes, respectively. Then, the interactions around secure transmission rate, i.e., secrecy rate, are modeled as two-person zero-sum security games. For each security game model, the existence of Nash equilibrium is proved, and the pure strategy Nash equilibrium and mixed-strategy the Nash equilibrium profile are solved and analyzed. Finally, numerical simulations are conducted to validate the theoretical results, and show that AS and RS schemes can improve the secrecy rate and further enhance the physical layer security performance of NOMA systems. By analyzing the Nash equilibrium of the proposed game model, we can shed some light on the decision-making motives, which is of great significance in the design of security schemes.

The main contributions of this paper can be summarized as follows:

•   We are the first to investigate artificial-signal-assisted and relay-station-assisted secure downlink transmission schemes for NOMA systems against external active eavesdropping within the framework of game theory, which integrates eavesdropper’s strategy in the design of secure transmission scheme, improves secrecy rate and further enhances physical layer security performance accordingly.

•   We model the confrontational interaction between them as a two-person zero-sum game with secrecy rate as utilities to characterize the impact mechanism of legitimate communicators and active eavesdropper’s strategies on the security performance of the Nash system, prove the existence of the Nash equilibrium, and give the optimal (equilibrium) strategy profile which sheds some light on the design of secure NOMA downlink transmission.

•   Through numerical simulations, we demonstrate that legitimate communicators can improve the security performance in terms of secrecy rate by with the help of artificial signals or relay stations, while the active eavesdropper choose to eavesdrop and impose interference signal simultaneously in AS scheme and only eavesdrop in RS scheme.

The rest of the paper is organized as follows. In Section 2, a detailed literature survey of physical layer security issues in NOMA system are discussed. Section 3 describes the system model, including channel model and signal model, in artificial-signal-assisted scheme and relay-assisted scheme, respectively. In Section 4, the interactions between the utility of the legitimate communication party and eavesdropper are modeled as two-person zero-sum game, the utilities are expressed in terms of secrecy rate, the existence of the Nash equilibrium of the proposed game models is proved, and the pure strategy the Nash equilibrium and the mixed-strategy Nash equilibrium profiles are solved and analyzed respectively. In Section 5, the proposed game models are evaluated and verified through numerical simulations. Finally, a conclusion is given in Section 6.

2  Related Works

In the pioneering works on secure communication in NOMA system from the perspective of physical layer security, existing studies in this field can be classified into two categories: the security-oriented system optimization and X-assisted security scheme. In this section, we introduce the security solutions for NOMA communication systems according to the above taxonomy.

2.1 Security-Oriented NOMA System Design

Security-oriented NOMA system design aims to achieve better security performance by optimizing the NOMA communication system in normal operation mode, such as beamforming, power allocation, user pairing, etc. In [11], the authors investigated the physical layer security problem of mm-Wave NOMA network, proposed an analysis framework of security outage probability, develop a minimal angle-difference user pairing scheme and two maximum ratio transmission beamforming schemes to further enhance the secrecy performance. The authors of [12] considered the application of NOMA to a multi-user network with mixed multicasting and unicasting traffic and proposed a design of beamforming and power allocation ensures that the unicasting performance is improved and maintaining the reception reliability of multicasting. In [13], a low-complexity subcarrier assignment scheme was proposed to maximize the achievable secrecy energy efficiency. In [14], the authors investigated the reliable and secure transmission problem of NOMA systems with untrusted near users, and proposed a joint beamforming and power allocation scheme to achieve reliable and secure transmission. The authors of [15] designed a secure transmission scheme based on beamforming optimization to guard against both internal and external eavesdropping of downlink MISO NOMA networks. In [16], the authors considered the PLS against internal eavesdropping and gave the beamforming design and optimal power allocation problems to guarantee the positive secrecy rate of the system.

2.2 X-Assisted Security Solution

Different from security-oriented NOMA system design, X-assisted security solution enhance security by utilizing external “X”, such as artificial signals, relays, etc. We mainly introduce the two mainstream techniques, artificial-signal (AS) and relay-station (RS)-assisted security solutions, respectively.

2.2.1 AS-Assisted Security Solution

The authors of [17] proposed the method of combining weak user information bearing signal and artificial signal in NOMA system to improve the security performance of the system. The security outage performance of artificial noise assisted full duplex downlink NOMA transmission in large-scale networks was investigated in [18]. In [19], the authors proposed a new hierarchical PLS model to ensure the security of the transmitted information. And an auxiliary optimal beamforming scheme was proposed to ensure the layered information security. In [20], a new frequency domain artificial noise assisted transmission strategy was proposed to improve the physical layer security of the information receiver and satisfied the energy acquisition requirements of the energy receiver. The authors investigated the problem for the design of artificial noise assisted beamforming in MISO channels from the perspective of security outage. The optimal structure was found by solving the security rate maximization problem constrained by the security outage in [21].

2.2.2 RS-Assisted Security Solution

In [22], the security communication problem in multi hop relay systems was considered, the authors proposed to use full duplex relay to enhance the security of the wireless physical layer. The authors of [23] proposed a new two-level secure relay selection scheme in order to protect legitimate communication from eavesdropping. In [24], the authors considered a NOMA network with a half-duplex decode-and-forward relay to improve the physical layer security of two users. Two relay selection schemes termed decode-and-forward and amplify-and-forward protocols based optimal relay selection was proposed in [25]. In [26], the authors proposed a novel cooperative NOMA scheme to guarantee the secure transmission of a specific user via two time slots.

Although scholars have provided many security schemes in the research of NOMA physical layer security, they rarely consider the dynamic confrontational interaction between the two parties. Using the method of game theory, this paper comprehensively considers the confrontation game relationship between the eavesdropper and the legitimate communicator, establishes the interaction behavior of the two sides as a zero-sum game model, and finally realizes the secure transmission of the legitimate communicator.

3  System Model

Consider the standard downlink transmission of a typical NOMA system, consisting of a base station (BS) equipped with N antennas, an external active eavesdropper (E), and two paired legitimate users (LU1 and LU2) equipped with a single antenna respectively. In NOMA paired users, the user with better channel condition is called the strong user, and the user with poor channel gain is called the weak user [1]. Without loss of generality, we assume LU1 is a strong user and LU2 is a weak user. In our system model, BS sends signals to legitimate users, and the signals can also be received at E who may decode the message from the received signals. Meanwhile, E may sends jamming signal to the legitimate user to decrease its data rate and therefore the secrecy rate. In addition, we also assume that E is only interested in the information of LU2, the working mode of LU1 and LU2 is half-duplex, and the working mode of E is full-duplex, which can simultaneously eavesdrop and interfere and cause a certain amount of self-interference to oneself. In order to improve the security of the physical layer, two solutions are considered: superimposing artificial signal (AS) in the orthogonal null space in the transmission direction of LU2 and adding a relay station (RS) on the transmission link of LU2, as shown in Figs. 1a and 1b, respectively.

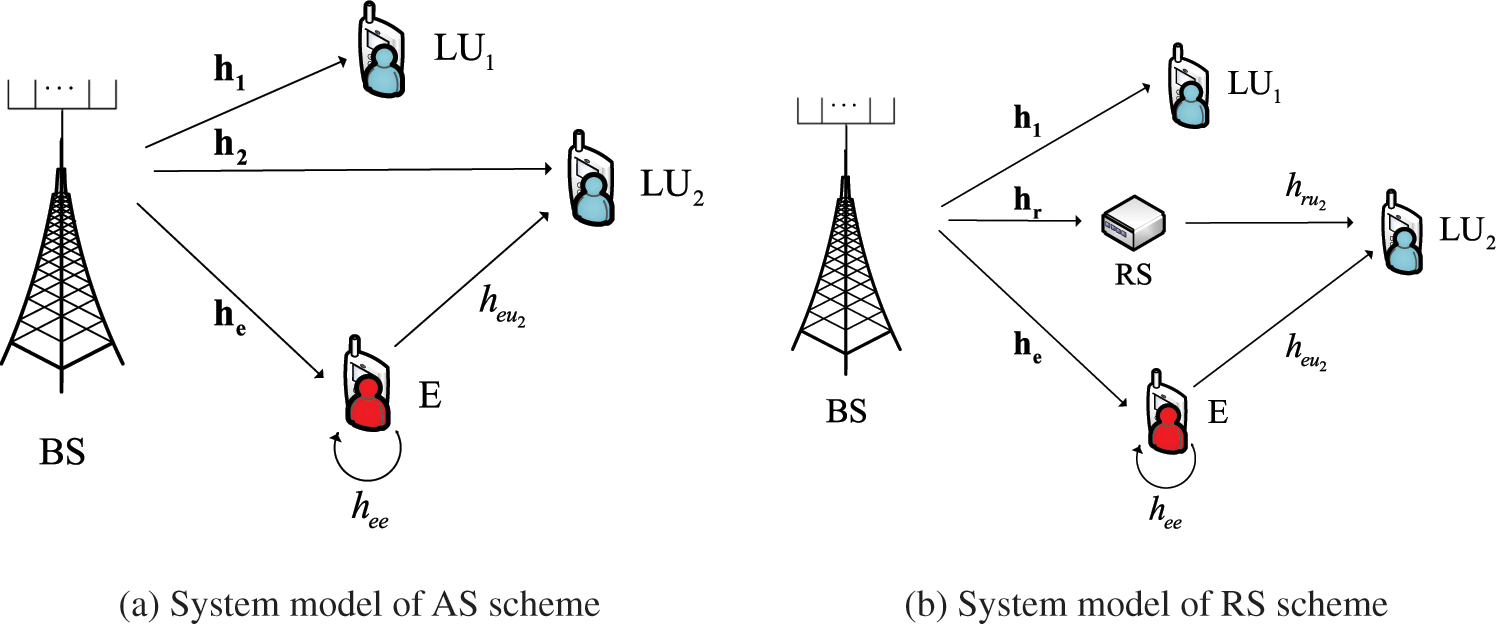
Figure 1: System model in AS and RS schemes

3.1 Channel Model

Assume that all channels experience independent quasi-static flat Rayleigh fading, where the channel coefficients remain unchanged within one time-frequency block but change independently between different time-frequency blocks, and suffer from additive white Gaussian noise (AWGN) [27,28]. The 1×N channel gain vectors from the BS to LUi(i∈{1,2}) and E are denoted as hi(i∈{1,2}) and he, respectively. The channel vector from E to LU2 is denoted as heu2, and E’s self-interference link gain as hee. Also, the 1×N channel gain vector from the BS to RS is denoted by hr, and the channel gain from RS to LU2 is denoted by hru2. We denote the noise power at LU1, LU2, RS and E as σ12, σ22, σr2 and σe2, respectively, with the same variance. We also assume that the quality of the relay channel in the system is better than that of the weak user, and the quality of the eavesdropping channel is worse than that of the weak user. It is reasonable to assume that the base station BS knows the channel state information (CSI) of all channels between BS and LUi(i∈{1,2}) perfectly due to the fact that they are normal transceivers in the NOMA system.

3.2 Signal Model

3.2.1 Signal Model of AS Scheme

In the system model of the AS scheme, the base station transmits superimposed signal to users. To protect the weak user from eavesdropping, the artificial signal is superimposed in the orthogonal null space of the transmission direction. The superimposed signal transmitted from BS to LUi(i∈{1,2}) can be expressed as

x=w1(α1Psx1+α2Psx2)+P3w2x3(1)

where x1 and x2 are the information-carrying signals to LU1 and LU2, x3 is the artificial signal, Ps is the power of effective signals in the superimposed signal at the base station BS, P3 is the transmission power of the artificial signal, α1 and α2 are the power sharing coefficients of LU1 and LU2 at the BS, with α1+α2=1 and α2>α1 for user fairness, w1=h2H||h2|| and w2 are well designed N×1 beamforming vectors for effective signals and artificial signal, respectively, and (⋅)H denotes the Hermitian (conjugate) transpose operation.

Then, the signals received at LU1 and LU2 are given by

y1=h1h2H||h2||(α1Psx1+α2Psx2)+h1w2P3x3+n1(2)

and

y2=h2h2H||h2||(α1Psx1+α2Psx2)+h2w2P3x3+heu2Pexe+n2,(3)

where hi∼CN(0,λi), n1 and n2 are the additive white Gaussian noise (AWGN) at LU1 and LU2, with ni(i∈{1,2})∼CN(0,σ2), where CN(⋅,⋅) is the complex Gaussian distribution, xe and Pe represent the interference signal and its power emitted by the eavesdropper E.

Since the artificial signal is allocated into the orthogonal null space of the channel for NOMA users, we have h1w2=0 and h2w2=0 [29]. Then formulas (2) and (3) can be rewritten as

y1=h1h2H||h2||(α1Psx1+α2Psx2)+n1(4)

and

y2=h2h2H||h2||(α1Psx1+α2Psx2)+heu2Pexe+n2.(5)

According to the power-domain NOMA principle, the strong user decodes his message by employing SIC after decoding the message of the weak user, and the weak user directly decodes his message by treating the signal of the strong user as noise. As a result, the signal-to-interference-to-noise ratio (SINR) at LU1 in the process of decoding its own information is

r12=α2ρs|hsu1|2α1ρs|hsu1|2+1(6)

and

r11=α1ρs|hsu1|2,(7)

where hsu1=h1h2H||h2||, and ρs=Psσ2 is the transmit signal to noise ratio (SNR) of BS. Then, the data rate for LU1 can be shown as

R1=log2⁡(1+r11).(8)

Similarly, LU2 decodes its own information directly, and the SINR can be expressed as

r22=α2ρs|hsu2|2α1ρs|hsu2|2+ρe|heu2|2+1,(9)

where hsu2=h2h2H||h2||, and ρe=Peσ2 denotes the transmit signal-to-noise ratio (SNR) from the eavesdropper E to the weak user. Then, the data rate for LU2 can be shown as

R2=log2⁡(1+r22).(10)

For the eavesdropper E, the received signal can be expressed as

ye=heh2H||h2||(α1Psx1+α2Psx2)+hew2P3x3+heeηPexe+ne(11)

where he∼CN(0,λe), ne∼CN(0,σ2), and η is the residual self-interference coefficient.

The SINR at the eavesdropper E to decode the message for LU2 can be expressed as

re=α2ρs|hse1|2α1ρs|hse1|2+ρ3|hse2|2+ηρe|hee|2+1,(12)

where hse1=heh2H||h2||, hse2=hew2, and ρ3=P3σ2. Then, the data rate of E to eavesdrop LU2 can be given by

Re=log2⁡(1+re).(13)

Similarly, when the eavesdropper E does not emit interference signals, i.e., ρe=0, or the BS does not superimpose artificial signals, then we have

{r22′=r22|ρe=0=α2ρs|hsu2|2α1ρs|hsu2|2+1,re′=re|ρe=0=α2ρs|hse1|2α1ρs|hse1|2+ρ3|hse2|2+1,re′′=re|ρ3=0=α2ρs|hse1|2α1ρs|hse1|2+ηρe|hee|2+1,re′′′=re|ρe=0,ρ3=0=α2ρs|hse1|2α1ρs|hse1|2+1.(14)

3.2.2 Signal Model of RS Scheme

In this scheme, the relay RS works in full duplex mode, and can decode and forward at the same time. In the transmission process, the base station BS first transmits a superimposed signal to the legitimate user LU1 and RS. After receiving the signal, the legitimate user LU1 uses SIC technology to decode the signal to obtain its own message, and the relay RS decodes the message for LU2 and forward it. Since the RS first decodes and then forward the message, it can perfectly eliminate the influence of self-interference [30]. The eavesdropper E eavesdrops at the base station BS, emits an interference signal at a certain power level to the legitimate user LU2, and suffers from the influence of self-interference which cannot be perfectly eliminated.

In the system model of the RS scheme, the superimposed signal transmitted to LU1 and RS at the BS is expressed as

x=w1(α1Psx1+α2Psx2).(15)

The signals received at LU1 and RS are respectively given by

y1=h1h2H||h2||(α1Psx1+α2Psx2)+n1(16)

and

yr=hrh2H||h2||(α1Psx1+α2Psx2)+nr,(17)

where hr∼CN(0,λr), nr∼CN(0,σ2), and the rest variables are similar to that in the AS scheme.

The SINR at RS to decode the message for LU2 can be expressed as

rsr=α2ρs|hsr|2α1ρs|hsr|2+1,(18)

where hsr=hrh2H||h2||.

The legitimate user LU2 receives the signal forwarded by the RS, which can be expressed as

y2=hru2Prx2+heu2Pew+ne,(19)

where hru2∼CN(0,λru2), heu2∼CN(0,λeu2), λru2 and λeu2 are the variance of complex Gaussian variables hru2 and heu2, respectively, and Pr is the transmit power of RS to forward the message for LU2 with Pr=Ps.

The SINR at LU2 to decode his own message can be expressed as

rr2=ρr|hru2|2ρe|heu2|2+1.(20)

For such a link from the BS to LU2 with the relay RS, the achievable data rate can be expressed as min{log2⁡(1+rsr),log2⁡(1+rr2)}, i.e., with an equivalent SINR as

r2=min{rsr,rr2},(21)

then the data rate for LU2 can be expressed as

R2=log2⁡(1+r2).(22)

For the eavesdropper E, the received signal can be given as

ye=heh2H||h2||(α1Psx1+α2Psx2)+heeηPew+ne,(23)

and the SINR at the eavesdropper E to decode the message for LU2 can be expressed as

re=α2ρs|hse|2α1ρs|hse|2+ηρe|hee|2+1,(24)

where hse=heh2H||h2||. Accordingly, the eavesdropping rate can be expressed as Re=log2⁡(1+re).

Similarly, when the eavesdropper E does not emit interference signals, i.e., ρe=0, we have

{rr2′=rr2|ρe=0=ρr|hru2|2,re′=re|ρe=0=α2ρs|hse|2α1ρs|hse|2+1.(25)

4  Game Model

In this article, we assume that the eavesdropper E only eavesdrops on LU2. Therefore, the secrecy rate of the system can be expressed as

Csec=[R2−Re]+(26)

where [⋅]+=max{⋅,0}.

In the downlink NOMA transmission system with external eavesdropper E, the legitimate user LU2 exerts to maximize the secrecy rate, which means that he needs to increase his own data rate and/or reduce the eavesdropping rate of E. On the contrary, for the eavesdropper E, he attempts to minimize the secrecy rate by increasing his own eavesdropping rate and/or reducing the data rate of LU2. This shows that one person or group can gain something only by causing another person or group to lose it, and the sum of the gains and losses is always ‘zero’. Therefore, we model the non-cooperative behavior between the legitimate users and the malicious eavesdropper in both AS and RS schemes as a non-cooperative two-person zero-sum game, respectively.

4.1 Game Modeling

4.1.1 Game Modeling for the AS Scheme

In the AS scheme, we regard the base station BS and users LUi(i∈{1,2}) as a legitimate party, who can choose to transmit only the effective signals or the signals superimposed with artificial signal to improve the secrecy rate of the system. The eavesdropper E can choose the strategy of only eavesdropping and not emitting the interference signal, or the strategy of eavesdropping while emitting the interference signal at the same time. We establish the zero-sum game model for secure downlink transmission in strategic form as follows.

Definition 4.1. In the AS scheme, the zero-sum game G1=(N1,(Si)i∈N1,(ui)i∈N1) is a triplet, where:

•   N1={L,E} is a set of players in the game. L represents the legitimate party consisting of the base station BS and the legitimate users LUi(i∈{1,2}), and E represents the external malicious eavesdropper.

•   Si is the set of possible strategies for player i∈N1. For L, its strategy set can be expressed as SL={A,O}, where A represents the strategy of transmitting the effective signals superimposed with artificial signal, and O represents the strategy of transmitting only the effective signals without artificial signal. For E, its strategy set can be expressed as SE={I,N}, where I means eavesdropping and emitting interference signal at the same time, and N means only eavesdropping and not emitting interference signal.

•   ui is the utility function of the player i∈N1. In this paper, the secrecy rate of the system is taken as the utility function of the game.

According to Definition 4.1, we can further formulate the utility matrix for the zero-sum game, as shown in Table 1. In the utility matrix, there are four strategy profiles in all, and they are (A,I), (A,N), (O,I) and (O,N). Take the profile (A,I) for example, it means the legitimate party L chooses the strategy A and the eavesdropper chooses the strategy I. We will analyze each strategy profile in detail and give their utility functions as follows.

For the profile (A,I), the legitimate party L chooses to superimpose the artificial signal AS in the null space of the weak user LU2 transmission direction to protect the message for the weak user LU2. The eavesdropper E chooses to emit an interference signal to the weak user LU2 while eavesdropping. In such a profile, the utility function of the legitimate party can be expressed as

CAIsec=[log2⁡(1+r22)−log2⁡(1+re)]+(27)

=[log2⁡(1+α2ρs|hsu2|2α1ρs|hsu2|2+ρe|heu2|2+1)−log2⁡(1+α2ρs|hse1|2α1ρs|hse1|2+ρ3|hse2|2+ηρe|hee|2+1)]+(28)

For the profile (A,N), the legitimate party L chooses to superimpose the artificial signal AS in the null space of the transmission direction. At this time, the eavesdropper E chooses to eavesdrop only, i.e., Pe=0. Then the utility function is given by

CANsec=[log2⁡(1+r22′)−log2⁡(1+re′)]+(29)

=[log2⁡(1+α2ρs|hsu2|2α1ρs|hsu2|2+1)−log2⁡(1+α2ρs|hse1|2α1ρs|hse1|2+ρ3|hse2|2+1)]+(30)

For the profile (O,I), the legitimate party L chooses not to superimpose the artificial signal AS to protect the message for LU2, i.e., P3=0. The eavesdropper E chooses to conduct both eavesdropping and interfering at the same time. The utility function can be expressed as

COIsec=[log2⁡(1+r22)−log2⁡(1+re′′)]+(31)

=[log2⁡(1+α2ρs|hsu2|2α1ρs|hsu2|2+ρe|heu2|2+1)−log2⁡(1+α2ρs|hse1|2α1ρs|hse1|2+ηρe|hee|2+1)]+(32)

For the profile (O,N), the legitimate party L does not choose the strategy of superimposing the artificial signal AS, and the eavesdropper E only conducts wiretapping. Then, the utility function is given by

CONsec=[log2⁡(1+r22′)−log2⁡(1+re′′′)]+(33)

=[log2⁡(1+α2ρs|hsu2|2α1ρs|hsu2|2+1)−log2⁡(1+α2ρs|hse1|2α1ρs|hse1|2+1)]+(34)

4.1.2 Game Modeling for the RS Scheme

In the system model of the RS scheme, the legitimate party L can choose to use the relay transmission strategy or the direct link transmission strategy. The eavesdropper E can choose from the strategies of eavesdropping strategy with or without emitting interference signal. We can establish the game model for the RS scheme as follows.

Definition 4.2. In the RS scheme, the zero-sum game G2=(N2,(Sj)j∈N2,(uj)j∈N2) is a triplet, where:

•   N2={L,E} is a set of players in the game. Same as in the game G1, L denotes the legitimate communication party, and E the eavesdropper.

•   Sj is the set of available strategies for the player j∈N2. For L, its strategy set can be expressed as SL={R,D}, where R represents the strategy of transmission with RS, and D represents the strategy of direct link transmission. For E, its strategy set can be expressed as SE={I,N}, where I means eavesdropping and emitting interference signals, and N means not emitting interference signals but only eavesdropping.

•   uj is the utility function of the player j∈N2.

Similarly, we can formulate the utility matrix as shown in Table 2, and the utility functions can be expressed as follows:

CRIsec=[log2⁡(1+min{rsr,rr2})−log2⁡(1+re)]+(35)

=[log2⁡(1+min{α2ρs|hsr|2α1ρs|hsr|2+1,ρr|hru2|2ρe|heu2|2+1})−log2⁡(1+α2ρs|hse|2α1ρs|hse|2+ηρe|hee|2+1)]+(36)

CRNsec=[log2⁡(1+min{rsr,rr2′})−log2⁡(1+re′)]+(37)

=[log2⁡(1+min{α2ρs|hsr|2α1ρs|hsr|2+1,ρr|hru2|2})−log2⁡(1+α2ρs|hse|2α1ρs|hse|2+1)]+(38)

CDIsec=[log2⁡(1+rs2)−log2⁡(1+re)]+(39)

=[log2⁡(1+α2ρs|hsu2|2α1ρs|hsu2|2+ρe|heu2|2+1)−log2⁡(1+α2ρs|hse|2α1ρs|hse|2+ηρe|hee|2+1)]+(40)

CDNsec=[log2⁡(1+rs2′)−log2⁡(1+re′)]+(41)

=[log2⁡(1+α2ρs|hsu2|2α1ρs|hsu2|2+1)−log2⁡(1+α2ρs|hse|2α1ρs|hse|2+1)]+(42)

where rs2 and rs2′ are the same with r22 and r22′ in the AS scheme, respectively.

4.2 Analysis of Game Equilibrium

In this subsection, we will first prove the existence of the Nash equilibrium for the zero-sum game in both AS and RS schemes, and then solve and analyze the pure strategy Nash equilibrium and the mixed strategy Nash equilibrium, respectively.

4.2.1 Existence of NE

We give the results of Nash Equilibrium of the games G1 and G2 by the following two theorems.

Theorem 4.1. There is at least one Nash equilibrium in the zero-sum game G1 of the AS scheme.

Proof. In the zero-sum game G1, the set of players N1={L,E} has two players, which is limited. Additionally, the set of strategies SL={A,O} and SE={I,N} are both limited. According to the existence theorem of Nash equilibrium, there is at least one Nash equilibrium in the game G1.

Theorem 4.2. There is at least one Nash equilibrium in the zero-sum game G2 of the RS scheme.

The proof is similar to that of Theorem 4.1 and thus omitted for simplicity.

4.2.2 Pure-strategy Nash Equilibrium

In this subsection, we solve the pure-strategy Nash equilibrium of the game G1 and G2, respectively. The pure-strategy Nash equilibrium and the corresponding strategies for the games in AS and RS schemes are provided by the following two theorems.

Theorem 4.3. The pure-strategy Nash equilibrium (A,I) exists in the game G1 provided CAIsec<CANsec and (A,N) exists provided CAIsec>CANsec.

Proof. According to the analysis aforementioned and Eqs. (28), (30), (32) and (34), it is easy to find that the utility functions in Table 1 satisfy the following conditions:

CANsec>CONsec,CAIsec>COIsec.(43)

Thus, the strategy A is the dominating strategy for the legitimate party in the game G1, that is, the legitimate party L will choose strategy A, no matter what E chooses. Next, we will prove the conditions for existence for two pure-strategy equilibrium, respectively.

First, if CAIsec<CANsec holds, we have CANsec>CAIsec>COIsec, and we can observe the following two facts. One is that the utility of L will decrease from CAIsec to COIsec if L changes its strategy from A to O, i.e., changing the strategy of superimposing artificial signals to not superimposing artificial signals, which violates his goal of maximizing the secrecy rate. Another, if the external eavesdropper E changes its strategy from I to N, i.e., changing the strategy of transmitting interference signals to not transmitting interference signals and only eavesdropping, the utility of E will increase from CAIsec to CANsec, and yet his goal is to minimize the secrecy rate. In summary, neither the legitimate party L nor the external eavesdropper E could benefit more by unilaterally deviating his strategy from the strategy profile (A,I). Therefore, the pure-strategy Nash equilibrium of the game is (A,I) provided CAIsec<CANsec.

Second, if CAIsec>CANsec holds, we have CAIsec>CANsec>CONsec. Similarly, we can also find that neither the legitimate party L nor the external eavesdropper E could benefit more by unilaterally deviating his strategy from the strategy profile (A,N), i.e., (A,N) is a pure-strategy Nash equilibrium of G1 provided CAIsec>CANsec.

This completes the proof.

Theorem 4.4. The pure-strategy Nash equilibrium (R,N) exists in the game G2 provided CRIsec>CRNsec, and (R,I) exists provided CRIsec<CRNsec.

Proof. Since we have assumed |hsr|2>|hsu2|2 and |hru2|2>|hsu2|2, according to the analysis aforementioned and Eqs. (36), (38), (40) and (42), it is easy to find that the utility functions in Table 2 satisfy the following conditions:

CRNsec>CDNsec,CRIsec>CDIsec.(44)

Thus, the strategy R is the dominating strategy for the legitimate party in the game G2, that is, the legitimate party L will choose strategy R, no matter what E chooses. Next, we will prove the conditions for existence for two pure-strategy equilibrium, respectively.

First, if CRIsec<CRNsec holds, we have CRNsec>CRIsec>CDIsec, and we can observe the following two facts. One is that the utility of L will decrease from CRIsec to CDIsec if L changes its strategy from R to D, i.e., changing the strategy of transmission with RS to without RS, which violates his goal of maximizing the secrecy rate. Another, if the external eavesdropper E changes its strategy from I to N, i.e., changing the strategy of transmitting interference signals to not transmitting interference signals and only eavesdropping, the utility of E will increase from CRIsec to CRNsec, and yet his goal is to minimize the secrecy rate. In summary, neither the legitimate party L nor the external eavesdropper E could benefit more by unilaterally deviating his strategy from the strategy profile (R,I). Therefore, the pure-strategy Nash equilibrium of the game is (R,I) provided CRIsec<CRNsec.

Second, if CRIsec>CRNsec holds, we have CRIsec>CRNsec>CDNsec. Similarly, we can also find that neither the legitimate party L nor the external eavesdropper E could benefit more by unilaterally deviating his strategy from the strategy profile (R,N), i.e., (R,N) is a pure-strategy Nash equilibrium of G1 provided CRIsec>CRNsec.

This completes the proof.

4.2.3 Algorithms for Pure Strategy Nash Equilibrium Strategy

According to the analysis in the previous section, there are two situations in the pure strategy Nash equilibrium of the game G1 and G2. Therefore, we propose two algorithms to determine the pure strategy Nash equilibrium strategy. The algorithms are described as follows.

4.2.4 Mixed-Strategy Nash Equilibrium

Different from the deterministic selection of a strategy in pure-strategy Nash equilibrium, a player may select each pure strategy with a certain probability, which leads to the concept of a mixed strategy. For each player, a mixed strategy consists of a number of possible actions and a probability distribution which corresponds to how frequently each action would be selected by the player. In this subsection, we will discuss the mixed-strategy Nash equilibrium of the game G1 and G2, respectively.

The mixed strategy Nash equilibrium in AS and RS schemes are given by the following two theorems.

Theorem 4.5. The utility of the mixed strategy Nash equilibrium (p∗,q∗) of the game G1 is written as

U∗(p∗,q∗)=CAIsecCONsec−CANsecCOIsecCAIsec+CONsec−COIsec−CANsec,

where p∗=CONsec−COIsecCAIsec+CONsec−COIsec−CANsec, q∗=CONsec−CANsecCAIsec+CONsec−COIsec−CANsec.

Proof. In the AS scheme, we define the probability distribution P=(p,1−p) for the legitimate party L, where 0≤p≤1 is the probability with which L selects the strategy A, i.e., the selection of superimposing artificial signals. Hence, 1−p is the probability with which L selects the strategy O. Similarly, we define the mixed strategy for the eavesdropper E as Q=(q,1−q), where 0≤q≤1 is the probability with which E selects the strategy I, i.e., the selection of emitting interference signals, and 1−q the probability of selecting the strategy N. Hence, the utility of the mixed strategy can be expressed as U(p,q)=PCQT.

The legitimate party L can find his optimal strategy by solving the following optimization problem: maxpminqPCQT, where C=[CAIsecCANsecCOIsecCONsec] is the utility matrix in Table 1, and (⋅)T is the transpose operation. The eavesdropper E can obtain his optimal strategy by solving the the problem: minqmaxpPCQT.

Solving the above two optimization problem yields the optimal probability value of each strategy selected by L and E as

p∗=CONsec−COIsecCAIsec+CONsec−COIsec−CANsec,q∗=CONsec−CANsecCAIsec+CONsec−COIsec−CANsec.

Then substitute p∗ and q∗ into PCQT, the Nash equilibrium utility of the mixed strategy of the game G1 is written as

U∗(p∗,q∗)=CAIsecCONsec−CANsecCOIsecCAIsec+CONsec−COIsec−CANsec.

This completes the proof.

Theorem 4.6. The utility of the mixed strategy Nash equilibrium (p∗,q∗) of the game G2 is written as

U∗(p∗,q∗)=CRIsecCDNsec−CRNsecCDIsecCRIsec+CDNsec−CDIsec−CRNsec,

where p∗=CDNsec−CDIsecCRIsec+CDNsec−CDIsec−CRNsec,q∗=CDNsec−CRNsecCRIsec+CDNsec−CDIsec−CRNsec.

The proof is similar to Theorem 4.5, and thus omitted for simplicity.

5  Numerical Simulation and Result Analysis

5.1 Simulation Setting

The main parameter settings in the simulation of AS and RS scheme are as follows. The power allocation coefficients of strong users and weak users in the NOMA system are α1=0.2, α2=0.8, respectively, the transmission signal-to-noise ratio at each node ranges from 0 to 30 dB, and the residual self-interference coefficient η during the process of eavesdropping transmitting interference power is 0.1.

5.2 Result Analysis in the AS Scheme

This subsection mainly analyzes the data rate of the weak user and the eavesdropper, as well as the gains of the pure and mixed strategy in the AS scheme.

5.2.1 Analysis of Data Rate

The curves in Fig. 2a show the data rate R2 of LU2 with respect to ρs under different ρe in the AS scheme. It can be seen from the figure that when ρe is constant, R2 increases as ρs increases; when ρs is constant, R2 decreases as ρe increases, which implies that, when the power of the interference signal transmitted by E is larger, the information transmission rate of LU2 can be reduced, so that the security rate of the system is smaller, and its purpose can be achieved. The legitimate party L can appropriately increase the total transmission power to weaken the influence of E interference.

Fig. 2b shows the change of the data rate of E with ρ3 in the AS scheme. It can be seen from the figure that when ρe is constant, Re decreases as ρ3 increases; when ρ3 is constant, Re decreases as ρe increases. It shows that while E is transmitting interference signals, although it can reduce the information transmission rate of LU2, it will also reduce its own information transmission rate. Therefore, E needs to consider the power value of the transmitted interference signal in the game. The legitimate party can reduce Re by increasing the power of the artificial signal, thereby increasing the security rate of the system and improving the security of the physical layer.

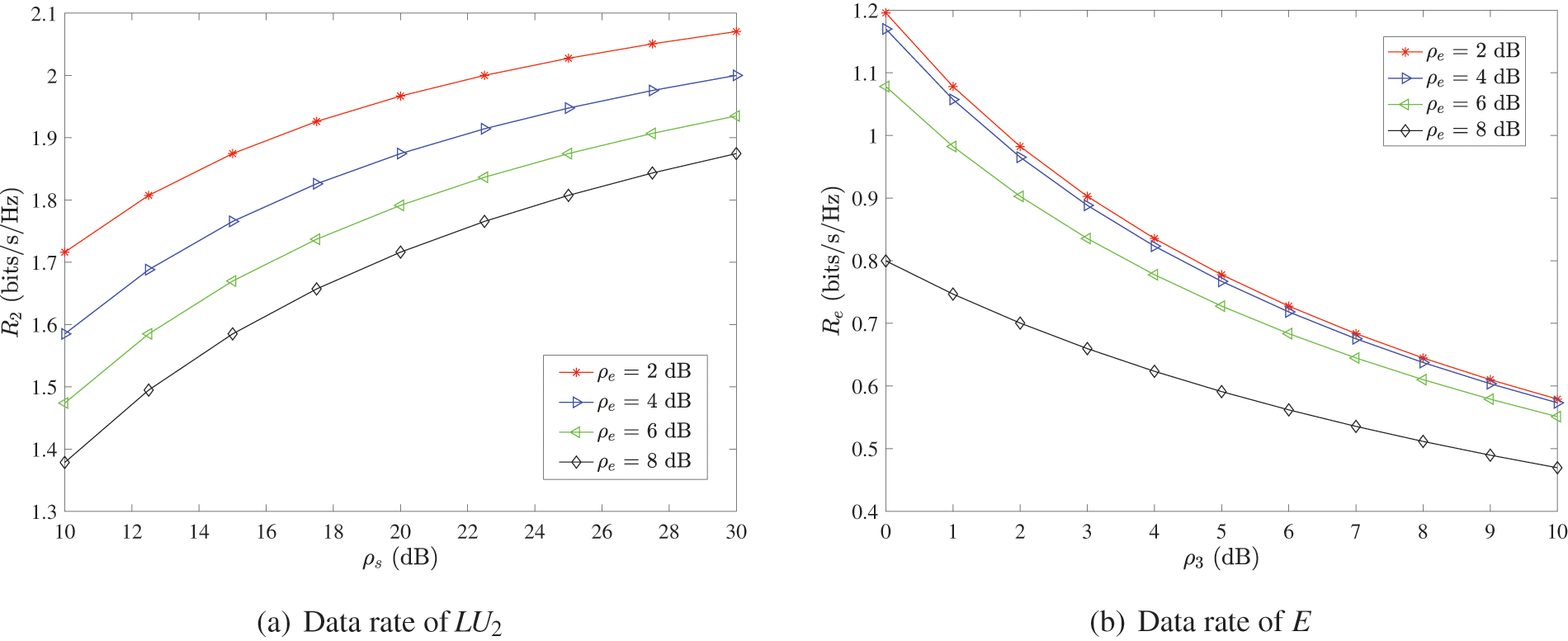
Figure 2: Data rate in the AS scheme

5.2.2 Analysis of the Pure Strategy Nash Equilibrium and Benefits

According to the aforementioned analysis, the pure strategy Nash equilibrium depends on the parameter ρe and ρ3. We show the effect of ρe and ρ3 on the pure strategy Nash equilibrium in Fig. 3, and we can find the following results. First, the equilibrium strategy changes from (A,N) to (A,I) as ρe increases if ρ3<M. Second, if ρ3>M the equilibrium strategy stays at (A,I) no matter how ρe changes. We also have similar results for ρe, ρ3 and some point M′ at the axis of ρe.

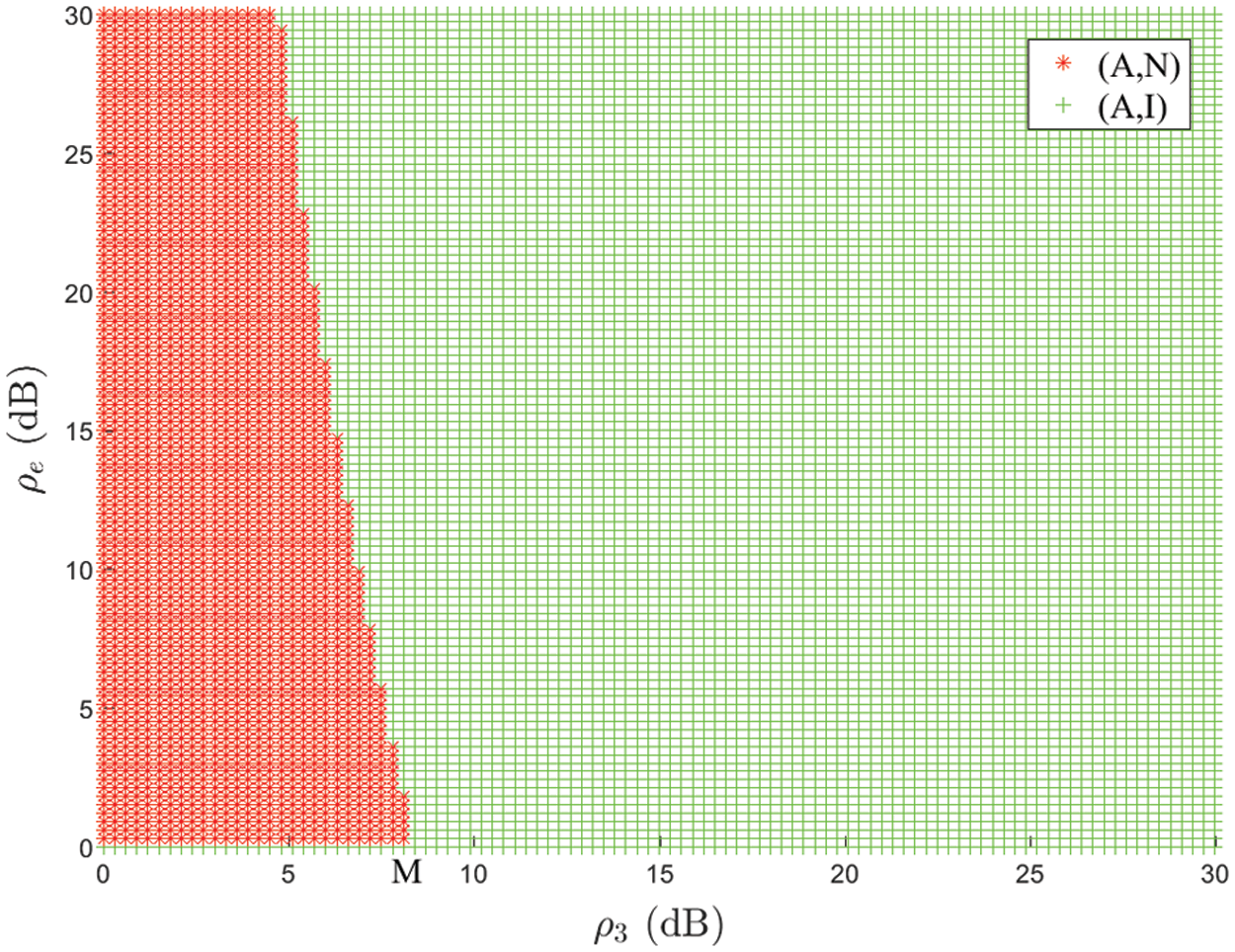
Figure 3: Effect of ρe and ρ3 with ρs=30 dB on pure strategy Nash equilibrium in the AS scheme

The curves in Fig. 4 show the benefits (Csec) of pure strategy in the AS scheme with respect to ρe and ρ3, respectively. From Fig. 4a, we can see that the curves of CANsec and CAIsec intersect at point A. When ρ3 in the range (0,X(A)) where X(A) denotes the operation of taking the abscissa value of point A, we have CONsec<CANsec<CAIsec, thus the pure strategy Nash equilibrium is (A,N) and the corresponding benefit is CANsec. When ρ3>X(A), we have CONsec<CAIsec<CANsec, thus the pure strategy Nash equilibrium is (A,I) and the corresponding benefit is CAIsec.

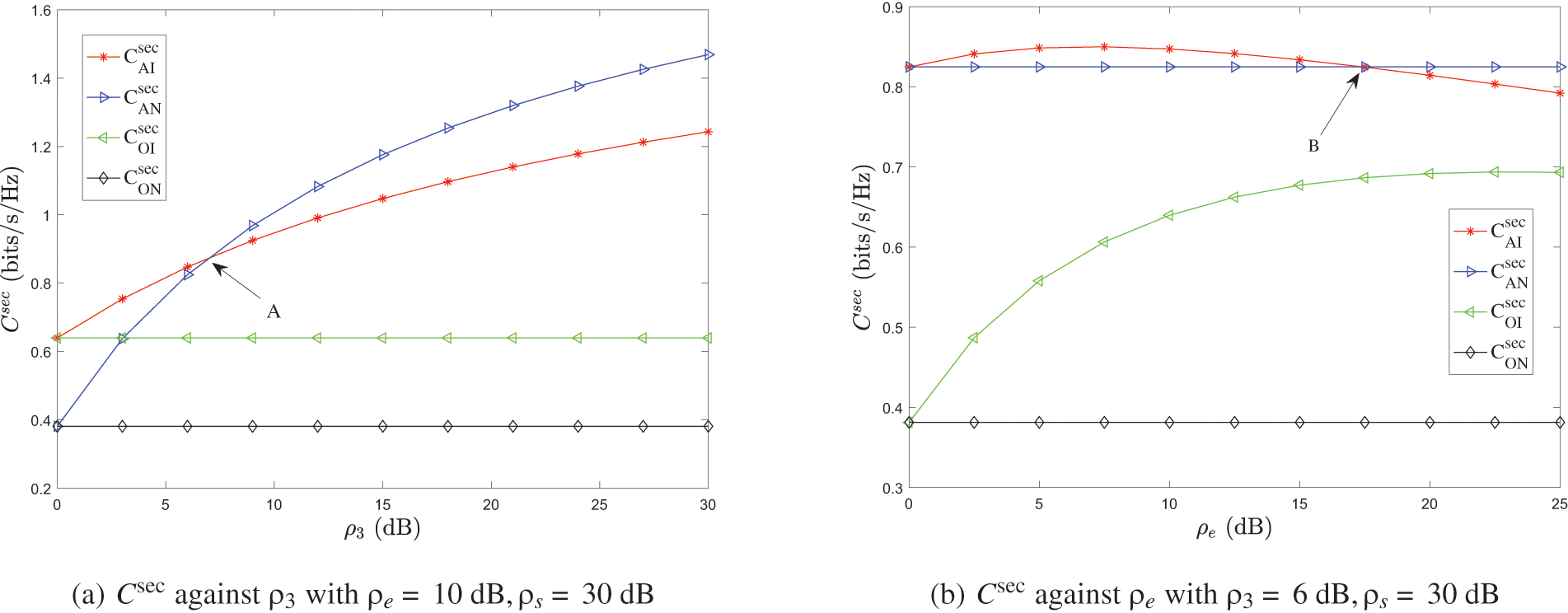
Figure 4: The benefits of pure strategy in the AS scheme

Likewise, from Fig. 4b, we can get similar results that the equilibrium strategy and the corresponding benefit is (A,N) and CANsec when 0<ρe<X(B), and the equilibrium strategy and the corresponding benefit is (A,I) and CAIsec when ρe>X(B).

5.2.3 Analysis of the Mixed Strategy Benefits

Fig. 5 shows the benefit variation of the mixed strategy in the AS scheme with respect to ρs. It can be seen from the figure that the revenue of the mixed strategy under AS scheme increases with the increase of ρs. The red curve represents the mixed strategy benefits under the best probability value, and the other three curves represent the mixed strategy benefits when ±ε, ±2ε and ±3ε are offset on the basis of the best probability value. The figure shows that the benefits of the mixed strategy under the optimal probability is the best, which verifies the previous theoretical analysis results.

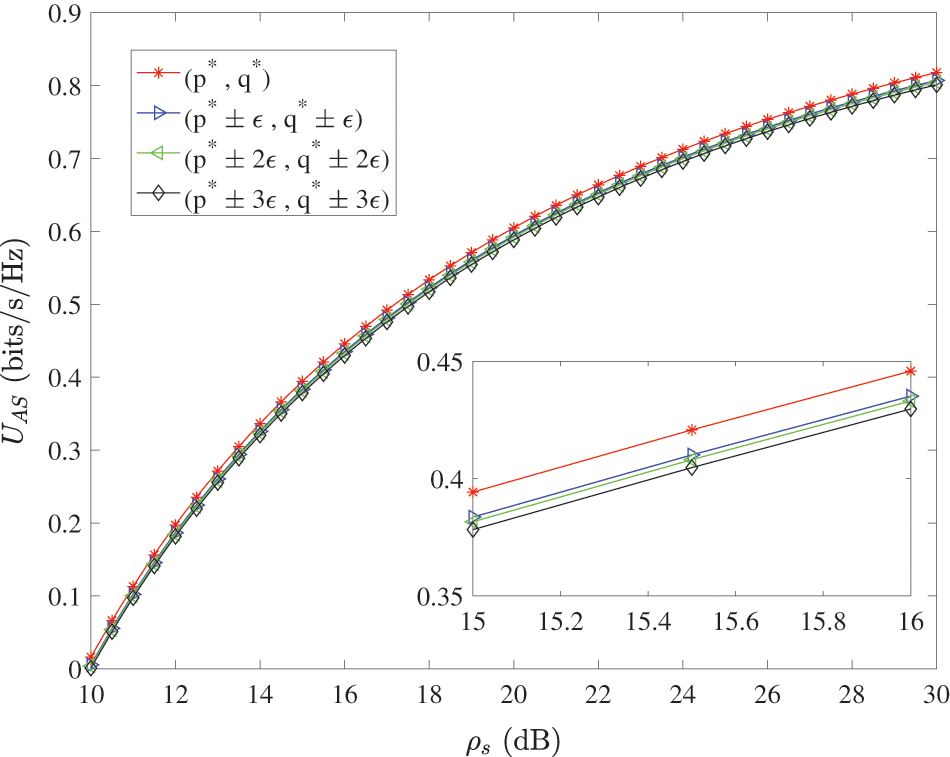
Figure 5: Benefits of mixed strategies in the AS scheme

Fig. 6 shows the comparison of benefits between the pure strategy Nash equilibrium and the mixed strategy Nash equilibrium in the AS scheme. From the local enlarged subplot, we can clearly find that the benefit curves of potential pure strategy Nash equilibrium profiles (A,I), (A,N) and the mixed strategy Nash equilibrium intersect at point X, Y and Z. With the increase of ρs, the equilibrium strategy profile will change from (A,I) to (A,N) when ρs goes across the abscissa of Z if the mixed strategy is not considered. Instead, if the mixed strategy is taken into consideration, the equilibrium strategy profile will change from (A,I) to the mixed strategy when ρs goes across the abscissa of X.

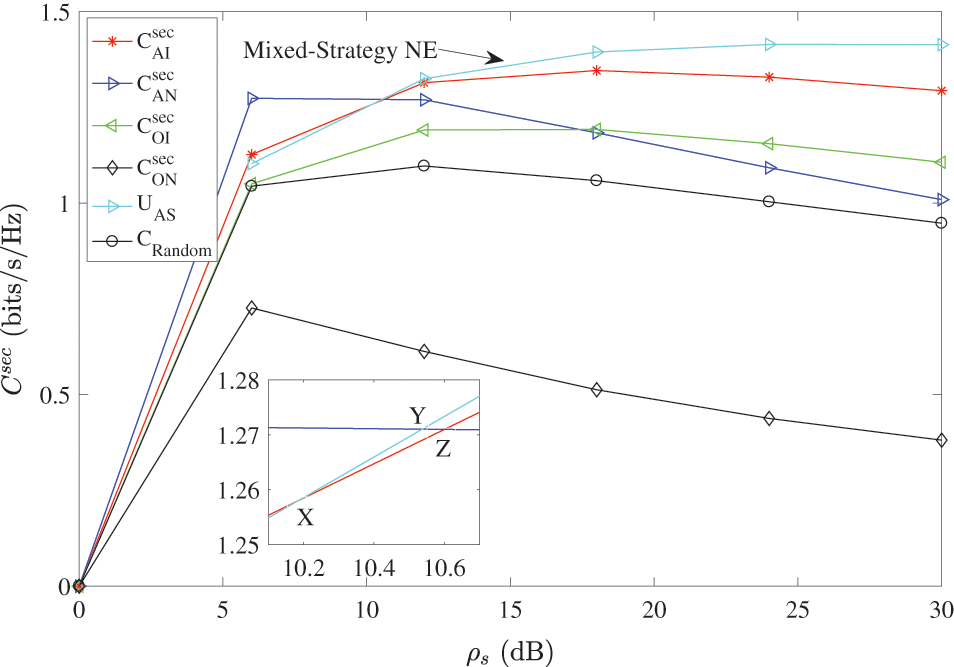
Figure 6: Comparison of the benefits between pure and mixed strategy NE in the AS scheme

Additionally, from Fig. 6, we can see that the curve of random-selection method is always below the curves of pure and mixed strategy NE. This is not good for legitimate communicators. Therefore, the legitimate communication party will not select the random-selection strategy to increase the secrecy rate, i.e., the random-selection strategy is unstable in the AS scheme.

5.3 Result Analysis in the RS Scheme

This subsection mainly analyzes the data rate of the weak user and the eavesdropper, as well as the benefits of the pure and mixed strategy in the RS schemes.

5.3.1 Analysis of Data Rate

Fig. 7a shows the relationship between the information transmission rate of LU2 and the selection of different strategies in the RS scheme. We can see that when the legitimate party selects strategy ‘R’ (add relay), the information transmission rate of LU2 is better than that of strategy ‘D’ (direct link). It shows that the RS scheme can improve the physical layer security performance of the system.

Fig. 7b shows the relationship between the information transmission rate of E and ρs in the RS scheme. When ρe is constant, Re increases with the increase of ρs; when ρs is constant, Re decreases with the increase of ρe. This shows that if E increases the power of transmitting interference signals, its own transmission rate will be reduced, and the security rate of the system will increase. If the legitimate party blindly increases the total transmission power, the security rate of the system will decrease. Therefore, in order to achieve their respective goals, both parties need to choose an appropriate power value.

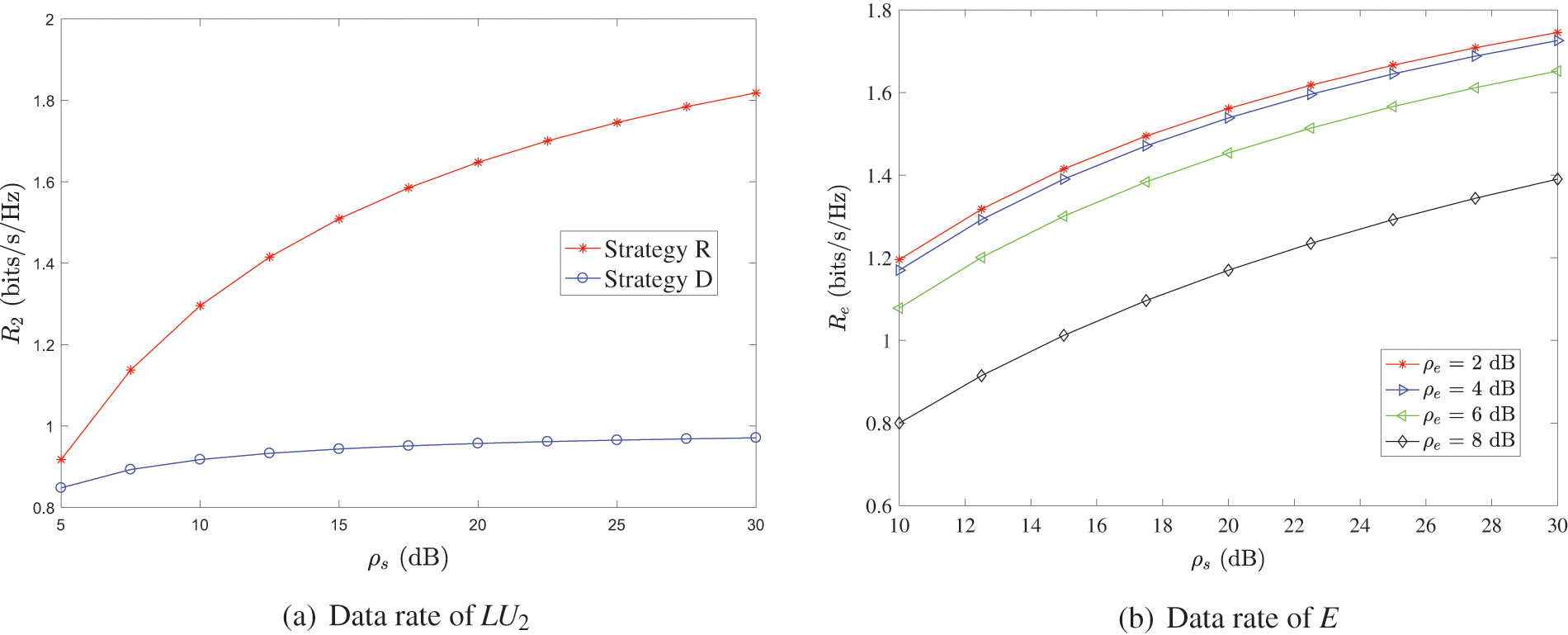
Figure 7: Data rate in the RS scheme

5.3.2 Analysis of the Pure Strategy Nash Equilibrium and Benefits

According to the analysis, the pure strategy Nash equilibrium depends on the parameter ρe and ρs. We show the effect of ρe and ρs on the pure strategy Nash equilibrium in Fig. 8, and we can find the following results. First, if ρs keeps constant, the equilibrium strategy changes from (R,N) to (R,I) as ρe increases. Second, if ρe keeps constant, the equilibrium strategy changes from (R,I) to (R,N) as ρs increases.

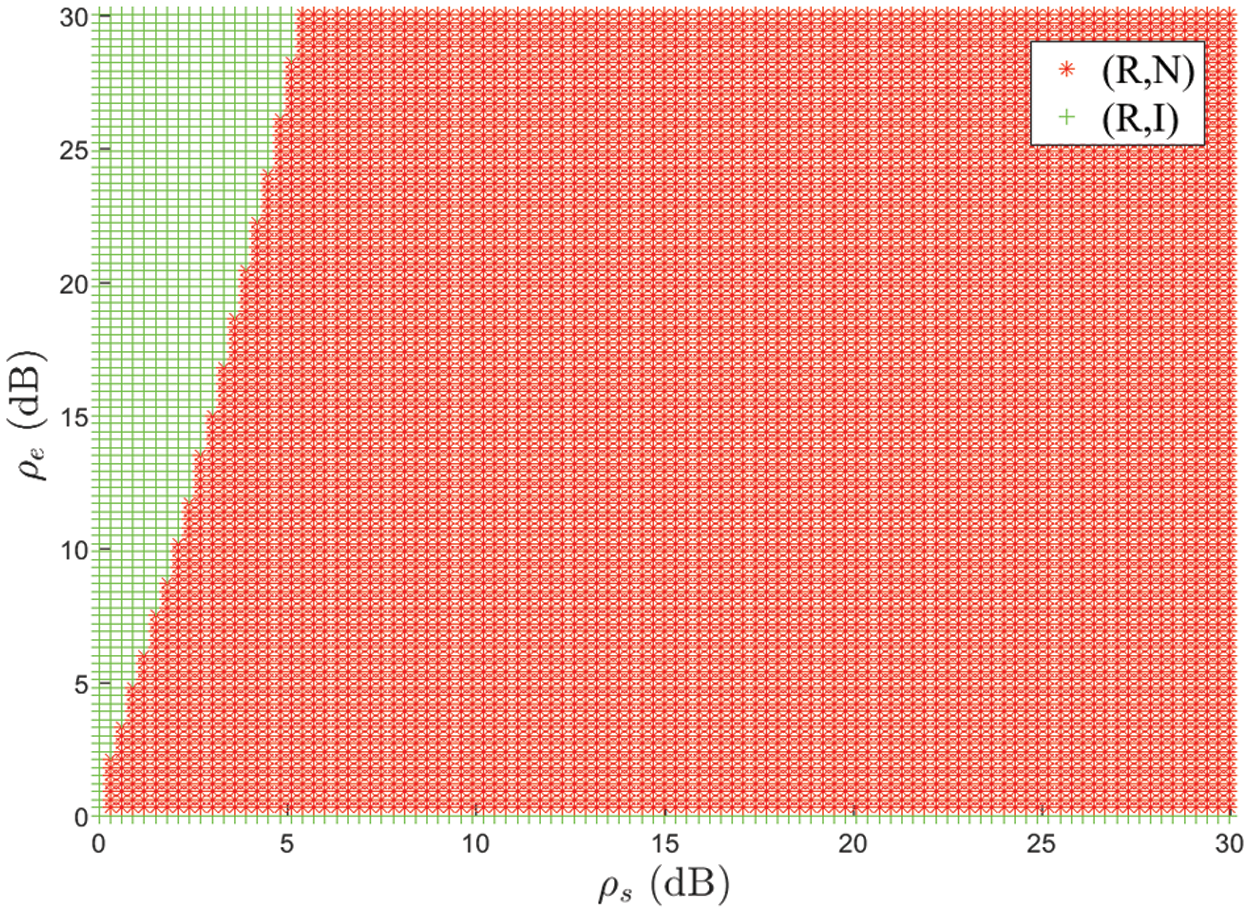
Figure 8: Effect of ρe and ρs on pure strategy Nash equilibrium in the RS scheme

Fig. 9 shows the pure strategy benefits under different conditions in the zero sum game of RS scheme. Fig. 9a shows the change of pure strategy benefits with ρs, and Fig. 9b shows the change of pure strategy benefits with ρe. It can be seen from the figure that the benefits of the pure strategy Nash equilibrium is CRNsec. When the legitimate party changes strategy ‘R’ to ‘D’, the benefits will change from CRNsec to CDNsec; When the eavesdropper changes strategy ‘N’ to ‘I’, the revenue will increase from CRNsec to CRIsec.

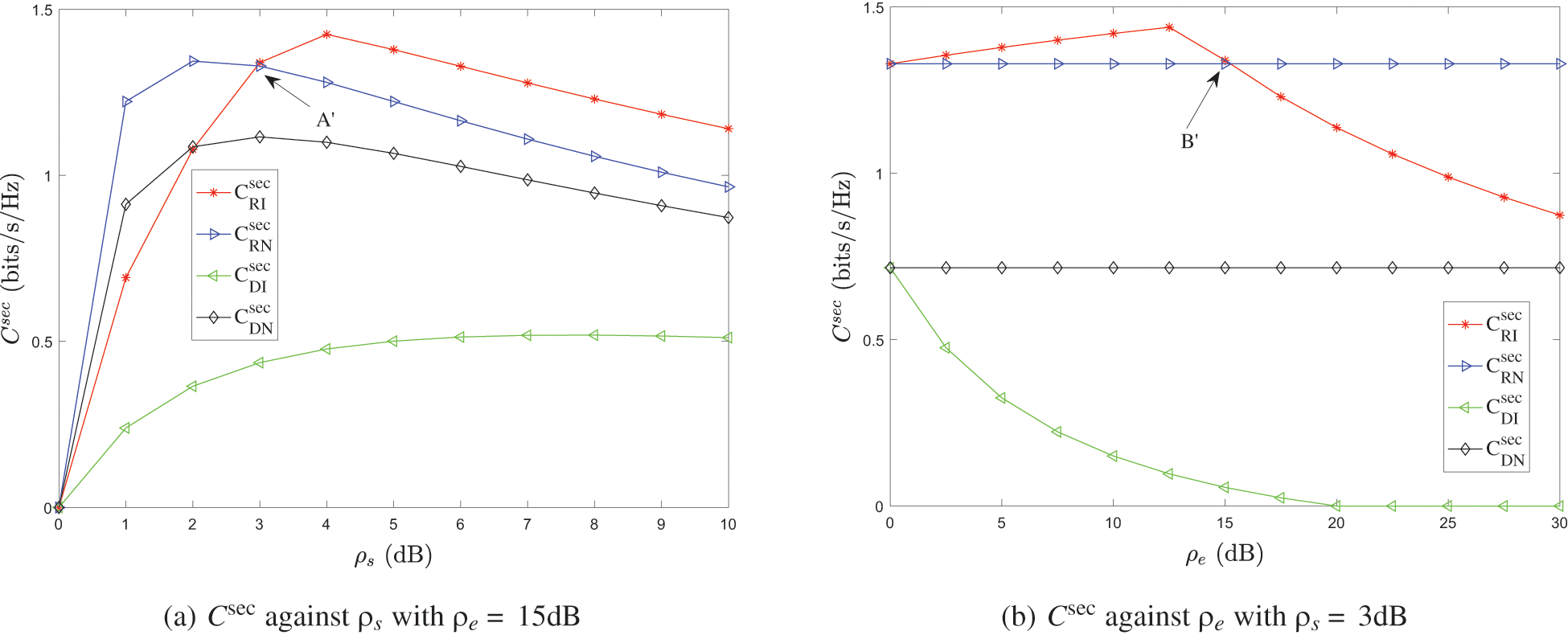
Figure 9: The benefits of pure strategy in the RS scheme

5.3.3 Analysis of the Mixed Strategy Benefits

Fig. 10 shows the change of the mixed strategy benefits of the zero sum game of RS scheme with ρs. It can be seen from the figure that the mixed strategy benefits under RS scheme decreases with the increases of ρs. The red curve represents the mixed strategy benefits under the best probability value, and the other three curves represent the mixed strategy benefits when ±ε, ±2ε and ±3ε are offset on the basis of the best probability value. The mixed strategy benefits the most under the optimal probability value, that is, the Nash equilibrium value of the mixed strategy.

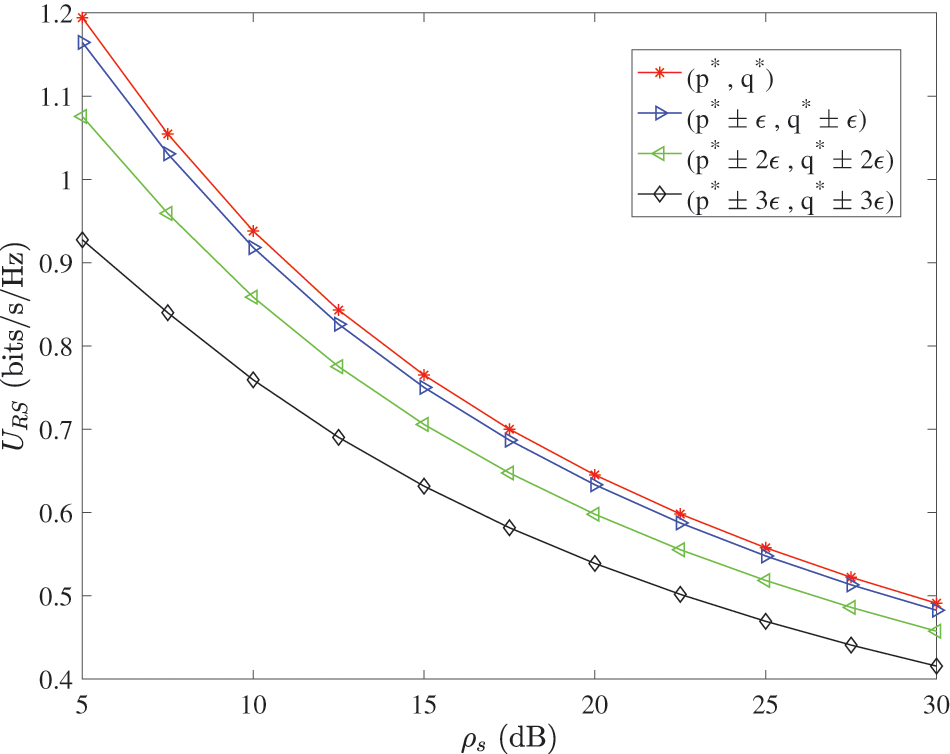
Figure 10: Benefits of mixed strategies in the RS scheme

Fig. 11 shows the comparison of benefits between the pure strategy Nash equilibrium and the mixed strategy Nash equilibrium in the RS scheme. It can be seen that the benefits of the mixed strategy Nash equilibrium are always smaller than that of the pure strategy Nash equilibrium. Therefore, both sides of the game will always choose a pure strategy. That is to say, in the zero-sum game of the RS scheme, both sides will choose the pure strategy NE profile (R,N), that is, the legitimate party L chooses the strategy of adding a relay station, and the eavesdropper E chooses the eavesdropping strategy.

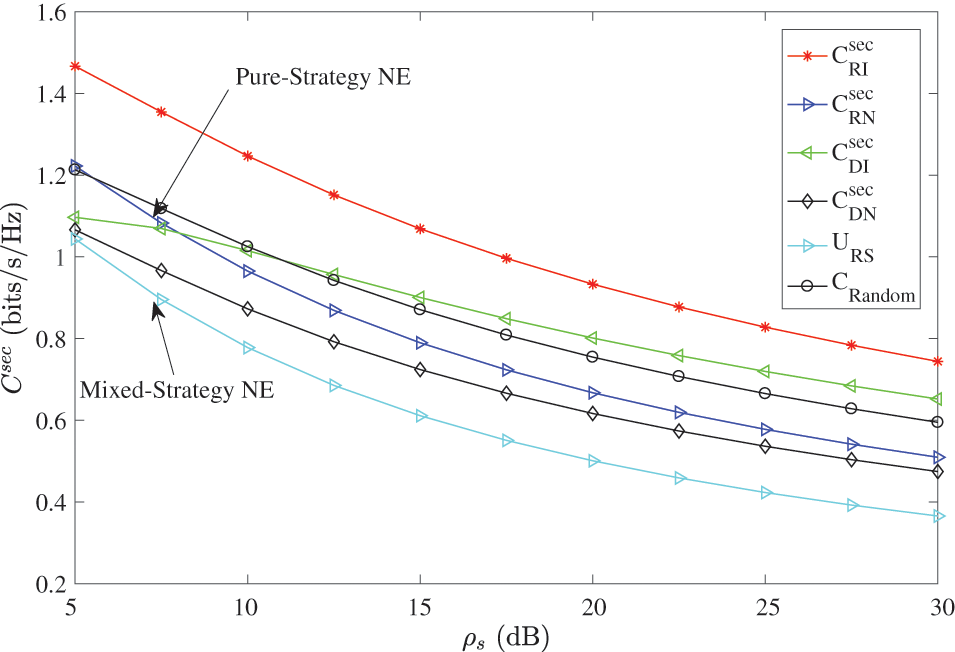
Figure 11: Comparison of the benefits between pure and mixed strategy NE in the RS scheme

Additionally, from Fig. 11, we can observe that the curve of random-selection method is always above the curves of pure and mixed strategy NE. This is not good for the active eavesdropper. Therefore, the active eavesdropper will not select the random-selection strategy to decrease the secrecy rate, i.e., the random-selection strategy is also unstable in the RS scheme.

6  Conclusion

In the scenario of the standard downlink NOMA transmission system, this paper considers two typical physical layer security design schemes based on artificial signals and relay assistance. The non-cooperative behavior between the legitimate communication party and the eavesdropping party under the two schemes is modeled as a two-person zero-sum game. The game is used to characterize the confrontational behavior relationship between the two parties and the process of mutual influence, and prove the existence of the game Nash equilibrium. Through the solution and analysis of the pure strategy and mixed strategy Nash equilibrium of the security game model, the best strategy profile of the two parties in the confrontation environment is given. Numerical simulation results show that both solutions can improve the physical layer security of the NOMA system. The physical layer security game model proposed in this paper can be extended to other scenarios (such as the combination of relay and artificial signals) and can be used to guide the analysis and design of security solutions. However, the cases where there are multiple eavesdroppers and multi-user pairs have not been considered in this paper, and need to be studied in the future.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This research was supported by the National Natural Science Foundation of China under Grants U1836104, 61801073, 61931004, 62072250, National Key Research and Development Program of China under Grant 2021QY0700, and The Startup Foundation for Introducing Talent of NUIST under Grant 2021r039.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Dai, L., Wang, B., Yuan, Y., Han, S., Chih-Lin, I. et al. (2015). Non-orthogonal multiple access for 5G: Solutions, challenges, opportunities, and future research trends. IEEE Communications Magazine, 53(9), 74–81. DOI 10.1109/MCOM.35. [Google Scholar] [CrossRef]

 2.  Ding, Z. G., Lei, X. F., Karagiannidis, G. K., Schober, R., Yuan, J. H. et al. (2017). A survey on non-orthogonal multiple access for 5G networks: Research challenges and future trends. IEEE Journal on Selected Areas in Communications, 35(10), 2181–2195. DOI 10.1109/JSAC.49. [Google Scholar] [CrossRef]

 3.  Liu, Y., Pan, G. F., Zhang, H. T., Song, M. (2016). On the capacity comparison between mimo-noma and mimo-oma. IEEE Access, 4, 2123–2129. DOI 10.1109/ACCESS.2016.2563462. [Google Scholar] [CrossRef]

 4.  Wu, Y. P., Khisti, A., Xiao, C. S., Caire, G., Wong, K. K. et al. (2018). A survey of physical layer security techniques for 5G wireless networks and challenges ahead. IEEE Journal on Selected Areas in Communications, 36(4), 679–695. DOI 10.1109/JSAC.2018.2825560. [Google Scholar] [CrossRef]

 5.  Yang, N., Wang, L. F., Geraci, G., Elkashlan, M., Yuan, J. H. et al. (2015). Safeguarding 5G wireless communication networks using physical layer security. IEEE Communications Magazine, 53(4), 20–27. DOI 10.1109/MCOM.35. [Google Scholar] [CrossRef]

 6.  Wang, Y., Zhou, X., Zhuang, Z., Sun, L., Qian, Y. et al. (2020). UAV-enabled secure communication with finite blocklength. IEEE Transactions on Vehicular Technology, 69(12), 16309–16313. DOI 10.1109/TVT.2020.3042791. [Google Scholar] [CrossRef]

 7.  Xia, G., Jia, L., Qian, Y., Shu, F., Zhuang, Z. et al. (2019). Power allocation strategies for secure spatial modulation. IEEE Systems Journal, 13(4), 3869–3872. DOI 10.1109/JSYST.2019.2918168. [Google Scholar] [CrossRef]

 8.  Shiu, Y. S., Chang, S. Y., Wu, H. C., Huang, S. C. H., Chen, H. H. (2011). Physical layer security in wireless networks: A tutorial. IEEE Wireless Communications, 18(2), 66–74. DOI 10.1109/MWC.2011.5751298. [Google Scholar] [CrossRef]